Сложение и вычитание десятичных дробей — как правильно? Правила и примеры
Понятие десятичной дроби
Прежде, чем перейдем к тому, как выполнить сложение и вычитание десятичных дробей, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это число в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель.
Конечная десятичная дробь — это когда количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
Основные свойства
|
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Сложение десятичных дробей
Мы знаем, что десятичная дробь состоит из целой и дробной части. При сложении десятичных дробей нужно отдельно сложить каждую часть.
Рассмотрим пример сложения 3,2 и 5,3. Для удобства используем метод столбика.
Для удобства используем метод столбика.
Запишем эти две дроби в столбик. При этом целая часть одной дроби должна быть под целой частью другой. В школе это называют «запятая под запятой». Вот так:
Складываем дробные части: 2 + 3 = 5. Запишем пятерку в дробной части ответа:
Теперь целые части: 3 + 5 = 8. Запишем восьмерку в целой части ответа:
Отделим запятой целую часть от дробной, чтобы запятая была под запятой:
Получили ответ: 3,2 + 5,3 = 8,5.
Вычитание десятичных дробей
Процесс вычитания десятичных дробей очень похож на сложение. Будем использовать те же правила: «запятая под запятой» и «равное количество цифр после запятой».
Пример 1. Найти значение выражения 2,5 − 2,2
Запишем в столбик выражение так, чтобы запятая была под запятой:
Вычислим дробную часть 5 − 2 = 3. Запишем тройку в десятой части ответа:
Вычислим целую часть 2 − 2 = 0. Запишем ноль в целой части ответа:
Отделим запятой целую часть от дробной:
Вот и ответ: 2,5 − 2,2 = 0,3.
Пример 2. Вычислить: 7,353 – 3,1
В этом выражении разное количество цифр после запятой: в 7,353 три цифры после запятой, а в 3,1 только одна. Значит в дроби 3,1 в конце добавим два нуля, чтобы уравнять количество цифр в обеих дробях. То есть: 3,1 = 3,100.
Запишем в столбик и посчитаем:
Ответ: 7,353 – 3,1 = 4,253.
Пример 3. Вычислить: 3 − 1,2
В этом примере из целого числа нужно вычесть десятичную дробь. Запишем это выражение столбиком так, чтобы целая часть десятичной дроби 1,23 была под числом 3. Вот так:
Сделаем количество цифр после запятой одинаковым:
Теперь вычитаем десятые части: 0 − 2. От нуля невозможно вычесть число 2. Поэтому займем единицу у соседнего разряда. Таким образом 0 превращается в число 10. Вычисляем десятые части: 10 − 2 = 8. Запишем восьмерку в десятой части ответа:
Сейчас вычтем целые части. В самом начале было число 3, но мы заняли у него единицу, поэтому оно обратилось в двойку. Поэтому: 2 − 1 = 1. Запишем единицу в целой части ответа:
Поэтому: 2 − 1 = 1. Запишем единицу в целой части ответа:
Отделим запятой целую часть от дробной:
Ответ: 3 − 1,2 = 1,8.
Мы рассмотрели несколько примеров сложения и вычитания десятичных дробей. Чтобы каждый ученик в 5 и 6 классе мог повторить эту последовательность, есть специальный алгоритм:
Алгоритм сложения (вычитания) десятичных дробей
|
Проще говоря, правило сложения (вычитания) десятичных дробей звучит так: чтобы сложить (вычесть) две десятичные дроби, нужно записать их в столбик друг под другом, запятая под запятой. А потом сложить как обыкновенные числа и снести запятую.
А потом сложить как обыкновенные числа и снести запятую.
Сложение и вычитание десятичных дробей 5 класс онлайн-подготовка на Ростелеком Лицей
Сложение и вычитание десятичных дробей
Научимся складывать и вычитать десятичные дроби.
Сложим десятичные дроби 3,7 и 2,651. Сначала уравняем количество цифр после запятой, приписав к первой дроби два нуля справа: 3,7=3,700. Потом запишем числа в смешанной форме.
Если сложить числа столбиком, получим тот же результат.
Теперь вычтем из 3,7 число 2,651.
Попробуем вычесть столбиком, и снова результат совпадёт.
Сформулируем правило сложения и вычитания десятичных дробей.
Чтобы сложить (вычесть) десятичные дроби, нужно:
1. Уравнять в этих дробях количество знаков после запятой.
2. Записать их друг под другом так, чтобы запятая была записана под запятой.
3. Выполнить сложение (вычитание), не обращая внимание на запятую.
4. Поставить в ответе запятую под запятой в данных дробях.
Теперь мы можем представлять дробь как сумму.
Число 0,444 равно сумме 4 десятых, 4 сотых, 4 тысячных:
Первый разряд после запятой называют разрядом десятых, второй – разрядом сотых, а третий – разрядом тысячных.
Сумму 0,4 + 0,004 + 0,004 называют разложением числа 0,444 по разрядным слагаемым.
Рассмотрим число 3258,912, в котором высшим разрядом являются тысячи, а низшим разрядом – тысячные. Это число содержит 3 тысячи, 2 сотни, 5 десятков, 8 единиц, 9 десятых, 1 сотую, 2 тысячные. Его разложением на сумму разрядных слагаемых будет 3258,912 = 3000 + 200 + 50 + 8 + 0,9 + 0,01 + 0,002
Десятичные дроби можно сравнивать по разрядам.
Например, 2,67<4,7, так как 2<4. Мы сравнили только высший разряд (единицы).
Сравним числа 2,681 и 2,69. Целые части одинаковы, и цифры в разряде десятых тоже одинаковы. Но число в разряде сотых меньше у первой десятичной дроби, чем у второй (8˂9). Значит, 2,681<2,69.
Значит, 2,681<2,69.
Действия с десятичными дробями
Десятичные дроби можно складывать, вычитать, умножать и делить. Также, десятичные дроби можно сравнивать между собой.
В этом уроке мы рассмотрим каждую из этих операций по отдельности.
Сложение десятичных дробейКак мы знаем, десятичная дробь состоит из целой и дробной части. При сложении десятичных дробей, целые и дробные части складываются по отдельности.
Например, сложим десятичные дроби 3,2 и 5,3. Десятичные дроби удобнее складывать в столбик.
Запишем сначала эти две дроби в столбик, при этом целые части обязательно должны быть под целыми, а дробные под дробными. В школе это требование называют «запятая под запятой».
Запишем дроби в столбик так, чтобы запятая оказалась под запятой:
Складываем дробные части: 2 + 3 = 5. Записываем пятёрку в дробной части нашего ответа:
Теперь складываем целые части: 3 + 5 = 8. Записываем восьмёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой»:
Для этого опять же соблюдаем правило «запятая под запятой»:
Получили ответ 8,5. Значит, выражения 3,2 + 5,3 равно 8,5
3,2 + 5,3 = 8,5
На самом деле не всё так просто как кажется на первый взгляд. Здесь тоже имеются свои подводные камни, о которых мы сейчас поговорим.
Разряды в десятичных дробях
У десятичных дробей, как и у обычных чисел, есть свои разряды. Это разряды десятых, разряды сотых, разряды тысячных. При этом разряды начинаются после запятой.
Первая цифра после запятой отвечает за разряд десятых, вторая цифра после запятой за разряд сотых, третья цифра после запятой за разряд тысячных.
Разряды в десятичных дробях хранят в себе нéкоторую полезную информацию. В частности, они сообщают сколько в десятичной дроби десятых частей, сотых частей и тысячных частей.
Например, рассмотрим десятичную дробь 0,345
Позиция, где находится тройка, называется разрядом десятых
Позиция, где находится четвёрка, называется разрядом сотых
Позиция, где находится пятёрка, называется разрядом тысячных
Посмотрим на данный рисунок.
Смотрим дальше. В разряде сотых располагается четвёрка. Это говорит о том, что в десятичной дроби 0,345 содержится четыре сотых .
Смотрим дальше. В разряде тысячных находится пятёрка. Это говорит о том, что в десятичной дроби 0,345 содержится пять тысячных .
Если мы сложим дроби , и то получим изначальную десятичную дробь 0,345
Сначала мы получили ответ , но перевели его в десятичную дробь и получили 0,345.
При сложении десятичных дробей соблюдаются те же правила что и при сложении обычных чисел. Сложение десятичных дробей происходит по разрядам: десятые части складываются с десятыми частями, сотые с сотыми, тысячные с тысячными.
Поэтому при сложении десятичных дробей требуют соблюдать правило «запятая под запятой»
. Запятая под запятой обеспечивает тот самый порядок, в котором десятые части складываются с десятыми, сотые с сотыми, тысячные с тысячными.
Пример 1. Найти значение выражения 1,5 + 3,4
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»:
В первую очередь складываем дробные части 5 + 4 = 9. Записываем девятку в дробной части нашего ответа:
Теперь складываем целые части 1 + 3 = 4. Записываем четвёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой»:
Получили ответ 4,9. Значит значение выражения 1,5 + 3,4 равно 4,9
1,5 + 3,4 = 4,9
Пример 2. Найти значение выражения: 3,51 + 1,22
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»
В первую очередь складываем дробную часть, а именно сотые части 1+2=3. Записываем тройку в сотой части нашего ответа:
Теперь складываем десятые части 5+2=7. Записываем семёрку в десятой части нашего ответа:
Теперь складываем целые части 3+1=4. Записываем четвёрку в целой части нашего ответа:
Записываем четвёрку в целой части нашего ответа:
Отделяем запятой целую часть от дробной, соблюдая правило «запятая под запятой»:
Получили ответ 4,73. Значит значение выражения 3,51 + 1,22 равно 4,73
3,51 + 1,22 = 4,73
Как и в обычных числах, при сложении десятичных дробей может произойти переполнение разряда. В этом случае в ответе записывается одна цифра, а остальные переносят на следующий разряд.
Пример 3. Найти значение выражения 2,65 + 3,27
Записываем в столбик данное выражение:
Складываем сотые части 5+7=12. Число 12 не поместится в сотой части нашего ответа. Поэтому в сотой части записываем цифру 2, а единицу переносим на следующий разряд:
Теперь складываем десятые части 6+2=8 плюс единица, которая досталась от предыдущей операции, получим 9. Записываем цифру 9 в десятой части нашего ответа:
Теперь складываем целые части 2+3=5. Записываем цифру 5 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 5,92. Значит значение выражения 2,65 + 3,27 равно 5,92
Значит значение выражения 2,65 + 3,27 равно 5,92
2,65 + 3,27 = 5,92
Пример 4. Найти значение выражения 9,5 + 2,8
Записываем в столбик данное выражение
Складываем дробные части 5 + 8 = 13. Число 13 не поместится в дробной часть нашего ответа, поэтому сначала записываем цифру 3, а единицу переносим на следующий разряд, точнее переносим её к целой части:
Теперь складываем целые части 9+2=11 плюс единица, которая досталась от предыдущей операции, получаем 12. Записываем число 12 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 12,3. Значит значение выражения 9,5 + 2,8 равно 12,3
9,5 + 2,8 = 12,3
При сложении десятичных дробей количество цифр после запятой в обеих дробях должно быть одинаковым. Если цифр не хватает, то эти места в дробной части заполняются нулями.
Пример 5. Найти значение выражения: 12,725 + 1,7
Прежде чем записывать в столбик данное выражение, сделаем количество цифр после запятой в обеих дробях одинаковым. В десятичной дроби 12,725 после запятой три цифры, а в дроби 1,7 только одна. Значит в дроби 1,7 в конце нужно добавить два нуля. Тогда получим дробь 1,700. Теперь можно записать в столбик данное выражение и начать вычислять:
В десятичной дроби 12,725 после запятой три цифры, а в дроби 1,7 только одна. Значит в дроби 1,7 в конце нужно добавить два нуля. Тогда получим дробь 1,700. Теперь можно записать в столбик данное выражение и начать вычислять:
Складываем тысячные части 5+0=5. Записываем цифру 5 в тысячной части нашего ответа:
Складываем сотые части 2+0=2. Записываем цифру 2 в сотой части нашего ответа:
Складываем десятые части 7+7=14. Число 14 не поместится в десятой части нашего ответа. Поэтому сначала записываем цифру 4, а единицу переносим на следующий разряд:
Теперь складываем целые части 12+1=13 плюс единица, которая досталась от предыдущей операции, получаем 14. Записываем число 14 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 14,425. Значит значение выражения 12,725+1,700 равно 14,425
12,725+ 1,700 = 14,425
Вычитание десятичных дробей
При вычитании десятичных дробей нужно соблюдать те же правила что и при сложении: «запятая под запятой» и «равное количества цифр после запятой».
Пример 1. Найти значение выражения 2,5 − 2,2
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»:
Вычисляем дробную часть 5−2=3. Записываем цифру 3 в десятой части нашего ответа:
Вычисляем целую часть 2−2=0. Записываем ноль в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 0,3. Значит значение выражения 2,5 − 2,2 равно 0,3
2,5 − 2,2 = 0,3
Пример 2. Найти значение выражения 7,353 — 3,1
В этом выражении разное количество цифр после запятой. В дроби 7,353 после запятой три цифры, а в дроби 3,1 только одна. Значит в дроби 3,1 в конце нужно добавить два нуля, чтобы сделать количество цифр в обеих дробях одинаковым. Тогда получим 3,100.
Теперь можно записать в столбик данное выражение и вычислить его:
Получили ответ 4,253. Значит значение выражения 7,353 − 3,1 равно 4,253
7,353 — 3,1 = 4,253
Как и в обычных числах, иногда придётся занимать единицу у соседнего разряда, если вычитание станет невозможным.
Пример 3. Найти значение выражения 3,46 − 2,39
Вычитаем сотые части 6−9. От число 6 не вычесть число 9. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда число 6 обращается в число 16. Теперь можно вычислить сотые части 16−9=7. Записываем семёрку в сотой части нашего ответа:
Теперь вычитаем десятые части. Поскольку мы заняли в разряде десятых одну единицу, то цифра, которая там располагалась, уменьшилась на одну единицу. Другими словами, в разряде десятых теперь не цифра 4, а цифра 3. Вычислим десятые части 3−3=0. Записываем ноль в десятой части нашего ответа:
Теперь вычитаем целые части 3−2=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,07. Значит значение выражения 3,46−2,39 равно 1,07
3,46−2,39=1,07
Пример 4. Найти значение выражения 3−1,2
В этом примере из целого числа вычитается десятичная дробь. Запишем данное выражение столбиком так, чтобы целая часть десятичной дроби 1,2 оказалась под числом 3
Запишем данное выражение столбиком так, чтобы целая часть десятичной дроби 1,2 оказалась под числом 3
Теперь сделаем количество цифр после запятой одинаковым. Для этого после числа 3 поставим запятую и допишем один ноль:
Теперь вычитаем десятые части: 0−2. От нуля не вычесть число 2. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда, 0 обращается в число 10. Теперь можно вычислить десятые части 10−2=8. Записываем восьмёрку в десятой части нашего ответа:
Теперь вычитаем целые части. Раньше в целой располагалось число 3, но мы заняли у него одну единицу. В результате оно обратилось в число 2. Поэтому из 2 вычитаем 1. 2−1=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,8. Значит значение выражения 3−1,2 равно 1,8
3 − 1,2 = 1,8
Умножение десятичных дробей
Умножение десятичных дробей это просто и даже увлекательно. Чтобы перемножить десятичные дроби, нужно перемножить их как обычные числа, не обращая внимания на запятые.
Чтобы перемножить десятичные дроби, нужно перемножить их как обычные числа, не обращая внимания на запятые.
Получив ответ, необходимо отделить запятой целую часть от дробной. Чтобы сделать это, надо посчитать количество цифр после запятой в обеих дробях, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Пример 1. Найти значение выражения 2,5 × 1,5
Перемножим эти десятичные дроби как обычные числа, не обращая внимания на запятые. Чтобы не обращать внимания на запятые, можно на время представить, что они вообще отсутствуют:
Получили 375. В этом числе необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в дробях 2,5 и 1,5. В первой дроби после запятой одна цифра, во второй дроби тоже одна. Итого две цифры.
Возвращаемся к числу 375 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 3,75. Значит значение выражения 2,5 × 1,5 равно 3,75
Значит значение выражения 2,5 × 1,5 равно 3,75
2,5 × 1,5 = 3,75
Пример 2. Найти значение выражения 12,85 × 2,7
Перемножим эти десятичные дроби, не обращая внимания на запятые:
Получили 34695. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 12,85 и 2,7. В дроби 12,85 после запятой две цифры, в дроби 2,7 одна цифра — итого три цифры.
Возвращаемся к числу 34695 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую:
Получили ответ 34,695. Значит значение выражения 12,85 × 2,7 равно 34,695
12,85 × 2,7 = 34,695
Умножение десятичной дроби на обычное число
Иногда возникают ситуации, когда требуется умножить десятичную дробь на обычное число.
Чтобы перемножить десятичную дробь и обычное число, нужно перемножить их, не обращая внимания на запятую в десятичной дроби. Получив ответ, необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в десятичной дроби, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Получив ответ, необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в десятичной дроби, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Например, умножим 2,54 на 2
Умножаем десятичную дробь 2,54 на обычное число 2, не обращая внимания на запятую:
Получили число 508. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,54. В дроби 2,54 после запятой две цифры.
Возвращаемся к числу 508 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 5,08. Значит значение выражения 2,54 × 2 равно 5,08
2,54 × 2 = 5,08
Умножение десятичных дробей на 10, 100, 1000
Умножение десятичных дробей на 10, 100 или 1000 выполняется таким же образом, как и умножение десятичных дробей на обычные числа. Нужно выполнить умножение, не обращая внимания на запятую в десятичной дроби, затем в ответе отделить целую часть от дробной, отсчитав справа столько же цифр, сколько было цифр после запятой в десятичной дроби.
Например, умножим 2,88 на 10
Умножим десятичную дробь 2,88 на 10, не обращая внимания на запятую в десятичной дроби:
Получили 2880. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,88. Видим, что в дроби 2,88 после запятой две цифры.
Возвращаемся к числу 2880 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 28,80. Отбросим последний ноль — получим 28,8. Значит значение выражения 2,88×10 равно 28,8
2,88 × 10 = 28,8
Есть и второй способ умножения десятичных дробей на 10, 100, 1000. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается вправо на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 2,88×10 этим способом. Не приводя никаких вычислений, сразу же смотрим на множитель 10. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 2,88 передвигаем запятую вправо на одну цифру, получим 28,8.
Видим, что в нём один ноль. Теперь в дроби 2,88 передвигаем запятую вправо на одну цифру, получим 28,8.
2,88 × 10 = 28,8
Попробуем умножить 2,88 на 100. Сразу же смотрим на множитель 100. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 2,88 передвигаем запятую вправо на две цифры, получаем 288
2,88 × 100 = 288
Попробуем умножить 2,88 на 1000. Сразу же смотрим на множитель 1000. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 2,88 передвигаем запятую вправо на три цифры. Третьей цифры там нет, поэтому мы дописываем ещё один ноль. В итоге получаем 2880.
2,88 × 1000 = 2880
Умножение десятичных дробей на 0,1 0,01 и 0,001
Умножение десятичных дробей на 0,1, 0,01 и 0,001 происходит таким же образом, как и умножение десятичной дроби на десятичную дробь. Необходимо перемножить дроби, как обычные числа, и в ответе поставить запятую, отсчитав столько цифр справа, сколько цифр после запятой в обеих дробях.
Например, умножим 3,25 на 0,1
Умножаем эти дроби, как обычные числа, не обращая внимания на запятые:
Получили 325. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 3,25 и 0,1. В дроби 3,25 после запятой две цифры, в дроби 0,1 одна цифра. Итого три цифры.
Возвращаемся к числу 325 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую. Отсчитав три цифры мы обнаруживаем, что цифры закончились. В этом случае нужно дописать один ноль и поставить запятую:
Получили ответ 0,325. Значит значение выражения 3,25 × 0,1 равно 0,325
3,25 × 0,1 = 0,325
Есть и второй способ умножения десятичных дробей на 0,1, 0,01 и 0,001. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается влево на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 3,25 × 0,1 этим способом. Не приводя никаких вычислений сразу же смотрим на множитель 0,1. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 3,25 передвигаем запятую влево на одну цифру. Передвинув запятую на одну цифру влево мы видим, что перед тройкой больше нет никаких цифр. В этом случае дописываем один ноль и ставим запятую. В результате получаем 0,325
Не приводя никаких вычислений сразу же смотрим на множитель 0,1. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 3,25 передвигаем запятую влево на одну цифру. Передвинув запятую на одну цифру влево мы видим, что перед тройкой больше нет никаких цифр. В этом случае дописываем один ноль и ставим запятую. В результате получаем 0,325
3,25 × 0,1 = 0,325
Попробуем умножить 3,25 на 0,01. Сразу же смотрим на множитель 0,01. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 3,25 передвигаем запятую влево на две цифры, получаем 0,0325
3,25 × 0,01 = 0,0325
Попробуем умножить 3,25 на 0,001. Сразу же смотрим на множитель 0,001. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 3,25 передвигаем запятую влево на три цифры, получаем 0,00325
3,25 × 0,001 = 0,00325
Нельзя путать умножение десятичных дробей на 0,1, 0,001 и 0,001 с умножением на 10, 100, 1000.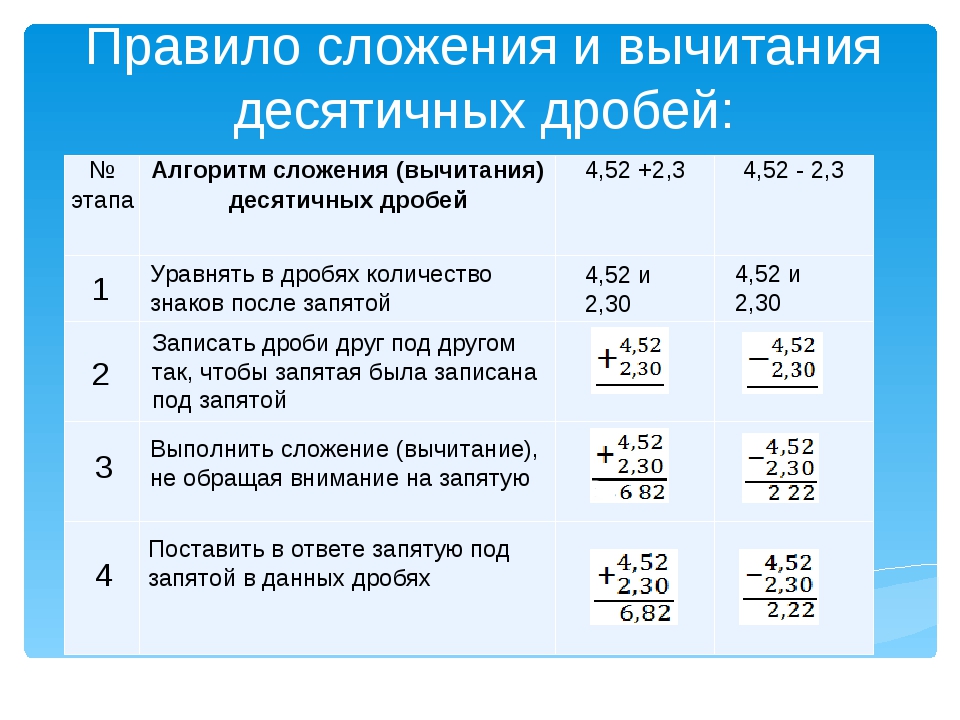 Типичная ошибка большинства людей.
Типичная ошибка большинства людей.
При умножении на 10, 100, 1000 запятая переносится вправо на столько же цифр сколько нулей во множителе.
А при умножении на 0,1, 0,01 и 0,001 запятая переносится влево на столько же цифр сколько нулей во множителе.
Если на первых порах это сложно запомнить, можно пользоваться первым способом, в котором умножение выполняется как с обычными числами. В ответе нужно будет отделить целую часть от дробной, отсчитав справа столько же цифр, сколько цифр после запятой в обеих дробях.
Деление меньшего числа на большее. Продвинутый уровень.
В одном из предыдущих уроков мы сказали, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель.
Например, чтобы разделить одно яблоко на двоих, нужно в числитель записать 1 (одно яблоко), а в знаменатель записать 2 (двое друзей). В результате получим дробь . Значит каждому другу достанется по яблока. Другими словами, по половине яблока. Дробь это ответ к задаче «как разделить одно яблоко на двоих»
Значит каждому другу достанется по яблока. Другими словами, по половине яблока. Дробь это ответ к задаче «как разделить одно яблоко на двоих»
Оказывается, можно решать эту задачу и дальше, если разделить 1 на 2. Ведь дробная черта в любой дроби означает деление, а значит и в дроби это деление разрешено. Но как? Мы ведь привыкли к тому, что делимое всегда больше делителя. А здесь наоборот, делимое меньше делителя.
Всё станет ясным, если вспомнить, что дробь означает дробление, деление, разделение. А значит и единица может быть раздроблена на сколько угодно частей, а не только на две части.
При разделении меньшего числа на большее получается десятичная дробь, в которой целая часть будет 0 (нулевой). Дробная часть же может быть любой.
Итак, разделим 1 на 2. Решим этот пример уголком:
Единицу на два просто так нацело не разделить. Если задать вопрос «сколько двоек в единице», то ответом будет 0. Поэтому в частном записываем 0 и ставим запятую:
Теперь как обычно умножаем частное на делитель, чтобы вытащить остаток:
Настал момент, когда единицу можно дробить на две части. Для этого справа от полученной единички дописываем ещё один ноль:
Для этого справа от полученной единички дописываем ещё один ноль:
Получили 10. Делим 10 на 2, получаем 5. Записываем пятёрку в дробной части нашего ответа:
Теперь вытаскиваем последний остаток, чтобы завершить вычисление. Умножаем 5 на 2, получаем 10
Получили ответ 0,5. Значит дробь равна 0,5
Половину яблока можно записать и с помощью десятичной дроби 0,5. Если сложить эти две половинки (0,5 и 0,5), мы опять получим изначальное одно целое яблоко:
Этот момент также можно понять, если представить, как 1 см делится на две части. Если 1 сантиметр разделить на 2 части, то получится 0,5 см
Пример 2. Найти значение выражения 4 : 5
Сколько пятёрок в четвёрке? Нисколько. Записываем в частном 0 и ставим запятую:
Умножаем 0 на 5, получаем 0. Записываем ноль под четвёркой. Сразу же вычитаем этот ноль из делимого:
Теперь начнём дробить (делить) четвёрку на 5 частей. Для этого справа от 4 дописываем ноль и делим 40 на 5, получаем 8. Записываем восьмёрку в частном.
Для этого справа от 4 дописываем ноль и делим 40 на 5, получаем 8. Записываем восьмёрку в частном.
Завершаем пример, умножив 8 на 5, и получив 40:
Получили ответ 0,8. Значит значение выражения 4 : 5 равно 0,8
Пример 3. Найти значение выражения 5 : 125
Сколько чисел 125 в пятёрке? Нисколько. Записываем 0 в частном и ставим запятую:
Умножаем 0 на 125, получаем 0. Записываем 0 под пятёркой. Сразу же вычитаем из пятёрки 0
Теперь начнём дробить (делить) пятёрку на 125 частей. Для этого справа от этой пятёрки запишем ноль:
Делим 50 на 125. Сколько чисел 125 в числе 50? Нисколько. Значит в частном опять записываем 0
Умножаем 0 на 125, получаем 0. Записываем этот ноль под 50. Сразу же вычитаем 0 из 50
Теперь делим число 50 на 125 частей. Для этого справа от 50 запишем ещё один ноль:
Делим 500 на 125. Сколько чисел 125 в числе 500. В числе 500 четыре числа 125. Записываем четвёрку в частном:
Записываем четвёрку в частном:
Завершаем пример, умножив 4 на 125, и получив 500
Получили ответ 0,04. Значит значение выражения 5 : 125 равно 0,04
Деление чисел без остатка
В уроке деление мы научились делить числа с остатком. Например, чтобы разделить 9 на 5, мы поступали следующим образом:
и далее говорили, что «девять разделить на пять будет один и четыре в остатке».
Теперь мы получили необходимые знания, чтобы разделить 9 на 5 без остатка. Наша задача раздробить остаток 4 на 5 частей. Другими словами, разделить меньшее число на большее.
Итак, поставим в частном после единицы запятую, тем самым указывая, что деление целых частей закончилось и мы приступаем к дробной части:
Допишем ноль к остатку 4
Теперь делим 40 на 5, получаем 8. Записываем восьмёрку в частном:
Что делать дальше мы уже знаем. Вытаскиваем остаток (если есть). Умножаем восьмёрку на делитель 5, и записываем полученный результат под 40:
40−40=0.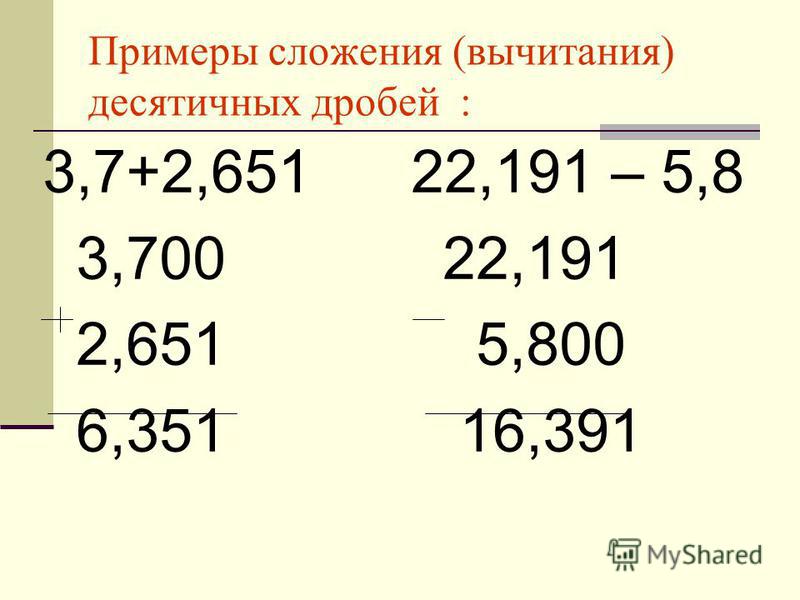 Получили 0 в остатке. Значит деление на этом полностью завершено. При делении 9 на 5 получается десятичная дробь 1,8:
Получили 0 в остатке. Значит деление на этом полностью завершено. При делении 9 на 5 получается десятичная дробь 1,8:
9 : 5 = 1,8
Пример 2. Разделить 84 на 5 без остатка
Сначала разделим 84 на 5 как обычно с остатком:
Получили в частном 16 и еще 4 в остатке. Теперь разделим этот остаток на 5. Поставим в частном запятую, а к остатку 4 допишем 0
Теперь делим 40 на 5, получаем 8. Записываем восьмерку в частном после запятой:
и завершаем пример, проверив есть ли еще остаток:
Деление десятичной дроби на обычное число
Десятичная дробь, как мы знаем состоит из целой и дробной части. При делении десятичной дроби на обычное число в первую очередь нужно:
- разделить целую часть десятичной дроби на это число;
- после того, как целая часть будет разделена, нужно в частном сразу же поставить запятую и продолжить вычисление, как в обычном делении.
Например, разделим 4,8 на 2
Запишем этот пример уголком:
Теперь разделим целую часть на 2. Четыре разделить на два будет два. Записываем двойку в частном и сразу же ставим запятую:
Четыре разделить на два будет два. Записываем двойку в частном и сразу же ставим запятую:
Теперь умножаем частное на делитель и смотрим есть ли остаток от деления:
4−4=0. Остаток равен нулю. Ноль пока не записываем, поскольку решение не завершено. Далее продолжаем вычислять, как в обычном делении. Сносим 8 и делим её на 2
8 : 2 = 4. Записываем четвёрку в частном и сразу умножаем её на делитель:
Получили ответ 2,4. Значение выражения 4,8 : 2 равно 2,4
Пример 2. Найти значение выражения 8,43 : 3
Делим 8 на 3, получаем 2. Сразу же ставим запятую после двойки:
Теперь умножаем частное на делитель 2 × 3 = 6. Записываем шестёрку под восьмёркой и находим остаток:
Далее продолжаем вычислять, как в обычном делении. Сносим 4
Делим 24 на 3, получаем 8. Записываем восьмёрку в частном. Сразу же умножаем её на делитель, чтобы найти остаток от деления:
24−24=0.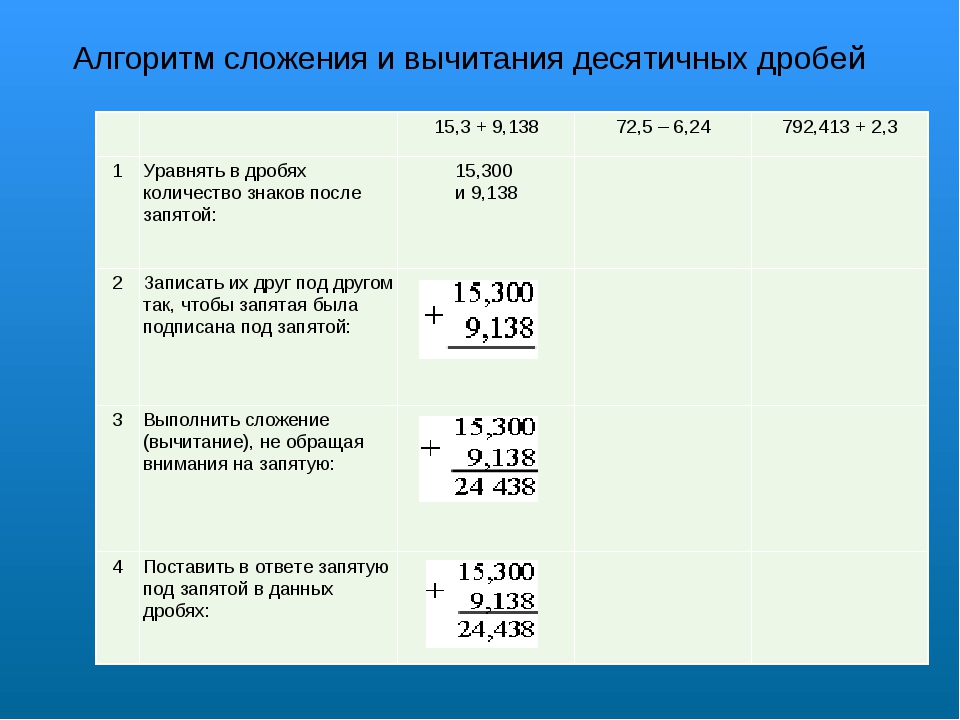 Остаток равен нулю. Ноль пока не записываем. Сносим последнюю тройку из делимого и делим на 3, получим 1. Сразу же умножаем 1 на 3, чтобы завершить этот пример:
Остаток равен нулю. Ноль пока не записываем. Сносим последнюю тройку из делимого и делим на 3, получим 1. Сразу же умножаем 1 на 3, чтобы завершить этот пример:
Получили ответ 2,81. Значит значение выражения 8,43 : 3 равно 2,81
Деление десятичной дроби на десятичную дробь
Чтобы разделить десятичную дробь на десятичную дробь, надо в делимом и в делителе перенести запятую вправо на столько же цифр, сколько их после запятой в делителе, и затем выполнить деление на обычное число.
Например, разделим 5,95 на 1,7
Запишем уголком данное выражение
Теперь в делимом и в делителе перенесём запятую вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит мы должны в делимом и в делителе перенести запятую вправо на одну цифру. Переносим:
После перенесения запятой вправо на одну цифру десятичная дробь 5,95 обратилась в дробь 59,5. А десятичная дробь 1,7 после перенесения запятой вправо на одну цифру обратилась в обычное число 17. А как делить десятичную дробь на обычное число мы уже знаем. Дальнейшее вычисление не составляет особого труда:
А как делить десятичную дробь на обычное число мы уже знаем. Дальнейшее вычисление не составляет особого труда:
Запятая переносится вправо с целью облегчить деление. Это допускается по причине того, что при умножении или делении делимого и делителя на одно и то же число, частное не меняется. Что это значит?
Это одна из интересных особенностей деления. Его называют свойством частного. Рассмотрим выражение 9 : 3 = 3. Если в этом выражении делимое и делитель умножить или разделить на одно и то же число, то частное 3 не изменится.
Давайте умножим делимое и делитель на 2, и посмотрим, что из этого получится:
(9 × 2) : (3 × 2) = 18 : 6 = 3
Как видно из примера, частное не поменялось.
Тоже самое происходит, когда мы переносим запятую в делимом и в делителе. В предыдущем примере, где мы делили 5,91 на 1,7 мы перенесли в делимом и делителе запятую на одну цифру вправо. После переноса запятой, дробь 5,91 преобразовалась в дробь 59,1 а дробь 1,7 преобразовалась в обычное число 17. На самом деле здесь происходило умножение на 10. Вот как это выглядело:
На самом деле здесь происходило умножение на 10. Вот как это выглядело:
5,91 × 10 = 59,1
1,7 × 10 = 17
Поэтому от количества цифр после запятой в делителе зависит то, на что будет умножено делимое и делитель. Другими словами, от количества цифр после запятой в делителе будет зависеть то, на сколько цифр в делимом и в делителе запятая будет перенесена вправо.
Деление десятичной дроби на 10, 100, 1000
Деление десятичной дроби на 10, 100, или 1000 осуществляется таким же образом, как и деление десятичной дроби на обычное число. Например, разделим 2,1 на 10. Решим этот пример уголком:
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится влево на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 2,1 : 10. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 2,1 нужно перенести запятую влево на одну цифру. Переносим запятую влево на одну цифру и видим, что там больше не осталось цифр. В этом случае перед цифрой дописываем ещё один ноль. В итоге получаем 0,21
Переносим запятую влево на одну цифру и видим, что там больше не осталось цифр. В этом случае перед цифрой дописываем ещё один ноль. В итоге получаем 0,21
2,1 : 10 = 0,21
Попробуем разделить 2,1 на 100. В числе 100 два нуля. Значит в делимом 2,1 надо перенести запятую влево на две цифры:
2,1 : 100 = 0,021
Попробуем разделить 2,1 на 1000. В числе 1000 три нуля. Значит в делимом 2,1 надо перенести запятую влево на три цифры:
2,1 : 1000 = 0,0021
Деление десятичной дроби на 0,1, 0,01 и 0,001
Деление десятичной дроби на 0,1, 0,01, и 0,001 осуществляется таким же образом, как и деление десятичной дроби на десятичную дробь. В делимом и в делителе надо перенести запятую вправо на столько цифр, сколько их после запятой в делителе.
Например, разделим 6,3 на 0,1. В первую очередь перенесём запятые в делимом и в делителе вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит переносим запятые в делимом и в делителе вправо на одну цифру.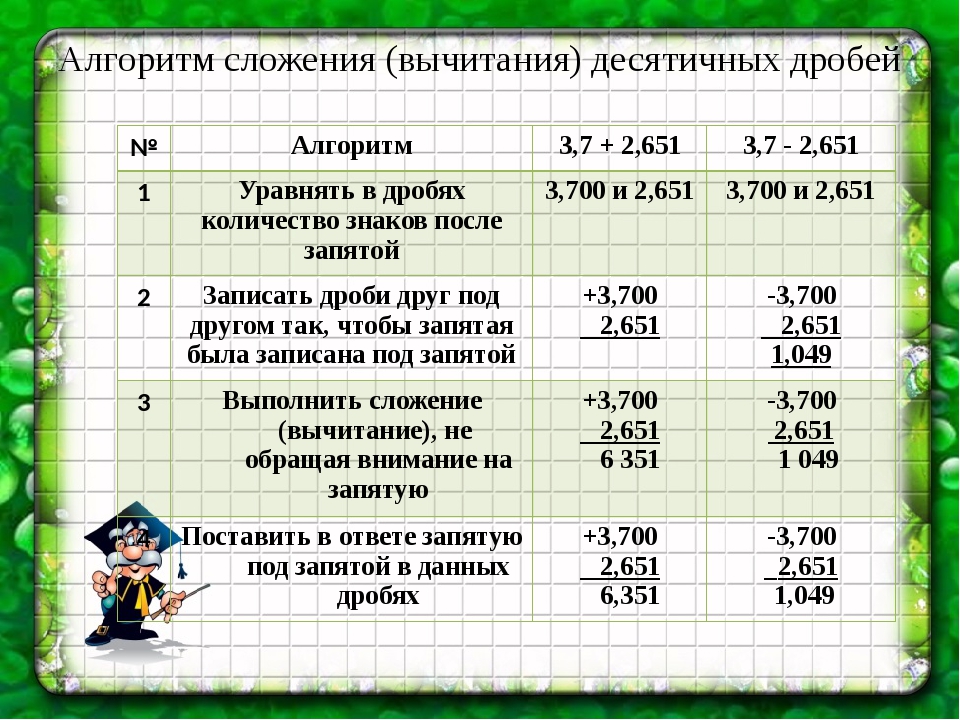
После перенесения запятой вправо на одну цифру, десятичная дробь 6,3 превращается в обычное число 63, а десятичная дробь 0,1 после перенесения запятой вправо на одну цифру превращается в единицу. А разделить 63 на 1 очень просто:
63 : 1 = 63
Значит значение выражения 6,3 : 0,1 равно 63
6,3 : 0,1 = 63
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится вправо на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 6,3 : 0,1. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 6,3 нужно перенести запятую вправо на одну цифру. Переносим запятую вправо на одну цифру и получаем 63
6,3 : 0,1 = 63
Попробуем разделить 6,3 на 0,01. В делителе 0,01 два нуля. Значит в делимом 6,3 надо перенести запятую вправо на две цифры. Но в делимом после запятой только одна цифра. В этом случае в конце нужно дописать ещё один ноль. В результате получим 630
В результате получим 630
6,3 : 0,01 = 630
Попробуем разделить 6,3 на 0,001. В делителе 0,001 три нуля. Значит в делимом 6,3 надо перенести запятую вправо на три цифры:
6,3 : 0,001 = 6300
Задания для самостоятельного решения
Задание 1. Выполните сложение:
0,6 + 0,3
Решение:
Задание 2. Выполните сложение:
1,2 + 5,3
Решение:
Задание 3. Выполните сложение:
1,6 + 0,4
Решение:
Задание 4. Выполните сложение:
0,8 + 0,5
Решение:
Задание 5. Выполните вычитание:
0,9 − 0,4
Решение:
Задание 6. Выполните вычитание:
2 − 0,3
Решение:
Задание 7. Выполните вычитание:
9 − 7,8
Решение:
Задание 8. Выполните вычитание:
4 − 1,8
Решение:
Задание 9. Выполните умножение:
3,2 × 1,8
Решение:
Задание 10. Выполните умножение:
9,3 × 5,8
Решение:
Задание 11. Выполните умножение:
Выполните умножение:
0,23 × 0,07
Решение:
Задание 12. Выполните умножение:
3,14 × 0,25
Решение:
Задание 13. Выполните деление:
9,36 : 6
Решение:
Задание 14. Выполните деление:
0,169 : 13
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Сложение и вычитание десятичных дробей
Чтобы найти сумму или разность двух чисел, записанных в десятичной форме, надо выполнить три шага:
- Записать числа в столбик таким образом, чтобы соответствующие разряды совпадали. Главный ориентир — десятичные точки. Они не являются отдельным разрядом, но должны стоять на одной вертикали;
- Сложить или вычесть полученные дроби столбиком — подобно тому, как мы складываем и вычитаем обычные числа.
 Не забудьте «внедрить» десятичную точку между соответствующими разрядами;
Не забудьте «внедрить» десятичную точку между соответствующими разрядами; - Полученное число и будет ответом — больше ничего делать не надо.
Как видите, сложение десятичных дробей почти ничем не отличается от сложения обычных чисел. Самое сложное — правильно сопоставить разряды слагаемых, чтобы десятичные точки находились на вертикальной прямой, друг под другом.
Задача. Найдите значение выражений: 8,125 + 17,4; 3,5 + 121,048.
Для каждого выражения приведем правильную запись и две неправильные (самые распространенные). Сначала — правильные:
Теперь рассмотрим неправильные решения. В первом случае все числа «прижаты» к левому краю, во втором — к правому. Ответы получатся совсем другие:
Как видите, ничего общего с тем, что должно получиться на самом деле.
Если в одном из слагаемых нет десятичной точки, ее ставят справа от всего числа. Например, возьмем числа 5,83 и 72. В этом случае операция сложения будет выглядеть так:
Кто-то скажет, что все эти отступы, сдвиги и запятые — ненужные сложности, и лучше работать «по старинке».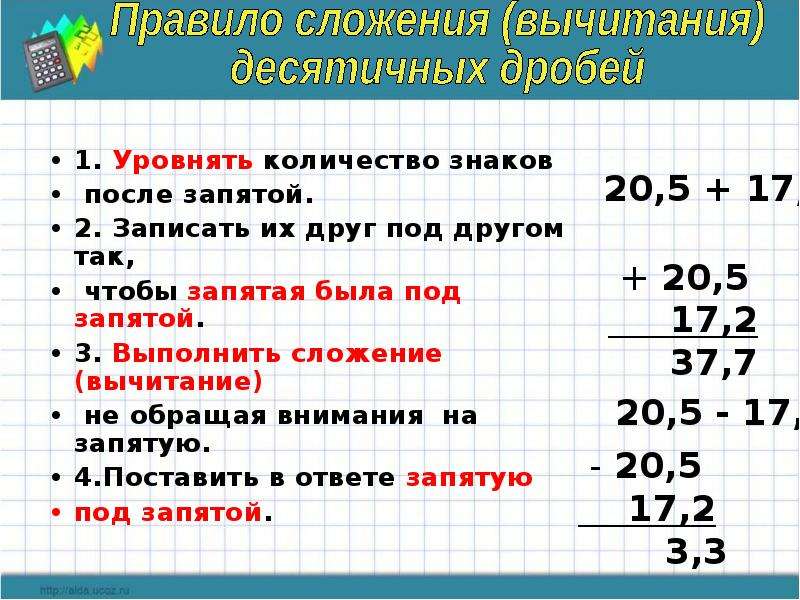 Что ж, я никого не собираюсь переубеждать. Отмечу лишь, что новая технология всегда требуют более высокой квалификации от тех, кто собирается ее использовать. В этом плане десятичные дроби — следующий уровень развития после обычных.
Что ж, я никого не собираюсь переубеждать. Отмечу лишь, что новая технология всегда требуют более высокой квалификации от тех, кто собирается ее использовать. В этом плане десятичные дроби — следующий уровень развития после обычных.
Задача. Найдите значение выражений: 7,34 + 18,5; 13 + 0,25;11,3 − 4,128; 5,21 − 11.
Эти примеры показывают, насколько упрощаются вычисления, когда дроби записаны в десятичной форме. Никаких дополнительных множителей, никаких общих знаменателей.
Чтобы почувствовать разницу, решим ту же задачу традиционным методом. Для этого переведем все десятичные дроби в обычные. Взгляните:
Задача. Найдите значение выражений: 7,34 + 18,5; 13 + 0,25;11,3 − 4,128; 5,21 − 11.
Итак, переводим все десятичные дроби в обычные и считаем по классической схеме:
Мы специально не стали выполнять обратный переход — от обычной дроби к десятичной — чтобы немного сократить вычисления.
Видно, что длина решения выросла многократно. Поэтому старайтесь работать с десятичными дробями везде, где это возможно.
Смотрите также:
- Умножение и деление десятичных дробей
- Как представить обычную дробь в виде десятичной
- Пробный ЕГЭ 2012. Вариант 3 (без логарифмов)
- Задача 7 — геометрический смысл производной
- Метод узлов в задаче B5
- Задача B5: площадь сектора
Сложение и вычитание десятичных дробей. Тест. — Kid-mama
Десятичные дроби складывают столбиком так же, как обыкновенные числа, при этом их записывают так, чтобы запятая находилась строго под запятой. Далее следуют алгоритму:
- Количество знаков после запятой уравнивают, приписывая нули на конце дроби.
- Выполняют сложение или вычитание как обычно, не обращая внимания на запятую.
- Ставят запятую под запятой в данных дробях.
Если вы складываете целое число и десятичную дробь, то просто прибавляете это число к целой части, которая находится перед запятой.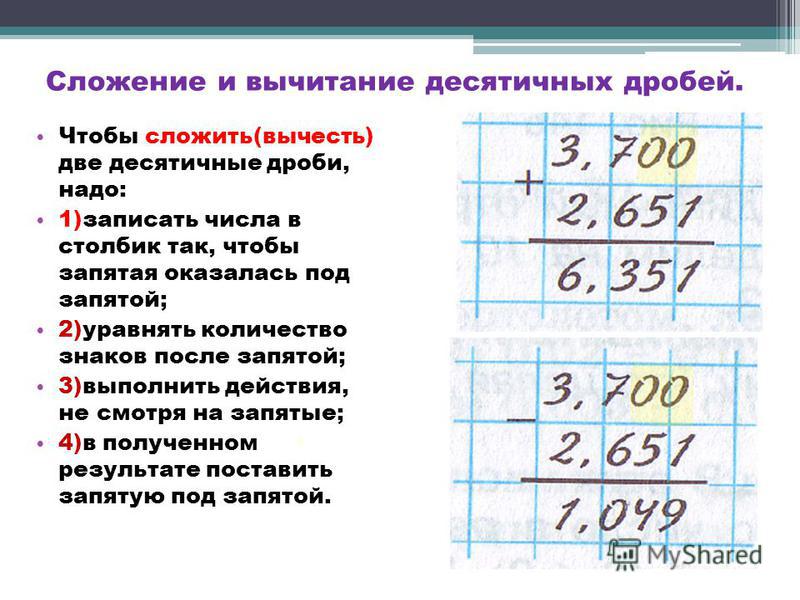 Например:
Например:
5 + 2,43 = 7,43
74 + 0,004 = 74,004
Если нужно из целого числа вычесть десятичную дробь, то уравниваете количество знаков после запятой и вычитаете столбиком, как описано в начале этой статьи. Например, как выполнить вычитание 52 — 3,614 = ?
Вы можете потренироваться решать примеры на сложение и вычитание десятичных дробей на нашем тренажёре.
Сложение и вычитание десятичных дробей
Лимит времени: 0
0 из 20 заданий окончено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Информация
Выполните сложение или вычитание и введите ответ. В ответе вставляйте запятую, а не точку, иначе будет засчитан неправильный ответ.
В ответе вставляйте запятую, а не точку, иначе будет засчитан неправильный ответ.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- С ответом
- С отметкой о просмотре
Этот тест можно проходить много раз. Задания каждый раз выпадают разные.
Задания каждый раз выпадают разные.
Сложение, вычитание, умножение и деление десятичных дробей
Сложение и вычитание десятичных дробей аналогично сложению и вычитанию натуральных чисел, но с определенными условиями.
Правило. Сложение и вычитание десятичных дробей производится по разрядам целой и дробной части как натуральных чисел.
При письменном сложении и вычитании десятичных дробей запятая, отделяющая целую часть от дробной, должна находиться у слагаемых и суммы или у уменьшаемого, вычитаемого и разности в одном столбце (запятая под запятой от записи условия до конца вычисления).
Примеры.
Сложение и вычитание десятичных дробей в строку:
243,625 + 24,026 = 200 + 40 + 3 + 0,6 + 0,02 + 0,005 + 20 + 4 + 0,02 + 0,006 = 200 + (40 + 20) + (3 + 4)+ 0,6 + (0,02 + 0,02) + (0,005 + 0,006) = 200 + 60 + 7 + 0,6 + 0,04 + 0,011 = 200 + 60 + 7 + 0,6 + (0,04 + 0,01) + 0,001 = 200 + 60 + 7 + 0,6 + 0,05 + 0,001 = 267,651
843,217 — 700,628 = (800 — 700) + 40 + 3 + (0,2 — 0,6) + (0,01 — 0,02) + (0,007 — 0,008) = 100 + 40 + 2 + (1,2 — 0,6) + (0,01 — 0,02) + (0,007 — 0,008) = 100 + 40 + 2 + 0,5 + (0,11 — 0,02) + (0,007 — 0,008) = 100 + 40 + 2 + 0,5 + 0,09 + (0,007 — 0,008) = 100 + 40 + 2 + 0,5 + 0,08 + (0,017 — 0,008) = 100 + 40 + 2 + 0,5 + 0,08 + 0,009 = 142,589
Сложение и вычитание десятичных дробей в столбик:
Сложение десятичных дробей требует верхней дополнительной строки для записи чисел, когда сумма разряда переходит через десяток. Вычитание десятичных дробей требует верхней дополнительной строки для того, чтобы отметить разряд, в котором одалживается 1.
Вычитание десятичных дробей требует верхней дополнительной строки для того, чтобы отметить разряд, в котором одалживается 1.
Если справа от слагаемого или уменьшаемого не хватает разрядов дробной части, то справа в дробной части можно дописывать столько нулей (увеличивать разрядность дробной части), сколько разрядов в другом слагаемом или уменьшаемом.
Умножение десятичных дробей производится так же, как и умножение натуральных чисел, по тем же правилам, но в произведении ставится запятая по сумме разрядов множителей в дробной части, считая справа налево (сумма разрядов множителей — это количество разрядов после запятой у множителей, вместе взятых).
Пример:
При умножении десятичных дробей в столбик первая справа значащая цифра подписывается под первой справа значащей цифрой, как и в натуральных числах:
Запись умножения десятичных дробей в столбик:
Запись деления десятичных дробей в столбик:
Подчеркнутые знаки — это знаки, за которые переносится запятая, потому что делитель должен быть целым числом.
Правило. При делении дробей делитель десятичной дроби увеличивается на столько разрядов, сколько разрядов в дробной его части. Чтобы дробь не изменилась, на столько же разрядов увеличивается и делимое (в делимом и делителе запятая переносится на одно и то же число знаков). Запятая ставится в частном на том этапе деления, когда целая часть дроби разделена.
Для десятичных дробей, как и для натуральных чисел, сохраняется правило: на ноль десятичную дробь делить нельзя!
Сложение десятичных дробей: правила и примеры
Сложение десятичных дробей можно выполнить двумя способами:
- Представить десятичные дроби в виде обыкновенных дробей и выполнить их сложение.
- Выполнить сложение десятичных дробей столбиком.
Сложение путём перевода в обыкновенные дроби
При сложении десятичных дробей путём их перевода в обыкновенные дроби следует руководствоваться следующим правилом:
- Нужно сравнить количество десятичных знаков у десятичных дробей.

- Если количество десятичных знаков одинаково, то переводим десятичные дроби в обыкновенные и складываем их.
- Если количество десятичных знаков различно, то сначала нужно уравнять их количество, приписав справа к десятичной дроби с меньшим количеством знаков необходимое число нулей.
Пример 1. Выполнить сложение чисел 3,1 и 4,7.
Решение. Так как количество десятичных знаков одинаково, то просто переводим десятичные дроби в обыкновенные и складываем. Десятичной дроби 3,1 соответствует обыкновенная дробь , а десятичной дроби 4,7 — обыкновенная дробь , значит:
Пример 2. Сложить числа 3,45 и 7,368.
Решение. Так как количество десятичных знаков различно, то сначала уравняем их количество, приписав справа к дроби 3,45 цифру 0. Десятичной дроби 3,450 соответствует обыкновенная дробь , а десятичной дроби 7,368 — обыкновенная дробь , значит:
Сложение десятичных дробей столбиком
Десятичные дроби можно складывать столбиком.
При сложении десятичных дробей столбиком следует руководствоваться следующим правилом:
- Записать десятичные дроби в столбик так, чтобы цифры одинаковых разрядов стояли друг под другом. Запятые десятичных дробей так же должны стоять друг под другом.
- Если количество десятичных знаков у дробей различно, для удобства можно уравнять их число, приписав справа к десятичной дроби с меньшим количеством десятичных знаков необходимое число нулей.
- Не обращая внимание на запятые, выполнить сложение так, как выполняется сложение столбиком натуральных чисел.
- В полученной сумме поставить запятую так, чтобы она стояла под запятыми слагаемых.
Пример 1. Сложить числа 3,1 и 4,7.
Решение. Выполняем сложение так, как выполняется сложение столбиком натуральных чисел, не обращая внимание на запятые:
Пример 2.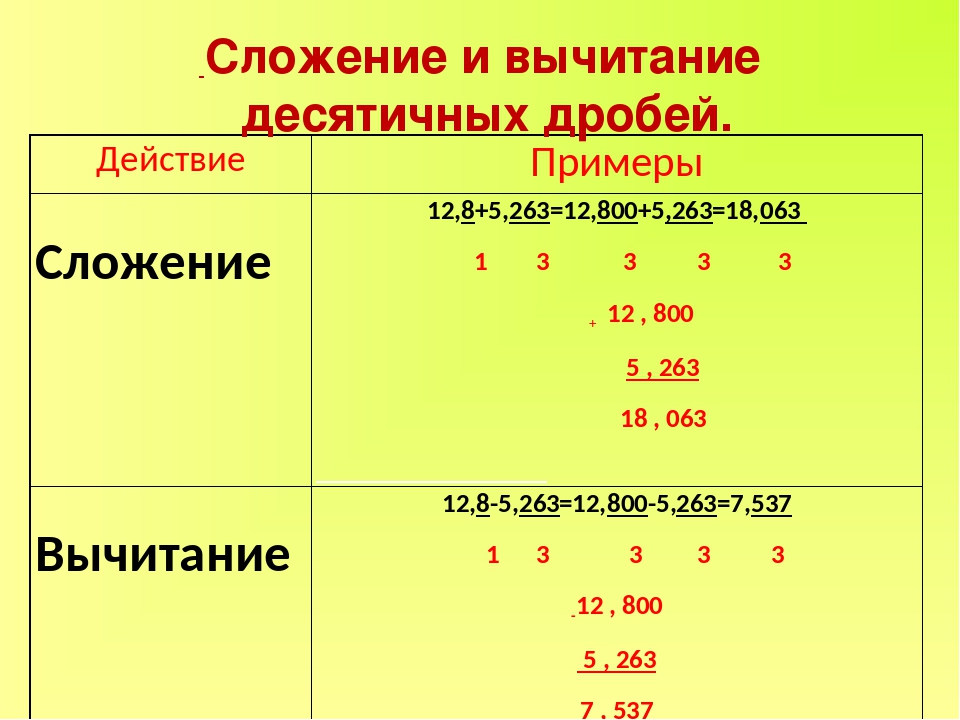 Сложить 3,45 и 7,368.
Сложить 3,45 и 7,368.
Решение. Выполняем сложение так, как выполняется сложение столбиком натуральных чисел. Для удобства, можно уравнять количество десятичных знаков в складываемых дробях:
Сложение десятичной дроби с натуральным числом
Правило сложения десятичных дробей с натуральными числами:
Чтобы сложить десятичную дробь и натуральное число, нужно данное натуральное число прибавить к целой части десятичной дроби, а дробную часть оставить без изменений.
Пример. Вычислить сумму 14,3 и 29.
Решение. Для удобства сложения, любое натуральное число можно представить в виде десятичной дроби. Для этого нужно поставить запятую после разряда единиц и приписать после запятой нужное количество нулей. Сложение выполняется по правилу сложения десятичных дробей столбиком:
Сложение десятичной дроби с обыкновенной дробью
Правило сложения десятичных дробей с обыкновенной дробью:
Сложение десятичной дроби с обыкновенной дробью сводится к сложению обыкновенных дробей. Для этого десятичная дробь переводится в обыкновенную дробь.
Для этого десятичная дробь переводится в обыкновенную дробь.
Что такое сложение и вычитание десятичных знаков?
Сложение и вычитание десятичных знаков
Десятичное число
Десятичное число — это дробь, знаменатель которой является степенью 10. Например, дробь 4 ⁄ 10 может быть записана в десятичной форме как 0,4, где:
Точка называется десятичной запятой.
Число справа от десятичной точки обозначает числитель дроби, то есть дробную часть.
Число слева от десятичной точки обозначает целую часть дроби.
Например, 4 3 ⁄ 10 выражается как 4,3, где 4 — это целая часть числа, а 0,3 — дробная часть.
Десятичная точка отделяет целую часть числа от дробной части.
Десятичные знаки в реальной жизни
Мы занимаемся сложением и вычитанием десятичных дробей в повседневной жизни, имея дело с:
десятичных знаков можно складывать или вычитать так же, как мы складываем или вычитаем целые числа.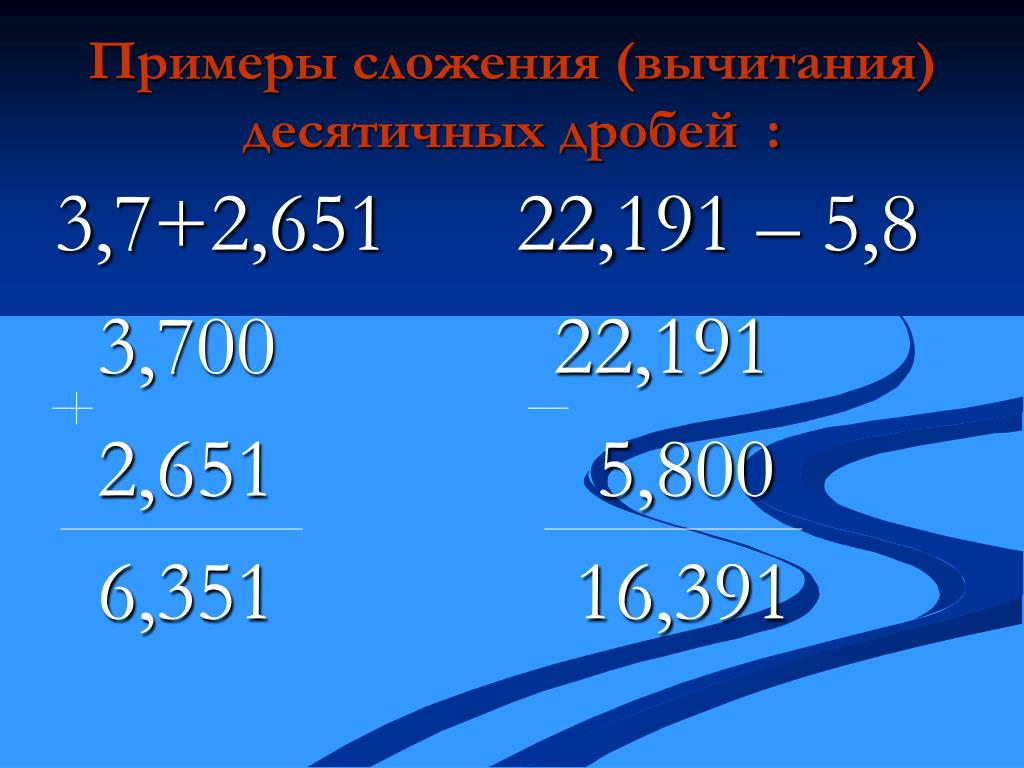
шагов для сложения или вычитания десятичных знаков:
Преобразует десятичные дроби в десятичные. (Десятичные дроби с одинаковым количеством цифр после запятой похожи на десятичные дроби).
Запишите десятичные дроби друг под другом в соответствии с местами цифр.
Добавляйте или вычитайте, начиная с крайней правой цифры и двигаясь к крайней левой цифре.
Поставьте десятичную точку под десятичной точкой в ответе.
Пример : прибавить 23,45; 13,101 и 345,5
1. Преобразовать в одинаковые десятичные числа : Наивысший десятичный разряд равен 3, поэтому мы добавляем нули в другие числа и получаем в них 3 десятичных разряда.
13.101
23,45 = 23,450
345,5 = 345,500
2. Выровнять десятичные знаки :
3. Добавить :
4. Место десятичной дроби в ответе :
Место десятичной дроби в ответе :
Пример : У Кайли было 25 м ленты. Для украшения юбки она использует 8 м и 13 см. Сколько ленты осталось у Кайли?
Решение :
Длина ленты у Кайли = 25 м = 25,00
Длина ленты Кайли = 8 м 13 см = 8,13
Оставшаяся длина ленты = 25,00 — 8,13
= 16.87
Интересные факты
|
Открытые учебники | Сиявула
Математика
Наука
- Читать онлайн
Учебники
Английский
Класс 7A
Марка 7Б
7 класс (A и B вместе)
Африкаанс
Граад 7А
Граад 7Б
Граад 7 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 8A
класс 8Б
Оценка 8 (вместе A и B)
Африкаанс
Граад 8А
Граад 8Б
Граад 8 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 9А
Марка 9Б
9 класс (A и B вместе)
Африкаанс
Граад 9А
Граад 9Б
Граад 9 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Класс 4A
Класс 4Б
Класс 4 (вместе A и B)
Африкаанс
Граад 4А
Граад 4Б
Граад 4 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 5А
Марка 5Б
Оценка 5 (вместе A и B)
Африкаанс
Граад 5А
Граад 5Б
Граад 5 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Класс 6A
класс 6Б
6 класс (A и B вместе)
Африкаанс
Граад 6А
Граад 6Б
Граад 6 (A en B saam)
Пособия для учителя
Наша книга лицензионная
Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.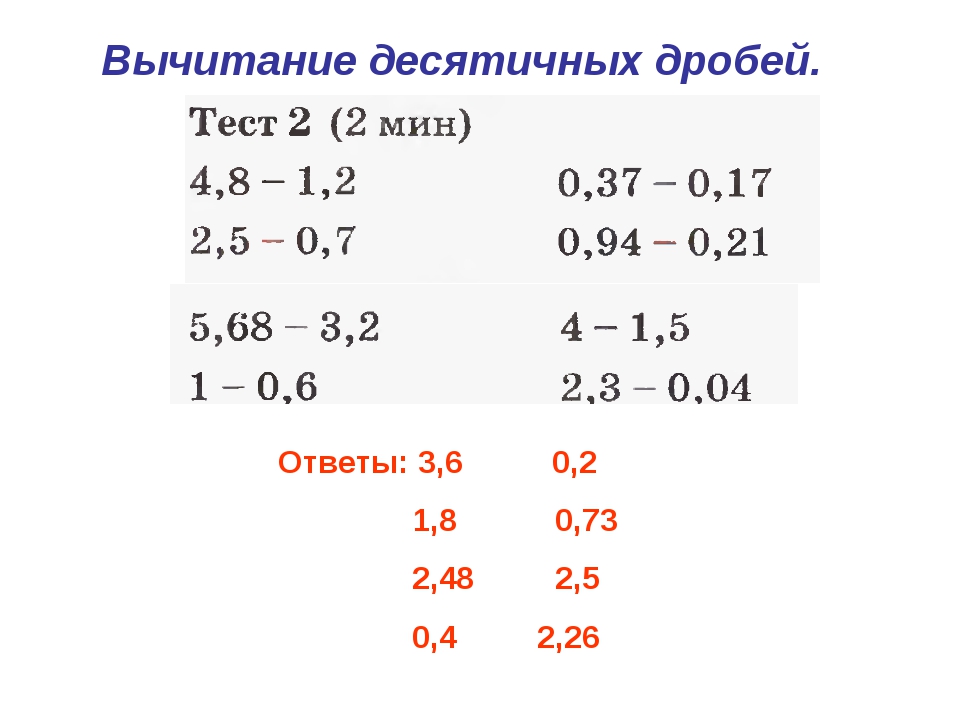 Вы можете делать ксерокопии, распечатывать и распространять их сколь угодно часто. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Вы можете делать ксерокопии, распечатывать и распространять их сколь угодно часто. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без марочного знака)
Эти небрендированные версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, модифицировать или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Как складывать десятичные дроби — определение, формула и примеры
В этом мини-уроке мы исследуем, как складывать десятичные дроби, выясняя, как складывать и вычитать десятичные дроби, а также методы, с помощью которых мы можем добавлять десятичные дроби к целым числам.
Но вот интересная мелочь: знаете ли вы, что греческий ученый Архимед (тот самый чувак, который пробежал через Сиракузы без одежды после того, как сделал одно из самых революционных открытий в физике) был человеком, который изобрел десятичную позиционную систему. Десятичное слово происходит от латинского слова decimus, означающего десятый. Следовательно, десятичная система имеет основу 10 и называется системой с основанием 10.
План урока Как складывать десятичные дроби? Прежде чем мы продолжим, давайте подведем итоги урока с десятичной дробью.
Можно применять все основные арифметические операции, сложение, вычитание, умножение и деление для десятичных знаков.
Добавление десятичных знаков показано ниже:
Мы узнаем о сложении и вычитании десятичных знаков в дальнейшем.
Важные примечания
- Мы всегда начинаем добавлять десятичные дроби с правой стороны, как в случае сложения двух чисел.
- Десятичные дроби всегда ставятся ниже десятичной точки.
Десятичные дроби добавляются следующим образом:
- Шаг 1: Запишите числа так, чтобы десятичные дроби были правильно выровнены.
- Шаг 2: Запишите нули там, где длина десятичных чисел не одинакова.
- Шаг 3: Теперь сложите десятичные числа и найдите результат сложения.
Давайте посмотрим на пример сложения десятичных знаков:
Добавить \ (8.6 \) и \ (2,8 \)- Шаг 1: Запишите числа так, чтобы десятичные дроби были правильно выровнены.

Цифры запишутся следующим образом:
- Шаг 2: Запишите нули там, где длина десятичных чисел не одинакова.
Этот шаг не применяется в данном случае, так как длина десятичных чисел такая же.
- Шаг 3: Теперь сложите десятичные числа и найдите результат для сложения.
Результатом сложения десятичных чисел является \ (11.4 \).
Советы и хитрости
- Сложение двух десятичных чисел может рассматриваться как сложение двух чисел изначально, а десятичное число может быть помещено в конце, чтобы избежать путаницы.
Узнайте о целых числах, прежде чем двигаться дальше.
Давайте посмотрим на несколько примеров сложения десятичных дробей с целыми числами.
Сложить \ (6.54 \) и \ (4 \)- Шаг 1: Запишите числа так, чтобы десятичные дроби были правильно выровнены.

Цифры запишутся следующим образом:
- Шаг 2: Поместите нули равными длине другого десятичного числа, что сделает его десятичным числом.
Поскольку 4 — это целое число, после десятичной дроби добавляются два нуля, теперь сложение будет выглядеть так:
- Шаг 3: Теперь сложите десятичные числа и найдите результат для сложения.
Результатом сложения десятичных чисел является \ (10.54 \).
Складываем \ (2.35 \) и \ (5 \)- Шаг 1: Запишите числа так, чтобы десятичные дроби были правильно выровнены.
Цифры запишутся следующим образом:
- Шаг 2: Поместите нули равными длине другого десятичного числа, что сделает его десятичным числом.
Поскольку 5 — это целое число, после десятичной дроби добавляются два нуля, теперь сложение будет выглядеть так:
- Шаг 3: Теперь сложите десятичные числа и найдите результат для сложения.

Результатом сложения десятичных чисел является \ (7.35 \).
сложить \ (13.24 \) и \ (25 \)- Шаг 1: Запишите числа так, чтобы десятичные дроби были правильно выровнены.
Цифры запишутся следующим образом:
- Шаг 2: Поместите нули равными длине другого десятичного числа, что сделает его десятичным числом.
Поскольку 25 — это целое число, после десятичной дроби добавляются два нуля, теперь сложение будет выглядеть так:
- Шаг 3: Теперь сложите десятичные числа и найдите результат для сложения.
Результатом сложения десятичных чисел является \ (38.24 \).
Посмотрите на симуляцию ниже:
Как складывать и вычитать десятичные дроби?
Сложение десятичных знаков
Мы научились добавлять десятичные дроби в разделе выше, давайте также посмотрим на их вычитание.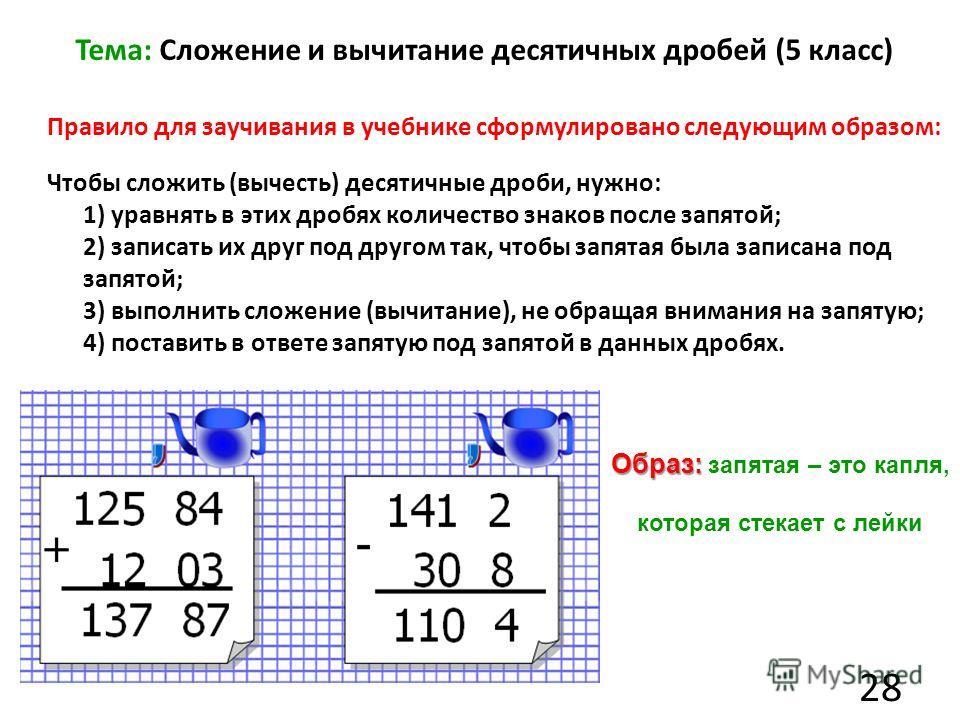
Вычитание десятичных знаков
Десятичные дроби вычитаются следующим образом:
- Шаг 1: Запишите числа так, чтобы десятичные дроби были правильно выровнены.
- Шаг 2: Запишите нули там, где длина десятичных чисел не одинакова.
- Шаг 3: Теперь вычтите десятичные числа и найдите результат для вычитания.
Давайте рассмотрим несколько примеров, чтобы лучше понять эту концепцию:
Вычесть \ (12.11 \) из \ (28.16 \)- Шаг 1: Запишите числа так, чтобы десятичные дроби были правильно выровнены.
Цифры запишутся следующим образом:
- Шаг 2: Запишите нули там, где длина десятичных чисел не одинакова.
Этот шаг не применяется в данном случае.
- Шаг 3: Теперь вычтите десятичные числа и найдите результат для вычитания.
Результат, полученный после вычитания десятичных чисел, равен \ (16. 05 \).
05 \).
- Шаг 1: Запишите числа так, чтобы десятичные дроби были правильно выровнены.
Цифры запишутся следующим образом:
- Шаг 2: Запишите нули там, где длина десятичных чисел не одинакова.
Это вычитание записывается как:
- Шаг 3: Теперь вычтите десятичные числа и найдите результат для вычитания.
Результат, полученный после вычитания десятичных чисел: \ (10.72 \)
Вычесть \ (10 \) из \ (18.56 \)- Шаг 1: Запишите числа так, чтобы десятичные дроби были правильно выровнены.
Цифры запишутся следующим образом:
- Шаг 2: Запишите нули там, где длина десятичных чисел не одинакова.
Это вычитание записывается как:
- Шаг 3: Теперь вычтите десятичные числа и найдите результат для вычитания.

Результат, полученный после вычитания десятичных чисел: \ (8.56 \)
Давайте посмотрим на симуляцию ниже:
Как складывать десятичные дроби с дробями?
Чтобы добавить десятичные дроби к дробям, выполните следующие действия:
- Шаг 1: Преобразуйте дробь в десятичную.
- Шаг 2: Запишите числа так, чтобы десятичные дроби были правильно выровнены.
- Шаг 3: Запишите нули там, где длина десятичных чисел не одинакова.
- Шаг 4: Теперь сложите десятичные числа и найдите результат сложения.
Давайте посмотрим на несколько примеров:
Добавить \ (7.28 \) к \ (\ dfrac {5} {8} \)- Шаг 1: Преобразуйте дробь в десятичную.
Дробь \ (\ frac {5} {8} \) в виде десятичной дроби записывается как \ (0.625 \)
- Шаг 2: Запишите числа так, чтобы десятичные дроби были правильно выровнены.

Цифры запишутся следующим образом:
- Шаг 3. Запишите нули там, где длина десятичных чисел не одинакова.
Это дополнение записывается как:
- Шаг 4: Теперь сложите десятичные числа и найдите результат для сложения.
Результатом сложения десятичного числа и дроби является \ (7.905 \).
Добавить \ (14.32 \) к \ (\ dfrac {1} {4} \)- Шаг 1: Преобразуйте дробь в десятичную.
Дробь \ (\ frac {1} {4} \) в виде десятичной дроби записывается как \ (0,25 \)
- Шаг 2: Запишите числа так, чтобы десятичные дроби были правильно выровнены.
Цифры запишутся следующим образом:
- Шаг 3. Запишите нули там, где длина десятичных чисел не одинакова.
Этот шаг здесь не применяется, так как длина числа после десятичной дроби такая же.
- Шаг 4: Теперь сложите десятичные числа и найдите результат для сложения.

Результат, полученный после сложения десятичного числа и дроби: \ (14.57 \)
Решенные примеры
Учитель Уильяма и Венди попросил их сложить 20,62 и 13,01 и найти ответ.Какой ответ они должны получить после сложения обоих чисел?
Решение
Они будут следовать приведенным ниже инструкциям, чтобы найти ответ:
- Шаг 1: Запишите числа так, чтобы десятичные дроби были правильно выровнены.
Цифры запишутся следующим образом:
- Шаг 2: Запишите нули там, где длина десятичных чисел не одинакова.
Этот шаг не применяется в данном случае, так как длина десятичных чисел такая же.
- Шаг 3: Теперь сложите десятичные числа и найдите результат для сложения.
Результат, полученный после сложения десятичных чисел: \ (33.63 \)
\ (\ поэтому \) Ответ \ (33. 63 \) 63 \) |
Как Шон вычтет 11,82 из 28,61? Помогите ему найти ответ.
Решение
Шон будет использовать следующие шаги, чтобы получить свой ответ:
- Шаг 1: Запишите числа так, чтобы десятичные дроби были правильно выровнены.
Цифры запишутся следующим образом:
- Шаг 2: Запишите нули там, где длина десятичных чисел не одинакова.
Этот шаг не применяется в данном случае, так как длина десятичных чисел такая же.
- Шаг 3: Теперь вычтите десятичные числа и найдите результат для вычитания.
Результатом сложения десятичных чисел будет \ (16.79 \)
| \ (\ поэтому \) Ответ: \ (16.79 \) |
Интерактивные вопросы
Вот несколько занятий для вас.
Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итоги
Надеемся, вам понравилось узнать, как добавлять десятичные дроби в практических вопросах.Теперь вы сможете легко найти ответы на вопросы, например, как складывать и вычитать десятичные дроби и как складывать десятичные дроби с целыми числами.
О компании CuemathВ Cuemath наша команда математиков стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу к обучению-обучению-обучению учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению.
Часто задаваемые вопросы (FAQ)
1.
 Как складывать и вычитать десятичные дроби?
Как складывать и вычитать десятичные дроби?Чтобы добавить десятичные дроби, выполните следующие действия:
Шаг 1: Запишите числа так, чтобы десятичные дроби были правильно выровнены.
Шаг 2: Запишите нули в тех местах, где длина десятичных чисел не одинакова.
Шаг 3: Теперь сложите десятичные числа и найдите результат для сложения.
Чтобы вычесть десятичные дроби, выполните следующие действия:
Шаг 1: Запишите числа так, чтобы десятичные дроби были правильно выровнены.
Шаг 2: Запишите нули в тех местах, где длина десятичных чисел не одинакова.
Шаг 3: Теперь вычтите десятичные числа и найдите результат для вычитания.
2. Как складывать десятичные дроби с целыми числами?
Чтобы добавить десятичные дроби к целым числам:
Шаг 1: Запишите числа так, чтобы десятичные дроби были правильно выровнены.
Шаг 2: Поместите нули равными длине другого десятичного числа, что сделает его десятичным числом.
Шаг 3: Теперь сложите десятичные числа и найдите результат для сложения.
Добавление десятичных знаков
Добавить десятичные дроби легко, если работа ведется аккуратно
Чтобы добавить десятичные дроби, выполните следующие действия:
- Запишите числа друг под другом, выровняв десятичных знаков
- Введите нули , чтобы числа имели одинаковую длину (почему это нормально, см. Ниже)
- Затем добавьте , используя сложение столбцов, не забывая поставить десятичную точку в ответе
Пример: прибавить 1.452 до 1,3
| Выровняйте десятичные точки: | 1.452 | ||
| + | 1,3 | ||
| «Pad» с нулями: | 1.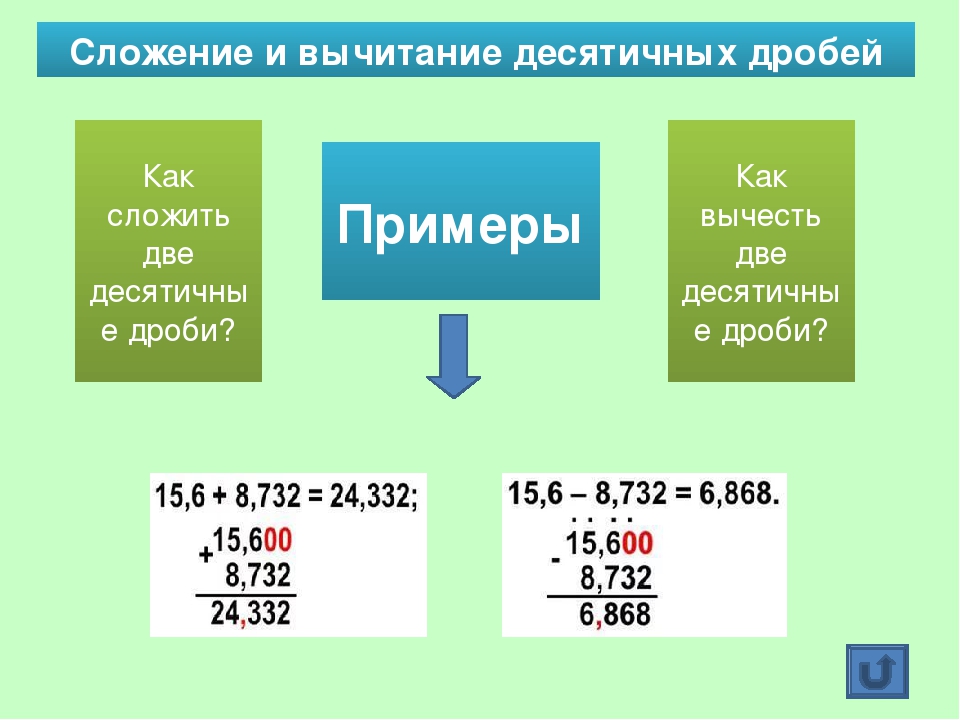 452 452 | ||
| + | 1.300 | ||
| Добавить: | 1.452 | ||
| + | 1,300 | ||
| 2,752 |
Пример: сложить 3,25, 0,075 и 5
| Выровняйте десятичные точки: | 3.25 | ||
| 0,075 | |||
| + | 5. | ||
| «Pad» с нулями: | 3,250 | ||
| 0,075 | |||
| + | 5.000 | ||
| Добавить: | 3,250 | ||
| 0,075 | |||
| + | 5.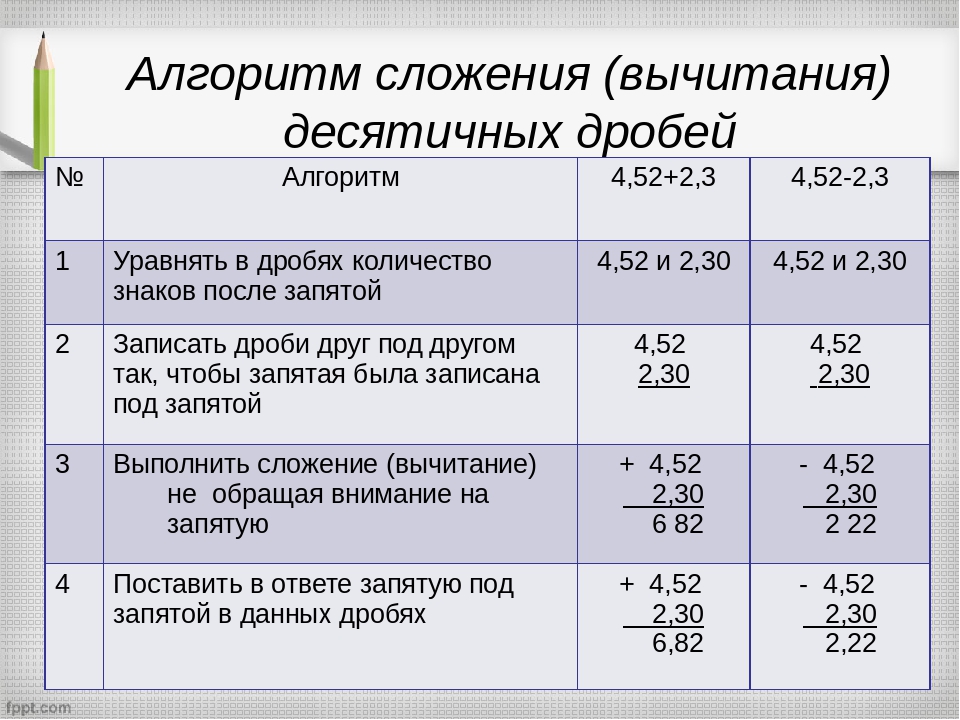 000 000 | ||
| 8,325 |
Вот и все: выровняйте десятичные точки, заполните нулями и сложите как обычно.
Вычитание
Чтобы вычесть, следуйте тому же методу: выровняйте десятичные точки, затем вычтите.
Пример: что такое 7,368–1,15?
| Выровняйте десятичные точки: | 7,368 | ||
| – | 1,15 | ||
| «Pad» с нулями: | 7.368 | ||
| – | 1,150 | ||
| Вычесть: | 7,368 | ||
| – | 1,150 | ||
| 6,218 |
Чтобы проверить , мы можем добавить ответ к вычитаемому числу:
Пример: проверьте, что 7.
 368 минус 1,15 равно 6,218
368 минус 1,15 равно 6,218Попробуем прибавить 6,218 к 1,15
| Выровняйте десятичные точки: | 6,218 | ||
| + | 1,15 | ||
| «Pad» с нулями: | 6.218 | ||
| + | 1,150 | ||
| Добавить: | 6,218 | ||
| + | 1,150 | ||
| 7,368 |
Он совпадает с номером, с которого мы начали, поэтому проверяется.
Ввод нулей
Почему можно ставить лишние нули?
Ноль на самом деле означает, что в этом десятичном разряде нет значения.
- В таком числе, как 10, ноль означает «нет»
- В таком числе, как 2,50, ноль означает «без сотых»
Так что можно безопасно взять число, например 2,5, и сделать его 2,50 или 2,500 и т. Д.
Д.
Но НЕ Берите 2,5 и не делайте это 20,5, это совершенно неправильно.
3.3: Объединение десятичных знаков — сложение и вычитание с десятичными знаками
Добавление десятичных знаков
Сложение десятичных чисел очень похоже на сложение целых чисел. Например, предположим, что нас просят добавить 2,34 и 5,25. Мы можем изменить эти десятичные числа на , смешанные дроби и сложить.
\ [\ begin {выровнено} 2,34 + 5,25 & = 2 \ frac {34} {100} + 5 \ frac {25} {100} \\ & = 7 \ frac {59} {100} \ end {выровнено} \ nonumber \]
Однако мы также можем выровнять десятичные числа по десятичным точкам и сложить по вертикали, как показано ниже.
\ [\ begin {массив} {r} 2.34 \\ + 5.25 \\ \ hline 7.59 \ end {array} \ nonumber \]
Обратите внимание, что эта процедура выравнивания дает тот же результат: «семь и пятьдесят девять сотых». Это мотивирует следующую процедуру сложения десятичных чисел.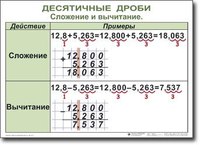
Добавление десятичных знаков
Чтобы добавить десятичные числа, действуйте следующим образом:
- Разместите добавляемые числа в вертикальном формате, выравнивая десятичные точки.
- Сложите числа, как если бы они были целыми числами.
- Разместите десятичную точку в ответе в том же столбце, что и десятичные точки над ней.
Пример 1
Складываем 3,125 и 4,814.
Решение
Поместите числа в вертикальном формате, выровняв их по десятичным точкам. Добавьте, а затем поместите десятичную точку в ответе в тот же столбец, что и десятичные точки, которые появляются над ответом.
\ [\ begin {array} {r} 3.125 \\ +4.814 \\ \ hline 7.939 \ end {array} \ nonumber \]
Таким образом, 3.125 + 4,814 = 7,939.
Упражнение
Добавить: 2.864 + 3.029
- Ответ
5,893
Пример 2
У Джейн в кошельке 4,35 доллара. У Джима в кошельке 5,62 доллара. Если они суммируют свои деньги, какова общая сумма?
У Джима в кошельке 5,62 доллара. Если они суммируют свои деньги, какова общая сумма?
Решение
Расположите числа в вертикальном формате, выравнивая десятичные точки, затем сложите.
\ [\ begin {array} {r} \ $ 4.35 \\ + \ $ 5.62 \\ \ hline \ $ 9.97 \ end {array} \ nonumber \]
Упражнение
У Алисы в кошельке 8,63 доллара, а у Джоанны — 2,29 доллара. Если они объединят свои деньги, какова общая сумма?
- Ответ
$ 10.91
Прежде чем перейти к другому примеру, напомним одно важное наблюдение.
Важное замечание
Добавление нулей в конец дробной части десятичного числа не меняет его значения.Точно так же удаление завершающих нулей в конце десятичного числа не меняет его значения.
Например, мы могли бы добавить два нуля в конце дробной части 7,25, чтобы получить 7,2500. Числа 7.25 и 7.2500 идентичны, как показывает следующий аргумент:
\ [\ begin {align} 7. 2500 & = 7 \ frac {2500} {10000} \\ & = 7 \ frac {25} {100} \\ & = 7.25 \ end {выравнивается} \ nonumber \]
2500 & = 7 \ frac {2500} {10000} \\ & = 7 \ frac {25} {100} \\ & = 7.25 \ end {выравнивается} \ nonumber \]
Пример 3
Складываем 7.5 и 12.23.
Решение
Расположите числа в вертикальном формате, выровняв их десятичные точки в столбце.Обратите внимание, что мы добавляем завершающий ноль, чтобы улучшить выравнивание по столбцам.
\ [\ begin {массив} {r} 7.50 \\ +12.23 \\ \ hline 19.73 \ end {array} \ nonumber \]
Следовательно, 7,5 + 12,23 = 19,73.
Упражнение
Добавить: 9.7 + 15.86
- Ответ
25,56
Пример 4
Найдите сумму: 12,2 + 8,352 + 22,44.
Решение
Расположите числа в вертикальном формате, выровняв их десятичные точки в столбце.Обратите внимание, что мы добавляем нули в конце, чтобы улучшить выравнивание по столбцам.
\ [\ begin {array} {r} 12. 200 \\ 8.352 \\ + 22.440 \\ \ hline 42.992 \ end {array} \ nonumber \]
200 \\ 8.352 \\ + 22.440 \\ \ hline 42.992 \ end {array} \ nonumber \]
Следовательно, 12,2 + 8,352 + 22,44 = 42,992.
Упражнение
Добавить: 12.9 + 4.286 + 33.97
- Ответ
51.156
Вычитание десятичных знаков
Вычитание десятичных чисел происходит почти так же, как и сложение десятичных чисел.
Вычитание десятичных знаков
Чтобы вычесть десятичные числа, действуйте следующим образом:
- Поместите числа для вычитания в вертикальном формате, выравнивая десятичные точки.
- Вычтите числа, как если бы они были целыми числами.
- Разместите десятичную точку в ответе в том же столбце, что и десятичные точки над ней.
Пример 5
Вычтем 12,23 из 33,57.
Решение
Расположите числа в вертикальном формате, выровняв их десятичные точки в столбце, а затем вычтите. Обратите внимание, что мы вычитаем 12,23 из 33,57.
Обратите внимание, что мы вычитаем 12,23 из 33,57.
\ [\ begin {массив} {r} 33,57 \\ -12,23 \\ \ hline 21,34 \ end {array} \ nonumber \]
Следовательно, 33,57 — 12,23 = 21,34.
Упражнение
Вычесть: 58,76 — 38,95
- Ответ
19,81
Как и при сложении, мы добавляем конечные нули к дробной части десятичных чисел, чтобы облегчить выравнивание по столбцам.
Пример 6
Найдите разницу: 13.3 — 8,572.
Решение
Расположите числа в вертикальном формате, выровняв их десятичные точки в столбце. Обратите внимание, что мы добавляем нули в конце дробной части 13,3, чтобы улучшить выравнивание по столбцам.
\ [\ begin {array} {r} 13.300 \\ -8.572 \\ \ hline 4.728 \ end {array} \ nonumber \]
Следовательно, 13,3 — 8,572 = 4,728.
Упражнение
Вычесть: 15,2 — 8,756
- Ответ
6.
 444
444
Сложение и вычитание десятичных чисел со знаком
Мы используем те же правила для сложения десятичных чисел со знаком, что и для сложения целых чисел.
Сложение двух десятичных знаков с одинаковыми знаками
Чтобы добавить два десятичных знака с одинаковыми знаками, действуйте следующим образом:
- Сложите величины десятичных чисел.
- Префикс общего знака.
Пример 7
Упростить: −3,2 + (- 18,95).
Решение
Чтобы добавить одинаковые знаки, сначала добавьте величины.
\ [\ begin {array} {r} 3.20 \\ +18.95 \\ \ hline 22.15 \ end {array} \ nonumber \]
Префикс общего знака. Следовательно, −3,2 + (- 18,95) = −22,15
.Упражнение
Упростить: -5,7 + (-83,85)
- Ответ
−89,55
Мы используем то же правило, что и для целых чисел, добавляя десятичные дроби с разными знаками.
Сложение двух десятичных знаков с разными знаками
Чтобы добавить два десятичных знака с разными знаками, действуйте следующим образом:
- Вычтите меньшую звездную величину из большей.
- Префикс знака десятичного числа с большей величиной.
Пример 8
Упростить: −3 + 2,24.
Решение
Чтобы добавить непохожие знаки, сначала вычтите меньшую величину из большей.
\ [\ begin {array} {r} 3.00 \\ -2,24 \\ \ hline 0,76 \ end {array} \ nonumber \]
Префикс знака десятичного числа с большей величиной. Следовательно, −3 + 2.24 = −0.76.
Упражнение
Упростить: −8 + 5,74
- Ответ
-2,26
Вычитание по-прежнему означает прибавить противоположное .
Пример 9
Упростить: −8,567 — (−12,3).
Решение
Вычитание сначала нужно заменить на сложение, добавив противоположное.
\ [- 8,567 — (-12,3) = -8,567 + 12,3 \ nonumber \]
У нас есть непохожие знаки. Во-первых, вычтите меньшую величину из большей.
\ [\ begin {array} {r} 12.300 \\ — 8.567 \\ \ hline 3.733 \ end {array} \ nonumber \]
Префикс знака десятичного числа с большей величиной. Отсюда:
\ [\ начало {выровнено} -8,567 — (-12,3) & = -8,567 + 12,3 \\ & = 3,733 \ конец {выровнено} \ nonumber \]
Упражнение
Упростить: −2.384 — (−15,2)
- Ответ
12,816
Порядок операций требует, чтобы мы сначала упростили выражения, содержащиеся в круглых скобках.
Пример 10
Упростить: −11,2 — (−8,45 + 2,7).
Решение
Сначала нужно добавить в круглые скобки. Поскольку у нас разные знаки, вычтите меньшую величину из большей.
\ [\ begin {array} {r} 8.45 \\ — 2.70 \\ \ hline 5.75 \ end {array} \ nonumber \]
Префикс знака числа с большей величиной. Следовательно,
Следовательно,
\ [- 11,2 — (−8,45 + 2,7) = −11,2 — (−5,75) \ nonumber \]
Вычитание означает сложение противоположного.
\ [- 11,2 — (−5,75) = −11,2 + 5,75 \ nonumber \]
Опять же, у нас непохожие знаки. Вычтите меньшую величину из большей.
\ [\ begin {array} {r} 11.20 \\ — 5.75 \\ \ hline 5.45 \ end {array} \ nonumber \]
Префикс знака числа с большой величиной.
\ [-11,2 + 5,75 = -5,45 \ nonumber \]
Упражнение
Упростить: −12,8 — (−7,44 + 3,7)
- Ответ
−9,06
Письмо по математике
Решение предыдущего примера должно быть записано следующим образом:
\ [\ begin {выровнено} -11,2 — (-8,45 + 2,7) & = -11,2 — (-5,75) \\ & = -11,2 + 5,75 \\ & = -5,45 \ конец {выровнено} \ nonumber \]
Любая скретч-работа, такая как вычисления в вертикальном формате в предыдущем примере, должна выполняться на полях или в блокноте.
Пример 11
Упростить: −12,3 — | — 4,6 — (−2,84) |.
Решение
Сначала мы упрощаем выражение внутри столбцов абсолютного значения, берем абсолютное значение результата, затем вычитаем.
\ [\ begin {align} -12,3 — | -4,6 — (- 2,84) | ~ \\ = -12,3 — | -4,6 + 2,84 | ~ & \ textcolor {red} {\ text {Добавьте противоположное.}} \\ = -12,3 — | -1,76 | ~ & \ textcolor {красный} {\ text {Добавить:} -4,6 + 2,84 = -1,76.} \\ = -12,3-1,76 ~ & \ textcolor {красный} {| -1.76 | = 1.76.} \\ = -12.3 + (-1.76) ~ & \ textcolor {red} {\ text {Добавить противоположное.}} \\ = -14.06 ~ & \ textcolor {red} {\ text {Добавить :} -12,3 + (-1,76) = -14,06.} \ End {выровнено} \ nonumber \]
Упражнение
Упростить: −8,6 — | — 5,5 — (−8,32) |
- Ответ
−11,42
Упражнения
В упражнениях 1–12 сложите десятичные дроби.
1. \ (31. 9 + 84.7 \)
9 + 84.7 \)
2. \ (9.39 + 7.7 \)
3.\ (4 + 97,18 \)
4. \ (2.645 + 2.444 \)
5. \ (4 + 87.502 \)
6. \ (23,69 + 97,8 \)
7. \ (95,57 + 7,88 \)
8. \ (18.7 + 7 \)
9. \ (52.671 + 5.97 \)
10. \ (9.696 + 28.2 \)
11. \ (4,76 + 2,1 \)
12. \ (1,5 + 46,4 \)
В упражнениях 13-24 вычтите десятичные дроби.
13. \ (9 — 2.261 \)
14. \ (98,14 — 7,27 \)
15. \ (80.9 — 6 \)
16.\ (9,126 — 6 \)
17. \ (55,672 — 3,3 \)
18. \ (4,717 — 1,637 \)
19. \ (60,575 — 6 \)
20. \ (8.91 — 2.68 \)
21. \ (39,8 — 4,5 \)
22. \ (8,210 — 3,7 \)
23. \ (8.1 — 2.12 \)
24. \ (7,675 — 1,1 \)
В упражнениях 25–64 складывайте или вычитайте десятичные дроби, как показано.
25. \ (- 19,13 — 7 \)
26. \ (- 8 — 79,8 \)
27. \ (6,08 — 76,8 \)
28. \ (5,76 — 36,8 \)
\ (5,76 — 36,8 \)
29. \ (- 34,7 + (- 56,214) \)
30. \ (- 7,5 + (- 7,11) \)
31. \ (8,4 + (- 6,757) \)
32. \ (- 1,94 + 72,85 \)
33. \ (- 50,4 + 7,6 \)
34. \ (1,4 + (- 86,9) \)
35. \ (- 43,3 + 2,2 \)
36. \ (0,08 + (-2,33) \)
37. \ (0,19 — 0,7 \)
38. \ (9 — 18.01 \)
39. \ (- 7 — 1,504 \)
40. \ (- 4,28 — 2,6 \)
41. \ (- 4.47 + (−2) \)
42. \ (- 9 + (- 43.67) \)
43. \ (71,72 — (−6) \)
44. \ (6 — (−8,4) \)
45. \ (- 9,829 — (-17,33) \)
46. \ (- 95,23 — (-71,7) \)
47. \ (2.001 — 4.202 \)
48. \ (4 — 11.421 \)
49. \ (2,6 — 2,99 \)
50. \ (3,57 — 84,21 \)
51. \ (- 4.560 — 2.335 \)
52. \ (- 4,95 — 96,89 \)
53. \ (- 54,3 — 3,97 \)
54. \ (- 2 — 29.285 \)
55. \ (- 6,32 + (-48,663) \)
56.\ (- 8,8 + (- 34,27) \)
57. \ (- 8 — (−3,686) \)
\ (- 8 — (−3,686) \)
58. \ (- 2,263 — (-72,3) \)
59. \ (9,365 + (−5) \)
60. \ (- 0,12 + 6,973 \)
61. \ (2,762 — (−7,3) \)
62. \ (65,079 — (-52,6) \)
63. \ (- 96,1 + (- 9,65) \)
64. \ (- 1.067 + (−4.4) \)
В упражнениях 65–80 упростите данное выражение.
65. \ (- 12,05 — | 17,83 — (-17,16) | \)
66. \ (15,88 — | — 5,22 — (-19,94) | \)
67.\ (- 6.4 + | 9.38 — (−9.39) | \)
68. \ (- 16,74 + | 16,64 — 2,6 | \)
69. \ (- 19,1 — (1,51 — (−17,35)) \)
70. \ (17,98 — (10,07 — (−10,1)) \)
71. \ (11,55 + (6,3 — (-1,9)) \)
72. \ (- 8,14 + (16,6 — (-15,41)) \)
73. \ (- 1,7 — (1,9 — (−16,25)) \)
74. \ (- 4,06 — (4,4 — (-10,04)) \)
75. \ (1,2 + | 8,74 — 16,5 | \)
76. \ (18,4 + | 16,5 — 7,6 | \)
77. \ (- 12,4 — | 3,81 — 16,4 | \)
78.\ (13,65 — | 11,55 — (−4,44) | \)
79. \ (- 11,15 + (11,6 — (-16,68)) \)
\ (- 11,15 + (11,6 — (-16,68)) \)
80. \ (8,5 + (3,9 — 6,98) \)
81. Крупные банки . Рыночная капитализация четырех крупнейших банков страны (по состоянию на 23 апреля 2009 г.)
| JPMorgan Chase & Co | 124,8 миллиарда долларов |
| Wells Fargo & Co | 85,3 миллиарда долларов |
| Goldman Sachs Group Inc. | 61,8 миллиарда долларов |
| Банк Америки | 56,4 миллиарда долларов |
Какова общая стоимость четырех крупнейших банков страны? Associated Press Times-Standard 22.04.09
82. Зеркало телескопа. Недавно запущенный телескоп Herschel имеет зеркало диаметром 11,5 футов, а зеркало Хаббла — 7,9 футов в диаметре. Насколько больше по диаметру зеркало Гершеля, чем зеркало Хаббла?
83.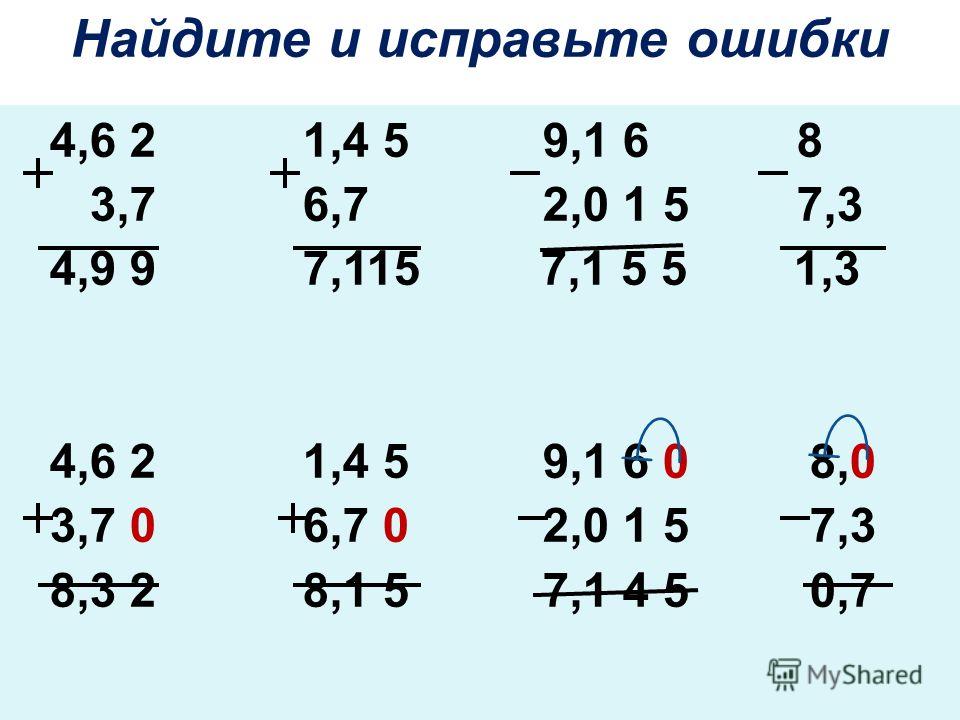 Средняя температура . Средние температуры в Сакраменто, штат Калифорния, в июле — высокая дневная температура 93,8 градуса по Фаренгейту и низкая ночная температура 60,9 градусов по Фаренгейту. Как меняется температура днем и ночью? Подсказка: См. Раздел 2.3, где приведена формула для сравнения температур.
Средняя температура . Средние температуры в Сакраменто, штат Калифорния, в июле — высокая дневная температура 93,8 градуса по Фаренгейту и низкая ночная температура 60,9 градусов по Фаренгейту. Как меняется температура днем и ночью? Подсказка: См. Раздел 2.3, где приведена формула для сравнения температур.
84. Средняя температура . Средние температуры в июле в Реддинге, штат Калифорния, представляют собой высокую дневную температуру 98,2 градуса по Фаренгейту и низкую ночную температуру 64.9 градусов по Фаренгейту. Как меняется температура днем и ночью? Подсказка: См. Раздел 2.3, где приведена формула для сравнения температур.
85. Собственный капитал . Чистая стоимость активов определяется как активы за вычетом обязательств. Активы — это все, что может быть конвертировано в наличные, а обязательства — это все долги. General Growth Properties, владельцы торгового центра Bayshore Mall, владеют активами на 29,6 млрд долларов и обязательствами на 27 млрд долларов и обанкротились.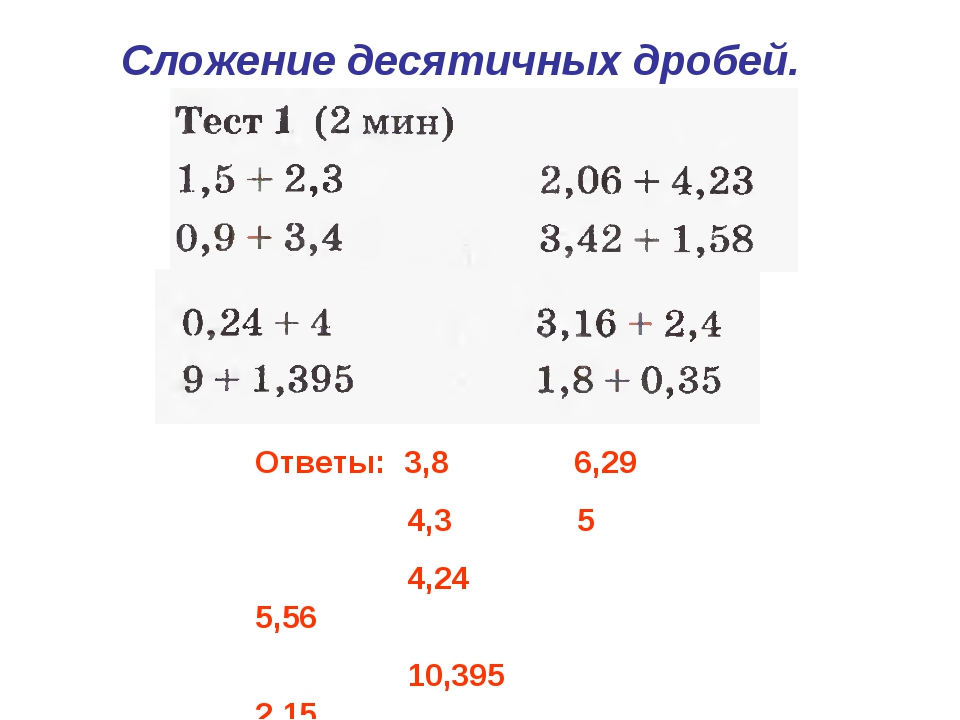 Какова была чистая стоимость активов General Growth Properties до банкротства? Times-Standard 17.04.2009
Какова была чистая стоимость активов General Growth Properties до банкротства? Times-Standard 17.04.2009
86. Виноградная дробленка . Предварительный отчет Калифорнийского министерства продовольствия и сельского хозяйства показывает, что в 2009 году в штате было произведено 3,69 миллиона тонн винного винограда. Это всего лишь меньше рекордных 3,76 миллиона тонн в 2005 году. На сколько тонн меньше рекорда был разгром 2009 года? Associated Press-Times-Standard Calif. Урожай винограда в 2009 году подскочил на 23%.
87. Оборот . Обследование вакансий и текучести кадров Департамента труда утверждает, что работодатели наняли около 4 человек.08 миллионов человек в январе 2010 года, в то время как 4,12 миллиона человек были уволены или иным образом уволились с работы. Насколько больше людей потеряли работу, чем были наняты? Преобразуйте свой ответ в целое число. Associated Press-Times-Standard 03/10/10 Количество вакансий резко увеличилось в январе до 2,7 млн.
Объединение десятичных знаков и дробей — элементарная математика
Представьте, что вам нужно решить следующую задачу сложения, в которой объединяет десятичные дроби и дроби:
Не так-то просто прибавить дробь к десятичной, правда? Гораздо проще добавлять дроби к дробям или десятичные дроби к десятичным.Итак, мы можем сделать это двумя способами:
- Измените десятичную дробь на дробь .
- Измените дробь на десятичную дробь .
Сегодня мы научимся делать первый вариант: заменить десятичные дроби на дроби . Для начала вам нужно узнать, как найти эквивалентные дроби.
В любом случае, в этом посте мы сделаем быстрый обзор поиска эквивалентных дробей:
Поиск эквивалентных дробей
Пример: Вот наша дробь…
И мы хотим сделать его знаменателем число 6, или другими словами:
Вы должны спросить себя, на какое число можно умножить 3 (знаменатель), чтобы получить 6… вот и все! Его умножили на 2.
Значит, числитель тоже нужно умножить на 2.
Если мы умножим 2 на 2, получим 4.
Хорошо, теперь, когда вы знаете, как найти эквивалентную дробь, мы собираемся заменить десятичную дробь на дробь.
Преобразование десятичной дроби в дробь
Допустим, у нас есть номер…
Как это сделать дробью? Мы собираемся следовать этой стратегии здесь, но сначала мы должны спросить себя, какой знаменатель имеет число… какой знаменатель может иметь любое число, которое позволило бы ему оставаться неизменным?… Вот и все! Число 1.
Теперь мы должны спросить себя, какое число нам нужно поставить в знаменатель эквивалентной дроби? Уловка состоит в том, чтобы использовать 1 и ставить после нее нули. Итак, первое, что мы сделаем, это попробуем с одним нулем, 10.
Поскольку мы должны умножить 1 на 10, чтобы получить 10, нам также нужно умножить 0,25 (числитель) на 10.
И мы остались с….
Мы еще не избавились от всех десятичных знаков, верно? Тогда давайте продолжим добавлять нули!
Если мы умножим на 100, у нас останется:
Хорошо, помните, что дроби можно упрощать.Если упростить эту дробь, у нас останется
Итак…
И все! Мы преобразовали десятичную дробь в дробь благодаря эквивалентным дробям.
Обзор
Подумайте, сколько нулей нам нужно было добавить после 1, чтобы избавиться от всех десятичных знаков в 0,25? В нем было два десятичных знака, и мы добавили к нему два нуля, или, говоря словами, по одному нулю для каждого десятичного знака, который у него был. Итак, каждый ноль отменяет один десятичный знак!
Подводя итог, когда мы хотим преобразовать десятичную дробь в дробь, мы должны:
- Заменить десятичную дробь на дробь больше 1.Итак, десятичная дробь будет числителем, а 1 — знаменателем.

- Найдите эквивалентную дробь. В знаменателе этой дроби будет 1 и столько нулей, сколько десятичных знаков в преобразуемом числе.
- Умножьте десятичную дробь на знаменатель эквивалентной дроби.
- Просто дробь.
А теперь вернемся к проблеме, которую мы видели в начале этого поста!
Затем,
Далее,
Теперь упрощаем,
Теперь проблема решена!
Я оставлю вам несколько ресурсов, которые вы можете использовать для анализа и практики:
А в Smartick вы найдете еще много упражнений.
Подробнее:
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
Вычисления, дроби, десятичные знаки и проценты
Вычисления, дроби, десятичные знаки и проценты Вычисления, дроби, десятичные дроби и проценты
Щелкните здесь, чтобы просмотреть указатель глоссария!
обыкновенные дроби
Состоит из двух чисел, разделенных горизонтальной или диагональной линией:
Знаменатель
нижнее число:
Указывает количество частей, на которые одна (1) делится
Числитель
Верхний номер:
Указывает количество тех частей, которые нас интересуют
Например, дробь половина, записанная как 1/2, означает, что одна была разделена на две части, поскольку нас интересует одна из этих двух частей. Дробь 3/4 означает, что одна была разделена на четыре части, и нас интересуют три из этих четырех частей
Дробь 3/4 означает, что одна была разделена на четыре части, и нас интересуют три из этих четырех частей
Правильные дроби
Числитель меньше знаменателя
1 = числитель
2 = знаменатель
3 = числитель
4 = знаменатель
Неправильные дроби
Числитель больше знаменателя
Происходит, когда дробь имеет значение больше 1
6 = числитель
5 = знаменатель
Здесь дробь имеет большее значение, чем 1
При работе с дробями полезно принять к сведению некоторые общие принципы, касающиеся того, что происходит, когда вы выполняете определенные математические операции с числителями и знаменателями.(Обратите внимание, что ниже мы внимательно указываем, что множитель или делитель больше (> 1). В каждом случае, если это число меньше единицы (<1), мы получаем противоположный результат.)
Операции с числителями
Если умножить числитель на число> 1, значение дроби увеличится
Если вы разделите числитель на число> 1, значение дроби уменьшится
Операции со знаменателями
Если знаменатель умножить на число> 1, значение дроби уменьшится
Если делить знаменатель на число> 1, значение дроби увеличивается
Операции над числителем и знаменателем
Общие принципы с дробями:
Если умножить числитель и знаменатель на одно и то же число, значение дроби останется прежним
Если вы разделите числитель и знаменатель на одно и то же число, значение дроби останется прежним
Эта информация пригодится при работе с дробями, поскольку позволяет выполнять определенные математические операции с дробями, когда вам необходимо изменить форму дроби. Различные примеры, приведенные ниже, иллюстрируют этот момент.
Различные примеры, приведенные ниже, иллюстрируют этот момент.
В аптеке от нас часто требуется выполнять математические операции с дробью. Наиболее распространенные операции проиллюстрированы ниже:
Сложение дробей
Сложите числа, знаменатели останутся прежними
Пример: сложение дробей (02040010)
Чтобы знаменатель оставался неизменным, он должен быть одинаковым для обеих добавляемых дробей.
Что делать, если знаменатели другие?
Пример: добавление разных знаменателей (02040020)
В этом случае можно применить принцип, который гласит, что если вы умножаете числитель и знаменатель на одно и то же число, значение дроби остается неизменным.Дробь 1/4 может быть заменена на дробь с тем же значением, но со знаменателем 8, умножив числитель и знаменатель фракции на число 2.
Сделайте знаменатели одинаковыми, умножив числитель и знаменатель на одно и то же число (см. Общие принципы)
Пример: общий знаменатель — 1 (02040030)
Заменить эту новую дробь, затем прибавить:
Пример: общий знаменатель — 2 (02040040)
Иногда формы обеих фракций должны быть изменены.
В этом случае ближайший общий знаменатель равен 12, поэтому числитель и знаменатель дроби 1/4 должны быть умножены на 3, чтобы получить 3/12, а числитель и знаменатель дроби 2/3 должны быть умножены на 4. сделать ставку 8/12
Тогда можно произвести сложение
Пример: сложение дробей (02040050)
Вычитание дробей
Вычитание дробей очень похоже на сложение дробей
Вычтем числители, знаменатель останется прежним
Пример: вычитание дробей (02040060)
Как и при сложении, если знаменатели разные, измените одну или обе дроби так, чтобы они были одинаковыми, а затем вычтите.
Пример: вычитание различных знаменателей (02040070)
Как и в приведенном выше примере, дробь 2/3 изменяется на 8/12, а дробь 1/4 изменяется на 3 // 12, и выполняется указанная математическая операция вычитания.
Пример: вычитание дробей (02040080)
Умножение дробей
Умножаем числители вместе = новый числитель
Умножаем знаменатели вместе = новый знаменатель
Пример: умножение дробей (02040090)
Умножение легко, потому что числители умножаются вместе. В отличие от сложения и вычитания, в знаменателе нет необходимости использовать общее число.
В отличие от сложения и вычитания, в знаменателе нет необходимости использовать общее число.
На дроби
Оберните делитель и произведите умножение.
Пример: деление дроби -1 (02040100)
Переверните 3/4 и умножьте:
Деление на дроби — 2 (02040200)
Сокращение обыкновенных дробей до наименьших членов
Дроби обычно выражаются в самой простой возможной форме = сокращение дроби до наименьшего числа.
Пример: сокращение обыкновенных дробей (02040300)
Разделите числитель и знаменатель на 3. Эта дробь выражается эквивалентной, но более простой дробью 4/5.
Это более простое выражение получается делением числителя и знаменателя на одно и то же число. Из общих принципов вы помните, что когда вы это сделаете, вы получите другую дробь, но с тем же значением.
Числитель и знаменатель дроби проверяются, чтобы определить, существует ли у каждой из них общий множитель.
В дроби 12/15 число 3 является общим множителем, поскольку и 12, и 15 делятся на 3. Это число делится как на числитель, так и на знаменатель.
Это число делится как на числитель, так и на знаменатель.
Пример: уменьшение дробей (02040400)
Сокращение неправильных дробей до наименьших членов
Неправильная дробь (у которой числитель больше знаменателя) сокращается до наименьших членов, заменяя дробь смешанным числом.
Разделите числитель на знаменатель, а остаток представьте в виде правильной дроби.
Пример № 1: Неправильная дробь — 1 (02040500)
Пример № 2: Неправильная дробь — 2 (02040600)
Умножение и деление смешанных чисел
Пример: умножение смешанной дроби (02040700)
Умножение и деление невозможно выполнить с использованием смешанных чисел:
Если смешанное число должно быть умножено или разделено, оно должно быть сначала заменено на неправильную дробь.
Чтобы преобразовать смешанное число в дробь, умножьте целое число на знаменатель и прибавьте его к числителю, затем запишите эти результаты как новый числитель над исходным знаменателем.
Пример: смешанные числа (02040800)
Подставьте эту неправильную дробь вместо смешанного числа, затем умножьте дробь.
Пример: замена неправильной дроби (02040900)
Выразите ответ 110/24 в виде смешанного числа, сокращенного до наименьшего числа.
Пример: сокращение смешанных чисел (02041000)
Десятичные дроби
Дробь, знаменатель которой равен 10 или кратен 10, называется десятичной дробью или десятичной дробью. Однако вместо записи дроби в виде двух чисел, разделенных линией, используется десятичная точка.
В десятичных дробях десятичная точка используется для обозначения числа, кратного десяти, в знаменателе.
Фактически записываются только числа числителя.
Пример: дроби как десятичная таблица (02041100)
При выполнении любой математической операции все термины должны быть в одной системе. Следовательно, если некоторые числа даны как обычные дроби, а некоторые как десятичные дроби, вы должны сначала преобразовать все числа в одну общую форму.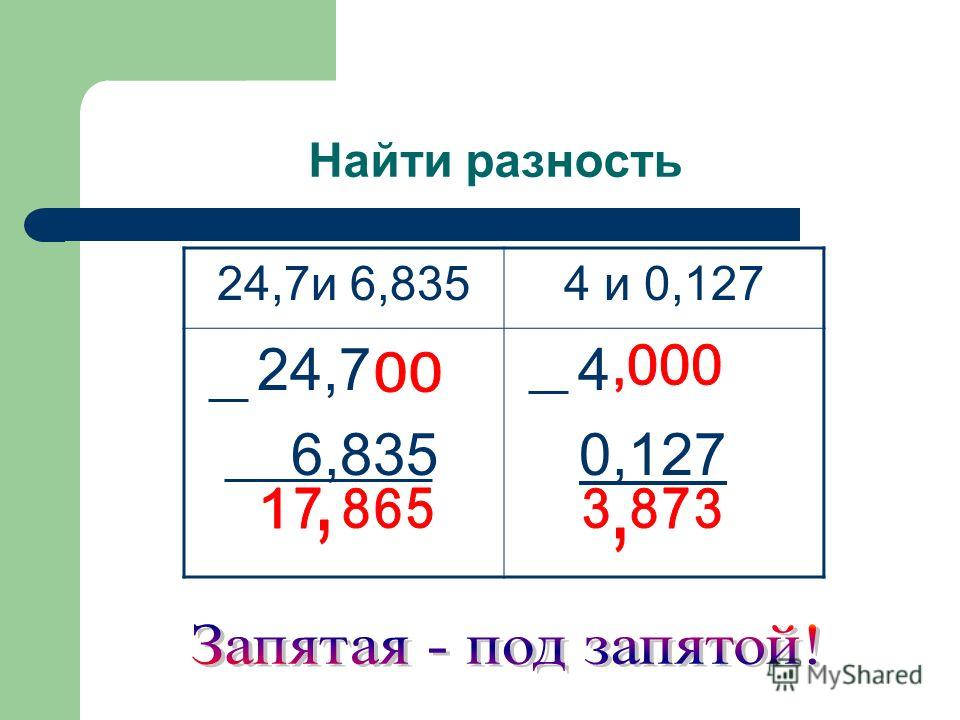
Преобразование между обыкновенной и десятичной дробями
Десятичное число = обыкновенные дроби
0,0011 = 11 / 10,000
Используйте десятичное число I (11) в качестве числителя.Знаменатель кратен десяти и определяется положением десятичной запятой. (Один ноль на каждое место.)
Обыкновенная дробь = Десятичная
5/8 = 0,625
Разделите числитель дроби на знаменатель. В приведенном выше примере разделите 5 на 8, чтобы получить 0,625.
Обратите внимание, что для некоторых дробей деление не получается четным и дает повторяющееся число. Например, 1/3 дает 0,333.
Математические операции с десятичными знаками
Чаще всего, когда мы выполняем математические операции с десятичными числами, мы используем калькулятор, и он автоматически дает ответ с десятичной дробью в нужном месте.Если вам пришлось выполнять эти операции вручную, следует запомнить несколько правил.
При сложении или вычитании десятичных знаков вы должны сначала выровнять числа так, чтобы десятичные точки находились непосредственно друг под другом.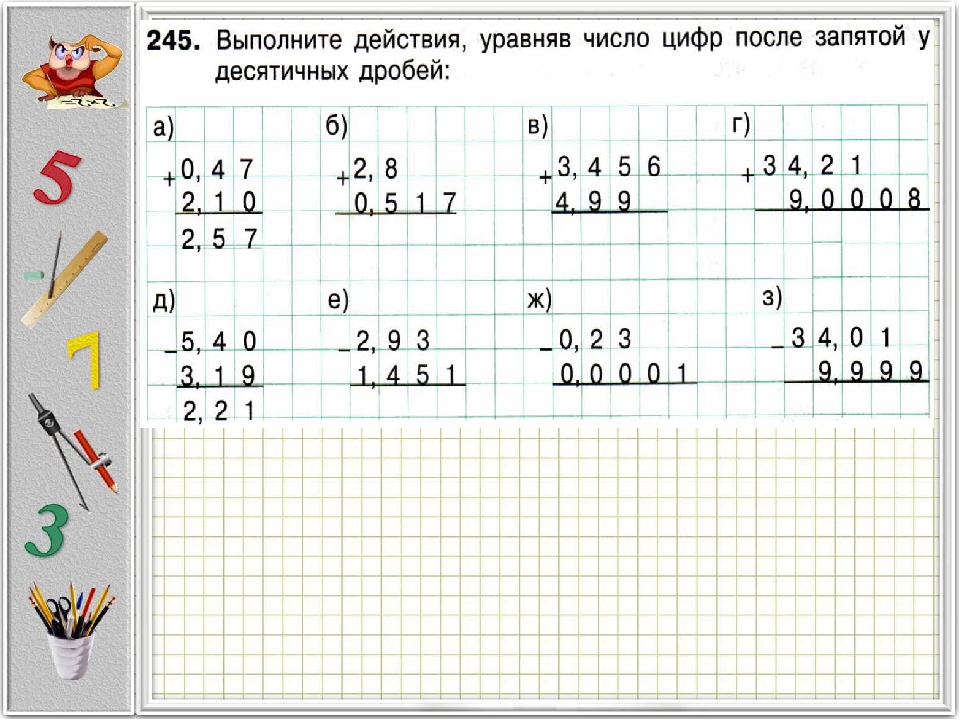 Затем сложите или вычтите, как если бы вы делали целые числа.
Затем сложите или вычтите, как если бы вы делали целые числа.
Чтобы добавить 0,1 + 0,33 + 0,017: Добавление десятичных знаков (02041200)
Чтобы вычесть 0,56 из 0,7: вычитание десятичных знаков (02041300)
Чтобы умножить десятичные дроби, умножайте числа так же, как и целые числа
Для определения позиции десятичной запятой в ответе:
Подсчитайте количество разрядов справа от десятичной точки для каждого из множителей.
Сложите это вместе.
Отсчитайте это количество знаков в ответе, начиная с крайнего правого числа.
Пример: при умножении 0,849 на 0,62 в двух множителях складываются пять знаков справа от десятичной дроби. Следовательно, при определении десятичного разряда в произведении 52638 отсчитайте пять разрядов слева от крайнего правого числа (в данном случае 8)
.Умножение десятичных знаков (02041400)
Если в ответе недостаточно чисел, используйте нули в качестве хранителей места. В приведенном выше примере, если число 0,62 равно 0,062 и нам нужно шесть десятичных знаков, ответ будет 0,052638.
В приведенном выше примере, если число 0,62 равно 0,062 и нам нужно шесть десятичных знаков, ответ будет 0,052638.
Чтобы разделить десятичные дроби, расположите числа для деления в столбик так же, как для целых чисел.
Если в делителе есть десятичная точка, переместите десятичную точку до упора вправо от числа, затем переместите десятичную точку делимого (делимого числа) на такое же количество разрядов вправо.
Если делимое целое число, вам нужно будет добавить ноль справа от последнего числа делимого для каждого необходимого десятичного разряда.Например, чтобы разделить 16,8 на 0,12, переместите десятичную запятую 0,12 вправо на два места, чтобы получить 12; аналогичным образом переместите десятичную запятую для делимого, 16.8, на две позиции вправо. Затем выполните деление как обычно.
Пример: разделение десятичных знаков (02041500)
Правила десятичных знаков при написании доз лекарств
Десятичные точки должны быть четко написаны при написании доз лекарственного средства, поскольку пропущенная или неверно прочитанная десятичная точка может привести к десятикратной ошибке в дозе
.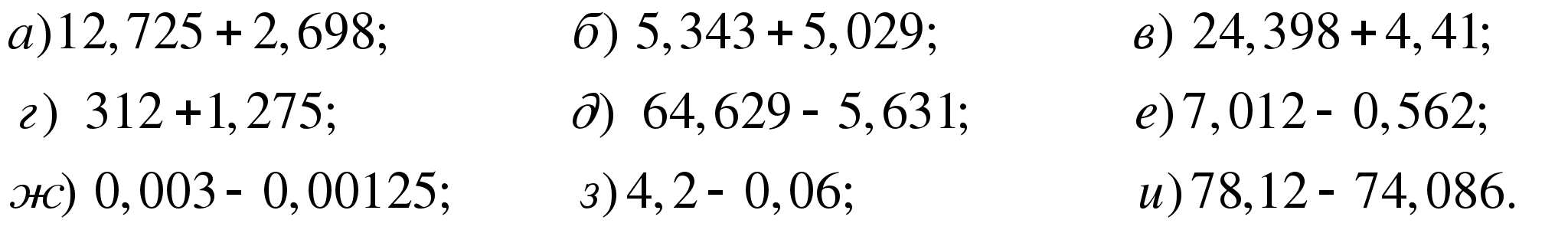
Никогда не добавляйте «конечный ноль» при записи целых чисел
Используйте 25 мг, а не 25.0 мг
Никогда не записывайте «голую десятичную дробь» при записи десятичной дроби вместо числа меньше 1
Используйте 0,25 мг, а не 0,25 мг
процентов
Проценты — это просто специальный вид дроби. Термин «процент» (обозначенный%) означает «за сотню».
Пример: 50% означает 50 на 100
Всегда переводите проценты в обыкновенные или десятичные дроби перед выполнением любых математических операций.
Процент =
в десятичной системеПереместите десятичную запятую на два разряда влево и опустите знак процента.
Пример: 50% = 0,50 или просто 0,5
Пример: 12,5% = 0,0125
Десятичное число =
процентовПереместите десятичную запятую на два разряда вправо и добавьте знак процента.
Пример: 0,5 = 50%
Пример: 0,0125 = 12,5%
Процент = правильная дробь
Используйте число в числителе и 100 в знаменателе.
50% = 50/100 (или 1/2 при сокращении до наименьшего значения)
Пример: 12.5%
Первая запись — обычная дробь —12,5 / 100
Поскольку мы обычно не смешиваем десятичные дроби в обычных дробях, эту дробь можно преобразовать в эквивалентную десятичную дробь без дроби, умножив числитель и знаменатель на 10 — 125/1000
Эта дробь может быть уменьшена до наименьшего числа путем деления числителя и знаменателя на общий множитель 125, что дает 1/8
.12,5% = 125./100 = 125/100 = 1/8 (при уменьшении до наименьшего значения)
Правильная дробь = Процент
Преобразуйте дробь в десятичную дробь, а затем преобразуйте десятичную дробь в проценты.
Пример: = 0,025 = 25%
Сами по себе проценты, как и обыкновенная и десятичная дробь, представляют собой просто числа без каких-либо единиц или размеров. Однако существуют определенные правила использования процентов при описании концентраций лекарственных препаратов.

 Не забудьте «внедрить» десятичную точку между соответствующими разрядами;
Не забудьте «внедрить» десятичную точку между соответствующими разрядами;

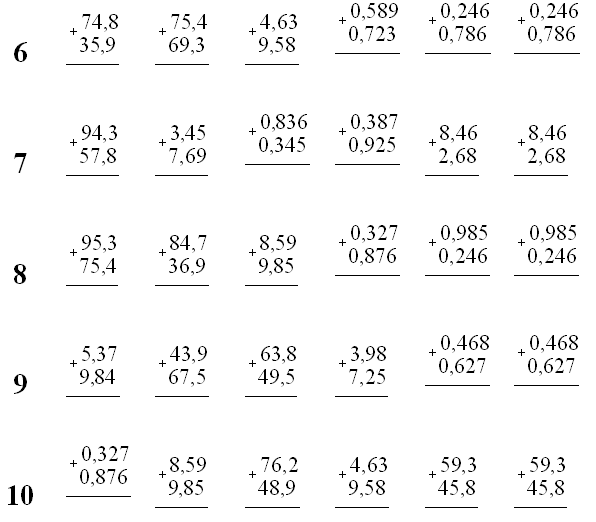




 444
444