Сложение и вычитание дробей с разными знаменателями
Замечание 1
Для сложения и вычитания алгебраических дробей с разными знаменателями выполняют действия, аналогичные тем, которые производят при сложении и вычитании обычных дробей с разными знаменателями.
Алгоритм:
Привести дроби к одинаковому знаменателю.
Найти дополнительные множители для каждой из дробей, которые являются произведением множителей, входящих в новый знаменатель и не входящие в старый.
Вычислить новый числитель для каждой дроби. Для этого надо старый числитель умножить на дополнительный множитель, найденный на $2$ шаге.
Выполнить сложение или вычитание дробей с одинаковым знаменателем.
Самое трудное в указанном алгоритме — это нахождение общего знаменателя. Общим знаменателем должно выступить выражение (одночлен или многочлен), которое делится на каждый из знаменателей исходных дробей без остатка.
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 29.04.2022
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
01Математика — 7 класс.
 Алгебра — Сложение и вычитание периодических дробей
Алгебра — Сложение и вычитание периодических дробей- Решение
- Видеорешение
Для того чтобы найти сумму \(\displaystyle 0,(3)+1,4,\) сперва распишем периодическую дробь:
\(\displaystyle 0,(3)=0,3333\ldots\)
Далее произведем сложение десятичных дробей, записывая одну дробь под другой так, чтобы одинаковые разряды располагались друг под другом, и запятая была под запятой:
| \(\displaystyle +\) | \(\displaystyle 0\) | \(\displaystyle ,\) | \(\displaystyle 3\) | \(\displaystyle 3\) | \(\displaystyle 3\) | \(\displaystyle 3\) | \(\displaystyle \ldots\) |
| \(\displaystyle 1\) | \(\displaystyle ,\) | \(\displaystyle 4\) | |||||
| \(\displaystyle ?\) | \(\displaystyle ,\) | \(\displaystyle ?\) | \(\displaystyle ?\) | \(\displaystyle ?\) | \(\displaystyle ?\) | \(\displaystyle ?\) |
Вначале сносим все цифры, стоящие над пустыми ячейками:
| \(\displaystyle +\) | \(\displaystyle 0\) | \(\displaystyle ,\) | \(\displaystyle 3\) | \(\displaystyle \color{red}{3}\) | \(\displaystyle \color{red}{3}\) | \(\displaystyle \color{red}{3}\) | \(\displaystyle \ldots\) |
| \(\displaystyle 1\) | \(\displaystyle ,\) | \(\displaystyle 4\) | |||||
| \(\displaystyle ?\) | \(\displaystyle ,\) | \(\displaystyle ?\) | \(\displaystyle \color{red}{3}\) | \(\displaystyle \color{red}{3}\) | \(\displaystyle \color{red}{3}\) | \(\displaystyle \ldots\) |
Далее складываем обычные десятичные дроби:
| \(\displaystyle +\) | \(\displaystyle \color{blue}{0}\) | \(\displaystyle ,\) | \(\displaystyle \color{blue}{3}\) | \(\displaystyle 3\) | \(\displaystyle 3\) | \(\displaystyle 3\) | \(\displaystyle \ldots\) |
| \(\displaystyle \color{blue}{1}\) | \(\displaystyle ,\) | \(\displaystyle \color{blue}{4}\) | |||||
| \(\displaystyle \color{blue}{1}\) | \(\displaystyle ,\) | \(\displaystyle \color{blue}{7}\) | \(\displaystyle 3\) | \(\displaystyle 3\) | \(\displaystyle 3\) | \(\displaystyle \ldots\) |
Таким образом,
\(\displaystyle 0,(3)+1,4=1,7333\ldots\)
и
\(\displaystyle 1,7333\ldots=1,7(3). \)
\)
Ответ: \(\displaystyle 1,7(3).\)
Математическое выражение: вычитание дробей
00:00:03.030
В этом уроке мы научимся вычитать дроби.
00:00:07.110
Теперь идея вычитания дроби аналогична сложению дроби.
00:00:13.070
Чтобы вспомнить, прибавим 3/5 к 1/5.
00:00:18.180
00:00:28.200
Следовательно, мы получаем 3 плюс 1,/5.
00:00:33.150
Из этого наблюдения видно, что при вычитании дробей 3/5 с 1/5 нам просто нужно вычесть числители, а знаменатели оставить прежними.
00:00:47.110
Отсюда получаем 3 минус 1/5.
00:00:52.110
Затем вычтите 3 из 1. Это даст 2. Наконец, мы получим дробь 2/5.
00:01:02.240
Хорошо, давайте наглядно посмотрим, как работает вычитание дробей. Мы видим, что, вычитая эти 3 зеленые части с этой 1 зеленой частью, мы получаем 2 зеленые части.
00:01:15.220
Две зеленые части представляют числитель 2, а все 5 частей в этой полосе представляют знаменатель 5. /9.
00:01:32.070
00:01:44.060
Из-за этого мы можем визуально увидеть, что мы не можем вычесть эти две дроби как есть.
00:01:51.120
Таким образом, единственный способ вычесть эти дроби — сделать все части одного размера. Это означает, что у этих дробей должны быть одинаковые знаменатели.
00:02:03.090
Для этого нам нужно использовать эквивалентные дроби.
00:02:08.080
Теперь, используя эквивалентные дроби, мы можем изменить этот знаменатель на 9, умножив числитель и знаменатель этой дроби на 3.
00:02:18.090
Это дает дробь 9.
00:02:22.230
У этих дробей одинаковые знаменатели. Это означает, что все части будут иметь одинаковый размер. Как вы можете видеть прямо здесь.
Как вы можете видеть прямо здесь.
00:02:34.240
Теперь мы можем вычесть эти две дроби, как в предыдущем примере. Таким образом, мы получаем 3 минус 2/9.
00:02:46.240
Минус 3 с 2. Это дает 1. Наконец, у нас есть дробь 1/9.
00:02:57.130
Следующий пример, давайте вычтем 1/3 из 1 1/2.
00:03:04.020
Обратите внимание, что эта дробь является смешанной дробью. Чтобы свести к минимуму ошибки, желательно преобразовать его в неправильную дробь.
00:03:13.000
Обратите внимание, что при преобразовании нам просто нужно сосредоточиться на этой смешанной дроби и игнорировать этот знак минус. Теперь мы умножаем 2 на 1. Это дает 2.
00:03:28.200
Затем мы добавляем 2 к 1. Это дает 3, которое становится числителем неправильной дроби. Теперь у нас есть неправильная дробь 3/2.
00:03:43.000
Обратите внимание, что мы не можем вычесть эти две дроби, потому что у них разные знаменатели.
00:03:49.190
Следовательно, единственный способ вычитания этих дробей — сделать их одинаковыми знаменателями.
00:04:01.240
Вот как. Мы можем сделать знаменатели одинаковыми, умножив числитель и знаменатель 1/3 на знаменатель другой дроби, равный 2, и умножив числитель и знаменатель 3/2 на знаменатель другой дроби, равный 3.
00:04:20.020
Так и сделаем. Умножение 1/3 на 2 и умножение 3/2 на 3. Это дает эквивалентные дроби, 2/6 и 9/6 соответственно. Знаменатели теперь одинаковы.
00:04:33.180
Теперь вычтем эти две дроби. Это дает 2 минус 9/6.
00:04:46.070
Вычитание 2 из 9 дает минус 7.
00:04:50.210
Обратите внимание на знак минус здесь? Мы можем переписать его таким образом, чтобы он выглядел аккуратнее. При этом у нас есть дробь, отрицательная 7/6.
00:05:01.200
Обратите внимание, что минус 7/6 — неправильная дробь. Таким образом, вместо того, чтобы оставлять ответ в таком виде, рекомендуется изменить его на смешанную дробь, используя длинное деление.
00:05:14. 080
080
Теперь при преобразовании нужно просто ориентироваться на эту дробь, а этот знак игнорировать.
00:05:22.040
Начнем. 7/6 — это то же самое, что 7 делит 6. Теперь это деление дает частное как 1. Это частное на самом деле является целым числом для смешанной дроби.
00:05:37.130
Затем мы умножаем 1 на 6. Это дает 6. 7 минус 6 дает остаток как 1.
00:05:47.200
Этот остаток, 1, фактически является числителем смешанной дроби.
00:05:54.240
Итак, здесь у нас есть окончательный ответ, минус 1 1/6.
00:06:03.160
На этом уроке все. Попробуйте ответить на практический вопрос, чтобы проверить свое понимание.
Вычитание дробей — Math28
Содержание
Что такое вычитание дробей?Вычитание дробей — одна из основных операций, позволяющая получить разность между двумя дробями в эквивалентной дроби, которая известна как «разность» или «вычитание».
Узнать больше о: « Вычитание » →
Символ или знак вычитания дробей Вычитание дробей представлено символом тире или промежуточной чертой «-», которая известна как «минус».
Узнать больше о: » Операции с дробями » →
Как мы вычитаем дроби?
Чтобы получить числовое значение в виде дроби, вы должны сначала определить, имеет ли вычитание дробей один и тот же знаменатель или разные знаменатели, поэтому есть две процедуры:
1) Вычитание дробей с одинаковым знаменателемВычитание дробей с одинаковым знаменателем или также известное как вычитание однородных дробей является наиболее упрощенной и простой процедурой, так как процедура вычитания основана на вычитании числителей, а знаменатель остается прежним.
3 / 4
—
1 / 4
=
2 / 4
3/4
1/4
2/4
Пример:
5 / 3
—
4 / 3
=
5 — 4 /
=
1 / 3
8 / 2
—
6 / 2
=
8 — 6 /
=
2 /
9 / 6
—
2 / 6
=
9 — 2 /
=
7 /
5 / 3
—
2 / 3
=
5 — 2 /
=
3 /
Из предыдущих примеров можно упростить 2/2 = 1 и 3/3 = 1.
Упражнение:
А)
5 / 3
—
3 / 3
= ?
Б)
9 / 2
—
5 / 2
= ?
С)
6 / 5
—
4 / 5
= ?
Д)
6 / 8
—
2 / 8
= ?
Для вычитания дробей с разными знаменателями или также известного как вычитание разнородных дробей рекомендуется знать, как получить наименьшее общее кратное (lcm), так как мы можем упростить уравнения.
Узнать больше о: « Наименьшее общее кратное » →
3 / 4
—
1 / 2
=
1 / 4
3/4
1/2
1/4
Рассмотрены два разных метода вычитания дробей с разными знаменателями, в данном случае первый метод соответствует прямой форме, так как мы не можем получить наименьшее общее кратное знаменателя, а второй метод соответствует получению наименьшего общего кратного.
Примечание : рекомендуется работать с ранее упрощенными дробями.
Примеры:
3 / 2
—
4 / 3
=
9 — 8 /
=
1 / 6
5 / 2
—
3 / 4
=
10 — 3 /
=
7 /
7 / 2
—
4 / 8
=
28 — 4 /
=
24 /
8 / 5
—
2 / 3
=
24 — 10 /
=
14 /
Из предыдущих примеров можно упростить 24/8 = 3.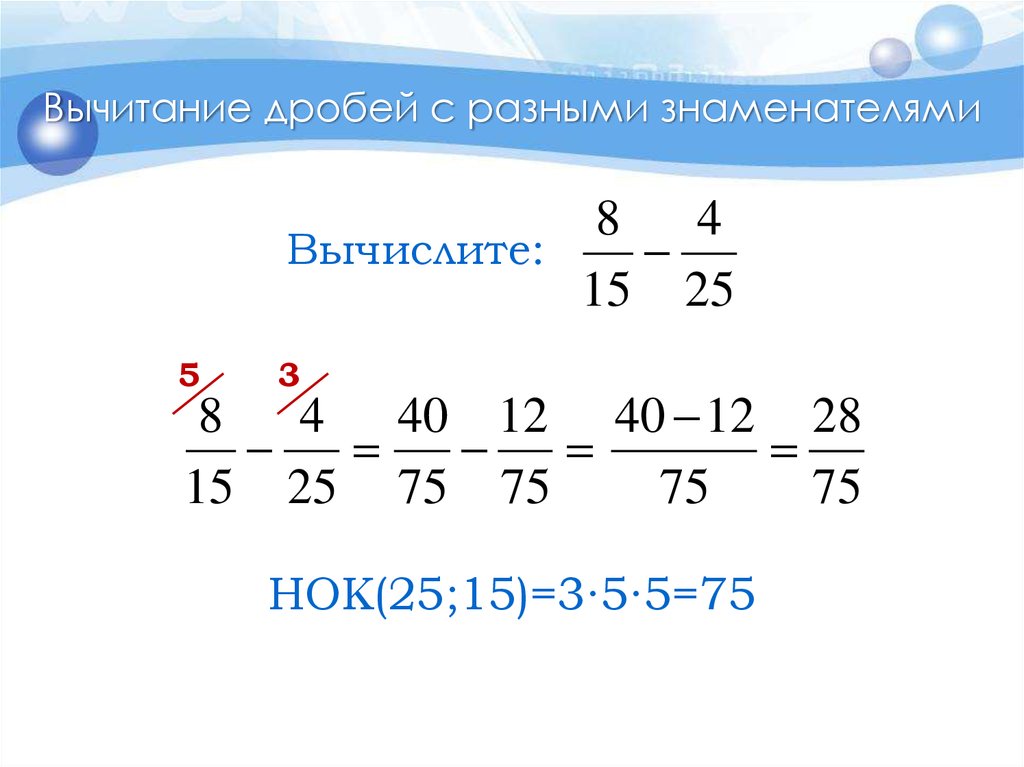
Упражнение:
А)
7 / 2
—
5 / 3
= ?
Б)
3 / 2
—
5 / 4
= ?
С)
3 / 4
—
3 / 5
= ?
Д)
6 / 6
—
2 / 2
= ?
Вычитание смешанных дробей
При вычитании смешанных дробей необходимо, чтобы вся часть выражалась в виде дроби с тем же знаменателем, что и в сопровождающей ее дробной части. Например, чтобы выполнить следующее смешанное вычитание:
4
2 / 5
— 3
4 / 8
- 1.
