Вычитание дробей, формулы и примеры решений

Содержание:

• Вычитание дробей с одинаковыми знаменателями
• Вычитание дробей с разными знаменателями
• Вычитание смешанных дробей

Определение

Вычитание дробей является действием, обратным к сложению. Вычесть из одной дроби другую — это означает найти такую третью дробь, которая в сумме со второй дробью дает первую.

Вычитание дробей с одинаковыми знаменателями

Чтобы вычесть дроби с одинаковыми знаменателями, нужно от числителя первой дроби отнять числитель второй, а знаменатель оставить без изменений.

Пример

Задание. Найти разность дробей $\frac{10}{11}$ и $\frac{7}{11}$

$$\frac{10}{11}-\frac{7}{11}=\frac{10-7}{11}=\frac{3}{11}$$

Ответ. $\frac{10}{11}-\frac{7}{11}=\frac{3}{11}$

Вычитание дробей с разными знаменателями

Чтобы вычислить дроби с разными знаменателями, нужно вначале привести их к наименьшему общему знаменателю, а затем отнимать их как дроби с одинаковым знаменателем.

{2}}{11}-\frac{1}{22}\right)=$$ $$=4+\frac{7 \cdot 2-1 \cdot 1}{22}=4+\frac{14-1}{22}=4+\frac{13}{22}=4 \frac{13}{22}$$

Ответ. $6 \frac{7}{11}-2 \frac{1}{22}=4 \frac{13}{22}$

В случае, когда дробь вычитаемого больше, чем дробь уменьшаемого, поступают следующим образом: берут одну единицу (целое) из целого числа уменьшаемого, записывают его как неправильную дробь, числитель и знаменатель которой равны между собой и равны знаменателю дробной части, и прибавляют к дробной части, далее отнимают две смешанные дроби, как описано выше.

Пример

Задание. Выполнить вычитание $5 \frac{4}{9}-1 \frac{11}{12}$

Решение. Дробь $\frac{4}{9}$ меньше ( сравнение дробей ), чем дробь $\frac{11}{12}$ (так как $4 \cdot 12 = 36 < 9 \cdot 11 = 99$ ), тогда

$$5 \frac{4}{9}-1 \frac{11}{12}=5+\frac{4}{9}-1 \frac{11}{12}=4+1+\frac{4}{9}-1 \frac{11}{12}=$$ $$=4+\frac{9}{9}+\frac{4}{9}-1 \frac{11}{12}=4 \frac{9+4}{9}-1 \frac{11}{12}=4 \frac{13}{9}-1 \frac{11}{12}=$$ $$=(4-1)+\left(\frac{13^{4}}{9}-\frac{11^{3}}{12}\right)=3+\frac{13 \cdot 4-11 \cdot 3}{36}=$$ $$=3+\frac{52-33}{36}=3+\frac{19}{36}=3 \frac{19}{36}$$

Ответ. $5 \frac{4}{9}-1 \frac{11}{12}=3 \frac{19}{36}$

Аналогичным образом поступают, когда надо вычесть из целого числа дробное.

Пример

Задание. Найти разность $4-3 \frac{3}{5}$

Решение. Выполним вычитание дробей по описанному выше правилу

$$4-3 \frac{3}{5}=3+1-3 \frac{3}{5}=3+\frac{5}{5}-3 \frac{3}{5}=3 \frac{5}{5}-3 \frac{3}{5}=$$ $$=(3-3)+\left(\frac{5}{5}-\frac{3}{5}\right)=0+\frac{5-3}{5}=\frac{2}{5}$$

Ответ. $4-3 \frac{3}{5}=\frac{2}{5}$

Замечание. Производить операции со смешанными числами можно и иначе: записать смешанное число в виде неправильной дроби и уже работать далее как с обыкновенными дробями.

Читать следующую тему: умножение дробей.

Как правильно вычитать обыкновенные дроби?

Оглавление

Время чтения:  5 минут

583

Дроби можно складывать, умножать, делить, а также вычитать. В этой статье мы рассмотрим вычисление разности таких дробей, которые имеют одинаковый или разный знаменатель. Также будет вычисление дроби из натурального числа и наоборот.

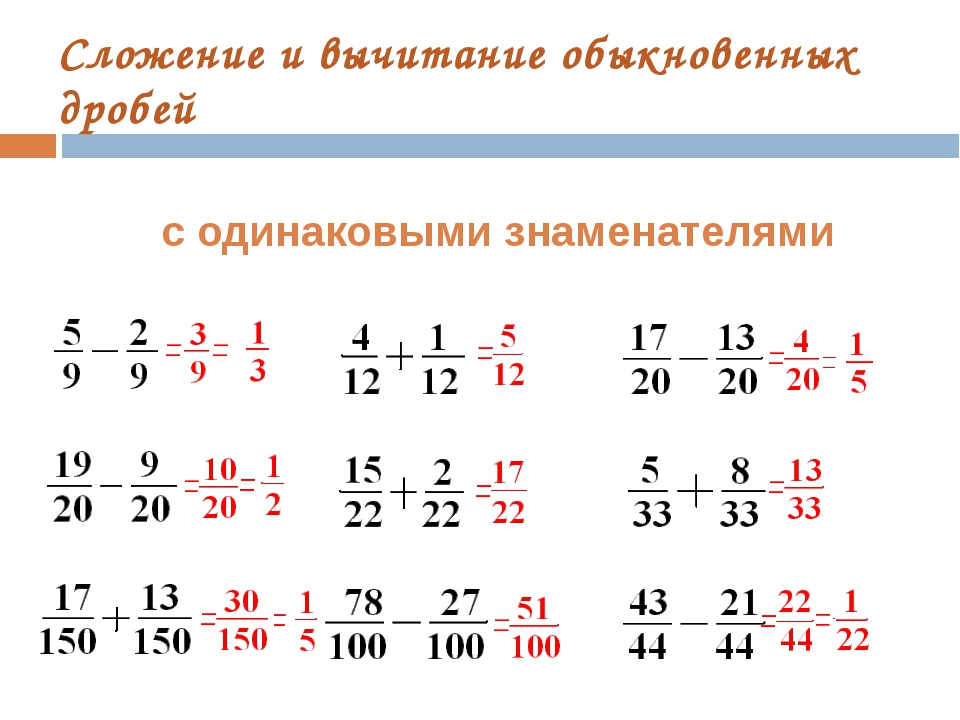
Вычитание дробей с одинаковыми знаменателями

Для нахождения разности дробей с одинаковыми знаменателями, необходимо вычесть один числитель из другого. Знаменатели не вычитаются.

Примеры

Найдите разность 4/8 – 3/8.

Решение:

Представьте, что у вас есть большая пицца, которая поделена на восемь частей. Вы взяли 4 куска, но съели лишь 3. Чтобы узнать, сколько осталось, нужно записать это так:

4/8 – 3/8 = 4-3/8 = 1/8

Выходит, что на тарелке остался 1 восьмой доли кусок пиццы. Из этого примера можно вывести формулу, которая подойдет для решения подобных примеров.

---

Рассмотрим ещё одно задание.

Пример 2:

Найдите разность 6/12 – 3/12.

Решение:

6/12 – 3/12 = 6-3/12 = 3/12 = 1/4 = 0.25

У этих дробей одинаковые знаменатели, поэтому нам нужно лишь вычесть 3 из 6. Мы получили 3/12 и сократили дробь делением на 3. Знак дроби означает деление, поэтому делим 1 на 4 и получаем 0.25.

Вычитание дробей с разными знаменателями

Если знаменатели разные, то нужно сделать так, чтобы они стали одинаковыми, т.е. привести дроби к общему знаменателю. После этого совершаем те же действия, что и выше.

Примеры

Пример 3:

Найдите разность 5/10 – 2/5.

Решение:

5/10 – 2/5 = 5/10 – 2•2/2•5 = 5/10 – 4/10 = 5-4/10 = 1/10 = 0.1

Чтобы найти общий знаменатель, нужно числитель и знаменатель второй дроби умножить на 2. Получим 4/10. Теперь можно находить разность как в прошлом примере.

---

Перейдем к следующему примеру.

Пример 4:

Найдите разность 52/24 – 14/12.

Решение:

52/24 – 14/12 = 52/24 – 2•14/2•12 = 52/24 – 28/24 = 52-28/24 = 24/24 = 1

Для того, чтобы привести к общему знаменателю, нужно умножить числитель и знаменатель второй дроби на 2. Будь в двух знаменателях 7 и 49, то мы бы умножали 7 не на 2, а на 7, чтобы получить в обоих знаменателях 49. Дальше все по формуле.

Вычитание натурального числа из обыкновенной дроби

Для того чтобы вычесть натуральное число из обыкновенной дроби, нужно представить натуральное число в виде обыкновенной дроби.

Рассмотрим на примере.

Примеры

Пример 5:

Найдите разность 288/36 – 6.

Решение:

288/36 – 6 = 288/36 – 6/1 = 288/36 – 36•6/36•1 = 288/36 – 216/36 = 288-216/36 = 72/36 = 2

Может показаться, что это сложно, но это не так. Число 6 можно представить в виде обыкновенной дроби: 6/1. Далее будем находить разность этих дробей. Приводим дроби к общему знаменателю, умножая знаменатель и числитель второй дроби на 36. Вычитаем, делим и получаем ответ.

Есть и второй вариант решения (для неправильных дробей, где числитель больше знаменателя) такого примера, более удобный и простой. Возьмем новые числа.

---

Пример 6:

Найдите разность 72/27 – 2.

Решение:

72/27 – 2 = 2 2/3 – 2 = 2/3

В этом случае не пришлось превращать натуральное число в дробь, 72/27 мы сделали смешанным числом, отняли двойки и получили ответ. Можно решать на основе прошлого примера, однако, это будет дольше и сложнее.

Понятия

• Смешанное число – это такая правильная дробь, в состав которой входит целое число.
• Неправильная дробь – это дробь, в которой числитель равен знаменателю или больше его.
• Правильная дробь – это дробь, в которой знаменатель больше числителя.

Для того, чтобы преобразовать неправильную дробь в смешанное число, необходимо поделить ее числитель на знаменатель. Неполное частное станет целой частью смешанной дроби, остаток будет числителем дробной части, а знаменатель неправильной дроби – знаменателем дробной части.

Вычитание обыкновенной дроби из натурального числа

Примеры

Сразу перейдем к примеру.

Пример 7:

Найдите разность 6 – 7/5.

Решение:

6 – 7/5 = 6/1 – 7/5 = 5•6/5•1 – 7/5 = 30/5 – 7/5 = 30-7/5 = 23/5 = 4 3/5 = 4.6

Все, как и ранее, натуральное число 6 представляем в виде дроби, приводим к общему знаменателю, а после
находим разность.

Есть ещё один способ. Он хорош в том случае, если приходится работать с большими числами.

Если вычитаемая дробь – правильная, то натуральное число необходимо предоставить как сумму двух чисел, где
одно из них равно 1. Последним действием является вычитание дроби из этой единицы. Рассмотрим на
примере.

---

Пример 8:

Найдите разность 1040 – 20/55.

Решение:

Отнимем от 1040 единицу и вычтем дробь:

1040 – 20/55 = (1039 + 1) – 20/55

Перейдем к поиску ответа. Для этого вспомним свойства вычитания, согласно которым можно записать получившееся
выражение как 1039 + (1 – 20/55). Просто так отнять единицу в виде натурального числа мы не можем, поэтому
предоставим ее как дробь 1/1.

А теперь можно находить разность:

1 – 20/55 = 1/1 – 20/55 = 55/55 – 20/55 = 35/55.

Но это не конец, ведь у нас ещё осталось число 1039. Здесь все легко, просто приписываем это число к нашей дроби и получаем ответ: 1039 35/55. Здесь можно сократить дробь и выйдет 1039 7/11.

Рассмотрим решение этого примера с помощью прошлого способа, чтобы определить то, какой из них более удобный:

1040 – 20/55 = 1040/1 – 20/55 = 55•1040/55•1 — 20/55 = 57200/55 = 11436•5/11•5 = 11436/11 = 1039 7/11.

Ответ одинаковый, но решение, очевидно, побольше.

---

Но что же делать с неправильной дробью? Нужно заменить ее смешанным числом, а далее все про инструкции.

Пример 9:

Найдите разность 378 – 35/6.

Решение:

Отделяем целую часть: 35/6 = 5 5/6

Теперь, как и ранее, совершаем следующие действия:

373 – 5/6 = (372 + 1) – 5/6 = 372 + (1 – 5/6) = 372 + 1/6 = 372 1/6.

Свойства, необходимые для вычитания дробей

Примеры

Свойства вычитания натуральных чисел действуют и на вычитание обыкновенных дробей.

Пример 10:

Найдите разность 16/6 – 2/4 – 6/3.

Решение:

Сначала находим разность первых двух дробей, а после уже отнимаем и третью:

16/6 – 2/4 = 2•16/2•6 – 3•2/3•4 = 32/12 – 6/12 = 32-6/12 = 26/12 – 6/3 = 26/12 – 4•6/4•3 = 26/12 – 24/12 = 2/12 = 1/6

Когда необходимо работать с дробями и натуральными числами, то следует их распределять по типам в группы.

---

Пример 11:

Найдите разность (86 + 15/24) – (4 + 2/4).

Решение:

Сгруппируем числа.

(86 + 15/24) – (4 + 2/4) = 86 + 15/24 – 4 – 2/4 = (86 – 4) + (15/24 – 2/4)

Теперь можно решать дальше:

(86 – 4) + (15/24 – 2/4) = 82 + (15/24 – 12/24) = 82 + 3/24 = 82 + 1/8 = 82 1/8.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Задания для практики

Задание 1: Найдите разность 20/10 – 15/10.

Задание 2: Найдите разность 54/6 – 9/6.

Задание 3: Выделите целую часть из неправильной дроби 7/3.

Задание 4: Выделите целую часть из неправильной дроби 9/5.

Задание 5: Найдите разность 63/2 – 42/8.

Задание 6: Найдите разность 101/25 – 4.

Задание 7: Найдите разность 1096 – 25/40.

Задание 8: Найдите разность 46/6 – 2/2 – 189/36.

Задание 9: Найдите разность (65 + 56/45) – (10 + 4/9).

Ответы

Решение задания 1: 20/10 – 5/10 = 20-15/10 = 5/10 = 1/2 = 0.5.

Решение задания 2: 54/6 – 9/6 = 54-9/6 = 45/6 = 15/2 = 7.5.

Решение задания 3: 7/3 = 7:3 = 2 (остаток 1) = 2 1/3.

Решение задания 4: 9/5 = 9:5 = 1 (остаток 4) = 1 4/5.

Решение задания 5: 63/2 – 42/8 = 4•63/4•2 – 42/8 = 252/8 – 42/8 = 252-42/8 = 210/8 = 26.25.

Решение задания 6: 101/25 – 4 = 101/25 – 4/1 = 101/25 – 100/25 = 101-100/25 = 1/25 = 0.04.

Решение задания 7: 1096 – 25/40 = (1095 + 1) – 25/40 = 1095 + (1 — 25/40) = 1/1 – 25/40 = 40/40 – 25/40 = 15/40 = 1095 15/40 = 1095 3/8 = 1095.375.

Решение задания 8: 46/6 – 2/2 – 189/36 = 46/6 – 2/2 = 46/6 – 3•2/3•2 = 46/6 – 6/6 = 46-6/6 = 40/6 – 189/36 = 6•40/6•6 – 189/36 = 240/36 – 189/36 = 240-189/36 = 51/36 = 1. 416.

Решение задания 9: (65 + 56/45) – (10 + 4/9) = 65 + 56/45 – 10 – 4/9 = (65 – 10) + (56/45 – 4/9) = 55 + 36/45 = 55 + 4/5 = 55 4/5.

Оценить статью (55 оценок):

Поделиться

Вычитание дробей – Примеры

Вычитание дробей – это арифметическая операция, которая должна выполняться для нахождения разницы между двумя дробями. Чтобы вычесть две одинаковые дроби, мы должны вычесть их числители и записать разницу над общим знаменателем, а чтобы вычесть две разные дроби, мы должны сначала преобразовать их в подобные дроби, взяв НОК знаменателей. Мы также можем вычесть целое число и дробь, записав целое число в дробной форме, например, 3 = 3/1. Давайте узнаем больше о вычитании дробей подробно в этой статье.

1.	Как вычитать дроби?
2.	Вычитание дробей с одинаковыми знаменателями
3.	Вычитание дробей с разными знаменателями
4.	Вычитание дробей из целых чисел
5.	Часто задаваемые вопросы о вычитании дробей

Как вычитать дроби?

Дроби считаются частью целого. Группа дробей может быть классифицирована как подобные дроби и разные дроби на основе значения знаменателя. Подобные дроби – это те, у которых одинаковые знаменатели. Например, 3/4 и 5/4. В то время как непохожими являются дроби, имеющие разные знаменатели, например, 2/3 и 4/7. Мы можем найти разницу между двумя одинаковыми дробями, в отличие от дробей и дробей и целых чисел. Шаги для вычитания дробей перечислены ниже:

• Шаг 1: Определите, имеют ли данные дроби одинаковые знаменатели или разные знаменатели.
• Шаг 2: В случае одинаковых дробей вычтите числители и запишите их разность над общим знаменателем. Например, 5/7 — 2/7 = (5 — 2)/7 = 3/7. С другой стороны, для разных дробей найдите НОК знаменателей.
• Шаг 3: Умножьте числитель и знаменатель каждой дроби на целое число, чтобы получить НОК в знаменателе. Это делается для преобразования неодинаковых дробей в подобные дроби.
• Шаг 4: Вычтите их числители и запишите разницу над общим знаменателем.

Вот как мы вычитаем две дроби. Есть два случая, которые возникают при изучении вычитания дробей: вычитание подобных дробей и непохожих дробей. Давайте узнаем о каждом подробно.

Вычитание дробей с одинаковыми знаменателями

Дроби с одинаковыми знаменателями легко вычитаются путем вычитания их числителей. Шаги для вычитания дробей с одинаковыми знаменателями приведены ниже:

• Вычесть числители.
• Запишите общий знаменатель как знаменатель результирующей дроби.
• Теперь полученный ответ можно при необходимости привести к низшей форме.

Вычтем дроби 4/5 и 2/5, используя прямоугольную модель. Мы представляем 4/5 в этой модели, заштриховывая 4 из 5 частей.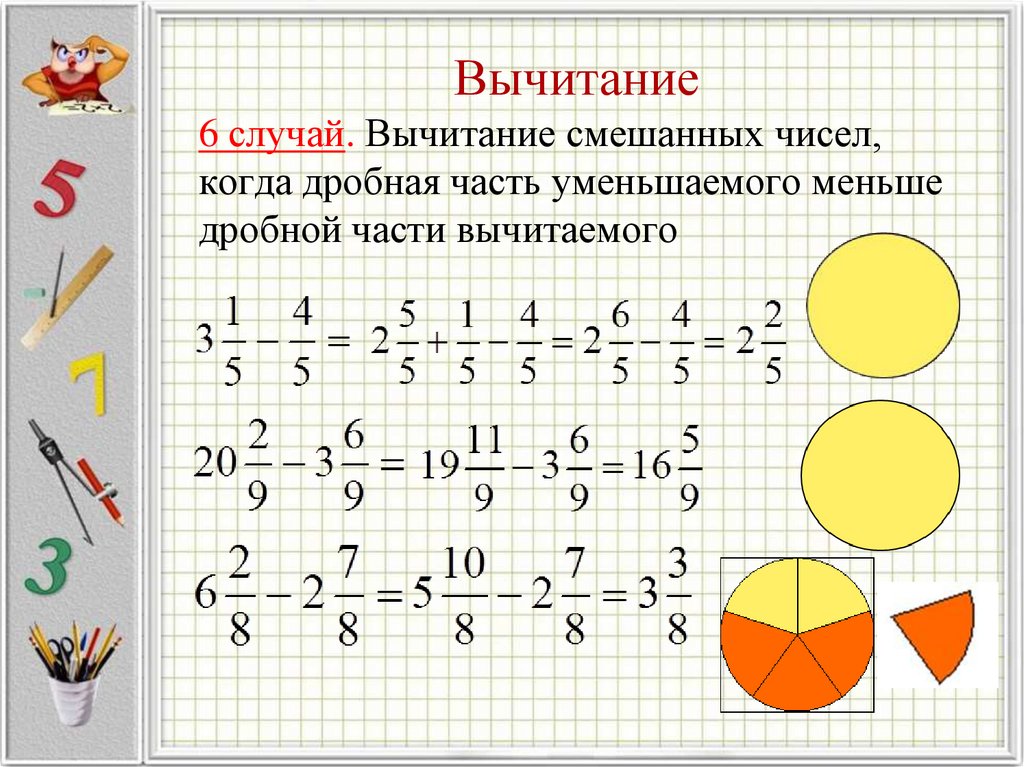 Далее мы заштрихуем 2 части из заштрихованных частей модели, чтобы представить удаление 2/5.

Теперь у нас осталось 2 части в заштрихованных частях модели. Таким образом, вычитание дробей дается как (4/5 — 2/5) = 2/5.

Вычитание дробей с разными знаменателями

Две дроби с разными или непохожими знаменателями можно вычесть, выполнив шаги, описанные ниже:

1. Сначала возьмите НОК знаменателей.
2. Преобразуем данные дроби в подобные дроби со знаменателем в виде НОК.
3. Теперь вычтите числители и запишите их разницу над общим знаменателем.
4. При необходимости упростите.

Давайте разберемся, как вычитать разные дроби, используя модель площади: (2/5 — 1/3). Это указывает на то, что мы должны удалить (1/3) часть ^rd из 2/5. Мы можем представить это, как показано ниже.

Поскольку наша модель разделена на 15 частей, это наш знаменатель. Это НОК знаменателей данных дробей. Первый прямоугольник показывает часть, представленную 2/5 (в строках) и 1/3 (в столбцах) в данной модели. Теперь переместите часть 1/3 на 2/5, чтобы мы могли вычесть 1/3 из 2/5. Мы видим, что осталась только 1 часть, которая не заштрихована. Таким образом, ответ дается как 2/5 — 1/3 = 1/15. Численно это можно выразить как

2/5 — 1/3

⇒ (2 × 3)/(5 × 3) — (1 × 5)/(3 × 5) [Поскольку НОК 5 и 3 равен 15]

⇒ 6 /15 — 5/15

⇒ 1/15

Следовательно, 2/5 — 1/3 = 1/15.

Воспользуйтесь нашим бесплатным онлайн-калькулятором дробей для вычитания, чтобы проверить свои ответы.

Вычитание дробей из целых чисел

Подобно вычитанию двух дробей, мы также можем вычесть дробь из целого числа и наоборот. Каждое целое число можно записать в дробной форме, написав 1 в качестве знаменателя, например, мы можем записать 7 как 7/1. Итак, для вычитания дроби и целого числа мы сначала заставляем их писать в дробной форме, затем мы можем легко найти разницу, применяя те же правила, что и вычитание двух непохожих дробей.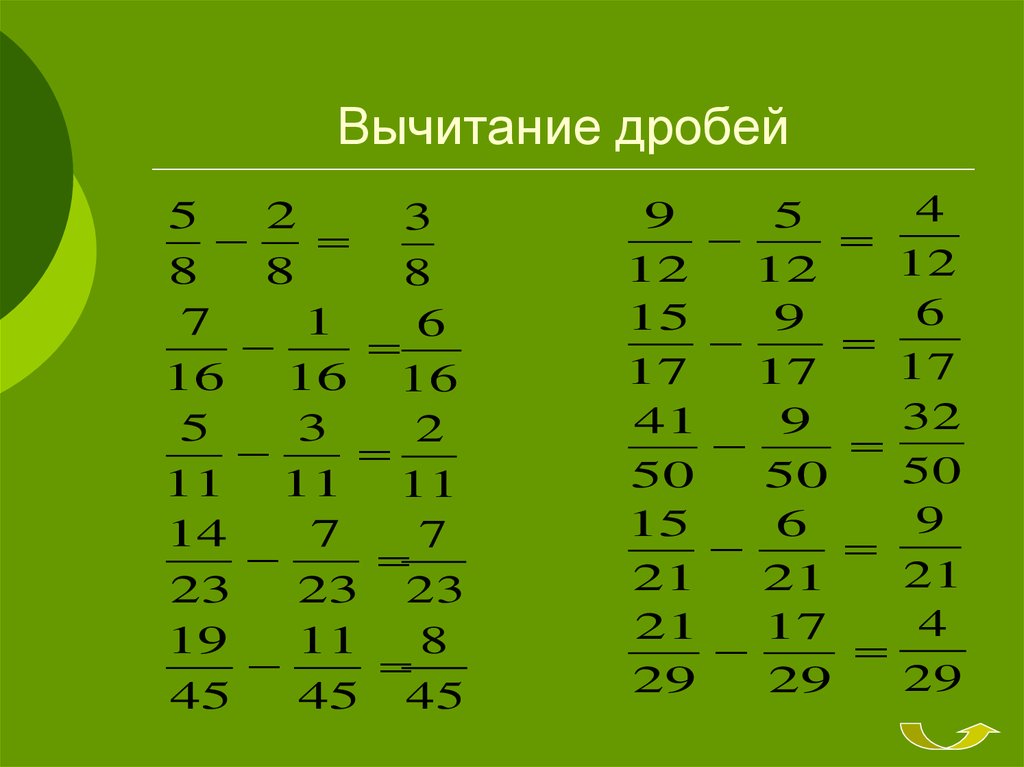 Чтобы вычесть дробь из целого числа, рассмотрим следующий пример: 2 — 1/4.

• Преобразуем целое число в дробную форму: 2 = 2/1.
• Теперь вычтите их как разные дроби.

Итак, чтобы вычесть 2/1 — 1/4, НОК 1 и 4 равно 4. Умножьте числитель и знаменатель 2/1 на 4, чтобы получить 4 в знаменателе.

2/1 — 1/4 = (2 × 4)/(1 × 4) — 1/4

= 8/4 — 1/4

= 7/4

= \(1\frac { 3}{4}\)

Следовательно, 2 — 1/4 = 7/4. Вот как мы вычитаем дроби с целыми числами.

Советы и рекомендации:

• Шагов вычитания дробей с разными знаменателями:

  а) Преобразуйте данные дроби в подобные дроби, взяв НОК знаменателей.
  б) Найдите эквивалентные дроби данных дробей, знаменатель которых равен НОК.
  в) Вычесть числители и оставить тот же знаменатель.

• Для разных дробей никогда не вычитайте числители и знаменатели напрямую.
  (3/5 — 2/3) ≠ (1/2)
• При вычитании разных дробей не нужно находить НОК знаменателей. Подойдет любое общее кратное. Таким образом, простое умножение двух знаменателей дает нам общее кратное. Это может привести к большим выглядящим числам, но его можно уменьшить до самой низкой формы.

► Похожие темы

Ознакомьтесь с этими интересными статьями, посвященными вычитанию дробей в математике.

• Умножение дробей
• Деление дробей
• Добавление дробей

Часто задаваемые вопросы о вычитании дробей

Что такое сложение и вычитание дробей?

Сложение и вычитание дробей — это две арифметические операции, выполняемые для сложения или вычитания дробей. Правила сложения и вычитания дробей одинаковы. Подобные дроби можно складывать/вычитать, добавляя/вычитая их числители и сохраняя общий знаменатель, в то время как разные дроби можно складывать/вычитать, сначала преобразовывая их в подобные дроби.

Как вычитать дроби?

Мы можем вычитать одинаковые и разные дроби, используя следующие шаги:

• Для одинаковых дробей вычесть числители и сохранить тот же знаменатель.
• Для вычитания разных дробей возьмите НОК знаменателей, преобразуйте дроби в одинаковые дроби и вычтите их.
• При необходимости уменьшите до наименьшего значения.

Что такое правило вычитания дробей?

Основное правило вычитания дробей состоит в том, чтобы сначала убедиться, что они имеют общий знаменатель. Если у них разные знаменатели, то мы сначала преобразуем их в одинаковые дроби.

Как вычитать дроби из целых чисел?

Мы можем использовать приведенные ниже шаги, чтобы вычесть дроби из целых чисел:

• Мы запишем целое число как дробь, написав 1 в знаменателе.
• Сделав это, мы получим две разные дроби.
• Теперь вычтем обе разные дроби и получим ответ.
• При необходимости полученное значение можно уменьшить до наименьшего значения.

Рассмотрим пример:

2 — 1/5 = 2/1 — 1/5
(2/1 × 5/5) — (1/5) = 10/5 — 1/5 = 9/5
= \(1\frac{4}{5}\)

Как вычитать дроби с разными знаменателями?

Выполните следующие действия, чтобы вычесть дроби с разными знаменателями:

• Найдите НОК знаменателей.
• Умножьте числитель и знаменатель каждой дроби на целое число, чтобы получить LCM в знаменателе.
• Вычтите их как дроби.
• При необходимости сократите окончательный ответ.

Как решить вычитание дробей?

Мы можем упростить вычитание дробей следующими способами:

• В случае одинаковых дробей дроби можно вычитать, вычитая их числители, и вывод можно легко упростить.
• У разнородных дробей сначала обобщаются знаменатели и только потом вычитаются дроби. После вычитания вывод можно легко упростить.

Давайте посмотрим на пример.
2/4 — 2/5 = (2/4 × 5/5) — (2/5 × 4/4)

= 10/20 — 8/20

= 2/20

= 1/10

Как вычитать неправильные дроби?

Неправильные дроби вычитаются так же, как и правильные дроби:

• Для одинаковых дробей вычесть числители и оставить тот же знаменатель.
• Для вычитания разных дробей возьмите НОК знаменателей, преобразуйте дроби в эквивалентные дроби и вычтите их как одинаковые дроби.

Если после вычитания полученный ответ представляет собой неправильную дробь, мы преобразуем дробь в смешанное число, чтобы записать ее в простейшей форме.

Вычитание дробей

Горячая математика

При вычитании дробей первое, что нужно проверить, это знаменатели одинаковы.

Вычитание дробей с одинаковыми знаменателями

Дроби с одинаковым знаменатели называются подобными дробями.

Чтобы вычесть дроби с одинаковыми знаменателями, вычтите числители , и запишите разницу над знаменателем.

5 7 − 4 7 «=» 1 7

Пример :

Находить 4 5 − 2 5 .

Так как знаменатели одинаковые, вычтите числители.

«=» 4 − 2 5

«=» 2 5

Вы можете получить ответ, которого нет в самые низкие условия , даже если дроби, которые вы складывали и вычитали, были одинаковыми. В этом случае вы должны уменьшить дробь .

8 9 − 2 9 «=» 6 9 «=» 6 ÷ 3 9 ÷ 3 «=» 2 3

Вычитание дробей с разными знаменателями

Если знаменатели не совпадают, то вы должны использовать эквивалентные дроби у которых есть общий знаменатель . Для этого нужно найти наименьший общий множитель (НОК) двух знаменателей.

Чтобы вычесть дроби с разными знаменателями, переименуйте дроби с общим знаменателем. Затем вычтите и упростите.

Например, предположим, что вы хотите добавить:

6 7 − 2 3

LCM 3 и 11 является 33 .