Умножение в столбик | интернет проект BeginnerSchool.ru
Умножение многозначных или многоразрядных чисел удобно производить письменно в столбик, последовательно умножая каждый разряд. Давайте разберем, как это делать. Начнем с умножения многоразрядного числа на одноразрядное число и постепенно увеличим разрядность второго множителя.
Для того чтобы умножить в столбик два числа, разместите их одно под другим, единицы под единицами, десятки под десятками и так далее. Сравните два множителя и меньший разместите под большим. Затем начинайте умножать каждый разряд второго множителя на все разряды первого множителя.
Пишем однозначное число под единицами многозначного.
Умножаем 2 последовательно на все разряды первого множителя:
Умножаем на единицы:
8 × 2 = 16
6 пишем под единицами, а 1 десяток запоминаем. Для того, чтобы не забыть пишем 1 над десятками.
Умножаем на десятки:
3 десятка × 2 = 6 десятков + 1 десяток(запоминали) = 7 десятков. Ответ пишем под десятками.
Умножаем на сотни:
4 сотни × 2 = 8 сотен. Ответ пишем под сотнями. В результате получаем:
438 × 2 = 876
Умножим трехзначное число на двухзначное:
924 × 35
Пишем двухзначное число под трехзначным, единицы под единицами, десятки под десятками.
1 этап: находим первое неполное произведение, умножив 924 на 5.
Умножаем 5 последовательно на все разряды первого множителя.
Умножаем на единицы:
4 × 5 = 20 0 пишем под единицами второго множителя, 2 десятка запоминаем.
Умножаем на десятки:
2 десятка × 5 = 10 десятков + 2 десятка (запоминали) = 12 десятков, пишем 2 под десятками второго множителя, 1 запоминаем.
Умножаем на сотни:
9 сотен × 5 = 45 сотен + 1 сотня (запоминали) = 46 сотен, пишем 6 под разрядом сотен, а 4 под разрядом тысяч второго множителя.
924 × 5 = 4620
2 этап: находим второе неполное произведение, умножив 924 на 3.
Умножаем 3 последовательно на все разряды первого множителя. Ответ пишем под ответом первого этапа, сдвинув его на один разряд влево.
Умножаем на единицы:
4 × 3 = 12 2 пишем под разрядом десятков, 1 запоминаем.
Умножаем на десятки:
Умножаем на сотни:
9 сотен × 3 = 27 сотен, 7 пишем в разряд тысяч, а 2 в разряд десятков тысяч.
3 этап: складываем оба неполных произведения.
Складываем поразрядно, учитывая сдвиг.
В результате получаем:
924 × 35 = 32340
Умножим трехзначное число на трехзначное:
Возьмем первый множитель из предыдущего примера, а второй множитель тоже из предыдущего, но больше на 8 сотен:
924 × 835
Итак, два первых этапа такие же, как в предыдущем примере.
3 этап: находим третье неполное произведение, умножив 924 на 8
Умножаем 8 последовательно на все разряды первого множителя. Результат пишем под вторым неполным произведением со сдвигом влево, в разряд сотен.
4 × 8 = 32, пишем 2 в разряд сотен, 3 запоминаем
2 × 8 = 16 + 3 (запоминали) = 19, пишем 9 в разряд тысяч, 1 запоминаем
9 × 8 = 72 + 1 (запоминали) = 73, пишем 73 в разряды сотен и десятков тысяч соответственно.
4 этап: складываем три неполных произведения.
В результате получаем:
924 × 835 = 771540
Итак, сколько разрядов во втором множителе, столько и будет слагаемых в сумме неполных произведений.
Возьмем два множителя с одинаковой разрядностью:
3420 × 2700
При умножении двух чисел оканчивающихся нулями пишем одно число под другим так, чтобы нули обоих множителей остались в стороне.
Теперь умножаем два числа, не обращая внимания на нули:
342 × 27 = 9234
Общее количество нулей приписываем к получившемуся произведению.
В результате получаем:
3420 × 2700 = 9234000
Подведем итог. Для того чтобы письменно в столбик умножить два числа друг на друга, надо:
1. Сравнить два числа и меньшее написать под большим, единицы под единицами, десятки под десятками и так далее. Если числа с нулями, то пишем одно число под другим так, чтобы нули обоих множителей остались в стороне.
2. Умножаем последовательно каждый разряд второго множителя, начиная с единиц, на все разряды первого множителя. На нули внимания не обращаем
3. Неполные произведения пишем друг под другом, сдвигая каждое неполное произведение на один разряд влево. Сколько во втором множителе значащих разрядов (не 0), столько будет неполных произведений.
4. Складываем все неполные произведения.
5. К полученному результату приписываем нули из обоих множителей.
Вот и все, спасибо, что Вы с нами!
Понравилась статья — поделитесь с друзьями:
Оставляйте пожалуйста комментарии в форме ниже
|
1. |
Мотивация. (самоопределе ние к учебной деятельности). Цель: Мотивация учащихся к учебной деятельности на личностно-значимом уровне |
Создаёт условия для возникновения внутренней потребности включения в деятельность. У: Добрый день ребята! Садитесь. Я приглашаю вас на урок «Математики». Ребята, для того, чтобы вы поверили в свои силы и вам легко работалось на уроке, повторите за мной следующие слова:
У: Повернитесь лицом к соседу, скажите ему:
Cегодняшний урок я хочу начать словами французского философа Ж.Ж. Руссо.
«Вы талантливые дети! Когда-нибудь вы сами приятно поразитесь, какие вы умные, как много и хорошо умеете, если будете постоянно работать над собой, ставить новые цели и стремиться к их достижению. Вы готовы к работе? Тогда в путь. |
Включаются в учебную деятельность. Слушают учителя.
Садятся за парты.
Хором повторяют.
Поддерживают диалог.
|
Личностные УУД: самоопределение |
2. |
Актуализация знаний. Цель: Готовность мышления и осознания потребности к построению нового способа действий. |
Ведёт подводящий диалог. ( Активизирует у учащихся мыслительные операции, внимание, память) 1. Проверка домашнего задания. — С домашним заданием все справились?
2. – Откройте тетради. Запишите число. Классная работа. Минутка чистописания. У вас на столах листы самоконтроля. По мере выполнения заданий вы будете себя оценивать.
3. Устный счет. Работа в парах. Заполните таблицу.
Проверка. -Как найти скорость? -Как найти расстояние? -Как найти время?
— Посмотрите внимательно на экран и предложите работу, которую мы можем выполнить.
Исследуйте первое выражение. -Какую закономерность вы установили.
-Предлагаю, прежде чем вы назовёте произведение, объяснить приём умножения. 1)6·9= 54 2) 26·3 3) 139·0 4) 264·10 5) 92· 100 6) 532·300 ( По мере поступления ответов на экране появляются результаты рассуждения) (Слайд 2) |
Участвуют в диалоге.
Все правильно выполнено — +; Одна ошибка – V; Больше ошибок — —.
Во время проверки таблицы вспоминают взаимосвязь между величинами: скорость, расстояние, время.
— Можно посчитать треугольники. — Можно выявить закономерность.
Вспомнить название чисел при умножении. 1) табличное умножение 2) внетабличное умножение ( разбиваем на разрядные слагаемые) 3) умножение на нуль 4) увеличение числа в 10 раз, приём умножения на 10 5) приём умножения на 100 6) затрудняются
|
Познавательные УУД: — Общеучебные; — Логические;
Коммуникативные УУД: — умение вступать в диалог и участвовать в коллективном обсуждении проблемы; |
3. |
Постановка учебной задачи. Создание проблемной ситуации. Цель: Выявление места и причины затруднения, постановка цели урока. |
1. Ведёт побуждающий диалог. — Почему вы затрудняетесь назвать произведение в 6 треугольнике? Побуждает к осознанию темы и цели урока.
— Как вы думаете, какова же тема нашего урока?
— Я предлагаю вам два варианта решения данной проблемы. 2. Стимулирует к деятельности. — Первый: Сама покажу вам приём умножения. Второй – на основе ранее полученных знаний попробуете решить сами. — Какой вариант выберете вы и почему?
|
Участвуют в диалоге. — Не можем, так как с этим приёмом умножения ещё не знакомы (умножение на числа, оканчивающееся нулями) Формулируют тему урока. —Умножение многозначных чисел на числа, которые оканчиваются нулями.
Дети предпочитают « открывать» новое знание сами.
|
Познавательные УУД: — постановка и формулирование проблемы — поиск и выделение необходимой информации
Регулятивные УУД: — целеполагание; Коммуникативные: — умение выражать свои мысли; |
4 |
« Открытие» детьми нового знания. Цель: Построение детьми нового способа действий и формирование способности к его выполнению. |
1. Организует деятельность. (Слайд 3) — Великий Сократ говорил о том, что научиться играть на флейте можно только, играя самому. —Так и вы можете научиться умножать такие числа, думая только своей головой и пытаясь решить самостоятельно. — У кого есть предположения, как можно его вычислить? Хорошо, если вычислим на калькуляторе, получим готовый ответ, мы пополним копилку наших знаний?
— Вы предложили устно выполнить вычисления. Как именно? — Какой закон математики вы применили? ( Слайд 4) — Всегда ли устно можно быстро и правильно выполнить умножение многозначного числа, учитывая то, что числа могут быть большими? — Какой способ мы можем ещё использовать? — Умеем мы это правильно делать?
— Дайте более точную формулировку темы нашего урока.
— Какую учебную задачу вы поставите перед собой?
2.- Запишите пример столбиком и самостоятельно решите его.
— Где мы можем проверить правильность наших рассуждений? — Откройте учебники на стр.13, внимательно рассмотрите образец и сравните со своим решением. — Я прошу поднять руку тех ребят, которые выполнили умножение так, как показано в учебнике. — Молодцы. Значит, вы умеете применять ранее полученные знания. — Открытые вами знания позволили найти произведение в 6 треугоьнике? ( Слайд 6)
— Сейчас объясним приём умножения на доске. 3. Вызывает к доске ученика, верно решившего пример.
— У кого другая запись?
4. Организует работу в парах по составлению алгоритма умножения. — Чтобы правильно решать такие примеры, нужно знать алгоритм решения. — Что такое алгоритм? — Сейчас мы его составим. У вас на партах конверты с карточками, на которых напечатаны действия алгоритма. Работая и обсуждая в парах, вы разложите карточки в нужном порядке.
Выводит алгоритм на экран. (Слайд 7) |
Выдвигают гипотезы: — устно — на калькуляторе
— столбиком. -Нет.
Объясняют приём умножения. 532·300= 532·(3·100)= 532·3·100=159600 — Сочетательный закон.
— Не всегда.
— Решение столбиком. -Нет. Дети формулируют тему и учебную задачу урока. — Письменное умножение на числа, оканчивающиеся нулями. — Мы должны научиться письменно умножать многозначные числа /в столбик/ на числа, которые оканчиваются нулями.
Пытаются решить пример самостоятельно.
— В учебнике.
Дети открывают учебники и сравнивают своё решение с образцом.
Называют произведение в треугольнике.
Объясняют приём умножения. — Выполняем умножение, не глядя на нули, а затем к результату приписываем столько нулей, сколько содержится во втором множителе.
— Пошаговое выполнение действий.
Открывают конверты. Располагают карточки в нужном порядке. Одна пара зачитывает.
1. 2.Умножаю многозначное число на число, не обращая внимания на нули. 3.К полученному результату приписываю нули. 4.Читаю ответ.
|
Познавательные УУД: — построение логической цепи рассуждений; — самостоятельное создание способов решения проблем поискового характера; Коммуникативные УУД: — инициативное сотрудничество в поиске и сборе информации со сверстниками и учителем; |
5. |
Первичное закрепление с проговарива- нием. Цель:
Зафиксировать способ письменного умножения на числа, оканчивающиеся нулями. |
1.Организует работу по закреплению нового знания. — Закрепим полученные знания, выполнив письменное умножение с объяснением на доске. ( с.13 №40 – 1 строчка) (К доске вызывает сначала « сильного» ученика, затем «слабого».) — Понятен ли вам этот вычислительный приём? — Как проверить, что вы его усвоили?
(Учитель даёт инструктаж по выполнению задания.) -Давайте проверим. — У каждого из вас имеется карточка. На ней записаны примеры. ( 735 ·500 6307 · 40)
Предлагаю спрогнозировать предполагаемый результат: в верхнем углу карточки вы видите круг. Закрасьте его зелёным цветом, если вы уверены в своих силах. Жёлтым цветом – если сомневаетесь. Красным цветом – если вам нужна помощь. Кому нужна помощь, обращайтесь к алгоритму. А теперь приступим. — Передайте карточку соседу. Выводит ответы к заданию на экран. ( Слайд 8) — Если нет ошибок, закрасьте нижний круг зелёным цветом, если есть ошибки – жёлтым. — Верните карточку владельцу. — Совпал ли ваш прогноз с результатом?
|
Два ученика работают у доски, остальные в тетради.
— Решить примеры самостоятельно.
Прогнозируют результат и выполняют задание.
Взаимопроверка по готовым ответам с доски.
— Ответы детей / Мой прогноз совпал с результатом, был уверен и правильно выполнил. — Мой прогноз не совпал с результатом, я был уверен, что справлюсь, но допустил ошибку./ |
КоммуникативныеУУД: Умение выражать свои мысли; Регулятивные УУД: Овладение алгоритмом умножения;
|
8. |
Включение нового в систему знаний и повторения. Цель: — закрепить умение решать текстовые задачи; — применение нового способа действия; — создание ситуации успеха. |
Организует индивидуальную работу с последующей проверкой в группе и самопроверкой по эталону.
1. Внимание на экран. ( Слайд 9) Перед вами 4 задания.
— Какое из них далеко от темы нашего урока?
А) 736·300 6 324· 50 Б) 6 895+ 72 456 + 658 В) 784 · 600 + 2 907 · 30 Г) х· 4= 432·30
Осталось 3 задания. — Выберите себе то, которое для вас более интересно и которое вы можете выполнить. Выполните его. / Учитель проходит по классу, наблюдает, какой уровень выбрал каждый из учащихся и кладёт рядом с его работой фишку (цвет фишки – уровень сложности выбранного задания)/ — А теперь, ребята, попрошу вас собраться в группы в соответствии с выполненным заданием. Проверьте своё решение с решением товарищей. — Садитесь на свои места, посмотрите внимательно на экран и сверьте свою работу с образцом. (слайд 10-12) |
Анализируют и делают вывод, что лишнее задание Б.
— Лишнее задание Б, так как оно не подходит к теме нашего урока. Формулируют уровень сложности заданий и конкретизируют их. А – выполнить умножение столбиком В- вспомнить порядок действий и вычислить. Г- решить уравнение.
Выбирают и выполняют задание.
Собираются в группы по цвету фишек с целью взаимопроверки.
Сверяют решение с образцом на слайдах. Исправляют ошибки и фиксируют затруднения. |
Познавательные УУД: — анализ с целью выделения главных признаков; — умение осознанно строить речевое высказывание в устной форме; — выделение и поиск необходимой информации;
Коммуникативные УУД: — умение достаточно полно и чётко выражать мысли;
-интегрирование в группы и продуктивное взаимодействие.
Регулятивные УУД: — планирование; — контроль; — коррекция; — самооценка.
|
9. |
Рефлексия учебной деятельности. Цель: — Оценить результаты собственной деятельности;
— Осознание метода построения границ применения нового знания.
|
Благодарит ребят за работу. Вы все очень постарались. — Огромное трудолюбие и ваша тяга к знаниям помогла нам сделать на уроке открытие. Эта удача приблизила ещё на один шаг каждого из вас к успеху. — Какая тема нашего урока?
— Какую учебную задачу мы ставили перед собой?
— Чему новому научились?
— Достигли мы успеха? На память о нашем уроке, чтобы вы ничего не забыли: домашнее задание, запишите в дневник. (Слайд 14) Проводит инструктаж домашнего задания. стр.13 № 40 (нижняя строчка)– обязательное для всех № 42 – предлагаю тем, кто не боится трудностей. Оценивание работы учащихся ВЫСТАВЛЕНИЕ ОЦЕНОК (по листу самоконтроля) — Где и в каких случаях знания, полученные на уроке, могут пригодиться в жизни?
|
Дети вспоминают тему и учебную задачу урока. — Умножение многозначных чисел на числа, которые оканчиваются нулями. — Научиться письменно умножать на числа, оканчивающиеся нулями.
— Научились письменно умножать на числа, оканчивающиеся нулями.
-Достигли.
Записывают задание в дневники.
Тот, кто поднялся, анализирует и оценивает свою работу на уроке. |
Регулятивные: — оценка того, что усвоено, осознание качества и уровня усвоения. Познавательные: — умение структурировать знания;
Коммуникативные УУД: — аргументировать свои высказывания;
|
Письменное умножение многозначных чисел на числа, оканчивающиеся нулями
Класс: 4 Предметная область: математика, УМК « Школа России» Составила учитель начальных классов: Завалищина Т.Ю.
Чкаловская школа – интернат московской области
Тип урока: урок «открытия» новых знаний. Первый урок в изучении темы.
Тема: «Письменное умножение на числа, оканчивающиеся нулями».
Цели: формировать у учащихся умения овладеть письменным приёмом умножения на числа, оканчивающиеся нулями; использовать данный прием в системе ране изученных знаний; совершенствовать вычислительные навыки, умение решать задачи.
Учебные задачи, направленные на достижение личностных результатов обучения:
— принятие и освоение социальной роли обучающегося, развитие мотивов учебной деятельности и формирование личностного смысла учения.
Учебные задачи, направленные на достижение метапредметных результатов обучения:
— овладение способностью принимать и сохранять цели и задачи учебной деятельности, поиска средств её осуществления;
— готовность анализировать, сравнивать, делать выводы, составлять алгоритм решения и пользоваться им; слушать собеседника и вести диалог; готовность признавать возможность существования различных точек зрения, излагать своё мнение и аргументировать свою точку зрения; готовность оценить свою работу.
Учебные задачи, направленные на достижение предметных результатов обучения:
— Формирование умения выполнять устно и письменно арифметические действия с числами и числовыми выражениями; составлять краткую запись и рассуждать по ней; решать текстовые задачи, уравнения, определять части круга, переводить одни единицы времени (длины) в другие; выполнять и строить алгоритм; представлять, анализировать данные.
Оборудование урока: ПК, презентация к уроку, раздаточный материал (карточки с заданиями, алгоритм умножения на карточках). Учеб
ник: М.И.Моро « Математика» 4 класс, часть 2.
Прогнозируемые результаты:
Предметные. В конце урока ученики должны знать: 1. Алгоритм письменного умножения на числа, оканчивающиеся нулями.
2.Уметь письменно умножать на числа, которые оканчиваются нулями.
Метапредметные
1.Умеют ставить учебную задачу и самостоятельно формулировать выводы.
2.Умеют слушать собеседника, излагать своё мнение и аргументировать свою точку зрения.
Личностные. Должны уметь сотрудничать с учителем и сверстниками
№ п./п
Этапы урока
Деятельность учителя
Деятельность учащихся
Формируемые УУД (называть виды с расшифровкой)
I.
Организационный
момент (1 мин)
Цель:
мотивация учащихся к учебной деятельности на личностно-значимом уровне
Создаю условия для возникновения внутренней потребности включения в деятельность.
Прозвенел звонок – начинается урок.
Чтоб урок прошёл прекрасно,
Хорошо, отлично, классно
Наберитесь вы терпенья,
Лень отбросьте и тогда, все получится, друзья!
Хором дополняют реплику учителя.
Садятся за парты
Личностные УУД:
Самоорганизация на учебную деятельность.
II
Этап подготовки
к активному, сознательному усвоению знаний.
/5 мин./
1.Устный счет: 9000 х 7; 2500 х 3; 4700 х 2
2.Проверка домашнего задания (Вычислить результаты удобным способом. № 36(с. 12))
— Проверим первый и четвертый примеры.
12 х (5 х7)
— Назовите значение выражения.
— Какой способ вам помог найти результат?
— Поднимите руку, кто выбрал такой же способ?
17 х (4 х 10)
— Почему?
— Каким свойством пользовались при вычислениях?
9 сот. х 7 = 63 сот. = 6300
Объясняют свой выбор
(420) (Ученик: «Я считаю, что удобно (12х5) х7, т. к. в первом действии получаю круглые десятки, а их легко умножить на 7)
(Все)
17 х (4 х 10) – способ выбрал 1 ребенок
(17х4)х10 – остальные ребята
Это удобнее, т.к. двузначное число легче умножать на однозначное нежели на трехзначное
-Применяли свойство умножения числа на произведение.
Актуализировать знания для проведения простейших математических вычислений
Развитие навыков формулировки личной оценки, аргументирования своего мнения
Познавательные УУД:
— Общеучебные;
— Логические;
III.
Постановка темы и задач урока
(3мин)
1.)Самоопределение к деятельности.
Коммуникативные УУД:
— умение вступать в диалог и участвовать в коллективном обсуждении проблемы;
Создание проблемной ситуации.
/Цели:
выявление места и причины затруднения, постановка цели урока;
.
6·9=
26·3 139·0
264·10
92· 100
532·300
Веду подводящий диалог.
— Посмотрите внимательно на экран и предложите работу, которую мы можем выполнить.
-Предлагаю, прежде чем вы назовёте произведение, объяснить приём умножения.
( По мере поступления ответов на экране появляются результаты рассуждения)
(Слайд 3)
Участвуют в диалоге, объясняют приемы умножения.
— Можно посчитать фигуры. (Считают)
— Можно назвать доли круга. (Называют)
— Можно найти значения выражений.
1) табличное умножение
2) внетабличное умножение
( разбиваем на разрядные слагаемые)
3) умножение на нуль.
4) умножение на 10 (умножить на 1 и добавить 0)
5) умножение на 100 (приписать к 92 два нуля)
6) В ¼ круга — такие примеры не решали
Цель:
активизировать у учащихся мыслительные операции, внимание, память и побудить к осознанию темы
2. Постановка темы и учебной задачи
Ведёт побуждающий диалог.
— Почему вы затруднились назвать произведение в 1/4 круга?
Побуждаю к осознанию темы и цели урока.
— Как вы думаете, какова же тема нашего урока?
Какие варианты решения данной проблемы вы можете предложить?
Используйте ранее полученные знания, попробуете решить сами.
— Какой вариант выберете и почему?
Участвуют в диалоге.
— Потому что с этим приёмом умножения ещё не знакомы (умножение на числа, оканчивающееся нулями, где первая цифра частного больше единицы)
Формулируют тему урока.
-Умножение многозначных чисел на числа, которые оканчиваются нулями.
Дети предпочитают « открывать» новое знание сами.
Познавательные УУД:
— постановка и формулирование проблемы
— поиск и выделение необходимой информации
Регулятивные УУД:
— целеполагание;
Коммуникативные:
— умение выражать свои мысли;
IV
.
«Работа по теме»
(Всего 15 мин)
1. « Открытие» детьми нового знания.
/5 мин./
Цель:
построение детьми нового способа действий и формирование способности к его выполнению
2. Составление алгоритма письменного умножения многозначного числа на число, которое оканчивается нулями (3 мин)
1. Организует деятельность.
— У кого есть предположения, как можно его вычислить?
— Вы предложили устно выполнить вычисления. Как именно?
— Какой закон математики вы применили? ( Слайд 4)
— Хорошо, если вычислим на калькуляторе, получим готовый ответ, мы пополним копилку наших знаний?
— Всегда ли устно можно быстро и правильно выполнить умножение многозначного числа, учитывая то, что числа могут быть достаточно большими?
— Какой способ мы можем ещё использовать?
— Умеем мы это правильно делать?
— Дайте более точную формулировку темы нашего урока.
— Какую учебную задачу вы поставите перед собой? ( Слайд 5)
2.Предлагаю записать пример столбиком самостоятельно и решить его.
— Где мы можем проверить правильность наших рассуждений?
— Откройте учебники на стр.13, внимательно рассмотрите образец и сравните со своим решением.
— Я прошу поднять руку тех ребят, которые выполнили умножение так, как показано в учебнике.
— Молодцы. Значит, вы умеете применять ранее полученные знания.
— Сейчас объясним приём умножения на доске.
3. Вызывает к доске ученика, верно решившего пример.
— Сделаем вывод
— Открытые вами знания позволят сформулировать алгоритм письменного умножения многозначного числа на числа, оканчивающиеся нулями.
4. Организую работу в парах по составлению алгоритма умножения.
— Чтобы правильно решать такие примеры, нужно знать алгоритм решения.
— Что такое алгоритм?
— Сейчас мы его составим.
У вас на партах карточки, на которых напечатаны действия алгоритма. Работая и обсуждая в парах, вы разложите карточки в нужном порядке.
Вывожу алгоритм на экран. (Слайд 6)
Выдвигают гипотезы:
1- устно 532 х (3 х 100) =(532 х 3) х100
— Сочетательный закон
2 — на калькуляторе
-Нет. ( Представьте, что нет источника питания)
3 — столбиком.
Дети формулируют тему и учебную задачу урока.
— Письменное умножение на числа, оканчивающиеся нулями.
— Мы должны научиться письменно умножать многозначные числа
/в столбик /на числа, которые оканчиваются нулями.
Пытаются решить пример самостоятельно.
— В учебнике.
Дети открывают учебники и сравнивают своё решение с образцом.
(8 человек решили так:
х 532
300
159600
2 человека решили так:
х 532
300
159600
Называют произведение в ¼ круга.
Объясняют приём умножения.
— 532 х 300
3х100, значит (опираясь на свойства умножения)
я сначала х532
3_
и получу 1596, а затем
умножу на 100, (умножу на 1 и добавлю 00)
и получу 159600
— Выполняем умножение, не глядя на нули, а затем к результату приписываем столько нулей, сколько содержится во втором множителе.
— Пошаговое выполнение действий.
Открывают конверты. Располагают карточки в нужном порядке.
Одна пара зачитывает.
1.Второй множитель записываю так, чтобы нули остались в стороне.
2.Умножаю многозначное число на число, не обращая внимания на нули.
3.К полученному результату приписываю нули.
4.Читаю ответ.
Познавательные УУД:
— построение логической цепи рассуждений;
— самостоятельное создание способов решения проблем поискового характера;
Коммуникативные УУД:
— инициативное сотрудничество в поиске и сборе информации со сверстниками и учителем;
Познавательные УУД:
— построение логической цепи рассуждений;
— самостоятельное создание способов решения проблем поискового характера;
Умение сравнивать, анализировать, давать оценку своим действиям
Создание алгоритма деятельности при решении проблемы.
V.
3. Первичное закрепление с проговарива-
нием.
/4 мин./
Цель:
Зафиксировать способ письменного умножения на числа, оканчивающиеся нулями в решении примеров.
4. Самостоятельная работа (3мин)
Включение нового в систему знаний и повторения.
/Всего13 мин./
1.Работа по карточками с прогнозированием результатов.
Закрепление новых знаний и повторение (3 мин)
Задачи перед детьми: прогнозировать свои результаты; сравнивать прогноз и результат; объяснять причину ошибки
Организую работу по закреплению нового знания.
1)Фронтальная работа с проговариванием вслух.
— Закрепим полученные знания, выполнив письменное умножение с объяснением на доске. ( С.13 №40 – 1 строчка)
— Понятен ли вам этот вычислительный приём?
— Как проверить, что вы его усвоили?
2) Самостоятельная работа (с.13 №40 – 2 строчка)
Даёт инструктаж по выполнению задания.
1)Работа с карточкой
— У каждого из вас имеется карточка. На ней записаны 2 задания: первое в виде теста, а второе — задача
1. Укажи произведение чисел 154 х 500
7700 77000 77200
2*. Пол в коридоре нужно покрыть прямоугольным куском линолеума длина которого 2м , а ширина 8 дм 5 см. Какова его площадь?
Предлагаю спрогнозировать предполагаемый результат: в верхнем углу карточки и около второго задания вы видите овалы.
— Закрасьте их зелёным цветом, если вы уверены в своих силах. Жёлтым цветом – если сомневаетесь. Красным цветом – если вам нужна помощь.
— Кому нужна помощь, обращайтесь к алгоритму. ( А тем, кто запутался с задачей предлагаю карточку с частичным планом решения)
— Критерий оценки – правильность счёта, безошибочность. А теперь приступим.
— Передайте карточку соседу.
Вывожу ответы к заданию на экран.
( Слайд 7)
— Если нет ошибок, закрасьте нижний треугольник зелёным цветом, если есть ошибки – жёлтым.
— Верните карточку владельцу.
— Совпал ли ваш прогноз с результатом?
Два ученика работают у доски, остальные в тетради.
— Решить примеры самостоятельно.
Решают. Выполняют взаимопроверку и, если понадобится, оказываю помощь друг другу.
Прогнозируют результат и выполняют задание.
Взаимопроверка по готовым ответам с со слайда.
— Ответы детей / Мой прогноз совпал с результатом, был уверен и правильно выполнил.
— Мой прогноз не совпал с результатом, я был уверен, что справлюсь, но допустил ошибку./
Решают.
Проверяют и сравнивают, закрашивают.
Делают вывод и, если надо, исправляют ошибки.
КоммуникативныеУУД:
Умение выражать свои мысли;
Регулятивные УУД:
Овладение алгоритмом умножения;
Регулятивные УУД:
Самоконтроль;
Коррекция
Взаимопроверка
Прогнозирование результатов.
Сравнение прогноза и результата
Коммуникативные УУД:
Учебное сотрудничество;
Физминутка
(2 мин)
Музыкальная пауза
;
2.Какое из заданий не отвечает теме нашего урока?
/5 мин./
Цель: учить анализировать с целью выделения новогоприема умножения среди материала для повторения..
Тренировать способность к самоконтролю по эталону и самооценке.
Учить работать в группах и четко выражать свои мысли.
3. Работа над задачей в учебнике
(5 мин)
Цель: создать условия для индивидуального рассуждения над ходом решения задачи, используя совместно составленную таблицу.
1) Организую индивидуальную работу с последующей проверкой в группе и самопроверкой по эталону.
-Внимание на доску. Перед вами 4 задания.
— Какое из данных заданий не отвечает теме нашего урока?
— обычное
а) 6 324· 50 — 736·300
б) х : 4= 432·200 — сложное
в)6 895+ (72 456 — 658)
г) 2сут. =_______мин — самое сложное
Осталось 3 задания.
— Выберите себе то, которое для вас более интересно и которое вы в силах выполнить.
— Выполните его.
/ Прохожу по классу, наблюдаю, какой уровень выбрал каждый из учащихся и кладу рядом с его работой фишку (цвет фишки – уровень сложности выбранного задания)/
— Ребята, попрошу вас собраться в группы в соответствии с выполненным заданием. Проверьте своё решение с решением товарищей.
— Посмотрите внимательно на доску и сверьте свою работу с образцом.
2) Организую работу над задачей.
— Вернёмся к учебнику. Задача № 43 (с. 13)
— Прочитайте задачу.
— О чём говорится в задаче?
— Что известно?
— Как звучит вопрос задачи?
— Как удобнее записать условие задачи?
— Правильно, в виде таблицы.
/В ходе работы составляется таблица/
— Обведите главный вопрос задачи.
— Можем ли мы сразу ответить на вопрос задачи?
-. Каких данных не хватает во второй строчке, чтобы ответить на этот вопрос?
— Что еще необходимо знать, чтобы найти количество фломастеров, если известно общее количество предметов?
— Какая строчка таблицы поможет найти число карандашей?
-Кто может провести свое рассуждение по таблице?
— Кто может рассказать ход решения задачи?
— Кто затрудняется? (Индивидуальный подход)
Предлагаю решить задачу в тетрадях.
Ответ обсуждаем всем классом.
Взаимоконтроль с проверкой по эталону.
/3 мин./
Цель:
-Тренировать способность к самоконтролю и самооценке.
— Проверить способность к умножению многозначных чисел на числа, оканчивающиеся нулями.
Анализируют и делают вывод, что лишнее задание в).
— Лишнее задание в), так как оно не подходит к теме нашего урока. Оно подошло бы к теме – сложение многозначных чисел и порядок действий.
Формулируют уровень сложности заданий и конкретизируют их.
а) – обозначить порядок действий, выполнить умножение и сложение столбиком
в)- решить уравнение
г) – перевести одни единицы времени в другие
Выбирают и выполняют задание.
Собираются в группы по цвету фишек с целью взаимопроверки.
Сверяют решение с образцом на доске
Исправляют ошибки.
Дети отвечают на вопросы учителя по содержанию задачи.
Кол-во в 1 кор.
Кол-во кор.
Всего штук
карандаши
12шт.
40 к.
?
560
фломастеры
? шт.
10 к.
?
1 ученик записывает решение задачи на доске.
(Количество фломастеров в одной ко-ке)
(- Нет)
(- Количество фломастеров в 10 кор-ках)
(- Надо знать количество карандашей в 40 коробках)
(- Первая)
Один из учеников рассказывает ход решения задачи.
Рассуждение начинают так: -Из первой строки таблицы могу найти количество карандашей в 40 коробках (40 х 12) – эту сумму вычту из 560 и найду недостающее число в 3 столбике, т. е. общее число фломастеров. Осталось ответить на главный вопрос.
( Решают.) Оценивают свою работу
Познавательные УУД:
— анализ с целью выделения главных признаков;
— умение осознанно строить речевое высказывание в устной форме;
— выделение и поиск необходимой информации.
Коммуникативные УУД:
— умение достаточно полно и чётко выражать мысли;
-интегрирование в группы и продуктивное взаимодействие.
Регулятивные УУД:
— планирование;
— контроль;
— коррекция;
— самооценка.
10.
11.
12
Итог урока
1 мин
Рефлексия учебной деятельности.
/ 2 мин./
Цель:
— Оценить результаты собственной деятельности.
Домашнее задание
(1 мин)
— Какая тема нашего урока?
— Какую учебную задачу мы ставили перед собой?
— Что надо помнить, выполняя умножение чисел, оканчивающихся нулями, столбиком?
— Поднимите руку кто уверен в том, что понял новое правило письменного умножения?
— Какой этап урока вам больше понравился? Оцените свою работу на уроке.
Провожу инструктаж домашнего задания.
С. 14 № 47
Дети вспоминают поставленную цель и учебную задачу урока.
— Умножение многозначных чисел на числа, которые оканчиваются нулями.
— Научиться письменно умножать на числа, оканчивающиеся нулями.
— Выполнять умножение, не глядя на нули, а затем к результату приписывать столько нулей, сколько содержится во втором множителе.
Ответы детей
Анализируют и оценивают свою работу на уроке.
.
Записывают задание в дневники.
Регулятивные:
— оценка того, что усвоено, осознание качества и уровня усвоения.
Познавательные:
— умение структурировать знания;
Коммуникативные УУД:
— аргументировать свои высказывания;
Цель:
— закрепить умение решать текстовые задачи;
— применение нового способа действия;
— создание ситуации успеха.
Б) Умножение на числа, оканчивающиеся нулями — Мегаобучалка
Следует отметить, что при изучении умножения, многозначных чисел на числа, оканчивающиеся нулями, вычисления обязательно опираются на случаи умножения и деления на числа 10, 100,1000. Эти случаи умножения и деления уже рассматривались с детьми при изучении еще нумерации многозначных чисел. Теперь к этим случаям умножения и деления обязательно следует вернуться. Причем их не целесообразно разделять, как это предлагают авторы учебников.
Теоретической основой вычислительного приема, используемого при умножении на числа, оканчивающиеся нулями, является правило умножения числа на произведение. Это правило является для детей новым. Его рассмотрению следует уделить внимание. Однако, по сравнению с другими правилами, при раскрытии его сути достаточно использовать только числовой материал.
Приведем вариант разговора с детьми, который может быть таким.
Учитель. Прочитайте выражение и вычислите его значение 2 • (3 • 4)
Дети. Число 2 умножить на произведение чисел 3 и 4. Чтобы вычислить значение, надо найти произведение (выполнить действие в скобках), получаем 12, а затем 2 умножить на 12, получим 24.
Учитель. Давайте запишем.
2 •(3•4) = 2 • 12=24.
А теперь давайте попробуем умножить число 2 на произведение чисел 3 и 4 по-другому. Умножим вначале число 2 на первый множитель 3. А затем, что надо сделать?
Дети. Полученный результат умножить на второй множитель 4.
Учитель. Верно, то есть, 2 • (3 • 4) = (2 • 3) • 4 = 6 • 4 = 24.
Ответ мы получили один и тот же. О чем это говорит?
Дети. Рассуждения ведем верно.
Учитель. А теперь давайте попробуем число 2 умножить на второй множитель:
2 • (3 • 4) = (2 • 4) • 3 = 8 • 3 = 24.
Видим, что результат один, значит, рассуждали верно. Давайте обобщим и сделаем вывод, как можно умножать число на произведение.
Дальнейшая работа над правилом продолжается в том же плане, как и для всех других:
— формируем умение применять все три способа вычислений;
— учим выделять удобный способ;
— учим применять правило для вычислений.
Затем переходим к рассмотрению случаев умножения многозначных чисел на числа, оканчивающиеся нулями. Начинаем с устного приема, чтобы показать ход рассуждений. Например:
12 • 40 = 12 • (4 • 10) = (12 • 4) • 10 = 48 • 10 = 480.
Подводим детей к выводу, что фактически умножаем 12 на 4 и приписываем столько нулей, сколькоих во втором множителе. Затем дается задание объяснить решение примера:
306 • 90 = 306 • (9 • 10) = (306 • 9) • 10 = 2754 • 10 = 27 540.
После этого переходим к рассмотрению письменного умножения на числа, оканчивающиеся нулями, т.е. к записи в столбик.
Предлагаем решить пример. 583 • 70. Выясняем, что устно решить трудно, Надо записать столбиком. Как это сделать? Это покажет ход рассуждений. 583 • 70 = 583 • (7 • 10) = (583 • 7) • 10 = 4081 • 10 = 40810.
Значит, 583 будем умножать на 7, а полученный результат умножим на 10. Отсюда запись: второй множитель 70 пишем так, чтобы цифра 7 стояла под цифрой 3.
583 583
Х х
7 70
4 081 41 810
Рассуждения: 583 умножим на 7, получим 4081 и приписываем ноль, получаем 40 810.
Отдельно выделяется и рассматривается случай, когда оба множителя оканчиваются нулями. Начинаем опять с устного приема, чтобы уяснить ход рассуждений.
30 • 50 = 3 дес. • (5 • 10) = (3 дес. • 5) • 10 = 150 дес. = 1500.
800 • 60 = 8 сот. • (6 • 10) = 48 сот. • 10 = 48 000.
2600 • 60 и т.д.
Подмечаем с детьми, что практически надо перемножить значащие части чисел и приписать столько нулей, сколько их в двух множителях вместе.
Такие примеры записываются в строчку и решаются устно. При письменном умножении запись делается в столбик, причем эта запись должна отражать ход рассуждений.
2600 4250 1860
х 80 х 70 х 300
208000 297500 558000
Следует обратить внимание на тот факт, что после ознакомления с новым приемом вычисления, где надо один из множителей представлять в виде произведения, учащиеся начинают путать этот прием умножения числа на произведение с приемом умножения числа на сумму.
1. Чтобы предупредить такие ошибки надо предлагать учащимся упражнение на сравнение соответствующих приемов вычисления. Например:
15 • 60= 15•(б • 10) = (15 •6) • 10 = 90 •10=900.
15 • 14 =15•(10+4)== 15• 10 + 15 • 4 = 150 + 60 = 210.
В) Умножение на двузначное и трехзначное число
Теоретическая основа вычислительных приемов, используемых при рассмотрении этих случаев умножения — правило умножения числа на 4 сумму, которое предварительно изучается.
Рассмотрение случаев умножения на двузначное число полезно начать с устного приема, чтобы показать ход рассуждений:
14•13 =14•(10+3)= 14 • 10 + 14 • 3 = 140 + 42 = 182.
Затем целесообразно усложнить задание. 67 • 45 = 67 • (40 + 5) = 67 • 40 + 67 • 5 = 2680 + 335 =3015.
Устно выполнить трудно, можно предложить сделать вычисления письменно.
67 67 2680
х х +
40 5 335
2680 335 3015
В ходе этих рассуждений подводим детей к выводу, что надо найти два неполных произведения и их сложить, то есть данное число умножаем на число десятков второго множителя; затем это число умножаем на число единиц второго множителя. Полученные результаты складываем. Если устно умножать трудно, лучше записать столбиком. Умножать начинаем с единиц. Показываем ход рассуждений при этом.
Х 45
+2680
Умножаем 67 на 5, получим 335 единиц. Теперь умножим 67 на 40. Для этого умножаем 67 на 4 и полученное число умножим на 10, получаем 2680. Обращаем внимание, что 335 и 2680 — это неполные произведения. Число 3015 — полное произведение, или окончательный результат.
Обращаем внимание учащихся на то, что второе неполное произведение — это результат умножения на круглые десятки, поэтому всегда в нем на месте единиц стоит 0, его обычно не пишут. Это неполное произведение указывает на количество десятков в нем, его и начинают записывать под десятками первого неполного произведения.
Таким образом, рассуждения ведем так: 67 умножим на 5 единиц, получаем 335 единиц — первое неполное произведение. Теперь 67 умножим на 4 десятка, получаем 268 десятков — второе неполное произведение. Складываем.
При умножении на трехзначное число следует подвести детей к выводу, что рассуждения в принципе те же, только здесь будет добавляться только третье неполное произведение, а значит, третье слагаемое — какое-то количество сотен. Третье неполное произведение начинаем записывать под сотнями первого неполного произведения.
Практика показывает, что для того чтобы выработать прочные навыки безошибочных вычислений, нужно прорешать значительно количество упражнений и необходима достаточная тренировка. Кроме того, успех зависит и от того, насколько прочны знания учащихся таблицы умножения и как уверенно дети овладели навыками сложения двух-трех чисел.
После того как рассмотрены общие случаи умножения на двузначное и трехзначное число, рассматриваются частные случаи умножения, а именно случаи умножения чисел с нулями в середине второго множителя, Фактически здесь учащиеся встречаются с тем же самым приемами вычислений, но с некоторыми особенностями.
Например, 829 • 703. Для первого такого примера целесообразно показать детям более подробную запись:
829
х
703
+
После обсуждения дети подводятся к выводу, что второе неполное произведение здесь можно убрать. Отсюда приходим к записи:
Х 703
+5803
Такой подход позволит предупредить возникновение у детей ошибок в записи второго неполного произведения для аналогичных случаев.
Умножение на числа, выходящие за пределы трехзначных (4-хзначные, 5-значные и др.) по существу не отличаются от умножения на трехзначное число. Поэтому, овладев навыками умножения на трехзначное число, ученики смогут овладеть умением умножать многозначные числа на любое число.
И опять после рассмотрения всех случаев умножения многозначных чисел вводится умножение составных именованных чисел, выраженных в метрических мерах. Здесь умножение целесообразно выполнять одним способом: составное именованное число заменяется простым, выполняют действие над отвлеченными числами, а затем полученное простое именованное число заменяют составным.
7 м 85 см·18 = 141 м 30 см 4 ц 90 кг • 26 = 127ц 40 кг
Х 18
+785
См)
При изучении всех случаев умножения прежде всего необходимо добиться понимания вычислительного приема, после чего вести работу по формированию вычислительных навыков. А для этого надо своевременно и разумно сокращать объяснение решения и переходить к кратким пояснениям. Большее значение в этом имеет тщательно подобранная система тренировочных упражнений.
2. | Актуализация знаний . /5 мин./ Цель: Готовность мышления и осознания потребности к построению нового способа действий. | Веду подводящий диалог. ( Активизирую у учащихся мыслительные операции, внимание, память) — Посмотрите внимательно на экран. Перед вами числовые выражения. -Какую закономерность вы установили, исследуя первое выражение.? -Предлагаю, прежде чем вы назовёте произведение, объяснить приём умножения. 1)6·9= 54 2) 26·3 3) 139·0 4) 264·10 5) 92· 100 6) 500·5 ( По мере поступления ответов на экране появляются результаты рассуждения) | Участвуют в диалоге. — Можно выявить закономерность. 1) табличное умножение 2) внетабличное умножение ( разбиваем на разрядные слагаемые) 3) умножение на нуль 4) увеличение числа в 10 раз, приём умножения на 10 5) приём умножения на 100 6) затрудняются | Познавательные УУД: — Общеучебные; — Логические; Коммуникативные УУД: — умение вступать в диалог и участвовать в коллективном обсуждении проблемы; | 3. | Постановка учебной задачи. Создание проблемной ситуации. /5 мин/ Цель: Выявление места и причины затруднения, постановка цели урока. | 1. Веду побуждающий диалог. — Почему вы затруднились назвать произведение в 6 снежинке? Побуждаю к осознанию темы и цели урока. — Как вы думаете, какова же тема нашего урока? — Я предлагаю вам два варианта решения данной проблемы. 2. Стимулирую к деятельности. Предлагаю два варианта: — Первый : Сама покажу вам приём умножения. Второй – на основе ранее полученных знаний попробуете решить сами. — Какой вариант выберете вы и почему | Участвуют в диалоге. — Не можем, так как с этим приёмом умножения ещё не знакомы (умножение числа, оканчивающегося нулями) Формулируют тему урока. -Умножение чисел, запись которых оканчивается нулями. Дети предпочитают « открывать» новое знание сами. | Познавательные УУД: — постановка и формулирование проблемы — поиск и выделение необходимой информации Регулятивные УУД: — целеполагание; Коммуникативные: — умение выражать свои мысли; | 4 | . « Открытие» детьми нового знания. /9 мин./ Цель: Построение детьми нового способа действий и формирование способности к его выполнению. | 1. Организую деятельность. — Великий Сократ говорил о том, что научиться играть на флейте можно только, играя самому. -Так и вы можете научиться умножать такие числа, думая только своей головой и пытаясь решить самостоятельно. — У кого есть предположения, как можно его вычислить? — Хорошо, если вычислим на калькуляторе, получим готовый ответ, мы пополним копилку наших знаний? Как будем выполнять? — Вы предложили устно выполнить вычисления. Как именно? Может кто-то из вас сможет объяснить, как можно умножить 500 на 5? 18000* 3 =18 тыс. * 3 = 54 тыс.= 54 000 — Какой способ мы можем ещё использовать? — Умеем мы это правильно делать? — Дайте более точную формулировку темы нашего урока. — Какую учебную задачу вы поставите перед собой? 2.Предлагаю записать пример столбиком самостоятельно и решить его. А сейчас научимся записывать столбиком.
380 .9 8400 .7 69000 . 4 380 8400 69000 9 7 4 3420 58800 276000
— Сейчас объясним приём умножения на доске. 3. Вызываю к доске ученика, верно решившего пример. 8400 * 7 — У кого другая запись? 4. Организую работу в парах по составлению алгоритма умножения. — Чтобы правильно решать такие примеры, нужно знать алгоритм решения. — Что такое алгоритм? — Сейчас мы его составим. У вас на партах карточки, на которых напечатаны действия алгоритма. Работая и обсуждая в парах, вы разложите карточки в нужном порядке. Вывожу алгоритм на экран. | Выдвигают гипотезы: — устно — на калькуляторе — столбиком. -Нет. -устно. Объясняют приём умножения. Умножаем числа без нулей, а потом их приписываем. — Не всегда. — Решение столбиком. Дети формулируют тему и учебную задачу урока. — Письменное умножение чисел, запись которых оканчивается нулями. — Мы должны научиться письменно умножать многозначные числа /в столбик Пытаются решить пример самостоятельно. Под первой цифрой справа отличной от нуля. Объясняют приём умножения. — Выполняем умножение, не глядя на нули, а затем к результату приписываем столько нулей, сколько содержится в множителе. — Пошаговое выполнение действий. Располагают карточки в нужном порядке. Одна пара зачитывает. 1.Второй множитель подписываю под первой цифрой справа, чтобы нули остались в стороне. 2.Умножаю многозначное число на число, не обращая внимания на нули. 3.К полученному результату приписываю столько нулей, сколько их на конце первого множителя. 4.Читаю ответ. | Познавательные УУД: — построение логической цепи рассуждений; — самостоятельное создание способов решения проблем поискового характера; Коммуникативные УУД: — инициативное сотрудничество в поиске и сборе информации со сверстниками и учителем; |
Конспект урока «Письменное умножение на числа, оканчивающиеся нулями»
Тема урока «Письменное умножение на числа, оканчивающиеся нулями»1. Орг. момент
— На этом уроке мы рассмотрим письменное умножение на числа, оканчивающиеся нулями. Узнаем, как правильно умножать подобные числа в столбик, как можно использовать правило умножения числа на произведение чисел для облегчения умножения. Решим несколько примеров обеими способами. Пример 1Рассмотрим выражение: . Воспользуемся правилом умножения числа на произведение чисел, для этого заменим число 20 на произведение чисел 2 и 10, получим:
Удобно сначала умножить 134 на первый множитель, а затем получившийся результат умножить на второй множитель, ведь второй множитель – круглое число.
Умножение данного выражения можно записать столбиком. Для этого число 20 запишем таким образом, чтобы цифра 2 оказалась под единицами первого множителя:
Число 20 – это 2, умноженное на 10, умножим сначала число 134 на 2, не обращая внимания на ноль. 4 единицы умножить на 2 – 8 единиц, 3 десятка умножить на 2 – 6 десятков, и 1 сотня умножить на 2 – 2 сотни, получаем результат:
Умножим его теперь на второй множитель 10 и получим ответ:
Ответ: 2680.
Пример 2Рассмотрим выражение: . Воспользуемся правилом умножения числа на произведение чисел, для этого заменим число 400 произведением чисел 4 и 100:
При умножении числа на произведение чисел можно умножить сначала число на первый множитель, а затем получившийся результат умножить на второй множитель.
При записи вычислений в столбик запишем число 400 так, чтобы цифра 4 была под цифрами единиц первого множителя.
Умножим 316 на 4, не обращая внимания на нули.
, 4 записываем, 2 десятка запоминаем.
Далее, , и еще два запоминали, записываем .
И сотни: .
Теперь умножим результат на второй множитель 100, для этого достаточно приписать два нуля:
Ответ: 126 400.
Пример 3Рассмотрим частный случай умножения, когда оба множителя заканчиваются нулями.
530 – это 53 десятка. Заменим число 300 на произведение чисел 3 и 100:
Умножим 53 десятка на первый множитель 3, а затем получившийся результат умножим на второй множитель 100, получим:
При записи умножения в столбик запишем число 300 таким способом, чтобы цифра 3 оказалась под цифрой десятков первого множителя.
Умножим 53 на 3, не обращая внимания на нули. – это единицы, – это десятки.
То есть, 53 дес. умножили на 3 и получили 159 дес. Теперь умножим на второй множитель 100. Для этого припишем два нуля.
Получили 15 900 дес. Перенесем один ноль, получим 159 000:
Ответ: 159 000.
ЗаключениеМы сегодня учились выполнять письменное умножение чисел, оканчивающихся нулями.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Festival.1september.ru (Источник).
Myshared.ru (Источник).
Infourok.ru (Источник).
Домашнее задание
Выполните умножение в столбик:
Познакомимся с письменным приёмом умножения на числа, оканчивающиеся нулями
Познакомимся с письменнымприёмом умножения на числа,
оканчивающиеся нулями.
Открой учебник на стр. 115.
Рассмотри решение примеров нового вида.
Обрати внимание на запись цифры 0.
Какой пример верный у меня?
423·300=12
423·30=12 690
690
Запишите и самостоятельно реши данное выражение столбиком.
423·30= 423
× 30
Проверь себя!
423
× 30
12690
Запишите и самостоятельно реши данное выражение столбиком.
423·300=423
× 300
Проверь себя!
423
× 300
126900
Алгоритм записи и решения
умножения на однозначное число.:
1) Записываем первый множитель.
2) Второй множитель записываем так, чтобы нули
остались в стороне.
3) Умножаем многозначное число на число, не
обращая внимания на нули.
4) К полученному результату приписываем нули.
5) Читаем ответ.
Самостоятельно реши числовые выражения,
записывая в тетрадь вычисления столбиком.
585·70=
1)
2)
3)
4)
5)
646·30=
Записываем первый множитель.
Второй множитель записываем так, чтобы нули остались в стороне.
Умножаем многозначное число на число, не обращая внимания на нули.
К полученному результату приписываем нули.
Читаем ответ.
Проверь себя .
585·70=40 950 646·30=19380
585
646
× 70
× 30
40950
19380
Проверь себя .
585·70=40 950 646·30=19380
585
646
× 70
× 30
40950
19380
718·300=
718
× 300
1)
2)
3)
4)
5)
2406·30=
2406
×
30
Записываем первый множитель.
Второй множитель записываем так, чтобы нули остались в стороне.
Умножаем многозначное число на число, не обращая внимания на нули.
К полученному результату приписываем нули.
Читаем ответ.
Приготовься самостоятельно
Записывать решения задач в тетрадь.
Вычисления делай столбиком.
Скорость моторной лодки 15 км/ч.
Сколько времени ей понадобится,
чтобы преодолеть расстояние в 90 км?
Запиши решение задачи в свою тетрадь.
Для записи ответа переведите часы в минуты.
Такой получился ответ?
240 мин
МОЛОДЕЦ!
А что нам помогло справиться
с трудностями?
Что было легко?
Как умножали на число
оканчивающееся нулями?
Умножение чисел с нулями
В сегодняшнем посте мы узнаем, как умножить чисел, после которых идут нули.
Вы можете перемножить их, как любое другое число, но у нас есть способ научить вас, и этому легко научиться!
Самое важное, когда вы изучаете трюк, — это помнить, почему он работает именно так; Итак, давайте начнем, и вы увидите, что вы узнаете это в кратчайшие сроки и запомните навсегда.
Пример # 1:
Первая задача умножения, которую мы рассмотрим, это…
Давайте решим задачу, как обычно, поместив числа в столбцы:
Посмотрите на проблему.После того, как вы хорошо его рассмотрите, продолжайте читать.
А теперь перейдем к чему-нибудь посложнее:
Если мы разместим числа в столбцах, мы увидим, что:
Подумайте, что происходит с нулями? Давайте попробуем поставить нули после 3…
Еще раз введем числа в столбцы:
Внимательно посмотрите на все решенные нами задачи умножения.Что случилось с нулями? Нули из 5 и 3 «перескочили» к окончательному ответу, верно? Теперь убери все нули из задач. Какие числа действительно нужно умножать?
Тогда вам просто нужно посчитать количество нулей и прибавить их к 15!
Давайте посмотрим на другие примеры:
Подводя итог, чтобы перемножить числа, после которых идут нули…
Здесь у нас есть задача умножения с числами, за которыми следуют нули:
Давайте выполним следующие шаги:
- Определите нули и сосчитайте их:
В этом примере у нас пять нулей, два позади 6 и три позади 8 .
- Умножение ненулевых чисел:
- Окончательным ответом будет число, полученное на шаге 2, за которым следуют нули, которые мы подсчитали на шаге 1:
Итак, осталось:
Что вы думаете? Это просто!
Нам нужно знать , как умножить , чтобы выполнить шаг 2, поэтому мы подготовили несколько ссылок, которые могут вам помочь:
Также не стесняйтесь зарегистрироваться в Smartick, чтобы продолжить изучение математики !!
Подробнее:
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создавать максимально качественные математические материалы.
Что означает ноль при многозначном умножении?
В течение последних двух недель я требовал от своих учеников проходить проверку вычислений каждый день, потому что, даже если они, возможно, усвоили навык, они плохо владеют ни одной из 4 операций. Каждый день ученики решают 4 вычислительных задачи, относящиеся к одной из 4 операций.Первая задача — это всегда вычитание с нулями, вторая задача — умножение двух цифр на две цифры, третья задача — деление, а последняя задача — вычитание с нулем в середине. Я ежедневно оцениваю задачи, чтобы ученики могли сразу же получить обратную связь, которая побудит их сделать лучше на следующий день.
С тех пор, как я выполнял проверку вычислений каждый день, я заметил, что некоторые из моих учеников более высокого уровня, которые очень хорошо решают задачи, испытывают трудности с вычислениями.Это стало настоящим открытием для меня, а также для этих студентов, потому что я стараюсь не обращать на них такого пристального внимания, потому что они не требуют такого внимания, как другие студенты. Что ж, этот один конкретный студент боролся с вычислениями до такой степени, что он постоянно получал 50 за каждый день. Итак, я решил привести его в свой класс вместе с другими учениками для репетиторства. Когда я обучаю двухзначному умножению на двузначное, я учу своих учеников видеть проблему как две отдельные задачи, потому что им легче увидеть ее таким образом; это помогает им разделить проблему на части вместо того, чтобы рассматривать ее как одну гигантскую проблему, состоящую из множества частей.Пока мы работали над проблемой, указанной ниже, студент спросил: «Могу ли я переставить 2?» Я ответил: «Вы можете переместить 2, но вам нужно добавить ноль, потому что 2 находится в разряде десятков, а вы фактически умножаете на 2 десятки, что составляет 20.»
Этот вопрос заставил меня понять, почему он был так сбит с толку, потому что я обучал каждому навыку в контексте значения места, но когда я обучал этому навыку, я не делал связи для студентов, явно говоря, что 2 в разряде десятков — это 2 десятки, что на самом деле 20.
На следующий день в классе я спросил студентов, почему мы ставим ноль на единицу, когда умножаем на десятки? Руки начали подниматься, но прежде, чем я позвал ученика, я сказал классу, что ответ был не ноль, а место. По всей комнате можно было видеть, как руки медленно опускаются. Это заставило меня понять, что многих моих студентов учили, что ноль — это заполнитель, и поэтому он НЕ имеет значения в системе счисления. Я не думаю, что учителя начальной школы понимают, что когда ученика учат, что ноль — это заполнитель, он посылает ученикам сообщение о том, что ноль всегда занимает место, и не укрепляет понимание того, что если ноль находится в числе, в этом нет ничего место.
Мой подход к обучению операциям с числами, имеющими ноль, изменился, потому что теперь я понимаю, что многие из моих учеников должны усвоить, что ноль имеет значение, даже если значение нуля — ничто.
Это полный урок с инструкциями и упражнениями для четвертого класса об умножении на целые десятки и сотни. В уроке объясняется, как работает ярлык, а также объясняется, почему он работает.Он содержит множество упражнений для студентов, в том числе словесную задачу.
1.Умножить.
2.А теперь попробуйте! Умножьте на 20 и 200.
3.Попробуй сам! Заполните.
4. Сарай Марка имеет размеры 20 на 15 футов. Какова его площадь? Напишите число
приговор. А = __________________________________ 5.
Напишите числовое предложение и найдите А = __________________________________ 6.Марку сказали, что ему нужно четыре грузовика гравия, чтобы покрыть подъездную дорожку.
7. Умножить.
8. Умножение.
Напишите числовое предложение для каждого вопроса. 9.В одном часе ______ минут. Сколько минуты в 24 часах? 10. В одном часе ______ минут, а в одном в минуте ______ секунд. Сколько секунд в часе? 11. Эд зарабатывает 30 долларов в час. а. Сколько он будет зарабатывать за 8-часовой рабочий день? г. Сколько он будет зарабатывать за 40-часовую рабочую неделю? г. Сколько дней ему нужно будет работать, чтобы заработать больше 1000 долларов? 12. Найдите недостающий фактор. Думайте «задом наперед»! Сколько нулей тебе нужно?
Этот урок взят из книги Марии Миллер «Math Mammoth Multiplication 2», размещенной на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер. | |||
Если умножить на 10, просто прибавишь ноль? Ужасы!?!
Мы спрашиваем, мы слушаем, мы учимся — одна из первых моих статей в блоге. (Я разместил его 5 января 2015 года.) Пост включает интервью нескольких студентов, ответивших на вопрос: Сколько будет 12,6 x 10?
В одном из видеоклипов Маллика Скотт берет интервью у Наташи, которая объясняет, как она решила дать неправильный ответ — 12.60. Наташа объясняет: «Любое число, умноженное на 10, вы можете добавить ноль в конце».
Несмотря на то, что я написал блог более трех лет назад, Уэстли Янг недавно опубликовал комментарий, который частично касается стратегии «добавить ноль»:
Уэстли (который пишет в Твиттере как @Cukalu) поднял вопросы, которые давно меня беспокоят. Одной из проблем является мое беспокойство по поводу того, что ученики начальных классов замечают шаблон для умножения целых чисел на 10, а затем ошибочно применяют этот шаблон к десятичным, как это сделала Наташа.
Моя вторая проблема — это мои затруднения с тем, что делать со своими проблемами.
В элементарной математике учащиеся имеют опыт поиска закономерностей. Это может быть хорошо. Они изучают алгоритмы. Это тоже может быть хорошо. Их язык часто неточен. Это не так уж и хорошо, но они в процессе обучения, и обучение идет беспорядочно. Обучение тоже беспорядочное.
Многие мысли проносятся в моей голове, когда я размышляю над этим видеоклипом Наташи и над комментарием Уэстли. Что я должен делать как учитель? Как я могу помочь Наташе и похожим на нее ученикам передумать?
Моя первая мысль
Что, если бы я сказал что-то вроде этого Наташе:
Если Наташа ответила «да», я бы хотел услышать, почему она думала, что это правда.(Я думаю, что важно попросить студентов объяснить свои рассуждения, даже если они верны. Может быть, даже особенно, когда они правы.) Затем я мог бы сказать что-то вроде: «Интересно, как я могу умножить число на 10 и перевернуть и получите такой же ответ, как и число до того, как я умножил «. Может ли это помочь? Куда это могло привести?
Моя вторая мысль
Что, если бы я сказал Наташе что-то вроде этого:
Ура, тогда я попал бы в семантическую дыру, которая больше стимулирует закатывание глаз у студентов, чем глубокое математическое мышление.Наташа добавляла ноль не в том смысле, что она выполняла операцию сложения; вместо этого она писала / прикрепляла / добавляла (или как бы вы это описали) ноль к числу. Для 8 x 10 она сделает это и получит 80. Для 12,6 она сделала это и получила 12,60.
Моя третья мысль
Что, если бы я сказал что-то вроде этого Наташе:
Это идея, которую я хотел бы, чтобы студенты поняли, как указал Уэстли в своем комментарии. В классной обстановке, возможно, я напишу это на доске, предложу ученикам сначала поговорить с партнером, а затем попросить учеников поделиться своими идеями с классом о том, почему то, что я сказал, является математически верным.Думаю, они согласятся.
Что ж, предположим, студенты согласны со всеми этими утверждениями. Поможет ли это им по-другому подумать об умножении на 10? Я не уверен. Судя по моему опыту преподавания, обучение через рассказ часто неэффективно. Мои утверждения могут быть мне понятны, но подобные утверждения слишком часто являются математическим бла-бла для студентов.
Когда я прочитал это, я сказал себе: «Да!»
Роль контекстов
Хорошо, еще одна мысль. Марк Чабб (который пишет как @ MarkChubb3) написал блог под названием The Importance of Contexts and Visuals .В разделе об использовании контекстов он написал:
Когда я прочитал это, я сказал себе: «Да!»
И тут мне вспомнился еще один клип из того же интервью с Малликой и Наташей. Через несколько вопросов после того, как Наташа решила 12,6 x 10, Маллика попросила ее решить задачу со словами: Одна ручка стоит 1,39 доллара. Сколько стоят десять ручек?
Здесь Наташа снова сталкивается с умножением на 10. Она повторяет то, что она сказала при умножении 12,6 x 10: «Каждый раз, когда вы умножаете число на 10, вы просто добавляете ноль в конец.Но здесь, в контексте покупки ручек, она получает правильный ответ — 13,90 доллара. Подумав о том, что написал Марк, контекст проблемы побудил Наташу дать разумный ответ, а не то, что она сделала с проблемой голого числа. Взглянуть.
Где мои мысли?
Я все еще думаю. Как писал Марк, при умножении десятичных чисел на 10, если мы обосновываем опыт учащихся в контексте, у них будет больше шансов применить рассуждения, чтобы придать смысл, чем применять шаблон, который они выучили для целых чисел.(Было бы интересно поговорить со студентами о том, почему «закрепка на нуле» работает с целыми числами, а не с десятичными. Но это будет позже.)
Кроме того, в ответ на комментарий Уэстли о важности того, что на самом деле происходит с математической точки зрения, когда мы умножаем целые числа на 10, я думаю, что мне нужно признать, что учащиеся узнают шаблон, но продолжать помогать им понять шаблон математически. Слишком многие ученики считают умножение на 10 чистой удачей, особенно когда им не так легко умножать на другие числа.
Я знаю, что не касался другой части комментария Уэстли о том, что студенты «перемещают десятичную точку» как стратегию умножения десятичных чисел на 10. Я тоже слышал это объяснение и согласен с тем, что десятичная дробь на самом деле не перемещается. Может еще один блог?
Я все еще думаю. Приветствую твои мысли.
Постскриптум
Я понимаю, что один пример мало что доказывает. Вот видеоклипы двух других студентов, Дженнифер и Серджио, которые отвечают на те же два вопроса, что и Наташа.Для 12,6 x 10 Серхио попросил пропустить его, заявив, что не может понять ответ без бумаги и карандаша, в то время как Дженнифер дала неправильный ответ — 120,6. На контекстную проблему покупки 10 ручек по 1,39 доллара каждая Серхио и Дженнифер получают правильный ответ, каждый из которых рассуждает по-своему.
Стратегии умножения — Метод коробки
Когда я перешла в 3/4 класс, мне на колени оказался совершенно новый мир учебной программы. Поскольку я никогда раньше не учил умножению двойных и тройных цифр, я, естественно, начал учить своих учеников делать это именно так, как я научился.В методе алгоритма определенно нет ничего плохого, но со временем я обнаружил, что очень полезно изучить несколько других методов решения этих проблем. Этот пост посвящен моему новому фавориту…. Коробочный метод!
Первый шаг метода коробки — нарисовать коробку. Если вы умножаете две цифры на две цифры, ваше поле должно состоять из двух строк на два столбца. Для задачи три цифры на две цифры потребуются три строки и два столбца или две строки на три столбца (в любом случае работает из-за свойства коммутативности).
Затем вы расширяете каждый из факторов в соответствии с числовой стоимостью. Таким образом, 24 становится 20 + 4, а 35 становится 30 + 5. Каждая часть расширенной записи написана либо сверху, либо сбоку поля.
Шаг третий — умножить числа в сетке. Это похоже на магический квадрат. Умножьте верхнее число на число сбоку и поместите ответ в поле, где пересекаются строка и столбец. На этом этапе я учу детей умножать числа, оканчивающиеся на ноль.Я заставляю их полностью игнорировать нули для начала. Поэтому вместо того, чтобы беспокоиться о 20 x 30, они просто работают с 2 x 3. После того, как они написали 6, они подсчитывают, сколько нулей они проигнорировали в первую очередь (2), и складывают их, получая 600. Это действительно дает смысл для них, и он охватывает еще один математический стандарт в процессе!
Последний шаг — сложить все числа в поле.
Вот и все! Как только дети поймут, как установить коробку, они отлично справятся с этой стратегией.При обучении методу ящика я сначала позволяю детям использовать таблицу умножения, чтобы помочь им. Меня больше беспокоит их понимание процесса умножения двух или трех цифр. Как только они получают процесс, я даю им задачи обойтись без диаграммы, но я придерживаюсь цифр от 0 до 5 во всех местах. Они лучше пропускают счет с меньшими числами и, как правило, знают эти таблицы с меньшим умножением. Последний «уровень» — это ввести в места более крупные цифры. Как только они смогут решать задачи типа 89 x 76, я знаю, что они понимают процесс и хорошо разбираются в своих таблицах умножения.
Вот еще несколько полных примеров:
Я планирую посвятить несколько постов другим стратегиям умножения и деления, которые я изучил за последние пару лет. Следующим будет…. Частичные продукты!
Определение нулевой матрицы
Нулевая матрица
Что такое нулевая матрица?
Вспомните из нашего урока по записи матриц, что матрица — это упорядоченный список чисел, заключенный в прямоугольную скобку. Для нулевой матрицы все упрощается, поскольку вам действительно не нужно беспокоиться о числах, содержащихся в прямоугольном массиве этой нотации, как и говорит название, есть только одно число, которое может содержаться внутри этих матриц, поскольку все его записи.
Таким образом, нулевая матрица — это матрица любых размеров, в которой все элементы ее элементов равны нулю. Математически нулевую матрицу можно представить выражением:
Уравнение 1: Математическое выражение для нулевой матрицы размеров mxnГде m представляет количество строк, а n количество столбцов, содержащихся в матрице. Следовательно, если мы должны записать нулевые матрицы разных размеров, нам просто нужно определить m и n в каждом случае и заполнить все записи внутри скобок матриц нулями.
Примеры нулевых матриц можно увидеть ниже:
Уравнение 2: Примеры нулевых матриц различных размеровИз приведенных выше примеров записи нулевой матрицы обратите внимание, что эти матрицы могут иметь любой размер и комбинацию измерений, и они не обязательно являются квадратными матрицами. Таким образом, вы можете иметь нулевую матрицу с любым количеством строк или столбцов, но помните, что для любого заданного размера можно получить только одну нулевую матрицу (что имеет смысл, поскольку есть только один способ иметь все нули в качестве записей в матрица определенного размера или размерной комбинации).
Не путайте нулевую матрицу с тем, что люди могут назвать «нулевой диагональной матрицей». Такая нулевая диагональная матрица обычно относится к полой матрице, где все диагональные элементы внутри нее равны нулю, а остальные ее элементы могут быть любым числом. Сходство между обычной нулевой матрицей и пустой матрицей происходит от их следа (сложения элементов на их диагоналях), поскольку у обоих есть все нулевые элементы, которые нужно добавить, чтобы получить след, равный нулю. Таким образом, оба этих типа матриц представляют собой то, что мы называем матрицей нулевого следа.
Важные замечания о нулевой матрице
После того, как мы изучили определение нулевой матрицы, давайте поговорим о некоторых особых характеристиках этой матрицы.
- Каков ранг нулевой матрицы?
Помните, что ранг матрицы соответствует максимальному количеству линейно независимых столбцов внутри матрицы. Мы можем определить ранг матрицы, вычислив ее форму эшелона строк, а затем подсчитав левые ненулевые строки, цель которых состоит в том, чтобы найти размерность векторного пространства для рассматриваемой матрицы.
Итак, если мы говорим о разрешимой системе линейных уравнений, преобразованной в матричную запись, определение ранга такой матрицы позволяет нам увидеть максимальное количество независимых переменных и, таким образом, размерные плоскости, для которых система может быть представлена графически.
Как же тогда получить это для нулевой матрицы? Для этого нам сначала нужно спросить себя, являются ли векторы внутри нулевой матрицы линейно независимыми друг от друга? Не совсем, все они одинаковые, и все они нулевые векторы.Так случилось ли, что они представляют собой какую-либо плоскость измерения? Нет. Можете ли вы на самом деле свести его к форме эшелона строк? Нет. Таким образом, если задуматься, нулевая матрица содержит нулевое количество линейно независимых столбцов и нулевое количество ненулевых строк, поэтому наш окончательный вывод состоит в том, что ранг нулевой матрицы должен быть равен нулю.
Если вы подумаете об этой идее более глубоко, вы поймете, что любая ненулевая матрица не может иметь ранг меньше единицы, другими словами, чтобы любая матрица имела ранг нуля, она должна содержать все нулевые элементы внутри, Итак, мы пришли к выводу, что только нулевые матрицы имеют нулевой ранг. - Обратима ли нулевая матрица?
Для практических целей мы оставим полное объяснение того, как узнать, является ли матрица обратимой или нет, и как инвертировать те, которые для наших следующих уроков будут говорить об обратимой матрице 2×2. А пока прямо скажем, что нулевая матрица необратима.
Есть несколько правил, которые могут доказать это, например, ее определитель равен нулю, а если матрица квадратная, то ее ранг меньше, чем ее размерность. Опять же, мы поговорим об этом немного больше в наших следующих уроках об инвертировании матриц.Но давайте задумаемся над этой идеей на минуту: если мы упомянули ранее, что для любой матрицы определенного размера или размеров существует только одна конфигурация, в которой все ее элементы равны нулю, поэтому не может быть другого способа, которым вы можете переставить нули, чтобы получить обратную матрицу тех же размеров. Если все записи одинаковы, матрица будет точно такой же, нет «обратного» или «противоположного» от этого. - Можно ли диагонализовать нулевую матрицу?
Мы все еще немного далеки от нашего урока по диагонализации, но пока мы можем сказать, что да, нулевая матрица диагонализуема, поскольку ее нулевые элементы могут легко содержать линейно независимые собственные векторы.Подробнее о диагонализации в последующих уроках.
Пустое пространство нулевой матрицы
Поскольку нулевая матрица сама по себе является небольшой и конкретной концепцией, которую можно использовать во многих наших уроках линейной алгебры, теперь мы вынуждены еще раз вернуться к теме следующего урока: нулевое пространство матрицы.
Давайте еще раз упростим и скажем, что для того, чтобы вектор был частью нулевого пространства матрицы, умножение такой матрицы на упомянутый вектор должно приводить к нулевому вектору, таким образом давая «нулевой» результат.Если рассматриваемая матрица представляет собой матрицу с именем A, которая умножается на вектор u, мы говорим, что u находится в нулевом пространстве A, если выполняется следующее условие:
Уравнение 3: Условие для того, чтобы вектор u был частью нулевого пространства A
Если мы возьмем то, что мы знаем из наших уроков о представлении линейной системы в виде матрицы и матричного уравнения Ax = b, мы можем заметить, что при таком умножении умножаемый вектор фактически представляет собой набор решений, заданных однородной системой.
Теперь, как это можно применить к нулевой матрице?Ну, любая нулевая матрица, умноженная на вектор, будет иметь в результате нулевой вектор. То есть, если размеры матрицы и вектора соответствуют правилам умножения матриц, другими словами, если умножение может быть определено, то результатом обязательно будет нулевой вектор.
Причина этого в том, что, учитывая, что нулевая матрица содержит только нулевые элементы, любая запись, умноженная на любой элемент в векторе, приведет к нулевому компоненту, который будет частью результирующего вектора.Итак, условие для нулевого пространства выполнено, и это приводит нас к чему-то важному, о котором мы до сих пор не упоминали: нулевая матрица — это то, что мы называем нулевой матрицей, и это можно ясно увидеть, следуя процессу, описанному выше, поскольку нет независимо от того, какой вектор к нему умножается, результат всегда будет содержать только нулевые элементы.
Сложение, вычитание и скалярное умножение нулевой матрицы
В этом разделе мы сосредоточимся на демонстрации примеров операций либо с нулевыми матрицами внутри, над которыми работают, либо с проблемами, приводящими к решениям с нулевыми матрицами.Для этого давайте сразу перейдем к примерам упражнений:
Пример 1
Начнем с добавления, содержащего нулевую матрицу. Это довольно простая операция, поэтому давайте начнем с добавления следующего вида:
Уравнение 4: сложение с нулевой матрицей Чтобы решить эту проблему, мы просто добавляем все соответствующие элементы в обе матрицы, чтобы получить результирующую матрицу (которая имеет те же размеры, что и те, из которых она была получена). Итак, результат выглядит так: Уравнение 5: Решение сложения с нулевой матрицей Этот первый пример задачи показывает нам важное свойство нулевой матрицы: когда нулевая матрица либо добавляется, либо вычитается из другой матрицы с такими же размерами, эта матрица остается неизменной и равна результату операции.Пример 2
Чтобы продолжить наш следующий пример, мы работаем над вычитанием матриц, где нулевая матрица вычитается из другой матрицы равного размера. Уравнение 6: вычитание с нулевой матрицей Операция следует тем же принципам, что и сложение в примере 1. Таким образом, решая эту операцию, мы получаем: Уравнение 7: Решение вычитания с нулевой матрицей Как мы уже упоминали в нашем уроке о сложении и вычитании матриц, хотя сложение матриц является коммутативным (вы можете изменить порядок матриц, и результат не изменится), вычитания матриц нет, и это хорошо видно на этом примере.
Если бы у вас была нулевая матрица справа от знака минус в уравнении 6, то результат был бы равен другой матрице, участвующей в операции. Но поскольку нулевая матрица была первой, результат операции оказывается отрицательным по сравнению с ненулевой матрицей.
Пример 3
В этом примере мы добавляем следующие две следующие матрицы: Уравнение 8: сложение противоположных матриц Заметили что-то особенное из приведенных выше матриц? Они представляют собой отрицательные матрицы друг друга, или, другими словами, если вы возьмете первую матрицу и умножите ее на отрицательную, вы получите вторую матрицу.Следовательно, эта конкретная операция эквивалентна вычитанию матрицы из самой себя. Чтобы показать это, давайте определим первую матрицу как A: Уравнение 9: Матрица A Затем мы записываем эквивалентную операцию, которую мы объяснили минуту назад: Уравнение 10: Преобразование сложения матриц в вычитание Обратите внимание, что скалярное умножение минус один на A было упрощено, чтобы просто записать его как вычитание двух матриц, которые к настоящему времени являются A, и поэтому то, что мы имеем в уравнении 10, можно просто записать как: что, очевидно, имеет нулевой результат.Но поскольку здесь речь идет не только о числах, а о матрицах, нулевой результат должен быть массивом тех же размеров, что и A, и поэтому: Уравнение 11: вычитание самой матрицы Обратите внимание, что субиндексы в правой части уравнения обозначают размеры нулевой матрицы, что означает, что результирующая нулевая матрица должна иметь «m из A» (такое же количество строк, что и A) и «N из A». «(такое же количество столбцов, как у A). Давайте получим результат двумя разными способами: добавлением исходной матрицы, показанным в уравнении 8, и вычитанием матрицы, найденным в конце уравнения 10, чтобы показать, как мы получим тот же результат: нулевую матрицу, чтобы доказать уравнение 11.Уравнение 12: Окончательное решение, полученное двумя разными способами Вывод из этой проблемы состоит в том, что всякий раз, когда вы вычитаете матрицу из самой себя, вы получаете нулевую матрицу с теми же размерами, что и ваши исходные матрицы. Пример 4
В этом примере мы увидим вычитание двух равных матриц, которые оказываются векторами-столбцами. Уравнение 13: вычитание двух равных векторов-столбцов Здесь снова используется принцип, объясненный в предыдущем упражнении: при вычитании двух равных матриц (которые в данном случае оказываются двумя векторами-столбцами, поскольку каждая из матриц состоит только из одного столбца), результатом является нулевая матрица того же размера. как оригинальные: Уравнение 14: Решение вычитания двух равных векторов-столбцов Пример 5
Вычислите следующее скалярное умножение матрицы: Уравнение 15: Скалярное умножение матрицы на ноль В этом конкретном случае должно быть ясно, что результат будет равен нулю, поскольку все, что вы умножаете на ноль, приведет к нулю.Интересная часть здесь связана с тем фактом, что вы умножаете матрицу, и поэтому каждый элемент будет умножен на скаляр снаружи, в данном случае ноль, и что произойдет, вместо того, чтобы получить просто ноль в результате, это умножение даст матрицу, в которой все ее элементы равны нулю, и, таким образом, результатом будет нулевая матрица: Уравнение 16: Результат скалярного умножения матрицы на ноль Что также можно записать как: Уравнение 17: нулевая матрица с размерами 3 x 2 Пример 6
Вычислить следующее скалярное умножение, содержащее нулевую матрицу Уравнение 18: Скалярное умножение нулевой матрицы Как и в случае с прошлыми проблемами, мы можем интуитивно записать ответ в виде нулевой матрицы, поскольку каждый элемент в матрице равен нулю, не имеет значения, умножаете ли вы на них любой другой скаляр, результат всегда будет равен нулю в каждом дело.Чтобы расширить операцию, вот как это происходит: Уравнение 19: Результат скалярного умножения нулевой матрицы Пример 7
Давайте изменим режим наших задач, теперь вам даны матрицы, показанные ниже: Уравнение 20: матрицы B и 0 Имея это в виду, верны ли следующие матричные уравнения? Если нет, поправьте их.
- B + 0 = B
Этот случай соответствует тому, что мы видели в примере 1: наличие двух матриц с одинаковыми размерами, одна из которых является нулевой матрицей, а другая — ненулевой матрицей, когда вы складываете их вместе, результат равна ненулевой матрице, поскольку нулевая матрица ничего не вносит при добавлении каждого соответствующего элемента в две матрицы, участвующие в операции.Следовательно, это выражение ПРАВИЛЬНО. - 0 — B = B
В этом случае мы можем взглянуть на пример 2 и понять, что это выражение НЕПРАВИЛЬНО. При вычитании матрицы из нулевой матрицы той же размерности результат равен отрицательному значению ненулевой матрицы.
Следовательно, правильным выражением будет 0 — B = -B - B — B = 0
Это выражение ПРАВИЛЬНО и соответствует тому, что мы видели в примерах 3 и 4: если вы вычитаете матрицу сама по себе, это приводит к записи путем вычитания записи самого числа, и, таким образом, результирующей матрицы в котором все его входные элементы будут равны нулю (нулевая матрица 0). - 0 + 0 = B
Вышеприведенное выражение НЕПРАВИЛЬНО. При добавлении нуля плюс ноль результат всегда равен нулю. Это случай для каждого элемента результирующей матрицы при добавлении нулевой матрицы и другой равной нулевой матрицы, результатом будет равная нулевая матрица. Таким образом, правильное выражение: 0 + 0 = 0. - 0 ⋅ \ cdot⋅ B = 0
Это выражение ПРАВИЛЬНО. Результатом умножения каждого элемента на элемент в результате этой операции будет ноль, в результате чего получится матрица с нулевыми элементами, то есть нулевая матрица 0. - B ⋅ \ cdot⋅ 0 = 0
Как и в случае e), это выражение ПРАВИЛЬНО, поскольку каждый соответствующий элемент из ненулевой матрицы будет умножен на ноль из нулевой матрицы.
Как упоминалось ранее, нулевая матрица — это очень конкретная концепция, поэтому на этом уроке действительно нечего сказать о ней, но это не значит, что она не будет использоваться во многих областях линейной алгебры. Так же, как число ноль в математике, нулевая матрица предоставляет нам представление нулевого пространства, которое мы все еще можем характеризовать, другими словами, она может содержать нулевые элементы, но ее качества остаются там, чтобы мы могли использовать их по своему усмотрению с другими матрицами.
Чтобы завершить наш урок, мы просто предоставим две дополнительные ссылки на случай, если вы захотите посетить их и посмотреть, как они определяют нулевую матрицу, и предоставим простой пример добавления с нулевой матрицей.На сегодня все, до встречи на следующем уроке!
macos — умножение AWK дает ноль
Я немного новичок в использовании awk. Моя цель — создать функцию bash формы:
значение столбца файла myfunction
Берет заданный номер столбца в файле, умножает его на значение и перезаписывает файл. А пока я написал следующее:
function multiply_column {
файл = $ 1
столбец = 2 доллара США
значение = 3 доллара США
awk -F "" '{print $ col * mul}' col = $ column mul = $ value $ file
}
Мой файл выглядит так:
0.400000E + 15 0,168933E + 00 -0,180294E-44 0,168933E + 00
0,401000E + 15 0,167689E + 00 -0,181383E-44 0,167689E + 00
0,402000E + 15 0,166502E + 00 -0,182475E-44 0,166502E + 00
0,403000E + 15 0,165371E + 00 -0,183569E-44 0,165371E + 00
0,404000E + 15 0,164298E + 00 -0,184666E-44 0,164298E + 00
0,405000E + 15 0,163284E + 00 -0,185766E-44 0,163284E + 00
0,406000E + 15 0,162328E + 00 -0,186868E-44 0,162328E + 00
0,407000E + 15 0,161431E + 00 -0,187972E-44 0,161431E + 00
0.408000E + 15 0,160593E + 00 -0,189080E-44 0,160593E + 00
0,409000E + 15 0,159816E + 00 -0,1E-44 0,159816E + 00
0,410000E + 15 0,159099E + 00 -0,191302E-44 0,159099E + 00
0,411000E + 15 0,158442E + 00 -0,192416E-44 0,158442E + 00
0,412000E + 15 0,157847E + 00 -0,193534E-44 0,157847E + 00
0,413000E + 15 0,157312E + 00 -0,194653E-44 0,157312E + 00
0,414000E + 15 0,156840E + 00 -0,195775E-44 0,156840E + 00
0,415000E + 15 0,156429E + 00 -0,196899E-44 0,156429E + 00
0.416000E + 15 0,156081E + 00 -0,198026E-44 0,156081E + 00
0,417000E + 15 0,155796E + 00 -0,199154E-44 0,155796E + 00
0,418000E + 15 0,155573E + 00-0,200285E-44 0,155573E + 00
0,419000E + 15 0,155413E + 00 -0.201418E-44 0,155413E + 00
0,420000E + 15 0,155318E + 00 -0,202554E-44 0,155318E + 00
0.421000E + 15 0.155285E + 00 -0.203691E-44 0.155285E + 00
0,422000E + 15 0,155318E + 00 -0,204831E-44 0,155318E + 00
0,423000E + 15 0,155414E + 00 -0,205973E-44 0,155414E + 00
0.424000E + 15 0,155575E + 00 -0,207116E-44 0,155575E + 00
0,425000E + 15 0,155802E + 00 -0,208262E-44 0,155802E + 00
Мне удалось просто напечатать первый столбец, но когда я умножаю его на свое значение, awk дает мне 0. Я пробовал свою функцию с другими файлами, где данные были отформатированы по-другому, и она работала отлично. Я тоже пытался совместить это с bc, безуспешно.
Кто-нибудь понимает, почему в этом случае awk дает 0?
Заранее спасибо!
######### РЕДАКТИРОВАТЬЯ только что узнал, что если в моем файле данных используются запятые, а не точки (т.
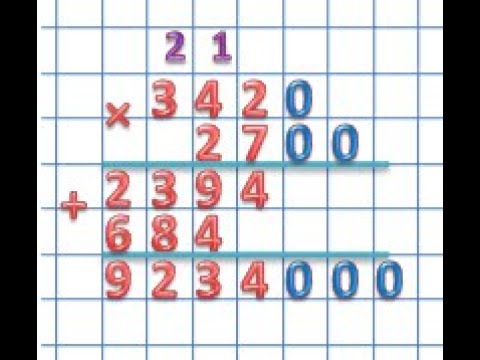



 Слайд 1
Слайд 1




 ( Слайд 5)
( Слайд 5)


 Второй множитель записываю так, чтобы нули остались в стороне.
Второй множитель записываю так, чтобы нули остались в стороне.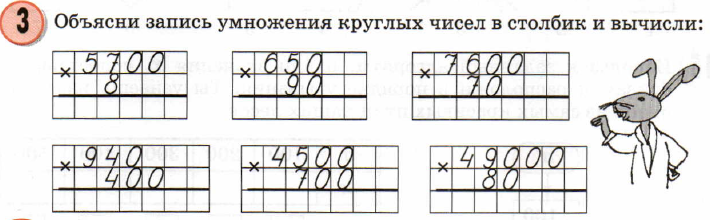
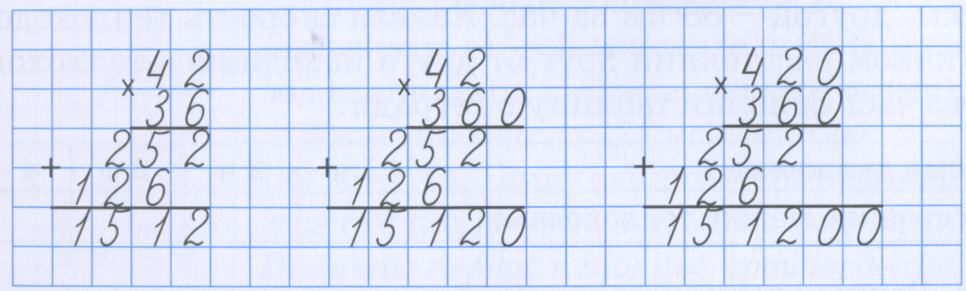

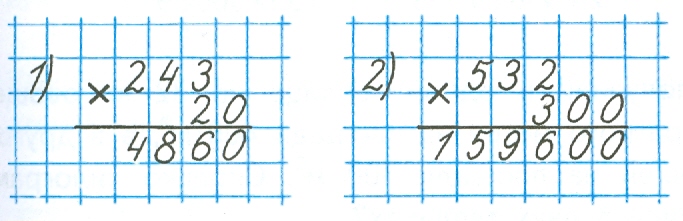

 Оно подошло бы к теме – сложение многозначных чисел.
Оно подошло бы к теме – сложение многозначных чисел.
