Как расставить порядок действий? — Ваша онлайн-энциклопедия
Содержание
- — Какие действия в математике делаются в первую очередь?
- — Как правильно решить пример без скобок?
- — Почему сначала идет умножение?
- — Как считать действия в скобках?
- — В каком порядке выполняются математические действия?
- — Что в примере делается первым?
- — В каком классе изучают порядок действий?
- — Что значит выражение в математике?
- — Почему умножение приоритетнее сложения?
- — Как называются числа при умножении?
- — Что сначала возведение в степень или умножение?
- — Что такое сложение и вычитание?
Какие действия в математике делаются в первую очередь?
Если в выражение без скобок входят не только сложение и вычитание, но и умножение или деление, то сначала выполняются по порядку умножение и деление, а затем сложение и вычитание также по порядку.
Как правильно решить пример без скобок?
Запомните правило:
- Если в примере нет скобок, сначала выполняем действия умножения и деления по порядку, слева направо. …
- Если в примере есть скобки, то сначала мы выполняем действия в скобках, затем умножение и деление, и затем — сложение и вычитание начиная слева направо.
Почему сначала идет умножение?
Так всё же почему умножение выполняется первое, а только потом сложение? Ответ довольно прост. При умножении двух разных единиц измерения получается новая единица измерения, при сложении единицы измерения не меняются. При умножении мы получаем эту самую новую единицу измерения.
Как считать действия в скобках?
- сначала выполняются действия, заключенные в скобки; при этом умножение и деление делаются в порядке из следования, но раньше, чем сложение и вычитание;
- затем выполняются остающиеся действия, причем опять умножение и деление делаются в порядке из следования, но раньше сложения и вычитания.

В каком порядке выполняются математические действия?
Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок: действия выполняются по порядку слева направо сначала выполняется умножение и деление, а затем — сложение и вычитание.
Что в примере делается первым?
Сначала умножение и деление, затем сложение и вычитание В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок: действия выполняются по порядку слева направо, причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
В каком классе изучают порядок действий?
3-й класс
Что значит выражение в математике?
Числовое выражение – это запись, состоящая из чисел и знаков действий между ними. Значение выражения – это результат выполненных действий. Сравнить числовые выражения – найти значение каждого из выражений и их сравнить. Порядок выполнения действий – это последовательность проводимых вычислений в данном выражении.
Значение выражения – это результат выполненных действий. Сравнить числовые выражения – найти значение каждого из выражений и их сравнить. Порядок выполнения действий – это последовательность проводимых вычислений в данном выражении.
Почему умножение приоритетнее сложения?
Неважность очерёдности действий умножения и деления при вычислении слагаемых в выражении — это основа безочерёдности этих действий, что значит, произведения и частные в выражении можно вычислять в любом порядке, как удобно, не соблюдая правило «слева направо».
Как называются числа при умножении?
Так же, как и при сложении и вычитании, числа при умножении тоже имеют свое название. Первое число при умножении называется первый множитель. Второе число при умножении называется второй множитель. Результат умножения называют произведение.
Результат умножения называют произведение.
Что сначала возведение в степень или умножение?
Для основных арифметических действий установлен следующий порядок: сначала выполняется возведение числа в степень, затем выполняется умножение и деление и в самую последнюю очередь выполняется сложение и вычитание.
Что такое сложение и вычитание?
Сложение – это объединение объектов в одно целое. Результатом сложения чисел является число, называемое суммой чисел (слагаемых). Вычитание – это такое действие, в котором отнимают меньшее число от большего. Большее число называется уменьшаемым, меньшее – вычитаемым, результат вычитания – разностью.
Интересные материалы:
Как установить будильник на телефоне Huawei?
Как установить будильник на телефоне Redmi?
Как установить другую операционную систему на телефон?
Как установить Google Play на телефон?
Как установить госуслуги на телефоне?
Как установить GTA San Andreas на телефон андроид?
Как установить Инстаграм на телефоне?
Как установить мелодию на звонок в телефоне?
Как установить на телефон NFC?
Как установить на телефон Viber?
| Табличка на двери |
В каком порядке выполняются математические действия. Конспект урока ««Порядок выполнения действий в выражениях без скобок и со скобками».
 «
«Тема урока: « Порядок выполнения действий в выражениях без скобок и со скобками».
Цель урока : создать условия для закрепления умений применять знания о порядке выполнения действий в выражениях без скобок и со скобками в различных ситуациях, умений решать задачи выражением.
Задачи урока.
Образовательные:
Закрепить знания учащихся о правилах выполнения действий в выражениях без скобок и со скобками; формировать у них умение пользоваться этими правилами при вычислении конкретных выражений; совершенствовать вычислительные навыки; повторить табличные случаи умножения и деления;
Развивающие:
Развивать вычислительные навыки, логическое мышление, внимание, память, познавательные способности учащихся,
коммуникативные навыки;
Воспитательные:
Воспитывать толерантное отношение друг к другу, взаимное сотрудничество,
культуру поведения на уроке, аккуратность, самостоятельность, воспитывать интерес к занятиям математикой.
Формируемые УУД:
Регулятивные УУД:
работать по предложенному плану, инструкции;
выдвигать свои гипотезы на основе учебного материала;
осуществлять самоконтроль.
Познавательные УУД:
знать правила порядка выполнения действий:
уметь разъяснить их содержание;
понимать правило порядка выполнения действий;
находить значения выражений согласно правилам порядка выполнения;
действий, используя для этого текстовые задачи;
записывать решение задачи выражением;
применять правила порядка выполнения действий;
уметь применять полученные знания при выполнении контрольной работы.
Коммуникативные УУД:
слушать и понимать речь других;
выражать свои мысли с достаточной полнотой и точностью;
допускать возможность различных точек зрения, стремиться понимать позицию собеседника;
работать в команде разного наполнения (паре, малой группе, целым классом), участвовать в обсуждениях, работая в паре;
Личностные УУД:
устанавливать связь между целью деятельности и её результатом;
определять общие для всех правила поведения;
выражать способность к самооценке на основе критерия успешности учебной деятельности.
Планируемый результат:
Предметные:
Знать правила порядка выполнения действий.
Уметь разъяснить их содержание.
Уметь решать задачи с помощью выражений.
Личностные:
Уметь проводить самооценку на основе критерия успешности учебной деятельности.
Метапредметные:
Уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение(Регулятивные УУД ).
Уметь оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им (Коммуникативные УУД ).
Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке (Познавательные УУД ).
Ход урока
1. Организационный момент.
Чтоб урок наш стал светлее,
Мы поделимся добром.
Вы ладони протяните,
В них любовь свою вложите,
И друг другу улыбнитесь.
Займите свои рабочие места.
Открыли тетради, записали число и классная работа.
2. Актуализация знаний.
На уроке нам с вами предстоит подробно рассмотреть порядок выполнения арифметических действий в выражениях без скобок и со скобками.
Устный счёт.
Игра «Найди правильный ответ».
(У каждого ученика лист с числами)
Я читаю задания, а вы, выполнив в уме действия, должны полученный результат, т. е. ответ, зачеркнуть крестиком.
Я задумала число, из него вычла 80, получила 18. Какое число я задумала? (98)
Какое число я задумала? (98)
Я задумала число, к нему прибавила 12, получила 70. Какое число я задумала? (58)
Первое слагаемое 90, второе слагаемое 12. Найдите сумму. (102)
Соедините полученные результаты.
Какую геометрическую фигуру вы получили? (Треугольник)
Расскажите, что вы знаете о данной геометрической фигуре. (Имеет 3 стороны, 3 вершины, 3 угла)
Продолжаем работать по карточке.
Найдите разность чисел 100 и 22. (78)
Уменьшаемое 99, вычитаемое 19. Найдите разность. (80).
Возьмите число 25 4 раза. (100)
Начертите внутри треугольника еще 1 треугольник, соединяя полученные результаты.
Сколько треугольников получилось? (5)
3. Работа над темой урока. Наблюдение за изменением значения выражения от порядка выполнения арифметических действий
В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
А в математике обязательно ли выполнять арифметические действия в определенном порядке?
Давайте проверим
Сравним выражения:
8-3+4 и 8-3+4
Видим, что оба выражения совершенно одинаковы.
Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).
Рис. 1. Порядок действий
В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
Видим, что значения выражений получаются разные.
Сделаем вывод: порядок выполнения арифметических действий менять нельзя .
Порядок выполнения арифметических действий в выражениях без скобок
Узнаем правило выполнения арифметических действий в выражениях без скобок.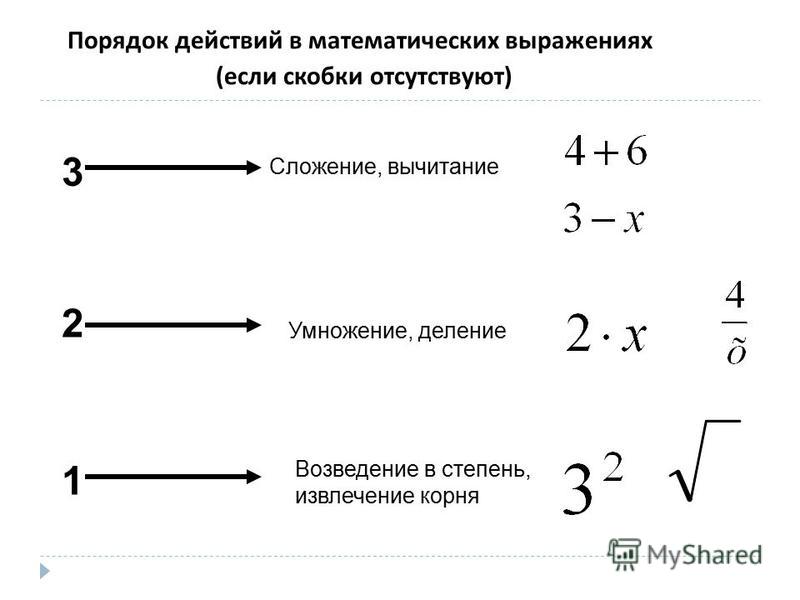
Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.
Потренируемся.
Рассмотрим выражение
В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени .
Выполняем действия слева направо по порядку (рис. 2).
Рис. 2. Порядок действий
Рассмотрим второе выражение
В этом выражении имеются только действия умножения и деления – это действия второй ступени.
Выполняем действия слева направо по порядку (рис. 3).
Рис. 3. Порядок действий
В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.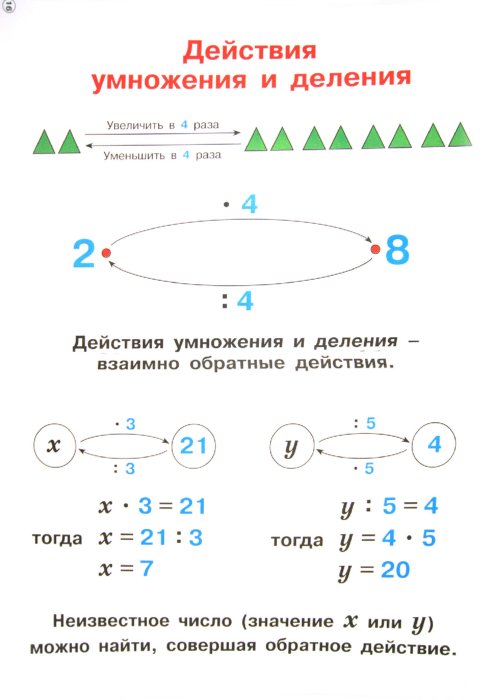
Рассмотрим выражение.
Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
Вычислим значение выражения.
18:2-2*3+12:3=9-6+4=3+4=7
Порядок выполнения арифметических действий в выражениях со скобками
В каком порядке выполняются арифметические действия, если в выражении имеются скобки?
Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.
Рассмотрим выражение.
30 + 6 * (13 — 9)
Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.
30 + 6 * (13 — 9)
Вычислим значение выражения.
30+6*(13-9)=30+6*4=30+24=54
Правило выполнения арифметических действий в выражениях без скобок и со скобками
Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?
Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
1. действия, записанные в скобках;
действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
Схема поможет запомнить это несложное правило (рис. 4).
Рис. 4. Порядок действий
4. Закрепление Выполнение тренировочных заданий на изученное правило
Потренируемся.
Рассмотрим выражения, установим порядок действий и выполним вычисления.
43 — (20 — 7) +15
32 + 9 * (19 — 16)
Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59
В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.
Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.
2*9-18:3=18-6=12
Узнаем, правильно ли определен порядок действий в следующих выражениях.
37 + 9 — 6: 2 * 3 =
18: (11 — 5) + 47=
7 * 3 — (16 + 4)=
Рассуждаем так.
37 + 9 — 6: 2 * 3 =
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37
Продолжаем рассуждать.
Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
18:(11-5)+47=18:6+47=3+47=50
В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
7*3-(16+4)=7*3-20=21-20=1
Выполним задание.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).
Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.
Проверим себя (рис. 6).
Рис. 6. Порядок действий
5. Подведение итогов.
Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками. В ходе выполнения заданий определяли, зависит ли значение выражений от порядка выполнения арифметических действий, узнали, отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренировались в применении изученного правила, искали и исправляли ошибки, допущенные при определении порядка действий.
Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.
Иначе говоря, арифметические действия имеют свой особый порядок выполнения.
Yandex.RTB R-A-339285-1
В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.
Определение 1
В случае выражений без скобок порядок действий определяется однозначно:
- Все действия выполняются слева направо.
- В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.
Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.
Пример 1
Условие: вычислите, сколько будет 7 − 3 + 6 .
Решение
В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:
7 − 3 + 6 = 4 + 6 = 10
Ответ: 7 − 3 + 6 = 10 .
Пример 2
Условие: в каком порядке нужно выполнять вычисления в выражении 6: 2 · 8: 3 ?
Решение
Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.
Пример 3
Условие: подсчитайте, сколько будет 17 − 5 · 6: 3 − 2 + 4: 2 .
Решение
Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:
17 − 5 · 6: 3 − 2 + 4: 2 = 17 − 10 − 2 + 2
Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:
17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7
Ответ: 17 − 5 · 6: 3 − 2 + 4: 2 = 7 .
Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.
Что такое действия первой и второй ступени
Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.
К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.
Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:
Определение 2
В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).
Порядок вычислений в выражениях со скобками
Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:
В таком случае нужное правило можно записать так:
Определение 3
Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.
Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.
Пример 4
Условие: вычислите, сколько будет 5 + (7 − 2 · 3) · (6 − 4) : 2 .
Решение
В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7:
7 − 2 · 3 = 7 − 6 = 1
Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .
Теперь нам нужно подставить получившиеся значения в первоначальное выражение:
5 + (7 − 2 · 3) · (6 − 4) : 2 = 5 + 1 · 2: 2
Начнем с умножения и деления, потом выполним вычитание и получим:
5 + 1 · 2: 2 = 5 + 2: 2 = 5 + 1 = 6
На этом вычисления можно закончить.
Ответ: 5 + (7 − 2 · 3) · (6 − 4) : 2 = 6 .
Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.
Пример 5
Условие: вычислите, сколько будет 4 + (3 + 1 + 4 · (2 + 3)) .
Решение
У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · (2 + 3) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .
Ответ: 4 + (3 + 1 + 4 · (2 + 3)) = 28 .
Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.
Допустим, нам надо найти, сколько будет (4 + (4 + (4 − 6: 2)) − 1) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6: 2 = 4 − 3 = 1 , исходное выражение можно записать как (4 + (4 + 1) − 1) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению (4 + 5 − 1) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .
Начинаем с выражения во внутренних скобках. Поскольку 4 − 6: 2 = 4 − 3 = 1 , исходное выражение можно записать как (4 + (4 + 1) − 1) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению (4 + 5 − 1) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.
Разберем пример такого вычисления.
Пример 6
Условие: найдите, сколько будет (3 + 1) · 2 + 6 2: 3 − 7 .
Решение
У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид (3 + 1) · 2 + 36: 3 − 7 .
Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид (3 + 1) · 2 + 36: 3 − 7 .
(3 + 1) · 2 + 36: 3 − 7 = 4 · 2 + 36: 3 − 7 = 8 + 12 − 7 = 13
Ответ: (3 + 1) · 2 + 6 2: 3 − 7 = 13 .
В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Октябрь 24th, 2017 admin
Лопатко Ирина Георгиевна
Цель: формирование знаний о порядке выполнения арифметических действий в числовых выражениях без скобок и со скобками, состоящих из 2-3 действий.
Задачи:
Образовательная: формировать у учащихся умение пользоваться правилами порядка выполнения действий при вычислении конкретных выражений, умение применять алгоритм действий.
Развивающая: развивать навыки работы в паре, мыслительную деятельность учащихся, умение рассуждать, сопоставлять и сравнивать, навыки вычисления и математическую речь.
Воспитательная: воспитывать интерес к предмету, толерантное отношение друг к другу, взаимное сотрудничество.
Типа: изучение нового материала
Оборудование: презентация, наглядности, раздаточный материал, карточки, учебник.
Методы: словесный, наглядно- образный.
ХОД УРОКА
- Организационный момент
Приветствие.
Мы сюда пришли учиться,
Не лениться, а трудиться.
Работаем старательно,
Слушаем внимательно.
Маркушевич сказал великие слова: “Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели .” Добро пожаловать на урок математики!
- Актуализация знаний
Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным. (Б. Паскаль)
Предлагаю выполнить логические задания. Вы готовы?
Вы готовы?
Какие два числа, если их перемножить, дают такой же результат, что и при их сложении? (2 и 2)
Из-под забора видно 6 пар лошадиных ног. Сколько этих животных во дворе? (3)
Петух, стоя на одной ноге весит 5кг. Сколько он будет весить, стоя на двух ногах? (5кг)
На руках 10 пальцев. Сколько пальцев на 6 руках? (30)
У родителей 6 сыновей. Каждый имеет сестру. Сколько всего детей в семье? (7)
Сколько хвостов у семи котов?
Сколько носов у двух псов?
Сколько ушей у 5 малышей?
Ребята, именно такой работы я и ждала от вас: вы были активны, внимательны, сообразительны.
Оценивание: словесное.
Устный счет
КОРОБКА ЗНАНИЙ
Произведение чисел 2 * 3, 4 * 2;
Частные чисел 15: 3, 10:2;
Сумма чисел 100 + 20, 130 + 6, 650 + 4;
Разность чисел 180 – 10, 90 – 5, 340 – 30.
Компоненты умножения, деления, сложения, вычитания.
Оценивание: ученики самостоятельно оценивают друг друга
- Сообщение темы и цели урока
“Чтобы переварить знания, надо поглощать их с аппетитом. ” (А.Франц)
” (А.Франц)
Вы готовы поглощать знания с аппетитом?
Ребята, Маше и Мише была предложена такая цепочка
24 + 40: 8 – 4=
Маша её решила так:
24 + 40: 8 – 4= 25 правильно? Ответы детей.
А Миша решил вот так:
24 + 40: 8 – 4= 4 правильно? Ответы детей.
Что вас удивило? Вроде и Маша и Миша решили правильно. Тогда почему ответы у них разные?
Они считали в разном порядке, не договорились, в каком порядке будут считать.
От чего зависит результат вычисления? От порядка.
Что вы видите в этих выражениях? Числа, знаки.
Как в математике называют знаки? Действия.
О каком порядке не договорились ребята? О порядке действий.
Что мы будем изучать на уроке? Какая тема урока?
Мы будем изучать порядок арифметических действий в выражениях.
Для чего нам нужно знать порядок действий? Правильно выполнять вычисления в длинных выражениях
«Корзина знаний» . (Корзина висит на доске)
(Корзина висит на доске)
Ученики называют ассоциации связанные с темой.
- Изучение нового материала
Ребята, послушайте, пожалуйста, что говорил французский математик Д.Пойя: “Лучший способ изучить что-либо — это открыть самому”. Вы готовы к открытиям?
180 – (9 + 2) =
Прочитайте выражения. Сравните их.
Чем похожи? 2 действия, числа одинаковые
Чем отличаются? Скобки, разные действия
Правило 1.
Прочитайте правило на слайде. Дети читают вслух правило.
В выражениях без скобок, содержащих только сложение и вычитание или умножение и деление, действия выполняются в том порядке, как они записаны: слева направо.
О каких действиях здесь говорится? +, — или : , ·
Из данных выражений найдите только те, которые соответствуют правилу 1. Запишите их в тетрадь.
Вычислите значения выражений.
Проверка.
180 – 9 + 2 = 173
Правило 2.
Прочитайте правило на слайде.
Дети читают вслух правило.
В выражениях без скобок сначала выполняются по порядку слева направо умножение или деление, а потом сложение или вычитание.
:, · и +, — (вместе)
Есть скобки? Нет.
Какие действия будем выполнять сначала? ·, : слева направо
Какие действия будем выполнять потом? +, — слева, направо
Найдите их значения.
Проверка.
180 – 9 * 2 = 162
Правило 3
В выражениях со скобками, сначала вычисляют значение выражений в скобках, затем выполняются по порядку слева направо умножение или деление, а потом сложение или вычитание.
А здесь какие арифметические действия указаны?
:, · и +, — (вместе)
Есть скобки? Да.
Какие действия будем выполнять сначала? В скобках
Какие действия будем выполнять потом? ·, : слева направо
А затем? +, — слева, направо
Выпишите выражения, которые относятся ко второму правилу.
Найдите их значения.
Проверка.
180: (9 * 2) = 10
180 – (9 + 2) = 169
Еще раз все вместе проговариваем правило.
ФИЗМИНУТКА
- Закрепление
“Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое.” , говорил М.В. Остроградский. Вот и мы сейчас вспомним, что мы только что изучили и применим новые знания на практике.
Страница 52 №2
(52 – 48) * 4 =
Страница 52 №6 (1)
Учащиеся собрали в теплице 700 кг овощей: 340 кг огурцов, 150 кг помидоров, а остальные – перец. Сколько килограммов перца собрали учащиеся?
О чем говорится? Что известно? Что нужно найти?
Давайте попробуем решить эту задачу выражением!
700 – (340 + 150) = 210 (кг)
Ответ: 210 кг перца собрали учащиеся.
Работа в парах.
Даны карточки с заданием.
5 + 5 + 5 5 = 35
(5+5) : 5 5 = 10
Оценивание:
- быстрота – 1 б
- правильность — 2 б
- логичность – 2 б
- Домашнее задание
Страница 52 № 6 (2) решить задачу, записать решение в виде выражения.
- Итог, рефлексия
Кубик Блума
Назови тему нашего урока?
Объясни порядок выполнения действий в выражениях со скобками.
Почему важно изучать эту тему?
Продолжи первое правило.
Придумай алгоритм выполнения действий в выражениях со скобками.
“Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе.” (М.И. Калинин)
Спасибо за работу на уроке!!!
ПОДЕЛИТЬСЯ Вы можете
Начальная школа подходит к концу, скоро ребёнок шагнёт в углубленный мир математики. Но уже в этот период школьник сталкивается с трудностями науки. Выполняя простое задание, ребёнок путается, теряется, что в результате приводит к отрицательной отметке за выполненную работу. Чтобы избежать подобных неприятностей, нужно при решении примеров, уметь ориентироваться в порядке, по которому нужно решать пример. Не верно распределив действия, ребёнок не правильно выполняет задание. В статье раскрываются основные правила решения примеров, содержащих в себе весь спектр математических вычислений, включая скобки. Порядок действий в математике 4 класс правила и примеры.
Не верно распределив действия, ребёнок не правильно выполняет задание. В статье раскрываются основные правила решения примеров, содержащих в себе весь спектр математических вычислений, включая скобки. Порядок действий в математике 4 класс правила и примеры.
Перед выполнением задания попросите своё чадо пронумеровать действия, которые он собирается выполнить. Если возникли затруднения – помогите.
Некоторые правила, которые необходимо соблюдать при решении примеров без скобок:
Если в задании необходимо выполнить ряд действий, нужно сначала выполнить деление или умножение, затем . Все действия выполняются по ходу письма. В противном случае, результат решения будет не верным.
Если в примере требуется выполнить , выполняем по порядку, слева направо.
27-5+15=37 (при решении примера руководствуемся правилом. Сначала выполняем вычитание, затем – сложение).
Научите ребёнка всегда планировать и нумеровать выполняемые действия.
Ответы на каждое решённое действие записываются над примером. Так ребёнку гораздо легче будет ориентироваться в действиях.
Так ребёнку гораздо легче будет ориентироваться в действиях.
Рассмотрим ещё один вариант, где необходимо распределить действия по порядку:
Как видим, при решении соблюдено правило, сначала ищем произведение, после — разность.
Это простые примеры, при решении которых, необходима внимательность. Многие дети впадают в ступор при виде задания, в котором присутствует не только умножение и деление, но и скобки. У школьника, не знающего порядок выполнения действий, возникают вопросы, которые мешают выполнить задание.
Как говорилось в правиле, сначала найдём произведение или частное, а потом всё остальное. Но тут же есть скобки! Как поступить в этом случае?
Решение примеров со скобками
Разберём конкретный пример:
- При выполнении данного задания, сначала найдём значение выражения, заключённого в скобки.
- Начать следует с умножения, далее – сложение.
- После того, как выражение в скобках решено, приступаем к действиям вне их.

- По правилам порядка действий, следующим шагом будет умножение.
- Завершающим этапом станет .
Как видим на наглядном примере, все действия пронумерованы. Для закрепления темы предложите ребёнку решить самостоятельно несколько примеров:
Порядок, по которому следует вычислять значение выражения уже расставлен. Ребёнку останется только выполнить непосредственно решение.
Усложним задачу. Пусть ребёнок найдёт значение выражений самостоятельно.
7*3-5*4+(20-19) 14+2*3-(13-9)
17+2*5+(28-2) 5*3+15-(2-1*2)
24-3*2-(56-4*3) 14+12-3*(21-7)
Приучите ребёнка решать все задания в черновом варианте. В таком случае, у школьника будет возможность исправить не верное решение или помарки. В рабочей тетради исправления не допустимы. Выполняя самостоятельно задания, дети видят свои ошибки.
Родители, в свою очередь, должны обратить внимание на ошибки, помочь ребёнку разобраться и исправить их. Не стоит нагружать мозг школьника большими объёмами заданий. Такими действиями вы отобьёте стремление ребёнка к знаниям. Во всём должно быть чувство меры.
Такими действиями вы отобьёте стремление ребёнка к знаниям. Во всём должно быть чувство меры.
Делайте перерыв. Ребёнок должен отвлекаться и отдыхать от занятий. Главное помнить, что не все обладают математическим складом ума. Может из вашего ребёнка вырастет знаменитый философ.
Мы рассмотрим в этой статье три варианта примеров:
1. Примеры со скобками (действия сложения и вычитания)
2. Примеры со скобками (сложение, вычитание, умножение, деление)
3. Примеры, в которых много действий
1 Примеры со скобками (действия сложения и вычитания)
Рассмотрим три примера. В каждом из них порядок действий обозначен цифрами красного цвета:
Мы видим, что порядок действий в каждом примере будет разный, хотя числа и знаки одинаковые. Это происходит потому, что во втором и третьем примере есть скобки.
*Это правило для примеров без умножения и деления. Правила для примеров со скобками, включающих действия умножения и деления мы рассмотрим во второй части этой статьи.
Чтобы не запутаться в примере со скобками, можно превратить его в обычный пример, без скобок. Для этого результат, полученный в скобках, записываем над скобками, далее переписываем весь пример, записывая вместо скобок этот результат, и далее выполняем все действия по порядку, слева направо:
В несложных примерах можно все эти операции производить в уме. Главное — сначала выполнить действие в скобках и запомнить результат, а затем считать по порядку, слева направо.
А теперь — тренажеры!
1) Примеры со скобками в пределах до 20. Онлайн тренажер.
2) Примеры со скобками в пределах до 100. Онлайн тренажер.
3) Примеры со скобками. Тренажер №2
4) Вставь пропущенное число — примеры со скобками. Тренажер
2 Примеры со скобками (сложение, вычитание, умножение, деление)
Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.
Сначала рассмотрим примеры без скобок:
Есть одна хитрость, как не запутаться при решении примеров на порядок действий. Если нет скобок, то выполняем действия умножения и деления, далее переписываем пример, записывая вместо этих действий полученные результаты. Затем выполняем сложение и вычитание по порядку:
Если нет скобок, то выполняем действия умножения и деления, далее переписываем пример, записывая вместо этих действий полученные результаты. Затем выполняем сложение и вычитание по порядку:
Если в примере есть скобки, то сначала нужно избавиться от скобок: переписать пример, записывая вместо скобок полученный в них результат. Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:
3 Примеры, в которых много действий
Если в примере много действий, то удобнее будет не расставлять порядок действий во всем примере, а выделить блоки, и решить каждый блок отдельно. Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).
Обратные операции: умножение и деление
Что такое обратные операции?
Обратные операции — это два разных типа вычислений, оказывающих противоположное влияние друг на друга. Например, вычитание — операция, обратная сложению, а деление — операция, обратная умножению.
Например, вычитание — операция, обратная сложению, а деление — операция, обратная умножению.
В математике слово «инверсия» означает «противоположное».
Обратные операции можно использовать для отмены исходной операции. Это приводит к возврату значения, с которого мы начали до первого вычисления.
Например, мы можем начать с числа 5, а затем умножить его на 4.
5 × 4 = 20. Мы начали с 5, но теперь их 20.
Чтобы вернуться от 20 к 5, мы используем обратную операцию.
20 ÷ 4 = 5. Мы можем вернуться от 20 к 5, разделив на 4.
Мы говорим, что умножение на 4 — это операция, обратная делению на 4.
Умножение 5 на 4 дало 20.
Разделив 20 на 4, мы вернулись к 5.
Умножение и деление являются примерами обратных операций.
Что такое обратное умножению?
Обратным умножением является деление. Если вы умножите на заданное число, а затем разделите на то же число, вы получите то же число, с которого начали. Деление имеет эффект, противоположный умножению.
Деление имеет эффект, противоположный умножению.
Например, здесь 3 × 2 = 6.
Мы начали с числа 3.
Мы умножили его на 2, чтобы увеличить от 3 до 6.
Для возврата от 6 к 3 необходимо использовать обратную операцию.
Противоположностью умножения на 2 является деление на 2.
Делим 6 на 2, чтобы вернуться к исходному числу 3.
Деление имело обратный эффект по отношению к умножению, выполненному в исходном расчете.
Деление и умножение обратны только в том случае, если деление и умножение на одно и то же число. В этом примере мы умножили и разделили на 2.
Что такое обратное делению?
Обратное деление — умножение. Если вы разделите на заданное число, а затем умножите на то же число, вы получите то же число, с которого начали. Умножение имеет эффект, противоположный делению.
Например, вот 10 ÷ 2 = 5.
Мы начали с числа 10.
Мы разделили его на 2, чтобы уменьшить 10 до 5.
Чтобы вернуться от 5 к нашему исходному числу 10, мы должны использовать обратную операцию.
Мы можем умножить 5 на 2, чтобы вернуться к исходному числу 10. 5 × 2 = 10.
Деление на 2 и умножение на 2 являются обратными операциями. Умножение на 2 привело к отмене деления на 2.
Как записать умножение в виде деления
Чтобы записать умножение как деление, выполните следующие действия:
- Запишите ответ умножения в начале деления перед знаком деления.
- Запишите два умножаемых числа после знака деления и после знака равенства соответственно.
- Два числа на втором шаге можно записать в любом порядке, чтобы образовать два разных предложения с делением.
Например, вот 7 × 8 = 56. Запишем это умножение как деление.
Каждое умножение можно переписать как деление, используя те же числа, но в другом порядке.
Если вы знаете ответ на данное умножение, вы можете сразу использовать его для создания деления без выполнения каких-либо вычислений. Просто переставьте числа.
Просто переставьте числа.
Первый шаг — написать ответ на умножение в начале предложения деления. Результат умножения теперь равен числу, на которое оно делится.
56 — это ответ на умножение 7 × 8 = 56. Мы начнем наше деление с 56.
Следующим шагом будет запись умножаемых чисел в предложении умножения после знака деления и после знака равенства в любом порядке.
Умножаются два числа: 7 и 8. Мы напишем 7 после знака деления и 8 после знака равенства.
Преобразуем умножение 7 × 8 = 56 в деление 56 ÷ 7 = 8. Используемые числа те же, но они записаны в другом порядке.
В то время как 56 должно идти в начале деления, два других числа 7 и 8 могут быть записаны в любом порядке. Для каждого умножения можно записать два разных деления.
На этот раз мы напишем эти два числа в другом порядке.
Преобразуем умножение 7×8=56 в деление 56÷8=7.
7 × 8 = 56 можно записать как 56 ÷ 7 = 8 или 56 ÷ 8 = 7.
Как записать деление как умножение
Чтобы записать деление как умножение, выполните следующие действия:
- Запишите делимое число как ответ в конце умножения.

- Запишите оставшиеся два числа в предложении деления, умноженные вместе в предложении умножения.
- Два числа из второго шага можно записать в любом порядке, чтобы получились два разных предложения умножения.
Например, вот 18 ÷ 6 = 3
Первый шаг — записать делимое число в начале деления как ответ в конце умножения.
18 — это число, которое нужно разделить. Это сформирует ответ в конце умножения.
Следующим шагом будет запись оставшихся двух чисел из деления, умноженных вместе, в предложении умножения.
Два других числа в делении — это 6 и 3.
Мы можем записать 18 ÷ 6 = 3 как 6 × 3 = 18.
Мы также можем записать 18 ÷ 6 = 3 как 3 × 6 = 18. Неважно, в каком порядке умножаются два числа.
Каждое предложение деления может быть записано как два разных предложения умножения.
18 ÷ 6 = 3 можно записать как 6 × 3 = 18 или 3 × 6 = 18.
Как обучать многозначному умножению и делению в длинное число
Узнайте, как лучше всего обучать многозначному умножению и делению в длинное число. Эта дифференцированная стратегия помогает учащимся 3-го, 4-го, 5-го классов и учащимся специального образования.
Эта дифференцированная стратегия помогает учащимся 3-го, 4-го, 5-го классов и учащимся специального образования.
Вы нашли отличное место для начала, если вам нужны лучшие стратегии для обучения многозначному умножению и делению в длинную сторону. Я обнаружил, что это самые простые методы обучения учащихся. Лучше всего они работают с учащимися 4-х классов, учащимися 5-х классов, учащимися из групп риска, борцами и учащимися специального образования — ВСЕ СТУДЕНТЫ !
Этот визуальный метод успешно работает для очень многих учеников!
Много лет назад обучение алгоритмам умножения и деления в раз вызывало у меня огромный страх. Традиционные методы, которые я использовал, просто не работали.
Мои ученики так запутались. Они забыли шаги. Они не могли выстроить свои числа и — они даже не могли прочитать свой собственный почерк.
Стратегии умножения и деления Shape Math™ Я знал, что должен быть лучший способ. Но, короче говоря, лучшего способа я не нашел. Итак, я разработал собственную стратегию, которую назвал Shape Math™.
Но, короче говоря, лучшего способа я не нашел. Итак, я разработал собственную стратегию, которую назвал Shape Math™.
Я много лет преподаю эту стратегию многозначного умножения и деления в своем классе, и я получил фантастических отзывов от других учителей об их успехах в использовании!
Рабочий лист для умножения с использованием двузначного органайзера для умножения Об организаторахМетоды Shape Multiplication™ и Shape Division™ используют форм и цветов , чтобы помочь учащимся запомнить последовательность шагов.
Формы и цвета помогают учащимся решать задачи до тех пор, пока они не освоятся в процессе. В конце концов, им больше не понадобится органайзер. это визуальный процесс, который подходит многим учащимся, в том числе учащимся, испытывающим затруднения !
Органайзеры для умножения выглядят так:
А вот органайзер для задач на деление:
Как я обучение двузначному умножению.
Ниже представлена пошаговая видеоинструкция деления в длину по стандартному алгоритму.
Инструктаж для всей группы
Обычно я использую SmartBoard (интерактивную доску) перед всем классом для групповых занятий, за которыми следуют небольшие группы и индивидуальная помощь.
Для начала я представляю органайзер и предлагаю ученикам обратить внимание на различные формы и цвета. Затем мы говорим о том, как различные формы и цвета помогают нам решать длинные математические задачи.
Затем мы говорим о том, как различные формы и цвета помогают нам решать длинные математические задачи.
Представляя эту стратегию, я начинаю с демонстрации основных задач на умножение (или деление). Например, я бы начал с задачи на 2 цифры x 1 с помощью органайзера. Затем, после беглого обзора, я подробно учу, как решать многошаговую задачу на умножение с помощью органайзера.
I подробно объяснить мои мысли вслух, чтобы ученики услышали. Например, я говорю: «Мне нужно умножить 5 в пятиугольнике единицы на 3 в круге». Я обязательно указываю на фигуры и числа и заполняю органайзер, пока говорю.
Студенты несколько раз смотрят, как я моделирую процесс. Пока я моделирую процедуру, я задаю вопросы о последовательности шагов.
Пока я сижу у интерактивной доски, ученики следуют вместе со своими органайзерами на своих местах. Учащимся нравится использовать органайзеры, помещенные в прозрачные пластиковые конверты с маркерами, стираемыми с помощью сухого стирания.
На фото ниже показано, что любая цифра, умноженная на 3 в красном кружке, дает произведение, указанное в красных кружках под цифрой 3. Вот почему я продолжаю повторять: «Круги идут с кругами».
Цифры, умноженные на 2 в синем квадрате, дают продукты, указанные в синих квадратах на органайзере. Поэтому я повторяю «Квадраты идут с квадратами» снова и снова.
2-значный органайзер для умножения на интерактивной доскеВо время обучения я звучу как заезженная пластинка, постоянно повторяя: «Круги идут кругами; квадраты идут с квадратами». Этот метод работает даже тогда, когда вы начинаете дифференцировать, исключая цвета и переходя к органайзеру черно-белых фигур.
Рабочие листы по умножению двузначных и трехзначных чиселИндивидуальное/малое обучение
Далее мы переходим от обучения всей группы к самостоятельной работе над заданием.
Пока ученики работают, я быстро прохожусь по классу и замечаю, какие ученики выглядят сбитыми с толку. В это время я обычно либо собираю студентов в небольшую группу за задним столом, либо предлагаю индивидуальную помощь.
В это время я обычно либо собираю студентов в небольшую группу за задним столом, либо предлагаю индивидуальную помощь.
Многоразовые прозрачные пластиковые футляры
Мне нравится использовать эти потрясающие футляры для сухого стирания ( Нажмите здесь, чтобы найти похожие на Amazon ). Я люблю их и использую почти каждый день по-разному для разных предметов.
Shape Math™ использует цвета и формы для дифференциацииДифференциация упрощается благодаря органайзерам и рабочим листам в наборах Shape Math. Универсальность позволяет вам подобрать необходимый уровень помощи для уникальных потребностей каждого учащегося.
Как выделиться с помощью органайзеровУвеличьте помощь учащимся, которым нужна максимальная поддержка, используя цвета и формы. По мере того, как учащиеся улучшают свои навыки, уменьшайте зависимость, убирая цвета и вводя готовые рабочие листы.
В конце концов, вы можете отказаться от форм и цветов и перейти к прилагаемым рабочим листам в виде миллиметровки.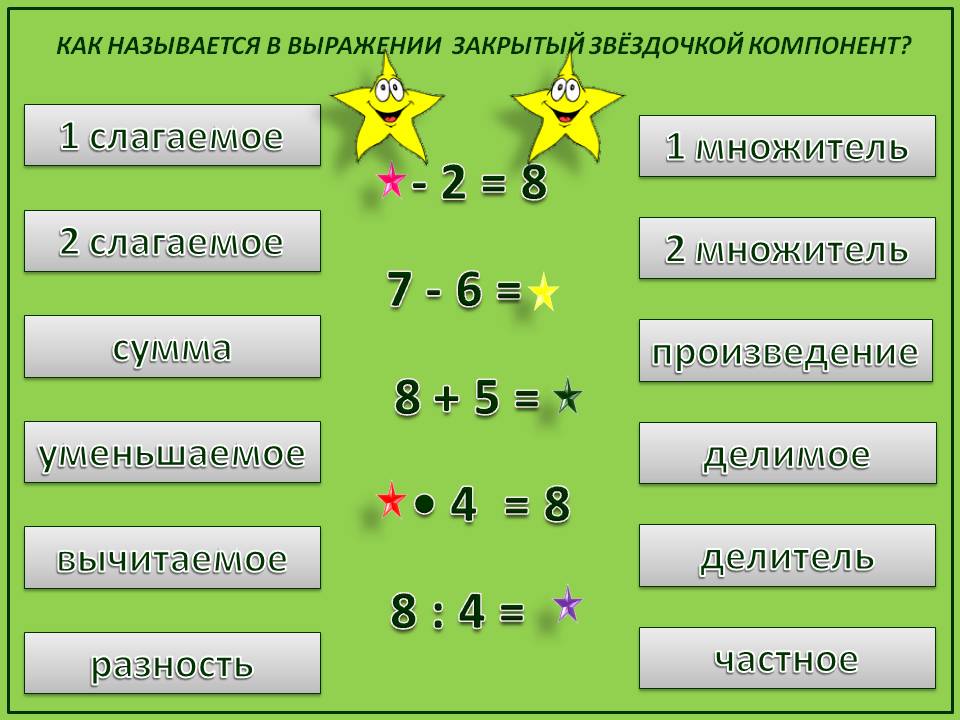 Затем, когда придет время, учащиеся смогут перейти к базовому алгоритму умножения или деления без использования цветов, фигур или миллиметровой бумаги.
Затем, когда придет время, учащиеся смогут перейти к базовому алгоритму умножения или деления без использования цветов, фигур или миллиметровой бумаги.
Варианты строительных лесов, предлагаемые в этих наборах, повышают уверенность и вовлеченность учащихся. Уверенность и вовлеченность ведут к возбуждению, гордости и стремлению учиться.
Набор для начинающих, 3-значный и 4-значный набор рабочих листов и органайзеровНаборы для умножения и деления включают множество органайзеров разного размера. Кроме того, предварительно разработанные рабочие листы позволяют выбрать правильное время для внедрения более сложных навыков.
Типовые лесаПрогресс обычно включает:
- Устранение цветов на органайзерах
- Устранение фигур
- Устранение органайзеров
- Переход на миллиметровую бумагу
- Переход от миллиметровой бумаги к независимости.
Сначала я удалил цвета на школьном органайзере на фотографии выше. Однако я заметил, что ему тяжело без цветов, поэтому я использовал маркеры, чтобы вернуть ему цвета. Есть много способов помочь вашим ученикам в обеспечении надлежащего уровня поддержки.
Однако я заметил, что ему тяжело без цветов, поэтому я использовал маркеры, чтобы вернуть ему цвета. Есть много способов помочь вашим ученикам в обеспечении надлежащего уровня поддержки.
Вы выбираете подходящее время для уничтожения цветов на органайзерах с конечной целью уничтожения органайзера. Затем учащиеся могут перейти на рабочие листы с миллиметровой бумагой, прежде чем перейти к самостоятельности без органайзеров или миллиметровой бумаги.
Щелкните изображение, чтобы узнать больше об этом ресурсе Анкерные диаграммы в классеЯ ОБОЖАЮ базовые диаграммы — их легко сделать, и они ПОТРЯСАЮЩИЕ справочные инструменты! Ниже приведена якорная таблица умножения, которую я использую и показываю в качестве справочной информации для своих учеников.
Якорная диаграмма двузначного умножения Якорная диаграмма с использованием визуального органайзера с цветами и формами Якорная диаграмма длинного деления Я начал использовать это мнемоническое устройство со старым добрым McDonald’s: 0 Делает
(разделитель)
 0084
0084Раньше я пользовался пульмонологическим устройством Division Family , но семьи могут выглядеть очень по-разному, поэтому вместо этого я переключился на поговорку McDonald’s.
- Daddy , (Divide)
- Mommy (Multiply),
- сестра (выброс),
- Brother (выброшен),
- (выброшен),
- .
Иногда у меня есть готовая задача в начале урока математики, например, утренняя работа.
Как только учащиеся усваивают правило деления в длинную, я меняю цифры на стикерах. Я делаю все, что в моих силах, чтобы он соответствовал цвету, но жизнь случается. Якорная диаграмма Sticky-Note делает изменение задач проще и веселее. В стикерах есть что-то, что нравится ученикам.
якорная диаграмма для заметок У меня есть одна последняя мысль о якорных диаграммах для заметок. Студенты любят быть ответственными за изменение чисел. Кроме того, некоторым учащимся требуется дополнительное внимание и повышение уверенности в себе.
Студенты любят быть ответственными за изменение чисел. Кроме того, некоторым учащимся требуется дополнительное внимание и повышение уверенности в себе.
Мне бы очень хотелось узнать, как вы используете стикеры в классе!
Статьи о многозначном умножении:
- 3 идеи для обучения многозначному умножению – Вот 3 идеи FAST для обучения многозначному умножению. Эти вмешательства просты и быстры для занятых учителей.
- Рабочие листы по умножению 2-значных чисел: дифференцированные – Вот визуальный метод обучения умножению 2-значных чисел с использованием дифференцированных визуальных подсказок, которые помогут учащимся добиться успеха в обучении.
- Двузначное умножение стало проще! – Вот как использовать организаторы двузначного умножения и рабочие листы.
Статьи о длинном делении:
- Дифференцированные рабочие листы на длинное деление БЕСПЛАТНО – Получите эти дифференцированные рабочие листы на длинное деление БЕСПЛАТНО и значительно повысьте успеваемость учащихся и ваши успехи в обучении!
- Вмешательство в математику с миллиметровой бумагой – В этой статье блога объясняется, как использовать миллиметровую бумагу в качестве быстрого и простого ресурса для вмешательства с вашими учащимися.
 Кроме того, он содержит ссылки на бесплатную печатную миллиметровую бумагу и идеи о том, как ее использовать в классе.
Кроме того, он содержит ссылки на бесплатную печатную миллиметровую бумагу и идеи о том, как ее использовать в классе.
Ресурсы для дифференцированного умножения:
- Набор рабочих листов и органайзеров для умножения двух цифр – Этот новый метод двузначного умножения использует цвета и формы, чтобы обеспечить наглядную конкретную стратегию обучения двузначному умножению.
- Рабочие листы и органайзеры для умножения 2 и 3 цифр – Этот метод многозначного (3 x 2 цифры) умножения использует цвета и формы для визуальной, конкретной стратегии.
- Рабочие листы и органайзеры для умножения 2-значных x 1-значных и 3-значных x 1-значных чисел – Этот набор включает умножение 2-значных x 1-значных и 3-значных x 1-значных значений с этими рабочими листами и органайзерами .
- 3-значные и 4-значные рабочие листы и органайзеры для умножения – Этот метод многозначного (3-значный x 3-значный и 4-значный x 3-значный) метод умножения использует цвета и формы для визуального, конкретного стратегия.

- Все ресурсы умножения – Ознакомьтесь со всеми ресурсами для умножения, которые я предлагаю в моем магазине для учителей.
Ресурсы для дифференцированных длинных разделов:
- Дифференцированные рабочие листы и органайзеры для длинных разделов — Посетите сайт Teachers Pay Teachers, чтобы увидеть полный набор органайзеров и рабочих листов, включенных в исходный комплект.
- Все ресурсы отдела – Ознакомьтесь со ВСЕМИ ресурсами для умножения, которые я предлагаю в моем магазине учителей для учителей.
- 2-значные делители Дифференцированные рабочие листы и органайзеры – Когда вы будете готовы перейти к двузначным делителям, это идеальный ресурс для продвижения продвинутого обучения длинных делений с вашими учащимися.
- Рабочие листы и органайзеры для умножения на 2 цифры — дифференцированный ресурс — Посетите сайт Teachers Pay Teachers, чтобы увидеть полный набор органайзеров и рабочих листов, включенных в этот оригинальный комплект.

Пожалуйста, следите за мной в моем магазине учителей , , Pinterest и Facebook , если вы нашли эту статью полезной! Я хотел бы услышать от вас!
Умножение и деление — Oxford Owl для дома
Вам не нужно быть экспертом, чтобы помочь ребенку с математикой! Вот четыре простых, но эффективных способа помочь вашему ребенку развить понимание умножения и деления:
1. Практическое изучение
Использование реальных предметов для раннего понимания умножения и деления. Например, используйте носки, перчатки или формочки для льда, чтобы считать двойками, пятерками или десятками. Используйте коробки для яиц или лотки для кексов, чтобы исследовать массивы. Практикуйте деление, разделяя бусинки между игрушками или раскладывая кубики по группам.
2. Тренировка таблицы умножения
Пойте, повторяйте или играйте в игры, чтобы помочь ребенку запомнить таблицу умножения. Дайте баллы за каждый факт, который они знают. Используйте реальные возможности для практики. Например, когда вы в супермаркете, спросите ребенка: «Сколько у нас будет пакетов, если мы купим 3 мультиупаковки по 6 штук в каждой?»
Дайте баллы за каждый факт, который они знают. Используйте реальные возможности для практики. Например, когда вы в супермаркете, спросите ребенка: «Сколько у нас будет пакетов, если мы купим 3 мультиупаковки по 6 штук в каждой?»
3. Объясните различные методы
Попросите ребенка объяснить каждый этап умножения или деления и почему он выбрал этот метод. Они могут использовать удвоение или деление пополам, применять факты таблицы умножения, использовать изображения для представления своих расчетов или писать свои методы. Поощряйте их сначала оценивать, а затем проверять с помощью другой стратегии.
4. Переходите на цифровые технологии и побеждайте!
Помимо множества ресурсов, доступных здесь, в Oxford Owl, есть широкий спектр онлайн-занятий и веселых игр, которые помогут быстро вспомнить факты умножения и деления. Наиболее популярны сайты, которые поощряют детей соревноваться со временем или бросать вызов своим друзьям, одноклассникам и даже учителям. Скорость – ключ к успеху.
Скорость – ключ к успеху.
Хотите узнать больше?
Чтобы помочь вашему ребенку учиться дальше, вы можете посмотреть некоторые видео, включенные в нашу специальную библиотеку по математике. Если вы ищете другие идеи для поддержки обучения дома, зайдите в наш блог по математике, чтобы изучить статьи, полные лучших советов и интересных занятий.
Умножение и деление в 1-м классе (возраст 5–6 лет)
В 1-м классе ваш ребенок должен уметь решать простые задачи на умножение и деление, используя в помощь предметы, рисунки и массивы. В том числе:
- считая шагами по 2, 5 и 10 и понимая, что, например, 3 × 2 равно 2 + 2 + 2
- совместное использование и группировка для решения задач деления
- начинает понимать взаимосвязь между умножением и делением.
Дополнительная информация и идеи для занятий в 1-м классе
Умножение и деление во 2-м классе (6–7 лет)
Во 2-м классе ваш ребенок должен будет использовать ряд методов для решения задач на умножение и деление, в том числе с помощью практические ресурсы и умственные методы. В том числе:
В том числе:
- знание и использование фактов умножения и деления для таблиц умножения на 2, 5 и 10
- распознавание и определение нечетных и четных чисел
- , используя символы ×, ÷ и = для записи операций умножения и деления.
Дополнительная информация и идеи для занятий для 2-го года
Умножение и деление в 3-м классе (возраст 7–8 лет)
В 3-м классе ваш ребенок должен будет использовать ряд стратегий для решения задач в уме и начнет учиться формальные письменные методы для краткого умножения и краткого деления. В том числе:
- знание и использование фактов умножения и деления для таблиц умножения на 3, 4 и 8
- умножение двузначных чисел на однозначные числа
- понимание того, что умножение и деление имеют обратную зависимость (т. е. они отменяют друг друга), и использование этого для проверки своих вычислений.
Дополнительная информация и идеи для занятий для 3-го класса
Умножение и деление в 4-м классе (8–9 лет)
Ожидается, что в 4-м классе ваш ребенок сможет уверенно использовать формальные письменные методы краткого умножения и краткого деления. В том числе:
В том числе:
- знание и использование фактов умножения и деления для всех таблиц умножения до 12 × 12
- умножение трехзначных чисел на однозначные числа
- умножение трех чисел
- готовится к проверке таблицы умножения для 4-х классов в июне.
Дополнительная информация и идеи для занятий для 4-го класса
Умножение и деление в 5-м классе (возраст 9–10 лет)
Ожидается, что в 5-м классе ваш ребенок сможет решать задачи на умножение и деление с использованием чисел до четырех цифр и начать учить длинное умножение. В том числе:
- умножение четырехзначных чисел на двузначные числа
- деление четырехзначных чисел на однозначные и интерпретация остатков
- понимание терминов кратное, множитель, общий множитель, простое, квадратное и кубическое числа.
Дополнительная информация и идеи для занятий для 5-го класса
Вычисления в 6-м классе (возраст 10–11 лет)
Ожидается, что в 6-м классе ваш ребенок будет способен умножать и делить большие числа, используя формальные письменные методы, включая деление в длинное число. . В том числе:
. В том числе:
- умножение четырехзначных чисел на двузначные с использованием длинного умножения
- деление четырехзначных чисел на двузначные с использованием длинного деления
- решение многоэтапных задач с использованием сложения, вычитания, умножения и деления, выбор методов для использования и объяснение причин.
Дополнительная информация и идеи для занятий для 6-го класса
об арифметических операторах — PowerShell
- Статья
- 11 минут на чтение
Краткое описание
Описывает операторы, выполняющие арифметические действия в PowerShell.
Подробное описание
Арифметические операторы вычисляют числовые значения. Вы можете использовать один или несколько
арифметические операторы для сложения, вычитания, умножения и деления значений, а также для
вычислить остаток (модуль) операции деления.
Оператор сложения ( + ) и оператор умножения ( * ) также работают на
строки, массивы и хеш-таблицы. Оператор сложения объединяет ввод.
Оператор умножения возвращает несколько копий ввода. Вы можете даже
смешивать типы объектов в арифметическом операторе. Метод, который используется для оценки
оператор определяется типом самого левого объекта в
выражение.
Начиная с PowerShell 2.0, все арифметические операторы работают с 64-битными числами.
Начиная с PowerShell 3.0, -шр (сдвиг-вправо) и -шл (сдвиг-влево)
добавлены для поддержки побитовой арифметики в PowerShell. Побитовые операторы
работают только с целочисленными типами.
PowerShell поддерживает следующие арифметические операторы:
Сложение (
+) — добавляет числа, объединяет строки, массивы и хэш-таблицы6 + 2 # результат = 8 "файл" + "имя" # результат = "имя файла" @(1, "один") + @(2.0, "два") # результат = @(1, "один", 2.
 0, "два")
@{"один" = 1} + @{"два" = 2} # результат = @{"один" = 1; "два" = 2}
0, "два")
@{"один" = 1} + @{"два" = 2} # результат = @{"один" = 1; "два" = 2}
Вычитание (
-) — Вычитание или отрицание чисел6 - 2 # результат = 4 - -6 # результат = 6 (Get-Date).AddDays(-1) # Вчерашняя дата
Умножение (
*) — умножение чисел или копирование строк и массивов указанное количество раз6 * 2 # результат = 12 @("!") * 4 # результат = @("!","!","!","!") "!" * 3 # результат = "!!!"Отдел (
/) — Делит числа6 / 2 # результат = 3
Модуль (
%) — возвращает остаток от операции деления.7 % 2 # результат = 1
Побитовое И (
- диапазон)5-диапазонный 3 # результат = 1
Побитовое НЕ (
-bnot)-bnot 5 # результат = -6
Побитовое ИЛИ (
-bor)5 -бор 0x03 # результат = 7
Побитовое исключающее ИЛИ (
-bxor)5 -bxor 3 # результат = 6
Сдвигает биты влево (
-шл)102 -шл 2 # результат = 408
Сдвигает биты вправо (
-shr)102 -shr 2 # результат = 25
Приоритет оператора
PowerShell обрабатывает арифметические операторы в следующем порядке:
| Приоритет | Оператор | Описание |
|---|---|---|
| 1 | () | Скобки |
| 2 | - | Для отрицательного числа или унарного оператора |
| 3 | * , / , % | Для умножения и деления |
| 4 | + , - | Для сложения и вычитания |
| 5 | - полоса , - шпилька | Для побитовых операций |
| 5 | -бор , -бксор | Для побитовых операций |
| 5 | -шр , -шл | Для побитовых операций |
PowerShell обрабатывает выражения слева направо в соответствии с
правила приоритета. В следующих примерах показано влияние приоритета
правила:
В следующих примерах показано влияние приоритета
правила:
3+6/3*4 # результат = 11 3+6/(3*4) # результат = 3,5 (3+6)/3*4 # результат = 12
Порядок, в котором PowerShell оценивает выражения, может отличаться от других языки программирования и сценариев, которые вы использовали. Следующий пример показывает сложный оператор присваивания.
$а = 0 $б = @(1,2) $с = @(-1,-2) $b[$a] = $c[$a++]
В этом примере выражение $a++ оценивается до $b[$a] . Оценка $a++ изменяет значение $a после использования в операторе $c[$a++] ,
но до того, как он будет использован в $b[$a] . Переменная $a в $b[$a] равна 1 , а не 0 . Поэтому оператор присваивает значение $b[1] , а не $b[0] .
Приведенный выше код эквивалентен:
$a = 0 $б = @(1,2) $с = @(-1,-2) $тмп = $с[$а] $а = $а + 1 $b[$a] = $tmp
Деление и округление
Если частное операции деления является целым числом, PowerShell округляет
значение до ближайшего целого числа. Когда значение равно
Когда значение равно .5 , округляется до ближайшего
четное целое.
В следующем примере показан эффект округления до ближайшего четного целого числа.
PS> [int]( 5 / 2 ) # Результат округляется в меньшую сторону 2 PS> [int]( 7 / 2 ) # Результат округляется в большую сторону 4
Вы можете использовать класс [Math] , чтобы получить другое поведение округления.
PS> [int][Math]::Round(5 / 2,[MidpointRounding]::AwayFromZero 3 PS> [int][Math]::Ceiling(5 / 2) 3 PS> [int][Math]::Floor(5 / 2) 2
Для получения дополнительной информации см. Math.Round метод.
Сложение и умножение нечисловых типов
Вы можете добавлять числа, строки, массивы и хеш-таблицы. И вы можете умножить числа, строки и массивы. Однако вы не можете умножать хеш-таблицы.
При добавлении строк, массивов или хэш-таблиц элементы объединяются.
Когда вы объединяете коллекции, такие как массивы или хеш-таблицы, новый объект
создается, который содержит объекты из обеих коллекций. Если вы попытаетесь
объединить хэш-таблицы с одним и тем же ключом, операция завершится ошибкой.
Если вы попытаетесь
объединить хэш-таблицы с одним и тем же ключом, операция завершится ошибкой.
Например, следующие команды создают два массива, а затем добавляют их:
$a = 1,2,3 $b = "А", "В", "С" $а + $б
1 2 3 А Б С
Вы также можете выполнять арифметические операции над объектами разных типов. операция, которую выполняет PowerShell, определяется типом Microsoft .NET самый левый объект в операции. PowerShell пытается преобразовать все объектов в операции к типу .NET первого объекта. Если это удастся при преобразовании объектов он выполняет операцию, соответствующую .NET Тип первого объекта. Если не удается преобразовать какой-либо из объектов, операция не удалась.
Следующие примеры демонстрируют использование сложения и умножения операторы в операциях, которые включают различные типы объектов.
$массив = 1,2,3 $red = [ConsoleColor]::Red $blue = [ConsoleColor]::Синий "файл" + 16 # результат = "файл16" $массив + 16 # результат = 1,2,3,16 $массив + "файл" # результат = 1,2,3,"файл" $массив * 2 # результат = 1,2,3,1,2,3 "файл" * 3 # результат = "файлфайлфайл" $синий + 3 # результат = красный $red - 3 # результат = Синий $синий - $красный # результат = -3 + '123' # результат = 123
Поскольку метод, используемый для оценки операторов, определяется
крайний левый объект, сложение и умножение в PowerShell не являются строго
коммутативный. Например,
Например, (a + b) не всегда равно (b + a) и (ab) .
не всегда равно (ba) .
Следующие примеры демонстрируют этот принцип:
PS> "файл" + 16 файл16 PS>16 + "файл" InvalidArgument: невозможно преобразовать значение «файл» в тип «System.Int32». Ошибка: "Входная строка имеет неверный формат."
Хэш-таблицы — это немного другой случай. Вы можете добавить хеш-таблицы в другой хэш-таблица, если в добавленных хеш-таблицах нет повторяющихся ключей.
В следующем примере показано, как добавлять хэш-таблицы друг к другу.
$hash2 = @{a=1; б=2; с=3}
$hash3 = @{c1="Server01"; c2="Сервер02"}
$хэш2 + $хэш3
Имя Значение ---- ----- c2 Сервер02 1 Би 2 c1 Сервер01 с 3
В следующем примере возникает ошибка, поскольку один из ключей дублируется в обе хеш-таблицы.
$hash2 = @{a=1; б=2; с=3}
$hash3 = @{c1="Server01"; c="Сервер02"}
$хэш2 + $хэш3
Операция остановлена:
Линия |
3 | $хэш2 + $хэш3
| ~~~~~~~~~~~~~~~
| Товар уже добавлен. Ключ в словаре: 'c' Добавляемый ключ: 'c'
Ключ в словаре: 'c' Добавляемый ключ: 'c'
Также к массиву можно добавить хеш-таблицу; и вся хеш-таблица становится элемент в массиве.
$array1 = @(0, "Hello World", [datetime]::Now)
$хэш2 = @{а=1; б=2}
$массив2 = $массив1 + $хэш2
$массив2
0 Привет, мир 12 июня 2017 г., 15:05:46 Ключ: а Значение : 1 Имя: а Ключ : б Значение : 2 Имя : б
Однако в хеш-таблицу нельзя добавить какой-либо другой тип.
$хеш2 + 2
InvalidOperation: хеш-таблицу можно добавить только в другую хеш-таблицу.
Хотя операторы сложения очень полезны, используйте операторы присваивания
для добавления элементов в хеш-таблицы и массивы. Для получения дополнительной информации см.
about_assignment_operators. Следующее
примеры используют += оператор присваивания для добавления элементов в массив:
$array = @()
(0..9).foreach{$массив += $_}
$массив
0 1 2
Преобразование типов для соответствия результату
PowerShell автоматически выбирает числовой тип . NET, который лучше всего выражает
результат без потери точности. Например:
NET, который лучше всего выражает
результат без потери точности. Например:
2 + 3,1 (2).ПолучитьТип().ПолноеИмя (2 + 3.1).ПолучитьТип().ПолноеИмя
5.1 Система.Int32 Система.Двойной
Если результат операции слишком велик для типа, тип результата расширяется для размещения результата, как в следующем примере:
(512 МБ).GetType().FullName (512MB * 512MB).GetType().FullName
System.Int32 Система.Двойной
Тип результата не всегда совпадает с одним из операндов. в
В следующем примере отрицательное значение нельзя преобразовать в целое число без знака, а
целое число без знака слишком велико для приведения к Int32 :
([int32]::minvalue + [uint32]::maxvalue).gettype().fullname
System.Int64
В этом примере Int64 может поддерживать оба типа.
Исключением является тип System.Decimal . Если любой из операндов имеет Десятичный тип , результатом будет Десятичный тип . Любой результат слишком велик для Десятичное значение является ошибкой.
Любой результат слишком велик для Десятичное значение является ошибкой.
PS> [Десятичный]::maxvalue 7
Арифметические операторы и переменные
Вы также можете использовать арифметические операторы с переменными. Операторы действуют на значения переменных. Следующие примеры демонстрируют использование арифметические операторы с переменными:
PS> $intA = 6 PS> $intB = 4 PS> $intA + $intB 10 PS> $a = "Мощность" PS> $b = "Оболочка" PS> $а + $б PowerShell
Арифметические операторы и команды
Обычно арифметические операторы используются в выражениях с числами, строки и массивы. Однако вы также можете использовать арифметические операторы с объекты, которые возвращаются командами, и со свойствами этих объектов.
В следующих примерах показано, как использовать арифметические операторы в выражениях. с командами PowerShell:
с командами PowerShell:
(дата получения) + (новый временной интервал -день 1)
Оператор скобок принудительно выполняет оценку командлета Get-Date и
оценка выражения командлета New-TimeSpan -Day 1 в указанном порядке. Оба
затем результаты добавляются с помощью оператора + .
Процесс получения | Где-Объект {($_.ws * 2) -gt 50mb}
Обрабатывает NPM(K) PM(K) WS(K) VM(M) CPU(s) Id ProcessName
------- ------ ----- ----- ----- ------ -- -----------
1896 39 50968 30620 264 1 572,55 1104 исследователь
12802 78 188468 81032 753 3 676,39 5676 ПРОГНОЗ
660 9 36168 26956 143 12,20 988 PowerShell
561 14 6592 28144 110 1 010,09 496 услуги
3476 80 34664 26092 234 ...45,69 876 свхост
967 30 58804 59496 416 930,97 2508 WINWORD
В приведенном выше выражении каждое рабочее пространство процесса ( $_.ws ) умножается на 2 ; и результат сравните с 50mb , чтобы увидеть, больше ли он.
Побитовые операторы
PowerShell поддерживает стандартные побитовые операторы, включая побитовое И
( -band ), включающие и исключающие операторы побитового ИЛИ ( -bor и -bxor ) и побитовое НЕ ( -bnot ).
Начиная с PowerShell 2.0, все побитовые операторы работают с 64-битными целыми числами.
Начиная с PowerShell 3.0, -шр (сдвиг-вправо) и -шл (сдвиг-влево)
введены для поддержки побитовой арифметики в PowerShell.
PowerShell поддерживает следующие побитовые операторы.
| Оператор | Описание | Выражение | Результат |
|---|---|---|---|
-ленточный | Побитовое И | 10-диапазонный 3 | 2 |
-бор | Побитовое ИЛИ (включительно) | 10 -бор 3 | 11 |
-бксор | Побитовое ИЛИ (исключающее) | 10-бксор 3 | 9 |
-bnot | Побитовое НЕ | -bНе 10 | -11 |
-шл | Сдвиг влево | 102 -шл 2 | 408 |
-шр | Сдвиг вправо | 102 -шр 1 | 51 |
Побитовые операторы действуют на двоичный формат значения. Например, бит
структура числа 10 — 00001010 (на основе 1 байта), а бит
структура числа 3 — 00000011. Когда вы используете побитовый оператор для
сравнить 10 с 3, сравниваются отдельные биты в каждом байте.
Например, бит
структура числа 10 — 00001010 (на основе 1 байта), а бит
структура числа 3 — 00000011. Когда вы используете побитовый оператор для
сравнить 10 с 3, сравниваются отдельные биты в каждом байте.
В побитовой операции И результирующий бит устанавливается в 1 только тогда, когда оба входных биты 1,
1010 (10) 0011 ( 3 ) -------------- группа 0010 ( 2 )
В операции побитового ИЛИ (включительно) результирующий бит устанавливается в 1, когда либо или оба входных бита равны 1. Результирующий бит устанавливается в 0 только тогда, когда оба входных бита биты установлены на 0.
1010 (10) 0011 ( 3 ) -------------- БОР (включительно) 1011 (11)
В операции побитового ИЛИ (исключающее) результирующий бит устанавливается в 1 только тогда, когда один входной бит 1.
1010 (10) 0011 ( 3 ) -------------- bXOR (эксклюзивный) 1001 ( 9)
Побитовый оператор НЕ является унарным оператором, который производит двоичное
дополнение стоимости. Биту 1 присваивается значение 0, а биту 0 присваивается значение 1.
Биту 1 присваивается значение 0, а биту 0 присваивается значение 1.
Например, двоичное дополнение 0 равно -1, максимальное целое число без знака (0xffffffff), а двоичное дополнение -1 равно 0.
-bNot 10
-11
0000 0000 0000 1010 (10) ------------------------- бНЕ 1111 1111 1111 0101 (-11, хфффффффф5)
В операции побитового сдвига влево все биты перемещаются на «n» позиций влево, где «n» — значение правого операнда. В единицы вставляется ноль место.
Если левый операнд представляет собой целое (32-разрядное) значение, младшие 5 битов правый операнд определяет, сколько битов левого операнда сдвигается.
Если левый операнд представляет собой длинное (64-битное) значение, младшие 6 бит правого операнд определяет, сколько битов левого операнда сдвигается.
| Выражение | Результат | Двоичный результат |
|---|---|---|
21 -шл 0 | 21 | 0001 0101 |
21 -шл 1 | 42 | 0010 1010 |
21 -шл 2 | 84 | 0101 0100 |
В операции побитового сдвига вправо все биты перемещаются на «n» позиций вправо,
где «n» задается правым операндом. Оператор сдвига вправо (-shr)
вставляет ноль в крайнее левое место при сдвиге положительного или беззнакового
значение вправо.
Оператор сдвига вправо (-shr)
вставляет ноль в крайнее левое место при сдвиге положительного или беззнакового
значение вправо.
Если левый операнд представляет собой целое (32-разрядное) значение, младшие 5 битов правый операнд определяет, сколько битов левого операнда сдвигается.
Если левый операнд представляет собой длинное (64-битное) значение, младшие 6 бит правого операнд определяет, сколько битов левого операнда сдвигается.
| Выражение | Результат | Двоичный | Шестнадцатеричный |
|---|---|---|---|
21 -шр 0 | 21 | 0001 0101 | 0x15 |
21 -шр 1 | 10 | 0000 1010 | 0x0A |
21 -шр 2 | 5 | 0000 0101 | 0x05 |
21 -шр 31 | 0 | 0000 0000 | 0x00 |
21 -шр 32 | 21 | 0001 0101 | 0x15 |
21 -шр 64 | 21 | 0001 0101 | 0x15 |
21 -шр 65 | 10 | 0000 1010 | 0x0A |
21 -шр 66 | 5 | 0000 0101 | 0x05 |
[число]::MaxValue -shr 1 | 1073741823 | 0x3FFFFFFFF | |
[число]::MinValue -shr 1 | -1073741824 | 0xC0000000 | |
-1 -шр 1 | -1 | 0xFFFFFFFF |
См.
 также
также- about_Arrays
- about_Hash_Tables
- about_Operators
- about_Assignment_Operators
- about_Comparison_Operators
- about_Variables
- Дата получения
- New-TimeSpan
4.2 — Арифметические вычисления с использованием арифметических операторов
Все, что мы сделали до сих пор, это сложили вместе переменные. Конечно, мы могли бы также вычитать, умножать, делить или возводить в степень переменные. Нам просто нужно убедиться, что мы используем символы, которые распознает SAS. Их:
| Операция | Символ | Заявление о назначении | Действия предприняты |
| дополнение | + | a = b + c ; | добавить b и c |
| вычитание | — | а = б — в ; | вычесть c из b |
| умножение | * | a = b * c ; | умножить b и c |
| отделение | / | a = b / c ; | разделить b на c |
| возведение в степень | ** | а = б ** в ; | возвести b в степень c |
| отрицательный префикс | — | = — ; | возьмите негатив b |
Как и в других языках программирования, в операторе присваивания можно выполнять более одной операции. Операции выполняются так же, как и для любого математического выражения, а именно:
Операции выполняются так же, как и для любого математического выражения, а именно:
- сначала выполняется возведение в степень, затем умножение и деление и, наконец, сложение и вычитание
- если в одном выражении встречаются несколько экземпляров сложения, несколько экземпляров вычитания или сложения и вычитания, операции выполняются слева направо
- если в одном выражении встречаются несколько экземпляров умножения, несколько экземпляров деления или умножение и деление, операции выполняются слева направо
- если в одном выражении встречается несколько экземпляров возведения в степень, операции выполняются справа налево
- операции в скобках выполняются первыми
Это последняя пуля, которую, я думаю, будет полезно знать. Если вы используете круглые скобки, чтобы специально указать SAS, что вы хотите вычислить в первую очередь, вам не нужно так сильно беспокоиться о других правилах. Давайте рассмотрим два примера.
Следующий пример содержит вычисление, иллюстрирующее стандартный порядок операций. Предположим, преподаватель статистики вычисляет итоговую оценку, взвешивая средний балл за экзамен на 0,6, балл за проект на 0,2 и итоговый экзамен на 0,2. Следующая программа SAS иллюстрирует, как преподаватель (неправильно) вычисляет 9 баллов учащихся.0161 финальные сорта:
Предположим, преподаватель статистики вычисляет итоговую оценку, взвешивая средний балл за экзамен на 0,6, балл за проект на 0,2 и итоговый экзамен на 0,2. Следующая программа SAS иллюстрирует, как преподаватель (неправильно) вычисляет 9 баллов учащихся.0161 финальные сорта:
DATA сорта; входное имя $ 1-15 e1 e2 e3 e4 p1 f1; финал = 0,6*e1+e2+e3+e4/4 + 0,2*p1 + 0,2*f1; ДАННЫЕ; Александр Смит 78 82 86 69 97 80 Джон Саймон 88 72 86 . 100 85 Патрисия Джонс 98 92 92 99 99 93 Джек Бенедикт 54 63 71 49 82 69 Рене Портер 100 62 88 74 98 92 ; БЕЖАТЬ; PROC PRINT данные = оценки; имя переменной e1 e2 e3 e4 p1 f1 final; БЕЖАТЬ;
Ну да ладно, инструктору лучше придерживаться статистики, а не математики. Как видно из заявления о задании, преподаватель пытается указать SAS усреднить четыре экзаменационных балла, сложив их и разделив на 4, а затем умножив результат на 0,6. Давайте посмотрим, что вместо этого делает SAS. Запустить и запустить программу SAS и просмотрите результат, чтобы понять, что сделала SAS, скажем, для первого студента Александра Смита. Если вы все еще не уверены, еще раз просмотрите правила порядка операций. Правила говорят нам, что SAS first:
Если вы все еще не уверены, еще раз просмотрите правила порядка операций. Правила говорят нам, что SAS first:
- берет первую экзаменационную оценку Александра 78 и умножает ее на 0,6, чтобы получить 46,8 .
- берет четвертый экзаменационный балл Александра 69 и делит его на 4, чтобы получить 17,25
- берет оценку проекта Александра 97 и умножает ее на 0,2, чтобы получить 19..4
- берет итоговый экзаменационный балл Александра 80 и умножает его на 0,2, чтобы получить 16,0
Затем SAS выполняет все сложения:
46,8 + 82 + 86 + 17,25 + 19,4 + 16,0
, чтобы получить окончательный результат 267,45. Теперь, может быть, это окончательная оценка, которую хочет Александр, но она все равно в корне неверна. Давайте посмотрим, сможем ли мы помочь инструктору по статистике, воспользовавшись последним правилом, согласно которому операции в скобках выполняются в первую очередь.
Следующий пример содержит вычисление, иллюстрирующее стандартный порядок операций. Предположим, преподаватель статистики вычисляет итоговую оценку, взвешивая средний балл за экзамен на 0,6, балл за проект на 0,2 и итоговый экзамен на 0,2. Следующая программа SAS иллюстрирует, как преподаватель (правильно) вычисляет итоговые оценки учащихся:
Предположим, преподаватель статистики вычисляет итоговую оценку, взвешивая средний балл за экзамен на 0,6, балл за проект на 0,2 и итоговый экзамен на 0,2. Следующая программа SAS иллюстрирует, как преподаватель (правильно) вычисляет итоговые оценки учащихся:
оценок DATA; входное имя $ 1-15 e1 e2 e3 e4 p1 f1; финал = 0,6*((e1+e2+e3+e4)/4) + 0,2*p1 + 0,2*f1; ДАННЫЕ; Александр Смит 78 82 86 6997 80 Джон Саймон 88 72 86 . 100 85 Патрисия Джонс 98 92 92 99 99 93 Джек Бенедикт 54 63 71 49 82 69 Рене Портер 100 62 88 74 98 92 ; БЕЖАТЬ; PROC PRINT данные = оценки; имя переменной e1 e2 e3 e4 p1 f1 final; БЕЖАТЬ;
Давайте еще раз разберем расчет окончательного результата Александра. Оператор присваивания для final сообщает SAS:
- сначала сложить четыре экзаменационных балла Александра (78, 82, 86, 69), чтобы получить 315
- , а затем разделите эти 315 на 4, чтобы получить средний балл за экзамен 78,75
- , а затем умножьте средний экзаменационный балл 78,75 на 0,6, чтобы получить 47,25 .
- , а затем возьмите оценку проекта Александра 97 и умножьте ее на 0,2, чтобы получить 19,4 .
- , а затем возьмите итоговый экзаменационный балл Александра 80 и умножьте его на 0,2, чтобы получить 16,0

Затем SAS выполняет сложение последних трех элементов:
47,25 + 19,4 + 16,0
, чтобы получить окончательный результат 82,65. Там это звучит гораздо лучше. Извините, Александр.
Запустить и запустить программу SAS, чтобы узнать, как мы это сделали. Просмотрите результаты процедуры печати, чтобы убедиться, что окончательные оценки были рассчитаны в соответствии с пожеланиями преподавателя. Кстати, обратите внимание еще раз, что SAS присваивает отсутствующее значение окончательной оценке для Джона Саймона.
В этом последнем примере мы подсчитали средние баллы студентов за экзамен, сложив их четыре экзаменационные оценки и разделив на 4. Вместо этого мы могли бы воспользоваться одной из многих числовых функций, доступных в SAS, а именно функцией СРЕДНЯЯ функция.
Умножение 2- и 3-значных чисел
Урок 2: Умножение 2- и 3-значных чисел
/en/multiplicationdivision/introduction-to-multiplication/content/
количество, вы увеличиваете много раз. В разделе «Введение в умножение» вы узнали, что умножение может быть способом понять, что происходит в реальной жизни. Например, представьте, что в магазине продаются ящики с грушами. В маленьких коробочках пять груш каждая. Вы покупаете два . Вы можете написать ситуацию следующим образом и использовать для ее решения таблицу умножения на :Теперь представьте, что вы решили купить две коробки большего размера, содержащие 14 груш в каждой. Эта ситуация будет выглядеть так:
Эту задачу решить сложнее. Подсчет груш займет некоторое время. К тому же в таблице умножения нет 14. К счастью, есть способ написать задачу так, чтобы ее можно было разбить на более мелкие части. Это называется штабелирование . Это означает, что мы будем писать числа друг над другом , а не рядом.
К тому же в таблице умножения нет 14. К счастью, есть способ написать задачу так, чтобы ее можно было разбить на более мелкие части. Это называется штабелирование . Это означает, что мы будем писать числа друг над другом , а не рядом.
Давайте потренируемся в этой задаче, 14 x 2.
Сначала напишите числа, одно над другим. Это хорошая привычка всегда писать большее число сверху. Если вы этого не сделаете, решить проблему будет сложнее.
Затем запишите знак раз к оставшимся
Вместо знака равно поставьте черту под числом внизу.
Обратите внимание, как числа выстроены справа от ?
Когда вы пишете задачу на умножение с накоплением, всегда следите за тем, чтобы числа выстраивались таким образом.
Например, давайте рассмотрим другую задачу, 5 x 112. Видите, как 2 находится прямо над 5?
Видите, как 2 находится прямо над 5?
Также обратите внимание, что мы поставили большее число сверху, хотя это было второе число в нашем исходном выражении.
Всегда решайте задачи на умножение с накоплением одинаково: с большим числом сверху…
Всегда устанавливайте задачи на умножение с накоплением одинаково: с большим числом сверху… и правильными цифрами выстроились.
Решение задач на умножение с накоплением
На первый взгляд задачи на умножение с накоплением могут показаться довольно сложными. Не волнуйся! Если вы сможете решить задачи из раздела «Введение в умножение», вы сможете научиться решать и эти задачи. Чтобы умножать большие числа, вам понадобятся те же базовые навыки, что и для умножения маленьких. Вы даже можете использовать такие же инструменты, как раз таблицы .
Давайте посмотрим, как работает решение задач на умножение с накоплением.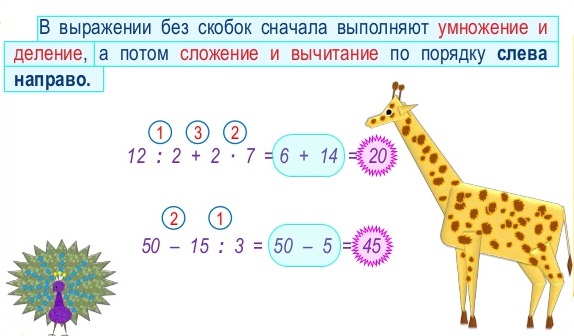
Помните пример с двумя коробками, в каждой из которых было по 14 груш? Чтобы узнать, сколько всего груш, мы решим эту задачу: 14 x 2.
Когда вы умножаете сложенные числа, вы начинаете с правой цифры в нижнем числе задачи. Наше нижнее число состоит только из одной цифры: 2.
Мы умножим 2 на верхнее число, 14. Поскольку в таблице умножения нет 14, нам придется умножать по одной цифре за раз.
Как обычно, решим задачу от направо налево . Итак, мы умножим 2 на цифру вверху справа. Вот, это 4.
Теперь пришло время решить 2 x 4. Мы можем использовать таблицу умножения.
2 x 4 равно 8. Запишем 8 под 2 и 4.
Теперь умножим 2 на следующую цифру слева: 1.
Теперь решим 2 x 1.
Всякий раз, когда вы умножаете число на 1, это число остается то же .
 Итак, 2 x 1 равно 2. Просто чтобы убедиться, мы проверим таблицу умножения.
Итак, 2 x 1 равно 2. Просто чтобы убедиться, мы проверим таблицу умножения.Напишите 2 под чертой, прямо под 1.
Готово! Всего у нас 28, или двадцать восемь. 14 x 2 = 28.
Давайте потренируемся с другой задачей, 31 x 7.
Всегда начинайте с цифры внизу справа . Здесь это 7.
Сначала умножьте 7 на цифру справа вверху, 1.
7 x 1 равно 7. Напишите 7 непосредственно под цифрами, которые мы только что перемножили.
Далее мы умножим 7 на следующую цифру слева. Это 3.
Мы воспользуемся таблицей умножения, чтобы найти 7 x 3.
7 x 3 равно 21. Убедитесь, что числа выстроены так, чтобы правая цифра 21, 1, была прямо под 3.
Наш ответ 217. Итак, 31 x 7 = 217.
Попробуйте это!
Сложите и решите эти задачи на умножение. Затем проверьте свой ответ, введя его в поле.
31 x 3 =
24 x 2 =
40 x 8 =
Использование переноса
На последней странице вы практиковались в умножении чисел, стоящих вертикально. Некоторые проблемы требуют дополнительного шага. Давайте рассмотрим следующую задачу:
Если вы попытаетесь умножить 9 x 5, вы заметите, что нет места для записи произведения, 45. Когда произведение двух чисел равно больше, чем 9 , вам нужно будет использовать метод под названием , несущий . Если вы знаете, как складывать большие числа, возможно, вы помните и об использовании переноса. Давайте посмотрим, как это работает в умножении.
Давайте попробуем решить задачу, которую мы только что рассмотрели, 29 x 5.
Как обычно, мы начнем с умножения 5 на верхнюю правую цифру, 9.
Согласно нашей таблице умножения , 5 x 9 равно 45, но нет места для записи обеих цифр под 5 и 9.
Запишем правую цифру 5 под чертой.
 ..
..Запишем правую цифру 5 под чертой… тогда запишем левую цифру , 4, до следующего набора цифр в задаче.
Видишь, как это работает? Мы умножили 5 и 9, чтобы получить 45. Мы поместили 5 под чертой, перенесли 4 и поместили ее над следующим набором цифр.
Теперь пришло время для следующего шага. Это то же самое, что и с любой другой задачей на умножение. Мы умножим 5 х 2,
5 х 2 = 10. Но 10 под чертой пока писать не будем — есть еще один шаг.
Помните номер, который мы носили, 4?
Мы должны к добавить к нашему продукту, 10.
4 + 10 равно 14.
Мы напишем 14 под чертой.
Итого 145. Теперь мы знаем, что 29 х 5 = 145.
Давайте попробуем решить еще одну задачу. 208 х 6,
Сначала мы умножаем нижнее число 6 на цифру справа вверху. Это 8.
6 x 8 равно 48.

Запишем 8 под чертой…
Запишем 8 под чертой… и перенесем 4. Мы поместим его над следующей цифрой.
Следующая цифра 0.
Все, что умножается на ноль, равно 0, поэтому мы знаем, что 6 x 0 = 0.
Помните, мы еще не пишем этот 0 под чертой. Мы должны добавить его к 4, которые мы только что перенесли.
4 + 0 = 4. Под чертой напишем 4.
Наконец, мы умножаем 6 на 2.
6 x 2 = 12, поэтому мы напишем 12 под чертой.
Готово! Ответ: 1248, или одна тысяча двести сорок восемь. 208 x 6 = 1248.
Попробуйте!
Сложите и решите эти задачи на умножение. Затем проверьте свой ответ, введя его в поле.
25 х 9=
98 x 2 =
103 x 5 =
Умножение больших чисел
На последних нескольких страницах вы практиковались в умножении больших чисел на маленькие. Что произойдет, если вам нужно умножить два больших числа?
Например, представьте, что ваш счет за мобильный телефон составляет 43 доллара в месяц . В году 12 месяцев, поэтому, чтобы узнать, сколько вы платите за свой телефон каждый год, вы можете решить 43 x 12. Вы должны написать выражение следующим образом:
В году 12 месяцев, поэтому, чтобы узнать, сколько вы платите за свой телефон каждый год, вы можете решить 43 x 12. Вы должны написать выражение следующим образом:
На первый взгляд эта проблема может показаться сложной, но не беспокойтесь. Если вы можете умножать маленькие числа, вы можете умножать и большие. Все, что вам нужно сделать, это разделить эту большую проблему на несколько более мелких. Как всегда, вы можете использовать свою таблицу умножения на , чтобы помочь.
Чтобы решить такую большую задачу, начните с тех же шагов, которые вы используете для решения любой другой задачи на умножение.
Как всегда, вы начинаете с цифры справа внизу. Вот, это 2.
Умножим на цифру справа вверху, 3.
Благодаря нашей таблице умножения мы знаем, что 3 x 2 равно 6.
Мы запишем 6 под линия, крайняя правая.
Далее умножаем 2 x 4.
2 x 4 равно 8.

Напишите 8 под чертой, прямо под 4.
90 OK. Первая половина задачи решена.Теперь пришло время снова взглянуть на нижний номер.
Мы собираемся умножить следующую цифру. Это 1.
Сначала умножьте 1 на верхнее число справа. Здесь это 3.
1 x 3 равно 3… но мы не собираемся писать 3 в обычном месте.
Вместо того, чтобы писать 3 справа от , как мы обычно делаем… это на одно место левее, под вторым набором цифр.
Рекомендуется отметить место, которое вы оставили пустым. Таким образом, вы будете знать, что случайно ничего туда не запишете. Мы добавим 0, так как ноль — это то же самое, что ничего .
Теперь давайте умножим последний набор чисел. Это 1 x 4.
1 x 4 = 4. Мы напишем 4 под чертой, слева от 3, которые мы только что написали.
Последний шаг.
 Чтобы получить окончательный ответ, нам нужно к 90 165 добавить 90 168 чисел, которые мы только что получили в результате умножения.
Чтобы получить окончательный ответ, нам нужно к 90 165 добавить 90 168 чисел, которые мы только что получили в результате умножения.Как всегда, мы начнем добавлять справа.
6 + 0 равно 6. Мы напишем 6 под чертой.
Далее, 8 + 3.
8 + 3 равно 11. Поскольку 11 — двузначное число, нам придется переносить.
Запишите правую цифру 1 под 8 и 3…
Запишите левую цифру 1 под 8 и 3… затем перенесите правую цифру и поместите ее над цифрой слева.
Наконец, мы добавим 4 к только что перенесенной 1.
4 + 1 равно 5.
Готово! Итого 516. Другими словами, 43 x 12 = 516.
Попробуйте!
Сложите и перемножьте эти двузначные числа. Затем проверьте свой ответ, введя его в поле.
33 x 21 =
52 x 17 =
81 x 34 =
Умножение двух трехзначных чисел
Умножение больших чисел всегда работает одинаково, независимо от того, сколько цифр в числах. Когда вы умножаете, будьте осторожны, записывая числа в правильных местах. Давайте рассмотрим задачу с двумя 3-значные номера , чтобы увидеть, как это работает с еще большими номерами.
Когда вы умножаете, будьте осторожны, записывая числа в правильных местах. Давайте рассмотрим задачу с двумя 3-значные номера , чтобы увидеть, как это работает с еще большими номерами.
Давайте попробуем решить эту задачу: 601 x 243.
Как всегда, начнем с умножения нижней правой цифры на верхнюю правую цифру. Итак, 3 x 1.
Благодаря нашей таблице умножения мы знаем, что 3 x 1 равно 3. Запишите число 3 под чертой справа.
Теперь умножьте 3 на следующее число, 0.
Любое число, умноженное на ноль, равно 0, поэтому напишите 0 под чертой, рядом с 3.
Далее, 3 x 6.
3 x 6 = 18. Напишите 18 под чертой.
Мы закончили с первой цифрой нижнего числа.
Затем умножьте на второе число внизу, 4.
4 x 1 равно 4. Помните, что вы не собираетесь писать 4 до конца справа.
Вместо этого напишите 4 на одну позицию левее под вторым набором цифр.

Чтобы все было выровнено, мы поместим ноль в качестве заполнителя справа от четырех.
Теперь давайте перейдем к следующему числу сверху — 0.
4 x 0 равно 0. Напишите 0 под чертой.
Затем умножьте 4 на последнюю цифру верхнего числа — 6.
4 x 6 равно 24. Напишите 24 под чертой.
Мы готовы умножить на последнюю цифру нашего нижнего числа — 2.
Как всегда, начните с верхней правой цифры, 1.
2 x 1 равно 2.
Напишем 2 под чертой, через два пробела справа.
Обратите внимание, куда мы поставили 2.
Когда мы умножили на первую цифру в нижнем числе… , мы выстроили товар до упора вправо .
Когда мы умножали на вторую цифру …
Когда мы умножали на вторую цифру .
 .. мы записывали произведение на один пробел слева.
.. мы записывали произведение на один пробел слева.Теперь, когда мы умножили на третью цифру …
Теперь, когда мы умножили на третью цифру … мы поместили произведение на два пробела слева от
Возможно, вы заметили закономерность. Каждый раз, когда мы умножали на новую цифру, мы записывали произведение на одну цифру дальше влево. Это верно независимо от того, сколько цифр в числах, на которые вы умножаете.
Вернемся к нашей проблеме. Мы просто умножили 2 x 1.
Следующая цифра 0.
2 x 0 равно 0. Напишите 0 под чертой.
Наконец, умножьте 2 x 6.
2 x 6 равно 12. Напишите 12 под чертой.
Время добавить. Как всегда, начните с крайних правых цифр. Здесь это означает, что мы добавляем 3 + 0 + 0.
3 + 0 + 0 = 3.
 Напишите 3 непосредственно под цифрами, которые мы только что добавили.
Напишите 3 непосредственно под цифрами, которые мы только что добавили.Далее мы добавим 0 + 4 + 0.
0 + 4 + 0 равно 4.
Теперь следующий набор цифр, 8 + 0 + 2.
7 9009 8 + 0 + 2 = 10. 10 — двузначное число, поэтому нам нужно нести . Напишите 0 под цифрами, которые мы только что добавили, и поместите 1 над следующим набором цифр.Пришло время добавить 1, которую мы только что перенесли. Это означает, что мы находим 1 + 1 + 4 + 0.
1 + 1 + 4 + 0 = 6. Напишите 6 под чертой.
Далее, 2 + 2.
2 + 2 = 4. Напишите 4 под чертой.
Слева только одна цифра — 1.
Один плюс ничего равно 1, поэтому под чертой напишем 1.
Наконец-то мы закончили! Всего у нас 146 043, или сто сорок шесть тысяч сорок три. 601 х 243 = 146 043.
Какое огромное количество! Если эта проблема показалась вам сложной, не волнуйтесь.

 Порядок выполнения действий, правила, примеры
Порядок выполнения действий, правила, примеры
 Сколько всего детей в семье? (7)
Сколько всего детей в семье? (7)
 Сравните их.
Сравните их.

 Во втором классе вы уже познакомились с некоторыми правилами порядка действий. Так, вы, наверное, помните, что руководят порядком в выполнении действий скобки. Они показывают, что действия нужно выполнить первым. Какие существуют другие правила порядка действий? Отличается ли порядок действий в выражениях со скобками и без скобок? На эти вопросы вам предстоит найти ответы в учебнике математики 3 класса при изучении темы «Порядок выполнения действий». Вы должны обязательно потренироваться в применении изученных правил, а если понадобиться, то найти и исправить ошибки в установлении порядка действий в числовых выражениях. Помните, пожалуйста, что порядок важен в любом деле, но в математике он имеет особое значение!
Во втором классе вы уже познакомились с некоторыми правилами порядка действий. Так, вы, наверное, помните, что руководят порядком в выполнении действий скобки. Они показывают, что действия нужно выполнить первым. Какие существуют другие правила порядка действий? Отличается ли порядок действий в выражениях со скобками и без скобок? На эти вопросы вам предстоит найти ответы в учебнике математики 3 класса при изучении темы «Порядок выполнения действий». Вы должны обязательно потренироваться в применении изученных правил, а если понадобиться, то найти и исправить ошибки в установлении порядка действий в числовых выражениях. Помните, пожалуйста, что порядок важен в любом деле, но в математике он имеет особое значение!

 действия, записанные в скобках;
действия, записанные в скобках; Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание.
Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание. Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

 Необходимость введения выражений, содержащих два и более арифметических действий одной ступени, возникает при знакомстве учеников с вычислительными приемами сложения и вычитания в пределах 10, а именно:
Необходимость введения выражений, содержащих два и более арифметических действий одной ступени, возникает при знакомстве учеников с вычислительными приемами сложения и вычитания в пределах 10, а именно: К моменту изучения во 2 классе темы «Порядок действий» учащиеся умеют находить значения выражений этого вида. Цель работы на данном этапе — опираясь практические умения учащихся, обратить их внимание на порядок выполнения действий в таких выражениях и сформулировать соответствующее правило. Учащиеся самостоятельно решают подобранные учителем примеры и объясняют, в каком порядке выполняли; действия в каждом примере. Затем формулируют сами или читают по учебнику вывод: если в выражении без скобок указаны только действия сложения и вычитания (или только действия умножения и деления), то их выполняют в том порядке, в каком они записаны (т.е. слева направо).
К моменту изучения во 2 классе темы «Порядок действий» учащиеся умеют находить значения выражений этого вида. Цель работы на данном этапе — опираясь практические умения учащихся, обратить их внимание на порядок выполнения действий в таких выражениях и сформулировать соответствующее правило. Учащиеся самостоятельно решают подобранные учителем примеры и объясняют, в каком порядке выполняли; действия в каждом примере. Затем формулируют сами или читают по учебнику вывод: если в выражении без скобок указаны только действия сложения и вычитания (или только действия умножения и деления), то их выполняют в том порядке, в каком они записаны (т.е. слева направо).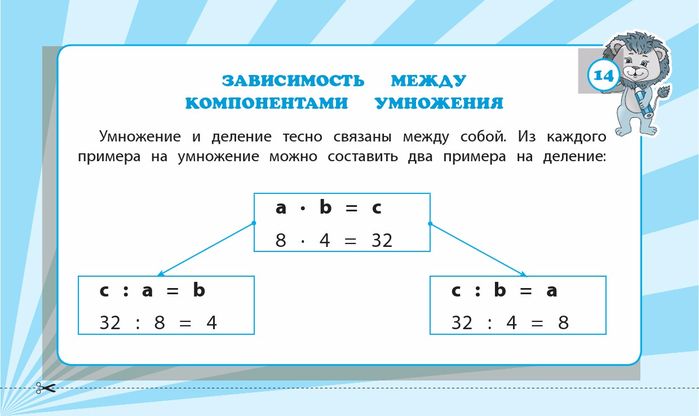 Использование скобок в числовых выражениях, содержащих действия сложения и вычитания, в дальнейшем получает свое развитие, которое связано с изучением таких правил, как прибавление суммы к числу, числа к сумме, вычитание суммы из числа и числа из суммы. Но при первом знакомстве со скобками важно нацелить учащихся на то, что сначала выполняется действие в скобках.
Использование скобок в числовых выражениях, содержащих действия сложения и вычитания, в дальнейшем получает свое развитие, которое связано с изучением таких правил, как прибавление суммы к числу, числа к сумме, вычитание суммы из числа и числа из суммы. Но при первом знакомстве со скобками важно нацелить учащихся на то, что сначала выполняется действие в скобках. Рассматривая эти выражения нетрудно показать, что действия в них выполняются не в том порядке, в каком записаны; чтобы показать другой порядок их выполнения, и использованы скобки.
Рассматривая эти выражения нетрудно показать, что действия в них выполняются не в том порядке, в каком записаны; чтобы показать другой порядок их выполнения, и использованы скобки.

 Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.  Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху. За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.
За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.  По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования. Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.
Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи. Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.
Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.

 Это не математическое действие.
Это не математическое действие.
 Какой еще туалет?
Какой еще туалет?

 Кроме того, он содержит ссылки на бесплатную печатную миллиметровую бумагу и идеи о том, как ее использовать в классе.
Кроме того, он содержит ссылки на бесплатную печатную миллиметровую бумагу и идеи о том, как ее использовать в классе.

 0, "два")
@{"один" = 1} + @{"два" = 2} # результат = @{"один" = 1; "два" = 2}
0, "два")
@{"один" = 1} + @{"два" = 2} # результат = @{"один" = 1; "два" = 2}
 Ключ в словаре: 'c' Добавляемый ключ: 'c'
Ключ в словаре: 'c' Добавляемый ключ: 'c'
 Итак, 2 x 1 равно 2. Просто чтобы убедиться, мы проверим таблицу умножения.
Итак, 2 x 1 равно 2. Просто чтобы убедиться, мы проверим таблицу умножения.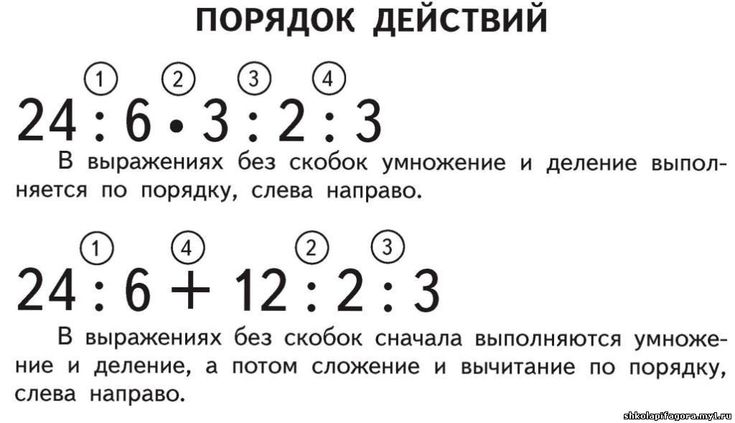 ..
..

 Чтобы получить окончательный ответ, нам нужно к 90 165 добавить 90 168 чисел, которые мы только что получили в результате умножения.
Чтобы получить окончательный ответ, нам нужно к 90 165 добавить 90 168 чисел, которые мы только что получили в результате умножения.
 .. мы записывали произведение на один пробел слева.
.. мы записывали произведение на один пробел слева. Напишите 3 непосредственно под цифрами, которые мы только что добавили.
Напишите 3 непосредственно под цифрами, которые мы только что добавили.