Действия с дробями: правила, примеры, решения
Данная статья рассматривает действия над дробями. Будут сформированы и обоснованы правила сложения, вычитания, умножения, деления или возведения в степень дробей вида AB, где A и B могут быть числами, числовыми выражениями или выражениями с переменными. В заключении будут рассмотрены примеры решения с подробным описанием.
Правила выполнения действий с числовыми дробями общего вида
Числовые дроби общего вида имеют числитель и знаменатель, в которых имеются натуральные числа или числовые выражения. Если рассмотреть такие дроби, как 35, 2,84, 1+2·34·(5-2), 34+782,3-0,8, 12·2, π1-23+π, 20,5ln 3, то видно, что числитель и знаменатель может иметь не только числа, но и выражения различного плана.
Определение 1Существуют правила, по которым идет выполнение действий с обыкновенными дробями. Оно подходит и для дробей общего вида:
- При вычитании дробей с одинаковыми знаменателями складываются только числители, а знаменатель остается прежним, а именно: ad±cd=a±cd, значения a, c и d≠0 являются некоторыми числами или числовыми выражениями.

- При сложении или вычитании дроби при разных знаменателях, необходимо произвести приведение к общему, после чего произвести сложение или вычитание полученных дробей с одинаковыми показателями. Буквенно это выглядит таком образом ab±cd=a·p±c·rs, где значения a, b≠0, c, d≠0, p≠0, r≠0, s≠0 являются действительными числами, а b·p=d·r=s. Когда p=d и r=b, тогда ab±cd=a·d±c·db·d.
- При умножении дробей выполняется действие с числителями, после чего со знаменателями, тогда получим ab·cd=a·cb·d, где a, b≠0, c, d≠0 выступают в роли действительных чисел.
- При делении дроби на дробь первую умножаем на вторую обратную, то есть производим замену местами числителя и знаменателя: ab:cd=ab·dc.
Обоснование правил
Определение 2Существуют следующие математические моменты, на которые следует опираться при вычислении:
- дробная черта означает знак деления;
- деление на число рассматривается как умножение на его обратное значение;
- применение свойства действий с действительными числами;
- применение основного свойства дроби и числовых неравенств.

С их помощью можно производить преобразования вида:
ad±cd=a·d-1±c·d-1=a±c·d-1=a±cd;ab±cd=a·pb·p±c·rd·r=a·ps±c·es=a·p±c·rs;ab·cd=a·db·d·b·cb·d=a·d·a·d-1·b·c·b·d-1==a·d·b·c·b·d-1·b·d-1=a·d·b·cb·d·b·d-1==(a·c)·(b·d)-1=a·cb·d
Примеры
В предыдущем пункте было сказано про действия с дробями. Именно после этого дробь нуждается в упрощении. Подробно эта тема была рассмотрена в пункте о преобразовании дробей.
Для начала рассмотрим пример сложения и вычитания дробей с одинаковым знаменателем.
Пример 1Даны дроби 82,7 и 12,7, то по правилу необходимо числитель сложить, а знаменатель переписать.
Решение
Тогда получаем дробь вида 8+12,7. После выполнения сложения получаем дробь вида 8+12,7=92,7=9027=313. Значит, 82,7+12,7=8+12,7=92,7=9027=313.
Ответ: 82,7+12,7=313
Имеется другой способ решения. Для начала производится переход к виду обыкновенной дроби, после чего выполняем упрощение. Это выглядит таким образом:
82,7+12,7=8027+1027=9027=313
Пример 2
Так как даны равные знаменатели, значит, что мы выполняем вычисление дроби при одинаковом знаменателе. Получим, что
1-23·log23·log25+1-233·log23·log25+1=1-2-233·log23·log25+1
Имеются примеры вычисления дробей с разными знаменателями. Важный пункт – это приведение к общему знаменателю. Без этого мы не сможем выполнять дальнейшие действия с дробями.
Процесс отдаленно напоминает приведение к общему знаменателю. То есть производится поиск наименьшего общего делителя в знаменателе, после чего добавляются недостающие множители к дробям.
Если складываемые дроби не имеют общих множителей, тогда им может стать их произведение.
Пример 3Рассмотрим на примере сложения дробей 235+1 и 12.
Решение
В данном случае общим знаменателем выступает произведение знаменателей. Тогда получаем, что 2·35+1. Тогда при выставлении дополнительных множителей имеем, что к первой дроби он равен 2, а ко второй 35+1. После перемножения дроби приводятся к виду 42·35+1.
235+1+12=2·22·35+1+1·35+12·35+1==42·35+1+35+12·35+1=4+35+12·35+1=5+352·35+1
Ответ: 235+1+12=5+352·35+1
Когда имеем дело с дробями общего вида, тогда о наименьшем общем знаменателе обычно дело не идет. В качестве знаменателя нерентабельно принимать произведение числителей. Для начала необходимо проверить, имеется ли число, которое меньше по значению, чем их произведение.
Пример 4Рассмотрим на примере 16·215 и 14·235, когда их произведение будет равно 6·215·4·235=24·245. Тогда в качестве общего знаменателя берем 12·235.
Рассмотрим примеры умножений дробей общего вида.
Пример 5Для этого необходимо произвести умножение 2+16 и 2·53·2+1.
Решение
Следую правилу, необходимо переписать и в виде знаменателя написать произведение числителей. Получаем, что 2+16·2·53·2+12+1·2·56·3·2+1. Когда дробь будет умножена, можно производить сокращения для ее упрощения.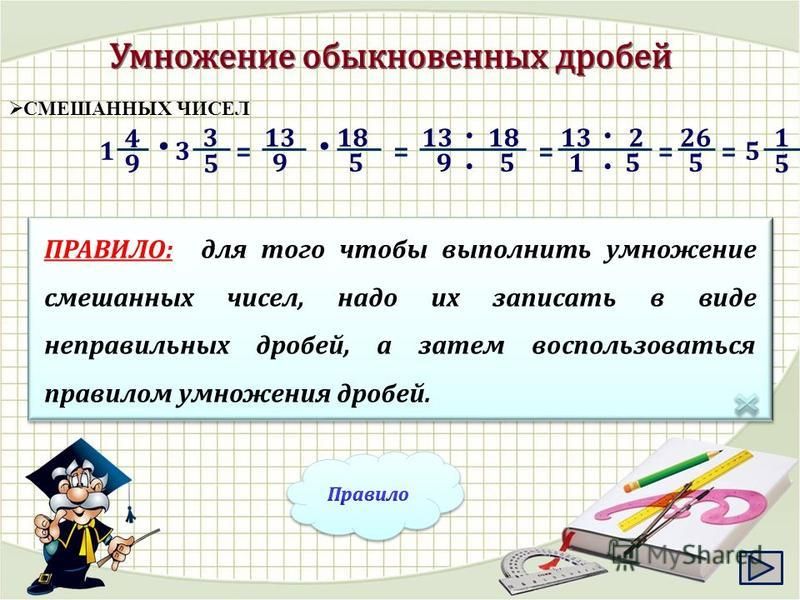 Тогда 5·332+1:1093=5·332+1·9310.
Тогда 5·332+1:1093=5·332+1·9310.
Используя правило перехода от деления к умножению на обратную дробь, получим дробь, обратную данной. Для этого числитель и знаменатель меняются местами. Рассмотрим на примере:
5·332+1:1093=5·332+1·9310
После чего должны выполнить умножение и упростить полученную дробь. Если необходимо, то избавиться от иррациональности в знаменателе. Получаем, что
5·332+1:1093=5·33·9310·2+1=5·210·2+1=32·2+1==3·2-12·2+1·2-1=3·2-12·22-12=3·2-12
Ответ: 5·332+1:1093=3·2-12
Данный пункт применим, когда число или числовое выражение может быть представлено в виде дроби, имеющую знаменатель, равный 1, тогда и действие с такой дробью рассматривается отдельным пунктом. Например, выражение 16·74-1·3 видно, что корень из 3 может быть заменен другим 31 выражением. Тогда эта запись будет выглядеть как умножение двух дробей вида 16·74-1·3=16·74-1·31.
Выполнение действие с дробями, содержащими переменные
Правила, рассмотренные в первой статье , применимы для действий с дробями, содержащими переменные.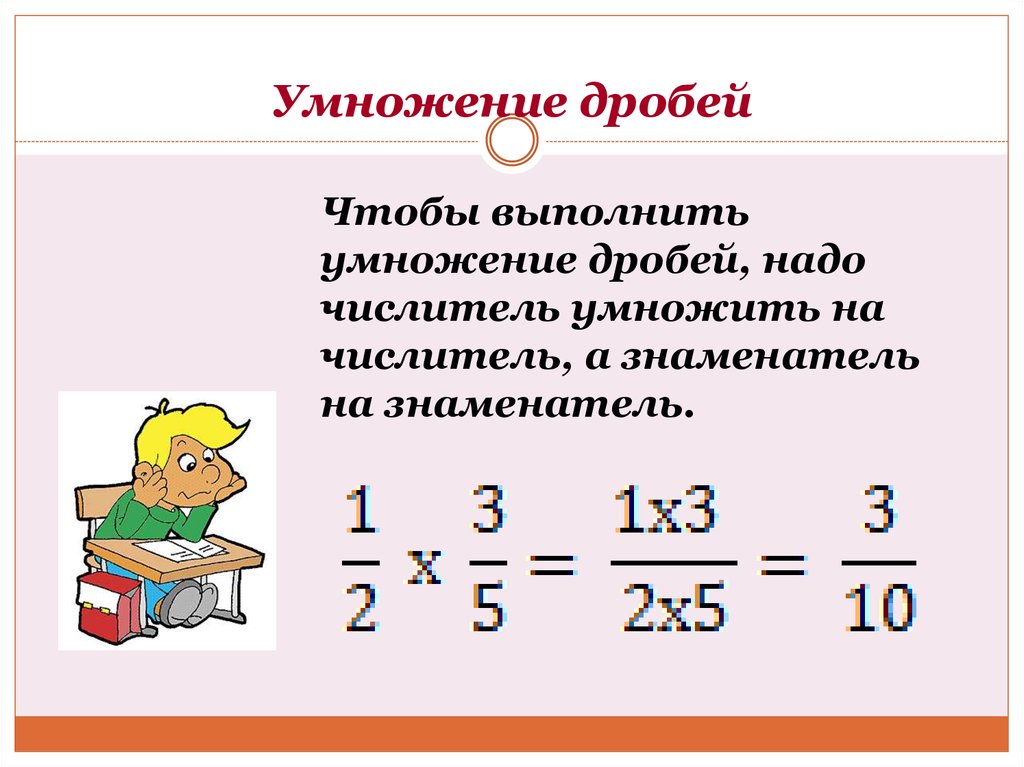 Рассмотрим правило вычитания, когда знаменатели одинаковые.
Рассмотрим правило вычитания, когда знаменатели одинаковые.
Необходимо доказать, что A, C и D (D не равное нулю) могут быть любыми выражениями, причем равенство AD±CD=A±CD равноценно с его областью допустимых значений.
Необходимо взять набор переменных ОДЗ. Тогда А, С, D должны принимать соответственные значения a0, c0 и d0. Подстановка вида AD±CD приводит разность вида a0d0±c0d0, где по правилу сложения получаем формулу вида a0±c0d0. Если подставить выражение A±CD, тогда получаем ту же дробь вида a0±c0d0. Отсюда делаем вывод, что выбранное значение, удовлетворяющее ОДЗ, A±CD и AD±CD считаются равными.
При любом значении переменных данные выражения будут равны, то есть их называют тождественно равными. Значит это выражение считается доказываемым равенством вида AD±CD=A±CD.
Примеры сложения и вычитания дробей с переменными
Когда имеются одинаковые знаменатели, необходимо только складывать или вычитать числители. Такая дробь может быть упрощена. Иногда приходится работать с дробями, которые являются тождественно равными, но при первом взгляде это незаметно, так как необходимо выполнять некоторые преобразования. Например, x23·x13+1 и x13+12 или 12·sin 2α и sin a·cos a. Чаще всего требуется упрощение исходного выражения для того, чтобы увидеть одинаковые знаменатели.
Например, x23·x13+1 и x13+12 или 12·sin 2α и sin a·cos a. Чаще всего требуется упрощение исходного выражения для того, чтобы увидеть одинаковые знаменатели.
Вычислить:1) x2+1x+x-2-5-xx+x-2, 2)lg2x+4x·(lg x+2)+4·lg xx·(lg x+2), x-1x-1+xx+1.
Решение
- Чтобы произвести вычисление, необходимо вычесть дроби, которым имеют одинаковые знаменатели. Тогда получаем, что x2+1x+x-2-5-xx+x-2=x2+1-5-xx+x-2. После чего можно выполнять раскрытие скобок с приведением подобных слагаемых. Получаем, чтоx2+1-5-xx+x-2=x2+1-5+xx+x-2=x2+x-4x+x-2
- Так как знаменатели одинаковые, то остается только сложить числители, оставив знаменатель:lg2x+4x·(lg x+2)+4·lg xx·(lg x+2)=lg2x+4+4x·(lg x+2)
Сложение было выполнено. Видно, что можно произвести сокращение дроби. Ее числитель может быть свернут по формуле квадрата суммы, тогда получим (lg x+2)2из формул сокращенного умножения. Тогда получаем, что
lg2x+4+2·lg xx·(lg x+2)=(lg x+2)2x·(lg x+2)=lg x+2x - Заданные дроби вида x-1x-1+xx+1 с разными знаменателями.
 После преобразования можно перейти к сложению.
После преобразования можно перейти к сложению.
Рассмотрим двоякий способ решения.
Первый способ заключается в том, что знаменатель первой дроби подвергается разложению на множители при помощи квадратов, причем с ее последующим сокращением. Получим дробь вида
x-1x-1=x-1(x-1)·x+1=1x+1
Значит, x-1x-1+xx+1=1x+1+xx+1=1+xx+1.
В таком случае необходимо избавляться от иррациональности в знаменателе.
Получим:
1+xx+1=1+x·x-1x+1·x-1=x-1+x·x-xx-1
Второй способ заключается в умножении числителя и знаменателя второй дроби на выражение x-1. Таким образом, мы избавляемся от иррациональности и переходим к сложению дроби при наличии одинакового знаменателя. Тогда
x-1x-1+xx+1=x-1x-1+x·x-1x+1·x-1==x-1x-1+x·x-xx-1=x-1+x·x-xx-1
Ответ: 1) x2+1x+x-2-5-xx+x-2=x2+x-4x+x-2, 2)lg2x+4x·(lg x+2)+4·lg xx·(lg x+2)=lg x+2x, 3)x-1x-1+xx+1=x-1+x·x-xx-1.
В последнем примере получили, что приведение к общему знаменателю неизбежно. Для этого необходимо упрощать дроби.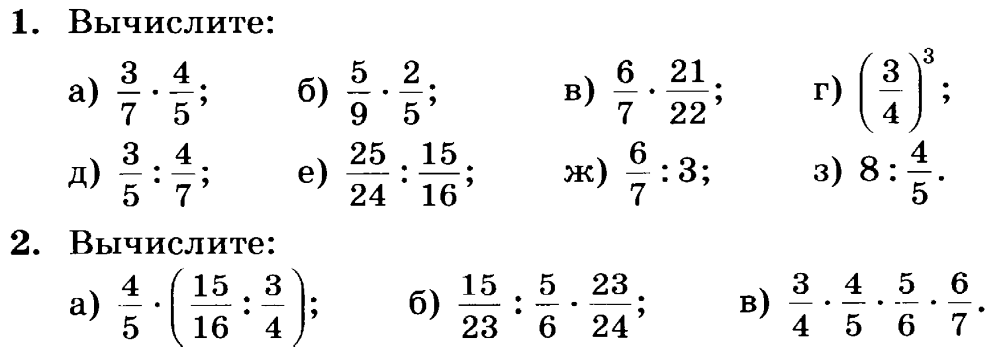
Вычислить значения дробей: 1) x3+1×7+2·2, 2) x+1x·ln2(x+1)·(2x-4)-sin xx5·ln(x+1)·(2x-4), 3) 1cos2x-x+1cos2x+2·cos x·x+x
Решение
- Никаких сложных вычислений знаменатель не требует, поэтому нужно выбрать их произведение вида 3·x7+2·2, тогда к первой дроби x7+2·2 выбирают как дополнительный множитель, а 3 ко второй. При перемножении получаем дробь вида x3+1×7+2·2=x·x7+2·23·x7+2·2+3·13·x7+2·2==x·x7+2·2+33·x7+2·2=x·x7+2·2·x+33·x7+2·2
- Видно, что знаменатели представлены в виде произведения, что означает ненужность дополнительных преобразований. Общим знаменателем будет считаться произведение вида x5·ln2x+1·2x-4. Отсюда x4 является дополнительным множителем к первой дроби, а ln(x+1) ко второй. После чего производим вычитание и получаем, что:
x+1x·ln2(x+1)·2x-4-sin xx5·ln(x+1)·2x-4==x+1·x4x5·ln2(x+1)·2x-4-sin x·lnx+1×5·ln2(x+1)·(2x-4)==x+1·x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4)=x·x4+x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4) - Данный пример имеет смысл при работе со знаменателями дробями.
 Необходимо применить формулы разности квадратов и квадрат суммы, так как именно они дадут возможность перейти к выражению вида 1cos x-x·cos x+x+1(cos x+x)2. Видно, что дроби приводятся к общему знаменателю. Получаем, что cos x-x·cos x+x2.
Необходимо применить формулы разности квадратов и квадрат суммы, так как именно они дадут возможность перейти к выражению вида 1cos x-x·cos x+x+1(cos x+x)2. Видно, что дроби приводятся к общему знаменателю. Получаем, что cos x-x·cos x+x2.
После чего получаем, что
1cos2x-x+1cos2x+2·cos x·x+x==1cos x-x·cos x+x+1cos x+x2==cos x+xcos x-x·cos x+x2+cos x-xcos x-x·cos x+x2==cos x+x+cos x-xcos x-x·cos x+x2=2·cos xcos x-x·cos x+x2
Ответ:
1) x3+1×7+2·2=x·x7+2·2·x+33·x7+2·2, 2) x+1x·ln2(x+1)·2x-4-sin xx5·ln(x+1)·2x-4==x·x4+x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4), 3) 1cos2x-x+1cos2x+2·cos x·x+x=2·cos xcos x-x·cos x+x2.
Примеры умножения дробей с переменными
При умножении дробей числитель умножается на числитель, а знаменатель на знаменатель. Тогда можно применять свойство сокращения.
Пример 8Произвести умножение дробей x+2·xx2·ln x2·ln x+1 и 3·x213·x+1-2sin2·x-x.
Решение
Необходимо выполнить умножение. Получаем, что
Получаем, что
x+2·xx2·ln x2·ln x+1·3·x213·x+1-2sin(2·x-x)==x-2·x·3·x213·x+1-2×2·ln x2·ln x+1·sin (2·x-x)
Число 3 переносится на первое место для удобства подсчетов, причем можно произвести сокращение дроби на x2, тогда получим выражение вида
3·x-2·x·x13·x+1-2ln x2·ln x+1·sin (2·x-x)
Ответ: x+2·xx2·ln x2·ln x+1·3·x213·x+1-2sin(2·x-x)=3·x-2·x·x13·x+1-2ln x2·ln x+1·sin (2·x-x).
Деление
Деление у дробей аналогично умножению, так как первую дробь умножают на вторую обратную. Если взять к примеру дробь x+2·xx2·ln x2·ln x+1 и разделить на 3·x213·x+1-2sin2·x-x, тогда это можно записать таким образом, как
x+2·xx2·ln x2·ln x+1:3·x213·x+1-2sin(2·x-x), после чего заменить произведением вида x+2·xx2·ln x2·ln x+1·3·x213·x+1-2sin(2·x-x)
Возведение в степень
Перейдем к рассмотрению действия с дробями общего вида с возведением в степень. Если имеется степень с натуральным показателем, тогда действие рассматривают как умножение одинаковых дробей. Но рекомендовано использовать общий подход, базирующийся на свойствах степеней. Любые выражения А и С, где С тождественно не равняется нулю, а любое действительное r на ОДЗ для выражения вида ACr справедливо равенство ACr=ArCr. Результат – дробь, возведенная в степень. Для примера рассмотрим:
Но рекомендовано использовать общий подход, базирующийся на свойствах степеней. Любые выражения А и С, где С тождественно не равняется нулю, а любое действительное r на ОДЗ для выражения вида ACr справедливо равенство ACr=ArCr. Результат – дробь, возведенная в степень. Для примера рассмотрим:
x0,7-π·ln3x-2-5x+12,5==x0,7-π·ln3x-2-52,5x+12,5
Порядок выполнения действий с дробями
Действия над дробями выполняются по определенным правилам. На практике замечаем, что выражение может содержать несколько дробей или дробных выражений. Тогда необходимо все действия выполнять в строгом порядке: возводить в степень, умножать, делить, после чего складывать и вычитать. При наличии скобок первое действие выполняется именно в них.
Пример 9Вычислить 1-xcos x-1cos x·1+1x.
Решение
Так как имеем одинаковый знаменатель, то 1-xcos x и 1cos x, но производить вычитания по правилу нельзя, сначала выполняются действия в скобках, после чего умножение, а потом сложение. Тогда при вычислении получаем, что
Тогда при вычислении получаем, что
1+1x=11+1x=xx+1x=x+1x
При подстановке выражения в исходное получаем, что 1-xcos x-1cos x·x+1x. При умножении дробей имеем: 1cos x·x+1x=x+1cos x·x. Произведя все подстановки, получим 1-xcos x-x+1cos x·x. Теперь необходимо работать с дробями, которые имеют разные знаменатели. Получим:
x·1-xcos x·x-x+1cos x·x=x·1-x-1+xcos x·x==x-x-x-1cos x·x=-x+1cos x·x
Ответ: 1-xcos x-1cos x·1+1x=-x+1cos x·x.
Урок математики по теме «Деление дробей в уравнениях»
Форма урока: объяснение нового материала.
Цели урока:
- Обучающая: выработать навыки учащихся умножать и делить обыкновенные дроби, решать и оформлять задачи на уравнения.
- Воспитательная: воспитывать самостоятельность, аккуратность
- Развивающая: развивать внимание,
математическую речь, вычислительные навыки
учащихся, интерес к математике.

Ожидаемые результаты: дети научаться решать задачи и уравнения на дроби.
Этапы урока |
Время (мин) | Слайды |
| Организационный момент. | 2 | Слайд 1 |
| Устная работа и повторение ранее изученного | 8 | Слайды 2, 3, 4, 5,6 |
| Формирование новых знаний и умений | 10 | Слайды 7, 8 |
| Физкультминутка | 2 | Слайды 9, 10 |
| Закрепление нового материала | 5 | Слайд 11 |
| Проверка знаний (с/р) | 10 | Слайд 12 |
| Постановка домашнего задания | 1 | Слайд 13 |
| Подведение итогов урока | 2 |
ХОД УРОКА
I. Организационный этап
Организационный этап
– Здравствуйте, мы проведем сегодня урок по
теме «Деление дробей в уравнених». Откройте
тетради, запишите число, классная работа и тему
урока.
Целью нашего урока является закрепление и
проверка умений умножать и делить обыкновенные
дроби, а также повторить навыки решения задач и
уравнений.
II. Устный опрос учащихся
Чтобы умным в жизни стать
Надо дроби изучать
1) Переведите смешанную дробь в неправильную (Приложение 1, слайд 3)
2) Выделите целую часть (Приложение 1, слайд 4)
3) Умножьте дроби (Приложение 1, слайд 5)
– Повторим правило умножения двух дробей:
Чтобы умножить дробь на дробь нужно перемножить
их числители и знаменатели и первое произведение
записать числителем, а второе знаменателем.
4) Выполните деление (в тетрадях с последующей взаимопроверкой, сосед у соседа) (Приложение 1, слайд 6)
– Повторим правило деления двух дробей: Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.
III. Формирование новых знаний и умений
– При изучении темы деление большое значение имеет умение решать уравнения. Рассмотрим пример и запишем его в тетрадь. (Приложение 1, слайд 7)
– Чтобы решить уравнение необходимо
определить какой компонент в уравнении является
неизвестным.
– Какой?
– 1 множитель
– Правильно! Чтобы найти неизвестный множитель,
что нужно сделать?
– Чтобы найти неизвестный множитель необходимо
произведение разделить на известный множитель.
– Находим корень уравнения, выполняя деление. Выполним проверку и запишем ответ.
Выполним проверку и запишем ответ.
– А теперь давайте проверим ваше умение решать задачи.
№ 597 (Приложение 1, слайд 7)
– Сколько всего прошел лыжник ? (26 км)
– Сколько километров прошел в первый день?
(неизвестно)
– Сколько километров прошел во второй день?
(неизвестно)
– Какую величину, с какой сравнивают?
– Что возьмем за х?
– Как найти дробь от числа?
– Сколько километров прошел за два дня?
– Как найти?
– Составим уравнение.
– 14 км лыжник прошел во второй день
26 – 14 = 12 км лыжник прошел в первый день.
№ 598 (Приложение 1, слайд 8)
– Вспомним что такое 1% (одна сотая)
– Какой дробью запишем 75% (75/100 = 3/4)
– Сколько грибов собрала белка? (неизвестно)
– Сколько грибов собрал бельчонок? (неизвестно)
– Какую величину, с какой сравнивают?
– Что обозначим за икс?
– Как найти дробь от числа?
– Сколько собрали вместе белка и бельчонок?
– Составим уравнение.
200 грибов собрала белка
350 – 200 = 150 грибов собрал бельчонок
IV. Физкультминутка
– Встаем и выполняем несколько упражнений.
А теперь, ребята, встали,
Быстро руки вверх подняли,
В стороны, вперёд, назад
Повернулись вправо, влево,
Тихо сели, вновь за дело.
V. Закрепление нового материала
№ 594
– Сколько собрал Митя?
– Сколько собрал Коля?
– Какую величину, с какой сравнивают?
– Что обозначим за икс?
– Как найти дробь от числа?
– Сколько собрали вместе мальчики?
28 грибов собрал Митя
64 – 28 = 36 грибов собрал Коля
VI. «Математический выбор»
Уравнения, оцениваемые в 3 балла: Уравнения, оцениваемые в 5 баллов:
1) 1)
2) 2)
3) 3)
4) 4)
Уравнения, оцениваемые в 6 баллов:
1)
2)
3)
4)
Оценки: 5 – 12 баллов; 4 – 9 баллов; 3 – 6 баллов.
Каждый выбирает себе уравнения по «плечу».
Учитель во время работы оценивает учеников.
VII. Итог урока
– С каким настроением вы сегодня работали на
уроке?
– Какая задача для вас была самой интересной?
– Ребята чему мы научились на сегодняшнем уроке?
– Как найти часть от числа?
– Как найти неизвестный множитель?
Оценки за урок.
VIII. Домашнее задание
– С листов решить любые три уравнения, из тех которые не решали в классе.
MathOnWeb — Электронная книга по алгебре — Дробные выражения и уравнения
В этой главе мы рассмотрим дроби в четвертый и последний раз. Давайте просмотрите наши предыдущие три встречи:
- Обыкновенные дроби. В разделе 1.2 мы представили
обозначение дроби, a / b ,
где a и b были целыми числами для
описать часть или часть целого объекта.
 Например, ¾ означало, что мы разбили объект на 4 равные части.
части и у нас было 3 из тех частей. Обратите внимание, что a / b было числом;
обозначения а / б не имели ничего общего с делением.
В разделе 1.2 мы также узнали, как преобразовать дробь в
самые низкие условия,
как складывать и вычитать дроби,
умножить дроби,
разделить дроби и как
преобразовать неправильную дробь
в смешанную дробь с помощью длинного деления.
Например, ¾ означало, что мы разбили объект на 4 равные части.
части и у нас было 3 из тех частей. Обратите внимание, что a / b было числом;
обозначения а / б не имели ничего общего с делением.
В разделе 1.2 мы также узнали, как преобразовать дробь в
самые низкие условия,
как складывать и вычитать дроби,
умножить дроби,
разделить дроби и как
преобразовать неправильную дробь
в смешанную дробь с помощью длинного деления. - Разделение номеров. В разделе 2.4
мы определили деление двух чисел в терминах умножения.
Мы сказали, что разделив a с помощью b произвел число c такое, что c умножить на b вернули a .
Мы использовали то же обозначение дроби, a / b , для обозначения деления a на b , потому что, когда a и b оба были целыми числами, тогда
деление на / b дало обыкновенную дробь a / b .
 Однако в любом другом случае деление давало действительное число.
В разделе 2.4 мы также узнали, что деление a на b может быть
заменяется умножением на на
обратное b .
Наконец, мы узнали правила деления с участием
знаки минус.
Однако в любом другом случае деление давало действительное число.
В разделе 2.4 мы также узнали, что деление a на b может быть
заменяется умножением на на
обратное b .
Наконец, мы узнали правила деления с участием
знаки минус. - Раздел выражений. В разделе 3.5
мы видели, что существует три различных способа разделения выражений в зависимости от
были ли числитель a и знаменатель b мономами, полиномами или полиномами.
- Если бы они были мономами, затем деление a на b просто равносильно записи алгебраическая дробь, a / b , и уменьшив его до наименьших значений, как обыкновенную дробь.
- Если бы это были многочлены, то a можно разделить на b с использованием длинного деления,
точно так же, как неправильная обыкновенная дробь может быть преобразована в смешанную дробь с помощью длинного деления.

- Если a было многочленом и b был одночленом, то мы разместили в каждом члене а над б так, чтобы результатом деления была сумма алгебраические дроби.
Осталось обсудить алгебраических дробей , то есть дробей, числитель и знаменатель являются алгебраическими выражениями. В этой главе обсуждаются алгебраические дроби и дробные уравнения. Он содержит следующие разделы:
- раздел 11.1 — В этом разделе мы говорим о упрощение алгебраических дробей. Главный новый результат состоит в том, что поскольку теперь мы знаем, как разложить выражение на множители, мы можем разложить числитель или знаменатель, и это открывает новый способ уменьшить алгебраическая дробь до младших членов.
- раздел 11.2 — В этом разделе мы
Расскажите об умножении и делении алгебраических дробей.

- раздел 11.3 — В этом разделе мы Расскажите о сложении и вычитании алгебраических дробей.
- раздел 11.4 — В этом разделе мы покажем, как решать уравнения, содержащие алгебраические дроби.
11.1 — Упрощение алгебраических дробей
Некоторые определения
- Обыкновенная дробь форма или а / б , где a , числитель , и b , знаменатель , оба являются целыми числами. Обыкновенная дробь используется для описания части или доли целого объекта. Обозначение означает, что мы разбиваем объект на b равные части, и у нас есть этих частей. Часть или часть объекта, который у нас есть это а / б .
- Раздел определяется с точки зрения умножения.
Деление числа a на число b дает число c такое, что c умножить на b дает обратно a .
 Мы используем то же обозначение дроби, a / b , для обозначения деления a на b , потому что, когда a и b оба были целыми числами, тогда
подразделение а / b дает обыкновенную дробь a / b .
Мы используем то же обозначение дроби, a / b , для обозначения деления a на b , потому что, когда a и b оба были целыми числами, тогда
подразделение а / b дает обыкновенную дробь a / b . - Алгебраическая дробь — это дробь, у которой числитель или знаменатель являются алгебраическими
выражения.
Два примера алгебраических дробей:
и .
- рациональная алгебраическая дробь — это алгебраическая дробь, числитель и знаменатель являются полиномами. Первый пример выше — это рациональная алгебраическая дробь; второй нет.
- A правильная обыкновенная дробь обыкновенная дробь, числитель которой меньше ее
знаменатель и неправильная обыкновенная дробь это тот, числитель которого больше или равен его знаменателю.
Смешанная дробь — это сумма целого числа и правильной дроби.
 Длинное деление можно использовать для преобразования
неправильную дробь в смешанную дробь.
Длинное деление можно использовать для преобразования
неправильную дробь в смешанную дробь. - A правильная алгебраическая дробь — рациональная алгебраическая дробь чей числитель младше степени чем его знаменатель, а неправильная алгебраическая дробь равна единице. числитель которого больше или равен знаменателю. Смешанное выражение представляет собой сумму многочлена и правильной алгебраической дроби. Длинное деление можно использовать для преобразования неправильную алгебраическую дробь к смешанному выражению.
Деление на ноль
Эта операция не допускается в математике. Нажмите здесь, чтобы узнать, почему. Это означает, что в алгебраической дроби
,
x не может равняться 1 или −3, потому что эти значения x вызовут
дробь, чтобы знаменатель был равен нулю.
Приведение алгебраической дроби к наименьшим членам
Посмотрите на алгебру, которую мы делаем здесь:
- Начнем с дроби a / b .
- Умножаем на 1. Это не изменит его значение.
- Запишем «1» как дробь d / d .
- Перемножаем две дроби. Числитель новой дроби равен ad и знаменатель bd .
- Последняя дробь равна эквивалентно в первой дроби.
Если мы пойдем в обратном направлении, то мы скажем, что сводим дробь к ее простейшая эквивалентная дробь или низшая дробь . Для этого находим любой множитель, который содержится и в числителе, и в знаменателе. и зачеркнуть или зачеркнуть , например:
Пример: Сократите обыкновенные дроби 10/6 и 10/5 до меньших значений.
| Разложите числитель и знаменатель на множители. Отмените общий делитель 2. | |
| Разложите числитель и знаменатель на множители. Отмените общий делитель 5. Результат деления — целое число. Мы говорим, что знаменатель делит без остатка . в числитель. |
Если числитель и знаменатель алгебраической дроби равны мономов , то выполните все следующие шагов, чтобы сократить дробь до наименьшего члена :
- Получите знак, используя правила для знаков.
- Уменьшить коэффициент до минимума.
- Отмена идентичных множителей, которые появляются как в числителе, так и в знаменателе.
- Объедините экспоненты с одинаковым основанием, используя
свойство деления экспонент.

Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
| Перед результатом ставится знак −
или перед числителем; никогда не стоит перед знаменателем. Уменьшить коэффициент 6/9к самые низкие условия. |
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
| Два знака — заменены знаком +, который нам не нужно отображать.
Коэффициент снижается до ¼.
Числитель содержит другие множители, поэтому 1 в числителе можно опустить. Объедините экспоненты с основанием x с использованием свойств экспоненты. |
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
| Знак − ставится впереди. Коэффициент снижается до 1/3. одинаковых множителей из x 3 в числителе и знаменателе сокращаются. Числитель не содержит других множителей, поэтому на этот раз должна отображаться 1. |
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
| После проведения всех упрощений знаменатель равен 1, поэтому нам не нужно его отображать. Таким образом, результатом является обычное выражение, не алгебраическая дробь. |
Если числитель и знаменатель алгебраической дроби равны многочленов , тогда в дополнение к шагам, перечисленным выше, попробуйте выполнить следующие шагов, чтобы сократить дробь до минимального значения :
- Разложите на множители числитель, знаменатель или оба.
 Иногда это вызывает новые
появляются аннулирующие факторы.
Иногда это вызывает новые
появляются аннулирующие факторы. - Множитель a − знак вне числителя или знаменателя. Иногда это приводит к появлению нового фактора отмены.
В следующих примерах мы будем предполагать, что вы уже знаете как сделать факторинг поэтому мы просто покажем, как использовать множители для сведения алгебраических дробей к самые низкие условия.
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
| Разложите числитель и знаменатель на множители. Отменить общий делитель x . |
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
Разложить числитель на множители. Отменить общий делитель x − 2. |
Пример: Уменьшить алгебраическую дробь на самые низкие условия.
Решение: Это та же алгебраическая дробь, что и в предыдущем примере, за исключением что знаменатель отличается знаком -.
| Разложить на множители числитель и фактор a − выйти
знаменателя. Отменить общий делитель x − 2. Подставить знак − к числителю и распространять его. |
11.2 — Умножение и деление алгебраических дробей
Умножение алгебраических дробей
Порядок умножения алгебраических дробей такой же, как и порядок умножения алгебраических дробей. умножение обыкновенных дробей.
| Умножение двух алгебраических дробей дает новую алгебраическую дробь.  Умножьте два числителя, чтобы получить новый числитель, и умножьте два знаменателя, чтобы получить новый
новый знаменатель: Затем упростите, сократив новую дробь до наименьших членов. Умножьте два числителя, чтобы получить новый числитель, и умножьте два знаменателя, чтобы получить новый
новый знаменатель: Затем упростите, сократив новую дробь до наименьших членов. |
Примеры:
Деление алгебраических дробей
Порядок деления алгебраических дробей такой же, как и порядок деления алгебраических дробей. деления обыкновенных дробей.
| Замените деление на дробь на умножение на обратную дробь , например: Затем выполните умножение двух дробей как описано выше. |
Обратите внимание, что вы берете обратную дробь внизу!
| Вот почему эта процедура работает: Суть в том, что вместо того, чтобы видеть дробь, деленную на дробь, ищите одну дробь, числитель и знаменатель которой являются дробями.  На первом шаге мы умножили эту дробь на UFOO
числитель и знаменатель которого являются дробями. НЛО был
выбран так, чтобы дроби в знаменателе сокращались и давали 1. После другого
упрощение, оставившее только окончательное умножение дробей. На первом шаге мы умножили эту дробь на UFOO
числитель и знаменатель которого являются дробями. НЛО был
выбран так, чтобы дроби в знаменателе сокращались и давали 1. После другого
упрощение, оставившее только окончательное умножение дробей. |
Примеры: Найдите следующие три шага: (1) инвертируйте нижнюю дробь, (2) умножить дроби, (3) упростить.
11.3 — Сложение и вычитание алгебраических дробей
Процедура сложения или вычитания алгебраических дробей такая же, как и процедура сложение или вычитание обыкновенных дробей.
Сложение дробей с одинаковыми знаменателями
Фракции, имеющие равные знаменатели, также называются , как и дроби .
| Чтобы сложить или вычесть две одинаковые дроби, просто сложите или вычтите числители и поднесите результат к общему знаменателю, так: |
Пример:
Сложение дробей с неравными знаменателями
| Чтобы сложить или вычесть дроби, у которых знаменатели не равны, их нужно сначала преобразовать к эквивалентным дробям, которые делают имеют общий знаменатель.  Вот шаги: Вот шаги:
|
Пример: . Чтобы вычесть эти дроби, выполните следующие действия:
- Найдите ЖК, это 10.
- Так как в знаменателе первой дроби уже есть LCD, нам нужно только умножьте вторую дробь на 5/5, чтобы преобразовать ее в эквивалентную дробь с знаменатель 10.
- Вычтите числители и поместите результат на ЖК-дисплей.
- Упростите, сократив дробь до меньших членов.

Пример: . Чтобы добавить эти дроби, выполните следующие действия:
- Найдите ЖК-дисплей, который имеет размер (4 x − 1)( x + 3).
- Умножить числитель и знаменатель первой дроби на ( x + 3) и числитель и знаменатель второй дроби на (4 x − 1):
- Обе дроби теперь имеют LCD в качестве знаменателя. Добавьте числители и поместите результат на ЖК-дисплей.
- Упростите, распределив числитель.
Сложение дробей с факторизуемыми знаменателями
| Вы должны всегда факторизовать знаменатели. Это единственный способ определить, является ли фактор появляется более чем в одном знаменателе.  |
Пример: . Чтобы добавить эти дроби, выполните следующие действия:
- Разложите знаменатель первой дроби на множители. Тогда мы видим, что факторы x — 2 и x — 3 появляются более чем в одном знаменателе:
- Найдите ЖК-дисплей, который равен ( x − 2)( x − 3).
- Умножьте числитель и знаменатель второй дроби на ( x − 3) и числитель и знаменатель третьей дроби на ( x — 2):
- Теперь обе дроби имеют LCD в качестве знаменателя. Добавьте числители и поместите результат на ЖК-дисплей.
- Упростите, распределив и добавив одинаковые члены в числителе.
Сложение дробей и не дробей (смешанные выражения)
| Чтобы сложить или вычесть дроби и не дроби, преобразуйте не дроби в дроби со знаменателем 1.  |
Пример: . Чтобы добавить эту дробь и не дробь, выполните следующие действия:
- Запишите не дробь в виде дроби со знаменателем 1:
- Найдите ЖК-дисплей, который, конечно же, ( x − 2).
- Умножить числитель и знаменатель первой дроби на ( х — 2):
- Обе дроби теперь имеют LCD в качестве знаменателя. Добавьте числители и поместите результат на ЖК-дисплей.
- Упростите, распределив и добавив одинаковые члены в числителе.
11.4 — Дробные уравнения
Прежде чем читать этот раздел, вы можете рассмотреть следующие темы:
- Основы решения уравнений.
- Техника очистки фракций для
решение линейных уравнений.

- Как найти наименьший общий знаменатель (ЖК) алгебраических дробей.
Дробное уравнение — это уравнение, содержащее дробные члены. В разделе 4.2 мы видели как решить линейное уравнение , содержащее дроби. Шаги для решения любого дробного уравнения точно такие же:
- Посмотрите на знаменателей всех дробей и найдите их наименьшее общее кратное (НОК) (это также называется наименьшим общим знаменателем (LCD) дробей).
- Умножьте обе части уравнения на LCM.
- Распределите LCM по обеим частям уравнения.
- Уравнение больше не содержит дробей, и вы можете продолжить его решение с помощью основных процедур решения уравнений.
- Проверьте решение. Это особенно важно для дробных уравнений. Там
две возможные проблемы:
- Если знаменатель любого члена дроби содержит x , то LCM будет
также содержат x , и умножение обеих частей уравнения на LCM даст
увеличьте степень x в уравнении.
 Это часто приводит к посторонним решениям.
Это часто приводит к посторонним решениям. - При подстановке решений обратно в исходное уравнение для их проверки, любое решение, в результате которого любой член дроби имеет нулевой знаменатель, должно быть отброшено. потому что деление на ноль запрещено в математике.
- Если знаменатель любого члена дроби содержит x , то LCM будет
также содержат x , и умножение обеих частей уравнения на LCM даст
увеличьте степень x в уравнении.
Пример 1: Решите это дробное уравнение для x :
Решение: Члены дробей имеют знаменатели 3, 2 и 6. НОК этих чисел равен 6. Умножьте обе части уравнения на 6. (Не забудьте заключить обе части уравнения в скобки.)
Распределите по обеим частям уравнения:
4 х — 3 = 6 x + 7.
Фракции теперь очищены, так что это больше не дробное уравнение. Завершите решение уравнения, собрав линейные члены в левой части и
постоянные члены в правой части. Это дает:
Завершите решение уравнения, собрав линейные члены в левой части и
постоянные члены в правой части. Это дает:
−2 x = 10.
Разделите обе части на −2. Это дает решение:
х = −5.
Проверьте его, подставив обратно в исходное уравнение. Это дает -23/6 = -23/6, так что решение проверено.
Пример 2: Решите это дробное уравнение для x :
Решение: Члены дробей имеют знаменатели x 2 + x − 2, x +
2, и x – 1.
Может показаться, что LCM является продуктом всех трех, но поскольку x 2 + x − 2 можно разложить на множители
как ( x + 2)( x — 1), LCM на самом деле просто ( x + 2)( x — 1). Умножьте на него обе части уравнения.
(Не забудьте заключить обе части уравнения в скобки.)
Умножьте на него обе части уравнения.
(Не забудьте заключить обе части уравнения в скобки.)
Распределите по обеим частям уравнения:
9 = 3 ( х — 1) + 7 ( х + 2).
Теперь дроби очищены, так что это больше не дробное уравнение; это линейное уравнение. Решите ее, используя обычные методы. Распределите еще раз на правой стороне:
9 = 10 x + 11.
Соберите постоянные члены в левой части:
−2 = 10 х .
Разделите обе части на 10. Это дает решение:
х = −1/5.
Проверьте его, подставив обратно в исходное уравнение.
Это дает -25/6 = -25/6, так что решение проверено.
Пример 3: Цель этого примера — проиллюстрировать решение, которое должно быть отклонено, потому что оно вызывает деление на ноль . Уравнение идентично один в предыдущем примере, за исключением того, что он отличается знаком одного термина. Решите это дробное уравнение для x :
Решение: Сравните каждый шаг здесь с соответствующим шагом в приведенном выше примере. Умножьте обе части уравнения на LCM, что снова равно ( х + 2)( х — 1):
Распределите по обеим частям уравнения:
9 = −3 ( x – 1) + 7 ( x + 2).
Распределите еще раз на правой стороне:
9 = 4 x + 17.
На этот раз решение x = -2.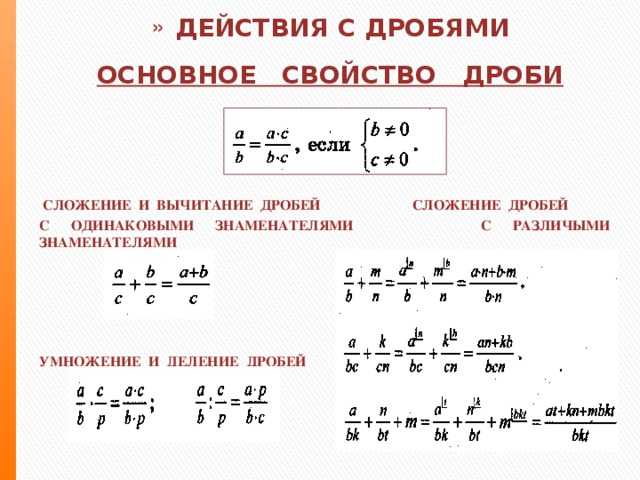

 После преобразования можно перейти к сложению.
После преобразования можно перейти к сложению. Необходимо применить формулы разности квадратов и квадрат суммы, так как именно они дадут возможность перейти к выражению вида 1cos x-x·cos x+x+1(cos x+x)2. Видно, что дроби приводятся к общему знаменателю. Получаем, что cos x-x·cos x+x2.
Необходимо применить формулы разности квадратов и квадрат суммы, так как именно они дадут возможность перейти к выражению вида 1cos x-x·cos x+x+1(cos x+x)2. Видно, что дроби приводятся к общему знаменателю. Получаем, что cos x-x·cos x+x2.
 Например, ¾ означало, что мы разбили объект на 4 равные части.
части и у нас было 3 из тех частей. Обратите внимание, что a / b было числом;
обозначения а / б не имели ничего общего с делением.
В разделе 1.2 мы также узнали, как преобразовать дробь в
самые низкие условия,
как складывать и вычитать дроби,
умножить дроби,
разделить дроби и как
преобразовать неправильную дробь
в смешанную дробь с помощью длинного деления.
Например, ¾ означало, что мы разбили объект на 4 равные части.
части и у нас было 3 из тех частей. Обратите внимание, что a / b было числом;
обозначения а / б не имели ничего общего с делением.
В разделе 1.2 мы также узнали, как преобразовать дробь в
самые низкие условия,
как складывать и вычитать дроби,
умножить дроби,
разделить дроби и как
преобразовать неправильную дробь
в смешанную дробь с помощью длинного деления. Однако в любом другом случае деление давало действительное число.
В разделе 2.4 мы также узнали, что деление a на b может быть
заменяется умножением на на
обратное b .
Наконец, мы узнали правила деления с участием
знаки минус.
Однако в любом другом случае деление давало действительное число.
В разделе 2.4 мы также узнали, что деление a на b может быть
заменяется умножением на на
обратное b .
Наконец, мы узнали правила деления с участием
знаки минус.

 Мы используем то же обозначение дроби, a / b , для обозначения деления a на b , потому что, когда a и b оба были целыми числами, тогда
подразделение а / b дает обыкновенную дробь a / b .
Мы используем то же обозначение дроби, a / b , для обозначения деления a на b , потому что, когда a и b оба были целыми числами, тогда
подразделение а / b дает обыкновенную дробь a / b . Длинное деление можно использовать для преобразования
неправильную дробь в смешанную дробь.
Длинное деление можно использовать для преобразования
неправильную дробь в смешанную дробь.
 Иногда это вызывает новые
появляются аннулирующие факторы.
Иногда это вызывает новые
появляются аннулирующие факторы.
 Это часто приводит к посторонним решениям.
Это часто приводит к посторонним решениям.