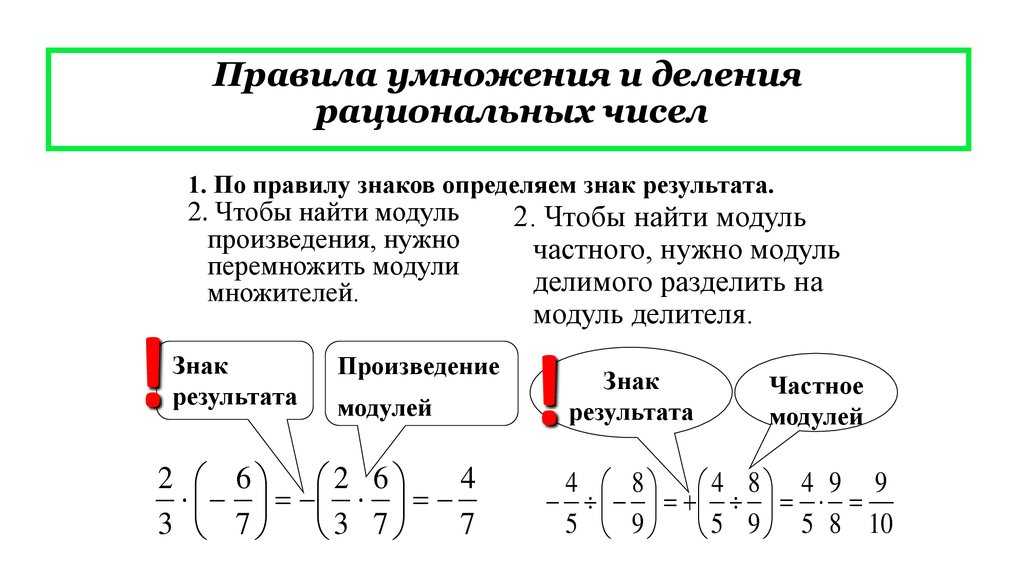
Как умножить дробь на отрицательное число?

Как умножить дробь на отрицательное число?

Чтобы найти произведение двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем перемножить дроби по правилу умножения дробей. Пример. При умножении отрицательной дроби на положительную результат будет отрицательным.

Как разделить и умножить дробь на дробь?

Как делить дробь на дробь? Выполняем следующую последовательность действий: числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби; знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.

Как делить обыкновенные дроби?

Правило. Чтобы разделить обыкновенную дробь , надо числитель делимого умножить на знаменатель делителя, а знаменатель делимого умножить на числитель делителя. Первое произведение взять числителем, а второе — знаменателем. Чтобы разделить обыкновенные дроби, можно делимое умножить на дробь, обратную делителю.

Как решить деление смешанных дробей?

Чтобы разделить одно смешанное число на другое, надо:

1. преобразовать смешанные дроби в неправильные;
2. умножить первую дробь на дробь, обратную второй;
3. сократить полученную дробь;
4. если получилась неправильная дробь преобразовать неправильную дробь в смешанную.

Как делить столбиком с запятыми?

Как разделить столбиком одну десятичную дробь на другую Переносим запятую в делимом и делителе вправо на то количество знаков, которое необходимо для превращения делителя в натуральное число. Если в делимом не хватит знаков, дописываем в него нули с правой стороны.

Как объяснить деление на двузначное число?

Алгоритм деления столбиком на двузначное число

1. Находим первое неполное делимое. Это число, которое делится на делитель с получением числа больше или равного 1. …
2. Определяем количество цифр в частном. …
3. Находим цифры в каждом разряде частного. …
4. Находим остаток (если есть). …
5. Деление нужно непременно проверить умножением.

Как правильно делить двузначное число на однозначное?

Чтобы разделить двузначное число на однозначное, надо двузначное число представить в виде суммы разрядных слагаемых и разделить эту сумму на однозначное число.

Как правильно делить в столбик?

Начинаем делить «512» на «8» следующим образом:

1. Определяем неполное частное. Для этого слева направо сравниваем цифры делимого и делитель. …
2. «51» больше «8». Значит это неполное частное. …
3. Приступаем к делению. Вспоминая таблицу умножения на «8», находим ближайшее к «51» произведение. …
4. В остатке получилось «3».

Как решать примеры с остатком?

Порядок решения примеров на деление с остатком.

1. Находим наибольшее число до «17», которое делится на «3» без остатка. Это «15». 15 : 3 = 5.
2. Вычитаем из делимого найденное число из пункта «1». 17 − 15 = 2.
3. Сравниваем остаток с делителем.

Как разделить 14 на 30 с остатком?

Ответ, проверенный экспертом Решение: 14:30=0 ( ост. 14) .

Как выполнить деление с остатком с проверкой?

Чтобы проверить деление с остатком, нужно делитель умножить на значение частного и прибавить остаток.

Как называют частное при делении с остатком?

Делимое, делитель, неполное частное, остаток от деления Натуральное число, на которое делят, называют делителем. В результате деления с остатком получаются два числа, одно из которых называют неполным частным, а другое – остатком.

Что такое неполное частное 4 класс?

«Неполное частное» – это число, показывающее какое максимальное количество раз, делитель содержится в делимом. 157. Выполни деление нацело и деление с остатком. Как получить делимое 60, используя значение частного и делитель?

Как найти делитель если известно делимое и частное с остатком?

Решение Чтобы найти делитель, если известны делимое, неполное частное и остаток, нужно от делимого отнять остаток, и полученную разность разделить на неполное частное.

§ Умножение отрицательных чисел. Умножение рациональных чисел

Координатная прямая Координаты точек на числовой оси Сложение отрицательных чисел Вычитание отрицательных чисел Умножение отрицательных чисел Деление отрицательных чисел

Используя понятие модуля числа, сформулируем правила умножения положительных и отрицательных чисел.

Умножение чисел с одинаковыми знаками

Первый случай, который может вам встретиться — это умножение чисел с одинаковыми знаками.

Чтобы умножить два числа с одинаковыми знаками надо:

• перемножить модули чисел;
• перед полученным произведением поставить знак «+» (при записи ответа знак «плюс» перед первым числом слева можно опускать).

Примеры умножения отрицательных и положительных чисел.

• (−3) · (−6) = +18 = 18
• 2 · 3 = 6

Умножение чисел с разными знаками

Второй возможный случай — это умножение чисел с разными знаками.

Чтобы умножить два числа с разными знаками, надо:

• перемножить модули чисел;
• перед полученным произведением поставить знак «−».

Примеры умножения отрицательных и положительных чисел.

• (−0,3) · 0,5 = −0,15
• 1,2 · (−7) = −8,4

Правила знаков для умножения

Запомнить правило знаков для умножения очень просто. Данное правило совпадает с правилом раскрытия скобок.

Запомните!

Минус на минус даёт плюс,

  Плюс на минус даёт минус.

+ · (+) = +	+ · (−) = −
− · (−) = +	− · (+) = −

В «длинных» примерах, в которых есть только действие умножение, знак произведения можно определять по количеству отрицательных множителей.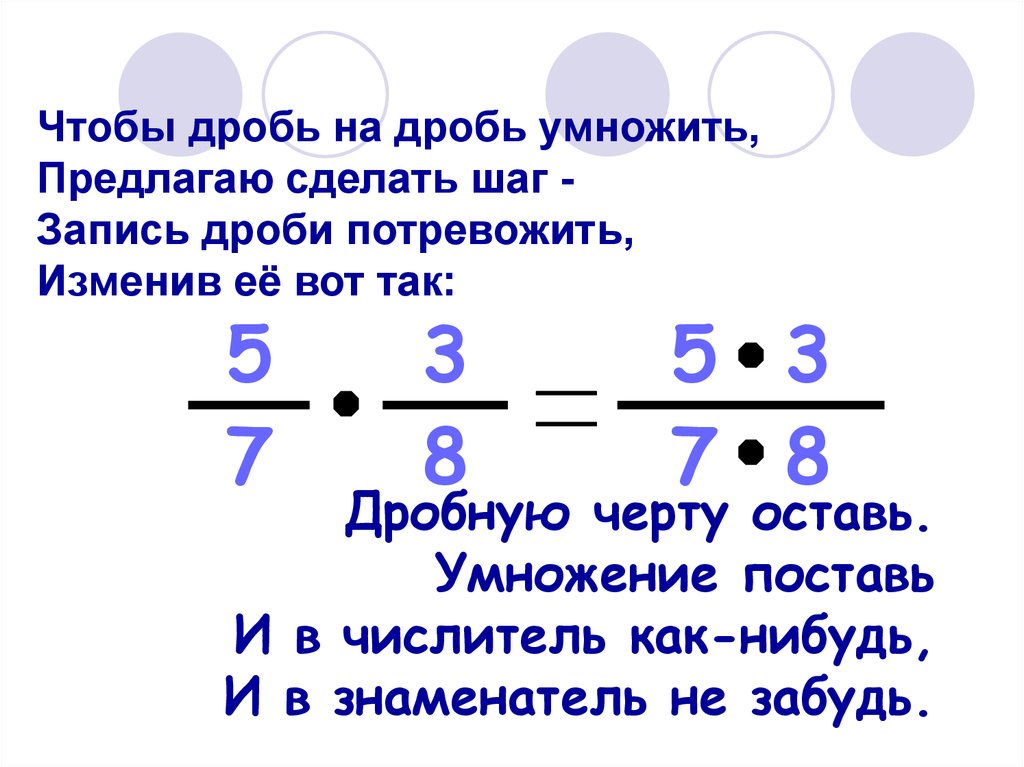

При чётном числе отрицательных множителей результат будет положительным, а при нечётном количестве — отрицательным.

Пример.

(−6) · (−3) · (−4) · (−2) · 12 · (−1) =

В примере пять отрицательных множителей. Значит, знак результата будет «минус».

Теперь вычислим произведение модулей, не обращая внимание на знаки.

6 · 3 · 4 · 2 · 12 · 1 = 1728

Конечный результат умножения исходных чисел будет:

(−6) · (−3) · (−4) · (−2) · 12 · (−1) = −1728

Умножение на ноль и единицу

Если среди множителей есть число ноль или положительная единица, то умножение выполняется по известным правилам.

• 0 · a = 0
• a · 0 = 0
• a · 1 = a

Примеры:

• 0 · (−3) = 0
• 0,4 · 1 = 0,4

Особую роль при умножении рациональных чисел играет отрицательная единица «−1».

Запомните!

При умножении на «−1» число меняется на противоположное.

В буквенном выражении это свойство можно записать:

a · (−1) = (−1) · a = −a

При совместном выполнении сложения, вычитания и умножения рациональных чисел сохраняется порядок действий, установленный для положительных чисел и нуля.

Пример умножения отрицательных и положительных чисел.

Координатная прямая Координаты точек на числовой оси Сложение отрицательных чисел Вычитание отрицательных чисел Умножение отрицательных чисел Деление отрицательных чисел

---

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».

Оставить комментарий:

Отправить

---

Обзор размножая дробные образовательные ресурсы

Целые рабочие личные листы, проводящие в библиотеке.

Результаты фильтрации

очистить все фильтры

By Grade

• Preschool
• Kindergarten
• 1st grade
• 2nd grade
• 3rd grade
• 4th grade
• 5th grade
• 6th grade
• 7th grade
• 8th grade

By Субъект

• Кодирование
•  Изобразительное искусство
•  иностранный язык

•  Математика

  •  Число 0018
  •  Addition
  •  Subtraction
  •  Multiplication
  •  Division
  •  Mixed Operations

  •  Fractions

    •  Fraction Models
    •  Равные дроби
    •  Сравнение дробей
    • Смешанные числа и неправильные дроби
    •  Сложение и вычитание дробей

    •  Multiplying and Dividing Fractions

      •  Multiplying Fractions

      • Division with Unit Fractions
      • Dividing Fractions
  •  Decimals
  •  Percents, Ratios, and Скорости
  •  Алгебра
  •  Геометрия
  •  Измерение
  •  9009  Время
  0010 Money Math
  •  Data and Graphing
  •  Math Word Problems
  • Math Puzzles
•  Reading & Writing
•  Science
•  Social emotional
•  Социальные исследования
•  Typing

по теме

•  Праздники

Стандарт

.

0015  Common Core

Дроби 4



Учебный урок

Дроби углубляются в изучение 9

3 Учащиеся будут применять предыдущие знания о нахождении эквивалентных дробей и преобразовании между дробями и смешанными числами, чтобы работать с дробями более сложными способами. Студенты будут продолжать использовать визуальные модели для обучения и практики сложения, вычитания, умножения и деления дробей.

5-й класс

Математика



Урок с пошаговыми инструкциями

Поиск Умножение дробей Образовательные ресурсы

Умножение дробей — отличная отправная точка для изучения арифметики, если ваш ребенок только начинает изучать арифметику. Этому навыку обычно обучают, начиная с четвертого класса, поэтому, если ваш ученик уже знаком с различными типами дробей, изучите наши ресурсы, чтобы помочь им освоить умножение дробей, прежде чем они перейдут к более сложным понятиям.

Узнайте больше об умножении дробей

Умножение дробей — одна из самых простых задач, потому что правил не так много. Ниже приведено пошаговое руководство по умножению правильных, неправильных и смешанных дробей.

Общие правила
Если обе дроби имеют числитель и знаменатель, правила очень просты:

1. Умножить числители (верхние числа)
2. Умножить знаменатели (нижние числа)
3. Упростить, если необходимо0018

Чтобы узнать, как умножать числа, посетите нашу страницу Умножение.

Дроби и целые числа
Если вы пытаетесь умножить дробь на целое число, преобразуйте целое число в дробь, присвоив ей знаменатель, равный 1 (3 станет ³ ⁄ ₁ ), и затем следуйте общим правилам умножения дробей.

Смешанные дроби
Чтобы умножать смешанные дроби, вы должны знать, как выполнять преобразование между смешанной дробью и неправильной дробью.

Если вашему ребенку нужна помощь с этой концепцией, взгляните на «Основы дробей» в нижней части страницы «Дроби» и поработайте с некоторыми рабочими листами.

1. Преобразование смешанной дроби в неправильную
2. Умножение дробей по общим правилам
3. Преобразование произведения обратно в смешанную дробь

Используйте эти правила, чтобы работать с различными рабочими листами и упражнениями на этой странице, пока ваш ребенок не станет профессиональным умножителем дробей!

Дроби

Дробь , или дробное число используются для представления части целого. Дроби состоят из двух чисел: числитель (над чертой) и знаменатель (под чертой).

Знаменатель говорит вам о количестве равных частей, на которые что-то делится. Числитель говорит вам, сколько из этих равных частей рассматривается. Таким образом, если дробь состоит из пирога, знаменатель 5 говорит вам, что пирог был разделен на пять равных частей, из которых 3 (числитель) находятся в дроби.

Иногда полезно подумать о разделительной линии (середина дроби) означает «из». Другими словами, также означает 3 из 5 равных частей от всего пирога.

Отрицательные дроби

Дроби могут быть отрицательными , а также положительными. (См. рисунок ниже.)

Однако отрицательные дроби обычно записываются следующим образом:

Сложение положительных и отрицательных дробей

Правила для чисел со знаком применимы и к дробям.

Пример 1

Добавьте следующее.

Вычитание положительных и отрицательных дробей

Правило вычитания чисел со знаком применимо и к дробям.

Пример 2

Вычтите следующее.

Умножение дробей

Чтобы умножить дроби, просто умножить числители, а затем умножить знаменатели. При необходимости уменьшите до самых низких условий.

Пример 3

Умножить.

Этот ответ пришлось сократить, потому что он не был в самом низком выражении. Поскольку целые числа также можно записать в виде дробей и т. д., проблему можно решить, заменив 3 на .

Ранняя редукция

Раннее сокращение при умножении дробей избавило бы вас от необходимости сокращать ваши ответы после завершения умножения. Чтобы уменьшить, найдите число, которое делится без остатка на один числитель и один знаменатель. В этом случае 2 будет делиться на 2 без остатка в числителе 2 (проходит один раз) и в знаменателе 12 (проходит шесть раз). Таким образом,

Помните, что раннее сокращение возможно только при умножении на дробей. Здесь также действуют правила умножения чисел со знаком.

Пример 4

Уменьшить, где это возможно, раньше, а затем умножить.

Умножение смешанных чисел

Чтобы умножить смешанные числа, сначала замените любое смешанное число неправильной дробью. Затем умножьте.

Пример 5

Умножить.

Измените ответ, если он в форме неправильной дроби, обратно на смешанное число и при необходимости уменьшите.