Вычитание дробей с одинаковыми знаменателями.

Для начала приведём пример, который позволит нам выяснить, как проводится вычитание дробей с одинаковыми знаменателями.

ПРИМЕР:

Пусть на тарелке находилось пять восьмых долей яблока, то есть, ⁵/₈  яблока. После чего две восьмых доли забрали. По смыслу вычитания, указанное действие можно записать так:

Понятно, что при этом на тарелке остаётся
5 – 2 = 3  восьмых доли  яблока, то есть

Рассмотренный пример иллюстрирует правило вычитания дробей с одинаковыми знаменателями.

Чтобы вычесть дробь из дроби с одинаковыми знаменателями, нужно вычесть числитель вычитаемого из числителя уменьшаемого и оставить прежний знаменатель.

Озвученное правило с помощью букв записывается так:

ПРИМЕР:

Выполните вычитание обыкновенной дроби  ¹⁷/₁₅  из обыкновенной дроби  ²⁴/₁₅.

РЕШЕНИЕ:

Знаменатели вычитаемых дробей равны. Числитель уменьшаемого равен  34, а числитель вычитаемого равен  17, их разность равна:

24 – 17 = 7.

Поэтому вычитание дробей с одинаковыми знаменателями²⁴/₁₅  и  ¹⁷/

Краткий вариант решения выглядит так:

ОТВЕТ:  ⁷/₁₅

При возможности нужно проводить сокращение дроби и (или) выделение целой части из неправильной дроби, которая получается при вычитании дробей с одинаковыми знаменателями.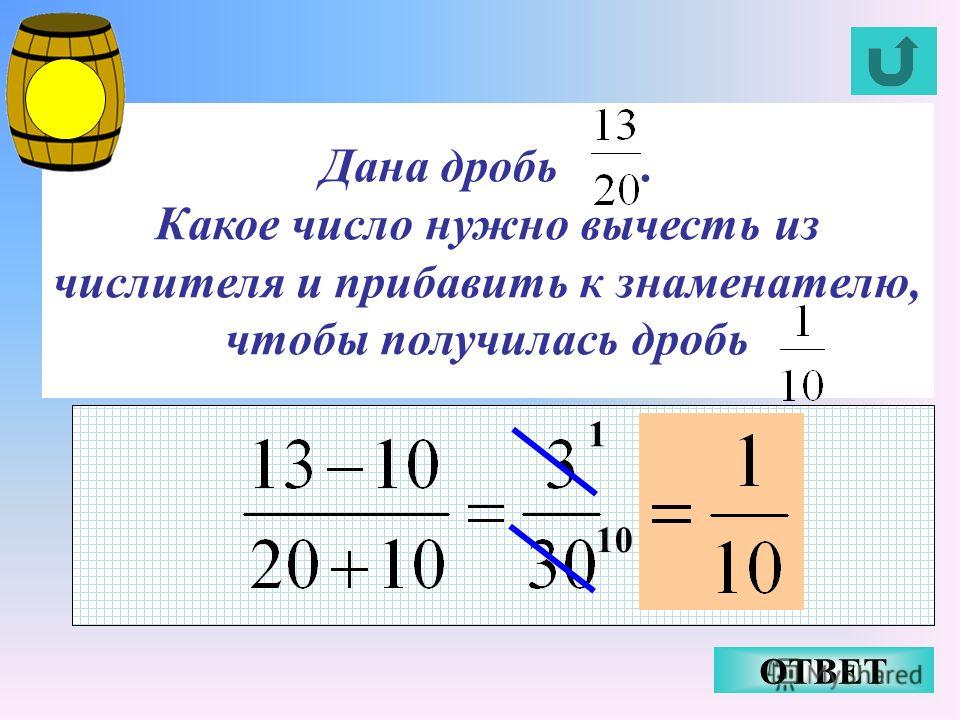

ПРИМЕР:

Вычислите разность:

РЕШЕНИЕ:

Воспользуемся формулой вычитания дробей с одинаковыми знаменателями.

Очевидно, что числитель и знаменатель полученной дроби делятся надва, то есть дробь  ²²/₁₂ –

Итак, вычисляемая разность дробей с одинаковыми знаменателями равна  1⁵/₆.
Краткий вариант решения выглядит так:

ОТВЕТ:  1⁵/₆ 

ПРИМЕР:

Вычитание дробей с разными знаменателями.

Вычитание дробей с разными знаменателями сводится к вычитанию дробей с одинаковыми знаменателями. Для этого дроби с разными знаменателями достаточно привести к общему знаменателю.

Чтобы вычесть дробь из дроби с разными знаменателями, нужно предварительно привести их к наименьшему общему знаменателю, затем из числителя уменьшаемого вычесть числитель вычитаемого и под их разностью подписать общий знаменатель.       

ПРИМЕР:

Отнимите от обыкновенной дроби  ²/₉  обыкновенную дробь  ¹/₁₅.

РЕШЕНИЕ:

Так как знаменатели вычитаемых дробей разные, то сначала выполним приведение дробей к наименьшему общему знаменателю. Так как

НОК (9; 15) = 45,

то дополнительным множителем дроби  ²/₉  является число

45 : 9 = 5,

а дополнительным множителем дроби  ¹/₁₅  является число:

45 : 15 = 3,

тогда

Осталось вычесть из дроби  ¹⁰/₄₅  дробь  ³/₄₅, получаем

что и даёт нам искомую разность дробей с разными знаменателями.
Краткое решение записывается так:

ОТВЕТ:  ⁷/₄₅

Не следует забывать про сокращение полученной после вычитания дроби, а также про выделение целой части.

ПРИМЕР:

Вычтите из дроби  ¹⁹/₉  дробь  ⁷/₃₆.

РЕШЕНИЕ:

После приведения дробей с разными знаменателям к наименьшему общему знаменателю  36, получим дроби  ⁷⁶/₃₆  и  ⁷/₃₆. Находим их разность:

Полученная дробь сократима, после её сокращения на  3, получаем  ²³/₁₂. А эта дробь неправильная, поэтому, выделив из неё целую часть, получим 

ОТВЕТ:  1¹¹/₁₂

ПРИМЕР:

Вычитание смешанных дробей.

Чтобы вычесть смешанные числа, сначала приведём дробные части уменьшаемого и вычитаемого к наименьшему общему знаменателю. Затем вычтем целое из целого и дробь из дроби.

ПРИМЕР:

Найти разность:

РЕШЕНИЕ:

ОТВЕТ:

ПРИМЕР:

Но бывают случаи, когда дробная часть вычитаемого больше дробной части уменьшаемого. В таких случаях нужно взять одну единицу из целой части уменьшаемого, раздробить её в те доли, в каких выражена дробная часть, и прибавить к дробной части уменьшаемого. А затем вычитание будет выполняться так же, как вычитание смешанных чисел.                                          

ПРИМЕР:

В случае, когда дробь вычитаемого больше, чем дробь уменьшаемого, поступают следующим образом: берут одну единицу (целое) из целого числа уменьшаемого, записывают его как неправильную дробь, числитель и знаменатель которой равны между собой и равны знаменателю дробной части, и прибавляют к дробной части, далее отнимают две смешанные дроби.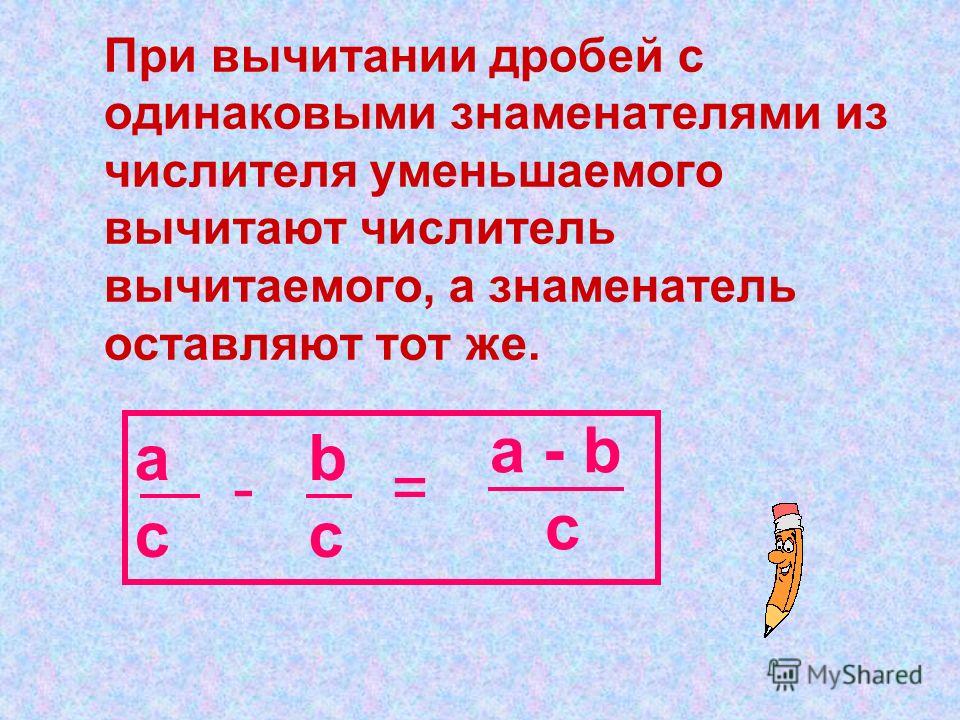

ПРИМЕР:

Выполнить вычитание:

РЕШЕНИЕ:

Дробь  ⁴/₉  меньше чем дробь  ¹¹/₁₂  так как

4 ∙ 12 = 36 < 9 ∙ 11 = 99,

тогда

ОТВЕТ:  3¹⁹/₃₆

Вычитание обыкновенной дроби из натурального числа.

Вычитание обыкновенной дроби из натурального числа можно свести к вычитанию обыкновенных дробей, представив натуральное число как дробь.

ПРИМЕР:

.

РЕШЕНИЕ:

Представим число  7  как дробь  ⁷/₁, после чего выполним вычитание:

Выделив целую часть из полученной дроби, получаем окончательный ответ.

ОТВЕТ:  5¹/₃

Рассмотрим ещё пример на вычитание смешанного числа из натурального числа.

ПРИМЕР:

Но существует более рациональный способ вычитания дроби из натурального числа. Его преимущества заметны тогда, когда уменьшаемое натуральное число и знаменатель вычитаемой дроби являются большими числами. Если вычитаемая дробь правильная, то уменьшаемое натуральное число можно заменить суммой двух чисел, одно из которых равно единице, отнять правильную дробь от единицы, после чего завершить вычисления.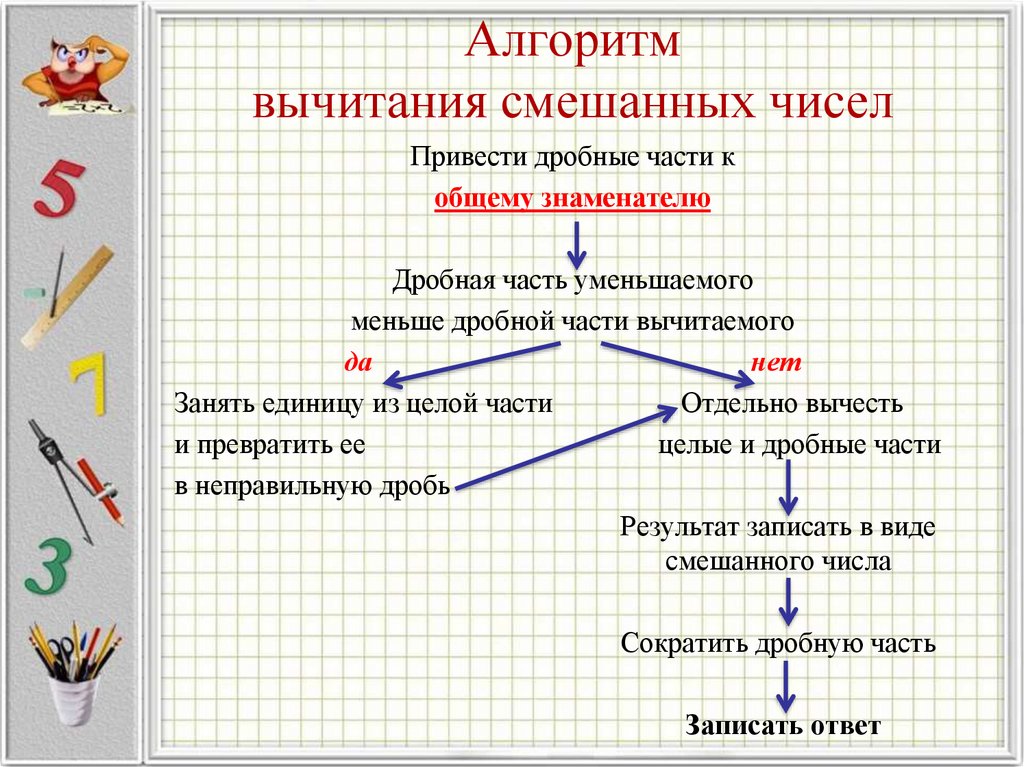

ПРИМЕР:

Найти разность:

РЕШЕНИЕ:

Выполним вычитание дробей по описанному выше правилу:

ОТВЕТ:  ²/₅

ПРИМЕР:

Выполните вычитание обыкновенной дроби  ¹³/₆₂  из натурального числа  1065.

РЕШЕНИЕ:

Вычитаемая обыкновенная дробь – правильная. Заменим число  1065  суммой

1064 + 1,

При этом получим:

Осталось вычислить значение полученного выражения. В силу свойств вычитания, полученное выражение можно переписать так:

Вычислим значение разности в скобках, заменив единицу дробью, ¹/₁:

Краткое решение записывается так: ОТВЕТ:  1064⁴⁹/₆₂

Рассмотрим ещё пример на вычитание смешанного числа из целого числа.                                                                                               

ПРИМЕР:

Если же вычитаемая дробь неправильная, то её можно заменить смешанным числом, после чего провести вычитание смешанного числа из натурального числа.

ПРИМЕР:

Отнимите обыкновенную дробь  ⁷³/₅  от натурального числа  644.

РЕШЕНИЕ:

Выделим целую часть из неправильной дроби:

Тогда

ОТВЕТ:  629²/₅

Вычитание натурального числа из обыкновенной дроби.

Вычитание натурального числа из дроби можно свести к вычитанию обыкновенных дробей. Для этого достаточно представить натуральное число в виде дроби со знаменателем  1.

ПРИМЕР:

Выполните вычитание числа  3  из обыкновенной дроби  ⁸³/₂₁.

РЕШЕНИЕ:

Так как число  3 = ³/₁  то:

ОТВЕТ:  ²⁰/₂₁

Вычитание натурального числа из неправильной дроби удобнее проводить, представив дробь в виде смешанного числа.

ПРИМЕР:

Отнимите число  3  от дроби  ⁸³/₂₁.

РЕШЕНИЕ:

Сначала выделим целую часть из неправильной дроби  ⁸³/₂₁, получим:

тогда

Осталось провести вычитание натурального числа из смешанного числа:

ОТВЕТ:  ²⁰/₂₁

Распространение свойств вычитания на дробные числа.

Все законы и свойства вычитания натуральных чисел справедливы и для дробных чисел. Их применение во многих случаях значительно упрощает процесс вычисления.

Вместо того, чтобы вычесть сумму дробей, можно вычесть каждое слагаемое последовательно, и обратно: вместо того, чтобы вычитать каждое число последовательно, можно вычесть сразу их сумму.

ПРИМЕР:

Вычислите значение выражения:

РЕШЕНИЕ:

Сначала вычислим разность

после чего от неё отнимем дробь  ⁵/₆. после выделения целой части из полученной неправильной дроби получим:

ОТВЕТ:  3¹¹/₁₂ 

ПРИМЕР:

Здесь использовано правило вычитания из чисел разности.

Когда выражение содержит и натуральные числа и дроби, то при вычислении удобно группировать числа с числами, а дроби с дробями.

ПРИМЕР:

Выполните вычитание суммы натурального числа и обыкновенной дроби

из суммы натурального числа и дроби

РЕШЕНИЕ:

Нам нужно вычислить разность

Свойства сложения и вычитания позволяют нам провести следующую группировку что упрощает вычисления. Осталось лишь закончить вычисления:

ОТВЕТ:  93¹/₄

Если уменьшаемое уменьшим на какое-нибудь число, не изменяя вычитаемого, то разность уменьшится на то же самое число.

Если вычитаемое увеличим на какое-нибудь число, то разность уменьшится на то же число.

Если вычитаемое уменьшим на какое-нибудь число, то разность увеличится на то же число.

Если уменьшаемое и вычитаемое увеличим или уменьшим на одно и то же число, то разность не изменится.

Задания к уроку 16

• Задание 1
• Задание 2
• Задание 3

ДРУГИЕ УРОКИ

• Урок 1. Нумерация
• Урок 2. Сложение натуральных чисел 
• Урок 3. Вычитание натуральных чисел
• Урок 4. Таблица умножения 
• Урок 5. Умножение натуральных чисел 
• Урок 6. Деление натуральных чисел
• Урок 7. Степень числа
• Урок 8. Измерение величины
• Урок 9. Деление с остатком
• Урок 10. Делимость натуральных чисел
• Урок 11. Наибольший общий делитель (НОД)
• Урок 12. Наименьшее общее кратное (НОК)
• Урок 13. Обыкновенные дроби
• Урок 14. Преобразование дробей
• Урок 15. Сложение дробей
• Урок 17. Умножение дробей
• Урок 18. Деление дробей
• Урок 19. Нахождение дроби от числа (задачи)
• Урок 20. Нахождение числа по известной его части (задачи)
• Урок 21. Конечные десятичные дроби
• Урок 22. Сложение десятичных дробей
• Урок 23. Вычитание десятичных дробей
• Урок 24. Умножение десятичных дробей
• Урок 25. Деление десятичных дробей
• Урок 26. Округление чисел

javascript — Как вычесть единицу из последней цифры его дробной части?

Вопрос задан 1 год 4 месяца назад

Изменён 1 год 4 месяца назад

Просмотрен 114 раз

var num = 21.58746;     // 21.58745
var num = 421;          // 420
var num = 0. 8527777857; // 0.8527777856

• javascript

5

Примерно так, но возможны неточности из-за указанных в комментариях проблем с плавающей точкой

var num1 = 21.58746;     // 21.58745
var num2 = 421;          // 420
var num3 = 0.8527777857; // 0.8527777856
function decOne(num) {
  // переводим в строку, вырезаем дробь, определяем длинну
  const frac_len = ((num + '').split('.')[1] || '').length
  return num - 1 / 10**frac_len
}
console.log(decOne(num1))
console.log(decOne(num2))
console.log(decOne(num3))

касательно дробной части:

числа хранятся в двоичном виде, отображение для пользователей осуществляется в десятичном виде, поскольку log(2)/log(10) — иррациональное число, то однозначное соответствие десятичной и двоичной записей (однозначная точность) возникает только в случае, если число (дробная часть числа) представимо как степень двойки

таким образом однозначно ваша задача решаема только в очень редких случаях

однако вы можете попытаться грубой силой проделать данную операцию

1. перевести число в строку
2. разбить строку на 2 части (до точки и после точки)
3. перевести разбитые части в числа
4. вычесть из числа, соответствующего дробной части 1
5. если получилось отрицательное число, то создать строку, содержащую 9 по кол-ву равному длине строки, содержащей дробную часть, а из числа, соответствующего целой части вычесть 1
6. перевести оба числа в строки 6. 1) при этом дополнить строку отвечающую дробной части 0 в начале, так чтобы длина строки соответствовала длине разбитой строки
7. соединить строки через .
8. перевести строку в число 🙂

вот только не удивляйтесь если после того как у числа 3.1415926 вы вычели единицу и получили (в виде строки) 3.1415925, после перевода в число вы все равно получили 3.1415926

P.S.

конечно можно сделать более грубое, но при этом более точное выполнение вашей задачи

1. перевести число в строку
2. разбить на целую и дробную части
3. узнать длину дробной части
4. получить число value = pow(10, -(len - 1))
5. вычесть из первоначального числа полученное

только опять же не удивляйтесь, если вместо 3.1415925 вы получите 3.1415925999998

P.P.S.

число пи просто привел для примера — на нем такого эффекта может и не быть

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

Вычитание дробей — Элементарная математика

Введение

Что такое вычитание дробей?

Общие основные стандарты

Как вычитать дроби

Советы по обучению вычитанию дробей

Легко совершать ошибки

Практические вопросы по вычитанию дробей

Часто задаваемые вопросы о добавлении фракций

Следующие уроки

Все еще застряли?

[БЕСПЛАТНО] Математические экзамены на конец года (4-й и 5-й классы)

Экзамены охватывают ряд тем, чтобы оценить успеваемость ваших учащихся по математике и помочь подготовить их к государственным экзаменам.

Скачать бесплатно

Введение

Что такое вычитание дробей?

Общие основные стандарты

Как вычитать дроби

Советы по обучению вычитанию дробей

Легко совершать ошибки

Практические вопросы по вычитанию дробей

Часто задаваемые вопросы о добавлении фракций

Следующие уроки

Все еще застряли?

Здесь вы узнаете, как вычитать дроби с одинаковыми знаменателями и с разными знаменателями. Вы также научитесь вычитать смешанные числа.

Учащиеся впервые узнают о вычитании дробей как части числа и операциях с дробями в начальной школе.

Что такое вычитание дробей?

Вычитание дробей — это вычитание двух или более дробей, чтобы найти разницу.

Для этого у дробей нужен общий знаменатель (нижнее число). Затем вы можете вычесть дроби на , вычитая числители (верхние числа).

Например,

\cfrac{7}{8}-\cfrac{3}{8}=

Поскольку знаменатели одинаковы, части имеют одинаковый размер. Вы вычитаете, чтобы увидеть, сколько частей осталось, 7-4=3.

Есть 3 части. Но какого размера детали? Они по-прежнему восьмые, поэтому знаменатель остается прежним.

\cfrac{7}{8}-\cfrac{4}{8}=\cfrac{3}{8}

Если знаменатели не совпадают, вы создаете эквивалентные дроби перед сложением.

Например,

\cfrac{2}{3}-\cfrac{5}{9}=

Уравнение выводит \cfrac{5}{9} из \cfrac{2}{3}.

Поскольку знаменатели НЕ совпадают, части НЕ имеют одинакового размера. Используйте эквивалентные дроби, чтобы создать общий знаменатель 9.

Умножить числитель и знаменатель \cfrac{2}{3} на 3.

\cfrac{2 \; \раз\; 3}{3 \; \раз\; 3}=\cfrac{6}{9}

Теперь используйте эквивалентную дробь для расчета \cfrac{6}{9}-\cfrac{5}{9}.

Вы вычитаете, чтобы увидеть, сколько частей осталось, 6-5=1.

Есть 1 деталь. Но какого размера часть? Это все еще девятая, поэтому знаменатель остается прежним.

\cfrac{6}{9}-\cfrac{5}{9}=\cfrac{1}{9}

Что такое вычитание дробей?

Общие базовые стандарты

Какое отношение это имеет к математике в 4-м и 5-м классах?

• Класс 4 – Числа и операции – Дроби (4.NF.B.3c)
  Сложение и вычитание смешанных чисел с одинаковыми знаменателями, например, путем замены каждого смешанного числа эквивалентной дробью и/или с использованием свойств операций и связи между сложением и вычитанием.
• Класс 5 – Числа и операции – Дроби (5.NF.A.1)
  Сложение и вычитание дробей с разными знаменателями (включая смешанные числа) путем замены данных дробей эквивалентными дробями таким образом, чтобы получить эквивалентную сумму или разность дробей с одинаковыми знаменателями.
  Например, \cfrac{2}{3} + \cfrac{5}{4} = \cfrac{8}{12} + \cfrac{15}{12} = \cfrac{23}{12}. (В общем, \cfrac{a}{b} + \cfrac{c}{d} = \cfrac{(ad\; + \;bc)}{bd}. )

Как вычитать дроби

Чтобы вычитать дроби с одинаковыми знаменателями:

1. Вычесть числители (верхние числа).
2. Запишите свой ответ в виде дроби.

Чтобы вычесть смешанные числа с одинаковыми знаменателями:

1. Вычтите дроби, при необходимости заимствуя.
2. Вычтите целые числа.
3. Запишите свой ответ в виде смешанного числа.

Для вычитания дробей с разными знаменателями:

1. Создайте общие знаменатели (нижние числа).
2. Вычтите числители (верхние числа).
3. Запишите свой ответ в виде дроби.

Чтобы вычесть смешанные числа с разными знаменателями:

1. Создайте общие знаменатели (нижние числа).
2. Вычитание дробей, при необходимости заимствование.
3. Вычтите целые числа.
4. Запишите свой ответ в виде смешанного числа.

[БЕСПЛАТНО] Проверка понимания дробей (для 4–6 классов)

Используйте этот тест, чтобы проверить понимание дробей учащимися 4–6 классов. Более 10 вопросов с ответами, охватывающими ряд тем 4-го, 5-го и 6-го классов, чтобы определить сильные стороны и поддержку!

СКАЧАТЬ БЕСПЛАТНО

Икс

[БЕСПЛАТНО] Проверка понимания дробей (для 4–6 классов)

Используйте этот тест, чтобы проверить понимание дробей учащимися 4–6 классов. Более 10 вопросов с ответами, охватывающими ряд тем 4-го, 5-го и 6-го классов, чтобы определить сильные стороны и поддержку!

СКАЧАТЬ БЕСПЛАТНО

Примеры вычитания дробей

Пример 1: вычитание дробей с одинаковыми знаменателями

Решить \cfrac{3}{5}-\cfrac{1}{5}.

1. Вычесть числители (верхние числа).

Уравнение отнимает \cfrac{1}{5} от \cfrac{3}{5}.

Так как знаменатели одинаковые, детали имеют одинаковый размер. Вы вычитаете, чтобы увидеть, сколько частей осталось: 3-1=2.

2 Запишите ответ в виде дроби.

Есть 2 части. Но какого размера детали? Они по-прежнему пятые, поэтому знаменатель остается прежним.

\cfrac{3}{5}-\cfrac{1}{5}=\cfrac{2}{5}

Пример 2: вычитание смешанных чисел с одинаковыми знаменателями

Решите 4 \cfrac{11}{12 }-1 \cfrac{7}{12}.

Вычитание дробей, при необходимости заимствование.

Уравнение убирает 1 \cfrac{7}{12} из 4 \cfrac{11}{12}.


Начните с дробей. Так как знаменатели одинаковы, то и части имеют одинаковый размер. Вы вычитаете, чтобы увидеть, сколько частей осталось: 11-7=4.


4 части. Но какого размера детали? Они по-прежнему двенадцатые, поэтому знаменатель остается прежним.


\cfrac{11}{12}-\cfrac{7}{12}=\cfrac{4}{12}

Вычесть целые числа.


4-1=3

Ответ запишите в виде смешанного числа.


4 \cfrac{11}{12}-1 \cfrac{7}{12}=3 \cfrac{4}{12}


Вы также можете записать этот ответ в виде эквивалентной дроби 3 \cfrac{1 {3}.

Пример 3: вычитание смешанных чисел с одинаковыми знаменателями

Решите 2 \cfrac{3}{10}-1 \cfrac{9}{10}.

Вычитание дробей, при необходимости заимствование.

Уравнение убирает 1 \cfrac{9}{10} из 2 \cfrac{3}{10}.


Начните с дробей. Так как знаменатели одинаковы, то и части имеют одинаковый размер. Однако деталей не хватит, чтобы взять 9от 3.


Одно целое можно разбить на \cfrac{10}{10} …


2 \cfrac{3}{10}=1 \cfrac{13}{10}


Теперь вы можете решить 1 \cfrac{13}{10}-1 \cfrac{9}{10}.


Вы вычитаете, чтобы увидеть, сколько частей осталось: 13-9=4.


4 части. Но какого размера детали? Они по-прежнему десятые, поэтому знаменатель остается прежним.


\cfrac{13}{10}-\cfrac{9}{10}=\cfrac{4}{10}

Вычтите целые числа.


1-1=0

Ответ запишите в виде смешанного числа.


Иногда ответ будет дробным.


1 \cfrac{13}{10}-1 \cfrac{9}{10}=\cfrac{4}{10}


Вы также можете записать этот ответ в виде эквивалентной дроби \cfrac{2}{ 5} или десятичное 0,4.

Пример 4: вычитание дробей с разными знаменателями

Решить \cfrac{3}{4}-\cfrac{1}{2}.

Создайте общие знаменатели (нижние числа).

Поскольку \cfrac{3}{4} и \cfrac{1}{2} не имеют одинаковых знаменателей, части НЕ имеют одинакового размера. Можно использовать общий знаменатель 4.


Умножьте числитель и знаменатель \cfrac{1}{2} на 2, чтобы получить эквивалентную дробь.


\cfrac{3}{4} \quad и \quad \cfrac{1 \; \раз\; 2}{2 \; \раз\; 2}=\cfrac{2}{4}

Вычесть числители (верхние числа).

Теперь используйте эквивалентную дробь для решения: \cfrac{3}{4}-\cfrac{2}{4}.


Так как знаменатели одинаковые, части имеют одинаковый размер. Вы вычитаете, чтобы увидеть, сколько частей осталось: 3-2=1.

Ответ запишите дробью.

Есть 1 часть. Но какого размера часть? Это все еще четверть, поэтому знаменатель остается прежним.


\cfrac{3}{4}-\cfrac{2}{4}=\cfrac{1}{4}

Пример 5: вычитание смешанных чисел с разными знаменателями

Решите 2 \cfrac{1}{2}-1 \cfrac{1}{3}.

Создайте общие знаменатели (нижние числа).

Уравнение забирает 1 \cfrac{1}{3} из 2 \cfrac{1}{2}.


Начните с дробей. Поскольку \cfrac{1}{2} и \cfrac{1}{3} не имеют одинаковых знаменателей, части НЕ имеют одинакового размера.


Умножьте числитель и знаменатель на противоположный знаменатель, чтобы получить эквивалентные дроби с общими знаменателями.


\cfrac{1 \; \раз\; 3}{2 \; \раз\; 3}=\cfrac{3}{6} \quad и \quad \cfrac{1 \; \раз\; 2}{3 \; \раз\; 2}=\cfrac{2}{6}

Вычесть дроби, при необходимости заимствуя.

Теперь используйте эквивалентные дроби, чтобы решить: 2 \cfrac{3}{6}-1 \cfrac{2}{6}.


Начните с дробей. Так как знаменатели одинаковы, то и части имеют одинаковый размер. Вы вычитаете, чтобы увидеть, сколько частей осталось: 3-2=1.


Есть 1 часть. Но какого размера часть? Это все еще шестая, поэтому знаменатель остается прежним.

\cfrac{3}{6}-\cfrac{2}{6}=\cfrac{1}{6}

Вычтите целые числа.


2-1=1

Ответ запишите в виде смешанного числа.


2 \cfrac{3}{6}-1 \cfrac{2}{6}=1 \cfrac{1}{6}

Пример 6: вычитание смешанных чисел с разными знаменателями

Решите 5 \cfrac {3}{8}-1 \cfrac{3}{4}.

Создайте общие знаменатели (нижние числа).

Уравнение убирает 1 \cfrac{3}{4} из 5 \cfrac{3}{8}.


Начните с дробей. Поскольку \cfrac{3}{8} и \cfrac{3}{4} не имеют одинаковых знаменателей, части НЕ имеют одинакового размера. Можно использовать общий знаменатель 8.


Умножьте числитель и знаменатель \cfrac{3}{4} на 2, чтобы получить эквивалентную дробь.


\cfrac{3}{8} \quad и \quad \cfrac{3 \; \раз\; 2}{4 \; \раз\; 2}=\cfrac{6}{8}

Вычесть дроби, при необходимости заимствуя.

Теперь используйте эквивалентные дроби для решения: 5 \cfrac{3}{8}-1 \cfrac{6}{8}.


Начните с дробей. Так как знаменатели одинаковы, то и части имеют одинаковый размер. Однако частей недостаточно, чтобы отнять 6 от 3.


Одно целое можно разбить на \cfrac{8}{8}…


5 \cfrac{3}{8}=4 \cfrac {11}{8}


Теперь вы можете решить 4 \cfrac{11}{8}-1 \cfrac{6}{8}.


Вы вычитаете, чтобы увидеть, сколько частей осталось: 11-6=5.


Осталось 5 деталей. Но какого размера детали? Они по-прежнему восьмые, поэтому знаменатель остается прежним.

\cfrac{11}{8}-\cfrac{6}{8}=\cfrac{5}{8}

Вычесть целые числа.


4-1=3

Ответ запишите в виде смешанного числа.


4 \cfrac{11}{8}-1 \cfrac{6}{8}=3 \cfrac{5}{8}

Учебные советы по вычитанию дробей

• Работа с дробями в 3-м классе сосредоточена вокруг понимание с помощью моделей, особенно моделей площадей и числовых линий. Чтобы опираться на это в 4-м и 5-м классах, всегда имейте физические или цифровые модели, чтобы учащиеся могли использовать их при необходимости.
• Чтобы представить эту тему, дайте учащимся задачу на вычитание дробей и дайте им время решить ее так, как им понятно. Затем пройдитесь по различным стратегиям решения всей группой.
• В начале вы можете придерживаться более мелких долей или задач, не связанных с заимствованием. Однако в какой-то момент важно перейти к показу учащимся всех видов задач на вычитание дробей, смешанных вместе. Это дает им возможность определить, какую стратегию решения использовать.
• Рабочие листы с дробями могут иметь свое место, когда учащиеся все еще развивают понимание сложения, но как только учащиеся освоят успешную стратегию и смогут гибко работать, включите математические игры или реальные проекты, связанные с вычитанием дробей.

Наши любимые ошибки

• Вычитание без одинаковых знаменателей
  При вычитании дроби должны иметь одинаковые знаменатели. Прежде чем вычитать дроби с разными знаменателями, приведите равные дроби к общему знаменателю.

• При вычитании дробей вычитаются только числители
  Знаменатель говорит нам, насколько велики части. Вы вычитаете количество частей (числители) и сохраняете знаменатель (размер частей) тем же самым.

Практические вопросы по вычитанию дробей

\cfrac{3}{6}

\cfrac{3}{0}

1 \cfrac{1}{6}

Уравнение принимает \cfrac{2}{6 } от \cfrac{5}{6}.

 

Поскольку знаменатели одинаковы, части имеют одинаковый размер. Вы вычитаете, чтобы увидеть, сколько частей осталось: 5-2=3.

 

 

Есть 3 части. Но какого размера детали? Они по-прежнему шестые, поэтому знаменатель остается прежним.

 

 

\cfrac{5}{6}-\cfrac{2}{6}=\cfrac{3}{6}

 

Вы также можете записать этот ответ в виде эквивалентной дроби \cfrac{1}{2}.

2 \cfrac{2}{4}

\cfrac{3}{4}

1 \cfrac{2}{4}

Уравнение отнимает 1 \cfrac{3}{4} от 3 \cfrac{1}{4}.

 

Начните с дробей. Так как знаменатели одинаковы, то и части имеют одинаковый размер. Однако частей недостаточно, чтобы из 1 вычесть 3.

 

Одно целое можно разбить на \cfrac{4}{4}…

 

3 \cfrac{1}{4}=2 \cfrac{5}{4}

 

 

Теперь вы можете решить 2 \cfrac{5}{4}-1 \cfrac{3}{4}.

 

Вы вычитаете, чтобы увидеть, сколько частей осталось: 5-3=2.

 

 

Есть 2 части. Но какого размера детали? Они по-прежнему четвертые, поэтому знаменатель остается прежним.

 

 

\cfrac{5}{4}-\cfrac{3}{4}=\cfrac{2}{4}

 

Вычтите целые числа.

 

 

2-1=1

 

 

2 \cfrac{5}{4}-1 \cfrac{3}{4}=1 \cfrac{2}{4}

 

Вы также можете записать этот ответ как эквивалентное смешанное число 1 \cfrac{1}{2}.

3 \cfrac{7}{10}

6 \cfrac{9}{10}

2 \cfrac{9}{10}

2 \cfrac{7}{10}

Уравнение принимает 2 \cfrac{1}{10} от 4 \cfrac{8}{10}.

 

Начните с дробей. Так как знаменатели одинаковы, то и части имеют одинаковый размер. Вы вычитаете, чтобы увидеть, сколько частей осталось: 8-1=7.

 

 

Всего 7 частей. Но какого размера детали? Они по-прежнему десятые, поэтому знаменатель остается прежним.

 

 

\cfrac{8}{10}-\cfrac{1}{10}=\cfrac{7}{10}

 

Вычтите целые числа.

 

 

4-2=2

 

 

4 \cfrac{8}{10}-2 \cfrac{1}{10}=2 \cfrac{7}{10}

 

Вы также можете записать этот ответ в виде десятичного числа 2.7.

\cfrac{1}{2}

\cfrac{7}{15}

\cfrac{3}{8}

\cfrac{7}{0}

Поскольку \cfrac{2}{3 } и \cfrac{1}{5} не имеют одинаковых знаменателей, части НЕ одного размера.

 

Умножьте числитель и знаменатель на противоположный знаменатель, чтобы получить эквивалентные дроби с общими знаменателями.

 

\cfrac{2 \; \раз\; 5}{3\; \раз\; 5}=\cfrac{10}{15} \quad и \quad \cfrac{1 \; \раз\; 3}{5 \; \раз\; 3}=\cfrac{3}{15}

 

Теперь используйте эквивалентные дроби для решения: \cfrac{10}{15}-\cfrac{3}{15}.

 

Поскольку знаменатели одинаковы, части имеют одинаковый размер. Вы вычитаете, чтобы увидеть, сколько частей осталось: 10-3=7.

 

 

Всего 7 частей. Но какого размера детали? Они по-прежнему пятнадцатые, поэтому знаменатель остается прежним.

 

 

\cfrac{10}{15}-\cfrac{3}{15}=\cfrac{7}{15}

4\cfrac{1}{12}

1\cfrac{5}{12}

2\cfrac{5}{12}

1\cfrac{7}{12}

Уравнение принимает 2\cfrac{1}{3} от 3\cfrac{3}{4}.

 

Начните с дробей. Поскольку \cfrac{3}{4} и \cfrac{1}{3} не имеют одинаковых знаменателей, части НЕ имеют одинакового размера.

 

Умножьте числитель и знаменатель на противоположный знаменатель, чтобы получить эквивалентные дроби с общими знаменателями.

 

\cfrac{3 \; \раз\; 3}{4 \; \раз\; 3}=\cfrac{9}{12} \quad и \quad \cfrac{1 \; \раз\; 4}{3 \; \раз\; 4}=\cfrac{4}{12}

 

Теперь используйте эквивалентные дроби для решения: 3 \cfrac{9}{12}-2 \cfrac{4}{12}.

 

Начните с дробей. Так как знаменатели одинаковы, то и части имеют одинаковый размер. Вы вычитаете, чтобы увидеть, сколько частей осталось: 9-4=5.

 

 

5 частей. Но какого размера детали? Они по-прежнему двенадцатые, поэтому знаменатель остается прежним.

 

 

\cfrac{9}{12}-\cfrac{4}{12}=\cfrac{5}{12}

 

Вычтите целые числа.

 

 

3-2=1

 

 

3 \cfrac{9}{12}-2 \cfrac{4}{12}=1 \cfrac{5}{12}

4\cfrac{1}{12}

1\cfrac{3}{12}

2\cfrac{5}{12}

1\cfrac{7}{12}

Уравнение принимает 3 \cfrac{5}{6} от 5 \cfrac{1}{12}.

 

Начните с дробей. Поскольку \cfrac{1}{12} и \cfrac{5}{6} не имеют одинаковых знаменателей, части НЕ имеют одинакового размера. Можно использовать общий знаменатель 12.

 

Умножьте числитель и знаменатель \cfrac{5}{6} на 2, чтобы получить эквивалентную дробь.

 

\cfrac{1}{12} \quad и \quad \cfrac{5 \; \раз\; 2}{6 \; \раз\; 2}=\cfrac{10}{12}

 

Теперь используйте эквивалентную дробь для решения: 5 \cfrac{1}{12}-3 \cfrac{10}{12}.

 

Начните с дробей. Так как знаменатели одинаковы, то и части имеют одинаковый размер. Однако частей недостаточно, чтобы из 1 вычесть 10.

 

Одно целое можно разбить на \cfrac{12}{12}…

 

5 \cfrac{1}{12}=4 \cfrac{13}{12}

 

 

Теперь вы можете решить 4 \cfrac{13}{12}-3 \cfrac{10}{12}.

 

Вы вычитаете, чтобы увидеть, сколько частей осталось: 13-10=3.

 

 

Осталось 3 детали. Но какого размера детали? Они по-прежнему двенадцатые, поэтому знаменатель остается прежним.

 

 

\cfrac{13}{12}-\cfrac{10}{12}=\cfrac{3}{12}

 

Вычтите целые числа.

 

 

4-3=1

 

 

4 \cfrac{13}{12}-3 \cfrac{10}{12}=1 \cfrac{3}{12}

 

Вы также можете записать этот ответ как эквивалентное смешанное число 1 \cfrac{1}{4}.

Часто задаваемые вопросы о добавлении дробей

Изменяет ли размер дроби умножение на общий множитель?

Нет, хотя создаются новый числитель и новый знаменатель, значение дроби остается прежним. Поскольку знаменатель новой дроби больше, части будут меньше, поэтому числитель также должен быть больше, чтобы сумма частей была того же размера, что и исходная дробь.

Должны ли все разности дробей быть в наименьшем выражении?

Нет, учащимся не нужно находить наименьший общий знаменатель, чтобы правильно ответить на вопрос о сложении дроби. Однако по мере того, как учащиеся продвигаются в своем понимании дробей, это хорошая привычка расти. Также важно помнить о стандартных ожиданиях, поскольку они могут варьироваться от штата к штату.

Сложение дробей похоже на вычитание дробей?

Да, вы выполняете многие из тех же шагов, чтобы сложить дроби, что также требует общих знаменателей. Единственное отличие состоит в том, что вы складываете числители, а не вычитаете.

Все еще зависает?

Компания Third Space Learning специализируется на оказании помощи учителям и школьным руководителям в оказании персонализированной помощи по математике большему количеству своих учеников с помощью высококачественных индивидуальных онлайн-репетиторских занятий по математике, проводимых экспертами-предметниками.

Каждую неделю наши преподаватели поддерживают тысячи учеников, которые рискуют не оправдать свои ожидания в классе, и помогают ускорить их прогресс и повысить уверенность в себе.

Узнайте, как мы можем помочь вашим ученикам добиться успеха с помощью наших программ обучения математике для начальной школы.

Мы используем необходимые и необязательные файлы cookie для улучшения работы нашего веб-сайта. Пожалуйста, ознакомьтесь с нашей Политикой в ​​отношении файлов cookie для получения информации о том, как мы используем файлы cookie и как управлять вашими настройками файлов cookie или изменять их. Принять

Калькулятор дробей


Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми числами, десятичными знаками и смешанные числа. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.

Правила выражений с дробями:

Дроби — для деления числителя на знаменатель используйте косую черту, т. е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.

Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .

Математические символы




Символ	Название символа	Символ Значение	Пример
+	Знак плюс	Сложение	1/2 + 1/3
—	Знак минус	Вычитание	2 8/390 1 91825 0923
*	звездочка	умножение	2/3 * 3/4 ​​
×	знак умножения	умножение	2/3 × 9099 5/6	3 1	:	знак деления	деление 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 ​​ • квадратный корень дроби: sqrt(1/16) • сокращение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций . Наиболее распространенные мнемоники для запоминания этого порядка операций: PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание. BEDMAS — Скобки, Экспоненты, Деление, Умножение, Сложение, Вычитание BODMAS — Скобки, Порядок, Деление, Умножение, Сложение, Вычитание. GEMDAS — символы группировки — скобки (){}, показатели степени, умножение, деление, сложение, вычитание. MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS. Будь осторожен; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо. В дробях Муравей за первый час поднимается на 2/5 шеста, а в следующий час – на 1/4 шеста. Какую часть шеста преодолевает муравей за два часа? Из 550 000,00 Из 550 000,00 было использовано 325 000,00. Какая часть от общей суммы была использована? Наименьшие члены 2 Мы можем записать выражение 4/12 в его наименьшем члене как 1/3. Чему равно 3/15 в наименьшем члене? Петрушка Бабушка Милка посадила 12 рядов овощей. 1/6 рядов — морковь. Остальное петрушка. Сколько рядов засажено петрушкой? Четверть Четверть числа 72: В столовой В классной комнате Джейкоба 18 учеников. Шесть учеников приносят обед в школу. Остальные обедают в столовой. Проще говоря, какая часть студентов обедает в столовой? Младенцы Двое взрослых, двое детей и четверо младенцев находятся в автобусе. Какую часть населения составляют младенцы? Корзина с фруктами Если в корзине семь яблок и пять апельсинов, какая часть апельсинов в корзине с фруктами? Кто-то Кто-то съел 1/10 торта, осталось только 9/10. Если вы съедите 2/3 оставшегося торта, сколько всего торта вы съедите? Знаменатель 2 Знаменатель дроби равен пяти, а числитель равен 7. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт