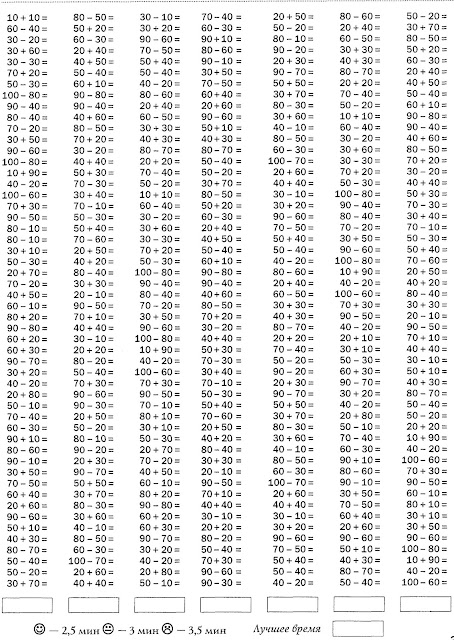
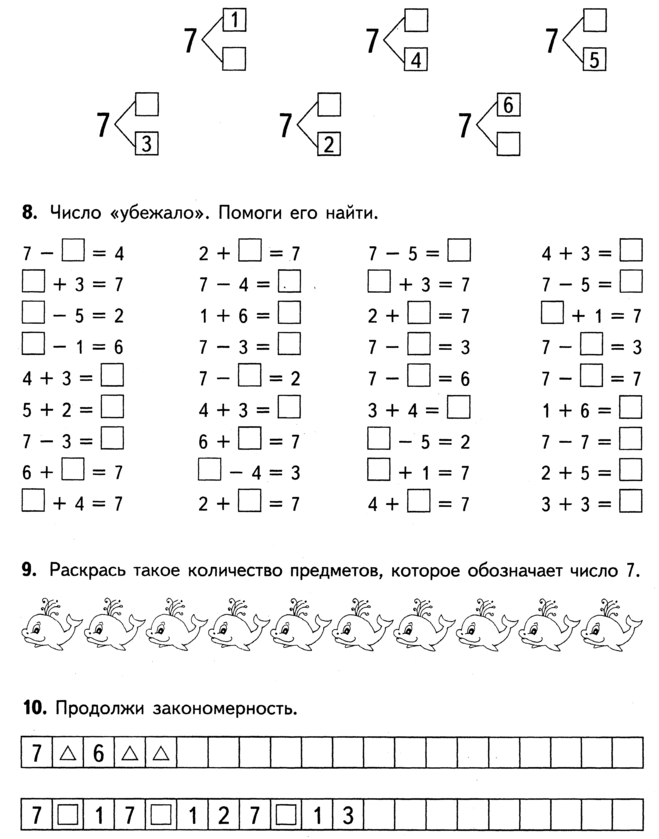
Тренажер счета в пределах 20
60,00 ₽
Примеры на сложение и вычитание в пределах 20 с автопроверкой для решения на компьютере (в Excel без печати).
Артикул: i-13526 Категория: Для учебы Метки: 1 класс, Сложение и вычитание простое
- Описание
- Детали
- Отзывы (0)
Описание
Тренажер счета в пределах 20 – это программа, которая формирует примеры на сложение и вычитание в пределах 20, чтобы решать их на компьютере (не распечатывая).
Программа будет полезна как дошкольникам, так и ученикам 1 класса. Практика счета поможет развить внимательность и закрепить навыки устного счета у детей. Для этого достаточно заниматься 10-15 минут в день.
Программа написана в Excel с помощью макросов.
Можно выбрать уровень сложности:
- примеры только на сложение, только на вычитание или на оба действия;
- примеры в пределах от 10 до 20 (на каждое число внутри диапазона).
При нажатии кнопки «Начать» запускается счетчик, который подсчитывает количество решенных примеров, в том числе правильных и решенных с ошибкой. При нажатии кнопки «Начать» счетчик обнуляется.
Для удобства внизу карточки есть кнопки с цифрами, которые нужно нажимать при выборе ответа.
Тренажер примеров по математике удобен, так как не нужно заранее покупать задачники и пособия по математике с примерами. Можно скачать файл и решать примеры в любое время независимо от подключения к интернету.
Если Вы хотите посмотреть принцип работы программы, можете скачать программу «Тренажер счета в пределах 10» бесплатно.
Карточки для печати в формате А4 можно получить в программе «Сложение и вычитание в пределах 20«.
Другие программы, которые помогут закрепить навыки счета в пределах 20:
- Состав числа от 11 до 20
- Цепочки примеров в пределах 20 (сложение и вычитание)
- Умная раскраска «Примеры до 20»
- Числовые пирамиды в пределах 10,20…100
- Головоломка «Судоку мини»
- Головоломка «Квадрат слагаемых»
- Сравнение чисел в пределах 10,20,100
- Математический диктант 1 класс
- Задание на неделю 1класс
На сайте представлен каталог программ, в котором все программы распределены по группам. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.
Вам также будет интересно…
Головоломка «Математический лабиринт (сложение и вычитание)»
Оценка 5.00 из 5
100,00 ₽В корзинуТренажер «Состав числа от 11 до 20»
Оценка 4.
60,00 ₽В корзину 50 из 5
50 из 5Сложение и вычитание в пределах 20
Оценка 5.00 из 5
60,00 ₽В корзинуЦепочки примеров в пределах 20 (сложение и вычитание)
Оценка 5.00 из 5
60,00 ₽В корзинуМатематический кроссворд (сложение и вычитание)
90,00 ₽В корзинуУмная раскраска «Примеры до 20»
70,00 ₽В корзинуЗадание на неделю 1 класс
Оценка 5.00 из 5
110,00 ₽В корзинуСостав числа от 11 до 20
Оценка 5.00 из 5
60,00 ₽В корзинуГоловоломка «Судоку мини»
70,00 ₽В корзину
Математика — Начальные классы — Сообщество взаимопомощи учителей Педсовет.su
Егорова Елена 5.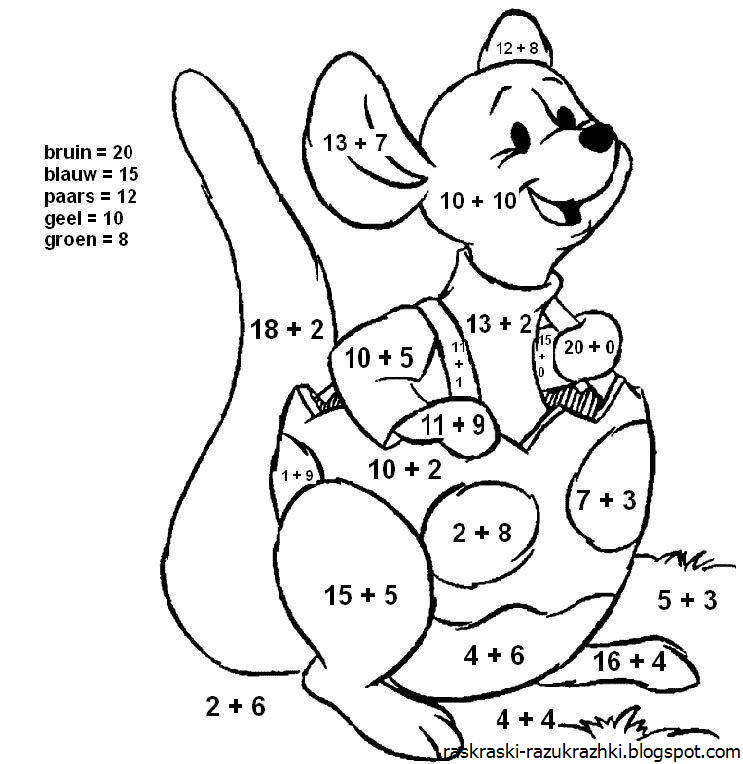 0
0Отзыв о товаре ША PRO Анализ техники чтения по классам
и четвертям
Хочу выразить большую благодарность от лица педагогов начальных классов гимназии «Пущино» программистам, создавшим эту замечательную программу! То, что раньше мы делали «врукопашную», теперь можно оформить в таблицу и получить анализ по каждому ученику и отчёт по классу. Великолепно, восторг! Преимущества мы оценили сразу. С начала нового учебного года будем активно пользоваться. Поэтому никаких пожеланий у нас пока нет, одни благодарности. Очень простая и понятная инструкция, что немаловажно! Благодарю Вас и Ваших коллег за этот важный труд. Очень приятно, когда коллеги понимают, как можно «упростить» работу учителя.
учитель химии и биологии, СОШ с. Чапаевка, Новоорский район, Оренбургская область
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ
по ХИМИИ
Спасибо, аналитическая справка замечательная получается, ОГЭ химия и биология. Очень облегчило аналитическую работу, выявляются узкие места в подготовке к
экзамену. Нагрузка у меня, как и у всех учителей большая. Ваш шаблон экономит
время, своим коллегам я Ваш шаблон показала, они так же его приобрели. Спасибо.
Очень облегчило аналитическую работу, выявляются узкие места в подготовке к
экзамену. Нагрузка у меня, как и у всех учителей большая. Ваш шаблон экономит
время, своим коллегам я Ваш шаблон показала, они так же его приобрели. Спасибо.
Чазова Александра 5.0
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ по
МАТЕМАТИКЕ
Очень хороший шаблон, удобен в использовании, анализ пробного тестирования занял считанные минуты. Возникли проблемы с распечаткой отчёта, но надо ещё раз разобраться. Большое спасибо за качественный анализатор.
Лосеева Татьяна Борисовна 5.0
учитель начальных классов, МБОУ СОШ №1, г. Красновишерск, Пермский край
Отзыв о товаре Изготовление сертификата или свидетельства конкурса
Большое спасибо за оперативное изготовление сертификатов! Все очень красиво.
Мой ученик доволен, свой сертификат он вложил в портфолио. Обязательно продолжим с Вами сотрудничество!
Обязательно продолжим с Вами сотрудничество!
Язенина Ольга Анатольевна 4.0
учитель начальных классов, ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Отзыв о товаре Вебинар Как создать интересный урок:
инструменты и приемы
Я посмотрела вебинар! Осталась очень довольна полученной
информацией.
Арапханова Ашат 5.0
ША Табель посещаемости + Сводная для ДОУ ОКУД
Хотела бы поблагодарить Вас за такую помощь. Разобралась сразу же, всё очень
аккуратно и оперативно. Нет ни одного недостатка. Я не пожалела, что доверилась и
приобрела у вас этот табель.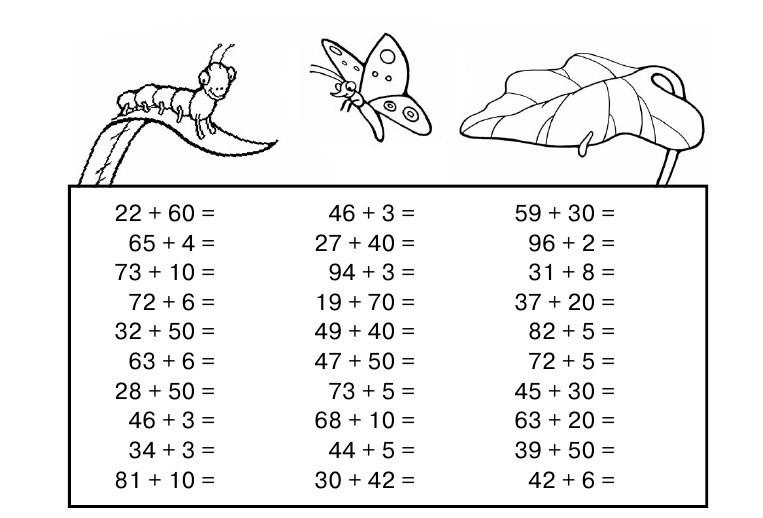 Благодаря Вам сэкономила время, сейчас же
составляю табель для работников. Удачи и успехов Вам в дальнейшем!
Благодаря Вам сэкономила время, сейчас же
составляю табель для работников. Удачи и успехов Вам в дальнейшем!
Дамбаа Айсуу 5.0
Отзыв о товаре ША Шаблон Excel Анализатор результатов ЕГЭ по
РУССКОМУ ЯЗЫКУ
Спасибо огромное, очень много экономит времени, т.к. анализ уже готовый, и особенно радует, что есть варианты с сочинением, без сочинения, только анализ сочинения! Превосходно!
20 Моделирование | R Programming for Data Science
20.1 Генерация случайных чисел
Посмотрите видео этого раздела
Моделирование — важная (и большая) тема как для статистики, так и для множества других областей, где необходимо ввести случайность. Иногда вам нужно реализовать статистическую процедуру, которая требует генерации или выборки случайных чисел (например, цепь Маркова Монте-Карло, бутстрап, случайные леса, бэггинг), а иногда вы хотите смоделировать систему, и для моделирования случайных входных данных можно использовать генераторы случайных чисел.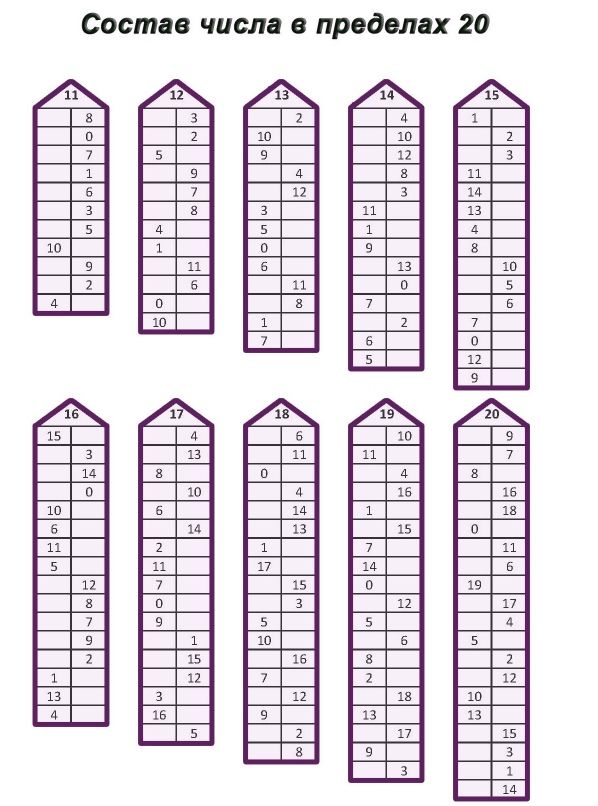
R поставляется с набором генераторов псевдослучайных чисел, которые позволяют моделировать известные распределения вероятностей, такие как нормальное, пуассоновское и биномиальное. Некоторые примеры функций для вероятностных распределений в R
-
rnorm: генерировать случайные нормальные переменные с заданным средним значением и стандартным отклонением -
dnorm: оценить нормальную плотность вероятности (с заданным средним/стандартным отклонением) в точке (или векторе точек) -
пнорм: оценить кумулятивную функцию распределения для нормального распределения -
rpois: генерировать случайные вариации Пуассона с заданной скоростью
Для каждого распределения вероятностей обычно доступны четыре функции, которые начинаются с букв «r», «d», «p» и «q». Функция «r» — это та функция, которая фактически моделирует случайные числа из этого распределения. Другие функции имеют префикс
-
dдля плотности . -
rдля генерации случайных чисел -
рдля накопительной раздачи -
qдля квантильной функции (обратное кумулятивное распределение)

Если вы заинтересованы только в моделировании случайных чисел, вам, скорее всего, понадобятся только функции «r», а не другие. Однако, если вы собираетесь моделировать произвольные распределения вероятностей, используя что-то вроде выборки отбраковки, вам понадобятся и другие функции.
Вероятно, наиболее распространенным распределением вероятностей, с которым можно работать, является нормальное распределение (также известное как гауссово). Для работы с нормальным распределением необходимо использовать следующие четыре функции:
dnorm(x, mean = 0, sd = 1, log = FALSE) pnorm(q, среднее = 0, sd = 1, нижний.хвост = ИСТИНА, log.p = ЛОЖЬ) qnorm(p, среднее = 0, sd = 1, нижний.хвост = ИСТИНА, log.p = ЛОЖЬ) rnorm(n, mean = 0, sd = 1)
Здесь мы моделируем стандартные нормальные случайные числа со средним значением 0 и стандартным отклонением 1,
> ## Имитация стандартных нормальных случайных чисел > х <- rнорм(10) > х [1] 0,01874617 -0,18425254 -1,37133055 -0,59916772 0,29454513 0,38979430 [7] -1,20807618 -0,36367602 -1,62667268 -0,25647839
Мы можем изменить параметры по умолчанию для моделирования чисел со средним значением 20 и стандартным отклонением 2.
> x <- rnorm(10, 20, 2) > х [1] 22,20356 21,51156 19,52353 21,97489 21,48278 20,17869 18,09011 19,60970 [9] 21,85104 20,96596 > резюме(х) Мин. 1 кв. Медиана Среднее 3-е кв. Максимум. 18.0919,75 21,22 20,74 21,77 22,20
Если вы хотите узнать, какова вероятность того, что случайная переменная Normal будет меньше, скажем, 2, вы можете использовать функцию pnorm() для выполнения этого вычисления.
> пнорм(2) [1] 0,9772499
Никогда не знаешь, когда этот расчет пригодится.
20.2 Установка начального числа случайных чисел
При моделировании любых случайных чисел необходимо установить начальное число случайных чисел . Установка начального числа случайного числа с set.seed() обеспечивает воспроизводимость последовательности случайных чисел.
Например, я могу сгенерировать 5 обычных случайных чисел с помощью rnorm() .
> сет.сид (1) > норм(5) [1] -0,6264538 0,1836433 -0,8356286 1,5952808 0,3295078
Обратите внимание, что если я снова вызову rnorm() , я, конечно, получу другой набор из 5 случайных чисел.
> rнорма(5) [1] -0,8204684 0,4874291 0,7383247 0,5757814 -0,3053884
Если я хочу воспроизвести исходный набор случайных чисел, я могу просто сбросить начальное число с помощью set.seed() .
> сет.сид (1) > rnorm(5) ## То же, что и раньше [1] -0,6264538 0,1836433 -0,8356286 1,5952808 0,3295078
В общем, всегда следует устанавливать случайное начальное число при проведении моделирования! В противном случае вы не сможете восстановить точные числа, полученные в результате анализа.
Можно генерировать случайные числа из других вероятностных распределений, таких как Пуассон. Распределение Пуассона обычно используется для моделирования данных, которые поступают в виде подсчетов.
> rpois(10, 1) ## Считает со средним значением 1 [1] 0 0 1 1 2 1 1 4 1 2 > rpois(10, 2) ## Считает со средним значением 2 [1] 4 1 2 0 1 1 0 1 4 1 > rpois(10, 20) ## Считает со средним значением 20 [1] 19 19 24 23 22 24 23 20 11 22
20.
 3 Моделирование линейной модели
3 Моделирование линейной моделиПосмотрите видео этого раздела
Моделирование случайных чисел полезно, но иногда мы хотим смоделировать значения, полученные из конкретной модели . Для этого нам нужно указать модель, а затем смоделировать ее с помощью функций, описанных выше. 92)\), \(\бета_0=0,5\) и \(\бета_1=2\). Переменная x может представлять собой важный предиктор исхода y . Вот как мы могли бы сделать это в R.
> ## Всегда устанавливайте начальное число! > сет.сид(20) > > ## Моделирование переменной-предиктора > х <- rнорм(100) > > ## Имитация термина ошибки > e <- rnorm(100, 0, 2) > > ## Вычислить результат с помощью модели > у <- 0,5 + 2 * х + е > резюме (у) Мин. 1 кв. Медиана Среднее 3-е кв. Максимум. -6,4084 -1,5402 0,67890,6893 2,9303 6,5052
Мы можем построить результаты моделирования модели.
> plot(x, y)
Что, если мы хотим смоделировать предикторную переменную x , которая является двоичной, а не имеет нормальное распределение.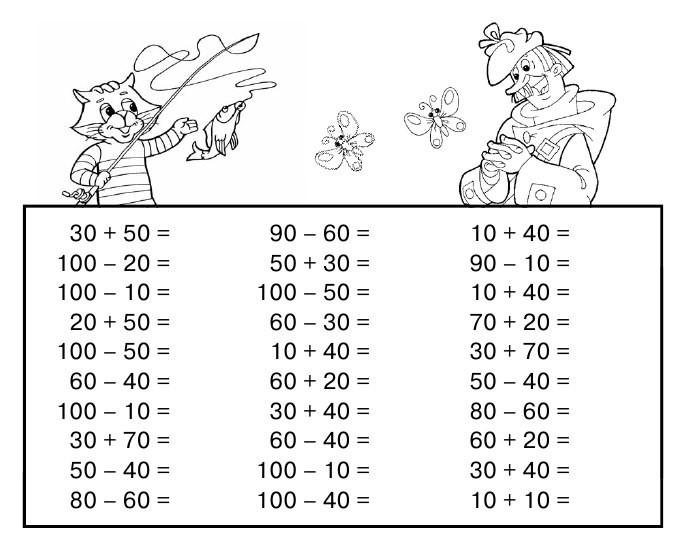 Мы можем использовать функцию
Мы можем использовать функцию rbinom() для моделирования двоичных случайных величин.
> сет.сид (10) > x <- rbinom(100, 1, 0,5) > str(x) ## 'x' теперь равно 0 и 1 int [1:100] 1 0 0 1 0 0 0 0 1 0 ...
Затем мы можем продолжить работу с остальной частью модели, как и раньше.
> е <- rнорма(100, 0, 2) > у <- 0,5 + 2 * х + е > plot(x, y)
Мы также можем смоделировать обобщенную линейную модель , где ошибки больше не из нормального распределения, а из какого-то другого распределения. Например, предположим, что мы хотим смоделировать лог-линейную модель Пуассона, где
\[ Y \sim Пуассон(\mu) \]
\[ \log \mu = \beta_0 + \beta_1 x \]
и \(\beta_0=0,5\) и \(\beta_1=0,3\). Нам нужно использовать rpois() функция для этого
> set.seed(1) > > ## Имитация переменной-предиктора, как и раньше > x <- rnorm(100)
Теперь нам нужно вычислить среднее логарифмическое значение модели, а затем возвести его в степень, чтобы среднее значение передавалось в rpois() .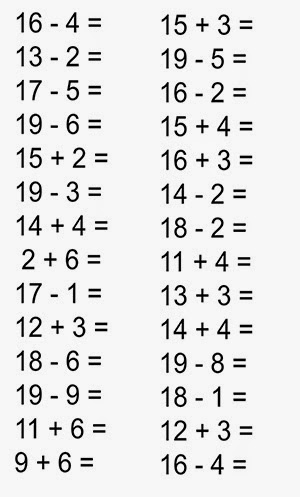
> лог.мю <- 0,5 + 0,3 * х > y <- rpois(100, exp(log.mu)) > резюме (у) Мин. 1 кв. Медиана Среднее 3-е кв. Максимум. 0,00 1,00 1,00 1,55 2,00 6,00 > график (х, у)
Подобные модели можно строить произвольной сложности, моделируя больше предикторов или выполняя преобразования этих предикторов (например, возведение в квадрат, логарифмическое преобразование и т. д.).
20.4 Случайная выборка
Посмотрите видео этого раздела
Функция sample() случайным образом выбирает из заданного набора (скалярных) объектов, что позволяет вам выбирать из произвольного распределения чисел.
> сет.сид (1) > образец (1:10, 4) [1] 9 4 7 1 > образец (1:10, 4) [1] 2 7 3 6 > > ## Не обязательно числа > образец (буквы, 5) [1] «р» «с» «а» «у» «ш» > > ## Сделать случайную перестановку > образец (1:10) [1] 10 6 92 1 5 8 4 3 7 > образец (1:10) [1] 5 10 2 8 6 1 4 3 9 7 > > ## Образец с заменой > образец (1:10, заменить = ИСТИНА) [1] 3 6 10 10 6 4 4 10 9 7
Для выборки более сложных вещей, таких как строки из фрейма данных или списка, вы можете выбирать индексы в объект, а не элементы самого объекта.
Вот как можно выбирать строки из фрейма данных.
> библиотека (наборы данных) > данные (качество воздуха) > голова (качество воздуха) Ozone Solar.R Температура ветра Месяц День 1 41 190 7,4 67 5 1 2 36 118 8,0 72 5 2 3 12 149 12,6 74 5 3 4 18 313 11,5 62 5 4 5 НП НП 14,3 56 5 5 6 28 NA 14.9 66 5 6
Теперь нам просто нужно создать индексный вектор, индексирующий строки фрейма данных, и сделать выборку непосредственно из этого индексного вектора.
> набор семян(20)
>
> ## Создать индексный вектор
> idx <- seq_len(nrow(качество воздуха))
>
> ## Выборка из индексного вектора
> образец <- образец (idx, 6)
> качество воздуха [samp, ]
Ozone Solar.R Температура ветра Месяц День
107 н/д 64 11,5 798 15
120 76 203 9,7 97 8 28
130 20 252 10,9 80 9 7
98 66 НП 4,6 87 8 6
29 45 252 14,9 81 5 29
45 NA 332 13,8 80 6 14 Таким способом можно семплировать и другие более сложные объекты, если существует способ индексации подэлементов объекта.
20.
 5 Резюме
5 Резюме- Создание выборок из конкретных вероятностных распределений может быть выполнено с помощью функций «r»
- Встроены стандартные распределения: нормальное, пуассоновское, биномиальное, экспоненциальное, гамма и т. д.
- Функцию
sample()можно использовать для получения случайных выборок из произвольных векторов - Установка начального числа генератора случайных чисел с помощью
set.seed()имеет решающее значение для воспроизводимости
python — это хорошая или плохая «симуляция» для Монти Холла? Как так?
спросил
Изменено 1 год, 1 месяц назад
Просмотрено 13 тысяч раз
Пытаясь объяснить другу задачу Монти Холла вчера во время урока, мы написали ее на Python, чтобы доказать, что если вы всегда меняете местами, вы выиграете 2/3 раза. Мы придумали это:
Мы придумали это:
import random as r
#iterations = int(raw_input("Сколько итераций? >> "))
итераций = 100000
двери = ["коза", "коза", "машина"]
выигрыши = 0,0
потери = 0,0
для i в диапазоне (итерации):
n = r.randrange (0,3)
выбор = двери[n]
если п == 0:
#print "Вы выбрали дверь 1."
#print "Монти открывает дверь 2. За этой дверью сидит коза."
#print "Вы переключились на дверь 3."
побед += 1
#print "Вы выиграли " + Doors[2] + "\n"
Элиф п == 1:
#print "Вы выбрали дверь 2."
#print "Монти открывает дверь 1. За этой дверью сидит коза."
#print "Вы переключились на дверь 3."
побед += 1
#print "Вы выиграли " + Doors[2] + "\n"
Элиф п == 2:
#print "Вы выбрали дверь 3."
#print "Монти открывает дверь 2. За этой дверью сидит коза."
#print "Вы переключились на дверь 1."
потери += 1
#print "Вы выиграли " + Doors[0] + "\n"
еще:
печатать "Ты облажался"
процент = (выигрыши/итерации) * 100
print "Выигрыши: " + str(выигрыши)
print "Потери: " + str(потери)
print "Вы выиграли " + str(процент) + "% случаев"
Мой друг подумал, что это хороший способ (и хорошая имитация), но у меня есть сомнения и опасения.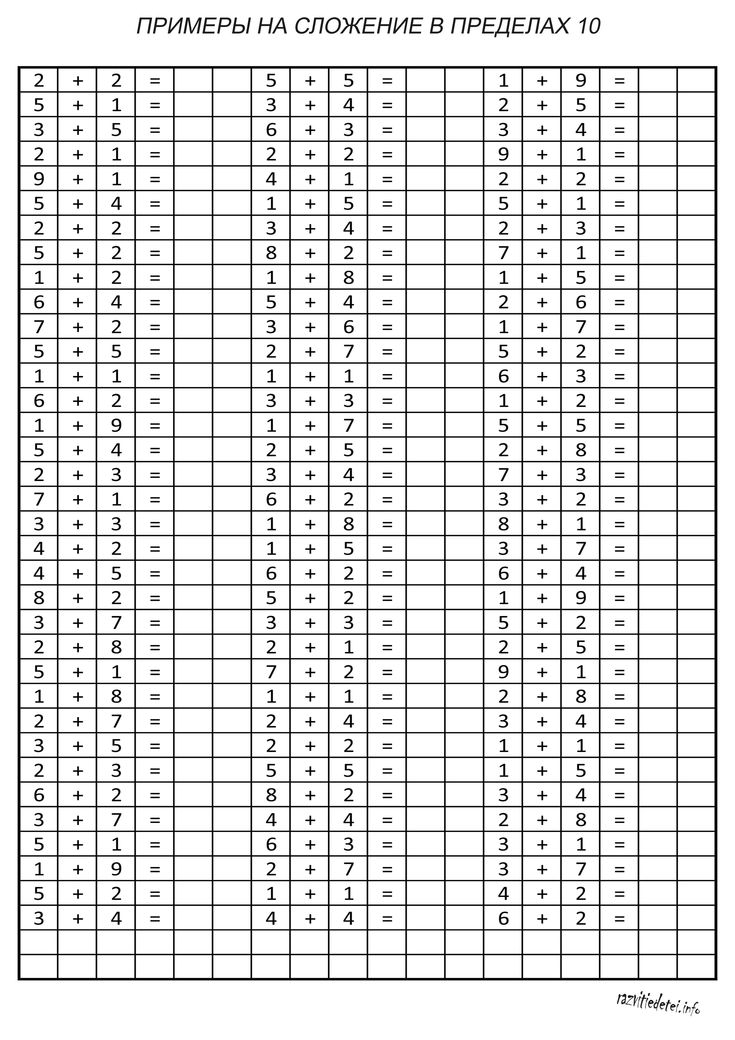 Действительно ли это достаточно случайно?
Действительно ли это достаточно случайно?
Проблема в том, что все варианты жестко закодированы.
Это хорошая или плохая «симуляция» задачи Монти Холла? Как так?
Можете ли вы придумать лучшую версию?
- питон
- не зависящий от языка
- вероятность
3
Ваше решение в порядке, но если вы хотите более строгого моделирования задачи в том виде, в каком она поставлена (и более качественного Python;-), попробуйте:
import random
итераций = 100000
двери = ["коза"] * 2 + ["машина"]
change_wins = 0
change_loses = 0
для i в xrange (итерации):
random.shuffle(двери)
# вы выбираете дверь n:
n = случайный.randrange(3)
# Монти выбирает дверь k, k!=n и Doors[k]!="car"
последовательность = диапазон (3)
random.shuffle(последовательность)
для k последовательно:
если k == n или door[k] == "car":
Продолжить
# теперь, если вы измените, вы потеряете iff door[n]=="car"
если двери [n] == "автомобиль":
change_loses += 1
еще:
change_wins += 1
print "Изменение имеет %s выигрышей и %s проигрышей" % (change_wins, change_loses)
perc = (100,0 * выигрыши_изменения) / (выигрыш_изменения + проигрыши_изменения)
print "IOW, меняя, вы выигрываете в %. 1f%% случаев" % perc
1f%% случаев" % perc
типичный вывод:
Изменение имеет 66721 выигрыш и 33279 проигрышей IOW, меняя, вы выигрываете в 66,7% случаев
8
Вы упомянули, что все варианты выбора жестко запрограммированы. Но если вы присмотритесь, то заметите, что то, что вы считаете «выбором», на самом деле вовсе не является выбором. Решение Монти не теряет общности, поскольку он всегда выбирает дверь, за которой стоит коза. Ваш обмен всегда определяется тем, что выбирает Монти, а поскольку «выбор» Монти на самом деле не был выбором, то и ваш выбор тоже. Ваша симуляция дает правильные результаты...
1
Мне нравится что-то подобное.
#!/usr/бин/питон
импортировать случайный
АВТОМОБИЛЬ = 1
КОЗА = 0
def one_trial(двери, переключатель=False):
"""Одно испытание конкурса Монти Холла."""
random.shuffle(двери)
first_choice = двери. pop()
если переключатель==False:
вернуть первый_выбор
двери elif.__contains__(CAR):
вернуть АВТОМОБИЛЬ
еще:
вернуть козла
def n_trials(переключатель=ложь, n=10):
"""Сыграйте в игру N раз и верните некоторую статистику."""
победы = 0
для n в xrange(n):
двери = [АВТОМОБИЛЬ, КОЗА, КОЗА]
wins += one_trial(двери, переключатель=переключатель)
напечатать "выиграно:", побед, "проиграно:", (n-выигрышей), "среднее:", (с плавающей запятой (победы) / с плавающей запятой (n))
если __name__=="__main__":
импорт системы
n_trials(переключатель=eval(sys.argv[1]), n=int(sys.argv[2]))
$ ./montyhall.py Правда 10000
выиграл: 6744 проиграл: 3255 в среднем: 0,674467446745
pop()
если переключатель==False:
вернуть первый_выбор
двери elif.__contains__(CAR):
вернуть АВТОМОБИЛЬ
еще:
вернуть козла
def n_trials(переключатель=ложь, n=10):
"""Сыграйте в игру N раз и верните некоторую статистику."""
победы = 0
для n в xrange(n):
двери = [АВТОМОБИЛЬ, КОЗА, КОЗА]
wins += one_trial(двери, переключатель=переключатель)
напечатать "выиграно:", побед, "проиграно:", (n-выигрышей), "среднее:", (с плавающей запятой (победы) / с плавающей запятой (n))
если __name__=="__main__":
импорт системы
n_trials(переключатель=eval(sys.argv[1]), n=int(sys.argv[2]))
$ ./montyhall.py Правда 10000
выиграл: 6744 проиграл: 3255 в среднем: 0,674467446745
Вот моя версия...
случайный импорт
победы = 0
для n в диапазоне (1000):
двери = [1, 2, 3]
carDoor = random.choice(двери)
playerDoor = random.choice(двери)
hostDoor = random.choice(list(set(doors) - set([carDoor, playerDoor])))
# Чтобы придерживаться, просто закомментируйте следующую строку. (playerDoor, ) = set(doors) - set([playerDoor, hostDoor]) # Игрок меняет двери местами.
если playerDoor == carDoor:
побед += 1
print str(round(wins / float(n) * 100, 2)) + '%'
(playerDoor, ) = set(doors) - set([playerDoor, hostDoor]) # Игрок меняет двери местами.
если playerDoor == carDoor:
побед += 1
print str(round(wins / float(n) * 100, 2)) + '%'
Вот интерактивная версия:
из случайного импорта в случайном порядке, выбор
машины,козы,итеры= 0, 0, 100
для i в диапазоне (итеры):
двери = ['коза А', 'коза Б', 'автомобиль']
перетасовать (двери)
moderator_door = 'автомобиль'
# Ход 1:
selected_door = выбор(двери)
распечатать выбранную_дверь
двери.удалить(выбранная_дверь)
print 'Вы выбрали дверь с неизвестным объектом'
#2 ход:
в то время как moderator_door == 'автомобиль':
moderator_door = выбор(двери)
двери.удалить(moderator_door)
print 'Модератор открыл дверь с помощью ', moderator_door
#Поворот 3:
solution=raw_input('Хотите поменять дверь? [yn]')
если решение=='y':
приз = двери[0]
print 'У вас есть дверь с', приз
Элиф решение == 'n':
приз = выбранная_дверь
print 'У вас есть дверь с', приз
еще:
приз = 'ОШИБКА'
итер += 1
напечатать 'ОШИБКА: неизвестная команда'
если приз == 'автомобиль':
автомобили += 1
Элиф приз! = 'ОШИБКА':
козы += 1
напечатать '==============================='
распечатать 'РЕЗУЛЬТАТЫ'
напечатать '==============================='
печать 'Козы:', козы
print 'Автомобили :', автомобили
Мое решение с пониманием списка для имитации проблемы
из случайного импорта randint
N = 1000
деф имитировать (N):
car_gate=[randint(1,3) для x в диапазоне(N)]
gate_sel=[randint(1,3) для x в диапазоне(N)]
score = sum([True, если car_gate[i] == gate_sel[i] или ([posible_gate для posible_gate в [1,2,3] if posible_gate != gate_sel[i]][randint(0,1)] == car_gate[i]) иначе False для i в диапазоне (N)])
return 'вы выигрываете %s раз, когда меняете свой выбор. ' % (с плавающей запятой (оценка) / с плавающей запятой (N))
' % (с плавающей запятой (оценка) / с плавающей запятой (N))
print simulator(N)
Образец не мой
# -*- Кодировка: utf-8 -*-
#!/usr/bin/python -Ou
# Автор: kocmuk.ru, 2008 г.
импортировать случайный
num = 10000 # количество игр, которые нужно сыграть
win = 0 # инициализируем количество побед, если не изменим наш первый выбор
for i in range(1, num): # играть в игры "num"
if random.randint(1,3) == random.randint(1,3): # если выиграть при первом выборе
win +=1 # увеличение количества побед
print "Я не меняю первый выбор и выигрываю:", win, " games"
print "Я меняю первоначальный выбор и выигрываю:", num-win, " games" # проигрыш "not_change_first_choice является выигрышем при изменении
Я обнаружил, что это самый интуитивный способ решения проблемы.
случайный импорт
# game_show вернет True/False, если участник выиграл/проиграл машину:
def game_show (knows_bayes):
двери = [i для i в диапазоне (3)]
# Пусть машина будет за этой дверью
car = random. choice(двери)
# Участник выбирает эту дверь..
выбор = random.choice(двери)
# ..поэтому хост открывает другую (случайную) дверь, за которой нет машины
open_door = random.choice([i для i в дверях, если я не в [автомобиле, выбор]])
# Если участник known_bayes, то теперь она поменяет двери
если know_bayes:
choice = [i для i в дверях, если я не в [choice, open_door]][0]
# Выиграл ли участник автомобиль?
если выбор == автомобиль:
вернуть Истина
еще:
вернуть ложь
# Давайте запустим game_show() для двух участников. Один знает_байес, а другой нет.
победы = [0, 0]
пробеги = 100000
для x в диапазоне (0, работает):
если game_show(Истина):
победы[0] += 1
если game_show(False):
победы[1] += 1
print "Если участник знает_bayes, он выигрывает в %d %% случаев." % (с плавающей запятой (выигрыши [0])/пробеги * 100)
print "Если участник НЕ знает_байес, он выигрывает в %d %% случаев." % (с плавающей запятой (победы [1])/пробеги * 100)
choice(двери)
# Участник выбирает эту дверь..
выбор = random.choice(двери)
# ..поэтому хост открывает другую (случайную) дверь, за которой нет машины
open_door = random.choice([i для i в дверях, если я не в [автомобиле, выбор]])
# Если участник known_bayes, то теперь она поменяет двери
если know_bayes:
choice = [i для i в дверях, если я не в [choice, open_door]][0]
# Выиграл ли участник автомобиль?
если выбор == автомобиль:
вернуть Истина
еще:
вернуть ложь
# Давайте запустим game_show() для двух участников. Один знает_байес, а другой нет.
победы = [0, 0]
пробеги = 100000
для x в диапазоне (0, работает):
если game_show(Истина):
победы[0] += 1
если game_show(False):
победы[1] += 1
print "Если участник знает_bayes, он выигрывает в %d %% случаев." % (с плавающей запятой (выигрыши [0])/пробеги * 100)
print "Если участник НЕ знает_байес, он выигрывает в %d %% случаев." % (с плавающей запятой (победы [1])/пробеги * 100)
Это выводит что-то вроде
Если участник know_bayes, он выигрывает в 66 % случаев.Если участник НЕ знает_байес, он выигрывает в 33 % случаев.
Прочитайте сегодня главу о знаменитой задаче Монти Холла. Это мое решение.
случайный импорт
защита one_round():
двери = [1,1,0] # 1==коза, 0=машина
random.shuffle(doors) # перетасовать двери
выбор = случайный.randint(0,2)
возвратные двери[выбор]
#Если выбран козел, это означает, что игрок проигрывает, если он/она не меняется.
#Этот метод возвращает, если игрок выигрывает или проигрывает, если он/она изменился. выигрыш = 1, проигрыш = 0
деф зал():
change_wins = 0
N = 10000
для индекса в диапазоне (0, N):
change_wins += one_round()
распечатать change_wins
зал()
Обновленное решение
Обновление, на этот раз с использованием модуля enum . Опять же, стремясь к краткости, используя наиболее выразительные возможности Python для рассматриваемой проблемы:
из enum import auto, Enum
из случайного импорта
Приз класса (перечисление):
КОЗА = авто ()
АВТОМОБИЛЬ = авто()
items = [Prize. GOAT, Приз.GOAT, Приз.CAR]
количество_испытаний = 100000
количество_выигрышей = 0
# Перетасовка призов за дверью. Игрок выбирает случайную дверь, а Монти выбирает
# первая из двух оставшихся дверей не является автомобилем. Затем игрок
# изменяет свой выбор на оставшуюся дверь, которая еще не была выбрана.
# Если это машина, увеличьте количество побед.
для испытания в диапазоне (num_trials):
перетасовать (предметы)
игрок = рандом (длина (предметы))
monty = next(i для i, p в enumerate(items), если i != игрок и p != Prize.CAR)
player = next(i for i in range(len(items)) if i не в (player, monty))
num_wins += items[player] is Prize.CAR
print(f'{num_wins}/{num_trials} = {num_wins / num_trials * 100:.2f}% побед')
GOAT, Приз.GOAT, Приз.CAR]
количество_испытаний = 100000
количество_выигрышей = 0
# Перетасовка призов за дверью. Игрок выбирает случайную дверь, а Монти выбирает
# первая из двух оставшихся дверей не является автомобилем. Затем игрок
# изменяет свой выбор на оставшуюся дверь, которая еще не была выбрана.
# Если это машина, увеличьте количество побед.
для испытания в диапазоне (num_trials):
перетасовать (предметы)
игрок = рандом (длина (предметы))
monty = next(i для i, p в enumerate(items), если i != игрок и p != Prize.CAR)
player = next(i for i in range(len(items)) if i не в (player, monty))
num_wins += items[player] is Prize.CAR
print(f'{num_wins}/{num_trials} = {num_wins / num_trials * 100:.2f}% побед')
Предыдущее решение
Еще одно «доказательство», на этот раз с Python 3. Обратите внимание на использование генераторов для выбора 1) какую дверь открывает Монти и 2) на какую дверь переключается игрок.
случайный импорт
items = ['коза', 'коза', 'машина']
количество_испытаний = 100000
количество_выигрышей = 0
для испытания в диапазоне (num_trials):
random. shuffle (предметы)
игрок = случайный.randrange(3)
monty = next(i для i, v в enumerate(items), если i != игрок и v != 'автомобиль')
player = next(x вместо x в диапазоне (3), если x не в (player, monty))
если items[player] == 'car':
число_выигрышей += 1
print('{}/{} = {}'.format(num_wins, num_trials, num_wins / num_trials))
shuffle (предметы)
игрок = случайный.randrange(3)
monty = next(i для i, v в enumerate(items), если i != игрок и v != 'автомобиль')
player = next(x вместо x в диапазоне (3), если x не в (player, monty))
если items[player] == 'car':
число_выигрышей += 1
print('{}/{} = {}'.format(num_wins, num_trials, num_wins / num_trials))
Монти никогда не открывает дверь машиной - в этом весь смысл шоу (он не твой друг и знает, что находится за каждой дверью)
3
Вот другой вариант, который мне кажется наиболее интуитивным. Надеюсь это поможет!
случайный импорт
класс МонтиХолл():
"""Игровой симулятор Монти Холла."""
защита __init__(сам):
self.doors = ['Дверь #1', 'Дверь #2', 'Дверь #3']
self.prize_door = случайный.выбор(self.doors)
self.contestant_choice = ""
self.monty_show = ""
self.contestant_switch = ""
self.contestant_final_choice = ""
само. результат = ""
def Contestant_Chooses (я):
self.contestant_choice = random.choice(self.doors)
защита Monty_Shows (я):
monty_choices = [дверь за дверью в self.doors, если дверь не в [self.contestant_choice, self.prize_door]]
self.monty_show = случайный.выбор(monty_choices)
def Contestant_Revises(я):
self.contestant_switch = random.choice([Истина, Ложь])
если self.contestant_switch == True:
self.contestant_final_choice = [дверь за дверью в self.doors, если дверь не в [self.contestant_choice, self.monty_show]][0]
еще:
self.contestant_final_choice = self.contestant_choice
Оценка защиты (самостоятельно):
если self.contestant_final_choice == self.prize_door:
self.outcome = "Победа"
еще:
self.outcome = "Проиграть"
деф _ShowState (я):
напечатать "-" * 50
print "Двери %s" % self.doors
print "Призовая дверь %s" % self.prize_door
print "Выбор участника %s" % self.
результат = ""
def Contestant_Chooses (я):
self.contestant_choice = random.choice(self.doors)
защита Monty_Shows (я):
monty_choices = [дверь за дверью в self.doors, если дверь не в [self.contestant_choice, self.prize_door]]
self.monty_show = случайный.выбор(monty_choices)
def Contestant_Revises(я):
self.contestant_switch = random.choice([Истина, Ложь])
если self.contestant_switch == True:
self.contestant_final_choice = [дверь за дверью в self.doors, если дверь не в [self.contestant_choice, self.monty_show]][0]
еще:
self.contestant_final_choice = self.contestant_choice
Оценка защиты (самостоятельно):
если self.contestant_final_choice == self.prize_door:
self.outcome = "Победа"
еще:
self.outcome = "Проиграть"
деф _ShowState (я):
напечатать "-" * 50
print "Двери %s" % self.doors
print "Призовая дверь %s" % self.prize_door
print "Выбор участника %s" % self. contestant_choice
print "Шоу Монти %s" % self.monty_show
print "Переключение участников %s" % self.contestant_switch
print "Окончательный выбор участника %s" % self.contestant_final_choice
напечатать "Результат %s" % self.outcome
напечатать "-" * 50
Switch_Wins = 0
NoSwitch_Wins = 0
Switch_Lose = 0
NoSwitch_Lose = 0
для x в диапазоне (100000):
игра = МонтиХолл()
game.Contestant_Chooses()
игра.Monty_Shows()
game.Contestant_Revises()
игра.Счет()
# Подсчитайте баллы
если game.contestant_switch и game.outcome == "Победа": Switch_Wins = Switch_Wins + 1
если нет (game.contestant_switch) и game.outcome == "Win": NoSwitch_Wins = NoSwitch_Wins + 1
если game.contestant_switch и game.outcome == "Проиграть": Switch_Lose = Switch_Lose + 1
если нет (game.contestant_switch) и game.outcome == "Проиграть": NoSwitch_Lose = NoSwitch_Lose + 1
напечатать Switch_Wins * 1.0 / (Switch_Wins + Switch_Lose)
вывести NoSwitch_Wins * 1.0 / (NoSwitch_Wins + NoSwitch_Lose)
contestant_choice
print "Шоу Монти %s" % self.monty_show
print "Переключение участников %s" % self.contestant_switch
print "Окончательный выбор участника %s" % self.contestant_final_choice
напечатать "Результат %s" % self.outcome
напечатать "-" * 50
Switch_Wins = 0
NoSwitch_Wins = 0
Switch_Lose = 0
NoSwitch_Lose = 0
для x в диапазоне (100000):
игра = МонтиХолл()
game.Contestant_Chooses()
игра.Monty_Shows()
game.Contestant_Revises()
игра.Счет()
# Подсчитайте баллы
если game.contestant_switch и game.outcome == "Победа": Switch_Wins = Switch_Wins + 1
если нет (game.contestant_switch) и game.outcome == "Win": NoSwitch_Wins = NoSwitch_Wins + 1
если game.contestant_switch и game.outcome == "Проиграть": Switch_Lose = Switch_Lose + 1
если нет (game.contestant_switch) и game.outcome == "Проиграть": NoSwitch_Lose = NoSwitch_Lose + 1
напечатать Switch_Wins * 1.0 / (Switch_Wins + Switch_Lose)
вывести NoSwitch_Wins * 1.0 / (NoSwitch_Wins + NoSwitch_Lose)
Вывод остается прежним: переключение увеличивает ваши шансы на победу: 0,665025416127 против 0,33554730611 из предыдущего запуска.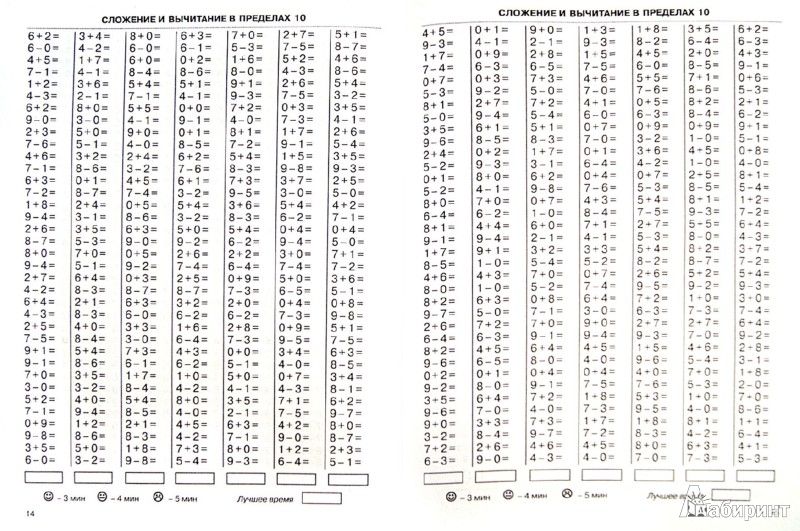
Вот один, который я сделал ранее:
import random
игра защиты():
"""
Установите три двери, одну случайным образом с автомобилем позади и две с
козы позади. Случайным образом выбираете дверь, затем ведущий забирает
одна из коз. Верните результат в зависимости от того, застряли ли вы с
ваш первоначальный выбор или переключился на другую оставшуюся закрытую дверь.
"""
# Ни стик, ни переключатель еще не выиграли, поэтому установите для них обоих значение False
палка = переключатель = ложь
# Установить все двери на козлы (нули)
двери = [0, 0, 0]
# Произвольно поменять одну из коз на машину (одну)
двери[random.randint(0, 2)] = 1
# Случайным образом выберите одну из трех дверей
выбор = двери[random.randint(0, 2)]
# Если бы нашим выбором была машина (единица)
если выбор == 1:
# Тогда побеждает палка
палка = правда
еще:
# В противном случае, потому что ведущий заберет другой
# козел, переключение всегда будет побеждать. переключатель = Истина
возврат (палка, переключатель)
переключатель = Истина
возврат (палка, переключатель)
У меня также был код для многократного запуска игры, и я сохранил его и образец вывода в этом репозитории.
Вот мое решение проблемы MontyHall, реализованное на python.
Это решение использует numpy для скорости, а также позволяет изменять количество дверей.
def montyhall (Испытания: «Количество испытаний», Двери: «Количество дверей», P: «Отладка вывода»):
N = Trials # количество проб
Размер двери = Двери+1
Ответ = (nprand.randint(1,DoorSize,N))
OtherDoor = (nprand.randint(1,DoorSize,N))
UserDoorChoice = (nprand.randint(1,DoorSize,N))
# это создаст вторую дверь, которая не является дверью, выбранной пользователем
C = np.where((UserDoorChoice==OtherDoor)>0)[0]
в то время как (len(C)>0):
OtherDoor[C] = nprand.randint(1,DoorSize,len(C))
C = np.where((UserDoorChoice==OtherDoor)>0)[0]
# поместите автомобиль в качестве другого варианта, если пользователь ошибся
D = np. where((UserDoorChoice!=Ответ)>0)[0]
ДругаяДверь[D] = Ответ[D]
'''
ЕслиПользователь Остается = 0
ЕслиПользовательские Изменения = 0
для n в диапазоне (0, N):
IfUserStays += 1 if Answer[n]==UserDoorChoice[n] else 0
IfUserChanges += 1 if Answer[n]==OtherDoor[n] else 0
'''
IfUserStays = float(len( np.where((Answer==UserDoorChoice)>0)[0]))
IfUserChanges = float(len( np.where((Answer==OtherDoor)>0)[0] ))
если П:
print("Ответ ="+str(Ответ))
print("Другое ="+str(ДругаяДверь))
print("UserDoorChoice="+str(UserDoorChoice))
print("ДругаяДверь ="+str(ДругаяДверь))
распечатать("результаты")
print("UserDoorChoice="+str(UserDoorChoice==Answer)+" n="+str(IfUserStays)+" r="+str(IfUserStays/N))
print("OtherDoor ="+str(OtherDoor==Answer)+" n="+str(IfUserChanges)+" r="+str(IfUserChanges/N))
возврат IfUserStays/N, IfUserChanges/N
where((UserDoorChoice!=Ответ)>0)[0]
ДругаяДверь[D] = Ответ[D]
'''
ЕслиПользователь Остается = 0
ЕслиПользовательские Изменения = 0
для n в диапазоне (0, N):
IfUserStays += 1 if Answer[n]==UserDoorChoice[n] else 0
IfUserChanges += 1 if Answer[n]==OtherDoor[n] else 0
'''
IfUserStays = float(len( np.where((Answer==UserDoorChoice)>0)[0]))
IfUserChanges = float(len( np.where((Answer==OtherDoor)>0)[0] ))
если П:
print("Ответ ="+str(Ответ))
print("Другое ="+str(ДругаяДверь))
print("UserDoorChoice="+str(UserDoorChoice))
print("ДругаяДверь ="+str(ДругаяДверь))
распечатать("результаты")
print("UserDoorChoice="+str(UserDoorChoice==Answer)+" n="+str(IfUserStays)+" r="+str(IfUserStays/N))
print("OtherDoor ="+str(OtherDoor==Answer)+" n="+str(IfUserChanges)+" r="+str(IfUserChanges/N))
возврат IfUserStays/N, IfUserChanges/N
Я только что обнаружил, что глобальный коэффициент выигрыша составляет 50%, а коэффициент проигрыша - 50%. .. Это соотношение выигрыша или проигрыша в зависимости от выбранного окончательного варианта.
.. Это соотношение выигрыша или проигрыша в зависимости от выбранного окончательного варианта.
- %Выигрышей (оставшихся): 16,692
- %Выигрышей (переключение): 33,525
- %Потери (оставшиеся) : 33,249
- %Потери (переключение) : 16,534
Вот мой код, который отличается от вашего + с комментариями, чтобы вы могли запускать его с небольшими итерациями:
import random as r
#iterations = int(raw_input("Сколько итераций? >> "))
итераций = 100000
двери = ["коза", "коза", "машина"]
wins_staying = 0
wins_switching = 0
loss_staying = 0
loss_switching = 0
для i в диапазоне (итерации):
# Перемешать варианты
r.shuffle (двери)
# print("Конфигурация дверей: ", двери)
# Хозяин всегда будет знать, где машина
car_option = двери.index("автомобиль")
# print("автомобиль в опции: ", car_option)
# Задаем параметры пользователю
доступные_опции = [0, 1, 2]
# Пользователь выбирает опцию
user_option = r.choice (доступные_опции)
# print("Опция пользователя: ", user_option)
# Убираем опцию
если (user_option != car_option ) :
# В случае, если дверь является козловой дверью для пользователя
# просто оставляем дверь машины и дверь пользователя
available_options = [user_option, car_option]
еще:
# В случае, если дверь является дверью автомобиля
# пытаемся оставить одну случайную дверь
available_options.
 50 из 5
50 из 5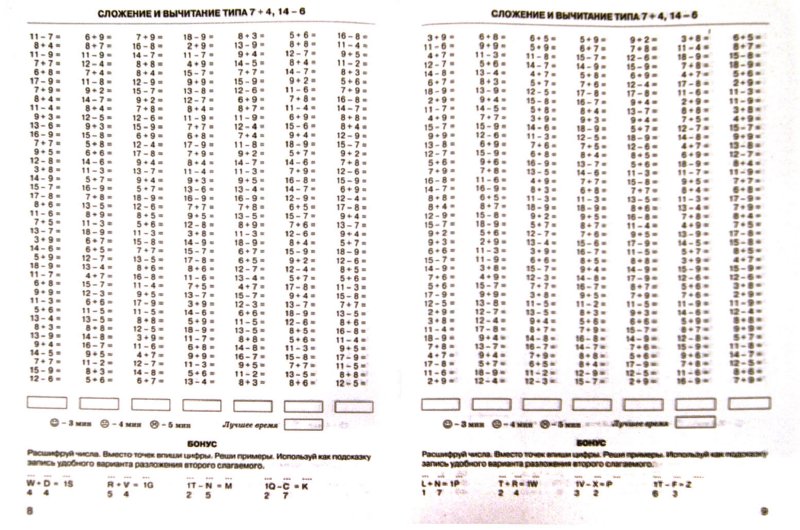 1f%% случаев" % perc
1f%% случаев" % perc
 pop()
если переключатель==False:
вернуть первый_выбор
двери elif.__contains__(CAR):
вернуть АВТОМОБИЛЬ
еще:
вернуть козла
def n_trials(переключатель=ложь, n=10):
"""Сыграйте в игру N раз и верните некоторую статистику."""
победы = 0
для n в xrange(n):
двери = [АВТОМОБИЛЬ, КОЗА, КОЗА]
wins += one_trial(двери, переключатель=переключатель)
напечатать "выиграно:", побед, "проиграно:", (n-выигрышей), "среднее:", (с плавающей запятой (победы) / с плавающей запятой (n))
если __name__=="__main__":
импорт системы
n_trials(переключатель=eval(sys.argv[1]), n=int(sys.argv[2]))
$ ./montyhall.py Правда 10000
выиграл: 6744 проиграл: 3255 в среднем: 0,674467446745
pop()
если переключатель==False:
вернуть первый_выбор
двери elif.__contains__(CAR):
вернуть АВТОМОБИЛЬ
еще:
вернуть козла
def n_trials(переключатель=ложь, n=10):
"""Сыграйте в игру N раз и верните некоторую статистику."""
победы = 0
для n в xrange(n):
двери = [АВТОМОБИЛЬ, КОЗА, КОЗА]
wins += one_trial(двери, переключатель=переключатель)
напечатать "выиграно:", побед, "проиграно:", (n-выигрышей), "среднее:", (с плавающей запятой (победы) / с плавающей запятой (n))
если __name__=="__main__":
импорт системы
n_trials(переключатель=eval(sys.argv[1]), n=int(sys.argv[2]))
$ ./montyhall.py Правда 10000
выиграл: 6744 проиграл: 3255 в среднем: 0,674467446745
 (playerDoor, ) = set(doors) - set([playerDoor, hostDoor]) # Игрок меняет двери местами.
если playerDoor == carDoor:
побед += 1
print str(round(wins / float(n) * 100, 2)) + '%'
(playerDoor, ) = set(doors) - set([playerDoor, hostDoor]) # Игрок меняет двери местами.
если playerDoor == carDoor:
побед += 1
print str(round(wins / float(n) * 100, 2)) + '%'
 ' % (с плавающей запятой (оценка) / с плавающей запятой (N))
' % (с плавающей запятой (оценка) / с плавающей запятой (N))
 choice(двери)
# Участник выбирает эту дверь..
выбор = random.choice(двери)
# ..поэтому хост открывает другую (случайную) дверь, за которой нет машины
open_door = random.choice([i для i в дверях, если я не в [автомобиле, выбор]])
# Если участник known_bayes, то теперь она поменяет двери
если know_bayes:
choice = [i для i в дверях, если я не в [choice, open_door]][0]
# Выиграл ли участник автомобиль?
если выбор == автомобиль:
вернуть Истина
еще:
вернуть ложь
# Давайте запустим game_show() для двух участников. Один знает_байес, а другой нет.
победы = [0, 0]
пробеги = 100000
для x в диапазоне (0, работает):
если game_show(Истина):
победы[0] += 1
если game_show(False):
победы[1] += 1
print "Если участник знает_bayes, он выигрывает в %d %% случаев." % (с плавающей запятой (выигрыши [0])/пробеги * 100)
print "Если участник НЕ знает_байес, он выигрывает в %d %% случаев." % (с плавающей запятой (победы [1])/пробеги * 100)
choice(двери)
# Участник выбирает эту дверь..
выбор = random.choice(двери)
# ..поэтому хост открывает другую (случайную) дверь, за которой нет машины
open_door = random.choice([i для i в дверях, если я не в [автомобиле, выбор]])
# Если участник known_bayes, то теперь она поменяет двери
если know_bayes:
choice = [i для i в дверях, если я не в [choice, open_door]][0]
# Выиграл ли участник автомобиль?
если выбор == автомобиль:
вернуть Истина
еще:
вернуть ложь
# Давайте запустим game_show() для двух участников. Один знает_байес, а другой нет.
победы = [0, 0]
пробеги = 100000
для x в диапазоне (0, работает):
если game_show(Истина):
победы[0] += 1
если game_show(False):
победы[1] += 1
print "Если участник знает_bayes, он выигрывает в %d %% случаев." % (с плавающей запятой (выигрыши [0])/пробеги * 100)
print "Если участник НЕ знает_байес, он выигрывает в %d %% случаев." % (с плавающей запятой (победы [1])/пробеги * 100)
 Если участник НЕ знает_байес, он выигрывает в 33 % случаев.
Если участник НЕ знает_байес, он выигрывает в 33 % случаев.
 GOAT, Приз.GOAT, Приз.CAR]
количество_испытаний = 100000
количество_выигрышей = 0
# Перетасовка призов за дверью. Игрок выбирает случайную дверь, а Монти выбирает
# первая из двух оставшихся дверей не является автомобилем. Затем игрок
# изменяет свой выбор на оставшуюся дверь, которая еще не была выбрана.
# Если это машина, увеличьте количество побед.
для испытания в диапазоне (num_trials):
перетасовать (предметы)
игрок = рандом (длина (предметы))
monty = next(i для i, p в enumerate(items), если i != игрок и p != Prize.CAR)
player = next(i for i in range(len(items)) if i не в (player, monty))
num_wins += items[player] is Prize.CAR
print(f'{num_wins}/{num_trials} = {num_wins / num_trials * 100:.2f}% побед')
GOAT, Приз.GOAT, Приз.CAR]
количество_испытаний = 100000
количество_выигрышей = 0
# Перетасовка призов за дверью. Игрок выбирает случайную дверь, а Монти выбирает
# первая из двух оставшихся дверей не является автомобилем. Затем игрок
# изменяет свой выбор на оставшуюся дверь, которая еще не была выбрана.
# Если это машина, увеличьте количество побед.
для испытания в диапазоне (num_trials):
перетасовать (предметы)
игрок = рандом (длина (предметы))
monty = next(i для i, p в enumerate(items), если i != игрок и p != Prize.CAR)
player = next(i for i in range(len(items)) if i не в (player, monty))
num_wins += items[player] is Prize.CAR
print(f'{num_wins}/{num_trials} = {num_wins / num_trials * 100:.2f}% побед')
 shuffle (предметы)
игрок = случайный.randrange(3)
monty = next(i для i, v в enumerate(items), если i != игрок и v != 'автомобиль')
player = next(x вместо x в диапазоне (3), если x не в (player, monty))
если items[player] == 'car':
число_выигрышей += 1
print('{}/{} = {}'.format(num_wins, num_trials, num_wins / num_trials))
shuffle (предметы)
игрок = случайный.randrange(3)
monty = next(i для i, v в enumerate(items), если i != игрок и v != 'автомобиль')
player = next(x вместо x в диапазоне (3), если x не в (player, monty))
если items[player] == 'car':
число_выигрышей += 1
print('{}/{} = {}'.format(num_wins, num_trials, num_wins / num_trials))
 результат = ""
def Contestant_Chooses (я):
self.contestant_choice = random.choice(self.doors)
защита Monty_Shows (я):
monty_choices = [дверь за дверью в self.doors, если дверь не в [self.contestant_choice, self.prize_door]]
self.monty_show = случайный.выбор(monty_choices)
def Contestant_Revises(я):
self.contestant_switch = random.choice([Истина, Ложь])
если self.contestant_switch == True:
self.contestant_final_choice = [дверь за дверью в self.doors, если дверь не в [self.contestant_choice, self.monty_show]][0]
еще:
self.contestant_final_choice = self.contestant_choice
Оценка защиты (самостоятельно):
если self.contestant_final_choice == self.prize_door:
self.outcome = "Победа"
еще:
self.outcome = "Проиграть"
деф _ShowState (я):
напечатать "-" * 50
print "Двери %s" % self.doors
print "Призовая дверь %s" % self.prize_door
print "Выбор участника %s" % self.
результат = ""
def Contestant_Chooses (я):
self.contestant_choice = random.choice(self.doors)
защита Monty_Shows (я):
monty_choices = [дверь за дверью в self.doors, если дверь не в [self.contestant_choice, self.prize_door]]
self.monty_show = случайный.выбор(monty_choices)
def Contestant_Revises(я):
self.contestant_switch = random.choice([Истина, Ложь])
если self.contestant_switch == True:
self.contestant_final_choice = [дверь за дверью в self.doors, если дверь не в [self.contestant_choice, self.monty_show]][0]
еще:
self.contestant_final_choice = self.contestant_choice
Оценка защиты (самостоятельно):
если self.contestant_final_choice == self.prize_door:
self.outcome = "Победа"
еще:
self.outcome = "Проиграть"
деф _ShowState (я):
напечатать "-" * 50
print "Двери %s" % self.doors
print "Призовая дверь %s" % self.prize_door
print "Выбор участника %s" % self. contestant_choice
print "Шоу Монти %s" % self.monty_show
print "Переключение участников %s" % self.contestant_switch
print "Окончательный выбор участника %s" % self.contestant_final_choice
напечатать "Результат %s" % self.outcome
напечатать "-" * 50
Switch_Wins = 0
NoSwitch_Wins = 0
Switch_Lose = 0
NoSwitch_Lose = 0
для x в диапазоне (100000):
игра = МонтиХолл()
game.Contestant_Chooses()
игра.Monty_Shows()
game.Contestant_Revises()
игра.Счет()
# Подсчитайте баллы
если game.contestant_switch и game.outcome == "Победа": Switch_Wins = Switch_Wins + 1
если нет (game.contestant_switch) и game.outcome == "Win": NoSwitch_Wins = NoSwitch_Wins + 1
если game.contestant_switch и game.outcome == "Проиграть": Switch_Lose = Switch_Lose + 1
если нет (game.contestant_switch) и game.outcome == "Проиграть": NoSwitch_Lose = NoSwitch_Lose + 1
напечатать Switch_Wins * 1.0 / (Switch_Wins + Switch_Lose)
вывести NoSwitch_Wins * 1.0 / (NoSwitch_Wins + NoSwitch_Lose)
contestant_choice
print "Шоу Монти %s" % self.monty_show
print "Переключение участников %s" % self.contestant_switch
print "Окончательный выбор участника %s" % self.contestant_final_choice
напечатать "Результат %s" % self.outcome
напечатать "-" * 50
Switch_Wins = 0
NoSwitch_Wins = 0
Switch_Lose = 0
NoSwitch_Lose = 0
для x в диапазоне (100000):
игра = МонтиХолл()
game.Contestant_Chooses()
игра.Monty_Shows()
game.Contestant_Revises()
игра.Счет()
# Подсчитайте баллы
если game.contestant_switch и game.outcome == "Победа": Switch_Wins = Switch_Wins + 1
если нет (game.contestant_switch) и game.outcome == "Win": NoSwitch_Wins = NoSwitch_Wins + 1
если game.contestant_switch и game.outcome == "Проиграть": Switch_Lose = Switch_Lose + 1
если нет (game.contestant_switch) и game.outcome == "Проиграть": NoSwitch_Lose = NoSwitch_Lose + 1
напечатать Switch_Wins * 1.0 / (Switch_Wins + Switch_Lose)
вывести NoSwitch_Wins * 1.0 / (NoSwitch_Wins + NoSwitch_Lose)
 переключатель = Истина
возврат (палка, переключатель)
переключатель = Истина
возврат (палка, переключатель)
 where((UserDoorChoice!=Ответ)>0)[0]
ДругаяДверь[D] = Ответ[D]
'''
ЕслиПользователь Остается = 0
ЕслиПользовательские Изменения = 0
для n в диапазоне (0, N):
IfUserStays += 1 if Answer[n]==UserDoorChoice[n] else 0
IfUserChanges += 1 if Answer[n]==OtherDoor[n] else 0
'''
IfUserStays = float(len( np.where((Answer==UserDoorChoice)>0)[0]))
IfUserChanges = float(len( np.where((Answer==OtherDoor)>0)[0] ))
если П:
print("Ответ ="+str(Ответ))
print("Другое ="+str(ДругаяДверь))
print("UserDoorChoice="+str(UserDoorChoice))
print("ДругаяДверь ="+str(ДругаяДверь))
распечатать("результаты")
print("UserDoorChoice="+str(UserDoorChoice==Answer)+" n="+str(IfUserStays)+" r="+str(IfUserStays/N))
print("OtherDoor ="+str(OtherDoor==Answer)+" n="+str(IfUserChanges)+" r="+str(IfUserChanges/N))
возврат IfUserStays/N, IfUserChanges/N
where((UserDoorChoice!=Ответ)>0)[0]
ДругаяДверь[D] = Ответ[D]
'''
ЕслиПользователь Остается = 0
ЕслиПользовательские Изменения = 0
для n в диапазоне (0, N):
IfUserStays += 1 if Answer[n]==UserDoorChoice[n] else 0
IfUserChanges += 1 if Answer[n]==OtherDoor[n] else 0
'''
IfUserStays = float(len( np.where((Answer==UserDoorChoice)>0)[0]))
IfUserChanges = float(len( np.where((Answer==OtherDoor)>0)[0] ))
если П:
print("Ответ ="+str(Ответ))
print("Другое ="+str(ДругаяДверь))
print("UserDoorChoice="+str(UserDoorChoice))
print("ДругаяДверь ="+str(ДругаяДверь))
распечатать("результаты")
print("UserDoorChoice="+str(UserDoorChoice==Answer)+" n="+str(IfUserStays)+" r="+str(IfUserStays/N))
print("OtherDoor ="+str(OtherDoor==Answer)+" n="+str(IfUserChanges)+" r="+str(IfUserChanges/N))
возврат IfUserStays/N, IfUserChanges/N