|
Организационный (2 мин) |
Организует актуализацию требований к ученику со стороны учебной деятельности.
Придумано кем-то просто и мудро При встрече здороваться «Доброе утро!» слайд 1 — А теперь тихо сядут те, у кого день рождения четного числа месяца, а теперь те, у кого нечетного числа. — Докажите! Молодцы! |
Слушают учителя. Демонстрируют готовность к уроку, организуют рабочее место, настраиваются на плодотворную работу. |
К – планируют учебное сотрудничество с учителем и сверстниками. Л – понимают значение знаний для человека; проявляют интерес к изучаемому предмету, понимают его важность Р – контролируют свои действия в подготовке к уроку. |
Актуализация знаний (5 мин) |
Создаёт условия для возникновения у учеников внутренней потребности включения в учебную деятельность.
Проводит устный счёт. Математика нас ждет Начинаем устный счет! Слайд 2
-Найдите значение выражений и разгадайте зашифрованное слово. — Произведение чисел 9 и 5 равно 40 или 46? — Первый множитель 7 второй 9, произведение равно 53 или 64? — Частное чисел 32 и 8 равно 3 или 6? — Какое число больше 8 в 7 раз 55 или 58? — 7 на 7 — 47 или 48? — Какое число меньше 72 в 8 раз 7 или 8? — Произведение 3 в 8 равно 25 или 29? — Какой ряд чисел у вас получился? 45, 63, 4, 56, 49, 9, 24. — Расположите числа в порядке убывания. — Расшифруйте слово. ПИФАГОР В листах самооценки поставьте знак + или — |
Выполняют задания. Вступают в диалог с учителем.
Фронтальная |
Р – осознают, что уже известно и что предстоит усвоить. П – анализируют, делают выводы.
К – обмениваются мнениями, выражают свою точку зрения, при этом не создают конфликтных ситуаций. Л – проявляют интерес к предмету |
Постановка цели и задач урока. (3 мин) |
Устанавливает тематические рамки. Организует уточнение темы и цели. — Кто такой Пифагор? Слайд 3. — Что вы о нем знаете? Слайд 4 — Как по-другому можно назвать таблицу Пифагора? Какое наибольшее число записано в таблице? —Назовите тему урока. Слайд 5-6 Цель урока. — Дополните предложения и назовите задачи нашего урока |
Внимательно слушают, вступают в диалог, высказывают свое мнение. Формулируют и уточняют тему урока, ставят цель. Мотивируют свою деятельность.
Таблица умножения в пределах 100. Познакомиться с таблицей умножения. |
Р – осознают, что уже известно и что предстоит усвоить. П – анализируют, делают выводы. К – обмениваются мнениями, выражают свою точку зрения, при этом не создают конфликтных ситуаций. Л – проявляют интерес к предмету |
Самоопределение к деятельности. (10 мин) |
Нацеливает на перспективу. Концентрирует устойчивое внимание учащихся. Создает ситуацию успеха. Организует выявление места затруднения. Организует фиксирование во внешней речи причины затруднения. Организует открытие нового знания. Создает ситуацию применения знаний в новой ситуации (перенос на практику). Слайд 7 — Прочитайте хором девиз нашего урока. — Следуя нашему девизу, сегодня на уроке вы станете ЮНЫМИ УЧЕНЫМИ и проведете свое маленькое исследование и, возможно, даже сделаете открытие. — Ваша тетрадь на сегодня станет журналом наблюдений юного ученого, поэтому записи в ней нужно вести аккуратно. -Вот первая запись. Слайд 8 — Готовясь к уроку, я распечатала вам таблицу, но краска закончилась, некоторые строчки остались пустыми. Помогите восстановить таблицу.
— Вам нужно, работая в группе, продолжить ряд чисел, разгадав закономерность. — Проверим, верно, ли вы заполнили пропуски. Молодцы! — Кто догадался, как устроена эта таблица? — Что за числа в левом столбике и верхней строке — Что обозначают остальные числа? — Имея под рукой таблицу Пифагора, вы можете без труда найти произведение двух чисел. Вы хотите научиться пользоваться ей? -У вас на столах лежат листочки, закончите предложения и расставьте их в таком порядке, чтобы получился алгоритм нахождения произведения двух чисел. — Давайте проверим, что у вас получилось? — Сверьте наш алгоритм с информацией в учебнике на с. 25 — По данному алгоритму найдите произведение 7*4 Оцените свою работу в листах самооценки. — Какую игру напоминает принцип работы с табл.? — Каким цветом обозначено произведение одинаковых множителей? Как они располагаются?-Обратите внимание на числа слева и справа от диагонали, что вы можете сказать про них? -Какие еще секреты скрывает таблица? — 1 поставленную задачу мы с вами выполнили, а вторая задача — научиться пользоваться ей. — Что для этого нужно? Потренироваться. С. 26 №1 2х9 7х9 9х6 8х7 9х8 9х9 4х5 5х6 45:5 6х4 8х8 |
Читают девиз урока. Записывают в тетради число. Внимательно слушают, вступают в диалог, высказывают свое мнение.
3 февраля. Классная работа.
Работают в группе
№1
— В левом столбике записан 1 множитель, в верхнем ряду – 2 множитель, а на пересечении произведение этих чисел.
Чтобы найти произведение двух чисел, нужно…. 1. В левом столбце…… 2. В верхнем ряду…… 3. Находим……
Симметрично относительно диагонали, вправо и вниз ответы повторяются, во 2 строке, в 5 строке, в последней строке, в 9 столбце. |
П –осуществляют осознанное и произвольное построение речевого высказывания, подведение под понятие; используют математические термины, символы и знаки. К – умеют слушать друг друга, строить понятные для партнёра по коммуникации речевые высказывания. Л – осознают свои возможности в учении; |
Открытие нового способа (10 мин)
Первичное закрепление |
Способствует самостоятельному применению знаний на практике. Развивает мыслительную деятельность через анализ и синтез. — Почему данный пример вызвал затруднение? -Можно ли с помощью таблицы умножения найти частное чисел? — Какая учебная задача стоит перед нами? Слайд 11 — Проведем исследование? -На какое слово нужно обратить внимание? — Что вы знаете о частном? — А что такое деление? — Какое предположение можно сделать?
— Составьте алгоритм. -Сверим наши догадки с информацией учебника на с. 25 — Верно ли мы определили способ нахождения частного? Слайд 12. Объясните, как 45:5 — Мы решили поставленную задачу? Молодцы! — Закончим решение примеров с помощью таблицы Пифагора и составленного нами алгоритма. 56:8 49:7 64:8
Физкультминутка Вы, наверное, устали? Ну, тогда все дружно встали, Ножками потопали, Ручками похлопали, Покружились, повертелись И за парты все уселись. Глазки крепко закрываем, Дружно до пяти считаем, Открываем, поморгаем И работать продолжаем. |
Мы не знаем алгоритма нахождения частного
С помощью таблицы умножения найти частное чисел.
Осуществляют поиск решения учебной задачи, строят предположения, решают учебную задачу с помощью открытого способа. |
П –осуществляют поиск решения проблемы, используя собственную систему знаний. К – умеют слушать друг друга, строить понятные для партнёра по коммуникации речевые высказывания. Л – осознают свои возможности в учении; |
Включение нового знания в систему знаний (10 мин) |
Развивает самоконтроль. Создает ситуацию успеха. Выявляет место и причины затруднения.
— Как вы думаете, для чего нужна эта таблица? -Поможет ли нам таблица в решении задач? — Решим задачу на С. 26 № 3
Работа у доски Спрогнозируйте свой результат. Нарисуйте кружок на полях в тетради. Решите задачу 2 способами. Слайд 13 Поставьте себе !, +, ?, —
Слайд 14 Самостоятельная работа дифференцированная №5 (12 + 6) : 3=6 (8 + 32) : 4=10 (14 + 49) : 7= 9 (32 +16) : 8=6
Самопроверка и самооценка.
Работа в парах № 6 Взаимопроверка. Самооценка. |
Самостоятельно решают задачу с экрана и оформляют решение в тетрадях. Организуют взаимопроверку.
Проверяют задание, исправляют ошибки
Поясняют решение задачи, исправляют ошибки. |
П – применяют полученные знания при решении задач; осуществляют логические действия при выполнении заданий; ориентируются в своей системе знаний. Р – принимают и сохраняют учебные цели и задачи; умеют проговаривать последовательность действий на уроке; умеют планировать своё действие в соответствии с поставленной задачей; умеют вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок. К – владеют навыками конструктивного взаимодействия. Л – способны к самооценке на основе критерия успешности учебной деятельности. |
Подведение итогов урока.
|
Организует фиксирование нового содержания. Организует рефлексию. Организует самооценку учебной деятельности. — Какие знания мы сегодня закрепляли? — Что нового узнали? Какие открытия сделали? — Достигли ли мы цели урока? Все ли поставленные задачи выполнили? Вернемся к нашим задачам.
— Вернитесь к листам самооценки, посчитайте знаки и оцените свою работу на уроке. — Кому было понятно и легко? — У кого были трудности, но он с ними справился? — Кому нужна помощь? — Сегодня на уроке вы прекрасно работали, но больше всех проявили активность следующие учащиеся: Им присваивается звание Юных ученых. |
Отвечают на вопросы. Делают выводы и обобщения. Задают уточняющие вопросы. |
П – ориентируются в своей системе знаний.
Р – принимают и сохраняют учебные задачи. Л – проявляют интерес к предмету, способны к самооценке на основе критерия успешности учебной деятельности. |
Постановка домашнего задания. (2 мин) |
Проводит инструктаж по выполнению домашнего задания. С.26 № 2, 4 обязательно, №7 по выбору Благодарит ребят за работу. Урок сегодня был удачный, Не прошёл для вас он зря. Вы все очень постарались. Вам понравилось, друзья? — Огромное трудолюбие и ваша тяга к знаниям помогла нам сделать на уроке открытие. Эта удача приблизила ещё на один шаг каждого из вас к успеху.- Спасибо вам за активное участие. |
Выполняют задание. Оценивают свою деятельность на уроке. |
П – ориентируются в своей системе знаний. Р – принимают и сохраняют учебные задачи. Л – проявляют интерес к предмету; |
Урок 12. таблица умножения и деления с числом 4. таблица пифагора — Математика — 3 класс
Математика, 3 класс
Урок №12. Таблица умножения и деления с числом 4.
Таблица Пифагора
Перечень вопросов, рассматриваемых в теме:
— Какая закономерность в составлении таблицы умножения с числом 4?
— Что представляет собой таблица Пифагора?
Глоссарий по теме:
В таблице умножения с числом 4 произведение чисел увеличивается на 4.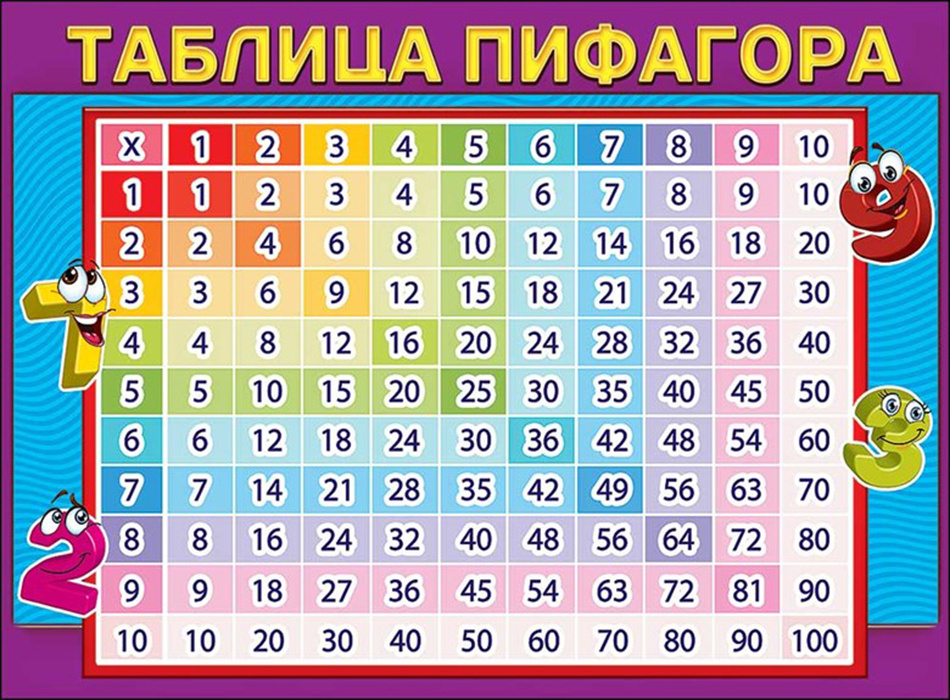
Значения таблицы умножения чисел 2, 3, 4 можно оформить в виде таблице.
В результате получится таблица умножения.
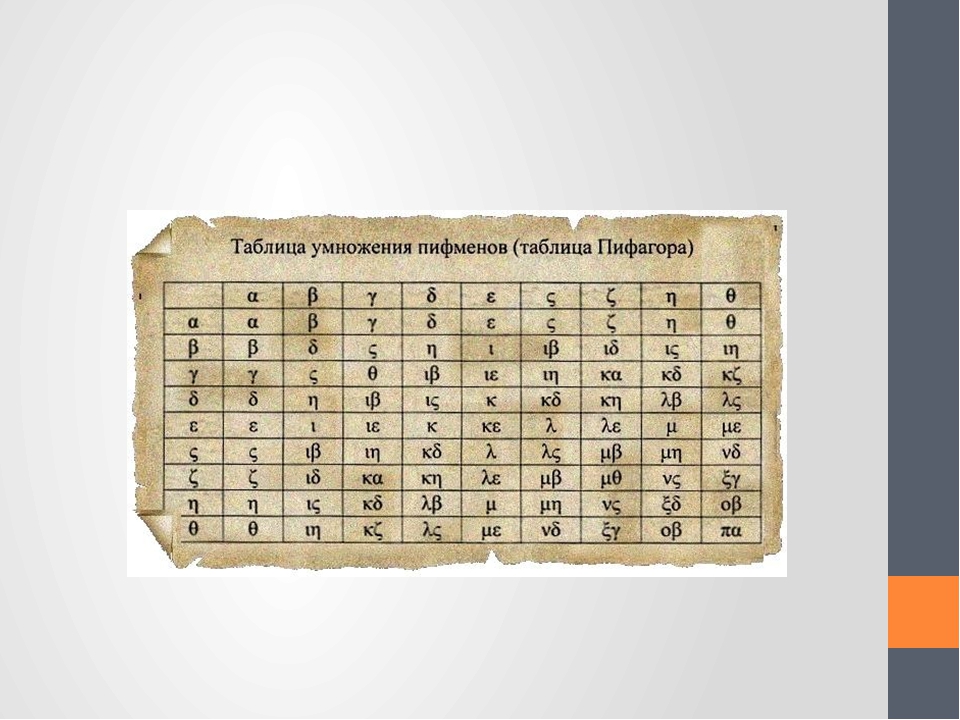
Впервые таблицу составил древнегреческий учёный Пифагор, живший до нашей эры.
Основная и дополнительная литература по теме урока
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с.34-35
2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 3 класс. Часть 1. М.; Просвещение, 2016. –
с. 17-18.
Теоретический материал для самостоятельного изучения
Четыре в комнате угла.
Четыре ножки у стола.
И по четыре ножки
У мышки и у кошки.
Известно детям в целом мире,
Что дважды два равно четыре.
Наша задача: составить таблицу умножения и деления с числом 4.
Заполним таблицу, зная таблицу умножения числа 2.
В первой строке записаны числа от 1 до 9. Умножим число 2 на каждое и запишем ответы во второй строке.
Добавим третью строку с числом 3. Умножим число 3 на каждое число из первой строчки.
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
Добавим в таблицу четвертую строку с числом 4.
Но заполнить строку с числом 4 труднее, так как не знаем таблицу умножения с числом 4.
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
4 |
Для составления можно воспользоваться рисунком.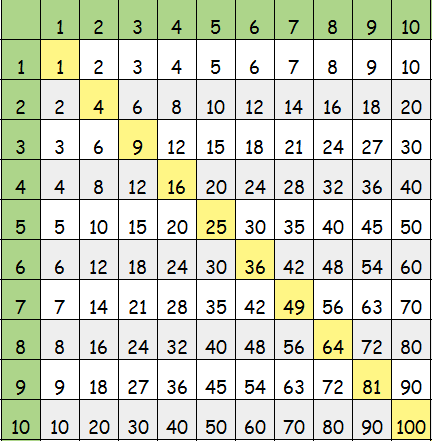
Начнём составлять таблицу умножения с числом 4 со случая
4 ∙ 4, так как знаем
4 ∙2 = 8
4∙3 = 12
4 ∙ 4 – число 4 нужно взять 4 раза и получится 16
4 ∙ 5 – число 4 нужно взять 5 раз, получится 20.
Произведение
увеличивается на 4.
Значит при умножении на 6, произведение равно 24, на 7 – 28, на 8 – 32, на 9 – 36.
4 ∙ 4 = 16
4 ∙ 5 = 20
4 ∙ 6 = 24
4 ∙ 7 = 28
4 ∙ 8 = 32
4 ∙ 9 = 36
Зная правило: от перестановки множителей произведение не меняется, составим таблицу умножения на 4. А правило: если произведение разделить на один множитель, то получим другой, поможет нам составить таблицу деления с числом 4.
5 ∙ 4 = 20 20 : 4 = 5 20 : 5 = 4
6 ∙ 4 = 24 24 : 4 = 6 24 : 6 = 4
7 ∙ 4 = 28 28 : 4 = 7 28 : 7 = 4
8 ∙ 4 = 32 32 : 4 = 8 32 : 8 = 4
9 ∙ 4 = 36 36 : 4 = 9 36 : 9 = 4
Теперь можно заполнить четвёртую строку в таблице.
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
Таким образом, мы можем заполнить таблицу умножения числа 5, 6, 7, 8, 9.
Получится таблица умножения, которую впервые составил древнегреческий учёный Пифагор.
Пифагор жил в 6 веке до нашей эры. Пифагор родился на греческом острове Самос в Эгейском море и, по сохранившимся преданиям, много путешествовал.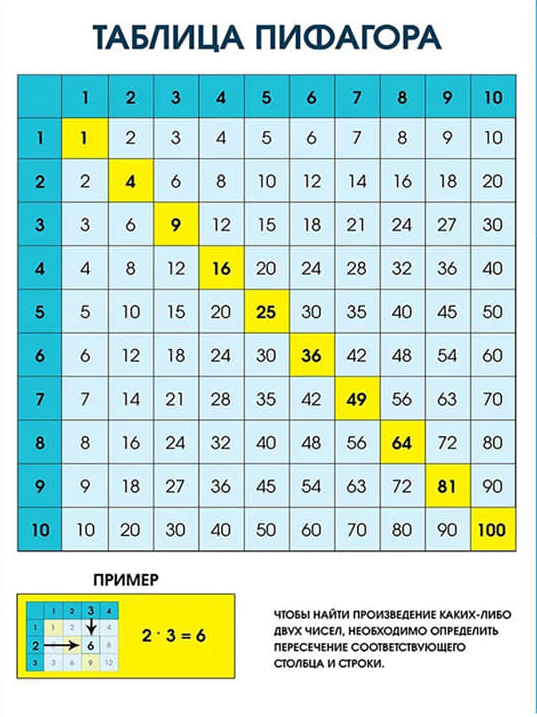 Жил Пифагор в Египте, Вавилоне, совершал путешествие в Индию, знакомился с достижениями науки этих стран. Потом он поселился на юге нынешней Италии, где основал пифогорейский союз – общество философов. Философы пифагорейского союза много занимались наукой, особенно математикой. Ими создана таблица умножения, они разделили все числа на чётные и нечётные.
Жил Пифагор в Египте, Вавилоне, совершал путешествие в Индию, знакомился с достижениями науки этих стран. Потом он поселился на юге нынешней Италии, где основал пифогорейский союз – общество философов. Философы пифагорейского союза много занимались наукой, особенно математикой. Ими создана таблица умножения, они разделили все числа на чётные и нечётные.
Сегодня таблицей Пифагора пользуются на уроках математике, по ней учат таблицу умножения.
Попробуем воспользоваться таблицей Пифагора и найти значения выражений.
2 ∙ 5; 3 ∙ 9; 4 ∙ 7;
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
Задания тренировочного модуля.
1. Вычислите устно. Значения, каких выражений равно 4.
36 : 9;
4 ∙ 8;
16: 4 ∙ 1;
24 : 8;
(6 ∙ 2) :3
Правильный ответ:
36 : 9;
16 : 4 ∙ 1;
(6 ∙ 2) : 3
3 класс. Математика. Закрепление. Таблица Пифагора. (Стр.31) | Методическая разработка (математика, 3 класс) по теме:
3 класс. Математика.
Урок 22.
Тема: Закрепление. Таблица Пифагора. (Стр.31)
Цель урока:
1.Проверить усвоение таблиц умножения и деления с числами 2,3, 4.
2.Закреплятьумения решать простые задачи на умножение и деления.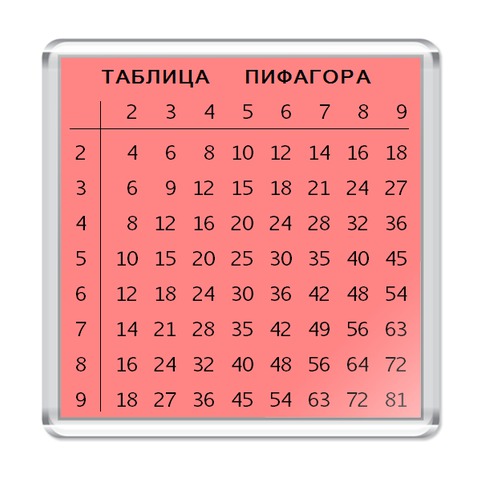
4.Совершенствоватьнавыки нахождения периметра квадрата.
5.Развивать внимание, мышление и память.
6.Познакомить с биографией Пифагора и его вкладом в математику. Развивать интерес к точным наукам.
Оборудование:
Мудрая Сова; Белка, Ёжик, Зайчик; запись ребуса о Пифагоре на доске; Бусины для задания Белки; два столбика примеров в виде снежков для задания зайца; таблица Пифагора расчерчивается на доске; карточки для составления таблицы Пифагора на каждого ученика; портрет Пифагора.
Ход урока:
1.Сообщение темы и целей урока и минутка чистописания.
Тётушка Сова приветствует вас и объявляет, что сегодняшний урок будет посвящён древнему философу и математику.
Вы узнаете его имя, если выпишите только чётные цифры и буквы под ними.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
А П Б И Д Ф У А Ж Г Л О З Р
Письмо цифр: 2 4 6 8 10 12 14
Ответ: ПИФАГОР
— Мы будем учиться составлять таблицу Пифагора и повторять таблицу умножения на 2,3,4.
2. Арифметический диктант.
Диктант проводится в тетради. Записываются только результаты ответа.
1.Найдите сумму чисел 34 и 18.
2.На сколько 43 меньше 81?
3.Найдите разность чисел 72 и 27.
4.На сколько 75 больше 35?
5.Уменьшаемое 78, вычитаемое 29. Найдите разность.
6.Первое слагаемое 9. Второе 3. Найдите сумму.
7.Первый множитель 3. Второй – 9. Найдите произведение.
8.Делимое 12. Делитель 4. Назовите частное.
Ответ: 52 38 45 40 49 12 27 3
3.Устный счёт.
1. Задание от Белочки.
-Из различных цифр я сделала бусы. Но бусы были порваны. Кто сможет их помочь собрать, тому бы я поставила пять!
5——-О———15———О——-О———О——-35——-О———О
16——-26——-О———О——-56———О———-О
2.Задание от Зайчика.
Игра «Кто быстрее?»
Циферки в снежки играли.
В некоторых попадали.
Ты попробуй-ка, найди,
Где какие циферки?
Класс делится на две команды. Кто быстрее заполнит пустые кружочки, тот и выиграл.
4 · 9 = О 7 · 4 = О
24 : 8 = О 27 : 9 = О
9 · 2 = О 8 · 2 = О
36 : 4 = О 21 : 3 = О
3 · 8 = О 4 · 8 = О
16 : 8 = О 16 6 4 = О
5 · 3 = О 3 · 6 = О
6 · 4 = О 12 : 6 = О
28 : 4 = О 4 · 4 = О
3. Задание от Ёжика.
Тетрадь Моро – стр.13, №17,18.
4.Работа над новым материалом.
1.Составление таблицы Пифагора.
— Какие цифры в первой строке?
— Какие цифры в первом столбике
— Умножь каждое из чисел на 2, а произведение запиши во второй строке.
— В третьей строке запиши произведения, полученные при умножении чисел первого ряда на 3, в четвёртой – на 4.
Получилась таблица, которую мы будем заполнять по мере изучения таблицы умножения.
Эту таблицу составил великий философ и учёный Пифагор, который жил в 6 веке до нашей эры. Пифагор родился на греческом острове Самос в Эгейском море и, по сохранившимся преданиям, много путешествовал.
Жил Пифагор в Египте, Вавилоне, совершал путешествие в Индию, знакомился с достижениями науки этих стран. Потом он поселился на юге нынешней Италии, где основал пифогорейский союз – общество философов.
Философы пифагорейского союза много занимались наукой, особенно математикой. Ими создана таблица умножения, они разделили все числа на чётные и нечётные.
Пифагорейцы придавали числам очень большое значение. Считалось, что через них можно выразить все закономерности в мире. И сами числа они наделяли разнообразными свойствами. Например считалось, что 5 символизирует цвет, 6 – холод, 7 – разум, здоровье, 8 – любовь, дружбу и т.д.
Самым знаменитым из открытий Пифагора стала «теорема Пифагора», которую вы будете изучать на уроках геометрии в старших классах. И с этим именем вы ещё не раз столкнётесь на уроке математики.
И с этим именем вы ещё не раз столкнётесь на уроке математики.
2. Выводы по поводу составления таблицы умножения 4.
— Что мы можем сказать о результатах умножения числа 4? ( Все произведения – чётные числа. То есть результатом умножения не может быть 13, 17, 25, 37 и т.д. )
— Какими законами умножения можно воспользоваться, чтобы легче было запомнить таблицу умножения 4? ( Часто лучше умножать не 4 на число, а воспользоваться переместительным свойством умножения и умножать число на 4, ведь от перемены мест множителей произведение не меняется. А затем сочетательным свойством, т.е. умножить число на 2, а потом полученный результат умножить ещё раз на 2.)
Например:
При вычислении произведения 4 · 6 можно рассуждать так:
1) Я помню, что 4 · 5 = 20, значит, что 4 · 6 = 4 · 5 + 4 = 20 + 4 = 24
2) Я знаю, что 4 · 10 = 40 и 4 · 4 = 16.
Тогда 4 · 6 = 4 · 10 – 4 · 4
40 – 16 = 24
3) 4 · 6 = 6 · 2 + 6 · 2 = 12 + 12 = 24
Итак, 4 · 6 = 24
3.Выполнение задания под № 2, стр.31 для закрепления таблицы Пифагора.
Физкультминутка.
Наступает в лесу тишина,
(Руки плавно поднять вверх, затем опустить)
Заблестела на небе луна.
(Покачать поднятыми руками)
Ёжик свернулся клубком,
(Руки на поясе, свести и развести локти)
Зайчик уснул под кустом.
(Присесть на корточки)
Только сове не спится,
(Руки в виде крыльев – в стороны)
В небе ночном кружится:
( Помахать вверх – вниз)
Покричала. Полетала.
Пошумела.
И на ветку дуба старого
Она тихо села.
(Наклонить туловище вперёд ,руки отвести назад. Присесть.)
5.Повторение изученного материала.
1.Решение геометрических задач.
№6, стр.31
Р = 4 · а
а = 3 см; 4 см, 6 мм , 7 мм
Р = 4 · 3 = 12 см
Р = 4 · 4 = 16 см
Р = 4 · 6 = 24 мм
Р = 4 · 7 = 28 мм
Задания по рядам – вычислить периметр квадрата со стороной
1 вар. – а = 5 см
– а = 5 см
2 вар. – а = 8 мм
3 вар. – а = 1 дм.
2. Решение задач.
№3, стр.31
Расход проволоки на одну клетку | Количество клеток | Расход проволоки на все клетки |
? | 2 шт. | 20 м |
10 м | 5 шт. | ? |
1) 20 : 2 = 10 ( м)
2) 10 · 5 = 50 (м)
3.Решение выражений.
№5, стр.31 – самостоятельная работа.
Дополнительно!
Тетрадь Моро – стр.13, №16
6.Итог урока.
— Тётушка Сова благодарит вас за урок и спрашивает, что больше всего вам на нём запомнилось, чему мы научились.
7.Домашняя работа.
№14, стр.28; №6, стр.32
Тетрадь Моро – стр.12, стр.21, №41
1.Составление таблицы Пифагора.
1.Составление таблицы Пифагора.
1.Составление таблицы Пифагора.
Этапы | Обучающие | Деятельность учителя | Деятель | Формы | Формируемые умения | |||||||
I. Мотивация | Эмоциональная, психологическая | Приветствует учащихся, проверяет готовность класса и оборудования; эмоционально настраивает на учебную деятельность. Мы сегодня не одни, БРР Послушайте притчу. Жил на свете великий мастер по стрельбе из лука, у него обучалось много учеников. На одном из уроков, повесив мишень на дерево, он спросил у учеников: – Что Вы видите? Притча о цели. Первым последовал ответ: – Я вижу дерево на котором висит мишень. Притча о цели. И вот учитель подошел к своему лучшему ученику и спросил: Притча о цели. (Чтобы были внимательными, собранными и сосредоточенными на своей цели) | Слушают учителя.
Записывают число: 18 октября. Классная работа. | Фронтальная, индивидуальная | К – планируют учебное сотрудничество | |||||||
II. Актуализация знаний | 1. Устный счёт, повторение теории. | — Как называется раздел, который мы сейчас изучаем? 8+8+8=8∙2 3+3+3+3=3∙4 6+6+7=6 * 3 — Докажите. Поиграем в игру «Лови ошибку» (приём развития критического мышления) (выражения написаны на листьях) Дети выходят к доске и убирают выражения с ошибками. 4∙5=20 16:2= 8 72:8=9 9:3=2 4∙7=27 — Верное ли выражение 72:8=9? (проблема) — Сможем мы сейчас ответить на этот вопрос? Почему? Каких нам знаний не хватает? — На этот вопрос в течение урока найдем ответ. — Найдите выражения, которые показывают взаимосвязь умножения и деления. — Как нашли первое частное? Второе? | Внимательно слушают. Числа от 1 до 100. Умножение и деление. | Фронтальная, индивидуальная | П – осуществляют | |||||||
2. Проверка домашнего задания. | — Какое было домашнее задание? (Запомнить таблицу умножения и деления с числом 4, и повторить с числом 2 и 3) Проверяем по учебнику с. 35. №1 — Взаимопроверка Кто доволен своим результатом? Поднимите руки. Оцените работу. | Заполнение таблицы
| ||||||||||
III. Самоопределение к деятельности | Целеполагание. | — У нас получилась таблица умножения. | Ученики берут листочки и встают по заданию. |
| ||||||||
IV. Изучение нового материала | 1. Рассказ о Пифагоре (слайд) | Таблицу составил великий учёный Пифагор, который жил в 6 веке до нашей эры. Известно, что родился Пифагор на острове Самос, расположенном в Эгейском море. Числам придавал очень большое значение. Числа казались ему чем-то таинственным. | По заданию записывают таблицу в тетрадь. | |||||||||
Физкультминутка | Организует проведение физкультминутки. | Выполняют движения |
| |||||||||
2. Работа по таблице (лист проверки д/з) | Рассмотрим структуру таблицы. Какую закономерность вы наблюдаете в каждой строке? В каждом столбце? (каждое следующее число больше предыдущего на 2 ед., 3 ед., 4 ед.) |
|
| |||||||||
3. Первичное закрепление. | Работа по учебнику. С.35, №2. — работа в парах |
|
| |||||||||
| 4. | — Сможем мы продолжить таблицу на 5 строку? Как? | Заполнение строки, соблюдая логическое построение таблицы. |
| ||||||||
5. Таблица Пифагора (сканир. с форзаца учебника) | — Эта таблица есть на форзаце нашего учебника. Найдите и рассмотрите. |
|
| |||||||||
Игра «Попади в цель» | Вспоминаем притчу. Что ученик видел перед собой? (только цель) | На карточке с таблицей Пифагора закрашивают клеточку с числом-ответом. |
| |||||||||
Физкульт | Под песню «Буратино» дети выполняют танцевальные движения. (1 куплет) |
|
| |||||||||
| А нам этот ключик поможет открыть секрет таблицы Пифагора. А нам он поможет увидеть симметрично расположенные числа. |
|
| |||||||||
V. Продолжение работы по теме урока. | 1. Решение задачи | №3, с. 35.
| Решают задачу самостоятельно. |
| ||||||||
2.Самостоятельная работа. | Решение примеров № 5, с. 35 |
|
|
| ||||||||
3. Разноуровневая самостоятельная работа. | (задания по уровням на листах, с. – Ребята, вспомните, что за фигура – квадрат. – Как же мы найдем периметр квадрата? 1 уровень: Найди периметр квадрата, длина стороны которого 5 см. 2 уровень: Найди периметр квадрата, длина стороны которого 6 дм. 3 уровень: Найди периметр квадрата, длина стороны которого 7 мм. | Вспоминают, как найти периметр квадрата. |
| |||||||||
4. Упражнение «Оратор» | Толковый словарь Ожегова. Тот, кто произносит речь, а также человек, обладающий даром красноречия. | |||||||||||
| 5. Это интересно! | В Российских школах значения таблицы Пифагора обычно доходят до 10×10, в других странах таблица может принимать значения до 12×12, н-р Великобритании, Индии. |
|
| ||||||||
VI. Итоги урока. Рефлексия деятель | Обобщение полученных на уроке | Вернемся к притче. К кому напоследок обратился великий мастер по стрельбе из лука? Почему он был лучшим учеником? — Ответим на контрольные вопросы. Запишите только ответы. Оценивание. — Какова была учебная задача урока? — На что были направлены все задания? Для чего мы их выполняли? — Какое задание показалось интересным? Трудным? Почему было трудно? — Что нового вы узнали на уроке? — Оцените свою работу, используя фразеологизмы. Засучив рукава – стараться изо всех сил. Считать ворон – быть невнимательным, рассеянным. Палец о палец не ударил – ничего не сделал. Работать спустя рукава – не стараться, относиться безответственно. Работать не покладая рук – стараться. — Эти фразеологизмы вы можете найти в словаре фразеологизмов. Дополнительную интересующую вас информацию о Пифагоре и тайнах таблицы вы можете найти на сайте «Почемучка» (сайт для детей и их родителей) pochemu4ka.ru и на сайте frazbook.ru — словарь фразеологизмов | Отвечают на вопросы | Фронтальная, индивидуальная | П – ориентируются | |||||||
VII. Домашнее задание | Инструктаж по выполнению домашнего задания | 1) Раскрасить картинку с опорой на таблицу Пифагора. | Задают уточняющие | Фронтальная, индивидуальная | Р – принимают и сохраняют учебные задачи |
№ 4. – Сформулируйте вопрос задачи. – Сколько всего минут передавали по радио сказку и концерт? | ||||
2. Работа | № 6. – Ребята, вспомните, что за фигура – квадрат. – А сколько сторон у квадрата? – Как же мы найдем периметр квадрата? | Вспоминают, как найти периметр квадрата. | ||
Физкультминутка. | Организует проведение физкультминутки. | Выполняют упражнения | ||
3. Сам. работа. | – Самостоятельно выполните задание № 5 (2, 4 столбики). | Выполняют задание. | ||
4. «Вопросник для смышленых» | 1) Какие часы два раза в сутки показывают верное время? | – Которые стоят. | ||
2) Что случится с красным платком, если его опустить на дно моря на 5 минут? | – Намокнет. | |||
3) Как далеко в лес может забежать заяц? 4) Можно ли в решете принести воду? 5) Летели 3 страуса, одного сбили. Сколько остались лететь? | – До середины, дальше уже из леса. – Можно, когда она замерзнет. – Страусы не летают. | |||
6) Когда мы смотрим на цифру 2, а говорим «10»? | – Когда смотрим на часы (минуты). | |||
7) В каком числе столько же цифр, сколько букв в его названии? (100 – сто). | ||||
8) Какие три числа, если их сложить или перемножить, дают один и тот же результат? (– 1, 2, 3. | ||||
9) Назовите пять дней, не называя чисел и дней недели (Позавчера, вчера, сегодня, завтра, послезавтра | ||||
Таблица умножения и деления с числом 4. Таблица Пифагора
Кхе-кхе… А вот и я, Матюша.
Соскучились? Сегодня я познакомлю вас с
таблицей умножения и деления с числом четыре.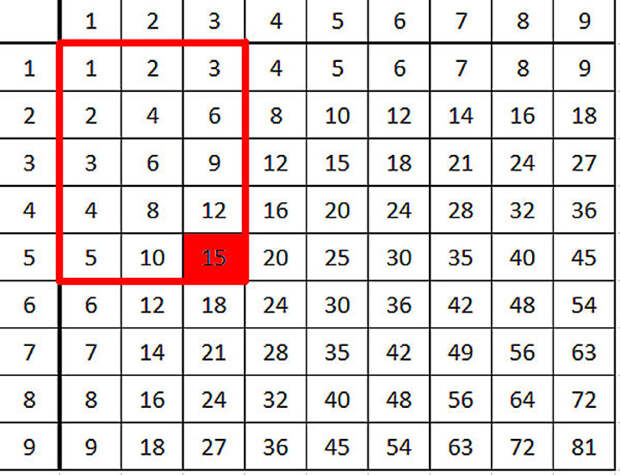 Я наслышан, что таблицу
умножения и деления с числами два и три вы уже знаете. Да и умножение на один,
надеюсь, труда для вас не составляет. Но, всё-таки, повторить умножение на эти
числа стоит. Повторение – мать учения. Итак, друзья, за работу.
Я наслышан, что таблицу
умножения и деления с числами два и три вы уже знаете. Да и умножение на один,
надеюсь, труда для вас не составляет. Но, всё-таки, повторить умножение на эти
числа стоит. Повторение – мать учения. Итак, друзья, за работу.
Четыре умножить на один – один. Один умножить на четыре – один.
Четыре умножить на два – восемь. Два умножить на четыре – восемь.
Четыре умножить на три – двенадцать. Три умножить на четыре – двенадцать.
Ну а дальше будем составлять. Смотрите-ка на ответы – четыре, восемь, двенадцать.
Как только второй множитель увеличивается на один, произведение увеличивается на четыре. Следующий пример у нас – четыре умножить на четыре. А ответ будет на четыре больше двенадцати, то есть шестнадцать. И во втором столбике – то же самое.
Четыре умножаем на пять. Ответ на четыре больше шестнадцати – двадцать. Ну и пять умножить на четыре, конечно, тоже двадцать.
От перестановки множителей произведение не меняется.
Четыре умножаем на шесть. Ответ на четыре больше двадцати – двадцать четыре. Шесть умножить на четыре – тоже двадцать четыре.
Четыре умножить на семь – двадцать восемь. Семь умножить на четыре двадцать восемь.
Четыре умножить на восемь – тридцать два. Восемь умножить на четыре – тридцать два.
Четыре умножить на девять – тридцать шесть. Девять умножить на четыре – тридцать шесть.
Ну а уж четыре умножить на десять – конечно сорок, как и десять умножить на четыре – сорок.
Вот таблицу умножения мы и составили.
А теперь посмотрите, сколько вы уже знаете и сколько осталось выучить.
Ну что, с умножением справились, пора
приниматься за деление. А ведь, как известно, деление – это действие
обратное умножению. И сейчас самое время вспомнить правило. Чтобы найти
неизвестный множитель, надо произведение разделить на известный множитель.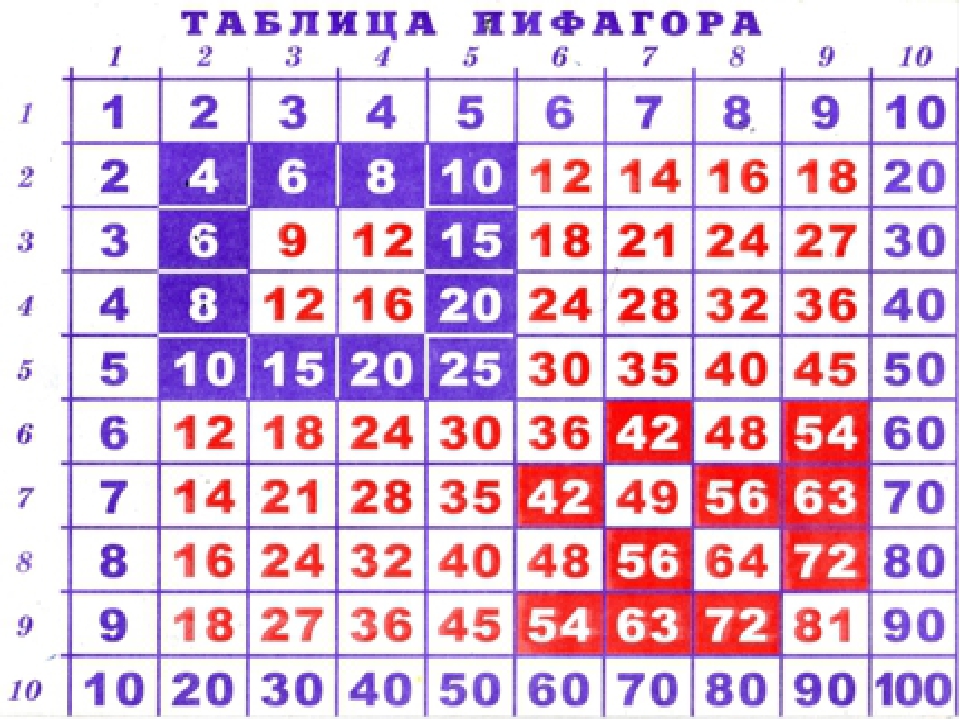 То есть, таблицу деления мы будем составлять на основе таблицы умножения.
То есть, таблицу деления мы будем составлять на основе таблицы умножения.
Вот эти примеры мы уже знаем.
Ну а шестнадцать разделить на четыре? Конечно, четыре.
Двадцать разделить на четыре? Пять. А двадцать разделить на пять – четыре.
Двадцать четыре разделить на четыре – шесть. Двадцать четыре разделить на шесть – четыре.
Двадцать восемь разделить на четыре – семь. Двадцать восемь разделить на семь – четыре.
Тридцать два разделить на четыре – восемь. Тридцать два разделить на восемь – четыре.
Тридцать шесть разделить на четыре – девять. Тридцать шесть разделить на девять – четыре.
Сорок разделить на четыре – разумеется, десять. А сорок разделить на десять – четыре.
Ого, сколько примеров получилось. А выучить-то надо гора-аздо меньше.
Но я чувствую, что вы немного устали. Впрочем, как и я. Поэтому я предлагаю вам совершить маленькую экскурсию в древние века.
Оказывается, старейшая известная таблица умножения обнаружена в Древнем Вавилоне и имеет возраст примерно 4000 лет.
В древнем Китае примерно 2000 лет назад пользовались таблицей умножения, более похожей на современную.
Но сейчас часто пользуются такой таблицей умножения, которую называют «Таблица Пифагора». Считают, что древнегреческий ученый и математик Пифагор Самосский, живший примерно полторы тысячи лет назад, составил эту таблицу умножения. Вот как она выглядит:
И сегодня я научу вас пользоваться этой таблицей.
Посмотрите, как в ней расположены числа. Сначала в горизонтальной строчке и в первом столбике числа от одного до десяти. Потом – все результаты умножения на два, то есть четные числа, Дальше – результаты умножения на три. Потом на четыре. И так далее.
Вот, например, вам надо умножить три на
четыре. Находим в первом столбике число три.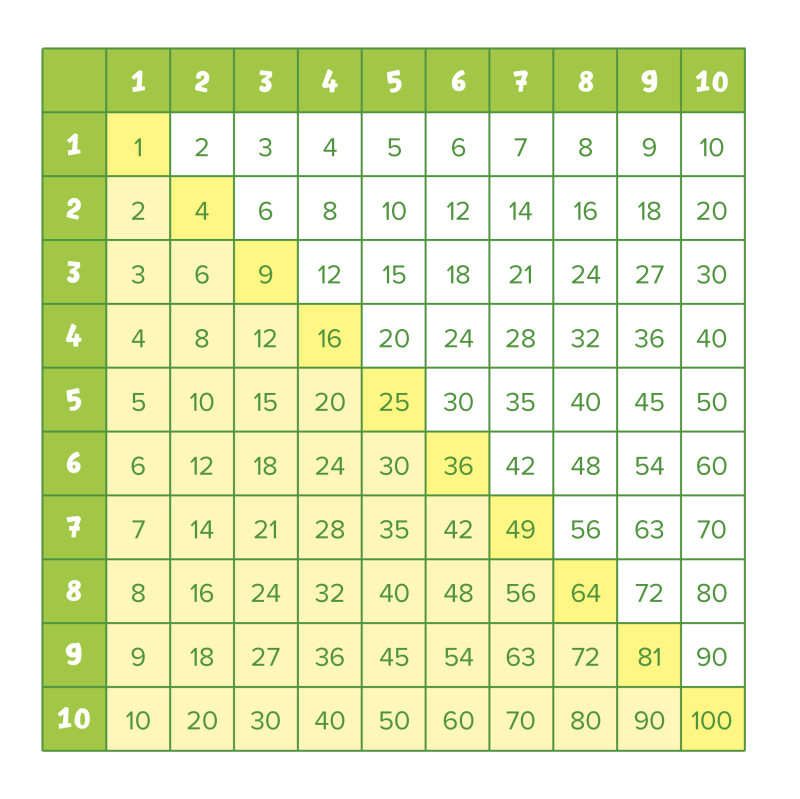 В верхней строчке число четыре.
Ведем от них навстречу друг другу линии, или стрелки. Число на месте
встречи и будет результатом умножения этих чисел, то есть,
произведением. Произведение чисел три и четыре равно двенадцати.
В верхней строчке число четыре.
Ведем от них навстречу друг другу линии, или стрелки. Число на месте
встречи и будет результатом умножения этих чисел, то есть,
произведением. Произведение чисел три и четыре равно двенадцати.
Но можно было и наоборот – в верхней строчке найти число три, а в первом столбике – четыре. Всё равно место встречи стрелок – число двенадцать. Неважно – первый множитель выбирать в первом столбце или в первой строке; второй множитель в первой строке или в первом столбце. Ведь вы помните, что от перестановки множителей произведение не меняется.
А теперь попробуем умножить число четыре на семь. Вот четыре, вот семь. Стрелки бегут навстречу. Произведение чисел четыре и семь равно двадцати восьми.
А как вы думаете, делить можно при помощи этой таблицы? Конечно, можно.
Например, двадцать четыре надо разделить на шесть. Теперь первое число выражения, двадцать четыре, мы ищем не в крайних рядах таблицы, а в её середине. Э, да здесь два числа двадцать четыре!
Какое из них выбрать? Посмотрите, одно из чисел находится на перекрестке линий от чисел три и восемь. Второе – на перекрестке чисел шесть и четыре. Так как нам надо найти частное чисел двадцать четыре и шесть, то конечно, мы выберем второе число. Так как это произведение чисел шесть и четыре, значит, двадцать четыре разделить на шесть, равно четыре.
А если, к примеру, надо найти частное чисел двадцать один и три? Находим в середине таблицы число двадцать один. От него можно провести стрелки к числам три и семь. Значит, двадцать один разделить на три, равно семь!
Ну что, вы поняли, как пользоваться таблицей Пифагора? Правда здорово? Это я Пифагору на ушко про эту таблицу рассказал. Не верите? Дело ваше.
А я свое дело сделал. Теперь вам
осталось только таблицы умножения и деления с числом четыре наизусть выучить,
да ещё потренироваться в работе с таблицей Пифагора.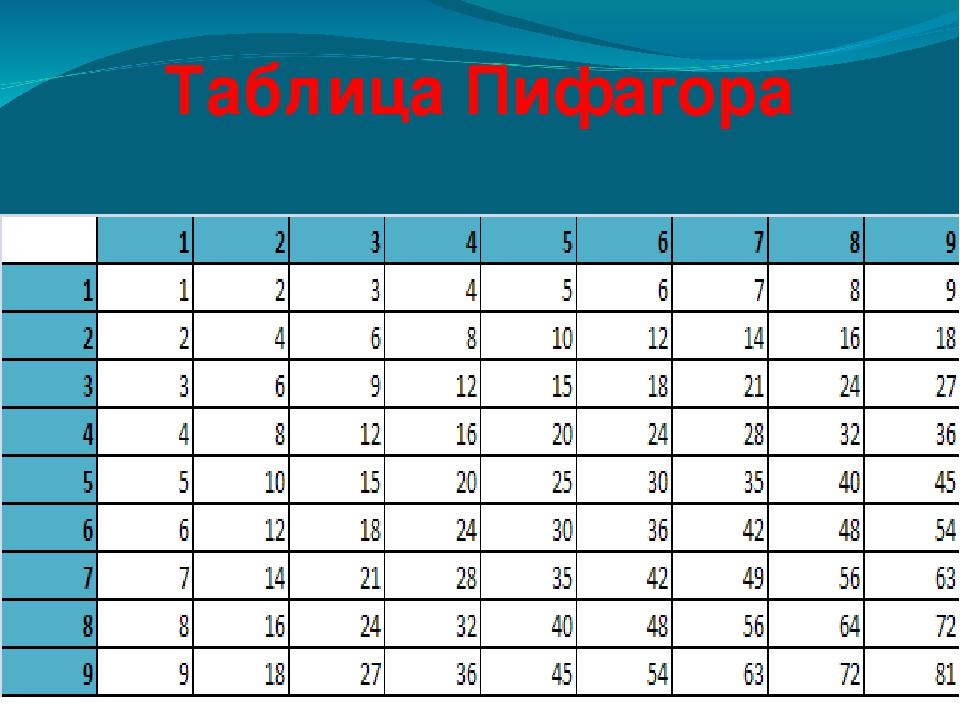 И перед тем,
как нам сегодня распрощаться, я хочу вам сказать слова великого Пифагора:
И перед тем,
как нам сегодня распрощаться, я хочу вам сказать слова великого Пифагора:
Не делай никогда того, чего ты не знаешь, но научись всему, что следует знать, и тогда ты будешь вести спокойную жизнь….
Ну всё. Пойду я немного прогуляюсь, а потом спать. Всем пока!
Как выучить таблицу умножения легко и быстро
1. Взломайте систему
Обычно таблица умножения на обратной стороне школьных тетрадок выглядит так.
Фото: Ramif / DepositphotosОдин вид этих бесконечных столбиков с цифрами способен вогнать энергичного младшеклассника в отчаяние. Поэтому без сомнений берите жирный маркер и на глазах ребёнка перечёркивайте математическую пытку. Это не просто перфоманс, а способ создать позитивный настрой.
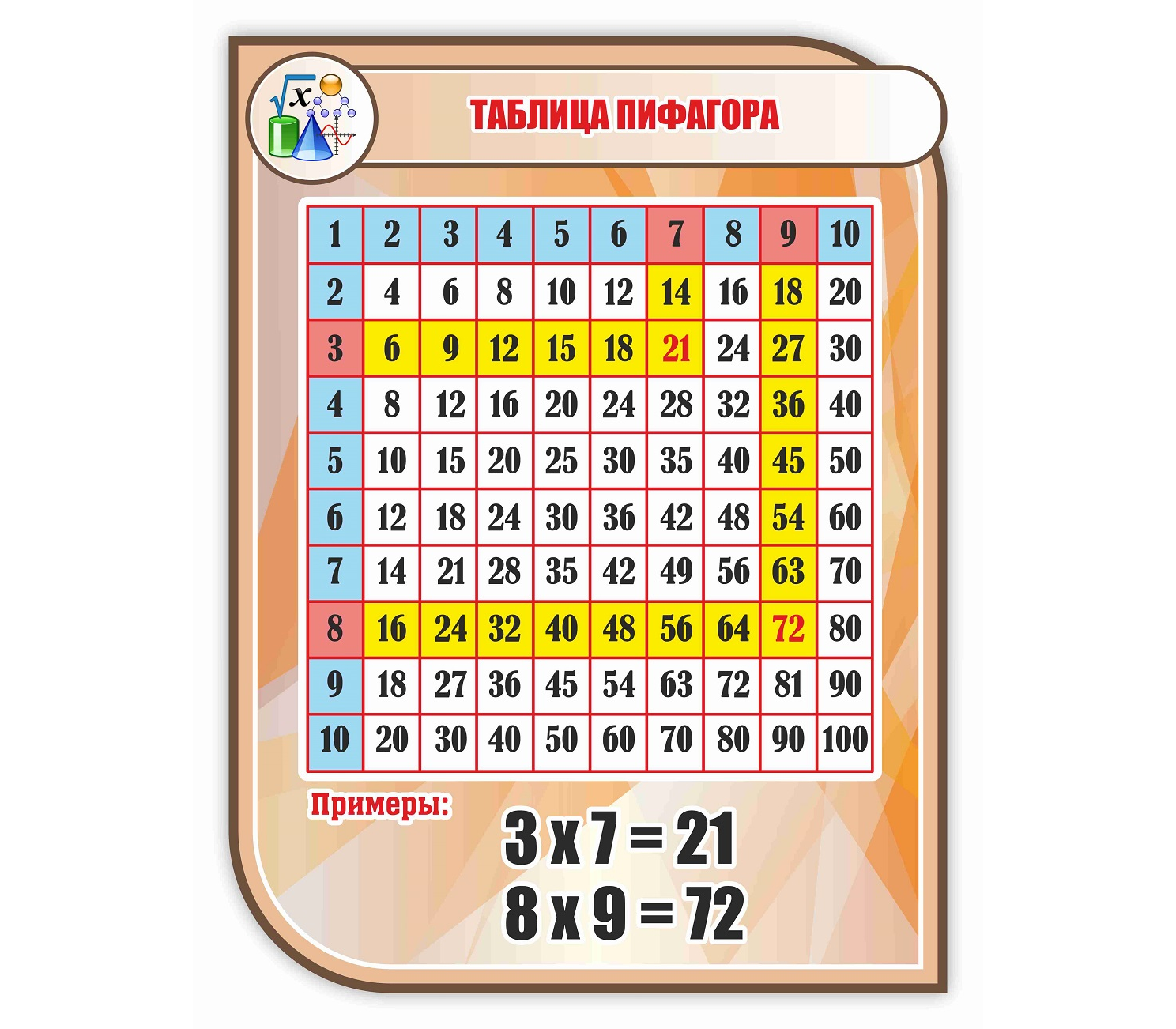
Вместо сложных примеров предложите школьнику таблицу Пифагора.
Это и есть настоящая таблица умножения. Покажите ребёнку, насколько легко ею пользоваться.
Результат умножения двух цифр — это число, которое находится на пересечении строки и столбика с соответствующими цифрами. Например, чтобы умножить 3 на 4, достаточно мысленно провести две линии: одну горизонтальную от цифры 3 в левом столбике, и вторую вертикальную — от цифры 4 в верхней строке. Результат — 12.
2. Объясните, что задача в два раза проще, чем кажется
Вместе умножьте 3 на 4. А теперь предложите ребёнку поменять цифры местами: выбрать 3 не в вертикальном столбике, а в горизонтальной строке. А 4, соответственно, в столбике слева. Обратите внимание, что результат будет тем же. И 3 × 4, и 4 × 3 равно 12.
Это правило называется свойством коммутативности. Или детским языком «от перемены мест множителей результат не меняется».
Не надо запоминать, сколько будет 3 × 4 или 4 × 3. Достаточно выучить, что цифры 3 и 4 в любом порядке при умножении друг на друга дают 12.
Из свойства коммутативности следует простой вывод. Таблица умножения — в два раза меньше и проще, чем кажется. Если вы знаете, сколько будет 4 × 7, значит, вам автоматически известно, сколько будет 7 × 4. Вам не надо это дополнительно учить.
Таблица умножения — в два раза меньше и проще, чем кажется. Если вы знаете, сколько будет 4 × 7, значит, вам автоматически известно, сколько будет 7 × 4. Вам не надо это дополнительно учить.
3. Помогите ребёнку понять физический смысл умножения
Это можно сделать, рисуя на таблице прямоугольники со сторонами, соответствующими умножаемым цифрам.
Например, вот так можно показать, что такое 2 × 4 — это два ряда по четыре клеточки в каждом.
Предложите ребёнку сосчитать, сколько клеточек помещается в получившемся прямоугольнике. Так он сам обнаружит, что 2 × 4 = 8.
Отсканируйте или распечатайте несколько копий таблицы Пифагора и вместе со школьником рисуйте другие прямоугольники — горизонтальные, вертикальные, маленькие и большие, подсчитывая, сколько в них клеточек. Таким образом вы заодно задействуете зрительную память: вспоминая, сколько будет, например, 3 × 4, ребёнок представит себе соответствующую фигуру — и легко ответит.
4. Найдите в таблице закономерности
Когда ребёнок самостоятельно обнаруживает закономерность, он запоминает её навсегда. Это более простой и эффективный способ освоить таблицу умножения, чем зубрёжка.
Вот некоторые закономерности, на которые стоит обратить внимание.
- При умножении на 1 любая цифра остаётся той же.
- Умножение на 2 — это просто цифра, к которой прибавили её же. Например, 3 × 2 означает, что к цифре 3 прибавили 3. 8 × 2 значит 8 + 8.
- Все примеры с умножением на 5 имеют результат, который оканчивается на 5 или на 0.
- Чтобы умножить на 5 любое чётное число, надо взять его половинку и приписать к ней 0. Например, 6 × 5: берём половинку от 6 — это цифра 3 — и приставляем к ней ноль: получается 30.
- При умножении на 9 сумма цифр в результате обязательно будет равна 9. Например, 2 × 9 = 18 (1 + 8 = 9). 3 × 9 = 27 (2 + 7 = 9). И так далее.
- Чтобы умножить любое число на 10, достаточно пририсовать к нему справа ноль.
5.
 Учите небольшими порциями
Учите небольшими порциямиНе нужно пытаться за один присест вызубрить всё. Начните с умножения на 1, 2 и 3 и посвятите изучению каждой такой темы день или два. Так вы постепенно подготовите ребёнка к усвоению более сложной информации.
Когда школьник разобрался и усвоил самые простые столбцы, переходите к числам посложнее: сначала к умножению на 4–7, а затем — на 8–9.
6. Повторяйте
Чем чаще, тем лучше. Сначала спрашивайте по порядку, а когда ответы станут уверенными — вразброс. Следите и за темпом: поначалу давайте больше времени на размышление, но постепенно просите ребёнка отвечать быстрее.
7. Распечатайте или купите обучающие плакаты
Лучше несколько. Развесьте их в тех местах, где ребёнок проводит много времени — в детской (игровой зоне), над рабочим столом, на холодильнике.
Плакаты должны быть большими и яркими. Можно использовать и те, на которых изображена не таблица Пифагора, а стандартные примеры. В любом случае ребёнок будет цепляться взглядом за красочное изображение, и оно закрепится в памяти.
8. Научите ребёнка математическим фокусам
Вот несколько простых примеров.
Фокус с умножением на 7
Вам понадобятся несколько игральных кубиков (костей). Скажите ребёнку, что, сколько бы костей он ни выбросил, вы сразу же скажете сумму точек на их верхних и нижних гранях — даже несмотря на то, что низ кубиков не видно.
Секрет прост: кубики устроены таким образом, что сумма точек на верхней и нижней поверхностях всегда равна 7. Таким образом, чтобы узнать правильный ответ, достаточно умножить количество брошенных кубиков на 7.
Предложите ребёнку показать фокус брату или сестре, бабушке с дедушкой, друзьям. Пусть школьник меняет число кубиков. Это поможет ему закрепить в памяти умножение на 7.
Фокус с умножением на 9
Фото: sqback / DepositphotosПоверните обе ладони к себе. Перед вами окажутся 10 пальцев. Мысленно пронумеруйте их от 1 до 10: большой палец левой руки — 1, указательный — 2 и так далее, вплоть до большого пальца правой руки, который будет соответствовать 10.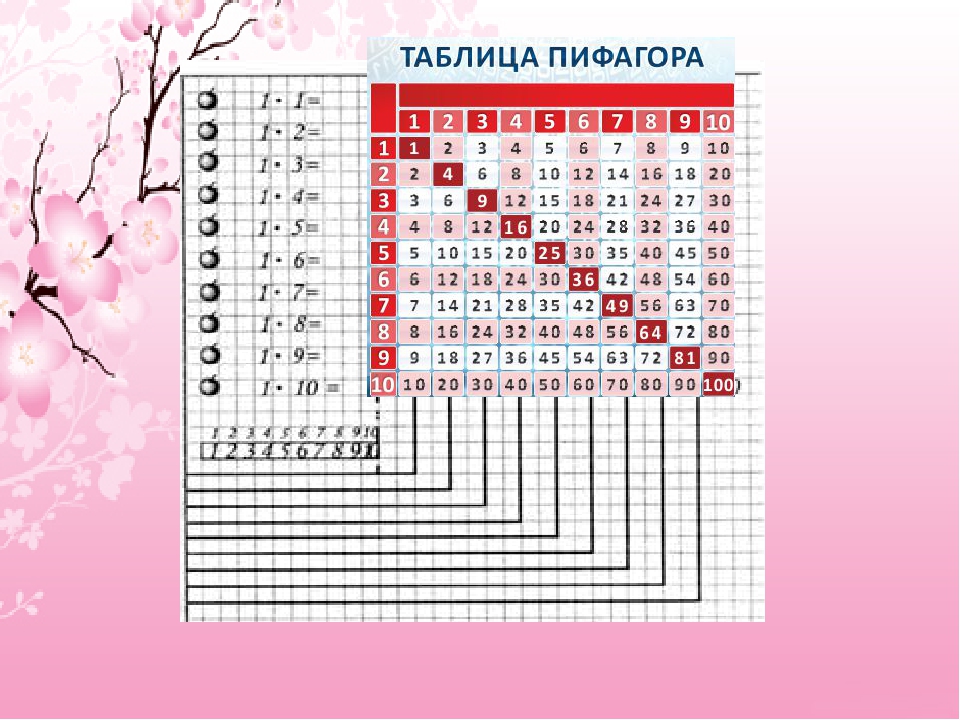 Дальше действуйте так.
Дальше действуйте так.
- Выберите цифру, на которую хотите умножить 9.
- Прижмите соответствующий ей палец вниз.
- Посчитайте, сколько пальцев останется слева от прижатого — это будут десятки в искомом ответе. Справа — единицы.
Например, вам нужно умножить 9 на 2. Вы прижимаете второй по счёту палец — левый указательный. Справа от него остаётся 1 палец (количество десятков), слева — 8 (количество единиц). Правильный ответ: 9 × 2 = 18.
9. Покажите, что математика полезна
Детям, да и взрослым, сложно запоминать абстрактные вещи — те, что не применяются в обычной жизни. Ваша задача — продемонстрировать ребёнку, что таблица умножения очень даже полезна. Это можно сделать разными способами.
Например, предложите школьнику, собирающемуся на прогулку, угостить друзей конфетами или печеньем. «На площадке тебя ждут Катя, Вася, Платон и Ира. Каждому из них ты собираешься дать по 2 конфеты. Сколько конфет тебе надо взять?»
Другой вариант: пусть ребёнок посчитает общее количество колёс у проезжающих мимо шести автомобилей. Или выяснит, сколько людей пойдёт на пикник, если вы собираетесь встретиться четырьмя семьями, в каждой из которых по три человека.
10. Играйте в математику
Сегодня можно купить множество обучающих пособий с красочными картинками и продуманными логическими задачами. Благодаря таким упражнениям обучение превращается в увлекательную игру. Но играть можно, и не тратясь на книжки.
Используйте готовые игры с кубиками
Подойдёт любая бродилка, в которой игрок продвигается на то количество клеток, которое указывает брошенный кубик. Скажите ребёнку, что сегодня все броски считаются двойными (или, положим, тройными). Как правило, детям очень нравится идея проходить в два или три раза дальше, чем показывает кубик.
Чтобы добавить интереса в игру, регулярно пытайтесь смошенничать. Например, говорите: «Так, у меня выпало 4, значит, я должен пройти в два раза дальше… На 10 клеточек!» Пусть ребёнок вас поправляет.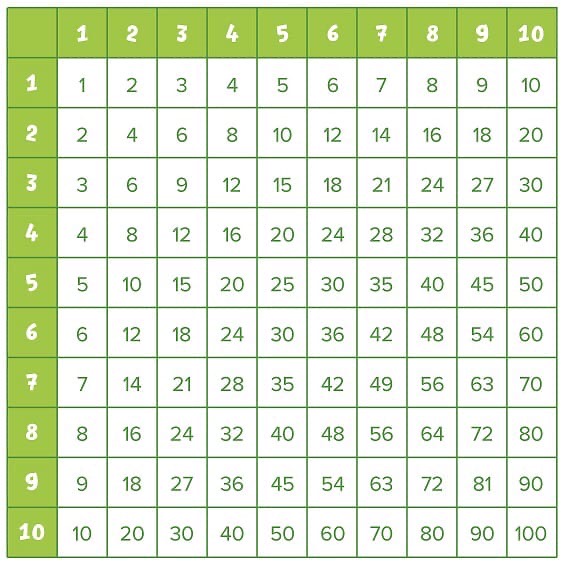
Предложите ребёнку опередить калькулятор
Вам понадобятся всё те же игральные кубики (если ребёнок учит умножение от 1 до 6) или колода игральных карт без картинок (если речь об умножении цифр от 6 до 10). Пусть школьник бросает два кубика или вытягивает две карты из колоды.
Увидев цифры, вы перемножаете их на калькуляторе, а ребёнок проделывает ту же процедуру в уме. Кто быстрее справится, тот получает очко.
Игра может длиться, например, до 7 очков. Победитель получает оговорённый заранее приз.
11. Не превращайте обучение в стресс
Нередко, контролируя детскую учёбу, родители слишком увлекаются и совершают одни и те же ошибки. Вот чего нельзя делать ни в коем случае.
- Заставлять ребёнка заниматься, если он не хочет. Попытайтесь мотивировать: учёба должна быть интересной, а не превращаться в пытку.
- Ругать за ошибки и пугать плохими оценками.
- Ставить в пример одноклассников. Когда тебя с кем-то сравнивают, это неприятно. И нередко вызывает протест: «Раз я хуже, то вообще ничего учить не буду!»
- Учить сразу всё. Ребёнка легко напугать и утомить большим объёмом новой информации.
- Игнорировать успехи. Хвалите ребёнка, когда он справляется с заданиями. Это снизит стресс и вызовет стремление учиться дальше.
Этот материал впервые был опубликован в январе 2017 года. В июле 2020-го мы обновили текст.
Читайте также ✂️✏️📐
Пифагорейских троек
«Тройка Пифагора» — это набор положительных целых чисел, a , b и c , который соответствует правилу:
a 2 + b 2 = c 2
Пример: наименьшая тройка Пифагора — 3, 4 и 5.
Проверим:
3 2 + 4 2 = 5 2
При вычислении получается:
9 + 16 = 25
Да, это трояк Пифагора!
Треугольники
Если стороны треугольника являются тройкой Пифагора, это прямоугольный треугольник.
Подробнее см. Теорему Пифагора.
Пример: тройка Пифагора из 3, 4 и 5 образует прямоугольный треугольник:
Вот еще две тройки Пифагора:
| 5, 12, 13 | 9, 40, 41 | |
| 5 2 + 12 2 = 13 2 | 9 2 + 40 2 = 41 2 | |
| 25 + 144 = 169 | (попробуйте сами) |
И у каждого треугольника есть прямой угол!
Список первых
Вот список первых нескольких троек Пифагора (, а не , включая «увеличенные» версии, упомянутые ниже):
| (3, 4, 5) | (5, 12, 13) | (7, 24, 25) | (8, 15, 17) |
| (9, 40, 41) | (11, 60, 61) | (12, 35, 37) | (13, 84, 85) |
| (15,112,113) | (16, 63, 65) | (17 144 145) | (19 180 181) |
| (20, 21, 29) | (20, 99 101) | (21 220 221) | (23 264 265) |
| (24 143 145) | (25 312 313) | (27 364 365) | (28, 45, 53) |
| (28,195,197) | (29 420 421) | (31 480 481) | (32 255 257) |
| (33, 56, 65) | (33 544 545) | (35 612 613) | (36, 77, 85) |
| (36 323 325) | (37 684 685) | … бесконечно много больше … | |
Масштабируйте их
Самый простой способ создать дополнительные тройки Пифагора — это увеличить набор троек.
Пример: масштабировать
3, 4, 5 на 2 дает 6, 8, 10Что также соответствует формуле a 2 + b 2 = c 2 :
6 2 + 8 2 = 10 2
36 + 64 = 100
Если вы хотите узнать о них больше, прочтите Pythagorean Triples — Advanced
Пифагорейских троек — Продвинутый
(Вы можете сначала прочитать теорему Пифагора
или Введение в тройки Пифагора)
«Тройка Пифагора» — это набор положительных целых чисел, a , b и c , который соответствует правилу:
a 2 + b 2 = c 2
Треугольники
И когда мы построим треугольник со сторонами a , b и c , это будет прямоугольный треугольник (подробнее см. Теорему Пифагора):
Теорему Пифагора):
Примечание:
- c — самая длинная сторона треугольника, называемая «гипотенузой»
- a и b — две другие стороны
Пифагорейские тройки
Известный пример троек Пифагора:
Еще два примера:
| 5, 12, 13 | 9, 40, 41 | |
| 5 2 + 12 2 = 13 2 | 9 2 + 40 2 = 41 2 | |
| 25 + 144 = 169 | (попробуйте сами) |
Бесконечный
Набор троек Пифагора бесконечен.
Мы можем доказать это с помощью первой тройки Пифагора (3, 4 и 5) :
Пусть n будет любым целым числом больше 1, тогда 3n, 4n и 5n также являются набором троек Пифагора. Это правда, потому что:
(3n) 2 + (4n) 2 = (5n) 2
Примеры:
| n | (3n, 4n, 5n) | |
|---|---|---|
| 2 | (6,8,10) | |
| 3 | (9,12,15) | |
| … | … и т.д … |
Таким образом, мы можем сделать бесконечно много троек, просто используя тройку (3,4,5).
Доказательство Евклида, что существует бесконечно много пифагоровых троек
Но Евклид использовал другое рассуждение, чтобы доказать, что набор троек Пифагора бесконечен.
Доказательство основывалось на том факте, что разность квадратов любых двух последовательных (одно за другим) чисел всегда является нечетным числом.
Примеры:
2 2 — 1 2 = 4 — 1 = 3 (нечетное число),
3 2 — 2 2 = 9 — 4 = 5 (нечетное число),
4 2 — 3 2 = 16 — 9 = 7 (нечетное число),
и т. Д.
Д.
Именно так (вы понимаете, почему?)
Нечетные числа и последовательные квадраты
См. Квадраты и нечетные числа или посмотрите на эту таблицу в качестве примера:
| n | n 2 | Разница |
|---|---|---|
| 1 | 1 | |
| 2 | 4 | 4−1 = 3 |
| 3 | 9 | 9−4 = 5 |
| 4 | 16 | 16−9 = 7 |
| 5 | 25 | 25−16 = 9 |
| … | … | … |
А нечетных чисел бесконечное количество. Поскольку полные квадраты образуют подмножество нечетных чисел, а дробная часть бесконечности также равна бесконечности, отсюда следует, что также должно быть бесконечное количество нечетных квадратов. Итак, существует бесконечное количество троек Пифагора.
Недвижимость
Интересный факт: тройка Пифагора всегда состоит из:
- все четные числа или
- два нечетных числа и четное число.
Пифагорейская тройка никогда не может состоять из всех нечетных чисел или двух четных чисел и одного нечетного числа. Это правда, потому что:
- Квадрат нечетного числа — это нечетное число, а квадрат четного числа — четное число.
- Сумма двух четных чисел является четным числом, а сумма нечетного числа и четного числа является нечетным числом.
Итак, когда и a, и b четны, c тоже. Точно так же, когда одно из a и b нечетное, а другое четное, c должно быть нечетным!
Построение пифагорейских троек
Строить множества пифагоровых троек несложно.
Когда m и n — любые два положительных целых числа (m> n):
- a = m 2 — n 2
- b = 2 млн
- c = m 2 + n 2
Тогда a, b и c образуют пифагорейскую тройку.
Пример: m = 2 и n = 1
- a = 2 2 — 1 2 = 4 — 1 = 3
- б = 2 × 2 × 1 = 4
- с = 2 2 + 1 2 = 4 + 1 = 5
Таким образом, мы получаем первую тройку Пифагора (3,4,5) .
Аналогичным образом, когда m = 3 и n = 2, мы получаем следующий тройной пифагорейский (5,12,13) .
Список первых
Вот список всех троек Пифагора, где a, b и c меньше 1000.
Но в списке есть только первый набор (a, b, c), который является тройкой Пифагора (называемой примитивной тройкой Пифагора), поэтому кратные (a, b, c), такие как (2a, 2b, 2c), (3a, 3b, 3c) и т. Д. Отсутствуют в списке.
Пример: (3,4,5) — тройка Пифагора.(6,8,10) также является троицей Пифагора, но не показано, поскольку оно просто (3,4,5) умноженное на 2.
| (3,4,5) | (5,12,13) | (7,24,25) | (8,15,17) | (9,40,41) |
| (11,60,61) | (12,35,37) | (13,84,85) | (15 112 113) | (16,63,65) |
| (17 144 145) | (19 180 181) | (20,21,29) | (20,99,101) | (21 220 221) |
| (23 264 265) | (24 143 145) | (25 312 313) | (27 364 365) | (28,45,53) |
| (28,195,197) | (29 420 421) | (31 480 481) | (32 255 257) | (33,56,65) |
| (33 544 545) | (35 612 613) | (36,77,85) | (36 323 325) | (37 684 685) |
| (39,80,89) | (39 760 761) | (40 399 401) | (41 840 841) | (43 924 925) |
| (44,117,125) | (44 483 485) | (48,55,73) | (48 575 577) | (51 140 149) |
| (52 165 173) | (52 675 677) | (56 783 785) | (57 176 185) | (60,91,109) |
| (60 221 229) | (60 899 901) | (65,72,97) | (68 285 293) | (69 260 269) |
| (75 308 317) | (76 357 365) | (84 187 205) | (84 437 445) | (85 132 157) |
| (87 416 425) | (88 105 137) | (92 525 533) | (93 476 485) | (95 168 193) |
| (96 247 265) | (100 621 629) | (104 153 185) | (105 208 233) | (105 608 617) |
| (108 725 733) | (111 680 689) | (115 252 277) | (116 837 845) | (119 120 169) |
| (120 209 241) | (120 391 409) | (123 836 845) | (124 957 965) | (129 920 929) |
| (132 475 493) | (133 156 205) | (135 352 377) | (136 273 305) | (140 171 221) |
| (145 408 433) | (152 345 377) | (155 468 493) | (156 667 685) | (160 231 281) |
| (161 240 289) | (165 532 557) | (168 425 457) | (168 775 793) | (175 288 337) |
| (180,299,349) | (184 513 545) | (185 672 697) | (189 340 389) | (195 748 773) |
| (200 609 641) | (203 396 445) | (204 253 325) | (205 828 853) | (207 224 305) |
| (215 912 937) | (216 713 745) | (217 456 505) | (220 459 509) | (225 272 353) |
| (228 325 397) | (231 520 569) | (232 825 857) | (240 551 601) | (248 945 977) |
| (252 275 373) | (259 660 709) | (260 651 701) | (261 380 461) | (273 736 785) |
| (276 493 565) | (279 440 521) | (280 351 449) | (280 759 809) | (287 816 865) |
| (297 304 425) | (300 589 661) | (301 900 949) | (308 435 533) | (315 572 653) |
| (319 360 481) | (333 644 725) | (336 377 505) | (336 527 625) | (341 420 541) |
| (348 805 877) | (364 627 725) | (368 465 593) | (369 800 881) | (372 925 997) |
| (385 552 673) | (387 884 965) | (396 403 565) | (400 561 689) | (407 624 745) |
| (420 851 949) | (429 460 629) | (429 700 821) | (432 665 793) | (451 780 901) |
| (455 528 697) | (464 777 905) | (468 595 757) | (473 864 985) | (481 600 769) |
| (504 703 865) | (533 756 925) | (540 629 829) | (555 572 797) | (580 741 941) |
| (615 728 953) | (616 663 905) | (696 697 985) |
Как научить детей младшего школьного возраста теореме Пифагора
Меня спросили,
В настоящее время я учусь в MCC.Я изучаю курс для учителей элементарной математики. Мы должны составить план урока, чтобы научить младших школьников пользоваться теоремой Пифагора. Мне нужно научиться разбирать теорему Пифагора для элементарного ребенка. Я застрял в квадратной корневой части.
Обычно теорему Пифагора изучают сразу после извлечения квадратного корня или в курсе геометрии. Обычно это происходит в средней школе, а не в начальных классах.
На мой взгляд, если детей еще не учили концепции квадратного корня, то вы не сможете объяснить ОБЕ теорему Пифагора И концепцию квадратного корня за один урок.Кроме того, прежде чем изучать квадратные корни, учащиеся должны знать о возведении в квадрат чисел (показателей).
Единственный способ, которым я могу это понять, — это если вы даже не пытаетесь объяснить, что такое квадратные корни, а просто скажите студентам, чтобы они получали их с помощью калькулятора. Таким образом, вы можете сконцентрироваться на обучении их этой основной идее:
Теорема Пифагора позволяет вам найти третью сторону прямоугольного треугольника, если вы уже знаете две другие стороны.
План урока
- Попросите каждого ученика нарисовать на бумаге ПРАВИЛЬНЫЙ треугольник.Учащимся необходимо использовать инструмент (например, треугольную линейку или угол какого-либо объекта), чтобы убедиться, что их треугольники имеют прямой угол. Попросите их измерить все стороны каждого треугольника.
- Сделайте несколько своих измерений и покажите (без использования символа квадрата), что
(сторона 1) · (сторона 1) + (сторона 2) · (сторона 2) = (самая длинная сторона) · (самая длинная сторона)
верно для некоторых нарисованных ими треугольников.Если они знают о переменных, то вы можете представить теорему, используя переменные.Если они знают о возведении в квадрат, используйте для этого соответствующий символ.
- Попросите студентов проверить это соотношение для своих треугольников.
 Конечно, поскольку измерения по своей природе всегда несколько неточны, они приблизятся только к получению истинного уравнения.
Конечно, поскольку измерения по своей природе всегда несколько неточны, они приблизятся только к получению истинного уравнения. - Не забудьте показать ученикам пространственный треугольник со сторонами 3, 4 и 5 единиц:
На изображении стороны прямоугольного треугольника имеют длину 3, 4 и 5 единиц. Боковые стороны получили «квадрат».Когда вы сложите все маленькие квадраты на двух ножках, вы увидите, что сумма квадратов на ножках равна общему количеству квадратов, нарисованных на гипотенузе.
- Затем вы можете показать студентам прямоугольный треугольник с вымышленными размерами двух сторон. Какова длина третьей стороны? Я предполагаю, что студенты скажут вам просто измерить это — зачем беспокоиться о вычислениях, если вы можете измерить?
Так что измените треугольник на вашем изображении, чтобы он был, скажем, частью крыши.Допустим, вы планируете построить крышу и вам нужно знать длину длинной стороны ДО того, как она будет построена. Вы еще не можете измерить его, так как он еще не построен.
Скажем, две ноги 20 футов и 6 футов. Мы получили:
(самая длинная сторона) · (самая длинная сторона) = 20 · 20 + 6 · 6 (самая длинная сторона) · (самая длинная сторона) = 436
Попросите их воспользоваться калькулятором, чтобы извлечь квадратный корень из 436 — и они нашли длину самой длинной стороны треугольника в футах.
Это может быть не очень элегантный урок, но, как я уже упоминал, я считаю, что теорему Пифагора не следует преподавать даже в младших классах. Сделать это будет довольно сложно. Также имейте в виду, что вы можете научить использовать теорему только для решения гипотенузы прямоугольного треугольника, а другие ситуации оставить на потом.
См. Также:
Интернет-ресурсы по теореме Пифагора
Вопросы по теореме Пифагора
Добро пожаловать в раздел «Вопросы по теореме Пифагора».
Здесь вы найдете помощь, поддержку и вопросы, которые помогут вам овладеть теоремой Пифагора и применить ее.
Здесь вы найдете нашу страницу поддержки, которая поможет вам научиться использовать и применять теорему Пифагора.
Обратите внимание: теорема Пифагора также называется «Теорема Пифагора»
Существует ряд листов, включающих поиск недостающих сторон прямоугольных треугольников, тестирование прямоугольных треугольников и решение словесные задачи с использованием теоремы Пифагора.
Использование этих листов поможет вашему ребенку:
- изучить теорему Пифагора о прямоугольном треугольнике;
- использовать и применять теорему в различных контекстах для решения проблем.
Теорема Пифагора утверждает, что в прямоугольном треугольнике (или прямоугольном треугольнике) сумма квадратов двух меньших сторон треугольника равна квадрату гипотенузы.
Другими словами, a 2 + b 2 = c 2 .
где c — гипотенуза (самая длинная сторона), а a и b — другие стороны прямоугольного треугольника.
Что это значит?
Это означает, что для любого прямоугольного треугольника оранжевый квадрат (который представляет собой квадрат с самой длинной стороной) имеет ту же площадь, что и два других синих квадрата, сложенных вместе.
Формулы прочие
В результате формулы a 2 + b 2 = c 2 , мы также можем вывести, что:
- b 2 = c 2 — a 2 и a 2 = c 2 — b 2
- c = √ (a 2 + b 2 )
- b = √ (c 2 — a 2 ) и a = √ (c 2 — b 2 )
Примеры
Пример 1
В этом примере нам нужно найти гипотенузу (самую длинную сторону прямоугольного треугольника).
Итак, используя пифагор, сумма двух меньших квадратов равна квадрату гипотенузы.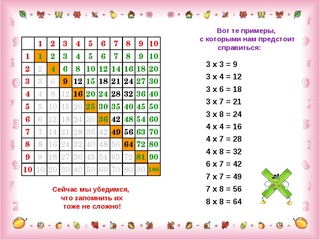
Это дает нам 4 2 + 6 2 =? 2
Так ? 2 = 16 + 36 = 52
Так ? должен быть равен √52 = 7,21 см до 2dp.
Пример 2
В этом примере нам нужно найти длину основания треугольника с учетом двух других сторон.
Итак, используя пифагор, сумма двух меньших квадратов равна квадрату гипотенузы.
Это дает нам? 2 + 5 2 = 8 2
Так ? 2 = 8 2 — 5 2 = 64 — 25 = 39
Так ? = √39 = от 6,25 см до 2dp.
Следующие вопросы включают использование теоремы Пифагора для поиска недостающей стороны прямоугольного треугольника.
Первый лист включает только поиск гипотенузы.
В треугольниках использовался ряд различных единиц измерения, которые не масштабированы.
Следующие вопросы включают использование теоремы Пифагора, чтобы выяснить, является ли треугольник прямоугольным. (есть ли у треугольника прямой угол).
Если теорема Пифагора истинна для треугольника, и c 2 = a 2 + b 2 , то треугольник — это прямоугольный треугольник.
Если теорема Пифагора ложна для треугольника и c 2 = a 2 + b 2 , то треугольник не является прямоугольным.
В треугольниках использовался ряд различных единиц измерения, которые не масштабированы.
Следующие вопросы включают использование теоремы Пифагора для решения ряда словесных задач, связанных с вопросами «из реальной жизни».
На первом листе нужно найти только гипотенузу, учитывая размеры других сторон.
Иллюстрации были предоставлены, чтобы помочь студентам решить эти текстовые задачи.
Здесь вы найдете страницу поддержки с множеством геометрических формул.
На этой странице приведены формулы для:
- площади и объемы 2D и 3D форм
- внутренние углы многоугольников
- уголки двухмерных фигур
- формулы и теоремы треугольника
Эта страница станет полезным справочником для всех, кому нужна геометрическая формула.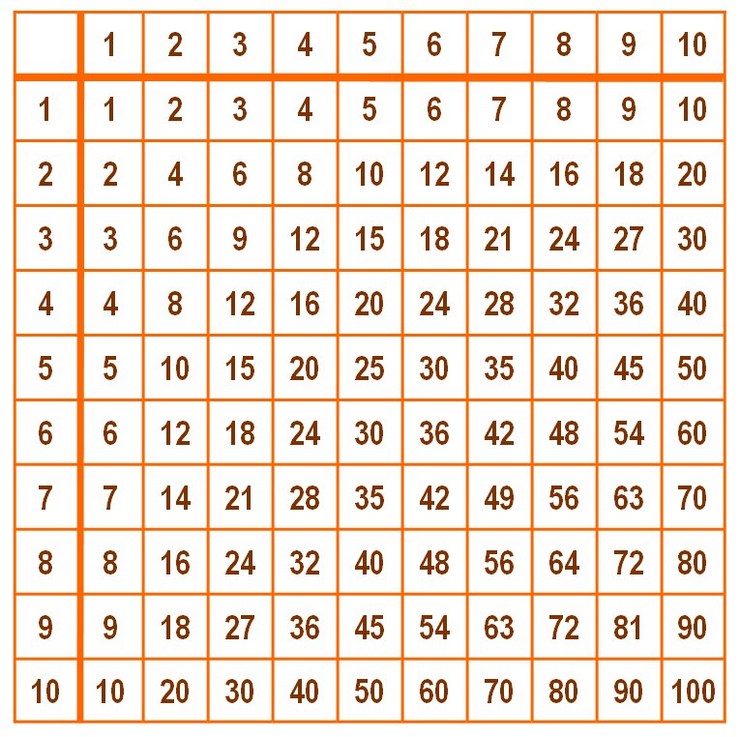
Здесь вы найдете страницу поддержки, которая поможет вам разобраться в некоторых особенности треугольников, особенно прямоугольных.
Использование этой страницы поддержки поможет вам:
- разбираться в различных типах и свойствах треугольников;
- понять, как найти площадь треугольника;
- знает и использует теорему Пифагора.
Все бесплатные печатные геометрические рабочие листы в этом раздел поддерживает тесты элементарной математики.
Здесь вы найдете ряд шпаргалок по геометрии, которые помогут вам ответить на ряд вопросов о геометрии.
Таблицы содержат информацию об углах, типах и свойствах двумерных и трехмерных фигур, а также общие формулы, связанные с двумерными и трехмерными фигурами.
На этой странице находятся:
- изображений обычных 2D- и 3D-форм;
- свойств 2D и 3D форм;
- формул, включающих двумерные формы, такие как площадь и периметр, теорема Пифагора, законы тригонометрии и т. Д .;
- формул, включающих трехмерные фигуры об объеме и площади поверхности.
Использование листов в этом разделе поможет вам понять и ответить на ряд вопросов о геометрии.
Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике. и все другие наши математические игры и ресурсы.
Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.
Теорема Пифагора о столбцах | Японская математика в период Эдо
Соотношение a 2 + b 2 = c 2 относительно трех сторон прямоугольного треугольника называется теоремой Пифагора .Эта теорема известна с древних времен, как следует из названия; и мы не уверены, есть ли неопровержимые доказательства того, что Пифагор (ок. до н. э. 570-ок. до н. э.) действительно открыл его.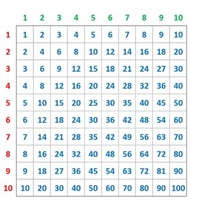
Теорема Пифагора
В третьем веке Диоген Лаэртиос писал в Philosophon bioi (Жизни выдающихся философов) , что «Согласно Аполлодору, арифметику, когда он обнаружил, что площадь квадрата на гипотенузе прямоугольного треугольника равна Сумма площадей двух квадратов на двух других сторонах, содержащих прямой угол, он принес в жертву сотню быков.«Однако мы не знаем никаких подробностей об этом арифметике Аполлодоре.
В третьем веке до нашей эры Евклид доказал теорему Пифагора в своей книге Стоихея (Элементы) , в которой он не упомянул имя Пифагора. Однако в году. В комментарии к первой книге «Элементы Евклида », написанной Проклосом в пятом веке, и в году «De Architectura », написанной Витрувием, римским архитектором, в первом веке до нашей эры, утверждается, что первооткрывателем этой теоремы был Пифагор.Эти древние документы были обнаружены в период Возрождения, и с тех пор Евклид включил в Элементы , что эта теорема на самом деле была открыта Пифагором. Однако наиболее распространенным современным мнением является то, что Пифагор не был первооткрывателем этой теоремы.
Эта теорема была названа законом Кукоген в китайской математике и обсуждалась в древних математических книгах Zhoubi suanjing и Jiuzhang suanshu .Даже после того, как теорема была представлена в Японии, в ней использовалось имя Koukogen . Kou (крючок) — это «прямоугольный крючок», что означает две короткие стороны, содержащие прямой угол; Ко (бедро) — «сустав ноги», означающий длинную сторону; и Gen (хорда) — тетива, что означает гипотенузу.
Эта теорема также была открыта в древней Вавилонии и древней Индии и считалась важной теоремой, используемой в геодезии, архитектуре, астрономических наблюдениях и т. Д.Тригонометрические функции также тесно связаны с теоремой Пифагора.
«Тетива» в комментарии к
Zhoubi suanjingЭтот комментарий поясняет цифрой, что 3 2 +4 2 = 5 2 справедливо для прямоугольного треугольника с тремя сторонами длиной 3, 4 и 5, и эта цифра может помочь нам доказать, что 2 + b 2 = c 2 также верно, когда длины равны a , b и c .Обратите внимание на следующие две цифры:
Нам известно, что существует несколько сотен методов доказательства теоремы Пифагора. Метод, принятый Евклидом для доказательства теоремы, заключается в использовании конгруэнтных треугольников и эквивалентной деформации; в дополнение к этому мы знаем алгебраический метод, использующий подобие; метод доказательства теоремы путем размещения тех же четырех прямоугольных треугольников в соответствующих местах и вычисления этих треугольников; и один, который включает создание двух квадратов на двух сторонах, содержащих прямой угол, разложение квадратов и наложение их на квадрат на гипотенузе.
Укладка одинаковых четырех прямоугольных треугольников
- На рисунке 1
Из рисунка 1 следует, что c 2 = 4 ・ ab / 2 + (ba) 2
= 2ab + b 2 -2ab + a 2
= a 2 + b 2- На рисунке 2
Из рисунка 2 следует, что c 2 = (a + b) 2 -4 ・ ab / 2
= a 2 + 2ab + b 2 -2ab
= a 2 + b 2
Эти методы доказательства, использующие области, связаны с теоремой Бойяи-Гервиена , а в Васане они рассматривались как задачи обрезки по размеру (которые будут объяснены позже).Книги, в которых собраны методы доказательства теоремы Пифагора, включают Предложение Пифагора (Вашингтон, округ Колумбия, 1968) Эллумиса, которое мы можем прочитать в предоставленной электронной библиотеке (http://www.eric.ed.gov/). ERIC (Информационный центр исследований в области образования) в США.
Пример раскроя по размеру (из Kanja otogi zoshi )
тройка Пифагора
Тройка (a, b, c), состоящая из трех натуральных чисел, удовлетворяющих a 2 + b 2 = c 2 , называется тройкой Пифагора и прямоугольными треугольниками, три стороны которых длины a , b и c называются треугольниками Пифагора .Самая известная тройка Пифагора — (3,4,5), в то время как другие тройки Пифагора включают (5,12,13) и (15,8,17) и т. Д.
Мы знаем, что существует бесконечное количество троек Пифагора; давайте рассмотрим причину этого. Если предположить, что n — любое натуральное число, и вычислить a 2 + b 2 для a = 3n , b = 4n получаем (3 n ) 2 + (4 n ) 2 = 25 n 2 = (5 n ) 2 .Тогда, если мы предположим, что c = 5 n , ( a, b, c ) является тройкой Пифагора. Поскольку n — любое натуральное число, мы можем быть уверены, что существует бесконечное количество троек Пифагора.
Когда мы предполагаем n = 1,2,3 …, мы получаем пифагоровы тройки вроде (3,4,5) (6,8,10) (9,12,15) …
Однако этот метод не позволяет нам получить тройку Пифагора (5,12,13) с любыми n .
Фактически, (5,12,13) является частным случаем, когда n = 2 при предположении a = 2 n +1, b = 2 n ( n +1), и c = 2 n 2 +2 n +1; для любого натурального числа n ,
(2 n +1) 2 + {2 n ( n +1)} 2 = 4 n 4 +8 n 3 +8 n 2 +4 n + 1 = (2 n 2 +2 n +1) 2 верно, и поэтому мы знаем, что (a, b, c) — пифагорова тройка .Когда мы предполагаем n = 1,2,3 …, мы получаем пифагоровы тройки, такие как (3,4,5) (5,12,13) (7,24,25) … Мы также можем обнаружить это со следующими свойствами четырехугольных чисел:
Четырехугольное число и тройка Пифагора
Если мы продолжаем последовательно складывать нечетные числа, мы получим квадратные числа (четырехугольные числа), например 1 = 1 2 , 1 + 3 = 2 2 , 1 + 3 + 5 = 3 2 и т. Д.
Сумма нечетных чисел представляет собой квадратное число
Из рисунка видно, что 1 + 3 = 2 2 , 1 + 3 + 5 = 3 2 , 1 + 3 + 5 + 7 = 4 2 , ・ ・ ・ и так далее.Представьте сумму первых n нечетных чисел двумя следующими способами:
S = 1 + 3 + 5 + …… + (2 n -3) + (2 n -1)
S = (2 n -1) + (2 n — 3) + (2 n -5) + …… + 3 + 1
Добавьте два вышеуказанных выражения:
2S = 2 n + 2 n + 2 n + … … + 2 n + 2 n
В итоге получаем S = n 2
Как показано на рисунке, верно 1 + 3 + 5 + ・ ・ ・ + (2 n ? 1) = n 2 .Используя это соотношение, мы можем найти тип троек Пифагора.
Из 4 2 = 1 + 3 + 5 + 7 и 5 2 = 1 + 3 + 5 + 7 + 9 = 4 2 +3 2 , (3,4,5) равно пифагорейская тройка.
Из 12 2 = 1 + 3 + 5 + ・ ・ ・ +23 и 13 2 = 1 + 3 + 5 + ・ ・ ・ +23+ 25 = 12 2 +5 2 , (5,12,13) - пифагорова тройка.
Из 24 2 = 1 + 3 + 5 + ・ ・ ・ +47 и 25 2 = 1 + 3 + 5 + ・ ・ ・ +47+ 49 = 24 2 +7 2 , (7,24,25) — тройка Пифагора.
Когда последнее добавленное нечетное число само является квадратным числом, сумма нечетных чисел до предпоследнего нечетного числа также является квадратным числом, и их сумма также будет квадратным числом, поэтому три числа являются пифагорейскими. тройной.
Представление последнего добавленного нечетного числа с (2 p +1) 2 в качестве квадратного числа и при условии, что числа четырехугольника равны ( n ? 1) 2 = 1 + 3 + 5 + ・ ・ ・+ (2 n ? 3) и n 2 = 1 + 3 + 5 + ・ ・ ・ + (2 n ? 3) + (2 p +1) 2 ,
получаем n = 2 p 2 +2 p +1 и n ? 1 = 2 p 2 +2 p = 2 p ( p +1 ) из 2 n = 4 p 2 +4 p +2 потому что (2 p +1) 2 = n 2 ? ( n ? 1) 2 = 2 n ? 1.Следовательно, (2 p +1, 2 p ( p +1), 2 p 2 +2 p +1) для любого натурального числа p является тройкой Пифагора.
Калькулятор теорем Пифагора
Этот калькулятор теорем Пифагора вычислит длину любой из недостающих сторон прямоугольного треугольника, если вам известны длины двух других его сторон. Сюда входит вычисление гипотенузы. Гипотенуза прямоугольного треугольника — это сторона, противоположная прямому углу, и самая длинная сторона.Эту сторону можно найти с помощью формулы гипотенузы, другого термина теоремы Пифагора, когда она решает гипотенузу. Напомним, что прямоугольный треугольник — это треугольник с углом в 90 градусов. Два других угла также должны составлять 90 градусов, так как сумма углов любого треугольника равна 180. Продолжайте читать, чтобы ответить «что такое теорема Пифагора и как она используется?»
Что такое теорема Пифагора?
Теорема Пифагора описывает, как три стороны прямоугольного треугольника связаны в евклидовой геометрии.В нем говорится, что сумма квадратов сторон прямоугольного треугольника равна квадрату гипотенузы. Вы также можете думать об этой теореме как о формуле гипотенузы. Если стороны прямоугольного треугольника равны a и b , а гипотенуза равна c , формула будет
a² + b² = c²
Теорема была приписана древнегреческому философу и математику Пифагору, жившему в шестом веке до нашей эры. Хотя ранее она использовалась индейцами и вавилонянами, Пифагор (или его ученики) были первыми, кто доказал эту теорему.Следует отметить, что нет никаких конкретных доказательств того, что сам Пифагор работал или доказал эту теорему.
Как использовать теорему Пифагора
- Введите две длины, которые у вас есть в формуле. Например, предположим, что вы знаете
a = 4,b = 8, и мы хотим найти длину гипотенузыc. - После ввода значений в формулу получаем
4² + 8² = c² - Возвести каждый член в квадрат, чтобы получить
16 + 64 = c² - Объедините похожие термины, чтобы получить
80 = c² - Извлеките квадратный корень из обеих частей уравнения, чтобы получить
c = 8.94. Не пропустите и проверьте это с помощью нашего калькулятора теорем Пифагора!
Обратите внимание, что если вы решаете для a или b , измените уравнение, чтобы изолировать желаемую переменную, прежде чем объединять одинаковые термины и извлекать квадратный корень
Калькулятор теорем Пифагора вычислит стороны так же, как мы показали выше. Мы включили метод, чтобы показать вам, как вы можете решить вашу проблему, если вы предпочитаете делать это вручную.
Что такое формула гипотенузы?
Формула гипотенузы просто берет теорему Пифагора и решает гипотенузу, c . Решая гипотенузу, мы просто извлекаем квадратный корень из обеих частей уравнения a² + b² = c² и решаем относительно c . При этом получаем c = √ (a² + b²) . Это просто расширение теоремы Пифагора и часто не связано с названием формулы гипотенузы .
Другие соображения при работе с треугольниками
Обратите внимание, что стороны треугольника имеют определенный уклон или наклон.Мы можем использовать калькулятор уклона, чтобы определить уклон каждой стороны. В прямоугольном треугольнике стороны, образующие прямой угол, будут иметь уклон, произведение которых равно -1. Формула для наклона, если вы хотите рассчитать вручную:
. (y₂ - y₁) / (x₂ - x₁)
Итак, если координаты (3,6) и (7,10) , наклон сегмента будет (10-6) / (7-3) = 1 . Если наклон другого сегмента, образующего угол, равен -1 , тогда линии будут перпендикулярными, поскольку 1 * -1 = -1 .Следовательно, треугольник — это прямоугольный треугольник.
Вы также можете вычислить недостающие длины сторон и углы прямоугольного треугольника с помощью калькулятора прямоугольного треугольника. Если углы, указанные в задаче, выражены в градусах и вы хотите преобразовать их в радианы или радианы в градусы, воспользуйтесь нашим конвертером углов. Существует простой способ преобразовать градусы в радианы и радианы в градусы.
Если угол в радианах
- Умножить на
180 / π
Если угол в градусах
- Умножить на
π / 180
Иногда вы можете столкнуться с проблемой, когда отсутствуют две или все три стороны.В таких случаях калькулятор теорем Пифагора не поможет — вы будете использовать тригонометрические функции для поиска этих недостающих частей. Это можно сделать вручную или с помощью нашего калькулятора треугольников.
Математика 8 класс, Блок 8.6
Краткое содержание урока 6
Прямоугольный треугольник — треугольник с прямым углом. В прямоугольном треугольнике сторона, противоположная прямому углу, называется гипотенузой , а две другие стороны называются ее катетами .Вот несколько прямоугольных треугольников с обозначением гипотенузы и катетов:
Мы часто используем буквы a и b для обозначения длины более коротких сторон треугольника и c для обозначения длины самой длинной стороны прямоугольного треугольника. Если треугольник прямоугольный, то a и b используются для обозначения длины катетов, а c используется для обозначения длины гипотенузы (поскольку гипотенуза всегда является самой длинной стороной прямоугольного треугольника). Например, в этом прямоугольном треугольнике a = \ sqrt {20}, b = \ sqrt5 и c = 5.2 Это свойство всех прямоугольных треугольников, а не только этих примеров, часто называют теоремой Пифагора . Название происходит от математика по имени Пифагор, жившего в Древней Греции около 2500 г. до н.э., но это свойство прямоугольных треугольников было независимо открыто математиками других древних культур, включая Вавилон, Индию и Китай. В Китае такое же отношение называют теоремой Шан Гао. В будущих уроках вы научитесь некоторым способам объяснить, почему теорема Пифагора верна для любого прямоугольного треугольника .
 Слайд 9
Слайд 9


 !, +, — Слайд 15
!, +, — Слайд 15
 Рефлексия (3 мин)
Рефлексия (3 мин)
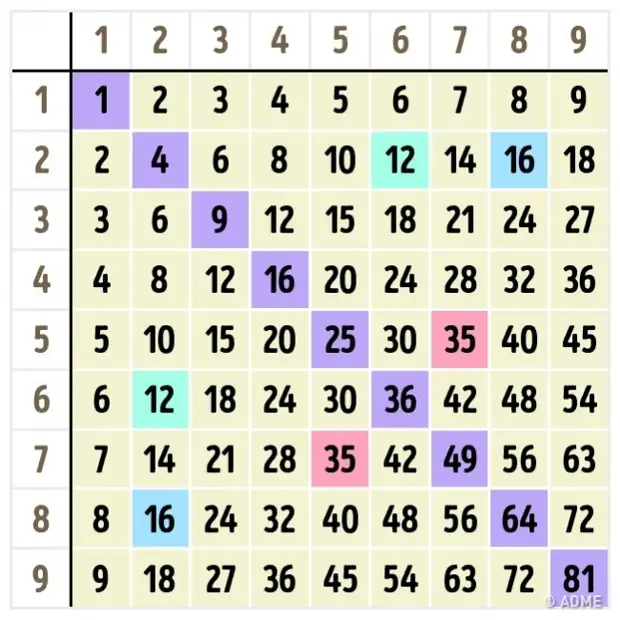 оценивают собственную деятельность на уроке.
оценивают собственную деятельность на уроке.



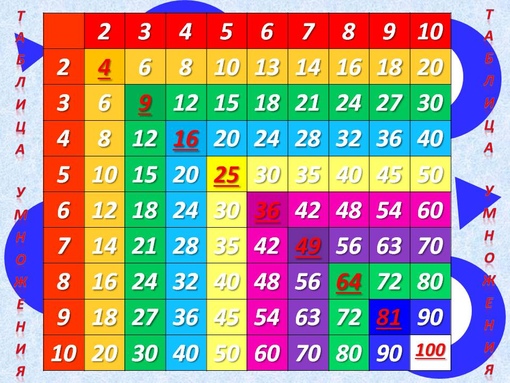

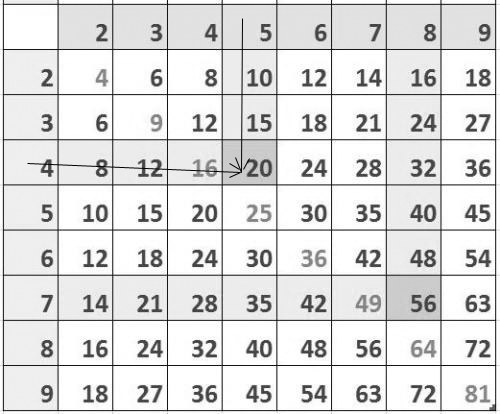 Работа по таблице (лист проверки д/з)
Работа по таблице (лист проверки д/з)
 35, № 6)
35, № 6)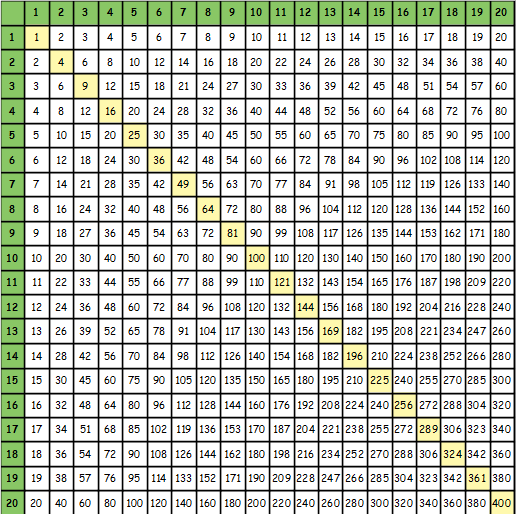

 Я изучаю курс для учителей элементарной математики. Мы должны составить план урока, чтобы научить младших школьников пользоваться теоремой Пифагора. Мне нужно научиться разбирать теорему Пифагора для элементарного ребенка. Я застрял в квадратной корневой части.
Я изучаю курс для учителей элементарной математики. Мы должны составить план урока, чтобы научить младших школьников пользоваться теоремой Пифагора. Мне нужно научиться разбирать теорему Пифагора для элементарного ребенка. Я застрял в квадратной корневой части.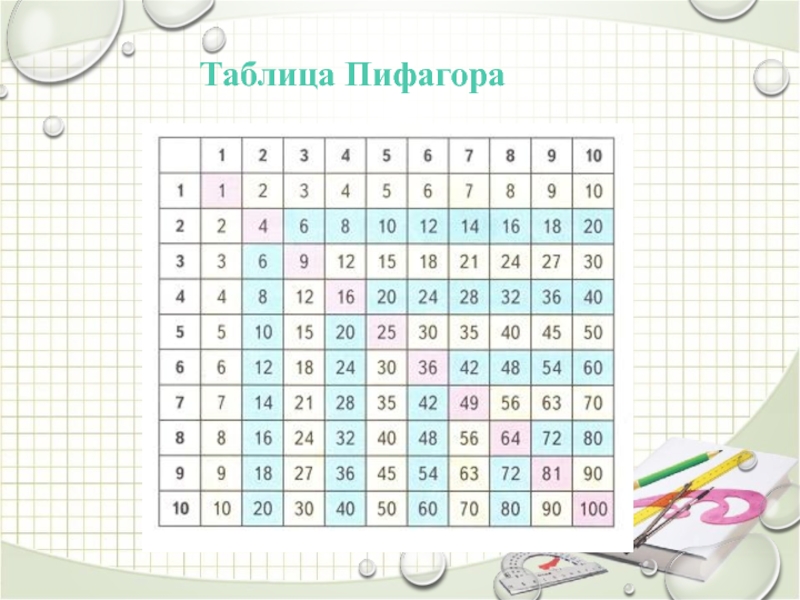 Конечно, поскольку измерения по своей природе всегда несколько неточны, они приблизятся только к получению истинного уравнения.
Конечно, поскольку измерения по своей природе всегда несколько неточны, они приблизятся только к получению истинного уравнения.