1 десяток. Состав числа 10
Цели урока.
1. Закрепить знание состава числа 10. Совершенствовать умения:
а) выполнять задания, требующие знание состава числа 10;
б) записывать выражения по рисунку или соотносить предложенные с рисунком;
в) выполнять группировку;
г) выявлять закономерности;
д) отмечать изменения.
2. Развивать внимание, память, логическое мышление, воображение, математическую речь.
3. Воспитывать интерес к предмету, аккуратность, чувство товарищества и взаимопомощи.
Оборудование: рисунок к загадке, модель капельки, карточки с числами, геометрические фигуры-маленькие и большие квадраты разного цвета, рисунок “волшебного колеса”, стопка тетрадей, перфокарты, капелька для каждого ученика.
Ход урока
I. Организация учащихся на работу
У: Какое время года?
Д: Весна.
У: Что изменилось в природе?
Д: Тает снег, солнце греет сильнее, на улице становится тепло.
У: Отгадайте загадку:
Растёт она вниз головой,
Не летом растёт, а зимой.
На солнце её припечёт,
Заплачет она и умрёт. (Сосулька)
У: Что значит заплачет?
Д: Капают капли.
Рисунок 1
У: Каждая упавшая капля пахнет весной, она не простая и предлагает вам задание. Если мы быстро и правильно выполним задание, то эта капля попадает в ручеёк знаний (пока что ещё маленький).
Рисунок 2
II. Чистописание (1-ая капелька)
У: Разгадайте правило, по которому составлен ряд чисел, и продолжите его (только однозначные числа)
4, 6, 5, 7, 6, …, …, …, …
Д: 4, 6, 5, 7, 6, 8, 7, 9, 8 (фронтальная проверка).
У: Уменьшите каждое число в ряду на 3.
На обратной стороне доски даны ответы
(самопроверка).
1, 3, 2, 4, 3, 5, 4, 6, 5,
У: Мы справились с заданием, и первая капелька попадает в ручеёк знаний (капельку помещаем в ручеёк).
III. Устный счёт (2-ая капелька)
1) У: На доске даны карточки с числами 1-9. Я говорю задание, вы должны подумать и выбрать карточку с нужным ответом:
- на сколько число 8 больше числа 4?
- на сколько число 7 меньше числа 9?
- число 9 уменьшить на 3;
- число 2 увеличить на 1;
- чему равна сумма чисел 2 и 5?
- чему равна разность чисел 7 и 6?
Д: 4, 2, 6, 3, 7, 1 (фронтальная проверка).
2) У: Вставьте вместо точек числа, чтобы получились верные записи. Использовать только числа, полученные в первом задании
… + …=… — …
… — …=… — …
… + …=… + …
Задание выполняется самостоятельно в тетрадях,
затем проверяется у доски. Рассматриваются все
варианты ответов.
У: Мы справились с заданием, и вторая капелька попадает в ручеёк знаний (капельку помещаем в ручеёк).
IV. Подготовка к работе (3-я капелька)
У: Назовите числа, которые нужно вставить в «окошки».
Рисунок 3
Учащиеся называют числа, выходят к доске и переворачивают карточки:
3, 9, 5, 1, 6, 10
У: Назовите лишнее число.
Д: 10.
У: Почему?
Д: Двузначное, один десяток.
У: Какую задачу урока ставим? Зачем?
Д: Повторение и закрепление состава числа 10, чтобы потом легко и быстро выполнять сложение и вычитание.
Сообщение темы и задач урока.
У: Мы справились с заданием, и третья капелька попадает в ручеёк знаний (капельку помещаем в ручеёк).
V. Повторение.
1) 4-ая капелька.
У: У меня в стопке тетради. Сколько их?
Д: 5 (считают).
У: Я добавила еще несколько. Сколько стало?
Сколько стало?
Д: 10 (считают).
У: Сколько я добавила тетрадей?
Д: 5.
У: Как получили 10?
Д: 5 + 5=10.
Выражение записывается на доске и в тетради.
2) 5-ая капелька.
Даны фигуры. Назовите их.
Рисунок 4
У: По какому признаку нужно разбить все фигуры на две группы, чтобы это соответствовало выражению 5 + 5?
Д: По цвету.
Ученик у доски делит фигуры по цвету на две группы.
У: По какому ещё признаку можно разбить фигуры?
Д: По размеру.
Ученик у доски делит фигуры по размеру на две группы и записывает выражение 6+4=10, 4+6=10. Дети записывают в тетрадь.
3) Физкультминутка “Хомка”.
Хомка-хомка, хомячок,
Полосатенький бочок.
Хомка раненько встаёт,
Щёки моет, шейку трёт.
Подметает хомка хатку
И выходит на зарядку.
Раз, два, три, четыре, пять!
Хомка хочет сильным стать.(Дети имитируют все движения хомячка.)
4) 6-ая капелька.
Игра «Волшебное колесо»
Рисунок 5
У: Расположите числа от 1 до 9 так, чтобы в любом направлении по прямой линии получилось в сумме 10.
Ученики выходят к доске и записывают пары чисел.
У: А теперь напишем новые выражения на доске и в тетради: 1+9=10; 9+1=10; 2+8=10; 8+2=10; 3+7=10; 7+3=10.
Прочитайте все выражения (записи в тетради).
У: Мы справились с этими заданиями, поэтому все капельки попадают в ручеёк знаний.
5) 7-ая капелька.
Работа по учебнику Н.Б.Истоминой. Страница 125 № 291 (работа в парах).
У: Рассмотрите каждую пару рисунков. Что происходит?
Д: Количество кругов увеличивается.
1-ая пара объясняет: число красных кругов увеличили на 2, стало 10 (8+2)
2-ая пара – число жёлтых кругов увеличили на 4, получили 10 (6+4)
3-я пара — число зелёных кругов увеличили на 5, получили 10 (5+5)
4-ая пара — число синих кругов увеличили на 3, получили 10 (7+3)
У: Какого случая не хватает?
Д: 9+1=10
6) 8-ая капелька.
Работа в тетради на печатной основе (ТПО). Страница 37 №79. Первое задание выполняется с объяснением.
У: В треугольнике 4 круга. Какой цифрой записали это число?
Д: 4.
У: Сколько надо дорисовать кругов до 1 десятка?
Д: 6.
У: Сколько всего кругов?
Д: 10. Для записи этого числа используем две цифры: 1 и 0.
Дальше задание выполняется самостоятельно. После выполнения – проверка.
У: Мы справились с заданием, и эти капельки тоже попадают в ручеёк знаний.
7) 9-ая капелька.
Работа с перфокартами.
У: У вас на столе перфокарта, с помощью которой я проверю, как вы усвоили состав числа 10. А опускать капельку в ручеёк или нет, я решу после проверки выполненной работы.
Рисунок 6
VI. Итог.
У: Что повторили на уроке? Какие задания больше понравились?
На столе у каждого маленькая капелька.
Дети выходят к доске и опускают свою капельку в “ручеёк знаний” (в конверт).
Список литературы:
- Истомина Н.Б. Математика: учебник для 1 класса общеобразовательных учреждений / Н.Б. Истомина. – 10-е изд. – Смоленск: Ассоциация XXI век, 2010. – 176 с.
- Истомина Н.Б., Редько З.Б. Математика: тетрадь к учебнику для 1 класса общеобразовательных учреждений. В 2 ч. Ч.2. / Н.Б. Истомина. – 13-е изд. – Смоленск: Ассоциация XXI век, 2010. – 64 с.
- Бугримова Т.А. Математика. 1 класс: Поурочные
планы (по учебнику Н.Б. Истоминой) / Т.
 А. Бугримова.
– Волгоград: Учитель, 2004. – 287 с.
А. Бугримова.
– Волгоград: Учитель, 2004. – 287 с.
Проверочный тест «Состав чисел до 10» для 1 класса от ЛогикЛайк
Математика / 1 класс / Тесты
Умение представлять число в виде суммы двух других чисел — основа навыков сложения и вычитания. Проверьте как первоклассник усвоил состав чисел. Предложенный онлайн-тест превратит обучение в весёлую игру!
Задания в тесте разноплановые: подобрать пару чисел, найти пропущенные числа, выбрать верное или неверное утверждение. Маленьким математикам нужно быть внимательными, чтобы ответить правильно на все вопросы.
Результат теста:
Более 2500 заданий для развития математических способностей и логического мышления — в онлайн‑курсе ЛогикЛайк.
Тест составлен на основе программного материала по математике для учеников 1 класса и соответствует требованиям ФГОС.
Какая пара чисел является составом числа 5?
Варианты ответов:
а) 3 и 2
б) 2 и 4
в) 1 и 3
Узнать ответ
Ответ: а) 3 и 2.
Какое число нужно вставить в «окошко»?
☐ — это 2 и 4
Варианты ответов:
а) 9
б) 8
в) 6
Узнать ответ
Ответ: в) 6.
Какая пара чисел не является составом числа 9?
Варианты ответов:
а) 7 и 2
б) 4 и 5
в) 3 и 8
Узнать ответ
Ответ: в) 3 и 8.
Какое число нужно вставить в «окошко»?
7 — это 3 и ☐
Варианты ответов:
а) 4
б) 5
в) 3
Узнать ответ
Ответ: а) 4.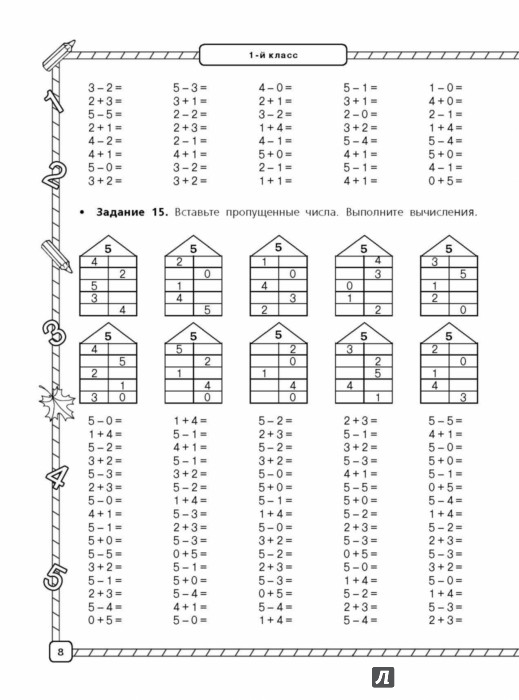
Какое утверждение верно?
Варианты ответов:
а) 7 – это 5 и 2
б) 8 – это 4 и 6
в) 6 – это 3 и 4
Узнать ответ
Ответ: а) 7 – это 5 и 2.
Какое число нужно вставить в «окошко»?
8 — это ☐ и 3
Варианты ответов:
а) 6
б) 5
в) 4
Узнать ответ
Ответ: б) 5.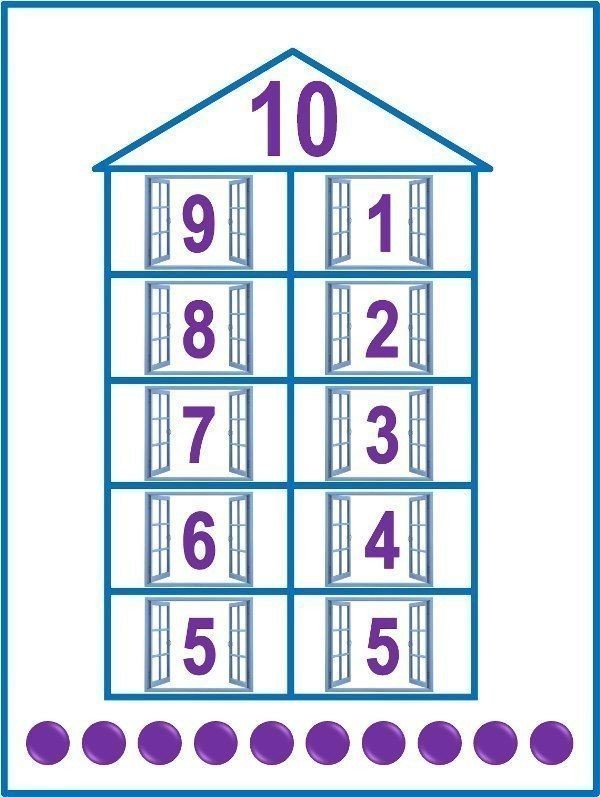
Какая пара чисел является составом числа 9?
Варианты ответов:
а) 5 и 6
б) 3 и 7
в) 4 и 5
Узнать ответ
Ответ: в) 4 и 5.
Какое число нужно вставить в «окошко»?
10 — это 7 и ☐
Варианты ответов:
а) 3
б) 5
в) 4
Узнать ответ
Ответ: а) 3.
Какое утверждение верно?
Варианты ответов:
а) 10 – это 2 и 6
б) 7 – это 5 и 2
в) 8 – это 4 и 5
Узнать ответ
Ответ: б) 7 – это 5 и 2.
Какое утверждение неверно?
Варианты ответов:
а) 9 – это 6 и 4
б) 6 – это 3 и 3
в) 8 – это 2 и 6
Узнать ответ
Ответ: а) 9 – это 6 и 4.
Попробуйте пройти другие «математические тесты для 1 класса» от ЛогикЛайк.
Состав Числа Примеры Тренировки Хитрости в Мышлении
Для чего нужно знать состав числа?
Как упражнения по составу чисел могут помочь вашему ребенку , Какая польза от знания состава числа.
Ответы на эти вопросы Вы можете получить у нас на сайте.
С составом числом знакомиться уже начинают в детском саду, в старших группах есть занятия по подготовке детей к школе. Малышей учат считать и решать простенькие примеры и задачи.
Малышей учат считать и решать простенькие примеры и задачи.
А для этого детям дают задание запомнить состав числа.
В возрасте 6-7 лет ребенка знакомят с составом чисел от 0 до 10 . Изучение состава числа поможет будущему школьнику легко освоить сложение и вычитание.
К этому возрасту ребенок знает наизусть прямой счет до 10, обратный счет в пределах 10, умеет пересчитывать и отсчитывать предметы, знает состав числа из единиц: понимает, что 3 — это 1 и 1 и 1. Все это говорит о том, что ваш ребенок готов к изучению состава чисел до 10 из двух меньших чисел.
Состав числа начинают изучать с опорой на наглядный материал. С помощью карандашей, орехов, конфет покажите ребенку все варианты состава чисел в пределах десяти. Например, число 6 — это 0 и 6, 1 и 5, 2 и 4, 3 и 3, 4 и 2, 5 и 1, 6 и 0. Одно занятие посвящайте одному числу. Пусть ребенок вначале отсчитает нужное число предметов, а затем распределит их по группам, применяя различные комбинации. Результаты своих вычислений ребенок может записывать в виде примеров. Не забывайте, что самый лучший тренажер и помощник, который всегда с собой – это пальцы ребенка. В первое время с помощью пальцев можно и нужно находить правильный ответ. Но результатом изучения состава числа должен стать счет в уме. Ребенок предстоит научиться отвечать на вопросы: 8 — это 3 и ? 5 это 2 и ?
Не забывайте, что самый лучший тренажер и помощник, который всегда с собой – это пальцы ребенка. В первое время с помощью пальцев можно и нужно находить правильный ответ. Но результатом изучения состава числа должен стать счет в уме. Ребенок предстоит научиться отвечать на вопросы: 8 — это 3 и ? 5 это 2 и ?
Когда мы просто складываем разные числа, результат может получиться любой. Но когда мы выясняем состав какого-то числа, то как бы идём в обратном направлении — от результата, который известен заранее. Мы учим определённые пары слагаемых — у каждого числа они свои, — чтобы получался именно этот результат.
Помните
Знание состава числа — залог быстрого счета, устного и письменного. Если во время подготовки к школе состав числа до 10 не уложился у ребенка в голове, надо обязательно уделить этому время в первом классе, а потом не забывать о закреплении состава числа до 20 и далее — это сильно сократит время на вычисления.
Я предлагаю действовать в таком порядке.
- Объяснить наглядно, как при одной и той же сумме одно слагаемое может увеличиваться, а второе — уменьшаться. Очень удобно это делать на предметах, которых всегда фиксированное и привычное глазу количество: отлично подходят коробки из-под яиц (10), прозрачные упаковки печенья или конфет (обычно 6, 8, 12), строчки календаря (7), упаковки акварели, пластилина и т.п.
- Ребёнок обязательно должен записать в тетрадь (или на листочек) все возможные варианты состава числа, проговорить их вслух, найти и соединить примеры с одинаковыми слагаемыми (7+1 и 1+7, например) если он конечно может писать.
- Очень советую сделать для закрепления состава числа карточки вида
7 + 1 = 8
6 + 2 = 8
5 + 3 = 8
4 + 4 = 8
Отдельную карточку на каждый пример. Зачем? Карточки составом числа дают нам много возможностей для заучивания комбинаций.
Обзаведитесь карточками на состав числа. Их можно купить или сделать. Они бывают нескольких типов, и лучше, чтобы они были двух видов. Разрезная карточка состоит из двух половинок. На одной изображён 1 предмет, на другой — 1, 2, 3 и больше точно таких же предметов. Половинки могут быть соединены знаком «+», но «плюс» можно сделать и отдельно. Второй комплект представляет собой набор картинок, на которых изображены эти же предметы одним множеством, без всякого разделения. Когда ребёнок хорошо научится сопоставлять число и цифру, можно сделать такие же карточки с цифрами. Их может быть несколько комплектов, чтобы представлять каждое число в разных вариантах.
Разрезная карточка состоит из двух половинок. На одной изображён 1 предмет, на другой — 1, 2, 3 и больше точно таких же предметов. Половинки могут быть соединены знаком «+», но «плюс» можно сделать и отдельно. Второй комплект представляет собой набор картинок, на которых изображены эти же предметы одним множеством, без всякого разделения. Когда ребёнок хорошо научится сопоставлять число и цифру, можно сделать такие же карточки с цифрами. Их может быть несколько комплектов, чтобы представлять каждое число в разных вариантах.
Проводите занятия регулярно. Покажите ребёнку карточку, на которой изображено, скажем, 5 предметов. Предложите подобрать картинки так, чтобы на всех вместе тоже было столько же яблок или кружочков. Периодически меняйтесь ролями. Пусть ребёнок тоже даёт вам задания, а вы его старательно выполняйте. Иногда делайте ошибки, ваш ученик должен научиться контролировать ваши действия.
Аналогичные задания поводите и с цифрами. Покажите, например, число 9 и точно так же, как в предыдущем случае, предложите найти несколько вариантов его состава.
Объясните ребёнку, что чем больше число — тем больше возможностей его составить.
Например:
- Раскладываем карточки по порядку.
- Просим ребёнка все их назвать.
- Переворачиваем, кладём карточки лицевой стороной вниз.
- Просим ребёнка их припомнить.
- Открываем, проверяем, хвалим!
Сделать столько раз, сколько понадобится, чтобы ребёнок назвал их все. Заниматься можно буквально по нескольку минут, между делом.
Поговорим о хитростях запоминания
Расскажите, что любое число всегда состоит из единицы и предыдущего числа. Таким образом, если нужно определить состав числа 8, у ребенка уже готов один ответ: 8 – это 1 и 7. Соответственно, чтобы определить, сколько будет 8 минус 1, нужно от 8 отчитать 1 в обратном порядке, то есть назвать предыдущее число.
Познакомьте ребенка также с отсчетом 2. Чтобы ответить на вопрос: 8 – это 2 и сколько?, нужно сначала отсчитать 1 в обратном порядке, а потом еще 1.
Больше практикиЧтобы довести определение состава числа до автоматизма, решайте как можно больше примеров.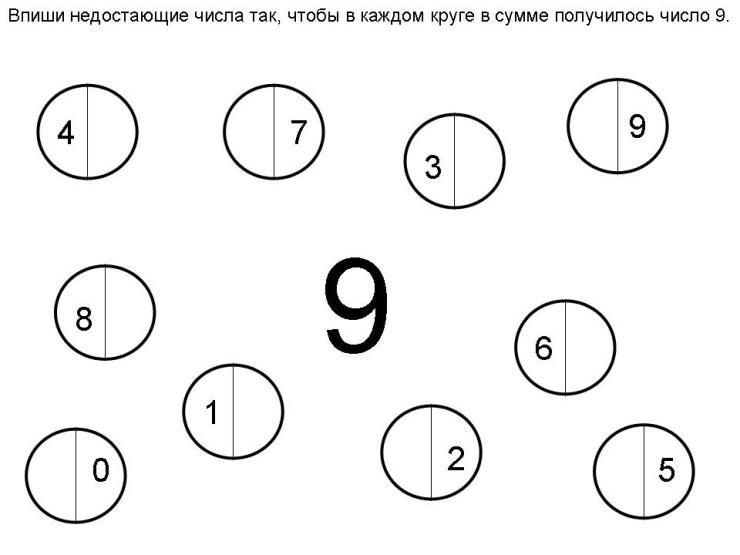 Можно играть в игру: вы называете число, состав которого нужно определить, ребенок как можно быстрее показывает любое уместное количество пальцев, вы показываете оставшееся количество. Потом меняетесь ролями. Эта игра также тренирует навык сравнения, ведь если вы назовете 4, ребенку нельзя показать 5 и более пальцев.
Можно играть в игру: вы называете число, состав которого нужно определить, ребенок как можно быстрее показывает любое уместное количество пальцев, вы показываете оставшееся количество. Потом меняетесь ролями. Эта игра также тренирует навык сравнения, ведь если вы назовете 4, ребенку нельзя показать 5 и более пальцев.
Это интересно, читайте также:
Изучаем Состав Числа в виде Игры
Тренировка
А теперь будем тренировать запоминание. Точнее, припоминание. Теперь наши задания направлены на то, чтобы ребёнок припоминал нужные примеры.
Задание 1. Я делаю так — даю листок с примерами, где есть и те примеры, которые мы сейчас учим, и другие. Инструкция для ребёнка: «Найди все примеры, которые мы сейчас учили, и запиши правильный ответ. На другие примеры сейчас не обращай внимания».
(Некоторые прилежные дети начинают всё равно решать все примеры. Поэтому я стараюсь подбирать такие «ненужные» примеры, которые они должны были уже освоить. )
)
Самое главное — наблюдать за ребёнком в процесс работы: он припоминает примеры (те, которые мы сейчас заучиваем) или заново считает? Если считает — ничего не получилось! Либо ребёнок их ещё не запомнил (тогда надо вернуться к пункту 3), либо не понимает, чего мы сейчас от него хотим. Нам нужно именно это: найти знакомые примеры!
Задание надо выполнить хотя бы 3- раза (не сразу, с интервалами, в один день не более двух раз через промежуток времени).
Задание 2. Снова даём ребёнку листок с примерами, где есть и те, которые мы «учили», и на состав других чисел. И просто просим решать примеры. Не подсказываем, что некоторые примеры он уже «помнит».
Наблюдаем. Делаем выводы: если вспоминает «наши» примеры и сразу пишет в них ответы — ура, получилось! Если нет — возвращаемся к пункту 3.
Примеры с вычитанием
Теперь нас ждёт непростой момент — мы должны научить ребёнка решать примеры на вычитание, используя знание состава числа.
Если мы помогаем первокласснику, необходимо использовать математические термины: «Когда мы складываем два слагаемых, у нас получается сумма. Это примеры на сложение. А что такое пример на вычитание? Это когда мы знаем сумму и знаем одно слагаемое, а второе слагаемое не знаем. Как его найти? Для этого из суммы мы вычитаем известное слагаемое.
Но если ты помнишь состав числа, то неизвестное слагаемое ты можешь просто припомнить. Мы с тобой выучили состав числа 8. Ты помнишь все комбинации? Перечисли!»
Ребёнок отвечает:
7 + 1 = 8
6 + 2 = 8
5 + 3 = 8
4 + 4 = 8
«Молодец! А теперь давай будем менять числа местами! Наши примеры будут на вычитание, поэтому сумму 8 мы всегда будем ставить на первое место. Вычитать можно только из самого большого числа! Вычитать будем одно из слагаемых, а второе будет получаться в ответе. Давай попробуем: называй любой пример на сложение с ответом 8!»
5 + 3 = 8
«Сейчас мы с тобой будем „прятать“ одно слагаемое, делать его неизвестным. Что у нас получится:
Что у нас получится:
8 — 5 = ?
Правильно, 3! Второе слагаемое!
Давай попробуем ещё раз:
6 + 2 = 8
А сколько будет:
8 — 6 = ?
Правильно, 2 — второе слагаемое!».
На этом этапе я даю детям вот такие примеры:
6 + 2 =
2 + 6 =
8 — 2 =
8 — 6 =
5 + 3 =
3 + 5 =
8 — 3 =
8 — 5 =
Такая последовательность примеров помогает ребёнку осознать связь сложения и вычитания. И опять же — всё направлено на запоминание. Когда мы решаем примеры на вычитание, можно посчитать, а можно припомнить. Припоминать — быстрее!
Момент связи сложения и вычитания очень важен для решения уравнений. Если ребёнок не улавливает эту связь, ему будет трудно решать уравнения.
Заполни пустые места или запоминанием состав числа
Скажем, 5 это 1 плюс 4, или 2 плюс 3, или 3 плюс 2, или 4 плюс 1.
Малыши заучивают это как стишок или скороговорку, зачастую просто не вникая или не понимая смысла.
Для того, чтобы состав чисел от 1 до 10 действительно отложился в детских головках, Ментальная Арифметика предлагает скачать карточки-задания на состав числа.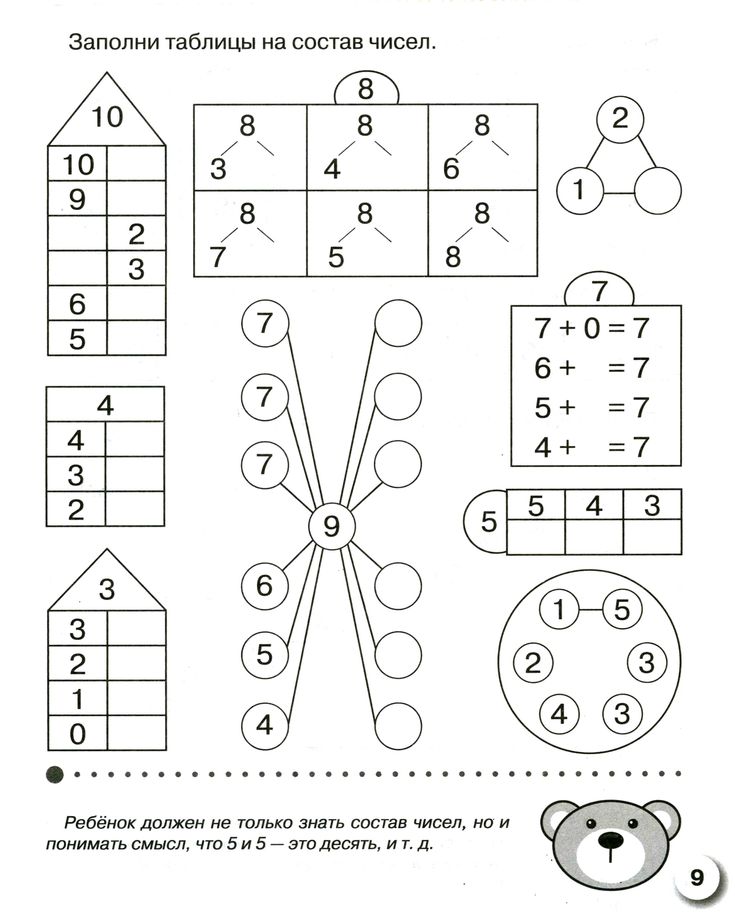
Для того, чтобы заполнить пустые места надо подумать. Раздумья ускоряют память детей и соответственно мысль.
Желаем Вам успехов в познании математических цифр.
Авторская статья от Аллы Ромашкиной
Ваш сайт Ментальная Арифметика.
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа для дошкольников. Учимся раскладывать числа на части
К возрасту 5-6 лет ребёнок способен считать до 10 в прямом и обратном порядке, умеет пересчитывать и отсчитывать предметы, знает, как разложить числа на единицы, например, 4 равно 1, 1, 1 и 1. Это значит, что малыш уже готов осваивать состав числа до 10.
Аудио-версия статьи «СОСТАВ ЧИСЛА ДЛЯ ДОШКОЛЬНИКОВ» Тег audio не поддерживается вашим браузером. Скачать. СОСТАВ ЧИСЛА ДЛЯ ДОШКОЛЬНИКОВ
Содержание
Зачем учить состав числа
Как быстро научиться раскладывать числа на части
- Действия с предметами
- Числовая линейка
- Наглядность
- Решение бытовых задач
- Знакомство с примерами
Игры и упражнения на закрепление состава чисел
- Сколько кругов?
- Прищепки
- Сколько в корзинке
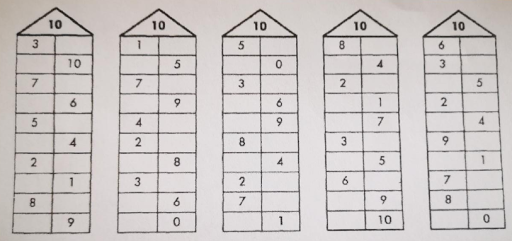
- Числовые домики
- Упражнения на закрепление нескольких чисел
- Наглядный способ решения примеров
Советы для мам
В современной начальной школе детям приходится считать в уме. Лучше заранее научить дошкольников раскладывать числа на составные части. Знание состава числа позволит быстро справляться с примерами на сложение и вычитание.
Лучше заранее научить дошкольников раскладывать числа на составные части. Знание состава числа позволит быстро справляться с примерами на сложение и вычитание.
Зачем учить состав числа
После 5 лет можно знакомить дошкольников с составом чисел. Это нужно для заблаговременной подготовки к будущим урокам математики. Малыш уже способен понять, что каждое число, кроме единицы, состоит из двух меньших.
К первому классу дети должны знать, что 10 можно разложить на 1 и 9, 5 и 5, 8 и 2, 7 и 3, 6 и 4, а 9 состоит из 5 и 4, 6 и 3 и так далее. Запомнив все парные сочетания в числах первого десятка, ребёнок с лёгкостью освоит сложение и вычитание.
Научившись раскладывать числа на части, малыши легко справляются с примерами. Например, с такими: 2+3=5 или 4+1=5. Ребятишки знают, что состав числа 5 — это 2 и 3 или 4 и 1, поэтому считают быстро и без ошибок.
Как быстро научиться раскладывать числа на части
Справиться с решением задачи вам поможет знание простых принципов. Чтобы малышу было понятней, всегда применяйте элемент игры и наглядность. Каждое занятие посвящайте одному числу.
Чтобы малышу было понятней, всегда применяйте элемент игры и наглядность. Каждое занятие посвящайте одному числу.
Обучение ребёнка разбейте на несколько этапов, переходя от простого к более сложному:
Действия с предметами
В самом начале дошкольникам объясняют состав числа с помощью знакомых вещей. Можно раскладывать орешки, жёлуди, камешки и прочие однотипные предметы.
Числовая линейка
Для запоминания состава числа и решения примеров пригодится обычная линейка.
Допустим, нужно сложить 4 и 2. Малыш ставит пальчик или карандашик на первое из чисел — 4 и перемещает его на 2 деления вправо, до цифры 6.
Важно донести до ребёнка принцип: если нужно сложить два числа, двигаем палец вправо. Когда вычитаем, то перемещаем влево.
Аналогичные действия выполняют с числовыми лучами.
Наглядность
Разместите в детской комнате красочные изображения числовых домиков и картинки с составом чисел. Обращайте на них внимание малыша, делайте пояснения. Благодаря зрительной памяти, информация усвоится быстрее.
Благодаря зрительной памяти, информация усвоится быстрее.
Решение бытовых задач
Дети хорошо усваивают знания, необходимые в повседневной жизни. Накрывая на стол, положите 1 ложку. Спросите малыша, сколько нужно добавить ложек, если в доме 4 человека.
Последует ответ ― 3. Значит, число 4 состоит из двух частей: 1 и 3. Принеси ложки и проверь. Как ещё их можно разложить? Правильно, 2 и 2.
Знакомство с примерами
Когда дошкольник запомнит состав чисел, переходите к примерам.
Используйте карточки с цифрами и знаками «плюс», «минус», «равно». Покажите малышу, как путём сложения и вычитания получить число 8 (2+6=8, 10—2=8) или другое. Постепенно у ребёнка сформируется представление о примерах.
Игры и упражнения на закрепление состава чисел
Регулярно занимаясь, дети быстро запоминают состав чисел до 10. Более сложная задача ― научиться раскладывать числа на части, понять, как это делается. В этом поможет подборка математических игр.
Сколько кругов?
В качестве наглядного пособия предлагаем использовать набор двусторонних карточек с кружочками. Одна сторона у них синего цвета, другая красного. Показываем малышу карточку с пятью красными кругами.
«Сосчитай количество кругов (5).
Один повернём синей стороной, сколько осталось красных (4)?
Запомни, число 5 состоит из двух частей — 4 и 1. Давай посмотрим, каким ещё может быть состав числа 5». Поочерёдно переворачиваем все круги, комментируя свои действия.
Прищепки
Для игры, кроме карточек с цифрами до 10, пользуемся бельевыми прищепками. Их можно заменить канцелярскими скрепками. Число 1 приравниваем к одной прищепке, 2 ― к двум и так до десяти.
Берём карточку с цифрой 4, прицепляем 4 прищепки с одной из сторон. Спрашиваем ребёнка: «Сколько всего прищепок? (4). Сейчас разделим число 4 на 2 части. Здесь оставляем три прищепки, на противоположной стороне прикрепим одну. Как ты думаешь, из каких частей состоит число 4? (3 и 1)».
Покажите, как можно разделить иначе: 2 и 2. Упражняйтесь со всеми числами первого десятка. Чтобы сделать состав числа понятным для дошкольников, возьмите прищепки либо скрепки двух цветов. Игра развивает математическое мышление и моторику.
Сколько в корзинке
Подготовьте комплекты карточек с числами от 1 до 10, их можно сделать самим. Ещё вам понадобятся 8 коробок, мисок или ведёрок. На каждой ёмкости нарисуйте число с трёх до десяти.
Объясните ребёнку, что во все миски нужно положить по 2 цифры или карточки. Если сложить их вместе, должно получиться нарисованное число. Покажите пример: в миску с числом 6 можно положить цифры 5 и 1, 3 и 3, 2 и 4. Задача малыша ― применить одно из возможных сочетаний.
Сначала играйте по очереди, чтобы кроха понял, как правильно действовать. Если ребёнок легко справляется, усложните задание: попросите использовать все комбинации.
Числовые домики
Игра поможет дошкольникам запомнить состав чисел первого десятка.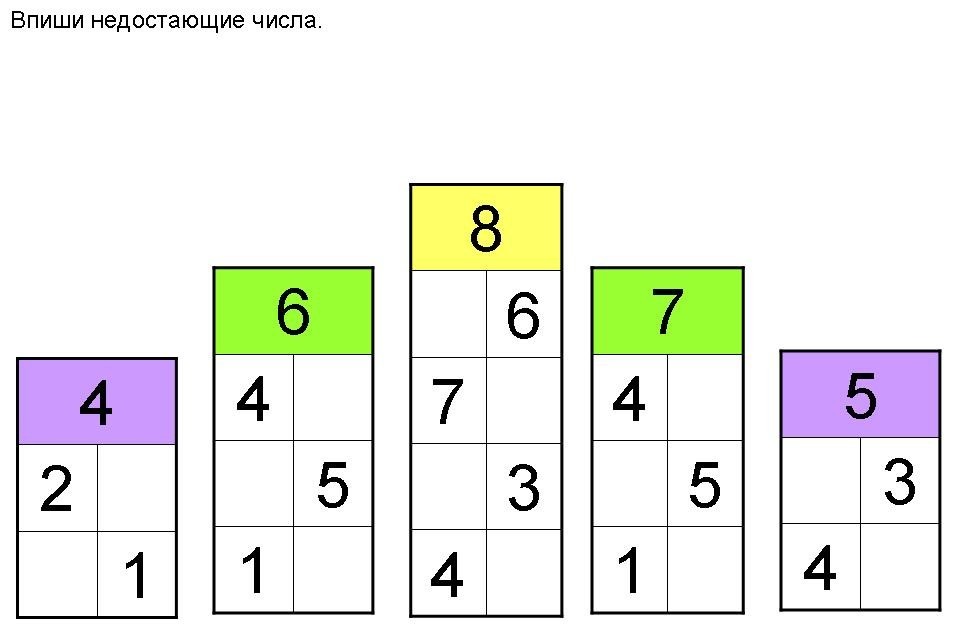 В качестве наглядного пособия используют 9 числовых домиков из нескольких этажей: от 2 до 10. Их можно скачать тут.
В качестве наглядного пособия используют 9 числовых домиков из нескольких этажей: от 2 до 10. Их можно скачать тут.
Расскажите малышу, что у домиков есть хозяева — числа, нарисованные на крыше. На каждом этаже 2 квартиры (два окошка). Общее количество жильцов одного этажа должно совпадать с числом на крыше. Тогда хозяин разрешит поселиться.
Покажите ребёнку, как заселить домик, где хозяйка цифра 4. Комментируйте ваши действия: «На первом этаже будут жить 0 и 4, вместе получим 4. На втором — пара 2 и 2, а на третьем (3 и 1)?» Спросите малыша, из каких чисел ещё состоит 4.
Затем предложите крохе самому заселять домики, начав с первого этажа.
Учите рассуждать вслух, сколько жильцов должно быть в каждой квартире? На первых занятиях можно применять счётные палочки. Играя с домиками, дети быстро научатся раскладывать числа на части.
Упражнения на закрепление нескольких чисел
Закрепить навыки счёта поможет подборка упражнений с картинками. Все задания можно скачать здесь.
Помоги корабликам найти свою пристань. На борту кораблей написаны по 2 цифры, образующие состав числа одной из пристаней внизу рисунка. Применив сложение или вычитание, ребёнок сможет найти пристань для каждого кораблика. Например, к пристани с числом 5 идут корабли, на которых написано 4+1 и 3+2. Путь лучше начертить карандашом.
Разложи на две части. Например, на картинке 10 яблок и 5 пар тарелок. Задача малыша – разложить яблоки так, чтобы в каждой паре их было 10. Повторяться нельзя. Другие задания:
Домики с пустыми квартирами. Ребёнку нужно вписать правильное число в каждую клеточку.
Похожее задание выполняют в упражнении «Числовой ряд» . Если кроха пока не умеет рисовать цифры, попробуйте применить карточки.
Скачать задания
Наглядный способ решения примеров
Использование счётных карточек и обычных предметов поможет научиться раскладывать числа на части.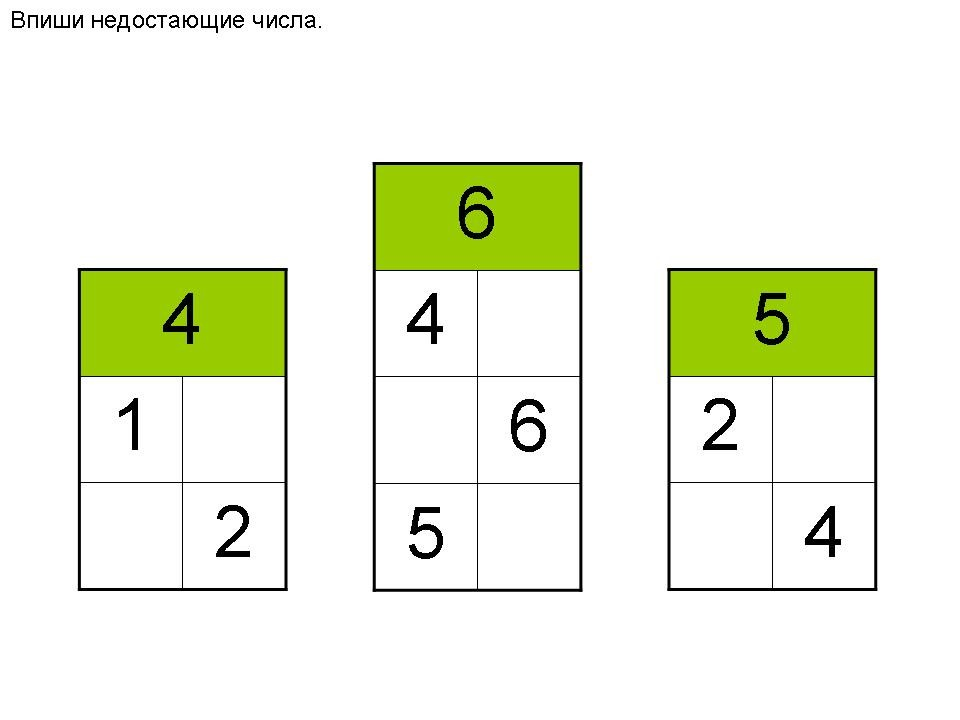 Наглядные действия облегчают выполнение заданий. Вот как можно решить пример с помощью любых орешков.
Наглядные действия облегчают выполнение заданий. Вот как можно решить пример с помощью любых орешков.
Скажите малышу, что белочка нашла 6 орешков. Ей нужно спрятать одну часть в дупло, а другую в норку. Как их разложить? Покажите ребёнку все возможные комбинации: 3 и 3, 2 и 4, 5 и 1. Используйте карточки.
Для изучения состава числа с дошкольниками подготовьте тетрадь в клетку и 2 карандаша разных цветов. Нарисуйте на странице шесть полосок размером 1 на 6 клеточек. Рядом напишите примеры.
Закрашивая клеточки в полосках, малыши видят, как квадратики одного цвета убывают, а другого прибавляются.
Советы для мам
Понять, что такое состав числа дошкольникам довольно сложно. Вам помогут игровые приёмы и маленькие хитрости:
1. На прогулке, в магазине и дома используйте любую возможность для практического применения счёта. Решайте бытовые задачки. Старайтесь, чтобы малышу было интересно.
2. В начале освоения нового материала разрешите считать с помощью привычного «калькулятора» — пальчиков.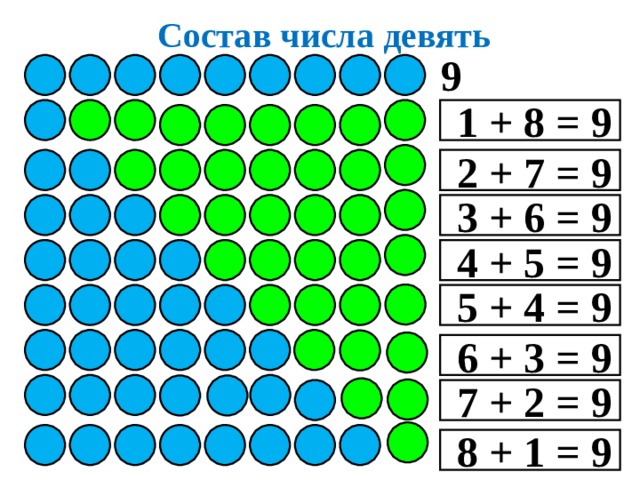 Постепенно приучайте ребёнка к счёту в уме. При систематических занятиях вопрос: «4 это 1 и сколько?» и ему подобные не вызовет затруднений.
Постепенно приучайте ребёнка к счёту в уме. При систематических занятиях вопрос: «4 это 1 и сколько?» и ему подобные не вызовет затруднений.
3. Поделитесь с малышом «большим секретом»: в состав каждого числа входит единица и предыдущее число. Например, 6 — это 1 и 5, 9 — 1 и 8. Так дети быстро научатся раскладывать числа на части и легче освоят вычитание. «Сколько будет, если от 9 отнять 1?» Ответ — 8.
4. Дошкольникам нравится меняться с мамой ролями, задавать аналогичные вопросы. Предоставьте возможность проявить инициативу, поощряйте самостоятельность будущих первоклашек. Устраивайте соревнования на скорость решения примеров.
В заключение повторим, что прочное запоминание состава чисел возможно лишь при условии регулярных упражнений. Чтобы ребёнок не утратил интерес к занятиям математикой, фантазируйте, меняйте игры и радуйтесь успехам малышей.
Состав числа 10. Решение задач. Конспект
Просмотр содержимого документа
«Состав числа 10.
 Решение задач. Конспект»
Решение задач. Конспект»
Конспект урока по математике 1 класс
Тема урока:. Состав числа 10. Решение задач.
Тип учебного занятия: комбинированный.
Вид учебного занятия: урок — путешествие.
Продолжительность – 45 минут.
Цели:
1 .Формирование вычислительных навыков и знания состава чисел в
пределах первого десятка.
Развитие логических операций: анализа, синтеза, обобщения, сравнения, способствуя развитию мышления в целом.
Развитие речи обучающихся, использование математических терминов и понятий.
Воспитание трудолюбия, усидчивости, активности, аккуратности, коллективизма.
Оборудование: компьютер, проектор, экран, презентация PowerPoint из 29 слайдов, компьютеры для школьников; учебник М.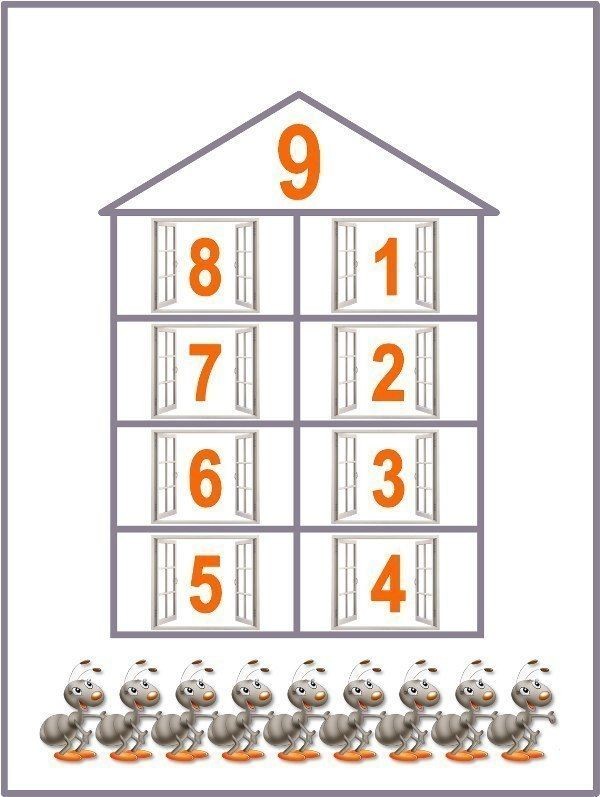 И.Моро «Математика. 1 класс».
И.Моро «Математика. 1 класс».
Ход учебного занятия:
Этап учебного занятия | Время | Цель | Методы | Формы | Презентация |
I. Орг. момент. Целеполагание. | 2 мин. | Организация класса. Настрой детей на работу. Организовать познавательную деятельность учащихся. | Беседа. Создание ситуации познавательной новизны. | Фрон-тальная | Слайд 1 |
Деятельность учителя | |
Математика – особая страна, Для путешествия смекалка нам нужна. Будем много думать и считать, И задачки не забудем мы решать. Сегодня на уроке мы отправимся в гости. А к кому именно – вы узнаете, если будете внимательны и правильно выполните задание | Слайд 1 |
Этап учебного занятия | Время | Цель | Методы | Формы | Презентация |
II.Актуализация знаний. Повторение пройденного. | 7 мин. | Побуждение к работе с новой информацией. Пробуждение интереса к теме. Активизация имеющихся у учащихся знаний. Подготовка к осознанному восприятию учебного материала. | Диалог учителя и детей. Наглядный. | Фрон- тальная | Слайды 2 — 7 |
Деятельность учителя | |
Устный счет. 1.Какое число предшествует при счете числу 9? 2. Какое число следует при счете за числом 5? 3. Какое число стоит между числами 3 и 5? 4. Какое число стоит правее числа 8? 5.Какое число стоит левее числа 3? — На этом уроке мы с вами отправимся в гости к гномам. Эти маленькие существа очень любят математику. Ведь математика – царица всех наук, и тот, кто занимается ею, сможет не только считать и решать задачи, но и станет находчивым, сообразительным, научиться логически мыслить и находить выход из любой ситуации. 2. 1. Какой домик нужно вставить в пустой квадрат? 2. У крышки стола 4 угла. Сколько останется углов, если 1 угол отпилить? 3. Куда войдет больше воды: в трехлитровый чайник или трехлитровый самовар? 4. Сколько зайцев в корзине? Почему ты так решил? | Слайд 2 Слайды 3 – 7 |
Этап учебного занятия | Время | Цель | Методы | Формы | Презентация |
III.Повторение пройденного материала | 15 мин. | Повторение алгоритма написания числа10. | Словесный; наглядный; частично-поисковый. | Фронтальная и индивидуальная самостоятельная работа | Слайды 8 — 16 |
Деятельность учителя | ||||||||
Подготовительный этап к изучению новой темы. — И вот мы в гостях у гнома Цветика. Чем он занят? — Верно, поливает свой любимый цветок. Но в лейке мало воды. Давайте поможем Цветику набрать в нее воды. Вы должны решить примеры, тогда капельки воды попадут в лейку. Готовы? Приступайте к работе. — Молодцы, ребята! Теперь в лейке Гнома Цветика достаточно воды для поливки его любимого цветка. Переход к следующему этапу урока с помощью физминутки для глаз. 2. — А сейчас я проверю, насколько вы были внимательны, когда решали примеры. — Назовите последний пример. Что заметили при его решении? -Что можно сказать о числе 10? — Сколько понадобилось гному Тото кубиков для башни? — Как вы думаете, о каком числе пойдет сегодня речь на уроке? Определите тему нашего урока. — Какие задачи поставим на урок? — Верно. Мы знакомимся с числом 10, составом числа 10, научимся его писать. — Количество предметов, равное 10, обозначается числом 10. 3. Работа в тетради. Запись числа 10. -Чем число 10 отличается от остальных? (при записи используем две цифры – 1 и 0). Ноль катился по странице и не значил ничего. Рядом встала единица, сделав ДЕСЯТЬ из него. Состав числа 10. — Какие числа нужно вставить? Почему? — Где вы встречаетесь с числом 10? ВЫВОД: Поскольку у человека на руках 10 пальцев, то число 10 с давних времен использовалось как укрупненная единица счета. | Слайды 8 — 12 Слайд 13 Слайд 14 Слайд 15 Слайд 16 Слайд 17 | |||||||
Этап учебного занятия | Время | Цель | Методы | Формы | Презентация | |||
IV.Работа по презентации | 5 мин. | Закрепить знание состава числа 10 Развивать речь обучающихся, используя математические термины и понятия.. | Самосто- ятельная работа | Слайды 18-19 | ||||
Деятельность учителя | |
А этого гнома зовут Молчун. -Покажите разбивку фигур в соответствии с данными выражениями, опираясь на образец. Обоснуйте свой выбор. — Какие числа нужно вставить? Почему? — Что записано на клеточках справа? — Какую взаимосвязь используем? — Прокоментируйте решение, указывая часть и целое, способ нахождения. МИКРОИТОГ: Как получить число 10? | Слайд 18 Слайд 19 |
Этап учебного занятия | Время | Цель | Методы | Формы | Презентация |
Физкультминутка | 3мин. | Снятие мышечной усталости, профилактика перенапряжения. |
Деятельность учителя | |
Вижу, сильно вы устали. Позову Весельчака, Проведет он физминутку, Всем понравится она. Жил-был маленький гном (присели, встали) С большим колпаком (вытянули руки вверх, соединили ладони) Он был путешественник-гном. (руки на пояс, шаги на месте) На лягушке он скакал: Прыг-скок, ква-ква! (прыгаем) И на стрекозе летал: (машем руками) Ух, высоко! (встали на носочки) По ручью плыл в чайной чашке: (плывем любым стилем) Буль-буль-буль! Ездил он на черепашке: (руки на пояс и потопать на месте) Топ-топ-топ! И, протопав все тропинки, Он качался в паутинке, (качаемся из стороны в сторону) Баю-бай! Баю-бай! Утро придет, (руки вверх, в стороны, вниз) Гном опять в поход пойдет! (шаги на месте) |
Этап учебного занятия | Время | Цель | Методы | Формы | Презентаия |
V. | 10 мин. | Обобщить полученные знания; уметь анализировать полноту и новизну приобретённых знаний. | Диалог учителя и детей. Письменная работа. | Фронтальная, работа в парах, самостоятельная работа. | Слайды 20-27 |
Деятельность учителя | |
Решение задач с результатом 10. Давайте познакомимся. Этого гнома зовут Хитрун. Он очень любит математику, но больше всего ему нравится решать задачи. Он приготовил вам интересные задачи. Раз к зайчонку на обед Прискакал дружок-сосед. На пенек зайчата сели И по 5 морковок съели. Кто считать, ребята, ловок? Сколько съедено морковок? Белка на елке грибочки сушила, Песенку пела и говорила: «Мне зимой не знать хлопот, Потому что есть грибок: Два масленка, два опенка, А лисичек ровно шесть. Ты попробуй все их счесть». -Интересные задачи? Гном Хитрун вам приготовил еще одну задачу. «У кормушки сидели 4 птички. К ним прилетели еще 6 птичек. Сколько птичек стало у кормушки?» (Во время разбора задачи при помощи подводящего диалога подвожу обучающихся к правильному оформлению схемы и решения задачи. Запись решения в тетрадь. Работа а парах – взаимопроверка решения задачи) Самостоятельная работа. -Наш урок подходит к концу. Нам осталось побывать в гостях у гнома Тихони . Он предлагает вам в силу ваших знаний и возможностей выбрать задание, которое, по-вашему мнению, вы сможете выполнить. ЗЕЛЕНАЯ КАРТОЧКА – сравнить выражения 10+0…10-0 10-2…10-5 3 +7…2+8 1+9…5-5 ЖЕЛТАЯ КАРТОЧКА – заполнить пропуски 10 — ? = 4 ? +5 = 10 7 + ? = 10 ? — 8 = 2 КРАСНАЯ КАРТОЧКА – придумать и записать 4 примера с числом 10. — Сверьте свое решение с решением гнома. — Почему нет результатов выполнения заданий на красной карточке? | Слайд 20 Слайд 21 Слайд 22 Слайд 23 Слайд 24 Слайд 25 Слайд 26-27 |
Этап учебного занятия | Время | Цель | Методы | Формы | Презентация |
VI. | 3 мин. | Осознание обучающимися своей учебной деятельности, самооценка результатов деятельности | Словесный (беседа) | Фронтальная дискуссия. | Слайды 28 |
Деятельность учителя | |
— Сегодня на уроке мы с вами были в гостях у весёлых, трудолюбивых гномов. Какие новые знания вы получили? — Какие знания и умения повторили и закрепили на уроке? — Где в жизни эти знания вам могут пригодиться? У вас на столе лежат смайлики. Возьмите, пожалуйста, тот, который соответствует вашему настроению. Веселый — Урок понравился: я справился со всеми заданиями. Я доволен собой. Серьезный — Настроение хорошее, но задания были не такими уж легкими. Мне было трудно, но я справился. Грустный — Задания на уроке оказались слишком трудные. — Все сегодня работали со старанием, показали своё трудолюбие. Я говорю вам всем сегодня: « Молодцы! Спасибо за урок!» | Слайд 28 Слайд 29 |
6
«Конспект ООД по ФЭМП «Состав числа 10 из двух меньших»
«Конспект ООД по ФЭМП «Состав числа 10 из двух меньших»
Конспект ООД по познавательно – исследовательской деятельности (ФЭМП)
на тему «Состав числа 10 из двух меньших» для детей подготовительной группы
Цель: Закрепление математических знаний и умений посредством игры ; совершенствовать умение счета в пределах 10,понимание отношений между числами натурального ряда, умение увеличивать число в пределах 10.
Обучающие задачи:
Учить составлять число 10 из двух меньших чисел и раскладывать его на 2 меньших числа.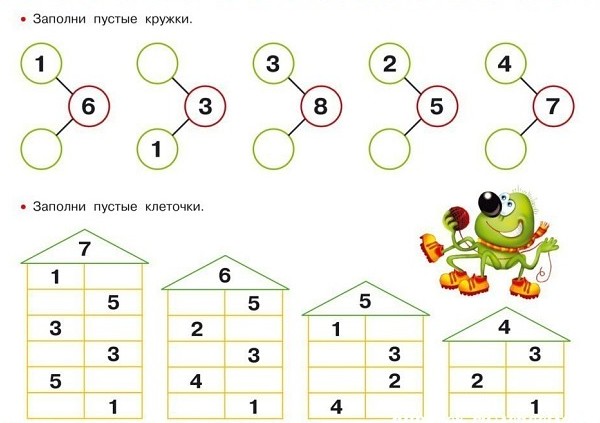
Закреплять умение определять предыдущее, последующее и пропущенное число к названному или обозначенному цифрой в пределах 10.
Продолжать формировать навыки ориентировки на листе бумаги в клетку.
Развивающие задачи:
Создать условия для развития логического мышления, сообразительности, внимания.
Способствовать формированию мыслительных операций, развитию речи, умению аргументировать свои высказывания.
Воспитательные задачи:
Воспитывать самостоятельность, умение понимать учебную задачу и выполнять её самостоятельно.
Воспитывать интерес к математическим занятиям.
Методические приёмы:
Игровой (использование сюрпризных моментов).
Наглядный (использование иллюстрации).
Словесный (напоминание, указание, вопросы, индивидуальные ответы детей).
Поощрение, анализ занятия.
Оборудование: магнитная доска, цифры.
Демонстрационный материал: иллюстрация паровозика, собачки, дерева ,домик, коврик.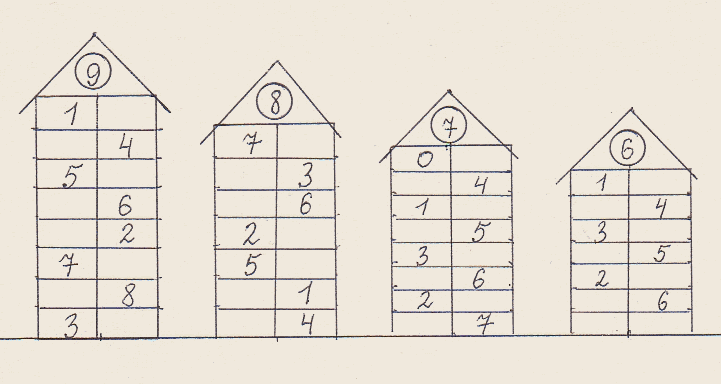
Раздаточный материал: набор цифр на каждого ребенка, листочки в клетку, карандаши, счетные палочки.
.
Ход занятия.
-Ребята, наше сегодняшнее задание будет необычном. Мы с вами отправимся в путешествие в страну Математики. На чем можно отправиться в путешествие?
-А чтобы узнать на чем мы поедем, отгадайте загадку:
Черный дом по рельсам мчится,
Только пар над ним клубится.(паровоз)
— Что нам нужно приобрести, чтобы попасть в вагон?
-Возьмите билеты и садитесь на свои места в соответствии с номером на вашем билете.
-Проходим в вагон и занимаем места (садятся за столы)
-Чтобы поезд тронулся нужно выполнить задания.
-Посчитай до 20
-Посчитай до 10 и обратно
-Посчитай от 9до5;от8до2;
-Поехали. А пока мы едем давайте познакомимся с соседями, поиграем в игру «Назови соседей».Я буду называть цифры, а вы покажите соседей этой цифры.
-Кто соседи у цифры7;8;5;9.
-Какое число предыдущее? последующее? почему?
-А вот и первая станция «Засели домик».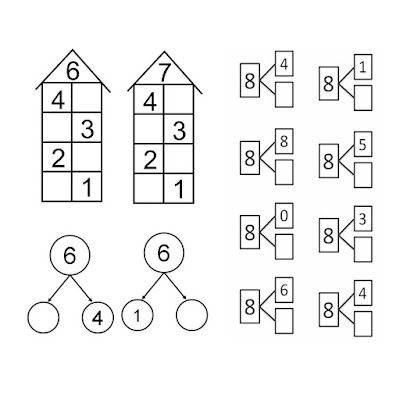
-Сколько этажей в доме? Сколько квартир в каждом этаже?
-Нам нужно заселить дом так, чтобы на каждом этаже жили 10 человек.
-Возьмите столько счетных палочек, сколько жильцов будут жить на каждом этаже?
-Как можно заселить жителей на1 этаже? во 2 этаже?.
-Перед тем как продолжить путь давайте мы с вами отдохнем.
Физкультминутка.
1-вперед наклонимся
2-назад прогнемся
И наклоны в стороны
Делать мы возьмемся
Приседания опять
Будем дружно выполнять
1,2,3,4,5
Кто там начал отставать?
На ходьбу мы перейдем
И занятия вновь начнем.
—Поехали дальше. А чтобы нам не было,скучно отгадаем загадки:
— Сколько солнышек на небе? (1)
— Сколько хвостов у 7 ослов? (7)
— Сколько ушей у 3 мышей? (6)
-На березе росли 4 груши,1 груша упала. сколько груш осталось на березе?
— В вазе 5 ромашек и 2 василька Сколько ромашек в вазе? (7)
— Наступил зима. На клумбе распустились 3 ромашки, а затем еще одна. Сколько ромашек распустилось? (зимой цветы на клумбе не цветут)
На клумбе распустились 3 ромашки, а затем еще одна. Сколько ромашек распустилось? (зимой цветы на клумбе не цветут)
— Сколько орехов в пустом стакане? (стакан пустой значит, в нем ничего нет)
— Молодцы! Отвечали быстро и правильно.
-Ребята, на нашем пути выросло дерево. Чтобы его обойти мы должны выполнить задание
А задание вот, какое. За деревом кто – то спрятался и наша задача узнать его.
Графический диктант «Собачка»
-Собачка не отпускает нас просто так. А давайте сделаем ей подарок. Что можно подарить
-А мы подарим коврик, чтобы ей было тепло лежать. Чем украшен наш коврик?
-Назовите фигуру, которая находится в правом вернем углу? в левом нижнем углу?
посередине? в левом верхнем углу? в правом нижнем углу?
-Собачка хочет чтобы мы еще измерили её коврик? С помощью чего мы можем это сделать (измерение с помощью мерки)
-А что еще может послужить меркой
-А теперь постройте мне прямоугольник дли на которой равна 4 счетным палочкам,а ширина равна 2 счетным палочкам.
-Молодцы, ребята! Справились и с этим заданием. Отправляемся дальше.
-Ребята, а вот и наша следующая станция. а что мы тут видим?
-Числа заблудились, они не могут найти свое место. Давайте им поможем?
-Ребята. нам пора возвращаться обратно. но для этого мы должны выполнить ещё одно задание «Сосчитай –ка»
На забор взлетел петух,
Повстречал ещё там двух.
Сколько стало петухов?
Пять цветочков у Наташи,
И ещё два дал ей Саша.
Кто тут сможет посчитать,
Сколько будет два и пять?
Четыре спелых груши
На веточке качалось
Две груши снял Алеша
А сколько груш осталось?
Стала курица считать
Маленьких цыпляток.
Желтых пять и белых пять,
А всего …
В класс вошла Алинка,
А за ней — Каринка.
А потом пришел Марат.
Сколько стало всех ребят?
Итог занятия.
-В какой стране мы побывали?
-Какие задания мы выполняли на пути?
-Какое задание вам понравилось больше? Какое задание вам показалось трудным?
Составление чисел в детском саду | Mrs.
 Albanese’s Kindergarten Class
Albanese’s Kindergarten ClassВсю последнюю неделю мы сосредоточились на составлении чисел от 5 до 10.
Мне нравится знакомить с этим понятием моих K-учеников в первой половине учебного года, так как это отличное введение в дополнение (что происходит ближе к концу учебного года).
Мы потратили хорошую неделю на все навыки, но вы можете легко растянуть это на 2 недели! В моем блоке есть уроки, центры, игры и мероприятия, которые легко подготовить и в которые можно играть!
Я создал подробный недельный план уроков, в котором изложено все, что вы видите ниже.
Вы можете скачать это для БЕСПЛАТНО ниже.
ДЕНЬ 1 — Что значит «сочинить»?
Мне нравится начинать с разговора со студентами о слове «составлять» и вводить слова «и» и «сделать». Мы также учимся составлять и читать математические предложения.
Я размещаю эти числа и простое математическое выражение на карманной таблице, чтобы ученики могли работать с ней, а также чтобы мы могли обращаться к ней в течение недели.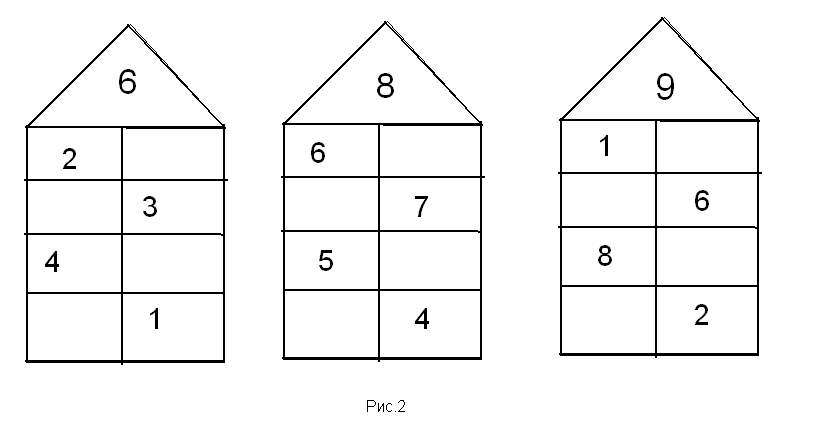 Вот забавная игра: возьмите кубики Unifix двух цветов. Выберите несколько из каждого и попросите студентов помочь вам сосчитать их. Смоделируйте, как мы можем составить математическое предложение на карманной таблице -> «У нас есть 4 синих и 2 красных — получается 6!»
Вот забавная игра: возьмите кубики Unifix двух цветов. Выберите несколько из каждого и попросите студентов помочь вам сосчитать их. Смоделируйте, как мы можем составить математическое предложение на карманной таблице -> «У нас есть 4 синих и 2 красных — получается 6!»
Я выбираю ученика, который подходит и берет по горсти каждого цвета, и мы пробуем еще раз.
Мне нравится продолжать это упражнение в малых группах, обращая внимание на то, как мы формулируем предложение, используя «и» и «сделать».
ДЕНЬ 2 — Я могу это сделать!
Это действительно отличное занятие для публикации на интерактивной доске. Выберите число, с которым вы хотите работать (например, 4 — очень легко начать!). Раздайте столько же двусторонних жетонов одному ученику. Попросите этого ученика придумать различные способы представления числа (например, 2 и 2, 3 и 1 и т. д.). Поначалу было сложно, но ученики сразу поняли! Я записывала все ответы на интерактивной доске, раскрашивая кружки в зависимости от наших ответов.
Мы даже попробовали это с другими номерами, так как им очень понравилось это занятие!
В моей небольшой группе я использовала коврик «Создание 5» (или «Создание 10» для учащихся 2-х классов) с цветными кубиками Unifix.
Мы попрактиковались в составлении числа различными способами, а затем ученики смогли заполнить буклет по составлению чисел.
Учащиеся 1-го класса (JK) поработали над составлением чисел до 5. Я сделала 2 квадрата разного цвета из плотной бумаги, и они приклеили разные ответы на каждую страницу.
Учащиеся 2-го класса (SK) смогли поработать над составлением чисел до 10. Я разбросал на столе различные 10-рамки с числами от 1 до 10. Они выбрали 2 и вклеили их в свой буклет. Затем они записали свои ответы.
ДЕНЬ 3 — Составление 5 (или 10)
Мы начинаем уделять больше внимания составлению 5 (или 10) в деталях, знакомя учащихся с вероятностью. Да, несколько игр, которые я создал в этом пакете, также касаются вероятности!
Я напечатал круги двух цветов и поместил их в карманный кубик (вы можете просто распечатать готовый к использованию кубик, входящий в этот набор, если у вас нет карманного кубика). Я выбрал ученика, который подошел и бросил кубик. Мы записывали то, что он/она катал, на рабочий лист, спроецированный на мою интерактивную доску. Мы продолжили прокатку и запись, а затем обсудили наши выводы.
Я выбрал ученика, который подошел и бросил кубик. Мы записывали то, что он/она катал, на рабочий лист, спроецированный на мою интерактивную доску. Мы продолжили прокатку и запись, а затем обсудили наши выводы.
Одинаковые ли рулоны? Сколькими способами мы сделали 5? 10?
В моей небольшой группе я закончил вчерашние буклеты. Я также предложил студентам возможность использовать математические манипуляции для чтения математических предложений и составления чисел.
ДЕНЬ 4 — ВЗЯТЬ И ПРОЛИВАТЬ!
Это одна из моих ЛЮБИМЫХ игр! Студентам тоже нравится! Я думаю, это потому, что они встряхивают жетоны в чашке и проливают их! Они получают кайф от этого!
После того, как я рассказал, как играть в эту игру всей группой, я настроил ее для небольшой группы. Одна вещь, которую я усвоил за эти годы: чтобы не перепутать счетчики, дайте ученикам салфетки (может быть и цветной лист плотной бумаги!) и пусть они встряхнут и прольют на него.
Я наткнулся на эту песню в прошлом году и думаю, что она идеально подходит для знакомства с простыми способами сделать 5!
ytimg.com/vi/gXwuwJqYwM4/0.jpg» frameborder=»0″ src=»https://www.youtube.com/embed/gXwuwJqYwM4?feature=player_embedded»>ДЕНЬ 5 — Что у меня в руке?
Вот еще одна веселая и простая игра — выберите карточку с числом и посчитайте столько же манипуляций. Попросите учащихся помочь вам считать. Без просмотра учениками разделите жетоны между обеими руками (т. е. числовая карточка = 5, положите 3 в одну руку и 2 в другую, покажите учащимся только 3). Предложите учащимся определить, сколько их в другой руке.
Это такая замечательная игра (и очень простая в настройке!), что, показав им пару раз, вы можете оставить ее в своем математическом центре и предложить учащимся сыграть в нее вместе!
С моей небольшой группой мы работали над «Roll It! Compose It!» Мне очень нравится это занятие как вызов для многих учеников! Они были к этому готовы после того, как узнали все о составлении чисел на этой неделе!
Для тех учеников, которым нужно было немного больше времени, чтобы поработать над составлением чисел, у меня было готово это задание, в котором они выбирали математическое предложение и строили его, используя манипуляторы/свободные части (мы использовали кнопки).
Вот несколько отличных онлайн-игр, которые можно установить на свои компьютеры!
Звездопад -> Candy Machine (составление и разложение чисел)
*ПРИМЕЧАНИЕ. Эта игра работает только на настольных компьютерах, НЕ на iPad) нужно)
В этой игре основное внимание уделяется составлению чисел с использованием 5-фрейма. Нажмите {ЗДЕСЬ}, чтобы играть.
Вы можете найти все эти задания в моем наборе «Сочинение чисел в детском саду» на TpT.
ПЛАН УРОКОВ НА 1 НЕДЕЛЮ
Я составил подробный план занятий на неделю, если вы хотите попробовать эти занятия в своем классе!
Нажмите на картинку ниже, чтобы скачать БЕСПЛАТНО!
Основы детского сада: Комбинации от чисел до 10
Донна работала учителем, тренером по математике, интервенционистом и координатором учебной программы. Часто выступая на государственных и национальных конференциях, она делится своей любовью к математике с мировой аудиторией через свой веб-сайт Math Coach’s Corner. Донна также является соавтором Guided Math Workshop.
Донна также является соавтором Guided Math Workshop.
Как выглядит математика в детском саду? Какими основными навыками должен овладеть каждый учащийся детского сада до первого класса? Хотите верьте, хотите нет, но беглость речи начинается в детском саду, когда ученики учатся составлять и раскладывать числа! Теперь, прежде чем вы достанете эти карточки (так многие из нас узнали наши «факты») или начнете проклинать меня за то, как дети теряют свое детство, прочитайте дальше, чтобы понять, что именно я имею в виду, и для игр и занятий в детском саду, которые более веселые. чем работать.
Этот пост содержит партнерские ссылки, что просто означает, что когда вы используете мою ссылку и покупаете продукт, я получаю небольшую комиссию. С вас не взимается дополнительная плата, и я ссылаюсь только на книги и продукты, которые лично рекомендую.
Во-первых, давайте взглянем на общие основные математические стандарты для детского сада (CCMS), связанные с развитием беглости фактов. Даже если вы не находитесь в штате, который следует CCMS, в вашем штате, вероятно, действуют аналогичные стандарты для детского сада. Я, например, в Техасе, и вы найдете очень похожие стандарты в нашем TEKS.
Даже если вы не находитесь в штате, который следует CCMS, в вашем штате, вероятно, действуют аналогичные стандарты для детского сада. Я, например, в Техасе, и вы найдете очень похожие стандарты в нашем TEKS.
CCSS.MATH.CONTENT.K.OA.A.3
Разлагать числа, меньшие или равные 10, на пары более чем одним способом, например, с помощью предметов или рисунков, и записывать каждое разложение с помощью рисунка или уравнение (например, 5 = 2 + 3 и 5 = 4 + 1).
CCSS.MATH.CONTENT.K.OA.A.4
Для любого числа от 1 до 9 найдите число, которое дает 10 при добавлении к данному числу, например, с помощью предметов или рисунков, и запишите ответ с рисунком или уравнением.
CCSS.MATH.CONTENT.K.OA.A.5
Свободно складывать и вычитать в пределах 5.
Нужен простой английский? Прежде всего, поймите, что они последовательные. Другими словами, каждый стандарт основывается на предыдущем. Читайте ниже перевод каждого из стандартов. Затем прокрутите вниз для получения дополнительной информации и бесплатных занятий для отработки навыков.
Затем прокрутите вниз для получения дополнительной информации и бесплатных занятий для отработки навыков.
- Первый стандарт гласит, что для каждого числа до десяти дети должны знать все различные способы составления (составления) или разбиения (разложения) этого числа. Начнем с 5. Пятерку можно составить (составить) из 0 и 5, 1 и 4 или 2 и 3. Ее также можно разбить (разложить) на те же самые части. Не упускайте из виду тот факт, что учащиеся должны приобрести этот навык с использованием объектов и изображений перед записью каждой декомпозиции в виде уравнения или рисунка. Учащиеся должны работать над одним целевым числом за раз и освоить все комбинации для этого числа, прежде чем переходить к следующему числу.
- В нашей системе счисления десять — это особое число, поэтому оно получает особый стандарт. Навык действительно ничем не отличается от первого стандарта.
- Это умение обращается к автоматизму. Это означает, что, хотя учащиеся могут по-прежнему нуждаться в предметах и/или картинках для комбинаций чисел выше пяти, они должны автоматически знать все комбинации цифр до пяти к концу детского сада.

Разложение чисел более чем одним способом
Определение целевого числа ребенка
Важно понимать, что дети должны освоить комбинации для одного числа, прежде чем переходить к следующему. Для ребенка бесполезно практиковаться в составлении и разложении 6, если он не знает комбинаций для 5. Вот тут-то и начинается дифференциация. Для определения беглости ребенка с каждым числом можно использовать процедуру, называемую «оценкой скрытия». Чтобы определить, знает ли ребенок все комбинации числа 3, попросите ребенка отсчитать 3 фишки. В качестве прилавка можно использовать что угодно – сушеные бобы, макароны, монетки. Любой небольшой предмет, на самом деле. мне нравятся эти маленькие сантиметровые кубики , потому что они легко помещаются под рукой и могут быть использованы для самых разных действий. Я рекомендую использовать все одного цвета, чтобы ребенок ориентировался на количество, а не на цвет. Так, например, если вы работаете с 5, используйте 5 зеленых кубиков.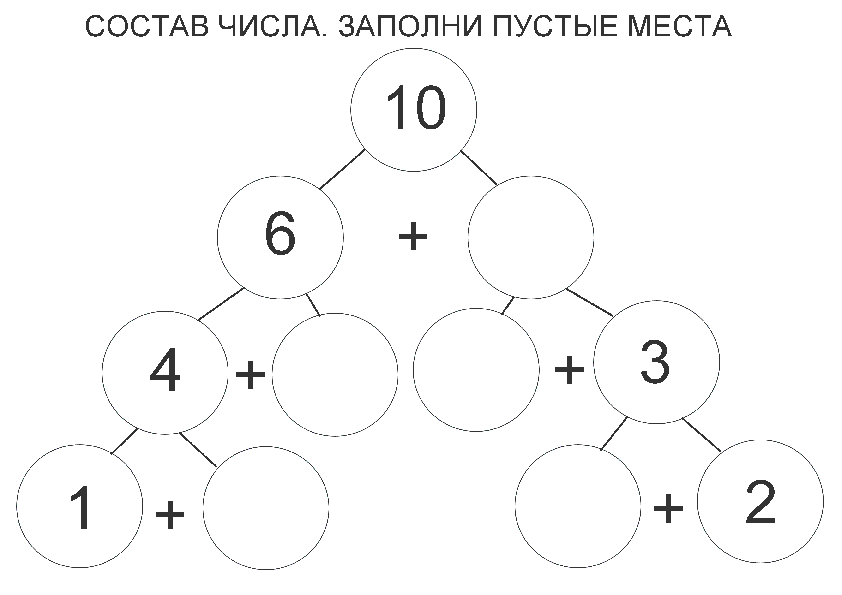
Скройте несколько фишек и покажите некоторые, попросив ребенка определить, сколько фишек скрыто. Например, скрыть 1 счетчик и показать 2. «Если у меня есть 3 счетчика и 2 отображаются, сколько скрыто?» Продолжайте эту процедуру для каждой комбинации для 3 (скрыть 3, показать 0; скрыть 2, показать 1; скрыть 0, показать 3). Если ваш ребенок может назвать все недостающие части для 3, попробуйте комбинации для 4. Когда ваш ребенок больше не может легко называть недостающие части, , становится его номером. Каждые несколько недель «проверяйте» своего ребенка, чтобы определить, готов ли он перейти к новому номеру. Вот видео оценки скрытия в действии.
Вы заметите, как этот ребенок знал комбинации для 5 автоматически, но замедлился на 6, в частности, на 2 и 4 для составления 6. Пока я продолжал проверять ребенка на 7, число, которое ему нужно для практики — его целевое число — 6.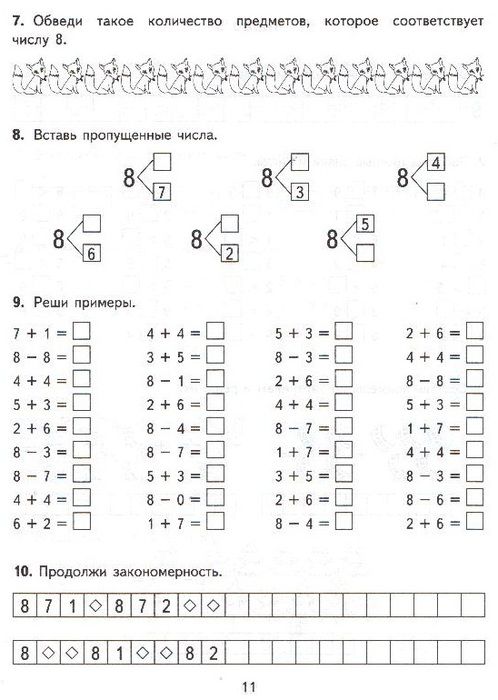 Я полагаю, что ему нужно будет поработать только над 6 на короткое время. Затем я бы перепроверил его на 6 и попробовал бы на 7. Скорее всего, его новым целевым числом было бы 7.
Я полагаю, что ему нужно будет поработать только над 6 на короткое время. Затем я бы перепроверил его на 6 и попробовал бы на 7. Скорее всего, его новым целевым числом было бы 7.
Отработка целевого числа ребенка
Теперь, когда вы определили целевое число вашего ребенка, пора играть! Помните, что вы можете использовать эти действия снова и снова с разными целевыми числами по мере продвижения вашего ребенка.
Первая игра называется Shake and Spill . По сути, вы используете целевой номер вашего ребенка; скажем, 5, например. Положите 5 фишек в чашку, встряхните ее и высыпьте фишки на коврик. Затем ребенок описывает, сколько человек упало на картинку и сколько упало (например, 3 на утке, 2 на утке, 3 и 2 составляют 5 ). Продолжайте этот процесс, пытаясь найти все комбинации для целевого числа. Вот подсказка. Поместите коврик для встряхивания во что-нибудь, например, в коробку , показанную на рисунке. Он содержит «разлив».
Следующая игра может называться В пещере , если у вас есть жетоны плюшевых мишек , или Под камнем , если у вас их нет. По сути, это игровая версия оценки скрытности. Для игры вам понадобятся фишки или мишки и пластиковый стаканчик (не может быть прозрачным). Используйте количество медведей или других счетчиков, равное целевому числу, которое вы практикуете. Например, если вы работаете над числом 5, используйте 5 медведей. Ребенок закрывает глаза, пока вы кладете несколько мишек «в пещеру» (под чашку). Затем она открывает глаза и говорит, сколько медведей спрятано. Убедитесь, что ваш ребенок произносит комбинацию (например, 2 и 3 дает 5), чтобы он тренировал свои комбинации вслух. Вы также можете попросить ребенка написать уравнение, соответствующее каждой комбинации (например, 2 + 3 = 5).
Вот ссылки на посты с некоторыми другими ресурсами для отработки комбинаций каждого числа:
- Mathemagician Make Ten , играл с колодой карт; можно адаптировать для практики любой номер
- Make 5 Go Fish , игра с колодой карт
- Семерка сверху , игра с колодой карт
- В этом посте есть несколько карточек, которые вы можете скачать с различными способами их использования
- Это бесплатный буклет для печати для отработки всех комбинаций на десятку
И наконец, здесь — невероятно захватывающая игра для отработки комбинаций любых чисел от 5 до 12.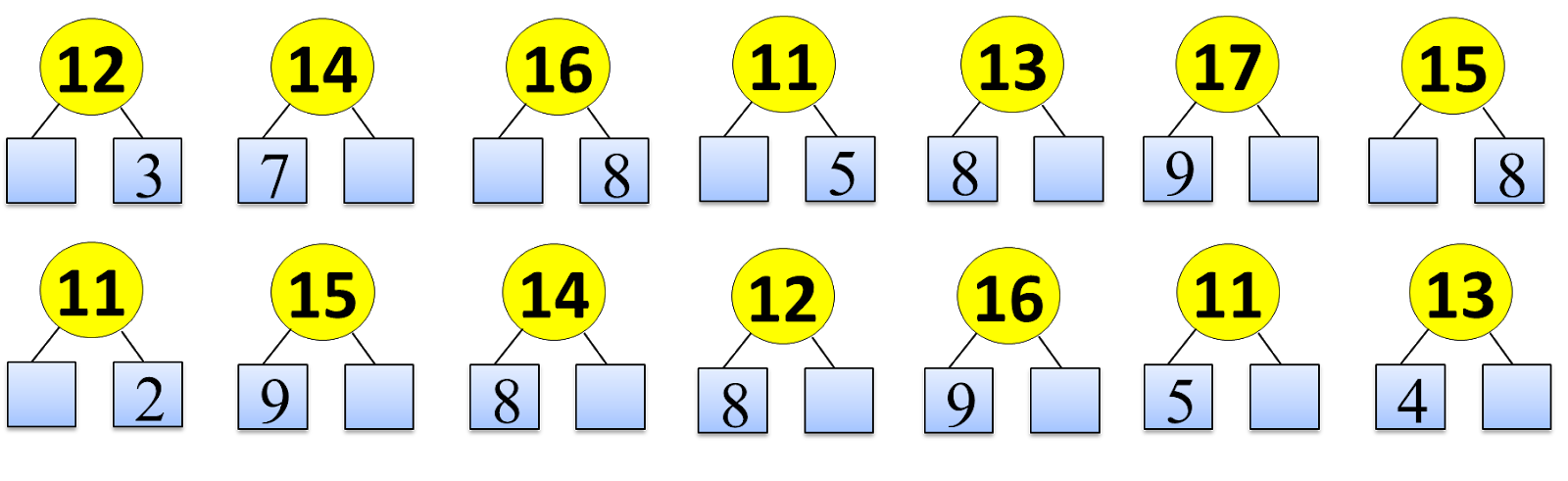
Если у вас есть дополнительные предложения по отработке этого важного навыка, пишите их в комментариях!
Как обучать представлению чисел
Многие ученики идут в детский сад, уже умея считать. Они могут назвать числа «один, два, три…» и так далее до 10. Но они не всегда понимают, что каждое произносимое ими число — это 9.0168 количество .
Кроме того, их может сбить с толку тот факт, что одно и то же число может быть представлено по-разному — его числовым именем («один») и его цифрой («1»). Путаница в отношении различных представлений чисел может затруднить учащимся изучение сложения и вычитания.
Использование различных способов представления числа может помочь учащимся понять каждое число как количество. С помощью этой стратегии вы будете использовать явные инструкции для обучения трем различным представлениям чисел от 1 до 10: имени числа, числу и изображению или набору объектов, показывающих количество.
Учащиеся пройдут серию совместных практических занятий с этими представлениями. Стратегия заканчивается оценкой обучения, а также вариантами дальнейшей практики.
Прокрутите вниз, чтобы найти советы по адаптации этой стратегии для дистанционного обучения.
Скачать: Головоломки с числами для печати
Головоломки с числами PDF
Читать: Как использовать эту стратегию представления чисел
Задание: Учащиеся узнают число по его написанному числу, названию числа и изображению повторяющихся объектов, показывающих количество.
Уровни обучения (со стандартами):
- K (Common Core K.CC.A.3: Запись чисел от 0 до 20. Представляйте количество объектов письменной цифрой от 0 до 20, где 0 представляет количество предметов.)
- K (Common Core K.CC.B.4.A: При подсчете предметов произносите имена чисел в стандартном порядке, соединяя каждый предмет с одним и только одним числовым именем, а каждое числовое имя с один и только один объект.
 )
) - K (Common Core K.CC.B.4.B: Поймите, что последнее названное число говорит о количестве подсчитанных объектов. Количество объектов одинаково, независимо от их расположения или порядка, в котором они были подсчитаны. )
- K (Общая основная математическая практика MP2: разум абстрактно и количественно.)
Лучше всего используется для инструкции с:
- ВСЕГО КЛАССА
- Маленькие группы
Как к подготовке: 9000 2
9000 2
9000 2 9000 22.0011 Собрать материалы. Распечатайте числовую головоломку для каждой группы из трех-пяти учащихся. Подумайте о том, чтобы заранее вырезать кусочки головоломки. Вы можете держать их вместе или в небольших пакетах. Печать на карточках или ламинирование частей головоломки облегчит учащимся работу с ними.
Подготовьте набор каталожных карточек для цифр 1–10. Напишите по одной цифре на каждой карточке.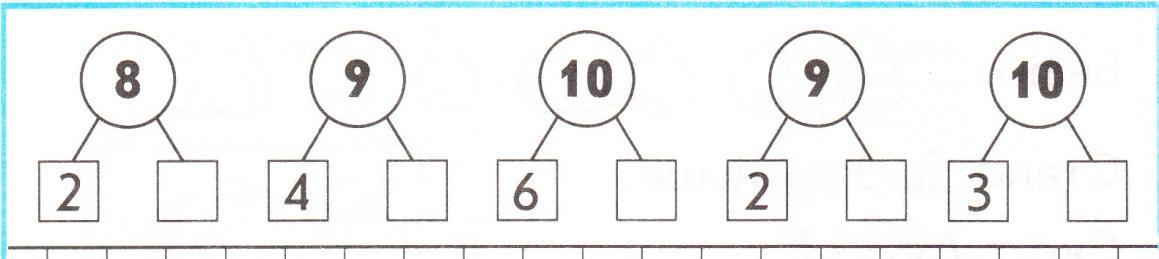 Подготовьте соответствующий набор для имен чисел.
Подготовьте соответствующий набор для имен чисел.
Объедините мелкие предметы, такие как соломинки, кубики, ластики или жетоны, в группы от одного до 10. Вы можете сгруппировать предметы в небольшие пластиковые пакеты или чашки, например, пять соломинок в одном пакете или шесть ластиков в чашке.
Совет учителю: Создайте стену слов, чтобы поддержать изучающих английский язык (ELL) и других учащихся, которым полезна визуальная поддержка. Наличие названий чисел рядом с письменными цифрами поможет учащимся выучить их как слова для зрения. Если стена слов невозможна, сделайте якорную диаграмму достаточно большой, чтобы ее могли видеть все учащиеся.
Как учить:
1. Разогрейтесь, повторив идентификацию номера. Напишите число от 1 до 10 на доске или укажите на число на стене слов или на якорной диаграмме. Произнесите номер вслух. Попросите учащихся повторить число. Затем попросите учащихся показать и сосчитать количество пальцев, чтобы совпасть с числом. Смоделируйте правильный ответ. Например, для числа 3 вы должны смоделировать ответ, подняв три пальца и сказав: «Правильно. Это 3». Затем громко посчитайте каждый палец. «Раз два три.»
Смоделируйте правильный ответ. Например, для числа 3 вы должны смоделировать ответ, подняв три пальца и сказав: «Правильно. Это 3». Затем громко посчитайте каждый палец. «Раз два три.»
После нескольких раундов объясните учащимся, что существует множество способов представления чисел, и использование пальцев — лишь один из них. Спросите: «Каким другим способом мы можем показать число 3?» Возьмите разные ответы от студентов. Смоделируйте ответы, написав, нарисовав и используя предметы в зависимости от того, что говорят учащиеся.
2. Модель, представляющая числа различными способами. Сообщите учащимся цель сегодняшнего урока. «Сегодня мы изучим три разных способа показать число. Вы можете использовать цифру. Вы можете использовать имя числа, которое является словом для числа. Или вы можете использовать картинку или набор предметов». Попросите учащихся повторить концепцию. Скажите: «Итак, вы можете использовать числительное. Скажи цифра со мной. Вы можете использовать числовое имя.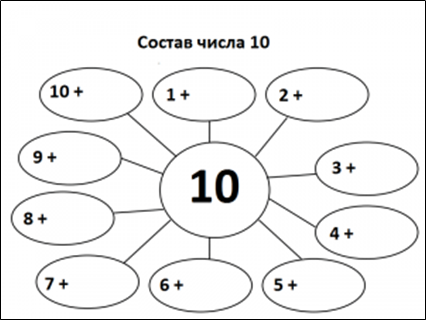 Произнеси со мной номер , имя . Или вы можете использовать картинку или набор объектов. Скажи картинку или набор предметов вместе со мной».
Произнеси со мной номер , имя . Или вы можете использовать картинку или набор объектов. Скажи картинку или набор предметов вместе со мной».
Покажите им, как выглядят эти изображения. Например, поднимите карточку с цифрой 5 и другую с цифрой «пять». Затем скажите: «Число 5 можно записать вот так. Но его также можно записать как слово пять . Пять. Пять. Пять – это имя числа. И это можно показать пятью одинаковыми предметами». Нарисуйте на доске пять квадратов, считая каждый по одному, пока не дойдете до пяти. «Раз, два, три, четыре, пять. Пять квадратов. Все они означают одно и то же: 5 (указать на написанное число), 5 (указать на название числа) и 5 (указать на квадраты)».
«Попробуем еще раз». Повторите шаги с другим числом из набора от 1 до 10.
Используйте предметы в комнате для представления количества. Вы можете использовать кубики, прилавки, кресла-мешки или что-нибудь большое и достаточно яркое, чтобы учащиеся могли видеть со своих мест.
3. Практика сопоставление числительных и числовых названий со счетными предметами. Прежде чем перейти к работе со всеми числами от 1 до 10 и их представлениями, попросите учащихся попрактиковаться с несколькими числами. Поместите набор предметов перед каждой группой учащихся, меняя количество предметов от группы к группе. Этими предметами могут быть жетоны, кубики, соломинки и т. д. Один учащийся должен нести ответственность за демонстрацию предметов, чтобы их могли видеть другие участники.
Затем раздайте учащимся четыре каталожные карточки: две с цифрами и две с совпадающими названиями цифр. Например, если перед группой стоят шесть предметов, они могут получить следующие четыре карточки: 1, 6, один, шесть. Попросите учащихся в группе решить, какие каталожные карточки (одна цифра и одно имя цифры) подходят к набору предметов. Пусть студенты обсудят это и придут к соглашению. Свяжитесь с каждой группой и предложите поддержку по мере необходимости. После того, как все группы приняли решение, пусть они разделятся. Пока они держат карточки, предложите им назвать число и написать название числа по буквам: «с-и-х… шесть».
Пока они держат карточки, предложите им назвать число и написать название числа по буквам: «с-и-х… шесть».
Поверните набор объектов из одной группы в другую и раздайте новый набор карточек каждой группе. Повторите те же действия. После двух раундов, если каждая группа успешно совпала, переходите к задаче с числовыми головоломками.
4. Попрактикуйтесь с числовыми головоломками. Раздайте каждой группе набор числовых головоломок (предварительно вырезанных или с помощью ножниц, если учащиеся собирают наборы). Дайте указания: «Теперь мы будем использовать головоломки с числами, чтобы попрактиковаться в том, как мы можем показывать числа. Рассортируйте все части головоломки по трем стопкам: цифры, названия чисел и картинки».
После того, как учащиеся соберут три стопки, попросите их перетасовать каждую стопку, чтобы ее части не располагались в определенном порядке. Скажите: «Теперь каждый ученик по очереди выбирает одну фишку из стопки с цифрами. Сообщите членам вашей группы номер, который вы выбрали.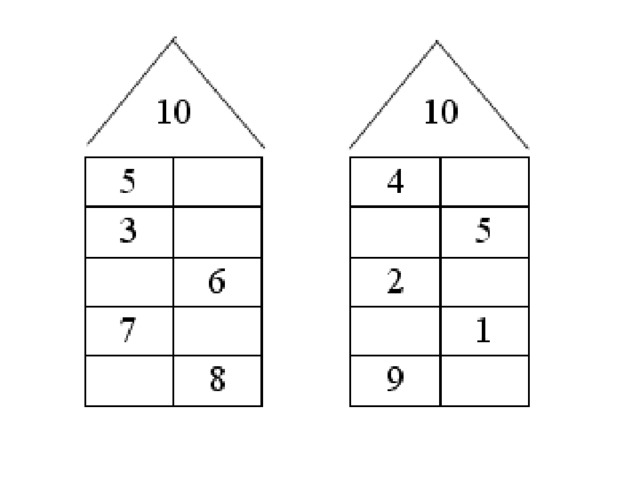 Вместе группа будет искать совпадающее имя числа и совпадающую карточку с изображением из двух других стопок, чтобы идти с числом. Продолжайте по очереди и соединяйте свои части вместе. Когда все части будут объединены в группы по три (число, название числа и изображение), поднимите руки, чтобы проверить свою работу». Продемонстрируйте, как составить соответствующий набор, прежде чем учащиеся начнут.
Вместе группа будет искать совпадающее имя числа и совпадающую карточку с изображением из двух других стопок, чтобы идти с числом. Продолжайте по очереди и соединяйте свои части вместе. Когда все части будут объединены в группы по три (число, название числа и изображение), поднимите руки, чтобы проверить свою работу». Продемонстрируйте, как составить соответствующий набор, прежде чем учащиеся начнут.
5. Оценка обучения. Предложите ученикам встретиться с вами один на один за столом с предметами на нем. Дайте каждому учащемуся цифру (каталожную карточку или из набора кусочков головоломки). Попросите учащихся показать вам соответствующее количество, используя предметы на столе. Затем попросите их выбрать совпадающее числовое имя из набора каталожных карточек или числовых кусочков головоломки. Предложите учащимся подсчитать предметы и произнести название числа, чтобы показать, что они понимают, что все три представляют одно и то же количество. Учащимся, у которых возникают трудности с этим заданием, следует дать дополнительные инструкции в малых группах, ориентированные на ограниченный набор чисел, таких как 1–5, а затем 6–10.
6. Продолжение практики. Дайте учащимся возможность продолжать практиковаться в представлении чисел. Попробуйте выполнить следующие упражнения для закрепления знаний:
- Сделайте из набора пазлов ожерелья, проделав отверстие с обеих сторон каждого кусочка и добавив веревку. Дайте каждому ученику ожерелье. Попросите их встать и найти двух других одноклассников, которые носят такой же «номер», но в другой форме.
- Используйте стену слов, чтобы отметить небольшие группы учащихся или отдельных лиц. Попросите их назвать число, произнести его название по буквам и сосчитать предметы.
- Показать число в любой форме, которую вы выберете. Дайте учащимся время подумать, какое это число. Попросите их найти примеры этого числа в комнате. Затем спросите студентов, где еще они могут встретить формы этого числа в своей жизни.
Поймите: почему эта стратегия работает
Ученикам, у которых проблемы с математикой в младших классах, особенно с пониманием чисел, часто трудно переключаться между различными представлениями чисел. Им трудно понять, что количество одинаковое. Непосредственно обучая трем представлениям одной и той же величины, вы можете помочь учащимся избежать этой путаницы.
Им трудно понять, что количество одинаковое. Непосредственно обучая трем представлениям одной и той же величины, вы можете помочь учащимся избежать этой путаницы.
Использование физических объектов и изображений для представления величин помогает учащимся практиковать и применять понятия стабильного порядка и однозначного соответствия. Эти понятия необходимы для понимания сложения, вычитания и сравнения величин.
Совместная учебная деятельность в этой стратегии числовой головоломки позволяет учащимся практиковаться в демонстрации и передаче своего понимания. Совместное обучение особенно полезно для ELL, потому что они могут найти сверстников более доступными и более понятными, чем учителя. Учащиеся, которые могут быть не готовы выполнить задание самостоятельно, также получают пользу от работы со сверстниками. Иногда сверстники могут предлагать корректирующую обратную связь, на которой другие учащиеся могут учиться.
Посоветуйте, как семьи могут практиковать представление чисел дома. Например, семьи могут дать учащимся числовое имя, написанное на маленьком листе бумаги, и попросить их найти это количество предметов. Или семьи могут попросить учащихся обозначить набор предметов в доме числовым или числовым названием на листе бумаги, чтобы показать количество.
Например, семьи могут дать учащимся числовое имя, написанное на маленьком листе бумаги, и попросить их найти это количество предметов. Или семьи могут попросить учащихся обозначить набор предметов в доме числовым или числовым названием на листе бумаги, чтобы показать количество.
Игры — это также отличный способ попрактиковаться в числах дома. Настольные игры, такие как Five Little Monkeys и Hi Ho Cherry-O, представляют количества более чем одним способом.
Адаптация: использование для дистанционного обучения
- Партнерство с семьями учащихся. Узнайте, какие ресурсы у них есть и что им может понадобиться для обучения дома.
- Проведите весь класс или небольшие группы учащихся по шагам синхронного онлайн-класса или запишите видео для асинхронного обучения. В любом случае, используйте UDL при планировании урока.
- При явном обучении представлению чисел используйте как картинки, так и физические объекты при подсчете каждого числа. Предложите учащимся вместе с вами попрактиковаться в сопоставлении количества с числами и названиями чисел.
 Предложите им найти и использовать набор из 10 предметов в своем доме, таких как цветные карандаши, игровые фигуры или монеты.
Предложите им найти и использовать набор из 10 предметов в своем доме, таких как цветные карандаши, игровые фигуры или монеты. - Попросите семьи распечатать пазлы с числами или написать их от руки. Или предложите им сыграть в онлайн-игру, например, «Представь числа в пределах 10 ».
- Создавайте онлайн-карточки, чтобы учащиеся могли практиковать различные представления чисел. Или покажите семьям, как делать карточки из любой бумаги, которая есть у них дома. Карточки можно настроить таким образом, чтобы с одной стороны отображалось имя числа, а с другой — цифра с изображенными объектами (например, точками) для подсчета.
Исследования, лежащие в основе этой стратегии
«Лучшее обучение посредством структурированного обучения: схема постепенного освобождения от ответственности (2-е изд.)», Дуглас Фишер и Нэнси Фрей
«Экспериментальная оценка влияния совместного обучения на детский сад способности детей к математике», из International Journal of Educational Research
«Переход от неформальных математических знаний к формальным: посредничество с помощью числовых знаний», из Журнал педагогической психологии
Связанные темы
Школьные поддержки
Стратегии и советы
Подростковые номера (здание с десятью)
Используйте ресурс 9013
или
70003Имя пользователя
Пароль
- Забыли пароль?
- Регистрация
Цель
Цель этого раздела последовательных уроков состоит в том, чтобы развить знания и понимание структуры позиционного значения чисел от десяти до двадцати.
Цели достижения
NA1-1: Используйте ряд стратегий подсчета, группировки и равного распределения с целыми числами и дробями.
Разработка AO и другие учебные ресурсы
NA1-3: Знать группы с пятью, в пределах десяти и с десятью.
Разработка AO и другие учебные материалы
NA1-4: Расскажите и объясните стратегии счета, группировки и равного распределения, используя слова, цифры и изображения.
Разработка АО и другие учебные ресурсы
Конкретные результаты обучения
- Мгновенное распознавание закономерностей для подростков.
- Соберите группы по десять человек и изобразите числа подростков с помощью материалов.
- Распознавать и записывать слова и символы для чисел для подростков.
- Поймите, что в подростковом числе 1 представляет одну группу из десяти.
- Расширьте нотацию чисел для подростков и поймите простое разрядное значение.
- Поймите и примените десять за один обмен.

- Поймите, как разложить десятку, чтобы вычесть.
Описание математики
Когда учащиеся встречают десять, они впервые встречают двузначное число. Они начинают осознавать, что числительные больше не нужно учить, и мы просто «перерабатываем» их. Это их вход в структурный мир нашей системы счисления, основанной на десятках.
Они знакомятся с языком цифр, места и значения. Это значительный концептуальный сдвиг для детей, когда они переходят от понимания номинального значения, что числительное представляет собой количество единиц, которые можно сосчитать, к пониманию позиционного значения, в котором числительное может представлять группу или ряд групп, которые сами по себе. состоит из единиц, которые можно посчитать. Это сложная идея.
Когда дети изучают подростковые числа, их значение и структуру (вместо того, чтобы просто «проговаривать» их в счетной последовательности), основное внимание уделяется развитию понимания того, что значение цифры зависит от ее места. Это не тривиально, и это усложняется языком подростковых чисел.
Это не тривиально, и это усложняется языком подростковых чисел.
Дети часто путают названия чисел, такие как «четырнадцать» и «сорок», потому что взрослые произносят окончания слов нечетко. Услышав слово «четырнадцать», дети могут ожидать, что сначала в символической форме появится цифра 4, потому что именно это число появляется первым, когда они его произносят. Таким образом, видя 14 и слыша «четыре — подросток», вы можете запутаться.
Детям нужно много возможностей, чтобы сделать эти цифры из материалов. При первом использовании материала с разрядным значением детям нужна возможность сгруппировать отдельные единицы, чтобы получилась одна десятка. Делая это, они приходят к пониманию того, что десять «единиц» или единиц действительно составляют одно « десять» . Таким образом, первое оборудование, которое следует использовать, — это то, что можно физически сгруппировать, одно за другим, чтобы составить или составить одну группу из десяти или «десятку», и которую можно распаковать или снова разложить на десять единиц. Когда это дополняется символической записью, которая точно соответствует представлению числа, развивается понимание двузначной записи. Оборудование, в котором десятки уже предварительно сгруппированы, можно использовать после того, как группировка для получения десятки будет хорошо понята.
Когда это дополняется символической записью, которая точно соответствует представлению числа, развивается понимание двузначной записи. Оборудование, в котором десятки уже предварительно сгруппированы, можно использовать после того, как группировка для получения десятки будет хорошо понята.
Для детей это значительный сдвиг в том, чтобы использовать материалы, в которых десять выглядит совершенно иначе, чем единицы (например, деньги), и доверять торговле «десять за один». Самая большая абстракция — это, конечно, цифры в нашей системе счисления, где десятки и единицы выглядят совершенно одинаково, но только их положение говорит об их значении.
Глубокое изучение разрядности с числами подростков необходимо, если наши ученики хотят работать с реальным пониманием чисел в нашей системе счисления.
Упражнения, предлагаемые в этой серии уроков, могут стать основой для самостоятельных практических заданий.
Ссылки на систему нумерации
Этапы 2-4
Возможности для адаптации и дифференциации
Возможности обучения в этом модуле можно дифференцировать, предоставляя или удаляя поддержку учащихся и изменяя требования к заданиям. Способы дифференцировать задания включают в себя:
Способы дифференцировать задания включают в себя:
- Предложение меньшего количества заданий на каждом занятии тем учащимся, которым нужна дополнительная поддержка.
- Работа с числами 11-15 перед введением чисел 16-19.
- Использование некоторых из предложенных заданий в качестве самостоятельных занятий для учащихся, которым нужны более сложные задачи.
Использование языковой структуры позиционного значения в Te Reo Māori для развития и укрепления понимания того, что подростковые числа представляют «десять и», является адаптацией, которая поддерживает Te Reo, идентичность и язык учащихся маори, а также концептуальное понимание подростковых чисел.
Требуемые ресурсы Материалы
- Десятки кадров (Материал 4-6)
- Палочки для льда
- Эластичные резинки для волос или резинки
- Пластиковые бобы
- Пластиковые контейнеры
- Карты стрел (Material Master 4–14)
Activity
Session 1
SLO:
- Мгновенное распознавание шаблонов для подростков.

- Соберите группы по десять человек и изобразите числа подростков с помощью материалов.
- Распознавать и записывать слова и символы для чисел для подростков.
Упражнение 1
- Покажите учащимся несколько десятков кадров. Пусть они покажут столько же пальцев, сколько точек, скажите и напишите цифру пальцем в воздухе или на коврике.
- Покажите два кадра с десятками, один из десяти, а другой из числа меньше десяти, вместе образуя число подростков. Попросите учеников «написать» пальцем, сколько точек они видят. Например:
13
Повторить с несколькими номерами для подростков.
- Напишите числа 11–19 в виде символов и слов на миллиметровой бумаге, подчеркивая несоответствия языка и исследуя для развлечения альтернативные формы некоторых подростковых чисел, например, одиннадцать (одиннадцать), двенадцать (двенадцать), тринадцать (тринадцать ), пятнадцать (пятнадцать). Для каждого слова подчеркните teen в слове, потренируйтесь произносить его и слышать конечную согласную «н».
 Установите связь между этим «подростковым» словом и «десятью». Сохраните эту диаграмму, чтобы добавить ее позже.
Установите связь между этим «подростковым» словом и «десятью». Сохраните эту диаграмму, чтобы добавить ее позже.
- Спросите, что ученики замечают во всех этих числах. (Все они имеют в конце слово «подросток», им десять и «что-то в этом роде»). Они известны как подростковые числа.
Занятие 2
Попросите учащихся работать в парах, чтобы они сыграли Пары подростков .
(Цель: распознавать и сопоставлять подростковые числа и слова «десять и ____»)
Учащиеся кладут между собой две стопки карт лицевой стороной вниз (Приложение 1). Стопка 1. Карточки с цифрами для подростков (показаны две рамки с десятками), Стопка 2. Карточки со словами «Десять» и «_____».
Учащиеся по очереди переворачивают одну карточку с десятками и называют количество точек, которые они видят. Затем они переворачивают карточки со словами и читают слова вслух. Если десятки кадров и карточка со словами совпадают, они сохраняют совпадающую пару, и победителем становится ученик с наибольшим количеством пар.
Например:
Занятие 3
- Теперь попросите учащихся «создать» свою группу из десяти человек. Дайте каждой паре сорок детских палочек или палочек для льда, две эластичные резинки для волос, ручки и листы бумаги.
- Пусть каждый ученик выберет и напишет символами число от одиннадцати до девятнадцати и возьмет столько же палочек. Пусть они посчитают и сделают одну связку из десяти, используя резинку для волос, а затем напишут и нарисуют то, что у них есть. Например:
12 – десять и два . - Пусть они развяжут палочки и вернут их в центр, а затем повторят с другим номером подростка, используя запасные палочки по мере необходимости.
- Попросите учеников вернуться ко всей группе со своими рисунками, спрятав их. Предложите учащимся по очереди описать классу/группе то, что они нарисовали, и попросите одноклассника сказать, какое это число. Затем показывается рисунок.
- В заключение учитель записывает слова «десять и _________» рядом с каждым числом подростков в таблице класса, начатой в предыдущем упражнении.
 Также рассмотрите возможность совместного изучения анимации детских палочек Place Value, доступной по адресу https://e-ako.nzmaths.co.nz/modules/PVanimations/ .
Также рассмотрите возможность совместного изучения анимации детских палочек Place Value, доступной по адресу https://e-ako.nzmaths.co.nz/modules/PVanimations/ .
Сессия 2
SLO:
- Сформируйте группы по десять человек и представьте числа подростков с помощью материалов.
- Распознавать и записывать слова и символы для чисел для подростков.
- Поймите, что в подростковом числе 1 представляет одну группу из десяти
Занятие 1
- Попросите учащихся сесть вместе с партнером. Скажите им, что каждая пара будет рисовать на пальцах цифры для подростков, и попросите их обсудить, как они будут это делать. Посмотрите и прислушайтесь к тем учащимся, которые сразу же узнают, что один из их пары будет «десяткой», поднимая каждый раз по десять пальцев.
- Поднимите несколько карточек с названиями чисел словами, символами и теми, которые читаются как «десять и ___». (Приложение 2). Каждый раз давайте карточку первой паре, чтобы добиться совместного представления на их пальцах.

- Учитель делает номер для подростков из детских кубиков или палочек для льда, заставляя учеников считать до десяти, пока собирается десятка.
Поднимите десять связок и спросите: «У меня еще есть десять палочек?» (да) «Сколько у меня пачек по десять штук?» (1). Запись на графике, например, у меня пятнадцать. 15 это десять и пять. 15 это 1 десяток и 5 единиц. Обсудите язык «единиц» и то, что иногда «единицы» можно назвать «единицами».
- Смоделируйте еще один пример, затем пусть учащиеся индивидуально нарисуют и напишут три своих любимых подростковых числа. Например, «12 — это 1 десяток и две единицы».
Занятие 2
Если возможно, пусть учащиеся поработают в небольших группах или парах, чтобы изучить, найти и показать четыре совпадающие карточки в карточной игре BSM 9-1-48.
В качестве альтернативы учащиеся могут составить классную игру-головоломку. Раздайте каждому учащемуся карточку, ручки и ножницы. Попросите их собрать свои собственные кусочки головоломки, которые затем можно будет объединить с теми, что сделали их одноклассники, и смешать их, чтобы получилась игра в пары.
Попросите их собрать свои собственные кусочки головоломки, которые затем можно будет объединить с теми, что сделали их одноклассники, и смешать их, чтобы получилась игра в пары.
Задание 3
- Вернитесь к таблице класса, начатой на занятии 1. Запишите слова маори для чисел для подростков, выделив «текау ма» — это «десять и», соединив этот математический язык с другими уже записанными выражениями.
- В небольших группах, используя карточки BSM 9-1-48, учащиеся играют в Teen Teams (цель: сопоставить словесные, графические и символьные изображения подростковых чисел).
Учащиеся раздают по 7 карточек. Оставшаяся стопка карт кладется в центр группы. Учащиеся по очереди спрашивают у одного другого игрока карточку, необходимую для заполнения набора из 5 семейных карточек подростков. Если у другого игрока нет искомой карты, запрашивающий игрок берет одну из стопки. Когда наборы готовы, учащиеся кладут их перед собой.
Победителем становится игрок с наибольшим количеством комплектов.
Сессия 3
SLO:
- Поймите, что в подростковом числе 1 представляет одну группу из десяти.
- Расширьте нотацию чисел для подростков и поймите простое разрядное значение.
- Поймите и примените десять за один обмен.
Упражнение 1
- Отобразите таблицу, начатую в Занятии 1. Запишите рядом с числами 11–19 описание «1 десяток и x единиц» для каждого из чисел.
- Используя увеличенные карточки со стрелками, продемонстрируйте и обсудите обозначения разрядов, которые мы используем, выделяя язык десятков и единиц.
- Познакомьте учащихся с пластиковыми фасолью и контейнерами. Попросите их работать в парах, чтобы составить контейнеры по десять бобов в каждом и обсудить, как эти контейнеры будут называться. (контейнер — это «один десяток» или «десять»). Предложите учащимся обсудить сходство между палочками, которые они использовали, и бобами.
Примечание. Контейнер для фасоли выглядит иначе, но его все же можно распаковать. Это тонкий и важный сдвиг. Также рассмотрите возможность совместного изучения анимации bean-компонентов в составе группы или класса, доступной по адресу https://e-ako.nzmaths.co.nz/modules/PVanimations/ .
Контейнер для фасоли выглядит иначе, но его все же можно распаковать. Это тонкий и важный сдвиг. Также рассмотрите возможность совместного изучения анимации bean-компонентов в составе группы или класса, доступной по адресу https://e-ako.nzmaths.co.nz/modules/PVanimations/ . - Дайте учащимся время ознакомиться с карточками «бобы» и «стрелки». Попросите их сделать и смоделировать как минимум три подростковых номера с помощью оборудования, объяснив это своему партнеру.
- Пусть каждый учащийся заполнит лист мыслительной доски (Приложение 3) или мини-плакат об одном из своих любимых номеров подростков. Отобразите их.
Занятие 2
Учащиеся играют в игру Go Teen парами.
(Цель: использовать десять единиц для получения одной группы из десяти при добавлении двух однозначных чисел.)
У учащихся есть игральные карты (туз — 9), перетасованные и лежащие лицом вниз между ними. У них есть одиночные бобы и пустые десятки контейнеров (или одиночные детские / ледяные палочки и резинки для волос), доступны однозначные и десятки карт со стрелками.
Игроки по очереди переворачивают две игральные карты. Когда два числа складываются, если получается меньше десяти, они возвращаются лицом вниз в стопку сброса.
Если они делают больше десяти, они сохраняют свои игральные карты, берут общее количество бобов, группируют материалы, показывая общее количество как 1 десяток и единицы. Они также показывают номер со стрелками.
Однако, если число уже составлено его партнером (карты со стрелками для этого числа были использованы), учащийся должен просто вернуть свои игральные карты в стопку сброса.
Победителем становится игрок, набравший наибольшее количество десятков (контейнеров с фасолью), когда все карты со стрелками будут израсходованы.
Сессия 4
SLO:
- Понимание и применение десяти за один обмен.
- Поймите, как разложить десятку, чтобы вычесть.
Занятие 1
- Учитель моделирует фигурку подростка из контейнеров и бобов и спрашивает: «Какая цифра здесь изображена?».
 Например, 18:
Например, 18:
Поставлена задача, в которой вычитаемое число требует «распаковать» или разложить десятку:
«Вот бобы, которые садовник Гэвин собирается сажать. Он сажает 9в первом ряду. Сколько бобов осталось посадить во втором ряду? Как мы можем это решить?»
Учащиеся обсуждают стратегии вычитания 9 и предлагают, что они могут сделать с материалами. Учитель моделирует этот и еще один пример вместе.
- Учащимся предоставляются оценочные материалы, и каждому дается не менее двух задач на вычитание для решения с разложением (Приложение 4). Учащиеся должны записать с помощью картинок, слов и уравнений, что они сделали и каков их результат.
- Поделитесь в классе/группе и обсудите. Можно ввести язык составления десяти (сочинение) и разбиения десяти (разложение).
Упражнение 2
- Учитель просит ученика смоделировать двадцать, используя материал с разрядностью. Обсудите, что это означает: два десятка равно двадцати.

- Предложите учащимся сыграть парами или небольшими группами От первого до двадцати .
(Цель: понять, как составлять и раскладывать десятку.)
У учащихся есть бобы и контейнеры, карточки с числами 11–14, набор игральных карт 2–5, игральные кости с символами + или –, отмеченными на каждой из шести граней. Карточки с цифрами раскладываются лицевой стороной вниз.
Каждый учащийся выбирает карточку и составляет это число, используя оборудование разряда.
Игроки по очереди бросают кости и переворачивают игральную карту. Они следуют инструкции, либо добавляя, либо вычитая из своих материалов. Каждый раз, когда у ученика есть очередь, он должен написать уравнение.
Победителем становится первый ученик, у которого есть два контейнера с десятью бобами (двадцать).
Например: ученик переворачивает и моделирует 13, бросает + и 3 и получает 16.
На следующем ходу ученику может понадобиться — 4, а на следующем ходу — — 3. Это потребует от ученика разложить десять.
Учащийся уже записал три хода:
13 + 3 = 16
16 – 4 = 12
12 – 3 = 9
- Завершите урок, сосредоточив внимание на словах «значение места». Учитель записывает «значение места» на диаграмме и спрашивает учащихся, что это может означать. Им предлагается просмотреть все записи подростковых номеров, сделанные на этих уроках. Примите все ответы, но в заключение выделите и запишите, что « место числительного в числе говорит нам, сколько оно стоит или его значение ». Покажите увеличенные карточки со стрелками, обращая внимание на слова десятки и единицы .
Домашняя ссылка
Уважаемые родители и whānau,
На уроке математики на этой неделе мы изучали числа для подростков и то, как они состоят из десяти и однозначного числа. Например, тринадцать — это 10 + 3. Мы также познакомились со значением разряда, узнав, что 1 из 13 на самом деле является одной группой из десяти.
Вы можете помочь своему ребенку попрактиковаться в этой очень важной идее, играя в игру Подростковый матч .
Разрежьте прикрепленную страницу, чтобы сделать отдельные карточки. Разложите их лицевой стороной вниз на столе. По очереди выбирайте пару карт. Если они совпадают, оставьте пару. Победителем становится тот, у кого больше всего пар.
[Включить копию Copymaster 5]
Приложения
Добавить в план
Первый уровень
Ранние вычислительные навыки и учащиеся с трудностями в математике
- Список журналов
- Рукописи авторов HHS
- PMC3756513
Фокус, кроме ребенка. Авторская рукопись; доступно в PMC 2013 29 августа.
Опубликовано в окончательной редакции как:
Фокус, кроме ребенка. 2012 январь; 44(5): 1–16.
PMCID: PMC3756513
NIHMSID: NIHMS367956
PMID: 23997274
, Доцент и лицензионная информация. . Некоторые дети понимают основы чисел и математики, в то время как другие испытывают трудности с базовым счетом, распознаванием чисел, пониманием символов, количественным различением и понятиями сложения и вычитания. Часто этот набор ранних числовых компетенций называют 9.0125 чувство числа или навыки раннего счета. Перед тем, как перейти к более сложным математическим задачам, учащиеся должны усвоить и понять эти компетенции. В этой статье описываются важные ранние вычислительные навыки и дается описание того, как этим навыкам можно научить учащихся, испытывающих трудности с математикой.
Прежде чем решать задачи по алгебре, геометрии, дробям и вычислениям, учащиеся должны иметь четкое представление о числах (Малофеева, Дэй, Сако, Янг и Чиансио, 2004). Иногда это называют числовой смысл (например, Джордан, 2007; Камински, 2002; Вагнер и Дэвис, 2010) или ранний счет (например, Аунио, Хаутамаки, Саданиеми и Ван Луит, 2009; Брайант и др., 2011; ВанДерХейден и др. др., 2011). Независимо от используемого термина, конструкция относится к ранним числовым навыкам, которые являются основой для развития математических способностей. В этой статье мы называем этот набор навыков ранними числовыми компетенциями.
Иногда это называют числовой смысл (например, Джордан, 2007; Камински, 2002; Вагнер и Дэвис, 2010) или ранний счет (например, Аунио, Хаутамаки, Саданиеми и Ван Луит, 2009; Брайант и др., 2011; ВанДерХейден и др. др., 2011). Независимо от используемого термина, конструкция относится к ранним числовым навыкам, которые являются основой для развития математических способностей. В этой статье мы называем этот набор навыков ранними числовыми компетенциями.
Что такое ранние числовые навыки?
Хотя единого определения ранних вычислительных навыков не существует, несколько исследователей выявили ранние числовые навыки, которые важны для младших школьников (Berch, 2005; Bryant et al., 2011; Gersten & Chard, 1999; Griffin & Case, 1997; Kaufmann, Handl, & Thony, 2003; Lago & DiPerna, 2010). См. схему ранних числовых компетенций. Некоторые темы (например, разрядное значение или основные комбинации чисел) требуют предварительных знаний по другим темам (например, распознавание чисел или сравнение чисел). Мы представляем эти ранние числовые навыки в виде коллекции, потому что развитие у учащихся ранних числовых навыков не всегда является линейным, и учащиеся различаются по временной шкале, за которую они приобретают эти навыки.
Мы представляем эти ранние числовые навыки в виде коллекции, потому что развитие у учащихся ранних числовых навыков не всегда является линейным, и учащиеся различаются по временной шкале, за которую они приобретают эти навыки.
Открыть в отдельном окне
Ранние числовые навыки
Важность ранних числовых навыков
Дети начинают ходить в школу (т. е. в детский сад) с широким спектром ранних числовых навыков. Некоторые дети уже умеют различать величины, знают названия своих чисел и могут решать простые задачи на сложение и вычитание; другим трудно идентифицировать числа и считать от 1 до 10 (Lembke & Foegen, 2009). Воздействие на первых этапах числовой деятельности дома, в дошкольном учреждении или в детском саду играет важную роль в формировании навыков счета у учащихся детского сада на раннем этапе (Baroody & Benson, 2001; Jung, 2011: Skwarchuk, 2009).). Чем больше учащиеся знакомятся с ранними числовыми способностями через игры, рассказы или игры до начала формального школьного обучения, тем лучше они понимают строительные блоки математики (Ramani & Siegler, 2008).
Одним из признаков того, что эти ранние вычислительные способности важны, является то, что они предсказывают более поздние достижения в математике. Например, Локуниак и Джордан (2008) протестировали 198 учащихся весной в детском саду по начальным числовым показателям и снова зимой во втором классе по показателю беглости вычислений. Учащиеся, набравшие ниже 25-го процентиля в начале детского сада, были отнесены к группе риска плохого развития математики. Ранние числовые меры включали вопросы счета, знания чисел, невербального счета, числовых комбинаций и задач на рассказы. Мера беглости вычислений состояла из 25 комбинаций сложения и 25 вычитания чисел. Ранняя вычислительная компетентность, измеренная в детском саду, была важным предиктором беглости счета во втором классе. Более 50% учащихся из группы риска (выявленных в детском саду) по-прежнему успевали ниже 25-го процентиля во втором классе, а 25% учащихся из группы риска показали результаты между 25-м и 50-м процентилями. Выводы Локуняка и Джордана показывают, что многие учащиеся с более слабыми навыками счета в детском саду будут продолжать демонстрировать более низкую успеваемость по математике после окончания детского сада. Джордан, Каплан, Локуняк и Раминени (2007) обнаружили аналогичную закономерность у 277 учащихся от детского сада до первого класса. Показатели чувства числа осенью в детском саду составляли 66% дисперсии тестов по математическим вычислениям и решению задач, проводимых в конце первого класса. Другие исследования (Duncan et al., 2007; Jordan, Glutting, Ramineni, & Watkins, 2010) также показывают, что ранние навыки счета предсказывают успехи в математике в более поздних классах.
Джордан, Каплан, Локуняк и Раминени (2007) обнаружили аналогичную закономерность у 277 учащихся от детского сада до первого класса. Показатели чувства числа осенью в детском саду составляли 66% дисперсии тестов по математическим вычислениям и решению задач, проводимых в конце первого класса. Другие исследования (Duncan et al., 2007; Jordan, Glutting, Ramineni, & Watkins, 2010) также показывают, что ранние навыки счета предсказывают успехи в математике в более поздних классах.
Трудности с ранними математическими навыками
Многие учащиеся испытывают трудности с ранними математическими навыками (Lembke & Foegen, 2009; Lloyd, Irwin, & Hertzman, 2009). В Соединенных Штатах различия проявляются в начале школьного обучения: некоторые дети приходят в школу с устоявшимся набором навыков счета в раннем возрасте, тогда как другие демонстрируют гораздо более низкие результаты при выполнении задач в раннем возрасте (Jordan et al., 2007). Например, Джордан, Каплан, Раминени и Локуняк (2009 г. ) применяли ранние числовые меры счета, распознавания чисел, сравнения, числовых комбинаций и задач на рассказы в детском саду. Учащиеся с более низким доходом в их выборке продемонстрировали значительно более низкие численные баллы в начале, чем их сверстники со средним доходом. Хотя низкий доход может быть не единственным фактором, влияющим на различия в умении считать в раннем возрасте, Jordan et al. (2009) продемонстрировали, что учащиеся детского сада демонстрируют различные уровни навыков счета в раннем возрасте. Та же тенденция сохраняется и для студентов в других странах (Ee, Wong, & Aunio, 2006; Lloyd et al., 2009).). Например, финские учащиеся в возрасте от 5 до 7 лет с особыми потребностями (т. е. с синдромом дефицита внимания, языковыми трудностями или трудностями в развитии) продемонстрировали значительно более низкие численные показатели в раннем возрасте, чем учащиеся без особых потребностей (Aunio et al., 2009).
) применяли ранние числовые меры счета, распознавания чисел, сравнения, числовых комбинаций и задач на рассказы в детском саду. Учащиеся с более низким доходом в их выборке продемонстрировали значительно более низкие численные баллы в начале, чем их сверстники со средним доходом. Хотя низкий доход может быть не единственным фактором, влияющим на различия в умении считать в раннем возрасте, Jordan et al. (2009) продемонстрировали, что учащиеся детского сада демонстрируют различные уровни навыков счета в раннем возрасте. Та же тенденция сохраняется и для студентов в других странах (Ee, Wong, & Aunio, 2006; Lloyd et al., 2009).). Например, финские учащиеся в возрасте от 5 до 7 лет с особыми потребностями (т. е. с синдромом дефицита внимания, языковыми трудностями или трудностями в развитии) продемонстрировали значительно более низкие численные показатели в раннем возрасте, чем учащиеся без особых потребностей (Aunio et al., 2009).
Поскольку учащиеся, которые хуже справляются с числовыми задачами в начальной школе, часто демонстрируют более низкую математическую компетентность в старшей начальной и средней школе (Duncan et al. , 2007), раннее выявление и раннее вмешательство являются ключевыми (Dowker, 2005). Хотя выявление учащихся, испытывающих затруднения, может быть затруднено из-за неадекватных оценок (Mazzocco, 2005), а некоторые учащиеся ошибочно идентифицируются как отстающие в математике (Locuniak & Jordan, 2008), исследования показывают, что раннее вмешательство может помочь учащимся с их ранними навыками счета (Berch, 2005; Брайант и др., 2011; Фукс и др., 2005а).
, 2007), раннее выявление и раннее вмешательство являются ключевыми (Dowker, 2005). Хотя выявление учащихся, испытывающих затруднения, может быть затруднено из-за неадекватных оценок (Mazzocco, 2005), а некоторые учащиеся ошибочно идентифицируются как отстающие в математике (Locuniak & Jordan, 2008), исследования показывают, что раннее вмешательство может помочь учащимся с их ранними навыками счета (Berch, 2005; Брайант и др., 2011; Фукс и др., 2005а).
Early Numerical Instruction
На основе экспериментальной работы со студентами, испытывающими трудности с математикой, Fuchs et al. (2008) предоставили несколько рекомендаций по важным компонентам обучения математике. Инструкция должна быть четкой с упором на концептуальные и процедурные знания. Обучение должно быть организовано осмысленно, чтобы свести к минимуму проблемы, а практика и повторение должны быть частью любой учебной программы. Фукс и др. также подчеркнул использование мотивационных инструментов, встроенных в обучение, чтобы помочь учащимся с поведением на задании и контролировать академический прогресс. Мониторинг успеваемости учащихся важен для того, чтобы у учителей были объективные индикаторы того, когда реакция учащихся на текущую учебную программу является неадекватной и вряд ли приведет к достижению цели. Когда данные учащегося указывают на неадекватную реакцию, учитель корректирует учебную программу учащегося.
Мониторинг успеваемости учащихся важен для того, чтобы у учителей были объективные индикаторы того, когда реакция учащихся на текущую учебную программу является неадекватной и вряд ли приведет к достижению цели. Когда данные учащегося указывают на неадекватную реакцию, учитель корректирует учебную программу учащегося.
Gersten et al. (2009) выделили четкое обучение, использование стратегий, вербальные выражения учащихся, использование визуальных представлений, мониторинг прогресса и использование различных примеров как важные учебные практики для учащихся, испытывающих трудности с математикой. В дополнение к этим пунктам Герстен и Чард (1999) предложили работать над беглостью математики, чтобы объединить обучение понятиям и процедурам с достаточной практикой. Эти рекомендации особенно важны для учащихся с математическими трудностями, и следующие примеры демонстрируют, как эти важные учебные рекомендации, используемые для обучения навыкам счета на ранних этапах, полезны для учащихся с математическими трудностями.
Например, Bryant et al. (2011) работали с первоклассниками (N = 224), которые показали результаты ниже 35-го процентиля при ранней оценке числовых компетенций. Некоторые учащиеся (n = 151) были назначены на начальную числовую программу, в то время как другие учащиеся (n = 73) остались в своем обычном учебном классе для обучения математике. Репетиторство в малых группах для учащихся начальных численных программ длилось 22 недели, четыре занятия в неделю, 25 минут каждое занятие. Студенты участвовали в подробном обучении с управляемой и независимой практикой процедурных и концептуальных идей счета, числовых отношений, наборов из 10, числовых комбинаций и разряда. В посттесте учащиеся, участвовавшие в начальной числовой программе, показали значительно более высокие результаты, чем учащиеся в контрольной группе, с величиной эффекта (ES) 0,18 при сравнении величин, 0,47 при сравнении числовых последовательностей, 0,39.на разрядное значение и 0,55 на числовые комбинации сложения и вычитания.
Фукс и др. (2005a) также проводили раннее обучение числам первоклассников (N = 127), у которых были проблемы с математикой. Студенты были случайным образом распределены для раннего обучения математике (n = 64) или для участия в обычном обучении математике без репетиторства (n = 63). Студенты получали репетиторство в течение 16 недель, три раза в неделю, по 40 минут. Репетиторство было сосредоточено на ранних числовых навыках, таких как идентификация и запись чисел, использование символов, счет, разрядное значение, а также комбинации сложения и вычитания. После того, как обучение закончилось, учащиеся, получившие обучение, превзошли студентов без обучения в тестах сложения фактов (ES = 0,40), фактов вычитания (ES = 0,14), вычислений (ES = 0,57), понятий и приложений (ES = 0,67) и задач на рассказ. (ES = 0,70).
В других странах также было показано, что ранние числовые программы улучшают успеваемость по математике учащихся, испытывающих затруднения. Кауфманн и др. (2003) работал с шестью учениками с трудностями в математике. Эти студенты участвовали в ранней числовой программе в течение 6 месяцев, три раза в неделю, по 25 минут. Учащиеся узнали о счете, символах, фактах, равных 10, фактах сложения и вычитания, а также о размещении значений посредством явных инструкций и перехода от конкретного (т. е. манипулятивного) к абстрактному (т. е. решения задач с числами и символами). Шестеро учеников добились значительного роста в ходе программы по сравнению со сверстниками, у которых не было проблем с математикой. Кауфманн, Делазер, Поль, Семенца и Даукер (2005) расширили эту работу, сравнив раннюю числовую программу, ориентированную на процедурное и концептуальное обучение, с программой, ориентированной на обучение базовым навыкам. Студенты, участвовавшие в процедурной и концептуальной программе, продемонстрировали значительный прогресс в показателях счета, количества элементов, сравнений и вычислений по сравнению со студентами, участвовавшими в программе базовых навыков. Van Luit и Schopman (2000) работали с учащимися детских садов (N = 124), которые по ранним числовым показателям показали результаты ниже 25-го процентиля.
Эти студенты участвовали в ранней числовой программе в течение 6 месяцев, три раза в неделю, по 25 минут. Учащиеся узнали о счете, символах, фактах, равных 10, фактах сложения и вычитания, а также о размещении значений посредством явных инструкций и перехода от конкретного (т. е. манипулятивного) к абстрактному (т. е. решения задач с числами и символами). Шестеро учеников добились значительного роста в ходе программы по сравнению со сверстниками, у которых не было проблем с математикой. Кауфманн, Делазер, Поль, Семенца и Даукер (2005) расширили эту работу, сравнив раннюю числовую программу, ориентированную на процедурное и концептуальное обучение, с программой, ориентированной на обучение базовым навыкам. Студенты, участвовавшие в процедурной и концептуальной программе, продемонстрировали значительный прогресс в показателях счета, количества элементов, сравнений и вычислений по сравнению со студентами, участвовавшими в программе базовых навыков. Van Luit и Schopman (2000) работали с учащимися детских садов (N = 124), которые по ранним числовым показателям показали результаты ниже 25-го процентиля. Половине студентов было поручено пройти раннее числовое обучение; другая половина участвовала в их обычной классной программе. Ранние числовые инструкции были сосредоточены на навыках счета, а обучение было явным и интерактивным и следовало последовательности от конкретного к репрезентативному и абстрактному (Hudson & Miller, 2006). После двадцати 30-минутных занятий учащиеся, участвовавшие в начальной числовой программе, превзошли контрольную группу по ранним числовым показателям сравнения чисел, счета и понимания значения чисел.
Половине студентов было поручено пройти раннее числовое обучение; другая половина участвовала в их обычной классной программе. Ранние числовые инструкции были сосредоточены на навыках счета, а обучение было явным и интерактивным и следовало последовательности от конкретного к репрезентативному и абстрактному (Hudson & Miller, 2006). После двадцати 30-минутных занятий учащиеся, участвовавшие в начальной числовой программе, превзошли контрольную группу по ранним числовым показателям сравнения чисел, счета и понимания значения чисел.
Эти результаты первых числовых исследований в Соединенных Штатах и за рубежом показывают, что учащиеся-математики, испытывающие затруднения, получают пользу от программ, ориентированных на ранние вычислительные навыки. Все инструкции в этих программах были явными и были сосредоточены на обучении студентов смыслу (т. Е. Концепциям), стоящим за ранними вычислительными способностями, а также процедурам решения математических задач.
В этой статье мы выделяем четыре основные категории ранних навыков работы с числами: счет, сравнение чисел, понимание символов и понятия сложения и вычитания. В этом разделе мы опишем каждую из этих категорий и то, как учащиеся могут бороться с навыками в этой категории. Затем мы представляем пример вмешательства, чтобы помочь учащимся, которые борются с этими ранними вычислительными способностями. Наконец, мы даем рекомендации для практиков.
В этом разделе мы опишем каждую из этих категорий и то, как учащиеся могут бороться с навыками в этой категории. Затем мы представляем пример вмешательства, чтобы помочь учащимся, которые борются с этими ранними вычислительными способностями. Наконец, мы даем рекомендации для практиков.
Счет
Счет — это нечто большее, чем простое повторение «1, 2, 3, 4, 5…». 2004; Брюс и Трелфолл, 2004). Например, учащиеся могут не придавать значения своему счету или понимать, что числовые слова сопоставляются со счетными элементами. Подсчет включает в себя пять принципов: стабильный порядок, однозначное соответствие, кардинальность, абстракция и нерелевантность порядка (Gelman & Gallistel, 19).78). Студенты могут бороться с одним или несколькими из этих принципов (Bruce & Threlfall, 2004). Эти принципы часто комбинируются (т. е. учащиеся произносят названия чисел и указывают на каждый счетный объект), и поэтому эти принципы следует практиковать вместе (Camos, Barrouillet & Fayol, 2001).
Многие учащиеся развивают навыки счета еще до поступления в детский сад (Gelman & Gallistel, 1978). Однако некоторые учащиеся приходят в школу с недостаточными навыками счета или непониманием принципов счета. Например, многие учащиеся могут без труда сосчитать до пяти, но могут испытывать затруднения при подсчете больших наборов (т. е. наборов больше 5 или 6), делать больше ошибок и не понимать, как использовать счет для определения количества элементов в наборе. набор (Каррасумада, Вендрель, Рибера и Монтсеррат, 2006 г.). Однако навыкам счета можно научить и улучшить с помощью инструкций и практики (Camos et al., 2001; Xin & Holmdal, 2003). Часто полезным способом понять, понимают ли учащиеся принципы счета, является демонстрация счета и неправильного счета с помощью куклы (Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007; Muldoon, Lewis, & Francis, 2007). Рекомендации по обучению счету могут определяться осведомленностью (или отсутствием) навыков счета у куклы. Например, если учащийся говорит, что для марионетки неправильно вести счет справа налево ученика, то учащийся должен пройти обучение принципу нерелевантности порядка счета.
Для счета учащиеся должны знать количество слов в порядке (Slusser & Sarnecka, 2011), понятие, называемое стабильным порядком. Эти слова обычно произносятся в прямом порядке (например, «один, два, три, четыре, пять»), и последовательность этих счетных слов должна использоваться последовательно (Frye, Braisby, Lowe, Maroudas, & Nicholls, 1989). ). Стабильный порядок часто изучается и практикуется с помощью песен, песнопений или историй.
Кроме того, при подсчете учащиеся должны сосчитать каждый элемент только один раз (Van De Walle, Karp, & Bay-Williams, 2010). это называется индивидуальная переписка. При обучении переписке один на один учащимся легче отслеживать элементы в ряду или элементы, которые были помечены и разделены, а не элементы, которые подсчитываются случайным образом (Potter & Levy, 1968). Чтобы считать с использованием однозначного соответствия, учащиеся должны знать названия чисел, ценить стабильный порядок и понимать взаимосвязь между счетами и названиями чисел (Potter & Levy, 1968). Индивидуальная переписка часто практикуется путем передачи предметов (например, файлов cookie) и обеспечения того, чтобы каждый учащийся получил один файл cookie (Van De Walle et al., 2010).
Индивидуальная переписка часто практикуется путем передачи предметов (например, файлов cookie) и обеспечения того, чтобы каждый учащийся получил один файл cookie (Van De Walle et al., 2010).
Комбинируя стабильный порядок и однозначное соответствие, учащиеся начинают считать наборы объектов, чтобы определить число в наборе (т. е. принцип мощности ). При подсчете набора предметов окончательный счет (например, «4» после подсчета четырех динозавров) представляет набор. Кардинальность относится к пониманию того, что окончательный или последний подсчет представляет собой общее количество подсчитанных элементов (Bermejo et al., 2004). Часто это практикуется, когда студентов просят сосчитать набор предметов, а затем просят их ответить на вопрос: «Сколько?» (Малдун, Льюис и Фриман, 2003 г.).
Хотя принцип счета абстракции не является обязательным для счета, учащимся полезно понять, что любые объекты могут составлять множество (Frye et al., 1989). Например, счетный набор не обязательно должен содержать только лягушек. Набор для счета может содержать лягушек, жаб, грузовиков и карандашей. Подсчет может применяться к любому набору элементов, независимо от того, насколько абстрактными могут быть эти элементы. Подобно абстракции, нерелевантность порядка не так важна, как другие принципы подсчета (Kamawar et al., 2010). Принцип нерелевантности порядка диктует, что порядок, в котором подсчитываются элементы, не имеет значения, пока каждый элемент подсчитывается только один раз (т. Е. Соответствие один к одному). Многие учащиеся считают слева направо и сверху вниз, потому что именно так они читают по-английски, поэтому таких учащихся может сбить с толку тот факт, что счет не должен происходить линейным образом.
Набор для счета может содержать лягушек, жаб, грузовиков и карандашей. Подсчет может применяться к любому набору элементов, независимо от того, насколько абстрактными могут быть эти элементы. Подобно абстракции, нерелевантность порядка не так важна, как другие принципы подсчета (Kamawar et al., 2010). Принцип нерелевантности порядка диктует, что порядок, в котором подсчитываются элементы, не имеет значения, пока каждый элемент подсчитывается только один раз (т. Е. Соответствие один к одному). Многие учащиеся считают слева направо и сверху вниз, потому что именно так они читают по-английски, поэтому таких учащихся может сбить с толку тот факт, что счет не должен происходить линейным образом.
Учащиеся должны перейти от подсчета предметов по одному к подсчету (Bruce & Threlfall, 2004; Hannula, Rasanen, & Lehtinen, 2007). Субитирование — это возможность мгновенно распознать, сколько предметов находится в группе. См. примеры субитизации. Учащиеся должны быть в состоянии посмотреть на каждый из примеров и сразу распознать, что есть четыре прямоугольника, три круга, один шестиугольник и шесть квадратов. Часто учащиеся, у которых проблемы с математикой, испытывают трудности с субитизацией (Schleifer & Landerl, 2011), но практика может помочь улучшить их навыки (Клементс, 19 лет).99; Фишер, Кенгетер и Хартнегг, 2008 г.). Субитация часто рассматривается как центральный компонент начальной вычислительной компетенции, и мы упоминаем ее здесь, потому что учащиеся могут субитизировать (вместо счета), чтобы сравнивать суммы и работать со сложением и вычитанием.
Часто учащиеся, у которых проблемы с математикой, испытывают трудности с субитизацией (Schleifer & Landerl, 2011), но практика может помочь улучшить их навыки (Клементс, 19 лет).99; Фишер, Кенгетер и Хартнегг, 2008 г.). Субитация часто рассматривается как центральный компонент начальной вычислительной компетенции, и мы упоминаем ее здесь, потому что учащиеся могут субитизировать (вместо счета), чтобы сравнивать суммы и работать со сложением и вычитанием.
Оценка количества
Субитирование связано с оценкой детьми количества, связанной с ними ранней числовой компетенцией. Иногда это называют количественной дискриминацией, величиной или сравнением чисел. На самом базовом уровне учащиеся смотрят на два числа (например, 4 и 9).) и ответьте на вопрос «Чего больше?» (9) или «Что меньше?» (4). Студенты могут использовать манипуляции или изображения, чтобы помочь в различении двух величин. Учащимся легче различать величины, которые намного дальше друг от друга (например, 9 и 2), чем те, которые ближе по величине (например, 9 и 8; Murray & Mayer, 1988). При сравнении больших двузначных чисел учащимся легче различать числа, в которых разряды десятков отличаются, чем когда разряды одни и те же, но разряды единиц различаются (Ganor-Stern, Pinhas, & Tzelgov, 2009).).
При сравнении больших двузначных чисел учащимся легче различать числа, в которых разряды десятков отличаются, чем когда разряды одни и те же, но разряды единиц различаются (Ganor-Stern, Pinhas, & Tzelgov, 2009).).
Учащиеся с трудностями в математике часто испытывают трудности со сравнением чисел и хуже справляются с заданиями на сравнение, чем их сверстники без математических трудностей (De Smedt & Gilmore, 2011; Holloway & Ansari, 2009). Интересно, что учащиеся могут лучше справляться с задачами на числовые величины, которые не включают числовые символы (Rousselle & Noel, 2007). Например, когда им предлагается группа из шести и четырех конфет, учащиеся могут определить, что шесть больше, чем четыре. сложно (De Smedt & Gilmore, 2011).
Учащиеся дошкольного возраста, когда им предъявляют два набора для сравнения, часто не считают и используют принцип кардинальности для сравнения двух наборов. Обычно учащиеся вместо этого полагаются на визуальный (то есть несимволический) осмотр (Чжоу, 2002). Опора на визуальное сканирование может помочь учащимся только на некоторое время, как правило, когда числа находятся в диапазоне от 1 до 3. Поэтому может быть полезно дать инструкции по счету для определения различий между наборами (Muldoon et al., 2003). Часто учащиеся не понимают, что счет можно использовать для сравнения, потому что учителя обычно спрашивают: «Сколько?» с каждым заданием на подсчет вместо вопросов типа «На сколько меньше?» или «У кого больше?»
Опора на визуальное сканирование может помочь учащимся только на некоторое время, как правило, когда числа находятся в диапазоне от 1 до 3. Поэтому может быть полезно дать инструкции по счету для определения различий между наборами (Muldoon et al., 2003). Часто учащиеся не понимают, что счет можно использовать для сравнения, потому что учителя обычно спрашивают: «Сколько?» с каждым заданием на подсчет вместо вопросов типа «На сколько меньше?» или «У кого больше?»
Математические символы
С ранними навыками счета учащиеся в конечном итоге будут ассоциировать счет (например, один, два, три) с числовыми символами (например, 1, 2, 3). Студенты часто могут повторять числовые слова в стабильном порядке, использовать взаимно однозначное соответствие и понимать количество элементов без использования числовых символов. Учащиеся также могут сравнивать суммы без использования числовых символов (т. е. при наличии визуальных представлений двух наборов). Однако, как только учащиеся поступают в детский сад, большинство занятий, связанных со счетом и сравнением чисел, требуют от учащихся знания числовых символов и значения этих символов для выполнения математических задач. Математические символы важны, потому что большая часть математики представлена с помощью символов.
Математические символы важны, потому что большая часть математики представлена с помощью символов.
Десять числовых символов (т. е. 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9) могут использоваться по отдельности или в сочетании для представления любого числа (например, 14 597). Помимо десяти числовых символов учащиеся младших классов изучают два символа операций: знак плюс (+) для сложения и знак минус (-) для вычитания. Учащиеся также используют знак равенства (=) в числовых предложениях. Учащиеся также могут использовать символы неравенства для обозначения больше (>) и меньше (<) при сравнении сумм. Студенты обычно изучают числовые символы раньше любых других символов (Zhou, Wang, Wang, & Wang, 2006).
Учащиеся должны научиться писать и интерпретировать символы, потому что они не придают значения символам автоматически. Значение символов развивается со временем и с практикой. Например, учащиеся узнают, что «три» или * * * или три медведя-манипулятора могут быть представлены письменным символом 3 и наоборот. Учащиеся должны научиться складывать предметы, когда они видят символ плюса (+), и убирать предмет или находить разницу, когда они видят символ минуса (-). Многие учащиеся понимают операции, обозначенные знаками плюс и минус, но меньше учащихся правильно интерпретируют знак равенства и символы неравенства (например, Hattikudur & Alibali, 2010; Matthews & Rittle-Johnson, 2009).; Макнейл. 2008). Знак равенства следует понимать как относительный символ, указывающий на то, что между числами по обе стороны от знака равенства (=) существует сбалансированная связь (Jacobs, Franke, Carpenter, Levi, & Battey, 2007). Символы неравенства (< и >) также следует понимать как реляционные, причем одна сторона символа представляет большее или меньшее количество.
Учащиеся должны научиться складывать предметы, когда они видят символ плюса (+), и убирать предмет или находить разницу, когда они видят символ минуса (-). Многие учащиеся понимают операции, обозначенные знаками плюс и минус, но меньше учащихся правильно интерпретируют знак равенства и символы неравенства (например, Hattikudur & Alibali, 2010; Matthews & Rittle-Johnson, 2009).; Макнейл. 2008). Знак равенства следует понимать как относительный символ, указывающий на то, что между числами по обе стороны от знака равенства (=) существует сбалансированная связь (Jacobs, Franke, Carpenter, Levi, & Battey, 2007). Символы неравенства (< и >) также следует понимать как реляционные, причем одна сторона символа представляет большее или меньшее количество.
К сожалению, учащиеся начинают неправильно понимать символы, поскольку учителя проводят инструкции или практику, не способствующую полному пониманию символа (Capraro, Ding, Matteson, Capraro, & Li, 2007; McNeil, 2008). Например, студенты часто практикуют сотни уравнений, таких как 2 + 3 = _, которые требуют небольшого понимания знака равенства в реляционной манере (Пауэлл, в печати). Напротив, учащиеся, даже те, у кого проблемы с математикой, учатся интерпретировать знак равенства относительно с помощью соответствующих инструкций и практики (Powell & Fuchs, 2010). Однако без надлежащего обучения и практики учащиеся продолжают неправильно использовать или неверно истолковывать символы в средних и старших классах (Knuth, Alibali, Hattikudur, McNeil, & Stephens, 2008; Rowntree, 2009).; Верикиос и Фармаки, 2010).
Напротив, учащиеся, даже те, у кого проблемы с математикой, учатся интерпретировать знак равенства относительно с помощью соответствующих инструкций и практики (Powell & Fuchs, 2010). Однако без надлежащего обучения и практики учащиеся продолжают неправильно использовать или неверно истолковывать символы в средних и старших классах (Knuth, Alibali, Hattikudur, McNeil, & Stephens, 2008; Rowntree, 2009).; Верикиос и Фармаки, 2010).
Понятия сложения и вычитания
Изучение понятий сложения и вычитания не обязательно следует за овладением счетом, сравнением чисел и математическими символами. Дети часто могут решать простые задачи на сложение и вычитание, представленные без символов (т. е. представленные устно и/или решенные с помощью манипуляций или счета; Cobb, 1987; Sherman & Bisanz, 2009). Однако для выполнения большинства задач на сложение и вычитание, с которыми сталкиваются учащиеся начальной школы, необходимы адекватные навыки счета, сравнения и знания символов.
Приступая к изучению комбинаций чисел на сложение и вычитание (т. е. основных фактов), учащиеся часто работают над простыми задачами с манипуляциями. С практикой учащиеся меньше полагаются на манипуляции и больше полагаются на свои пальцы при счете (Groen & Resniek, 1977). Поскольку счет часто связан с решением комбинаций чисел сложения и вычитания, важны навыки счета (Baroody, Bajwa, & Eiland, 2009). В большинстве случаев младшие школьники используют счет единицами в качестве механизма счета по умолчанию. Счет двойками или другими способами или использование навыков субитизации не распространены до второго класса или позже (Camos, 2003). Затем учащиеся переходят от счета к решению комбинаций чисел, используя стратегии рассуждения или по памяти. Мастерство и беглость, конечно, являются конечной целью числовых комбинаций. Как правило, к концу первого класса учащиеся должны знать все 100 комбинаций сложения и 100 вычитаний (Baroody et al., 2009).).
е. основных фактов), учащиеся часто работают над простыми задачами с манипуляциями. С практикой учащиеся меньше полагаются на манипуляции и больше полагаются на свои пальцы при счете (Groen & Resniek, 1977). Поскольку счет часто связан с решением комбинаций чисел сложения и вычитания, важны навыки счета (Baroody, Bajwa, & Eiland, 2009). В большинстве случаев младшие школьники используют счет единицами в качестве механизма счета по умолчанию. Счет двойками или другими способами или использование навыков субитизации не распространены до второго класса или позже (Camos, 2003). Затем учащиеся переходят от счета к решению комбинаций чисел, используя стратегии рассуждения или по памяти. Мастерство и беглость, конечно, являются конечной целью числовых комбинаций. Как правило, к концу первого класса учащиеся должны знать все 100 комбинаций сложения и 100 вычитаний (Baroody et al., 2009).).
Приступая к сложению и вычитанию, учащиеся часто решают задачи на сложение более успешно, чем задачи на вычитание (Shinskey, Chan, Coleman, Moxom, & Yamamoto, 2009). Это связано с тем, что учащиеся учатся считать вперед задолго до того, как им удается считать назад. Навыки сложения учащихся, даже тех, у кого проблемы с математикой, как правило, сильнее, чем их навыки вычитания. Это проявляется в том, что многие учащиеся решают задачи на вычитание более эффективно, когда используют навыки сложения (Torbeyns, De Smedt, Stassens, Ghesquiere, & Verschaffel, 2009).). Например, когда им предлагается задача 14 – 9 = _, многим учащимся легче подумать: «Что я могу добавить к 9, чтобы получить 14?» и может быть использована стратегия подсчета вперед.
Это связано с тем, что учащиеся учатся считать вперед задолго до того, как им удается считать назад. Навыки сложения учащихся, даже тех, у кого проблемы с математикой, как правило, сильнее, чем их навыки вычитания. Это проявляется в том, что многие учащиеся решают задачи на вычитание более эффективно, когда используют навыки сложения (Torbeyns, De Smedt, Stassens, Ghesquiere, & Verschaffel, 2009).). Например, когда им предлагается задача 14 – 9 = _, многим учащимся легче подумать: «Что я могу добавить к 9, чтобы получить 14?» и может быть использована стратегия подсчета вперед.
Хотя учащиеся могут понять принцип вычитания, они часто отстают в своей способности понять, что вычитание является обратным сложением (Baroody, Lai, Li, & Baroody, 2009). Поскольку учащиеся не понимают автоматически обратной зависимости между сложением и вычитанием, это понятие следует сделать более явным посредством обучения и практики (Baroody, 19).99). Учащиеся, которые понимают взаимосвязь между сложением и вычитанием (т. е. сложение является обратным действием вычитанию и наоборот), демонстрируют лучшие концептуальные знания и лучшие результаты вычитания, чем учащиеся, которые не понимают этой взаимосвязи (Gilmore & Papadatou-Pastou, 2009).
е. сложение является обратным действием вычитанию и наоборот), демонстрируют лучшие концептуальные знания и лучшие результаты вычитания, чем учащиеся, которые не понимают этой взаимосвязи (Gilmore & Papadatou-Pastou, 2009).
Стратегии счета (т. е. счет, чтобы найти ответ на комбинацию чисел сложения или вычитания) помогают учащимся решать комбинации. Однако не все учащиеся используют стратегию подсчета (Saxton & Cakir, 2006). Некоторые студенты просто предполагают. Для многих учащихся, особенно для тех, кто борется с начальными навыками счета, стратегии счета для решения числовых комбинаций полезны и могут быть изучены относительно легко. Есть несколько стратегий счета, которые учащиеся могут использовать при решении комбинаций чисел сложения и вычитания. См. схемы. При подсчете всех учащиеся подсчитывают первое слагаемое, подсчитывают второе слагаемое, а затем считают оба слагаемых вместе, начиная с 1. Обычно это первая стратегия подсчета для сложения, которую используют учащиеся (Fuson & Secada, 19). 86). Стратегия подсчета всех не очень эффективна и, учитывая необходимое количество подсчетов, часто приводит к неправильным ответам. Студенты обычно отказываются от подсчета всех в пользу более продвинутой стратегии «подсчета» или «подсчета» (Fuson & Secada, 1986). Подсчет можно проводить двумя способами: начать с большего слагаемого и подсчитывать меньшее слагаемое (т. е. стратегия «минимум», потому что студент считает минимальное количество) или наоборот (т. учащийся считает максимальную сумму). Прежде чем учащиеся узнают о коммутативном свойстве сложения (т. е. порядок сложения не влияет на сумму), они часто начинают с первого слагаемого в числовом предложении (например, 4 из 4 + 9).= _), не осознавая большей эффективности, если начинать с большего слагаемого и подсчитывать меньшее слагаемое (Groen & Parkman, 1972). Например, если представлено 5 + 9 = _, учащиеся начинают с 9 и считают еще 5: «10, 11, 12, 13, 14». Учащиеся часто развивают эту стратегию счета на основе опыта и практики (Weiland, 2007), но может быть необходимо, особенно для учащихся, испытывающих затруднения с математикой, дать подробные инструкции по этой более эффективной стратегии счета (Powell, Fuchs, Fuchs, Cirino, & Флетчер, 2009 г.
86). Стратегия подсчета всех не очень эффективна и, учитывая необходимое количество подсчетов, часто приводит к неправильным ответам. Студенты обычно отказываются от подсчета всех в пользу более продвинутой стратегии «подсчета» или «подсчета» (Fuson & Secada, 1986). Подсчет можно проводить двумя способами: начать с большего слагаемого и подсчитывать меньшее слагаемое (т. е. стратегия «минимум», потому что студент считает минимальное количество) или наоборот (т. учащийся считает максимальную сумму). Прежде чем учащиеся узнают о коммутативном свойстве сложения (т. е. порядок сложения не влияет на сумму), они часто начинают с первого слагаемого в числовом предложении (например, 4 из 4 + 9).= _), не осознавая большей эффективности, если начинать с большего слагаемого и подсчитывать меньшее слагаемое (Groen & Parkman, 1972). Например, если представлено 5 + 9 = _, учащиеся начинают с 9 и считают еще 5: «10, 11, 12, 13, 14». Учащиеся часто развивают эту стратегию счета на основе опыта и практики (Weiland, 2007), но может быть необходимо, особенно для учащихся, испытывающих затруднения с математикой, дать подробные инструкции по этой более эффективной стратегии счета (Powell, Fuchs, Fuchs, Cirino, & Флетчер, 2009 г. ).
).
Открыть в отдельном окне
Стратегии подсчета
При использовании каждой из этих стратегий учащиеся могут поднимать пальцы вверх, сгибать пальцы или постукивать пальцами. Учащиеся могут работать, повернув ладони к себе или от себя. Кроме того, учащиеся могут считать слева направо или справа налево. Они могут начать считать указательным, большим или другим пальцем.
Чтобы решить числовые комбинации с вычитанием, учащиеся часто считают в обратном порядке. То есть они начинают с уменьшаемого и отсчитывают количество вычитаемого. Для 9– 4 = _, учащиеся начинают с 9 и отсчитывают до 4: «8, 7, 6, 5». Обратный или обратный счет затруднен для учащихся, особенно учащихся с трудностями в математике, потому что беглость обратного счета ограничена по сравнению с беглостью прямого счета (Passolunghi & Cornoldi, 2008). Учащиеся также склонны делать гораздо больше ошибок при обратном счете, чем при прямом. Более эффективная стратегия решения задач на вычитание — счет вверх. Учащиеся начинают с вычитаемого и считают до уменьшаемого. Для 9– 4 = _, учащиеся начинают с 4 и считают «5. 6. 7, 8, 9». Они считают по 5 пальцев или делают 5 счетов, поэтому 9 – 4 = 5. Эта стратегия использует навыки быстрого прямого счета учащихся и оказалась полезной стратегией для учащихся с трудностями в математике (Fuchs et al., 2009; Fuchs). , Пауэлл и др., 2010). Использование подсчета для вычитания также подчеркивает тот факт, что вычитание представляет собой разницу между двумя суммами (то есть уменьшаемым и вычитаемым).
Учащиеся начинают с вычитаемого и считают до уменьшаемого. Для 9– 4 = _, учащиеся начинают с 4 и считают «5. 6. 7, 8, 9». Они считают по 5 пальцев или делают 5 счетов, поэтому 9 – 4 = 5. Эта стратегия использует навыки быстрого прямого счета учащихся и оказалась полезной стратегией для учащихся с трудностями в математике (Fuchs et al., 2009; Fuchs). , Пауэлл и др., 2010). Использование подсчета для вычитания также подчеркивает тот факт, что вычитание представляет собой разницу между двумя суммами (то есть уменьшаемым и вычитаемым).
Сложение и вычитание, практика использования стратегий счета и работа над беглостью речи улучшают успеваемость учащихся, испытывающих затруднения (Fuchs, Powell, et al., 2010). Учащиеся должны понимать концепции, лежащие в основе числовых комбинаций (Baroody, Lai, et al., 2009).), но им также необходимо рутинно, даже ежедневно, практиковаться, чтобы развить беглость речи и помочь учащимся часто и правильно проводить ассоциации между основами задачи и их ответами (Fuchs, Powell, et al. , 2010). Это приводит к тому, что учащиеся строят представления в долговременной памяти и помогают учащимся полагаться на наиболее эффективную стратегию решения задач на сложение и вычитание: автоматический поиск ответов (Fuchs et al., 2011). По этой причине учащиеся должны практиковаться на всех комбинациях чисел, особенно на комбинациях чисел, которые включают двузначные числа (например, 9).+ 7 = 16; 14 – 8 = 6), потому что они, как правило, больше знакомы с более простыми комбинациями чисел (Hamann & Ashcraft, 1986).
, 2010). Это приводит к тому, что учащиеся строят представления в долговременной памяти и помогают учащимся полагаться на наиболее эффективную стратегию решения задач на сложение и вычитание: автоматический поиск ответов (Fuchs et al., 2011). По этой причине учащиеся должны практиковаться на всех комбинациях чисел, особенно на комбинациях чисел, которые включают двузначные числа (например, 9).+ 7 = 16; 14 – 8 = 6), потому что они, как правило, больше знакомы с более простыми комбинациями чисел (Hamann & Ashcraft, 1986).
Мы обсудили четыре первых числовых навыка: счет, сравнение чисел, понимание символов и понятия сложения и вычитания. Хотя это и не исчерпывающий список навыков раннего численного обучения, эти четыре являются важными компонентами эффективной программы раннего численного обучения для учащихся, испытывающих затруднения. Четыре компонента связаны друг с другом и дополняют друг друга по мере того, как учащиеся изучают все больше и больше математики в начальных классах. В то время как учащиеся могут испытывать трудности с одной или несколькими из этих начальных вычислительных способностей, обучение и практика могут улучшить начальные численные навыки учащихся.
В то время как учащиеся могут испытывать трудности с одной или несколькими из этих начальных вычислительных способностей, обучение и практика могут улучшить начальные численные навыки учащихся.
В следующем разделе мы опишем начальную числовую программу для первоклассников, у которых проблемы с математикой. Мы описываем эту программу, чтобы проиллюстрировать, как учителя и родители учащихся, испытывающих затруднения, могут включить в успешную учебную программу для учащихся, испытывающих затруднения, четыре первых числовых навыка, обсуждаемых в этой статье. Это не единственное доступное раннее численное вмешательство, поэтому преподавателям следует изучить варианты, прежде чем выбирать программу для своих учеников. 9Программа 0125 Galaxy Math, , также известная как Number Rockets, (Fuchs et al., 2011), была разработана, чтобы помочь предотвратить долговременные трудности в математике, устраняя ранние дефициты числовых навыков и способствуя знанию чисел и навыкам с комбинациями чисел и другими Основные элементы школьной программы по математике в первом классе. Программа называется Galaxy Math , потому что на уроках используется космическая тема, чтобы мотивировать учащихся. Преподаватели призывают учащихся «Отправиться в математическую галактику!» а ученики используют математические манипуляторы в форме ракет. См. пример диаграммы мотивации на тему галактики.
Программа называется Galaxy Math , потому что на уроках используется космическая тема, чтобы мотивировать учащихся. Преподаватели призывают учащихся «Отправиться в математическую галактику!» а ученики используют математические манипуляторы в форме ракет. См. пример диаграммы мотивации на тему галактики.
Открыть в отдельном окне
Галактика Математика Мотивационная таблица
Экспериментальное исследование Галактики Математика
В начале первого класса учащиеся с согласия родителей прошли скрининг для выявления тех, кто подвержен риску неадекватного развития математики, хотя большинство учащихся не имели школьной диагностированной неспособности к обучению. Эти учащиеся были случайным образом распределены для продолжения своей обычной школьной программы (т. е. контрольной группы) или для одной из двух версий Математика Галактики. В обеих версиях Galaxy Math основное внимание (25 минут каждого 30-минутного занятия) уделяется типам начальных числовых компетенций, обсуждаемых в этой статье. Одна версия Galaxy Math (стандартная версия) добавляла 5 минут практики в конце каждого занятия; другая версия добавила 5 минут игр. В обоих условиях обучения. студентов Galaxy Math получили 48 индивидуальных занятий три раза в неделю.
Одна версия Galaxy Math (стандартная версия) добавляла 5 минут практики в конце каждого занятия; другая версия добавила 5 минут игр. В обоих условиях обучения. студентов Galaxy Math получили 48 индивидуальных занятий три раза в неделю.
См. список из Galaxy Math единиц и концепций. В Единице 1 учащиеся используют манипулятивные средства, такие как числовая линия, подсчет бобов и «Мистер Уайт». Greater Gator», чтобы узнать величины, попрактиковаться в счете, сравнить числа и выучить символы. См. и, например, действия по подсчету и изучению терминологии равных. Эти занятия проводятся во время первых нескольких уроков Galaxy Math. См. образец строки номера. Числа в числовой строке увеличиваются в размере по мере увеличения значения чисел, чтобы помочь учащимся понять величину чисел. Обратитесь к мистеру Большому Аллигатору. У этого аллигатора широко открыта пасть с символами неравенства (то есть больше или меньше знаков), наложенными на открытую пасть. Учащиеся узнают, что аллигатор очень голоден и хочет съесть большее количество, когда ему дают две порции. Открытый рот всегда обращен к большему числу. Также в Блоке 1 учащиеся изучают стратегии подсчета (для сложения) и подсчета (для вычитания). При счете учащиеся держат меньшее слагаемое на пальцах, а затем считают, складывая по одному пальцу за раз, пока не останется пальцев (т. Е. Сжатый кулак). Например, с 3 + 6 ученик поднимает 3 пальца и затем считает: «7» (загибает 1 палец), «8» (загибает другой палец), «9».(загибает последний палец). Ответ — это последнее число, которое сказал ученик (в данном случае 9). Подсчет — это одна из версий стратегии подсчета. Подсчет оказался полезным для первоклассников, потому что он помогал им следить за суммой подсчета. С подсчетом на вычитание учащиеся начинают со сжатым кулаком. Они начинают с вычитаемого и пальцами считают до уменьшаемого. Например, при 9-3 учениках считают «4, 5, 6, 7, 8, 9» (каждый раз поднимая другой палец). Как только учащиеся доходят до уменьшаемого, они подсчитывают количество пальцев (в данном случае 6), и 6 записывается как ответ.
Учащиеся узнают, что аллигатор очень голоден и хочет съесть большее количество, когда ему дают две порции. Открытый рот всегда обращен к большему числу. Также в Блоке 1 учащиеся изучают стратегии подсчета (для сложения) и подсчета (для вычитания). При счете учащиеся держат меньшее слагаемое на пальцах, а затем считают, складывая по одному пальцу за раз, пока не останется пальцев (т. Е. Сжатый кулак). Например, с 3 + 6 ученик поднимает 3 пальца и затем считает: «7» (загибает 1 палец), «8» (загибает другой палец), «9».(загибает последний палец). Ответ — это последнее число, которое сказал ученик (в данном случае 9). Подсчет — это одна из версий стратегии подсчета. Подсчет оказался полезным для первоклассников, потому что он помогал им следить за суммой подсчета. С подсчетом на вычитание учащиеся начинают со сжатым кулаком. Они начинают с вычитаемого и пальцами считают до уменьшаемого. Например, при 9-3 учениках считают «4, 5, 6, 7, 8, 9» (каждый раз поднимая другой палец). Как только учащиеся доходят до уменьшаемого, они подсчитывают количество пальцев (в данном случае 6), и 6 записывается как ответ. В Блоке 1 учащиеся также решают сюжетные задачи с манипуляциями, картинками или действиями. Например, при появлении проблемы «У Джона в тележке для продуктов 4 яблока. Он кладет в тележку еще 1 яблоко. Сколько яблок сейчас в тележке Джона?» учащиеся могли рисовать яблоки или использовать блоки-манипуляторы для решения задачи.
В Блоке 1 учащиеся также решают сюжетные задачи с манипуляциями, картинками или действиями. Например, при появлении проблемы «У Джона в тележке для продуктов 4 яблока. Он кладет в тележку еще 1 яблоко. Сколько яблок сейчас в тележке Джона?» учащиеся могли рисовать яблоки или использовать блоки-манипуляторы для решения задачи.
TABLE 1
Galaxy Math Lessons
| Unit | Lessons | Topics | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1–3 | Number line (0–9) | |||||||||||
| Counting вслух | |||||||||||||
| чтение и запись чисел | |||||||||||||
| подсчет предметов | |||||||||||||
| 1001 | |||||||||||||
| 4 | Using hands to show numbers less than 10 | ||||||||||||
| Discussion of 0 and numbers 11–19 | |||||||||||||
| Counting forwards | |||||||||||||
| Counting backwards | |||||||||||||
| 5 | Определение наибольшего и наименьшего чисел с помощью числовой строки | ||||||||||||
| 6, 7 | Сравнение чисел с помощью языка и символов | ||||||||||||
| 8 | Концепция добавления | ||||||||||||
| Значение + и = | |||||||||||||
| 9 | Дополнение 1 с номером | ||||||||||||
. | |||||||||||||
| 10 | Сложение 0 и 1 с числовой строкой | ||||||||||||
| Использование манипуляций, изображений и действий для решения сюжетных задач | |||||||||||||
| 11 | Подсчет в | ||||||||||||
| 12 | Добавление 0, 1 и 2 с подсчетом | ||||||||||||
| 13 | Концепция субтрега | 13 | . для сложения для сложения | ||||||||||
| 14 | Сложение и вычитание 1 с числовой строкой | ||||||||||||
| Использование манипуляций, изображений и действий для решения сюжетных задач | |||||||||||||
| 15 | Addition of 0 and 1 with number line | ||||||||||||
| Using manipulatives, pictures, and actions to solve story problems | |||||||||||||
| 16 | Counting up | ||||||||||||
| 17 | Сложение и вычитание 0, 1 и 2 со счетом in/up | ||||||||||||
| 18 | Просмотр счета in/up | ||||||||||||
| 2 | Doubles 19–20 | 06||||||||||||
| 3 | 21–24 | 5 Set | |||||||||||
| 25–28 | 6 Set | ||||||||||||
| 29–32 | 7 Set | ||||||||||||
| 33–36 | 8 Set | ||||||||||||
| 37–40 | 9 Set | ||||||||||||
| 41–44 | 10 Set | ||||||||||||
| 45–48 | 11 Set | ||||||||||||
| 49–52 | 12 Set | ||||||||||||
| 4 | 53 | Number line to 100 | |||||||||||
| Numbers 20–29 | |||||||||||||
| 54–56 | Number line to 100 | ||||||||||||
| Double-digit addition | |||||||||||||
| 57 | Счет десятками | ||||||||||||
| Использование рук для представления десятков и единиц | |||||||||||||
| 58 | Знакомство со значением разряда 9 15039 909 006 | Introduction to rods and cubes | |||||||||||
| Regrouping 10 cubes into 1 rod | |||||||||||||
| 60 | Regrouping | ||||||||||||
| 61 | Representing one- and two-digit numbers with rods and cubes | ||||||||||||
| Значение 0 в разряде | |||||||||||||
| 62 | Представление одно- и двузначных чисел палочками и кубами | ||||||||||||
| 63 631006 | Identifying larger and smaller numbers using place value and number line | ||||||||||||
| 64–66 | Practicing place value | ||||||||||||
| 5 | 67–74 | Review |
Open in a separate window
В Разделе 2 учащиеся используют бобы и числовую линейку, чтобы узнать о двойных числах от 0 до 6 (т. е. 0 + 0, 1 + 1, 2 + 2, 3 + 3, 4 + 4, 5 + 5, 6 + 6). , 0 – 0, 2 – 1, 4 – 2, 6 – 3, 8 – 4, 10 – 5, 12 – 6). Двойные числа отрабатываются в начале программы, потому что учащиеся обычно не испытывают особых трудностей с запоминанием двойных чисел, и учащиеся могут использовать двойные числа для решения других числовых комбинаций (Van De Walle et al., 2010).
е. 0 + 0, 1 + 1, 2 + 2, 3 + 3, 4 + 4, 5 + 5, 6 + 6). , 0 – 0, 2 – 1, 4 – 2, 6 – 3, 8 – 4, 10 – 5, 12 – 6). Двойные числа отрабатываются в начале программы, потому что учащиеся обычно не испытывают особых трудностей с запоминанием двойных чисел, и учащиеся могут использовать двойные числа для решения других числовых комбинаций (Van De Walle et al., 2010).
В Разделе 3 учащиеся начинают изучать комбинации чисел в наборах. Каждый набор включает все комбинации чисел с суммой и уменьшаемым концом в качестве номера целевого набора. Например, набор 5 состоит из комбинаций альтернативных чисел с суммой 5 или 5 в качестве уменьшаемого (т. е. 0 + 5, 1 + 4, 2 + 3, 3 + 2, 4 + 1, 5 + 0, 5 – 0, 5 – 1, 5 – 2, 5 – 3, 5 – 4, 5 – 5). Репетиторы начинают с 5-го набора и продолжают 12-й. При работе над каждым комплектом тьютор проводит с учеником пять видов деятельности. Во-первых, преподаватель и ученик используют кубики unifix, чтобы увидеть, как можно по-разному комбинировать кубики, чтобы получить комбинации чисел сложения и вычитания из набора. См. примеры из набора 5. С манипуляторами учащиеся также могут увидеть, как 1 + 4, 4 + 1, 5 – 1 и 5 – 4 связаны как «семья», а второе задание каждого урока сосредоточено на семьях, составляющих соответствующий набор. В-третьих, учащиеся либо отвечают на задачи набора числовых комбинаций на листе, либо показывают все комбинации в числовом наборе с манипулятивными ракетами. Затем репетитор и ученик работают вместе, чтобы решить сюжетную задачу, включающую комбинацию чисел из набора. Учащийся решает задачу и объясняет, почему задача истории специфична для набора чисел. Пятое занятие каждый день — это устный обзор предыдущих наборов чисел.
См. примеры из набора 5. С манипуляторами учащиеся также могут увидеть, как 1 + 4, 4 + 1, 5 – 1 и 5 – 4 связаны как «семья», а второе задание каждого урока сосредоточено на семьях, составляющих соответствующий набор. В-третьих, учащиеся либо отвечают на задачи набора числовых комбинаций на листе, либо показывают все комбинации в числовом наборе с манипулятивными ракетами. Затем репетитор и ученик работают вместе, чтобы решить сюжетную задачу, включающую комбинацию чисел из набора. Учащийся решает задачу и объясняет, почему задача истории специфична для набора чисел. Пятое занятие каждый день — это устный обзор предыдущих наборов чисел.
Открыть в отдельном окне
Манипулятивные примеры из 5 наборов
Над каждым набором студенты работают от одного до четырех уроков. После первого урока в наборе каждый последующий урок начинается с контрольного теста с карточками, с помощью которого учащиеся могут перейти к следующему набору, правильно отвечая на карточки. Студенты должны ответить в течение 3 секунд, допустив не более одной ошибки. Студенты, достигшие мастерства до полного набора четырех уроков в каждом наборе, завершают набор из 12. Другие учащиеся завершают набор из 10 предметов, а затем переходят к Разделу 4. Это правило обеспечивает надлежащий охват материала.
Студенты, достигшие мастерства до полного набора четырех уроков в каждом наборе, завершают набор из 12. Другие учащиеся завершают набор из 10 предметов, а затем переходят к Разделу 4. Это правило обеспечивает надлежащий охват материала.
В Уроке 4 акцент делается на разрядность: счет десятками до 100, показ и запись единиц и десятков, перегруппировка и сложение двузначных чисел. Учащиеся также просматривают числовые наборы во время этого раздела. Модуль 5 предназначен для учащихся, демонстрирующих мастерство при работе с наборами чисел. В этом разделе учащиеся рассматривают числовые наборы и концепции разряда.
В последние 5 минут каждого занятия Fuchs et al. (2011) выделили эффекты предоставления практики. Для этого половина студентов в исследовании выполняла систематическую практику в течение последних 5 минут; другая половина играла в игры. В практических и игровых условиях содержание было одинаковым: материал, относящийся к уроку сегодняшнего дня. Случайное задание определяло, участвовали ли учащиеся в играх или практиковались в конце каждого дневного урока.
В условии игр учащиеся играют в игры с манипулятивными ракетами для отработки понятий. Например, в одной игре учащиеся вращаются, чтобы узнать, сколько ракет вызвано на космическую станцию, и помещают это количество ракет на игровое поле. Затем снова крутятся, чтобы посмотреть, сколько ракет отозвано обратно на землю, и убирают соответствующее количество ракет с доски. Затем они генерируют числовое предложение, представляющее эту серию событий. Во время игр наставники поощряют учеников знать ответ или использовать пальцы, бобы или числовые линии для вычисления ответа. Преподаватели объясняют, что «знание ответа сразу» является предпочтительной стратегией, если ученик уверен в ответе.
При выполнении условия «Практика » учащиеся практикуют содержание уроков с помощью упражнения «Набери или превзойди свой результат», которое основано на карточках. Например, как только введены наборы сложения/вычитания, учащиеся тренируются в комбинациях чисел. Воспитатели предлагают детям вспомнить комбинацию по памяти или, если они не уверены в ответе, использовать стратегию счета, которую они изучили в Galaxy Math , чтобы решить комбинацию. Когда учащийся отвечает правильно, карточки кладутся стопкой на парту. Когда учащийся отвечает неправильно, репетитор требует, чтобы учащиеся использовали стратегию подсчета (т. е. подсчитывали или подсчитывали), чтобы найти правильный ответ. Затем исправленная карта кладется в стопку на столе. В конце 90 секунд, учащийся графически показывает количество правильно отвеченных карточек. См. образец графика флэш-карты. Затем у учащихся есть два шанса набрать или превзойти свой первый результат по флеш-карте.
Когда учащийся отвечает правильно, карточки кладутся стопкой на парту. Когда учащийся отвечает неправильно, репетитор требует, чтобы учащиеся использовали стратегию подсчета (т. е. подсчитывали или подсчитывали), чтобы найти правильный ответ. Затем исправленная карта кладется в стопку на столе. В конце 90 секунд, учащийся графически показывает количество правильно отвеченных карточек. См. образец графика флэш-карты. Затем у учащихся есть два шанса набрать или превзойти свой первый результат по флеш-карте.
Открыть в отдельном окне
Практика Flash Card Graph
В обоих случаях репетиторы поощряют выполнение задания и мотивацию к усердной работе (Fuchs et al., 2008), используя систематическую программу вознаграждения. Репетиторы учат студентов, что поведение на задании означает внимательность и старание правильно отвечать на вопросы. Учащиеся узнают, что поведение при выполнении задания важно для «отрыва в математическую галактику». Учащиеся получают стикеры за поведение на задании и усердную и правильную работу. Они прикрепляют свои стикеры к таблице Galaxy Math (см. ). Учащиеся получают приз (например, небольшую игрушку, наклейку или карандаш), когда достигают солнца на карте галактики.
Они прикрепляют свои стикеры к таблице Galaxy Math (см. ). Учащиеся получают приз (например, небольшую игрушку, наклейку или карандаш), когда достигают солнца на карте галактики.
Результаты исследования (Fuchs et al., 2011) показали, что учащиеся, участвовавшие в репетиторстве Galaxy Math , улучшили свои знания чисел, простых арифметических операций, более сложных вычислений и решения текстовых задач значительно лучше, чем учащиеся из контрольной группы. Учащиеся в практических условиях улучшили более простые арифметические и более сложные вычисления, чем учащиеся в играх, без ущерба для их знаний о числах или производительности в текстовых задачах. Это, наряду с другими исследованиями раннего численного вмешательства (например, Bryant et al., 2011; Fuchs et al., 2005b), демонстрирует положительные результаты для учащихся из групп риска, когда раннее численное вмешательство проводится рано и интенсивно. Фукс и др. (2011) также показывает особую важность включения частых, хорошо продуманных упражнений, которые поддерживают правильное реагирование.
Поскольку учащиеся поступают в детский сад и часто переходят в первый класс с разной степенью начальной вычислительной компетенции, практикующие врачи должны обеспечить раннюю оценку и раннее вмешательство, чтобы помочь учащимся, которые борются с основами математики. Для оценки могут использоваться меры мониторинга прогресса (например, Lembke & Foegen, 2009; Seethaler & Fuchs, 2011) и меры скрининга, нацеленные на конкретные математические навыки (например, Geary et al., 2007; Jordan et al., 2009). чтобы определить, какие студенты требуют раннего численного вмешательства.
После выявления учащихся, у которых в детском саду или в первом классе возникают проблемы с начальными вычислительными навыками, практикующим специалистам необходимо оценить программы для начальных числовых вычислений и выбрать программу, которая наилучшим образом соответствует потребностям учащихся.
Основываясь на экспериментальной работе с младшими учащимися (например, Bryant et al., 2011; Fuchs et al. , 2011), программы раннего развития числовых компетенций должны включать следующее; (а) подробное обучение, сосредоточенное на концептуальных знаниях и процедурных навыках, (б) последовательность инструкций, которая является значимой и актуальной, (в) повторение ранее изученных тем, (г) отработка текущих тем и (д) беглая работа над комбинации сложения и вычитания чисел. Направленность обучения (т. е. навыки счета, понятия сложения) должна определяться исходя из потребностей учащихся. Одна программа не может быть лучшей для всех учащихся, поэтому практикующие врачи должны следить за успеваемостью учащихся, пока учащиеся участвуют в обучении, чтобы определить реакцию. Если учащиеся не демонстрируют надлежащего обучения, их учебная программа должна быть изменена для формирующей разработки программы, адаптированной к потребностям учащегося.
, 2011), программы раннего развития числовых компетенций должны включать следующее; (а) подробное обучение, сосредоточенное на концептуальных знаниях и процедурных навыках, (б) последовательность инструкций, которая является значимой и актуальной, (в) повторение ранее изученных тем, (г) отработка текущих тем и (д) беглая работа над комбинации сложения и вычитания чисел. Направленность обучения (т. е. навыки счета, понятия сложения) должна определяться исходя из потребностей учащихся. Одна программа не может быть лучшей для всех учащихся, поэтому практикующие врачи должны следить за успеваемостью учащихся, пока учащиеся участвуют в обучении, чтобы определить реакцию. Если учащиеся не демонстрируют надлежащего обучения, их учебная программа должна быть изменена для формирующей разработки программы, адаптированной к потребностям учащегося.
Поскольку ранние навыки счета в детском саду предсказывают математические успехи в более поздних классах (Duncan et al., 2007; Jordan et al., 2010), жизненно важно своевременно оказывать помощь учащимся, которым не хватает навыков в начальных навыках счета. Исследователям необходимо продолжать совершенствовать ранние числовые оценки и вмешательства, которые помогут школам в своевременной идентификации и эффективном вмешательстве, чтобы обеспечить компетентность учащихся в основных строительных блоках математики.
Исследователям необходимо продолжать совершенствовать ранние числовые оценки и вмешательства, которые помогут школам в своевременной идентификации и эффективном вмешательстве, чтобы обеспечить компетентность учащихся в основных строительных блоках математики.
Это исследование было поддержано наградой № R01HD059179 от Национального института детского здоровья и развития Юнис Кеннеди Шрайвер Университету Вандербильта. Содержание является исключительной ответственностью авторов и не обязательно отражает официальную точку зрения Национального института детского здоровья и развития Юнис Кеннеди Шрайвер.
Доктор Сара Р. Пауэлл, Департамент учебной программы, обучения и специального образования Университета Вирджинии.
Доктор Линн С. Фукс, факультет специального образования Университета Вандербильта.
- Аунио П., Хаутамаки Дж., Саяниеми Н., Ван Луит Дж.Э.Х. Ранний счет у слабоуспевающих детей раннего возраста. Британский журнал исследований в области образования.
 2009;35(1):25–46. 10.1080/01411920802041822. [Google Scholar]
2009;35(1):25–46. 10.1080/01411920802041822. [Google Scholar] - Баруди А.Дж. Реляционные знания детей о сложении и вычитании. Познание и обучение. 1999;17(2):137–175. [Google Scholar]
- Баруди А.Дж., Баджва Н.П., Эйланд М. Почему Джонни не может вспомнить основные факты? Обзоры исследований нарушений развития. 2009 г.;15(1):69–79. 10.1002/ддрр.45. [PubMed] [Google Scholar]
- Baroody AJ, Benson A. Инструкция по раннему номеру. Обучение детей математике. 2001;8(3):154–158. [Google Scholar]
- Baroody AJ, Lai M, Li X, Baroody AE. Понимание дошкольниками принципов вычитания. Математическое мышление и обучение: международный журнал. 2009;11(1–2):41–60. [Google Scholar]
- Berch DB. Осмысление числа смысла: последствия для детей с математическими отклонениями. Журнал неспособности к обучению. 2005;38(4):333–339.. [PubMed] [Google Scholar]
- Bermejo V, Morales S, deOsuna JG. Способствовать развитию у детей понимания кардинальности. Обучение и инструкция.
 2004;14(4):381–398. [Google Scholar]
2004;14(4):381–398. [Google Scholar] - Брюс Р.А., Трелфолл Дж. Раз, два, три и так далее. Образовательные исследования по математике. 2004;55(1–3):3–26. [Google Scholar]
- Брайант Д.П., Брайант Б.Р., Робертс С., Вон С., Пфаннштиль К.Х., Портерфилд Дж., Герстен Р. Программа раннего обучения математике для первоклассников, испытывающих трудности с математикой. Исключительные дети. 2011;78(1):7–23. [Академия Google]
- Камос В. Стратегии счета от 5 лет до совершеннолетия: адаптация к особенностям строения. Европейский журнал психологии образования – EJPE. 2003;18(3):251–265. [Google Scholar]
- Camos V, Barrouillet P, Fayol M. Объясняет ли координация вербальной и моторной информации развитие счета у детей? Журнал экспериментальной детской психологии. 2001;78(3):240–62. [PubMed] [Google Scholar]
- Капраро М.М., Дин М., Маттесон С., Капраро Р.М., Ли С. Репрезентативные последствия для понимания эквивалентности. Школьная наука и математика. 2007;107(3):86–88.
 [Академия Google]
[Академия Google] - Каррасумада С., Вендрель Р., Рибера Г., Монтсеррат М. Когнитивные процессы, связанные со счетом у учащихся с особыми образовательными потребностями. Европейский журнал специального образования. 2006;21(2):135–150. [Google Scholar]
- Клементс Д.Х. Субитация. Обучение детей математике. 1999;5(1):400–405. [Google Scholar]
- Кобб П. Исследование академического арифметического контекста детей младшего возраста. Образовательные исследования по математике. 1987;18(2):109–24. [Google Академия]
- Де Смедт Б., Гилмор К.К. Неисправный номерной модуль или нарушение доступа? обработка числовых величин у первоклассников с математическими трудностями. Журнал экспериментальной детской психологии. 2011;108(2):278–292. [PubMed] [Google Scholar]
- Даукер А. Раннее выявление и вмешательство для учащихся с трудностями в математике. Журнал неспособности к обучению. 2005;38(4):324–332. [PubMed] [Google Scholar]
- Duncan GJ, Dowsett CJ, Claessens A, Magnuson K, Huston AC, Klebanov P, American PA.
 Подготовка к школе и более поздние достижения. Развивающая психология. 2007;43(6):1428–1446. [PubMed] [Академия Google]
Подготовка к школе и более поздние достижения. Развивающая психология. 2007;43(6):1428–1446. [PubMed] [Академия Google] - Ee J, Wong KY, Aunio P. Счет детей младшего возраста в Сингапуре, Пекине и Хельсинки. Журнал дошкольного образования. 2006;33(5):325–332. [Google Scholar]
- Фишер Б., Кенгетер А., Хартнегг К. Влияние ежедневной практики на субитизацию, визуальный счет и базовые арифметические навыки. Оптометрия и развитие зрения. 2008;39(1):30–34. [Google Scholar]
- Фрай Д., Брейсби Н., Лоу Дж., Марудас С., Николлс Дж. Понимание маленькими детьми счета и количества элементов. Развитие ребенка. 1989;60(5):1158. 10.1111/1467-8624.ep9676220. [PubMed] [Google Scholar]
- Fuchs LS, Compton DL, Fuchs D, Paulsen K, Bryant JD, Hamlett CL. Профилактика, выявление и когнитивные детерминанты математических трудностей. Журнал педагогической психологии. 2005а; 97(3):493–513. 10.1037/0022-0663.97.3.493. [Google Scholar]
- Fuchs LS, Compton DL, Fuchs D, Paulsen K, Bryant J, Hamlett CL.
 Реакция на вмешательство: предотвращение и выявление математических способностей. Обучение исключительных детей. 2005b;37(4):60–63. [Академия Google]
Реакция на вмешательство: предотвращение и выявление математических способностей. Обучение исключительных детей. 2005b;37(4):60–63. [Академия Google] - Fuchs LS, Fuchs D, Powell SR, Seethaler PM, Cirino PT, Fletcher JM. Интенсивное вмешательство для учащихся с математическими отклонениями: семь принципов эффективной практики. Ежеквартальный отчет по неспособности к обучению. 2008;31(2):79–92. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Fuchs LS, Geary DC, Fuchs D, Schatschneider C, Hamlett CL, DeSelms-Wolfe J, Changas P. Понимание и продвижение математического развития учащихся из групп риска в первом классе : рандомизированное контрольное исследование. 2011 г. Рукопись передана в печать. [Академия Google]
- Fuchs LS, Powell SR, Seethaler PM, Cirino PT, Fletcher JM, Fuchs D, Hamlett CL. Влияние обучения стратегическому счету с преднамеренной практикой и без нее на навыки комбинации чисел у учащихся с трудностями в математике. Обучение и индивидуальные различия.
 2010;20(2):89–100. [Бесплатная статья PMC] [PubMed] [Google Scholar]
2010;20(2):89–100. [Бесплатная статья PMC] [PubMed] [Google Scholar] - Fuchs LS, Powell SR, Seethaler PM, Cirino PT, Fletcher JM, Fuchs D, Zumeta RO. Устранение дефицита комбинации чисел и словесных задач среди учащихся с математическими трудностями: рандомизированное контрольное испытание. Журнал педагогической психологии. 2009 г.;101(3):561–576. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Fuson KC, Secada WG. Учить детей складывать, считая с помощью рисунков пальцев одной руки. Познание и обучение. 1986;3(3):229–260. [Google Scholar]
- Ганор-Штерн Д., Пинхас М., Цельгов Дж. Сравнение двузначных чисел: важность совместного представления. Ежеквартальный журнал экспериментальной психологии. 2009;62(3):444–452. 10.1080/174702108023
. [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Byrd-Craven J, Nugent L, Numtee C. Когнитивные механизмы, лежащие в основе дефицита успеваемости у детей с нарушением способности к математическому обучению. Развитие ребенка.
 2007; 74(4):1343–1359.. 10.1111/j.1467-8624.2007.01069.х. [Бесплатная статья PMC] [PubMed] [Google Scholar]
2007; 74(4):1343–1359.. 10.1111/j.1467-8624.2007.01069.х. [Бесплатная статья PMC] [PubMed] [Google Scholar] - Gelman R, Gallistel CR. Представление ребенка о числе. Кембридж, Массачусетс: Издательство Гарвардского университета; 1978. [Google Scholar]
- Герстен Р., Чард Д. Чувство чисел: переосмысление инструкций по арифметике для учащихся с математическими отклонениями. Журнал специального образования. 1999;33(1):18–28. [Google Scholar]
- Gersten R, Chard DJ, Jayanthi M, Baker SK, Morphy P, Flojo J. Обучение математике для учащихся с ограниченными возможностями обучения: метаанализ учебных компонентов. Обзор образовательных исследований. 2009 г.;79(3):1202–1242. [Google Scholar]
- Gilmore CK, Papadatou-Pastou M. Модели индивидуальных различий в концептуальном понимании и арифметических навыках: метаанализ. Математическое мышление и обучение. 2009;11(1):25–40. 10.1080/10986060802583923. [Google Scholar]
- Гриффин С., Кейс Р. Переосмысление учебной программы по математике в начальной школе: подход, основанный на когнитивной науке.
 Проблемы в образовании. 1997;3(1):1–49. [Google Scholar]
Проблемы в образовании. 1997;3(1):1–49. [Google Scholar] - Groen GJ, Parkman JM. Хронометрический анализ простого сложения. Психологический обзор. 1972;79(4):329–343. [Google Scholar]
- Groen G, Resnick LB. Могут ли дети дошкольного возраста изобретать алгоритмы сложения? Журнал педагогической психологии. 1977;69(6):645–652. [Google Scholar]
- Хаманн М.С., Эшкрафт М.Х. Представление в учебнике основных фактов сложения. Познание и обучение. 1986;3(3):173–192. [Google Scholar]
- Ханнула М.М., Расанен П., Лехтинен Э. Развитие навыков счета: роль спонтанного сосредоточения внимания на числе и перечисления на основе субитизации. Математическое мышление и обучение: международный журнал. 2007;9(1): 51–57. [Google Scholar]
- Хаттикудур С., Алибали М.В. Изучение знака равенства: помогает ли сравнение с символами неравенства? Журнал экспериментальной детской психологии. 2010;107(1):15–30. [PubMed] [Google Scholar]
- Holloway ID, Ansari D. Отображение числовых величин в символы: эффект числового расстояния и индивидуальные различия в математических достижениях детей.
 Журнал экспериментальной детской психологии. 2009;103(1):17–29. [PubMed] [Google Scholar]
Журнал экспериментальной детской психологии. 2009;103(1):17–29. [PubMed] [Google Scholar] - Хадсон П., Миллер С.П. Разработка и внедрение инструкций по математике для учащихся с различными потребностями в обучении. Бостон: Пирсон; 2006. [Google Академия]
- Джейкобс В.Р., Франке М.Л., Карпентер Т.П., Леви Л., Бэтти Д. Профессиональное развитие сосредоточено на алгебраическом мышлении детей в начальной школе. Журнал исследований в области математического образования. 2007;38(3):258–288. [Google Scholar]
- Джордан, Северная Каролина. Потребность в чувстве числа. Образовательное лидерство. 2007;65(2):63–66. [Google Scholar]
- Jordan NC, Glutting J, Ramineni C, Watkins MW. Проверка инструмента проверки правильности чисел для использования в детском саду и первом классе: прогнозирование математических знаний в третьем классе. Обзор школьной психологии. 2010;39(2): 181–195. [Google Scholar]
- Джордан Н.С., Каплан Д., Локуняк М.Н., Раминени С. Прогнозирование успеваемости по математике в первом классе на основе траекторий развития чувства чисел.
 Исследования и практика с ограниченными возможностями обучения. 2007;22(1):36–46. 10.1111/j.1540-5826.2007.00229.х. [Google Scholar]
Исследования и практика с ограниченными возможностями обучения. 2007;22(1):36–46. 10.1111/j.1540-5826.2007.00229.х. [Google Scholar] - Jordan NC, Kaplan D, Ramineni C, Locuniak MN. Ранняя математика имеет значение: знание чисел в детском саду и более поздние результаты математики. Развивающая психология. 2009;45(3):850–867. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Юнг М. Числовые отношения в дошкольных учреждениях. Обучение детей математике. 2011;17(9):550–557. [Google Scholar]
- Камавар Д., ЛеФевр Дж., Бизанц Дж., Фаст Л., Скварчук С., Смит-Чант Б., Пеннер-Вилгер М. Знание принципов счета: насколько релевантна нерелевантность порядка? Журнал экспериментальной детской психологии. 2010;105(1):138–145. 10.1016/j.jecp. 2009.08.004. [PubMed] [Google Scholar]
- Камински Э. Содействие математическому пониманию: смысл чисел в действии. Журнал исследований в области математического образования. 2002; 14(2):133–49.. [Google Scholar]
- Кауфманн Л.
 , Делазер М., Поль Р., Семенца С., Даукер А. Эффекты специальной программы обучения математике у детей дошкольного возраста: пилотное исследование. Образовательные исследования и оценка. 2005;11(5):405–431. 10.1080/13803610500110497. [Google Scholar]
, Делазер М., Поль Р., Семенца С., Даукер А. Эффекты специальной программы обучения математике у детей дошкольного возраста: пилотное исследование. Образовательные исследования и оценка. 2005;11(5):405–431. 10.1080/13803610500110497. [Google Scholar] - Кауфманн Л., Хэндл П., Тони Б. Оценка программы вмешательства в арифметику, ориентированной на базовые числовые знания и концептуальные знания: экспериментальное исследование. Журнал неспособности к обучению. 2003;36(6):564–573. [PubMed] [Академия Google]
- Кнут Э.Дж., Алибали М.В., Хаттикудур С., Макнил Н.М., Стивенс А.С. Важность понимания знака равенства в средних классах. Преподавание математики в средней школе. 2008;13(9):514–519. [Google Scholar]
- Lago RM, DiPerna JC. Чувство числа в детском саду: факторно-аналитическое исследование конструкции. Обзор школьной психологии. 2010;39(2):164–180. [Google Scholar]
- Лембке Э., Фоген А. Определение показателей раннего счета для учащихся детского сада и первоклассников.
 Исследования и практика с ограниченными возможностями обучения. 2009 г.;24(1):12–20. [Google Scholar]
Исследования и практика с ограниченными возможностями обучения. 2009 г.;24(1):12–20. [Google Scholar] - Ллойд Дж.Е.В., Ирвин Л.Г., Херцман С. Готовность к школе в детском саду и результаты грамотности и счета в четвертом классе детей с особыми потребностями: популяционное исследование. Образовательная психология. 2009;29(5):583–602. [Google Scholar]
- Locuniak MN, Jordan NC. Использование чувства числа в детском саду для прогнозирования беглости счета во втором классе. Журнал неспособности к обучению. 2008;41(5):451–459. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Малофеева Е., Дэй Дж., Сако Х., Янг Л., Чансио Д. Построение и оценка теста на чувствительность к числам с форой у детей. Журнал педагогической психологии. 2004;96(4):648–659. [Google Scholar]
- Мэтьюз П., Риттл-Джонсон Б. В погоне за знаниями: сравнение самообъяснений, концепций и процедур как педагогических инструментов. Журнал экспериментальной детской психологии. 2009;104(1):1–21.
 [PubMed] [Google Scholar]
[PubMed] [Google Scholar] - Mazzoceo MMM. Проблемы в определении целевых навыков для скрининга и вмешательства по математике. Журнал неспособности к обучению. 2005;38(4):318–323. [PubMed] [Google Scholar]
- McNeil NM. Ограничения в обучении детей 2 + 2 = 4: Типичные арифметические задачи могут помешать обучению математической эквивалентности. Развитие ребенка. 2008;79(5): 1524–1537. 10.1111/j.1467-8624.2008.01203.х. [PubMed] [Google Scholar]
- Малдун К.П., Льюис С., Фрэнсис Б. Использование кардинальности для сравнения величин: роль социально-когнитивного конфликта в ранней арифметике. Наука о развитии. 2007;10(5):694–711. 10.1111/j.1467-7687.2007.00618.x. [PubMed] [Google Scholar]
- Muldoon K, Lewis C, Freeman NH. Использование счета в работе: понимание дошкольниками кардинального расширения. Международный журнал образовательных исследований. 2003;39(7):695–718. [Google Scholar]
- Мюррей, П.Л., Майер, Р.Э. Суждения дошкольников о числовой величине.
 Журнал педагогической психологии. 1988;80(2):206–209. [Google Scholar]
Журнал педагогической психологии. 1988;80(2):206–209. [Google Scholar] - Passolunghi MC, Cornoldi C. Нарушения рабочей памяти у детей с арифметическими трудностями. Детская нейропсихология. 2008;14(5):387–400. л0.1080/09297040701566662. [PubMed] [Google Scholar]
- Potter MC, Levy EI. Пространственное перечисление без подсчета. Развитие ребенка. 1968; 39 (1): 265–272. [PubMed] [Академия Google]
- Пауэлл С.Р. Уравнения и знак равенства в учебниках по элементарной математике. Журнал начальной школы в печати. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Powell SR, Fuchs LS. Вклад обучения с равными знаками помимо обучения словесным задачам для учащихся третьего класса с трудностями по математике. Журнал педагогической психологии. 2010;102(2):381–394. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Powell SR, Fuchs LS, Fuchs D, Cirino PT, Fletcher JM. Влияние репетиторства по поиску фактов на учащихся третьего класса с математическими трудностями с трудностями чтения и без них.
 Исследования и практика с ограниченными возможностями обучения. 2009 г.;24(1):1–11. 10.1111/j.1540-5826.2008.01272.х. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Исследования и практика с ограниченными возможностями обучения. 2009 г.;24(1):1–11. 10.1111/j.1540-5826.2008.01272.х. [Бесплатная статья PMC] [PubMed] [Google Scholar] - Ramani GB, Siegler RS. Содействие широкому и стабильному улучшению числовых знаний детей из малообеспеченных семей посредством настольных игр с числами. Развитие ребенка. 2008;79(2):375–394. [PubMed] [Google Scholar]
- Руссель Л., Ноэль М. Основные числовые навыки у детей с ограниченными возможностями обучения математике: сравнение обработки величин символических и несимволических чисел. Познание. 2007; 102(3):361–39.5. [PubMed] [Google Scholar]
- Rowntree RV. Понимание и неправильное понимание учащимися алгебраических неравенств. Школьная наука и математика. 2009;109(6):311–312. [Google Scholar]
- Сакстон М., Чакир К. Расчет, торговля и разделение: влияние обучения и предварительных знаний на выполнение задач с основанием 10. Развитие ребенка. 2006;77(3):767–785. 10.1111/j.1467–8624.
 2006.00902.x. [PubMed] [Google Scholar]
2006.00902.x. [PubMed] [Google Scholar] - Шлейфер П., Ландерл К. Субитирование и подсчет в типичном и атипичном развитии. Наука о развитии. 2011;14(2):280–29.1. 10.1111/J.1467-7687.2010.0O976.X. [PubMed] [Google Scholar]
- Seethaler PM, Fuchs LS. Использование измерения на основе учебной программы для мониторинга развития математики дошкольников. Оценка эффективного обучения. 2011;36(4):219–229. 10.1177/1534508411413566. [Google Scholar]
- Шерман Дж., Бизанц Дж. Эквивалентность в символическом и несимволическом контекстах: преимущества решения проблем с помощью манипулятивных средств. Журнал педагогической психологии. 2009;101(1):88–100. [Google Академия]
- Шински Дж. Л., Чан Ч., Коулман Р., Моксом Л., Ямамото Э. Несимволическая арифметика дошкольников с большими множествами: сложение точнее вычитания? Журнал экспериментальной детской психологии. 2009;103(4):409–420. [PubMed] [Google Scholar]
- Скварчук С. Как родители поддерживают обучение дошкольников счету дома? Журнал дошкольного образования.
 2009;37(3):189–197. [Google Scholar]
2009;37(3):189–197. [Google Scholar] - Slusser EB, Sarnecka BW. Найдите изображение восьми черепах: связь между счетом детей и их знанием семантики числовых слов. Журнал экспериментальной детской психологии. 2011;110(1):38–51. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Торбейнс Дж., Де Смедт Б., Стассенс Н., Гескьер П., Вершаффель Л. Решение задач на вычитание с помощью косвенного сложения. Математическое мышление и обучение. 2009;11(1):79–91. 10.1080/10986060802583998. [Google Scholar]
- Ван де Валле Дж. А., Карп К. С., Бэй-Уильямс Дж. М. Математика в начальной и средней школе: Преподавание в целях развития. 7. Бостон: Аллин и Бэкон; 2010. [Google Scholar]
- Van Luit JEH, Schopman EAM. Улучшение раннего счета детей младшего возраста с особыми образовательными потребностями. Корректирующее и специальное образование. 2000;21(1):21–40. [Академия Google]
- VanDerHeyden AM, Broussard C, Snyder P, George J, Lafleur SM, Williams C. Измерение понимания детсадовцами ранних математических понятий.
 Обзор школьной психологии. 2011;40(2):296–306. [Google Scholar]
Обзор школьной психологии. 2011;40(2):296–306. [Google Scholar] - Верикиос П., Фармаки В. От уравнения к неравенству с использованием функционального подхода. Международный журнал математического образования в области науки и техники. 2010;41(4):515–530. [Google Scholar]
- Вагнер Д., Дэвис Б. Чувство числа: Заземляющий смысл числа в смысле количества. Образовательные исследования по математике. 2010;74(1):39–51. 10.1007/s10649-009-9226–9. [Google Scholar]
- Вейланд Л. Опыт, который поможет детям научиться считать. Обучение детей математике. 2007;14(3):188–192. [Google Scholar]
- Xin JF, Holmdal P. Закуски и навыки: Обучение детей навыкам функционального счета. Обучение исключительных детей. 2003;35(5):46–51. [Google Scholar]
- Чжоу С. Использование детьми дошкольного возраста счета для сравнения двух наборов в кардинальных ситуациях. Раннее развитие ребенка и уход. 2002;172(2):99–111. [Google Scholar]
- Zhou X, Wang Y, Wang L, Wang B.
 Представление детей в детском саду и понимание письменных числовых символов. Раннее развитие и уход за детьми. 2006;176(1):33–45. 10.1080/0300443042000302645. [Академия Google]
Представление детей в детском саду и понимание письменных числовых символов. Раннее развитие и уход за детьми. 2006;176(1):33–45. 10.1080/0300443042000302645. [Академия Google]
Числа до 10 заданий для маленьких учеников
Математика | Номера
Создание прочной основы для понимания чисел имеет решающее значение для долгосрочного успеха учащихся в математике, и это начинается в раннем возрасте. Это эквивалентно изучению названий букв и звуков букв при чтении.
Для наших учеников важно развить глубокое понимание отдельных чисел, их количества, того, как они представлены и как они соотносятся с другими числами. Чувство числа развивается посредством большого количества моделирования, практики и воздействия.
Сегодня я хотел поделиться некоторыми идеями, которые помогут вашим маленьким ученикам попрактиковаться и выучить числа, но я также хочу поделиться простым бесплатным тестом, который вы можете использовать для отслеживания прогресса ваших учеников в изучении чисел до 10.
Вот некоторые из моих любимых упражнений для отработки чисел. Упражнения просты в подготовке и могут быть использованы для утренней ванны, математических занятий или быстрых финишеров. Это свежие, интерактивные и увлекательные занятия, которые обязательно привлекут внимание ваших маленьких учеников.
Match and Cover:Match and Cover включает 25 различных ковриков для занятий с двумя типами ковриков, как показано на рисунках выше и ниже. Учащиеся используют пластиковые математические кубики {или медведей} и цветовой код на правой стороне коврика, чтобы показать свои ответы.
На коврике, изображенном выше, ученики просто сопоставляют число с числом. Используя маты, изображенные ниже, учащиеся определят число, представленное каждой картинкой, и используют цветовой код, чтобы покрыть картинки, чтобы показать число.
Pocket Chart Activity: Этот ресурс Pocket Chart прекрасно работает в качестве центра или математической доски объявлений . Учащиеся сопоставляют карточки с картинками, на которых изображено число, с соответствующим заголовком числа. На заголовок/номер приходится шесть карточек с картинками. Если вы используете это как центр, учащиеся могут выполнять это задание, используя карманную схему, на полу или за столом. В качестве дополнительного бонуса в этот пакет включены числа до 20!
Учащиеся сопоставляют карточки с картинками, на которых изображено число, с соответствующим заголовком числа. На заголовок/номер приходится шесть карточек с картинками. Если вы используете это как центр, учащиеся могут выполнять это задание, используя карманную схему, на полу или за столом. В качестве дополнительного бонуса в этот пакет включены числа до 20!
Если у вас завалялись мини-ластики, вот несколько отличных способов найти им хорошее применение. Этот ресурс Build the Number включает в себя четыре различных типа действий , которые помогут вашим учащимся идентифицировать и строить числа.
Если у вас нет мини-ластиков, пластиковые кубики или другие маленькие манипуляторы в классе тоже подойдут.
Закройте номер: Закройте номер — это простое в приготовлении задание. Просто распечатайте и вставьте защитную пленку для страниц. Учащиеся определяют номер мишени на коврике. Они смотрят на различные объекты (или картинки), чтобы определить, какие из них показывают целевой номер. Они используют кубики, мини-ластики или другие манипуляции в классе, чтобы скрыть свои ответы.
Учащиеся определяют номер мишени на коврике. Они смотрят на различные объекты (или картинки), чтобы определить, какие из них показывают целевой номер. Они используют кубики, мини-ластики или другие манипуляции в классе, чтобы скрыть свои ответы.
В этот ресурс включено 33 различных числовых коврика . Учащиеся определяют каждое число на коврике и используют магнитные числа, чтобы показать свой ответ. Вы также можете заламинировать их и попросить учеников использовать маркеры для сухого стирания. Числа отображаются в виде костяшек домино, счетных меток, десяти кадров и многого другого.
Найди номер: Это задание Найди номер лучше всего работает с карманной картой. В нее можно играть как всей группой, так и в небольшой группе. Чтобы играть, учитель прячет специальные карточки за несколькими числами. Учащиеся по очереди угадывают, за каким числом скрываются специальные карточки.
6 различных круглогодичных тематических наборов . Этот ресурс включает числа до 20, но вам не нужно использовать все числа, чтобы играть в игру. Вы можете играть с числами до 5, до 10 или вплоть до 20. Также имеется необязательная страница прогнозов, чтобы учащиеся могли записывать числа, за которыми, по их мнению, скрываются специальные карточки.
Сопоставьте:Сопоставьте включает в себя десять различных наборов одинаковых карточек для чисел до 10. Темы круглогодичные, поэтому вы можете использовать их круглый год. Есть справочная страница для учащихся и несколько различных вариантов листа записи, так что вы можете использовать их в качестве центра. Конечно, они совершенно необязательны, и студенты определенно могут выполнить это задание без них.
Числа до 10: счетные действия Включено 12 различных счетных действий. У каждого есть несколько версий, поэтому вы можете использовать их более одного раза, не объясняя заново направления. Для занятий потребуются основные школьные принадлежности, такие как пластиковые математические кубики, математические мишки, мини-ластики {если они у вас есть} и игральные кости.
Для занятий потребуются основные школьные принадлежности, такие как пластиковые математические кубики, математические мишки, мини-ластики {если они у вас есть} и игральные кости.
Для этих занятий нет листов для записей, поэтому они отлично подходят для утреннего принятия ванны, быстрого финиширования или работы в небольших группах.
Цифры до 10: Математические центрыВот краткое описание математических центров. Есть 15 различных центров:
Учащиеся считают каждую группу медведей, чтобы определить общее количество. Используя манипуляции в классе, они покажут свой ответ на десяти кадрах. Для всех центров включены визуальные указания «Я могу»!
Учащиеся пересчитывают каждый набор предметов на счетном коврике, чтобы определить общее количество каждого из них. Они найдут соответствующий набор картинок на листе для записи и запишут число, чтобы показать итоги.
Учащиеся выбирают карточку и считают, чтобы определить недостающие числа. Они найдут на листе соответствующую серию картинок и запишут недостающие числа.
Они найдут на листе соответствующую серию картинок и запишут недостающие числа.
Вы можете найти все упражнения, которыми я поделился, в Числах до 10 по математике НАБОР . Нажмите на картинку ниже, чтобы проверить это в моем магазине TpT.
Числа до 10 Оценка:
Эта бесплатная оценка состоит из нескольких компонентов. Существует контрольный список для учителей и соответствующие страницы для учащихся. Эта оценка поможет вам контролировать способность ваших учащихся называть числа, механически считать до 10 и определять количество.
Существует два варианта оценки счетных количеств. Вы можете просто предложить учащимся определить количество семян в каждом яблоке или использовать печатную версию, чтобы учащиеся записали числа. {Вы получите бонусную оценку написания чисел, используя печатную версию!} Все, что включено в этот бесплатный подарок, представлено в черно-белом варианте. Вы можете распечатать на цветной бумаге, чтобы добавить изюминку.
 (Дети имитируют все
движения хомячка.)
(Дети имитируют все
движения хомячка.)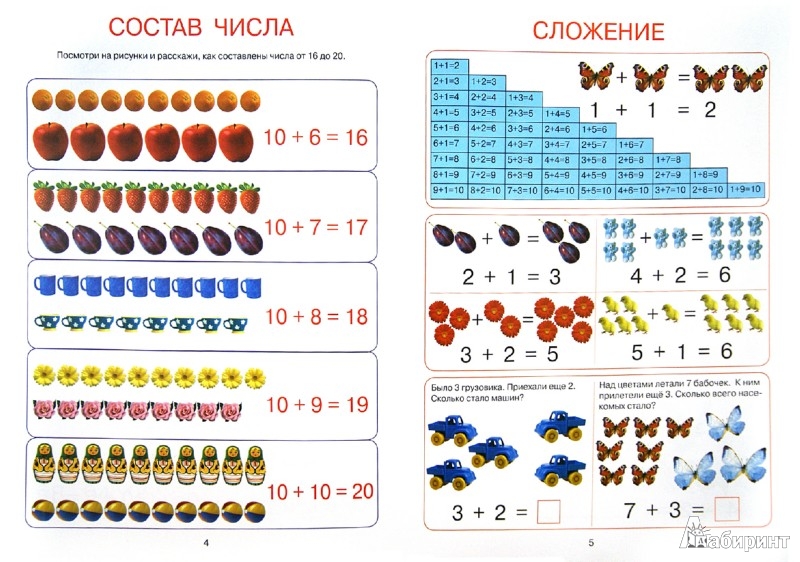 А. Бугримова.
– Волгоград: Учитель, 2004. – 287 с.
А. Бугримова.
– Волгоград: Учитель, 2004. – 287 с.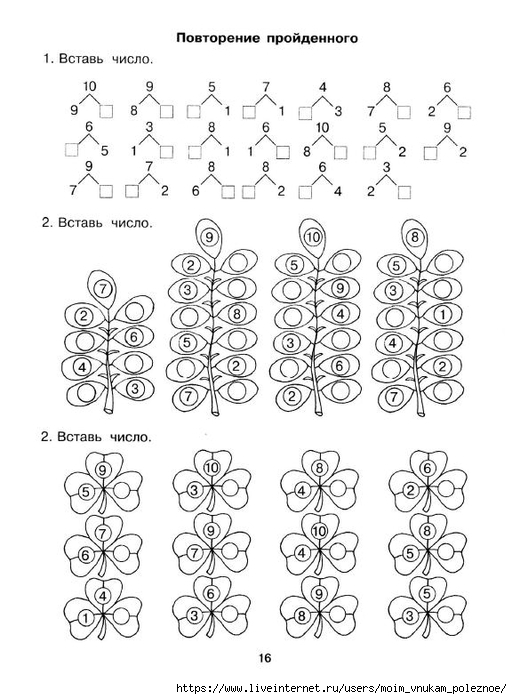 Объясните ребёнку, что чем больше число — тем больше возможностей его составить.
Объясните ребёнку, что чем больше число — тем больше возможностей его составить.

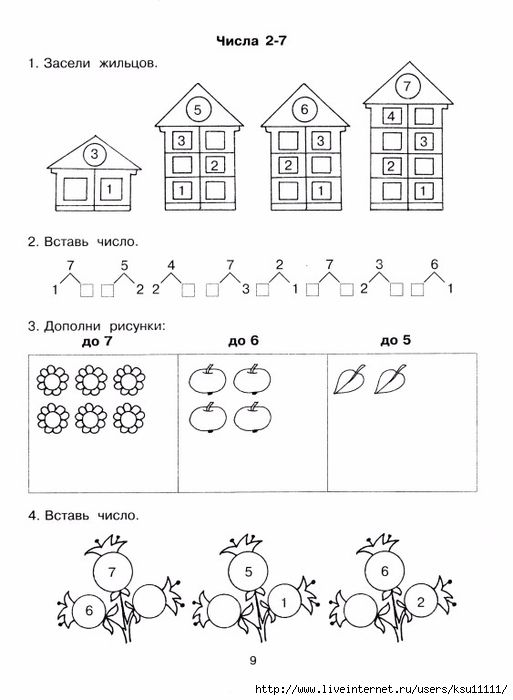 Зарядка для ума (задания на развитие логического мышления).
Зарядка для ума (задания на развитие логического мышления).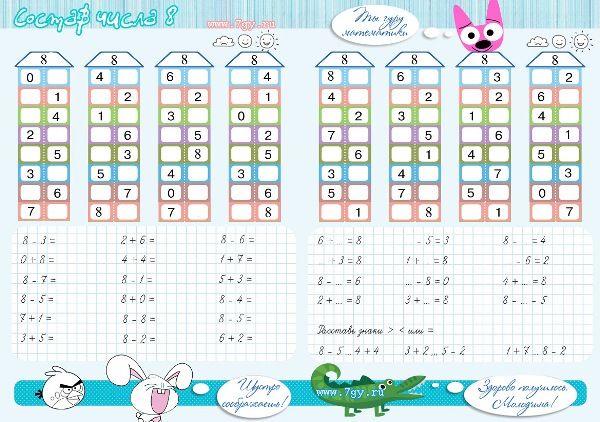
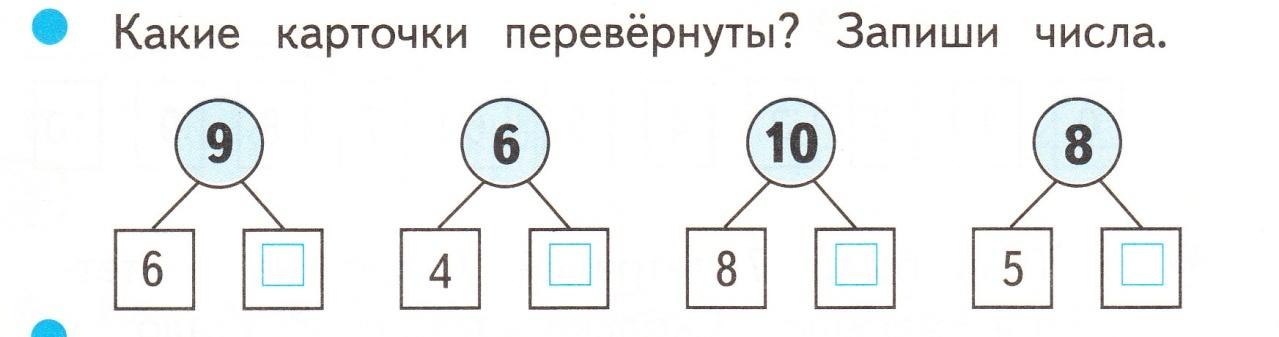 Повторение алгоритма написания числа 10. Определение темы и задач урока.
Повторение алгоритма написания числа 10. Определение темы и задач урока.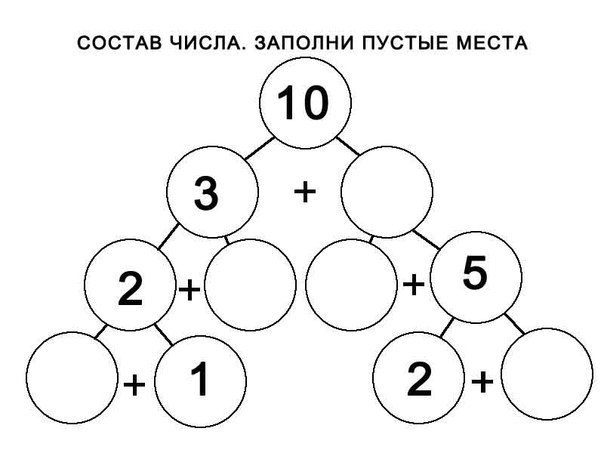 С этим связано и обозначение десятка: 1десяток 0 единиц – 10.
С этим связано и обозначение десятка: 1десяток 0 единиц – 10. Он предлагает вам задания в
Он предлагает вам задания в
 Закрепление и систематизация знаний.
Закрепление и систематизация знаний.
 Подведение итогов урока. Рефлексия
Подведение итогов урока. Рефлексия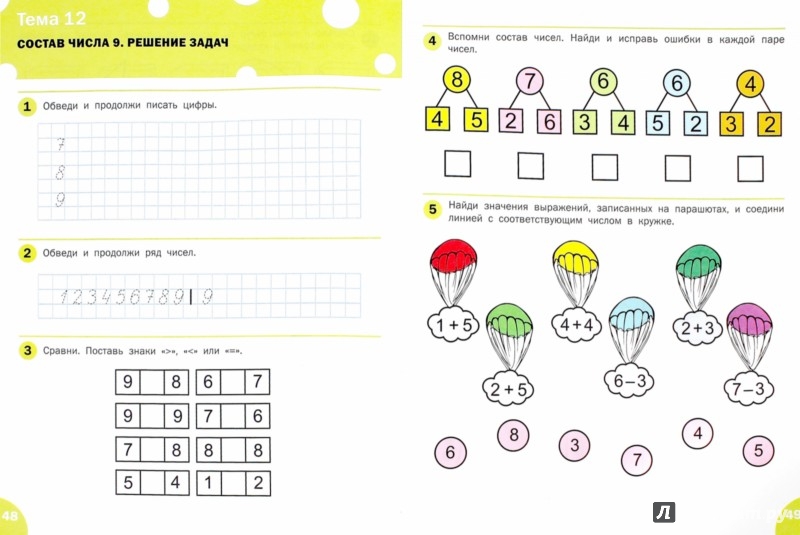 Мне нужна помощь!
Мне нужна помощь!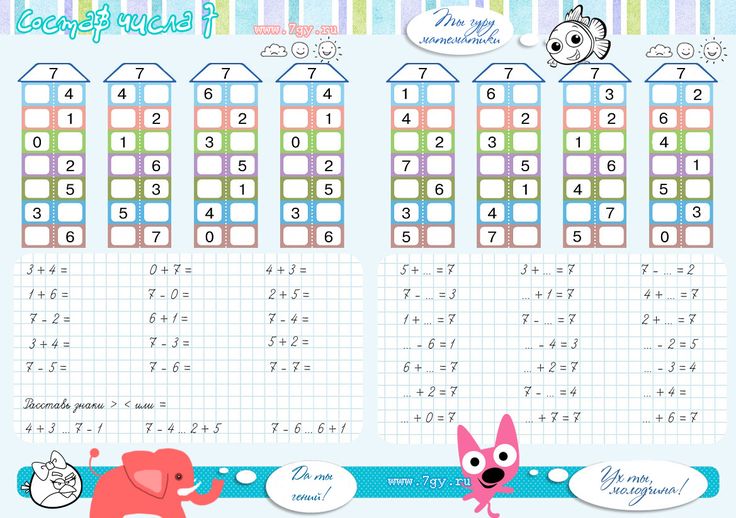
 )
)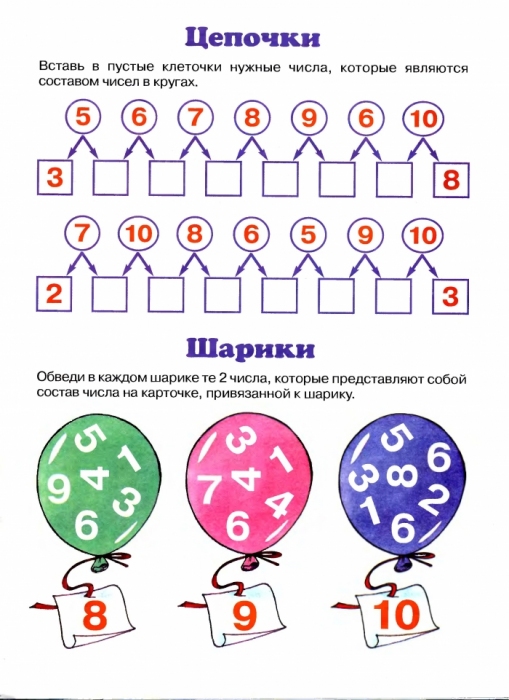 Предложите им найти и использовать набор из 10 предметов в своем доме, таких как цветные карандаши, игровые фигуры или монеты.
Предложите им найти и использовать набор из 10 предметов в своем доме, таких как цветные карандаши, игровые фигуры или монеты.