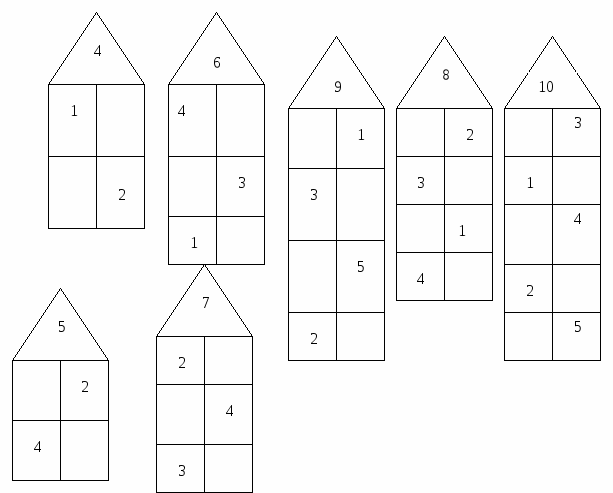
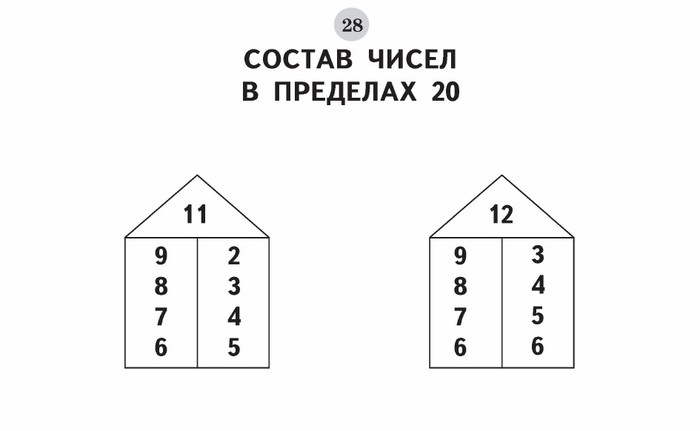
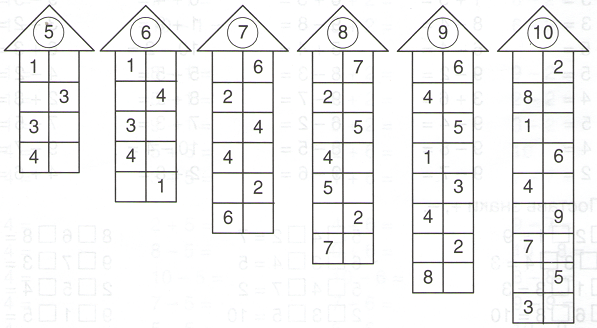
Домики чисел в пределах 10
Похожие презентации:
Тренажер «Домики». Состав числа в пределах 10
Тенажер. Состав числа в пределах 10
Сложение и вычитание чисел в пределах 10
Интерактивный тренажёр. Состав чисел в пределах 10
Нумерация чисел в пределах 10. (1 класс)
Сложение и вычитание в пределах 10
Счёт в пределах 10
Тренажер. Счет в пределах 10
Сложение чисел в пределах 10
Устный счёт в пределах 10
выход
Тренажер «ДОМИКИ».
Состав числа в пределах 10.
2
6
3
7
10
4
8
2-10
5
9
меню
выход
2
1
?
1 2 3 4 5 6 7 8 9 10
меню
выход
3
2
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
3
1
?
1 2 3 4 5 6 7 8 9 10
меню
выход
4
3
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
4
1
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
4
2
?
1 2 3 4 5 6 7 8 9 10
выход
5
3
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
5
1
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
5
4
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
5
2
?
1 2 3 4 5 6 7 8 9 10
меню
выход
6
2
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
6
1
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
6
4
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
6
3
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
6
5
?
1 2 3 4 5 6 7 8 9 10
меню
выход
7
1
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
7
3
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
7
2
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
7
6
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
7
5
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
7
4
?
1 2 3 4 5 6 7 8 9 10
меню
выход
8
5
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
8
1
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
8
3
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
8
4
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
8
7
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
8
2
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
8
6
?
1 2 3 4 5 6 7 8 9 10
меню
выход
9
4
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
9
1
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
9
5
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
9
3
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
9
6
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
9
8
?
1 2 3 4 5 6 7 8 9 10
далее
меню
9
2
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
9
7
?
1 2 3 4 5 6 7 8 9 10
меню
выход
10
1
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
10
3
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
10
6
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
10
4
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
10
2
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
10
7
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
10
5
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
10
9
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
10
8
?
1 2 3 4 5 6 7 8 9 10
меню
выход
4
2
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
9
2
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
2
1
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
5
4
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
3
2
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
10
6
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
6
1
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
8
7
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
3
1
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
6
3
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
6
4
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
7
2
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
10
9
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
5
2
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
6
5
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
10
2
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
7
4
?
1 2 3 4 5 6 7 8 9 10
далее
выход
8
4
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
7
6
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
8
1
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
9
5
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
10
8
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
8
3
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
7
3
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
8
5
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
9
1
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
8
2
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
4
3
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
7
1
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
9
3
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
9
6
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
10
4
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
10
1
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
7
5
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
9
7
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
10
3
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
8
6
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
4
1
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
9
8
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
5
1
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
10
5
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
6
2
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
10
7
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
5
3
?
1 2 3 4 5 6 7 8 9 10
далее
меню
выход
9
4
?
1 2 3 4 5 6 7 8 9 10
English Русский Правила
Плакат состав числа до 10 домики в Казани: 57-товаров: бесплатная доставка, скидка-50% [перейти]
Партнерская программаПомощь
Казань
Каталог
Каталог Товаров
Одежда и обувь
Одежда и обувь
Стройматериалы
Стройматериалы
Здоровье и красота
Здоровье и красота
Текстиль и кожа
Текстиль и кожа
Детские товары
Детские товары
Продукты и напитки
Продукты и напитки
Электротехника
Электротехника
Дом и сад
Дом и сад
Мебель и интерьер
Мебель и интерьер
Вода, газ и тепло
Вода, газ и тепло
Сельское хозяйство
Сельское хозяйство
Все категории
ВходИзбранное
Плакат состав числа до 10 домики
253
520
Плакат «Состав числа» А2 Тип: Обучающий плакат, Размер: Длина 70.
000 Ширина 50.000 Высота 3.000,
В МАГАЗИНЕще цены и похожие товары
125
250
Обучающий плакат А2 (картон) «Состав числа» + наклейки на тетради, артикул СА-П-009 Тип: Обучающий
В МАГАЗИНЕще цены и похожие товары
305
449
Обучающий плакат СОСТАВ ЧИСЛА Тип: Обучающий плакат, Размер: Длина 43.000 Ширина 7.000 Высота
В МАГАЗИНЕще цены и похожие товары
Состав числа. Плакат
В МАГАЗИНЕще цены и похожие товары
234
364
Обучающий плакат счет от 1 до 10, постер в детскую комнату, для школы, для сада, для оформления детской комнаты, картон, 69.7х50.5см Мир открыток
ПОДРОБНЕЕЕще цены и похожие товары
Литур/Плакат Состав числа 550х770 мм Производитель: Литур, Пол: для девочек, для мальчиков, унисекс
ПОДРОБНЕЕЕще цены и похожие товары
234
289
Эмеральд Груп/Школьные плакаты для детей обучающие по математике «Состав числа» для начальной школы, детского сада
ПОДРОБНЕЕЕще цены и похожие товары
Числовые домики.
Оформительский и Дидактический набор. 130 картинок Производитель: Творческий Центр
ПОДРОБНЕЕЕще цены и похожие товары
139
199
ФЕНИКС+/Обучающий плакат-листовка Феникс+ «состав числа«, А4, 1 л. Производитель: Феникс+, Пол: для
ПОДРОБНЕЕЕще цены и похожие товары
ПЛ-8529 Плакат А3. Состав числа Производитель: Творческий Центр СФЕРА, Пол: для девочек, для
ПОДРОБНЕЕЕще цены и похожие товары
243
541
Состав числа/А2. Обучающий плакат. Производитель: Без бренда, Пол: для девочек, для мальчиков,
ПОДРОБНЕЕЕще цены и похожие товары
234
364
Обучающий плакат счет от 1 до 10, постер в детскую комнату, для школы, для сада, для оформления детской комнаты, картон, 69.7х50.5см Мир открыток
ПОДРОБНЕЕЕще цены и похожие товары
290
427
Обучающий плакат состав числа Производитель: Альмарин, Возраст: 14+, Пол: для девочек, для
ПОДРОБНЕЕЕще цены и похожие товары
245
546
Математика.
Состав чисел от 1 до 10/А2. Обучающий плакат для начальной школы Производитель: Без
ПОДРОБНЕЕЕще цены и похожие товары
Улитина Н.В. «Состав числа от 1 до 10. Наглядное пособие для начальной школы» Класс: 1 класс, 2
ПОДРОБНЕЕЕще цены и похожие товары
*ПЛ-8529 Плакат А3. Состав числа (в индивидуальной упаковке с европодвесом и клеевым клапаном)
ПОДРОБНЕЕЕще цены и похожие товары
Гузь А. (худ.): Обучающий плакат-листовка «Состав числа» Пол: для девочек, для мальчиков, унисекс
ПОДРОБНЕЕЕще цены и похожие товары
202
505
Состав числа/А5. Обучающий плакат. Производитель: Без бренда, Пол: для девочек, для мальчиков,
ПОДРОБНЕЕЕще цены и похожие товары
Числовые домики.
Обучающие карточки Пол: для девочек, для мальчиков, унисекс
ПОДРОБНЕЕЕще цены и похожие товары
Числовые домики. Учим состав чисел Пол: для девочек, для мальчиков, унисекс, Цифры и счет: Да
ПОДРОБНЕЕЕще цены и похожие товары
139
149
Числовые домики. Учим состав чисел Производитель: Литур, Пол: для девочек, для мальчиков, унисекс
ПОДРОБНЕЕЕще цены и похожие товары
ПЛ-8529 Плакат А3. Состав числа Производитель: Творческий Центр СФЕРА, Пол: для девочек, для
ПОДРОБНЕЕЕще цены и похожие товары
Домики: состав числа (катаемся на лифте, считаем жильцов, красим окна). Пол: для девочек, для
ПОДРОБНЕЕЕще цены и похожие товары
231
576
Состав числа/А3. Обучающий плакат.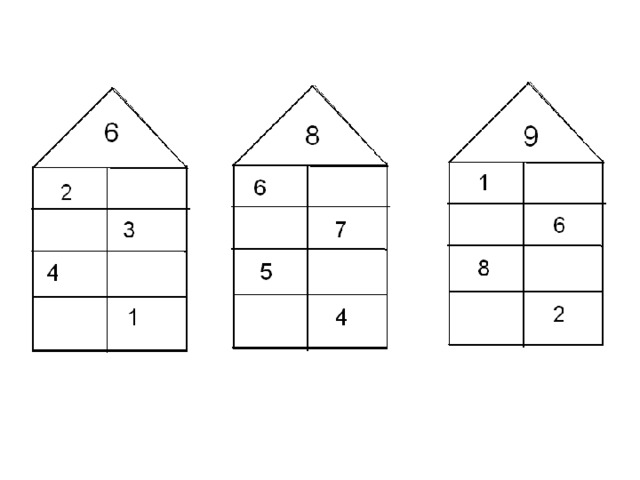
ПЛ-8529 Производитель: Без бренда, Пол: для девочек, для
ПОДРОБНЕЕЕще цены и похожие товары
218
448
Состав чисел постер А4 / постер для школы / Обучающий плакат Производитель: Без бренда, Пол: для
ПОДРОБНЕЕЕще цены и похожие товары
200
446
Состав числа. А4/Ш-7705. Обучающий плакат. Производитель: Без бренда, Пол: для девочек, для
ПОДРОБНЕЕЕще цены и похожие товары
Плакат Дрофа-Медиа Состав числа 3415 Тип: печатный плакат, Производитель: Дрофа-Медиа, Тема
ПОДРОБНЕЕЕще цены и похожие товары
Тренажер ДОМИКИ Состав числа в пределах 10
Тренажер «ДОМИКИ» . Состав числа в пределах 10. Ячменева Мария Александровна Учитель начальных классов «МОУ СОШ № 38» 2 6 3 7 10 4 8 2 -10 выход 5 9
меню выход 2 1 ? 1 2 3 4 5 6 7 8 9 10
меню выход 3 2 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 3 1 ? 1 2 3 4 5 6 7 8 9 10
меню выход 4 3 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 4 1 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 4 2 ? 1 2 3 4 5 6 7 8 9 10
меню выход 5 3 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 5 1 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 5 4 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 5 2 ? 1 2 3 4 5 6 7 8 9 10
меню выход 6 2 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 6 1 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 6 4 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 6 3 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 6 5 ? 1 2 3 4 5 6 7 8 9 10
меню выход 7 1 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 7 3 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 7 2 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 7 6 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 7 5 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 7 4 ? 1 2 3 4 5 6 7 8 9 10
меню выход 8 5 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 8 1 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 8 3 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 8 4 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 8 7 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 8 2 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 8 6 ? 1 2 3 4 5 6 7 8 9 10
меню выход 9 4 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 9 1 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 9 5 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 9 3 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 9 6 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 9 8 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 9 2 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 9 7 ? 1 2 3 4 5 6 7 8 9 10
меню выход 10 1 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 10 3 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 10 6 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 10 4 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 10 2 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 10 7 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 10 5 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 10 9 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 10 8 ? 1 2 3 4 5 6 7 8 9 10
меню выход 4 2 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 9 2 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 2 1 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 5 4 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 3 2 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 10 6 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 6 1 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 8 7 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 3 1 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 6 3 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 6 4 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 7 2 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 10 9 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 5 2 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 6 5 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 10 2 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 7 4 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 8 4 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 7 6 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 8 1 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 9 5 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 10 8 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 8 3 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 7 3 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 8 5 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 9 1 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 8 2 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 4 3 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 7 1 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 9 3 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 9 6 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 10 4 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 10 1 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 7 5 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 9 7 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 10 3 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 8 6 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 4 1 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 9 8 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 5 1 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 10 5 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 6 2 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 10 7 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 5 3 ? 1 2 3 4 5 6 7 8 9 10 далее
меню выход 9 4 ? 1 2 3 4 5 6 7 8 9 10
Лучшие занятия по разложению математического центра
Халява | Математика
Я пишу, чтобы поделиться занятиями в математическом центре по декомпозиции, которые вы можете использовать для закрепления идей декомпозиции. Продолжайте читать, чтобы получить халяву в конце этого сообщения в блоге.
Раньше я участвовал в разложении. Я люблю учить разложению! Это сложная концепция, но есть МНОЖЕСТВО упражнений, которые вы можете использовать, чтобы научить этому навыку первоклассников.
Что разлагается?
Разложение — это разбиение числа на части. Учащиеся привыкли работать с целыми числами (используя предметы для составления числа 5) и теперь узнают, что числа можно разбить на части (2 и 3 равны 5). Они будут разлагать числа, рисуя и используя предметы. Некоторые учащиеся будут готовы писать уравнения, но когда мы впервые узнаем о разложении, они используют слова для объяснения своего мышления.
Студенты должны разложить числа в пределах 10, найти число, которое составляет 10, и решить текстовые задачи путем разложения.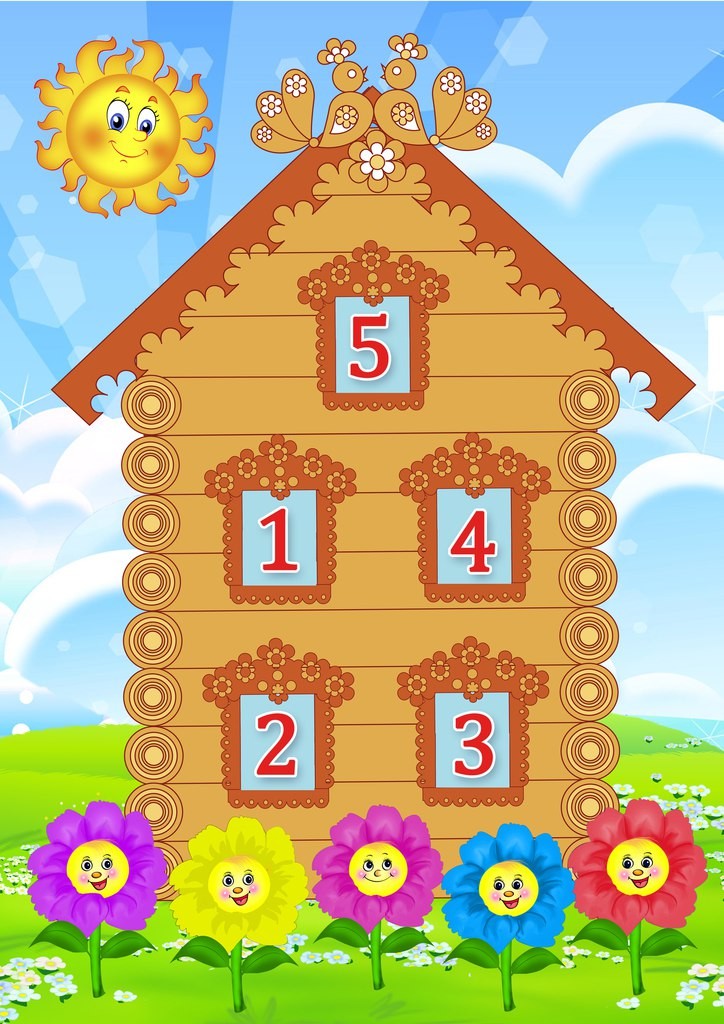
Цель состоит в том, чтобы развить понимание учащихся о числах, например, узнать, что числа являются гибкими.
Стратегии, которые работают
Вот несколько стратегий, которые вы можете использовать, чтобы помочь своим ученикам decompose:
- Научите их языку, моделируя – покажите учащимся, как разложить число, моделируя, как это сделать. Думайте вслух, когда вы разлагаете число. Предложите студентам поделиться тем, что они заметили или что их смущает, и используйте это время как возможность прояснить любые недоразумения. Некоторые новые словарные слова, которые вы хотите использовать при моделировании того, как разлагаться, это разложение, соединение и , разделяющие .
- Предоставьте учащимся множество возможностей и различных средств для демонстрации своего мышления. Позвольте им рисовать картинки, разыгрывайте их всем телом и пальцами, а также с помощью предметов.
- Научите учащихся пользоваться такими средствами обучения, как s часть-часть-кто le, числовые связи и десять рамок для моделирования того, как разлагать числа.
Упражнения по разложению чисел
Ниже приведены некоторые упражнения, которые дают учащимся значимые возможности разложить числа.
Показать 3 способа
Учащиеся выбирают карточку с номером. Они разлагают число с помощью кубиков, разбивая кубики на 2 части. Они пишут уравнение или числовое предложение и рисуют картинку.
Сдвинь и разложи
Учащиеся расставляют по кругу 5 или 10 фишек или предметов. Попросите учащихся передвинуть несколько фишек в верхний и нижний прямоугольники. Они пишут, как они разлагают число как уравнение или числовое предложение.
Мат «Часть-Часть-Целое»
Учащиеся выбирают число и разлагают его, используя Мат «Часть-Часть-Целое».
Числовые связи
Выбрав число, учащиеся разлагают это число, используя числовое соединение.
Облигация огромного количества
Иногда больше может быть лучше! Учащиеся могут разложить число, используя большое число, и написать, как они разложили число, на столе (или на листе записи!)
Переверни и разложи
Эта игра очень веселая! Учащиеся переворачивают карточку и используют рамку с десяткой, чтобы показать, сколько еще предметов им нужно, чтобы сделать 10.
Они также тренируются в изготовлении 5.
Постройте и запишите пропущенное число
Учащиеся выбирают уравнение и используют десятичную рамку, чтобы решить пропущенное число.
Сделай это 3 способами
Это задание очень понравилось моим ученикам! Моих учеников всегда больше всего увлекли самые простые игры! Учащиеся выбирают целевое число и разлагают его тремя способами. Вы можете предложить им использовать предметы или нарисовать картинку. Затем они написали предложение или уравнение, чтобы показать, как они разложили число.
Головоломки, головоломки и еще раз головоломки!
Мои ученики любят головоломки! Это отличная партнерская игра, которая заставит ваших учеников говорить о разложении. Они выбирают уравнение и сопоставляют его с правильным номером.
Реши и найди
Это отличная игра, которая поможет учащимся подумать о различных способах разложения числа. Они выбирают домино, складывают числа, чтобы найти сумму, и закрывают ответ на игровом поле.
Вращай и решай
Мои ученики обожают эту практическую игру! Тем более, что я купил пластиковые спиннеры, и им больше не нужно пользоваться карандашом и скрепкой (их волнуют именно мелочи!). Они крутят спиннер, выясняют, сколько еще нужно, чтобы получилось 10, и закрывают рамку с десятью, которая отображает это число на игровом поле.
Сделай 10!
Учащиеся считают монеты в копилке и с помощью десятичной рамки показывают, сколько еще монет им нужно, чтобы получилось 10.
Math Talk Mat
Это отличное занятие, помогающее учащимся развить словарный запас для разложения чисел. Я преподаю английский как второй язык, и это занятие помогло мне увидеть и произнести «часть» и «целое» число. Учащиеся выбирают числовую связь и моделируют ее, используя коврик «часть-часть-целое». Затем они пишут, как разложили число, и делятся своей работой с партнером.
Разыграй!
Есть 3 Действуй! коврики для задач со словами. Учащиеся разыгрывают словесные задачи, используя предметы, и записывают их разложение, составляя уравнение или числовое предложение.
Сделай 5! Настольная игра
Это партнерская игра. Один ученик переворачивает карточку и говорит, показывают ли пальцы способ получить 5 или не получить 5. Если это способ сделать 5, он перемещает свою пешку на одно место вверх. Они продолжают играть, пока не дойдут до конца.
Фу! Это много разлагающих игр!
Get Decomposing Math Centers
Вы хотите, чтобы все занятия по декомпозиции занимались в центре математики? Нажмите на изображение ниже, чтобы купить в моем магазине TpT!
Разложение чисел Freebie Math Center
Занятий в математическом центре никогда не бывает слишком много. Вот халява из моего пакета Decomposing Math Center. Вы можете получить это задание с низкой подготовкой, заполнив форму ниже.
Какие еще упражнения на разложение вы использовали в своем обучении? Дайте мне знать в разделе комментариев ниже.
Счастливого обучения,
Тройник
Почтовые теги: #сложение#разложение#разложение математических центров#разложение чисел в детском саду#бесплатные распечатки#БЕСПЛАТНЫЕ#математика#занятия в математическом центре#математические центры#операции и алгебраическое мышление#словные задачи
Похожие сообщения
Subitising
Маленькие дети обладают замечательным умением: они могут распознавать количество предметов, не считая.
Это называется субитизация, и она развивается с самого раннего возраста. Очень маленькие дети могут различать не только одну и две, но и большое количество точек, когда их вдвое больше в одной группе, например, 16 и 8 (Sarama and Clements, 2009).). Маленькие дети также обладают мощным
визуальную память, а некоторым может быть легче запоминать изображения, чем слова: трехлетние дети могут распознавать три вещи, хотя они могут и не произносить слова. Субитирование может помочь детям создавать образы для чисел, визуализировать и запоминать факты о числах. Например, большинство четырехлетних детей легко учатся распознавать пять точек на игральной кости, что помогает им понять кардинальное значение или
«сколько» числа пять, которое они могут связать со словом и символом для числа 5. Структурированные изображения, подобные этому, также помогают детям начать видеть числа внутри чисел, например, видеть четыре и один в пределах пяти.
Как обучать субитизации?
Способность детей к субитизации можно развить путем обучения.
Игры дают повторяющийся опыт интерпретации точечных изображений, чтобы решить, на сколько клеток нужно переместиться, как в нашем упражнении «Игра в Incey Wincey Spider», или сколько вещей нужно собрать, как в нашем упражнении «Кости», где точечное число определяет, сколько животных нужно переместить. вставь свою ручку. (Чтобы найти оба этих действия, прокрутите вниз
набор задач EYFS на основе чисел.) Для детей, которые не знакомы с точечными изображениями, игральные кости можно адаптировать только для отображения чисел до трех. Большие точечные кубики хороши для подвижных игр, например, прыжков по дорожке. Спиннеры с точками представляют собой альтернативу, как у ребенка на картинке, у которого есть свой спиннер на шнурке: он крутит его, а затем делает это.
много прыжков по кольцевой трассе, затем делает то же самое снова, и снова, и снова..! Наличие собственного игрального кубика или спиннера — хороший вариант для детей младшего возраста, который позволяет не ждать своей очереди.
Большие напольные костяшки домино приглашают детей сопоставлять числовые шаблоны в помещении или на улице.
Пальцы также предоставляют изображения, которые можно заменить числами, с дополнительным преимуществом, заключающимся в том, что они воплощены в мышечной памяти. Ключевым навыком здесь является демонстрация всех пальцев одновременно: Marton & Neuman (1990) обнаружили, что дети старшего возраста с трудностями в математике, как правило, считают пальцы по одному, а не используют все сразу «цифры пальцев». Вы можете попросить маленьких детей сначала «вырасти», а затем «показать».
и, наконец, «выбросить» номера пальцев.
Использование ряда предметов и приспособлений в различном расположении помогает детям познакомиться с различными изображениями чисел, а также подчеркивает различные свойства чисел. Например, Numicon представляет числа как четные или нечетные, тогда как связанные кубики отображают числа как длины: соединение всех этих изображений помогает детям построить богатую сеть понимания, чтобы связывать числовые слова и
символы.
Игры с субитаризацией могут включать в себя менее распространенное расположение объектов.
Игры, предполагающие обнаружение спрятанных предметов, побуждают маленьких детей сказать, сколько предметов они видят (см. задание NRICH «Скрытые драгоценности»). В одной из игр перевернутые тарелки скрывают три, четыре и пять предметов, их быстро меняют местами и предлагают детям следить за тарелкой с четырьмя.
Когда вы останавливаетесь и ненадолго поднимаете тарелку, дети интуитивно подсчитывают показанное число. Это упражнение взято с очень полезного веб-сайта Клементса и Сарамы, на котором представлена траектория обучения субитизации, подкрепленная видеороликами с упражнениями для каждого этапа. (Если вы еще этого не сделали, вам необходимо создать учетную запись перед доступом к бесплатным ресурсам.)
https://www.learningtrajectories.org/math-activities/fantastic-five-tricky-two
Деятельность включает в себя слуховое субитирование или распознавание ряда звуков, таких как хлопки или удары барабана, связывая их с движением и музыкой.
Концептуальное субитирование
Субитирование также может помочь детям изучить факты сложения и вычитания.
На некоторых изображениях ниже общее число пять распознается путем добавления подгрупп, таких как три и два или четыре и один (назад, 2014 г. — см. статью NRICH Early Number Sense). Это предполагает осознание части-целого, что позволяет детям одновременно видеть целое число и числа, из которых оно состоит.
вверх. Способность думать о числах как о композициях других чисел была описана Резником (19).83) как «вероятно, главное концептуальное достижение младших школьных лет».
Распознавание количества путем объединения количества меньших подгрупп называется концептуальным субитированием: это более продвинутое, чем перцептивное субитизирование, которое включает мгновенное распознавание (Clements, 1999). Восприятие чисел как комбинаций других чисел помогает детям развивать понимание части и целого и знакомиться с комбинациями чисел. Кроме того, это намного эффективнее, чем давать дети должны составлять предложения, считая кубики и надеясь, что они запомнят соответствующие числа!
Номер разговоры
Показ детям «быстрых изображений» и вопрос, сколько они видят, является одним из способов развития субитизации.
Альтернативный способ развития концептуального субитизации — показать детям несколько точек и попросить их сказать, как они видят это число (см. задание NRICH «Разговоры о числах»). Учительница Джанин Давеналл привлекает маленьких детей, показывая изображение и спрашивая: «Какие числа вы можете
увидеть скрытый внутри этого числа?’
Они могут ответить: «Я вижу три и четыре», или «шесть и один», или «два и два, и два и один». Это инклюзивное занятие с множеством «правильных» ответов и возможностью обнаружить, что другие видят одно и то же по-другому. Дети также узнают обо всех различных комбинациях, которые могут составить одно и то же число. Альтернативой является использование гигантских магнитных кнопок на подносе, который вы переворачиваете. тайком переставлять и показывать разные комбинации одного и того же числа.
(www.teachingchannel.org/videos/visualizing-number-combinations)
Дети младшего возраста не только больше реагируют на реальные объекты, чем на изображения на экране, но они также видят, что количество кнопок остается прежним.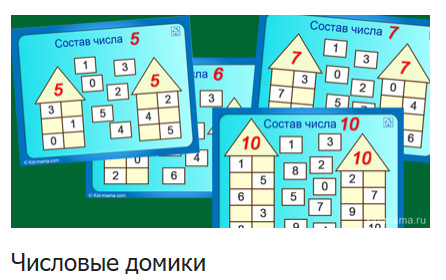
то же самое, несмотря на перестановку.
Более сложные изображения могут представлять большие трудности для некоторых детей. Маллиган и Митчелмор (2009) показали маленьким детям треугольник из 6 точек и попросили нарисовать его по памяти: они обнаружили, что их ответы значительно различаются, а некоторые просто рисуют много точек.
Даже когда пятилетних детей просят скопировать изображение, многие пятилетние дети рисуют треугольники из точек, подобные показанному справа, очевидно, им трудно сосредоточиться на количестве и расположении точек (Gifford & Thouless, 2018). . Это означает, что некоторым детям потребуется гораздо больше практики, чтобы смотреть и говорить о числовых закономерностях, чтобы увидеть, как они организованы. Ежедневные «разговоры о числах» могут помочь детей анализировать и визуализировать числовые образы, формируя понимание кардинальных значений, таких как «шесть» из шести.
Детям, работающим в приемной, нравится создавать свои собственные расстановки чисел, таких как семь и девять, и видеть, какие из них легче всего узнают их друзья.
Дети старшего возраста с трудностями в математике сочли изображение «семерки леденца» наиболее запоминающимся, в то же время узнавая ключевой факт числа, что четыре и три составляют семь (Emerson & Babtie, 2010).
В Венгрии детей учат распознавать такие числа, как «пять с небольшим», используя изображение кости для 5 и связывая их с числами пальцев (см. статью NRICH «От объектов и изображений к математическим идеям»).
В Нидерландах исследователи разработали бисерные нити и рекенреки (счетные рамки), используя группы по пять человек, поскольку они обнаружили, что это помогает детям быстрее «видеть» числа (Gravemeijer, 1991). Способность подразделять группы способствует пониманию детьми больших чисел и более позднему мультипликативному мышлению: например, распознавание больших чисел путем подсчета групп из двух, трех или пять.
(Изображения выше взяты с веб-сайта Number Talk Images.)
Субитировать с повседневными предметами сложнее, чем с более простыми формами, такими как точки.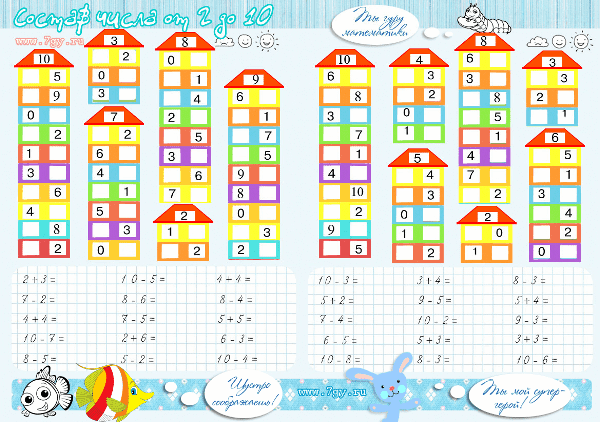
Тем не менее, детям может быть интереснее обсуждать изображения, которые представляют для них особый интерес и актуальность, или даже создавать свои собственные изображения для числовых разговоров.
Благодарности:
Janine Davenall
Buckinghamshire, Berkshire & Oxfordshire Mathematical Pedagogy Work Group
Ссылки:
Back, J. (2014) Early Number Sense
Clements, D.H. (1999) Субитизинг: что это такое? Зачем этому учить? Обучение детей математике 5(7) 400-405
Emerson, J. & Babtie, P . (2010) Оценка дискалькулии: Emerson House Mathematics London: Continuum.
Таулесс, Х. и Гиффорд, С. . (2018) «Треугольники точек: два разных подхода к анализу реакции детей младшего возраста на активность репликации паттерна» в Голдинге, Дж., Бретчер, Н., Крисан, К., Гераниу, Э., Ходжен Дж.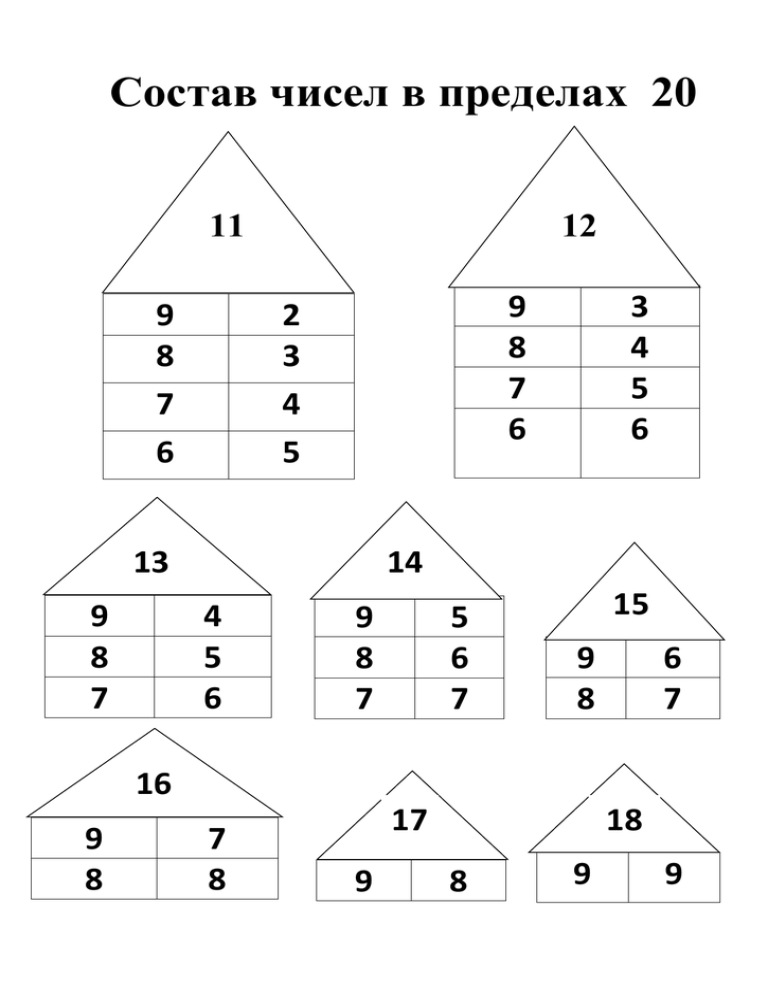
и К. Морган ( ред.). (2018) Research Proceedings
9-го Британского конгресса по математическому образованию (3–6 апреля 2018 г., Уорикский университет, Великобритания) 175-182 Онлайн на www.bsrlm.org.uk/bcme-9/
Gravemeijer, K.P.E. (1991) Учебно-теоретические размышления об использовании манипулятивных средств в Streefland, L. Реалистическое математическое образование в начальной школе . Утрехт: Институт Фройденталя 57-76
Мартон, Ф. и Нойман, Д. (1990) «Конструктивизм, феноменология и происхождение арифметических навыков» в Стеффе, Л.П. и Вуд, Т. (1990) Преобразование детского математического образования: международные перспективы Нью-Джерси: Lawrence Earlbaum Associates 62-75
Resnick, L.B. (1983) «Теория развития понимания чисел» в Гинзбурге, Х. (ред.) Развитие математического мышления . London Academy Press 109–181.
Сарама, Дж. С., и Клементс, Д. Х.
(2009). Исследования в области математики для детей младшего возраста . Лондон: Рутледж.
Скачать pdf здесь.
Включение одной функции в другую: объяснение композиции
Наборы точекФункции в точкахОбласти и декомпозицииСловесные пробыОбратные функции
Purplemath
До сих пор мы выполняли композицию по точкам, причем эти точки либо перечислены в наборах, либо отображены на графиках; и мы оценили композиции при заданных входных значениях.
Мы также можем оценивать композиции символически; то есть без числового входного значения. Легче оценивать композицию в какой-то момент, потому что вы можете упростить по мере продвижения, так как вы всегда будете просто подставлять числа и упрощать.
Содержимое продолжается ниже
MathHelp.com
Составные функции
Вычисление символьной композиции, когда вы сначала подставляете x к какой-то функции, а затем подключаете эту функцию к какой-то другой функции, может быть намного сложнее.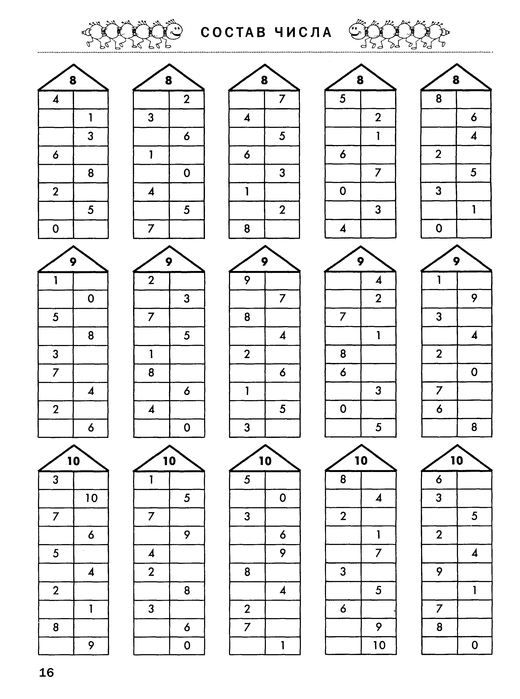
Но этот процесс работает точно так же, как и композиция по номеру, и использование скобок — чтобы быть более точным на каждом этапе — будет даже полезнее.
Какой пример составления формулы одной функции с другой?
- Дано F ( x ) = 2 x +3 и G ( x ) = — x 2 53) = — x . ( х ).
В этой композиции я не пытаюсь найти определенное числовое значение. Вместо этого я пытаюсь найти формулу, полученную в результате подстановки формулы для г ( x ) в формулу для f ( x ).
Я буду писать формулы на каждом шаге, используя круглые скобки, чтобы указать, куда должны идти входные данные: ))
= f (− x 2 + 5)
= 2( ) + 3
= 2(− x 2 + 5) + 3
= −2 x 2 + 10 + 3
= −2 x 2 + 13
Эта последняя строка, максимально упрощенная, дает мне ответ.
( f ∘ g )( x ) = −2 x 2 + 13
:
( f ∘ g )(1) = −2(1) 2 + 13
= −2 + 13 = 11
Это тот же ответ, который мы получили раньше, когда мы вычисляли точку. Раньше мы подставляли число в g ( x ), находили новое значение, подставляли его в f ( x ) и упрощали результат. На этот раз мы подставили формулу в f ( x ), упростили формулу, подставили то же число, что и раньше, и упростили результат. Окончательные числовые ответы были одинаковыми.
Если вы правильно выполнили символическую композицию (композицию с формулами), вы получите одинаковые значения в любом случае, независимо от значения, которое вы выберете для x . Это может быть удобным способом проверки вашей работы.
- Дано F ( x ) = 2 x +3 и G ( x ) = — x 2 9063, находка x 2 906+5, нахождение x 2 906+5, нахождение x 2 906+5, нахождение x 9053 2 ) = — x 2 ). )( х ).
На этот раз я буду делать пыхтение в другом порядке.
( г ∘ f )( x ) = г ( f ( x ))
= г (2 x + 3)
= −( ) 2 + 5
= −(2 x + 3) 2 + 5
= −(4 x 2 + 12 x + 9) + 5
= −4 x 2 − 12 x − 9 + 5
= −4 x 2 − 12 x − 4
Дальше ничего не упрощается, так что я закончил.
( г ∘ f )( x ) = −4 x 2 − 12 x − 4
8 Эти два примера должны быть символическими. Посмотрите на результаты, которые я получил: ( f ∘ g )( x ) = −2 x 2 + 13
( G & Compfn; F ) ( x ) = −4 x 2 — 12 x — 4
, который составляет ( F и 40003
) не совпадает с ( г ∘ f )( x ). Это верно в целом. Следует исходить из того, что композиции ( f ∘ г )( x ) и ( г ∘ f )( x ) будут разными.
В частности, композиция — это не то же самое, что умножение. Открытая точка «∘» это не то же самое, что точка умножения «•», и это не то же самое.
Умножение:
всегда верно
f ( x ) • г ( x ) = г ( x ) • f ( x )
Состав:
обычно ложно
( f ∘ g )( x ) = ( g ∘ f )( x ∘ f )( x ) 9000 с правильным результатом. Композиция не является гибкой, как умножение; композиция — это совершенно другой процесс. Не пытайтесь умножать функции, когда вы должны вставлять их друг в друга.
Кстати, если вы помните, что изучали ассоциативные, коммутативные и транзитивные свойства действительных чисел, и если вы помните, задавались вопросом: «Зачем мне это знать?», то вот почему: чтобы вы могли узнавать здесь свойство коммутативности не выполняется.
Композиция функций — это «операция», которая не является коммутативной.
- Дано f ( x ) = 2 x + 3 и г ( x ) = − x
2 06 + 5, найти ( f ∘ f )( x ).
Не путайте эту композицию с квадратом функции f ( x ). Поскольку композиция функций некоммутативна, результат *не* будет равен ( f ( x )) 2 , что равно 4 x 2 + 12 x (
5
3 f ∘ f )( x ) = ф ( ф ( х ))
= f (2 x + 3)
= 2( ) + 3
= 2(2 x + 3) + 3
= 4 x + 6 + 3
= 4 x + 9
Это максимально упрощенное выражение, поэтому у меня есть ответ:
( f ∘ f )( x )) = 4 x + 9
- Given f ( x ) = 2 x + 3 and g ( x ) = − x 2 + 5, найти ( г ∘ г )( x ).
Моя работа выглядит так:
( г ∘ г )( x ) = g( г ( x ))
= −( ) 2 + 5
= −(− x 2 + 5) 2 + 5
= −( x 4 − 10 x 2 + 25) + 5
= − x 4 + 10 x 2 − 25 + 5
= − x 4 + 10 x 2 − 20
Это полностью упрощено, поэтому мой ответ:
( g & compfn; G ) ( x ) = — x 4 + 10 x 2 — 20 0003
. com/modules/fcncomp3.htm Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в композиции функций. Попробуйте введенное упражнение или введите свое собственное упражнение.