Сокращение дробей умножение дробей: Сокращение дробей: умножение и деление числителя и знаменателя на число

admin

Как умножать дроби

Пожаловаться

Шпак Юлия

, автор статей | Создано 

Содержание:

Виды дробей

Умножение дробей

Умножение десятичных дробей

Как умножить дробь на натуральное число

Умножение трёх и более дробей

Дробь в математике – это результат деления меньшего числа a на большее число b.

Часто в жизни нам приходится вспоминать правила математики

Существует две формы записи дробей:

  • В столбик через черту: a/b, где а – делимое или числитель, b – делитель или знаменатель.
  • Одним числом через «,» после ноля: 0,5. Такие дроби называют десятичными.

В обычной жизни редко встречаются случаи, когда меньшее число делится на большее красиво. Легко разделить в уме на 2, 4, 5, 8, 10. А вот деление на 3, 7, 11, 13 и кратные им числа представляет сложность в виде бесконечного ряда цифр после запятой. Поэтому такие числа легче и проще записывать дробями.

Виды дробей

По содержанию дроби делятся на:

  • математические, то есть записанные цифрами – 5/6;
  • алгебраические, то есть записанные буквами или буквенными выражениями – a/(a—b).

По свойствам дроби бывают:

  • правильными – числитель меньше знаменателя (5/6);
  • неправильными – числитель больше знаменателя (
    6/5)    .

В неправильной дроби сначала находят целое, а после выделяют дробный остаток

6/5=1 1/5 (одна целая и одна пятая часть числа). Иначе такое число называют смешанным.

Это базовые знания о дробях, которые помогут вам справиться с их умножением.

Умножение дробей

Главное правило: произведение двух дробей равно отношению произведения их числителей на произведение их знаменателей.

В теории всё просто: чтобы перемножить дроби, умножьте числитель первой дроби на числитель второй, аналогично поступите со знаменателями:

a/b * c

/d = a * c/b * d

С математическими дробями работать интереснее. Вот простой пример:

½ * 3/5 = 1 * 3/2 * 5 =3/10

Если есть числа второго и более порядка, попробуйте до умножения сократить дроби. Например:

30/40 * 21/70

Первую дробь сократите на 10. Получится 3/4.

Вторую дробь сократите на 7. Получится 3/7.

С учётом сокращений пример изменится:

¾ * 3/7 = 3 * ¾ * 7 = 9/28

Когда требуется умножить смешанное число на дробь, перед умножением нужно привести смешанное число к дроби.

1 1/5  * 2/3 = 6/5 * 2/3 = 6 * 2/5 * 3 (можно провести сокращение на 3) = 2 * 2/5 * 1 = 4/5

Умножение десятичных дробей

В обычной жизни редко встречаются случаи, когда меньшее число делится на большее красиво

Десятичные дроби умножают в столбик, как и любые многозначные числа. Выглядит это так:

3,12 * 0,02

х 3,12

   0,02

_______

   624

Теперь нужно понять, где ставить 0 и запятые. После запятых будет столько знаков, сколько их суммарно в двух множителях, то есть в нашем примере – 4. Ответ будет выглядеть так: 0,0624.

Как умножить дробь на натуральное число

Правило: произведение дроби на натуральное число равно отношению произведения числителя дроби на натуральное число к знаменателю дроби.

При умножении обычной дроби на натуральное число, нужно умножить только числитель:

2/3 * 4 = 8/3

С полученным результатом можно работать дальше, например, выделить целую часть числа: 2 2/3.

Другой пример:

2/4  *5 = 10/4

Такую дробь можно сократить на 2. Получим

5/2 или 2 ½.

Иногда в результате умножения дроби на натуральное число удаётся сократить дробь до натурального числа. Этим активно пользуются в математике.

2/3 * 6 = 12/3 = 4

Умножение десятичной дроби на натуральное число производят в столбик.

1,324 * 3

Сначала перемножают числа, не обращая внимания на запятые:

х1,324

         3

_______

   3972

После запятой должно остаться столько же цифр, как и в дроби. В нашем примере их три.

Ответ: 3,972.

Умножение трёх и более дробей

Когда требуется умножить между собой 3 и более дроби, вспомните главное правило умножения. Оно будет распространяться и на умножение дробей.

Правило: от перемены мест множителей произведение не меняется.

Как это выглядит на примере? Умножим четыре дроби:

2/3 *4/7 * 3/8 * 12/20 = 2 * 4 * 3 * 12/3 * 7 * 8 * 20

Для начала сократим дробь. Для удобства запишем:

2 * 3 * 4 * 12 / 20 * 3 * 8 * 7

В результате сокращения получим:

1 * 1 * 1 * 3/5*1*1*7

Ответ: 3/35.

Знание правил умножения дробей может оказаться полезным, когда нет под рукой калькулятора. К тому же обычный калькулятор не умеет умножать обычные дроби, для этого есть специальные программы.

Фото: © Shutterstock.com

РубрикаОбучение

В жизни пригодится: основы финансовой грамотности для детей

Славянский календарь: удивительные факты из жизни наших предков

Первый подарок матери — жизнь, второй — любовь, и третий — понимание

Комментарии

‘ + ‘

‘ + tooltips[tooltip][0] + ‘

‘ + » + tooltips[tooltip][1] + » + ‘

‘ + ‘

Узнавай и участвуй

Клубы на Бэби.ру — это кладезь полезной информации

Смотри сейчас! Тест на Беременность 4 Кто такие Коробыши? Давайте знакомиться!Проблемы у родителей: кто поможет?Зимний отдых: что выбрать?Есть ли альтернатива школе?Речевое развитие детей: когда начинать?

Технологическая карта урока.

Умножение дробей. 6-й класс Технологическая карта урока. Умножение дробей. 6-й класс

Разделы: Математика, Общепедагогические технологии

Класс: 6

Ключевые слова: умножение дробей

Класс

6

УМК

Учебник Математика. 6 класс. Мерзляк А.Г. и др. (М.: Вентана-Граф, 2019)

Тип урока

Урок открытия новых знаний и их первичное закрепление

Цель урока

  • Формирование у учащихся умений умножать обыкновенные дроби.
  • Расширение понятийной базы за счет включения в нее новых элементов.

Задачи урока

Образовательные:

  • повторить основные действия (сокращение, сложение, вычитание) с обыкновенными дробями;
  • ввести правило умножения обыкновенных дробей закрепить правило при выполнении заданий.

Развивающие:

  • способствовать развитию мотивации изучения предмета;
  • развивать грамотную математическую речь;
  • активизировать мыслительную деятельность учащихся посредством участия каждого из них в процессе решения задач;
  • развивать коммуникативные компетенции.

Воспитательные:

  • воспитывать настойчивость и целеустремленность, умение оценивать;
  • воспитание культуры общения;
  • способствовать формированию математической компетентности учащихся.

Планируемые результаты

Предметные:

  • знать правило умножения обыкновенной дроби на натуральное число, а также правило умножения обыкновенных дробей;
  • уметь применять ЗУН по умножению обыкновенных дробей на примерах и текстовых задачах, а также оценивать свою деятельность по заданным критериям.

Личностные:

  • формирование познавательного интереса к изучению нового, способам обобщения и систематизации знаний;
  • воспитание культуры личности;
  • развивать навыки сотрудничества со сверстниками и умения находить решения в спорных ситуациях.

Метапредметные:

  • планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями её реализации; способствовать приобретению учащимися навыков общения при совместной работе;
  • делать выводы на основе обобщения знаний.

Основные понятия

Умножение дробей, умножение десятичной дроби на натуральное число, свойства умножения

Методы обучения

Наглядно-иллюстративный, исследовательский

Организация пространства

Фронтальная, индивидуальная

Ресурсы

Учебник, компьютер, проектор, презентация

Организационная структура урока

Дроби — Умножение дробей — Первый взгляд

Дроби — Умножение дробей — Первый взгляд
Дом | Учитель | Родители | Глоссарий | О нас

Чтобы умножить дроби:

  1. Упростить дроби, если не в самых низких терминах.
  2. Умножить числители дробей, чтобы получить новый числитель.
  3. Умножить знаменатели дробей, чтобы получить новый знаменатель.

Упрощение результирующую дробь, если это возможно.

Нажмите на примере.

Помощь с домашним заданием | Предварительная алгебра | Дроби Отправить эту страницу другу по электронной почте
Поиск






  ·   Умножение дробей








Первый Взгляд   В Глубина   Примеры   Тренировка

Умножение дробей

Упрощение дробей — ChiliMath

Поиск

Дробь считается «упрощенной», если она выражена младшим членом . Это означает, что у единственный общий делитель между числителем и знаменателем равен 1 и никакому другому.

Метод 1. Упрощение дробей путем многократного деления

  • Продолжайте делить числитель и знаменатель на общий делитель до тех пор, пока не останется единственный общий делитель 1.
  • Хотя нет правильного способа, какой общий делитель использовать в начале, я бы предложил использовать первые пять (5) простых чисел в порядке возможного общего делителя:

2, 3, 5, 7, 11 , …

Метод 2. Упрощение дробей с использованием наибольшего общего делителя

  • Найдите наибольший общий делитель (НОД) числителя и знаменателя.
  • Разделите верхние и нижние числа дроби на GCF, чтобы сократить до наименьшего члена.
  • Вы можете найти GCF либо методом проб и ошибок , когда числа относительно невелики, либо с помощью простой факторизации.

Это простая иллюстрация, показывающая, что дробь \Large{8 \over {12}} приводится к простейшей форме. Вы видите закономерность?

Давайте рассмотрим еще несколько примеров с подробными пояснениями.

Примеры упрощения дробей

Пример 1 : Упростите приведенную ниже дробь.

Упростите, используя метод 1: метод повторного деления

Очевидно, что 1 не является единственным общим делителем между числителем и знаменателем. Поскольку они оба четные числа, они должны делиться на 2.

  • Разделите верхнее и нижнее число на 2. Вот что у нас получилось.

Выходная дробь после деления верхней и нижней частей на 2 равна \Large{2 \over 4}. Мы можем остановиться здесь? Еще нет! Их все еще можно уменьшить вторым делением на 2.

  • Снова разделите верхнюю и нижнюю часть на 2. Ответ: \Large{1 \over 2} (как простейшая форма \Large{4 \over 8}, потому что только делитель числителя и знаменателя равен 1

Упростить, используя метод 2: метод наибольшего общего множителя

В приведенном выше решении с использованием повторного деления мы упростили \Large{4 \over 8}, разделив его числитель и знаменатель два раза на число 2. Но подождите! Есть ли какой-нибудь короткий путь? Некоторые из вас, возможно, заметили, что использование общего делителя 4 может напрямую упростить это за один шаг!

На самом деле, Наибольший общий делитель (НОД) этой дроби равен 4, потому что это НАИБОЛЬШЕЕ число, которое равномерно делит числитель и знаменатель. Поскольку числа невелики, GCF можно определить методом проб и ошибок.

Пример 2 : Упростите приведенную ниже дробь.

Упростите, используя метод 1: метод повторного деления

Начните упрощать, используя первые несколько простых чисел (2, 3, 5, 7, 11 и т. д.).

  • Разделите верхнее и нижнее числа на первое простое число, равное 2.
  • У нас все еще есть общий делитель! Разделите верх и низ на следующее большее простое число, равное 3. После этого шага мы должны получить окончательный ответ.

Упростите, используя метод 2: метод наибольшего общего делителя

Чтобы найти наибольший общий делитель, мы собираемся разложить каждое число на простые множители. Затем определите общие факторы между ними. Наконец, умножьте общие множители, чтобы получить требуемый GCF, который может упростить дробь.

Поскольку GCF = 6, используйте это число, чтобы разделить числитель и знаменатель, чтобы получить ответ за один шаг.

Пример 3 : Упростите приведенную ниже дробь.

Упрощение с использованием метода 1: метод повторного деления

Мы можем начать тестирование с чисел 2, 3, 5 и т. д., чтобы упростить это. Но есть очевидный делитель, который выделяется! Поскольку оба числа оканчиваются на ноль, они должны делиться на 10.

Теперь на 2 нельзя разделить оба числа, поэтому попробуйте 3.

Упростите, используя Метод 2: метод наибольшего общего множителя

Разложите каждое число на простые множители и получите произведение общих множителей для получения необходимого НОД.

Упростите данную дробь за один шаг, используя делитель GCF = 30.

Пример 4 : Упростите приведенную ниже дробь.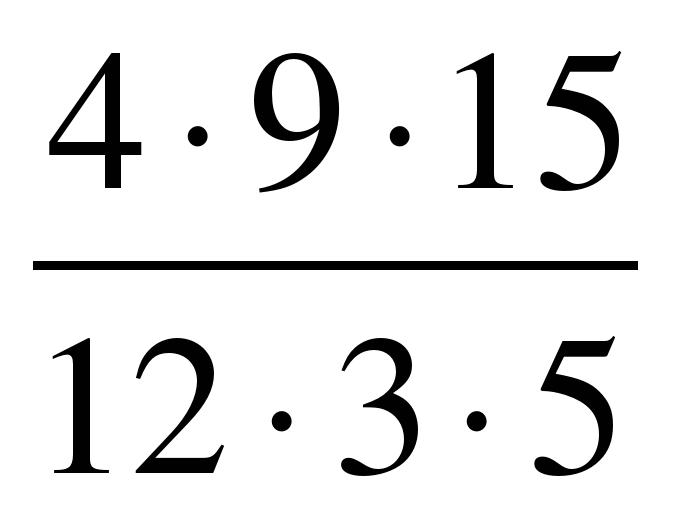

Решение:

Разделите числитель и знаменатель на общий делитель 3.

Пример 5 : Упростите дробь.

Решение:

Упростите, используя метод повторного деления.

  • Разделить числитель и знаменатель на 3, два раза !

Пример 6 : Упростите приведенную ниже дробь.

Решение:

Упростите эту дробь методом наибольшего общего множителя.

  • Найдите GCF, разложив на простые множители числитель и знаменатель. Определите общие факторы. Перемножьте их вместе, чтобы получить требуемый GCF.
  • После определения GCF разделите числитель и знаменатель, чтобы получить окончательный ответ.

Пример 7 : Упростите приведенную ниже дробь.

Решение:

Найдите наибольший общий делитель между числителем и знаменателем и используйте это число, чтобы упростить дробь.

admin

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *