Свойства сложения. Законы сложения

ГДЗ 1 класс

ГДЗ 10 класс

  

Категория: Математика

Прибавить одно число к другому довольно просто. Рассмотрим пример, 6+3=9. Это выражение означает, что к шести единицам добавили три единицы и в итоге получили девять единиц. Или, если рассмотреть числовой отрезок: сначала по нему передвинулись на 6 единиц, а затем на 3, и оказались в точке 9. Числа 6 и 3, которые мы сложили, называются слагаемыми. А результат сложения — число 9 —  называется суммой. В виде буквенного выражения этот пример будет выглядеть так: a+b=c, где a — слагаемое, b — слагаемые, c – сумма.
Если мы к 3 единицам добавим 6 единиц, то в результате сложения получим тот же результат, он будет равен 9. Из этого примера делаем вывод, что как бы мы не меняли местами слагаемые, ответ остается неизменным: 6+3=3+6=9

Называется такое свойство слагаемых переместительным законом сложения.

Переместительный (коммуникативный) закон сложения:

a + b = b + a.

От перемены мест слагаемых сумма не меняется.

Примеры:

55 + 21 = 21 + 55 = 76
108 + 2 = 2 + 108 = 110

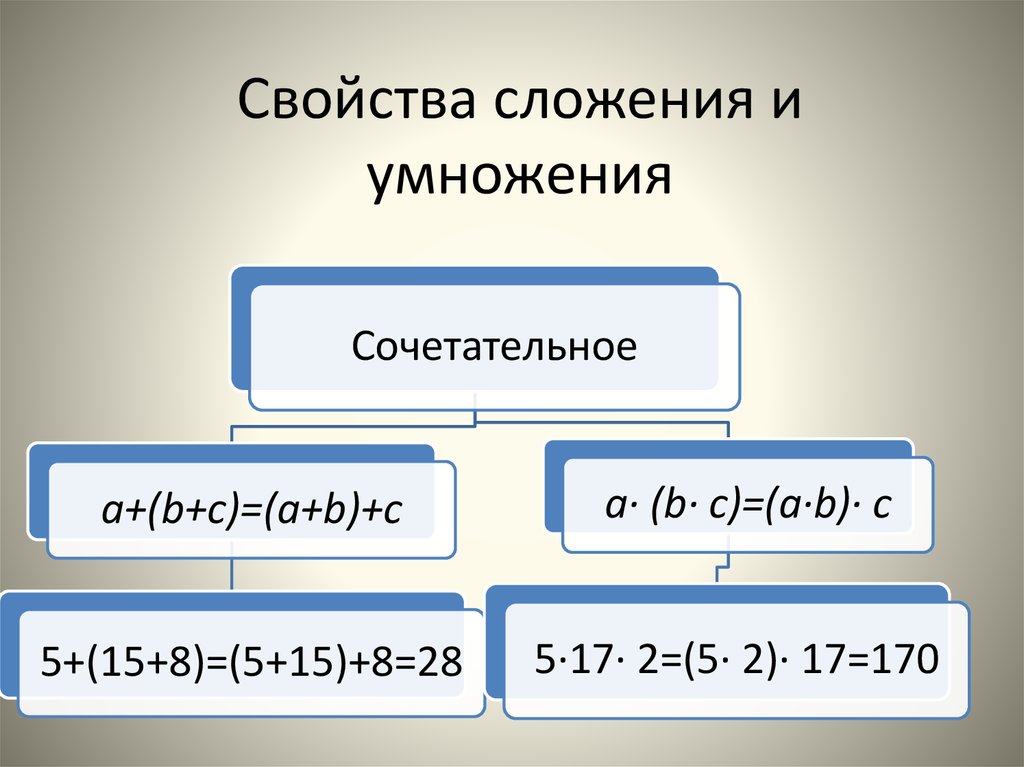
Если же мы рассмотрим три слагаемых, например, возьмем числа 1, 2 и 6 и выполним сложение в таком порядке, сначала прибавим 1+2, а потом прибавим к получившейся сумме 6, то получим выражение: (1+2)+6=9
Можем сделать наоборот, сначала сложить 2+6, а потом к полученной сумме прибавить 1. У нас пример будет выглядеть так: 1+(2+6)=9
Ответ остался прежним. У обоих видов сложения одного и того же примера ответ одинаковый. Делаем вывод: (1+2)+6=1+(2+6)

Это свойство сложения называется сочетательным законом сложения.

Сочетательный (ассоциативный) закон сложения:

a + b + c = a + (b + c).

Сумма не меняется, если какую-нибудь группу рядом стоящих слагаемых заменить их суммой.

Пример:

197 + 23 + 77 = 197 + (23 + 77) = 197 + 100 = 297.

 

Примечание от 7 гуру: оба закона справедливы для любого количества слагаемых. Переместительный и сочетательный законы сложения работают для всех неотрицательных чисел.

Переместительное и сочетательное свойства используются для удобства и упрощения вычислений при сложении.

Пример:

Нужно найти сумму 23 + 9 + 7
Пользуясь переместительным законом, поменяем местами слагаемые 9 и 7, получим 23 + 7 + 9,
теперь, пользуясь сочетательным свойством, объединяем 23 и 7, так как они дают круглое число: (23 + 7) + 9,
Сначала складываем 23 и 7, их сумма равна 30.
Затем прибавляем девять:       30 + 9 = 39.
Итак:  23 + 9 + 7 = (23 + 7) + 9 = 36

Свойство сложения с нулем.

Прибавление к числу нуля не изменяет этого числа: a + 0 = 0 + a = 0.

Пример:

99 + 0 = 0 + 99 = 99

 

• Назад
• Вперед

 
умножить наподелить на

 

org/BreadcrumbList»>
• Уроки
• Математика

Вам может пригодиться:

Сложение натуральных чисел / Натуральные числа и действия над ними / Справочник по математике 5-9 класс

1. Главная
2. Справочники
3. Справочник по математике 5-9 класс
4. Натуральные числа и действия над ними
5. Сложение натуральных чисел

К нескольким натуральным числам прибавим 1:

Мы видим, что когда мы прибавляем к натуральному числу 1, получаем следующее за ним натуральное

число, т.е. следующее число больше предыдущего на единицу. Теперь к 4 прибавим 3: 4+3: для этого к 4 прибавим 3 раза единицу. Учитывая, что при прибавлении к числу единицы получаем следующее число, получим:

Но мы записываем коротко: 4+3=7.

Запомните: Числа, которые складываются, называются слагаемыми, число, которое получается в результате сложения, называется суммой.

Сложение чисел на координатном луче

Изобразим координатный луч. Отметим на нем начало координат, единичный отрезок и несколько чисел, следующих друг за другом:

Рассмотрим наш пример: 4+3. Для того чтобы к 4 прибавить 3 на координатном луче, необходимо от точки 4

вправо отложить 3 единичных отрезка: 

И мы попадем в точку 7, следовательно 4+3=7.

Теперь попробуем отложить на луче, от точки  3 6 единичных отрезков, и от точки 6 3 единичных отрезка, другими словами к 3 прибавим 6 и  к 6 прибавим 3 :

Мы видим, что и в первом и во втором случае мы попадаем в одну и ту же точку: 9, следовательно сумма чисел 3 и 6 и 6 и 3 одинакова и равна 9. Это можно записать с помощью равенства:

В этом случае мы меняем местами слагаемые и получаем первое свойство сложения — переместительное свойство:

• От перестановки слагаемых сумма не меняется

---

Рассмотрим с помощью координатного луча следующие суммы: и , для этого от  точки 3 сначала отложим (6+7) единичных отрезков, а затем от точки 3, отложим сначала 6 единичных отрезков, а затем от получившийся точки отложим еще 7 единичных отрезков:

Заметим, что и в первом и во втором случае мы попадаем в одну точку: 16. Это можно записать равенством:

Мы получили второе свойство сложения — сочетательное свойство:

•  Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом к полученной сумме прибавить второе слагаемое

---

К натуральному числу можно прибавлять не только натуральное число, но еще и нуль, изобразим на луче прибавление нуля к 7:

Так как нам необходимо отложить от точки 0 единичных отрезков, то мы попадаем снова в ту же точку,т. е. значение числа от прибавления к нему нуля не изменилось: 7+0=7 . Применив переместительное свойство получим: 7+0=0+7=7, отсюда получаем третье свойство сложения — свойство нуля:

• Если прибавить к нулю какое-нибудь число, то получится прибавленное число

Свойства сложения

1. Переместительное свойство

От перестановки слагаемых сумма не меняется

Пример: 9+8=8+9=17

 

2. Сочетательное свойство

Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом к полученной сумме прибавить второе слагаемое

Пример: 7+(3+9)=(7+3)+9=19

 

3. Свойство нуля

Если прибавить к нулю какое-нибудь число, то получится прибавленное число

Пример: 0+10=10

Сравнение сумм натуральных чисел

Сравним (15+81) и (15+77), для этого рассмотрим слагаемые этих двух сумм: Мы видим, что первые слагаемые у них одинаковые, поэтому переходим к сравнению вторых слагаемых: 81 >77, поэтому (15+81)>(15+77).

Теперь сравним (21+15) и (34+54), для этого опять рассмотрим слагаемые, в данном случае одинаковых у нас нет, но мы видим, что слагаемые первой суммы меньше слагаемых второй суммы, а значит мы можем записать: (21+15)<(34+54).

Бывают случаи, когда нельзя однозначно сказать, какая сумма больше. Например сравним суммы: (26+33) и (18+43), мы видим, что первое слагаемое первой суммы больше первого слагаемого второй суммы, но второе слагаемое первой суммы меньше второго слагаемого второй суммы. В таком случае необходимо наши суммы привести к виду первого примера, т.е. 26=18+8, следовательно, 26+33=(18+8)+33=18+8+33=18+41, теперь мы сравниваем (18+41) и (18+43), первые слагаемые равны, а 41<43, следовательно(18+41)<(18+43) и мы можем сказать, что (26+33)<(18+43).

Из выше сказанного, делаем вывод: При увеличении слагаемых сумма увеличивается, а при уменьшении уменьшается.

Письменный прием сложения («сложение в столбик»)

Часто при решении задач, нам необходимо складывать многозначные числа, поэтому считать в «уме» или чертить координатный луч не целесообразно, для решения таких задач был придуман письменный прием сложения или «сложение в столбик»

, который помогает сложение многозначных чисел свести к сложению однозначных чисел, которое мы можем производить легко. Рассмотрим пример:

	1	1	1
+	4	5	8	7	1
		4	3	8	2
	5	0	2	5	3

Сложение начинаем справа, с разряда единиц: 1+2=3, записываем 3 под единицами, и переходим в разряд десятков: 7+8=15 >10, значит единицы десятков(5) записываем под десятками, а десяток десятков — это единица сотен, записываем ее над разрядом сотен, чтобы не забыть и переходим в следующий разряд: 8+3+1=12 >10, поступаем аналогично, единицы(2) записываем под рассматриваемым разрядом, а десятки записываем над следующим разрядом, далее складываем единицы тысяч: 5+4+1=10=10, здесь 0 единиц, поэтому под рассматриваемым разрядом ставим нуль, а десяток переносим в разряд десятков тысяч: 4+1=5.

Получаем, что 45871+4382=50253.

Вывод: Если при сложении чисел одного разряда число получается больше или равное 10, то 1 десяток записываем над следующим разрядом, а единицы под рассматриваемым разрядом.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Понятие о натуральном числе

Вычитание натуральных чисел

Умножение натуральных чисел

Деление натуральных чисел

Порядок выполнения действий

Степень числа. Квадрат и куб числа

Меньше или больше

Меньше или больше на сколько? во сколько раз?

Формулы

Уравнения

Натуральные числа и действия над ними

Правило встречается в следующих упражнениях:

5 класс

Задание 509, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 735, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 793, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 910, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1169, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1521, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1763, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 178, Мерзляк, Полонский, Якир, Учебник

Номер 435, Мерзляк, Полонский, Якир, Учебник

Номер 1051, Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 70, Мерзляк, Полонский, Якир, Учебник

Номер 122, Мерзляк, Полонский, Якир, Учебник

Номер 308, Мерзляк, Полонский, Якир, Учебник

Номер 1183, Мерзляк, Полонский, Якир, Учебник

Номер 1190, Мерзляк, Полонский, Якир, Учебник

Задание 330, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 533, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 766, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 891, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 4, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1

7 класс

Номер 6, Мерзляк, Полонский, Якир, Учебник

Номер 7, Мерзляк, Полонский, Якир, Учебник

Номер 11, Мерзляк, Полонский, Якир, Учебник

Номер 17, Мерзляк, Полонский, Якир, Учебник

Номер 177, Мерзляк, Полонский, Якир, Учебник

Номер 497, Мерзляк, Полонский, Якир, Учебник

Номер 564, Мерзляк, Полонский, Якир, Учебник

Номер 671, Мерзляк, Полонский, Якир, Учебник

Номер 706, Мерзляк, Полонский, Якир, Учебник

Номер 1006, Мерзляк, Полонский, Якир, Учебник

8 класс

Номер 67, Мерзляк, Полонский, Якир, Учебник

---

Ассоциативное свойство – объяснение с примерами

Слово « ассоциативный » взято из слова « ассоциированный, », что означает группу. Следовательно, ассоциативное свойство связано с группировкой. Открытие ассоциативного закона вызывает споры. Его представил не один человек.

В начале 18 ^го века математики начали анализировать абстрактные виды вещей, а не числа, и они хотели говорить о свойствах чисел, которые объясняют эти объекты. В 1919, Гамильтон употребил фразу «ассоциативный характер операции».

Что такое ассоциативная собственность?

Согласно свойству ассоциативности в математике, если вы складываете или умножаете числа, не имеет значения, где вы ставите скобки. Вы можете добавить их куда угодно. Это означает, что группировка чисел не важна во время сложения.

Только сложение и умножение ассоциативны, а вычитание и деление неассоциативны.

Ассоциативное свойство сложения

Согласно ассоциативному свойству сложения, если сложить три или более чисел, результат будет одним и тем же независимо от того, как числа расположены или сгруппированы.

Предположим, что если сложить числа a , b и c , и результат будет равен некоторому числу m , то если сначала сложить a и b , а затем c или добавить b и C Сначала, а затем A , результат по -прежнему равен M, , т. Е.

( A + B ) + C = A + ( B + 788. ) = m

Числа a , b и c называются слагаемыми.

Это свойство также работает для более чем трех номеров.

Пример 1

Покажите, что следующие числа подчиняются ассоциативному свойству сложения:

2, 6 и 9

Раствор

2 + 6 + 9

= (2 + 6) + 9 = 8 + 9 = 17

Или

= 2 + (6 + 9) = 2 + 15 = 17

Результат одинаков в обоих случаях. Следовательно,

(2 + 6) + 9 = 2 + (6 + 9)

В качестве реального примера ассоциативного свойства, если я иду в кафе и трачу 8 долларов на пиццу, 5 долларов на мороженое и 3 доллара на на кофе, то деньги, которые я должен кассиру, можно записать в виде суммы:

($8 + $5) + $3

Или

8 долларов + (5 долларов + 3 доллара)

Сумма обоих составляет 16 долларов.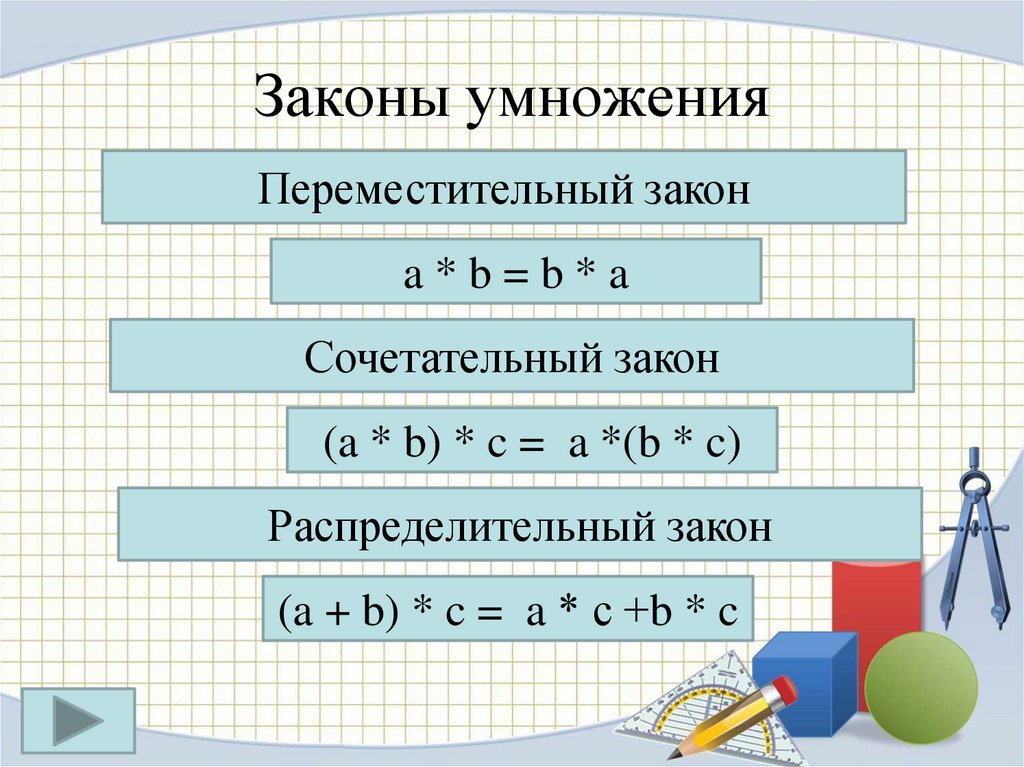

Ассоциативное свойство умножения

Согласно ассоциативному свойству умножения, если умножить три или более чисел, результат будет одинаковым, независимо от того, как числа расположены или сгруппированы.

Предположим, что если перемножить числа a , b и c , и результат будет равен некоторому числу n , то если мы умножим a и b сначала, а затем c , или умножьте b и c сначала, а затем a , результат все равно равен n , т.е. b ) × c = a × ( b × c ) = n

Это свойство также работает для более чем трех чисел.

Композиции функций и умножения матриц не являются ассоциативными.

Пример 2

Показать, что следующие числа подчиняются ассоциативному свойству умножения: 9 = 108

2 × 6 × 9 = 2 × (6 × 9) = 2 × 54 = 108

Результат одинаков в обоих случаях. Следовательно,

(2 × 6) × 9 = 2 × (6 × 9)

Почему вычитание и деление неассоциативны?

Чтобы понять, почему вычитание и деление не следуют ассоциативному правилу, следуйте приведенным ниже примерам.

Пример 3

Укажите, верно ли следующее выражение.

( а – б ) – с = а – ( б – с )

• Что нужно показать?

( A — B )- C = A -( B — C )

• Шаг. справа.

( a – b ) – c

• Шаг 3: Откройте скобки.

a – b – c

• Шаг 4: Объедините b и c в скобках.

a – ( b + c )

• Шаг 5: Посмотрите, получили ли вы желаемый результат.

( а – б ) – c = a – ( b + c )

• Шаг 6: Сформулируйте свои выводы.

С

( A — B ) — C = A — ( B + C )

HENT 9007 777777. )

HEND

7777777777777777777. )

HENT 9007 (777777. ). – c ≠ a – ( b – c )

Следовательно, данное выражение ложно и не следует свойству ассоциативности.

Пример 4

Укажите, верно ли следующее выражение.

(4 a ÷ 2 a ) ÷ a = 4 a ÷ (2 a ÷ a ) Что нужно показать?

(4 A ÷ 2 A ) ÷ A = 4 A ÷ (2 A ÷ A )

• ÷ A )
  • ÷ A )
    • STATE 2:.

    (4 a ÷ 2 a ) ÷ a

    • Шаг 3: Решить.

    (4 a ÷ 2 a ) ÷ a = (2) ÷ a = 2/ a

    4 a ÷ (2 a ÷ a ) = 4 a ÷ (2) = 2 a

  • 9020 Укажите ваши результаты.

  С

  (4 A ÷ 2 A ) ÷ A = 2/ A

  4 A ÷ A ÷ A ) = 2 A ÷ A ) = 2 A ÷ A ) = 2 A ÷ A ) = 2 A ÷ A ) = 2 A

  Следовательно,

  (4 а ÷ 2 а ) ÷ а ≠ 4 а ÷ (2 а ÷ а ) Следовательно, данное выражение не следует за ассоциативным выражением

  , 9000 имущество.

  Ассоциативное свойство

  Ассоциативное свойство

  Набор имеет свойство ассоциативности при определенной операции, если результат операции один и тот же независимо от того, как мы группируем любые наборы из 3 или более элементов, соединенных операцией. Это определение станет более понятным, когда мы рассмотрим несколько примеров.

  Более формально, если x , y и z являются переменными, представляющими любые 3 произвольных элемента в наборе, на который мы смотрим (назовем набор, который мы рассматриваем A), а символ # представляет нашей операции, то ассоциативное свойство для A с операцией # будет:

  ( x#y )# z = x #( y#z ).

  Это означает, что свойство ассоциативности имеет место только для множества A и операции # if, независимо от того, какие элементы мы возьмем из A и подставим вместо x , y и z , ( x# y )# z всегда будет давать нам тот же результат, что и x #( y#z ).

  Помните, что скобки просто говорят нам какую пару делать первой .

  Обратите внимание, что при всех операциях операция может воздействовать только на одну пару элементов за раз . Таким образом, выражение x#y#z не имеет смысла, если только мы не установим правило, которое говорит нам сначала идти слева направо или сначала идти справа налево, потому что у нас нет способа узнать , которое операция, которую нужно выполнить первой : должны ли мы сначала выполнить x#y или y#z? Когда мы делаем сложение, вычитание, умножение или деление, у нас есть правило, которое говорит нам просто идти слева направо. Но это правило не обязательно для произвольных операций! Если мы работаем с какой-либо операцией, которая является , а не сложением, вычитанием, умножением или делением, то мы должны иметь круглые скобки для любого выражения с более чем двумя элементами, чтобы мы знали, какое вхождение операции нужно выполнить первым !

  Давайте рассмотрим несколько примеров, чтобы мы могли более четко понять ассоциативное свойство:

  Сначала рассмотрим несколько бесконечных множеств с уже знакомыми нам операциями:

   

  а) Набор из натуральных чисел ассоциативен относительно операции сложения , потому что верно, что для любые два натуральных числа x, y и z, (x+y)+z = x+(y +з).

   

  b) Набор из целых чисел является , а не ассоциативным при операции деления , потому что для любых трех целых чисел x, y и z во многих случаях (x ÷ y) ÷ z ≠ x ÷ (y ÷ г)! Например:

  (10 ÷ 5) ÷ 2 = 2 ÷ 2 = 1

  10 ÷ (5 ÷ 2) = 10 ÷ 2,5 = 2

  1 ≠ 2!

  Так (10 ÷ 5) ÷ 2 ≠ 10 ÷ (5 ÷ 2)

  Итак, (x ÷ y) ÷ z = x ÷ (y ÷ z) равно , а не верно для всех целых чисел x, y и z!

  , чтобы увидеть еще несколько примеров!

  в) Множество из рациональных чисел ассоциативно по действию умножение , потому что верно, что для любые три рациональных числа x, y и z, (xy)z=x(yz). (Опять же обратите внимание, что мы не всегда записываем символ операции для умножения. Традиционно, когда мы пишем умножение, оставляем символ умножения, так что x×y просто записывается как xy.)

   

  d) Набор из действительных чисел является , а не ассоциативным при операции вычитания , потому что для любых трех действительных чисел x, y и z существует много случаев, когда (x – y) – z ≠ x – (у – з)! Например:

  (2 – 5) – 12 = (–3) – 12 = –15

  2 – (5 – 12) = 2 – (–7) = 2 + 7 = 9

  –15 ≠ 9!

  Так (2 – 5) – 12 ≠ 2 – (5 – 12)

  Итак, (x – y) – z = x – (y – z) равно , а не верно для всех действительных чисел x, y и z!

  Если все, что у нас есть, это таблица операций, может быть немного сложнее определить, обладает ли множество свойством ассоциативности при конкретной операции. Чтобы понять, как это сделать,

  Давайте посмотрим на несколько простых наборов с операционными таблицами и проверим, обладают ли они свойством ассоциативности.

  e) Вот таблица операций для набора {a,b,c} и операции *:

  *	и	б	с
  и	и	б	с
  б	б	и	с
  с	с	с	и

  Чтобы проверить ассоциативность, мы должны проверить все возможные экземпляры уравнения (x*y)*z = x*(y*z). Это означает, что мы должны думать о каждой возможной комбинации того, чем могут быть x, y и z.

   

  Использование приведенной выше таблицы для записи всех возможных комбинаций элементов, которые могут использоваться для x, y и z, а затем вычисление (x*y)*z и сравнение с x*(y*z) дает нам следующую таблицу. :

   

  Значения x, y, z	(х*у)*г	х*(у*г)	(x*y)*z = x*(y*z)?
  х=а, у=а, г=а	(а*а)*а = а*а = а	а*(а*а) = а*а = а	а = а, Итак, (а*а)*а = а*(а*а).
  х=а, у=а, г=б	(а*а)*б = а*б = б	а*(а*б) = а*б = б	b = b, поэтому (a*a)*b = a*(a*b).
  х=а, у=а, г=с	(а*а)*с = а*с = с	а*(а*с) = а*а = с	с = с, Итак, (а*а)*с = а*(а*с).
  х=а, у=б, г=а	(а*б)*а = б*а = б	а*(б*а) = а*б = б	b = b, поэтому (a*b)*a = a*(b*a).
  х=а, у=б, г=б	(а*б)*б = б*б = а	а*(б*б) = а*а = а	а = а, Итак, (а*b)*b = а*(b*b).
  х=а, у=б, г=с	(а*б)*с = б*с = с	а*(б*с) = а*с = с	c = c, Итак, (a*b)*c = a*(b*c).
  х=а, у=с, г=а	(а*с)*а = с*а = с	а*(с*а) = а*с = с	с = с, Итак, (а*с)*а = а*(с*а).
  х=а, у=с, г=б	(а*с)*b = с*b = с	а*(с*б) = а*с = с	c = c, Итак, (a*c)*b = a*(c*b).
  х=а, у=с, г=с	(а*с)*с = с*с = а	а*(с*с) = а*а= а	а = а, Итак, (а*с)*с = а*(с*с).
  х=б, у=а, г=а	(б*а)*а = б*а = б	б*(а*а) = б*а = б	b = b, поэтому (b*a)*a = b*(a*a).
  х=б, у=а, г=б	(б*а)*б = б*б = а	б*(а*б) = б*б = а	а = а, Итак, (b*a)*b = b*(a*b).
  х=б, у=а, г=с	(б*а)*с = б*с = с	б*(а*с) = б*с = с	c = c, Итак, (b*a)*c = b*(a*c).
  х=б, у=б, г=а	(б*б)*а = а*а = а	б*(б*а) = б*б = а	а = а, поэтому (b*b)*a = b*(b*a).
  х=б, у=б, г=б	(б*б)*б = а*б = б	б*(б*б) = б*а = б	b = b, поэтому (b*b)*b = b*(b*b).
  х=б, у=б, г=с	(б*б)*с = а*с = с	б*(б*с) = б*с = с	c = c, Итак, (b*b)*c = b*(b*c).
  х=б, у=в, г=а	(b*c)*a = c*a = c	б*(с*а) = б*с = с	c = c, Итак, (b*c)*a = b*(c*a).
  х=б, у=в, г=б	(b*c)*b = c*b = c	б*(с*б) = б*с = с	с = с, поэтому (b*c)*b = b*(c*b).
  х=б, у=с, г=с	(b*c)*c = c*c = a	б*(с*с) = б*а = б	a ≠ b, Итак, (b*c)*c ≠ b*(c*c)!
  х=с, у=а, г=а	(с*а)*а = с*а = с	с*(а*а) = с*а = с	с = с, Итак, (с*а)*а = с*(а*а).
  х=с, у=а, г=б	(с*а)*b = с*b = с	с*(а*б) = с*б = с	c = c, Итак, (c*a)*b = c*(a*b).
  х=с, у=а, z=с	(с*а)*с = с*с = а	с*(а*с) = с*с = а	а = а, Итак, (с*а)*с = с*(а*с).
  х=с, у=б, г=а	(с*б)*а = с*а = с	с*(б*а) = с*б = с	c = c, Итак, (c*b)*a = c*(b*a).
  х=с, у=b, z=b	(с*б)*б = с*б = с	с*(б*б) = с*а = с	c = c, Итак, (c*b)*b = c*(b*b).
  х=с, у=b, z=с	(с*б)*с = с*с = а	с*(б*с) = с*с = а	а = а, так что (с*b)*с = с*(b*с).
  х=с, у=с, z=а	(с*с)*а = а*а = а	с*(с*а) = с*с = а	а = а, так что (с*с)*а = с*(с*а).
  х=с, у=с, z=b	(с*с)*b = а*b = b	с*(с*b) = с*с = а	b ≠ a, Итак, (c*c)*b ≠ c*(c*b)!
  х=с, у=с, z=с	(с*с)*с = а*с = с	с*(с*с) = с*а = с	с = с, Итак, (с*с)*с = с*(с*с).

   

  Таким образом, набор {a,b,c} при операции * равен не ассоциативный, потому что у нас есть по крайней мере один пример , где (x*y)*z ≠ x*(y*z)! На самом деле у нас есть два примера, когда это не удается: (b*c)*c ≠ b*(c*c) и (c*c)*b ≠ c*(c*b)! Когда x равно b, y равно c и z равно c, (x*y)*z ≠ x*(y*z)! И когда x равно c, y равно c и z равно b (x*y)*z ≠ x*(y*z)!

   

   

  Хотя на самом деле нет хорошего ярлыка, который можно использовать, чтобы попытаться увидеть, является ли множество под операцией, заданной таблицей операций, ассоциативным, есть несколько вещей, которые вы можете найти, которые могут сократить количество экземпляров, которые вам нужно проверить:

  Если набор имеет идентификатор , то нам не нужно проверять какие-либо экземпляры, включающие этот идентификатор. Почему? Давайте посмотрим, что произойдет, если мы вычислим экземпляр, содержащий идентификатор. Для этой цели мы позволим e представлять единичный элемент нашего множества, а x и y будем представлять любые два элемента нашего множества.

  Давайте посмотрим, верно ли (e* x )* y = e*( x * y ).

  Сначала мы вычислим (e* x )* y . Поскольку тождество по определению не изменяет элементы, когда действует на них операцией, мы должны иметь e* x= x . Итак, (e* x )* y= x * y .

  Теперь мы вычислим e*( x * y ). Опять же, поскольку тождество по определению не изменяет элементы, когда действует на них с помощью операции, мы должны иметь e*( x * у ) = х * у . Итак, (e* x )* y = e*( x * y ) верно.

  Мы можем использовать аналогичные рассуждения, чтобы увидеть, что ( x *e)* y = x *(e* y ) верно и что ( x * y )*e= x *( y *e) верно.

  Таким образом, выражения, содержащие тождество, всегда будут ассоциативными. Это означает, что для того, чтобы проверить, обладает ли набор ассоциативным свойством, нам нужны только выражения проверки, которые содержат только элементы, которые НЕ являются тождественными.

  Это может значительно сократить количество проверяемых элементов. Чтобы убедиться в этом, давайте снова посмотрим на наш пример:

  .

  Пример:

  Вот таблица операций для набора {a,b,c} и операции *:

  *	и	б	с
  и	и	б	с
  б	б	и	с
  с	с	с	и

  Обратите внимание, что этот набор имеет тождество: a, потому что всякий раз, когда a умножается на любой элемент в наборе справа или слева, он оставляет этот элемент неизменным.

  Таким образом, чтобы проверить ассоциативность, мы должны проверить все возможные экземпляры уравнения (x*y)*z = x*(y*z), которое не включает a (поскольку a является тождеством, а мы не необходимо проверять комбинации, включающие тождество).

   

  Значения x, y, z	(х*у)*г	х*(у*г)	(x*y)*z = x*(y*z)?
  х=б, у=б, г=б	(б*б)*б = а*б = б	б*(б*б) = б*а = б	b = b, поэтому (b*b)*b = b*(b*b).
  х=б, у=б, г=с	(б*б)*с = а*с = с	б*(б*с) = б*с = с	c = c, Итак, (b*b)*c = b*(b*c).
  х=б, у=в, г=б	(b*c)*b = c*b = c	б*(с*б) = б*с = с	с = с, поэтому (b*c)*b = b*(c*b).
  х=б, у=с, г=с	(б*с)*с = с*с = а	б*(с*с) = б*а = б	a ≠ b, Итак, (b*c)*c ≠ b*(c*c)!
  х=с, у=b, z=b	(с*б)*б = с*б = с	с*(б*б) = с*а = с	c = c, Итак, (c*b)*b = c*(b*b).
  х=с, у=b, z=с	(с*б)*с = с*с = а	с*(б*с) = с*с = а	а = а, так что (с*b)*с = с*(b*с).
  х=с, у=с, z=b	(с*с)*b = а*b = b	с*(с*b) = с*с = а	b ≠ a, Итак, (c*c)*b ≠ c*(c*b)!
  х=с, у=с, z=с	(с*с)*с = а*с = с	с*(с*с) = с*а = с	с = с, Итак, (с*с)*с = с*(с*с).

  Обратите внимание, что, проверяя только экземпляры, которые не содержат идентификатор a , мы сократили количество комбинаций, которые нам нужно проверить, с 27 до 8! Это большое улучшение!

  Будьте осторожны! Многие студенты делают ошибку, заключая, что набор ассоциативен, проверив лишь несколько примеров.