Примеры в столбик на сложение, вычитание и умножение: заполнить пропуски
Рейтинг 5.00 из 5 на основе опроса 1 пользователя
(1 отзыв клиента)
120,00 ₽
Примеры на сложение, вычитание и умножение в столбик. В каждом примере пропущены цифры (разряды): в слагаемом, уменьшаемом, вычитаемом, множителе или в ответе. В задании нужно заполнить пустые клетки (пропущенные цифры), чтобы получилось верное равенство. С ответами. Для печати А4.
Количество товара Примеры в столбик на сложение, вычитание и умножение: заполнить пропуски
Артикул: i-10135 Категория: Для учебы Метки: Примеры в столбик, 2 класс, 3 класс, 4 класс
- Описание
- Детали
- Отзывы (1)
Описание
Программа формирует  В каждом примере пропущены цифры (разряды): в слагаемом, уменьшаемом, вычитаемом, множителе или в ответе. В задании нужно заполнить пустые клетки (пропущенные цифры), чтобы получилось верное равенство.
В каждом примере пропущены цифры (разряды): в слагаемом, уменьшаемом, вычитаемом, множителе или в ответе. В задании нужно заполнить пустые клетки (пропущенные цифры), чтобы получилось верное равенство.
Это будет способствовать повторению правил письменного выполнения различных арифметических действий с переходом через разряд. Выполняя задание, ребенок будет развивать математическое мышление, навыки устного счета, внимательность, умение слагать и вычитать, осуществляя записи в столбик.
Программа представляет собой тренажер для счета. Она имеет внутренние настройки, выбирая которые можно создать примеры на сложение, вычитание и умножение в столбик для детей разного возраста и уровня подготовки:
- в пределах 100 на сложение и вычитание двузначных чисел,
- в пределах 1 000 на сложение и вычитание трехзначных чисел,
- с большими числами до 10 000.

Поэтому программа будет полезна как для учеников начальной школы 2-4 классов, так и для более старших классов.
Программа счета написана в Excel с помощью макросов. Формируются примеры на листе формата А4. Примеры генерируются случайным образом, количество генераций не ограничено. При записи примеров разряды чисел формируются друг под другом, что позволяет легко ориентироваться в примерах.
В конце карточки формируются ответы на примеры, которые после печати карточки можно отрезать.
Генератор примеров по математике будет очень удобен как для родителей, так и для учителей. Не нужно заранее покупать задачники и пособия по математике с примерами. Можно скачать файл и сгенерировать карточки в любое время независимо от подключения к интернету и распечатать.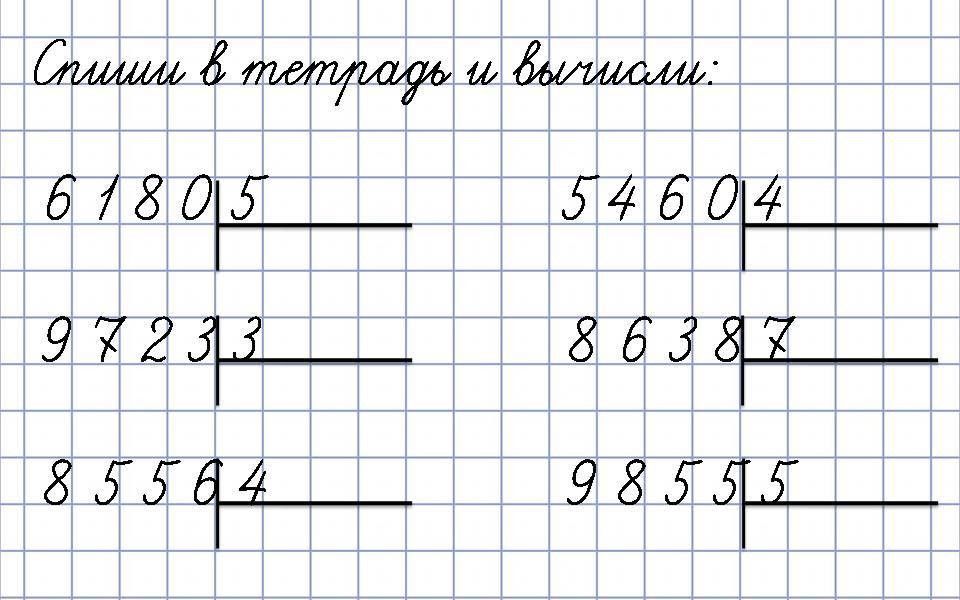
Для ознакомления с программой можно бесплатно скачать примеры, которые получаются при использовании программы. Для получения новой карточки примеров достаточно скачать, нажать на кнопку генерации и распечатать.
На сайте представлен каталог программ, в котором все программы распределены по группам. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.
Вам также будет интересно…
Деление в столбик
75,00 ₽В корзинуУмножение трехзначного числа на однозначное по схеме
75,00 ₽В корзинуЗадачи на движение (разные виды)
100,00 ₽В корзинуДеление с остатком на число (с выбором делимого и делителя)
Оценка 3.00 из 5
80,00 ₽В корзинуПродолжить ряд чисел
125,00 ₽В корзинуРаскрытие скобок и порядок действий до 1000 (сложные примеры)
130,00 ₽В корзинуВсе действия в столбик 3 (со словами для самоконтроля)
Оценка 5.
175,00 ₽В корзину 00 из 5
00 из 5Выражения с именованными числами (разные единицы измерения)
90,00 ₽В корзинуСложение и вычитание в столбик
Оценка 5.00 из 5
70,00 ₽В корзину
Вычитание столбиком до 1000000.
Главная / Генератор примеров по математике.
Распечатать. Печатается 2 листа. Первый — задания, Второй — задания с ответами.
После решения обязательно проведите проверку !
Задания каждый раз выдаются разные.
Задание
Вычитание столбиком до 1000000.| — | 343865 307859 |
| — | 563626 549062 |
| — | 12940 10765 |
| — | 39326 37406 |
| — | 209395 56664 |
| — | 349841 233007 |
| — | 653387 641057 |
| — | 491005 445892 |
| — | 358563 24006 |
| — | 949014 111012 |
| — | 533089 394040 |
| — | 686747 34111 |
| — | 774055 437995 |
| — | 914792 370789 |
| — | 431460 397450 |
| — | 627028 522405 |
| — | 357034 227787 |
| — | 313850 235907 |
| — | 734002 36094 |
| — | 344610 326524 |
| — | 63984 15013 |
| — | 964183 771749 |
| — | 163158 84666 |
| — | 828643 823548 |
| — | 240876 159782 |
| — | 396610 320285 |
| — | 914019 235379 |
| — | 595211 276766 |
| — | 109438 43524 |
| — | 90910 15588 |
Ответы
Вычитание столбиком до 1000000.
| — | 343865 30785936006 |
| — | 563626 54906214564 |
| — | 12940 107652175 |
| — | 39326 374061920 |
| — | 209395 56664152731 |
| — | 349841 233007116834 |
| — | 653387 64105712330 |
| — | 491005 44589245113 |
| — | 358563 24006334557 |
| — | 949014 111012838002 |
| — | 533089 394040139049 |
| — | 686747 34111652636 |
| — | 774055 437995336060 |
| — | 914792 370789544003 |
| — | 431460 39745034010 |
| — | 627028 522405104623 |
| — | 357034 227787129247 |
| — | 313850 23590777943 |
| — | 734002 36094697908 |
| — | 344610 32652418086 |
| — | 63984 1501348971 |
| — | 964183 771749192434 |
| — | 163158 8466678492 |
| — | 828643 8235485095 |
| — | 240876 15978281094 |
| — | 396610 32028576325 |
| — | 914019 235379678640 |
| — | 595211 276766318445 |
| — | 109438 4352465914 |
| — | 90910 1558875322 |
Основные операции (сложение, вычитание, умножение, деление) Рабочие листы Mega Bun
Это набор продуктов для следующих основных операций (сложение, вычитание, умножение, деление). Все эти рабочие листы не требуют подготовки. Просто выберите из нужной папки, распечатайте и будьте готовы к уроку.
Все эти рабочие листы не требуют подготовки. Просто выберите из нужной папки, распечатайте и будьте готовы к уроку.
- Дополнительные рабочие листы
- Рабочие листы на вычитание
- Рабочие листы умножения
- Рабочие листы разделов
Что вы получите
Вы получите несколько файлов для печати. Это 2-страничные файлы с ключами ответов. Они организованы в папки для быстрого доступа. Просто выберите файл и распечатайте.
1. ДОПОЛНЕНИЕ
Всего 12 типов. Каждый тип экзамена сгруппирован по количеству цифр в дополнениях. В каждой группе по 15 рабочих листов. В целом, у вас есть сотни рабочих листов на выбор.
- 1 цифра + 1 цифра — идеально подходит для арифметики в уме
- 1 цифра + 2 цифры
- 2 цифры + 2 цифры
- 2 цифры + 3 цифры
- 3 цифры + 3 цифры
- 3 цифры + 4 цифры
1. Найдите сумму.
Сложения выровнены по вертикали, чтобы учащиеся могли выполнять сложение непосредственно на рабочем листе.
2. Сложите числа и напишите их сумму в соответствующем поле.
Детям может понадобиться использовать отдельную бумагу для сложения.
3. Добавить числа, показать решение.
Учащиеся должны переписать и выровнять добавления, а затем выполнить сложение.
4. Раскрасьте правильный ответ (2 варианта)
Для каждого пункта даются варианты ответов, и детей просят раскрасить правильный ответ.
5. Раскрасьте правильный ответ (3 варианта)
Для каждого пункта даются варианты ответов, и детей просят раскрасить правильный ответ. (3 варианта)
6. Выберите правильный ответ из списка.
Впишите букву правильного ответа в отведенное место.
7. Сопоставьте два столбца.
Сопоставьте слагаемые в левом столбце с суммой в правом столбце.
8. Найдите недостающее дополнение.
Учащиеся должны дополнить уравнение недостающим слагаемым.
9. Найдите недостающее сложение или сумму.
Дети должны заполнить пробелы, чтобы завершить уравнение.
10. Сложение 3 чисел.
Указанные числа выровнены. Ученикам просто нужно выполнить сложение.
11. Добавление 3 чисел.
Учащиеся должны переписать и выровнять три числа, а затем выполнить сложение.
12. Сложить 3 цифры, 2 суммы.
Детям нужно сложить первые два числа, а затем добавить результат к третьему числу.
2. ВЫЧИТАНИЕ
Всего 11 типов. Каждый тип экзамена сгруппирован по количеству цифр вычитаемого/уменьшаемого. В каждой группе по 15 рабочих листов. В целом, у вас есть сотни рабочих листов на выбор.
- 1 цифра — 1 цифра — идеально подходит для арифметики в уме
- 2-значный — 1-значный – идеально подходит для ментальной арифметики
- 2 цифры — 2 цифры
- 3 цифры — 2 цифры
- 3 цифры — 3 цифры
- 4 цифры — 3 цифры
- 4 цифры — 4 цифры
1. Вычитание чисел
Числа выровнены по вертикали, чтобы учащиеся могли выполнять вычитание прямо на рабочем листе.
2. Найдите разницу
Вычтите числа и напишите их разницу в соответствующем поле. Учащимся может потребоваться использовать отдельную бумагу (для черновиков) для выполнения вычитания.
3. Вычтите числа, покажите решение
Учащиеся должны переписать и выровнять числа, а затем выполнить вычитание.
4. Раскрасьте правильный ответ (2 варианта)
Вычтите числа, а затем раскрасьте прямоугольник правильного ответа.
5. Раскрасьте правильный ответ (3 варианта ответа)
Вычтите числа. Раскрасьте прямоугольник правильного ответа (из трех вариантов)
6. Выберите правильный ответ из списка
Вычтите числа и выберите ответ из поля. Впишите букву правильного ответа в отведенное место.
7. Сопоставьте два столбца
Сопоставьте числа в левом столбце с разницей в правом столбце. Напишите букву вашего ответа в отведенном месте.
8. Найдите недостающее уменьшаемое или вычитаемое
В уравнении отсутствует уменьшаемое или вычитаемое. Учащиеся должны заполнить пропуски, чтобы завершить уравнение.
Учащиеся должны заполнить пропуски, чтобы завершить уравнение.
9. Найдите пропущенное уменьшаемое, вычитаемое или разность
В уравнении отсутствует уменьшаемое, вычитаемое или разность. Учащиеся должны заполнить пропуски, чтобы завершить уравнение.
10. Вычитание трех чисел, показать решение
Учащиеся должны переписать и выровнять три числа, а затем выполнить вычитание.
11. Вычесть 3 числа, 2 ответа
Ученикам нужно будет вычесть первые два числа, а затем вычесть результат из третьего числа.
3. УМНОЖЕНИЕ
Всего 10 типов. Каждый тип экзамена сгруппирован по количеству цифр факторов. В каждой группе по 15 рабочих листов. В целом у вас есть сотни рабочих листов на выбор.
В каждом разделе есть смешанный набор рабочих листов для умножения на ваш выбор, в том числе:
- 1 x 1 цифра — идеально подходит для ментальной арифметики
- 2 x 1 цифры
- 2 x 2 цифры
- 3 x 1 цифра
- 3 x 2 цифры
- 4 x 1 цифра
- Кратность 10
1. Умножьте числа
Умножьте числа
Числа расположены в стандартной форме, и учащиеся должны найти произведения.
2. Найдите продукт (горизонтальный)
Данные числа расположены горизонтально, и учащиеся должны вычислить продукты.
3. Умножьте числа, покажите решение
Учащиеся должны преобразовать числа в стандартную форму, а затем выполнить умножение, показав свое решение.
4. Раскрасьте правильный ответ (2 варианта)
Умножьте числа, а затем раскрасьте прямоугольник правильного ответа.
5. Раскрасьте правильный ответ (3 варианта)
Умножьте числа, а затем раскрасьте прямоугольник правильного ответа.
6. Выберите правильный ответ из списка
Умножьте числа и выберите ответ из поля. Впишите букву правильного ответа в отведенное место.
7. Сопоставьте два столбца
Сопоставьте числа в левом столбце с продуктами в правом столбце. Напишите букву вашего ответа в отведенном месте.
8. Найдите недостающий множитель
В уравнении отсутствует множитель.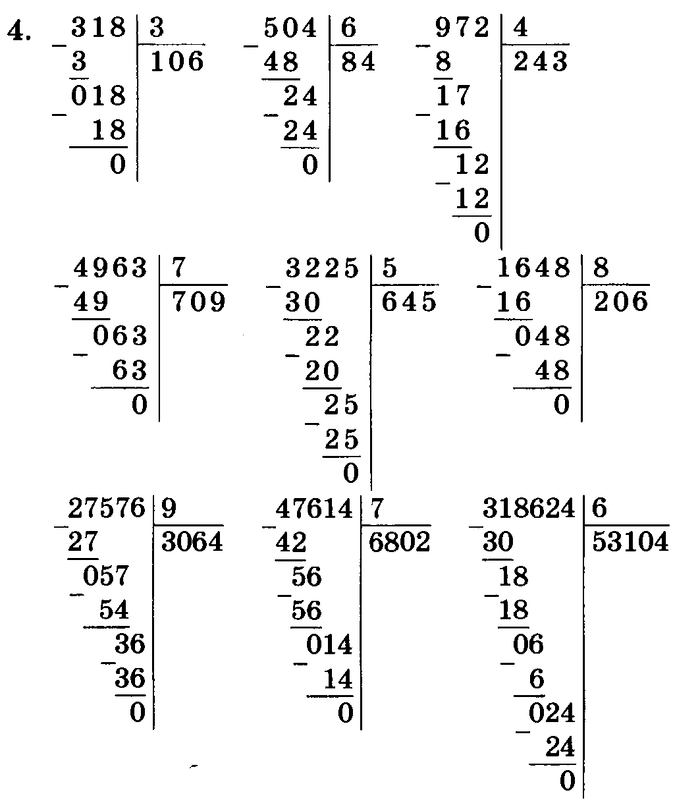 Учащиеся должны заполнить пропуски, чтобы завершить уравнение.
Учащиеся должны заполнить пропуски, чтобы завершить уравнение.
9. Найдите недостающий множитель или произведение
В каждом уравнении есть недостающий множитель или произведение. Учащиеся должны заполнить пропуски, чтобы завершить уравнение.
10. Таблица умножения
Создание таблицы
Заполните поля
4. ОТДЕЛ
Всего существует 9 типов. Каждый тип экзамена сгруппирован по количеству цифр делимого/делителя. В каждой группе 15 рабочих листов, что дает вам сотни рабочих листов на выбор.
- 2 цифры на 1 цифру — идеально подходит для арифметики в уме
- 2 цифры по 1 или 2 цифры
- 3 цифры по 1 или 2 цифры
- 4 цифры по 1 или 2 цифры
- 4 цифры по 2 или 3 цифры
- Кратность 10 (25 рабочих листов)
1. Разделить числа (Стандартная форма)
Числа расположены в стандартной форме, и учащиеся должны найти частное.
2. Разделите числа (горизонтальное уравнение)
Разделите числа (горизонтальное уравнение)
Данные числа расположены горизонтально, и учащиеся должны вычислить частное.
3. Разделите числа, покажите решение
Учащиеся должны привести числа к стандартной форме, а затем выполнить деление, показав свое решение.
4. Раскрасьте правильный ответ (2 варианта)
Разделите числа, а затем раскрасьте прямоугольник правильного ответа.
5. Раскрасьте правильный ответ (3 варианта)
Разделите числа, а затем раскрасьте прямоугольник правильного ответа. (3 варианта)
6. Выберите правильный ответ из списка
Разделите числа и выберите ответ из поля. Впишите букву правильного ответа в отведенное место.
7. Сопоставьте два столбца
Сопоставьте числа в левом столбце с ответами в правом столбце. Напишите букву вашего ответа в отведенном месте.
8. Найдите недостающее делимое или делитель
В уравнении отсутствует делимое или делитель. Учащиеся должны заполнить пропуски, чтобы завершить уравнение.
9. Найдите пропущенное делимое, делитель или частное
В каждом уравнении отсутствует делимое, делитель или частное. Учащиеся должны заполнить пропуски, чтобы завершить уравнение.
Операции над матрицами в R
Матрицы в R представляют собой набор значений, действительных или комплексных чисел, расположенных в группе с фиксированным числом строк и столбцов. Матрицы используются для отображения данных в структурированном и хорошо организованном формате. Элементы матрицы необходимо заключать в круглые скобки или скобки. Матрица с 9элементы показаны ниже. Эта матрица [M] имеет 3 строки и 3 столбца. К каждому элементу матрицы [M] можно обращаться по номеру строки и столбца. Например, 23 = 6 Порядок матрицы : Порядок матрицы определяется количеством строк и столбцов. Порядок матрицы = количество строк × количество столбцов. Следовательно, матрица [M] является матрицей порядка 3 × 3.
Операции с матрицами
Существует четыре основных операции, т. е. DMAS (деление, умножение, сложение, вычитание ), что можно сделать с матрицами. Обе матрицы, участвующие в операции, должны иметь одинаковое количество строк и столбцов.
е. DMAS (деление, умножение, сложение, вычитание ), что можно сделать с матрицами. Обе матрицы, участвующие в операции, должны иметь одинаковое количество строк и столбцов.
Сложение матриц
Сложение двух одинаковых упорядоченных матриц и дает матрицу, в которой каждый элемент представляет собой сумму соответствующих элементов входных матриц.
Python3
В приведенном выше коде nrow(B) задает количество строк в B, а ncol(B) задает количество столбцов. Здесь sum — это пустая матрица того же размера, что и B и C. Элементы sum — это сложение соответствующих элементов B и C через вложенные циклы for. Использование оператора «+» для добавления матрицы: Аналогично, следующий скрипт R использует встроенный оператор +: 4444447. 33333333. 444447 901,10447 |
|
Вывод:
[1] [2] [3]
[1,] 1 3 5
[2,] 2 4 6
[1] [2] [3]
[1,] 7 9 11
[2,] 8 10 12
[1] [2] [3]
[1,]-6-6-6
[2,]-6-6-6
Здесь в приведенном выше коде элементы матрицы различий являются вычитанием соответствующих элементов B и C через вложенные циклы for. Использование оператора «-» для вычитания матриц: Аналогично, следующий скрипт R использует встроенный оператор «-»:
Python3
|
Output:
[1] [ 2] [3] [1,] -1+0i 5.3+0i 0+0i [2,] 2+3i 0.0+0i 0+0i
Свойства вычитания матриц:
- Некоммутативный: B – C != C – B
- Неассоциативный: Для n числа матриц A – (B – C) != (A – B) – C
- Порядок задействованных матриц должен быть одинаковым.
Умножение матриц
Умножение двух одинаковых упорядоченных матриц и дает матрицу, в которой каждый элемент является произведением соответствующих элементов входных матриц.
Python3
|
Выход:
[ 1] [2] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3]
[1,] 1 3 5
[2,] 2 4 6
[1] [2] [3]
[1,] 7 911
[2,] 8 10 12
[1] [2] [3]
[1,] 7 27 55
[2,] 16 40 72 Элементы суммы являются произведением соответствующих элементов B и C через вложенные циклы for. Использование оператора « *» для умножения матрицы: Аналогично, в следующем сценарии R используется встроенный оператор *:
Python3
|
Выход:
[1] [2] [3] [1,] 2+0i -3+2i 0.54+0i
Свойства умножения матриц:
- Коммутативный: B * C = C * B
- Ассоциативный: Для n * числа матриц (B * C) = (A * B) * C
- Порядок задействованных матриц должен быть одинаковым.

Деление матриц
Деление двух одинаковых упорядоченных матриц дает матрицу, в которой каждый элемент представляет собой частное соответствующих элементов первого матричного элемента, деленного на второй.
Python3
, 8 , 9 , 10 , 11 , 12 ), nrow = 2 , ncol = 3 )
|
Выход:
[ 1] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3] [3]
[1,] 1 3 5
[2,] 2 4 6
[1] [2] [3]
[1,] 7 911
[2,] 8 10 12
[1] [2] [3]
[1,] 0,1428571 0,3333333 0,4545455
[2,] 0. 2500000 0.4000000 0.5000000
2500000 0.4000000 0.5000000 Элементы матрицы div представляют собой деление соответствующих элементов B и C через вложенные циклы for. Использование оператора «/» для деления матрицы: Аналогично, следующий скрипт R использует встроенный оператор /:0304 4 , 6i , - 1 ), nrow = 1 , ncol = 3 )
C = matrix(c( 2 , 2i , 0 ), nrow = 1 , ncol = 3 )
печать (B / C)
Вывод:
[] [1,] 2+0i 3+0i -Inf+NaNiСвойства деления матрицы:
- Некоммутативный: B / C != C / B
- Неассоциативный: количество матриц A / (B / C) != (A / B) / C
- Порядок задействованных матриц должен быть одинаковым.


 00 из 5
00 из 5


 2500000 0.4000000 0.5000000
2500000 0.4000000 0.5000000 