5.4.7. Примеры на сложение и вычитание обыкновенных дробей.
Автор Татьяна Андрющенко На чтение 2 мин. Просмотров 4.1k. Опубликовано
I. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
Примеры.
II. Если нужно сложить дроби с разными знаменателями, то сначала дроби приводят к наименьшему общему знаменателю, а затем складывают дроби с одинаковыми знаменателями.
Примеры.
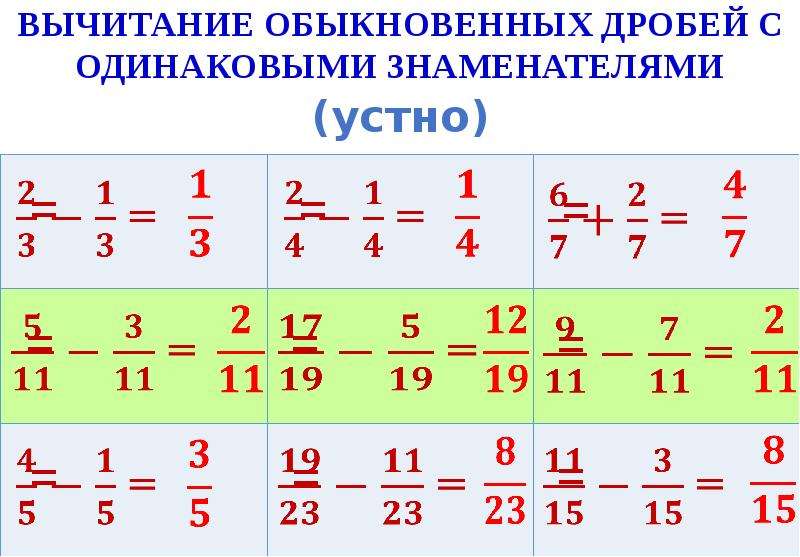
III. Чтобы выполнить вычитание дробей с одинаковыми знаменателями, из числителя первой дроби вычитают числитель второй дроби, а знаменатель оставляют тот же.
Примеры.
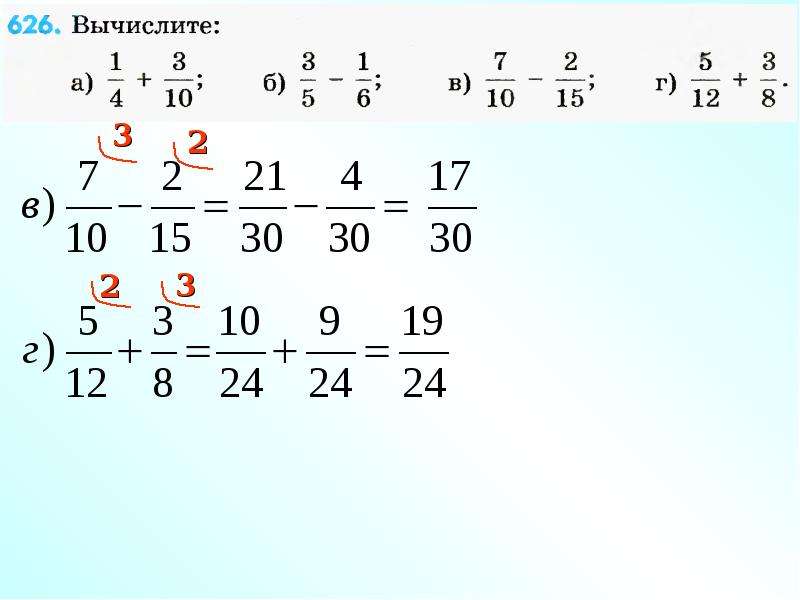
IV. Если нужно выполнить вычитание дробей с разными знаменателями, то их сначала приводят к общему знаменателю, а затем выполняют вычитание дробей с одинаковыми знаменателями.
Примеры.
V. При выполнении действий сложения или вычитания смешанных чисел эти действия выполняют отдельно для целых частей и для дробных частей, а затем результат записывают в виде смешанного числа.
Примеры.
Да, складывать нужно отдельно целые части и отдельно дробные части смешанного числа.
Нет, не нужно расписывать целые и дробные части смешанных чисел по отдельности.
Важно: не начинайте выполнять сложение, пока не приведете дробные части данных смешанных чисел к наименьшему общему знаменателю (НОЗ).
Помним, что единицу можно представить в виде обыкновенной дроби, числитель и знаменатель которой, являются любыми равными друг другу числами.
Важно: не начинайте выполнять вычитание, пока не приведете дробные части данных смешанных чисел к наименьшему общему знаменателю (НОЗ) и не убедитесь, что из числителя первой дроби можно вычесть числитель второй дроби.
А если нельзя вычесть?
Тогда «занимаете» у целой части уменьшаемого одну целую единицу, представляете ее в виде неправильной дроби с таким же знаменателем (НОЗ), и добавляете эту неправильную дробь (раздробленную единицу) к дробной части уменьшаемого.
Сложение дробей — как складывать дроби 🤔
Понятие дроби
Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между ними означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел, например, 5/9 или (1,5 — 0,2)/15.
- Алгебраические — состоят из переменных, например, (x + y)/(x — y).
В этом случае значение дроби зависит от данных значений букв.
В этом случае значение дроби зависит от данных значений букв.Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1\4.
Основные свойства дробей1. Дробь не имеет значения, при условии, если делитель равен нулю. 2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля. 3. Равными называются такие a/b и c/d, если: 4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь. |
Как плюсовать дроби
Сложение — это арифметическое действие, в результате которого получается новое число.
Оно содержит в себе сумму заданных чисел.
Свойства сложения
- От перестановки мест слагаемых сумма не меняется: a + b = b + a.
- Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа: (a + b) + c = a + (b + c).
- Если к числу прибавить ноль, получится само число: a + 0 = 0 + a = a
- При сложении числа можно переставлять и объединять в группы, результат от этого не изменится.
Давайте рассмотрим несколько вариантов сложения обыкновенных дробей.
Сложение дробей с одинаковыми знаменателями
Чтобы получить результат суммы двух дробей с равными знаменателями, нужно сложить числители исходных дробей, а знаменатель оставить прежним.
Не забудьте проверить, можно ли сократить дробь.
Сложение дробей с разными знаменателями
Как складывать дроби с разными знаменателями — для этого нужно найти наименьший общий знаменатель (далее — НОЗ), а затем воспользоваться предыдущим правилом.
Вот, что делать:
1. Найдем наименьшее общее кратное (далее — НОК) для определения единого делителя.
Для этого записываем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
2. Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:
- 90 : 15 = 6,
- 90 : 18 = 5.
Полученные числа записываем справа сверху над числителем.
3. Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
4. Проверим полученный результат:
- если делимое больше делителя, нужно преобразовать в смешанное число;
- если есть что сократить, нужно выполнить сокращение.
Еще раз ход решения одной строкой:
Сложение смешанных чисел
Сложение смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей.
Для этого нужно действовать поэтапно:
1. Сложить целые части.
2. Сложить дробные части.
Если знаменатели разные, воспользуемся знаниями из предыдущего примера и приведем к общему.
3. Суммируем полученные результаты.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Если урок в самом разгаре и посчитать нужно быстро — можно воспользоваться онлайн-калькулятором. Вот несколько подходящих:
Прибавление и вычитание дробей — смежные темы: принципы и закономерности очень похожи. Чтобы закрепить знания, нужно решать примеры сложения дробей, как можно чаще.
Запишите вашего ребенка на бесплатный вводный урок математики в детскую школу Skysmart: порешаем задачки на интерактивной платформе, порисуем фигуры на онлайн-доске и покажем, что учиться можно с интересом и в удовольствие.
Повторение «Правила сложения обыкновенных дробей»
Текст этой презентации
Слайд 1
СКАЗКАПравила сложенияв царстве обыкновенных дробей
Слайд 2
—
1) 2)
3) 4) 5) 6)
сказка
Слайд 3
Сказка ложь,
Но в ней намёк,
Добрым молодцам
И красным девицам урок.
Слайд 4
В 3/9 царстве, в 3/10 государстве жили-были обыкновенные дроби. Были они разные.
Египтяне употребляли
только дроби с числителем единица и дробь 2/3.
Римляне тоже пользовались
одним знаменателем, равным 12.
В древнем Вавилоне предпочитали, наоборот, -постоянный знаменатель, равный 60.
Дроби в древней Руси
назывались долями, позднее «ломаными числами».
1/2 — полтина, 1/4 -четь, 1/8 – полчеть, 1/3 – треть, 1/6 – полтреть, 1/12 — полполтреть
Слайд 5
Действия с дробями в средние века считались самой сложной областью математики. До сих пор немцы говорят про человека, попавшего в затруднительное положение, что он «попал в дроби».
Слайд 6
Поставил царь перед своими подданными проблему:
найти интересные способы сложения обыкновенных дробей.
… И дал на раздумье только одну ночь.
Слайд 7
Первым вышел простак и предложил складывать дроби так:
Загудели дроби.
Как же так?
Слайд 8
Вторым вышел Тугодум. Он изобрёл оригинальный способ:
Восхитился царь!
2
3
Слайд 9
Слайд 10
Чем хорош этот способ?
Просто меняем знаменатели – способ легкий!
Чем плох?
Сокращать ответ приходится
Слайд 11
А Зануда прочитал в умной книге, что сначала нужно найти НОК знаменателей
8
4
2
1
2
2
2
6
3
1
2
3
НОК (8;6) = 2*2*2*3=24
Не по душе пришёлся подданным этот способ!
3
4
Слайд 12
Тогда Умник говорит:
8 и 6 делятся на 2.
8 : 2 = 4, 6 : 2 = 3.
Поменяем местами.
3
4
Вот увидите: этот способ в XXI веке будет самым удобным у шестиклассников!
Слайд 13
Слайд 14
А царь спросил у Умника:как сложить три дроби?
Задумались подданные…
Слайд 15
Но тут вышли три мудреца и предложили свой способ:
Делим больший знаменатель на два других
12:6=2, 12:8=неудача!
Тогда 12+12=24 и проверяем снова.
24:8=3, 24:6=4, 24:12=2
Слайд 16
Слайд 17
Если ты ленишься думать – пользуйся способом Тугодума (просто меняй знаменатели).
Если ты посообразительней – твой способ Умника.
Если ты – творец, то НОК дробей возникает у тебя в голове сразу.
Итак:
Слайд 18
Вот и сказочке конец, а кто слушал и понял – молодец!
Сложение и вычитание простых дробей с одинаковыми знаменателями
Описание
Программа формирует примеры на сложение и вычитание простых дробей с одинаковыми знаменателями.
Случайным образом генерируется десять примеров. Ответ каждого предыдущего примера является первым числом следующего, что позволяет сформировать цепочку взаимосвязанных примеров. Итоговый ответ, который печатается в правом нижнем углу страницы, позволяет проверить правильность решения всех примеров без проверки каждого из них.
Это дает возможность самостоятельно проверить правильность решения без возможности посмотреть ответ в процессе работы.
Правило сложения / вычитания простых дробей с одинаковыми знаменателями:
для того, чтобы сложить / вычесть две простые дроби с одинаковым знаменателем, необходимо сложить / вычесть числители этих дробей, а знаменатель оставить без изменений.
При необходимости проводится сокращение дроби. Если получившаяся дробь является неправильной (числитель больше знаменателя), дробь преобразуется в смешанную.
Программа написана в Excel с помощью макросов. Примеры генерируются случайным образом, количество генераций не ограничено. Для ознакомления с программой можно скачать образец примеров, которые получаются при использовании программы.
Для получения новой карточки примеров достаточно скачать, нажать на кнопку и распечатать.
Основные виды дробей, их основное свойство, а также все операции, которые можно выполнять с дробями: сокращение, приведение, сравнение, сложение, вычитание, умножение и деление описаны в статье «Математические дроби – просто о сложном».
Другие программы, которые помогут закрепить навыки счета с дробями:На сайте представлен каталог программ, в котором все программы распределены по группам с указанием различий в программах внутри каждой группы. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.
Презентация «Сложение и вычитание обыкновенных дробей»
Слайды и текст этой онлайн презентации
Слайд 1
Сложение и вычитание
обыкновенных дробей
5 класс
Слайд 2
Каждый может за версту Видеть дробную черту.
Над чертой – _________, знайте, Под чертою – __________. Дробь такую, непременно, Надо звать ____________.
числитель
знаменатель
обыкновенной
Слайд 3
Какая часть квадрата закрашена на рисунках?
Слайд 4
В году 365 дней. В феврале – 28 дней, а в декабре 31 день.
Какую часть года составляет февраль, а какую – декабрь?
Слайд 5
Воронёнок спит 9 часов в сутки, а учится 5 часов.
Какую часть суток он спит, а какую – учится?
Слайд 6
Расположите дроби в порядке возрастания с соответствием букв, и вы прочтете имя древнегреческого ученого – основателя библиотеки в городе Александрии, жившего в Древнем Египте
во II веке до н.э. Он впервые высказал предположение о том, что Земля имеет круглую форму.
13
24 21
24 6
24 3
24 8
24 23
24 22
24 19
24 4
24
О Ф А Э Т Н Е С Р
Эратосфен
Слайд 7
Расположите дроби в порядке убывания, и вы прочтете название самой маленькой страны в мире.
16:21 6:21 8:21 19:21 5:21 11:21 13:21
А А К В Н И Т
16
21 6
21 8
21 19
21 5
21 11
21 13
21
А А К В Н И Т
Ватикан
Слайд 8
В корзинку помещается 600 г земляники. Наташа набрала корзинки. Сколько граммов ягод набрала Наташа?
3
4
Слайд 9
450 г
Слайд 10
У пристани находится 10 двухместных лодок и 30 одноместных. Какую часть всех лодок составляют двухместные лодки?
Слайд 11
1 4
Слайд 12
Задания на карточкахСлайд 13
+
Фиалка наскальная
+ Стерис альпийский
— Родиола розовая
— Купальница открытая
+ Мак полярный
Вычислите и установите соответствие между названием и изображением редких цветковых растений, внесенных в Красную книгу НАО.
Слайд 14
Ответы
1-й вариант 2-й вариант
Слайд 15
Учебник,§33, Задачник №331,№ 334, №343, №347 (по желанию)
Домашнее задание:
Слайд 16
16
Ну вот и закончилось наше познавательное путешествие.
«Сложение и вычитание, деление и умножение обыкновенных дробей» (стр. 1 из 2)
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ КАЗАХСТАН
КОСТАНАЙСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ
Реферат
На тему: «Сложение и вычитание, деление и умножение обыкновенных дробей».
Костанай
2011 год
СОДЕРЖАНИЕ
1. Из истории обыкновенных дробей ………………………………………..3
2. Действия с обыкновенными дробями …………..…………………………..5
2.1. Сложение и вычитание обыкновенных дробей …………………………..5
2.2. Умножение и деление обыкновенных дробей ………………………….7
3. Примеры на сложение, вычитание, умножение и деление дробей ……. 10
4. Список литературы ……………………………………………………………11
1. Из истории возникновения обыкновенных дробей.
Дроби появились в глубокой древности. При разделе добычи, при измерениях величин, да и в других похожих случаях люди встретились с необходимостью ввести дроби.
Древние египтяне уже знали, как поделить 2 предмета на троих, для этого числа –2/3- у них был специальный значок. Между прочим, это была единственная дробь в обиходе египетских писцов, у которой в числителе не стояла единица – все остальные дроби непременно имели в числителе единицу (так называемые основные дроби): 1/2; 1/3; 1/28; … . Если египтянину нужно было использовать другие дроби, он представлял их в виде суммы основных дробей. Например, вместо 8/15 писали 1/3+1/5. Иногда это бывало удобно. В папирусе Ахмеса есть задача :
«Разделить 7 хлебов между 8 людьми». Если резать каждый хлеб на 8 частей, придётся провести 49 разрезов.
А по-египетски эта задача решалась так: Дробь 7/8 записывали в виде долей: 1/2+1/4+1/8. Значит каждому человеку надо дать полхлеба, четверть хлеба и восьмушку хлеба; поэтому четыре хлеба разрезали пополам, два хлеба- на 4 части и один хлеб на 8 долей, после чего каждому дали его часть.
Но складывать такие дроби было неудобно. Ведь в оба слагаемых могут входить одинаковые доли, и тогда при сложении появится дробь вида 2/n.
А таких дробей египтяне не допускали. Поэтому, папирус Ахмеса начинается с таблицы, в которой все дроби такого вида от 2/5 до 2/99 записаны в виде суммы долей. С помощью этой таблицы выполняли и деление чисел. Вот, например, как 5 делили на 21: 5/21
Умели египтяне также умножать и делить дроби. Но для умножения приходилось умножать доли на доли, а потом, быть может, снова использовать таблицу. Ещё сложнее обстояло с делением.
В древнем Вавилоне предпочитали наоборот, — постоянный знаменатель, равный 60-ти. Шестидесятеричными дробями, унаследованными от Вавилона, пользовались греческие и арабские математики и астрономы. Но было неудобно работать над натуральными числами, записанными по десятичной системе, и дробями, записанными по шестидесятеричной. А работать с обыкновенными дробями было уже совсем трудно. Поэтому голландский математик Симон Стевин предложил перейти к десятичным дробям.
Интересная система дробей была в Древнем Риме. Она основывалась на делении на 12 долей единицы веса, которая называлась асс.
Двенадцатую долю асса называли унцией. А путь, время и другие величины сравнивали с наглядной вещью- весом. Например, римлянин мог сказать, что он прошел семь унций пути или прочел пять унций книги. При этом, конечно, речь шла не о взвешивании пути или книги. Имелось в виду, что пройдено 7/12 пути или прочтено 5/12 книги. А для дробей, получающихся сокращением дробей со знаменателем 12 или раздроблением двенадцатых долей на более мелкие, были особые названия.
Даже сейчас иногда говорят:”Он скрупулёзно изучил этот вопрос.” Это значит, что вопрос изучендо конца, что не одной самой малой неясности не осталось. А происходит странное слово “скрупулёзно” от римского названия 1/288 асса — “скрупулус”. В ходу были и такие названия: ”семис”- половина асса, “секстанс”- шестая его доля, “семиунция”- половина унции, т.е. 1/24 асса и т.д. Всего применялось 18 различных названий дробей. Чтобы работать с дробями, надо было помнить для этих дробей таблицу сложения и таблицу умножения. Поэтому римские купцы твёрдо знали, что при сложении триенса (1/3 асса) и секстанса получается семис, а при умножении беса (2/3 асса) на сескунцию( 2/3 унции, т.
е.1/8 асса) получается унция. Для облегчения работы составлялись специальные таблицы, некоторые из которых дошли до нас.
Современную систему записи дробей с числителем и знаменателем создали в Индии. Только там писали знаменатель сверху, а числитель — снизу, и не писали дробной черты. А записывать дроби в точности, как сейчас, стали арабы.
Обыкновенная дробь – это число вида
, где m и n – натуральные числа, например . Число m называется числителем дроби, n – знаменателем. Среди обыкновенных дробей различают правильные и неправильные дроби. Дробь называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателя или равен ему.2. Действия с обыкновенными дробями.
2.1. Сложение и вычитание обыкновенных дробей.
Сложение обыкновенных дробей выполняется так:
а) если знаменатели дробей одинаковы, то к числителю первой дроби прибавляют числитель второй дроби и оставляют тот же знаменатель, т.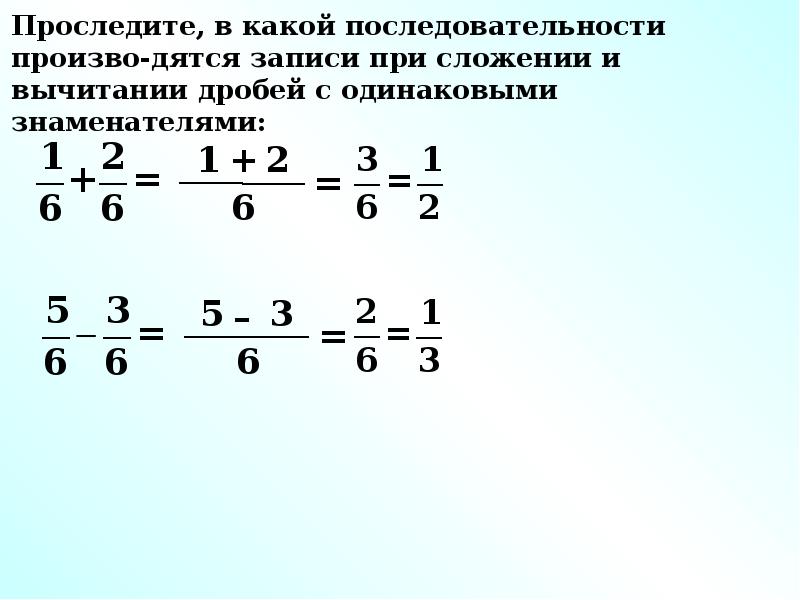
е.
б) если знаменатели дробей различны, то дроби сначала приводят к общему знаменателю, предпочтительнее к наименьшему, а затем к числителю первой дроби прибавляют числитель второй дроби, т.е.
.Вычитание обыкновенных дробей выполняют следующим образом:
а) если знаменатели дробей одинаковы, то от числителя первой дроби вычитают числитель второй дроби и оставляют тот же знаменатель, т.е.
.б) если знаменатели различны, то сначала дроби приводят к общему знаменателю, а затем от числителя первой дроби вычитают числитель второй дроби, т.е.
.Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то для того, чтобы сложить дроби, надо сложить их числители, а для того, чтобы вычесть дроби, надо вычесть их числители (в том же порядке). Полученная сумма или разность будет числителем результата; знаменатель останется тем же.
Например:
1.
2.
3.
4.
5.
6.
Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю.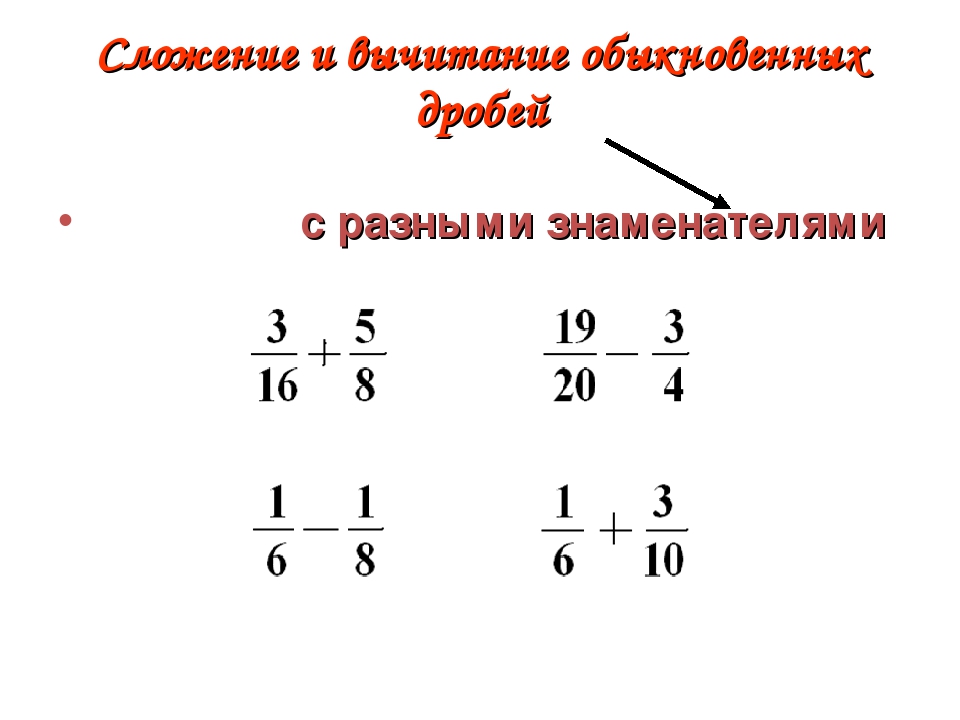
При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел мы рекомендуем сначала преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется, к виду смешанного числа.
Например:
1.
2.
3.
4.
5.
6.
7.
8.
2.2. Умножение и деление обыкновенных дробей.
Умножение обыкновенных дробей выполняется следующим образом:
,т.е. перемножаются отдельно числители, отдельно знаменатели, первое произведение делают числителем, второе – знаменателем.
При умножении дроби на натуральное число, числитель дроби умножают на это число, а знаменатель оставляют без изменения.
Если множители являются смешанными числами, то сначала их нужно записать в виде неправильных дробей, затем воспользоваться правилом умножения дробей.
Деление обыкновенных дробей выполняют следующим образом:
,т.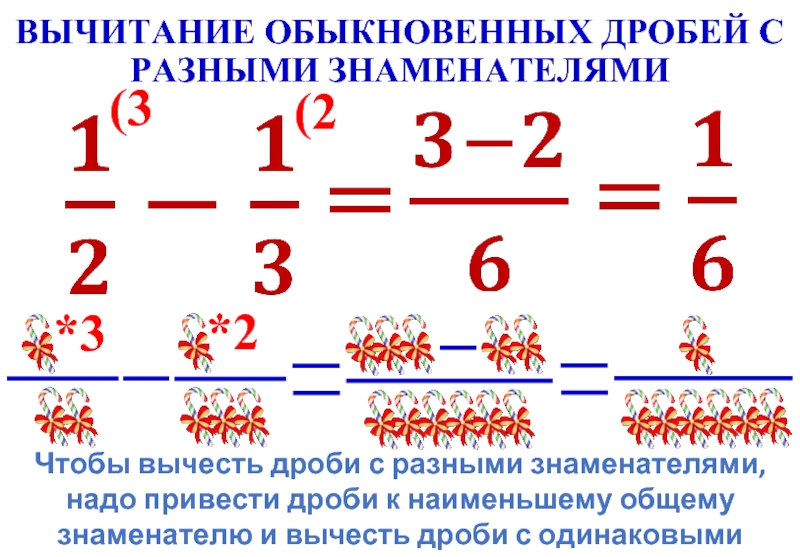
е. делимое
Умножение обыкновенной дроби на целое число.
Чтобы умножить дробь на целое число, достаточно числитель дроби умножить на это число, оставив прежний знаменатель.
Открытый урок на тему «Сложение и вычитание обыкновенных дробей»
Разработка урока математики
Дата проведения: 10.12.13
Учитель: Машканцева Елена Владимировна
Класс: 5
Тема урока: «Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями»
Кол-во часов: 1
Тип урока: комбинированный урок.
Цель урока: повторить, обобщить, систематизировать изученный материал; провести контроль приобретенных знаний.
Задачи урока:
Образовательные: повторить и обобщить изученный материал; закрепить правила сложения и вычитания обыкновенных дробей; контроль и оценка знаний, полученных в ходе изучения темы.
Развивающие: развитие логического и пространственного мышления обучающихся, памяти, навыки устного счета
Воспитательные: эстетическое воспитание, воспитание ответственности, умения работать в коллективе, самостоятельности.
Формы работы: индивидуальная, фронтальная.
Методы обучения: словесный, наглядный, практический.
Оборудование: мультимедийный проектор, раздаточный материал(карточки).
Учебно- методическое обеспечение: учебник «Математика,5 класс» И.И.Зубарева, А.Г.Мордкович.
Примечание к уроку: В разработке представлен заключительный урок по теме«Сложение и вычитание обыкновенных дробей».Урок такого плана подготовлен в системе, для достижения оптимального результата. Предлагаемая организация урока обеспечивает работу всех каналов восприятия: познавательной учебной деятельностью обеспечены и аудиалы, и визуалы, и кинестетики. Образовательная деятельность направлена на повышение результативности, производительности педагогического труда путем перевода обучающихся с позиции объекта деятельности учителя в позицию субъекта учения, содействует развитию потенциала каждого ребенка, раскрытию заложенных в нем возможностей. Таким образом, урок полностью отвечает требованиям деятельностного подхода в образовании.
Ход урока.
I. Организационно этап.
II. Мотивация учебной деятельности обучающихся, постановка цели и задач урока.
III. Актуализация знаний.
Устная работа.
Проводится с помощью презентации с заданиями. Работа направлена на повторение основных составляющих знаний по правилам работы с обыкновенными дробями (составление дробей и смешенных чисел по предлагаемым карточкам
Цель: развитие внимательности, устного счета и памяти у обучающихся.
1)Из истории дробей (слайды ).
2) Устная работа (слайды ).
IV. Работа над нестандартными заданиями (слайды )
V. Воспроизведение заданий на новом уровне (слайды ).
VI.
VII.
VIII.
IX. Итоги урока.
Учитель готовит бланк с таблицей выставления отметок каждому обучающемуся по 4 основным этапам урока (устная работа, работа со схемой, с/р).
X. Домашнее задание.
XI.Рефлексия.
Карточки для рефлексии.
Понравился ли тебе урок?
Что не понравилось на уроке?
Оцени свою деятельность на уроке.
Какой фрагмент урока был самым интересным?
Добавление дробей | Как сложить дроби + примеры
Сегодня мы рассмотрим несколько примеров сложения дробей .
Перед тем, как прочитать этот пост, вы можете проверить предыдущий пост, в котором мы объясняем, как добавлять дроби шаг за шагом.
Начнем с простейшего примера:
Сложение дробей с одинаковым знаменателемНапример:
Единственное, что нам нужно сделать, это сложить числители и оставить знаменатель в покое .Ответ: :
. Сложение чисел и дробиНапример:
Первое, что нам нужно сделать в этом случае, — это преобразовать 2 в дробь. Как вы уже знаете, мы можем просто поставить 1 в знаменателе любого числа, не меняя его значения:
Когда у нас есть две дроби, мы можем начать искать общий знаменатель .
В этом примере это довольно просто, потому что этим числом является наименьшее общее кратное 1 и любому числу.Итак:
Теперь нам нужно только умножить 2 на 4, и мы получим:
… и теперь мы добавляем его в нашу задачу сложения:
Сложение дробей с совпадающими простыми знаменателямиПомните, что два числа взаимно просты, если их наибольший общий делитель равен 1 . Например, в задаче:
Знаменатели взаимно простые, потому что:
Проблемы такого рода легко решить, потому что единственное, что нам нужно сделать, чтобы найти новые числители, — это умножить каждый числитель на знаменатель другой дроби, как показано ниже:
А мы просто умножаем знаменатели вместе.Итак, получаем:
и
И единственное, что осталось сделать, это сложить две дроби вместе:
Общее сложение дробейНапример:
Нам нужно вычислить наименьшее общее кратное знаменателей :
Что нам делать дальше? Давайте разберемся.
Во-первых, давайте посмотрим на дробь:
Чтобы найти числитель , нам нужно разделить НОК на знаменатель дроби:
Нам нужно умножить числитель дроби на 2.Итак:
И мы видим, что новый числитель — 6.
В качестве знаменателя нам просто нужно использовать GCM (18):
Теперь мы проделаем то же самое с другой дробью. Чтобы найти числитель, нам нужно разделить:
И умножаем на числитель:
Затем мы подставляем GCM в качестве знаменателя, что дает нам:
Теперь осталось сложить дроби вместе …
И все!
Фактически мы складываем все дроби таким образом, первые примеры были проще благодаря GCM, с которым было легче работать.Однако способ решения проблем всегда оставался прежним.
Подводя итог, шаги для сложения дробей :
- Найдите GCM двух знаменателей.
- Разделите GCM на знаменатель и умножьте это на числитель, чтобы преобразовать каждую дробь в дробь, в которой GCM является новым знаменателем.
- Когда мы выполнили два предыдущих шага со всеми дробями, расположите их по порядку и сложите их числители.
Если вы хотите продолжить изучение математики, зарегистрируйтесь сегодня в Smartick!
Удачи в добавлении дробей — немного попрактиковавшись, вы увидите, что это совсем несложно, и получите это в кратчайшие сроки!
Подробнее:
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
Сложение дробей с одинаковыми знаменателями |
Чтобы складывать или вычитать элементы, единицы должны быть одинаковыми. Например, посмотрите на добавляемые ниже элементы.
2 яблока + 3 яблока = 5 яблок
6 апельсинов + 3 апельсина = 9 апельсинов
2 четверти + 5 четвертей = 7 кварталов
2 никеля + 3 никеля = 5 никель
Мы не можем добавлять яблоки и апельсины, если не называем их «фруктами».
Точно так же мы не можем добавлять четвертинки и пятаки, если не называем их «центами». В названии дроби знаменателем является единица измерения. Например, в дроби «4 десятых» используется знаменатель: десятых . Следовательно, 4 десятых + 5 десятых = 9 десятых. Посмотрите на пример 1 ниже.
Пример 1: Пицца была разделена на восемь равных частей (ломтиков). Если Дженни съела пять ломтиков, а Эрик — два, то какую часть пиццы они съели вместе?
Анализ: Дженни съела «5 восьмых» пиццы, а Эрик съел «2 восьмых».В каждой из этих дробей используется знаменатель: восьмых . Поскольку обе дроби имеют одинаковые единицы, мы можем сложить их вместе.
Решение: «5 восьмых + 2 восьмых = 7 восьмых».
Знаменатель дроби обозначает то, что мы считаем. В примере 1 мы считаем восьмые. Это показано в числовой строке ниже.
Нарисовать числовую прямую не всегда удобно. Итак, нам нужна арифметическая процедура сложения дробей.
Задача из примера 1 записана с использованием математической записи, представленной ниже:
Знаменатель дроби указывает единицу измерения. Числитель показывает, сколько их. Например, в дроби пять восьмых единица восьмая, а их 5. Для сложения дробей знаменатели должны совпадать с . То есть они должны иметь общий знаменатель .
У этих дробей общий знаменатель (знаменатели совпадают).Если бы знаменатели не были общими, вы не смогли бы сложить эти дроби.
Это приводит нас к следующей процедуре сложения дробей с общим знаменателем.
Процедура: Чтобы сложить две или более дробей с одинаковыми знаменателями, сложите числители и поместите полученную сумму над общим знаменателем. При необходимости упростите результат.
Давайте рассмотрим несколько примеров сложения дробей с помощью этой процедуры.
|
|
В примере 3 нам нужно было упростить результат: мы сократили шесть девятых до наименьших членов, то есть двух третей.
|
В примере 4 мы упростили результат, преобразовав неправильную дробь в целое число.
Избегайте этой распространенной ошибки!
Некоторые студенты по ошибке складывают знаменатели и числители. Это математически неверно, как показано ниже.
|
Знаменатели не складывать!
Чтобы сложить дроби, складывайте только числители и ставьте сумму над общим знаменателем.
Пока что мы добавляли только две дроби за раз. Мы можем сложить более двух дробей, используя описанную выше процедуру. Это показано в примерах ниже.
|
|
Сводка:
Чтобы сложить две или более дробей с одинаковыми знаменателями, сложите числители и поместите полученную сумму над общим знаменателем. При необходимости упростите результат.
Упражнения
Указания: складывайте дроби в каждом упражнении ниже. Обязательно упростите ваш результат, если необходимо. Щелкните один раз в ОКНО ОТВЕТА и введите свой ответ; затем нажмите ENTER. После того, как вы нажмете ENTER, в БЛОКЕ РЕЗУЛЬТАТОВ появится сообщение, указывающее, правильный или неправильный ваш ответ. Чтобы начать заново, нажмите ОЧИСТИТЬ.
Примечание. Чтобы записать дробь в три четверти, введите в форму 3/4.
| 1. | |
2. | |
| 3. | |
| 4. | |
| 5. | |
Сложение дробей
Эта страница содержит ссылки на бесплатные математические рабочие листы для задач сложения дробей.
Нажмите одну из кнопок ниже, чтобы увидеть все рабочие листы в каждом наборе. Вы также можете использовать меню «Рабочие листы» сбоку на этой странице, чтобы найти рабочие листы по другим математическим темам.
Общий знаменатель, без целых частей
Общий знаменатель, смешанные ответы
Смешанные дроби с общим знаменателем
Половинки, четверти, восьмые
20 Рабочие листы сложения дробей
Эти рабочие листы дробей предоставляют практические навыки сложения общих дробей с половинками, четвертями и восьмыми.
Половинки, четверти, восьмыеРазличные знаменатели
24 Таблицы сложения дробей
Эти рабочие листы имеют практические проблемы для сложения дробей с разными знаменателями.
Разные знаменателиНеправильно с тем же знаменателем
Неправильно с другим знаменателем
Как сложить дроби
Шаги по сложению дробей могут быть очень простыми, если проблема настроена правильно.
Рабочие листы на этой странице содержат примеры задач, которые иллюстрируют возрастающие уровни сложности для развития навыков, необходимых для решения любых задач сложения дробей.
В простейших случаях у двух дробей уже будет общий знаменатель. В этом случае сложите числители, а затем уменьшите полученную дробь.
Если числитель ответа больше знаменателя, то ответ является неправильной дробью. Эту дробь следует превратить в правильную дробь, вычеркнув из числителя целые числа, пока числитель не станет меньше знаменателя.
При сложении дробей без общего знаменателя перед сложением числителей необходимо найти общий знаменатель. Найдите две эквивалентные дроби, определив наименьшее общее кратное двух знаменателей и используя его в качестве знаменателя для обеих дробей.
Эти шаги кажутся более сложными, чем кажется, но очень хороший способ визуализировать процесс сложения дробей — использовать калькулятор дробей по ссылке ниже.
Сложение и вычитание дробей | Промежуточная алгебра
Результаты обучения
- Найдите общий знаменатель двух или более дробей
- Используйте общий знаменатель для сложения или вычитания дробей
- Упростите дробь до наименьшего значения
Введение
Прежде чем мы начнем, вот несколько важных терминов, которые помогут вам понять концепции работы с дробями в этом разделе.
- произведение: результат умножения
- коэффициент : что-то перемножаемое — для [латекс] 3 \ cdot 2 = 6 [/ latex] оба [latex] 3 [/ latex] и [latex] 2 [/ latex] являются факторами [latex] 6 [ / латекс]
- числитель : верхняя часть дроби — числитель дроби [латекс] \ dfrac {2} {3} [/ latex] равен [latex] 2 [/ latex]
- знаменатель : нижняя часть дроби — знаменатель дроби [латекс] \ dfrac {2} {3} [/ латекс] равен [латекс] 3 [/ латекс]
Инструкции по математическим вопросам
Учебники по математике и учителя используют много разных слов, чтобы дать ученикам инструкции о том, что им делать с той или иной задачей.Например, в примере этого модуля вы можете увидеть такие инструкции, как «Найти» или «Упростить». Важно понимать, что означают эти слова, чтобы вы могли успешно решать задачи этого курса. Вот краткий список слов, которые могут помочь вам понять, как решать проблемы в этом модуле.
| Инструкция | Интерпретация |
|---|---|
| Найти | Выполните указанные математические операции, которые могут включать сложение, вычитание, умножение, деление. |
| Упростить | 1) Выполните указанные математические операции, включая сложение, вычитание, умножение, деление. 2) Напишите математическое утверждение в кратчайшие сроки, чтобы не было никаких других математических операций, которые можно было бы выполнить — часто встречается в задачах, связанных с дробями и порядком операций |
| Оценить | 1) Выполните указанные математические операции, включая сложение, вычитание, умножение, деление. 2) Заменить заданное значение переменной в выражении, а затем выполнить указанные математические операции |
| Уменьшить | Напишите математическое утверждение в наименьшем или наименьшем значении, чтобы не было других математических операций, которые можно было бы выполнить — часто встречается в задачах, связанных с дробями или делением. |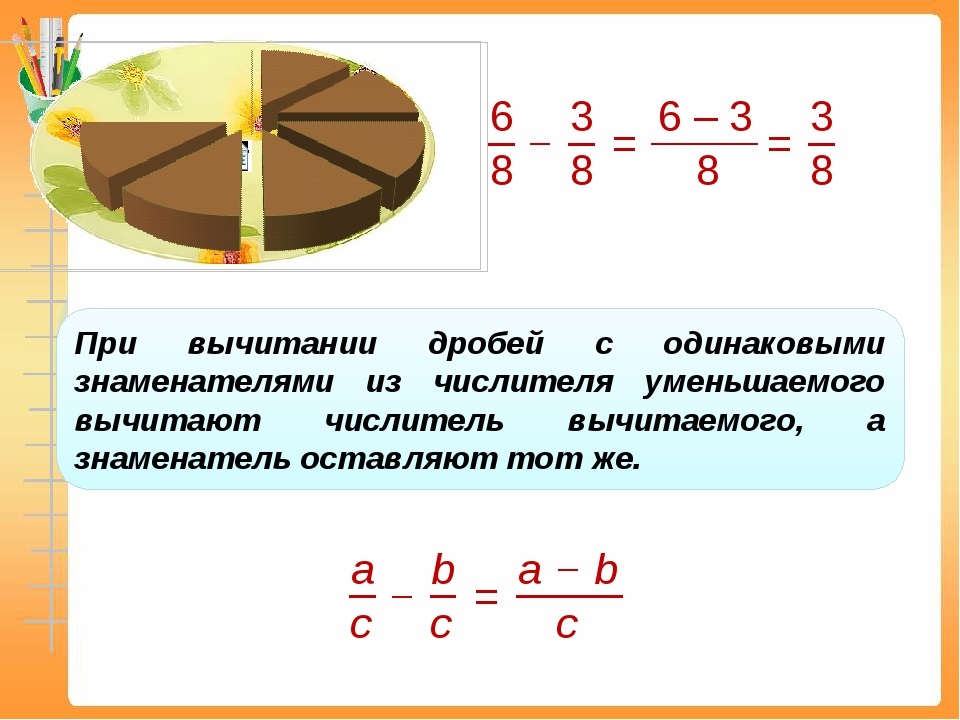
Сложение дробей
Когда вам нужно сложить или вычесть дроби, вам нужно сначала убедиться, что дроби имеют одинаковый знаменатель.Знаменатель сообщает вам, на сколько частей было разбито целое, а числитель говорит вам, сколько из этих частей вы используете.
Концепцию «частей целого» можно смоделировать с помощью пиццы и кусочков пиццы. Например, представьте, что пицца разрезана на [латекс] 4 [/ latex] куска, и кто-то берет [латекс] 1 [/ latex] кусок. Теперь [латекс] \ dfrac {1} {4} [/ latex] пиццы исчез, а [latex] \ dfrac {3} {4} [/ latex] остается.
Обратите внимание, что обе эти фракции имеют знаменатель [латекс] 4 [/ латекс], который относится к количеству ломтиков, на которые была нарезана вся пицца.Что делать, если у вас есть другая пицца, которая была разрезана на [латекс] 8 [/ latex] равных частей, а [латекс] 3 [/ latex] этих частей исчезли, оставив [латекс] \ dfrac {5} {8} [/ латекс]?
Как вы можете описать общее количество пиццы, которое осталось между двумя пиццами? Теперь есть две очень разные дроби, и их трудно сравнивать.
Вам понадобится общий знаменатель, технически называемый наименьшим общим кратным . Помните, что если одно число кратно другому, вы можете разделить их и не иметь остатка.
Один из способов найти наименьшее общее кратное двух или более чисел — сначала умножить каждое на [latex] 1, 2, 3, 4 [/ latex] и т. Д. Например, найти наименьшее общее кратное для [latex] 2 [/ латекс] и [латекс] 5 [/ латекс].
| Сначала перечислите все кратные [latex] 2 [/ latex]: | Затем перечислите все числа, кратные 5: |
| [латекс] 2 \ cdot 1 = 2 [/ латекс] | [латекс] 5 \ cdot 1 = 5 [/ латекс] |
| [латекс] 2 \ cdot 2 = 4 [/ латекс] | [латекс] 5 \ cdot 2 = 10 [/ латекс] |
| [латекс] 2 \ cdot 3 = 6 [/ латекс] | [латекс] 5 \ cdot 3 = 15 [/ латекс] |
| [латекс] 2 \ cdot 4 = 8 [/ латекс] | [латекс] 5 \ cdot 4 = 20 [/ латекс] |
| [латекс] 2 \ cdot 5 = 10 [/ латекс] | [латекс] 5 \ cdot 5 = 25 [/ латекс] |
Наименьшее кратное, которое у них есть общее, будет общим знаменателем для двух! В приведенном выше примере это [латекс] 10 [/ латекс].
Пример
Опишите количество пиццы, оставшееся в приведенных выше примерах, используя общие термины.
Показать решениеПерепишите дроби [latex] \ dfrac {3} {4} [/ latex] и [latex] \ dfrac {5} {8} [/ latex] как дроби с наименьшим общим знаменателем.
Найдите наименьшее общее кратное знаменателей. Это наименьший общий знаменатель.
Кратные [latex] 4: 4, \ textbf {8}, 12,16, \ textbf {24} [/ latex]
Кратное [latex] 8: \ textbf {8}, 16, \ textbf {24} [/ latex]
Наименьший общий знаменатель [латекс] 8 [/ латекс] — наименьшее общее кратное.
Перепишите [латекс] \ dfrac {3} {4} [/ latex] со знаменателем [латекс] 8 [/ latex]. Вам нужно умножить верхнюю и нижнюю части на [latex] 2 [/ latex], чтобы не изменить отношения между ними (потому что [latex] \ dfrac {2} {2} = 1 [/ latex]).
[латекс] \ dfrac {3} {4} \ cdot \ dfrac {2} {2} = \ dfrac {6} {8} [/ латекс]
Нам не нужно перезаписывать [latex] \ dfrac {5} {8} [/ latex], поскольку у него уже есть общий знаменатель.
Ответ
У [latex] \ dfrac {6} {8} [/ latex] и [latex] \ dfrac {5} {8} [/ latex] одинаковый знаменатель, и вы можете описать, сколько пиццы осталось, с помощью общих терминов. , и сравнивать значения будет проще.
Чтобы сложить дроби с разными знаменателями, вам нужно сначала переписать их с общими знаменателями. Тогда вы знаете, что делать! Шаги показаны ниже.
Сложение дробей с разными знаменателями
- Найдите общий знаменатель.
- Перепишем каждую дробь, используя общий знаменатель.
- Теперь, когда дроби имеют общий знаменатель, можно складывать числители.
- Упростите, отбросив все общие множители в числителе и знаменателе.
Упрощение дроби
Часто, если ответ на проблему дробный, вас просят написать его в кратчайшие сроки. Это обычное соглашение, используемое в математике, подобно тому, как предложение начинается с заглавной буквы и заканчивается точкой. В этом курсе мы не будем вдаваться в подробности о методах уменьшения фракций, потому что их много.
Процесс упрощения дроби часто называют уменьшением дроби . Мы можем упростить, отбросив (разделив) общие множители в числителе и знаменателе дроби.Мы можем это сделать, потому что дробь представляет собой деление.
Например, чтобы упростить [latex] \ dfrac {6} {9} [/ latex], вы можете переписать [latex] 6 [/ latex] и [latex] 9 [/ latex], используя наименьшие возможные коэффициенты:
[латекс] \ dfrac {6} {9} = \ dfrac {2 \ cdot3} {3 \ cdot3} [/ латекс]
Поскольку и в числителе, и в знаменателе есть [латекс] 3 [/ латекс], а дроби можно считать делением, мы можем разделить [латекс] 3 [/ латекс] в верхней части на [латекс] 3 [/ латекс] внизу, чтобы уменьшить до [латекс] 1 [/ латекс].
[латекс] \ dfrac {6} {9} = \ dfrac {2 \ cdot \ cancel {3}} {3 \ cdot \ cancel {3}} = \ dfrac {2} {3} \ cdot1 = \ dfrac { 2} {3} [/ латекс]
Переписывание дробей с наименьшими возможными множителями часто называется разложением на простые множители.
В следующем примере вам показано, как сложить две дроби с разными знаменателями, а затем упростить ответ.
Пример
Добавьте [латекс] \ dfrac {2} {3} + \ dfrac {1} {5} [/ latex]. Упростите ответ.
Показать решение Поскольку знаменатели не одинаковы, найдите общий знаменатель, умножив знаменатели.[латекс] 3 \ cdot5 = 15 [/ латекс]
Запишите каждую дробь со знаменателем [латекс] 15 [/ латекс], умножив его на [латекс] 1 [/ латекс].
[латекс] \ begin {array} {c} \ dfrac {2} {3} \ cdot \ dfrac {5} {5} = \ dfrac {10} {15} \\\\\ dfrac {1} {5 } \ cdot \ dfrac {3} {3} = \ dfrac {3} {15} \ end {array} [/ latex]
Сложите дроби, сложив числители и сохранив знаменатель прежним. Убедитесь, что дробь не может быть упрощена.
[латекс] \ dfrac {10} {15} + \ dfrac {3} {15} = \ dfrac {13} {15} [/ латекс]
Ответ
[латекс] \ dfrac {2} {3} + \ dfrac {1} {5} = \ dfrac {13} {15} [/ латекс]
Вы можете найти общий знаменатель, найдя общие кратные знаменателей.
Наименьшее общее кратное — самый простой в использовании.
Пример
Добавьте [латекс] \ dfrac {3} {7} + \ dfrac {2} {21} [/ latex]. Упростите ответ.
Показать решение Поскольку знаменатели не одинаковы, найдите наименьший общий знаменатель, найдя наименьшее общее кратное (НОК) 7 и 21.Кратное [латекс] 7: 7, 14, \ textbf {21} [/ latex]
Кратное [латекс] 21: \ textbf {21} [/ latex]
Запишите каждую дробь со знаменателем [латекс] 21 [/ латекс].
[латекс] \ begin {array} {c} \ dfrac {3} {7} \ cdot \ dfrac {3} {3} = \ dfrac {9} {21} \\\\\ dfrac {2} {21 } \ end {array} [/ latex]
Сложите дроби, сложив числители и сохранив знаменатель прежним.Убедитесь, что дробь не может быть упрощена.
[латекс] \ dfrac {9} {21} + \ dfrac {2} {21} = \ dfrac {11} {21} [/ латекс]
Ответ
[латекс] \ dfrac {3} {7} + \ dfrac {2} {21} = \ dfrac {11} {21} [/ латекс]
В следующем видео вы увидите пример того, как сложить две дроби с разными знаменателями.
Вы также можете сложить более двух дробей, если сначала найдете для них общий знаменатель. Пример суммы трех дробей показан ниже.В этом примере вы будете использовать метод простой факторизации, чтобы найти НОК.
Подумай об этом
Добавьте [латекс] \ dfrac {3} {4} + \ dfrac {1} {6} + \ dfrac {5} {8} [/ latex]. Упростите ответ и напишите смешанное число.
Чем этот пример отличается от предыдущих? Воспользуйтесь рамкой ниже, чтобы записать несколько мыслей о том, как сложить три дроби с разными знаменателями.
Показать решение Поскольку знаменатели не похожи, найдите наименьший общий знаменатель, найдя наименьшее общее кратное (НОК) [латекс] 4, 6 [/ латекс] и [латекс] 8 [/ латекс].[латекс] 4 = 2 \ cdot2 \\ 6 = 3 \ cdot2 \\ 8 = 2 \ cdot2 \ cdot2 \\\ текст {LCM}: \, \, 2 \ cdot2 \ cdot2 \ cdot3 = 24 [/ латекс]
Запишите каждую дробь со знаменателем [латекс] 24 [/ латекс].
[латекс] \ begin {array} {c} \ dfrac {3} {4} \ cdot \ dfrac {6} {6} = \ dfrac {18} {24} \\\\\ dfrac {1} {6 } \ cdot \ dfrac {4} {4} = \ dfrac {4} {24} \\\\\ dfrac {5} {8} \ cdot \ dfrac {3} {3} = \ dfrac {15} {24 } \ end {array} [/ latex]
Сложите дроби, сложив числители и сохранив знаменатель прежним.
[латекс] \ dfrac {18} {24} + \ dfrac {4} {24} + \ dfrac {15} {24} = \ dfrac {37} {24} [/ латекс]
Запишите неправильную дробь как смешанное число и упростите дробь.
[латекс] \ dfrac {37} {24} = \ normalsize 1 \, \, \ dfrac {13} {24} [/ latex]
Ответ
[латекс] \ dfrac {3} {4} + \ dfrac {1} {6} + \ dfrac {5} {8} = \ normalsize 1 \ dfrac {13} {24} [/ latex]
Вычитание дробей
Когда вы вычитаете дроби, вы должны подумать, есть ли у них общий знаменатель, как при сложении дробей. Ниже приведены несколько примеров вычитания дробей, знаменатели которых не совпадают.
Пример
Вычтите [латекс] \ dfrac {1} {5} — \ dfrac {1} {6} [/ latex].Упростите ответ.
Показать решениеУ дробей разные знаменатели, поэтому вам нужно найти общий знаменатель. Напомним, что общий знаменатель можно найти, умножив два знаменателя вместе.
[латекс] 5 \ cdot6 = 30 [/ латекс]
Записываем каждую дробь как эквивалентную дробь со знаминателем [латекс] 30 [/ латекс].
[латекс] \ begin {array} {c} \ dfrac {1} {5} \ cdot \ dfrac {6} {6} = \ dfrac {6} {30} \\\\\ dfrac {1} {6 } \ cdot \ dfrac {5} {5} = \ dfrac {5} {30} \ end {array} [/ latex]
Вычтите числители.При необходимости упростите ответ.
[латекс] \ dfrac {6} {30} — \ dfrac {5} {30} = \ dfrac {1} {30} [/ латекс]
Ответ
[латекс] \ dfrac {1} {5} — \ dfrac {1} {6} = \ dfrac {1} {30} [/ латекс]
Пример ниже показывает, как использовать кратные, чтобы найти наименьшее общее кратное, которое будет наименьшим общим знаменателем.
Пример
Вычтите [латекс] \ dfrac {5} {6} — \ dfrac {1} {4} [/ latex]. Упростите ответ.
Показать решение Найдите наименьшее общее кратное знаменателей — это наименьший общий знаменатель.Кратное [латекс] 6: 6, \ textbf {12}, 18, 24 [/ latex]
Кратные [latex] 4: 4, 8, \ textbf {12}, 16, 20 [/ latex]
[латекс] 12 [/ латекс] является наименее распространенным кратным [латекса] 6 [/ латекса] и [латекса] 4 [/ латекса].
Запишите каждую дробь со знаменателем [латекс] 12 [/ латекс].
[латекс] \ begin {array} {c} \ dfrac {5} {6} \ cdot \ dfrac {2} {2} = \ dfrac {10} {12} \\\\\ dfrac {1} {4 } \ cdot \ dfrac {3} {3} = \ dfrac {3} {12} \ end {array} [/ latex]
Вычтите дроби. При необходимости упростите ответ.
[латекс] \ dfrac {10} {12} — \ dfrac {3} {12} = \ dfrac {7} {12} [/ латекс]
Ответ
[латекс] \ dfrac {5} {6} — \ dfrac {1} {4} = \ dfrac {7} {12} [/ латекс]
В следующем видео вы увидите пример вычитания дробей с разными знаменателями.
Сложение дробей: все, что вам нужно знать
Джерри строит небольшой скворечник. Он просматривает планы и определяет длину деревянных блоков, которые ему понадобятся для завершения своего проекта.К сожалению, не все измерения были равны полному дюйму. Следовательно, Джерри нужно использовать дроби для перечисления необходимых ему измерений. Затем ему нужно добавить дроби, чтобы определить, сколько древесины нужно закупить.
Дроби используются для обозначения частей целого. Если у вас меньше целого пирога, вы можете использовать дроби, чтобы показать, сколько у вас действительно пирога. Некоторые дроби включают:
Когда Джерри готов сложить дроби, ему нужно кое-что знать, чтобы быть уверенным, что у него будет достаточно древесины.
Как складывать дроби с одинаковыми знаменателями
Сложить дроби довольно просто, если вы начинаете с одинаковых знаменателей. Знаменатель — это нижнее число, а числитель — это верхнее число. Допустим, у вас есть следующая проблема:
Поскольку знаменатели одинаковы (6), все, что вам нужно сделать, это сложить числители вместе:
Может быть, вы купили два пирога: вишневый и яблочный. После того, как несколько ваших гостей приготовили себе десерт, вы обнаружите, что у одного пирога осталось 2 ломтика из 6, которые вы нарезали, а у другого осталось 3 ломтика из 6.Сложив их вместе, вы узнаете, что у вас осталось 5 фрагментов, которыми вы можете поделиться с другими.
Упрощение дробей
После сложения дробей важно дать ответ в простейшей форме. Итак, нужно убедиться, что решение сведено к минимальным срокам. Например,
Прежде чем перейти к следующему уравнению, вам необходимо проверить свой ответ и убедиться, что его нельзя упростить. Для этого
- 1.Рассмотрим множители числителя и знаменателя.
- 2. Определите GCF (наибольший общий коэффициент). Это наибольшее число, которое делится на числитель и знаменатель.
- 6 — 1, 2, 3, 6
12 — 1, 2, 3, 4, 6, 12
Для приведенного выше примера GCF равен 6.
- 3. Если мы разделим числитель и знаменатель на это число, мы получим ½. Это самый низкий член из возможных для этого уравнения.
Важно убедиться, что дробь не может быть уменьшена ниже.Это особенно верно, если вы не можете найти GCF, поэтому вам следует продолжать делить верхнюю и нижнюю части на одно и то же число, пока вы не уменьшите дробь как можно больше.
Смешанные числа и неправильные дроби
Смешанное число — это число, которое содержит как дробную, так и целую дробь, например:
Сложить эти числа бывает сложно. Чтобы упростить процесс, сначала преобразуйте число в неправильную дробь. У неправильной дроби числитель больше знаменателя.По этой причине важно упростить дробь после нахождения решения, поскольку вы, вероятно, получите другое смешанное число. Посмотрите это уравнение:
В этом уравнении вы знаете, что 1 = 4/4. Следовательно, 2 = 8/4. Сложите дробь к преобразованному целому числу:
После нахождения решения пора упростить дробь. В этом случае окончательное решение — это просто целое число 3.
Сложение дробей с разными знаменателями
Знание основных принципов сложения дробей важно, но часто в уравнениях дроби имеют разные знаменатели.Когда это произойдет, что делать? Прежде чем складывать дроби, вам нужно иметь одинаковые знаменатели.
Один из самых простых способов найти общие знаменатели — это умножить первый знаменатель на второй и наоборот. При этом важно умножить числитель и знаменатель на одно и то же число, чтобы значение не изменилось. Если вы не знаете, что это значит, взгляните на этот пример:
Допустим, мы начинаем со следующего уравнения:
Поскольку дроби имеют разные знаменатели, первое, что нам нужно сделать, это преобразовать дроби, чтобы получить общие знаменатели.Для этого посмотрите на знаменатели и умножьте каждый на другой знаменатель. И умножьте числитель на то же число, что и знаменатель, чтобы значение не изменилось:
Как только у дробей будет одинаковый знаменатель, сложите числители:
Окончательное решение — неправильная дробь, поэтому вам нужно преобразовать его в смешанное число и упростить решение:
Разделив числитель и знаменатель на 2, вы можете упростить решение до:
Взгляните на следующие 5 практических примеров.Если вам нужно преобразовать знаменатели, убедитесь, что вы сначала выполнили этот шаг. Затем решайте и упрощайте!
Практические примеры
Практический пример 1 Решение
Поскольку дроби не имеют одинаковых знаменателей, первое, что нужно сделать, это преобразовать дроби. Самый простой способ сделать это — умножить дроби на противоположный знаменатель. Не забудьте умножить числитель и знаменатель на одно и то же число. Вы также можете заметить, что оба числа являются множителями 30, поэтому вы можете умножить их на соответствующий коэффициент, чтобы получить знаменатель 30 (6 x 5 и 10 x 3).
После того, как дроби будут иметь одинаковые знаменатели, сложите числители. Поскольку сумма является неправильной дробью, измените ее на смешанное число, прежде чем упрощать дробь.
Практический пример 2 Решение
В этой практической задаче вам нужно изменить дроби, чтобы знаменатели были одинаковыми. Конечно, вы можете умножить знаменатели друг на друга. Однако, поскольку 3 — это коэффициент 12, вы можете умножить только одну из дробей, чтобы получить аналогичные знаменатели, прежде чем решать уравнение и упрощать.
Так как сумма является неправильной дробью, вам нужно уменьшить уравнение до смешанного числа и упростить окончательную дробь.
Практический пример 3 Решение
Для практической задачи 3 уравнение имеет смешанные числа, поэтому начните с неправильной дроби. Поскольку 1 = 4/4, мы можем предположить, что 2 = 8/4. Добавьте это число в числитель (3). Затем пора убедиться, что в уравнении есть одинаковые знаменатели. Как и в предыдущем примере, 4 — это коэффициент 12.Следовательно, вы можете умножить числитель и знаменатель первой дроби на 3, чтобы преобразовать дробь.
Сумма является неправильной дробью. Тридцать восемь можно трижды разделить на 12 (12 × 3 = 36). Это дает вам остаток 2. Затем проверьте, является ли это самой простой формой.
Практический пример 4 Решение
Еще раз, вы можете начать решать уравнение, переводя дроби в одинаковые знаменатели. Умножьте каждую дробь на знаменатель другой дроби, чтобы получить новый знаменатель 56.
После преобразования дроби сложите числители и посмотрите, сможете ли вы упростить дробь.
Решение — неправильная дробь. Поэтому сначала превратите число в смешанное число. Затем упростите решение. Множители 56 включают 1, 2, 4, 7, 8, 14, 28 и 56. Множители 25 включают 1, 5 и 25. Поскольку у них нет общих множителей, окончательное решение будет:
Практический пример 5 Решение
Для последней практической задачи начните с преобразования смешанного числа в неправильную дробь.Для этого уравнения 1 = 8/8, поэтому 3 = 24/8.
Затем убедитесь, что у дробей одинаковые знаменатели. Каждую дробь можно умножить на знаменатель другой дроби. Затем сложите продукты.
Если решение представляет собой неправильную дробь, упростите его до смешанного числа:
Тогда упростите! Множители 51 включают 1, 3, 17, 51. Множители 72 включают 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72. Оба числа можно разделить на 3.Разделите числитель и знаменатель на 3 и получите:
.Так как 17 простое число, дробь максимально упрощена.
Как вы справились с практическими вопросами? Какие вопросы у вас есть по поводу сложения дробей? Расскажите нам в комментариях ниже.
Сложение, вычитание и эквивалентные дроби
Назначение
Цель этой серии уроков — развить понимание эквивалентных дробей и операций сложения и вычитания с дробями.
Конкретные результаты обучения
- Сложить и вычесть дроби с одинаковыми знаменателями.
- Найдите и запишите эквивалентные дроби для простых дробей в повседневном использовании.
- Учтите, что эквивалентные дроби занимают одно и то же место в числовой строке.
- Распознайте и примените мультипликативные отношения между простыми эквивалентными дробями.
- Поймите, что дроби могут иметь бесконечное количество имен.
- Поймите обратную природу умножения и деления и как эти знания можно использовать для упрощения дробей.
- Применяйте знания об эквивалентных дробях для решения задач, которые включают сравнение, сложение и вычитание дробей с разными знаменателями.
Описание математики
В этом разделе студенты учатся находить эквивалентные дроби и применять эквивалентность при сложении и вычитании дробей с разными знаменателями.Основная идея сложения и вычитания состоит в том, что объединяемые, разделяемые или сравниваемые единицы имеют одинаковый размер. В простой задаче сложения, такой как 6 + 7 = 13, предполагается, что 6, 7 и 13 относятся к одним и тем же единицам, таким как яблоки или сантиметры.
Сложение и вычитание дробей требует большей сложности, чем целые числа.
Например, 3/4 + 2/5 =? включает две фракции, состоящие из разных единиц. Три четверти относятся к трем единицам размером в одну четверть, а две пятых относятся к двум единицам, размер которых составляет одну пятую.Поскольку четверти и пятые — единицы разного размера, их нельзя добавить. Обратите внимание, что знаменатель указывает размер единиц, из которых состоит дробь.
Переименование дробей в единицы одинакового размера предполагает создание общего знаменателя. Общим знаменателем может быть любое общее кратное знаменателей добавляемых или вычитаемых дробей. Например, решить 4/5 — 2/3 =? общий знаменатель 3 и 5 может быть 15, 30, 45 и т. д. Для простоты обычно используется наименьшее общее кратное 15.Разделение пятых на три равные части дает пятнадцатые, поэтому 4/5 = 12/15. Разделение третей на пять равных частей дает пятнадцатые, поэтому 2/3 = 10/15. Обратите внимание, что переименование дроби в эквивалентной форме похоже на умножение на единицу в форме дроби. 4/5 x 3/3 = 12/15 и 2/3 x 5/5 = 10/15. 3/3 и 5/5 — имена для одного.
После того, как 4/5 и 2/3 переименованы в эквивалентные дроби с одинаковым знаменателем, единицы имеют одинаковый размер, и их можно разделить или сравнить. Итак, 4/5 — 2/3 = 12/15 — 10/15 = 2/15.
Возможности адаптации и дифференциации
Возможности обучения в этом модуле можно дифференцировать, предоставляя или прекращая поддержку учащимся, изменяя требования к заданиям. Способы поддержки студентов включают:
- продолжение работы над умножением и делением основных фактов посредством диагностики и практики упущенных фактов
- последовательное использование конкретных материалов, таких как бумажные полоски или листы, дробные полоски или круги, с упором на то, чтобы учащиеся предвидели результаты своих действий
- явное моделирование действий над материалами с соответствующим опросом о задействованных фракциях и размере единицы
- , связывая слова и материалы с символами, чтобы учащиеся могли соединить символы дроби с количеством
- использование множества ситуаций, к которым применяется сложение и вычитание.Ситуации включают объединение, разделение и сравнение количеств.
Задачи можно варьировать разными способами, в том числе:
- , начиная с дробей, которые возникают в результате симметричного разделения единицы, т. Е. Половин, четвертей, восьмых и т. Д., До использования более сложных разделов, таких как трети, пятые и седьмые
- работая сначала с задачами сложения и вычитания, где равное разделение единиц легко воспроизвести и визуализировать, например половинки, трети, четверти
- с использованием физических и схематических моделей до использования символов, а затем с использованием обоих вместе
- совместных групп, чтобы студенты могли поддерживать других.Требование объяснений и обоснований от групп студентов
- снижение спроса на продукт, например диаграммы, вначале меньше полагающиеся на написание уравнений, но постепенно переходящие к беглому владению уравнениями
- с использованием цифровых технологий, таких как виртуальные манипуляторы, для облегчения визуализации и принятия рисков.
Контексты этого раздела могут быть адаптированы к интересам и культурным особенностям ваших учащихся. Дроби возникают в результате равного распределения и измерения.Справедливая доля является общей чертой многих культур, особенно общин Пасфика, где усилия и вознаграждение принадлежат коллективу. Совместная еда — это универсальное культурное явление. В полинезийских культурах доли, предоставляемые семьям в результате коллективного сбора еды и материалов или охоты, часто основываются на количестве членов семьи, поэтому доли часто неравны. Контексты измерения повсеместны в современной жизни из-за использования метрических мер. Длина, площадь, масса, объем и вместимость возникают в повседневных условиях: от распределения воды до создания предметов из ткани и расчета нагрузок.Исторические меры, такие как размах рук, окружность головы и длина стопы, также обеспечивают контекст для использования дробей, что связано с необходимостью точности.
Необходимые ресурсные материалы
- Кубы Unifix
- Клейкая лента
- Колоды игральных карт
- Полосы из бумаги формата А3
- Перекидная доска сотен
- Копирайтеры один, два, три, четыре, пять и шесть.
Деятельность
Сессия 1SLO:
- Укрепите понимание того, где дроби помещаются на числовой прямой.
- Сложить и вычесть дроби с одинаковыми знаменателями.
- Начните это занятие с пропуска прямого и обратного счета с обычными дробями и смешанными числами.
Например: «одна четверть, две четверти, три четверти, одна, одна и одна четверть, одна и две четверти, одна и три четверти, две, две и одна четверть…»
Используйте набор полосок дробей (Copymaster One) чтобы построить модель числовой линии в процессе счета.
Почему 4/4 называется единицей?
Почему 6/4 называется 1 ½? - Спросите: «Как написать 1 четвертями?» (4/4).Как написать 2 (8/4), 3 (12/4) и 4 (16/4)?
Напишите в таблице класса / группы словами и символами:
Четыре четверти такие же, как одна: 4/4 = 1,
Восемь четвертей такие же, как две: 8/4 = 2 и т. Д.
Выделите знак равенства . Попросите учащихся обсудить значение знака = (то же самое, что сумма на одной стороне эквивалентна по значению сумме на другой стороне).
Запишите свои идеи.
Равно означает одинаковое количество. Итак, 8/4 и 2 — это два способа записать одно и то же число. - Задайте и запишите эту задачу в таблице класса / группы.«В доме Илии устраивается вечеринка с пиццей. Остались следующие кусочки пиццы: 1 1/8 вегетарианской, 3/4 любителя мяса, 1 5/8 пепперони, 1/2 гавайской, 1 1/4 маргариты и 7/8 морепродуктов. В целом, сколько пиццы осталось? »
Попросите учащихся работать в парах, чтобы найти решение. Раздайте студентам «Копимастер 2: кусочки пиццы», чтобы они могли использовать их при необходимости. Поделитесь стратегиями всем классом и запишите их на диаграмме класса. Поощряйте студентов мыслить гибко.
Легко ли сложить пары дробей? (е.грамм. 1 1/8 + 7/8). Почему?
Сколько всего осталось восьмых пиццы?
Учащиеся могут разделить общую сумму 6 ½ пиццы и преобразовать это количество в 52/8. В качестве альтернативы они могут изменить каждую дробь на восьмые и суммировать восьмые. - Выдайте каждой паре учащихся липкую ленту и две полоски бумаги длиной A3 (42 см).
Создайте свою собственную строку с дробным числом, начиная с нуля и заканчивая восьмеркой, где находится правый край.Свяжите обе полоски вместе, чтобы получилась хорошая длина.
Какой номер пойдет на хоин?
Где вы найдете 1? 7? 4 ½, 6 3/4?
Пожалуйста, покажите все половинки, четверти и восьмые от 0 до 8.
Проследите, чтобы ученики поместили все числа, включая дроби, на отметках, а не в пробелах. - После того, как учащиеся заполнят числовые строки, обратитесь к дробям в задаче о пицце, изложенной в части 3 выше.
Попросите учащихся начать с нуля и добавить 1 1/8 (оставшаяся вегетарианская пицца) в числовой строке.Они могут использовать колышек, чтобы отмечать общее количество пиццы каждый раз, когда добавляется каждая фракция.
Как мы можем определить, куда упадет ¾ больше, добавляя остатки мяса?
Три четверти больше, чем 1 1/8 равняется 1 7/8, тогда можно добавить 1 целую пиццу, чтобы получить 2 7/8 пиццы. Сначала можно добавить 1, а затем 7/8, и ответ будет таким же.
Используйте свою числовую строку, чтобы сложить доли остатков. Убедитесь, что наш исходный ответ правильный.
Прогуляйтесь по комнате, чтобы убедиться, что ученики правильно складывают дроби, переименовывая единицы, половинки, четверти и восьмые по мере необходимости, и распознавая, когда создается еще одна (целая). - Устно задавать другие проблемы, говоря очень медленно; например 2 1/2 + 3/4 + 3/4 + 1 3/4 + 3/4 = ☐
Попросите учащихся решить задачу, представив числовую прямую. Попросите учащихся поделиться своим результатом с партнером. Убедитесь, что записанные дроби видны учащимся.
Повторите то же самое с другими примерами, включающими половинки, четверти и восьмые. При необходимости используйте кусочки пиццы для подтверждения суммы. - Дайте каждой группе еще две полоски и кусок липкой ленты.Задайте следующую задачу:
Создайте новую числовую линию, начинающуюся с нуля и заканчивающуюся восьмеркой. Соедините полоски, как в прошлый раз.
На этот раз ваша числовая строка должна показывать половинки, трети и шестые.
Как вы разделите каждую единицу на трети?
Как разделить трети на шестые? - Бродить по комнате, пока студенты работают.
Правильно ли они размещают целые числа?
Сделана ли третья часть из единицы на три равные части?
Знают ли учащиеся, что половина одной трети равна одной шестой? - Соберите класс, обсудите и наметьте основные выводы, извлеченные из этого занятия.Сосредоточьте внимание студентов на необходимости использования общего знаменателя при объединении дробей (сложение) и на том, что одно и то же количество может быть представлено разными дробями.
Вы можете выровнять первую и вторую числовые линии.
Используя числовые линии, сколько имен для 1 ½ мы можем найти?
1 2/4, 6/4, 1 4/8, 12/8, 1 3/6, 9/6.
Что будет, если мы добавим 3/4 и 5/6? Каков был бы ответ?
Студенты должны понимать, что ответ 19/12 не может быть выражен точным числом четвертей или шестых.Вы можете использовать дробные полоски, чтобы показать, что для выражения ответа необходимы двенадцатые доли.
SLO:
- Помните, что знаменатели должны быть одинаковыми, чтобы складывать или вычитать дроби.
- Поймите значение эквивалента.
- Найдите и запишите эквивалентные дроби для простых дробей в повседневном использовании.
- Сложите и вычтите простые дроби с разными знаменателями.
- Начните занятие с постановки задачи на вычитание, в которой знаменатели совпадают.
Например: у строителя есть бревна длиной 3 1/4 метра. Отрезает 1 3/4 метра. Какая длина дров осталась?
Предложите учащимся вычислить ответ, а затем сверить свои ответы с полосками с дробями (Copymaster One). Физическое действие — это удаление. Убрать 1 1/4 просто, но нужно разбить единицу одного метра, чтобы удалить другие 2/4. Остается 1 2/4 или 1 1/2.
Просмотрите стратегии из занятия 1. Как и в случае с сложением, для вычитания дробей необходимы единицы с одинаковым знаменателем. - Поставьте задачу, в которой знаменатели нелегко связать.
Например: Строитель имеет бревна длиной 4 3/4 метра. Отрезает 2 1/3 метра. Какая длина дров осталась?
Попросите учащихся работать в парах, чтобы попытаться решить задачу. Поощряйте доступ к их предыдущим числовым линиям и дробным полосам. - Поддержите учащихся, использующих модель полосы и вопросы о строительных лесах, например:
Как вы можете найти оставшуюся длину? (Либо прибавьте к 2 1/3, пока не получите 4, либо удалите 2 1/3 из 4).
Оцените оставшуюся длину. (2 метра и доля метра)
Какая дробь равна с отведенной 1/3? Куски какого размера подойдут? (Двенадцатые) - После подходящего времени соберите класс для обсуждения стратегии. Смоделируйте проблему с помощью дробных полосок, чтобы символы могли быть связаны с величинами.
Запишите проблему, используя пустую числовую строку, чтобы зафиксировать удаление деталей.
В чем проблема с 3/4 — 1/3 ? (Разные знаменатели означают части разного размера)
Можно ли переименовать 3/4 и 1/3, используя другой знаменатель? Какой знаменатель?
Студенты, возможно, уже обнаружили, что двенадцатая часть соответствует промежутку между 2 и ответом на числовой прямой.
Сколько двенадцатых равно 3/4? Сколько двенадцатых равняется 1/3? (Выровняйте части фракционной полосы, если необходимо, чтобы убедиться, что 3/4 = 9/12 и 1/3 = 4/12) - Используйте уравнения для моделирования проблемы:
4 3/4 — 1 1/3 = 4 9/12 — 2 4/12
= 2 5/12 (сначала вычитая единицы, затем двенадцатые)
Зачем нам нужен общий знаменатель из двенадцати, чтобы решить эту проблему? ( Сложение и вычитание возможно только при одинаковых единицах измерения.) - Напишите в таблице класса / группы: «Что означает , эквивалентная дробь ?»
Жизненно важно, чтобы учащиеся осознавали, что эквивалентные средства равной ценности, то есть различные выражения одной и той же величины.½ и 5/10 эквивалентны, потому что они представляют одну и ту же сумму и занимают одно и то же место на числовой прямой между нулем и единицей. - Запишите ответы учащихся, включая примеры, которые они приводят, например, 1/2 = 2/4
Обратитесь к записи таблицы класса / группы из Сессии 1:
4/4 = 1, 8/4 = 2, 12/4 = 3, 16/4 = 4 и выделенный знак = .
Согласны ли учащиеся с тем, что равенство означает «такое же, как» или «что сумма на одной стороне равна сумме на другой стороне»? - Раздайте учащимся бумажные полоски одинаковой длины, вырезанные из фотокопировальной бумаги.
Используйте продольную складку, чтобы проиллюстрировать, как можно найти эквивалентные дроби.
Вот пример 2/3 = 4/6 = 8/12 =…
- Запишите уравнения эквивалентности, например 2/3 = 4/6 = 8/12.
Что будет дальше в уравнении? Откуда вы знаете? (= 16/24 = 32/48…)
Какие закономерности вы замечаете в числах?
Ученики должны заметить, что числитель и знаменатель удваиваются.
Почему это произошло ? (С каждой половинной складкой количество частей, составляющих единицу (знаменатель), удваивается, так что количество закрашенных частей удваивается) - Приведите два других примера складывания, например:
Начните с 3/4 и несколько раз делите пополам, чтобы получить 3/4 = 6/8 = 12/16
Начните с 1/2 и несколько раз подряд получите 1/2 = 3/6 = 9/18 - Предоставьте своим ученикам дробные полоски (второй копии) и кусочки пиццы (второй копии).
Найдите как можно больше эквивалентных фракций, используя эти материалы. Запишите дроби, используя уравнения и диаграммы. Создайте плакат своей работы, объясняющий, как работают эквивалентные дроби.
Дайте студентам достаточно времени для изучения. Бродите по комнате и ищите:
Уверены ли учащиеся в значении числителя как счета и знаменателя как размера подсчитываемых фигур?
Ожидают ли учащиеся взаимоотношений между предметами разного размера?
Ожидают ли учащиеся эффекта деления пополам и трети частей родительской фракции?
Правильно ли учащиеся записывают эквивалентность, используя уравнения? - По прошествии подходящего времени соберите класс, чтобы поделиться плакатами.Ищите закономерности в уравнениях, особенно умножение и деление числителей и знаменателей на один и тот же коэффициент.
Например:- Эти дроби эквивалентны
- Они одинаковой длины
- Дроби имеют одинаковое значение
SLO:
- Учтите, что эквивалентные дроби занимают одно и то же место в числовой строке.
- Распознайте и примените мультипликативные отношения между простыми эквивалентными дробями.
- Предложите учащимся еще раз просмотреть плакаты с эквивалентными дробями. Вместе запишите в таблице класса / группы, что ученики замечают об эквивалентных дробях, выделяя эти эквивалентные дроби:
- имеют такое же значение
- имеют одинаковую длину
- имеют разные числители и знаменатели.
- Дайте каждой паре учеников по две полоски бумаги, вырезанные по длине из бумаги формата А3.
Вот несколько эквивалентных дробей, которые я нашел:
2/3 = 4/6 = 8/12
Я хочу отметить каждую дробь числовой строкой. - Начните с использования единицы длины из дробной полосы, установленной для отметки нуля и единицы соответственно на левом и правом концах.
Как мне найти место для отметки двух третей? (Две копии одной трети с нуля)
Как мне найти место, чтобы отметить четыре шестых? (Четыре копии одной шестой с нуля)
Как мне найти место, чтобы отметить восемь двенадцатых? (Восемь копий, одна двенадцатая от нуля)
Какие другие дроби будут эквивалентны двум третям? - Попросите своих учеников создать числовую линию, показывающую некоторые из эквивалентных дробей, которые они определили.По прошествии подходящего времени соберите полоски и разложите их вертикально на стене или доске.
Посмотрите на вертикальное выравнивание, чтобы проверить правильность расстановки дробей и эквивалентности. - Мы использовали длины. Интересно, работает ли эквивалентность и с областями.
Раздайте каждому учащемуся три чистых листа бумаги формата А4 и попросите их сложить их таким образом.
Вам нужно будет подумать, как была сложена бумага.
Не забудьте пометить каждый кусок правильной дробью.
- Собери класс.
Используйте листочки бумаги, чтобы показать партнеру, что:- Три четверти эквивалентны шести восьмым (3/4 = 6/8).
- Две трети эквивалентны восьми двенадцатым (2/3 = 8/12).
- Пять шестых равны двадцатью двадцать четвертым (5/6 = 20/24).
- Дайте студентам достаточно времени, чтобы репетировать свои демонстрации эквивалентности.Обратите внимание на признаки того, что ученики замечают взаимосвязь между дробями единиц, например, двадцать четвертые — это четверти шестых.
- Поделитесь результатами всем классом, наклеив соответствующие листы бумаги на доску, чтобы проверить соответствие площади. Вы можете попробовать менее очевидные примеры, когда умножение числителя и знаменателя на целочисленный коэффициент не работает. Хорошие примеры счетчиков:
Сколько шестых равняется трем четвертям ? (3/4 = 9/12 и 1/6 = 2/12. В трех четвертях 4 ½ шестых)
Сколько восьмых эквивалентно одной трети? (1/3 = 8/24 и 1/8 = 3/24.В одной трети 2 2/3 восьмых) - Прибавить к очкам с начала деятельности:
Эквивалентные дроби:- имеют такое же значение
- имеют одинаковую длину или площадь
- имеют разные числители и знаменатели
- занимают то же место в числовой строке.
- Напишите в таблице класса / группы: 1/2 = 2/4 = 4/8
Спросите учащихся, что они замечают, что происходит с числителем (он удваивается каждый раз) и что происходит со знаменателем (он удваивается каждый раз). время).
Спросите студентов, как это можно показать. Примите их предложения, придя к пониманию, что это можно показать таким образом.
- Вместе признать, что значение 2/2 равно 1 и что когда любое целое число умножается на 1, произведение равно этому числу. Мы можем умножить дробь на 2/2, 3/3, 4/4 и т. Д., Чтобы найти эквивалентные дроби без изменения значения представленной суммы.
- Попросите учеников сыграть Fractions Fish , которые можно сделать из «Копимастера 3».
Цель: распознать мультипликативную взаимосвязь между эквивалентными дробями)
Эта игра предназначена для двух или трех игроков, и правила включены в Copymaster.
SLO:
- Поймите, что дроби могут иметь бесконечное количество имен.
- Поймите обратную природу умножения и деления и как эти знания можно использовать для упрощения дробей.
- Используйте умножение и деление для вычисления эквивалентных дробей.
- Начните это занятие с совместного чтения заключительного утверждения, сделанного на занятии 3.
Обратитесь к этому выражению и попросите учащихся предложить, как продолжается паттерн эквивалентных дробей.
Как долго может продолжаться эта модель получения дробей, эквивалентных половине? - Попросите учащихся обсудить это в парах и согласовать свой ответ. «Навсегда. Мы можем продолжать идти дальше ».
- Задайте вопрос: Какая из этих дробей будет в списке эквивалентна половине?
Откуда ты знаешь? (обратите внимание, что некоторые дроби равны 1/2, но не встречаются в двойном списке)
50/100 64/128 36/72 256/512 22/44
Общее свойство всех дробей, эквивалентных 1/2, состоит в том, что знаменатель — удвоенный числитель. - Обсудите и сделайте вывод, что существует бесконечное количество имен для любой дроби. Вы можете попробовать другие дроби, такие как 2/3 и 3/5, чтобы увидеть, не закончились ли у вас возможные эквивалентные дроби. Например: 2/3 x 3/3 = 6/9 = 18/27 = 54/81 =…
- Напишите 9/12.
Есть ли более простой способ записать эту дробь?
Предложите учащимся исследовать вопрос в парах и записать свои идеи.
Идеи могут быть:- Мы пошли «назад» (несколько раз разделили числитель и знаменатель на 2).
- Мы знаем, что 3/12 — это то же самое, что ¼.
- Мы знаем, что 9 — это три четверти от 12.
- Создайте изображение задачи в виде полосы с дробями:
Если мы посмотрим на числители и знаменатели дробей, можем ли мы узнать простейшую дробь без использования полос?
Запишите равенство как:
9/12 = 3/4
Мы знаем, что мы можем превратить три четверти в девять двенадцатых, умножив на единицу. Мы используем 3/3 как имя для одного.
Что отменит умножение числителя и знаменателя на три?
Студенты могут понять, что 9 ÷ 3 = 3 и 12 ÷ 3 = 4, что дает числитель и знаменатель 3/4. - Приведите еще несколько примеров упрощения дробей путем определения общего множителя. При необходимости используйте дробные полоски для моделирования каждой проблемы. Обратите внимание, что учащимся нужно будет считать двадцатые как половину десятых, а двадцать четвертых — как половину двенадцатых.
Например:
8/12 (2/3) 6/10 (3/5) 15/20 (3/4) 9/24 (3/8) - Обобщите выводы о том, как упростить дроби:
- Чтобы упростить дробь, вы можете разделить числитель и знаменатель на одно и то же целое число.
- Умножение и деление — обратные операции, одно отменяет другое.
- Попросите учащихся сыграть в парах Simplify Secrets .
Цель: Упростить дроби и определить, какие дроби можно упростить.
Пары учащихся разделяют колоду перетасованных игральных карт с картинками и удаленными джокерами. Каждому из них понадобится карандаш и лист бумаги.
Игроки по очереди переворачивают две карты. Первая карточка — числитель, а вторая — знаменатель.Игрок записывает свою долю. Рядом с дробью они пишут более простую эквивалентную дробь, если могут, показывая, на что они разделили числитель и знаменатель. Если их партнер соглашается, они отмечают свою запись.
Фракции, для которых они не могут найти более простую дробь, записываются, и ничего больше не добавляется.
Например:
Если игрок вытягивает 6, а затем 8, он пишет 6/8 = ¾, оправдывает коэффициент деления, и как только его партнер соглашается, он может добавить галочку ✔.
Если игрок вытягивает 7, а затем 9, он пишет 7/9, но галочка не ставится.
Если дробь является неправильной дробью, которая заменяется смешанным числом без упрощения, галочка не ставится, поскольку это не упрощает дробь. Например: 7/2 = 3 ½ не заработать тик, бит 9/3 = 3/1 заработать тик.
Ученики играют и записывают 10 раундов (минимум). Затем им следует внимательно изучить дроби, которые они смогли упростить (✔), и те, которые им не удалось.
Они должны обсудить, согласиться и написать «Секрет упрощения дробей…» - Соберите класс после игры, чтобы сделать вывод о том, что дробь можно упростить, если и числитель, и знаменатель имеют общий множитель.
- Для практики в нахождении эквивалентных дробей попросите учащихся самостоятельно заполнить MM8-9 часть 1, Эквивалентные дроби: уравнение и объяснение.
- Кратко опишите в таблице класса / группы то, что было изучено на этом занятии.
Например:- У дроби может быть бесконечное количество имен, если мы продолжаем умножать числитель и знаменатель на одно и то же число.
- Некоторые дроби можно упростить, разделив числитель и знаменатель на одно и то же число.
SLO:
- Найдите общее кратное и используйте его для получения эквивалентных дробей.
- Применяйте знания об эквивалентных дробях для решения задач, которые включают сравнение, сложение и вычитание дробей с разными знаменателями.
- Для начала задайте вопрос:
Когда будет полезно узнать об эквивалентных дробях ?
Запишите предложения студентов и попросите их привести примеры.Они могут предложить следующие проблемы:- Если мы сравниваем разные виды дробей, чтобы увидеть, какая дробь больше. Например, у вас может быть 3/4 метра ткани, а вам нужно 2/3 метра. Вам будет достаточно?
- Если мы складываем разные дроби. Допустим, у вас было 3/4 пиццы и еще 1/3 пиццы. Из этого получится 1 целая пицца?
- Если у вас есть сумма, и вы отдали ее дробь, и вы хотите вычислить, что у вас осталось. Как будто у вас есть 5/8 чего-то, а вы раздали 1/4.
- Предложите учащимся решить эти две задачи в парах перед тем, как поделиться с классом.
- У вас две работы. Стрижка газона занимает 3/4 часа. Мойка и полировка машины занимает 2/3 часа.
Сколько времени в часах требуется для выполнения обеих работ?
(3/4 + 2/3 = 9/12 + 8/12 = 17/12 = 1 5/12) - В бутылке осталось 1 4/5 литра сока. Вы наливаете из бутылки 3/4 литра.
Сколько сока осталось в бутылке?
(1 4/5 — 3/4 = 9/5 — 3/4 = 1 16/20 — 15/20 = 1 1/20)
- У вас две работы. Стрижка газона занимает 3/4 часа. Мойка и полировка машины занимает 2/3 часа.
- Смоделируйте каждую задачу с помощью дробных полос. Обсудить:
Почему для решения обеих проблем необходимо найти общий знаменатель?
Какие общие знаменатели вы использовали? Почему вы выбрали именно эти числа?
Когда вы использовали эквивалентные дроби для решения задач? - Задайте вопрос:
Как лучше всего найти общий знаменатель?
В качестве примера возьмем 2/3 + 4/5.
Из предыдущей работы студенты могли знать, что трети и пятые могут быть поровну разделены на пятнадцатые.
На сколько равных частей разбита каждая треть, чтобы образовались пятнадцатые? (пять)
Возможно, вам потребуется продемонстрировать разбиение с помощью дробных полос. Учащимся необходимо понять, что размер частей зависит от того, сколько из этих частей составляют одно (целое).
Сколько пятнадцатых эквивалентно двум третям? (напишите 2/3 = 10/15) - Задайте те же вопросы для четырех пятых (пятые делятся на три равные части, чтобы получить пятнадцатые, поэтому 4/5 = 12/15)
- Суммируем:
Мы ищем наименьшее общее кратное 3 и 5 (НОК), поэтому обе дроби могут иметь одинаковый знаменатель. - Раздайте ученикам Копимастер Четыре, представляющий собой лист из сотен досок. Покажите, как можно найти общие числа, кратные 3 и 5. Студенты могут скопировать вас на своей странице.
Оттенять кратные трем одним цветом; 3, 6, 9,…
Закрасьте числа, кратные пяти, другим цветом; 5, 10, 15,…
Продолжайте, пока не будут найдены все кратные.
Как узнать, какие числа являются общим кратным 3 и 5? (двойной цвет)
Какое наименьшее общее кратное 3 и 5? (15)
Пусть студенты поработают над этими задачами, используя Copymaster Four в качестве поддержки.- Найти общее кратное 2 и 3?
- Найти общее кратное 2 и 5?
- Найти общее кратное 5 и 6?
- Найти общее кратное 4 и 6?
- Найти общее кратное 7 и 13?
- Обсудите результаты. Обратите внимание на:
Почему в правом столбце указаны общие кратные 2 и 5?
Почему 12 НОК 4 и 6, когда 4 x 6 = 24?
Почему у 7 и 13 только одно общее кратное меньше 100? - Когда мы решаем задачу типа 1/3 + ½ = □, какой общий знаменатель мы можем использовать? Почему?
Обратите внимание, что подойдет любое общее кратное, но использовать LCM проще всего.
Запишите мышление, используя следующую таблицу:
- Используйте тот же формат, чтобы найти общий знаменатель для задач из раздела 2.
3/4 + 2/3 =
1 4/5 — 3/4 - Попросите своих учеников больше поработать с обыкновенными кратными (Copymaster Five). Некоторым студентам потребуется поддержка, чтобы понять, что от них требуется. При необходимости смоделируйте решение первой проблемы, а затем предложите учащимся работать самостоятельно.
- Бродите по комнате и ищите:
Ищут ли ваши ученики закономерность в появлении кратных чисел?
Например, общие кратные 3 и 8 встречаются в каждой восьмой ячейке в столбце и строке 3 и в каждой третьей ячейке в столбце и строке 8.
Могут ли они идентифицировать LCM в каждой проблеме? - Попросите учащихся сыграть в игру, Я могу это сделать, в парах . (Копимастер Шесть).
Цель: Применить знание эквивалентных дробей для решения задач.
Это игра для двух игроков. Карты историй и фракций перемешиваются и складываются лицевой стороной вниз в две стопки. Каждый игрок берет две карты историй и 6 карт фракций и кладет их перед собой лицевой стороной вверх.
Игроки по очереди:- Проверьте, позволяет ли одна из их карточек дроби ответить на одну из проблем, а другую — на карточку проблемы.Если это так, игрок сопоставляет две карты и складывает две карты в пару. Второй игрок проверяет совпадение.
- Могут ли они составить пару или нет, игрок добавляет дополнительную дробь и проблемную карту из двух стопок, или они предлагают обмен одной карты каждого типа с другим игроком.
Побеждает игрок, у которого больше всего пар.
Примечание: останется 7 дробных карт, потому что некоторые из них являются «трюковыми».
- Попросите каждого ученика написать по крайней мере три задачи на сложение или вычитание дробей, которые должен решить партнер.У каждой проблемы должен быть типовой ответ. Составьте классную книгу задач на сложение и вычитание.
Дополнительная работа:
Ученики могут работать над некоторыми Дробностями e-ako, чтобы закрепить изучение концепций, разработанных на этих уроках. Эти e-ako находятся на правом конце полки уровня 3 на путях аддитивного и мультипликативного мышления.
Учащиеся работают самостоятельно, чтобы заполнить MM8-9 — часть 2, объяснение какой дроби больше.Попросите их объединиться в пары, поделиться и обсудить.
Учащиеся смотрят следующие видеоролики, чтобы узнать, как можно использовать модель кубов unifix для сложения и вычитания дробей:
Домашняя ссылка
Уважаемые родители и ванау,
В математике мы изучаем эквивалентные дроби. Мы научились играть в игру под названием Fraction Fish, в которой мы находим эквивалентные дроби. Ваш ребенок принес домой пластиковый пакет с игральными картами и инструкциями.Они объяснят, как в это играют.
Наслаждайтесь вызовом.
Помощь при сложении / вычитании дробей
Сложение или вычитание дробей — другой знаменательУбедитесь, что ваш ребенок понимает эквивалентные дроби, прежде чем приступать к сложению или вычитанию дробей.
Необходимо найти общий знаменатель при сложении или вычитании дробей с разными знаменателями. Это самый важный (и, вероятно, самый сложный) шаг в сложении или вычитании дробей.Общий знаменатель всегда можно найти, умножив знаменатели.
Если у двух дробей одинаковый знаменатель, числители можно складывать или вычитать, при этом знаменатель остается таким же, как показано в первом примере выше.
Урок по дробям: сложение и вычитание дробейВ этом коротком уроке шаг за шагом показано, как складывать и вычитать дроби.
Вышеупомянутый урок включает аудио (поэтому не забудьте включить динамики).Используйте кнопку воспроизведения / паузы, если вам нужно остановить и начать урок. Вы найдете больше похожих на Уроки по фракциям здесь.
Сложение или вычитание смешанных чиселЕсть два метода сложения и вычитания смешанных чисел. Либо сложите целые числа, а затем сложите дробные части, либо преобразуйте каждое смешанное число в неправильную дробь перед вычислением. напомните ребенку, что нужно сократить все ответы до самого низкого уровня и заменить неправильные дроби на смешанные числа.
Советы и напоминанияПри сложении / вычитании смешанных чисел:
- Сложите целое число частей.
- Измените требуемые дроби на их эквивалентные значения, чтобы у всех дробей был один и тот же знаменатель.
- Сложить / вычесть числители. Знаменатель оставьте как есть.
Пример ниже показывает сложение двух смешанных чисел.
Примечание. Альтернативой описанному выше методу является изменение смешанных чисел на неправильные дроби (7/3 и 15/4), преобразование их в эквивалентные значения (28/12 и 45/12), их сложение и, наконец, изменение неправильных дробей. дробь к смешанному числу.
Рабочие листы — сложение, вычитание дробейИспользуйте приведенные ниже рабочие листы, чтобы попрактиковаться в сложении и вычитании дробей
Попробуйте генератор рабочего листа дробей.