Сложение и вычитание обыкновенных дробей – правило (5 класс, математика)

3.9

Средняя оценка: 3.9

Всего получено оценок: 206.

3.9

Средняя оценка: 3.9

Всего получено оценок: 206.

Сложение и вычитание обыкновенных дробей достаточно простая процедура. Самое сложное для ученика 5 класса найти общий знаменатель дробей, но, даже найдя его, легко допустить ошибку по невнимательности. Чтобы избежать таких ошибок в будущем досконально разберемся в теме вопроса.

Сложение и вычитание чисел

Что собой представляет сложение и вычитание чисел? Это перенос точки, означающей число вперед или назад по числовой прямой. Под словом вперед подразумевается перенос точки вправо относительно нуля. Соответственно, под словом назад подразумевается перенос точки числа влево на числовой прямой.

В результате вычитания может получиться отрицательное число: если при переносе числа влево точка уйдет за границу нуля. Это вполне логично. Но может ли получится отрицательное число при сложении?

Может. Потому что операция сложения может производится не только с положительными числами, но и с отрицательными.

Под точкой числа подразумевается точка на числовой прямой, которой соответствует определенное число. Число может быть абсолютно любым, так как на числовой прямой может быть отмечено любое существующее действительное число.

Запомните, при сложении двух отрицательных чисел результатом всегда будет отрицательное число. При этом, если прибавлять к отрицательному числу положительное, то отрицательное получится только если отрицательное число больше положительному по модулю.

Значит, чтобы число переменило знак на противоположный, нужно чтобы при переносе точки числа, она пересекла рубеж нуля. Например:

30-46=0-16=-16 – точка зашла за рубежную отметку нуля на 16 единиц.

Обыкновенные дроби

Что такое дробь? Дробь это запись части числа. На практике это значит, что если взять какой-то целый предмет и поделить его на число частей, равное числу в знаменателе, а потом взять количество частей, равное числу в числителе, то получится число, равное дроби.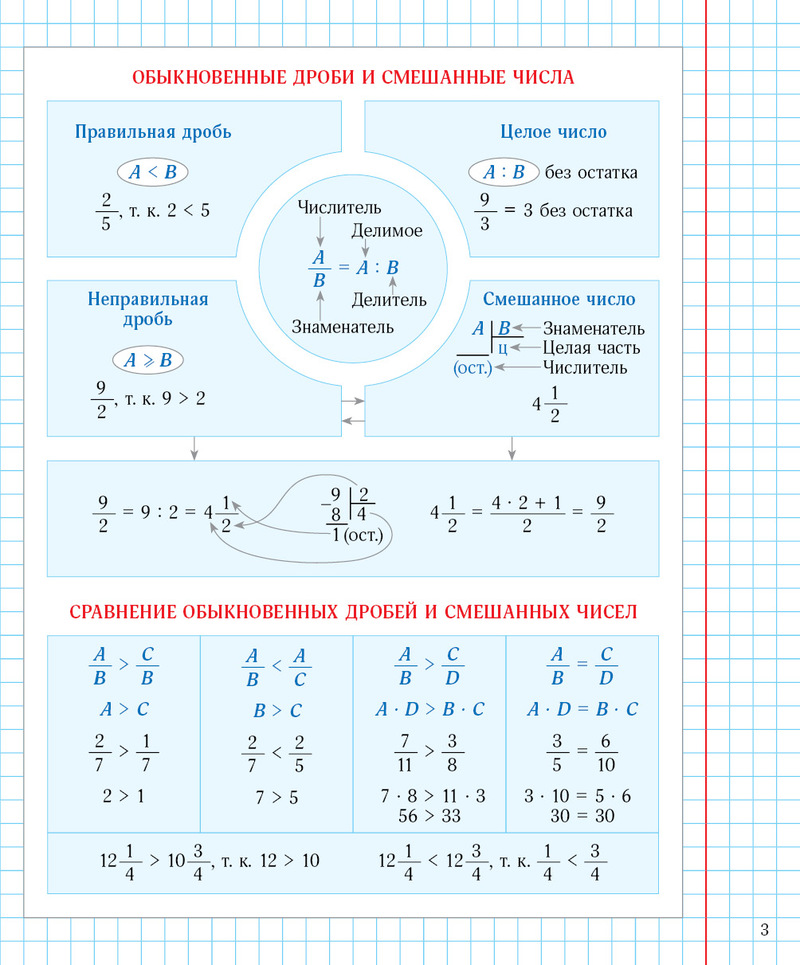

Если говорить проще, то дробь, это запись, которая позволяет работать с незаконченным делением, как с готовым числом. Например:

$$5:16={5\over{16}}$$ – так это записывается на практике.

Учителя любят следующую формулировку этого свойства: «Знак дроби заменяет деление» – эта формулировка проще, она легче запоминается, но не так понятна.

Что подразумевается под обыкновенной дробью? Под обыкновенной дробью подразумевается дробь, у которой числитель меньше знаменателя. То есть обыкновенная дробь, это дробь, которая меньше знаменателя или дробь, у которой нельзя выделить целую часть. Любая из трех формулировок считается правильной.

Противоположностью обычной дроби являются смешанные и неправильные дроби. Неправильные дроби это дроби, у которых числитель больше знаменателя. А смешанные дроби это дроби с выделенной целой частью.

Сложение и вычитание обыкновенных дробей

И сложение, и вычитание дробей имеет одинаковый алгоритм:

• Ищем общий знаменатель. Для того, чтобы определить общий знаменатель двух дробей, нужно найти наименьшее общее кратное двух знаменателей.
• Приводим к общему знаменателю обе дроби, для этого нужно домножить числитель и множитель каждой дроби так, чтобы оба знаменателя стали равными НОК.
• Записываем две дроби под общим знаменателем с сохранением операции сложения или вычитания в числителе.
• Выполняем операцию в числителе и при необходимости сокращаем результат.

Что мы узнали?

Мы поговорили о смысле сложения и вычитания. Выяснили, что такое обыкновенная дробь и чем она отличается от неправильной или смешанной. Привели правило сложения и вычитания обыкновенных дробей.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Татьяна Винникова

  10/10

Оценка статьи

3.9

Средняя оценка: 3.9

Всего получено оценок: 206.

---

А какая ваша оценка?

Сложение ⭐ обыкновенных дробей с одинаковыми знаменателями

Что такое дроби

Определение 1

Обыкновенная дробь является записью числа в виде ab при b, отличном от нуля, которая обозначает деление числа a на число b.

Компоненты обыкновенной дроби:

a — числитель;

b — знаменатель.

Определение 2

Правильной дробью называют дробь, в которой числитель меньше по сравнению со знаменателем.

Определение 3

Неправильной дробью называют дробь, в которой числитель больше по сравнению со знаменателем.

Нередко в результате решения самостоятельных задач и примеров на уроках в классе в ответе получается неправильная дробь. В этом случае можно выделить целую часть.

Свойства дробей:

1. При умножении пары обыкновенных дробей требуется найти произведение их числителей и знаменателей: ab·cd=a·cb·d.
2. При умножении дроби на число следует найти произведение числителя дроби на данное число: ab·n=a·nb.
3. Для того чтобы решать уравнения на деление одной дроби с каким-то знаком на вторую, нужно найти произведение первой дроби и дроби, которая является обратной ко второй: ab:cd=ab·dc=a·db·c.
4. При сравнении пары дробей требуется привести данные дроби к общему знаменателю и сравнить числители дробей. Дробь с большим числителем больше по сравнению с дробью, у которой числитель меньше.

Определение 4

Основное свойство дробей: допустимо умножать и делить числитель и знаменатель дроби на одинаковое число, что не приводит к изменению значения дроби:

ab=a·kb·k

Сложение обыкновенных дробей

Правило 1

Сложение или вычитание дробей, которые имеют одинаковые знаменатели, выполняется путем сложения или вычитания числителей этих дробей:

ab±cb=a±cb

Заметим, что в правиле указано понятие одинаковых знаменателей. В связи с этим при решении задач полезно владеть навыками приведения дробей к общему знаменателю. Алгоритм действий такой:

• определение минимального общего кратного для знаменателей данных дробей, то есть наименьшего общего знаменателя;
• деление наименьшего общего знаменателя, который был определен на предыдущем шаге, на знаменатели данных дробей, то есть поиск дополнительного множителя для каждой из дробей;
• умножение числителя и знаменателя каждой из дробей на ее дополнительный множитель, который был найден на предыдущем шаге.

Предположим, что имеются две дроби:

13 и 35

Наименьшим числом, которое можно поделить и на 3, и на 5, является 15. Это будет наименьший общий знаменатель для рассматриваемых дробей. Таким образом:

1·53·5=515

3·35·3=915

Правило 2

При сложении или вычитании дробей, которые имеют разные знаменатели, требуется привести эти дроби к общему знаменателю и сложить или вычесть числители:

ab±cd=ad±bcb·d

Рассмотрим несколько типичных примеров. Попробуем найти сумму двух обыкновенных дробей:

12+13=36+26=56

Знаменатели 2 и 3 обладают НОК, равным 6. Приведем дробь 12 к знаменателю со значением 6 путем умножения числителя и знаменателя на число 3. В результате получается дробь 36.

Затем обратимся ко второй дроби 36. Для того чтобы привести данную дробь к такому же знаменателю, как у первой дроби, умножим числитель и знаменатель дроби на число 2. В результате получим дробь 26.

В другом примере требуется найти сумму дробей, которые отличаются знаменателями:

23+12

Согласно алгоритму приведения дробей к общему знаменателю, найдем наименьшее общее кратное для чисел 2 и 3. Тогда общий знаменатель равен 6. Выполним вычисления:

23+12=46+36=76=116

Сложение смешанного числа и натурального числа

Пример 1

Рассмотрим равенство, в котором присутствуют дроби:

112=1+12

Исходя из полученного результата, можно сделать вывод о работе со смешанными дробями.

Правило 3

Какую-либо смешанную дробь можно записать в виде суммы целого числа и дроби:

abc=a+bc

Пример 2

Рассмотрим такой пример:

112+2=1+12+2

Зная, что при перестановке слагаемых сумма останется прежней, преобразуем выражение:

112+2=1+12+2=1+2+12=312

Исходя из полученного результата, запишем следующее правило.

Правило 4

При сложении натурального (целого) числа и смешанного числа требуется сложить целое число с целой частью смешанного числа, а дробную часть оставить прежней:

abc+d=a+d+bc

Пример решения задачи

Задача 1

Вычислить значение следующего выражения:

(35+74)·103

Решение

В первую очередь нужно вычислить значение выражения, заключенного в скобки:

35+74=3·4+7·55·4=4720

Далее приступим к умножению:

4720·103=47·1020·3=47·102·10·3=476

Ответ: 476

Задача 2

Дано несколько дробей, которые необходимо привести к общему знаменателю:

56,49 и 83

Решение

Заметим, что числа 6, 9 и 3 представляют собой делители для числа 18. Данное число является общим знаменателем. Таким образом, чтобы решить задачу, следует умножить числитель и знаменатель первой дроби на число 3, вторую дробь нужно умножить на число 2, а множитель для третьей дроби равен 6. Запишем результаты:

56=5·36·3=1518

49=4·29·2=818

83=8·63·6=4818

Ответ: 1518,818,4818.

Задача 3

Найти сумму двух дробей:

15+25

Решение

Воспользуемся правилом сложения дробей с одинаковыми знаменателями:

15+25=1+25=35

Ответ: 35

Задача 4

Сложить две дроби:

37+27

Решение

Воспользуемся правилом сложения дробей с одинаковыми знаменателями:

37+27=3+27=57

Задача 5

Туристы совершают пеший поход. В течение первого дня им удалось преодолеть 15 от всего пути. За второй день туристы прошли путь, равный 25 от всего пути. Требуется определить общее расстояние, пройденное туристами в течение двух дней.

Решение

Воспользуемся правилом сложения дробей с одинаковыми знаменателями:

15+25=1+25=35

Ответ: туристы прошли 35 от всего пути.

Задача 6

Найти сумму двух дробей:

34 и 27

Решение

Воспользуемся правилом сложения обыкновенных дробей, которые имеют разные знаменатели. В первую очередь приведем дроби к общему знаменателю. Для чисел 4 и 7 таким числом является 28. Тогда множителем для первой дроби является число 7, а вторую дробь требуется умножить на 4. Получим:

34+27=3×7+2×44×7=21+828=2928=1128

Ответ: 1128

Задача 7

Найти сумму пары смешанных чисел:

3611 и 1311

Решение

Воспользуемся правилом сложения смешанных чисел и запишем вычисления:

3611+1311=(3+611)+(1+311)=(3+1)+(611+311)=4+(6+311)=4+911=4911

Ответ: 4911

Задача 8

Выполнить сложение смешанных чисел:

718 и 216

Решение

Заметим, что дробные части данных смешанных чисел отличаются знаменателями. Поэтому в первую очередь следует привести эти дроби к общему знаменателю. Этим числом является 24. Множитель для первой дроби 718 равен 3, а вторую дробь 216 умножим на 4. Запишем вычисления:

718+216=71×38×3=21×46×4=7324+2424=9724

Ответ: 9724

Задача 9

Требуется определить, можно ли при сложении пары правильных дробей получить правильную дробь или неправильную дробь при сложении двух неправильных дробей на конкретных примерах.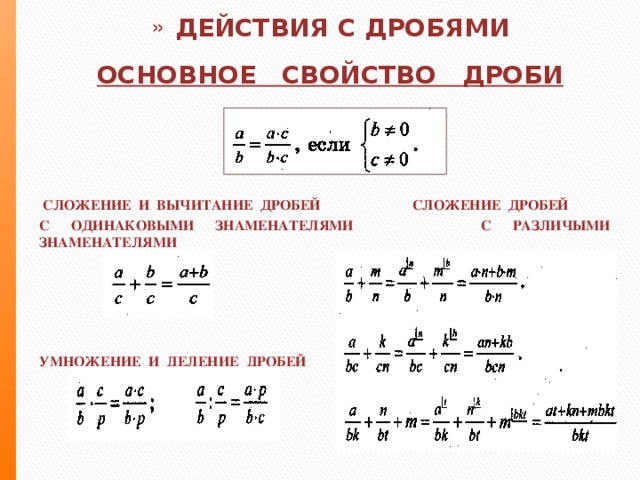

Решение

Представим сумму двух правильных дробей:

27+37=2+37=57

В данном случае, дробь 57 является правильной дробью. Это результат сложения двух правильных дробей 27 и 37.

Далее суммируем две неправильные дроби:

25+89=2×9+8×55×9=18+4045=5845

Заметим, что результатом сложения двух неправильных дробей 25 и 89 является неправильная дробь 5845.

Ответ: при сложении двух правильных дробей можно получить правильную дробь, при сложении двух неправильных дробей можно получить неправильную дробь.

Задача 10

Вычислить сумму дробей:

311+511

13+29

Решение:

311+511=3+511=811

13+29=1×33×3+29=39+29=59

Ответ: 811,59.

Задача 11

Требуется представить смешанную дробь, как сумму натурального числа и правильной дроби:

1947

513

Решение

1947=1+947

513=5+13

Ответ: 1+947,5+13.

Задача 12

Сложить дроби:

857+217

2913+213

725+3415

Решение

857+217=(8+2)+(57+17)=10+67=1067

2913+213=2+(913+213)=21113

725+3415=72×35×3+3415=7615+3415=(7+3)+(615+415)=10+1015=101015=1023

Ответ: 1067,21113,1023.

Задача 13

В обед было съедено 811 от целого пирога. За ужином было съедено еще 311 пирога. Требуется определить, пирог был съеден полностью, или какая-то его часть осталась?

Решение

Так как по заданию в знаменателе дроби записано число 11, можно сделать вывод о том, что пирог был разрезан на 11 частей. Суммируем части пирога, которые были съедены в течение обеда и ужина:

8 + 3 = 11

Получается, что всего было съедено 11 из 11 кусочков пирога, то есть весь пирог:

811+311=1111=1

Ответ: все кусочки пирога были съедены.

Сложение и вычитание дробей с переменными

Чтобы сложить или вычесть дроби:

• У вас должен быть общий знаменатель.
• Чтобы найти L восток C оммон Д эноминатор ( ЖК ), взять наименьшее общее кратное отдельные знаменатели.

Пример

Вопрос: Объедините в одну фракцию: $$ \cssId{s12}{\frac{2}{x+3} — \frac{3x}{x-1}} $$

Решение: Обратите внимание, что LCD это $\,(x+3)(x-1)\,.$

92 — 7x — 2}{(x+3)(x-1)}$

$\displaystyle\frac{2}{x+3} — \frac{3x}{x-1}$	оригинальное выражение
$\displaystyle = \ гидроразрыва {2} {х + 3} \ cdot \ гидроразрыва {х-1} {х-1} $ $\displaystyle \qquad -\ \frac{3x}{x-1}\cdot\frac{x+3}{x+3} $	получить общий знаменатель через умножение на $\,1\,$
$\displaystyle = \frac{2(x-1)-3x(x+3)}{(x+3)(x-1)}$	объединять подобные термины; записать числитель в стандартной форме

Оставьте знаменатель в факторизованной форме для вашего окончательного ответа.

Концептуальная практика

4.4: Сложение и вычитание дробей

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

9845

• Мишель Манес
• Гавайский университет

Вот две очень похожие дроби: \(\frac{2}{7}\) и \(\frac{3}{7}\). Что может означать их добавление? Может показаться разумным сказать:

\[\frac{2}{7}\; \text{представляет 2 пирога, разделенных на 7 детей} \ldotp \nonumber \]

\[\frac{3}{7}\; \text{представляет 3 пирога, разделенных на 7 детей} \ldotp \nonumber \]

Таким образом, возможно, \(\frac{2}{7} + \frac{3}{7}\) представляет 5 пирогов среди 14 детей, что дает ответ \(\frac{5}{14}\).

Очень заманчиво сказать, что «добавление дробей» означает «добавление пирогов и прибавление детей».

Беда в том, что дробь не пирог, и дробь не дитя. Таким образом, добавление кругов и добавление детей на самом деле не является добавлением дробей. Дробь это нечто другое. Это связано с пирогами и детьми, но что-то более тонкое. Дробь — это количество пирога на ребенка .

Нельзя добавлять пироги, нельзя добавлять детей. Вместо этого нужно добавить суммы, которые получают отдельные дети.

Пример: 2/7 + 3/7

Давайте потихоньку. Рассмотрим дробь \(\frac{2}{7}\). Вот изображение суммы, которую получает отдельный ребенок, когда семь детей получают два пирога:

Рассмотрим дробь \(\frac{3}{7}\). Вот картина суммы, которую получает отдельный ребенок, когда три пирога даются семи детям:

Сумма \(\frac{2}{7} + \frac{3}{7}\) соответствует сумма:

Ответ на картинке: \(\frac{5}{7}\).

Подумай / Соедини / Поделись

Помните, что \(\frac{5}{7}\) означает «количество пирога, которое получает один ребенок, когда семь детей делят пять пирогов». Внимательно объясните почему это то же самое, что и изображение, данное суммой выше:

В вашем объяснении должны использоваться как слова, так и изображения!

Большинство людей читают это как «две седьмых плюс три седьмых дает пять седьмых» и думают, что задача так же проста, как сказать «два яблока плюс три яблока дает пять яблок». И, в конце концов, они правы!

Вот как студентов сначала учат складывать дроби: Складывать дроби с одинаковым знаменателем кажется так же просто, как складывать яблоки:

4 десятых + 3 десятых + 8 десятых = 15 десятых.

\[\frac{4}{10} + \frac{3}{10} + \frac{8}{10} = \frac{15}{10} \ldotp \nonumber \]

(И, если хотите, \(\frac{15}{10} = \frac{5 \cdot 3}{5 \cdot 2} = \frac{3}{2}\).)

82 шестьдесят пятых + 91 шестьдесят пятых = 173 шестьдесят пятых:

\[\frac{82}{65} + \frac{91}{65} = \frac{173}{65} \ldotp \nonumber \]

Мы действительно добавляем сумм на ребенка не сумм, но ответы совпадают.

Мы можем использовать «Модель пирогов на ребенка», чтобы объяснить , почему сложение дробей с одинаковыми знаменателями работает таким образом.

Пример: 2/7 + 3/7

Подумайте о задаче на сложение \(\frac{2}{7} + \frac{3}{7}\):

\[\begin{split} \text {количество пирога, которое получит каждый ребенок, если 7 детей поделят по 2 пирога} & \\ +\; \text{количество пирогов, которое получит каждый ребенок, если 7 детей поделят по 3 пирога} \\ \hline ????? \qquad \qquad \qquad \qquad & \end{split} \nonumber \]

Поскольку в обоих случаях у нас есть 7 детей, делящих пироги, мы можем представить, что в обоих случаях это одни и те же 7 детей. Сначала они делят 2 пирога. Затем они делят еще 3 пирога. Сумма, которую каждый ребенок получает к тому времени, когда все пироги будут разделены, будет такой же, как если бы 7 детей только что поделили 5 пирогов для начала. То есть:

\[\begin{split} \text{количество пирога, которое получит каждый ребенок, если 7 детей поделят 2 пирога} & \\ +\; \text{количество пирога, которое получит каждый ребенок, если 7 детей разделят 3 пирога} \\ \hline \text{количество пирога, которое получит каждый ребенок, если 7 детей разделят 5 пирогов} \ldotp & \end{split} \nonumber \]

\[\frac{2}{7} + \frac{3}{7} = \frac{5}{7} \ldotp \nonumber \]

Теперь давайте подумаем об общем случае. Мы утверждаем, что

\[\frac{a}{d} + \frac{b}{d} = \frac{a + b}{d} \ldotp \nonumber \]

Переводя на нашу модель, у нас есть дети. Во-первых, они делят между собой пироги, а \(\frac{a}{d}\) представляет собой сумму, которую получает каждый ребенок. Затем они делят больше пирогов, поэтому каждый ребенок получает дополнительное количество пирога, равное \(\frac{b}{d}\). Сумма, которую получает каждый ребенок, равна \(\frac{a}{d} + \frac{b}{d}\).

Но не так уж важно, что дети сначала поделятся пирогами, а потом поделятся пирогами. Сумма, которую получает каждый ребенок, такая же, как если бы они начали со всех пирогов — всех \(a + b\) из них — и поделили их поровну. Это количество пирога представлено как \(\frac{a + b}{d}\).

Подумай / Соедини / Поделись

• Как можно вычесть дроби с одинаковым знаменателем? Например, что такое $$\frac{400}{903} — \frac{170}{903} ?$$
• Используйте модель «Pies Per Child», чтобы подробно объяснить, почему $$\frac{a}{d} — \frac{b}{d} = \frac{a — b}{d} \ldotp$$
• Объясните, почему тот факт, что знаменатели одинаковы, является существенным для этого метода сложения и вычитания. Где этот факт используется в объяснениях?

Этот подход к сложению дробей внезапно становится сложным, если задействованные знаменатели не являются одним и тем же общим значением. Например, что такое \(\frac{2}{5} + \frac{1}{3}\)?

Сформулируем этот вопрос в терминах пирогов и детей:

Предположим, Пойндекстер входит в команду из пяти детей, которые делят два пирога. Позже он становится частью команды из трех детей, которые делят один пирог. Сколько всего пирога получает Пойндекстер?

Подумай / Соедини / Поделись

Прежде чем читать дальше, обсудите эти вопросы с партнером. На самом деле это очень сложная проблема! Что может сказать ученик, если он еще не знает о сложении дробей? Запишите любые свои мысли.

1. Вы видите, что это та же проблема, что и вычисление \(\frac{2}{5} + \frac{1}{3}\)?
2. Каков наилучший подход к решению проблемы?

Один из способов ответить на этот вопрос о сложении — написать \(\frac{2}{5}\) в ряде альтернативных форм, используя наше правило ключевой дроби (то есть умножить числитель и знаменатель на 2, а затем каждый по 3, а затем каждый по 4 и так далее) и сделать то же самое для \(\frac{1}{3}\):

\[\begin{split} \frac{2}{5} + \frac{1}{3} & \\ \frac{4}{10} \quad \frac{2}{6} & \\ \textcolor{red}{\frac{6}{15}} \quad \frac{3}{9} & \\ \frac{8}{20}\; \; \frac{4}{12} & \\ \frac{10}{25}\; \; \textcolor{red}{\frac{5}{15}} & \\ \vdots \qquad \vdots\; & \end{split} \nonumber \]

Мы видим, что задача \(\frac{2}{5} + \frac{1}{3}\) на самом деле такая же, как \(\frac{6} {15} + \frac{5}{15}\). Таким образом, мы можем найти ответ, используя метод того же знаменателя:

\[\frac{2}{5} + \frac{1}{3} = \frac{6}{15} + \frac{5}{15} = \frac{11}{15} \ldotp \ nonumber \]

Пример: 3/8 + 3/10

Вот еще один пример сложения дробей с разными знаменателями: \(\frac{3}{8} + \frac{3}{10}\). В данном случае Валери входит в группу из 8 детей, которые делят 3 пирога. Позже она входит в группу из 10 детей, которые делят 3 разных пирога. Сколько всего пирога получила Валери?

\[\begin{split} \frac{3}{8} + \frac{3}{10} & \\ \frac{6}{16}\; \; \frac{6}{20} & \\ \frac{9{24}\; \; \frac{9}{30} & \\ \frac{12}{32}\; \; \textcolor{red}{\frac{12}{40}} & \\ \textcolor{red}{\frac{15}{40}}\; \; \frac{15}{50} & \\ \vdots \qquad \vdots\; & \end{split} \nonumber \]

\[\frac{3}{8} + \frac{3}{10} = \frac{15}{40} + \frac{12}{40} = \frac{17}{40} \ldotp \nonumber \]

Конечно, вам не нужно перечислять все эквивалентные формы каждой дроби, чтобы найти общий знаменатель. Если вы можете сразу увидеть знаменатель (или придумать более быстрый метод, который всегда работает), действуйте!

Подумай / Соедини / Поделись

Кэсси предлагает следующий метод для приведенного выше примера:

Когда знаменатели совпадают, мы просто добавляем числители. Итак, когда числители одинаковы, не следует ли просто сложить знаменатели? Вот так: \[\frac{3}{8} + \frac{3}{10} = \frac{3}{18} \ldotp \nonumber \]

Что вы думаете о предложении Кэсси? Имеет ли это смысл? Что бы вы сказали, если бы были учителем Кэсси?

Самостоятельно

Попробуйте выполнить эти упражнения самостоятельно. Для каждого упражнения на добавление также запишите интерпретацию задачи «Pies Per Child». Вы также можете нарисовать рисунок.

1. Что такое \(\frac{1}{2} + \frac{1}{3}\)?
2. Что такое \(\frac{2}{5} + \frac{37}{10}\)?
3. Что такое \(\frac{1}{2} + \frac{3}{10}\)?
4. Что такое \(\frac{2}{3} + \frac{5}{7}\)?
5. Что такое \(\frac{1}{2} + \frac{1}{4} + \frac{1}{8}\)?
6. Что такое \(\frac{3}{10} + \frac{4}{25} + \frac{7}{20} + \frac{3}{5} + \frac{49{50}\)?

Теперь попробуйте эти упражнения на вычитание.

1. Что такое \(\frac{7}{10} — \frac{3}{10}\)?
2. Что такое \(\frac{7}{10} — \frac{3}{20}\)?
3. Что такое \(\frac{1}{3} — \frac{1}{5}\)?
4. Что такое \(\frac{2}{35} — \frac{2}{7} + \frac{2}{5}\)?
5. Что такое \(\frac{1}{2} — \frac{1}{4} — \frac{1}{8} — \frac{1}{16}\)?

---

Эта страница под названием 4.