Сложение или умножение первое действие: Какое из действий (умножение, деление, сложение или вычитание) нужно выполнить первым, определяя значение выражения (31⋅1−0):31+81…

Содержание

Выражения без скобок — урок. Математика, 2 класс. — «Семья и Школа»

Содержание

Как правильно решить пример без скобок?

Запомните правило:

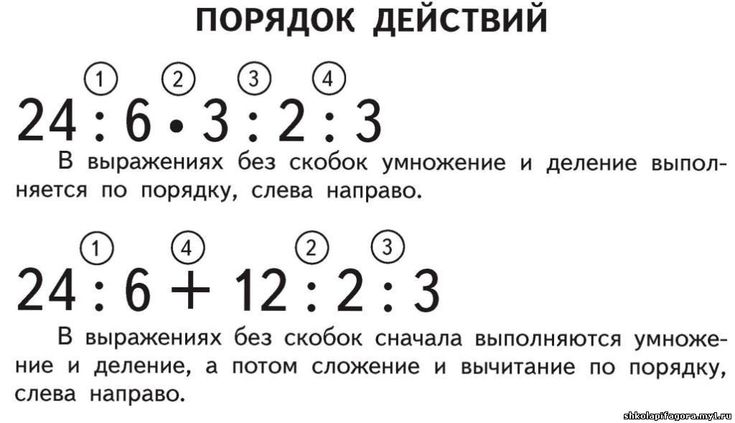
Если в примере нет скобок, сначала выполняем действия умножения и деления по порядку, слева направо. …
Если в примере есть скобки, то сначала мы выполняем действия в скобках, затем умножение и деление, и затем — сложение и вычитание начиная слева направо.

Какое первое действие в примере без скобок?

Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.

Какие первые действия в математике?

Сначала умножение и деление, затем сложение и вычитание В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок: действия выполняются по порядку слева направо, причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Что сначала делается сложение или умножение?

При умножении двух разных единиц измерения получается новая единица измерения, при сложении единицы измерения не меняются. При умножении мы получаем эту самую новую единицу измерения. Если она такая же, как и у первого слагаемого, тогда мы можем выполнить сложение. Это просто правило.

Что это вычитание?

Вычитание — операция обратная сложению. Вычитание возможно только, если оба аргумента принадлежат одному множеству элементов (имеют одинаковый тип).

Что такое сложение и вычитание?

Сложение – это объединение объектов в одно целое. Результатом сложения чисел является число, называемое суммой чисел (слагаемых). Вычитание – это такое действие, в котором отнимают меньшее число от большего. Большее число называется уменьшаемым, меньшее – вычитаемым, результат вычитания – разностью.

Как решать дроби Сложение и вычитание?

Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений. Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.

Как называется сложение в математике?

Сложение чисел Результат сложения двух или более чисел называется суммой, а сами числа — слагаемыми. … Складываем числа, аналогично положительным, записываем результат со знаком «минус». Например, (-6)+(-5,3)=-(6+5,3)=-11,3. От перестановки мест слагаемых сумма не изменяется a+b=b+a.

Как называется в математике плюс?

Знаки «плюс» и «минус» (+ и −) — математические символы, используемые для обозначения операций сложения и вычитания, а также положительных и отрицательных величин.

Как называется математическое действие Если стоит знак плюс?

В стране математики живут не только цифры и числа, но и разные математические знаки. Сегодня вы с Лисёнком познакомитесь с ними. … В математике это действие называется сложением и ставится знак плюс.

Как называется действие с минусом?

Вычитание – действие обратное сложению. Уменьшаемое – число, из которого вычитают. Вычитаемое – число, которое вычитают. Разность – результат вычитания.

Как называется при умножении?

Так же, как и при сложении и вычитании, числа при умножении имеют свое название. Первое число при умножении называется множитель. Второе число при умножении тоже называется множитель. Результат умножения называют произведение.

Что такое результат умножения?

Умноже́ние — одна из основных математических операций над двумя аргументами (множителями или сомножителями). Иногда первый аргумент называют множимым, а второй множителем; результат умножения двух аргументов называется их произведением.

Как умножить два отрицательных числа?

Умножение отрицательных чисел Правило умножения отрицательных чисел: чтобы умножить два отрицательных числа, нужно перемножить их модули. Это значит, что для любых отрицательных чисел -a, -b верно равенство: (-а) * (-b) = a * b.

Как умножить натуральное число на отрицательное?

Правило умножения отрицательных чисел заключается в том, что для того, чтобы умножить два отрицательных числа, необходимо перемножить их модули. Данное правило записывается так: для любых отрицательных чисел –a, −b данное равенство считается верным. (−а)⋅(−b)=a⋅b.

Примеры со скобками: какой порядок действий

Помню, в школе на зимние каникулы учительница всегда давала нам большой листок с примерами, которые нужно было решить. Чтобы мы за пару недель не забыли всё, что выучили. Почти все одноклассники вспоминали об этих примерах в воскресенье вечером перед школой. Страдальчески садились за стол и пытались включить мозг. Получалось не всегда. Спустя годы после школы тем более сложно что-то вспомнить. Поэтому у многих даже простые задания вызывают недоумение. Что ж, проверим, хорошо ли тебя натаскала математичка. А также расскажем, что стоит помнить, решая математические примеры со скобками.

Математические примеры со скобками

8 / 4(3 – 1) = ?

Посчитай и скажи, сколько у тебя вышло. Проверить себя можешь в конце статьи. А если возникают затруднения, мы всегда поможем!

Алгоритмы решения примеров

Начнем с простых примеров без скобок. Чтобы решить такие примеры, нужно помнить одно главное правило: все действия выполняются слева направо. Сначала сделай умножение и деление, а затем сложение и вычитание. © Depositphotos

Посчитаем: 5 х 4 – 8 / 2 = ?

Иди слева направо, но помни, что сначала выполняются умножение и деление. Так:

1) 5 х 4 = 20. Это умножение, и оно будет первым, если идти слева направо.

2) 8 / 2 = 4. Это деление, и, хотя оно идет после вычитания, деление выполняется первым.

3) 20 – 4 = 16. Теперь обычный порядок: после умножения и деления переходим к вычитанию.

Ответ: 5 х 4 – 8 / 2 = 16.

Как решать примеры со скобками

Пример может содержать круглые скобки, которые используются для изменения обычного порядка математических действий. Чтобы сделать всё правильно, запомни такие правила.

Сначала проделай все действия, указанные в скобках. Затем — всё остальное слева направо. Первыми всегда, как мы уже говорили, идут умножение и деление, а затем вычитание и сложение. Те же правила применяются к круглым скобкам.

Ответ на наш пример

Решая этот пример, легко перепутать порядок действий. Правильный порядок таков: сначала вычисли результат в скобках, затем подели 8 на 4, а результат умножь на то, что получил в скобках. Итак, ты получишь: 8 / 4(3 – 1) = 8 / 4 х 2 = 2 х 2 = 4.

А ты получил правильный ответ? Делись с нами в комментариях.

Екатерина Кукиб

Редактор, который не пишет статьи, а просто общается с читателем как с хорошим другом. Главные ориентиры в жизни — свобода и безбарьерность. Катя любит людей и их истории, которые собирает для своей собственной, чтобы потом рассказать ее миру. Любимая книга — «Искусство любить» Эриха Фромма.

0.1.1 — Порядок работы

Акроним PEMDAS, или мнемоника « p аренда e извините m y d ear a unt S ally», иногда используется, чтобы помочь учащимся запомнить основной порядок операций, где P = круглые скобки, E = показатели степени (и квадратные корни), M = умножение, D = деление, A = сложение и S = вычитание.

При выполнении ряда математических операций начинайте в скобках. Затем вычислите любые показатели степени или квадратные корни. Затем умножение и деление. И, наконец, сложение и вычитание. Для более глубокого ознакомления мы рекомендуем урок «Порядок операций» Академии Хана.

СкобкиПоказатель степени и квадратный кореньУмножение и делениеСложение и вычитание

В этом курсе мы будем часто использовать дроби. При работе с дробями можно представить, что операции в числителе заключены в скобки, а операции в знаменателе — в скобках. Ниже приведены несколько примеров математических операций, которые будут применяться в этом курсе. Мы узнаем о применении этих операций позже в курсе, здесь мы сосредоточимся только на математических операциях. 9* = 2,080\).

Сначала мы подставим заданные значения.

\(5,770 \pm 0,355(2,080)\)

В скобках нет операций, степеней или квадратных корней, поэтому следующим шагом будет умножение.

\(5,770 \pm 0,697\)

Символ ± говорит об использовании как вычитания, так и сложения.

\(5,770 — 0,697 = 5,073\)

\(5,770 + 0,697 = 6,467\)

Доверительный интервал (5,073, 6,467).

Пример: объединенная доля Раздел

Пример: тестовая статистика для доли Раздел

Статистические данные теста для проверки гипотезы пропорции одной выборки могут быть вычислены с использованием уравнения \(z = \frac {\hat p — p_0}{\sqrt{\frac{p_0 (1-p_0)}{n}}} \). Давайте проработаем эту формулу, используя следующие значения: \(\шляпа p = 0,87\), \(p_0 = 0,8\) и \(n=100\).

Сначала мы подставим заданные значения.

\(z = \frac {0,87 — 0,8}{\sqrt{\frac{0,8 (1- 0,8)}{100}}}\)

В первых шагах мы будем работать с числителем и знаменателем отдельно . Начнем с числителя, который содержит только вычитание.

\(z = \frac {0,07}{\sqrt{\frac{0,8 (1- 0,8)}{100}}}\)

Теперь сосредоточимся на знаменателе. Операция в скобках должна выполняться первой.

\(z = \frac {0,07}{\sqrt{\frac{0,8 (0,2)}{100}}}\)

В знаменателе мы можем сначала работать с вершиной дроби,

\(z = \frac {0,07}{\sqrt{\frac{0,16}{100}}}\)

Найдите дробь под квадратным корнем в знаменателе.

\(z = \frac {0,07}{\sqrt{0,0016}}\)

Затем извлеките квадратный корень из знаменателя.

\(z = \frac {0.07}{0.04}\)

И, наконец, разделите числитель на знаменатель.

\(z = 1,75\)

Экспоненты, умножение и сложение – MathFour

Рубрики: Алгебра; Будьте первым, кто поделится своими мыслями — оставьте комментарий ниже!

Это четвертая книга из серии Объяснение порядка действий.
Чтобы ознакомиться с другими статьями этой серии, нажмите здесь, чтобы перейти к введению.

Изображение из Википедии

Порядок операций можно свести к трем «настоящим» операциям.

Скобки — это просто способ сгруппировать элементы, а не настоящая операция. Поэтому они не считаются реальной операцией.

Поскольку деление — это просто умножение, перевернутое с ног на голову, нам не нужно включать его отдельно. Точно так же вычитание — это сложение на слуху. Так что его тоже выкидываем.

Теперь у нас их всего три: показатели степени, умножение и сложение.

Экспоненты — это быстрый способ умножения.

В предыдущей статье о запоминании правил экспоненты я записал это видео о экспонентах:

Вы видите, что 3 x 3 x 3 x 3 равно 3 ⁴ . Экспонента — это сокращение для умножения.

Умножение — это быстрый способ сложения.

Точно так же, когда мы перегружены сложением одних и тех же чисел снова и снова, как в видео, 4 + 4 + 4 + 4 + 4, мы можем использовать умножение, чтобы сократить это: 5 x 4.

Следуйте сокращению эволюция.

Эволюция быстрого доступа выглядит следующим образом:

Сначала появилось дополнение.
Затем мы создали умножение, чтобы упростить сложение.
Затем мы создали показатели степени, чтобы упростить умножение.

Итак, когда вы занимаетесь арифметикой, мы должны сначала использовать «недавние» сокращения (возведение в степень), затем «старые» сокращения (умножение), а затем «обычные» арифметические действия (сложение). Помните, что вычитание — это сложение, а деление — это умножение.

И имейте в виду, что нам нужно следить за группировкой или чем-либо изолированным скобками, барами абсолютного значения или дробью. Инструменты группировки/изоляции всегда важнее других правил работы.

Изображение из Википедии

Что, если ваш ответ не совпадает с ответом на обратной стороне книги?

В некоторых учебниках умножение выполняется перед делением. Это означает, что задача 9 3 x 2 будет показывать другой ответ (3/2) на страницах решения этого учебника, чем тот, который вы получили бы после ОоО, которое я здесь описываю (6).

Арифметические действия с десятичными дробями

4 части по 48 карточек с примерами на отдельное арифметическое действие (сложение, вычитание, умножение и деление).

Все карточки однотипны и включают в себя по 12 примеров различной трудности с учетом практически всех частных случаев, встречающихся при выполнении данного действия.

Все задания всех вариантов снабжены ответами.

dd_1_zadanija.doc
dd_2_zadanija.doc
dd_3_zadanija.doc
dd_4_zadanija.doc

dd_1_4_otvety.doc

Примеры

Сложение десятичных дробей

Вариант 1. 1.
Выполни сложение:
1) 15,0084 + 0,4548;
2) 2,773 + 78,73;
3) 4,929 + 0,0762;
4) 0,5867 + 0,4133;
5) 2,878 + 47,122;
6) 23,08 + 95,884;
7) 0,0065 + 71;
8) 92,02 + 94,98;
9) 0,001084 + 6,247;
10) 4 + 3,7305;
11) 0,00067165 + 0,00597835;
12) 0,003192 + 0,004808.

Вариант 1.2.
Выполни сложение:
1) 0,005407 + 0,05741;
2) 9,403 + 490,597;
3) 10 + 9,944;
4) 3,095 + 7,067;
5) 0,12733 + 0,04267;
6) 9,0695 + 0,00954;
7) 4,721 + 1,279;
8) 0,305 + 18;
9) 6654,2 + 39,68;
10) 0,019285 + 0,404985;
11) 0,9617 + 0,0383;
12) 0,017996 + 0,026004.

Вариант 1.3.
Выполни сложение:
1) 7,1589 + 81,418;
2) 3,1979 + 9,5937;
3) 0,80118 + 0,7761;
4) 74 + 0,28;
5) 80,727 + 97,273;
6) 0,0016077 + 0,0052923;
7) 84,124 + 5,876;
8) 666,73 + 610,97;
9) 9,4559 + 58;
10) 0,99737 + 0,00263;
11) 0,2356 + 0,0093663;
12) 30,294 + 29,106.

Ответы

1. 1.
1) 15,4632; 2) 81,503; 3) 5,0052; 4) 1;
5) 50; 6) 118,964; 7) 71,0065; 8) 187;
9) 6,248084; 10) 7,7305; 11) 0,00665; 12) 0,008.

1.2.
1) 0,062817; 2) 500; 3) 19,944; 4) 10,162;
5) 0,17; 6) 9,07904; 7) 6; 8) 18,305;
9) 6693,88; 10) 0,42427; 11) 1; 12) 0,044.

1.3.
1) 88,5769; 2) 12,7916; 3) 1,57728; 4) 74,28;
5) 178; 6) 0,0069; 7) 90; 8) 1277,7;
9) 67,4559; 10) 1; 11) 0,2449663; 12) 59,4.

Умножение десятичных дробей

Вариант 3.1.
Выполни умножение:
1) 10000 • 0,00012;
2) 0,7424 • 0,2;
3) 475 • 0,36;
4) 1000 • 0,8;
5) 2,15 • 1,8;
6) 0,0001 • 451;
7) 1,5 • 636;
8) 0,0999 • 33;
9) 4,015 • 0,084;
10) 0,8 • 27,5;
11) 0,01 • 80,7;
12) 18 • 9,1.

Вариант 3.2.
Выполни умножение:
1) 0,045 • 0,0672;
2) 100 • 0,0668;
3) 0,0001 • 611;
4) 645 • 6,4;
5) 0,00998 • 9,4;
6) 0,25 • 756;
7) 0,034 • 48;
8) 25 • 9,7;
9) 0,1 • 1,5;
10) 59,2 • 2,5;
11) 44,2 • 1000;
12) 0,216 • 0,0095.

Вариант 3.3.
Выполни умножение:
1) 57 • 38,7;
2) 8,75 • 1,4;
3) 62 • 41,5;
4) 201,5 • 0,098;
5) 17,5 • 0,8;
6) 0,071 • 56;
7) 0,001 • 0,895;
8) 0,00661 • 10;
9) 0,007 • 0,96086;
10) 9,2 • 100;
11) 958 • 0,01;
12) 375 • 0,76.

Ответы

3.1.
1) 1,2; 2) 0,14848; 3) 171; 4) 800;
5) 3,87; 6) 0,0451; 7) 954; 8) 3,2967;
9) 0,33726; 10) 22; 11) 0,807; 12) 163,8.

3.2.
1) 0,003024; 2) 6,68; 3) 0,0611; 4) 4128;
5) 0,093812; 6) 189; 7) 1,632; 8) 242,5;
9) 0,15; 10) 148; 11) 44200; 12) 0,002052.

3.3.
1) 2205,9; 2) 12,25; 3) 2573; 4) 19,747;
5) 14; 6) 3,976; 7) 0,000895; 8) 0,0661;
9) 0,00672602; 10) 920; 11) 9,58; 12) 285.

Автор: Ермолин Сергей Александрович.

Отменить умножение (сложение) с делением (вычитание)

Свойства равенства, о которых упоминалось ранее, некоторыми учащихся, реализуется неправильно даже тогда, когда ситуация требует их использование. Например, при решении уравнения как

требуются два шага:

а также

Обратите внимание, что в выражении порядок операций диктует, что умножение на 3 предшествует добавлению 7, и «отмены» этих процессов — вычитание 7 и деление на 3 — производилось в обратном порядке. Это не сказать, что мы не могли бы отменить вещи в другом порядке, но студенты, которые делают это, часто делают следующую ошибку. Деление на 3, они часто пренебрегают тем, что все термины с обеих сторон должны быть разделены на 3. Другими словами, после деления на 3 они записывать

Они слишком увлечены идеей, что будут вычитать 7 из обеим сторонам понять, что, разделив сначала на 3, это не 7, а , который нужно вычесть, давая тот же ответь как раньше. Здесь уместно еще одно замечание. Если круглые скобки появляются в уравнении, таком как

то порядок операций выгружается (вычитание внутри скобки стоят перед умножением на 3).

При решении для , мы можем, конечно, распределить 3, тем самым исключив круглые скобки и сделать проблему похожей на последнюю обсуждалось. Требуется еще меньше шагов, если просто «отменить» умножение и вычитание в обратном порядке:

а потом

Теперь вернемся к уравнению

и исследуйте более красноречивые ошибки, которые дали названия UMD и UAS в этот раздел. Немного учащиеся осознают необходимость за два шага (подобно тем, которые выполнялись, когда это уравнение было рассмотрено выше) изолировать , но мало чувствовать для каких операций это будет достигнуто. За например, понимая, что, как и в правой части уравнение, является «не-» термином, учащийся может написать

недоразумение, что она вычла 7 слева стороны, но делится на 7 на Обратная сторона. Исходное уравнение и новое больше не имеют те же решения в результате. Тот же ученик может затем признать, что ей нужно переместить на другую сторону.

Так как 3 умножается на , она должна «отменить» это на деля обе стороны на 3. Но она может (ошибочно) написать

разделив слева, но вычитая справа. Опять таки, решение отличается от того, которое решило исходное уравнение , а именно .

Еще хуже, когда ученик думает, что может решить за один шаг. (то есть позаботьтесь как об умножении на 3, так и о сложении из 7 за одну операцию). Такой студент может написать что-то вроде

Опять же, ответ, который получает этот студент, , отличается чем правильный.

главных ошибок в алгебре, сделанных студентами, изучающими исчисление (полный документ)
Полный список кодов оценок

Томас Л. Скофилд 2003-09-04

Порядок операций | Новозеландская математика

Цель

Цель этого раздела — развить понимание учащимися того, как ведут себя операции с числами, осознать необходимость правил, которые бы направляли нас в порядке, в котором мы выполняем эти операции, а также интерпретировать и применять эти правила в проблемных ситуациях.

Цели достижения

NA3-6: Запишите и интерпретируйте аддитивные и простые мультипликативные стратегии, используя слова, диаграммы и символы, с пониманием равенства.

Разработка АО и другие учебные ресурсы

Конкретные результаты обучения

Признать, что порядок действий имеет значение в практических ситуациях реальной жизни.
Понимать и объяснять связь между сложением и вычитанием, а также между умножением и делением.
Распознавайте неоднозначность выражений и уравнений, включающих более одной операции.
Распознавать порядок операций в задачах с произношением чисел.
Поймите и объясните правила порядка операций, включая объяснение аббревиатуры BEDMAS.
Применить порядок операций для решения проблем.

Описание математики

Когда учащиеся понимают и правильно используют общие символы для отношений (=, ≠, <, >) и числовых операций (+ — x ÷), они могут выражать простые математические идеи и проблемные ситуации, используя эти символы, а также может интерпретировать (и решать) знакомые математические уравнения и выражения. Однако когда они сталкиваются с проблемами, включающими более одной операции, они могут быть озадачены неоднозначностью некоторых выражений и уравнений. Это может привести к различным интерпретациям и результатам. Например, 4 + 2 х 5 = ☐. Это равно 30 или 14?

В устной и письменной речи мы принимаем как должное очень важную пунктуацию, которую используем. Спорное утверждение «Женщина без своего мужчины ничто», например, имеет совершенно иное значение, когда пунктуация ставится таким образом: «Женщина: без нее мужчина ничто». «Четыре плюс два, умноженное на пять, равно чему?» или «Четыре плюс два, умноженное на пять, равно чему?»

При отсутствии этой пунктуации установлены правила, в которых скобки (скобки) и изложенный порядок выполнения числовых операций, устранить любую двусмысленность. В то время как научные калькуляторы дают правильные ответы на многоступенчатые уравнения, учащиеся должны понимать необходимость согласованного порядка, знать правильные соглашения и уметь применять их для решения задач.

Упражнения, предлагаемые в этой серии уроков, могут стать основой для самостоятельных практических заданий.

Ссылки на систему нумерации
Мультипликатив
Расширенный мультипликатив

Необходимые материалы

Диаграммная бумага
Цветные (фломастеры) ручки
Калькуляторы
Научные калькуляторы
Копирайтеры Один и Два

Деятельность

Сессия 1

SLO:

Знайте, что порядок операций имеет значение в реальных жизненных ситуациях.
Понимать и объяснять связь между сложением и вычитанием, а также между умножением и делением.
Исследуйте предположения и доказательства.
Распознавайте неоднозначность выражений и уравнений, включающих более одной операции.
Распознавать порядок операций в задачах с произношением чисел.

Упражнение 1

Распечатайте на карточке наборы утверждений о действиях в Copymaster 1.
Начните с раздачи по одному каждому учащемуся в классе. Попросите учащихся всей группой прочитать свои утверждения вслух и внимательно выслушать утверждения друг друга. Затем учащиеся формируют группы связанных утверждений и договариваются о логическом порядке своих утверждений о действиях.
Попросите группы представить свои действия по порядку перед всем классом. Например:
1. Встаньте с постели. 2. Примите душ. 3. Оденьтесь. 4. Выйдите из дома. 5. Прийти в школу.
Попросите несколько групп затем прочитать их вне порядка , чтобы подчеркнуть тот факт, что это ерунда, и что существует разумный порядок их действий и что одни действия должны быть выполнены раньше других .

Занятие 2

Попросите учащегося записать в классной таблице числовые операции (используйте этот термин). Попросите учащихся объяснить каждый из символов операции, + — x ÷ .
Предложите учащимся обсудить в парах связь между операциями сложения и вычитания, а также между умножением и делением.
Выделите обратную связь в каждой паре операций. Попросите учащихся объяснить это с помощью уравнений и словесных примеров, например:
30 + 4 = 34 и 34 – 4 = 30
«У Пип в кошельке тридцать долларов банкнотами и четыре доллара монетами. Всего тридцать четыре доллара. Она платит четыре доллара за кофе, и у нее остается тридцать долларов».0003 Вычитание без сложения. Это обратная операция.
16 x 4 = 64 и 64 ÷ 4 = 16
Четыре друга заработали по шестнадцать долларов каждый. Всего работодатель выплатил шестьдесят четыре доллара. Каждый взял свою долю в шестнадцать долларов, так что получилось шестьдесят четыре, деленное на четыре.
Деление отменяет умножение. Это обратная операция.

Действие 3

См. задачу заказа действий в Упражнении 1, Шаг 1 (выше). Заказ был важен.
Поза: ‘ В математике порядок, в котором мы выполняем операции с числами, не меняет результат/результат’.
Запишите и обсудите их идеи. Опираясь на это:
Запишите это уравнение на классной таблице.
12 + 4 x 5 – 4 = ☐
Попросите пары учащихся решить уравнение и объяснить свое решение(я).
Иметь трех учеников прочитайте уравнение вслух тремя разными способами .
Напишите их, используя слова, подчеркивая различные знаки препинания .
Двенадцать плюс четыре, умножить на пять, минус четыре, равно семьдесят шесть.
Двенадцать плюс четыре умножить на пять минус четыре равно двадцати восьми.
Двенадцать плюс четыре, умноженное на пять минус четыре, равно шестнадцати.
Пусть учащиеся поработают в парах, чтобы записать каждую из этих трех интерпретаций в виде уравнений, изобретая свои собственные «математические знаки препинания» . Попросите их поделиться этим, написав это на карточке класса, чтобы другие могли видеть. Примите и изучите все предложения.
Согласитесь, что скобки полезны, и запишите их. Объясните, что скобки также известны как скобки .
(12 + 4) х 5 – 4 = 76
12 + (4 х 5) – 4 = 28
(12 + 4) х (5 – 4) = 16
Предложите учащимся обсудить и предложить возможных практических сценариев для каждого представления проблемы. Например:
(12 + 4) x 5 – 4 = 76
Льюис зарабатывает двенадцать долларов в час, упаковывая коробки, но получает бонус в размере четырех долларов каждый час, если он превышает общее количество коробок, установленное в качестве цели в час. Он работает пять часов, получая премию каждый час. После того, как он потратил четыре доллара на кофе, у него осталось семьдесят шесть долларов.

Занятие 4

Раздайте учащимся бумагу для рисования и цветные ручки.
Попросите пары учащихся вместе написать на диаграммах не менее трех из своих многошаговых уравнений, каждое из которых состоит из слов с пунктуацией и символов из .
Пусть они напишут сценарии из реальной жизни хотя бы для одной версии каждой из своих проблем.
Пусть учащиеся попарно поделятся этим.
НБ. Графики будут добавлены во время сеанса 2, когда будет представлена система BEDMAS.

Занятие 5

Завершите сессию рассмотрением гипотезы, сформулированной в Упражнении 3, Шаг 1 (выше).
«Порядок, в котором мы выполняем числовые операции, не влияет на результат».
Не согласен с утверждением. Согласитесь с тем, что порядок, в котором выполняются числовые операции , влияет на результат и что использование скобок помогает нам понять порядок операций.

Сессия 2
SLO:
Понимать и объяснять правила порядка операций, включая объяснение аббревиатуры BEDMAS.
Применить порядок операций для решения проблем.
Мероприятие 1
Просмотрите порядок действий, предпринятых в начале Занятия 1, и выводы по этому занятию.
Объясните учащимся, что математики согласовали порядок операций или математических действий. Напишите BEDMAS, пояснив, что это аббревиатура от согласованного соглашения.
Спросите: «Что такое аббревиатура ?»
Кто подскажет другую известную аббревиатуру?
Что такое соглашение ?
Что может означать BEDMAS ?
Предложите учащимся обсудить каждый из этих вопросов, а затем запишите их идеи рядом с аббревиатурой в таблице класса. (E для показателей может быть неизвестен).
B: кронштейны. E: показатели степени, D: деление, M: умножение, A: сложение, S: вычитание.
Объясните, что порядок операций иногда называют приоритетом операций . Это правило, которое мы используем, чтобы уточнить, какую операцию мы делаем в первую очередь. (до предшествует означает идти (или идти) раньше или первым.)
Если не совсем понятно, объясните возведение в степень , показав, что оно повторяется умножение : т. е. 4 ² = 4 x 4 = 16, или 10 ³ = 10 х 10 х 10 = 1000
Занятие 2
Раздайте копирайтеру 2. Объясните, что учащиеся должны исследовать, как работает БЕДМАС, применяя ее к уравнениям. Напомните им, что может быть полезно сначала прочитать каждую задачу вслух, чтобы понять уравнение, «услышав» его.
Предложите учащимся решить задачи в парах. Они должны записать, какую операцию они выполнили первой, и объяснить словами, почему. Они также должны обсуждать и записывать любые возникающие у них вопросы.
Попросите учащихся в парах поделиться своими решениями каждого из уравнений, объяснив порядок операций, которые они применяли в каждом примере. Сделайте следующие обучающие точки по мере их выполнения:
Деление и умножение выполняются в порядке их следования слева направо.
Сложение и вычитание выполняются в порядке их следования слева направо.
Обратите внимание в примерах 3, 4, 5, 6, 13 и 15 на эффект использования обратных операций.
При решении того, что в скобках, применяется порядок действий.
Занятие 3
Соберитесь всем классом. Предложите учащимся прочитать несколько уравнений вслух, расставляя запятые (паузы) там, где выражения заключены в скобки, например:
9. (25 – 5) ÷ 5 = ☐
Двадцать пять минус пять, разделить на пять, равно четырем.
и прерывая чтение запятыми (паузами), чтобы понять порядок операций, например:
13. 25 + 5 x 5 ÷ 5 ² = ☐
Двадцать пять плюс, пять раз пять разделить на пять в квадрате, равно двадцати шести.
Сделать вывод, что порядок, в котором мы выполняем числовые операции, конечно действительно меняет результат/результат .
Занятие 4
Попросите пары учащихся дополнить таблицы, начатые в Занятии 1. Объяснить порядок операций своими словами , показать значение аббревиатуры BEDMAS и выделить «эффект пунктуации» скобок.
Сессия 3
SLO:
Применять порядок операций для решения проблем.
Действие 1
Поза: Наличие соглашения BEDMAS означает, что мы все согласны со значением неизвестной величины в уравнении.
Пусть учащиеся обсудят это в парах, а затем поделятся с классом, объяснив причины своего согласия или несогласия с утверждением.
В ходе обсуждения поясните, что является неизвестным в уравнении типа (25 – 5) ÷ 5 = ☐. Также уточните, что иногда неизвестное (сумма) отображается с буквенным символом , например ‘n’ .
Занятие 2
Предоставьте каждому учащемуся бумагу и карандаши.
Поставьте эту задачу. «Я думаю о числе. Мы назовем это число «n». Я добавляю шесть к этому. Я удваиваю. Это равно двадцати восьми».
Спросите: Можете ли вы написать эту задачу в виде уравнения? [Уравнение: (n + 5) x 2 = 28]
Попросите некоторых учащихся записать свое уравнение в классную таблицу. Обсудите идеи учащихся, подчеркнув важность использования квадратных скобок для обозначения порядка операций. Основное внимание уделяется правильной записи уравнения в этот момент, а не нахождению значения n.
Поставьте еще две задачи, например:
«Я думаю о числе. Я вычитаю из него 10. Я делю это на девять. Это равно десяти». [Уравнение: (n – 10) ÷ 9 = 10 ]
«Я думаю о числе. Я вычитаю два. Я квадратю и получаю двадцать пять. [Уравнение: (n – 2) ² = 25]
и предложите учащимся записать каждое уравнение, поделиться и обсудить написанное .
Теперь посмотрим на каждое из уравнений по очереди.
(п + 5) х 2 = 28
(n – 10) ÷ 9 = 10
(n – 2) ² = 25
Попросите учащихся предложить, как они могут определить, какое число вы задумали в каждом примере (n).
Подчеркните сделанные в Занятии 1, Упражнении 2 замечания о том, что существует обратная связь между сложением и вычитанием, а также между умножением и делением. Обратная операция «отменяет» другую операцию.
Работайте в обратном порядке по первому примеру, применяя обратную операцию: 28 ÷ 2 = 14, 14 – 5 = 9и проверьте, что n = 9, подставив его вместо n в исходное уравнение. (9 + 5) х 2 = 28
Предложите учащимся обсудить два других примера в парах и поделиться своими решениями.
Занятие 3
Раздайте каждому учащемуся 2 небольших листа бумаги и карандаши. Пусть каждый учащийся напишет пять своих собственных: «Какое число я думаю?» проблемы. Они должны написать слова каждой из задач на одном листе бумаги, а на втором листе свои решения задач, с числом, которое они думают, вместо «n».
Предложите учащимся обменяться своими проблемами с партнером. Предложите учащимся записывать свои решения проблем своего партнера отдельно от страницы с проблемами. Затем эти проблемы могут быть обменены с другой парой студентов и обсуждены.
Упражнение 4
Предложите учащимся сравнить способ, которым простые и научные калькуляторы дают различных результатов для своих задач.
Они должны ввести решения своих уравнений, но опустить сумму. Например, для исходной задачи (n + 5) x 2 = 28 введите вместо этого: 9 + 5 x 2 = ☐
Научные калькуляторы были запрограммированы так, чтобы следовать соглашениям, в то время как простые калькуляторы в классе — нет.
Предложите учащимся решить свои проблемы и обсудить результаты, полученные с помощью обоих видов калькуляторов.
Занятие 5
Завершите занятие, попросив учащихся записать одну из своих словесных задач «Я думаю о числе» с уравнением внизу своего плаката из Занятий 1 и 2. Покажите плакаты и задуматься об обучении.
Подумайте о символах, выражениях и уравнениях, которые мы используем для выражения математических задач и которые помогают нам их обдумывать.