Карточки по теме «Сложение и вычитание столбиком» 2 класс | Консультация по математике (2 класс) на тему:
Самостоятельная работа Вариант 1. Фамилия _________________________
1.Решите задачи.
Оля собрала 25 грибов, а мама- 35 грибов. Вечером мама пожарила 42 гриба. Сколько грибов осталось?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В вазе было 30 конфет.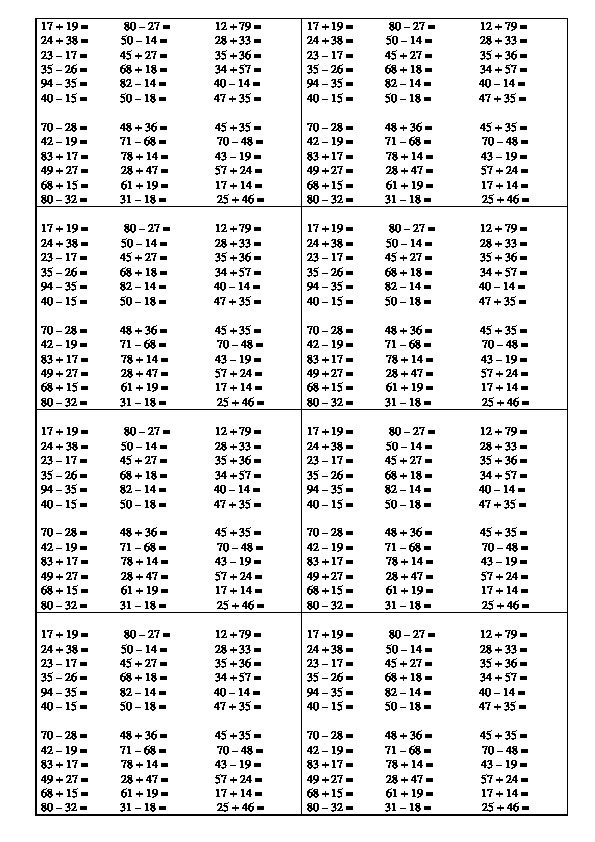 Лена взяла 12 конфет, а Таня 15 конфет. Сколько конфет осталось в вазе?
Лена взяла 12 конфет, а Таня 15 конфет. Сколько конфет осталось в вазе?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Реши примеры столбиком.
Реши примеры столбиком.
67- 38 65- 48 64 — 26 87- 43
36- 24 84 – 5 6 75 — 25 95 — 49
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Самостоятельная работа Вариант 2. Фамилия _________________________
Фамилия _________________________
1.Решите задачи.
В порту стояло 15 кораблей. Вскоре в порт вошло ещё 23 корабля. Через некоторое время порт покинуло 17 кораблей. Сколько кораблей осталось в порту?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У Вовы 14 яблок, у Димы – 7 яблок.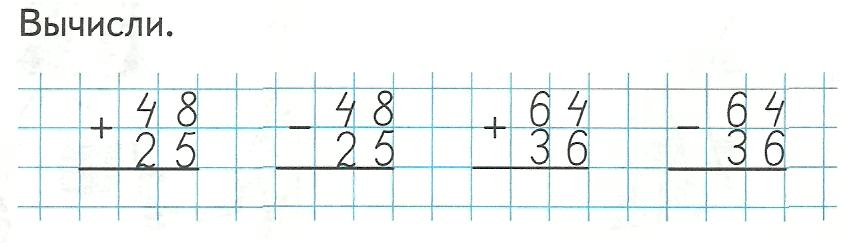 Сколько яблок у Дениса, если известно, что у него на 3 яблока меньше, чем у Вовы и Димы вместе?
Сколько яблок у Дениса, если известно, что у него на 3 яблока меньше, чем у Вовы и Димы вместе?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Реши примеры столбиком.
Реши примеры столбиком.
85- 25 66 — 39 67 – 38 74 – 4 9
44 — 35 77 — 44 87 — 53 8 5 – 67
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Карточки «Решение примеров в столбик» 2 класс
Ф. И._________________________________________________ вариант — 1
И._________________________________________________ вариант — 1
Решите примеры, записывая их столбиком
98 – 43 54 + 25 27 – 4 34 +2
52 +36 67 – 21 26 +70 48 – 24
Ф.И._________________________________________________ вариант — 2
Решите примеры, записывая их столбиком
48 +50 86 – 43 24 + 35 47 – 4
50 + 17 35 – 13 56 + 3 86 – 25
Ф.И._________________________________________________ вариант — 3
Решите примеры, записывая их столбиком
56 + 4 63 + 7 44 +6 75 + 5
31 + 9 52 +8 58 + 2 47 +3
Ф.И._________________________________________________ вариант — 4
Решите примеры, записывая их столбиком
52 +8 57 + 3 25 +5 77 +3
28 +2 64 + 6 36 +4 61 +9
Ф.И._________________________________________________ вариант — 5
52 +18 57 + 23 25 +65 77 +13
28 +42 64 + 16 36 +54 61 +29
Ф.И._________________________________________________ вариант — 6
Решите примеры, записывая их столбиком
56 + 24 63 + 27 44 +26 75 + 15
31 + 49 52 +38 58 +32 47 + 43
Ф.И._________________________________________________ вариант — 7
Решите примеры, записывая их столбиком
70 — 4 80 – 6 40 – 5 30 – 7
20 – 8 50 – 3 60 – 9 90 – 2
Ф.И._________________________________________________ вариант — 8
Решите примеры, записывая их столбиком
70 — 8 80 – 9 40 – 3 30 – 2
20 – 5 50 – 4 60 – 6 90 – 7
Ф.И._________________________________________________ вариант — 9
Решите примеры, записывая их столбиком
70 — 54 80 – 66 40 – 35 30 – 17
20 – 18 50 – 23 60 – 49 90 –52
Ф.И._________________________________________________ вариант — 10
Решите примеры, записывая их столбиком
70 — 54 80 – 56 40 – 25 30 – 27
20 – 18 50 –33 60 – 39 90 – 62
Ф.И._________________________________________________ вариант — 11
Решите примеры, записывая их столбиком
77 +16 35 + 48 27 + 34 34 +38
43 +29 15 + 29 56 + 37 53 + 17
Ф. И._________________________________________________ вариант — 12
И._________________________________________________ вариант — 12
Решите примеры, записывая их столбиком
67 +16 25 + 48 47 + 34 54 +38
53 +29 15 + 49 56 + 27 63 +17
Ф.И._________________________________________________ вариант — 13
Решите примеры, записывая их столбиком
54 – 28 84 – 27 65 – 29 45 – 16
53 — 29 67 — 38 56 — 27 63 — 17
Ф.И._________________________________________________ вариант — 14
Решите примеры, записывая их столбиком
38 – 19 95 – 47 53 – 36 44 — 36
63 – 17 42 – 25 87 – 58 61 — 33
Решите примеры, записывая их столбиком
45 +31 80 – 24 45 – 37 34 + 57 50 – 4 56 +47 63 +24 60 — 21
54 +28 73 – 64 26 +57 50 – 8 70 – 46 38 +27 70 – 15 45 +57
Ф.И._________________________________________________ вариант — 16
Решите примеры, записывая их столбиком
45 +34 80 – 28 45 – 39 34 + 56 50 – 5 56 +49 63 +24 60 — 23
55 +28 72 – 64 28 +57 50 – 6 70 – 36 39 +27 70 – 17 45 +56
Ф.И._________________________________________________
Решите примеры, записывая их столбиком
50 – 7 +22 70 – 8 +36 76 – 23 +42
38 +12 – 9 84 – 34 – 18 98 – 18 — 15
урок с примерами, карточками и видео
Если в вычитании чисел меньше 10 нет ничего сложного, то с двузначными и трёхзначными всё немного сложнее. Требуется зрительное восприятие ребёнком символов. Перед тем как переходить на сложение и вычитание столбиком двузначных и трёхзначных чисел, нужно хорошо изучить устный счёт.
Вычитание чисел столбиком: правила и советы
Результат вычитания можно проверить сложениемПеред усвоением нового способа вычитания, следует объяснить ребёнку, что такое разрядность числа.
Пример: 1385 — четырёхзначное число, где:
- 5 — единицы;
- 8 (80) — десятки;
- 3 (300) — сотни;
- 1 (1000) — тысячи.

Соответственно, самые младшие разряды (единицы) находятся справа, чем левее разряд относительно единиц, тем он старше — десятки, тысячи и т. д.
Принцип действий при вычитании столбиком таков:
- Записываем первое число.
- Строго под ним пишем второе число, но так, чтобы единицы оказались под единицами, десятки — под десятками, сотни — под сотнями.
- Согласно правилу, сначала из единиц вычитаются единицы. В случае когда число, из которого вычитаем, меньше вычитаемого числа, нужно «занять» десяток из следующего разряда. Чтобы избежать путаницы, над тем разрядом, из которого «брали» десятку, нужно поставить точку.
- Операции с остальными разрядами проводятся так же.
Главное — не забывать про те разряды, из которых брали десятки, их значения уменьшаются на единицу.
Карточки для уроков
Вычитание столбиком начинается с самой правой цифрыНа уроках для формирования практических навыков в решении примеров на вычитание столбиком можно раздать детям распечатанные карточки.
Для учеников 2 класса подойдут карточки с примерами на вычитание столбиком двухзначных чисел.
Большее число (уменьшаемое) записывается в столбике сверхуС помощью раздаточного материала на уроке можно проводить небольшие проверочные работы.
Все упомянутые действия по решению примеров на вычитание столбиком выполняются в умеОтдельно можно порешать примеры без перехода через десяток.
Черта в столбике означает знак равенстваУченикам 3–4 класса следует практиковаться в решении примеров с трёхзначными и четырёхзначными числами.
Если при вычитании столбиком над нулём стоит точка, ноль превращается в 9Для учеников среднего звена полезными будут более сложные примеры.
Вычитание в столбик полезно при выполнении действий с большими числамиВидео: как вычитать числа столбиком
Вычитание в столбик — простая арифметическая операция. Для закрепления знаний нужна лишь практика.
Для закрепления знаний нужна лишь практика.
Комплект карточек (10) «Обучающий калейдоскоп. Сложение и вычитание в столбик»
Комплект карточек предназначен для использования на уроках математики в начальной школе. Учитель может использовать карточки в качестве основного вида деятельности на уроке, а также во внеурочной деятельности, в группах продленного дня и математических кружках.
Используется вместе с наглядно-дидактическим пособием «Обучающий калейдоскоп»
Технические характеристики и комплектность
| Габаритные размеры в упаковке (дл.*шир.*выс.), см | 14*28*1 |
| Вес, кг, не более | 0,2 |
| В комплект входят: | |
| карточки с заданиями | 10 шт. |
| руководство по эксплуатации | 1 шт. |
Пособие состоит из 10 полноцветных, напечатанных на картоне и ламинированных пленкой карточек. Карточки снабжены маркировкой, где буква обозначает предмет, первая цифра – код темы, вторая цифра – порядковый номер (тему) карточки в серии, последняя цифра – вариант (I или II).
М18.1.I, М18.1.II. Нахождение числа, записанного словами. Повторение и закрепление знания разрядов многозначных чисел.Рекомендуется использовать во 2, 3 и 4 классах как задания для устного счета.
М18.2.I, М18.2.II. Для учащихся 3 и 4 классов. Вычисления в столбик. Сложение и вычитание трех и четырехзначных чисел с переходом через разряд.Рекомендуется записывать решения в тетрадь.
Вычисления в столбик. Сложение и вычитание трех и четырехзначных чисел с переходом через разряд.Рекомендуется записывать решения в тетрадь.
М18.3.I. Для учащихся 3 и 4 классов. Вычисления в столбик. Сложение и вычитание трех и четырехзначных чисел с переходом через разряд. В четырех заданиях из десяти требуется отыскать число, обозначающее пропущенный разряд вычитаемого или одного из слагаемых.
М18.3.II. Для учащихся 3 и 4 классов. Действия с многозначными числами, оформленные в таблицу, в которой необходимо правильно выбрать действие сложения или вычитания, опираясь на название компонента действия (уменьшаемое, вычитаемое, разность, слагаемое, сумма), и произвести вычисления, используя данные таблицы.Рекомендуется записывать решения в тетрадь.
М18.4.I. Для учащихся 3 и 4 классов. Действия с многозначными числами, оформленные в таблицу, в которой необходимо правильно выбрать действие сложения или вычитания, опираясь на название компонента действия (уменьшаемое, вычитаемое, разность, слагаемое, сумма), и произвести вычисления, используя данные таблицы.
М18.4.
II. Для учащихся 3 и 4 классов. Действия с трехзначными числами, оформленные в таблицу. Необходимо правильно выбрать действие сложения или вычитания и произвести вычисления, опираясь на данные таблицы, в которой указаны длины сторон треугольника и периметр. Рекомендуется записывать условия и решение в тетрадь.М18.5.I. Для учащихся 3 и 4 классов. Сложные примеры на все действия с определением порядка действий и последовательных вычислений, для которых потребуется вычислять в столбик. Задания оформлены в схемы. Не рекомендуется предлагать учащимся выполнение всех десяти заданий сразу. Рекомендуется использовать в качестве дополнительных упражнений по одному–два задания на уроке.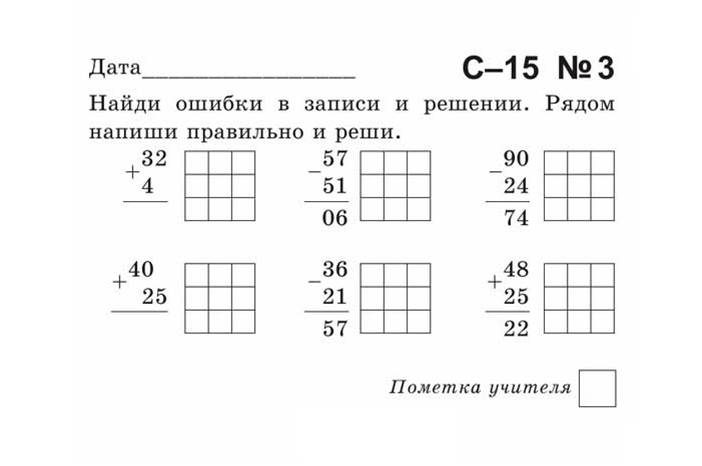 Выполнение заданий развивает логику и требует высокой концентрации внимания.
Выполнение заданий развивает логику и требует высокой концентрации внимания.
1.Организационный момент. Цель: придаёт чувство уверенности в себе и своих силах. 2. Актуализация знаний. Готовность мышления к восприятию учебного материала и осознание потребности в них. 3. Постановка учебной задачи и цели урока. 4. Создание проблемной ситуации. Новые знания. 5. Закрепление полученных знаний. 6. Работа с текстовыми задачами. Рефлексия. | Прочитайте на доске девиз нашего урока « Только вера в свои знания и силы нам помогут добиться успеха». Я желаю вам сегодня добиться не только успеха в учёбе, усовершенствовать свои математические способности, но и получить новые знания. Первое задание вы будете выполнять в парах. Вспомним правила работы в парах. — Возьмите карточку №1. Прочитайте внимательно задание. Обсудите его и выполните в тетради. -Прочитайте: какие числа вы выписали? Числа: 12, 40, 33, 100. -На какие две группы можно разделить эти числа? -Какие числа можно заменить суммой разрядных слагаемых? — Замените эти числа суммой разрядных слагаемых. — Проверка самостоятельной работы. — Для чего нам нужно уметь заменять числа разрядными слагаемыми? — Как вы думаете, какая тема сегодня будет на уроке? Тема урока: Сложение и вычитание двузначных чисел. Цель: Совершенствовать навыки сложения и вычитания многозначных чисел в строчку и в столбик. — Какие задания ещё можно выполнить с записанными числами? — Из данных чисел составить выражения и найти их значения. — В первый столбик записать суммы, а во второй – разности. — Прочитайте: какие выражения вы записали на сложение, на вычитание. 12+33=45 33-12=21 12+40=52 40-33=7 12+100=112 40-12=28 33+40=73 100-12=88 33+100=133 100-33=67 40+100=140 100-40=60 — Какие приёмы счёта вы использовали? Ед.+ед. ед.-ед. Дес.+дес. Дес.-дес. — Как вы записывали выражения? — Решение с объяснением в столбик с переходом через разряд. 1) 81 – 27 95 – 38 80 – 57 64 + 29 — Запишите выражение в столбик: 100 — 67 — Не получается? Почему? — Какое правило мы должны соблюдать при записи вычисления чисел в столбик? — Так как же нам записать это выражение в столбик? 2) 100 – 36 100 – 72 100 – 28 200 – 74 — Объяснение записи выражений в столбик и их вычисление. Самостоятельная работа: карточка №2. Записать примеры в столбик и вычислить. 37 + 12 67 – 28 100 – 54 49 – 24 90 – 53 100 – 43 Самопроверка по эталону: 29 39 46 25 37 57 Составьте с числами 12, 40. 33, 100 простую задачу. — Решите задачу самостоятельно. Анализ составной задачи — Прочитайте текст задачи. В пачке было 100 листов бумаги. В один день израсходовали 33 листа бумаги, во второй день 40 листов. Сколько листов бумаги осталось? — Как эту задачу записать кратко? Анализ задачи. — Прочитайте вопрос задачи. — Можно ли сразу на него ответить? — Что необходимо знать, чтобы ответить на вопрос задачи? — Во сколько действий будем решать задачу? — Почему? — Что узнаем первым действием? — Что узнаем вторым действием? 1.Запись решения задачи: 33 + 40 = 73 (Л.) – израсходовали 100 – 73= 27 (л.) – осталось 2. Составить выражение к этой задаче. 100 – 33 — 40 =27 (л.) – осталось 3. Второй способ: составить уравнение 100 – х = 33 + 40 Ответ: 27 листа бумаги осталось. — Какие новые знания вы сегодня получили? — Проверьте оценочный лист. Всё ли вы заполнили в нём? — Урок закончен. Спасибо за работу. | Дети читают девиз. Дети называют правила работы в парах. Дети читают задание и выполняют его. Учащиеся проверяют самостоятельную работу в парах и отмечают её результат в оценочном листе. — Чётные и нечётные; Круглые и некруглые; Двузначные и трёхзначные. 12, 33 Дети работают самостоятельно. В оценочном листе отмечают выполнение задания. Ответы детей. Можно составить: Выражения Задачу Уравнения Работа в парах. Самопроверка. Отмечают результат в оценочном листе. Ответы детей. В строчку Дети объясняют вычисления выражений в столбик. Дети пытаются записать выражение на доске столбиком. Объясняют свои действия. Единицы под единицами, десятки под десятками. Дети работают самостоятельно. Проверяют работу и отмечают её результат в оценочном листе. Дети составляют задачи разного вида. Запись решения задачи. Дети предлагают виды краткой записи. Строят модель к задаче. Рассуждение детей о решении задачи. Дети проверяют оценочный лист. | Личностные: понимание причин успеха в учёбе. Коммуникативные: учащиеся получают возможность договариваться между собой и приходить к общему решению. Познавательные: поиск нужной информации в тексте. Регулятивные: контролировать и оценивать свои действия. Коммуникативные: участие в диалоге Познавательные: умение проводить классификацию Предметные: представление чисел в виде суммы разрядных слагаемых. Регулятивные: контролировать и оценивать свои действия. Регулятивные: принимать и сохранять учебную задачу. Личностные: формирование интереса к различным видам учебной деятельности. Коммуникативные: умение работать в парах, уважать мнение товарища. Регулятивные: контролировать и оценивать свои действия. Предметные: умение выявить приёмы сложения и вычитания. Предметные: умение складывать и вычитать числа. Регулятивные: умение оценивать успешность работы. Предметные: умение составлять и решать простые задачи. Коммуникативные: участие в диалоге Предметные: умение решать составную задачу с помощью рассуждений. Регулятивные: самооценка |
Ход урока | Примечания | |||
Деятельность учителя | Деятельность учащихся | |||
1. | — Прозвенел звонок и смолк – начинается урок, мы за парты тихо сели и соседа не задели. — Здравствуйте, ребята, меня зовут Наталья Сергеевна. Сегодня я проведу у вас урок Математики. | — Дети приветствуют учителя. | — СЛАЙД 1 | |
2.Актуализация знаний (Устный счёт) | — Ребята, сегодня у нас с вами будет необычный урок. Как выдумаете, почему? — Дело в том, что у нас сегодня гостья — к нам на урок приехала Мудрая Черепаха. Черепаха приехала к нам с необыкновенно красивого, тропического острова. Вы хотите узнать, как же называется этот необычный остров? Тогда вам нужно будет поработать в парах и выполнить задание: соотнести каждое число с порядковым номером буквы алфавита. 12 | 21 | 2 | 1 |
К | У | Б | А | — Ответы детей. — Да. — Дети в парах выполняют задание на карточках. — КУБА. — Дети оформляют тетради. — Дети письменно выполняют задание. — 36. — Да. — Ребёнок выходит к доске и показывает более рациональный способ записи. — Это двузначное число. — 3. 6. — Дети письменно выполняют задание. — Оксана записывает на доске свой результат. — Дети по цепочке выходят к доске и записывают равенства. — 18 + 18 = 36 — Ответы детей. — Да. — Да. — Карточки с выражениями. — Ответы детей. — Ответы детей (будем учиться решать выражения такого вида – в столбик). — Сложение и вычитание двузначных чисел в столбик. — Ответы детей (научиться решать выражения такого виды и т.д.) | — СЛАЙД 2 — Карточки с заданием. — СЛАЙД 3 — СЛАЙД 4 — Работа в тетрадях. — Работа у доски. — Работа в тетради. — Работа у доски. — Работа у доски. — СЛАЙД 5 — Работа у доски. — СЛАЙД 6 — Конверт с выражениями. |
3.Работа над новой темой | — Итак, начинаем работу. — Ребята, посмотрите внимательно на первое выражение — сложение, знакома ли вам такая запись? — Что нового вы увидели в такой записи? — Как записаны числа? — Как вы думаете, почему? — Как нашли сумму? — Итак, давайте с вами проверим, правильно ли мы с вами всё предположили. А для этого откройте учебник на стр.76, задание №1. Прочитайте в рамочке правило, как записывают двузначные числа, складывая их в столбик. Оксана, прочитай для всех правило в рамочке. Спасибо! — Итак, какие в этом тексте можно выделить главные слова, которые помогут составить нам алгоритм сложения в «столбик»? Совершенно верно! — Мудрая Черепаха решила нам помочь и принесла нам алгоритм сложения в «столбик», чтобы нам было легче работать. — Итак, с алгоритмом сложения мы с вами познакомились. Посмотрите, Мудрая Черепаха ещё принесла нам конверт. Давайте скорей узнаем, что же там лежит. Маша, выйди и открой нам конверт. Итак, что на этот раз отправила нам Черепаха? А что нужно сделать с этим выражением? — Давайте выполним задние Черепахи. Я буду работать у доски, а вы будьте внимательны. Итак, выражение 43 + 55. Записываю в столбик. Пишу первое слагаемое 43, под ним пишу второе слагаемое 55 так, чтобы единицы были под единицами, десятки под десятками. Между ними ставлю знак «+». Черта под вторым слагаемым означает знак «=». Начинаю складывать единицы: 3 + 5 = 8. Записываю 8 под единицами. Складываю десятки: 4 + 5 = 9. Записываю 9 под десятками. Читаю: сумма чисел 43 и 55 равна 98. — Итак, мы выполнили задние Мудрой Черепахи? — Тогда продолжаем работу дальше. — Ребята, посмотрите внимательно на второе выражение – вычитание. Такая запись вам уже знакома. Скажите, как нашли разность? — Итак, давайте с вами снова проверим, правильно ли мы всё предположили. А что нам для того нужно сделать? Совершенно верно! Стр.76, задание №2. Прочитайте в рамочке правило, как записывают двузначные числа, вычитая их в столбик. Катя, прочитай для всех правило в рамочке. Спасибо! — Итак, а какие в этом тексте можно выделить главные слова, которые помогут составить нам алгоритм вычитания в «столбик»? Совершенно верно! — Мудрая Черепаха решила нам снова помочь и принесла нам алгоритм вычитания в «столбик», чтобы нам было легче работать. — Итак, с алгоритмом вычитания мы с вами познакомились. Посмотрите, Мудрая Черепаха ещё принесла нам конверт. Давайте скорей узнаем, что же там лежит. Таня, выйди и открой нам конверт. Итак, что отправила нам Черепаха? А что нужно сделать с этим выражением? — Давайте выполним задание Мудрой Черепахи. Я буду работать у доски, а вы будьте внимательны. Итак, выражение 98 — 55. Записываю в столбик. Пишу первое число 98, под ним пишу второе число 55 так, чтобы единицы были под единицами, десятки под десятками. Между ними ставлю знак «-». Черта под вторым числом означает знак «=». Начинаю вычитать единицы: 8 — 5 = 3. Записываю 3 под единицами. Вычитаю десятки: 9 — 5 = 4. Записываю 4 под десятками. Читаю: разность чисел 98 и 55 равна 43. — Итак, мы выполнили задние Мудрой Черепахи? | — Ответы детей. — Ответы детей. — Ответы детей (друг под другом, дес. под дес., ед. под ед.) — Ответы детей. — Ответы детей. — Дети читают правило. — Ребёнок читает правило в рамочке вслух. — Записываю… Складываю единицы… Складываю десятки… Читаю ответ… — Какое-то выражение. — Решить выражение в столбик. — Да. — Ответы детей. — Обратиться к учебнику. — Дети читают правило. — Ребёнок читает правило в рамочке вслух. — Записываю… Вычитаю единицы… Вычитаю десятки… Читаю ответ… — Какое-то выражение. — Решить выражение в столбик. — Да. | — Карточка со сложением. — Работа в учебнике. — Алгоритм сложения в «столбик». — Конверт с выражением 43 + 55. — Работа у доски (учитель показывает сложение в столбик с объяснением) — Карточка с вычитанием. — Работа в учебнике. — Алгоритм вычитания в «столбик». — Конверт с выражением 98 — 55. — Работа у доски (учитель показывает сложение в столбик с объяснением) | |
Физкультминутка | А теперь отдохнём. Встали. Мы писали и решали. Глазки наши подустали. Мы зажмурим глазки крепко. Раз! Открывает глазки класс. Вверх посмотрим дружно мы Посчитаем: раз, два, три! Вниз посмотрим на четыре. Глазки к полу опустили. Мы на пять посмотрим влево. Будем делать мы умело. Вправо смотрим. Это шесть. А теперь прошу всех сесть. Отдохнули и теперь Будем все решать смелей. | |||
4.Работа над пройденным материалом ЕСЛИ УСПЕЕМ | — Итак, продолжаем работу. Мудрая Черепаха предлагает выполнить нам следующее задание — поработать с учебником. Стр. 77 в учебнике, задание №3: вычислите с объяснением. Посмотрите, два выражения мы отсюда уже научились решать, значит, их мы рассматривать не будем. Работать будем по цепочке. Итак, 43 + 5, 43 + 50, 48 – 5, 93 – 50. Молодцы! — Следующее задание — №4: сравните (больше, меньше или равно). Оксана, пойдём к доске. Записываем 1 выражение: а + (54 + 42) * 97 + а Можем ли мы сразу же сравнить? Что сначала нужно сделать? Правильно! Считаем. Сколько получится? Итак, тогда какое выражение у нас сейчас получится: а + 96 * 97 + а Записываем. А сейчас мы можем сравнить? Сравниваем. Читаем результат. Верно! — Следующее задание — №5 под буквой Б: решите задачу. — Прочитайте текст задачи. Маша, прочитай нам задачу ещё раз вслух — Прочитайте условие задачи. О чём говорится в задаче? Сколько в коробку сложили катушек с красными нитками? Сколько катушек с синими нитками? Сколько катушек с зелёными нитками? А сколько катушек с белыми нитками? — Давайте схематически изобразим катушки ниток кругами. Таня, изобрази нам красные нитки. Катя, изобрази нам синие нитки. Оксана, изобрази нам зелёные нитки. А что сказано про белые нитки? К.Н. к к к С.Н. с с с с З. Б.Н. ? — Что требуется найти в задаче? — Какое нам ещё дополнительное условие открылось? — Значит, чем ещё мы должны дополнить нашу схему? Дополняем. К.Н. к к к С.Н. с с с с З.Н. з з з з з 28 Б.Н. бббббббббббббббб — Вот такая получилась у нас краткая запись. — Итак, что узнаем 1 действием? Каким действием? Записываем 1 действие. Таня, запиши 1 действие на доске: 1)3 + 4 = 7 (к.) — Что узнаем 2 действием? Каким действием? Записываем 2 действие. Маша, запиши 2 действие на доске: 2)7 + 5 = 12 (к.) — Что узнаем 3 действием? Каким действием? Записываем 3 действие. Катя, запиши 3 действие на доске: 3)28 – 12 = 16 (к.) — Итак, мы с вами нашли, сколько катушек с белыми нитками положили в коробку? Оксана, дополни нашу схему, дорисуй белые нитки. — Итак, мы с вами ответили на вопрос задачи? Запишите ответ самостоятельно: Ответ: 16 катушек с белыми нитками положили в коробку. — Следующее задание — №6. Выполняем устно. — Как называются такие математические записи? — Назовите всевозможные значения переменной: 9 – а 18 – (6 + с) (d — 7) + 10 | — Дети устно по цепочке выполняют задние. — Дети письменно выполняют задание, один ребёнок у доски. — Нет. — Посчитать в скобках. — 96. — Да. — а + 96 меньше 97 + а. — Дети читают задачу. — В задаче говорится о катушках ниток. — 3. — 4. — 5. — Несколько. — Дети выходят к доске и изображают катушки ниток. — Неизвестно. — Сколько катушек белых ниток положили в коробку, если в ней стало 28 катушек с нитками? — Что всего катушек с нитками стало 28. — Фигурной скобкой. — Сколько всего катушек с красными и синими нитками. — Сложением. — Сколько было всего катушек с красными, синими и зелёными нитками. — Сложением. — Сколько было катушек с белыми нитками. — Вычитанием. — Да. — Да. — Дети устно выполняют задание. — Выражения с переменной. — Ответы детей. | — Работа в учебнике. — Работа в учебнике. — Работа в тетради и у доски. — Работа в учебнике. — Работа у доски. — Работа в тетради. — Работа у доски. — Работа в учебнике. | |
5.Итог | — К сожалению, нашей сегодняшней гостье уже пора возвращаться обратно на свой остров. Давайте скажем ей большое спасибо за работу и попрощаемся с ней. — Наш урок тоже подходит к концу. Пора подводить итог. — Ребята, скажите, достигли ли вы целей, которые ставили себе на урок? — А чем сегодня на уроке мы с вами занимались? — Что нового на уроке вы узнали? — Какие вычисления мы с вами сегодня учились делать? | — Ответы детей. — Решали выражения, задачу и т.д. — Ответы детей. — Сложение и вычитание двузначных чисел в столбик. | ||
6.Домашнее задание | — Итак, дома обязательно стр. 77, №5 под буквой А и по желанию стр. 77, №4 сравнить оставшиеся выражения. | — Дети записывают Д/З. | — СЛАЙД 7 | |
7.Рефлексия | — Итак, оцените себя и свою работу на уроке: — Похлопайте в ладоши те, кто научился складывать и вычитать двузначные числа в столбик и может научить этому другого. Спасибо! — Потопайте ногами те, кто не понял, не научился складывать и вычитать двузначные числа в столбик. — Спасибо за работу, урок окончен. Отдыхайте! | — Дети оценивают себя. | — СЛАЙД 8 |
Индивидуальные карточки для 3 класса по теме «ПИСЬМЕННЫЕ ПРИЁМЫ СЛОЖЕНИЯ И ВЫЧИТАНИЯ В ПРЕДЕЛАХ 1000»
МБОУ «Верхнемедведицкая средняя общеобразовательная школа»
Курского района Курской области
ИНДИВИДУАЛЬНЫЕ КАРТОЧКИ
ДЛЯ 3 КЛАССА ПО ТЕМЕ:
Учитель начальных классов
первой квалификационной категории
Алферова Галина Николаевна
__________________________________________________________________________________________
Карточка № 1
Реши примеры, записывая столбиком:
345+498, 936-629, 298+635, 845-287, 689+288, 996-359
___________________________________________________________________________________________
Карточка № 2
Реши примеры, записывая столбиком:
326+289, 801-526, 425+ 397, 723-284, 981-423, 209+316
_________________________________________________________________________________________
Карточка № 3
Реши примеры, записывая столбиком:
563+355, 794-425, 638+197, 932-495, 279+631, 804-467
___________________________________________________________________________________________
__________________________________________________________________________________________
Карточка № 4
Реши примеры, записывая столбиком:
864-246, 564+276, 612-495, 175+388, 795- 218, 239+533
___________________________________________________________________________________________
Карточка № 5
Реши примеры, записывая столбиком:
816-257, 729+188, 564-286, 255+ 377, 565-458, 563+375,
_________________________________________________________________________________________
Карточка № 6
Реши примеры, записывая столбиком:
667-248, 436+375, 856-568, 347+255, 922- 567, 564+576
___________________________________________________________________________________________
__________________________________________________________________________________________
Карточка № 7
Реши примеры, записывая столбиком:
413+187, 536-249, 109+178, 583-268, 903-286, 652+ 289
___________________________________________________________________________________________
Карточка № 8
Реши примеры, записывая столбиком:
444+478, 854-287, 653+277, 675-286, 557+395, 775-388
_________________________________________________________________________________________
Карточка № 9
Реши примеры, записывая столбиком:
944-276, 564+88, 674-99, 545+297, 777-389, 222+399
___________________________________________________________________________________________
__________________________________________________________________________________________
Карточка № 10
Реши примеры, записывая столбиком:
268+556, 742-384, 354+378, 463-389, 232+629, 323-154
___________________________________________________________________________________________
Карточка № 11
Реши примеры, записывая столбиком:
197+226, 926-648, 858-599, 268+169, 880-677, 62+715
_________________________________________________________________________________________
Карточка № 12
Реши примеры, записывая столбиком:
269+721, 604+286, 892-283, 542-372, 298+570, 751-478
___________________________________________________________________________________________
__________________________________________________________________________________________
Карточка № 13
Реши примеры, записывая столбиком:
202+159, 183+387, 126+544, 384-279, 846-577, 262-93
___________________________________________________________________________________________
Карточка № 14
Реши примеры, записывая столбиком:
281+182, 181+719, 271+439, 593-239, 362-177, 723-232
_________________________________________________________________________________________
Карточка № 15
Реши примеры, записывая столбиком:
554+49, 29+481, 29+755, 547-128, 794-259, 823-309
___________________________________________________________________________________________
__________________________________________________________________________________________
Карточка № 16
Реши примеры, записывая столбиком:
453-149, 832-348, 736-417, 265+458, 453+138, 685+295
___________________________________________________________________________________________
Карточка № 17
Реши примеры, записывая столбиком:
649-181, 321-207, 361-86, 48+403, 696+149, 35+569
___________________________________________________________________________________________
Карточка № 18
Реши примеры, записывая столбиком:
507+389, 160+579, 89+818, 623-144, 390+297, 628+83
___________________________________________________________________________________________
__________________________________________________________________________________________
Карточка № 19
Реши примеры, записывая столбиком:
427+509, 87+376, 582-185, 79+830, 605-262, 708-242
___________________________________________________________________________________________
Карточка № 20
Реши примеры, записывая столбиком:
169+691, 142+338, 874-796, 808-238, 607-246, 865+91
_________________________________________________________________________________________
Карточка № 21
Реши примеры, записывая столбиком:
265+195, 92+419, 232+679, 323-153, 957-869, 663-95
___________________________________________________________________________________________
__________________________________________________________________________________________
Карточка № 22
Реши примеры, записывая столбиком:
508+459, 491+369, 415+395, 953-384, 946-267, 702-68
___________________________________________________________________________________________
Карточка № 23
Реши примеры, записывая столбиком:
763+99, 514+395, 769+131, 854-59, 807-279, 465-10 6
_________________________________________________________________________________________
Карточка № 24
Реши примеры, записывая столбиком:
583+268, 668-266, 57+377, 883-534, 701+219, 777+56
___________________________________________________________________________________________
_____________________________________________________________________________________
Карточка № 25
Реши примеры, записывая столбиком:
777+56, 328+358, 206+473, 294-79, 600-294, 950-668
___________________________________________________________________________________________
Карточка № 26
Реши примеры, записывая столбиком:
866-497, 700-77, 644-308, 850-167, 477-188, 905-609
_________________________________________________________________________________________
Карточка № 27
Реши примеры, записывая столбиком:
345+453, 540+168, 621+149, 456-134, 405-145, 400-174
___________________________________________________________________________________________
__________________________________________________________________________________________
Карточка № 28
Реши примеры, записывая столбиком:
546+354, 654+166, 432+469, 500-135, 604-336, 543-177
___________________________________________________________________________________________
Карточка № 29
Реши примеры, записывая столбиком:
407-238, 254+247, 317+291, 107+277, 530-132, 600-146
_________________________________________________________________________________________
Карточка № 30
Реши примеры, записывая столбиком:
360+273, 740-143, 534-287, 600-127, 575+278, 428+344
___________________________________________________________________________________________
Свободное владение языком с добавлением и вычитанием
Мир чисел чрезвычайно обширен, и это основная идея, которую изучают ученики 2-го класса. Они расширяют свои знания о числах от 100 до 1000 и повторяют операции, которые они выучили в 1-м классе, с большими числами. Свободное владение сложением и вычитанием, которое ученики усвоили в этом учебном году, создает прочную основу для умножения и деления, с которыми они столкнутся в 3-м классе.
В учебной программе 2-го класса «Счастливые числа» учащиеся много работают с разрядами, так как им необходимо понимать числовые позиции, чтобы освоить операции с трехзначными числами.Они изучают новые инструменты для математических операций, такие как диски с числовыми значениями и диаграмма с числовыми значениями, и расширяют свои знания процедурной беглости, изучая стандартный алгоритм сложения и вычитания столбцов и ментальных стратегий. Студенты практикуют эти навыки, используя осязаемые и яркие визуальные модели, представленные в нескольких представлениях, чтобы создать прочную и мощную основу для будущих математических достижений.
Изучите ниже многие задания и учебные сценарии для 2-го класса!
Все упражнения, упомянутые ниже, являются частью курса «Счастливые числа» для 2-х классов.Посетите HappyNumbers.com, чтобы ознакомиться с нашей полной учебной программой и подписаться на бесплатную пробную версию.
Основы свободного владения
Happy Numbers помогает студентам развить беглость речи в несколько этапов. Во-первых, они учатся делать десять.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Затем они прибавляют единицы к десяти или вычитают единицы из двузначного числа, чтобы получить десять.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Кроме того, учащиеся складывают и вычитают однозначное число и двузначное число, не переходя через десять.
Чтобы увидеть полное упражнение, перейдите по этой ссылке.
И, наконец, проделайте это через десятку.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
В Модуле 1 студенты работают с числами до 100.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Измерение длины
В 1 классе ученики познакомились с концепцией единицы измерения длины. Сначала они рассматривают его через реальный сценарий с кроссовками.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Затем «Счастливые числа» напоминают им об использовании сантиметров…
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
… и представляет линейку.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
С линейкой студенты изучают понятие миллиметра и его отношение к сантиметру.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Наконец, они используют обе единицы измерения для определения сумм и разностей длин.
Чтобы увидеть полное упражнение, перейдите по этой ссылке.
Трехзначные числа и значение разряда
Студенты начинают практиковаться с трехзначными числами на знакомой модели предметов в десятикадрах.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Они развивают беглость в числовой последовательности выше 100, решая упражнения с числовой линией.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Студенты учатся составлять трехзначное число, используя представление блока Base-10.Очевидно, что эта модель ограничивается большими числами, поэтому «Счастливые числа» в это упражнение также включают в себя карточки с номинальными значениями. Они усиливают репрезентативность и помогают определить ценность места.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Затем учащиеся практикуют разложение числа на сотни, десятки и единицы, используя только карточки с числовыми значениями.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Кроме того, они изучают единичные, стандартные, развернутые и словоформы чисел в запоминающихся визуальных сценариях, подобных этому с милыми осьминогами. В Happy Numbers все упражнения озвучены на английском и испанском языках, поэтому учащиеся могут читать и слушать инструкции на языке по своему выбору.
Чтобы увидеть полное упражнение, перейдите по этой ссылке.
Студенты знакомятся с таблицей стоимости. Это очень полезно при работе с составными числами.Представление более абстрактное, чем предыдущие, и удобное, так как студенты могут перетаскивать диски по диаграмме в качестве манипуляторов. Сначала они учатся использовать его для двузначных чисел.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Затем они начинают тренироваться с трехзначными числами.
Чтобы увидеть полное упражнение, перейдите по этой ссылке.
Посредством различных упражнений и визуальных представлений Happy Numbers помогает учащимся узнать, что такое эквивалентность между единицами, десятками, сотнями и тысячами.Они подкрепляют знания через диалог с забавными болванами.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Чтобы развить навыки определения числовой ценности, Happy Numbers заставляет учащихся решать «более или менее» задачи. Они складывают и вычитают 1, 10 или 100 к разным трехзначным числам или из них.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Игровые сценарии делают математику увлекательной и помогают отрабатывать новые навыки!
Чтобы увидеть полное упражнение, перейдите по этой ссылке.
Наконец, учащиеся могут определять схемы подсчета и составлять в соответствии с ними числовые ряды.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Сравнение трехзначных чисел
Чтобы учащиеся могли свободно владеть числами до 1000 и их разрядами, Happy Numbers дополняет учебную программу упражнениями по упорядочиванию и сравнению чисел. Во-первых, учащиеся понимают разницу между двузначными и трехзначными числами с помощью визуальных структур.
Чтобы увидеть полное упражнение, перейдите по этой ссылке.
Затем они учатся сравнивать два трехзначных числа. Карточки с разнесенными ценностями помогают определить разницу между числами в сотнях, десятках или единицах.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Кроме того, студенты практикуются в сложных задачах, где им нужно сначала построить числа на основе визуальных представлений, а затем расположить их в порядке возрастания и убывания.
Чтобы увидеть полное упражнение, перейдите по этой ссылке.
Сложение и вычитание столбцов
Во 2-м классе учащиеся также изучают стандартные алгоритмы сложения и вычитания столбцов, чтобы научиться бегло говорить с учетом разряда. Это потрясающе мощный фундамент для развития математического мышления! Мы начинаем использовать его в сочетании с картами количественной ценности, чтобы помочь учащимся понять, что здесь им необходимо применять знания о числовой ценности, которые у них уже есть.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Только после этого они переходят к использованию одних только столбцов для сложения двузначных чисел без перегруппировки.
Чтобы увидеть полное упражнение, перейдите по этой ссылке.
Вдобавок тренируются на модели диска. Happy Numbers использует эти представления по отдельности или вместе, чтобы показать масштабируемость математической операции и построить сложное понимание концепции.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Например, вот как это выглядит, когда студенты учатся складывать с обменом на сотни.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Happy Numbers предоставляет пошаговые инструкции для объяснения каждой новой концепции. Посмотрите, как учащиеся учатся вычитать с помощью обмена с помощью пошаговых подсказок.
Чтобы увидеть полное упражнение, перейдите по этой ссылке.
Позже учащиеся используют этот навык для решения задачи вычитания двух- и трехзначных столбцов.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Наконец, они работают по стандартному алгоритму с двумя трехзначными числами.
Чтобы увидеть полное упражнение, перейдите по этой ссылке.
Столбцы будут использованы позже для умножения, поэтому очень важно изучить эту процедуру качественно.Happy Numbers предоставляет студентам большое количество разнообразных заданий для практики и развития его использования.
Психологические стратегии
Модуль 5 учебной программы «Счастливые числа» для 2-го класса сконцентрирован на разработке ментальных стратегий сложения и вычитания в пределах 1000. Ментальные стратегии также основаны на числовом значении, и «Счастливые числа» сначала объясняют эту связь с помощью формы единиц и дисков с указанием значений. . Студенты видят, что сложить круглые числа так же просто, как сложить однозначные числа.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Шаг за шагом Happy Numbers дает учащимся меньше подсказок и больше свободы решать удобным для них способом.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Тем не менее, мы не хотим, чтобы учащиеся забывали сначала сделать 10 или 100…
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
… навык, который также применим к вычитанию, обратной стороне сложения.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
После этой практики с трех- и двузначными числами ученики решают задачи только с трехзначными числами. Они готовы!
Чтобы увидеть полное упражнение, перейдите по этой ссылке.
Подготовка к 3 классу
После существенной практики сложения и вычитания студенты переходят к основам умножения и деления.Во 2-м классе они еще не будут напрямую участвовать в этих математических операциях, но они познакомятся с основными концепциями равных групп, повторного сложения и массива.
Поскольку это самое начало, мы начинаем с манипуляторов, которые выглядят так же, как реальные объекты.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Учащиеся плавно перетаскивают числа и знаки на экране, создавая глубокий и ощутимый опыт.
Чтобы увидеть полное упражнение, перейдите по этой ссылке.
Далее идет повторное сложение предложений на основе массива.
Чтобы увидеть полное упражнение, перейдите по этой ссылке.
Это вдвойне мощно, потому что массивы будут использоваться не только при формировании умножения, но и при измерении области, которую они будут изучать в 3-м классе. Учащиеся выполняют задания, которые закладывают эту основу в Теме C Модуля 6.
Чтобы просмотреть полное упражнение, перейдите по этой ссылке.
Цветные квадраты выглядят так же, как единицы площади, и используются здесь в качестве манипуляторов для построения простых геометрических фигур, которые ученики научатся измерять в 3 классе.
Практика ведет к совершенству
Когда учитель не может каждую минуту стоять за спиной учеников, очень важно выбрать инструмент, который привлечет внимание и адаптируется к потребностям каждого ученика.Об этом мы думали, создавая упражнения для вашего класса. В конце концов, чтобы освоить что-либо в математике, нужно пробовать, пробовать и пробовать снова. Поэтому Happy Numbers подготовили большое количество упражнений с яркими и понятными визуальными моделями, поддержкой озвучивания и увлекательными сценариями. Дружественная и отзывчивая программа погрузит учащихся в математику и поможет им с удовольствием освоить стандарты 2-го класса. Изучите учебную программу 2-го класса и развивайте беглость речи в своем классе!
Как можно улучшить свои инструкции с помощью счастливых чисел?
Принести счастливые числа в класс невероятно легко, и вы можете сделать это в любой момент учебного года.Зарегистрируйтесь сейчас или посмотрите минутное видео, которое проведет вас через настройку:
Если у вас возникнут дополнительные вопросы, наша служба поддержки всегда готова помочь вам. Щелкните синий значок программы обмена сообщениями в правом нижнем углу этой страницы, чтобы начать с ними разговор.
Сложение слева направо: стратегия сложения
Сложение слева направо (также известное как внешнее сложение или метод частичных сумм) — одна из самых мощных математических стратегий в уме для обучения сложению двух- или трехзначных чисел.Однако многих сбивает с толку, почему это важно и почему оно может быть более эффективным, чем традиционное вертикальное добавление.
ПОЧЕМУ ЭТО ТАК ЭФФЕКТИВНО?
Самое лучшее в сложении слева направо — то, что эта стратегия способствует реальному пониманию.
Когда вы решаете уравнение с помощью стандартного алгоритма (вероятно, так, как вы научились складывать многозначные числа), вы используете серию шагов. Это включает в себя сначала добавление единиц, перенос при необходимости, затем добавление десятков, перенос при необходимости и т. Д.Эти шаги навсегда останутся в вашей памяти, и для тех, у кого есть отличные навыки запоминания, это может быть эффективным.
ОДНАКО стандартный алгоритм не способствует пониманию разряда и смысла числа. Это основная причина того, что современные инструкции по математике, как правило, уклоняются от традиционного алгоритма в начальных классах. Мы хотим, чтобы наши студенты действительно понимали, что они делают. Когда учеников обучают методам, которые стимулируют мысленную математику, они могут более гибко думать не только об этой изолированной концепции, но и о других математических концепциях.
ПРИМЕРЫ
Давайте посмотрим на несколько примеров сложения слева направо в действии.
В этом примере мы складываем 25 + 34. Сначала мы складываем десятки: 20 + 30, чтобы получилось 50. Затем мы складываем единицы: 5 + 4, чтобы получилось 9. Наконец, мы прибавляем 50 + 9, чтобы получить 59. Хотя это может показаться запутанным, если написано, как оно есть , этот процесс происходит очень быстро, когда учащийся понимает его — обычно это можно решить максимум за пару секунд.
Сложение слева направо также эффективно для добавления 3-значных плюс 3-значных чисел. В этом примере мы видим, что сначала складываем сотни, затем десятки, а затем единицы. Наконец, мы складываем все эти суммы вместе.
Когда учащиеся выполняют сложение таким образом, они хорошо понимают значение места и его значение. Например, в приведенном выше уравнении ученики видят «1» в 147 как 100, а не просто 1.«4» в 147 понимается как 40, а не просто 4. Это важное знание, если мы хотим, чтобы наши ученики стали эффективными математиками.
Всякий раз, когда мы преподаем математические стратегии, важно преподавать их таким образом, чтобы улучшить концептуальное понимание. Конкретно-репрезентативная абстрактная модель — отличная обучающая модель для этого. В видео ниже я подробнее расскажу о том, как можно обучить сложению слева направо с помощью модели CRA.
СЛЕДУЮЩИЕ ШАГИ:
- Если вам нужна полная поддержка для обучения стратегиям сложения в вашем классе, ознакомьтесь с The Addition Station ЗДЕСЬ. Вы найдете стратегию сложения слева направо на дополнительных станциях для старших классов. Эти математические станции представляют собой станции для самостоятельного обучения, ориентированные на учащихся, для освоения основных математических стратегий. Студенты продвигаются по уровням в своем собственном темпе, гарантируя, что они всегда сталкиваются с проблемами, и работают в полную силу.
- Прочтите другие сообщения на этом сайте о стратегиях сложения ЗДЕСЬ.
- Загрузите БЕСПЛАТНОЕ упражнение для отработки стратегии сложения слева направо ЗДЕСЬ.
- Ознакомьтесь со стратегией добавления слева направо » ЗДЕСЬ.
- Здесь вы можете найти карточки с заданиями, чтобы усилить стратегию сложения слева направо:
Первые математические навыки и учащиеся с математической сложностью
Дети идут в начальную школу с различными математическими навыками. Некоторые дети понимают основы чисел и математики, в то время как другие борются с основами счета, распознавания чисел, понимания символов, количественного различения и концепций сложения и вычитания.Часто этот набор начальных числовых умений называется числовыми умениями, или начальными умениями считать. Студенты должны освоить и понять эти компетенции, прежде чем переходить к более сложным математическим задачам. В этой статье описываются важные ранние числовые навыки и дается описание того, как этим навыкам можно научить учащихся, испытывающих трудности с математикой.
РАННИЕ ЧИСЛОВЫЕ КОМПЕТЕНТНОСТИ И УЧАЩИЕСЯ С МАТЕМАТИЧЕСКИМИ ТРУДНОСТЬЮ
Перед тем как решать задачи по алгебре, геометрии, дробям и вычислениям, студенты должны хорошо понимать числа (Malofeeva, Day, Saco, Young, & Ciancio, 2004).Иногда это называется числом , смыслом (например, Jordan, 2007; Kaminski, 2002; Wagner & Davis, 2010) или ранней математикой (например, Aunio, Hautamaki, Sajaniemi, & Van Luit, 2009; Bryant et al., 2011; VanDerHeyden et al., 2011). Независимо от используемого термина, конструкция относится к ранним численным компетенциям, которые лежат в основе развития компетенций в математике. В этой статье мы называем этот набор навыков начальными числовыми компетенциями.
Что такое ранние численные компетенции?
Хотя не существует единого определения ранних числовых компетенций, несколько исследователей определили ранние числовые компетенции, которые важны для молодых студентов (Berch, 2005; Bryant et al., 2011; Герстен и Чард, 1999; Гриффин и Кейс, 1997; Кауфманн. Хэндл и Тони, 2003; Lago & DiPerna, 2010). См. Диаграмму ранних численных компетенций. Некоторые темы (например, числовые значения или базовые комбинации чисел) требуют предварительных знаний по другим темам (например, распознавание чисел или сравнение чисел). Мы представляем эти ранние числовые компетенции как совокупность, потому что развитие учащихся ранних числовых компетенций не всегда линейно, и учащиеся различаются по срокам, по которым они приобретают эти навыки.
Ранние числовые компетенции
Важность ранних численных компетенций
Дети идут в школу (то есть в детский сад) с широким набором начальных числовых навыков. Некоторые дети уже знают числа, знают их названия и могут решать простые задачи на сложение и вычитание; другим сложно определить числа и считать от 1 до 10 (Lembke & Foegen, 2009). Раннее участие в числовой деятельности дома, в дошкольном учреждении или в детском саду играет важную роль в формировании у учеников детского сада ранних числовых компетенций (Baroody & Benson, 2001; Jung, 2011: Skwarchuk, 2009).Чем больше учащиеся знакомятся с ранними числовыми компетенциями в играх, рассказах или играх до начала формального обучения, тем лучше они понимают строительные блоки математики (Ramani & Siegler, 2008).
Одним из признаков того, что эти ранние числовые навыки важны, является то, что они предсказывают более поздние достижения в математике. Например, Locuniak и Jordan (2008) протестировали 198 учеников весной детского сада по ранним числовым мерам и снова зимой второго класса по мерам беглости вычислений.Учащиеся с показателями ниже 25-го процентиля в начале детского сада были отнесены к группе риска плохого развития математики. Первые числовые меры включали вопросы о счете, знании чисел, невербальном вычислении, числовых комбинациях и задачах рассказа. Измерение беглости вычислений состояло из 25 комбинаций чисел сложения и 25 чисел вычитания. Ранняя числовая компетентность, измеренная в детском саду, была важным показателем беглости вычислений во втором классе. Более 50% учащихся из группы риска (выявленных в детском саду) по-прежнему показывают результаты ниже 25-го процентиля во втором классе, а 25% учащихся из группы риска показывают результаты между 25-м и 50-м процентилями.Результаты Локуньяка и Джордана показывают, что многие учащиеся с более слабыми математическими навыками в детском саду будут продолжать демонстрировать более низкие результаты по математике после детского сада. Jordan, Kaplan, Locuniak и Ramineni (2007) обнаружили аналогичную картину с 277 учениками от детского сада до первого класса. На способность распознавать числа в осеннем детском саду приходилось 66% отклонений в тестах по математике и решению задач, проводимых в конце первого класса. Другие исследования (Duncan et al., 2007; Jordan, Glutting, Ramineni, & Watkins, 2010) также указывают на то, что первые навыки работы с числами позволяют прогнозировать успеваемость по математике в более поздних классах.
Трудности с ранними числовыми компетенциями
Многие молодые студенты испытывают трудности с ранними числовыми компетенциями (Lembke & Foegen, 2009; Lloyd, Irwin, & Hertzman, 2009). В Соединенных Штатах различия проявляются в начале обучения в школе: некоторые дети приходят в школу с установленным набором начальных числовых компетенций: другие демонстрируют гораздо более низкие результаты при начальных числовых задачах (Jordan et al., 2007). Например, Jordan, Kaplan, Ramineni и Locuniak (2009) применяли ранние числовые методы подсчета, распознавания чисел, сравнения, числовых комбинаций и задач рассказа в детском саду. Учащиеся с низкими доходами в их выборке продемонстрировали значительно более низкие начальные числовые баллы, чем их сверстники со средним доходом. Хотя низкий доход может быть не единственным фактором, способствующим различиям в ранней числовой компетенции, Jordan et al. (2009) продемонстрировали, что учащиеся детского сада демонстрируют разный уровень навыков счета в раннем возрасте.Та же тенденция характерна для студентов из других стран (Ee, Wong, & Aunio, 2006; Lloyd et al., 2009). Например, финские учащиеся в возрасте от 5 до 7 лет с особыми потребностями (т. Е. Синдром дефицита внимания, языковые трудности или трудности в развитии) продемонстрировали значительно более низкие показатели в начале обучения, чем учащиеся без особых потребностей (Aunio et al., 2009).
Поскольку учащиеся, которые хуже справляются с ранними числовыми задачами, часто демонстрируют более низкие математические способности в более поздних начальных и средних школах (Duncan et al., 2007), раннее выявление и раннее вмешательство являются ключевыми (Dowker, 2005). Хотя выявление учащихся, испытывающих трудности, может быть затруднено из-за неадекватных оценок (Mazzocco, 2005), а некоторых учащихся ошибочно определяют как учащихся, испытывающих трудности в математике (Locuniak & Jordan, 2008), исследования показывают, что раннее вмешательство может помочь учащимся в их начальных числовых навыках (Berch, 2005; Bryant et al., 2011; Fuchs et al., 2005a).
Раннее численное обучение
Основываясь на экспериментальной работе со студентами, которые борются с математикой, Fuchs et al.(2008) предоставили несколько рекомендаций по важным компонентам обучения математике. Инструкция должна быть четкой с акцентом на концептуальные и процедурные знания. Обучение должно быть осмысленным, чтобы минимизировать проблемы, а практика и повторение должны быть частью любой учебной программы. Fuchs et al. также подчеркнули использование инструментов мотивации, встроенных в инструкции, чтобы помочь учащимся вести себя при выполнении задания и контролировать успеваемость. Мониторинг успеваемости учеников важен для того, чтобы у учителей были объективные индикаторы того, когда ученик реагирует на текущую учебную программу неадекватно и вряд ли приведет к достижению цели.Когда данные ученика указывают на неадекватный ответ, учитель корректирует учебную программу ученика.
Gersten et al. (2009) выделили подробное обучение, использование стратегий, вербализацию учащихся, использование визуальных представлений, мониторинг прогресса и использование различных примеров в качестве важных учебных практик для учащихся, которые борются с математикой. Добавляя к этим пунктам, Герстен и Чард (1999) предложили работать над беглостью математики, чтобы интегрировать инструкции по концепциям и процедурам с достаточной практикой.Эти рекомендации особенно важны для учащихся с математическими трудностями, и следующие примеры демонстрируют, как эти важные учебные рекомендации, когда они используются для обучения навыкам вычисления в раннем возрасте, полезны для учащихся с математическими трудностями.
Например, Bryant et al. (2011) работали с первоклассниками (N = 224), которые показали результаты ниже 35-го процентиля при ранней числовой оценке компетенций. Некоторые ученики (n = 151) были назначены на начальную числовую программу, тогда как другие ученики (n = 73) остались в своем обычном учебном классе для обучения математике.Репетиторство в малых группах для студентов начальных этапов числовой программы длилось 22 недели, четыре занятия в неделю, 25 минут каждое. Студенты участвовали в подробном обучении с управляемой и независимой практикой по процедурным и концептуальным идеям счета, числовым отношениям, наборам из 10, числовым комбинациям и разряду. На итоговом тесте студенты, которые участвовали в ранней числовой программе, показали значительно более высокие результаты, чем студенты из контрольной группы, с величиной эффекта (ES) 0,18 при сравнении величины, 0.47 по числовым последовательностям, 0,39 по разрядам и 0,55 по числовым комбинациям сложения и вычитания.
Fuchs et al. (2005a) также проводил обучение по числовым методам для первоклассников (N = 127), которые испытывали трудности с математикой. Учащиеся были случайным образом распределены для раннего обучения численным навыкам (n = 64) или для участия в обычном обучении математике без дополнительных занятий (n = 63). Студенты получали репетиторство в течение 16 недель, три раза в неделю, по 40 минут за сеанс. Репетиторство было сосредоточено на начальных навыках работы с числами, таких как идентификация и написание чисел, использование символов, счет, разметка, а также комбинации сложения и вычитания.По окончании репетиторства ученики, получившие репетиторство, превзошли учеников без репетиторства по тестам на добавление фактов (ES = 0,40), фактов вычитания (ES = 0,14), вычислений (ES = 0,57), концепций и приложений (ES = 0,67) и задач рассказа (ES = 0,70).
В других странах ранние программы счисления также показали, что они улучшают успеваемость по математике учащихся, испытывающих трудности. Кауфманн и др. (2003) работали с шестью учениками с математическими трудностями. Эти студенты участвовали в начальной числовой программе в течение 6 месяцев три раза в неделю по 25 минут в каждой сессии.Учащиеся узнали о счетах, символах, фактах, равных 10, фактах сложения и вычитания, а также расстановке ценностей с помощью явных инструкций и работы от конкретного (т.е. манипулятивного) к абстрактному (то есть решения задач с числами и символами). Шесть учеников продемонстрировали значительный рост в ходе программы по сравнению со сверстниками, не испытывавшими трудностей по математике. Кауфманн, Делазер, Поль, Семенца и Даукер (2005) расширили эту работу, сравнив раннюю числовую программу, ориентированную на процедурное и концептуальное обучение, с программой, ориентированной на обучение базовым навыкам.Студенты, участвовавшие в процедурной и концептуальной программе, продемонстрировали значительный выигрыш в показателях подсчета, мощности, сравнений и вычислений по сравнению со студентами, которые участвовали в программе основных навыков. Ван Луит и Шопман (2000) работали с учениками детского сада (N = 124), которые показали результаты ниже 25-го процентиля по раннему числовому критерию. Половине студентов было назначено раннее обучение числовому обучению; другая половина участвовала в их обычной школьной программе.Ранние числовые инструкции были сосредоточены на навыках счета, а обучение было явным и интерактивным и следовало последовательности от конкретного к репрезентативному и абстрактному (Hudson & Miller, 2006). После двадцати 30-минутных занятий студенты, которые участвовали в ранней числовой программе, превзошли учащихся контрольной группы в ранних числовых измерениях, таких как сравнение чисел, счет и понимание значения чисел.
Эти результаты ранних численных исследований в Соединенных Штатах и за рубежом показывают, что учащиеся, испытывающие трудности, математики извлекают выгоду из программ, ориентированных на ранние численные навыки.Все инструкции в этих программах были четкими и были сосредоточены на обучении студентов значению (т.
РАННИЕ ЧИСЛОВЫЕ КОМПЕТЕНЦИИ
В этой статье мы выделяем четыре основные категории ранних числовых компетенций: счет, сравнение чисел, понимание символов, а также концепции сложения и вычитания. В этом разделе мы описываем каждую из этих категорий и то, как учащиеся могут бороться с навыками в этой категории.Затем мы представляем пример вмешательства, чтобы помочь студентам, которые борются с этими ранними числовыми компетенциями. Наконец, мы даем рекомендации для практикующих.
Счет
Счет — это не только повторение «1, 2, 3, 4, 5.…». Студенты часто могут считать до 10, но они могут не понимать, что означают числа (Bermejo, Morales, & deOsuna, 2004; Брюс и Трелфолл, 2004). Например, учащиеся могут не придавать значения своему счету или осознавать, что числовые слова отображаются на счетных элементах.Подсчет включает пять принципов: стабильный порядок, взаимно однозначное соответствие, мощность, абстракцию и нерелевантность порядка (Gelman & Gallistel, 1978). Студенты могут бороться с одним или несколькими из этих принципов (Bruce & Threlfall, 2004). Эти принципы часто комбинируются (т.е. ученики произносят числовые названия и указывают на каждый подсчитываемый объект), и поэтому эти принципы следует практиковать вместе (Camos, Barrouillet, & Fayol, 2001).
Многие учащиеся развивают навыки счета еще до поступления в детский сад (Gelman & Gallistel, 1978).Однако некоторые ученики приходят в школу с недостаточными навыками счета или непониманием принципов счета. Например, многие учащиеся могут без труда сосчитать до пяти, но они могут столкнуться с трудностями при подсчете больших наборов (т. Е. Наборов, превышающих 5 или 6), совершать больше ошибок и не понимать, как использовать счет для определения количества элементов в задании. набор (Carrasumada, Vendrell, Ribera, & Montserrat, 2006). Однако навыкам счета можно научить и улучшить с помощью инструкций и практики (Camos et al., 2001; Xin & Holmdal, 2003). Часто полезным способом понять, понимают ли учащиеся принципы счета, является демонстрация счета и неправильного счета с помощью марионетки (Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007; Muldoon, Lewis, & Francis, 2007). Рекомендации по обучению счету могут быть основаны на знании (или отсутствии) навыков счета марионеток. Например, если ученик говорит, что марионетка неправильно считать справа налево ученика, тогда ученик должен получить инструкции по принципу подсчета, не имеющему отношения к порядку.
Для подсчета учащиеся должны знать числовые слова по порядку (Slusser & Sarnecka, 2011). Эта концепция называется стабильным порядком . Эти слова обычно произносятся в прямом порядке (например, «один, два, три, четыре, пять»), и последовательность этих счетных слов должна использоваться последовательно (Frye, Braisby, Lowe, Maroudas, & Nicholls, 1989 ). Стабильный порядок часто изучается и практикуется с помощью песен, песнопений или рассказов.
Кроме того, при подсчете учащиеся должны считать каждый предмет только один раз (Van De Walle, Karp, & Bay-Williams, 2010).Это называется взаимно-однозначным соответствием . Практикуя индивидуальную переписку, ученикам легче отслеживать элементы в ряду или элементы, которые были помечены и разделены, чем элементы, которые подсчитываются случайным образом (Potter & Levy, 1968). Чтобы считать с использованием однозначного соответствия, учащиеся должны знать названия чисел, ценить стабильный порядок и понимать взаимосвязь между счетами и названиями чисел (Potter & Levy, 1968). Индивидуальная переписка часто практикуется путем раздачи элементов (например, файлов cookie) и обеспечения того, чтобы каждый учащийся получил один файл cookie (Van De Walle et al., 2010).
Комбинируя стабильный порядок и взаимно однозначное соответствие, учащиеся начинают подсчитывать наборы объектов, чтобы определить число в наборе (то есть, по принципу мощности ). При подсчете набора предметов окончательный счет (например, «4» после подсчета четырех динозавров) представляет набор. Количество элементов относится к пониманию того, что окончательный или последний счет представляет собой общее количество подсчитанных элементов (Bermejo et al., 2004). Часто это практикуется, когда учеников просят сосчитать набор предметов, а затем просят их ответить на вопрос: «Сколько?» (Малдун, Льюис и Фриман, 2003).
Хотя принцип счета абстракции не является необходимостью для подсчета, студентам полезно понимать, что любые объекты могут составлять набор (Frye et al., 1989). Например, счетный набор не обязательно должен содержать только лягушек. В счетный набор могут входить лягушки, жабы, грузовики и карандаши. Подсчет может применяться к любому набору элементов, независимо от того, насколько абстрактными они могут быть. Подобно абстракции, нерелевантность порядка не так важна, как другие принципы подсчета (Kamawar et al., 2010). Принцип нерелевантности порядка диктует, что порядок, в котором подсчитываются предметы, не имеет значения, пока каждый предмет подсчитывается только один раз (т. Е. Взаимно однозначное соответствие). Многие студенты считают слева направо и сверху вниз, потому что именно так они читают по-английски, поэтому этих студентов может сбить с толку тот факт, что счет не обязательно должен производиться линейно.
Ученики должны перейти от подсчета заданий один за другим к субитизации (Брюс и Трелфолл, 2004; Ханнула, Расанен и Лехтинен, 2007). Субитизация — это способность мгновенно распознать, сколько элементов находится в группе. См. Примеры субитализации. Учащиеся должны уметь смотреть на каждый из примеров и сразу распознавать четыре прямоугольника, три круга, один шестиугольник и шесть квадратов. Часто студенты, которые борются с математикой, борются с субитизацией (Schleifer & Landerl, 2011), но практика может помочь улучшить их навыки (Clements, 1999; Fischer, Köngeter, & Hartnegg, 2008). Субитизация часто рассматривается как центральный компонент ранней числовой компетенции, и мы упоминаем об этом здесь, потому что учащиеся могут субитизировать (вместо подсчета), чтобы сравнивать суммы и работать со сложением и вычитанием.
Оценка количества
Субитизация связана с оценкой детьми количества, связанной с этим ранней числовой компетенцией. Иногда это называют количественной дискриминацией, величиной или сравнением чисел. На самом базовом уровне ученики смотрят на два числа (например, 4 и 9) и отвечают на вопрос: «Что больше?» (9) или «Что меньше?» (4). Учащиеся могут использовать манипуляторы или изображения, чтобы помочь различить эти две величины. Студентам легче различать величины, которые намного дальше друг от друга (например,g., 9 и 2), чем более близкие по величине (например, 9 и 8; Murray & Mayer, 1988). Сравнивая более крупные двузначные числа, учащимся легче различать числа, где разряды десятков различаются, чем когда декады совпадают, а разряды единиц различаются (Ganor-Stern, Pinhas, & Tzelgov, 2009).
Учащиеся с трудностями в математике часто испытывают затруднения при сравнении чисел и хуже справляются с задачами сравнения, чем их сверстники без трудностей по математике (De Smedt & Gilmore, 2011; Holloway & Ansari, 2009).Интересно, что учащиеся могут лучше выполнять задачи с числовой величиной, не связанные с числовыми символами (Rousselle & Noel, 2007). Например, при представлении группы из шести конфет и четырех конфет учащиеся могут определить, что шесть — это больше, чем четыре. Когда учащимся нужно сравнить два числовых символа (например, «6» и «4»), это обычно больше. сложно (Де Смедт и Гилмор, 2011).
Учащиеся дошкольных учреждений, которым для сравнения представлены два набора, часто не учитывают и используют принцип мощности для сравнения двух наборов.Обычно студенты вместо этого полагаются на визуальный (т.е. несимволический) осмотр (Zhou, 2002). Опора на визуальное сканирование может помочь учащимся лишь на время, как правило, когда числа от 1 до 3. Поэтому инструкции по счету для определения различий между наборами могут быть полезны (Muldoon et al., 2003). Часто ученики не понимают, что для сравнения можно использовать счет, потому что учителя обычно спрашивают: «Сколько?» с каждым заданием на подсчет вместо вопросов типа «На сколько меньше?» или «У кого больше?»
Математические символы
С начальными навыками счета, в конечном итоге ученики будут ассоциировать счет (например,g., one, two, three) с числовыми символами (например, 1, 2, 3). Студенты часто могут повторять числовые слова в стабильном порядке, использовать взаимно однозначное соответствие и понимать количество элементов без использования цифровых символов. Учащиеся также могут сравнивать суммы без использования цифровых символов (т. Е. При наличии визуального представления двух наборов). Однако после того, как учащиеся пойдут в детский сад, большинство действий, связанных со счетом и сравнением чисел, требует, чтобы учащиеся знали числовые символы и значение этих символов для выполнения математических задач.Математические символы важны, потому что большая часть математики представлена с помощью символов.
Десять цифровых символов (например, 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9) могут использоваться по отдельности или вместе для представления любого числа (например, 14 597). Помимо десяти числовых символов, ученики начальной школы изучают два символа операций: знак плюса (+) для сложения и знак минус (-) для вычитания. Студенты также используют знак равенства (=) в числовых предложениях. Студенты также могут использовать символы неравенства для значений больше (>) и меньше (<) при сравнении сумм.Студенты обычно изучают числовые символы раньше любых других символов (Zhou, Wang, Wang, & Wang, 2006).
Учащимся необходимо научиться писать и интерпретировать символы, потому что они не придают значения символам автоматически. Значение символов развивается со временем и с практикой. Например, учащиеся узнают, что «три» или * * * или три медведя-манипулятора могут быть представлены письменным символом 3 и наоборот. Учащиеся должны научиться складывать предметы, когда они видят символ плюса (+), и брать предмет или находить разницу, когда они видят символ минуса (-).Многие студенты понимают операции, обозначенные знаками плюс и минус, но меньшее количество студентов правильно интерпретируют знак равенства и символы неравенства (например, Hattikudur & Alibali, 2010; Matthews & Rittle-Johnson, 2009; McNeil, 2008). Знак равенства следует понимать как символ отношения, указывающий на наличие сбалансированной связи между числами по обе стороны от знака равенства (=) (Jacobs, Franke, Carpenter, Levi, & Battey, 2007). Символы неравенства (<и>) также следует понимать как относительные, причем одна сторона символа представляет большую или меньшую величину.
К сожалению, ученики неправильно понимают символы, поскольку учителя дают инструкции или практику, которые не способствуют полному пониманию символа (Capraro, Ding, Matteson, Capraro, & Li, 2007; McNeil, 2008). Например, студенты часто практикуют сотни уравнений типа 2 + 3 = _, которые требуют небольшого понимания знака равенства в реляционной манере (Пауэлл, в печати). Напротив, студенты, даже те, кто борется с математикой, учатся интерпретировать знак равенства в зависимости от отношений с помощью соответствующих инструкций и практики (Powell & Fuchs, 2010).Однако без надлежащего обучения и практики учащиеся продолжают неправильно использовать или неверно истолковывать символы в средней и старшей школе (Knuth, Alibali, Hattikudur, McNeil, & Stephens, 2008; Rownree, 2009; Verikios & Farmaki, 2010).
Концепции сложения и вычитания
Изучение концепций сложения и вычитания не обязательно означает овладение счетом, сравнением чисел и математических символов. Дети часто могут решать простые задачи на сложение и вычитание, представленные без символов (т.е., представленный устно и / или решенный с помощью манипуляций или подсчета голосов; Кобб, 1987; Sherman & Bisanz, 2009). Однако адекватные навыки счета, сравнения и знания символов необходимы для выполнения большинства задач на сложение и вычитание, которые ставятся перед учащимися начальной школы.
Приступая к изучению числовых комбинаций сложения и вычитания (т. Е. Основных фактов), студенты часто работают над простыми задачами с помощью манипуляторов. По мере практики студенты меньше полагаются на манипуляторы и больше полагаются на свои пальцы при счете (Groen & Resniek, 1977).Поскольку при решении комбинаций чисел сложения и вычитания часто используется счет, навыки счета важны (Baroody, Bajwa, & Eiland, 2009). В большинстве случаев молодые студенты используют счет по одному в качестве механизма счета по умолчанию. Счет по два или другие приращения или использование навыков субитализации не распространены до второго класса или позже (Camos, 2003). Затем учащиеся переходят от счета к решению числовых комбинаций, используя стратегии рассуждения или по памяти. Мастерство и беглость, конечно же, являются конечной целью числовых комбинаций.Как правило, к концу первого класса ученики должны знать все 100 комбинаций чисел сложения и 100 вычитания (Baroody et al., 2009).
Начиная с сложения и вычитания, учащиеся часто решают задачи на сложение более успешно, чем задачи на вычитание (Шински, Чан, Коулман, Моксом и Ямамото, 2009). Это связано с тем, что ученики учатся считать вперед задолго до того, как им удастся считать в обратном направлении. Навыки сложения учащихся, даже учащихся, которые борются с математикой, обычно сильнее, чем их навыки вычитания.Это проявляется в том, что многие ученики решают задачи на вычитание более эффективно, когда они используют навыки сложения (Torbeyns, De Smedt, Stassens, Ghesquière, & Verschaffel, 2009). Например, при решении задачи 14 — 9 = _ многим ученикам легче подумать: «Что я могу добавить к 9, чтобы получить 14?» и может быть использована стратегия подсчета вперед.
Хотя учащиеся могут понять принцип вычитания, они часто отстают в своей способности понять, что вычитание — это обратное сложению (Baroody, Lai, Li, & Baroody, 2009).Поскольку учащиеся не понимают автоматически обратную связь между сложением и вычитанием, эту концепцию следует сделать более явной через инструкции и практику (Baroody, 1999). Студенты, которые понимают взаимосвязь между сложением и вычитанием (т.е. сложение является обратным вычитанию и наоборот), демонстрируют лучшие концептуальные знания и лучшие результаты вычитания, чем студенты, которые не понимают эту взаимосвязь (Gilmore & Papadatou-Pastou, 2009).
Стратегии подсчета (т. Е. Подсчет для поиска ответа на комбинацию чисел сложения или вычитания) помогают учащимся решать комбинации. Однако не все учащиеся используют стратегию подсчета (Saxton & Cakir, 2006). Некоторые студенты просто догадываются. Для многих студентов, особенно тех, кто борется с начальными навыками работы с числами, полезны стратегии подсчета для решения числовых комбинаций, и их можно относительно легко изучить. Есть несколько стратегий подсчета, которые студенты могут использовать при решении числовых комбинаций сложения и вычитания.См. Диаграммы. При подсчете всего учащиеся отсчитывают первое слагаемое, отсчитывают второе слагаемое, а затем считают оба слагаемых вместе, начиная с 1. Обычно это первая стратегия подсчета для сложения, которую применяют студенты (Fuson & Secada, 1986). Стратегия подсчета всего не очень эффективна и, учитывая количество требуемых подсчетов, часто приводит к неправильным ответам. Студенты обычно отказываются от использования подсчета всех в пользу более продвинутой стратегии «подсчета» или «расчета на» (Fuson & Secada, 1986).Подсчет может быть выполнен двумя способами: начать с большего слагаемого и подсчитать меньшее слагаемое (т. Е. Стратегия «мин», потому что ученик считает минимальное количество) или наоборот (т. Е. Стратегия «макс.», Потому что студент считает максимальную сумму). Прежде чем студенты узнают коммутативное свойство сложения (т. Е. Порядок сложения не влияет на сумму), они часто начинают с первого слагаемого в числовом предложении (например, 4 из 4 + 9 = _), не осознавая, что большая эффективность, начиная с большего слагаемого и считая меньшее слагаемое (Groen & Parkman, 1972).Например, если представить 5 + 9 = _, учащиеся начинают с 9 и считают еще 5: «10, 11, 12, 13, 14.» Студенты часто разрабатывают эту стратегию счета на основе опыта и практики (Weiland, 2007), но может быть необходимо, особенно для студентов, которые борются с математикой, дать подробные инструкции по этой более эффективной стратегии счета (Powell, Fuchs, Fuchs, Cirino и Флетчер, 2009).
Стратегии подсчета
С каждой из этих стратегий учащиеся могут поднимать пальцы, складывать пальцы или касаться пальцами.Студенты могут работать ладонями к себе или от них. Кроме того, учащиеся могут считать слева направо или справа налево. Они могут начать считать указательным, большим или другим пальцем.
Чтобы решить числовые комбинации на вычитание, ученики часто ведут обратный отсчет. То есть они начинают с уменьшаемого и отсчитывают количество вычитаемого. Если 9 — 4 = _, ученики начинают с 9 и считают 4: «8, 7, 6, 5.» Обратный отсчет или обратный отсчет затруднен для студентов, особенно для студентов с математическими трудностями, потому что беглость обратного счета ограничена по сравнению с беглым обратным счетом (Passolunghi & Cornoldi, 2008).Ученики также склонны делать гораздо больше ошибок, считая в обратном порядке, чем в обратном направлении. Более эффективная стратегия решения задач на вычитание — это подсчет. Учащиеся начинают с вычитаемого и считают до убавляемого. Если 9 — 4 = _, ученики начинают с 4 и считают «5. 6. 7, 8, 9. ” Они считают 5 пальцев или делают 5 счетов, поэтому 9 — 4 = 5. Эта стратегия использует навыки быстрого прямого счета учащихся и зарекомендовала себя как полезная стратегия для учащихся с трудностями в математике (Fuchs et al., 2009; Fuchs, Powell, et al., 2010). Использование подсчета для вычитания также подчеркивает тот факт, что вычитание представляет собой разницу между двумя суммами (то есть уменьшаемым и вычитаемым).
С помощью сложения и вычитания практика использования стратегий счета и работа над беглостью речи улучшает успеваемость учащихся, испытывающих трудности (Fuchs, Powell, et al., 2010). Учащимся необходимо понимать концепции, лежащие в основе числовых комбинаций (Baroody, Lai, et al., 2009), но им также необходимо предоставить рутинную, даже ежедневную практику, чтобы развивать беглость и помогать учащимся часто и правильно определять ассоциации между основами проблемы и их ответы (Fuchs, Powell, et al., 2010). Это приводит к тому, что учащиеся создают представления в долговременной памяти, и помогает учащимся полагаться на наиболее эффективную стратегию решения задач сложения и вычитания: автоматический поиск ответов (Fuchs et al., 2011). По этой причине учащимся необходимо попрактиковаться во всех комбинациях чисел, особенно в комбинациях чисел, состоящих из двузначных цифр (например, 9 + 7 = 16; 14-8 = 6), потому что они, как правило, гораздо больше знакомятся с более простыми комбинациями чисел (Hamann И Эшкрафт, 1986).
ПРИМЕР РАННЕЙ ЧИСЛЕННОЙ ВМЕШАТЕЛЬСТВА ДЛЯ БОРЬБЫ УЧАЩИХСЯ
Мы обсудили четыре ранние числовые навыки: счет, сравнение чисел, понимание символов и концепции сложения и вычитания. Хотя это не исчерпывающий список начальных числовых компетенций, эти четыре являются важнейшими компонентами эффективной ранней числовой программы для учащихся, испытывающих трудности. Эти четыре компонента связаны друг с другом и дополняют друг друга по мере того, как учащиеся изучают все больше и больше математики в младших классах начальной школы.Хотя учащиеся могут испытывать трудности с одной или несколькими из этих начальных числовых компетенций, обучение и практика могут улучшить начальные числовые навыки учащихся.
В этом следующем разделе мы описываем начальную числовую программу для первоклассников, у которых проблемы с математикой. Мы описываем эту программу, чтобы проиллюстрировать, как учителя и родители учащихся, испытывающих трудности, могут включить четыре ранние числовые компетенции, обсуждаемые в этой статье, в успешную учебную программу для учащихся, испытывающих трудности.Это не единственное доступное раннее численное вмешательство, поэтому учителя должны изучить варианты, прежде чем выбирать программу для своих учеников. Galaxy Math, , также называемый Number Rockets, (Fuchs et al., 2011) был разработан, чтобы помочь предотвратить долгосрочные трудности в математике, устраняя ранние дефициты числовых навыков и продвигая знания чисел и навыки с числовыми комбинациями и другими ключевые компоненты учебной программы по математике для первого класса. Программа называется Galaxy Math , потому что на всех уроках используется космическая тема, которая помогает мотивировать учащихся.Репетиторы поощряют студентов «Стремиться в галактику математики!» и студенты используют математические манипуляторы в форме ракет. См. Пример таблицы мотивации на тему галактики.
Galaxy Math Мотивационная таблица
Экспериментальное исследование Galaxy Math
В начале первого класса учащиеся с согласия родителей были проверены для выявления тех, кто подвержен риску неадекватного развития математики, хотя у большинства учащихся не было диагностировано в школе неспособность к обучению.Этих учеников случайным образом распределили для продолжения их обычной школьной программы (то есть контрольной группы) или одной из двух версий Galaxy Math. В обеих версиях Galaxy Math основное внимание (25 минут каждого 30-минутного учебного занятия) уделяется типам ранних численных навыков, обсуждаемых в этой статье. Одна версия Galaxy Math (стандартная версия) добавляла 5 минут практики в конце каждого занятия; в другой версии добавлено 5 минут игр.В обоих условиях обучения. Galaxy Math студентов прошли 48 индивидуальных занятий три раза в неделю.
См. Список модулей и концепций Galaxy Math . В Блоке 1 ученики используют такие манипуляторы, как числовая линия, подсчет бобов и «Мистер. Greater Gator », чтобы узнать величины, потренироваться в счете, сравнить числа и выучить символы. Посмотрите, например, деятельность по подсчету и изучению терминологии равных. Эти задания проводятся во время первых нескольких уроков Galaxy Math. См. Образец числовой строки. Числа на числовой строке увеличиваются в размере по мере того, как числа увеличиваются в значении, чтобы помочь учащимся понять величину чисел. Посмотрите на мистера Большого Аллигатора. У этого аллигатора широко открытая пасть с символами неравенства (то есть больше или меньше знаков), наложенными на открытую пасть. Учащиеся узнают, что аллигатор очень голоден и хочет съесть большее количество, когда ему предложат два количества. Открытый рот всегда смотрит на большее число.Также в Блоке 1 учащиеся изучают стратегии счета: счет (для сложения) и счет (для вычитания). Во время счета ученики держат меньшее слагаемое на пальцах, а затем считают, складывая по одному пальцу за раз, пока не останется ни одного пальца (например, сжатый кулак). Например, с 3 + 6 ученик поднимает 3 пальца и затем считает: «7» (складывает 1 палец), «8» (складывает еще один палец), «9» (складывает последний палец). Ответ — это последнее число, которое произносит учащийся (в данном случае 9).Подсчет — это одна из разновидностей стратегии подсчета. Подсчет оказался полезным для первоклассников, потому что он помогал им следить за подсчетом суммы. Счет для вычитания ученики начинают со сжатым кулаком. Они начинают с вычитания и пальцами считают до минимума. Например, с 9–3 учениками считается «4, 5, 6, 7, 8, 9» (каждый раз поднимая другой палец). Когда ученики достигают минимума, они подсчитывают количество пальцев (в данном случае 6), и 6 записываются как ответ.В Блоке 1 учащиеся также решают сюжетные задачи с помощью манипуляторов, изображений или действий. Например, когда ему задают вопрос: «У Джона в тележке с продуктами 4 яблока. Он кладет в тележку еще 1 яблоко. Сколько яблок сейчас в тележке Джона? » студенты могли рисовать яблоки или использовать манипулятивные блоки для решения задачи.
ТАБЛИЦА 1
| Блок | Уроки | Темы | ||
|---|---|---|---|---|
| 1 | 1–3 | Номер строки (0–9) | ||
| 907 907 | Чтение и запись чисел | |||
| Подсчет объектов | ||||
| Показывать числа меньше 10 | ||||
| руками, чтобы показать числа 907 чем 10 | ||||
| Обсуждение 0 и чисел 11–19 | ||||
| Подсчет вперед | ||||
| Подсчет в обратном направлении | 907 наименьшие числа с числовой строкой||||
| 6, 7 | Сравнение чисел с языком и символами | |||
| 8 | Концепция сложения | |||
| Значение + и = | ||||
| 9 | Сложение 1 строка||||
| Использование манипуляторов, изображений и действий для решения сюжетных задач | ||||
| 10 | Сложение 0 и 1 с числовой строкой | |||
| 907 и действия для решения сюжетных задач | ||||
| 11 | Подсчет | |||
| 12 | Сложение 0, 1 и 2 с подсчетом | |||
| 7 | 13 | Концепция вычитания 907|||
| Значение — Проверка учета на добавление | ||||
| 14 | Сложение и вычитание 1 с числовой строкой | |||
| Использование манипуляторов, изображений и действий для решения сюжетных задач | ||||
| 15 | с добавлением числа 0 строка | |||
| Использование манипуляторов, изображений и действий для решения сюжетных задач | ||||
| 16 | Подсчет | |||
| 17 | Сложение и вычитание с подсчетом в / до | |||
| 18 | Проверка счета в / до | |||
| 2 | 19–20 | Двойные | ||
| 3 | 21–24 | 90725–28 | 6 набор | |
| 29–32 | 7 набор | |||
| 33–36 | 8 Набор | |||
| 37–40 | 9 Набор | |||
| 41–44 | 10 Набор | |||
| 457 1148 1148 | 49–52 | 12 Набор | ||
| 4 | 53 | Номер до 100 | ||
| Номера 20–29 | ||||
| – | Номер||||
| Номер 907 100 | ||||
| Двузначное сложение | ||||
| 57 | Подсчет по десяткам | |||
| Использование рук для представления десятков и единиц | 907 для размещения значения | |||
| 59 | Введение в стержни и кубы | |||
| Re группировка 10 кубиков в 1 стержень | ||||
| 60 | Перегруппировка | |||
| 61 | Представление одно- и двузначных чисел со стержнями и кубиками | |||
| 907 значение | ||||
| 62 | Представление одно- и двузначных чисел стержнями и кубиками | |||
| 63 | Определение больших и малых чисел с помощью разряда и числовой строки | |||
| 66 | Практика разряда | |||
| 5 | 67–74 | Обзор |
В Модуле 2 учащиеся используют бобы и числовую линию, чтобы узнать о числах с двойным числом от 0 до 6 (т.е., 0 + 0, 1 + 1, 2 + 2, 3 + 3, 4 + 4, 5 + 5, 6 + 6, 0 — 0, 2 — 1, 4 — 2, 6 — 3, 8 — 4 , 10 — 5, 12 — 6). Двойные упражнения практикуются на ранних этапах программы, потому что учащимся обычно не сложно запоминать двойные числа, а учащиеся могут использовать их для решения других числовых комбинаций (Van De Walle et al., 2010).
В Блоке 3 учащиеся начинают изучать комбинации чисел в наборах. Каждый набор включает в себя все числовые комбинации с суммой и уменьшением в качестве номера целевого набора. Например, набор 5 состоит из комбинаций альтернативных чисел с суммой 5 или 5 в качестве уменьшаемого (т.е., 0 + 5, 1 + 4, 2 + 3, 3 + 2, 4 + 1, 5 + 0, 5 — 0, 5 — 1, 5 — 2, 5 — 3, 5 — 4, 5 — 5 ). Репетиторы начинают с 5-го подхода и продолжают 12-й подход. Работая над каждым набором, тьютор проводит с учеником пять заданий. Во-первых, наставник и ученик используют кубы unifix, чтобы увидеть, как кубики можно комбинировать по-разному, чтобы получить комбинации чисел сложения и вычитания набора. См. Примеры из 5 комплекта. С помощью манипуляторов учащиеся также могут увидеть, как 1 + 4, 4 + 1, 5-1 и 5-4 связаны как «семья», а второе задание каждого урока фокусируется на семьях, составляющих соответствующий набор.В-третьих, учащиеся либо отвечают на задачи из набора цифр на листе, либо показывают все комбинации из набора чисел с помощью управляемых ракет. Затем наставник и ученик вместе решают задачу-рассказ, в которой используется комбинация чисел из набора. Учащийся решает задачу и объясняет, почему задача рассказа относится к конкретному набору чисел. Пятое упражнение каждый день — это устный обзор предыдущих наборов чисел.
Примеры манипуляции с 5 наборами
Для каждого набора учащиеся работают от одного до четырех уроков.После первого урока в наборе каждый последующий урок начинается с теста на усвоение карточек, с помощью которого учащиеся могут перейти к следующему набору, правильно ответив на карточки. Студенты должны ответить в течение 3 секунд, не более одной ошибки. Студенты, которые достигли мастерства до полного набора из четырех уроков в каждом наборе, завершают 12 наборов. Другие учащиеся завершают набор из 10, а затем переходят к разделу 4. Это правило обеспечивает соответствующий охват содержания.
В Блоке 4 основное внимание уделяется разряду: счет от десятков до 100, отображение и запись единиц и десятков, перегруппировка и сложение двузначных чисел.Студенты также просматривают наборы чисел во время этого раздела. Блок 5 предназначен для учащихся, демонстрирующих мастерство при работе с наборами чисел. В этом модуле учащиеся рассматривают числовые наборы и концепции разметки.
За последние 5 минут каждого занятия Fuchs et al. (2011) изолировали влияние практики обеспечения. Для этого половина студентов в исследовании систематически практиковалась в течение последних 5 минут; другая половина играла в игры. В условиях практики и игр содержание было тем же: материал, относящийся к уроку того дня.Случайное задание определяло, участвовали ли учащиеся в играх или в тренировках в конце урока.
В условии игр учащиеся играют в игры с управляемыми ракетами для отработки концепций. Например, в одной игре учащиеся вращаются, чтобы узнать, сколько ракет вызывается на космическую станцию, и помещают это количество ракет на игровое поле. Затем они снова вращаются, чтобы увидеть, сколько ракет отозвано назад, на землю, и снимают соответствующее количество ракет с доски.Затем они генерируют числовое предложение, представляющее эту серию событий. В играх репетиторы побуждают учащихся знать ответ или использовать пальцы, бобы или числовые линии для вычисления ответа. Репетиторы объясняют, что «знать ответ сразу же» является предпочтительной стратегией, если ученик уверен в ответе.
В условии практика учащиеся отрабатывают материалы уроков с помощью упражнения «Собери или побей свой результат», основанного на флэш-карточках. Например, после введения наборов сложения / вычитания учащиеся практикуют числовые комбинации.Репетиторы поощряют детей извлекать комбинацию из памяти или, если они не уверены в ответе, используют стратегию счета, которую они изучили в Galaxy Math , чтобы решить комбинацию. Когда ученик отвечает правильно, флеш-карта складывается стопкой на стол. Когда ученик отвечает неправильно, репетитор требует, чтобы ученики использовали стратегию подсчета (то есть подсчет или подсчет), чтобы найти правильный ответ. Исправленная карта кладется в стопку на столе. По истечении 90 секунд учащийся отображает количество правильно отвеченных флеш-карточек.См. Образец графика флеш-карты. Затем у студентов есть два шанса встретить или побить свой первый результат на карточке.
Практическая флеш-карта
В обоих случаях наставники поощряют поведение при выполнении задания и мотивацию к тяжелой работе (Fuchs et al., 2008), используя программу систематического вознаграждения. Репетиторы учат студентов, что поведение при выполнении задания означает внимательность и упорные попытки правильно ответить на вопросы. Учащиеся узнают, что поведение при выполнении задания важно для «прыжка в галактику математики».«Учащиеся зарабатывают стикеры за выполнение заданий и усердную правильную работу. Они размещают свои наклейки на диаграмме Galaxy Math (см.). Учащиеся получают приз (например, маленькую игрушку, наклейку или карандаш), когда достигают Солнца на карте галактики.
В исследовании (Fuchs et al., 2011) результаты показали, что учащиеся, участвовавшие в репетиторстве Galaxy Math , улучшили свои знания чисел, простой арифметики, более сложных вычислений и текстовых задач значительно лучше, чем учащиеся контрольной группы.Учащиеся, участвовавшие в практике, улучшили больше, чем учащиеся-игры, по простой арифметике и более сложным вычислениям, без вреда для их числовых знаний или успеваемости по задачам со словами. Это, наряду с другими ранними исследованиями численного вмешательства (например, Bryant et al., 2011; Fuchs et al., 2005b), демонстрирует положительные результаты для учащихся из групп риска, когда раннее численное вмешательство происходит рано и с интенсивностью. Fuchs et al. (2011) исследование также показывает особую важность включения частых, хорошо продуманных практик, поддерживающих правильное реагирование.
ПРЕДЛОЖЕНИЯ ДЛЯ ПРАКТИКОВ
По мере того, как учащиеся поступают в детский сад и часто переходят в первый класс с разной степенью ранней числовой грамотности, практикующие должны проводить раннюю оценку и раннее вмешательство, чтобы помочь учащимся, которые борются с основами математики. Что касается оценки, мер мониторинга прогресса (например, Lembke & Foegen, 2009; Seethaler & Fuchs, 2011) и мер скрининга, направленных на конкретные математические навыки (например, Geary et al., 2007; Jordan et al., 2009) можно использовать для определения того, какие ученики заслуживают раннего численного вмешательства.
После выявления учащихся, которым в детском саду или первом классе сложно овладеть числовыми навыками на начальном этапе, практикующим необходимо оценить начальные числовые программы и выбрать программу, которая наилучшим образом соответствует потребностям их учеников.
Основываясь на экспериментальной работе с молодыми студентами (например, Bryant et al., 2011; Fuchs et al., 2011), программы начальных числовых компетенций должны включать следующее: (a) подробное обучение, сфокусированное на концептуальных знаниях и процедурных навыках, (b) последовательность инструкций, которая имеет смысл и актуальность, (c) обзор ранее преподаваемых тем, (d) практика текущих тем и (e) беглость работы над комбинации чисел сложения и вычитания.Основное направление обучения (например, навыки счета, концепции сложения) следует определять в зависимости от потребностей учащихся. Одна программа не может быть лучшей для всех студентов, поэтому практикующие должны следить за успеваемостью студентов, пока студенты участвуют в обучении, чтобы определить реакцию. Если учащиеся не демонстрируют надлежащего обучения, их учебную программу следует изменить, чтобы сформировать программу, адаптированную к потребностям учащегося.
Поскольку первые навыки счета в детском саду предопределяют математические достижения в более поздних классах (Duncan et al., 2007; Jordan et al., 2010), своевременное вмешательство учащихся, которым не хватает навыков в начальных числовых компетенциях, имеет жизненно важное значение. Исследователям необходимо продолжать совершенствовать ранние численные оценки и вмешательства, которые помогут школам своевременно выявлять и принимать эффективные меры для обеспечения компетентности учащихся в основных строительных блоках математики.
Дополнение со стратегиями перегруппировки — Lucky Little Learners
Я большой сторонник обучения студентов WHY до ПРОЦЕДУРА при изучении новой математической концепции.Я твердо верю, что учителя обязаны своим ученикам научить их множеству способов решения математических задач. Все мы изучаем концепции по-разному, и математика не исключение. С учетом сказанного, в этом посте будет объяснено несколько различных дополнений к стратегиям перегруппировки, которым вы можете научить своих учеников, чтобы они могли лучше понять эту концепцию.
Добавление с перегруппировкой — это очень систематическая концепция для обучения учащихся, и без твердого понимания числовой ценности нет смысла продолжать обучение.Важно, чтобы учащиеся твердо придерживались своих практических навыков, прежде чем переходить к сложению с перегруппировкой. В зависимости от того, где вы преподаете, вам может потребоваться обучать сложению двух и трех цифр по-разному. Итак, я предлагаю вам множество стратегий, которые вы можете попробовать со своими учениками. Если вы видите стратегию, которую не можете использовать, продолжайте прокручивать. Я обещаю, что будет кое-что, что вам будет полезно.
Разрядные коврики
Перед тем, как я начну свое прибавление к перегруппировочной единице, я провожу месяц за обучением числовой оценке.Учащиеся должны твердо понимать свое месторасположение, чтобы по-настоящему понять, ЧТО и ПОЧЕМУ добавляются при перегруппировке. В первый день обучения этому навыку мои ученики получают кубики unifix и узнают, как выглядит перегруппировка. Вы также можете использовать блоки с числовыми значениями, но мне нравится, что кубы unifix можно разделить и сдвинуть вместе. Мы всегда начинаем с двузначного числа вверху и однозначного числа внизу. Вот как я этому учу:
Пока я прохожу этот урок, у меня есть ученики, которые, кажется, могут понять концепцию, подходят и показывают классу, как все это делать, одновременно объясняя, что они делают.Когда студенты объясняют свое мышление и мыслительный процесс, это очень действенно.
Через день или два обучения этой концепции с использованием циновки с числовыми значениями, я попрошу их перейти к решению задач на бумаге и карандаше, но все же предоставлю им свои кубики unifix и мат с числовыми значениями для построения и решения каждой задачи. Обязательно возьмите свой БЕСПЛАТНЫЙ мат, прежде чем идти дальше! Зарегистрируйтесь ниже, чтобы получить халяву.
Успех! Теперь проверьте свою электронную почту, чтобы подтвердить подписку и получить бесплатную информацию о размещаемой стоимости.Если письма нет в вашем почтовом ящике, проверьте папку со спамом! -Angie 🙂 Lucky Little Learners
Один совет — дайте своим ученикам маркеры, пусть они просмотрят свой рабочий лист и выделят нужные места, чтобы у них было визуальное напоминание о том, с чего начать решать свои математические задачи.
Остерегайтесь тех, кто просто хочет взять двузначное число и рассчитывать на него. Хотя это практический способ решения этих проблем, вы также должны думать о концепции, которой вы пытаетесь их научить… перегруппировке.
Далее мы переходим к двузначным числам сверху и снизу. Конечно, мы возвращаемся к математическим манипуляциям, чтобы помочь им увидеть и понять процесс перегруппировки.
Продолжаем выделять единичные места на данном этапе. Я хочу, чтобы мои ученики всегда начинали с первых мест. Для них эта концепция сложнее, чем мы думаем. Их учат читать и писать слева направо, поэтому включение их с правой стороны задачи, как правило, вызывает затруднения у некоторых учеников.
Как я уже говорил в начале этого поста, я твердо верю в то, что нужно обучать студентов нескольким способам решения проблем, потому что никогда не знаешь, что с ними связано. Вот еще несколько способов, с помощью которых я показал своим ученикам, как решать сложение с помощью задач перегруппировки.
Метод прикрепления заметок
Метод слома
Метод нарезки и разделения
Как только ваши ученики найдут один или два метода, которые им комфортно использовать, важно предоставить множество возможностей для практики! Вот несколько ресурсов, которые вы можете начать использовать в своем классе уже сегодня! (ссылки под изображением)
МАТЕМАТИЧЕСКИЕ РЕСУРСЫ ДЛЯ ВАШЕГО КЛАССА
2-значные карты задач сложения
3-значные карты задач сложения
2-значные цвета по номеру годовой пакет
Добавление с перегруппировкой Math Notebook
2-значное добавление с помощью карт задач QR-кодов
Добавление 3-х цифр с помощью карточек с QR-кодами
Math Toothy ® Task Kit Bundle
Math Puzzles Bundle
2 Grade Math Centres Bundle
Успех! Теперь проверьте свою электронную почту, чтобы подтвердить подписку.
Сложение и вычитание KS2
последовательные номера
Возраст от 7 до 14 лет
Уровень испытания
Расследование, включающее сложение и вычитание наборов последовательных чисел. Много чего нужно узнать, много чего исследовать.
Бросьте эти кости
Возраст от 7 до 11
Уровень задания
Бросьте два красных кубика и один зеленый кубик. Сложите два числа на красных кубиках и уберите число на зеленом.Какие есть разные варианты ответов?
Лабиринт 100
Возраст от 7 до 11
Уровень задания
Сможете ли вы пройти через этот лабиринт так, чтобы числа, которые вы прошли, складывались точно в 100?
Domino Square
Возраст от 7 до 11
Уровень задания
Используйте домино «двойные 3 вниз», чтобы сделать квадрат так, чтобы на каждой стороне было по восемь точек.
4 Дом
Возраст от 5 до 16
Уровень испытания
Используйте эти четыре домино, чтобы создать квадрат с одинаковым количеством точек на каждой стороне.
Покупка воздушного шара
Возраст от 7 до 11
Уровень задания
Лолла купила воздушный шар в цирке. Она дала клоуну шесть монет, чтобы заплатить за это. Сколько могла Лолла заплатить за воздушный шар?
Домино Эми
Возраст от 7 до 11
Уровень задания
У Эми есть коробка с костяшками домино, но она не думает, что это полный набор. Какая из ее частей домино отсутствует?
Двадцать разделены на шесть
Возраст от 7 до 11
Уровень задания
У Кэти была колода из 20 карт, пронумерованных от 1 до 20.Она сложила карты в 6 неравных стопок, каждая из которых складывалась в одну и ту же стопку. Каков был итог и как это можно было сделать?
Супер Фигуры
Возраст от 7 до 11 лет Короткий
Уровень испытания
Значение круга меняется в каждой из следующих задач. Можете ли вы обнаружить его ценность в каждой проблеме?
Дальность 100
Возраст от 7 до 14 лет
Уровень испытания
Выберите четыре разные цифры от 1 до 9 и поместите по одной в каждое поле, чтобы в результате четыре двузначных числа в сумме составили 100.
Герметичный раствор
Возраст от 7 до 11
Уровень задания
Десять карточек помещаются в пять конвертов, так что в каждом конверте по две карточки. Сумма чисел внутри него написана на каждом конверте. Какие числа могут быть внутри конвертов?
Понятно
Возраст от 7 до 14 лет
Уровень испытания
Игра для двоих, или играть онлайн. Имея заданное число, скажем, 23, и диапазон чисел на выбор, скажем, 1-4, игроки по очереди добавляют к итоговой сумме, чтобы достичь своей цели.
Марка 37
Возраст от 7 до 14 лет
Уровень испытания
Четыре пакета содержат большое количество цифр 1, 3, 5 и 7. Выберите любые десять чисел из сумок выше, чтобы их общее количество равнялось 37.
Смешанные часы
Возраст от 7 до 11
Уровень задания
Есть циферблат, на котором перепутались числа. Сможете ли вы узнать, куда делись все цифры из этих десяти утверждений?
В поисках пятнадцати
Возраст от 7 до 11
Уровень задания
У Тима было девять карт с разными числами от 1 до 9.Как он мог сложить их в три стопки, чтобы в каждой стопке было 15?
Четыре Го
Возраст от 7 до 11
Уровень задания
Это испытание — игра для двух игроков. Выберите два числа, которые хотите умножить или разделить, затем отметьте свой ответ в числовой строке. Можно четыре подряд?
Вычеркни
Возраст от 5 до 11
Уровень испытания
Используйте свои навыки сложения и вычитания в сочетании со стратегическим мышлением, чтобы победить своего партнера в этой игре.
Всего шесть десять
Возраст от 7 до 11
Уровень задания
Эта задача сочетает в себе сложение, умножение, настойчивость и даже доказательство.
Шесть пронумерованных кубиков
Возраст от 7 до 11
Уровень задания
Эта задача сочетает пространственное восприятие со сложением и умножением.
Это был 2010 год!
Возраст от 5 до 11
Уровень испытания
Если ответ 2010, в чем может быть вопрос?
Планирование школьной поездки
Возраст от 7 до 11
Уровень задания
Вы организуете школьную поездку и вам нужно написать письмо родителям, чтобы сообщить им об этом дне.Используйте карточки, чтобы собрать всю необходимую информацию.
Пятнадцать карт
Возраст от 7 до 11
Уровень задания
Можете ли вы использовать эту информацию, чтобы узнать, какие карты я использовал?
Три соседа
Возраст от 7 до 11
Уровень задания
Посмотрите на трех «соседей по соседству» среди счетных цифр. Сложите их вместе. Что ты заметил?
Игральные кости в углу
Возраст от 7 до 11
Уровень задания
Как можно сложить хотя бы два кубика в стопку, чтобы общее количество видимых пятен равнялось 18?
Поезд в кости
Возраст от 7 до 11
Уровень задания
Эта цепочка игральных костей создана по определенным правилам.Сколько разных поездов можно сделать?
Играть до 37
Возраст от 7 до 11
Уровень задания
В этой игре для двух игроков идея состоит в том, чтобы по очереди выбрать 1, 3, 5 или 7. Победитель первым наберет 37.
Построй его
Возраст от 7 до 11
Уровень задания
Можете ли вы найти все способы получить 15 на вершине этого треугольника чисел? Много возможностей работать по-разному.
Сюрприз вычитания
Возраст от 7 до 14 лет
Уровень испытания
Проведите несколько расчетов.Вы удивлены результатами?
Y Вас также может заинтересовать эта подборка упражнений с веб-сайта STEM Learning, которые дополняют действия NRICH, указанные выше.
Сложение и вычитание в 3 классе (возраст 7–8 лет)
Как помочь дома
Существует множество простых и быстрых способов помочь ребенку понять сложение и вычитание. Вот лишь несколько повседневных идей, которые помогут вашему ребенку учиться:
1.Используйте язык сложения и вычитания
Использование правильного математического словаря поможет вашему ребенку разбираться в словесных задачах и познакомит его со словами, которые они будут слышать в школе.
Попробуйте использовать математический язык, например, , прибавьте , всего , еще , плюс , всего , и при сложении суммируют . Когда ваш ребенок найдет ответ на сложение, предложите ему использовать слово всего или сумма .Если они говорят о том, что вы можете складывать числа в любом порядке и получать одинаковый ответ, предложите им использовать слово , коммутативное .
Есть также много математической лексики, связанной с вычитанием. Когда ваш ребенок скажет вам ответ на вычисление вычитания, предложите ему называть это разницей . Например, «7 — 3 = 4» можно прочитать как «разница между 7 и 3 равна 4». Они также должны попытаться использовать язык отнять , вычесть , минус , минус , меньше и т. Д.
Попробуйте записать символы сложения и вычитания (‘+’ и ‘-‘) вместе со связанными словами на карточках (например, добавить , всего , еще , плюс , всего , сумма , отнять , вычесть , минус , минус и на меньше) . Помогите ребенку связать слова с правильным символом. Если необходимо, помогите им прочитать некоторые слова.
2. Попробуйте вычислить мысленно
Вашему ребенку важно развить свои умственные вычислительные навыки.Это полезно в повседневной жизни, особенно когда технологии (и бумага) могут быть недоступны или уместны, например, когда вы ходите по магазинам. Уверенность в математике в уме поможет вашему ребенку делать быстрые оценки и проверять свои расчеты.
Поощряйте вашего ребенка использовать различные методы при мысленном вычислении, такие как подсчет, обратный отсчет и разделение чисел. Ваш ребенок должен использовать свои знания о числовом значении, округлении и обратных операциях, чтобы делать оценки и проверять свои ответы.
Если ваш ребенок работает над проблемой и объявляет ответ, попросите его объяснить, как он решил проблему. Они могли рисовать картинки или диаграммы, чтобы помочь им объяснить свой метод.
Попросите ребенка выполнить указанные ниже действия, используя математические вычисления в уме, чтобы сохранить свои навыки на высоком уровне!
Дополнение + | Основы арифметики
Эта страница является частью нашей серии статей, посвященной основам арифметики — простейшему способу работы с числами.
Здесь вы узнаете основы сложения (+): как сложить, суммировать или объединить два или более чисел, чтобы получить новое число — итог.Умение «складывать» важно во всех сферах жизни, дома, в школе, на работе и в обществе.
См. Другие наши страницы, чтобы узнать о вычитании, умножении и делении.
Краткие сведения о добавлении:
- Сложение — это термин, используемый для описания сложения двух или более чисел.
- Знак плюс « + » используется для обозначения сложения: 2 + 2.
- При необходимости + можно использовать несколько раз: 2 + 2 + 2.
- Для более длинных списков чисел обычно проще записать числа в столбец и выполнить вычисление внизу.
- Слово «сумма» или символ ∑ также могут использоваться для сложения.
- Не имеет значения, в каком порядке вы складываете группу чисел, потому что ответ всегда будет одним и тем же:
1 + 2 + 3 + 4 дает тот же ответ (10), что и 4 + 2 + 1 + 3 - Добавление 0 к любому числу не имеет значения 2 + 0 = 2.
Базовое сложение — это шаг вперед от счета и обычно легко усваивается учащимися.
Как только ученик может сосчитать до десяти, он обычно может быстро прибавить до десяти.
Например, если учащемуся дают две стопки карт, одна стопка содержит 4 карты, а другая — 3 карты, он может пересчитать все карты и получить ответ: 7.
Использование пальцев — обычное дело при обучении счету и сложению. Добавление точек, нарисованных на листе бумаги, а затем использование «числовой линии» — это следующие шаги в обучении, на этот раз нет физических предметов, которые нужно было бы обрабатывать.
Наконец, когда цифры распознаны, можно вычислить ту же сумму, посмотрев на 3 + 4.
Сложить одно и то же число самому себе (или удвоить) также довольно просто, если вы усвоили базовое понимание умножения, например, 3 + 3 = 6.
Сложить одно и то же число с собой аналогично умножению числа на 2:
3 + 3 также можно записать как
3 x 2 (устно 3 умножить на 2).
Добавление столбца
При сложении большого количества чисел полезно записывать их в столбцы, обозначая единицы, десятки и сотни (примеры см. На нашей странице чисел).Если нам нужно было добавить 4, 15, 23, 24, 35, 42
Шаг 1:
Расположите числа в столбцах, Сотни, Десятки и Единицы по мере необходимости:
| Десятки | шт. |
| 4 | |
| 1 | 5 |
| 2 | 3 |
| 2 | 4 |
| 3 | 5 |
| 4 | 2 |
Сложите числа в правом столбце (единицы).Это должно дать вам ответ 23. Две десятки и три единицы. Напишите 3 в столбце «Единицы измерения».
Перенесите 2 десятка — это число обычно ставится под общей суммой, оно нам понадобится на следующем шаге.
| Десятки | шт. | |
| 4 | ||
| 1 | 5 | |
| 2 | 3 | |
| 2 | 4 | |
| 3 | 5 | |
| 4 | 2 | |
| = | ||
| Итого | 3 | |
| Перенесено | 2 |
Шаг 2:
Сложите числа в столбце десятков, не забывая включить 2, которые были перенесены.Вы должны получить ответ 14.
То есть 4 десятка (поскольку мы работаем в столбце десятков) и 1 для переноса в следующий столбец, сотни.
| Сот | Десятки | шт. | |
| 4 | |||
| 1 | 5 | ||
| 2 | 3 | ||
| 2 | 4 | ||
| 3 | 5 | ||
| 4 | 2 | ||
| = | |||
| Итого | 4 | 3 | |
| Перенесено | 1 | 2 |
Шаг 3:
Следующим шагом будет сложение чисел в столбце сотен.
В столбце сотен нет чисел, кроме 1, перенесенного из столбца десятков.
Так как больше добавить нечего, доведите до общей суммы.
У нас больше не осталось чисел, поэтому мы пришли к нашему ответу: 143 .
| Сот | Десятки | шт. | |
| 4 | |||
| 1 | 5 | ||
| 2 | 3 | ||
| 2 | 4 | ||
| 3 | 5 | ||
| 4 | 2 | ||
| = | |||
| Итого | 1 | 4 | 3 |
| Перенесено | 1 | 2 |
Вы можете использовать тот же метод для сложения все больших и больших чисел, добавляя дополнительные столбцы слева по мере необходимости для тысяч, десятков тысяч и т. Д.
Примеры добавления
Есть много примеров, когда сложение полезно в повседневных ситуациях. При разработке маршрута для путешествия вы можете сложить количество миль (или километров) для каждого шага путешествия, чтобы найти общее количество миль, которые вы пройдете. Это может помочь вам, например, спланировать остановки заправки.
Вы можете использовать сложение, чтобы вычислить, сколько времени потребуется. Например, если вы сядете в автобус в 11:00, а поездка займет 25 минут, во сколько вы приедете? Точно так же вы можете складывать дни, недели, месяцы или годы.
При добавлении минут или секунд всегда помните, что в минуте 60 секунд, а в часе 60 минут. Следовательно, 100 минут равны не часу, а 1 часу 40 минутам. См. Нашу страницу Расчет со временем для получения дополнительной информации.
Пожалуй, одно из самых распространенных повседневных применений сложения — это работа с деньгами. Например, суммирование счетов и чеков. Следующий пример — типичный чек из супермаркета.Сложите все индивидуальные цены, чтобы найти общую стоимость посещения.
Поскольку SkillsYouNeed является британским сайтом, используется символ валюты — £ (фунты). Добавление в $ (доллары), € (евро) или любую другую валюту аналогично — просто измените символ валюты.
| Сыр Чеддер | £ 2,99 | |
| Простая мука | £ 0,79 | |
| Сахарный песок | £ 1.20 | |
| Масло | £ 1,24 | |
| Морковь | 0,16 фунтов стерлингов | |
| Бытовая химия | £ 1,89 | |
| Молоко | £ 1,25 | |
| Молочный шоколад | £ 0,69 | |
| Моющее средство | £ 6.50 | |
| Яйца | £ 1.10 |
Добавьте цены в чек, как в предыдущем примере.
На этот раз у вас есть десятичная точка (.), Чтобы показать доли одной единицы (фунт £). При вычислении сложения столбцов вы можете игнорировать десятичную точку, пока не дойдете до конца. Начните с сложения чисел в правом столбце, как и раньше, работая по столбцам справа налево и перенося любые «десятки» в следующий столбец.
Не забудьте включить десятичную точку в конце ваших вычислений; у вас должно быть два столбца справа от него.Технически эти столбцы должны быть помечены как «Десятые» и «Сотые». Однако попробуйте складывать числа, не используя заголовки столбцов.
Возможно, вам будет проще написать или распечатать этот пример.
Ваш окончательный ответ должен быть: 17,81 фунта стерлингов.
Если вы пришли к другому ответу, проверьте свою работу и попробуйте еще раз.
Предупреждение!
Важно отметить, что не все мировые валюты основаны на десятичной системе счисления и не все валюты имеют два десятичных знака.Например, у некоторых есть ноль десятичных знаков (например, японская иена), а у некоторых — три десятичных разряда (например, динар во многих странах).
Примеров недесятичных валют очень мало. Мавритания (где 1 угия = 5 кумов) и Мадагаскар (где 1 ариари = 5 ираимбиланджа) только теоретически недесятичны, поскольку в обоих случаях стоимость каждой подъединицы слишком мала, чтобы иметь какое-либо практическое применение сегодня, а монеты Номиналы единиц больше не в обращении. Официальной валютой Суверенного военного Мальтийского ордена является мальтийское скудо, которое подразделяется на 12 тари, каждый из которых составляет 20 грани с 6 пикчоли на грано.
Все остальные мировые валюты либо десятичные, либо вообще не имеют подединиц, либо потому, что они были упразднены, либо потому, что они потеряли всякую практическую ценность и больше не используются.




 Оргмомент
Оргмомент Оксана, запиши на доске, что у тебя получилось.
Оксана, запиши на доске, что у тебя получилось.




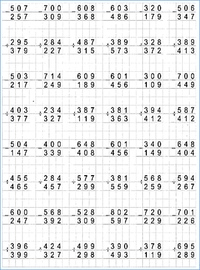 Н. з з з з з
Н. з з з з з