Сложение дробей — как складывать дроби 🤔
Понятие дроби
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Существует два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между ними означает деление.
Дроби бывают двух видов:
Числовые — состоят из чисел, например, 5/9 или (1,5 − 0,2)/15.
Алгебраические — состоят из переменных, например, (x + y)/(x − y). В этом случае значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной называют такую дробь, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1/4.
Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1/4.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Как плюсовать дроби
Сложение — это арифметическое действие, в результате которого получается новое число. Оно содержит в себе сумму заданных чисел.
Свойства сложения
- От перестановки мест слагаемых сумма не меняется: a + b = b + a.

- Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа: (a + b) + c = a + (b + c).
- Если к числу прибавить ноль, получится само число: a + 0 = 0 + a = a
- При сложении числа можно переставлять и объединять в группы, результат от этого не изменится.
Давайте рассмотрим несколько вариантов сложения обыкновенных дробей.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
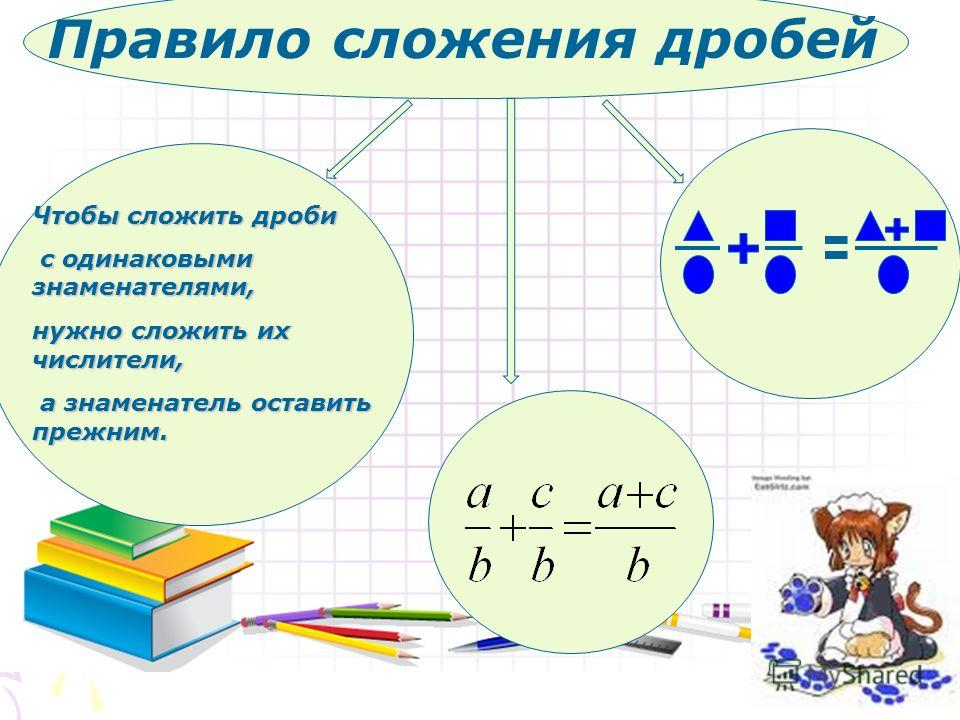
Сложение дробей с одинаковыми знаменателями
Чтобы получить сумму двух дробей с равными знаменателями, нужно сложить числители исходных дробей, а знаменатель оставить прежним.
Не забудьте проверить, можно ли сократить дробь.
Сложение дробей с разными знаменателями
Как складывать дроби с разными знаменателями — для этого нужно найти наименьший общий знаменатель (далее — НОЗ), а затем воспользоваться предыдущим правилом. Вот, что делать:
Вот, что делать:
1. Найдем наименьшее общее кратное знаменателей (далее — НОК) для определения единого делителя.
Для этого записываем в столбик числа, которые в произведении дают значения знаменателей складываемых дробей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 × 2 × 3 × 5 = 90
2. Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:
- 90 : 15 = 6,
- 90 : 18 = 5.
Полученные числа записываем справа сверху над числителем.
3. Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
4. Проверим полученный результат:
- если делимое больше делителя, нужно преобразовать в смешанное число;
- если есть что сократить, нужно выполнить сокращение.
Еще раз ход решения одной строкой:
Сложение смешанных чисел
Сложение смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
Для этого нужно действовать поэтапно:
1. Сложить целые части.
2. Сложить дробные части.
Если знаменатели разные, воспользуемся знаниями из предыдущего примера и приведем к общему.
3. Суммируем полученные результаты.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Прибавление и вычитание дробей — смежные темы: принципы и закономерности очень похожи. Чтобы закрепить знания, тренируйтесь решать примеры на сложение дробей как можно чаще.
Мерзляк 5 класс — § 27. Сложение и вычитание дробей с одинаковыми знаменателями
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
1. Сформулируйте правило сложения двух дробей с одинаковыми знаменателями.
Чтобы сложить две дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить прежним.
+ =
2. Сформулируйте правило вычитания двух дробей с одинаковыми знаменателями.
Чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.
— =
Решаем устно
1. Сравните:
1) >
2) >
3) < 1
4) > 1
5) = 1
6) <
2. Какие цифры можно поставить вместо звёздочки, чтобы дробь была правильной?
, , — правильные дроби.
Значит вместо звёздочки можно поставить числа 7, 8 или 9.
3. На шахматной доске стоят 14 фигур, из которых 5 — чёрные.
Какую часть всех фигур составляют белые фигуры?
14 — 5 = 9 (фигур) — белые
Значит, белые фигуры составляют части всех фигур.
Какую часть чёрных фигур составляют белые?
Белые фигуры составляют от чёрных фигур.
Какую часть белых фигур составляют чёрные?
Чёрные фигуры составляют от белых фигур.
4. Из суммы чисел 19 и 23 вычтите 34.
(19 + 23) — 34 = 42 — 34 = 8
5. К сумме чисел 18 и 16 прибавьте их разность.
(18 + 16) + (18 — 16) = 34 + 2 = 36
6. Удвойте сумму 37 + 100 + 63.
(37 + 100 + 63) • 2 = (37 + 63 + 100) • 2 = (100 + 100) • 2 = 200 • 2 = 400
7. Утройте разность 143 — 43.
(143 — 43) • 3 = 100 • 3 = 300
8. Назовите в порядке убывания числа:
, , 1, , , , , , .
Упражнения
743. Выполните действия:
1) + = =
2) + = =
3) — = =
4) — = =
5) + — = =
6) — — = =
744. Выполните действия:
1) + = =
2) — = =
3) + — = =
4) — — = =
745. Решите уравнение:
Решите уравнение:
1) + х =
х = —
х =
х =
2) — х =
х = —
х =
х =
3) х — =
х = +
х =
х =
746. Решите уравнение:
1) + х =
х = —
х =
х =
2) — х =
х = —
х =
х =
747. В первый день Миша прочитал книги, а во второй день — книги. Какую часть книги прочитал Миша за два дня?
1) + = = (книги) — прочитал Миша за 2 дня.
Ответ: книги.
748. Для перевозки груза использовали несколько грузовиков. На один из них положили груза, а на второй — груза. Какую часть груза положили на эти два грузовика?
1) + = = (груза) — положили на эти два грузовика.
Ответ: груза.
749. Кот Базилио съел за обедом кг сосисок, а лиса Алиса — на кг больше, чем Базилио. Сколько килограммов сосисок съели за обедом Базилио и Алиса вместе?
Сколько килограммов сосисок съели за обедом Базилио и Алиса вместе?
1) + = = (кг) — сосисок съела лиса Алиса.
2) + = = (кг) — сосисок съели лиса Алиса и кот Базилио вместе.
1 кг = 1 000 г
3) 1 000 : 20 • 21 = 50 • 21 = 1 050 (г) — сосисок съели лиса Алиса и кот Базилио вместе.
1 050 г = 1 кг 50 г.
Ответ: Лиса и кот вместе съели 1 кг 50 г сосисок или кг сосисок.
750. Отправившись на прогулку, черепаха Тортила за первый час проползла км, что на км больше, чем за второй час. Сколько километров проползла Тортила за два часа?
1) — = = (км) — проползла Тортила за второй час.
2) + = = (км) — проползла Тортила за два часа.
1 км = 1 000 м
3) 1 000 : 50 • 41 = 20 • 41 = 820 (м) — проползла Тортила за два часа.
Ответ: Тортила проползла за 2 часа 820 м или км.
751. Решите уравнение:
1) — =
= —
=
=
x = 27
2) + =
= —
=
=
x = 9
3) ( + x) — =
+ x = +
+ x =
+ x =
x = —
x =
x =
4) (x — ) + =
x — = —
x — =
x — =
x = +
x =
x =
752. Решите уравнение:
Решите уравнение:
1) — =
= +
=
=
x = 42
2) ( — a) — =
— a = +
— a =
— a =
a = —
a =
a =
3) — (b — ) =
b — = —
b — =
b — =
b = +
b =
b =
4) — (m + ) =
m + = —
m + =
m + =
m = —
m =
m =
753. Овощной магазин реализовал 240 кг картофеля. В первый день было продано картофеля, а во второй — . Сколько килограммов картофеля магазин реализовал за два дня?
1) + = = (картофеля) — было продано за 2 дня.
2) 240 : 16 • 10 = 15 • 10 = 150 (кг) — картофеля было продано за 2 дня.
Ответ: 150 кг.
754. Протяжённость построенной дороги составляет 92 км. За первый месяц построили дороги, а за второй месяц — . Сколько километров дороги было построено за два месяца?
Сколько километров дороги было построено за два месяца?
1) + = = (дороги) — построили за два месяца.
2) 92 : 23 • 15 = 4 • 15 = 60 (км) — дороги построили за два месяца.
Ответ: 60 км.
Упражнения для повторения
755. Найдите числа, которых не хватает в цепочке вычислений:
1) a = 5; b = 31; c = 5; d = 47; m = 9; n = 912.
2) x = 92; y = 12; z = 48; p = 8; q = 323; m = 61.
756. Найдите все натуральные числа, при делении которых на 7 неполное частное будет равно остатку.
Пусть х — искомое число, а а — это неполное частное и остаток, полученные при делении числа х на 7. Так как остаток от деления всегда меньше делителя, то а может равняться числам 1, 2, 3, 4, 5 и 6.
Найдём число х:
- если а = 1, то х = 7 • 1 + 1 = 7 + 1 = 8
- если а = 2, то х = 7 • 2 + 2 = 14 + 2 = 16
- если а = 3, то х = 7 • 3 + 3 = 21 + 3 = 24
- если а = 4, то х = 7 • 4 + 4 =27 + 4 = 32
- если а = 5, то х = 7 • 5 + 5 = 35 + 5 = 40
- если а = 6, то х = 7 • 6 + 6 = 42 + 6 = 48
Ответ: числа 8, 16, 24, 32, 40 и 42.
Задача от мудрой совы
757. В коробке лежат 4 белых, 5 чёрных и 6 красных шаров. Какое наименьшее количество шаров надо вынуть из коробки, чтобы среди них обязательно оказались:
1) 3 шара одного цвета
Предположим, что нам не везёт и мы всё время достаём из коробки шары разного цвета, а не подряд одного цвета. Тогда через 6 попыток мы достанем по 2 шара каждого цвета, а седьмая попытка станет удачной в любом случае, потому что какого цвета шар мы бы не вытянули — он станет третьим шаром одного из цветов:
- Белый
- Чёрный
- Красный
- Белый
- Чёрный
- Красный
- Любой цвет (белый, красный или черный)
Ответ: 7 шаров.
2) шары всех трёх цветов
Представим, что нам опять не везёт и мы всё время вытаскиваем из коробки шары одного цвета.
Самое большое количество шаров — красного цвета. Значит предположим, что сначала мы вытянули все 6 шаров красного цвета.
На втором месте по количеству — чёрные шары. Предположим, что после красных нам стали попадаться только чёрне шары и мы вытащим все 5 чёрных шаров из коробки.
А вот следующая попытка окажется удачной и нам обязательно попадётся белый шар, поскольку других в коробке уже не осталось. Значит количество попыток 12 (6 + 5 + 1 = 12):
- Красный
- Красный
- Красный
- Красный
- Красный
- Красный
- Чёрный
- Чёрный
- Чёрный
- Чёрный
- Чёрный
- Белый.
Ответ: 12 шаров.
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Сложение и вычитание алгебраических дробей с одинаковыми знаменателями (более сложные случаи) 8 класс онлайн-подготовка
Тема 10: Алгебраические дроби. Профильный уровень
Урок 6: Сложение и вычитание алгебраических дробей с одинаковыми знаменателями (более сложные случаи)
- Видео
- Тренажер
- Теория
Заметили ошибку?
Пример №1 на сложение/вычитание дробей с одинаковыми знаменателями
Вспомним изученное на прошлом уроке правило сложения и вычитания алгебраических дробей с одинаковым знаменателем:
Примечательно то, что оно одинаково применимо и для простейших случаев, рассмотренных ранее, и для более сложных, которые мы сейчас разберем на примерах.
Пример 1. Сложить и вычесть указанные дроби: .
Решение. Очевидно, что указанные дроби уже с одинаковым (общим) знаменателем, и мы можем воспользоваться упомянутым ранее правилом их сложения/вычитания.
.
Прокомментируем последовательность действий. В процессе применения правила сложения/вычитания дробей следует помнить, что такой знак, как минус перед дробью, относится ко всему числителю, и вычитать его необходимо в скобках. После приведения подобных слагаемых необходимо попытаться разложить знаменатель и числитель дроби на множители в надежде сократить на какой-то из них, что мы успешно и проделали. Затем при удачном стечении обстоятельств дробь сокращается, как в нашем случае, например, на . При этом стоит помнить, что любые сокращенные элементы необходимо учесть в области недопустимых значений переменных, так как они пропадают из дроби, и о них можно забыть. В нашем случае запишем, что .
Ответ..
Пример №2 на сложение/вычитание дробей с одинаковыми знаменателями
Пример 2. Сложить и вычесть указанные дроби:.
Решение. В указанном условии неочевидно, одинаковы ли знаменатели у дробей. Чтобы это проверить, разложим их на множители. При разложении на множители первого знаменателя видим, что он почти такой же, как и у второй дроби, противоположен только знак второго множителя. Чтобы привести знаменатели к одинаковому виду, вынесем минус из второго множителя второй дроби, и он окажется перед дробью, так как знак знаменателя и числителя относятся и ко всей дроби сразу:
.
Знаменатель третьей дроби тоже очень похож на знаменатель первой до разложения. Поступим с ним аналогично – вынесем минус и разложим на множители:
.
Все полученные преобразования дробей подставим в исходное условие (знак перед третьей дробью получится положительным, т. к. «минус на минус дает плюс»).
.
В числителе воспользовались формулой квадрата разности. После сокращения учтем, что
Ответ. .
Рассмотрим теперь пример на применение умения складывать дроби с одинаковыми знаменателями в других целях.
Пример на применение сложение/вычитания дробей при доказательстве положительности выражения
Пример 3. Доказать, что выражение принимает положительные значения при всех допустимых значениях переменной.
Решение. Поскольку необходимо исследовать выражение при всех допустимых значениях переменной, определим эти значения. По уже известному принципу, это все значения , кроме . Следовательно, . Выполним действия:
.
После приведения подобных слагаемых мы воспользовались формулой квадрата разности , далее, т. к. , то . Числитель и знаменатель положительные числа, значит, и дробь положительна.
Доказано.
На следующих уроках мы поговорим уже о сложении и вычитании дробей с разными знаменателями, используя похожую на изученную нами технику.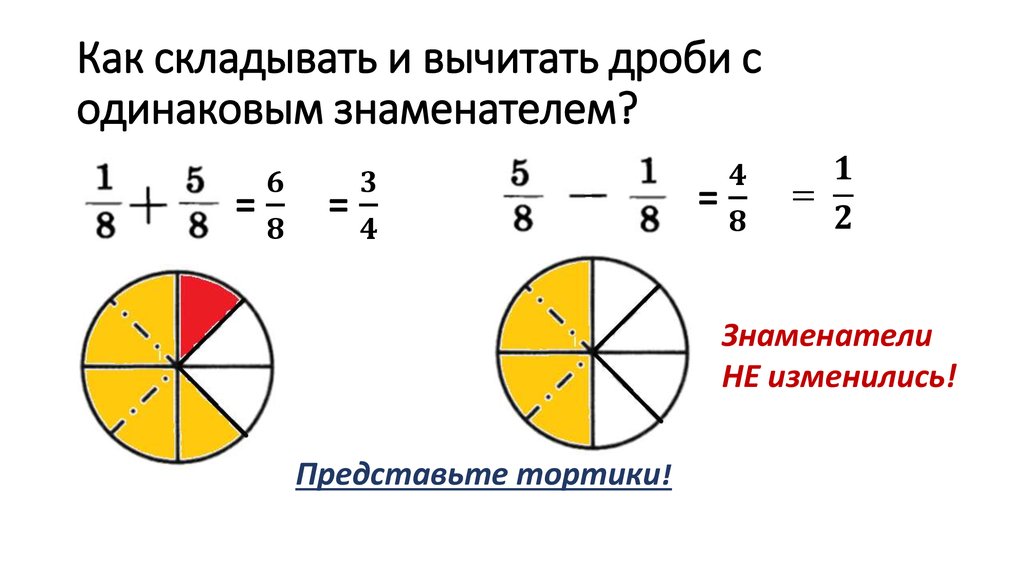
Список литературы
- Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- ЕГЭ по математике (Источник).
- Сайт учителя математики Зубаревой Веры Анатольевны (Источник).
Домашнее задание
- №58, 59, 60. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
- Упростить выражение .
- Упростить выражение .
- Упростить выражение .
Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.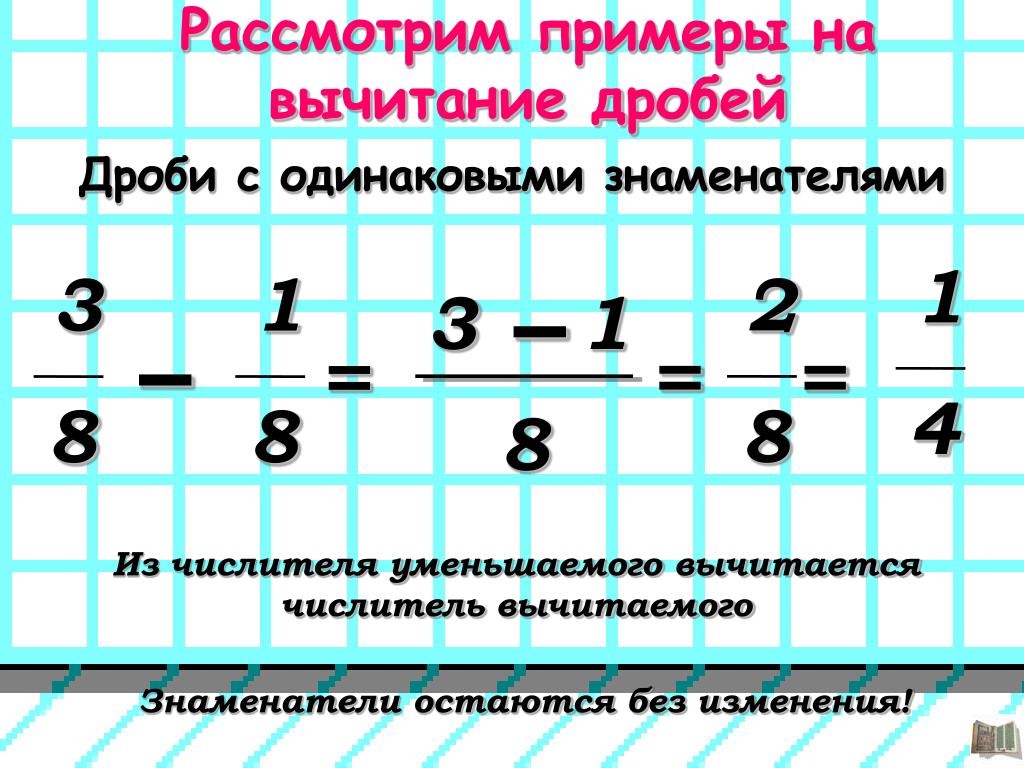
Алгебраические дроби — сложение и вычитание дробей с разными знаменателями
Сложение и вычитание простых дробей
См. также: более сложный уровень — сложение и вычитание дробей с алгебраическими выражениями и переменными.
Для проведения операции вычисления сложения простых дробей руководствуются следующим алгоритмом:
Сложение и вычитание простых дробей с одинаковым знаменателем
Для того, чтобы сложить две простые дроби с одинаковым знаменателем, необходимо сложить числители этих дробей, а знаменатель оставить без изменений.
- Числители каждой из дробей складываются, а знаменатели остаются без изменения
- При необходимости проводится сокращение дроби
- Если получившаяся дробь является неправильной (числитель больше знаменателя), дробь преобразуется в смешанную
Общая формула сложения простых дробей с одинаковым знаменателем приведена на картинке.
Примеры сложения дробей с одинаковыми знаменателями и их пояснение.
Складываем 2/9 и 5/9
Поскольку обе простые дроби имеют общий одинаковый знаменатель, то складываем числители
2+5 = 7
Ответ: 7/9
Складываем 1/8 и 3/8
Поскольку обе простые дроби имеют общий одинаковый знаменатель, то складываем числители
1+3=4
Таким образом, 1/8 + 3/8 = 4/8
Получившаяся дробь имеет кратные друг другу числитель и знаменатель, поэтому она подлежит сокращению. Сокращаем числитель и знаменатель на 4
4/8 = 1/2
Ответ: 1/2
Складываем 7/12 + 11/12
Поскольку обе простые дроби имеют общий одинаковый знаменатель, то складываем числители
7+11=18
Таким образом, 7/12 + 11/12 = 18/12
Получившаяся дробь имеет кратные друг другу числитель и знаменатель, поэтому она подлежит сокращению. Сокращаем числитель и знаменатель на 6
Сокращаем числитель и знаменатель на 6
18/12 = 3/2
Получившаяся дробь является неправильной (числитель больше знаменателя). Преобразуем ее в смешанную
3/2 = 1 1/2
Ответ: 1 1/2
Для того, чтобы вычесть из одной простой дроби другую простую дробь, если обе дроби имеют одинаковый знаменатель, необходимо из числителя первой дроби, вычесть числитель второй дроби, а знаменатель оставить без изменения
- Из числителя первой дроби вычитается числитель второй дроби, а знаменатели остаются без изменения
- При необходимости проводится сокращение дроби
Примеры вычитания дробей с одинаковыми знаменателями и их пояснение.
Вычитаем: 8/9 — 1/9
Поскольку обе простые дроби имеют общий одинаковый знаменатель, то вычитаем из числителя первой дроби числитель второй дроби
8-1 = 7
Ответ: 8/9 — 1/9 = 7/9
Вычитаем: 7/8 — 1/8
Поскольку обе простые дроби имеют общий одинаковый знаменатель, то вычитаем из числителя первой дроби числитель второй дроби
7-1 = 6
Получившаяся дробь имеет кратные друг другу числитель и знаменатель, поэтому она подлежит сокращению. Сокращаем числитель и знаменатель на 2
Сокращаем числитель и знаменатель на 2
6/8 = 3/4
Ответ: 7/8 — 1/8 = 3/4
В случае, когда обе дроби имеют разные знаменатели, пользуются правилами, описанными ниже.
Сложение и вычитание простых дробей с разными знаменателями (сложение и вычитание обыкновенных дробей)
Сложение обыкновенных дробей проводится по следующему алгоритму:
- Обе дроби приводятся к общему знаменателю
- Числители каждой из дробей складываются, а знаменатели остаются без изменения
- При необходимости проводится сокращение дроби
- Если получившаяся дробь является неправильной (числитель больше знаменателя), дробь преобразуется в смешанную
Примеры сложения простых дробей с разными знаменателями с пояснением.
Складываем 1/3 и 1/4
Поскольку знаменатели у обоих дробей — разные, их необходимо привести к общему знаменателю.
В данном случае, наименьшее общее кратное для 3 и 4 — это число 12. Соответственно, числитель и знаменатель первой дроби ( 1/3 ) умножаем на 4, а числитель и знаменатель второй дроби ( 1/4 ) умножаем на 3.
Получаем 4/12 и 3/12
Теперь у нас обе дроби имеют одинаковый знаменатель — 12. Поэтому складываем числители первой и второй дроби
4 + 3 = 7
Знаменатель остается без изменений 4/12 + 3/12 = 5/12
Ответ: 1/3 + 1/4 = 5/12
Складываем 2/3 и 3/4
Поскольку знаменатели у обоих дробей — разные, их необходимо привести к общему знаменателю.
В данном случае, наименьшее общее кратное для 3 и 4 — это число 12. Соответственно, числитель и знаменатель первой дроби ( 1/3 ) умножаем на 4, а числитель и знаменатель второй дроби ( 1/4 ) умножаем на 3.
Получаем 8/12 и 9/12
Теперь у нас обе дроби имеют одинаковый знаменатель — 12. Поэтому складываем числители первой и второй дроби
8 + 9 = 17
Знаменатель остается без изменений 8/12 + 9/12 = 17/12
Полученная дробь является неправильной (числитель больше знаменателя). Преобразуем ее в смешанную
Преобразуем ее в смешанную
17/12 = 1 5/12
Ответ: 2/3 + 3/4 = 1 5/12
См. также: более сложный уровень — сложение и вычитание дробей с алгебраическими выражениями и переменными.
2080.1947
Скорость поедания яблока | Описание курса | Сложение и вычитание дробей. Додавання і віднімання дробів
Технологическая карта урока математики в 5-м классе «Сложение и вычитание дробей с одинаковыми знаменателями»
- Нарейко Евгения Генадьевна
Разделы: Математика
Класс: 5
Ключевые слова: дроби, Сложение и вычитание дробей с одинаковыми знаменателями
Тема урока: Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями.
Класс: 5
Цель урока: научиться находить сумму и разность дробей с одинаковыми знаменателями.
Планируемые результаты:
- Предметные: ввести правила сложения и вычитания дробей с одинаковыми знаменателями; развивать умение анализировать, сравнивать, обобщать, делать выводы, развивать внимание;развивать познавательный интерес через игровые моменты взаимоконтроля, взаимопроверки.
- Метапредметные:
- регулятивные: выполнять оценку и самооценку; осознавать, что уже усвоено и что ещё следует усвоить, качество и уровень усвоения;
- познавательные: самостоятельно выделять, формулировать познавательные цели; моделировать, выстраивать логические цепи рассуждения; приводить доказательства на основе схем, моделей; составлять устно монологическое высказывание по данной теме;
- коммуникативные: инициативное сотрудничество в поиске и выборе информации с соседом по парте, в малой и большой группах; распределять работу и роли в группах, уметь выполнять свою часть работы и встраивать её в общее рабочее поле; контролировать, корректировать и оценивать действия партнёра.

- Личностные: учитывать чужую точку зрения; оказывать интеллектуальную помощь сквозным героям, которые в этом нуждаются, при решении трудных задач.
Тип урока: изучение нового материала.
Учебно-методическое обеспечение: учебник «Математика. 5 класс» автора Виленкина Н.Я., презентация, приложение.
Оборудование: компьютер, мультимедийный проектор, доска, мел.
Этапы урока | Задачи этапа | Время | Деятельность учителя | Деятельность учащихся | УУД |
1.Организационный момент | Создать благоприятный психологический настрой на работу. Обеспечить мотивацию учения детьми, принятие ими целей урока. |
4 мин | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. (слайд№3) -Вспомните, с чем вы знакомились на прошлых уроках? К нам на урок сегодня пришёл Незнайка и попросил помочь ему разобраться с понятием обыкновенные дроби и научится задачи с помощью дробей. И как вы уже догадались, на этом уроке мы продолжим работу с обыкновенными дробями. -Тема сегодняшнего урока (слайд №1) «Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями». -Какие цели мы поставим на данном уроке? (слайд № 4-7) | Включаются в деловой ритм урока. С обыкновенными дробями. Научились отличать правильные и неправильные дроби и сравнивать их. Учащихся пишут дату и тему урока в тетради. Цели урока:
| Личностные: самоопределение. Регулятивные: целеполагание. Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. |
2. Актуализация знаний и умений | Актуализация опорных знаний и способов действий; повторение умения переводить текст в запись в виде дроби, восстановление определения правильной и неправильной дроби, фиксирование индивидуальных затруднений | 8 мин | И вот первые вопросы от Незнайки; -Чем натуральные числа отличаются от дробных? — Что показывает знаменатель и где его пишут? — Что показывает числитель и где его пишут? Работа с рисунками. -Прочтите полученные ответы, а как ещё читаются эти дроби? (слайд №12) Устная работа. (слайд№13) -Помогите Незнайке собрать груши, на которых записаны неправильные дроби. -Какую дробь называют правильной? -Какую дробь называют неправильной? (слайд №14) Самостоятельная работ. (слайд №15) | Целые числа обозначают целые единицы а дробные –части единиц. Знаменатель показывает, на сколько долей делят и пишут его под чертой. Числитель показывает, сколько долей было взято и пишут его над чертой. Учащиеся пишут ответы на вопросы по слайдам в тетради. 1/2 — Половина 8/8; 17/13; 11/9. Дробь в которой числитель меньше знаменателя, называет правильной дробью. Дробь в которой числитель больше знаменателя, называет неправильной дробью. Работа в парах. | Личностные: оценивание усваиваемого материала. Коммуникативные: умение использовать речь для регуляции своего действия, строить понятные для окружающих высказывания. Регулятивные: контроль иоценка процесса и результатов деятельности. Познавательные: структурирование собственных знаний. |
3.Целеполагание и мотивация. | Обеспечение мотивации учения детьми, принятие ими целей урока | 8 мин | Ребята Незнайка очень удивлен, что дроби можно сравнивать так легко. Покажем ему, что ещё можно выполнит с обыкновенными дробями. Предлагаю построить ломаную из трёх отрезков по 2 см каждый и вычислить её длину в см. (слайд № 16) Проблемная ситуация; -Попробуйте вычислите длину ломаной в дм. Подсказка: -Найдите какую часть составляют 2 см от дециметра. (слайд №17-18) -Каким образом вы смогли вычислить длину в дм? А теперь попробуем вместе сформулировать правило сложения дробей с одинаковыми знаменателями. (слайд№19) Запишем правило сложения с помощью букв. Незнайка попросил помочь ему решить задачу. (слайд № 20) — К нему в гости пришли друзья, он решил угостить их яблоками положил на тарелку 10 (долей), 4 доли съели сколько долей осталось? -С помощью какого действия решили задачу? Сформулируйте правило вычитания дробей с одинаковыми знаменателями. Запишем это правило с помощью букв. (слайд № 21) | В тетради выполняют рисунок и вычисляют; 2+2+2=6см. Учащихся сталкиваются с проблемой 2см от дм., 2/10дм. Отмечают на рисунке и снова вычисляют длину ломаной. 2/10+2/10+2/10=2+2+2/10=6/10 Выполнили сложение дробей. При сложении дробей с одинаковыми знаменателями числители складывают, а знаменатель оставляется тот же. В тетради записывают правило с помощью букв 10/10-4/10=10-4/10=6/10 При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тот же. В тетради записывают правило с помощью букв
| Познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме. Личностные: самоопределение. Регулятивные: целеполагание. Коммуникативные: проявление активности во взаимодействии для решения познавательных задач; умение использовать речь для регуляции своего действия, строение понятные для окружающих высказывания. |
4. Применение знаний и умений в новой ситуации | Обеспечение восприятия, осмысления и первичного запоминания детьми изученной темы: «Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями». | 7 мин | — Итак одну из обучающих целей нашего урока вы выполнили ,выявили правила сложения и вычитания дробей с одинаковыми знаменателями осталось научиться применять эти правила на практике. Для этого поработаем с учебником; (слайд № 22) 1.Стр. 156, №1005.
— Прочитайте ответ.
— Прочитайте ответ. -Какую массу гвоздей получила первая бригада? — На сколько тонн меньше получила вторая бригада? -Сколько тонн гвоздей получила вторая бригада? | Решение задач по новой теме | Познавательные: формирование интереса к данной теме. Личностные: формирование готовности к самообразованию. Коммуникативные: умение оформлять свои мысли в устной форме; слушать и понимать речь других. Регулятивные: планирование своей деятельности для решения поставленной задачи и контроль полученного результата. |
5. Физкультминутка | Смена деятельности. | 2 мин | Сменить деятельность, обеспечить эмоциональную разгрузку учащихся. Физкультминутка | Учащиеся сменили вид деятельности и готовы продолжить работу. |
|
6. Первичное закрепление | Установление правильности и осознанности изучения темы. | 8 мин | -Далее я предлагаю вам проверить, как вы усвоили правила, выполнив самостоятельно № 1011, стр. 156. — Первые пять учеников справившихся с работой получают оценки. -А чтобы мы смогли быстро проверить правильность решения. приглашаю к доске 4 ученика. У доске каждый выполняет по одному столбику. К нам за помощью обратился Незнайка, он просит вас, проверить работу которую он выполнил. (слайд №24) | Самостоятельная работа: (слайд № 25) | Регулятивные: осуществление констатирующий и прогнозирующий контроль по результату и по способу действия. Познавательные: — умение ориентироваться в системе своих знаний, Коммуникативные: контроль, коррекция, оценка. |
7. Контроль усвоения, обсуждение допущенных ошибок и их коррекция. | Дать качественную оценку работы класса и отдельных обучаемых. | 3 мин | -Что изучили сегодня на уроке? -Кто желает сформулировать правило нахождения сложения дробей с одинаковыми знаменателями. | Учащихся формулируют правило сложения и вычитания дробей с одинаковыми знаменателями. | Личностные: формирование позитивной самооценки Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли; Регулятивные: умение самостоятельно анализировать правильность выполнения действий и вносить необходимые коррективы. |
8. |
| 3 мин | Было трудно … Было интересно … Я научился … Меня удивило … У меня……….настроение? (слайд № 26) | Учащихся отвечают на вопросы. Высказывают свои мнения. | Регулятивные: оценивание собственной деятельности на уроке. Коммуникативные: умение анализировать собственные успехи, неудачи, определять пути коррекции. Познавательные: рефлексия. |
9. Информация о домашнем задании | Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания | 2 мин | Сообщает домашнее задание: Прочитать теоретический материал п. Выполнить письменно | Открывают дневники, записывают домашнее задание, задают вопросы. |
Литература:
- Виленкин Н.Я., «Математика 5», «Мнемозина», 2007 г.
- Чесноков А.С., «Дидактические материалы по математике, 5 кл», М, 2010 г
- Супер-физкультминутка http://videouroki.net/diski.php
Сложение и вычитание дробей с одинаковыми знаменателями
Скачать 20.74 Kb.
|
С этим файлом связано 18 файл(ов). Среди них: funktsionalnaya_gramotnost.pptx, 00067d0a-56b25aca.doc, поурочный 9ю3.docx, 7 класс.pdf, 3kl_fizkult_-2019-2020.docx, ЕГ_7_Малярия_критерии.docx, 2021d6129e3c921d3ccd3d959dd60923.docx, blanki-oge-2021.pdf, Список детей.docx, 11.pdf, 56.pdf, График дежурств учителей МБОУ.docx, рабочая программа 9 класс геометрия (автовосстановление).docx, ЕГ_7 класс_вариант 2_система оценивания.docx, Анализ воспитательной работы за 1 полугодие 2021-2022.doc, Практическая работа № 1.doc, Практическая работа 4.docx, практическая работа 3.docx и ещё 8 файл(а). Показать все связанные файлы Подборка по базе: Разработка открытого урока обобщения знаний по теме Умножение и , Самостоятельная работа по теме «Сложение и вычитание смешанных ч, тренажер сложение.  docx, Сравнение, сложение и вычитание дробей с разными знаменателями.d, карточка сложение смешаных.docx, с.р. вычитание целых чисел.docx, Задания на сложение и сравнение целых чисел.docx, технологическая карта умножение десятичных дробей.doc, Конспект урока по математике в 1 классе по УМК «Начальная школа , Конспект урока.Сложение и вычитание смешанных чисел.docx docx, Сравнение, сложение и вычитание дробей с разными знаменателями.d, карточка сложение смешаных.docx, с.р. вычитание целых чисел.docx, Задания на сложение и сравнение целых чисел.docx, технологическая карта умножение десятичных дробей.doc, Конспект урока по математике в 1 классе по УМК «Начальная школа , Конспект урока.Сложение и вычитание смешанных чисел.docxПлан-конспект открытого урока по математике в 5 классе Тема: Сложение и вычитание дробей с одинаковыми знаменателями Учитель: Хадисов М.Х. – учитель математики МКОУ «Митлиурибская ООШ» Тип урока: урок получения новых знаний Цель урока: формирование навыков сложения и вычитания дробей с одинаковыми знаменателями, развитие умения складывать и вычитать дроби с одинаковыми знаменателями Задачи: Повторить понятие обыкновенной дроби; Сформулировать правила сложения и вычитания обыкновенных дробей с одинаковыми множителями через решение проблемной ситуации; Формировать навыки сложения и вычитания дробей с одинаковыми знаменателями.  Планируемые результаты:учащиеся познакомятся с правилами сложения и вычитания обыкновенных дробей с одинаковыми знаменателями, научаться применять данные правила на практике, при решении задач. Личностные УУД: проявление учебно-познавательного интереса, формирование мотивации к изучению нового материала. Предметные УУД: знать и использовать основные правила работы на уроке; научиться использовать правила сложения и вычитания обыкновенных дробей с одинаковыми знаменателями. Метапредметные УУД: Регулятивные: ставить учебную задачу урока, решать учебную задачу под руководством учителя, определять цель учебного задания, работать в соответствии с планом; находить и исправлять ошибки, отвечать на итоговые вопросы, оценивать свои достижения и работу одноклассников Познавательные: формировать навыки сложения и вычитания дробей с одинаковыми знаменателями; научить правильно читать и записывать выражения, содержащие обыкновенные дроби; формировать умение решать задачи на сложение и вычитание дробей с одинаковыми знаменателями; применять полученные знания при решении задач. Коммуникативные: воспитывать любовь к математике, уважение друг к другу, умение слушать, дисциплинированность, самостоятельность мышления. Репродуктивный (стимулирование учебной деятельности) Наглядный Проблемно – поисковый Эвристическая беседа Формы работы учащихся: Фронтальная Парная Ход урока Организационный момент. Приветствие, проверка готовности учащихся к занятию, организация внимания детей. Здравствуйте, ребята! Пожалуйста, убедитесь в своей готовности к уроку! Я желаю вам успешной и плодотворной работы! Садитесь. Актуализация знаний.  Учитель направляет деятельность учащихся, определяет содержание урока (продолжение изучения обыкновенных дробей). Ребята, на прошлых занятиях мы с Вами уже успели познакомиться и подружиться с понятием обыкновенной дроби. Давайте вспомним всё то, что мы уже знаем об обыкновенных дробях? Ученикам предлагается ответить на вопросы и выполнить ряд заданий: Почему люди стали использовать дробные числа? (Деление целого на равные части привело людей к использованию дробных чисел). Как записывается обыкновенная дробь? (С помощью дробной черты) Как называют число, которое стоит над чертой дроби? Под чертой дроби? Что показывает знаменатель обыкновенной дроби? Что показывает числитель? Какие дроби называются правильными обыкновенными дробями? А какие называются неправильными дробями? Прочитайте дроби. Из представленных на доске дробей, ребята, сидящие на первом варианте, пусть выпишут все неправильные обыкновенные дроби.  Ребята, сидящие на втором варианте – выпишите все правильные дроби. Ребята, сидящие на втором варианте – выпишите все правильные дроби.А теперь расположите выписанные вами дроби в порядке убывания. Учащиеся устно отвечают на вопросы, письменно выполняют два последних задания, повторяют уже изученный материал. Создание проблемной ситуации. Учитель создает проблемную ситуацию, тем самым мотивирует учащихся искать решение, развивая логическое мышление. Рассмотрим задачу: Папа съел 6/12 частей пиццы, мама съела ещё 2/12 частей пиццы, а сын съел 3/12частей пиццы. Кто съел больше всех? Сколько пиццы съедено всего? На сколько папа съел больше, чем мама? Какое действие поможет нам ответить на первый вопрос в задаче? (Сравнение дробей). Какие действия необходимо выполнить, чтобы ответить на остальные вопросы? (Сложение и вычитание). При направляющей помощи учителя ученики отвечают на вопросы, делают выводы. Формулирование проблемы.  Мы уже умеем сравнивать дроби. А чему же нам предстоит научиться сегодня? (Сложению и вычитанию дробей). Правильно! Сегодня мы научимся складывать и вычитать обыкновенные дроби с одинаковыми знаменателями, и с помощью этих знаний мы будем решать задачи. Какую тему урока мы запишем в тетрадь? (Сложение и вычитание дробей с одинаковыми знаменателями). Ученики записывают тему и число. Изучение нового материала. При направляющей помощи учителя дети выполняют задания: По математике задали решить 6 примеров. Вася решил 3 примера и отправился на прогулку. Какую часть домашнего задания по математике выполнил Вася? (3/6). После прогулки Вася решил ещё 2 примера. Какую часть заданий он решил после прогулки? (2/6). Какую часть домашнего задания сделал Вася? (5/6). Как мы определили, что Вася решил именно 5/6 задания? (Дети формулируют правило сложения дробей с одинаковыми знаменателями). Давайте запишем решение данной задачи в тетрадь! Торт разрезали на 6 частей. Откроем учебник на странице 155 и прочтем правила сложения и вычитания дробей. При сложении дробей с одинаковыми знаменателями числители складывают, а знаменатель не меняют. При вычитании дробей с одинаковыми знаменателями числители вычитают, а знаменатель не меняют. Запишем в тетради буквенную запись правил! Эти правила надо выучить! Физминутка (слежение глазами за подвижными объектами) Первичное применение нового знания. Ещё раз вслух повторим правила сложения и вычитания дробей! Молодцы. Давайте вернемся к нашей задаче. Теперь мы сможем ответить на все вопросы? (Да). Ученики отвечают на вопросы. Запишем решение задачи в тетрадь. Самостоятельная работа с учебником. Ребята, теперь попробуйте самостоятельно выполнить задание по учебнику № 1005, № 1006. Рабочая тетрадь №1, №2, №3 Если вы затрудняетесь с решением, я помогу. Справились с заданием? Молодцы! Теперь давайте проверим результаты! Для проверки поменяйтесь тетрадками, ошибки подчеркиваем и оцениваем работу. «5» — задание выполнено без ошибок, 1-2 ошибки – «4», 3 ошибки «3». Рефлексия. Какую тему урока мы сегодня изучали? Какие цели были поставлены? Достигнуты ли они? Что показалось сложным? Повторите правило сложения дробей с одинаковыми знаменателями. Повторите правило вычитание дробей с одинаковыми знаменателями. Домашнее задание. Запишите в дневники домашнее задание: Выучить правила на стр. 155, решить 1041(а-в), №1049 (а). Дата проведения: 31.01.2019г. |
Добавление дробей
PGSG8gJWt1g
Дробь типа 3 4 говорит, что у нас есть 3 из 4 частей, на которые делится целое.
Чтобы сложить дроби, нужно выполнить три простых шага:
- Шаг 1: Убедитесь, что нижние числа ( знаменатели ) совпадают
- Шаг 2: Сложите верхние числа ( числителей ), поместите этот ответ в знаменатель
- Шаг 3: Упростите дробь (если возможно)
Пример:
1 4 + 1 4
Шаг 1 . Нижние числа (знаменатели) уже одинаковы. Сразу переходите к шагу 2.
Шаг 2 . Сложите верхние числа и поставьте ответ над тем же знаменателем:
.1 4 + 1 4 знак равно 1 + 1 4 знак равно 2 4
Шаг 3 . Упростите дробь:
Упростите дробь:
2 4 знак равно 1 2
На картинке это выглядит так:
| 1 4 | + | 1 4 | = | 2 4 | = | 1 2 |
… и вы видите, как 2 4 проще, как 1 2 ? (см. Эквивалентные дроби.)
Пример:
1 3 + 1 6
Шаг 1 : Нижние числа разные. Видите, как кусочки разного размера?
Видите, как кусочки разного размера?
| 1 3 | + | 1 6 | = | ? | ||
Нам нужно сделать их одинаковыми, прежде чем мы сможем продолжить, потому что мы не можем добавить их вот так.
Число «6» в два раза больше, чем «3», поэтому, чтобы сделать нижние числа одинаковыми, мы можем умножить верхнюю и нижнюю части первой дроби на 9.0016 2 , например:
| × 2 |
| 1 3 | = | 2 6 |
| × 2 |
Важно: вы умножаете как сверху, так и снизу на одинаковую величину,
чтобы сохранить значение дроби одинаковым
Теперь дроби имеют одинаковое нижнее число («6»), и наш вопрос выглядит так:
| 2 6 | + | 1 6 | ||||
Нижние числа теперь одинаковы, поэтому мы можем перейти к шагу 2.
Шаг 2 : Сложите верхние числа и поместите их над одним знаменателем:
2 6 + 1 6 знак равно 2 + 1 6 знак равно 3 6
На картинке это выглядит так:
| 2 6 | + | 1 6 | = | 3 6 | ||
Шаг 3 : Упростить дробь:
3 6 знак равно 1 2
В графической форме весь ответ выглядит так:
| 2 6 | + | 1 6 | = | 3 6 | = | 1 2 |
С ручкой и бумагой
А вот как это сделать ручкой и бумагой (нажмите кнопку воспроизведения):
Играй! Попробуйте сложить дроби. |
Стихотворение, которое поможет вам вспомнить
♫ «Если вашей целью является сложение или вычитание,
нижние числа должны совпадать!
♫ «Измените низ, используя умножение или деление,
Но то же самое нужно применить и к верху,
♫ «И не забудьте упростить,
Пока не пришло время прощаться»
Пример:
1 3 + 1 5
Опять же, нижние цифры разные (ломтики разного размера)!
| 1 3 | + | 1 5 | = | ? | ||
Но давайте попробуем разделить их на более мелкие, чтобы были одинаковыми :
| 5 15 | + | 3 15 | ||||
Первая дробь: умножив верх и низ на 5, мы получили 5 15 :
| × 5 |
| 1 3 | = | 5 15 |
| × 5 |
Вторая дробь: умножив верх и низ на 3, мы получили 3 15 :
| × 3 |
| 1 5 | = | 3 15 |
| × 3 |
Нижние числа теперь одинаковы, поэтому мы можем добавить верхние числа:
| 5 15 | + | 3 15 | = | 8 15 | ||
Результат настолько прост, насколько это возможно, поэтому ответ:
1 3 + 1 5 знак равно 8 15
Делаем знаменатели одинаковыми
Откуда в предыдущем примере мы узнали, что нужно разрезать их на 1 / 15 тысяч, чтобы знаменатели совпадали? Мы просто перемножили два знаменателя (3 × 5 = 15).
Прочтите о двух основных способах приведения знаменателей в соответствие здесь:
- Метод общего знаменателя или
- Метод наименьшего общего знаменателя
Они оба работают, используйте тот, который вам больше нравится!
Пример: Кексы
Вы хотите испечь и продать кексы:
- Друг может предоставить ингредиенты, если вы дадите им 1 / 3 продаж
- Прилавок на рынке стоит 1 / 4 продаж
Сколько это вообще?
нам нужно добавить 1 / 3 и 1 / 4
1 3 + 1 4 = ? ?
Первые делают нижние числа (знаменатели) одинаковыми.
Умножить верх и низ 1 / 3 на 4 :
1×4 3×4 + 17 90 0
90 ?
и размножается верхняя и нижняя часть 1 / 4 на 3 :
1 × 4 3 × 40010 + 1 × 3 4 × 3 = + 1 × 3 4 × 3 = + 0007 ? ?
Сейчас Сделайте расчеты:
4 12 + 3 12 = 4 + 3 12 = 7 12
9001 7 12 сбываний идут в ингридиентах и ценах рынка.
Добавление смешанных фракций
У нас есть специальная (более продвинутая) страница по добавлению смешанных фракций.
930 931, 1399 932, 1400 933, 1401, 1402, 3564, 3565
Сложение дробей с одинаковыми знаменателями
Сложение дробей с одинаковыми знаменателями
Сложение дробей с одинаковыми знаменателями довольно просто, если следовать правилам. Этот урок посвящен сложению дробей с одинаковыми знаменателями. Мы включим всю информацию, которая вам понадобится, чтобы упростить работу с задачами на общий знаменатель!
Уравнение выше показывает Правило сложения . Итак, если вы имеете дело с одним и тем же (общим) знаменателем (b), ответом будет сумма числителей (a и c) по их общему знаменателю. Помните, что дробь относится к количеству частей в «целом», а ЦЕЛОЕ, о котором мы говорим, всегда является числом в знаменателе (внизу). Итак, все, что нам нужно сделать, это сложить части и сохранить одну и ту же точку отсчета.
Инструкция по сложению дробей с одинаковыми знаменателями
Чтобы складывать дроби, знаменатели должны быть равны. Выполните следующие шаги, чтобы добавить две дроби.
- Постройте каждую дробь (если необходимо) так, чтобы оба знаменателя были равны.
- Сложите числители дробей.
- Новый знаменатель будет знаменателем составных дробей.
- При необходимости сократите или упростите свой ответ.
- Разложить числитель на множители.
- Разложите знаменатель на множители.
- Отмена 9Дробь 0009 смешивает со значением 1.
- Перепишите ответ в виде упрощенной или сокращенной дроби.
ПОМНИТЕ: Мы НЕ складываем знаменатели
Вот и все!
Вот пример сложения дробей с одинаковым знаменателем…
Хотите проверить свою работу? Попробуйте наш новый Калькулятор сложения дробей для сложения до 5 дробей, целых чисел, смешанных чисел или неправильных дробей с одинаковыми или разными знаменателями.
Теперь, когда вы разобрались со сложением дробей, давайте копнем немного глубже…
Вы хотите быть «умником» в дробях? Верно?
Хорошо!
Было бы здорово, если бы указанное выше правило было всем, что вам нужно знать о сложении дробей. Но есть еще несколько вещей, о которых нам нужно поговорить, чтобы завершить этот урок. Итак, давайте приступим к делу.
Нажмите здесь , чтобы узнать, как переписать ответ в виде упрощенной или сокращенной дроби.
Как упростить ответы
Иногда, когда вы складываете дроби любого типа, вам нужно упростить ответ. На самом деле это означает, что вы должны показать свои результаты в «лучшей» возможной дробной форме. В результате есть еще несколько вещей для размышления…
Во-первых, ваш ответ может быть более высокой эквивалентной дробью, которая лучше представлена в сокращенной форме. Многие учителя будут настаивать на том, чтобы вы по возможности сокращали дробь.
Кроме того, сложение двух дробей может привести к так называемой неправильной дроби. Здесь числитель больше знаменателя. Чтобы записать эти ответы в их простейшей форме, вам придется преобразовать их в смешанное число. Это покажет представление целых частей и дробных частей.
Здесь числитель больше знаменателя. Чтобы записать эти ответы в их простейшей форме, вам придется преобразовать их в смешанное число. Это покажет представление целых частей и дробных частей.
Итак, давайте продолжим с подробной информацией о сложении дробей в этих особых случаях.
Приведение дробей к наименьшему эквиваленту
Вот ситуация. Вы хорошо добавили дроби, но ваш ответ может не показывать наименьшую эквивалентную дробь. Так как же убедиться, что при сложении дробей ваш ответ отображается в наименьшем эквиваленте?
Давайте рассмотрим простой пример сложения дробей, чтобы вы поняли суть…
Обратите внимание, что первоначальный ответ на сложение дробей в нашей тестовой задаче — «2/4». Чтобы определить, является ли наш ответ простейшей формой, мы должны разложить числитель и знаменатель на его простые числа.
Щелкните здесь, чтобы просмотреть обзор простых чисел.
Делители числа — это числа, которые при умножении дают это число. Самый простой способ убедиться, что вы учли ВСЕ делители числа, содержащиеся в дроби, — это разбить их на простые числа.
Самый простой способ убедиться, что вы учли ВСЕ делители числа, содержащиеся в дроби, — это разбить их на простые числа.
То, что мы ищем , это простые числа, которые являются общими делителями как в числителе, так и в знаменателе дроби. Если мы найдем эти общие факторы, мы сможем их отменить. Результатом будет наименьшая дробная эквивалентная дробь.
Поскольку «2» является общим множителем как в числителе, так и в знаменателе нашего примера, это означает, что наш ответ не является дробью в ее простейшей форме. Поэтому мы сократим (/) одну из двоек как в числителе, так и в знаменателе, разделив на «2». Результатом является уменьшенная дробь в ее простейшей форме.
Вот правило…
Всегда помните…
Что бы вы ни делали с числителем дроби, вы должны делать это и со знаменателем дроби. Таким образом, если вам нужно разделить числитель на число, вы также должны разделить знаменатель на то же число. Таким образом, вы не измените общее значение дроби.
Давайте добавим более сложную дробь, чтобы убедиться, что она у вас есть…
В этой задаче «2» и «3» можно найти как множители как в числителе, так и в знаменателе числа. дробная часть. Обратите внимание, как мы отменяем только один к одному! Сначала делим числитель и знаменатель на «2», затем делим и числитель, и знаменатель на «3». Так что в числителе осталось 1 x 1 x 3 = 3 , а знаменатель равен 1 x 2 x 2 x 1 = 4 . Это оставляет использование с уменьшенной дробью, равной 3/4.
Упростить неправильную дробь
Вы, наверное, помните, что в неправильной дроби числитель больше знаменателя. Поэтому каждый раз, когда вы складываете две дроби и ваш ответ оказывается неправильной дробью, вы должны упростить свой ответ. Результат будет в виде смешанного числа.
Чтобы преобразовать неправильную дробь в смешанное число, просто разделите числитель на знаменатель. Результатом будет целая часть числа и дробная часть.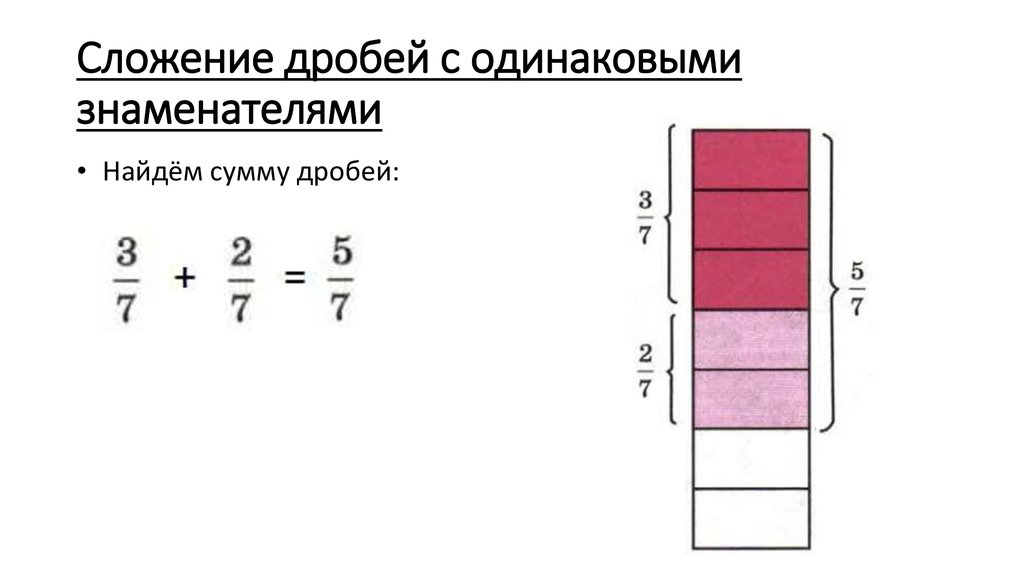
Вот пример…
Как видите, это довольно простая операция. Но имейте в виду, что если остатка нет, ответом будет только ЦЕЛОЕ ЧИСЛО.
Теперь у вас есть простой способ складывать дроби с одинаковыми знаменателями.
[fusion_separator style_type=”shadow” top_margin=”40″ bottom_margin=”40″ sep_color=”” icon=”” width=”” class=”” id=””/]
Дополнительная справка
Таблица факторизации простых чисел
Рабочие листы сложения дробей
Как складывать дроби с разными знаменателями
Если дроби, которые вы хотите сложить, имеют разные знаменатели, это можно сделать несколькими способами.Легко складывать дроби
В какой-то момент вашей жизни какой-то учитель где-то сказал вам эти золотые слова мудрости: «Нельзя складывать две дроби с разными знаменателями». Ваш учитель ошибся! Вы можете использовать простой способ, когда числители и знаменатели малы (скажем, 15 или меньше).Вот как это сделать:
Перемножьте две дроби и сложите результаты вместе, чтобы получить числитель ответа.

Предположим, вы хотите сложить дроби 1/3 и 2/5. Чтобы получить числитель ответа, перемножьте. Другими словами, умножьте числитель одной дроби на знаменатель другой:
1*5 = 5
2*3 = 6
Сложите результаты, чтобы получить числитель ответа:
5 + 6 = 11
Умножьте два знаменателя, чтобы получить знаменатель ответа.
Чтобы получить знаменатель, просто перемножьте знаменатели двух дробей:
3*5 = 15
Знаменатель ответа равен 15.
Запишите свой ответ в виде дроби.
Поскольку и числитель, и знаменатель — четные числа, вы знаете, что дробь можно уменьшить. Так что попробуйте разделить оба числа на 2:
Эту дробь нельзя уменьшить, поэтому 37/40 — окончательный ответ.
В некоторых случаях может потребоваться добавить более одной дроби. Метод аналогичен, с одной небольшой поправкой.
Начните с умножения числителя первой дроби на знаменателя всех остальных дробей.
(1*5*7) = 35
Проделайте то же самое со второй дробью и прибавьте это значение к первой.
35 + (3*2*7) = 35 + 42
Проделайте то же самое с оставшимися фракциями.
35 + 42 + (4*2*5) = 35 + 42 + 40 = 117
Когда вы закончите, у вас будет числитель ответа.
Чтобы получить знаменатель, просто умножьте все знаменатели вместе:
Вам может понадобиться уменьшить или заменить неправильную дробь смешанным числом. В этом примере вам просто нужно изменить номер на смешанный:
Добавление дробей методом быстрого трюка
Вы не всегда можете использовать этот метод, но вы можете использовать его, когда один знаменатель кратен другому. Посмотрите на следующую задачу:Сначала решите ее простым способом:
Это большие числа, и вы еще не справились, потому что числитель больше знаменателя. Ответ — неправильная дробь. Что еще хуже, числитель и знаменатель являются четными числами, поэтому ответ все равно нужно сократить.
Ответ — неправильная дробь. Что еще хуже, числитель и знаменатель являются четными числами, поэтому ответ все равно нужно сократить.
При некоторых проблемах со сложением дробей существует более разумный способ работы. Хитрость заключается в том, чтобы превратить задачу с разными знаменателями в более простую задачу с тем же знаменателем.
Прежде чем складывать две дроби с разными знаменателями, проверьте знаменатели, чтобы узнать, кратен ли один из них другому. Если это так, вы можете использовать быстрый трюк:
Увеличьте члены дроби с меньшим знаменателем, чтобы она имела больший знаменатель.
Взгляните на предыдущую задачу по-новому:
Как видите, 12 делится на 24 без остатка. В этом случае вы хотите возвести члены 11/12 так, чтобы в знаменателе было 24:
Чтобы заполнить вопросительный знак, трюк состоит в том, чтобы разделить 24 на 12, чтобы узнать, как связаны знаменатели; затем умножьте результат на 11:
? = (24 ÷ 12) 11 = 22
Перепишите задачу, подставив эту увеличенную версию дроби, и дополните.

Теперь вы можете переписать задачу так:
Как видите, цифры в этом случае намного меньше и с ними проще работать. Ответ здесь — неправильная дробь; превратить его в смешанное число легко:
Сложение дробей традиционным способом
Используйте традиционный способ только тогда, когда вы не можете использовать ни один из других методов (или когда вы знаете наименьшее общее кратное [НОК], просто взглянув на знаменатели).Вот традиционный способ сложения дробей с двумя разными знаменателями:
Найдите НОК двух знаменателей.
Предположим, вы хотите сложить дроби 3/4 + 7/10. Сначала найдите НОК двух знаменателей, 4 и 10. Вот как найти НОК, используя метод таблицы умножения:
Кратность 10: 10, 20, 30, 40
Кратность 4: 4, 8, 12, 16, 20
Таким образом, НОК 4 и 10 равно 20.
Увеличьте члены каждой дроби так, чтобы знаменатель каждой равнялся НОК.

Увеличьте каждую дробь до большего члена так, чтобы знаменатель каждой был равен 20.
Замените эти две новые дроби исходными и сложите.
На данный момент у вас есть две дроби с одинаковым знаменателем:
Когда ответ представляет собой неправильную дробь, вам все равно нужно изменить ее на смешанное число:
Об этой статье
Эту статью можно найти в категории:
- Предварительная алгебра,
Сложение дробей — шаги, примеры
Сложение дробей немного отличается от обычного сложения чисел так как дробь имеет числитель и знаменатель, разделенные чертой. сложение дробей можно легко сделать, если знаменатели равны. В то время как одинаковые дроби имеют общие знаменатели, разные дроби преобразуются в одинаковые дроби, чтобы упростить сложение. Давайте подробнее рассмотрим , добавив дроби в этой статье.
Давайте подробнее рассмотрим , добавив дроби в этой статье.
| 1. | Как складывать дроби? |
| 2. | Сложение дробей с одинаковыми знаменателями |
| 3. | Сложение дробей с разными знаменателями |
| 4. | Сложение дробей с целыми числами |
| 5. | Добавление дробей с переменными |
| 6. | Часто задаваемые вопросы о сложении дробей |
Как складывать дроби?
Дроби являются частью целого. Прежде чем перейти к сложению дробей, давайте быстро повторим, что такое дроби. Дроби состоят из двух частей, числителя и знаменателя. Общее представление дроби — это a/b, где «a» — числитель, «b» — знаменатель, а «b» не может быть нулевым. Например, 2/3, 14/5, 6/7, 28/9.и 21/43. Как и с другими числами, мы можем выполнять арифметические операции сложения, вычитания, умножения и деления дробей. Сложение дробей означает нахождение суммы двух или более дробей. Теперь давайте изучим основные шагов сложения дробей с помощью следующего примера.
Сложение дробей означает нахождение суммы двух или более дробей. Теперь давайте изучим основные шагов сложения дробей с помощью следующего примера.
Пример: Сложить 1/4 + 2/4
Решение: Сложим эти дроби, выполнив следующие действия.
- Шаг 1: Проверить, совпадают ли знаменатели. (Здесь знаменатели совпадают, поэтому переходим к следующему шагу)
- Шаг 2: Сложите числители и поместите сумму над общим знаменателем. Это означает, что (1 + 2)/4 = 3/4
- Шаг 3: При необходимости упростите дробь до наименьшей формы. Здесь он не нужен. Итак, сумма данных дробей равна 1/4 + 2/4 = 3/4 .
В математике есть разные типы дробей. При добавлении дробей нам нужно проверить, похожи ли они на дроби или не похожи на дроби. Подобные дроби — это группа дробей с общим знаменателем, а разные дроби — это группа дробей с разными знаменателями. Изучая сложение дробей, мы можем столкнуться со следующими сценариями.
Изучая сложение дробей, мы можем столкнуться со следующими сценариями.
- Сложение дробей с одинаковыми знаменателями: 3/4 + 1/4
- Сложение дробей с разными знаменателями: 3/5 + 1/2
- Сложение дробей с целыми числами: 1/2 + 2
- Сложение дробей с переменными: 3/5г + 1/4г
Теперь давайте более подробно узнаем о вышеупомянутых случаях.
Сложение дробей с одинаковыми знаменателями
Сложение дробей с одинаковыми знаменателями осуществляется путем записи суммы числителей над общим знаменателем. Давайте разберемся в этом с помощью примера.
Пример: Сложите дроби 2/4 + 1/4
Решение: Мы видим, что знаменатели данных дробей совпадают. Эти дроби называются подобными дробям.
Сложение одинаковых дробей можно произвести, сложив числители данных дробей и сохранив общий знаменатель. В этом случае мы сохраняем знаменатель равным 4 и добавляем числители. Это можно выразить как 2/4 + 1/4 = (2 + 1)/4 = 3/4. Это дает сумму как 3/4.
Это можно выразить как 2/4 + 1/4 = (2 + 1)/4 = 3/4. Это дает сумму как 3/4.
Сложение дробей с разными знаменателями
Мы только что научились складывать дроби с одинаковыми знаменателями. Теперь давайте разберемся, как складывать дроби с разными или непохожими знаменателями. Когда знаменатели разные, дроби называются непохожими дробями . В таких дробях первым делом нужно преобразовать их в подобные дроби, чтобы знаменатели стали общими. Это делается путем нахождения наименьшего общего кратного (НОК) знаменателей. Давайте разберемся в этом с помощью следующего примера.
Пример: Сложите дроби 1/3 и 3/5.
Решение: Мы будем использовать следующие шаги, чтобы сложить эти дроби.
- Шаг 1: Поскольку знаменатели в данных дробях разные, мы находим НОК 3 и 5, чтобы сделать их одинаковыми. НОК 3 и 5 = 15,
- Шаг 2: Теперь умножьте 1/3 на 5/5, (1/3) × (5/5) = 5/15 и 3/5 на 3/3, (3/5) × (3).
 /3) = 9/15, что преобразует их в одинаковые дроби с одинаковыми знаменателями.
/3) = 9/15, что преобразует их в одинаковые дроби с одинаковыми знаменателями. - Шаг 3: Теперь знаменатели совпадают, поэтому мы просто складываем числители и записываем сумму над общим знаменателем. Новые дроби с общими знаменателями — 5/15 и 9/15. Итак, 5/15 + 9/15 = (5 + 9)/15 = 14/15.
Сложение дробей с целыми числами
Простой способ сложить целое число и правильную дробь состоит в том, чтобы объединить их и представить в виде смешанной дроби. Например, 5 + 1/2 можно объединить и выразить как 5½ = 11/2. Точно так же 3 + 1/7 = \(3\frac{1}{7} \) = 22/7. Однако есть и другой способ сложения дробей с целыми числами. Давайте поймем это с помощью следующего примера.
Пример: Сложить 3 + 4/5
Решение: Сложим эти числа, выполнив следующие шаги:
- Шаг 1: запись 1 в качестве его знаменателя. Здесь 3 — это целое число, и его можно записать как 3/1 .
- Шаг 2: Теперь к 4/5 можно прибавить 3/1, то есть 3/1 + 4/5. Мы добавим их, сделав знаменатели одинаковыми, потому что они не похожи на дроби. Отсюда следует, что (3/1) + (4/5) = (3/1) × (5/5) + (4/5) × (1/1) = 15/5 + 4/5 = 19./5 = \(3\frac{4}{5} \)

Добавление дробей с переменными
Теперь, когда мы увидели сложение дробей с одинаковыми и разными дробями, мы можем расширить ту же концепцию для сложения дробей с переменными. Давайте разберемся в этом с помощью следующего примера.
Пример: Добавьте y/5 + 2y/5, где ‘y’ — переменная.
Решение: Складываем эти дроби, используя следующие шаги:
- Шаг 1: Данные дроби y/5 + 2y/5 подобны дробям, поскольку у них один и тот же знаменатель, и мы видим, что ‘y’ является общим.
- Шаг 2: Мы можем убрать общий множитель и переписать его как: y/5 + 2y/5 = (1/5 + 2/5)y = 3y/5
- Шаг 3: Следовательно, сумма y/5 + 2y/5 = 3y/5
Теперь давайте научимся складывать разные дроби на следующем примере.
Пример: Добавить д/2 + д/3
Решение: Давайте сложим дроби, выполнив следующие шаги.
- Шаг 1: Поскольку данные дроби y/2 + y/3 не похожи друг на друга, мы возьмем НОК знаменателей и преобразуем их в подобные дроби.
- Шаг 4: Далее нам нужно взять общую переменную и переписать ее следующим образом: LCM (2, 3) = 6; y/2 = (y/2) × (3/3) = 3y/6 и y/3 = (y/3 × (2/2) = 2y/6
- Шаг 5: Мы получили две дроби с общими знаменателями, (3y/6) + (2y/6) = (3y + 2y)/6 = 5y/6. Следовательно, сумма y/2 + y/3 = 5y/6
Следует отметить, что в некоторых случаях, когда у нас есть разные переменные, такие как «x» и «y», они рассматриваются как разные термины и не могут быть дополнительно упрощены, например, x/2 + y/3
Советы и рекомендации по сложению дробей
При работе со сложением дробей полезно помнить следующие моменты:
- В отличие от дробей, мы не складываем числители и знаменатели напрямую.
 1/5 + 2/3 ≠ 3/8
1/5 + 2/3 ≠ 3/8 - Чтобы сложить разные дроби, сначала преобразуйте данные дроби в одинаковые дроби, взяв НОК знаменателей.
- Сложите числители и сохраните общий знаменатель, чтобы получить сумму дробей.
☛ Похожие темы
- Вычитание дробей
- Умножение дробей
- Деление дробей
- Подобные дроби и отличные дроби
- Добавление калькулятора дробей
Часто задаваемые вопросы о сложении дробей
Как складывать дроби?
Процесс сложения дробей немного отличается от обычного сложения целых чисел. Первым шагом при сложении дробей является проверка, совпадают ли знаменатели данных дробей. Затем мы используем следующую процедуру, чтобы добавить их.
- Если дроби имеют общие знаменатели, то мы можем легко сложить числители и сохранить тот же знаменатель, чтобы получить сумму. Например, 2/4 + 1/4 = (2 + 1)/4 = 3/4
- Если знаменатели разные, мы делаем знаменатели равными, переводя их в эквивалентные дроби, находя НОК знаменателей.
 После этого можно делать прибавку. Например, 1/2 + 2/3 = (1/2 × 3/3) + (2/3 × 2/2) = 3/6 + 4/6 = (3 + 4)/6 = 7/6. = \(1 \dfrac{1}{6}\)
После этого можно делать прибавку. Например, 1/2 + 2/3 = (1/2 × 3/3) + (2/3 × 2/2) = 3/6 + 4/6 = (3 + 4)/6 = 7/6. = \(1 \dfrac{1}{6}\)
Каково правило сложения дробей?
Основное правило для сложения дробей — сделать знаменатели дробей одинаковыми. Если дроби имеют одинаковый знаменатель, мы можем просто сложить числители, сохраняя тот же знаменатель. Однако, если знаменатели разные, нам нужно преобразовать их в одинаковые дроби с одинаковыми знаменателями. Это делается путем записи их эквивалентных дробей с использованием НОК знаменателей. Как только они преобразуются в одинаковые дроби, дроби можно легко складывать, потому что нам просто нужно работать с числителями, сохраняя при этом тот же знаменатель.
Как складывать дроби с целыми числами?
Чтобы сложить дробь с целым числом, мы сначала преобразуем целое число в дробь. Например, если нам нужно сложить 3 и 1/2, целое число 3 можно легко преобразовать в дробь, например 3/1, и прибавить к другой дроби. Давайте посмотрим, как это работает. (3/1) + (1/2) = (3/1) × (2/2) + (1/2) = 6/2 + 1/2 = 7/2 = 3½. Другой способ складывать дроби и целые числа — просто комбинировать и представлять их в виде смешанных дробей. Например, 6 + 1/2 можно объединить и записать как \(6 \dfrac{1}{2}\)
Давайте посмотрим, как это работает. (3/1) + (1/2) = (3/1) × (2/2) + (1/2) = 6/2 + 1/2 = 7/2 = 3½. Другой способ складывать дроби и целые числа — просто комбинировать и представлять их в виде смешанных дробей. Например, 6 + 1/2 можно объединить и записать как \(6 \dfrac{1}{2}\)
Как складывать дроби с разными знаменателями?
Дроби с разными знаменателями можно сложить, сделав знаменатели общими. Это делается путем умножения числителя и знаменателя каждой из дробей на подходящее число так, чтобы все дроби стали как дроби. Чтобы сложить дроби 3/5 + 4/3, нам нужно обе дроби умножить на число, при котором знаменатели равны. Для этого нам понадобится НОК знаменателей, который в данном случае равен 15. Числитель и знаменатель первой дроби 3/5 нужно умножить на 3, а числитель и знаменатель второй дроби 4/3 умножить на 5. Следовательно, мы имеем (3/5 × 3/3) + (4/3 × 5/5) = (9/15) + (20/15) = (9 + 20)/15 = 29/15 = \(1 \dfrac{14}{15}\)
Как сложить три дроби с разными знаменателями?
Сложение трех дробей аналогично сложению двух дробей с разными знаменателями. Прежде всего, нам нужны НОК всех трех знаменателей. Соответственно, знаменатели всех трех дробей становятся общими путем умножения числителя и знаменателя каждой из дробей на подходящее число, чтобы они были преобразованы в одинаковые дроби. Теперь, когда знаменатели являются общими, добавляются числители, чтобы получить сумму дробей. Давайте поймем это с помощью этой задачи на сложение: 2/3 + 4/5 + 1/6. НОК 3, 5 и 6 равен 30. Теперь мы умножим каждую дробь на подходящее число, чтобы их знаменатели были общими: (2/3 × 10/10) + (4/5 × 6/6) + ( 1/6 × 5/5) = (20/30) + (24/30) + (5/30) = (20 + 24 + 5)/30 = 49/30 = \(1 \dfrac{19}{30}\)
Прежде всего, нам нужны НОК всех трех знаменателей. Соответственно, знаменатели всех трех дробей становятся общими путем умножения числителя и знаменателя каждой из дробей на подходящее число, чтобы они были преобразованы в одинаковые дроби. Теперь, когда знаменатели являются общими, добавляются числители, чтобы получить сумму дробей. Давайте поймем это с помощью этой задачи на сложение: 2/3 + 4/5 + 1/6. НОК 3, 5 и 6 равен 30. Теперь мы умножим каждую дробь на подходящее число, чтобы их знаменатели были общими: (2/3 × 10/10) + (4/5 × 6/6) + ( 1/6 × 5/5) = (20/30) + (24/30) + (5/30) = (20 + 24 + 5)/30 = 49/30 = \(1 \dfrac{19}{30}\)
Что такое элемент идентичности для сложения дробей?
Идентификационным элементом для сложения является 0, что означает, что для любого действительного числа «а» а + 0 = а. Точно так же для сложения дробей элемент идентичности равен 0. Для дроби вида a/b имеем a/b + 0 = 0 + a/b = a/b. Использование элемента идентичности для сложения не меняет значение дроби.
Что такое вычитание и сложение дробей?
При вычитании и сложении дробей, во-первых, следует приравнять знаменатели дробей. Процесс начинается с LCM знаменателей. Затем дроби умножаются на подходящее число, в результате чего все знаменатели становятся равными. Наконец, числители добавляются или вычитаются в соответствии с вопросом, а новый знаменатель остается прежним.
Сложение дробей с одинаковыми знаменателями |
Форма поиска
Поиск
Чтобы добавить или вычесть элементы, единицы должны быть одинаковыми. Например, посмотрите на добавляемые элементы ниже.
2 яблока + 3 яблока = 5 яблок
6 апельсинов + 3 апельсина = 9 апельсинов называть их «фруктами». Точно так же мы не можем добавлять четвертаки и пятаки, если не называем их «центами». В названии дроби единицей является знаменатель. Например, в дроби «4 десятых» единицей измерения является знаменатель, 9.0484 десятых . Следовательно, 4 десятых + 5 десятых = 9 десятых. Посмотрите на пример 1 ниже.
Следовательно, 4 десятых + 5 десятых = 9 десятых. Посмотрите на пример 1 ниже.
Пример 1: Пицца была разделена на восемь равных частей (ломтиков). Если Дженни съела пять кусочков, а Эрик — два, то какую часть пиццы они съели вместе?
Анализ: Дженни съела «5 восьмых» пиццы, а Эрик съел «2 восьмых». В каждой из этих дробей единицей является знаменатель, восьмых . Поскольку обе дроби имеют одинаковые единицы измерения, мы можем сложить их вместе.
Решение: «5 восьмых + 2 восьмых = 7 восьмых».
Знаменатель дроби называет то, что мы считаем. В примере 1 мы считаем восьмые. Это показано на числовой строке ниже.
Начертить числовую линию не всегда практично. Итак, нам нужна арифметическая процедура сложения дробей. Задача из примера 1 записывается с использованием следующих математических обозначений:
Знаменатель дроби называет единицу. Числитель показывает, сколько их. Например, в дроби пять восьмых единицей являются восьмые и их 5. Чтобы складывать дроби, знаменатели должен совпадать с . То есть они должны иметь общий знаменатель .
Чтобы складывать дроби, знаменатели должен совпадать с . То есть они должны иметь общий знаменатель .
У этих дробей общий знаменатель (знаменатели одинаковы). Если бы знаменатели не были общими, вы не могли бы складывать эти дроби.
Это приводит нас к следующей процедуре сложения дробей с общим знаменателем.
Процедура: Чтобы сложить две или более дроби с одинаковыми знаменателями, сложите числители и поместите полученную сумму над общим знаменателем. При необходимости упростите результат.
Давайте рассмотрим несколько примеров сложения дробей с помощью этой процедуры.
|
|
В примере 3 нам нужно было упростить результат: мы сократили шесть девятых до наименьших членов, что составляет две трети.
|
В примере 4 мы упростили результат, превратив неправильную дробь в целое число.
Избегайте этой распространенной ошибки!
Некоторые учащиеся ошибочно складывают знаменатели вместе с числителями. Это математически неверно, как показано ниже.
|
Не добавлять знаменатели!
Чтобы сложить дроби, сложите только числители и поместите сумму над общим знаменателем.
До сих пор мы добавляли только две дроби за раз. Мы можем добавить более двух дробей, используя описанную выше процедуру. Это показано в примерах ниже.
|
|
Итог:
Чтобы сложить две или более дроби с одинаковыми знаменателями, сложите числители и поместите полученную сумму над общим знаменателем. При необходимости упростите результат.
При необходимости упростите результат.
Упражнения
Указания: Сложите дроби в каждом упражнении ниже. При необходимости обязательно упростите результат. Щелкните один раз в ПОЛЕ ОТВЕТА и введите свой ответ; затем нажмите ВВОД. После того, как вы нажмете ENTER, в ОКНЕ РЕЗУЛЬТАТОВ появится сообщение, указывающее, является ли ваш ответ правильным или неправильным. Чтобы начать заново, нажмите ОЧИСТИТЬ.
Примечание: Чтобы записать дробь три четверти, введите 3/4 в форму.
| 1. | |
| ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ: | |
| 2. | |
| ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ: | |
3. | |
| ОТВЕТЫ: ОКНО РЕЗУЛЬТАТОВ: | |
| 4. | |
| ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ: | |
| 5. | |
| ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ: | |
| Уроки сложения и вычитания дробей и смешанных чисел | |
1. | Сложение дробей с одинаковыми знаменателями |
| 2. | Вычитание дробей с одинаковыми знаменателями |
| 3. | Сложение и вычитание дробей с разными знаменателями |
| 4. | Добавление смешанных номеров |
| 5. | Вычитание смешанных чисел |
| 6. | Решение словесных задач |
| 7. | Практические упражнения |
| 8. | Упражнения с вызовом |
| 9. | Решения |
Подпишитесь на нашу БЕСПЛАТНУЮ рассылку!
Подпишитесь на нашу БЕСПЛАТНУЮ рассылку новостей!
Адрес электронной почты *
5.
 1: Сложение и вычитание дробей с одинаковыми знаменателями
1: Сложение и вычитание дробей с одинаковыми знаменателями- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 48857
- Денни Бурзински и Уэйд Эллис-младший
- Колледж Южной Невады через OpenStax CNX
Цели обучения
- уметь складывать и вычитать дроби с одинаковыми знаменателями
Сложение дробей с одинаковыми знаменателями
Рассмотрим следующую диаграмму.
2 пятых и 1 одна пятая заштрихованы.
В заштрихованных областях диаграммы показано, что
(2 пятых) + (1 одна пятая) = (3 пятых)
То есть
\(\dfrac{2}{5} + \dfrac{1}{5} = \dfrac{3}{5}\)
Исходя из этого наблюдения, мы можем предложить следующее правило.
Метод сложения дробей с одинаковыми знаменателями
Чтобы сложить две или более дробей с одинаковыми знаменателями, сложите числители и поместите полученную сумму над общим знаменателем. Уменьшите, если необходимо.
Sample Set A
Найдите следующие суммы.
\(\dfrac{3}{7} + \dfrac{2}{7}\). Знаменатели одинаковы. Сложите числители и поместите эту сумму на 7.
Решение
\(\dfrac{3}{7} + \dfrac{2}{7} = \dfrac{3 + 2}{7} = \dfrac{5}{7}\)
Набор образцов A
\(\dfrac{1}{8} + \dfrac{3}{8}\). Знаменатели одинаковы. Сложите числители и поместите сумму на 8. Уменьшите.
Решение
\(\dfrac{1}{8} + \dfrac{3}{8} = \dfrac{1 + 3}{8} = \dfrac{4}{8} = \dfrac{ 1}{2}\)
Набор образцов A
\(\dfrac{4}{9} + \dfrac{5}{9}\). Знаменатели одинаковы. Сложите числители и поместите сумму больше 9.
Решение
\(\dfrac{4}{9} + \dfrac{5}{9} = \dfrac{4 + 5}{9} = \dfrac{9}{9} = 1\)
Набор образцов A
\(\dfrac{7}{8} + \dfrac{5}{8}\). Знаменатели одинаковы. Сложите числители и поместите сумму над 8.
Знаменатели одинаковы. Сложите числители и поместите сумму над 8.
Решение
\(\dfrac{7}{8} + \dfrac{5}{8} = \dfrac{7 + 5}{8} = \dfrac {12}{8} = \dfrac{3}{2}\)
Sample Set A
Чтобы увидеть, что произойдет, если мы по ошибке сложим знаменатели , а также числители, добавим
\(\dfrac{1}{2} + \dfrac{1}{2}\)
Сложение числителей и по ошибке сложение знаменателей дает
\(\ dfrac{1}{2} + \dfrac{1}{2} = \dfrac{1 + 1}{2 + 2} = \dfrac{2}{4} = \dfrac{1}{2}\)
Это означает, что два \(\dfrac{1}{2}\) равны одному \(\dfrac{1}{2}\). Нелепо! Мы не складываем знаменатели .
Тренировочный набор A
Найдите следующие суммы.
\(\dfrac{1}{10} + \dfrac{3}{10}\)
- Ответить
\(\dfrac{2}{5}\)
Тренировочный набор A
\(\dfrac{1}{4} + \dfrac{1}{4}\)
- Ответить
\(\dfrac{1}{2}\)
Тренировочный набор A
\(\dfrac{7}{11} + \dfrac{4}{11}\)
- Ответить
\(1\)
Тренировочный набор A
\(\dfrac{3}{5} + \dfrac{1}{5}\)
- Ответить
\(\dfrac{4}{5}\)
Тренировочный набор A
Покажите, почему сложение и числителей, и знаменателей нелепо, сложив \(\dfrac{3}{4}\) и \(\dfrac{3}{4}\) и изучив результат.
- Ответить
\(\dfrac{3}{4} + \dfrac{3}{4} = \dfrac{3 + 3}{4 + 4} = \dfrac{6}{8} = \dfrac{3}{4} }\), так что два \(\dfrac{3}{4}\) = один \(\dfrac{3}{4}\), что нелепо.
Вычитание дробей с одинаковыми знаменателями
Мы можем представить концепцию вычитания дробей примерно так же, как мы представляли сложение.
Исходя из этого наблюдения, мы можем предложить следующее правило для вычитания дробей с одинаковыми знаменателями:
Вычитание дробей с одинаковыми знаменателями
общий знаменатель. Уменьшите, если возможно.
Набор образцов B
Найдите следующие отличия.
\(\dfrac{3}{5} — \dfrac{1}{5}\). Знаменатели одинаковы. Вычтите числители. Поместите разницу над 5.
Решение
\(\dfrac{3}{5} — \dfrac{1}{5} = \dfrac{3 — 1}{5} = \dfrac{2}{ 5}\)
Набор образцов B
\(\dfrac{8}{6} — \dfrac{2}{6}\). Знаменатели одинаковы. Вычтите числители. Поместите разницу на 6.
Знаменатели одинаковы. Вычтите числители. Поместите разницу на 6.
Решение
\(\dfrac{8}{6} — \dfrac{2}{6} = \dfrac{8 — 2}{6} = \dfrac{6}{6} = 1\)
Набор образцов B
\(\dfrac{16}{9} — \dfrac{2}{9}\). Знаменатели одинаковы. Вычтите числители и поместите разницу в 9.
Решение
\(\dfrac{16}{9} — \dfrac{2}{9} = \dfrac{16 — 2}{9} = \dfrac{ 14}{9}\)
Sample Set B
Чтобы посмотреть, что произойдет, если мы ошибочно вычтем знаменатели, рассмотрим
\(\dfrac{7}{15} — \dfrac{4}{15} = \dfrac{7 — 4}{15 — 15} = \dfrac{3}{0}\)
Получаем деление на ноль, который не определен. Мы не вычитаем знаменатели.
Тренировочный набор B
Найдите следующие отличия.
\(\dfrac{10}{13} — \dfrac{8}{13}\)
- Ответить
\(\dfrac{2}{13}\)
Тренировочный набор B
\(\dfrac{5}{12} — \dfrac{1}{12}\)
- Ответить
\(\dfrac{1}{3}\)
Тренировочный набор B
\(\dfrac{1}{2} — \dfrac{1}{2}\)
- Ответить
0
Тренировочный набор B
\(\dfrac{26}{10} — \dfrac{14}{10}\)
- Ответить
\(\dfrac{6}{5}\)
Тренировочный набор B
Покажите, почему вычитание числителей и знаменателей ошибочно, выполнив вычитание \(\dfrac{5}{9} — \dfrac{2}{9}\)
- Ответить
\(\dfrac{5}{9} — \dfrac{2}{9} = \dfrac{5 — 2}{9 — 9} = \dfrac{3}{0}\), что не определено
Упражнения
Для следующих задач найдите суммы и разности. Обязательно уменьшайте.
Обязательно уменьшайте.
Упражнение \(\PageIndex{1}\)
\(\dfrac{3}{8} + \dfrac{2}{8}\)
- Ответить
\(\dfrac{5}{8}\)
Упражнение \(\PageIndex{2}\)
\(\dfrac{1}{6} + \dfrac{2}{6}\)
Упражнение \(\PageIndex{3}\)
\(\dfrac{9}{10} + \dfrac{1}{10}\)
- Ответить
1
Упражнение \(\PageIndex{4}\)
\(\dfrac{3}{11} + \dfrac{4}{11}\)
Упражнение \(\PageIndex{5}\)
\(\dfrac{9}{15} + \dfrac{4}{15}\)
- Ответить
\(\dfrac{13}{15}\)
Упражнение \(\PageIndex{6}\)
\(\dfrac{3}{10} + \dfrac{2}{10}\)
Упражнение \(\PageIndex{7}\)
\(\dfrac{5}{12} + \dfrac{7}{12}\)
- Ответить
1
Упражнение \(\PageIndex{8}\)
\(\dfrac{11}{16} — \dfrac{2}{16}\)
Упражнение \(\PageIndex{9}\)
\(\dfrac{3}{16} — \dfrac{3}{16}\)
- Ответить
0
Упражнение \(\PageIndex{10}\)
\(\dfrac{15}{23} — \dfrac{2}{23}\)
Упражнение \(\PageIndex{11}\)
\(\dfrac{1}{6} — \dfrac{1}{6}\)
- Ответить
0
Упражнение \(\PageIndex{12}\)
\(\dfrac{1}{4} + \dfrac{1}{4} + \dfrac{1}{4}\)
Упражнение \(\PageIndex{13}\)
\(\dfrac{3}{11} + \dfrac{1}{11} + \dfrac{5}{11}\)
- Ответить
\(\dfrac{9}{11}\)
Упражнение \(\PageIndex{14}\)
\(\dfrac{16}{20} + \dfrac{1}{20} + \dfrac{2}{20}\)
Упражнение \(\PageIndex{15}\)
\(\dfrac{12}{8} + \dfrac{2}{8} — \dfrac{1}{8}\)
- Ответить
\(\dfrac{1}{2}\)
Упражнение \(\PageIndex{16}\)
\(\dfrac{11}{16} + \dfrac{9}{16} — \dfrac{5}{16}\)
Упражнение \(\PageIndex{17}\)
\(\dfrac{4}{20} — \dfrac{1}{20} + \dfrac{9}{20}\)
- Ответить
\(\dfrac{3}{5}\)
Упражнение \(\PageIndex{18}\)
\(\dfrac{7}{10} — \dfrac{3}{10} + \dfrac{11}{10}\)
Упражнение \(\PageIndex{19}\)
\(\dfrac{16}{5} — \dfrac{1}{5} — \dfrac{2}{5}\)
- Ответить
\(\dfrac{13}{5}\)
Упражнение \(\PageIndex{20}\)
\(\dfrac{21}{35} — \dfrac{17}{35} + \dfrac{31}{35}\)
Упражнение \(\PageIndex{21}\)
\(\dfrac{5}{2} + \dfrac{16}{2} — \dfrac{1}{2}\)
- Ответить
10
Упражнение \(\PageIndex{22}\)
\(\dfrac{1}{18} + \dfrac{3}{18} + \dfrac{1}{18} + \dfrac{4}{18} — \dfrac{5}{18}\)
Упражнение \(\PageIndex{23}\)
\(\dfrac{6}{22} — \dfrac{2}{22} + \dfrac{4}{22} — \dfrac{1}{22} + \dfrac{11}{22}\)
- Ответить
\(\dfrac{9}{11}\)
Следующее правило сложения и вычитания двух дробей нелепо. Покажите, почему, выполнив операции, используя правило для следующих двух задач.
Покажите, почему, выполнив операции, используя правило для следующих двух задач.
Нелепое правило
Чтобы сложить или вычесть две дроби, просто сложите или вычтите числители и поместите результат над суммой или разностью знаменателей.
Упражнение \(\PageIndex{24}\)
\(\dfrac{3}{10} — \dfrac{3}{10}\)
Упражнение \(\PageIndex{25}\)
\(\dfrac{8}{15} + \dfrac{8}{15}\)
- Ответить
\(\dfrac{16}{30} = \dfrac{8}{15}\) (используя нелепое правило)
Упражнение \(\PageIndex{26}\)
Найдите общую длину винта.
Два месяца назад женщина выплатила \(\dfrac{3}{24}\) кредит. Месяц назад она выплатила \(\dfrac{5}{24}\) от общей суммы кредита. В этом месяце она снова погасит \(\dfrac{5}{24}\) от общей суммы кредита. В конце месяца, какую часть своего общего кредита она выплатит?
- Ответить
\(\dfrac{13}{24}\)
Упражнение \(\PageIndex{27}\)
Найдите внутренний диаметр трубы.




 (слайд №8-11)
(слайд №8-11) Учащихся меняются тетрадями и выполняют проверку оценивая друг друга.
Учащихся меняются тетрадями и выполняют проверку оценивая друг друга.





 Рефлексия (подведение итогов урока)
Рефлексия (подведение итогов урока) 26 на стр.158.
26 на стр.158.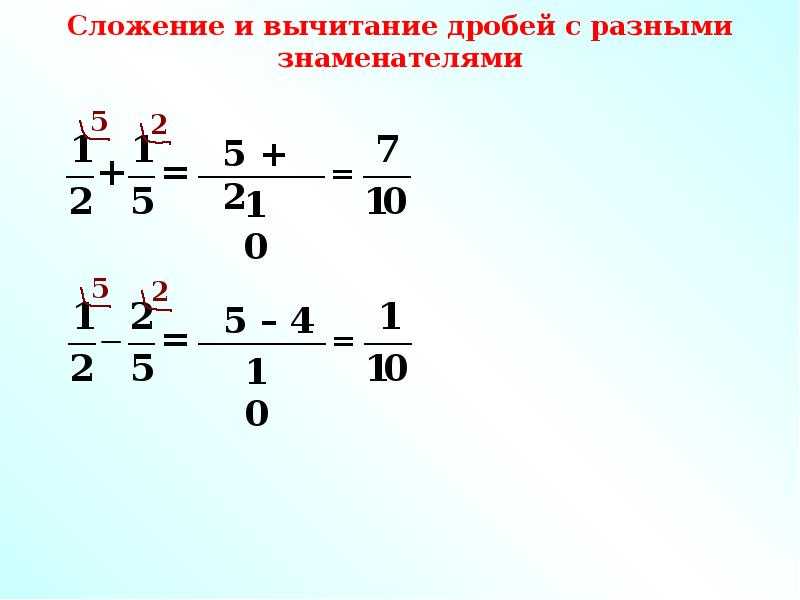

 1/6 часть торта съел Сережа. Сколько частей торта осталось? (5/6). Маша и Даша съели ещё 2/6 торта. Сколько частей торта осталось на тарелке? (3/6). Как нам удалось выполнить вычисления? (Дети формулируют правило вычитания дробей с одинаковыми знаменателями). Запишем решение данной задачи в тетрадь.
1/6 часть торта съел Сережа. Сколько частей торта осталось? (5/6). Маша и Даша съели ещё 2/6 торта. Сколько частей торта осталось на тарелке? (3/6). Как нам удалось выполнить вычисления? (Дети формулируют правило вычитания дробей с одинаковыми знаменателями). Запишем решение данной задачи в тетрадь.
 Спасибо за урок!
Спасибо за урок!

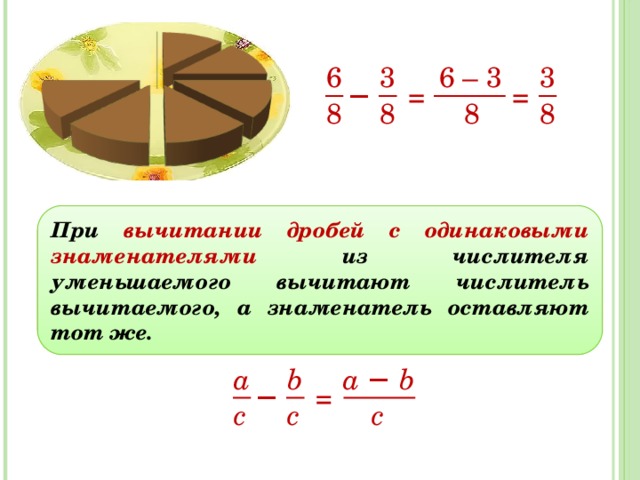

 /3) = 9/15, что преобразует их в одинаковые дроби с одинаковыми знаменателями.
/3) = 9/15, что преобразует их в одинаковые дроби с одинаковыми знаменателями. 1/5 + 2/3 ≠ 3/8
1/5 + 2/3 ≠ 3/8 После этого можно делать прибавку. Например, 1/2 + 2/3 = (1/2 × 3/3) + (2/3 × 2/2) = 3/6 + 4/6 = (3 + 4)/6 = 7/6. = \(1 \dfrac{1}{6}\)
После этого можно делать прибавку. Например, 1/2 + 2/3 = (1/2 × 3/3) + (2/3 × 2/2) = 3/6 + 4/6 = (3 + 4)/6 = 7/6. = \(1 \dfrac{1}{6}\)