Чтение и запись десятичных дробей

Часто бывает, что показать значение лучше в дробном выражении. К примеру, одну десятую часть дециметра можно представить так: \[\frac{1}{10} \text{дм}\].

Выражение обозначает, что дециметр разделили на 10 равных частей, и одна из этих частей была взята. В данном случае эта часть будет равна 1 сантиметру.

Если нужно показать в дробном виде 6 см и 3 мм в сантиметрах, представим выражение в виде десятичной дроби. Один миллиметр – это десятая часть сантиметра, соответственно 3 мм это три десятых, записываются так: \[\frac{3}{10} \mathrm{см}\].

Выражение обозначает, что один сантиметр был разделен на 10 равных частей и взяли три из них. В результате получается: \[6 \frac{3}{10}см\].

Дробь можно прочитать как шесть целых три десятых сантиметра. Если знаменатель дроби представлен числами 10, 100, 1000 эту дробь можно записать без знаменателя в виде целой и дробной части без знаменателя. Целая и дробная часть между собой разделяются запятой, получается 6,3 см. Каждое число, записанное в таком виде, считается десятичной дробью.

Что такое десятичная дробь

Десятичные дроби представляют собой целые числовые выражения, в знаменатель которых десять в какой-либо степени.

Для чего нужны десятичные дроби

• удобнее сравнивать;
• сокращение вычислений;
• удобная запись в одну строчку.

Чтобы записать десятичную дробь выполняют следующие действия:

1. Отдельно написать числитель.
2. Передвинуть десятичную точку на количество нулей знаменателя.
3. После того, как десятичная точка сдвинулась, зачеркните нули, которые остались в конце записи.

Если на втором шаге недостаточно цифр для завершения действия, на недостающих позициях проставляются нули. Примеры десятичной записи.

\[\frac{73}{10} ; \frac{9}{100} ; \frac{10029}{1000} ; \frac{10500}{1000}\]

В знаменателе первой дроби стоит 10, значит, числитель первой дроби 73 сдвинем на один знак. Получается 7,3.

Знаменатель второй дроби 100, а числитель 9. Сдвигаем десятичный знак на два знака и получаем 0,09.

Знаменатель третьей дроби 1000, а числитель 10029. Сдвигаем десятичную точку на три знака и получаем 10,029.

В последней дроби числитель 10500, перемещаем точку на три знака 10,500. Образовавшиеся в конце записи нули убираем, и получаем ответ 10,5.

Два последних примера показывают, как правильно поступать с нулями. Если нули получились справа в конце – их следует зачеркнуть, а если в середине, как в третьем примере, то их оставляем. Это цифры внутри числа.

Конечные десятичные дроби

Определение

Конечные десятичные дроби – это вид десятичной дроби, в которых содержится конечное число знаков после запятой. Например: 0,367; 3,7. Каждую из этих дробей можно записать как смешанном числом либо обыкновенной дроби.

Приведем пример, конечную десятичную дробь 5,63 легко представить как \[5 \frac{63}{100}\], десятичную дробь 0,2 можно привести к виду \[\frac{2}{10}\].

Обратные процесс записи обыкновенной дроби в десятичном виде выполняется не в каждом случае. Например, дробь \[\frac{5}{13}\] заменить, на аналогичную дробь со знаменателем 100, 10 нельзя.

Класс периодических и непериодических дробей

Если в десятичной дроби после запятой стоит бесконечное количество цифр, такие дроби называют бесконечными.

Такие дроби целиком записать невозможно, следовательно, при записи указывается лишь часть из них, далее записывается многоточие. Это обозначает бесконечную последовательность знаков после запятой. Примеры класса бесконечных десятичных дробей: 0,143346732…; 3,1415989032…; 2,6666666666…

После запятой могут стоять периодичные повторения одного знака или группы знаков.

Определение

Периодические дроби – это бесконечные десятичные дроби, в которых после запятой стоят повторяющиеся группы цифр или повторяется одна цифра.

Например, для десятичной дроби 3,444444… периодом будет 4, для 76,134134134134… периодом будет группа чисел 134.

Чтобы записать представить запись десятичной периодичной бесконечной дроби в сокращенном виде, достаточно указать период одни раз в скобках. Так для 3,444444… запись выглядит так 3,(4), дробь 76,134134134134… можно представить в виде 76,(134). Смысл остается тем же самым. Такую запись используют, чтобы избежать ошибок. В скобки заключают максимально короткую последовательность цифр, которые расположены ближе всего к запятой.

Каждую конечную дробь можно выразить как периодическую. В таком случае, добавляют бесконечное множество нулей в правой части выражения. Например, конечная дробь 45,32 в периодическом виде записывается как 45,32(0). Таким образом, добавление нулей в правую часть десятичной дроби дает равную ей дробь.

Бесконечные десятичные периодические дроби являются рациональными числами. Любую десятичную можно записать в виде обыкновенной и наоборот.

Дроби, у которых нет бесконечной последовательности после запятой, называют непериодическими. Внешне они бывают похожими на периодические, с записями наподобие 9,03003000300003… нужно быть внимательно, знаки после запятой одинаковые, но не повторяются. Такие дроби являются иррациональными и в обыкновенные дроби их не переводят.

Арифметические действия с десятичными дробями

Теоритические и практические уроки предполагают следующие действия с десятичными дробями, их можно: складывать, вычитать, умножать делить, сравнивать между собой.

Правила действий с десятичными дробями

1. Сделать одинаковым число знаков после запятой.
2. Выполнить запись в столбик друг под другом, запятая должна быть под запятой.
3. Выполнить сложение (вычитание).

Действия с десятичными дробями: сложение

Действия удобнее выполнять в столбик. Целые и дробные части складывают по отдельности. Например, выполним сложение дробей 3,2 и 5,3. Для этого запишем две дроби в столбик, при этом целые части следует записать под целыми, а дробные под дробными (запятая под запятой).

\[\begin{array}{r} + \begin{array}{r} 3,2\\ 5,3\\ \end{array} \\ \hline \begin{array}{r} 8,5 \end{array} \end{array}\]

В первую очередь складываем дробные части и записываем пятерку под чертой. Далее складываем целые части, пишем восьмерку в целой части ответа. Дробную часть от целой отделяем запятой. Получаем ответ 8,5.

Пример правильной записи:

\[\begin{array}{r} + \begin{array}{r} 10,234\\ 0,12\;\,\\ \end{array} \\ \end{array}\]

Пример неправильной записи:

\[\begin{array}{r} + \begin{array}{r} 10,234\\ 0,12\\ \end{array} \\ \end{array}\]

Место расположения цифр в десятичной дроби влияет на значение в десятичной дроби. Разряды, расположенные до запятой, носят названия аналогичные натуральным числам, после запятой первая цифра обозначает разряд десятых, вторая – сотых, третья – тысячных.

Разряды различаются по старшинству, если рассматривать цифры слева на право, то будем двигаться от старших разрядов к младшим.

В качестве примера возьмем десятичную дробь 0,345

Позиция тройки находится в разряде десятых.

Позиция четверки – в разряде сотых.

Пятерки – тысячных.

Расположение тройки в разряде десятых сообщает о том, что в рассматриваемой дроби 0,345 содержится три десятых \[\frac{3}{10}\]; четыре сотых \[\frac{4}{100}\]; пять десятитысячных \[\frac{5}{1000}\]. При сложении дробей получим изначальную.

\[\frac{100 / 3}{10}+\frac{10 / 4}{100}+\frac{1 / 5}{1000}=\frac{3 * 100}{10 * 100}+\frac{4 * 10}{100 * 10}+\frac{5 * 1}{1000 * 1}=\frac{300}{1000}+\frac{40}{1000}+\frac{5}{1000}=\frac{345}{1000}=0,345\]

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Сложение десятичных дробей

Правила сложения десятичных дробей те же, аналогичные сложению обычных чисел. Сложение выполняется согласно разрядам: десятки с десятками, сотые с сотыми. Соблюдение правила «запятая под запятой» обеспечит этот порядок. Сложение начинают с крайнего правого ряда и двигаются влево к предыдущему.

Математические действия с десятичными дробями:

• для сложения периодических десятичных дробей следует их заменить обыкновенными;
• бесконечные непериодические дроби складывают, предварительно округлив до некоторого разряда, чем меньше разряд, тем выше точность;
• для сложения десятичной дроби и натурального числа, натуральное число складывают с целой частью десятичной дроби, а дробную оставляют неизменной.

Вычитание десятичных дробей

Для выполнения вычитания соблюдаются правила, идентичные сложению: запятая под запятой и одинаковое количество цифр после запятой.

Пример

Найти значение разности 2,5 — 2,2

Записываем выражение, соблюдая правило запятой и вычисляем дробную часть 5-2=3. Далее выполняем действие с
целой частью 2-2=0. Получаем следующую запись:

\[\begin{array}{r}-\begin{array}{r}2,5\\2,2\\\end{array} \\\hline\begin{array}{r}0,3\end{array}\end{array}\]

Ответ: 2,5-2,2=0,3

Действия с десятичными дробями: примеры

>Пример 1

Вычислить 7,353-3,1

Для решения выражения, нужно сделать равным количество цифр в дробях. Для этого следует добавить два нуля в
дроби 3,1. Записываем выражение в столбик:

\[\begin{array}{r}-\begin{array}{r}7,353\\3,100\\\end{array}
\\\hline\begin{array}{r}4,253\end{array}\end{array}\]

Ответ: 4,253

При выполнении вычитания десятичных дробей, в отдельных случаях придется занимать единицу, как и в обычных числах.

Умножение десятичных дробей производится аналогично натуральным числам. Метод вычисление столбиком тоже подходит. Выполняя действие, на запятые можно не обращать внимание. Вычислив ответ, нужно отделить дробную часть от целой. Для этого в обеих дробях подчитайте количество цифр после запятой. В ответе подсчитываем столько же цифр и ставим запятую.

Пример 2

Вычислить 2,5х1,5

Перемножаем дроби, не обращая внимания на запятые.

\[\begin{array}{r}*\begin{array}{r}25\\15\\\end{array}
\\\hline+\begin{array}{r}125\\25\\\hline\begin{array}{r}375\end{array}\end{array}\end{array}\]

\[\begin{array}{r}*\begin{array}{r}2,5\\1,5\\\end{array} \\\hline\begin{array}{r}3,75\end{array}\end{array}\]

Запятая сдвигается на два знака, с учетом того, что в первой дроби один знак и во второй один знак.

Ответ: 3,75

Деление десятичной дроби на натуральное число производят по правилам деления в столбик. при выполнении действия на запятую не обращают внимания. В полученном частном запятая проставляется, когда заканчивается целая часть делимого. В случае, когда целая часть делимого меньше делителя, тогда в частном будет 0 целых.

Сравнение десятичных дробей

При сравнении двух дробей, большей будет та, у которой больше целая часть.

7,99>6,399

Если целые части дробей одинаковы, большей будет та, у которой больше десятых. Если равны десятые, то больше сотые и т.д.

85,7>85,679

Сложение, вычитание и умножение десятичных дробей

Сложение, вычитание и умножение десятичных дробей

Сложение и вычитание десятичных дробей выполняются так же, как сложение и вычитание целых чисел; нужно   только записывать каждый разряд под   разрядом того же наименования.

Пример. 2,3 + 0,02 + 14,96= 17,28.

Умножение десятичных дробей. Перемножаем данные числа как целые, не обращая внимания на запятую. Затем ставим в результате запятую, пользуясь следующим правилом: в произведении число знаков после запятой равно сумме чисел знаков после запятой во всех сомножителях.

Пример 1.          2,064 • 0,05. Перемножаем целые числа 2064 • 5 = 10 320. В первом сомножителе было три знака после запятой, во втором — два. В произведении число знаков после запятой должно быть пять.
Отделяем их справа; получаем 0,10320. Нуль, стоящий в конце дроби, можно отбросить: 2,064 · 0,05 =- 0,1032.

До постановки запятой отбрасывать нули при этом способе нельзя.

Пример 2. 1,125 • 0,08; 1125 • 8 = 9000. Число
знаков после запятой должно быть 3 + 2 = 5. Приписывая к 9000 нули слева (009000), отделяем справа пять знаков. Получаем 0,09000 = 0,09.

 

                                         Деление десятичной дроби на целое число

Если делимое меньше делителя, записываем в целой части частного нуль и ставим после него запятую. Затем, не обращая внимания на запятую, присоединяем к целой части делимого первую цифру его дробной части; если получается число, меньшее делителя, ставим после запятой нуль и присоединяем еще одну цифру делимого; если и после этого получаем число, меньшее делителя, ставим еще нуль и т. д., пока не получим числа, превосходящего делитель. В дальнейшем деление совершается так же, как с целыми числами, причем делимое можно неограниченно «расширять» вправо от запятой, приписывая в конце нули.

Замечание. Возможно, что описанный процесс деления никогда не закончится. В таком случае
частное нельзя точно выразить десятичной дробью, но, остановившись на некоторой цифре, получим приближенный результат.

 

                 Обращение десятичной дроби в простую и обратно

Чтобы обратить десятичную дробь в простую, нужно, отбросив запятую, сделать получившееся
число числителем дроби; знаменателем же нужно взять число, показывающее, какие доли представляет последний десятичный знак. Полученную дробь желательно сократить, если это возможно.

Если десятичная дробь превосходит единицу, то предпочтительно обращать в простую дробь только ту ее часть, которая стоит после запятой, целую же часть оставить без изменения.

Пример:   0,0125 обратить в простую дробь.
Последний десятичный знак представляет десятитысячные доли. Поэтому знаменатель будет 10 000 имеем      

Пример:    

Предпочтительно, однако, производить вычисление первым из двух указанных способов, т. е., оставляя без изменения двойку, стоящую слева от запятой, обращать в простую дробь число 0,75.

Пример:  дробь   обратить в десятичную. Делим 7:8 получаем 0,875.

В большинстве случаев этот процесс деления может продолжаться бесконечно. Тогда простая дробь не может быть обращена в десятичную точно. На практике этого никогда и не требуется. Деление заканчивают в тот момент, когда в частном получены все те десятичные доли, которые имеют практический интерес.

Пример: Требуется разделить 1 кг сахара на три равные части Масса каждой части  . Чтобы взвесить это количество, нужно выразить его в десятичных долях килограмма. Делим 1 на 3, получим 1:3=0.333……. Деление можно продолжать до бесконечности в частном будут появляться все новые тройки. Практический интерес имеют лишь сотые доли килограмма (10 г). Поэтому берем   

Для большей точности принято учитывать величину первой отбрасываемой цифры. Если она превышает 5, то удерживаемая цифра увеличивается на 1

Пример:  Обратить дробь    в десятичную. Точное значение будет 0,21875. В зависимости от требуемой степени точности, деление заканчивается на второй, третьей и т.д. цифре частного и берут  

 

                           Исторические сведения о дробях

Понятие о дроби могло возникнуть у людей лишь после того, как у них образовались некоторые представления о целых числах. Как и понятие целого числа, понятие дроби появилось не сразу. Представление о «половине» возникло гораздо раньше, чем о «третях» и «четвертях», а об этих последних— раньше, чем о дробях с другими знаменателями Первые представления о пелом число возникли в процессе счета; первые представления о дробях — и г; процесса измерения (длин, площадей, массы и т. д.). Следы исторической связи исчисления дробей и системы мер можно обнаружить у многих народов. Так, в вавилонской системе мер массы (и денег) 1 талант составлял 60 мин, а одна мина — 60 шекелей. Соответственно с этим в вавилонской математике широко применялись шестидесятеричные дроби. В древнеримской системе измерения массы 1 асе делился на 12 унций; согласно с этим римляне пользовались двенадцатеричными дробями. Дробь, которую мы называем 1/12 , римляне именовали «унцией», даже если бы она употреблялась для измерения длины или иной величины; дробь, которую мы называем 1/8 , римляне называли «полторы унции» и т. п.

Наши «обыкновенные дроби» широко употреблялись древними греками и индийцами. Правила действий с дробями, изложенные индийским ученым Брамагуптой (8 в. н. э.), лишь немногим отличаются от наших. Наша запись дробей тоже совпадает с индийской; только дробной черты индийцы не писали; греки записывали сверху знаменатель, а снизу числитель, но чаще пользовались другими записями, например писали (конечно, своими знаками) 3 5х (три пятых).

Индийское обозначение дробей и правила действий над ними были усвоены в 9 веке в мусульманских странах благодаря Мухаммеду Хорезмскому (аль-Хваризми,. Они были перенесены в Западную Европу итальянским купцом и ученым Леонардо Фибоначчи иг Пизы (13 в.)

Наряду с «обыкновенными» дробями применялись (преимущественно в астрономии) шестидесятеричные дроби. Они были позднее вытеснены десятичными дробями. Последние впервые ввел выдающийся самаркандский ученый Гиясэддин Джемшид г Каши (14—15 вв.). В Европе десятичные дроби были введены в практику нидерландским купцом и выдающимся
ученым-инженером Симоном Стевином (1548—1620).

Сложение десятичных знаков

Сложение десятичных знаков очень похоже на сложение целых чисел. Начнем наш урок с простого. Обратите внимание на следующие дополнения. Вы можете ясно видеть, что нет большой разницы между сложением десятичных знаков и сложением целых чисел. Тем не менее, есть несколько важных правил, которым нужно следовать, чтобы убедиться, что вы получили правильный ответ.

Правила сложения десятичных знаков

Просто следуйте трем приведенным ниже правилам в том порядке, в котором они перечислены здесь!

Правило №1

Убедитесь, что добавляемые десятичные числа соответствуют десятичным числам.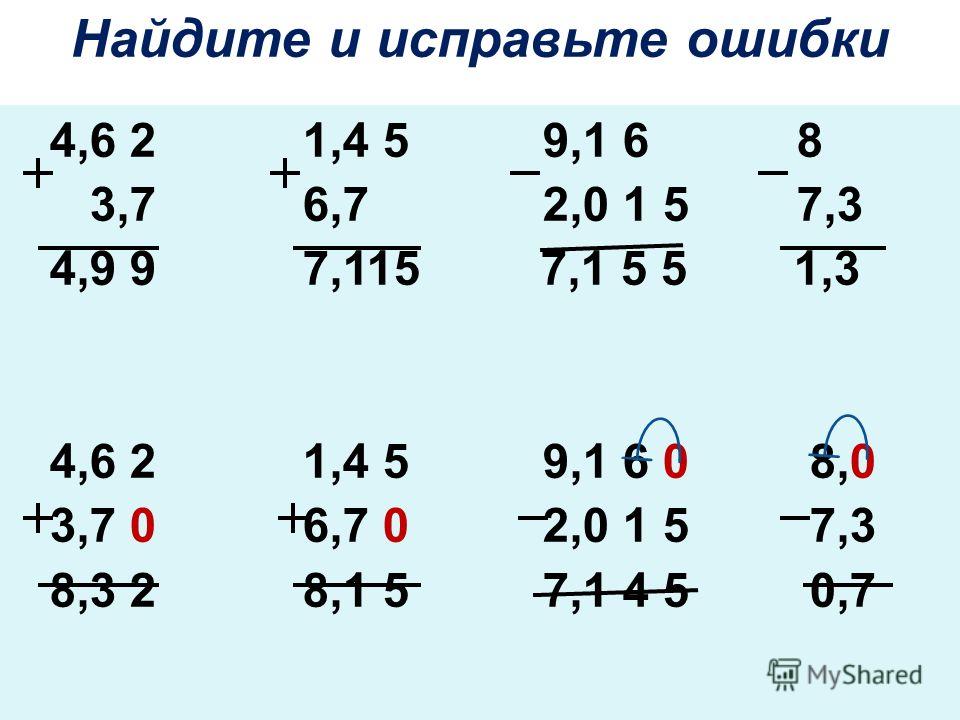 Например, 2,325 и 4,8 не похожи на десятичные дроби, поскольку у них разное количество знаков после запятой или количество цифр справа от запятой.

Просто добавляйте нули в качестве заполнителей, пока десятичные дроби не станут похожими на десятичные дроби. Например, просто добавьте два нуля в качестве заполнителей после 8, чтобы получить 4.800. Теперь 2,325 и 4,800 имеют одинаковое количество знаков после запятой.

Правило № 2

После того, как десятичные дроби представлены в вертикальном формате, самым важным правилом, на мой взгляд, является выравнивание десятичных точек и сохранение цифр с одним и тем же разрядом в одном и том же столбце. Это гарантирует, что вы не будете прибавлять десятые к сотым или сотые к тысячным и так далее…

Правило №3

Если вы выполнили правило №1 и правило №2 , вы готовы добавить цифры, которые имеют то же значение разряда. Не забывайте использовать числа, когда это необходимо, точно так же, как вы делаете это при сложении целых чисел.

Наконец, не забудьте написать десятичную точку, которая находится между цифрой в разряде единиц и цифрой в разряде десятых!

В первой задаче на сложение мы прибавляем 0,5 к 0,4. Поскольку правило № 1 и правило № 2 уже действуют, просто перейдите прямо к правилу № 3 , добавив цифры.

1. Сначала сложите десятые (5 и 4), чтобы получить 9 десятых
2. Затем сложите единицы (0 и 0), чтобы получить ноль.
3. Наконец, напишите десятичную дробь. Он ставится сразу после числа в разряде единиц.

Теперь попробуйте добавить следующие десятичные дроби.

Обратите внимание, что добавление десятых даст число больше, чем 10 десятых или 1. Следовательно, чтобы сложить эти десятичные дроби, мы должны перенести 1 на разряд единиц. Напомним также, что 1 десятая = 0,1, поэтому 10 десятых = 10 × 0,1 = 1

Ниже показано, как сложить первые две задачи:

последнюю задачу сами и получите 1. 6 за ответ.

Как складывать десятичные дроби по горизонтали

Вы могли бы получить ответы, складывая по горизонтали.

0,6 + 0,7 = 0,6 + 0,4 + 0,3 = 1 + 0,3 = 1,3 (0,7 = 0,4 + 0,3)

0,8 + 0,8 = 0,8 + 0,2 + 0,6 = 1 + 0,6 = 1,6 (0,8 = 0,2 + 0,64) 0,6 0,9 + 0,7 = 0,9 + 0,1 + 0,6 = 1 + 0,6 = 1,6 (0,7 = 0,1 + 0,6)

На практике при сложении по вертикали нет необходимости записывать все эти десятые доли. Вы можете притвориться, что десятичной точки не существует, и попробовать складывать десятичные дроби, как если бы вы складывали целые числа.

Вот как, если мы складываем 0,6 к 0,7 и 0,8 к 0,8

Как складывать десятичные дроби с целыми числами

Вам просто нужно следовать правилу № 1, когда вы складываете десятичные дроби с целыми числами.

Например, сложите вместе 42 и 3,0147.

42 = 42,0000, так как нам нужно использовать четыре нуля в качестве заполнителей. Теперь 42.0000 и 3.0147 имеют одинаковое количество знаков после запятой.

  42,0000
 + 3,0147
———————
  45,0147

42 и 3,0147 = 45,0147

Дополнительные примеры, показывающие, как складывать десятичные дроби

Начните с использования 0 в качестве заполнителей, а затем добавляйте, как если бы вы складывали целые числа.

Теперь пришло время сделать более сложный пример. Добавьте следующие четыре десятичных числа: 0,5, 35,25, 8,369 и 4,002

. Начните с использования 0 в качестве заполнителей

Затем внимательно изучите и выполните следующие 5 шагов:

Пройдите тест на сложение десятичных знаков, чтобы узнать, насколько хорошо вы поняли этот урок 9.0006

Чем сложение десятичных знаков похоже на сложение целых чисел? – Angola Transparency

Мы узнали, что сложение и вычитание десятичных чисел, чисел с десятичной точкой, аналогично сложению и вычитанию целых чисел. С той лишь разницей, что мы выстраиваем числа по десятичной точке . Кроме того, не имеет значения, какой номер идет внизу.

Содержание

• Является ли добавление десятичных дробей таким же, как и целых чисел?
• Как десятичные дроби связаны с целыми числами?
• Что я узнал, сложение десятичных знаков очень похоже на сложение?
• В чем сходство процесса сложения вычитания десятичных чисел?
• Что такое сложение десятичных чисел?
• Как складывать и вычитать десятичные дроби из целых чисел?
• Как десятичные дроби связаны с целыми числами и дробями?
• В чем разница между десятичным числом и числом?
• Считаются ли десятичные дроби целыми числами?
• Как вы пишете десятичные дроби в 5 классе?
• Как складывать десятичные дроби пятиклассникам?
• В каком классе вы учитесь складывать десятичные дроби?
• Каково определение сложения и вычитания десятичных знаков?
• Как научить складывать и вычитать десятичные дроби?
• Как умножить целое число на десятичное?
• Каковы правила сложения десятичных знаков?
• Как складывать целые числа?
• Что означает целое число?
• Может ли дробь быть целым числом?
• Является ли 10,0 целым числом?
• Является ли 0 действительным числом?

Является ли сложение десятичных дробей таким же, как и целые числа?

Сложение десятичных знаков аналогично обычному сложению целых чисел .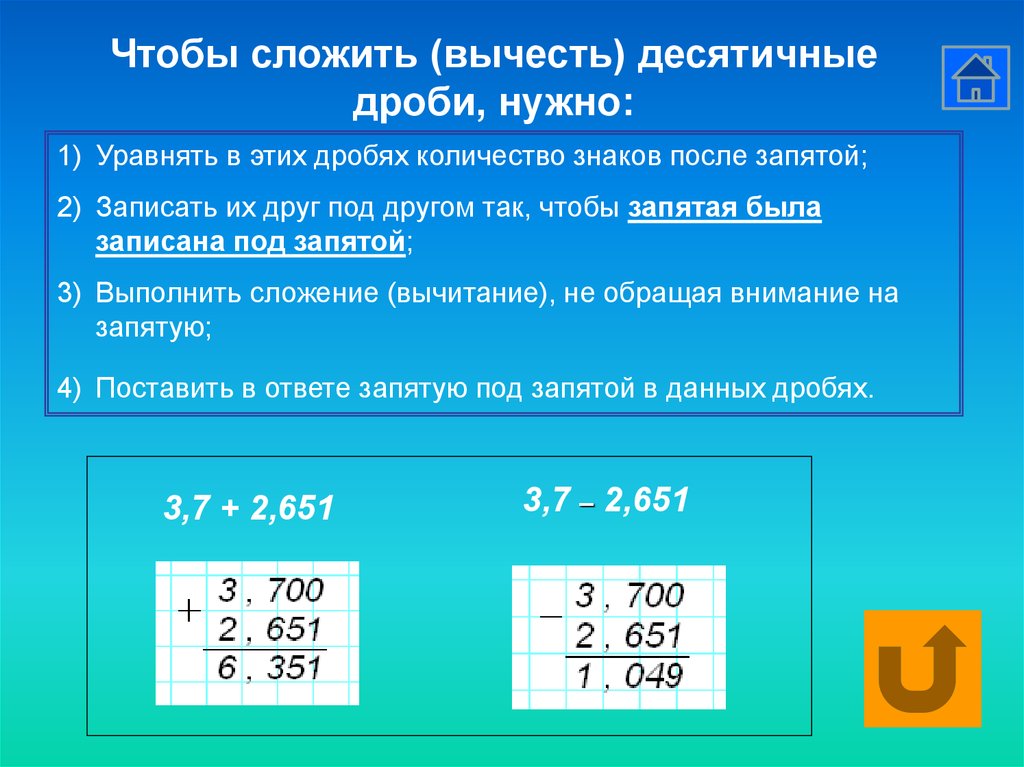 Мы знаем, что десятичное число — это число, состоящее из целой части и дробной части, разделенных десятичной точкой.

Как десятичные дроби связаны с целыми числами?

Ответ: Целые числа — это множество действительных чисел, включающее ноль и все положительные счетные числа. Принимая во внимание, что исключаются дроби, отрицательные целые числа, дроби и десятичные числа. ясно сказано, что десятичных знаков не входят в набор целых чисел .

Что я узнал, сложение десятичных знаков очень похоже на сложение?

Сложение и вычитание десятичных дробей. Сложение десятичных знаков очень похоже на сложение целых чисел , за исключением нескольких дополнительных технических деталей и учета . Напомним, что десятичные дроби — это просто дроби.

В чем сходство процесса сложения вычитания десятичных чисел?

Вычитание десятичных знаков использует ту же настройку, что и сложение десятичных знаков: выровняйте десятичные точки, а затем вычтите . В тех случаях, когда вы вычитаете два десятичных знака, которые распространяются на разные разрядные значения, часто имеет смысл добавить дополнительные нули, чтобы выровнять два числа — это немного упрощает выполнение вычитания.

Что такое сложение десятичных чисел?

Чтобы добавить десятичные знаки, выполните следующие действия: Запишите числа, одно под другим, выровняв десятичные запятые. Вставьте нули, чтобы числа имели одинаковую длину (см. ниже, почему это нормально). Затем добавьте, используя сложение столбцов, не забывая ставить десятичную точку в ответе.

Как складывать и вычитать десятичные дроби из целых чисел?

Как десятичные дроби связаны с целыми числами и дробями?

И дроби, и десятичные дроби — это всего лишь два способа представления чисел. Дроби записывают в виде p/q, где q≠0, а в десятичных дробях целая часть числа и дробная часть соединяются через запятую, например, 0,5. Дроби и десятичные дроби представляют отношение части к целому .

В чем разница между десятичным числом и числом?

ЦИФРОВОЙ определяет точную точность и масштаб. DECIMAL определяет только точную шкалу ; точность равна или превышает указанную кодером.

Считаются ли десятичные дроби целыми числами?

Основная идея: Целые числа не включают отрицательные числа, дроби или десятичные дроби .

Как вы пишете десятичные дроби в 5 классе?

Цитата из видео: Один два и семь так вот у меня три цифры до и три цифры после главное что нужно знать о значении десятичного разряда это числа после запятой стоят.

Как складывать десятичные дроби пятиклассникам?

Цитата из видео: Разрядное значение может помочь нам складывать десятичные дроби. Мы складываем десятичные числа друг на друга так, чтобы их десятичные точки были выровнены по вертикали.

В каком классе вы учитесь складывать десятичные дроби?

Возьмите сложение десятичных знаков. Обычно это часть обучения математике класса 5 .

Каково определение сложения и вычитания десятичных знаков?

Что такое сложение и вычитание десятичных дробей? Сложение десятичных знаков аналогично сложению чисел, но эти числа содержат десятичные точки. Вычитание десятичных дробей — это процесс вычитания десятичного числа с меньшей целой частью из десятичного числа с большей целой частью.

Как научить складывать и вычитать десятичные дроби?

Цитата из видео: Вы можете добавить нули справа от десятичной дроби, и это не изменит значение этого числа. Итак, вы снова можете использовать нули-заполнители справа от десятичного знака, и это не изменит значение.

Как умножить целое число на десятичное?

Чтобы умножить десятичное число на целое, выполните следующие действия:

1. Умножение. как и с целыми числами.
2. Подсчитайте общее количество знаков после запятой в ваших множителях.
3. Переместите десятичную точку в произведении на одно место влево для каждого подсчитанного десятичного знака.

Каковы правила сложения десятичных знаков?

ДОБАВИТЬ ИЛИ ВЫЧИТАТЬ ДЕСЯТИЧНЫЕ ЗНАКИ:
1) Выровнять десятичные точки вертикально. Вставьте любые 0, где это необходимо. 2) Сложите или вычтите числа, как если бы они были целыми числами. 3) Поместите десятичную точку в сумме или разнице так, чтобы она выровнялась вертикально с числами, которые добавляются или вычитаются.

Как складывать целые числа?

Цитата из видео: Один плюс два плюс три равно шести, а в столбце сотен семь плюс ноль равно семи. Итак у нас 762 это значит что сумма 37. А 725 это семьсот шестьдесят два.

Что означает целое число?

Целое число — это просто

любое положительное число, которое не включает дробную или десятичную часть .