Как найти Область Допустимых Значений (ОДЗ)

Поможем понять и полюбить математику

Начать учиться

122.9K

В математике все должно быть точно и понятно. Чтобы научиться решать примеры еще быстрее, необходимо учитывать ОДЗ. Давайте разберемся, что это такое и чем оно может быть полезно. В статье найдете все необходимые определения и примеры решений.

Допустимые и недопустимые значения переменных

В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.

Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.  

Чтобы дать верное определение области допустимых значений, разберемся, что  такое допустимые и недопустимые значения переменной. 

Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.

Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.

Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.

Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.

Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.

Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.

Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.

Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми. 

В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного. 

Пример 1

Рассмотрим выражение

В выражении три переменные (a, b, c). 

Запишем значения переменных в виде: a = 0, b = 1, c = 2.

Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:

Таким же образом можем выяснить, какие значения переменных  — недопустимые. 

a = 1, b = 2, c = 1.

Подставим значения переменных в выражение

На ноль делить нельзя.  

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Что такое ОДЗ

ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».

Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.

Запоминаем!

ОДЗ относится к выражениям. Область определения функции относится к функциям и не относится к выражениям.

Пример 2

Рассмотрим выражение

ОДЗ такого выражения выглядит следующим образом: ( — ∞; 3) ∪ (3; +∞).

Читать запись нужно вот так:
Область допустимых значений переменной x для выражения  — это числовое множество ( — ∞; 3) ∪ (3; +∞).

Пример 3
Рассмотрим выражение

ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.

Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Как найти ОДЗ: примеры решения

Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.

Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено. 

Мы не можем вычислить значение выражения, если:

• требуется извлечение квадратного корня из отрицательного числа;
• присутствует деление на ноль (математическое правило номер раз: никогда не делите на ноль).

Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.  

Давайте потренируемся находить ОДЗ.

Пример 4

Найдем область допустимых значений переменной выражения a

3 + 4 * a * b − 6.

Как решаем:

В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a³ + 4 * a * b − 6 при любых значениях переменной. 

ОДЗ переменных  a и b — это множество таких пар допустимых значений (a, b), где a — любое число и  b — любое число. 

Ответ: (a и b), где a — любое число и b — любое число.

Пример 5

Найдем область допустимых значений (ОДЗ) переменной выражения 

Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.  

Это значит, что мы может сказать, что ОДЗ переменной a в выражении — пустое множество.

Пустое множество изображается в виде вот такого символа Ø.

Пример 6

Найдем область допустимых значений (ОДЗ) переменных в выражении

Если  есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.

Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.

Лайфхак

Чтобы не потратить зря время на решение нерешаемого примера, всегда обращайтесь к списку условий, при которых выражение не может быть решено.

Запомните

• Если число входит в ОДЗ, то около числа ставим квадратные скобки.
• Если число не входит в ОДЗ, то около него ставятся круглые скобки.  

Например, если х > 6, но х < 8, то  записываем интервал [6; 8).

Зачем учитывать ОДЗ при преобразовании выражения

Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.

Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.

Тождественное преобразование может:

• расширить ОДЗ
• никак не повлиять на ОДЗ
• сузить ОДЗ

Рассмотрим каждый случай в отдельности.

Пример 7

Рассмотрим выражение a + 4/a — 4/a

Поскольку мы должны следить за тем, чтобы в выражении не возникало деление на ноль, определяем условие a ≠ 0.

Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).

В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a. 

ОДЗ для a — это R — множество всех вещественных чисел. 

Преобразование расширило ОДЗ — добавился ноль. 

Пример 8

Рассмотрим выражение a² + a + 4 * a

ОДЗ a для этого выражения — множество R.

В выражении есть подобные слагаемые, выполним тождественное преобразование. 

После приведения подобных слагаемых выражение приняло вид  a² + 5 * a 

ОДЗ переменной a для этого выражения — множество R.

Это значит, что тождественное преобразование никак не повлияло на ОДЗ. 

Пример 9

Рассмотрим выражение

ОДЗ a определяется неравенством (a — 1) * (a — 4) ≥ 0.

Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).

Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.

Приведем выражение к виду

ОДЗ переменной a для этого выражения определяется неравенствами:
a — 1 ≥ 0
a — 4 ≥ 0

Решив систему линейных неравенств, получаем множество [4; + ∞).

Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; +

∞).

Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.

Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Анастасия Белова

К предыдущей статье

174. 1K

Как перевести периодическую дробь

К следующей статье

Деление числа на произведение

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Таблица степеней 🆕

Поможем понять и полюбить математику

Начать учиться

143.8K

После изучения арифметических основ в виде сложения, вычитания, деления и умножения, открывается математика и ее большой мир. В этом материале рассмотрим такое понятие, как степень.

Основные понятия

Степень числа с натуральным показателем — это результат многократного умножения числа на себя.

Само число называют основанием степени, а количество операций умножения — показателем степени.

• aⁿ = a × a × … × a, где a — основание степени,
• n — натуральный показатель степени.

Запись читается, как «a» в степени «n».

Вот пример для наглядности:

• 3⁵ = 3 × 3 × 3 × 3 × 3 = 243

Эту запись можно прочитать тремя способами:

• 3 в 5 степени;
• пятая степень числа три;
• возвести число три в пятую степень.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Свойства степеней

Свойства степеней обычно используют, чтобы сократить или упростить сложные примеры. Удобно использовать вместе с таблицей степеней и таблицей умножения.

a1 = а a0 = 1 (a ≠ 0) a−n = 1 : an am × an = am+n am : an = am-n (a × b)n = an × bn (am)n = am×n (a : b)n = an : bn

Подготовка к ЕГЭ по математике онлайн поможет снять стресс перед экзаменом и повысит шансы на высокий балл.

Таблица степеней от 1 до 10

Таблица степеней — это перечень чисел от 1 до 10, возведенных в степень от 1 до 10. Ниже приведены два вида таблиц: выберите ту, которая удобнее для вас, скачайте на телефон или распечатайте и положите в учебник.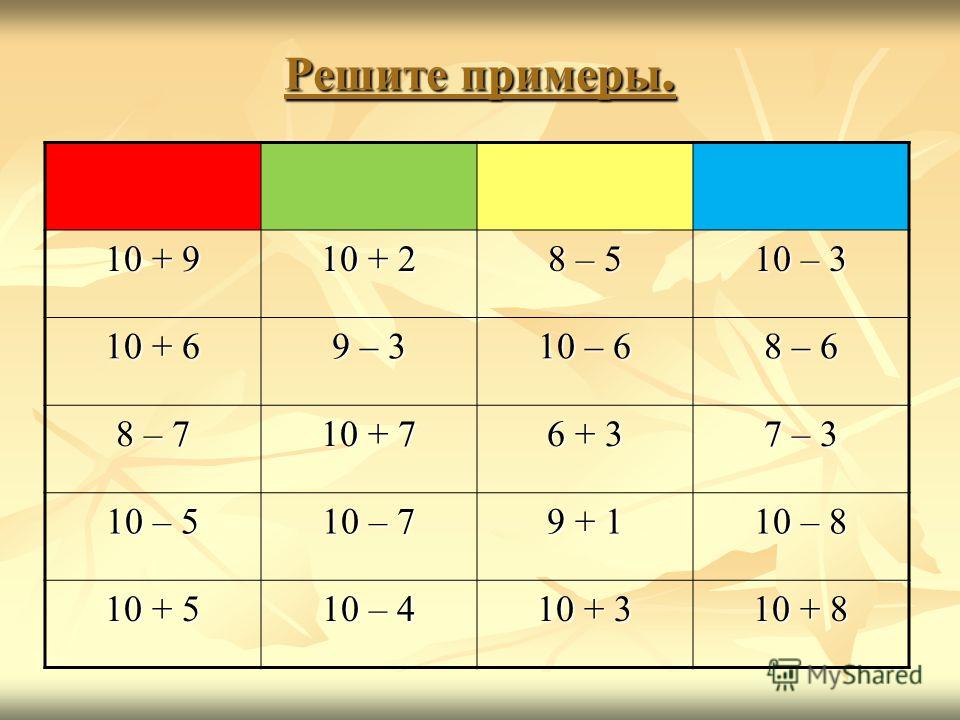

Как найти необходимые значения в этой таблице:

• В первом столбце находим число, которое обозначает степень. Запомним номер этой строки.
• В первой строке находим показатель степени. Запомним найденный столбец.
• На пересечении строки и столбца находится ответ.

В этой табличке мы просто ищем нужное нам число в степени и получаем ответ.

А если ответ нужно получить как можно быстрее, можно использовать онлайн-калькулятор степеней.

Решение задач

Задание 1. Упростить и решить выражение 5

2 × 5³.

Как решаем:

5² × 5³ = 5²⁺³ = 5⁵ = 3125

Задание 2. Упростить и решить выражение 2⁴ × 3³ × 2⁵.

Как решаем:

2⁴ × 3³ × 2⁵ = 2⁴⁺⁵ × 3³ = 2⁹ × 3³ = 512 × 27 = 13 824

Задание 3. Найти 36⁴.

Как решаем:

При условии, что у нас есть только таблица до 10, разложим основание степени на множители:

36⁴ = 6⁴ × 6⁴ = 1296 × 1296 = 1 679 616

36⁴ = 6⁴ × 6⁴ = 6⁸ = 1 679 616

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

293.4K

Как решать систему уравнений

К следующей статье

420. 2K

Сокращенное умножение: правила, формулы

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Решение неравенств с помощью пошагового решения математических задач

В этой главе мы разработаем некоторые приемы, помогающие решать задачи, сформулированные словами. Эти методы включают переписывание задач в виде символов. Например, поставленная задача

«Найдите число, которое при прибавлении к 3 дает 7»

можно записать так:

3 + ? = 7, 3 + n = 7, 3 + x = 1

и т. д., где символы ?, n и x представляют число, которое мы хотим найти. Такие сокращенные версии поставленных задач мы называем уравнениями или символическими предложениями. Такие уравнения, как x + 3 = 7, являются уравнениями первой степени, поскольку показатель степени равен 1. Члены слева от знака равенства составляют левый член уравнения; те, что справа, составляют правый член. Таким образом, в уравнении x + 3 = 7 левая часть равна x + 3, а правая часть равна 7.

РЕШЕНИЕ УРАВНЕНИЙ

Уравнения могут быть истинными или ложными, так же как словесные предложения могут быть истинными или ложными. Уравнение:

3 + x = 7

будет ложным, если вместо переменной подставить любое число, кроме 4. Значение переменной, для которой уравнение верно (4 в этом примере), называется решением уравнения. Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.

Пример 1. Определить, является ли значение 3 решением уравнения член.

4(3) — 2 = 3(3) + 1

12 — 2 = 9 + 1

10 = 10

Ответ. 3 это решение.

Уравнения первой степени, которые мы рассматриваем в этой главе, имеют не более одного решения. Решения многих таких уравнений можно определить путем проверки.

Пример 2 Найдите решение каждого уравнения путем проверки.

а. х + 5 = 12
б. 4 · x = -20

Решения а. 7 является решением, так как 7 + 5 = 12,
b. -5 является решением, поскольку 4(-5) = -20.

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ

В разделе 3.1 мы решили некоторые простые уравнения первой степени путем проверки. Однако решения большинства уравнений не сразу очевидны при осмотре. Следовательно, нам нужны некоторые математические «инструменты» для решения уравнений.

ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ

Эквивалентные уравнения – это уравнения, имеющие одинаковые решения. Таким образом,

3x + 3 = x + 13, 3x = x + 10, 2x = 10 и x = 5

эквивалентны уравнениям, поскольку 5 является единственным решением каждого из них. Обратите внимание, что в уравнении 3x + 3 = x + 13 решение 5 не очевидно при проверке, но в уравнении x = 5 решение 5 очевидно при проверке. При решении любого уравнения мы преобразуем данное уравнение, решение которого может быть неочевидным, в эквивалентное уравнение, решение которого легко заметить.

Следующее свойство, иногда называемое свойством сложения-вычитания , является одним из способов генерирования эквивалентных уравнений.

Если к обоим элементам добавляется или вычитается одно и то же количество уравнения, полученное уравнение эквивалентно исходному уравнение.

В символах

a — b, a + c = b + c и a — c = b — c

являются эквивалентными уравнениями.

Пример 1 Напишите уравнение, эквивалентное

x + 3 = 7

путем вычитания 3 из каждого члена.

Решение Вычитание 3 из каждого члена дает

x + 3 — 3 = 7 — 3

или

x = 4

Обратите внимание, что x + 3 = 7 и x = 4 являются эквивалентными уравнениями, поскольку решение одно и то же. для обоих, а именно 4. Следующий пример показывает, как мы можем сгенерировать эквивалентные уравнения, сначала упростив один или оба члена уравнения.

Пример 2 Напишите уравнение, эквивалентное

4x- 2-3x = 4 + 6

путем объединения одинаковых терминов, а затем добавления 2 к каждому элементу.

Объединение одинаковых членов дает

x — 2 = 10

Добавление 2 к каждому члену дает

x-2+2 =10+2

x = 12

Чтобы решить уравнение, мы используем сложение-sub тяга свойство преобразовывать данное уравнение в эквивалентное уравнение формы x = a, из которого мы можем найти решение путем проверки.

Пример 3 Решить 2x + 1 = x — 2.

Мы хотим получить эквивалентное уравнение, в котором все члены, содержащие x, находятся в одном члене, а все члены, не содержащие x, — в другом. Если мы сначала прибавим -1 к каждому элементу (или вычтем из него 1), мы получим

2x + 1- 1 = x — 2- 1

2x = x — 3

Если мы теперь прибавим -x к каждому члену (или вычтем x из него), мы получим

2x-x = x — 3 — х

х = -3

где решение -3 очевидно.

Решением исходного уравнения является число -3; однако ответ часто отображается в виде уравнения x = -3.

Поскольку каждое уравнение, полученное в процессе, эквивалентно исходному уравнению, -3 также является решением 2x + 1 = x — 2. В приведенном выше примере мы можем проверить решение, подставив — 3 вместо x в исходном уравнение

2(-3) + 1 = (-3) — 2

-5 = -5

Симметричное свойство равенства также полезно при решении уравнений. Это свойство указывает

Если a = b, то b = a

Это позволяет нам менять местами члены уравнения в любое время, не заботясь о смене знака. Таким образом,

Если 4 = x + 2, то x + 2 = 4

Если x + 3 = 2x — 5, то 2x — 5 = x + 3

Если d = rt, то rt = d

Может быть несколько различные способы применения вышеуказанного свойства сложения. Иногда один метод лучше другого, а в некоторых случаях также полезно симметричное свойство равенства.

Пример 4 Решите 2x = 3x — 9. (1)

Решение Если мы сначала прибавим -3x к каждому элементу, мы получим

2x — 3x = 3x — 9 — 3x

-x = -9

где переменная имеет отрицательный коэффициент. Хотя при проверке мы видим, что решение равно 9, поскольку -(9) = -9, мы можем избежать отрицательного коэффициента, добавляя -2x и +9 к каждому члену уравнения (1). В этом случае получаем

2х-2х + 9 = 3х- 9-2х+ 9

9 = х

откуда решение 9очевидно. Если мы хотим, мы можем записать последнее уравнение как x = 9 по симметричному свойству равенства.

Решенные уравнения с использованием Свойства Отдела

Рассмотрим уравнение

3x = 12

Решение этого уравнения равно 4. Также обратите внимание, что если мы разделим каждый член уравнения на 3, мы получаем уравнения

, решение которого также равно 4. В общем случае мы имеем следующее свойство, которое иногда называют свойством деления.

Если оба члена уравнения разделить на одно и то же (отличное от нуля) полученное уравнение эквивалентно исходному уравнению.

В символах

эквивалентны уравнениям.

Пример 1 Напишите уравнение, эквивалентное

-4x = 12

, разделив каждый член на -4.

Решение Деление обоих членов на -4 дает

При решении уравнений мы используем вышеуказанное свойство для получения эквивалентных уравнений, в которых переменная имеет коэффициент 1.

Пример 2 Решите 3y + 2y = 20.

Сначала мы объединяем одинаковые члены, чтобы получить

5y = 20

Затем, разделив каждый член на 5, мы получаем

В следующем примере мы используем дополнение — свойство вычитания и свойство деления для решения уравнения.

Пример 3 Решить 4x + 7 = x — 2.

Решение Сначала мы добавляем -x и -7 к каждому члену, чтобы получить

4x + 7 — x — 7 = x — 2 — x — 1

Далее , объединение одинаковых членов дает

3x = -9

Наконец, мы делим каждый член на 3, чтобы получить

РЕШЕНИЕ УРАВНЕНИЙ, ИСПОЛЬЗУЯ СВОЙСТВО УМНОЖЕНИЯ решение этого уравнения равно 12. Также обратите внимание, что если умножая каждый член уравнения на 4, мы получаем уравнения

, решение которых также равно 12. В общем случае мы имеем следующее свойство, которое иногда называют свойством умножения.

Если оба члена уравнения умножить на одну и ту же ненулевую величину, полученное уравнение эквивалентно исходному уравнению.

В символах

a = b и a·c = b·c (c ≠ 0)

являются эквивалентными уравнениями.

Пример 1 Напишите уравнение, эквивалентное

, умножив каждый член на 6.

Решение Умножив каждый член на 6, получим

дроби.

Пример 2 Решить

Решение Сначала умножьте каждый член на 5, чтобы получить

Теперь разделите каждый член на 3,

Пример 3 Решите .

Решение Сначала упростим над дробной чертой, чтобы получить

Затем умножим каждый член на 3, чтобы получить

Наконец, разделив каждый член на 5, получим

ДОПОЛНИТЕЛЬНОЕ СОЛНЦЕ РЕШЕНИЯ УРАВНЕНИЙ

Теперь мы знаем все методы, необходимые для решения большинства уравнений первой степени. Нет определенного порядка, в котором следует применять свойства. Любой один или несколько из следующих шагов, перечисленных на странице 102, могут быть подходящими.

Шаги для решения уравнений первой степени:

1. Объедините одинаковые члены в каждом члене уравнения.
2. Используя свойство сложения или вычитания, напишите уравнение со всеми членами, содержащими неизвестное в одном члене, и всеми членами, не содержащими неизвестного в другом.
3. Объедините одинаковые термины в каждом элементе.
4. Используйте свойство умножения для удаления дробей.
5. Используйте свойство Division, чтобы получить коэффициент 1 для переменной.

Пример 1 Решите 5x — 7 = 2x — 4x + 14.

Решение Сначала мы объединяем одинаковые члены, 2x — 4x, чтобы получить

5x — 7 = -2x + 14

Затем мы добавляем +2x и +7 к каждому члену и объединяем одинаковые члены, чтобы получить

5x — 7 + 2x + 7 = -2x + 14 + 2x + 1

7x = 21

Наконец, мы делим каждый член на 7, чтобы получить

В следующем примере мы упрощаем дробную черту перед применением свойств, которые мы изучали.

Пример 2 Решить

Решение Сначала мы объединяем одинаковые члены, 4x — 2x, чтобы получить

Затем мы добавляем -3 к каждому члену и упрощаем

Затем мы умножаем каждый член на 3, чтобы получить

Наконец, мы делим каждый член на 2, чтобы получить

РЕШЕНИЕ ФОРМУЛ

Уравнения, которые включают переменные для измерения двух или более физических величин, называются формулами. Мы можем найти любую переменную в формуле, если известны значения других переменных. Мы подставляем известные значения в формулу и находим неизвестную переменную методами, которые мы использовали в предыдущих разделах.

Пример 1 В формуле d = rt найдите t, если d = 24 и r = 3.

Решение Мы можем найти t, подставив 24 вместо d и 3 вместо r. То есть

d = rt

(24) = (3)t

8 = t

Часто бывает необходимо решать формулы или уравнения, в которых имеется более одной переменной для одной из переменных в терминах другие. Мы используем те же методы, что и в предыдущих разделах.

Пример 2 В формуле d = rt найдите t через r и d.

Решение Мы можем найти t через r и d, разделив оба члена на r, чтобы получить

, откуда по симметричному закону

В приведенном выше примере мы нашли t, применив свойство деления для создания эквивалентного уравнения. Иногда необходимо применить более одного такого свойства.

Пример 3 В уравнении ax + b = c найдите x через a, b и c.

Решение Мы можем найти x, сначала добавив -b к каждому члену, чтобы получить

, затем разделив каждый элемент на a, мы получим

Одно решение, нет решения, бесконечный рабочий лист решений и пример

Рабочие листы по математике для 8 класса

Теперь мы рассмотрим каждый из вышеупомянутых типов решения линейного уравнения и разберем их на примерах.

Примеры линейных уравнений с одним решением

Пример 1: Рассмотрим уравнение 7 x – 35 = 0,

на решении мы имеем 7 x = 35 или x = 5. Вышеупомянутое линейное уравнение является только правдой, если x = 5 и, следовательно 5.

Пример 2: Рассмотрим уравнение 9( x – 1) – 35 = 8 x + 37.

При решении имеем 9 x – 9 – 35 = 8 9 0382 х + 37.

Собираем одинаковые слагаемые с обеих сторон переносом их, у нас

9x – 8x = 37 + 35 + 9 = 80, что дает x = 80.

Приведенное выше линейное уравнение верно, только если x = 80

Следовательно, данное линейное уравнение имеет только одно решение 903 84 т. е. x = 80.

Из приведенных выше примеров мы видим, что переменная x не исчезает после решения, и мы говорим, что линейное уравнение будет иметь одно решение , если ему удовлетворяет ровно одно значение переменная.

Если вам нужна дополнительная помощь в освоении этой или любой другой математической концепции, вы можете выбрать наши услуги репетитора по математике для 8-го класса. Вы можете получить бесплатный сеанс перед покупкой, чтобы понять, как работают наши сеансы.

Линейные уравнения без решения (нулевое решение) Примеры

Узнайте больше о линейных уравнениях и других важных темах с репетиторством по математике для 8-го класса на eTutorWorld. Наши опытные преподаватели естественных наук разбивают темы на интерактивные индивидуальные занятия. Мы также предлагаем индивидуальные планы уроков, гибкий график и удобство обучения на дому.

  Пример 1: Рассмотрим уравнение 7 x – 35 = 5 x + 2 x – 27.

При решении имеем 7 903 82 х – 35 = 7х – 27

Вычитание 7 x с обеих сторон. 7 x – 7 x – 35  = 7 x – 7 x – 27

мы имеем -35 = -27, что является ложным утверждением, поскольку оно не может быть истинным для любого значения переменной х.

Следовательно, данное линейное уравнение имеет нулевое решение или число решений равно нулю.

Пример 2: Рассмотрим уравнение 3( x + 9) + 21 x = 24 x + 9.

90 002 При решении имеем 3 х + 27 + 21 x = 24 x + 9 или 24 x + 27 = 24 x + 9

Вычитание 24 x с обеих сторон, 24 x – 2 4 х + 27 = 24 х – 24 х + 9.

У нас есть 27 = 9, что является ложным утверждением, поскольку оно не может быть истинным ни при каком значении переменной х.

Следовательно, данное линейное уравнение не имеет решения или число решений равно нулю .

Из приведенных выше примеров мы видим, что переменная x исчезает / устраняется, поэтому мы говорим, что линейное уравнение будет иметь нулевое решение или не будет иметь никакого решения , если оно не может быть удовлетворено ни одним значением переменной или не существует любое значение переменной, которое делает данное уравнение истинным утверждением.

Линейные уравнения с бесконечными решениями Примеры

Пример 1: Рассмотрим уравнение 25 x – 35 = 5 (5 x 9038 3 + 4) – 55.

При решении имеем 25 x – 35 = 25 x + 20 – 55 или 25 x – 35 = 25 x – 35.

Вычитание 25 x с обеих сторон, 2 5 х – 25 х – 35 = 25 х – 25 х – 35

У нас есть -35 = -35, что является верным утверждением и будет истинным для любого значения переменной x .

Следовательно, данное линейное уравнение имеет бесконечное число решений или число решений бесконечно.

Пример 2: Рассмотрим уравнение 15 ( х + 9) = 24 х + 9 – (9 х – 126)

Решая имеем 15 х + 144 = 24 х + 9 – 9 х + 126 или 15 х + 144 = 15 х + 144.

Вычитание 15 х с обеих сторон. 15 x – 15 x +144 = 15 x – 15 x + 144

У нас есть 144 = 144, что является верным утверждением и будет истинным для любого значения переменной х .

Следовательно, данное линейное уравнение имеет бесконечное число решений или число решений бесконечно.

Из приведенных выше примеров мы можем сказать, что линейное уравнение будет иметь бесконечные решения , если ему удовлетворяет любое значение переменной или каждое значение переменной делает данное уравнение истинным утверждением.

Одно решение, нет решений, бесконечное количество решений – практические задачи по линейным уравнениям

Решите следующие линейные уравнения и определите, имеют ли данные линейные уравнения одно решение, нет решений или бесконечные решения.

1. 17 х – 75 = 6 + 14 х .
2. 3 х – 105 = 4 ( х – 20) – 1 ( х + 5).
3. 10 х + 2 7 = 2 (5 х + 99).
4. 7 х – 33 + 75 = 6 ( х + 7) + х.
5. 24 х + 60 = 4 ( х – 25).
6. 13 х + 10 – 4 х = 4 ( х – 26) + 5 х .

Ищете дополнительную помощь в понимании отсутствия решения, одного решения и бесконечных решений линейных уравнений? Попросите наших опытных наставников помочь вам! Вы можете записаться на бесплатное занятие, прежде чем приобретать пакеты репетиторства по математике для 8-го класса.

Ключ ответа

1. Одно решение, т. е. x = 27.
2. Бесконечные решения.
3. Нулевой раствор.
4. Бесконечные решения.
5. Одно решение, т. е. x = – 8.
6. Нулевой раствор.

Узнайте больше о линейных уравнениях и других важных темах с репетиторством по математике для 8-го класса на eTutorWorld. Наши опытные преподаватели естественных наук разбивают темы на интерактивные индивидуальные занятия. Мы также предлагаем индивидуальные планы уроков, гибкий график и удобство обучения на дому.

Часто задаваемые вопросы (FAQ)

Как вы определяете, имеет ли решение одно решение, не имеет решения или имеет бесконечное решение с помощью графического метода?

Чтобы узнать, есть ли у решения одно решение, нет ли решений или имеется бесконечное количество решений, с помощью графического метода, нанесите уравнения на график и посмотрите, где они пересекаются. Если они пересекаются в одной точке, то решение одно. Если они не пересекаются, то решения нет. Если уравнения перекрываются, то существует бесконечное количество решений.

Как с помощью алгебраического метода определить, имеет ли решение одно решение, не имеет решения или имеет бесконечное число решений?

Чтобы узнать, имеет ли решение одно решение, не имеет решения или имеет бесконечное число решений с помощью алгебраического метода, решите уравнения алгебраическим способом. Если вы получаете уникальное решение для каждой переменной, существует одно решение. Если вы получаете противоречие типа 0 = 1, то решения нет. Если вы получаете уравнение, которое всегда верно, например, 0 = 0, то существует бесконечное количество решений.

Что такое отсутствие решений и бесконечность решений?

«Нет решения» означает, что никакие значения не удовлетворяют всем уравнениям, а «бесконечное количество решений» означает, что удовлетворяет бесконечное множество значений. Первое происходит, когда уравнения представляют параллельные линии, второе, когда они эквивалентны.

Какой пример линейного уравнения не имеет решения?

Пример линейного уравнения без решения:

2x + 3y = 7

4x + 6y = 12

, так как второе уравнение в два раза больше первого уравнения, представляющего ту же прямую, решений нет.

Что является примером линейного уравнения с одним решением?

Пример линейного уравнения с одним решением:

2x + 3y = 7

5x – y = 2

, так как два уравнения представляют две пересекающиеся прямые с единственным решением (x,y)=(1,1) .

Что является примером линейного уравнения с бесконечным решением?

Пример линейных уравнений с бесконечным решением:

2x + 3y = 7

4x + 6y = 14

, поскольку второе уравнение в два раза больше первого уравнения, представляющего одну и ту же прямую, и, следовательно, существует бесконечно много решения.

Персонализированное онлайн-обучение

eTutorWorld предлагает доступное индивидуальное онлайн-обучение для классов K-12, помощь в подготовке к стандартным тестам, таким как SCAT, CogAT, MAP, SSAT, SAT, ACT, ISEE и AP. . Вы можете запланировать уроки онлайн-репетиторства в удобное для вас время с гарантией возврата денег. Первый индивидуальный онлайн-урок всегда БЕСПЛАТНЫЙ, никаких обязательств по покупке, кредитная карта не требуется.

Чтобы получить ответы/решения на любой вопрос или изучить понятия, возьмите БЕСПЛАТНАЯ ПРОБНАЯ ВЕРСИЯ Сессия.

Запланировать бесплатный сеанс

Кредитная карта не требуется, никаких обязательств по покупке.