Примеры на деление трехзначных чисел на двузначное, как делить двухзначные на двухзначные с остатком? Разное

❤ 2623 , Категория: Разное,   ⚑ 03 Июн 2020г

---

Содержание

• 1 Деление столбиком на двузначное число
• 2 Алгоритм деления столбиком на двузначное число
• 3 Разбор примеров на деление столбиком на двузначное число
• 4 Пример на деление с остатком
• 5 Деление с нулем в частном
• 6 Примеры на деление для самопроверки
• 7 Деление на двузначное число — способы и примеры решений
• 8 Деление на двузначное число устно
• 9 Деление в столбик на двузначное число
• 10 Примеры деления в столбик на двузначное число
  • 10.1 Пример 1
  • 10.2 Пример 2
  • 10.3 Пример 3
  • 10.4 Пример 4
  • 10.5 Пример 5
• 11 Письменное деление с остатком на двузначное число
  • • • 11.0.0.1 Этот видеоурок доступен по абонементу
  • 11. 1 С помощью этого урока вы сможете пройти тему «Деление на двузначное число». В ходе урока учитель напомнит пройденный материал, когда в частном при делении будет находиться однозначное или двухзначное число. Далее расскажет о правилах письменного деления в случае, если частное представлено трехзначным числом.
• 12 Деление на двузначное число без остатка
• 13 Деление на двузначное число с остатком
• 14 Заключение

Деление столбиком на двузначное число

Деление столбиком или, правильнее сказать, письменный прием деления уголком, школьники проходят уже в третьем классе начальной школы, но зачастую этой теме уделяется так мало внимания, что к 9-11 классу не все ученики могут им свободно пользоваться.

Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.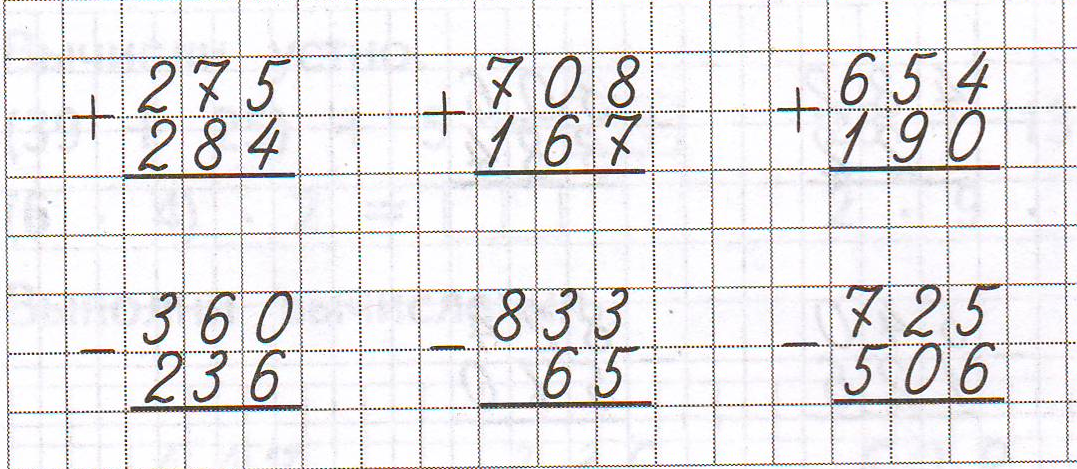

Очевидно, что уделив делению столбиком больше внимания, чем заложено в школьной программе, ребенок облегчит себе выполнение заданий по математике вплоть до 11 класса. А для этого нужно немногое — понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.

Для начала повторим кратко, как делить столбиком на однозначное число:

А что если деление с остатком? Смотрим в следующем видео:

Алгоритм деления столбиком на двузначное число

Как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к делению более мелких единиц.

1. Находим первое неполное делимое. Это число, которое делится на делитель с получением числа больше или равного 1. Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака.

Примеры 76 8:24. Первое неполное делимое 76
265 :53 26 меньше 53, значит не подходит.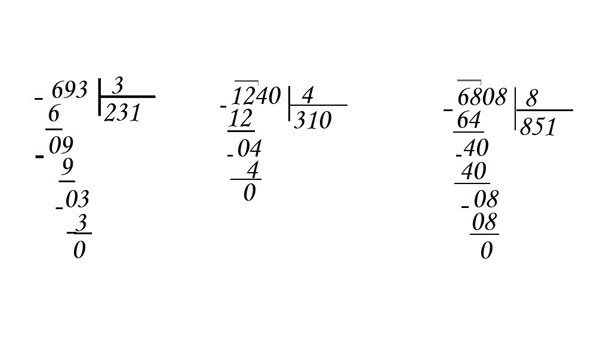 Нужно добавить следующую цифру (5). Первое неполное делимое 265.

2. Определяем количество цифр в частном. Для определения числа цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого — еще по одной цифре частного.

Примеры 768:24. Первое неполное делимое 76. Ему соответствует 1 цифра частного. После первого неполного делителя есть еще одна цифра. Значит в частном будет всего 2 цифры.
265:53. Первое неполное делимое 265. Оно даст 1 цифру частного. Больше в делимом цифр нет. Значит в частном будет всего 1 цифра.
15344:56. Первое неполное делимое 153, а после него еще 2 цифры. Значит в частном будет всего 3 цифры.

3. Находим цифры в каждом разряде частного. Сначала найдем первую цифру частного. Подбираем такое целое число, чтобы при умножении его на наш делитель получилось число, максимально приближенное к первому неполному делимому. Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя.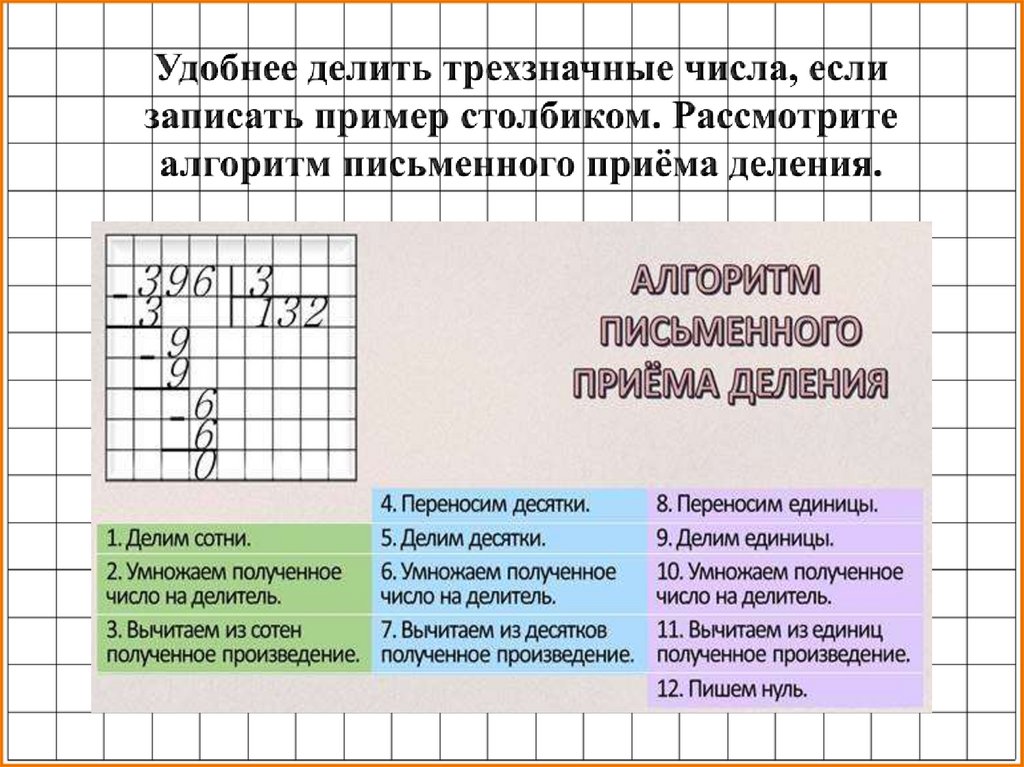 Записываем остаток. Проверяем, что он меньше делителя.

Затем находим вторую цифру частного. Переписываем в строку с остатком цифру, следующую за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.

4. Находим остаток (если есть).

Если цифры частного закончились и получился остаток 0, то деление выполнено без остатка. В ином случае значение частного записывается с остатком.

Так же выполняется деление на любое многозначное число (трехзначное, четырехзначное и т. д.)

Разбор примеров на деление столбиком на двузначное число

Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.

— Найдем значение частного чисел 265 и 53.

Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.

Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.

Значение частного чисел 265 и 53 равно 5.

Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.

— Найдем значение частного чисел 184 и 23.

В частном будет однозначное число.

Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8.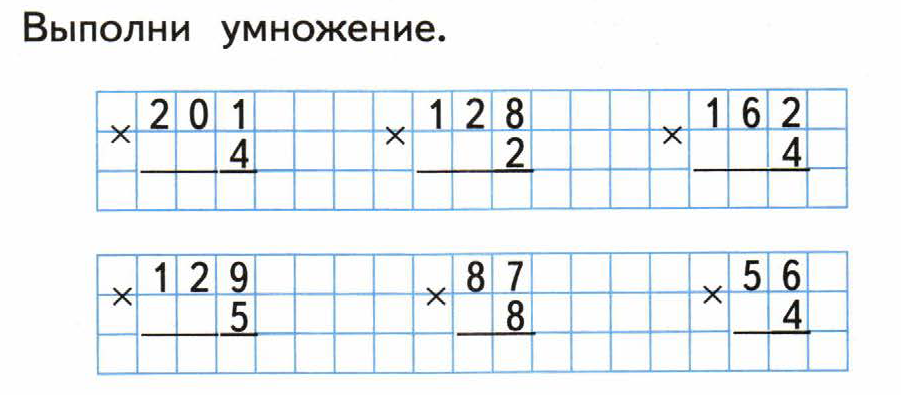 Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.

Значение частного чисел 184 и 23 равно 8.

Рассмотрим более сложные случаи деления.

— Найдем значение частного чисел 768 и 24.

Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.

Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.

Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.

Значение частного чисел 768 и 24 равно 32.

— Найдем значение частного чисел 15344 и 56.

Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.

Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.

Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое 414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414_10=41(ост.4). 41_5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.

Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.

Значение частного чисел 15344 и 56 равно 274.

Пример на деление с остатком

Чтобы провести аналогию, возьмем пример, похожий на пример выше, и отличающийся лишь последней цифрой

— Найдем значение частного чисел 15345:56

Делим сначала точно так же, как в примере 15344:56, пока не дойдем до последнего неполного делимого 225. Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.

Значение частного чисел 15345 и 56 равно 274 (остаток 1).

Деление с нулем в частном

Иногда в частном одним из чисел получается 0, и дети зачастую пропускают его, отсюда неправильное решение. Разберем, откуда может взяться 0 и как его не забыть.

— Найдем значение частного чисел 2870:14

Первое неполное делимое — 28 сотен. Значит в частном будет 3 цифры. Ставим под уголок три точки. Это важный момент. Если ребенок потеряет ноль, останется лишняя точка, которая заставит задуматься, что где-то упущена цифра.

Определим первую цифру частного. Разделим 28 на 14. Подбором получается 2. Проверим, подойдет ли цифра 2. Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.

Получился нулевой остаток. Мы обозначили его розовым для наглядности, но записывать его не нужно. Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.

Теперь переписываем в ту же строку последнюю цифру делимого (количество единиц).

70:14=5 Записываем вместо последней точки в частном цифру 5. 70-70=0. Остатка нет.

Значение частного чисел 2870 и 14 равно 205.

Деление нужно непременно проверить умножением.

Примеры на деление для самопроверки

Найдите первое неполное делимое и определите количество цифр в частном.

3432:66 2450:98 15145:65 18354:42 17323:17

Усвоили тему, а теперь потренируйтесь решить несколько примеров столбиком самостоятельно.

1428 : 42 30296 : 56 254415 : 35 16514 : 718

2924 : 68 136576 : 64 710278 : 91 15830 : 293

Деление на двузначное число — способы и примеры решений

Деление на двузначное число похоже на тот же процесс с однозначным числом, но занимает больше времени. Однако есть немало методов, которые упрощают процесс. Научиться выполнять деление быстро помогут основные правила и серьезная практика.

Деление на двузначное число устно

Осуществляется такое деление методом подбора.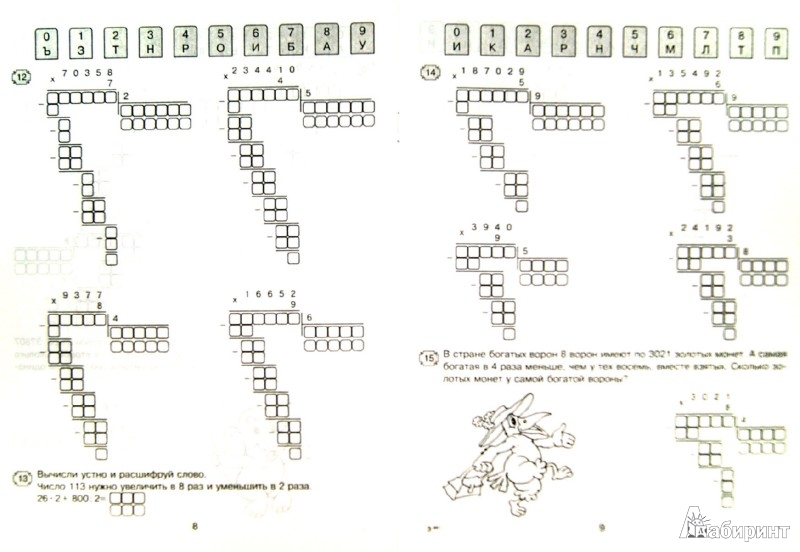 Например, нужно разделить число 90 на двузначное число 15 без остатка.

Чтобы это сделать устно, нужно подобрать такое число, которое при умножении его на 5 (15 оканчивается на 5) даст число, оканчивающееся на 0 (так как 90 оканчивается на ноль).

Какое число при умножении на 5 даст в результате число с цифрой 0 на конце? Их несколько.

Теперь проверяем. Если цифра нам подходит, то, умножив ее на 15, получим 90:

Последняя цифра 6 подходит. Мы выполнили деление: 90 : 15 = 6.

Деление в столбик на двузначное число

Деление в столбик школьники проходят еще в младших классах на уроках математики. В дальнейшем его применяют как вспомогательное средство при решении задач. Но если не пройти в нормальном виде деление уголков, то могут возникнуть затруднения и с трехзначными числами.

На рисунке 1 показан принцип деления и названия основных элементов процесса. Как и при делении на однозначные числа, работает алгоритм перехода от крупных к мелким единицам.

Порядок действий опишем, взяв для примера вычисление, представленное на рисунке 1:

Выделить самое маленькое двузначное число 63, которое можно поделить на делитель 61. Оно всегда больше того, которое является делителем.

Делим 63 на 61. Сколько раз 61 поместится в 63? Один. Записываем под уголком единицу. Это первая цифра частного.

Умножаем делитель на эту первую цифру: 61 * 1 = 61, вычитаем из 63 число 61, проводим черту и пишем разность — 2.

Сносим следующую цифру делимого — 4. Получаем число 24. Оно не делится на 61, потому записываем ноль на место второй цифры частного (это место рядом с цифрой 1 в нашем примере).

Сносим следующую (последнюю в нашем примере) цифру, это 4. Получаем число 244. Делим его на 61. Применим правило устного деления, описанное выше. Нужно подобрать такую цифру, которая при умножении на последнюю цифру (у 61 последняя цифра 1) даст ответ, оканчивающийся на последнюю цифру делимого (у 244 последняя цифра 4, она нам и нужна). Т. е. 4 * 1 = 4. Проверка: 61 * 4 = 244. Мы подобрали цифру 4 и она нам подошла.

Вписываем 4 третьей цифрой частного в уголок, получаем 104. Умножаем 61 на 4 и вычитаем результат из 244. Получаем 0. Деление выполнено.

В данном примере делимое — трёхзначное число. В общем случае процесс сноса цифр делимого и деления их на делитель продолжается до тех пор, пока не закончатся все цифры делимого. Этот принцип подходит для трехзначных, четырехзначных и других многозначных чисел.

Примеры деления в столбик на двузначное число

Рассмотрим некоторые примеры. Они довольно простые и помогут понять основные моменты данного способа.

Пример 1

Найдём значение частного чисел 265 и 53:

Пример 2

Найдем результат деления чисел 624 и 52:

Пример 3

Рассмотрим более сложные случаи деления в столбик. Найдем значение частного чисел 1610 и 35:

Пример 4

Деление пятизначного числа на двузначное. Узнаем значение частного чисел 10150 и 35:

Пример 5

Деление многозначного числа на двузначное с остатком. Вычислим, чему будет равно частное чисел 1978 и 38:

Деление на двузначное число можно выполнять в столбик и устно, но многозначные числа устно считать намного сложнее. Немногие школьники могут похвастаться подобными умениями.

Освоение процесса деления поможет школьникам в дальнейшем обучении. Так же существует немало тренажеров и онлайн-калькуляторов, которые можно использовать в свою пользу.

Письменное деление с остатком на двузначное число

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

С помощью этого урока вы сможете пройти тему «Деление на двузначное число». В ходе урока учитель напомнит пройденный материал, когда в частном при делении будет находиться однозначное или двухзначное число. Далее расскажет о правилах письменного деления в случае, если частное представлено трехзначным числом.

Деление на двузначное число без остатка

Рассмотрим сначала, как выполнить деление на двузначное число без остатка.

В значении частного будет одна цифра. Чтобы легче было подобрать цифру частного, разделим 312 не на 52, а на 50:

(ост. )

6 – это пробная цифра, ее нельзя сразу записывать в частном, ведь мы делим не на 50, а на 52. Сначала нужно проверить, подойдет ли цифра 6. Умножим 52 на 6.

Цифра подошла. Значение частного будет 6.

Рассмотрим еще один случай деления.

В значении частного будет одна цифра. Чтобы легче было подобрать цифру частного, разделим 469 не на 67, а на 60.

7 – это пробная цифра, ее нельзя сразу записывать в частном, ведь мы 469 делим не на 60, а на 67. Сначала нужно проверить, подойдет ли цифра 7. Умножим 67 на 7.

Мы видим, что цифра 7 подходит. Значит, значение частного будет 7.

Деление на двузначное число с остатком

При делении на двузначное число с остатком рассуждать нужно так же.

1. Найдем частное.

В частном будет одна цифра. Чтобы легче было найти цифру частного, разделим 299 не на 34, а на 30.

(ост. 29)

9 – это пробная цифра частного, ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 34 на 9.

306 больше, чем делимое 299. Значит, цифра 9 не подходит. Проверим цифру 8.

Значит, цифра 8 подойдет. Остаток меньше, чем делитель. Записываем в частном цифру 8.

Значение частного чисел 299 и 34 – 8 и остаток 27.

2. Рассмотрим еще один случай деления.

В частном будет одна цифра. Чтобы легче было найти цифру частного, разделим 191 не на 46, а на 40.

(ост. 31)

4 – это только пробная цифра, ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 46 на 4.

Остаток 7 меньше, чем делитель 46. Значит, цифра частого 4 подходит, запишем ее.

Значение частного чисел 191 и 46 – 4 и остаток 7.

Заключение

На уроке мы учились выполнять деление на двузначные числа без остатка и с остатком.

Список литературы

1. Математика. Учебник для 4 кл. нач. шк. В 2 ч./М.И. Моро, М.А. Бантова – М.: Просвещение, 2010.
2. Демидова Т.Е., Козлова С.А., Тонких А.П. Математика. 4 класс. Учебник в 3 ч. . 2-е изд., испр. – М.: 2013.; Ч.1 – 96 с., Ч.2 – 96 с., Ч.3 – 96 с.
3. Математика: учеб. для 4-го кл. общеобразоват. учреждений с рус. яз. обучения. В 2 ч. Ч. 1 / Т.М. Чеботаревская, В.Л. Дрозд, А.А. Столяр; пер. с бел. яз. Л.А. Бондаревой. – 3-е изд., перераб. – Минск: Нар. асвета, 2008. – 134 с.: ил.
4. Математика. 4 класс. Учебник. В 2 ч./Гейдман Б.П. и др. – 2010. – 120 с., 128 с.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Домашнее задание

Выполните деление с остатком и без остатка.

Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.

Источники:

http://7gy.ru/shkola/matematika/1312-delenie-stolbikom-na-dvuznachnoe-chislo. html
http://nauka.club/matematika/delenie-na-dvuznachnoe-chislo.html
http://interneturok.ru/lesson/matematika/4-klass/delenie-na-dvuznachnoe-chislo/pismennoe-delenie-s-ostatkom-na-dvuznachnoe-chislo

Статью нашли по запросам:

• деление трехзначнвх надвузначные методом под бора 3 класс ответы
• примеры деления трехзначного числа на двузначное без остатка
• примеры для 4 класса по математике на деление и умножение в столбик трехзначные на двузначные

ГДЗ по математике 4 класс учебник Моро, Бантова 2 часть

❤️️Ответ к странице 72. Математика 4 класс учебник 2 часть. Авторы: М.И. Моро, М.А. Бантова.

Номер 279.

1) Выполни деление с объяснением.
2) Объясняя так же, найди частное и остаток.

Ответ:

1)

Нужно разделить 954 на 318. Чтобы легче было найти цифру частного, разделим 954 на 300. Для этого разделим 9 на 3, в частном получим 3. Это пробная цифра, ее нужно проверить. Умножим 318 на 3, получится 954. Значит, частное 3.
Нужно разделить 876 на 219. Чтобы легче было найти цифру частного, разделим 876 на 200. Для этого разделим 8 на 2, в частном получим 4. Это пробная цифра, ее нужно проверить. Умножим 219 на 4, получится 876. Значит, частное 4.
Нужно разделить 2940 на 735. Чтобы легче было найти цифру частного, разделим 2940 на 700. Для этого разделим 29 на 7, в частном получим 4. Это пробная цифра, ее нужно проверить. Умножим 735 на 4, получится 2940. Значит, частное 4.

Нужно разделить 2544 на 424. Чтобы легче было найти цифру частного, разделим 2544 на 400. Для этого разделим 25 на 4, в частном получим 6. Это пробная цифра, ее нужно проверить. Умножим 424 на 6, получится 2544. Значит, частное 6.
2)

Нужно разделить 875 на 354. Чтобы легче было найти цифру частного разделим 875 на 300. Для этого разделим 8 на 3, в частном получим 2. Это пробная цифра, ее нужно проверить. Умножим 354 на 2, получится 708. Вычтем 708 и 875, получим 167. 167 — остаток. Проверка:
Значит, частное 2, остаток 167.
Нужно разделить 912 на 219. Чтобы легче было найти цифру частного, разделим 912 на 200. Для этого разделим 9 на 2, в частном получим 4. Это пробная цифра, ее нужно проверить. Умножим 219 на 4, получится 876. Вычтем 876 из 912, получим 36. 36 − это остаток. Проверка:
Значит, частное 4, остаток 36.
Нужно разделить 3964 на 526. Чтобы легче было найти цифру частного, разделим 3964 на 500. Для этого разделим 39 на 5, в частном получим 7. Это пробная цифра, ее нужно проверить. Умножим 526 на 7, получится 3682. Вычтем 3682 из 3964, получим 282. 282 − это остаток. Проверка:
Значит, частное 7, остаток 282.
Нужно разделить 2051 на 642. Чтобы легче было найти цифру частного, разделим 2051 на 600. Для этого разделим 20 на 6, в частном получим 3. Это пробная цифра, ее нужно проверить. Умножим 642 на 3, получится 1926. Вычтем 1926 из 2051, получим 125. 125 − это остаток. Проверка:
Значит, частное 3, остаток 125.

Номер 280.

На стройку привезли 120 т цемента, песка – в 2 раза больше, а щебёнки – в 4 раза больше, чем цемента. Для получения бетона израсходовали третью часть всех этих материалов. Поставь вопрос и реши задачу.

Ответ:

Вариант 1: Сколько тонн привезенных материалов израсходовали для приготовления бетона?

1) 120 ∙ 2 = 240 (т) – песка привезли на стройку. 2) 120 ∙ 4 = 480 (т) – щебня привезли на стройку. 3) 480 + 120 + 240 = 840 (т) – масса всех материалов, которые привезли на стройку. 4) 840 : 3 = 280 (т) – материалов израсходовали для приготовления бетона. Ответ: 280 т.
Вариант 2: Сколько тонн привезенных материалов всего осталось?

1) 120 ∙ 2 = 240 (т) – песка привезли на стройку. 2) 120 ∙ 4 = 480 (т) – щебня при везли на стройку. 3) 480 + 120 + 240 = 840 (т) – масса всех материалов, которые привезли на стройку. 4) 840 : 3 = 280 (т) – материалов израсходовали для приготовления бетона. 5) 840 − 280 = 560 (т) – материалов всего осталось неиспользованными. Ответ: 560 т.

Номер 281.

На 21 детскую простыню требуется столько же полотна, сколько на 15 простыней для взрослых. Сколько полотна расходуют на 1 простыню для взрослых, если на 1 детскую простыню расходуют 1 м 50 см? (Вырази длину в сантиметрах.)

Ответ:

1 м 50 см = 150 см 1) 150 ∙ 21 = 3150 (см) – общий расход на изготовления 21 детской простыни или 15 взрослой. 2) 3150 : 15 = 210 (см) – полотна потребуется для одной взрослой простыни.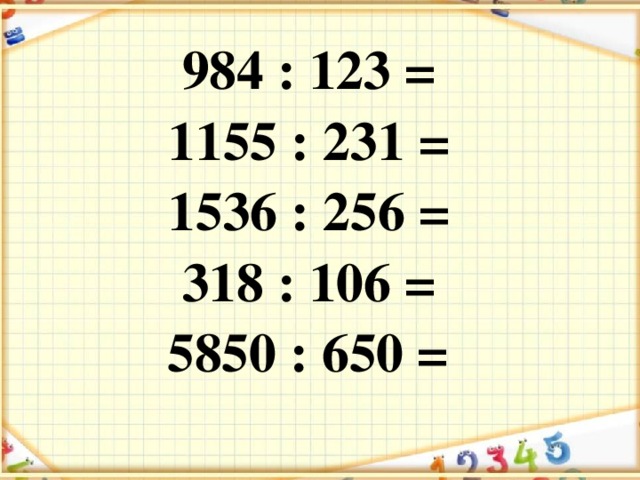

Ответ:210 см = 2 м 10 см.

Номер 282.

Составь по данному чертежу задачу и реши её.

Ответ:

ИИз двух пунктов одновременно навстречу друг другу выехали два автомобиля. Один ехал со скоростью 60 км/ч, а другой – 80 км/ч. Через 2 часа расстояние между ними стало равняться 420 км. Каково расстояние между пунктами, из которых выехали автомобили? 1) 60 + 80 = 140 (км/ч) – скорость сближения. 2) 140 ∙ 2 = 280 (км) – расстояние, пройденное автомобилями. 3) 420 + 280 = 700 (км) – расстояние между пунктами. Ответ: 700 км.

Номер 283.

Ответ:

Задание внизу страницы

Вычисли.

Ответ:

Задание на полях страницы

Лабиринт.

Ответ:

Как выполнить это задание? Лабиринт — головоломка, в которой нужно найти верный путь, ведущий от начала лабиринта к центру.

В данном случае ребенку предстоит решить математический лабиринт. Над лабиринтом стоит значок (квадрат делить на квадрат). Он означает, что в данном лабиринте записаны: на внешнем круге — делимое, на втором круге — делитель, а в центре — частное. То есть ребенку нужно составить 4 примера, сочетающих такие комбинации чисел, чтобы каждый раз при делении получалось число 6.
Первый вариант: Делимое — 420 Частное — 6 Значит, делитель — 70. 420 : 70 = 6
Второй вариант: Делимое — 540 Частное — 6 Значит, делитель — 90. 540 : 90 = 6
Третий вариант: Делимое — 360 Частное — 6 Значит, делитель — 60. 360 : 60=6
Четвертый вариант: Делимое — 480 Частное — 6 Значит, делитель — 80. 480 : 80 = 6

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

2 часть

4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111	112	113	114	115	116	117	118	119	120	121	122	123	124	125	126	127

Типы задач на умножение и деление

Проблемы со словами могут быть такой проблемой. Особенно в 3-х классах и выше, когда учащимся приходится решать все операции и многошаговые словесные задачи. Студенты часто пытаются определить представленную операцию или пропускают часть шагов, необходимых для решения. Явное преподавание типов словесных задач может помочь нашим ученикам распознавать операции в контексте. Стандарты Common Core State излагают различные типы задач на умножение и деление, которые должны знать учащиеся. Обучая их явно, мы помогаем учащимся понять умножение и деление в контексте, чтобы помочь им по-настоящему понять операции. Мы связываем то, как математика, которую они изучают, имеет отношение к их реальной жизни. Сосредоточив внимание на текстовых задачах и их типах, мы сосредоточимся на том, что делает умножение и деление тем, чем они являются.

В этом посте подробно рассматриваются все типы задач на умножение и деление слов. Я также даю несколько полезных ссылок внизу, в которых обсуждаются когнитивно-управляемые инструкции или типы задач CGI.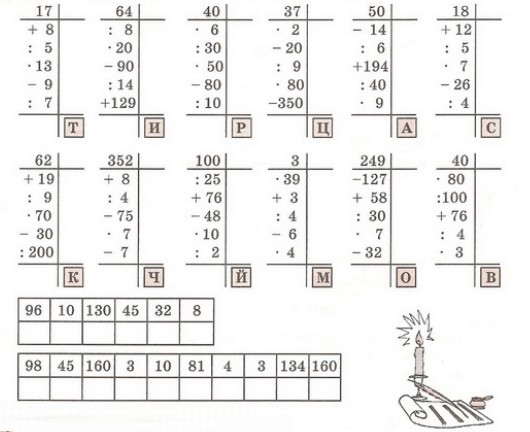 Они используют несколько иную лексику, чем CCSS, но имеют тот же набор навыков. Важное примечание: когда я говорю об обучении типам задач на умножение и деление слов в явном виде, я не имею в виду, что они практикуются только во время определенного раздела или что мы обучаем определенным ключевым словам для каждого типа задач. Учащиеся должны прочитать задачу и понимать контекст. Распознавание типа проблемы может поддержать эту работу, но оно не сосредоточено на ключевых словах. Кроме того, я ежедневно решаю задачи со словами вне нашей основной работы. Я твердо верю в спираль стандартов в текстовых задачах, чтобы учащиеся должны были сосредоточиться на контексте для решения. Для получения дополнительной помощи в решении проблем ознакомьтесь с моей публикацией «Почему ваши учащиеся борются с задачами в Word и что вы можете с этим поделать».

 

Важное замечание, прежде чем мы начнем: на протяжении всего нашего исследования обеих операций мы часто возвращаемся к всего .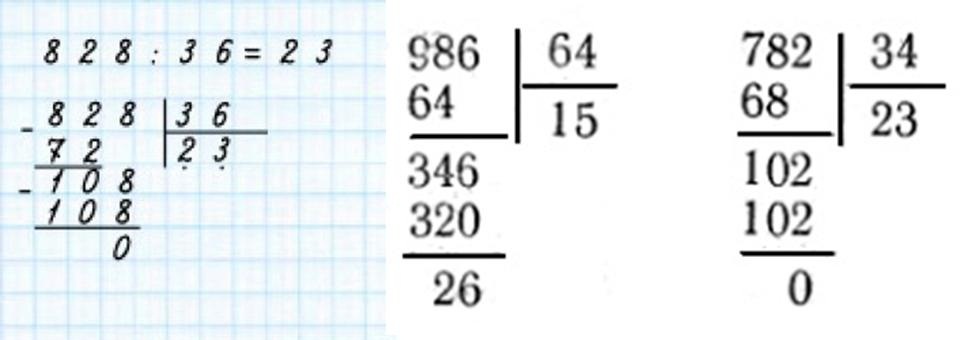 На первом уроке мы определили, что умножение позволяет нам найти общее количество предметов, расположенных в равных группах. Когда мы начинаем исследовать деление, мы знаем общее количество объектов, которые у нас есть, и должны найти неизвестное в связи с группами. На протяжении всей нашей работы с массивами, площадями и равными группами мы продолжаем возвращаться к понятию в сумме , чтобы помочь учащимся определить необходимую операцию. Именно путем определения суммы как известной или неизвестной учащиеся по-настоящему поймут операции умножения и деления. Как вы увидите, это основное внимание в каждом из типов задач на умножение и деление.

 Равные группы как умножение и деление

В своих постах «Введение в умножение и работу с делением» я прохожу практические, увлекательные уроки, которые я использую для ознакомления с каждой операцией. При введении обеих операций мы ориентируемся на равные групповые договоренности. Для учащихся крайне важно понять, что умножение и деление работают с равными группами, поэтому имеет смысл начать здесь. Когда мы впервые начинаем работать со словесными задачами на умножение и деление, я прошу учащихся определить элементы, которые расположены в группах, и определить, на что похожа эта группа. Например, группа может быть коробкой или сумкой. Эти объекты также могут быть просто объектами в других сценариях. Таким образом, определение того, что объект сгруппирован внутри чего-либо, помогает учащимся понять проблему слова и то, что присутствует сценарий равной группы.

	УМНОЖЕНИЕ	КОЛИЧЕСТВЕННЫЙ ПОДРАЗДЕЛ	ЧАСТНОЕ ПОДРАЗДЕЛЕНИЕ
	ВСЕГО НЕИЗВЕСТНО	# из ГРУППЫ НЕИЗВЕСТНО	# в каждом ГРУППА НЕИЗВЕСТНО
	4 х 6 = ? ? ÷ 4 = 6	? Х 6 = 24 24 ÷ ? = 6	4 х ? = 24 24 ÷ 4 = ?
Равные группы	На прилавке было 4 сумки. В каждом пакете было по 6 яблок. Сколько яблок было всего?	В мешках поровну разложено 24 яблока. В каждом пакете по 6 яблок. Сколько мешков с яблоками?	24 яблока поровну разделены на 4 мешка. Сколько яблок в каждом мешке?

УМНОЖЕНИЕ – Всего неизвестно

Это задачи со словами, которые мы обычно думаем с умножением. Это расположение элементов в равные группы, чтобы найти общее количество элементов. Определение того, что количество групп и количество элементов в каждой группе известно, а общее количество неизвестно, помогает учащимся решать эти словесные задачи.

ЧИТАТЕЛЬНОЕ ДЕЛЕНИЕ – количество групп неизвестно

Когда количество групп неизвестно, это проблема квотного деления. Поясню, я не учу своих студентов термину кавычка . Скорее, я учу их тому, что есть два типа разделения. Когда учащиеся могут определить, что общее количество объектов известно, но количество групп неизвестно, они знают, что они делятся. Важно, чтобы студенты имели много практики с обоими типами разделения.

ЧАСТИЧНОЕ ДЕЛЕНИЕ – # в каждой группе Неизвестно

Если в текстовой задаче указано общее количество элементов и их расположение, но не указано число в каждой группе, это деление на части. Думайте об этом как разделение . Количество групп известно, поэтому известны и разделы. Опять же, я не учу этому термину своих студентов, но важно, чтобы студенты знали, что деление представлено двумя способами.

После того, как обе операции будут представлены и отработаны по отдельности, мне нравится использовать мои карточки с заданиями по умножению и делению, чтобы практиковаться в написании уравнений и понимании группового расположения в контексте. Я считаю, что удаление всех компонентов словесной задачи и работа только с общей и групповой информацией помогает учащимся по-настоящему понять операции, связанные с равными группами. Это помогает им затем применить свои знания в текстовых задачах. Студенты получают практику с различными способами группировки элементов, что помогает им искать и определять отношения группировки в текстовых задачах позже.

Массивы как умножение и деление

В связи с обучением равным групповым расположениям, описанным выше, также должны быть включены массивы. Массивы — это то, как учащиеся впервые знакомятся с умножением во 2-м классе. Учащиеся должны иметь базовые знания с строк и столбцов словарного запаса. Массивы — это то, как я связываю то, что мы изучаем сейчас, с тем, что они узнали раньше. Поэтому я преподаю массивы в то же время, что и равные групповые аранжировки. Соотношу ряды и количество групп. Я всегда подчеркиваю, что столбцы совпадают с числом в каждой строке (или группе).

 

	УМНОЖЕНИЕ	КОЛИЧЕСТВЕННЫЙ ПОДРАЗДЕЛ	ЧАСТНОЕ ПОДРАЗДЕЛЕНИЕ
	ВСЕГО НЕИЗВЕСТНО	# из ГРУППЫ НЕИЗВЕСТНО	# в каждом ГРУППА НЕИЗВЕСТНО
	4 х 6 = ? ? ÷ 4 = 6	? Х 6 = 24 24 ÷ ? = 6	4 х ? = 24 24 ÷ 4 = ?
Массивы	Есть 4 ряда мешков по 6 мешков в каждом ряду. Сколько сумок? Сумки расположены в 4 ряда и 6 столбцов. Сколько сумок?	24 мешка расположены рядами по 6 штук. Сколько рядов мешков? 24 мешка расположены в 6 колонках. Сколько рядов мешков?	24 мешка расположены равномерно в 4 ряда. Сколько мешков в каждом ряду? 24 мешка расположены равномерно в 4 ряда. Сколько столбцов мешков есть?

Важно отметить, что CCSS предлагает две строгости задач с массивами слов: те, в которых представлены элементы в строках, и те, которые дают задачи со словами в строках и столбцах. Благодаря постоянному воздействию и практике студенты понимают, что они взаимозаменяемы. Задачи со словами-массивами не очень распространены, но определенно являются тем типом задач, с которым учащиеся должны ознакомиться и попрактиковаться. Они также закладывают основу для работы учащихся с нашим следующим типом словесных задач: область 9.0003

Площадь как умножение и деление

Площадь является важным компонентом нашей работы по умножению и делению. Это основная часть обучения математике в 3-м классе, и важно, чтобы учащиеся работали со многими текстовыми задачами, где они должны распознавать область в контексте и решать. Это особенно важно, чтобы научиться различать площадь и периметр, устанавливая связи между массивами и тем, что известно об умножении и делении. Площадь должна быть представлена ​​массивами и связана с моделью площади. Этот конкретный наглядный пример помогает учащимся связать то, что они уже знают (массивы), со своим новым обучением (областью). Единичные квадраты написаны в стандартах, чтобы быть этим мостом. Модели площадей продолжаются по мере того, как вы работаете с более сложными прямолинейными фигурами, и помогают учащимся понять распределительное свойство умножения. CCSS не перечисляет проблемы области как отдельную строку, а включает их в массивы. Хотя это, безусловно, имеет смысл, поскольку массивы могут быть созданы внутри прямоугольника, и именно так следует вводить площадь, в большинстве задач со словами с площадями не используются строки или столбцы при задании длин сторон. Я думаю, что важно рассматривать задачи со словами отдельно от массивов.

		ДЛИНА СТОРОНЫ НЕИЗВЕСТНА	ДЛИНА СТОРОНЫ НЕИЗВЕСТНА
Зона	У прямоугольника одна сторона равна 6 футам, а другая — 4 футам. Чему равна площадь прямоугольника?	Прямоугольник имеет площадь 24 квадратных фута. Если одна сторона имеет длину 6 футов, какой длины должна быть перпендикулярная сторона?	Прямоугольник имеет площадь 24 квадратных фута. Если одна сторона имеет длину 6 футов, какой длины должна быть перпендикулярная сторона?

УМНОЖЕНИЕ

Решение проблем области снова соединяется с общим числом и известными/неизвестными значениями. Когда учащиеся пытаются определить общую площадь фигуры и им даны длины обеих сторон, учащиеся должны умножить, чтобы найти площадь.

ДЕЛЕНИЕ

Когда учащимся дается общая площадь фигуры , но им нужно найти недостающую длину стороны, они должны разделить.

В конечном счете, если учащиеся хорошо понимают задачи на умножение и деление и их связь с  всего , они, скорее всего, успешно справятся с задачами на площадь.

Задания на сравнение

На мой взгляд, самыми сложными задачами на умножение и деление являются задачи на сравнение. Подобно тому, как они связаны со сложением и вычитанием, структура этих задач делает их более сложными, чем другие. Для них важно рассмотреть каждый из различных типов проблем и переварить то, что дается. Я использую процедуру «3 чтения» при работе с текстовыми задачами, и эти задачи всегда вызывают наибольшее обсуждение, поскольку учащиеся борются с представленной информацией.

		СРАВНЕНИЕ НЕИЗВЕСТНО	ПОСТОЯННАЯ НЕИЗВЕСТНАЯ
Сравнить	Небольшой пакет яблок стоит 4 доллара. Ящик яблок стоит в 6 раз дороже. Сколько стоит коробка яблок?	Небольшой пакет яблок стоит 4 доллара. Ящик яблок стоит 24 доллара. Во сколько раз коробка дороже мешка с яблоками?	Ящик яблок стоит 24 доллара, что в 6 раз больше, чем стоимость маленького мешка яблок. Сколько стоит маленькая сумка?

Примеры умножения и деления на части (постоянная неизвестная) имеют очень похожие формулировки, поскольку они оба имеют оператор сравнения: «в 6 раз больше». Это описание отношений между двумя группами — общей и группой сравнения. Пример с кавычками (сравнение) формулируется по-другому, поскольку неизвестное представляет собой отношение сравнения: «Во сколько раз больше, чем больше»

Ключ к пониманию задач мультипликативного сравнения заключается в том, что сравнение представляет собой повторяющиеся группы, тогда как константа — это размер группы. .

В словесной задаче на умножение вам сообщается сумма в группе сравнения, 6, и константа, 4. Каждый мешок яблок стоит 4 доллара, поэтому, если это в 6 раз больше, это то же самое, что иметь 6 мешков. Таким образом, 4 x 6.

В делении ( долей) словесная задача вам дано общее число (стоимость ящика яблок). Как только вы разделите или разделите эту стоимость на 6 равных групп, вы сможете определить стоимость одной из этих групп, которая равна стоимости маленького мешка яблок, и это то же самое, что и количество утки.

В ( в кавычках) делении словесной задачи вам дана константа, стоимость маленького мешка, а также стоимость ящика яблок. Неизвестно, каковы отношения между ними. В этих текстовых задачах формулировка вопроса часто может сбить учащихся с толку.

Как только учащиеся смогут разложить задачу на слова, чтобы определить сумму и сравнение, они смогут связать это с тем, что они уже знают об умножении и делении, чтобы помочь им при решении. Ключевым моментом является обучение студентов внимательному чтению слова «проблема». Чтобы узнать больше о моей рутине 3 чтения, вы можете щелкнуть изображение ниже.

Ищете дополнительные ресурсы? Вы можете скачать мой справочный лист «Типы задач на умножение и деление» и использовать его, чтобы определить и написать различные типы задач на слова для занятий в классе.

Хотите попрактиковаться в задачах на умножение и деление? У меня есть набор БЕСПЛАТНЫХ карточек с задачами на умножение и деление слов. Каждый из типов задач на умножение и деление слов, обсуждаемых здесь, отрабатывается в наборе из 24 карточек с заданиями. Это отличная практика для более поздних лет, чтобы учащиеся имели достаточную практику с каждым типом. Это даже было бы отличным инструментом, чтобы помочь учащимся обсудить различные типы проблем и то, как они представлены. Чтобы загрузить карточки с задачами на умножение и деление слов, просто заполните форму ниже, и они будут отправлены прямо на вашу электронную почту.

>

Информационный бюллетень

Подпишитесь, чтобы получать бесплатные карточки с задачами на умножение и деление! После подтверждения электронной почты вы получите файл и будете подписаны на мою еженедельную рассылку.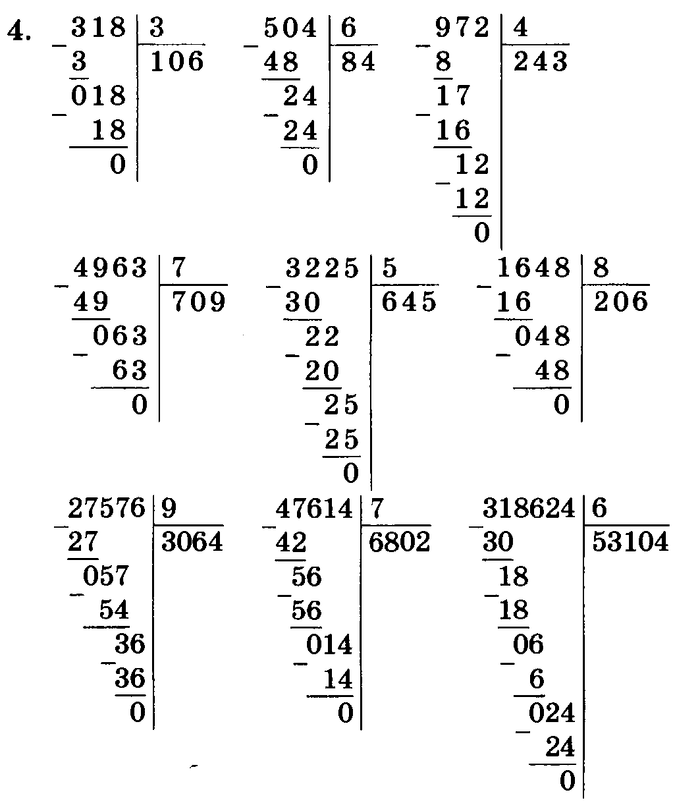

Загрузка…

 

Вам также могут быть полезны следующие ссылки.

Деление на части и цитаты из SFUSD

Ресурсы CGI из LAUSD

Задачи на умножение и деление из ND Counts

Два способа мышления о делении из Langford Math

Значение – Математика для учителей начальных классов

Дроби

Деление дробей — одна из самых сложных задач по математике в начальной школе. Вы уже привыкли к правилу: чтобы разделить на дробь, умножьте на обратную. («перевернуть и умножить»). Но спросите себя: почему это правило работает? Это действительно имеет смысл для вас? Можете ли вы объяснить, почему это имеет смысл для третьеклассника?

Мы собираемся перейти к правилу «перевернуть и умножить», но по пути мы найдем несколько более значимых способов понять деление дробей. Поэтому, пожалуйста, подыграйте: притворитесь, что вы еще не знаете правило «перевернуть и умножить», и решите задачи этой главы другими методами.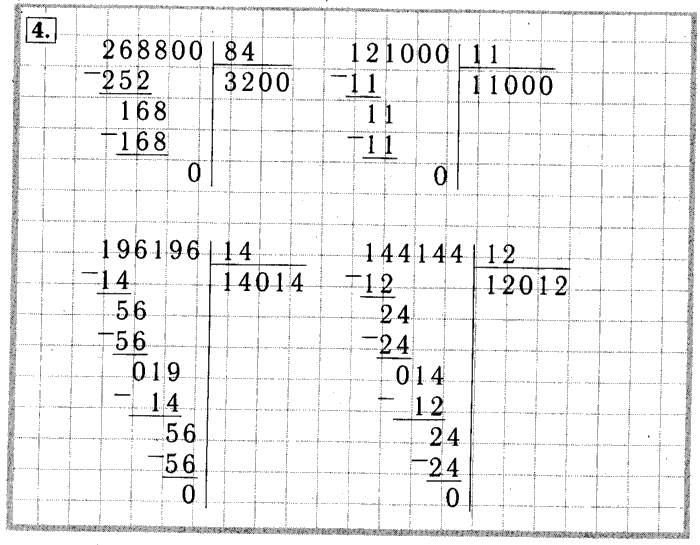

Запомните модель деления в кавычках: означает:

Сколько групп по 3 я могу найти в 18?

Мы начинаем с 18 точек (или шоколадных батончиков, или молекул) и делаем группы из 3 точек (или 3 любых других). Мы спрашиваем: сколько групп мы можем сделать?

18 точек, разделенных на группы по 3 точки. Так как групп 6, то 18 ÷ 3 = 6.

Та же идея применима, когда мы делим дроби. Например,  означает:

.

Сколько групп я могу найти в 6?

Пример: 6 ÷ 2/3

Давайте нарисуем 6 кругов и посмотрим, сколько групп мы можем найти:

Мы нашли девять одинаковых групп размера , поэтому мы заключаем, что

   

К сожалению, найти равные группы не всегда так просто. Например, задает вопрос:

Сколько групп я могу найти в ?

Пример: 3/4 ÷ 1/3

Давайте нарисуем круг и посмотрим, сколько групп мы можем найти:

На первом рисунке показан круг. На втором рисунке показаны две равные группы внутренней части , но осталось немного. Делаем вывод

   

Но сколько еще? Можем ли мы понять это точно?

Вот метод, который позволит вам выполнить вычисления точно. Мы будем использовать прямоугольные круги и разделим их на строки и столбцы на основе знаменателей делимых чисел.

Пример: 3/4 ÷ 1/3

Начните с рисования двух одинаковых прямоугольников, в каждом из которых 4 строки (от знаменателя и 3 столбца (от знаменателя).

Оттенок первого прямоугольника (это ровно три строки) и оттенок второго прямоугольника (так что это один столбец).0003

Теперь спросите: сколько копий  я могу найти в ? Ну, равно четырем меньшим квадратам. Итак, мы находим группы, равные этому:

На изображении мы можем найти:

• две группы из четырех квадратов (две группы ), и
• остался один квадрат из той группы, которую мы ищем.

Делаем вывод:

   

 

Подумай / Соедини / Поделись

Используйте любой метод, описанный выше, чтобы найти следующие частные. Помните, притворитесь, что вы не знаете никакого метода деления дробей, кроме нахождения групп одинакового размера.

   

   

Подумай / Соедини / Поделись

Решите каждую из следующих задач на деление дробей, используя метод «группы равного размера»:

   

   

Что вы заметили?

Это приводит к нашему первому методу деления дроби:

Метод общего знаменателя

Если две дроби имеют одинаковый знаменатель, то при их делении можно просто разделить числители. В символах

   

 

Подумай / Соедини / Поделись

• Используйте метод общего знаменателя, чтобы найти эти частные:

   

• Что делать, если дроби не имеют общего знаменателя? Является ли метод бесполезным, или вы можете найти способ заставить его работать? Можете ли вы решить эти проблемы?

   

Мы знаем, что всегда можем превратить задачу деления в задачу умножения с «недостающим множителем».