Вычисления с дробями • Образавр

Содержание

В $5$ классе вы уже начали проходить действия с дробями: сложение, вычитание, умножение и деление. В этом уроке вспомним и закрепим правила, по которым выполняют вычисления с дробями.

Сумма и разность

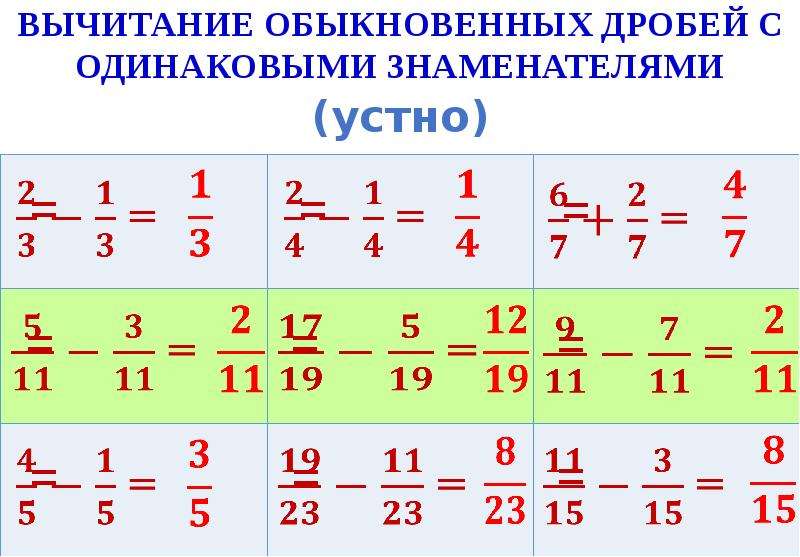
Чтобы найти сумму или разность дробей с одинаковыми знаменателями, нужно найти сумму или разность их числителей, а знаменатель оставить прежним.

То есть, сложение и вычитание всегда выполняется только с числителями, а не знаменателями. Например:

$$\frac{5}{20}+\frac{6}{20}=\frac{5+6}{20}=\frac{11}{20}$$

$$\frac{7}{12}-\frac{1}{12}=\frac{7-1}{12}=\frac{6}{12}$$

Подсказка

Вспомните предыдущий урок и основное свойство дроби.

Если в результате сложения или вычитания получается дробь, которую можно сократить, то её надо сократить, чтобы получить окончательный ответ:

$$\frac{6}{12}=\frac{6:6}{12:6}=\frac{1}{2}$$

Если знаменатели у дробей различаются, то к вычислениям добавляется ещё один шаг:

Чтобы найти сумму или разность дробей с разными знаменателями, нужно сначала привести эти дроби к общему знаменателю.

{(3}=\frac{5}{15}+\frac{6}{15}=\frac{5+6}{15}=\frac{11}{15}$$

Подсказка

У дробей «побольше», например, $\frac{9}{20}$ и $\frac{3}{16}$, может быть трудно сразу определить наименьший общий знаменатель. Конечно, всегда можно просто умножить первый знаменатель на второй, но тогда вычисления выйдут громоздкими.

Чтобы облегчить себе дальнейшие вычисления, лучше найти НОК — наименьшее общее кратное.

Как найти НОК?

Закрыть

1. Разложите на простые множители первое число

   $20=4\cdot5=2\cdot2\cdot5$

2. Разложите на простые множители второе число

   $16=4\cdot4=2\cdot2\cdot2\cdot2$

3. Запишите все множители вместе

   $НОК=2\cdot2\cdot5\cdot2\cdot2\cdot2\cdot2$

4. Вычеркните множители, одинаковые для первого и второго числа

   В нашем случае это две двойки — они встречаются и в первом, и во втором шаге.
   $НОК=\cancel{2}\cdot\cancel{2}\cdot5\cdot2\cdot2\cdot2\cdot2$
5. Найдите произведение

   $НОК=5\cdot2\cdot2\cdot2\cdot2=10\cdot8=80$

Общий знаменатель для дробей $\frac{9}{20}$ и $\frac{3}{16}$ равен $80$. {\space3}}{\cancel5}=\frac{2\cdot3}{1}=6$

Ответ: $6$.

Часто задаваемые вопросы

Как складывать дроби?

Чтобы сложить дроби, нужно привести их к общему знаменателю, а затем сложить числители.

Как вычитать дроби?

Чтобы из дроби вычесть дробь, нужно привести их к общему знаменателю, а затем выполнить вычитание с числителями.

Как умножать дроби?

Чтобы умножить дробь на дробь, нужно перемножить их числители и их знаменатели и первое произведение записать в числителе, а второе — в знаменателе.

Как делить дроби?

Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.

Алгебра 7-9 классы. 14. Решение типовых заданий по теме: «Дробные рациональные выражения»

Подробности

Категория: Алгебра 7-9 классы

 

Сумма и разность дробей

 

 

 Сложение и вычитание дробей с одинаковыми знаменателями

 


При сложении обыкновенных дробей с одинаковыми знаменателями складывают их числители, а знаменатель оставляют прежним.

Например:

Таким же образом складывают любые рациональные дроби с одинаковыми знаменателями:

где а, b и с — многочлены, причем с — ненулевой многочлен.

Это равенство выражает правило сложения рациональных дробей с одинаковыми знаменателями:

 

чтобы сложить рациональные дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тем же

 

Вычитание рациональных дробей выполняется аналогично сложению:

 

Чтобы выполнить вычитание рациональных дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тем же.

 

Пример 1. Сложим дроби

 

 

Пример 2. Вычтем дроби

 

 

Пример 3. Упростим выражение

Здесь удобно сложение и вычитание дробей выполнять не последовательно, а совместно:

 

 

 

Сложение и вычитание дробей с разными знаменателями


Сложение и вычитание рациональных дробей с разными знаменателями сводится к сложению и вычитанию рациональных дробей с одинаковыми знаменателями. Для этого данные дроби приводят к общему знаменателю.

Пример 1. Сложим дроби

Знаменатели дробей представляют собой одночлены. Наиболее простым общим знаменателем является одночлен . Коэффициент этого одночлена равен наименьшему общему кратному коэффициентов знаменателей дробей, а каждая переменная взята с наибольшим показателем, с которым она входит в знаменатели дробей. Дополнительные множители к числителям и знаменателям этих дробей соответственно равны .

Имеем

Пример 2. Преобразуем разность

Чтобы найти общий знаменатель, разложим знаменатель каждой дроби на множители:

Простейшим общим знаменателем служит выражение Дополнительные множители к числителям и знаменателям этих дробей соответственно равны b и а.

Имеем

Преобразование рационального выражения, которое является суммой или разностью целого выражения и дроби, сводится к преобразованию суммы или разности дробей.

Пример 3. Упростим выражение

Представим выражение а — 1 в виде дроби со знаменателем 1 и выполним вычитание дробей:

 

 

 

 

 

Произведение и частное дробей

 

 

 Умножение дробей. Возведение дроби в степень

При умножении обыкновенных дробей перемножают отдельно их числители и их знаменатели и первое произведение записывают в числителе, а второе — в знаменателе дроби. Например:

Таким же образом перемножают любые рациональные дроби:

где а, b, с и d — некоторые многочлены, причем b и d — ненулевые многочлены. Это равенство выражает правило умножения рациональных дробей:

 

чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе — знаменателем дроби.

Пример 1. Умножим дробь на дробь

Воспользуемся правилом умножения дробей:

 

Пример 2. Умножим дробь на дробь

Имеем

 

Пример 3. Представим произведение в виде рациональной дроби.

Имеем

 

Пример 4. Умножим дробь на многочлен

При умножении дроби на многочлен этот многочлен записывают в виде дроби и затем применяют правило умножения дробей:

Правило умножения дробей распространяется на произведение трех и более рациональных дробей. Например:

Выясним теперь, как выполняется возведение рациональной дроби в степень.

Рассмотрим выражение , являющейся  n-й степенью  рациональной дроби и докажем, что

По определению степени имеем

Применяя правило умножения рациональных дробей и определение степени, получим

Следовательно , 

Из доказанного тождества следует правило возведения рациональной дроби в степень:


чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй — в знаменателе дроби.

Пример 5. Возведем дробь в третью степень.

Воспользуемся правилом возведения в степень:

 

 

Деление дробей

 

При делении обыкновенных дробей первую дробь умножают на дробь, обратную второй. Например:

Так же поступают при делении любых рациональных дробей:

где а, b, с и d — некоторые многочлены, причем b, c и d — ненулевые многочлены.

Это равенство выражает правило деления рациональных :

 

чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.

 

Пример 1. Разделим дробь на дробь .

Воспользуемся правилом деления дробей:

 

Пример 2. Разделим дробь на дробь

Имеем

 

Пример 3. Разделим дробь на многочлен a + 3.

При делении дроби на многочлен этот многочлен записывают в виде дроби и затем применяют правило деления дробей:

 

 

 

Преобразование рациональных выражений

 

 

 

 Рациональное выражение представляет собой частное от деления суммы рациональных дробей многочлен. Деление на  можно заменить умножением на дробь Поэтому преобразование данного выражения сводится к сложению дробей и умножению результата на дробь  Вообще преобразование любого рационального выражения можно свести к сложению, вычитанию, умножению или делению рациональных дробей.

Из правил действий с дробями следует, что сумму, разнос произведение и частное рациональных дробей всегда можно предс вить в виде рациональной дроби. Значит, и всякое рациональное выражение можно представить в виде рациональной дроби.

Пример 1. Преобразуем в рациональную дробь выражение

Сначала выполним умножение дробей, затем полученный результат вычтем из многочлена x + 1:

 

 

Запись можно вести иначе:

 

 

 

Пример 2. Представим выражение

в виде рациональной дроби.

Сначала сложим дроби, заключенные в скобки, затем найденный результат умножим на дробь и, наконец, к полученному произведению прибавим 1:

 

Сравнение дробей с одинаковыми знаменателями | Математика 3-го класса

      Для дробей с одинаковыми знаменателями , дробь с большим числителем равна больше !

Поскольку 5 > 3, вы знаете, что 5/8 больше, чем 3/8.

Это было очень быстро! 🚀

Пример 2

Какая дробь самая большая: 4/6, 3/6 или 5/6?

Эти дроби имеют одинаковые знаменатели.

Итак, все, что нам нужно сделать, это сравнить с числителями .

👉 4 больше 3.

Это означает, что 4/6 больше 3/6.

👉 5 больше 4.

Значит 5/6 больше 4/6.

Это означает, что 5 / 6 является самым большим из .

Давайте проверим, правы ли мы. 😁

По барным моделям видно, что да, 5/6 самый большой.

Последний пример

Джун пошла в хозяйственный магазин, чтобы купить синюю веревку и зеленую веревку. Длина синей веревки 6 / 8 из ярдов . Длина зеленой веревки 7 / 8 из ярдов . Какая веревка была на длиннее ?

Нам нужно найти, какая веревка на длиннее. 😀

Как? 🤔

Нам нужно сравнить длины канатов 2 . 😎

6/8 и 7/8 имеют одинаковые знаменатели.

Итак, мы просто сравниваем с числителями . 😁

Поскольку 7 больше 6, значит, 7/8 на больше , чем 6/8.

Итак, зеленая веревка длиннее синей веревки! 😁

Теперь завершите практику. 😺 Вы узнаете больше и будете помнить дольше.

Вычитание дробей с общим знаменателем

Результаты обучения

• Используйте круги дробей, чтобы найти разницу между двумя дробями с одинаковыми знаменателями
• Вычитание дробей с одинаковыми знаменателями без дробных кругов
• Вычитание дробей с одинаковыми знаменателями, которые содержат переменные

Модель Вычитание дробей

Вычитание двух дробей с общими знаменателями очень похоже на сложение дробей. Представьте себе пиццу, нарезанную на [латекс]12[/латекс] кусочков. Предположим, что за ужином съедено пять штук. Это означает, что после обеда в коробке осталось семь кусков (или [латекс]{\большой\фрак{7}{12}}[/латекс] пиццы). Если Леонардо съест [латекс]2[/латекс] из этих оставшихся кусков (или [латекс]{\большой\фрак{2}{12}}[/латекс] пиццы), сколько останется? Осталось [латекс]5[/латекс] кусочков (или [латекс]{\большой\фрак{5}{12}}[/латекс] пиццы).

[латекс] {\ Большой \ гидроразрыва {7} {12}} — {\ Большой \ гидроразрыва {2} {12}} = {\ Большой \ гидроразрыва {5} {12}} [/латекс]

Давайте используйте дробные круги для моделирования того же примера, [латекс] {\ большой \ гидроразрыв {7} {12}} — {\ большой \ гидроразрыва {2} {12}} [/латекс].

Начните с семи [латексных] {\ больших \ гидроразрывов {1} {12}} [/ латексных]. Уберите два куска [латекс]{\Large\frac{1}{12}}[/latex]. Сколько двенадцатых осталось?


Опять же, у нас есть пять двенадцатых, [латекс] {\ большой \ гидроразрыв {5} {12}} [/латекс].

Пример

Используйте дробные круги, чтобы найти разницу: [латекс] {\ большой \ гидроразрыв {4} {5}} — {\ большой \ гидроразрыва {1} {5}} [/латекс]

Решение:
Начните с четырех [латексных] {\ больших \ гидроразрывов {1} {5}} [/латексных] частей. Уберите один кусок [латекса]{\Large\frac{1}{5}}[/latex]. Посчитайте, сколько пятых осталось. Осталось три куска [латекс]{\большой\фрак{1}{5}}[/латекс].

Попробуйте

Вычитание дробей с общим знаменателем

Мы вычитаем дроби с общим знаменателем почти так же, как складываем дроби с общим знаменателем.

Вычитание дроби

Если [latex]a,b,\text{ и }c[/latex] — числа, где [latex]c\ne 0[/latex], то

[latex]{\Large\frac{a}{ c}}-{\Large\frac{b}{c}}={\Large\frac{a-b}{c}}[/latex]

Чтобы вычесть дроби с общим знаменателем, мы вычитаем числители и помещаем разность над общим знаменателем.