Запишите распределительный закон для целых чисел а, b, c, сформулируйте его.

Все вопросы /Математика / класс

0 /10000

Ответы2

Распределительный закон умножения относительно сложения

Рассмотрим распределительный закон умножения относительно сложения.

• Для любых целых чисел а, b, c справедливо равенство (a + b) · с= a · с + b · с.
• Чтение равенства (a + b) · с= a · с + b · с: произведение суммы чисел а и b на число с равно сумме произведений а на с и b на с.
• Рабочая формулировка: для того, чтобы умножить сумму на число, достаточно, каждое слагаемое умножить на число и полученные результаты сложить.

В школе изучаются: свойство умножения суммы на число и свойство умножения числа на сумму.

Свойство умножения суммы на число.

Умножить сумму на число можно разными способами:

• 1 способ: (4+3) ∙ 2 = 7 ∙ 2 = 14; можно вычислить сумму и полученный результат умножить  на число;
• 2 способ: (4+3) ∙ 2 = 4 ∙ 2 + 3 ∙ 2 = 8 + 6 = 14; можно каждое слагаемое умножить на число и полученные результаты сложить.

Свойство умножения числа на сумму.

Умножить число на сумму можно разными способами:

• 1 способ. 16∙(2+3)=16∙5=80; вычислить сумму и число умножить на полученный результат;
• 2 способ. 16∙(2+3)=16∙2+16∙3=80; умножить число на каждое слагаемое и полученные произведения сложить.

Распределительный закон умножения относительно вычитания

Рассмотрим распределительный закон умножения относительно вычитания.

• Для любых целых чисел а, b, c справедливо равенство (a — b) · с= a · с — b · с.
• Чтение равенства (a — b) · с= a · с — b · с: произведение разности чисел а и b на число с равно разноси произведений а на с и b на с.
• Рабочая формулировка: для того, чтобы умножить разность на число, достаточно, уменьшаемое умножить на число, вычитаемое умножить на число и найти разность полученных результатов.
• Хотя этот закон можно рассматривать и как распределительный закон умножения относительно сложения (a + (- b)) · с= a · с + (- b) · с = a · с — b · с.

• Умножение разности на число: 99 · 3 = (100 — 1) ·3 = 100 · 3 — 1 · 3 = 300 – 3 = 297; 

• умножение числа на разность 247 · 98 = 247 · (100 — 2) = 247 · 100 — 247 · 2 = 24 700 — 494 = 24 206.

Существует распределительный закон относительно сложения и вычитания.

Сформулируем распределительный закон относительно сложения  для целых чисел а, b, c:

чтобы сумму чисел а и b умножить на число с, можно умножить на  число с каждое слагаемое, то есть числа а и b и сложить полученные произведения ((а + b) * с = а * с + b * с).

Сформулируем распределительный закон относительно вычитания  для целых чисел а, b, c:

чтобы разность чисел а и b умножить на число с, можно умножить на  число с уменьшаемое и вычитаемое отдельно и из первого произведения вычесть второе ((а — b) * с = а * с — b * с).

Большая энциклопедия школьника

Большая энциклопедия школьникауникальное издание, содержащее весь свод знаний, необходимый ученикам младших классов. Для детей, собирающихся в 1-й класс, она послужит незаменимым помощником для подготовки к школе. В этой энциклопедии ребенок сможет найти любую интересующую его информацию, в понятном и простом для него изложении. Вы подбираете слова и определения для простых вещей, которые надо объяснить ребенку? Сомневаетесь в формулировках? Просто возьмите «Большую энциклопедию школьника» и найдите нужный ответ вместе с малышом!

Математика в стихах
Развитие речи
Азбука в картинках
Игры на развитие внимания
Как правильно выбрать школу
Ваш ребенок левша
Как готовить домашнее задание
Контрольные и экзамены

Большая энциклопедия школьника

— это твой надёжный путеводитель в мире знаний. Она проведёт сквозь извилистые лабиринты наук и раскроет завесу великих тайн Вселенной. С ней ты поднимешься высоко к звёздам и опустишься на дно самых глубоких морей, ты научишься видеть мельчайшие организмы и осязать огромные пространства Земли. Отправившись в это увлекательное путешествие, ты значительно расширишь свой кругозор и поднимешься на новую ступень развития. Отныне никакие вопросы учителей не смогут поставить тебя в тупик, ты сможешь найти выход из любой ситуации. Мир знаний зовёт тебя. В добрый путь!

Ребенок не хочет учить буквы Ребенок не хочет учить буквы — Понимаете, ведь надо что-то делать! — с тревогой говорила мне полная, хорошо одетая дама, едва умещающаяся на стуле. Ее ноги в аккуратных лодочках были плотно сжаты (юбка до середины колена казалась слегка коротковатой для такой монументальной фигуры), руки сложены на коленях. — Ей же на тот год в школу, все ее сверстники уже читают, а она даже буквы …

Past continuous passive Страдательный залог образуется с помощью вспомогательного глагола ‘to be’. Страдательный залог глагола ‘to repair’ в группе ‘continuous’ : To be repaired = Быть исправленным. The road is being repaired = Дорогу чинят. The road is not being repaired = Дорогу не чинят. Is the road being repaired? = Чинят ли дорогу? The road was being repaired = Дорогу чинили. The road was not being repaired = Дорогу не чинили. Was the road being repaired? = Чинили ли дорогу? Страдательный …

Определение формулы органического вещества по его молярной массе Задание: Определить формулу углеводорода, если его молярная масса равна 78 г. № п/п Последовательность действий Выполнение действий 1. Записать общую формулу углеводорода. Общая формула углеводорода СхНу 2. Найти молярную массу углеводорода в общем виде. М(СхНу)=12х +у 3. Приравнять найденное в общем виде значение молярной массы к данному в …

У У ЗВУК (У). 1) Удобная буква! Удобно в ней то, Что можно на букву Повесить пальто. У – сучок, В любом лесу Ты увидишь букву У. 2) ФОНЕТИЧЕСКАЯ ЗАРЯДКА. — Как воет волк! ( у – у – у ) 3) ЗАДАНИЯ. а) Подними руку, если услышишь звук (у): паук, цветок, лужа, диван, стол, стул, голуби, курица. б) Где стоит (у)? Зубы, утка, наука, кенгуру …

законов и теорем булевой алгебры

законов и теорем булевой алгебры

1а.	Х • 0 = 0		1б.	Х + 1 = 1		Закон об аннулировании
2а.	Х • 1 = Х		2б.	Х + 0 = Х		Закон о личности
3а.	Х • Х = Х		3б.	Х + Х = Х		Закон идемпотента
4а.	Х • Х = 0		4б.	Х + Х = 1		Закон о дополнении
5.	Х = Х					Закон двойного отрицания
6а.	Х • У = У • Х		6б.	Х + У = У + Х		Коммунативное право
7а.	X (Y Z) = (X Y) Z = (X Z) Y = X Y Z					Ассоциативный закон
7б.	X + (Y + Z) = (X + Y) + Z = (X + Z) + Y = X + Y + Z					Ассоциативный закон
8а.	Х • (Г + Z) = Х У + Х Z		8б.	Х + Y Z = (Х + Y) • (Х + Z)		Распределительный закон
9а.	Х • У = Х + У		9б.	Х + У = Х • У		Теорема де Моргана
10а.	Х • (Х + У) = Х		10б.	Х + Х У = Х		Закон о поглощении
11а.	(X + Y) • (X + Y) = X		11б.	Х У + Х У = Х		Закон об увольнении
12а.	(X + Y) • Y = XY		12б.	Х У + У = Х + У		Закон об увольнении
13а.	(X + Y) • (X + Z) • (Y + Z) = (X + Y) • (X + Z)					Закон о консенсусе
13б.	ХУ + Х Z + Y Z = Х У + Х Z					Закон о консенсусе
14а.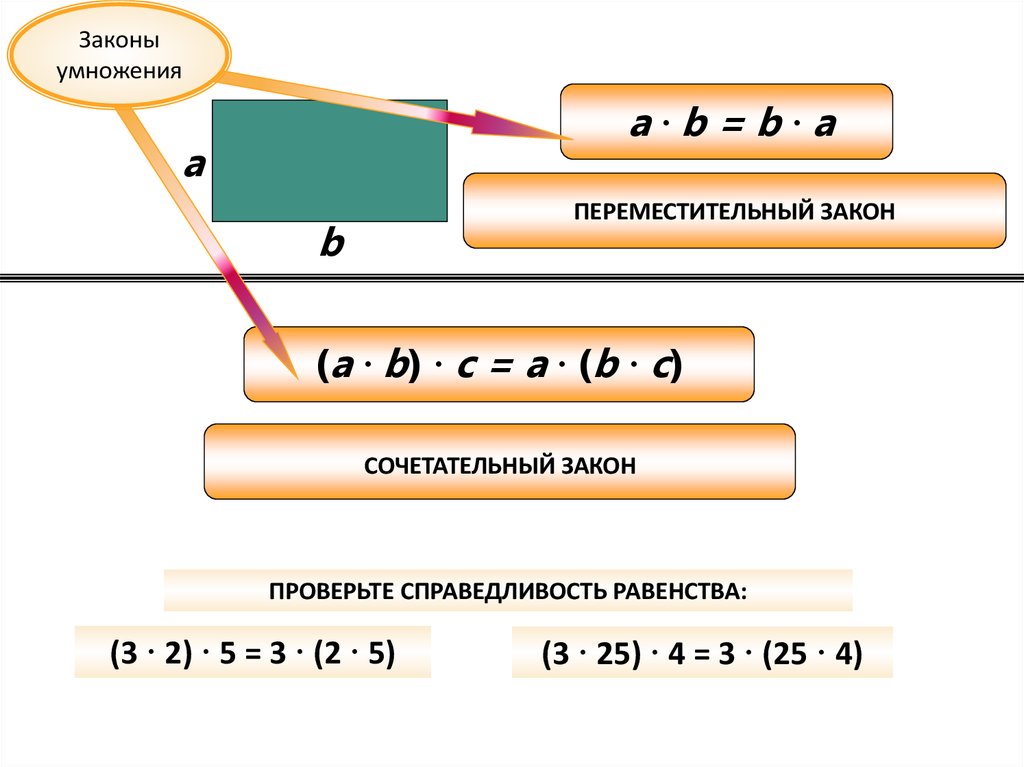	Х ⊕ Y = (Х + Y) • (Х + Y)		14б.	X ⊕ Y = X Y + X Y		Ворота исключающего ИЛИ
15а.	X ⊙ Y = (X + Y) • (X • Y)		15б.	Х ⊙ У = Х У + Х У		Ворота XNOR
15в.	X ⊙ Y = (X + Y) • (X + Y)					Ворота XNOR

ДеМоргана

	Стандартный
НАНД	Х = А • В	Х = А + В
И	Х = А • В	Х = А + В
НО	Х = А + В	Х = А • В
ИЛИ	Х = А + В	Х = А • В

Распределительная собственность — ChiliMath

Поиск

Дистрибутивное свойство умножения над сложением позволяет нам исключить символ группировки, обычно в виде скобки. Следующая диаграмма иллюстрирует основной шаблон или формулу, как ее применять.

---

Несколько примечаний:

• Это делается путем умножения внешнего члена на каждый член в скобках.

• Итак, возьмем терм a, стоящий вне скобок, и распределим его по каждому терму внутри скобок.

• Обратите внимание, что ab означает a, умноженное на b.

• Аналогично, ac означает a, умноженное на c.

---

Объединение похожих терминов с использованием распространяемого свойства

Пример 1: Распределить, а затем упростить приведенное ниже выражение.

Можно ли сразу совместить x-термины? Не так быстро! Термин 2x находится внутри скобок, а 3x снаружи. Мы не можем их объединить, потому что они находятся в разных местах.

Что нам нужно сделать, так это сначала исключить символ скобки, прежде чем мы сможем комбинировать одинаковые термины, которые возникнут при добавлении или вычитании. Вот где полезность этого свойства вступает в игру.

На этом этапе скобки больше нет, и все x-термины можно комбинировать. Я бы переставил их, разместив похожие термины рядом, прежде чем выполнять требуемую операцию.

---

Пример 2: Распределите, затем упростите приведенное ниже выражение.

Так как здесь две круглые скобки, мы должны применить это свойство дважды. Это должно избавиться от группирующих символов и позволить нам комбинировать похожие термины.

После удаления двух скобок теперь можно комбинировать одинаковые термины. Перед выполнением необходимой операции сложения или вычитания обязательно переставьте термины таким образом, чтобы похожие термины располагались рядом.

---

Пример 3: Распределите, затем упростите приведенное ниже выражение.

Я надеюсь, что теперь вы видите схему. Имея три круглых скобки, мы также должны применить их три раза.

Поскольку все термины теперь не в скобках, продолжайте комбинировать похожие термины.

---

Пример 4: Распределите, затем упростите приведенное ниже выражение.

Решение:

---

Пример 5: Распределите, затем упростите приведенное ниже выражение.

Решение:

---

Пример 6: Распределите, затем упростите приведенное ниже выражение.

Решение:

Сначала примените распределительное свойство к внутренним скобкам и объедините одинаковые термины. Наконец, избавьтесь от символа квадратной скобки, раздав еще раз.

---

Вы также можете использовать Распределительное свойство при решении уравнений .

Решение линейных уравнений с использованием распределительного свойства

Пример 7: Решите приведенное ниже линейное уравнение, используя Распределительное свойство.

Как видите, внешнее число 3, расположенное непосредственно слева от круглой скобки, предполагает, что мы можем применить это свойство для устранения символа группировки.

• Возьмите это число 3 и умножьте на каждый член в скобках.

• После этого символ скобки должен исчезнуть. Затем мы можем приступить к обычным шагам решения уравнения. В этом примере мы изолируем переменную «x» слева от уравнения. После распределения вычтите обе части на 3, а затем разделите -\,6 на обе стороны уравнения, чтобы получить окончательный ответ.

---

Пример 8: Решите приведенное ниже линейное уравнение, используя Распределительное свойство.

Наличие двух скобок в левой части уравнения означает, что мы должны распределять дважды.

Избавившись от группирующих символов, теперь мы можем комбинировать одинаковые термины и изолировать переменную в левой части уравнения.

---

Пример 9: Используйте Распределительное свойство для решения уравнения.

Решение:

Начните с распределения 4 в первой скобке, а затем распределения — 1 во второй скобке.