Открытый урок математики в 6-м классе «Применение распределительного свойства умножения»
- Агаева Галимат Гусеновна
Разделы: Математика, Конкурс «Презентация к уроку»
Класс: 6
Ключевые слова: распределительное свойство умножения
Презентация к уроку
Загрузить презентацию (463 кБ)
Тип урока: закрепление и совершенствование знаний.
Формы работы:
- Фронтальная устная работа
- Работа на доске и в тетрадях
- Работа в парах
- Самостоятельная работа.
Методы работы:
- словесный
- наглядный
- игровые
Технологии:
- рефлексивные
- здоровье сберегающие
- информационные.

Цели урока: научиться применять данные свойства относительно действий с обыкновенными дробями, смешанными числами, научится упрощать выражения и составлять выражения для решения задач.
Учебные задачи:
- Проверка знаний, умений и навыков учащихся по теме;
- Закрепление изученного — повторение теоретического материала, применение его на практике при решении поставленных задач;
- Контроль за уровнем усвоения материала;
- Отработка умений и навыков самостоятельной работы;
- Развитие творческих способностей учащихся.
Воспитательные задачи:
- Интерес к предмету и воспитание потребности и умений учиться математике;
- Содействовать профилактике утомляемости использованием специальных приёмов для поддержания работоспособности;
- Воспитание у учащихся ответственного отношения к учению;
Практические задачи:
- Умение применять полученные знания для решения простейших задач жизненной практики;
- Умение работать коллективно;
- Вызвать интерес к изучению темы посредством создания игровых проблемных ситуаций.

План урока:
- Организационный момент.
- Проверка домашнего задания.
- Устная разминка и теоретический опрос
- Практическая работа «Математические прятки»
- Физкультминутка.
- Работа по теме урока.
- Дифференцированная самостоятельная работа.
- Итог урока, оценки, домашнее задание.
Ход урока
1. Организационный моментПроверка наличия всего необходимого для урока.
Постановка цели урока — научится применять распределительного свойства умножения относительно действий с обыкновенными дробями, смешанными числами, научится упрощать выражения и составлять выражения для решения задач.
2. Проверка домашнего задания Самопроверка по готовым ответам и выставление оценки. (Ответы и критерии учащиеся видят на экране компьютера).
№ 529
Ответ: 200 га.
№ 568(а, в)
А) 7 2/3; в) 63.
№ 522
17,6, 4,6.
Критерии оценок:
- 5 заданий — «5»
- 4 заданий — «4»
- 3 заданий — «3»
- Менее 3 заданий — «2»
Учитель: Соотнесите свои ответы домашней работы с буквами, (в порядке убывания) и вы получите математический термин, о котором мы будем говорить на уроке.
200 | 63 | 17,6 | 7+ 2/3 | 4,6 |
Д | Р | О | Б | Ь |
Ответ: Дробь.
Учитель: Эпиграф нашего урока «Без знания дробей никто не может признаться знающим арифметику…»
В древности и в Средние века учение о дробях считалось хотя и самым трудным, но и самым важным разделом арифметики. Римский оратор Цицерон, живший в 1 веке до нашей эры, сказал: «Без знания дробей никто не может признаться знающим арифметику.»
На сегодняшнем уроке мы с Вами попытаемся заслужить признания нас- знающими арифметику. Для этого вам надо быть настойчивыми и внимательными.
Задача сегодняшнего урока рассказать и изучить действия и свойства дробей.
3. Устная разминка. Теоретический опросУстно решить на доске / на экране компьютера/
4. Работа по карточкам. Теоретический опрос (работа в парах) — «Математические прятки»Ответы: Математические прятки.
1. Деление числителя и знаменателя на их общий делитель, отличный от единицы, называется сокращением дроби. Деление числителя и знаменателя на их общий делитель, отличный от единицы, называется сокращением дроби.Пример: |
2. Чтобы сложить (вычесть) дроби с разными знаменателями, надо: Пример: |
3. Число, содержащее целую и дробную части, называют смешанным. Пример: |
4. Чтобы перевести обыкновенную дробь в десятичную надо: числитель дроби разделить на знаменатель дроби. Пример: |
5. Чтобы умножить дробь на дробь, надо: Пример: |
6. Пример: |
7. Чтобы найти несколько процентов от числа, нужно проценты перевести в обыкновенную или десятичную дробь и умножить число на эту дробь. Пример: |
| 8. Распределительное свойство умножения Чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе. Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения. |
Учитель: С этим свойством мы уже знакомы:
Умножим 26 • 4 = 104
Как мы это делаем:
(20 + 6) • 4 = 20 • 4 + 6 • 4 = 104
49 • 3 = 147
(50 — 1) • 3 = 150 — 3 = 147
Что же даёт нам применение распределительного свойства:
УПРОЩАТЬ ВЫЧИСЛЕНИЯ.
Давайте запишем формулировку данного свойства:
- относительно суммы: (a+b)c=ac+bc
- относительно вычитания: (a-b)c=ac-bc, где a>b
Работа по теме урока на экране компьютера:
Учитель:
Тренировочные упражнения
1. Решить № 540 (а). Решение объясняет учитель.
Решение.
7. Дифференцированная самостоятельная работаДифференцированный контроль знаний. Предлагается два уровня сложности. Ученик сам выбирает уровень по силам.
Критерии оценок:
- 4 заданий — «5»
- 3 заданий — «4»
- 2 задания — «3»
- 1 задание — «2»
Ответы:
1 вариант | 2 вариант |
Уровень А | Уровень А |
1. | 1. А) 13; Б)10,5; в) 4; |
Уровень Б | Уровень Б |
2. 5/28 | 2. ответ: х=1/3 |
Домашнее задание: № 544, № 545, № 546.
8. Оценки. ИтогЗаполните лист ответив на 8 вопрос.
Какое, свойство мы научились применять относительно действий, с обыкновенными дробями, смешанными числами?
Сегодня на уроке мы хорошо поработали. Закончить урок, мне хочется словами Аристотеля «Ум заключается не только в знаниях, но и в умении применять знания на деле».
Я надеюсь, мы с вами сможем на уроках не только получать знания, но и уметь применять их.
Что мы вспомнили и повторили?
Спасибо всем за урок. Урок окончен.
Урок окончен.
Онлайн урок: Применение распределительного свойства умножения по предмету Математика 6 класс
В этом уроке мы узнаем, как умножать смешанное число на натуральное, и разберем, как использовать распределительное свойство умножения для рационализации вычислений с обыкновенными дробями и смешанными числами.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Это свойство говорит нам о том, что если необходимо умножить одно число, назовем его a, на сумму двух других чисел, обозначим их b и c, то ответом будет сумма двух произведений: произведения a и b и произведения a и c
Напомним, коммутативное свойство — это научный термин для обычного правила, которое гласит, что перемена мест слагаемых (или множителей) не влияет на результат.
Вторая строка говорит о том же самом, что и первая; просто показывает, что коммутативное свойство умножения работает и в этом случае.
В уроке «Умножение дробей» мы уже касались этих моментов. Теперь рассмотрим их более подробно.
Самый простой способ умножения смешанного числа на натуральное заключается в том, чтобы перевести смешанное число в неправильную дробь, домножив целую часть на знаменатель и прибавив его к числителю, а далее домножить полученную неправильную дробь на натуральное число, перемножив числитель дроби и натуральное число.
Это и будет результатом.
Пример:
\(\mathbf{43\frac{1}{3}\cdot2=\frac{43\cdot3+1}{3}\cdot2=\frac{129+1}{3}\cdot2=\frac{130}{3}\cdot2=\frac{130\cdot2}{3}=\frac{260}{3}=86\frac{2}{3}}\)
Этот пример нам показывает, что даже такая простая операция, как умножение на 2, приводит нас к множеству умножений, сложений и даже делению. Для больших чисел такой путь неудобен. Стоит только представить, что целая часть смешанного числа будет больше 100, и знаменатель также также весьма сложный, то мы получим операции, которые с трудом делаются в уме.
Здесь нас выручит распределительное свойство.
Если представить \(\mathbf{43\frac{1}{3}}\) как сумму его целой и дробной частей, то есть
\(\mathbf{43\frac{1}{3}=43+\frac{1}{3}}\), то нам нужно будет в дальнейшем умножать только 43 и \(\mathbf{\frac{1}{3}}\), что значительно проще.
Посмотрим, как это все будет выглядеть целиком:
\(\mathbf{43\frac{1}{3}\cdot2=(43+\frac{1}{3})\cdot2=(43\cdot2)+(\frac{1}{3}\cdot2)=86+\frac{2}{3}=86\frac{2}{3}}\)
Можно заметить, что несмотря на то, что мы удлинили запись выражения, сами вычисления стали проще.
Может возникнуть необходимость выделения целой части, про это забывать нельзя. Но даже в таком случае делимое будет значительно меньше, чем если бы мы выносили целую часть из произведения, полученного классическим способом.
Пример:
\(\mathbf{25\frac{2}{5}\cdot3=(25+\frac{2}{5})\cdot3=(25\cdot3)+(\frac{2}{5}\cdot3)=75+\frac{6}{5}=75+1\frac{1}{5}=76\frac{1}{5}}\)
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Все те же свойства умножения выполняются не только по отношению к смешанному числу и натуральному, но и по отношению к смешанному числу и дроби (как и к любым другим числам).
Если необходимо умножить смешанное число на дробь, то можно разложить его как сумму и умножать на дробь отдельные слагаемые, а потом сложить результат.
Для понимания того, насколько это упрощает вычисления, снова разберем один и тот же пример двумя способами: «в лоб», то есть приводя смешанное число к дроби, и используя распределительное свойство.
Посчитаем выражение \(\mathbf{45\frac{2}{5}\cdot\frac{1}{3}}\)
I Первый способ (преобразовывая смешанное число в дробь):
\(\mathbf{45\frac{2}{5}\cdot\frac{1}{3}=\frac{45\cdot5+2}{5}\cdot\frac{1}{3}=\frac{227}{5}\cdot\frac{1}{3}=\frac{227\cdot1}{5\cdot3}=\frac{227}{15}=15\frac{2}{15}}\)
II Второй способ (используя распределительное свойство умножения):
\(\mathbf{45\frac{2}{5}\cdot\frac{1}{3}=(45+\frac{2}{5})\cdot\frac{1}{3}=(45\cdot\frac{1}{3})+(\frac{2}{5}\cdot\frac{1}{3})=\frac{45}{3}+\frac{2\cdot1}{5\cdot3}=15+\frac{2}{15}=15\frac{2}{15}}\)
Можем заметить, что при подсчете вторым способом самым крупным числом было 45, которое уже находилось в условии, в то же время при подсчете первым способом появилось число 227, которое больше, и в уме с ним работать уже менее комфортно.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Интересен тот факт, что ничего нам не запрещает применять распределительное свойство дважды.
Посмотрим на изображение выше.
На ней мы хотим перемножить две суммы.
Будем смотреть на первую скобку как на цельное выражение и обозначим его буквой А заглавной.
В этом случае надо, как и раньше, умножить A на c и прибавить к этому результат умножения A на d
Далее вспомним, что А — это тоже сумма, и применим распределительное свойство к выражениям \(\mathbf{(a+b)\cdot c}\) и \(\mathbf{(a+b)\cdot d}\)
Тогда получим именно то, что и получилось в конце: сумма четырех произведений.
В дальнейшем вы привыкните делать такие вещи в уме, беря по слагаемому из каждой скобки, и сможете обойтись без промежуточного вычисления.
Но пока что оно добавляет наглядности и объясняет, почему все происходит именно так.
Прежде чем перейти к смешанным числам посмотрим на пример с натуральными числами.
Пример:
\(\mathbf{(40+5)(20+3)=(40+5)\cdot20+(40+5)\cdot3=}\)
\(\mathbf{=40\cdot20+5\cdot20+40\cdot3+5\cdot3=800+100+120+15=1035}\)
Опять же, выражение стало более длинным, но согласитесь, все умножения, которые в итоге пришлось сделать, были проще, чем перемножение 45-ти и 23-х.
Теперь применим этот мощный инструмент к перемножению смешанных чисел.
Как вы могли догадаться, мы снова будем представлять смешанное число как сумму натурального числа и обыкновенной дроби. Таким образом, произведение двух смешанных чисел будет равно произведению сумм натурального числа и обыкновенной дроби каждого из этих чисел.
Сразу перейдем к примерам, ибо в них вся наглядность.
Пример:
\(\mathbf{12\frac{2}{3}\cdot9\frac{1}{5}=(12+\frac{2}{3})\cdot(9+\frac{1}{5})=(12+\frac{2}{3})\cdot9+(12+\frac{2}{3})\cdot\frac{1}{5}=}\)
\(\mathbf{=12\cdot9+\frac{2}{3}\cdot9+12\cdot\frac{1}{5}+\frac{2}{3}\cdot\frac{1}{5}=}\)
\(\mathbf{=108+\frac{18}{3}+\frac{12}{5}+\frac{2}{15}=108+\frac{90}{15}+\frac{36}{15}+\frac{2}{15}=}\)
\(\mathbf{=108+\frac{90+36+2}{15}=108+\frac{128}{15}=108+8\frac{8}{15}=116\frac{8}{15}}\)
И для сравнения классическим способом:
\(\mathbf{12\frac{2}{3}\cdot9\frac{1}{5}=\frac{12\cdot3+2}{3}\cdot\frac{9\cdot5+1}{5}=\frac{38}{3}\cdot\frac{46}{5}=\frac{38\cdot46}{3\cdot5}=\frac{1748}{15}=116\frac{8}{15}}\)
Видно, что в одном способе больше действий, а в другом сложнее вычисления. Смотрите что для вас проще и понятнее, и выбирайте соответствующий способ.
Смотрите что для вас проще и понятнее, и выбирайте соответствующий способ.
Пример:
\(\mathbf{20\frac{1}{4}\cdot5\frac{3}{5}=(20+\frac{1}{4})\cdot(5+\frac{3}{5})=(20+\frac{1}{4})\cdot5+(20+\frac{1}{4})\cdot\frac{3}{5}=}\)
\(\mathbf{=20\cdot5+\frac{1}{4}\cdot5+20\cdot\frac{3}{5}+\frac{1}{4}\cdot\frac{3}{5}=}\)
\(\mathbf{=100+\frac{5}{4}+\frac{60}{5}+\frac{3}{20}=100+\frac{25}{20}+12+\frac{3}{20}=}\)
\(\mathbf{=112+\frac{25+3}{20}=112+\frac{28}{20}=112+\frac{7}{5}=112+1\frac{2}{5}=113\frac{2}{5}}\)
И снова сравним с классическим способом:
\(\mathbf{20\frac{1}{4}\cdot5\frac{3}{5}=\frac{20\cdot4+1}{4}\cdot\frac{5\cdot5+3}{5}=\frac{81}{4}\cdot{28}{5}=\frac{81\cdot28}{4\cdot5}=\frac{81\cdot7}{5}=\frac{567}{5}=113\frac{2}{5}}\)
Итог точно такой же: с распределительным свойством больше вычислений, меньше сложность каждого конкретного вычисления, а при классическом способе наоборот.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Современный человек может не понять, зачем нужно распределительное свойство, ведь под рукой есть калькулятор, которому на первый взгляд безразлично, насколько большие числа в нем вычислять. Поэтому расскажу немного о том, как представлены числа в компьютерах и почему иногда важно уменьшить обрабатываемые числа.
Целые числа в компьютере представлены в двоичной системе счисления.
Она на самом деле весьма похожа на десятичную, только в ней всего лишь две цифры: 0 и 1
| Таблица соотвествия десятеричного и двоичного представления чисел | |
| Числа в десятичной системы счисления | Числа в двоичной системе системе счисления |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
| 16 | 10000 |
На уроках информатики вы узнаете, как именно связаны двоичная система счисления и десятичная, а пока просто запомним, что в компьютерах все числа представлены как нули и единицы.
В зависимости от реализации под числа выделяется какое-то количество бит — ячеек, способных принимать значение 0 или 1
Например, популярно выделять под целое число 32 бит.
Как видим, хоть целые числа могут быть сколь угодно малыми или сколь угодно большими, на практике появляются вполне реальные ограничения.
Так в языке программирования Java целые числа принимают значения от -2 147 483 648 до +2 147 483 647
Да, если мы делаем какие-то бытовые расчеты, этого хватает с запасом.
А если вычисления делает банк или правительство, где числа совсем другие?
На практике часто начинают выделять больше памяти под числа или использовать другие специальные технологии, тогда пользователь может снова не думать про размер чисел.
Но мысль о том, что размер чисел имеет значение, весьма важна.
распределительное-свойство-примеров-умножения-4-го класса — Googlesuche
AlleBilderVideosShoppingMapsNewsBücher
suchoptionen
Распределительное свойство умножения гласит, что умножение суммы двух или более слагаемых на число даст тот же результат, что и умножение каждое дополнение по отдельности по номеру, а затем сложение продуктов вместе. Например: 2 × (4 + 5) = (2 × 4) + (2 × 5) = 18.
Например: 2 × (4 + 5) = (2 × 4) + (2 × 5) = 18.
Каково распределительное свойство умножения? — Куэмат
www.cuemath.com › вопросы › какое-распределительное-свойство-множества…
Hervorgehobene Snippets
Ähnliche Fragen
Что такое распределительное свойство для умножения 4-го класса?
Что является примером распределительного свойства умножения?
Какое распределительное свойство умножения для малышей?
Каковы 4 свойства умножения с примером?
Умножение с использованием свойства распределения. 4 класс – YouTube
www.youtube.com › смотреть
16.12.2020 · Вы можете использовать распределительное свойство, чтобы умножить двузначное число на однозначное число. 4 класс …
Dauer: 2:41
Прислан: 16.12.2020
4 класс Math 2.5, Multiply with Distributive Property — YouTube
www.youtube.com › смотреть
14.03.2016 · Как умножить · используя дистрибутивное свойство умножения. Объяснение частичного…
Объяснение частичного…
Дауэр: 08:55
Прислан: 14.03.2016
4-й класс, математика 2.5, умножение с использованием свойства распределения — YouTube
www.youtube.com › смотреть
20.09.2019 · Свойство распределения утверждает, что умножение суммы на число равносильно умножению …
Дауэр: 15:28
Gepostet: 20.09.2019
Bilder
Alle Anzeigen
Alle Anleigen
Рабочие листы по недвижимости — Умножение — K5. Умножение
Распределительное свойство умножения говорит нам, что 5 x (2 + 3) равно 5 x 2 + 5 x 3. Мы можем использовать это для преобразования сложного умножения (3 x …
[PDF] ПРИЛОЖЕНИЕ ДЛЯ 4 КЛАПА — The Math Learning Center
www.mathlearningcenter.org › сайты › default › файлы › pdf
Переместительное свойство Меняйте порядок двух чисел Ассоциативное свойство Сгруппируйте по-разному Распределительное свойство Разбейте число на части и умножьте на единицу .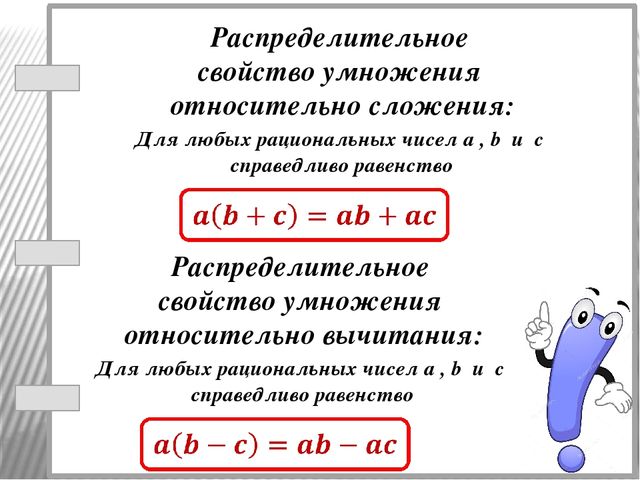 ..
..
Свойства умножения | Математика 4 класса — класс Ace
www.classace.io › учить › свойства-умножения…
Свойство распределения говорит о том, что мы можем распределять или раздавать 8 x каждому из слагаемых. Начало распределительной собственности. После того, как мы распространим …
Что такое распространяемая собственность? Определение, пример формулы, факты
www.splashlearn.com › математический словарь › алгебра
В соответствии с этим свойством умножение суммы двух или более слагаемых на число дает тот же результат, что и умножение каждого слагаемого по отдельности на …
Результаты для распределительного свойства рабочего листа умножения 4-й класс
www.teacherspayteachers.com › Диапазон цен › Бесплатно
Результаты 1–14 из 14+ дома. Он содержит множество тестов по математике, которые помогают детям развивать …
Ähnlichesuchanfragen
Распределительное свойство умножения Лист для 4-го класса
Умножение с использованием рабочих листов по распределительному свойству
Ассоциативное свойство умножения 4 класс
Коммутативное свойство умножения 4 класс
Распределительное свойство умножения 5 класс
Распределительное свойство умножения рабочие листы PDF
Распределительное свойство умножения 3 класс
Распределительная собственность «Распространить» означает разделить одно целое на множество частей. Распределительное свойство умножения основано на этой концепции и утверждает, что
Распределительное свойство умножения основано на этой концепции и утверждает, что
«Умножение числа на сумму двух или более слагаемых дает тот же результат, что и при умножении числа на каждое слагаемое по отдельности и последующем сложении произведений».
Давайте рассмотрим пример, чтобы понять, что это значит. Мы должны выполнить умножение для следующего выражения:
4(2 + 3)
Правило математики «порядок операций» соблазняет нас решить это выражение, используя следующие шаги:
Шаг 1: Выполните сложение внутри скобки, чтобы получить 4 x 5
Шаг 2: Выполните умножение, чтобы получить результат = 20
Свойство распределения меняет подход. Сначала мы распределяем умножаемое число по слагаемым. Последующие новые шаги:
Шаг 1: Разделите скобки, чтобы распределить 4. Получим (4 x 2) + (4 x 3)
Шаг 2: Выполните умножение внутри скобок, чтобы получить 8 + 12
Шаг 3 : Сложите продукты, чтобы получить результат = 20
Мы замечаем, что результат одинаков в обоих случаях, и свойство распределения действительно выполняется.
 Визуально мы можем представить это как:
Визуально мы можем представить это как:Ознакомьтесь с нашими рабочими листами!
Интересно отметить, что распределительное свойство умножения справедливо не только для сложения, но и для вычитания. Например, предположим, что нам нужно решить выражение:
3(5 — 2)
Мы можем использовать обычный подход, чтобы вычислить его как:
3(5 — 2) = 3 x 3 = 9
Используя распределительное свойство, мы можем вычислить его как:
3(5 — 2) = (3 x 5) – (3 x 2) = 15 – 6 = 9
Еще раз, мы можем видеть, что результат тот же в оба случая и свойство дистрибутивности выполняются, как и ожидалось. На самом деле это свойство действительно, даже если у нас есть комбинация сложения и вычитания внутри круглых скобок, как показано ниже.
Имея дело с комбинацией сложения и вычитания внутри скобок, мы должны быть особенно осторожны со знаками + и -. На этом этапе мы можем изменить утверждение о распределительном свойстве умножения, чтобы теперь утверждать, что
«Умножение числа на сумму или разность двух или более чисел (называемых операндами) дает тот же результат, что и при умножении числа к каждому операнду в отдельности, а затем добавляя или вычитая произведения (в зависимости от операции)».
Почему мы используем распределительное свойство умножения?
Из приведенных выше примеров кажется, что использование дистрибутивного свойства делает умножение длинным, потому что мы используем три шага, чтобы сделать то, что можно было сделать за два шага. Однако в некоторых случаях использование дистрибутивного свойства упрощает расчеты. Например, давайте рассмотрим выражение:
6(57)
Большинству детей это умножение покажется сложным, но если мы воспользуемся дистрибутивным свойством умножения вместо сложения, мы можем упростить это выражение как:
6(50 + 7) = 300 + 42
= 342
Это выражение решить проще, потому что теперь мы умножаем 6 на кратное 10 и на однозначное число. Есть еще некоторая возможность просто продолжить умножение. Если мы воспользуемся распределительным свойством умножения над вычитанием вместо сложения, то получим:
6(60 — 3) = 360 – 18
= 342
с числами как можно меньшими. Это, очевидно, проще, чем умножение на сложное число, состоящее из двух или более цифр. Теперь рассмотрим пример с трехзначным числом в скобках: 9.0003
Теперь рассмотрим пример с трехзначным числом в скобках: 9.0003
3(597) = 3(500 + 90 + 7)
= 1500 + 270 + 21
= 1791
В этом примере лучше использовать вычитание. Можете ли вы догадаться, почему?
3(597) = 3(600 — 3)
= 1800 – 9
= 1791
Используя вычитание, мы уменьшаем количество раз, которое нам нужно умножать – мы делаем это дважды, а не трижды. Кроме того, число 3 меньше, чем 9 и 7, что ускоряет расчеты.
В обоих вышеприведенных примерах, поскольку трехзначное число кратно сотне, мы, по сути, умножаем 3 только на однозначное число — либо на 5, либо на 6, и просто добавляем два нуля в конце. Мы эффективно сократили трехзначное умножение на 39.7 в простое однозначное умножение.
Однако всегда использовать прямое вычитание тоже не лучшая идея. Если бы нам нужно было вычислить такое выражение, как 5(287), было бы лучше использовать смесь сложения и вычитания. И вот почему:
Изучите 3 шага
Чтобы помочь вашему ребенку
наверстать упущенное в школе
Программа на 12 недель обновлена 7 февраля 2023 г.
 Уровень!
Уровень!- Прямое вычитание даст нам 5 (300 – 13), где 13 — двузначное число.
- Итак, мы делаем один шаг вперед и разделяем 13.
- Мы можем записать 13 либо как 10+3, либо как 20–7. Первый вариант лучше, потому что 3<7.
Следовательно,
5(286) = 5(300 — (10 + 3))
= 5(300 — 10 — 3)
= 1500 — 50 -15
= 14035 90 В этой точке вы, вероятно, задаетесь вопросом – существуют ли какие-либо правила, определяющие, какой подход следует использовать в том или ином случае? Ответ — нет. Выяснить, нужно ли и как разбивать термин в скобках, можно научиться только с практикой. Личные предпочтения также имеют значение — некоторым детям умножение двух цифр может показаться проще и веселее, чем сложение или вычитание трех цифр.
Как родитель или учитель, вы должны обучать детей концепции распределения, но не заставлять их всегда ее использовать. Дайте им свободу выбора подхода, который им наиболее удобен.
Как дистрибутивность работает с делением?
Учитывая, что деление является обратным умножению, мы не можем ожидать, что дистрибутивность будет работать одинаково в обоих случаях. При умножении у нас есть свобода разделить любое из двух умножаемых чисел. Например, в 124 х 35 (100 + 20 + 4) х 35, а также 124 х (30 + 5) будет один и тот же ответ при распространении.
Однако, если бы мы вычислили 124 ÷ 35, то (100 + 20 + 4) ÷ 35 не даст такого же результата, как 124 ÷ (30 + 5), как показано ниже.
Дистрибутивность как строительный блок для переменных и неизвестных
Помимо упрощения вычислений, одной из важных причин обучения детей дистрибутивности является то, что она служит подготовкой к работе с такими переменными, как «x» и «y». Когда у нас есть разные термины в скобках, мы часто используем дистрибутивность для решения уравнений. Например, если нам нужно решить уравнение 5(3 + x) = 17, мы распределяем 5 по слагаемым в скобках, чтобы получить:
5(3 + x) = 17
или 15 + 5x = 17
или 5x = 2
или x = 5/2
Как вы можете заставить детей практиковать свойство распределения?
Теперь, когда у вас есть примеры, советы и рекомендации по распределению, пришло время помочь детям применить эту концепцию.


 Чтобы найти дробь от числа, нужно умножить число на эту дробь.
Чтобы найти дробь от числа, нужно умножить число на эту дробь. А) 17; Б) 5 2/3; В) 1 ¼
А) 17; Б) 5 2/3; В) 1 ¼