ГДЗ по математике 4 класс учебник Моро, Бантова 1 часть

❤️️Ответ к странице 73. Математика 4 класс учебник 1 часть. Авторы: М.И. Моро, М.А. Бантова.

Номер 22.

Дополни задачу недостающими данными и реши её. Из неисправного водопроводного крана в секунду капают 2 капли, а за 12 мин наполняется 1 полный стакан. Сколько литров воды может зря вылиться из такого крана в течение часа? в течение суток? (Считать в литре ☐ стаканов.)

Ответ:

Считать, что в 1 литре 5 стаканов, потому что в одном стакане 200 мл.
Сколько стаканов воды выльется за 1 час? 60 : 12 = 5 (ст.) – за 1 час и это 1 л. Значит за 1 час выливается 1 литр воды. За сутки (24 с) выльется 24 литра. Ответ: 1 л и 24 л.

Номер 23.

Какую площадь занимает картофельное поле, если одна пятая часть этой площади составляет 200 м²?

Ответ:

Все поле – ? м² 1/5 часть – 200 м

2 200 ∙ 5 = 1000 (м²) Ответ: 1000 м² занимает картофельное поле.

Номер 24.

Какие числа пропущены в таблице?

Ответ:

1 см² = 100 мм²    1 м² = 100 дм² 1 дм² = 100 см²    1 км² = 1000000 м²

Номер 25.

Запиши вычисления столбиком.

Ответ:

45 км 530 м + 37 км 470 м = 83 км 45 км 530 м = 45530 м 37 км 470 м = 37470 м 83000 м = 83 км

---

24 км 040 м − 9 км 008 м = 15 км 032 м 24 км 040 м = 24040 м 9 км 008 м = 9008 м 15032 м = 15 км 032 м

---

32 т 820 кг − 8 т 950 кг = 23 т 870 кг 32 т 820 кг = 32820 кг 8 т 950 кг = 8950 кг 23 т 870 кг = 23870 кг

---

3 ч 15 мин − 45 мин = 2 ч 30 мин 3 ч 15 мин = 195 мин 195 мин − 45 мин = 150 мин 150 мин = 2 ч 30 мин

Номер 26.

Из двух одинаковых квадратов составили прямоугольник со сторонами 3 см и 1 см 5 мм. Сделай к задаче чертёж. Вырази длины сторон прямоугольника в миллиметрах и вычисли периметр этого прямоугольника и каждого квадрата.

Ответ:

3 см = 30 мм 1 см 5 мм − 15 мм
Периметр прямоугольника: (30 + 15) ∙ 2 = 90 (мм) Периметр квадрата: 15 ∙ 4 = 60 (мм) Ответ: периметр прямоугольника — 9 см, периметр каждого квадрата — 6 см.

Номер 27.

Начерти такие фигуры в тетради. В фигуре 1 найди одну девятую долю и закрась четыре таких доли, а в фигуре 2 закрась семь шестнадцатых долей. Найди площадь незакрашенной части фигуры 1.

Ответ:

3 ∙ 3 = 9 см² 9 − 4 = 5 см² Ответ: 5 см² площадь незакрашенной части фигуры 1.

Номер 1.

Как называются числа и соответствующие выражения при сложении? вычитании?

Ответ:

При сложении: первое слагаемое, второе слагаемое, сумма. При вычитании: уменьшаемое, вычитаемое, разность.

Номер 2.

Какие свойства сложения ты знаешь?

Ответ:

• Переместительное свойство сложения – от перестановки мест слагаемых значение суммы не меняется a + b = b + a
• Сочетательное свойство сложения – можно складывать слагаемые в любом порядке. Значение суммы от этого не поменяется (Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа.) (a + b) + c = a + (b + c)
• Свойство нуля при сложении – если к числу прибавить 0, получится тоже самое число. a + 0 = 0 + a = a

Номер 3.

Чему равна сумма двух слагаемых, если одно из них равно нулю? разность, если вычитаемое равно нулю?

Ответ:

Сумма равна слагаемому неравному нулю. Разность равна уменьшаемому.

Номер 4.

Что получится, если из суммы двух слагаемых вычесть одно слагаемое? если к вычитаемому прибавить разность? если из уменьшаемого вычесть разность?

Ответ:

Получится число, равное другому слагаемому. Получится уменьшаемое. Получится вычитаемое.

Номер 5.

Как можно проверить сложение? вычитание?

Ответ:

Из суммы вычесть одно из слагаемых. К разности прибавить вычитаемое или из уменьшаемого отнять разность.

Номер 6.

Какие ты знаешь правила о порядке выполнения действий в выражениях без скобок? в выражениях со скобками?

Ответ:

Сначала выполняются умножение и деление, а затем сложение и вычитание. Сначала выполняются действия в скобках.

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

2 часть

4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111	112	113	114	115	116	117	118	119	120	121	122	123	124	125	126	127

НОД и НОК

Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД и НОК.

НОД — это наибольший общий делитель.

НОК — это наименьшее общее кратное.

Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.

Наибольший общий делитель

Определение. Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.

Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа. Например, вместо переменной a подставим число 12, а вместо переменной b — число 9. Теперь попробуем прочитать это определение:

Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 12 и 9 делятся без остатка.

Из определения понятно, что речь идёт об общем делителе чисел 12 и 9. Причем делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.

Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.

Второй и третий способы довольны просты и дают возможность быстро найти НОД. Рассмотрим все три способа. А какой применять на практике — выбирать вам.

Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9.

Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.

12 : 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)

12 : 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)

12 : 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)

12 : 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)

12 : 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)

12 : 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)

12 : 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)

12 : 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)

12 : 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)

12 : 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)

12 : 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)

12 : 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)

Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9

9 : 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)

9 : 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)

9 : 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)

9 : 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)

9 : 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)

9 : 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)

9 : 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)

9 : 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)

9 : 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)

Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:

Выписав делители, можно сразу определить какой является наибольшим и общим.

Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3

И число 12 и число 9 делятся на 3 без остатка:

12 : 3 = 4

9  : 3 = 3

Значит НОД (12 и 9) = 3

---

Второй способ нахождения НОД

Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.

Пример 1. Найти НОД чисел 24 и 18

Сначала разложим оба числа на простые множители:

Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.

Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:

Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.

Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.

Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:

Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:

2 × 3 = 6

Значит НОД (24 и 18) = 6

---

Третий способ нахождения НОД

Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.

Пример 1. Найти НОД чисел 28 и 16.

В первую очередь, раскладываем числа 28 и 16 на простые множители:

Получили два разложения:  и 

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семёрка. Её и вычеркнем из первого разложения:

Теперь перемножаем оставшиеся множители и получаем НОД:

Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:

28 : 4 = 7

16 : 4 = 4

 НОД (28 и 16) = 4

---

Пример 2. Найти НОД чисел 100 и 40

Раскладываем на множители число 100

Раскладываем на множители число 40

Получили два разложения: 2 × 2 × 5 × 5 и 2 × 2 × 2 × 5

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения

Перемножим оставшиеся числа:

Получили ответ 20. Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:

100 : 20 = 5

40 : 20 = 2

 НОД (100 и 40) = 20.

---

Пример 3. Найти НОД чисел 72 и 128

Раскладываем на множители число 72

Раскладываем на множители число 128

Получили два разложения: 2 × 2 × 2 × 3 × 3 и 2 × 2 × 2 × 2 × 2 × 2 × 2.

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:

Перемножим оставшиеся числа:

Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:

72 : 8 = 9

128 : 8 = 16

 НОД (72 и 128) = 8

---

Нахождение НОД для нескольких чисел

Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.

Например, найдём НОД для чисел 18,  24  и  36

Разложим на множители число 18

Разложим на множители число 24

Разложим на множители число 36

Получили три разложения:

Теперь найдём и подчеркнём общие множители:

Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Эти множители входят во все три разложения. Перемножив эти множители, мы получим НОД, который ищем:

2 × 3 = 6

Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:

18 : 6 = 3

24 : 6 = 4

36 : 6 = 6

 НОД (18, 24 и 36) = 6

---

Пример 2. Найти НОД для чисел 12, 24, 36 и 42

Разложим на простые множители каждое число. Затем найдём произведение общих простых множителей.

Разложим на множители число 12

Разложим на множители число 24

Разложим на множители число 36

 

Разложим на множители число 42

Получили четыре разложения:

Теперь найдём и подчеркнём общие множители:

Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:

2 × 3 = 6

Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:

12 : 6 = 2

24 : 6 = 4

36 : 6 = 6

42 : 6 = 7

 НОД (12, 24 , 36 и 42) = 6

---

Наименьшее общее кратное

Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.

Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, причем оно должно быть максимально маленьким.

Определение. Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно a и b. Другими словами, это такое маленькое число, которое делится без остатка на число a и число b.

Определение содержит две переменные a и b. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:

Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12. Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12.

Из определения понятно, что наименьшее общее кратное это наименьшее число, которое делится без остатка на 9 и на 12. Это наименьшее общее кратное требуется найти.

Для нахождения наименьшего общего кратного (НОК) можно пользоваться тремя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.

В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9.

Итак, начнём. Кратные будем выделять синим цветом:

Теперь находим кратные для числа 12. Для этого поочерёдно умножим число 12 на все числа 1 до 12:

Теперь выпишем кратные обоих чисел:

 

Теперь найдём общие кратные обоих чисел. Найдя, сразу подчеркнём их:

Общими кратными для чисел 9 и 12 являются кратные 36 и 72. Наименьшим же из них является 36.

Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:

36 : 9 = 4

36 : 12 = 3

НОК (9 и 12) = 36

---

Второй способ нахождения НОК

Второй способ заключается в том, что числа для которых ищется наименьшее общее кратное раскладываются на простые множители. Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.

Применим данный способ для предыдущей задачи. Найдём НОК для чисел 9 и 12.

Разложим на множители число 9

Разложим на множители число 12

Выпишем первое разложение:

Теперь допишем множители из второго разложения, которых нет в первом разложении. В первом разложении нет двух двоек. Их и допишем:

Теперь перемножаем эти множители:

Получили ответ 36. Значит наименьшее общее кратное чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:

36 : 9 = 4

36 : 12 = 3

НОК (9 и 12) = 36

Говоря простым языком, всё сводится к тому, чтобы организовать новое разложение куда входят оба разложения сразу. Разложением первого числа 9 являлись множители 3 и 3, а разложением второго числа 12 являлись множители 2, 2 и 3.

Наша задача состояла в том, чтобы организовать новое разложение куда входило бы разложение числа 9 и разложение числа 12 одновременно. Для этого мы выписали разложение первого числа и дописали туда множители из второго разложения, которых не было в первом разложении. В результате получили новое разложение 3 × 3 × 2 × 2. Нетрудно увидеть воочию, что в него одновременно входят разложение числа 9 и разложение числа 12

---

Пример 2. Найти НОК чисел 50 и 180

Разложим на множители число 50

Разложим на множители число 180

Выпишем первое разложение:

Теперь допишем множители из второго разложения, которых нет первом разложении. В первом разложении нет ещё одной двойки и двух троек. Их и допишем:

Теперь перемножаем эти множители:

Получили ответ 900. Значит наименьшее общее кратное чисел 50 и 180 это число 900. Данное число делится на 50 и 180 без остатка:

900 : 50 = 18

900 : 180 = 5

НОК (50 и 180) = 900

---

Пример 3. Найти НОК чисел 8, 15 и 33

Разложим на множители число 8

Разложим на множители число 15

Разложим на множители число 33

Выпишем первое разложение:

Теперь допишем множители из второго и третьего разложения, которых нет первом разложении. Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:

Теперь перемножаем эти множители:

Получили ответ 1320. Значит наименьшее общее кратное чисел 8, 15 и 33 это число 1320. Данное число делится на 8, 15 и 33 без остатка:

1320 : 8 = 165

1320 : 15 = 88

1320 : 33 = 40

НОК (8, 15 и 33) = 1320

---

Третий способ нахождения НОК

Есть и третий способ нахождения наименьшего общего кратного. Он работает при условии, что его ищут для двух чисел и при условии, что уже найден наибольший общий делитель этих чисел.

Данный способ разумнее использовать, когда одновременно нужно найти НОД и НОК двух чисел.

К примеру, пусть требуется найти НОД и НОК чисел 24 и 12. Сначала найдем НОД этих чисел:

Теперь для нахождения наименьшего общего кратного чисел 24 и 12, нужно перемножить эти два числа и полученный результат разделить на их наибольший общий делитель.

Итак, перемножим числа 24 и 12

Разделим полученное число 288 на НОД чисел 24 и 12

Получили ответ 24. Значит наименьшее общее кратное чисел 24 и 12 равно 24

НОК (24 и 12) = 24

---

Пример 2. Найти НОД и НОК чисел 36 и 48

Найдем НОД чисел 36 и 48

Перемножим числа 36 и 48

Разделим 1728 на НОД чисел 36 и 48

Получили 144. Значит наименьшее общее кратное чисел 36 и 48 равно 144

НОК (36 и 48) = 144

Для проверки можно найти НОК обычным вторым способом, которым мы пользовались ранее. Если мы всё сделали правильно, то должны получить 144

Не расстраивайтесь, если сразу не научитесь находить НОД и НОК. Главное понимать, что это такое и как оно работает. А ошибки вполне естественны на первых порах. Как говорят: «На ошибках учимся».

---

Задания для самостоятельного решения

Задание 1. Найдите НОД чисел 12 и 16

Решение:

Показать решение

Задание 2. Найдите НОК чисел 12 и 16

Решение:

Показать решение

Задание 3. Найдите НОД чисел 40 и 32

Решение:

Показать решение

Задание 4. Найдите НОК чисел 40 и 32

Решение:

Показать решение

Задание 5. Найдите НОД чисел 54 и 86

Решение:

Показать решение

Задание 6. Найдите НОК чисел 54 и 86

Решение:

Показать решение

Задание 7. Найдите НОД чисел 98 и 35

Решение:

Показать решение

Задание 8. Найдите НОК чисел 98 и 35

Решение:

Показать решение

Задание 9. Найдите НОД чисел 112 и 82

Решение:

Показать решение

Задание 10. Найдите НОК чисел 112 и 82

Решение:

Показать решение

Задание 11. Найдите НОД чисел 24, 48, 64

Решение:

Показать решение

Задание 12. Найдите НОК чисел 24, 48, 64

Решение:

Показать решение

Задание 13. Найдите НОД чисел 18, 48, 96

Решение:

Показать решение

Задание 14. Найдите НОК чисел 18, 48, 96

Решение:

Показать решение

Задание 15. Найдите НОД чисел 28, 24, 76

Решение:

Показать решение

Задание 16. Найдите НОК чисел 28, 24, 76

Решение:

Показать решение

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано Автор

What?, Methods, Long, Properties & Examples

Процесс нахождения произведения двух или более чисел называется умножением.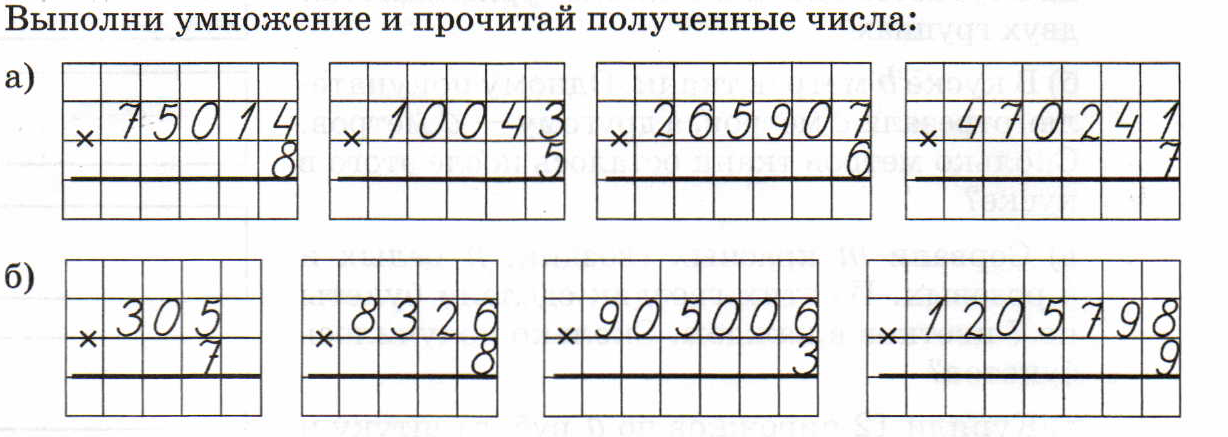 Полученный таким образом результат называется продуктом . Предположим, вы купили 6 ручек в один день и 6 ручек на следующий день. Всего ручек, которые вы купили, теперь 2 умножить на 6 или 6 + 6 = 12.

Это также можно записать как 2 x 6 = 12

Не тот символ, который используется для умножения. Символ (x) обычно используется для обозначения умножения. Другими распространенными символами, которые используются для умножения, являются звездочка (*) и точка (.) 

Важные термины при умножении

Некоторые важные термины, используемые при умножении:

Множимое — Число, которое нужно умножить, называется множимым.

Множитель — Число, на которое мы умножаем, называется множителем.

Произведение – Результат, полученный после умножения множителя на множимое, называется произведением.

Связь между множителем, множимым и произведением может быть выражена как:

Множитель  ×  Множитель = Произведение

Разберем это на примере.

Предположим, у нас есть два числа 9 и 5. Мы хотим умножить 9 на 5.

Итак, мы выражаем это как 9 x 5, что дает нам 45.

Следовательно, 9 x 5 = 45

Здесь 9 равно множимое, 5 — множитель, 45 — произведение.

Существует два метода умножения чисел, а именно метод расширенной записи и метод столбца.

Метод расширенной записи

В методе расширенной записи мы расширяем множимое по разрядным значениям, а затем умножаем каждое число на множитель. Затем мы суммируем все полученные результаты, чтобы получить окончательный ответ. Давайте разберемся на примере.

Например, умножьте 1235 на 4

Решение

Мы решим это шаг за шагом.

Шаг 1. Запишите число (множимое) в развернутой форме. Получаем,

1235 = 1000 + 200 + 30 + 5

Шаг 2. Умножьте каждое число на заданное число (множитель) по одному. Получаем,

1000 х 4 + 200 х 4 + 30 х 4 + 5 х 4

= 4000 + 800 + 120 + 20

Шаг 3 — Складываем полученные результаты. Мы получаем

4000 + 800 + 120 + 20 = 4940, что является нашим окончательным результатом

Следовательно, 1235 x 4 = 4940

Этот метод, хотя и простой, может не подходить для больших чисел. Но он используется для понимания основных понятий умножения.

Колоночный метод

В этом методе мы разбиваем числа на столбцы и умножаем числа на множимое одно за другим. Есть два сценария использования этого метода.

Давайте разберемся с ними один за другим

Умножение без перегруппировки

Этот метод вступает в силу, когда у нас есть меньшие числа, которые не требуют переноса каких-либо чисел на следующий разряд. Давайте разберемся на примере.

Например, умножить 1021 на 3

 Решение

Мы будем использовать следующие шаги, чтобы получить наш результат.

Шаг 1. Сначала мы записываем множимое и множитель в столбцах.

Шаг 2. Теперь умножаем число, стоящее в разряде единиц, на 3. Получаем

Шаг 3. Теперь умножаем число в разряде десятков на 3. Получаем

. Шаг 4. Далее умножаем число в разряде сотен на 3. Получаем

Шаг 5 – Наконец, умножаем число в разряде тысяч на 3. Получаем

Следовательно, 1021 x 3 = 3063

Умножение с перегруппировкой

В приведенном выше случае у нас есть небольшие умножения, которые ни на одном шаге не давали двузначных результатов. Но в случае больших чисел потребуется перенести число на число со следующим значением разряда. Это называется умножением с перегруппировкой. Давайте разберемся на примере.

Например, умножить 5092 на 5

Решение

Мы будем использовать следующие шаги, чтобы получить наш результат.

Шаг 1. Сначала мы записываем множимое и множитель в столбцах.

Шаг 2. Умножьте цифру единиц на 5. У нас 2 x 5 = 10. Запишите 0 в колонке единиц и перенесите 1 в колонку десятков.

Шаг 3 – Умножьте цифру десятков на 5. Получаем 9 x 5 = 45. Добавьте к ней 1, которая была перенесена, чтобы получить 45 + 1 = 46. Теперь запишите 6 в столбце десятков и перенесите 4 в сотню. столбец.

Шаг 4 – Умножаем цифру сотен на 5. Получаем 0 x 5 = 5. Теперь прибавляем к ней перенесенное 4 и получаем 4. Записываем 4 в столбец сотен.

Шаг 5 – Умножьте 5 на цифру тысячи. Получаем 5 x  = 25. Запишите 5 в столбце тысяч и 2 в столбце десятков тысяч.

Следовательно, конечный продукт равен 25460.

Длинное умножение похоже на метод столбца, за исключением того факта, что здесь мы умножаем большие числа. Этот метод используется, когда множимое больше 9, т. е. множимое больше однозначного числа. Этот метод включает следующие шаги –

1. Сначала мы записываем множимое и множитель в столбцах.
2. Сначала умножьте число, стоящее на месте множителя, на все числа множимого и запишите их горизонтально.
3. Убедитесь, что вы записываете числа справа налево и каждое число находится под соответствующим разрядом множимого.
4. Теперь перейдите к следующей строке.
5. Поставьте 0 на месте единицы в этой строке.
6. Теперь найдите цифру в разряде десятков множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили 0,9.0136
7. Снова перейти на следующую строку.
8. Поставьте 0 на месте единиц и десятков в этой строке.
9. Теперь найдите цифру в разряде сотен множителя. Умножьте число, стоящее в сотенном разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили два нуля.
10. Продолжайте в том же духе, добавляя дополнительный ноль в каждой строке, пока не дойдете до конца множителя
11. Сложите числа по вертикали в соответствии с их разрядностью.
12. Полученное таким образом число и есть ваш результат.

Давайте разберем это на примере

Например, Умножьте 132 на 13

Решение

1. Сначала мы запишем множимое и множитель в столбцах.

2. Сначала умножьте число, стоящее на месте единицы множителя, на все числа множимого и запишите их горизонтально.

3. Поставьте 0 на месте единицы следующей строки

4. Теперь найдите цифру в разряде десятков множителя. Умножьте число в десятом разряде множителя на все числа множимого и запишите их горизонтально в строке, где вы отметили 0.

5. В множимом больше нет числа. Теперь сложите числа по вертикали в соответствии с их разрядностью.

6. Окончательный ответ 1716. Следовательно, 132 x 13 = 1716

Давайте посмотрим на другой пример, где мы 3 цифры в множимом.

Например, Умножьте 364 на 123

Решение

1. Сначала запишем множимое и множитель в столбцы

2. Сначала умножим число на единицу множитель со всеми числами множимое и запишем их горизонтально.

3. Поставьте 0 на месте единицы следующей строки

4. Теперь найдите цифру в разряде десятков множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили 0,9.0005

5. Поставьте 0 на месте единиц и десятков в следующей строке.

6. Теперь найдите цифру в разряде сотен множителя. Умножьте число, стоящее в сотенном разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили два нуля.

7. В множимом больше нет числа. Теперь сложите числа по вертикали в соответствии с их разрядностью.

8. Следовательно, конечный продукт равен 44 772. Мы можем сказать, что 364 х 123 = 44772

• Чтобы умножить число на 10, поставьте 0 справа от числа. Например, 435 х 10 = 4350
• Чтобы умножить число на 100, нужно поставить два нуля справа от числа. Например, 435 х 100 = 43500
• Чтобы умножить число на 1000, поставьте справа от числа три нуля. Например, 435 x 1000 = 435000
• Чтобы умножить число на произведение 10, 100 и 1000 на счетные числа, умножьте числа на ненулевые числа, а затем добавьте к результату количество нулей. Например, умножьте 45 на 200. Чтобы решить это, мы сначала умножим 45 на 200. Получаем 45 х 2 = 90. Теперь мы добавляем 2 нуля (поскольку у 200 было 2 нуля) справа от 90. Получаем 9000.
• Следовательно, 45 x 20 = 9000

Коммутативное свойство

Коммутативное свойство утверждает, что при выполнении операции над два числа, порядок расположения чисел не имеет значения. Это означает, что если одно число умножается на другое, не имеет значения, какое число помечено как множитель, а какое число помечено как множимое. Справедливо ли это для умножения? Давайте узнаем.

Возьмем два числа 8 и 5.

Сначала отметим 8 как множитель и 5 как множимое.

Получаем, 8 х 5 = 40.

Теперь обратим порядок, т.е. 5 станет множителем, а 8 станет множимым.

Теперь мы получаем 5 x 8 = 40.

Оба процесса дают нам один и тот же ответ.

Следовательно, мы можем сказать, что умножение удовлетворяет коммуникативному свойству. Получаем

a x b = b x a

Следовательно, умножение коммуникативно.

Ассоциативное свойство

Ассоциативное свойство указывает, что при выполнении операции над более чем двумя числами порядок, в котором расположены числа, не имеет значения. В случае умножения это означает, что если мы хотим умножить 3 числа, сначала можно выбрать два из них, одно как множитель, а второе как множимое. Результат умножения будет служить множителем, а третье число — множителем для получения окончательного ответа. Является ли умножение ассоциативным? Давайте узнаем.

Возьмем 3 числа, 8, 5 и 2.

Возьмем сначала 8 и 5.

Сначала мы помечаем 8 как множитель и 5 как множимое.

Получаем, 8 х 5 = 40.

Теперь умножаем 40 на 2, получаем 40 х 2 = 80

Теперь давайте обратим порядок и сначала выберем 5 и 2.

Получаем, 5 х 2 = 10

Теперь умножаем этот результат на 8, получаем 10 х 8 = 80

Оба процесса дают нам одинаковый ответ.

Следовательно, мы можем сказать, что умножение удовлетворяет ассоциативному свойству. мы получаем

(a x b) x c =  a x (b x c)

Следовательно, умножение ассоциативно.

Мультипликативное свойство «0»

Произведение числа на 0 всегда равно 0. Например,

45 x 0 = 0 x 45 = 0

Свойство тождества умножение, если число, умноженное на это тождественное число, дает само число. Здесь

1 является элементом идентичности для умножения . Давайте посмотрим, почему?

4 x 1 = 4

15 x 1 = 15

20 x 1 = 20

Таким образом, любое число при умножении на 1 дает само число. Это тождественное свойство умножения.

Мультипликативное обратное

Число называется мультипликативным обратным, если число умножается на мультипликативное обратное, полученный результат является тождеством операции, в данном случае 1 (1 — мультипликативное тождество всех чисел).

Это означает, что для всех ненулевых чисел числа, умноженные на их обратные числа, дадут ответ как 1, т.е.

4 x 1/4 = 1

Следовательно, 1/a , которое также записывается как ^-1 , является мультипликативной инверсией a.

Распределительное свойство умножения на сложение/вычитание

Когда два числа складывают или вычитают, а результат умножают на другое число, их можно умножать отдельно.

Следовательно, для любых трех чисел, a, b и c, распределительное свойство умножения над сложением утверждает, что

a x ( b + c) = (a x b) + (a x c) 9Например, пусть сначала рассмотрим 10 x (18 + 12)

Есть два способа решить эту проблему.

Первый способ

Сначала складываем 18 и 12, получаем 30. Теперь умножаем 30 на 10, получаем 10 х 30 = 300

  Второй способ

Теперь мы используем распределительное свойство умножения вместо сложения.

Имеем 10 х (18 + 12)

 = (10 х 18) + (10 х 12)

 = 180 + 120

 = 300

Оба метода дают одинаковый ответ . Следовательно,

10 х (18 + 12) = (10 х 18) + (10 х 12)

Теперь давайте рассмотрим 10 х (18 – 12)

Снова давайте решим это обоими методами.

Первый способ

Находим разницу между 18 и 12. Имеем 18 – 12 = 6

Теперь мы умножаем 10 на 6. Получаем 10 x 6 = 60.

Второй метод

Теперь мы используем распределительное свойство умножения вместо вычитания.

Мы имеем 10 x (18 — 12)

= (10 x 18) — (10 x 12)

= 180 — 120

= 60

по обоим методам, мы получаем одинаковый ответ. Следовательно,

10 х (18 – 12) = (10 х 18) – (10 х 12)

Мы используем умножение при решении наших повседневных задач. Давайте посмотрим на некоторые примеры.

Пример 1 : На стадионе 287 рядов. Сколько студентов можно разместить на этом стадионе, если в каждом ряду 165 мест?

Решение

Нам известно, что

Количество рядов на стадионе = 287

Количество мест в каждом ряду = 165

Общее количество студентов, которые могут сидеть на стадионе = 287 x 16 5 = 47335.

Пример 2 : Генри купил 15 упаковок печенья. Каждый пакет содержит 35 файлов cookie. Сколько всего печенья у Генри?

Решение

Нам дано, что

Количество пакетов печенья, купленных Генри = 15

Количество печенья в каждом пакете = 35

Общее количество печенья, которое есть у Генри = 15 x 35 = 525 90 005

Умножение и решение задач на деление (на тему Хэллоуина) Рабочие листы по математике
Умножение рациональных алгебраических выражений с одинаковыми знаменателями (на тему аптеки) Рабочие листы
Умножение целых чисел с разными знаками (на тему банковского дела и финансов) Рабочие листы

Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!

8 забавных игр на умножение для ваших математических центров

Я ОБОЖАЮ играть в игры (не буду врать, известно, что я слишком серьезно отношусь к одной или двум играм в «Монополию»).

Но это не только я. Мои ученики ОБОЖАЛИ играть в игры. Я никогда не видел такой увлеченной группы, как когда мы играли в математические игры в течение 904:29 Первая пятница.

Хотите узнать самое лучшее о математических играх для класса?

Математические игры — это не только весело, но и невероятно хороший способ попрактиковаться в математических навыках! Они превращают скучную математическую практику в веселое мотивационное упражнение. На самом деле, игры настолько увлекательны, что ученики даже не знают, что они учатся!

Тссс..только не говорите моим ученикам.

Я хочу поделиться с вами 8 забавными играми на умножение, которые вы можете использовать в своих математических центрах. Одна из причин, по которой я люблю эти игры на умножение, заключается в том, что они не требуют от вас покупать что-то особенное. Вы можете использовать материалы, которые уже есть у вас в классе или дома.

Так что доставай кости, игральные карты, математические счетчики и давай поиграем в математические игры!

Математические игры для каждого этапа изучения математики

В этом посте мы рассказали о различных этапах мультипликативного мышления, которые учащиеся проходят на пути к овладению навыками умножения.

На конкретном этапе учащиеся изучают концептуальное значение умножения. На этом этапе они извлекают пользу из практики умножения с помощью практических манипуляций, таких как счетчики и кубы unifix.

На репрезентативном этапе учащиеся понимают, что значит умножать, и теперь они учатся применять более стратегические способы решения задач на умножение, такие как рисование массивов и пропуск счета для поиска ответа. На этом этапе они извлекают пользу из практики умножения, которая включает в себя рисование картинок или диаграмм.

На абстрактном этапе учащиеся решают задачи на умножение без использования манипуляций или рисунков. Они практикуют различные эффективные стратегии решения проблем, например, опираясь на известные факты. На этом этапе учащиеся получают пользу от практики вспоминания математических фактов по памяти, играя в веселые игры, такие как война умножения.

Игры на умножение, которые я описываю ниже, можно отнести к одной из этих трех фаз развития умножения. Некоторые игры следует использовать, когда учащиеся впервые учатся умножению и нуждаются в практической практике, в то время как другие игры лучше подходят для учащихся, которые уже некоторое время изучают умножение, но нуждаются в большей практике, вспоминая факты по памяти.

Небольшое замечание: я обнаружил, что некоторые из моих учеников специального образования, особенно те, кто боится или не любит математику, не любят играть в игры, в которых есть победитель и проигравший. Они могут чувствовать себя особенно побежденными, если в конечном итоге проиграют игру, что противоречит цели заинтересовать их математикой! В этом случае я превращу следующие игры в действия и уберу аспект выигрыша и проигрыша.

В моем БЕСПЛАТНОМ онлайн-курсе узнайте, как точно оценить навыки умножения и деления ваших учеников! Читать дальше и зарегистрироваться здесь.

Игры на умножение для бетонной фазы

Массивы умножения

Описание:

Это математическая игра с игральными картами и счетчиками. Учащиеся составляют массивы, представляющие уравнения умножения. Играйте с 2-4 учениками в каждой группе.

Материалы:

• математические счетчики
• колода игральных карт (в зависимости от размера коробки вы должны удалить некоторые из игральных карт. Например, на коробке выше всего 5 столбцов и 6 рядов, поэтому я бы взял все карты больше 6 ).
• большую коробку (обычно я могу найти коробки хорошего размера в магазинах с оптовыми складами, таких как Costco. Ищите большие контейнеры для яиц или яблок). игральных карт. Первая карта, которую они переворачивают, представляет количество столбцов. Вторая карта, которую они переворачивают, представляет количество рядов.
• Учащиеся используют счетчики для создания массива. В приведенном выше примере учащийся создал массив из красных счетчиков с 4 строками и 5 столбцами.
• Учащийся с наибольшим произведением выигрывает этот раунд и собирает все карточки.
• Затем учащиеся должны удалить все счетчики из своего массива и начать сверху. Каждый учащийся должен перевернуть еще 2 карточки и построить новый ряд.
• Ученик с наибольшим количеством карточек в конце игры выигрывает игру!
• Совет: вместо жетонов я иногда использую монетки в этой игре. Я обнаружил, что некоторые из моих учеников с математическими отклонениями легче усваивают математику, когда ее выражают в деньгах. Вместо подсчета всех жетонов в приведенном выше примере учащиеся могут пересчитать все монеты, чтобы вычислить, что 5 рядов по 4 монеты равны 20 копейкам.

Группы умножения

Описание:

В этой игре на умножение используются фишки, кости и бумажные тарелки. Учащиеся бросают кубик и составляют группы, представляющие уравнения умножения. Играйте по 2 ученика в группе.

Материалы:

• математические счетчики
• бумажные тарелки
• 4 кубика
• бумага и карандаш для подсчета очков

Направления:
900 05

• Каждый ученик бросает 2 кубика. Первое число, которое они бросают, представляет собой количество групп, а второе число представляет количество жетонов в каждой группе. В приведенном выше примере учащийся выбросил 3 и 5, что представляет собой 3 группы по 5 жетонов.
• Учащиеся берут столько бумажных тарелок, сколько им нужно, чтобы сформировать группы. Если я сначала выкину 3, я возьму 3 тарелки, чтобы составить 3 группы.
• Item»> Учащиеся берут столько жетонов, сколько им нужно, чтобы заполнить тарелки. Если выпадет 5, я положу по 5 жетонов на каждую тарелку.
• Учащиеся считают, чтобы найти общее количество жетонов. В приведенном выше примере учащийся составляет 3 группы по 5 фишек, всего 15 фишек.
• Учащийся с наибольшим количеством счетчиков побеждает в этом раунде и получает очко. Студенты должны вести учет своих баллов на отдельном листе бумаги.
• Верните счетчики и начните снова с шага №1. Учащиеся продолжают бросать кости и объединяются в группы с жетонами. Вы можете продолжать эту игру столько, сколько захотите, хотя я считаю, что около 15 минут — это достаточное количество времени. Студент, набравший наибольшее количество очков в конце игры, становится победителем!

Игры на умножение для репрезентативного этапа

Стеки умножения

Описание:

В этой математической игре учащиеся бросают кости и создают стопки из кубиков unifix. Они используют многократное сложение или пропускают счет, чтобы решить задачу на умножение и найти общее количество кубиков. Играйте с 2-4 учениками в каждой группе.

Материалы:

• кубики unifix или другой тип связующего кубика
• 2 кубика на каждого ученика
• доска для сухого стирания
• бумага и карандаш для подсчета очков

Инструкции:

• Каждый ученик бросает свою пару игральных костей. Первое число, которое они выбрасывают, говорит им, сколько стеков нужно сделать. Второе число, которое они выбрасывают, говорит им, насколько большой должна быть каждая стопка.
• Учащиеся складывают свои унификсы или соединяющие кубы, чтобы сделать свои стопки. В приведенном выше примере учащийся выбросил 4 и 7, поэтому он сделал 4 стопки по 7 кубиков унификса в каждой.
• Учащиеся пропускают счет или используют многократное сложение, чтобы найти общее количество кубиков unifix, которые они поставили друг на друга. Они должны показать свою работу на доске.
• Учащийся с наибольшим произведением побеждает в этом раунде и получает очко. Студенты должны вести учет своих баллов на отдельном листе бумаги.
• Снова начните с шага №1. Учащиеся продолжают бросать кости и составлять стопки, соединяя кубики. Вы можете продолжать эту игру столько, сколько захотите, хотя я считаю, что около 15 минут — это достаточное количество времени. Студент, набравший наибольшее количество очков в конце игры, становится победителем!

Заштрихуйте их

Описание: 

В этой математической игре учащиеся заштриховывают матрицы умножения на миллиметровой бумаге. Они бросают кости, чтобы узнать, из скольких строк и столбцов получится их массив. Играйте с 2 учениками в каждой группе.

Материалы:

• миллиметровая бумага (вы также можете использовать мою печатную миллиметровую бумагу, которую я даю бесплатно как часть моей электронной книги «Как научить умножению и делению». Загрузите мою электронную книгу ниже, чтобы получить бесплатную копию Stack ’em up! )
• обычный карандаш или цветной карандаш
• Пара игральных костей

Как проехать:

• Ученики ходят по очереди. Первый учащийся бросает два кубика, которые обозначают строки и столбцы массива.
• Первый ученик закрасил нужное количество строк и столбцов в любом месте на миллиметровке. В приведенном выше примере учащийся только что выкинул 1 и 5. Он может закрасить 1 строку и 5 столбцов или 5 строк и 1 столбец.
• Теперь очередь второго ученика. Второй ученик бросает кости и заштриховывает ряд, представленный кубиками.
• Учащиеся продолжают по очереди бросать кости и заштриховывать ряды. Первый ученик, которому не хватило места и который не может найти место для тени в своем массиве, проигрывает. Другой ученик – победитель!

Игры на умножение для бетонной фазы

Война на умножение

Описание:

Я объявляю войну! В классической игре учащиеся переворачивают по две карточки и умножают числа на карточках. Играйте в эту математическую карточную игру с 2–4 учащимися в каждой группе (хотя, если вы играете с более чем 2 учащимися, вам следует объединить 2 колоды игральных карт).

Материалы:

• Item»> колода игральных карт (вы можете сделать A равным 1 и убрать J, Q и K. В качестве альтернативы, если ваши ученики готовы умножать большие числа, вы можете сделать J равным 10, Q – 11, K – 12.)

Направления:

• Перетасуйте карты и переверните их стопкой.
• Учащиеся по очереди берут по две карты с верха стопки.
• Учащиеся переворачивают свои карточки. Число на каждой карточке представляет коэффициенты, которые необходимо умножить. Учащиеся умножают свои множители и произносят произведение вслух. Например, если бы я перевернул 8 и 7, я бы сказал: 8 x 7 равно 56.
• Учащийся с наибольшим произведением выигрывает этот раунд и собирает все карточки.
• Вернитесь к шагу №1. Учащиеся продолжают умножать две игральные карты до тех пор, пока карт не останется. Ученик, собравший больше всего карточек к концу игры, становится победителем!

Домино для умножения

Описание:

В этой математической игре используются домино, чтобы помочь учащимся попрактиковаться в умножении. Учащиеся переворачивают костяшки домино и умножают числа с обеих сторон костяшки. Играйте с 2–4 учащимися в каждой группе (хотя, если вы играете с более чем 2 учащимися, вы можете объединить 2 колоды домино.)

Материалы:

• набор костяшек

Направления:

• Перемешайте костяшки домино и положите их лицевой стороной вниз на стол.
• Каждый ученик выбирает одну костяшку домино, чтобы перевернуть ее одновременно.
• Item»> Числа на каждой стороне костяшки домино представляют факторы. Учащиеся умножают два числа, чтобы найти произведение. Например, если у меня есть 1 и 6, я умножаю 1 x 6 = 6.
• Учащийся с наибольшим результатом выигрывает все костяшки домино в этом раунде.
• Вернитесь к шагу №1. Учащиеся продолжают переворачивать костяшки домино и умножать множители. Ученик, собравший к концу игры наибольшее количество костяшек домино, становится победителем!

Умножение дженга

Описание:

Мне нравится «математизировать» уже существующие игры в моем классе. Вы можете прикрепить факты умножения к плиткам дженга, и учащиеся будут решать задачи по ходу игры. Играйте в «Умножение дженга» с 2 — 6 студентов в группе

Материалы:

• Item»> Дженга игра
• уравнения умножения. Вы можете распечатать или написать от руки задачи на умножение на небольших листочках бумаги и приклеить их к верхней части каждой плитки Дженга.

Направления:

• Первый ученик выбирает плитку дженги, чтобы убрать ее с башни и положить на вершину. После того, как ученик вытащил плитку Дженги, он должен решить уравнение умножения, прежде чем положить ее обратно на башню.
• Следующий ученик делает ход и повторяет шаг №1.
• Учащиеся продолжают решать задачи на умножение, наклеенные на плитки Дженга, в свой ход.
• Совет для профессионалов: вы можете перепрофилировать Jenga, чтобы помочь вашим ученикам практиковать и другие математические факты! Наклейте на плитки факты сложения, вычитания или деления, чтобы сделать вычисления более увлекательными.

Настольные игры умножение

Описание:

Подобно дженге, мне нравится перепрофилировать любимые настольные игры и «математизировать» их для практики умножения. «Жёлобы и лестницы» всегда были любимой игрой в классе, даже среди моих старших учеников, хотя вы можете использовать любую настольную игру, которая есть в вашем классе. По мере прохождения игры учащиеся решают факты умножения. Играйте с 2-6 учениками в группе.

Материалы:

• карточки фактов умножения. Вы можете использовать карточки или записать факты умножения на каталожных карточках.
• настольная игра. Вы можете использовать любую настольную игру, которая есть у вас в классе.

Как добраться:

• Item»> Перетасуйте карточки для умножения или каталожные карточки и переверните их стопкой.
• Каждый раз, когда учащийся делает ход, он должен сначала взять карту умножения с верха стопки и решить уравнение. Как только они решат уравнение, они могут бросить кости и продолжить игру.
• Учащиеся по очереди переворачивают карточку умножения и решают задачу в начале своего хода.

ЗАКЛЮЧЕНИЕ…

Надеюсь, некоторые из этих игр на умножение пригодятся вам в ваших математических центрах! Подобные увлекательные математические игры, особенно те, в которых используются манипуляции и рисунки, особенно полезны для учащихся специального образования, которым необходимо укрепить свое концептуальное понимание.

Обязательно загрузите электронную книгу «Как научить умножению и делению» ниже, чтобы получить бесплатную копию двух игр на умножение и одной игры на деление.