6 – 1 | 5+0 | |
3+2 | 1+3 | 7+1 |
4+1 | 7-2 | 10 – 5 |
9 — 2 | 3+3 | 3+1+1 |
2+3 | 7-1-1 | 8 — 3 |
Конспект урока математики «Сложение и вычитание в пределах 10» в 1 классе
.
Урок математики «Сложение и вычитание в пределах 10»
ФИО учителя | Кузнецова Ольга Васильевна | |
Место работы | МБОУ СОШ № 1 | |
Должность | Учитель начальных классов | |
Предмет | Математика | |
Класс | 1 |
Тема: «Сложение и вычитание в пределах 10»
(закрепление пройденного).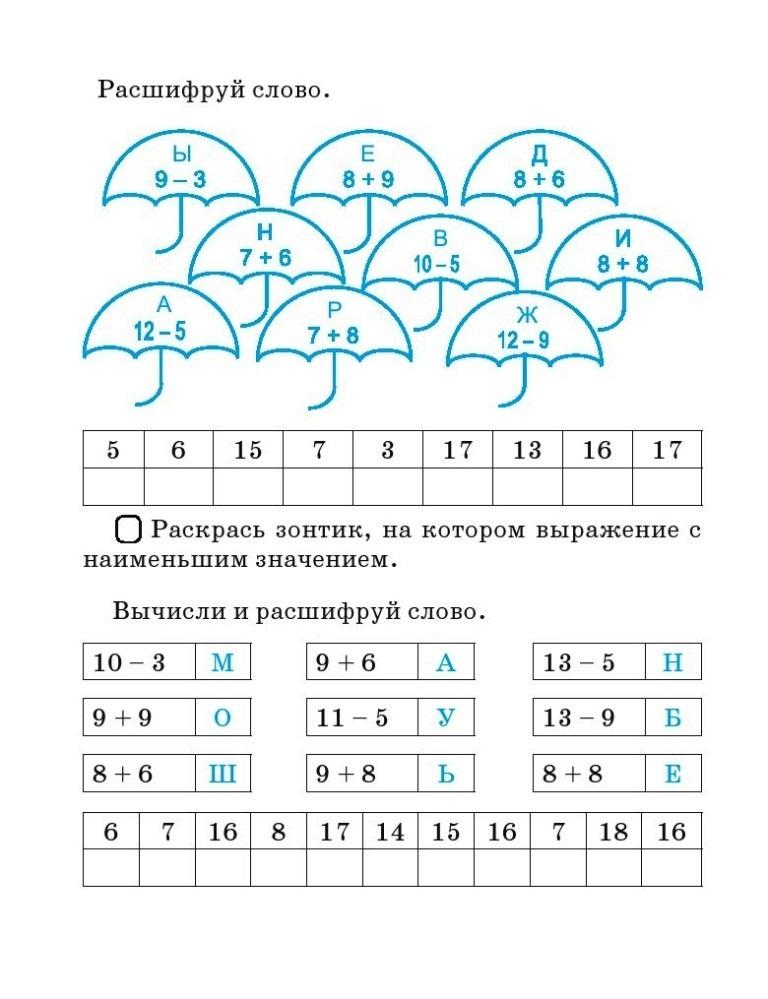
Цель урока: закрепить изученный материал
Задачи:
Выявить у учащихся уровень знаний состава числа 10, умение выполнять действия сложения и вычитания в пределах 10, решать задачи на уменьшение числа на несколько единиц, связанные со сравнением двух групп предметов,.
Развивать воображение детей, математическую речь, логическое мышление, память, внимание.
Воспитывать бережное отношение к здоровью.
Оборудование: картинки с изображением обезьянок, попугаев, Бармалея с попугаем на плече, доктора Айболита.
Ход урока.
Организационный момент.
Учитель. Улыбнитесь друг другу, садитесь.
Руки?
Дети. На месте!
Учитель. Ноги?
Ноги?
Дети. На месте!
Учитель. Локти?
Дети. У края.
Учитель. Спина?
Дети. Прямая!
Объявление темы урока.
Учитель. Ребята, все вы, наверное, знаете замечательное произведение Корнея Ивановича Чуковского «Доктор Айболит». Это сказочный доктор, который лечит зверей. Сегодня мы побываем у него в гостях. Но так как это сказка, в ней могут быть самые удивительные и непредвиденные ситуации. Чтобы выйти победителями из таких ситуаций, нам потребуются ваши знания и умения. Вы должны показать, как научились решать примеры, задачи, как вы знаете состав чисел, а значит, будут нужны ваши дружба и внимательность.
Повторение изученного материала.
Пространственная ориентировка.
На доске висит картина, где под деревом сидит доктор Айболит и около него звери.
Добрый доктор Айболит,
Он под деревом сидит.
Приходи к нему лечиться
И корова, и волчица,
И жучок, и червячок,
И медведица!
Всех излечит, исцелит
Добрый доктор Айболит!
Учитель. Сегодня мы в гостях у доктора Айболита. К нему пришли его друзья. Этих зверей и птиц он уже вылечил. Они здоровые, посмотрите, какие они весёлые, жизнерадостные, у них всё хорошо.
Учитель. Ребята, скажите, сколько сказочных героев расположены слева?
Дети. 3.
Учитель. А сколько героев справа?
Дети. 4.
Учитель. Где сказочных героев больше, слева или справа?
Дети. Справа.
Учитель. На сколько?
На сколько?
Дети. На 1 .
Учитель. Что можете сказать о сказочных героях, которые стоят слева и перед доктором Айболитом?
Дети. Их поровну.
Устный счёт.
Учитель. Ребята, доктор Айболит и его друзья принесли вам задание. Они хотят посмотреть, как вы решаете устно, читая выражения по — разному.
(Карточки с примерами)
4+1 3+2 5+3
6-1 7-2 5-3
Минутка чистописания.
Учитель. Ребята, сколько всего сказочных героев пришли в гости к доктору Айболиту?
Дети. 10.
Учитель. Сегодня на минутке чистописания будем писать число 10. Охарактеризуйте его.
Дети. Оно двузначное,чётное, состоит из двух знаков: из цифр 1 и 0.
Работа по теме урока.
Учитель. Ребята, смотрите, кто это? (Змея).
Посмотрите, какая она необычная. Сейчас вы должны быть внимательными.
— Прочитайте числа. В каком порядке они записаны?
Дети. В порядке возрастания.
Учитель. Как получается следующее число?
Дети. К числу прибавляют 2 и получают число через одно.
Учитель. Назовите следующие числа.
Дети. Это числа 8, 10.
Учитель. Какое из всех чисел лишнее?
Дети. «Лишнее» число 10 – оно двузначное, другие однозначные.
Учитель. Назовите геометрические фигуры.
Дети. Треугольник, круг, квадрат.
Учитель. Какая фигура «лишняя»?
Дети. Круг- нет углов. (по форме)
Треугольник – другого цвета. (по цвету)
Учитель. Какой записан арифметический знак?
Дети. Знак плюс.
Учитель. Назовите по-другому.
Дети. Знак сложения.
Учитель. В какой части формулировки задачи используется знак…
(Учитель показывает карточку со знаком вопроса).
Дети. В вопросе.
Учитель. Из каких частей ещё состоит задача?
Дети. Условие, решение, ответ.
Учитель. Ещё раз внимательно посмотрите на змею и запишите всё, что вы видели в строчку в том порядке, в каком записано на змее, начиная с головы.
Учитель закрывает змею. Дети выполняют задание. Проверка.
Учитель. Пока вы пишете, доктор Айболит будет лечить змею.
Учитель. Поднимите руку те, кто допустил 1 ошибку, 2 ошибки.
Зазвонил телефон. (Магнитофонная запись). Учитель берёт трубку телефона.
Учитель. Кто говорит?
— Крокодил.
Учитель. Что случилось?
— Наши детки заболели. Приезжайте в Африку скорей и вылечите наших малышей.
Учитель. Ребята, Айболиту срочно надо попасть в Африку. Может быть и мы отправимся вместе с доктором? Не боитесь опасностей?
Дети. Нет!
Учитель. Чтобы нам быстрее добраться. Полетим на самолёте. Нас много, и, чтобы побыстрее завершить посадку, подниматься в самолет будем по двум лестницам, каждая из которых состоит из пяти ступенек.
Учитель вызывает к доске двух учеников.
Учитель. Ваша задача: я даю вам по 6 карточек, а вы должны выбрать такие, которые выражали бы состав числа 10.
4+6 9-1
8+2 3+6
7+3 2+8
5+4 3+7
1+9 6+4
5+5 5+5
Остальные работают по карточкам.
7 3 5 2 4 9 1 3 8 2 5 8 4 5 5 2 3 9 6 4 2 1 0 10 |
Учитель. Обведите на каждой строчке числа, при сложении которых получается 10.
Обведите на каждой строчке числа, при сложении которых получается 10.
— Эти карточки будут билетом для вас для посадки на самолёт.
Карточки сдают учителю. Проверка детей, работающих у доски.
Физкультминутка.
Руки ставим мы вразлёт.
Появился самолёт.
Мах крылом туда-сюда.
Делай раз и делай два.
Раз и два, раз и два.
Руки в стороны держите,
Друг на друга посмотрите,
Раз и два, раз и два.
Опустите руки вниз,
И на место все садись.
Решение задач.
Учитель. Чтобы дорога показалась нам недолгой, а летим мы в Африку, будем решать задачи про её жителей.
Посмотрите внимательно на картинку и составьте задачу.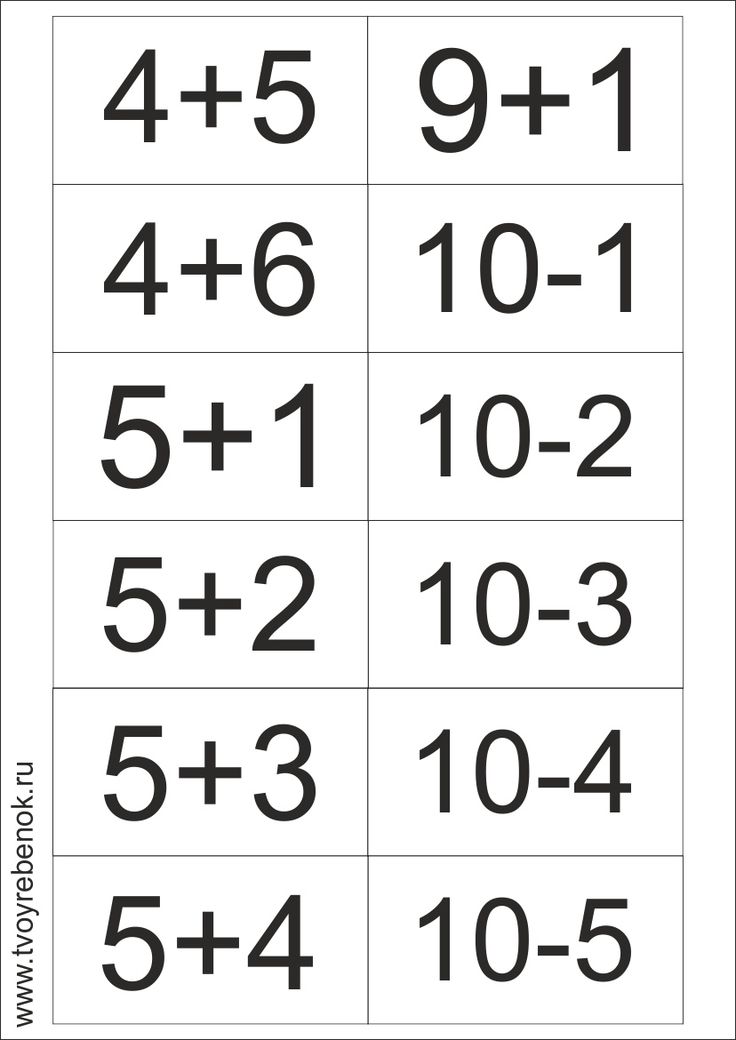
Дети видят пальму, на ней сидят 4 попугая. К ним летит ещё1.
.
Дети. На пальме сидели 4 попугая, к ним прилетел ещё 1 попугай. Сколько попугаев стало?
Учитель. О ком говорится в задаче?
Дети. О попугаях.
Учитель. Что нам известно?
Дети. Что их было 4, к ним прилетел ещё 1.
Учитель. Что неизвестно?
Дети. Сколько их стало?
Учитель. Их стало больше или меньше?
Дети. Больше.
Учитель. Каким действием выполним решение?
Дети. Сложением.
(Решение записывают в тетрадь).
(Проверка индивидуальных карточек)
Учитель. На второй пальме сидели обезьяны (они закрыты, дети их не видят). Их на 2 меньше, чем попугаев. Сколько обезьян на пальме?
Их на 2 меньше, чем попугаев. Сколько обезьян на пальме?
— О ком говорится в задаче? (О попугаях и об обезьянках)
— Что известно в задаче? (Что попугаев было 5)
— Что сказано про обезьянок ? (Их неизвестно, но сказано, что их было на 2 меньше.)
— А что значит на 2 меньше? (Столько же, но без двух).
— Каким действием решаем задачу?(Вычитанием).
— Запишите решение в тетрадь.(Один у доски)
Учитель. Будьте ещё внимательнее. Узнайте теперь, сколько всего попугаев и обезьянок на двух пальмах. (устно)
Физминутка.
(Дети танцуют под музыку «Чунга- чанга»)
Учитель. Наш самолёт совершил посадку. Ребята, посмотрите, кто это?
Ребята, посмотрите, кто это?
Дети. Это разбойник Бармалей.
Бармалей. Я – разбойник,
Я – злодей,
Я – ужасный Бар – ма — лей!
(Голос Бармалея записан на магнитофонной ленте.)
Бармалей. Не пущу я вас к больным, пока не решите мою задачу.
Масса моего попугая, стоящего на двух ногах – 3 кг. Какова будет масса
попугая, если он встанет на одну ногу?
(Ответы детей).
Бармалей. Да, справились, молодцы, но мы с вами ещё встретимся.
Учитель. А вот и больной. Да у вас ангина! Пока доктор Айболит лечит больного, и, чтобы ему стало легче, мы выполним математический диктант.
Какое число на 1 больше, чем 9?
Какое число на 1 меньше, чем 7?
К 3 прибавьте 1.

Первое слагаемое 2, второе слагаемое 3, найдите сумму.
10 уменьшить на 2.
5 увеличить на 2.
У доски один ученик пишет ответы, остальные – в тетрадях.
Проверка.
Учитель. Вот и вылечили больных! Звери благодарят вас и желают вам, чтобы вы были здоровы, счастливы.
Итог урока.
Учитель. Вот и закончилось наше путешествие. Кому понравилось сегодняшнее путешествие?
Нам пора домой. Пока летим обратно, скажите, какие математические задания вы выполняли?
О других путешествиях доктора Айболита вы узнаете, прочитав книгу «Доктор Айболит»
Оценивание.
лекция1
Лекция
1
Типы весов и уровни измерения
Дискретные и
непрерывные переменные
В тексте Даниэля различаются дискретные и непрерывные переменные. Эти
являются техническими различиями, которые не будут так важны для нас в этом
учебный класс. Согласно тексту, дискретные переменные — это переменные, в которых
промежуточные значения невозможны. Например, количество телефонных звонков.
вы получаете в день. Вы не можете принимать телефонные звонки 6.3. Непрерывные переменные
все остальное; любая переменная, которая теоретически может иметь значения между
баллы (например, от 153 до 154 фунтов). Оказывается, это
не все, что полезно различия для наших целей. Что на самом деле больше
важным для статистических соображений является уровень измерения использовал. Когда я говорю, что это более важно, я действительно преуменьшаю это.
Понимание уровня измерения переменной (или шкалы, или меры)
Первое и самое важное различие, которое необходимо сделать о переменной, когда
занимаюсь статистикой!
Эти
являются техническими различиями, которые не будут так важны для нас в этом
учебный класс. Согласно тексту, дискретные переменные — это переменные, в которых
промежуточные значения невозможны. Например, количество телефонных звонков.
вы получаете в день. Вы не можете принимать телефонные звонки 6.3. Непрерывные переменные
все остальное; любая переменная, которая теоретически может иметь значения между
баллы (например, от 153 до 154 фунтов). Оказывается, это
не все, что полезно различия для наших целей. Что на самом деле больше
важным для статистических соображений является уровень измерения использовал. Когда я говорю, что это более важно, я действительно преуменьшаю это.
Понимание уровня измерения переменной (или шкалы, или меры)
Первое и самое важное различие, которое необходимо сделать о переменной, когда
занимаюсь статистикой!
Уровни
измерения
Статистики часто ссылаются на «уровни измерения»
переменная, мера или шкала, чтобы различать измеряемые переменные, которые
имеют разные свойства. Различают четыре основных уровня: номинальный, порядковый,
интервал и отношение.
Различают четыре основных уровня: номинальный, порядковый,
интервал и отношение.
Номинальная
Переменная, измеренная по «номинальной» шкале,
переменная, которая на самом деле не имеет никакого оценочного различия. Одно значение
на самом деле не больше, чем другой. Хорошим примером номинальной переменной является
пол (или пол). Информация в наборе данных о поле обычно кодируется как 0 или 1, 1.
указывает на мужчину и 0 указывает на женщину (или наоборот — 0 для мужчин, 1
для женского пола). 1 в данном случае является произвольным значением и не больше и не больше.
лучше, чем 0. Между 0 и 1 существует только номинальная разница. При номинальном
переменных, существует качественная разница между значениями, а не количественная
один.
Порядковый номер
Нечто, измеряемое по «порядковой» шкале
имеет оценочный оттенок. Одно значение на больше или больше или лучше
чем другой. Продукт А предпочтительнее продукта Б, поэтому А получает
значение 1, а B получает значение 2. Другим примером может быть оценка вашего
удовлетворенность работой по шкале от 1 до 10, где 10 означает полное
удовлетворение. С порядковыми шкалами мы знаем только, что 2 равно
лучше 1 или 10 лучше 9; мы не знаем, насколько. Это может варьироваться. Расстояние между 1 и 2 может быть короче, чем между 9и 10.
Другим примером может быть оценка вашего
удовлетворенность работой по шкале от 1 до 10, где 10 означает полное
удовлетворение. С порядковыми шкалами мы знаем только, что 2 равно
лучше 1 или 10 лучше 9; мы не знаем, насколько. Это может варьироваться. Расстояние между 1 и 2 может быть короче, чем между 9и 10.
Интервал
Переменная, измеренная по интервальной шкале, дает
информация о большем или лучшем качестве порядкового номера
шкалы делают, но интервальные переменные имеют одинаковое расстояние между каждым значением.
Расстояние между 1 и 2 равно расстоянию между 9 и 10.
Хорошим примером является температура в градусах Цельсия или Фаренгейта.
такая же разница между 100 градусами и 90, как и между 42 и 32.
отношение
свойства, которыми обладает интервальная шкала, за исключением того, что при масштабировании отношений
абсолютный нуль. Примером является температура, измеряемая в градусах Кельвина. Здесь нет
возможное значение ниже 0 градусов Кельвина, это абсолютный ноль. вес это другое
например, 0 фунтов. является осмысленным отсутствием веса. Баланс вашего банковского счета составляет
еще один. Хотя у вас может быть отрицательный или положительный баланс счета, существует
определенное и непроизвольное значение счета
остаток 0.
вес это другое
например, 0 фунтов. является осмысленным отсутствием веса. Баланс вашего банковского счета составляет
еще один. Хотя у вас может быть отрицательный или положительный баланс счета, существует
определенное и непроизвольное значение счета
остаток 0.
Можно думать о номинальном, порядковом, интервал и отношение как ранжированные по отношению друг к другу. Соотношение более сложный, чем интервал, интервал более сложный, чем порядковый номер, и порядковый более сложный, чем номинальный. Я не знаю, есть ли ранги равноудалены или нет, вероятно, нет. Так что же это за уровень измерения? ранжирование уровней измерения?? Я бы сказал порядковый. В статистике лучше быть немного консервативен, когда сомневаешься.
Два
Общие классы переменных (кого это волнует?)
Хорошо, помните, я сказал, что это первое и самое важное отличие
при использовании статистики? Вот почему. В большинстве случаев статистики или
исследователи кончают тем, что заботятся только о разнице между номинальными и всеми
другие. Как правило, существует два класса статистики: те, которые имеют дело с
номинальные зависимые переменные и те, что имеют дело с порядковыми, интервальными,
или относительные переменные. (Сейчас мы сосредоточимся на зависимой переменной и
позже мы обсудим независимую переменную). Когда я описываю эти типы
два общих класса переменных, я (и многие другие) обычно называю их
«категорический» и «непрерывный». (Иногда я буду использовать «дихотомический»
вместо «категорический»). Отметим также, что
«непрерывный» в этом смысле не совсем то же самое, что
«непрерывный» используется в главе 1 текста при различении
между дискретным и непрерывным. Это гораздо более свободный термин. Категоричность и
дихотомические обычно означают, что шкала является номинальной. «Непрерывный»
переменные обычно являются порядковыми или лучше.
Как правило, существует два класса статистики: те, которые имеют дело с
номинальные зависимые переменные и те, что имеют дело с порядковыми, интервальными,
или относительные переменные. (Сейчас мы сосредоточимся на зависимой переменной и
позже мы обсудим независимую переменную). Когда я описываю эти типы
два общих класса переменных, я (и многие другие) обычно называю их
«категорический» и «непрерывный». (Иногда я буду использовать «дихотомический»
вместо «категорический»). Отметим также, что
«непрерывный» в этом смысле не совсем то же самое, что
«непрерывный» используется в главе 1 текста при различении
между дискретным и непрерывным. Это гораздо более свободный термин. Категоричность и
дихотомические обычно означают, что шкала является номинальной. «Непрерывный»
переменные обычно являются порядковыми или лучше.
Порядковые шкалы с несколькими категориями
(2,3 или, возможно, 4), а номинальные меры часто классифицируются как категориальные.
и анализируются с использованием биномиального класса статистических тестов, тогда как порядковые
шкалы со многими категориями (5 или более), интервалом и отношением, как правило,
проанализированы с помощью нормального теоретического класса статистических тестов.
Общие классы
Статистика (О, думаю, мне все равно)
Итак, у нас есть эти две общие категории (т. е. непрерывная и категоричная),
что дальше? Ну, это различие (как бы нечетко оно ни звучало) имеет очень важное значение.
последствия для типа используемой статистической процедуры, и мы будем делать
решения, основанные на этом различии на протяжении всего курса
 Итак, вот таблица
обобщить.
Итак, вот таблица
обобщить.
Тип зависимого Переменная (или шкала) | Уровень Измерение | Общий класс
Статистика | Примеры Статистические процедуры |
Категориальный (или дихотомический) | номинальный, порядковый номер с 2, 3 или 4 уровни | бином | хи-квадрат, логистическая регрессия |
Непрерывный | порядковый номер с более чем 4 категории | обычный | Дисперсионный анализ, регрессия, корреляция, t-критерий |
Опрос
Вопросы и меры: некоторые распространенные примеры
На практике исследователи
и проблемы исследования реальной жизни не говорят вам, как зависимая переменная
должны быть разделены на категории, поэтому я обозначу несколько типов вопросов для опроса или
другие общепринятые меры.
Да/Нет
Вопросы
Шкала Лайкерта
В опросе особого типа используется набор
ответы, упорядоченные таким образом, что один ответ больше другого.
термин Шкала Лайкерта названа в честь изобретателя,
Ренсис Лайкерт, чье имя
произносится как «Ликерт». Как правило, это
термин используется для любого вопроса, который имеет около 5 или более возможных вариантов. Ан
Примером может быть: «Как бы вы оценили администратора вашего отдела?»
1=очень некомпетентен, 2=несколько некомпетентен, 3=не компетентен, 4=несколько
компетентный или 5 = очень компетентный. шкалы Лайкерта
либо порядковый, либо интервальный, и многие психометристы
утверждал бы, что они являются интервальными шкалами, потому что, когда они хорошо построены,
является равным расстоянием между каждым значением.
Физический
Меры
Большинство физических мер, таких как
рост, вес, систолическое артериальное давление, расстояние и т. д., являются интервалом или соотношением
шкалы, поэтому они попадают в общую «непрерывную»
категория. Поэтому статистика типа нормальной теории также используется, когда такая мера служит зависимой переменной в анализе.
анализ.
Подсчеты
Подсчеты сложны. Если переменная измеряется счетом, например, если
Исследователь подсчитывает количество дней, в течение которых пациент находился в больнице.
госпитализации, переменная находится на шкале отношений и рассматривается как непрерывная
переменная. Однако часто рекомендуются специальные статистические данные, т.к.
переменные часто имеют очень асимметричное распределение с
большое количество случаев с нулевым счетом (см. Agresti,
1990, с.

Что такое простое число? Объяснение для родителей, учителей и детей
Простое число — это число, которое можно разделить только само на себя и на 1 без остатка. Здесь мы объясним, что именно это означает, дадим вам список простых чисел, которые дети должны знать в начальной школе, и предоставим вам несколько практических вопросов и примеров.
Что такое простое число?
Простое число — это целое число больше 1, имеющее только два делителя — самих себя и 1.
Простое число нельзя разделить ни на какие другие положительные целые числа без остатка, десятичной дроби или дроби.
Примером простого числа является 13. Его делителями являются только 1 и 13. Деление простого числа на другое натуральное число приводит к остатку чисел, например. 13 ÷ 6 = 2 остаток 1.
15 не является примером простого числа, потому что его можно разделить на 5 и 3, а также само на себя и 1.
15 является примером составного числа, поскольку оно имеет более двух делителей.
Простые числа часто рассматриваются математиками в качестве «строительных блоков» в теории чисел. Основная теорема арифметики гласит, что составное число можно представить в виде произведения простых чисел.
См. также: Правила делимости
Примеры простых чисел
Как определить, является данное число простым или нет, на основе свойств простых чисел.
Какие простые числа?
- Есть 8 простых чисел меньше 20: 2, 3, 5, 7, 11, 13, 17 и 19.
- Первые 10 простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
- Существует 25 простых чисел от 1 до 100.
- Простые числа включают большие числа и могут продолжаться далеко за пределы 100.
- Например, 21 577 — простое число.
Список простых чисел до 100
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
Обратите внимание, что этот список простых чисел содержит только нечетные числа, кроме 2.
Наименьшее простое число
2 — наименьшее простое число. Это также единственное четное простое число — все остальные четные числа могут делиться сами на себя, по крайней мере, на 1 и 2, то есть они будут иметь как минимум 3 делителя.
Наибольшее простое число
Греческий математик Евклид (один из самых известных математиков классической эпохи) записал доказательство того, что среди множества простых чисел нет наибольшего простого числа. Тем не менее, многие ученые и математики все еще пытаются найти его в рамках Великого Интернет-поиска простых чисел Мерсенна.
наибольшее известное простое число (по состоянию на ноябрь 2020 г.) равно 2 82 589 933 − 1, число, состоящее из 24 862 048 цифр при записи по основанию 10. До этого самым большим известным простым числом было 2 77 232 917 90 имеющий 23 249 425 цифр.
К тому времени, как вы это прочтете, он может стать еще больше, но вы можете следить за его развитием в Википедии.
Часто задаваемые вопросы о простых числах
Что такое простое число в математике?
Простое число — это число, которое можно разделить только на себя и на 1 без остатка.
Какие простые числа от 1 до 100?
Простые числа от 1 до 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Почему 1 не является простым числом?
1 не является простым числом, потому что оно имеет только один делитель, а именно 1. Простые числа должны иметь ровно два делителя.
Почему 2 простое число?
2 — простое число, потому что его единственными делителями являются 1 и оно само.
Является ли 51 простым числом?
51 не является простым числом, потому что оно имеет 3 и 17 в качестве делителей, а также само себя и 1. Другими словами, 51 имеет четыре делителя.
Рабочие листы с простыми числами
БЕСПЛАТНЫЕ рабочие листы, содержащие 29 вопросов и ответов по простым числам для 5-го и 6-го классов!
Простые числа в начальной школе
Простые числа не вводятся в Великобритании до 5-го класса.
Согласно национальной учебной программе, дети 5-го класса должны знать и использовать словарь простых чисел, простых множителей и составных (не простых) чисел. установить, является ли число до 100 простым, и вспомнить простые числа до 19».
В 6-м классе дети должны уметь «находить общие делители, общие кратные и простые числа» .
Как простые числа используются в реальном мире?
Одним из наиболее важных применений простых чисел является кибербезопасность — обеспечение большей безопасности информации, передаваемой через Интернет.
Чтобы зашифровать (защитить) такие вещи, как данные кредитной карты, медицинские записи и даже некоторые службы обмена сообщениями, такие как WhatsApp, инженеры-программисты создают алгоритмы, используя простые числа.
Перемножая два очень больших простых числа (некоторые компании используют простые числа, состоящие из сотен цифр!), мы получаем еще большее число, исходные множители которого (два очень больших простых числа) известны только нам. Затем мы используем это еще большее число для шифрования нашей информации.
Если кто-то еще хочет узнать, какую информацию мы посылаем, он должен выяснить, каковы были наши первоначальные факторы. С такими длинными простыми числами, как те, которые мы использовали, им могут потребоваться годы или даже десятилетия постоянных проб и ошибок, прежде чем они найдут хотя бы одно. Такая криптография с открытым ключом обеспечивает безопасность нашей информации.
Хотите знать, как объяснить своим детям другие ключевые слова по математике? Загляните в наш Начальный математический словарь или попробуйте эти основные математические термины:
- Что такое число в кубе: разъяснения для основных родителей и детей
- Что такое наименьшее общее кратное: объяснение для основных родителей и детей
- Что такое самый высокий общий фактор: объяснение для основных родителей и детей
Вопросы о простых числах
1) Квадратное число и простое число имеют в сумме 22. Какие это два числа?
Какие это два числа?
A: 9 и 13
2) Эмма думает о двух простых числах. Она складывает два числа вместе. Ее ответ — 36. Напишите все возможные пары простых чисел, которые могла придумать Эмма.
A: 5 и 31, 7 и 29, 13 и 23, 17 и 19
3) Обведите два простых числа – 29, 59, 39, 69, 29
A: 29 и 59
4
4) Запишите три простых числа, при умножении которых получается 231.A: 3 x 7 x 11
ЗАДАНИЕ: Чен выбирает простое число. Он умножает его на 10, а затем округляет до ближайшей сотни. Его ответ — 400. Напишите все возможные простые числа, которые мог выбрать Чен.
A: 37, 41 или 43.
Онлайн-центр Third Space Learning Maths Hub содержит сотни математических ресурсов для учителей начальной школы и родителей, которые можно использовать в школе и дома. Регистрация на бесплатных математических ресурсах выполняется быстро, легко и доступна для всех сотрудников вашей школы. Чтобы получить доступ к премиум-ресурсам, вашей школе потребуется премиум-подписка Maths Hub. Кроме того, доступ ко всем ресурсам премиум-класса включен бесплатно для школ, подписавшихся на наше онлайн-обучение по математике.
Чтобы получить доступ к премиум-ресурсам, вашей школе потребуется премиум-подписка Maths Hub. Кроме того, доступ ко всем ресурсам премиум-класса включен бесплатно для школ, подписавшихся на наше онлайн-обучение по математике.
Рабочие листы с простыми числами
- Готовые уроки Умножение и деление 5 класса (осенний блок 4) Слайды и рабочие листы
- Готовые уроки 6 класс 4 Операции (Осенний блок 2) Слайды и рабочие листы
- Рабочий лист 5-го класса: умножение и деление 1
- Рабочий лист 6-го класса: четыре операции
Видео с простыми числами
- Как учить простые и составные числа
Индивидуальные онлайн-уроки по математике, которым доверяют школы и учителя
Каждую неделю репетиторы-специалисты по математике Third Space Learning проводят еженедельные индивидуальные онлайн-уроки и математические вмешательства для тысяч учащихся начальной школы. С 2013 года мы помогли более 130 000 детей стать более уверенными в себе и способными к математике.

 Пчелёнок приготовил следующее задание:
Пчелёнок приготовил следующее задание: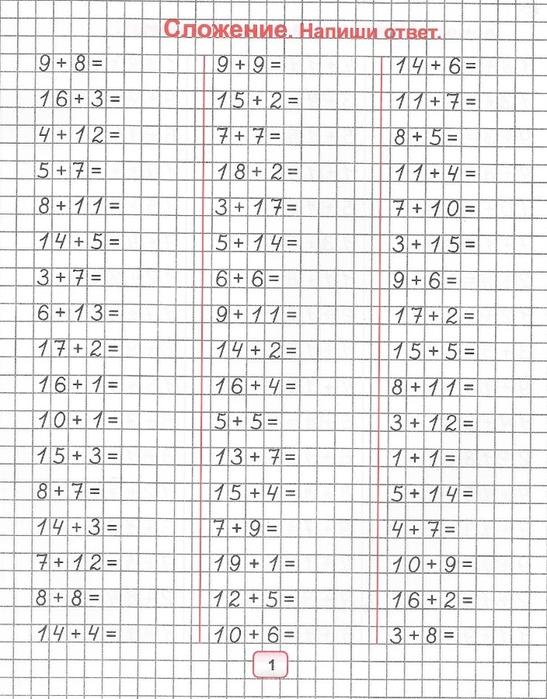 .
.

