Задачи в два действия: математика 2, 3 класс
Занимательная математика / 2 класс / Задачи в два действия
Поделитесь с друзьями:
Решение задач в несколько действий помогает развивать навыки анализа условий математических задач и текстовой информации вообще.
Образовательный проект ЛогикЛайк помогает детям научиться решать любые задачи по методике «от простого к сложному».
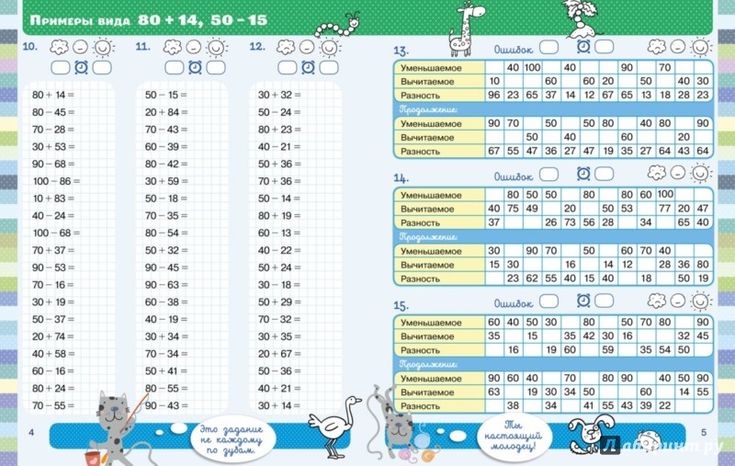
Типовые составные задачи для 1-2 класса
Простая с точки зрения математики задача решается в одно арифметическое действие. Чтобы решить составную задачу, ее нужно разложить на две или более простые или составные задачи.
Типовые задания на сложение и вычитание
Маша съела 4 мандарина, а Саша съел на 2 мандарина меньше Маши.
Сколько всего мандаринов съели ребята?
Решение:
4−2=2; 4+2=6.
Сравни выражения:
10 + 25 ? 15 + 20.
Решение:
10 + 25 = 35; 15 + 20 = 35.
Следовательно: 10 + 25 = 15 + 20.
Это довольно скучные задачи, решать которые захочется не каждому ребенку. Есть и другой подход.
Интересные составные задачи для 2-3 класса
Задача 1. Арифметический ребус
В математических ребусах одинаковые картинки скрывают одинаковые цифры. Подобные задания вызывают интерес к математике даже у дошкольников.
Показать решение
Гриб повторяется в обоих примерах. Чтобы узнать, какое число спрятано за звездой:
1. Решим пример 10-3. За грибом прячется 7.
2. Заменим гриб семеркой и решим пример 7+1.
Ответ: 8.
Задача 2. Что тяжелее, а что легче?
Фрукты взвесили 2 раза. Определи какой из наборов фруктов самый легкий.
Показать решение
Для решения задачи мы выполняем два действия:
1. Описываем неравенства из условий задачи: виноград легче ананаса, апельсин легче винограда.
2. Делаем вывод: апельсин легче, чем ананас. Итоговое неравенство:
Масса апельсина < масса винограда < масса ананаса.
Ответ: апельсин.
Задача 3. Кто больше съел?
Фиолетовый монстрик съел 4 целых апельсина, а Красный — 7 половинок таких же апельсинов. Кто съел больше?
Показать решение
1. 1 целый апельсин = 2 половинки. Посчитаем количество половинок, которое съел фиолетовый монстрик:
4 целых апельсина = 2 + 2 + 2 + 2 = 8 половинок.
2. Сравниваем количество частей апельсинов, которые съели монстрики: 8 > 7.
Ответ: фиолетовый монстрик.
Задача 4. Кто что выбрал?
На отдыхе семья взяла напрокат 2 скутера и 3 велосипеда. Папа и мама выбрали разные транспортные средства, а папа и дочка — одинаковые. У мамы и сына оказался разный транспорт. На чем поехала бабушка?
Показать решение
Подобные задачи начинают решать с группировки объектов.
1. Из условий задачи видно, что в одну группу попадают папа и дочка. Из условий про пары папа-мама, мама-сын можно сделать вывод, что сын и папа — в одной группе. С ними и дочка.
Ответ: Бабушка поехала на скутере.
Более 100 000 ребят уже занимаются логикой на ЛогикЛайк – присоединяйтесь!
Начать обучение
17 категорий, 5 уровней сложности, более 2500 заданий
Текстовые задачи на отношения — что это, определение и ответ
Отношения встречаются в различных задачах и важно понимать, как с ними работать. Отношение – это какая-то уже сокращенная дробь. То есть данные в заданиях отношения – не реальная величина, а уже сокращенная, и мы должны узнать, на сколько.
Отношение = дробь, можно сокращать и расширять.
Если это тяжело принять, то можно поступить проще: представить, что в отношениях даны не величины, а какие-то деления. Отношение обычно записывается через двоеточие, например 3:5.
Отношение обычно записывается через двоеточие, например 3:5.
Например, рассматриваем отношение конфет на двух столах – представляем, что единицы отношения – это вазочки с одинаковым количеством конфет, мы должны узнать, сколько вазочек находится на одном столе, а сколько – на другом; если рассматриваем отношение цветов, то единицы отношения – это клумбы с одинаковым количеством цветов.
Пример 1
В магазине в наличии есть карамель, шоколадные конфеты и мармеладные конфеты в соотношении \(3:5:7\) соответственно.
1. Каково отношение между карамелью и шоколадными конфетами?
Необходимо поделить количество коробок с карамелью на количество коробок с шоколадными конфетами, то есть \(3:5\).
2. Каково отношение между карамелью и мармеладными конфетами?
Необходимо поделить количество коробок с карамелью на количество коробок с мармеладными, то есть \(3:7.\)
3. Какую часть составляют мармеладные конфеты от всех конфет?
Нужно сложить количество всех коробок. Всего у нас \(3 + 5 + 7 = 15\) единиц отношения. Далее поделим единицы отношения мармеладных конфет на единицы отношения всех конфет. Таким образом, мармеладные конфеты по отношению ко всем конфетам составляют \(7:15.\ \)
Всего у нас \(3 + 5 + 7 = 15\) единиц отношения. Далее поделим единицы отношения мармеладных конфет на единицы отношения всех конфет. Таким образом, мармеладные конфеты по отношению ко всем конфетам составляют \(7:15.\ \)
4. Если в магазине есть 20 шоколадных конфет, то каково количество мармеладных?
В этом вопросе мы встречаемся с переходом от единиц отношения к абсолютной величине. Вспоминаем, что наши конфеты разложены по коробкам. То есть у нас есть 5 коробок, в которых 20 шоколадных конфет. Коробки — это единицы отношения, а шоколадные конфеты – это абсолютная величина.
Количество шоколадных конфет разделим на количество клеток \(20:5 = 4\), т.е. в каждой коробке 4 шоколадные конфеты.
Помним, что размер единицы отношения равен для всех элементов этого отношения. Значит, что во всех коробках в магазине находится по 4 конфеты.
Тогда всего в магазине 28 мармеладных конфет.
Пример 2
Отношение объема воды в большом и малом бассейне равно 3:2. Для того, чтобы поменять воду в этих двух бассейнах, потребуется 500 воды. Сколько воды в малом бассейне?
Для того, чтобы поменять воду в этих двух бассейнах, потребуется 500 воды. Сколько воды в малом бассейне?
Решение:
Представим, что вся вода из большого бассейна хранится в 3 бочках, из малого в 2 точно таких же, это будут единицы отношения. Абсолютная величина – это весь объем бассейна.
Если у нас 2 бочки от малого бассейна и 3 от большого, то всего их 5.
Мы знаем, что в 5 бочках находится 500 воды. Узнаем сколько в одной:
(500) : 5 = 100
Итак, узнаем, во сколько бочек вместится вся вода из малого бассейна, знаем их размерность, найдем объем малого бассейна.
Ответ: 200
Единицы отношения в геометрии
Единицы отношений могут встретиться и в задачах по геометрии. Смысл останется тем же: отношение — это какая-то сокращенная дробь. Например, может быть дано соотношение сторон или углов в задаче: стороны прямоугольного треугольника ABC AB и BC относятся как 3:4.
Так как отношение — это некая сокращенная дробь, то отношение сторон должно быть представлено следующим образом:
\(\frac{\text{AB}}{\text{BC}} = \frac{3x}{4x}\)
То есть мы вводим переменную, чтобы показать, что отношение не является реальным значением сторон.
Стороны могут составлять 3 и 4, 6 и 8, 333 и 444 соответственно, а также принимать любые другие значения при условия сохранения данного соотношения.
Аналогичным образом можно представить углы или другие измеряемые величины.
Примеры уроков второго шага | Второй шаг
Цифровые программы
Доступны для детей от детского сада до 8 класса
Изучите образцы всех классов младше
Детский сад
__Урок 18: Извинения могут помочь __
На этом уроке учащиеся узнают, как извиняться как способ проявления доброты и как инструмент для решения проблем в различных сценариях.
План урока (PDF)
Презентация урока
1 класс
Урок 9: Чувство разочарования
На этом уроке учащиеся узнают, какие подсказки подскажут им, когда другие могут быть разочарованы, и новый способ успокоиться, когда они сами расстроены.
План урока (PDF)
Презентация урока
2 класс
Урок 16: Как сказать о проблеме
обвинять.
План урока (PDF)
Презентация к уроку
Раздаточный материал к уроку (PDF)
3 класс
Урок 14. Задавайте вопросы
На этом уроке учащиеся узнают, как задавать вопросы, чтобы узнать, что чувствует другой человек, и понять, чего могут хотеть его друзья. или нужно.
План урока (PDF)
Презентация урока
Раздаточный материал к уроку (PDF)
4 класс
Урок 17. Уважительное высказывание
На этом уроке учащиеся узнают, как принимать во внимание точку зрения другого человека и говорить они хотят или нуждаются уважительным образом.
План урока (PDF)
Презентация урока
Раздаточный материал к уроку A (PDF)
Раздаточный материал к уроку B (PDF)
5 класс
Урок 17: Когда? Где? ВОЗ?
На этом уроке учащиеся узнают, как определить, когда и где работать над решением проблемы и кого следует привлечь.
План урока (PDF)
Презентация урока
6 класс
Раздел 4, урок 23: Уважительное общение
На этом уроке учащиеся узнают, как общаться во время конфликта, чтобы не допустить его эскалации путем самостоятельных размышлений опыт, определение уважительного общения и практика использования языка, который поможет разрешить конфликты.
Образец этого урока
План урока (PDF)
Раздаточный материал для учащихся (PDF)
7 класс
Раздел 3, урок 18: Практика позитивного внутреннего диалога
поговорите, чтобы переосмыслить сложные ситуации, в том числе обсудите, почему не всегда легко увидеть положительные стороны, и потренируйтесь замечать положительные вещи в их повседневной жизни.
Образец этого урока
План урока (PDF)
Раздаточный материал для учащихся (PDF)
8 класс
Раздел 2, урок 10: Факторы окружающей среды, способствующие издевательствам
выявление факторов окружающей среды для обсуждения правил и норм в своем собственном школьном сообществе.
Образец этого урока
План урока (PDF)
Раздаточный материал для учащихся (PDF)
Комплекты для занятий
Доступно для раннего обучения до 5 класса
Изучите образцы из всех классов младше
Раннее обучение
Тема недели 6: Спрашивайте, что вам нужно или хотите
Тематическая карточка на неделю
- 117 9004 Занятие на вынос 9000 004 Brain Builder: Остановись и Начало
Правила прослушивания
Карточки с чувствами
Детский сад
9000 Внимание 2: Фокусировка 9 190 6
Карточка еженедельного урока
Карточка выполнения
Правила прослушивания
Занятие на вынос 6 0102
6
6
6
6
6
6
6 de 1Урок 11: Проявление заботы и заботы
Еженедельная карточка урока
Brain Builder: Хлопай и жди
Карточка Follow Through
Плакат Empathy
Задание на вынос
2 класс
Урок 17.
 Решение задач, часть 1 Через карту
Решение задач, часть 1 Через картуНавыки обучения
Создатель мозга: Предложение Switcheroo
Как успокоиться Плакат
Шаги по решению проблем Плакат
3 класс
Урок 8: Принятие разногласий
Карточка еженедельных уроков
Карточка «Прохождение»
Навыки обучения
- 6
1 4
Раздаточный материал для учащихся
4 класс
Урок 15: Обращение Записи
Карточка «Преподавание урока»
Раздаточный материал для учащихся
Карточка «Прохождение»
5 класс
Урок 21: Борьба с давлением сверстников
Карточка «Преподавание урока»
Раздаточный материал для учащихся
900 Через 604
4
4
Отдел по предотвращению издевательств
Доступен для детей от детского сада до класса 5
Исследуйте примеры из классов 2 и 5 ниже
Класс 2
Урок 3: Отказ от травли
Образцы уроков
Занятие в классе
Занятие на вынос
5 класс
8 Урок 3: Отказ 0113
Образцы уроков
Занятия в классе
Возьмите- Домашнее задание
Отдел защиты детей
Доступно для раннего обучения до 5 класса
Исследуйте образцы из раннего обучения и 2 и 5 классов до
Раннее обучение
Тема недели 3: Безопасные и небезопасные прикосновения
Образцы тем на неделю
Занятия в классе
7 90-1414 4 0117
2 класс
Урок 3: Безопасность и небезопасные прикосновения
Образцы уроков
Занятия в классе
Занятия на вынос
Класс 5
004 Урок 3: Небезопасные и нежелательные прикосновенияОбразцы уроков
Занятие в классе
Занятие на вынос 9002-7 9002-
1 School TimeДоступно для детей от детского сада до 5 класса
Подробнее образцы из детского сада и 1-го класса нижеДетский сад – 1-й класс
Раздел 1, Тема 2: уверенное решение проблем
это может помочь им справиться с трудностями, а затем использовать эти стратегии, чтобы построить башню из 10 случайных предметов.

Что такое подсчет пропусков? Определение и примеры счета с пропуском
Счет с пропуском имеет дело со счетом по числу, отличному от 1. Например, с пропуском счета на 2, с пропуском счета на 3, с пропуском счета на 5, 10 или 100. Нас учат считать с пропуском в наших начальных классах, изучая подсчет чисел. Это помогает детям быстро считать предметы.
Основным применением подсчета с пропуском являются таблицы умножения или кратные числа, где мы пропускаем подсчет каждого числа, чтобы получить его кратное. Например, чтобы найти таблицу из 5, мы должны пропустить счет на 5, чтобы получить его множители, такие как 5, 10, 15, 20, 25, 30 и так далее.
Давайте изучим здесь примеры подсчета пропусков.
Что такое подсчет пропусков?
Подсчет с пропуском — это метод подсчета чисел путем добавления числа каждый раз к предыдущему числу. Например, пропускаем счет на 2, получаем 2, 4, 6, 8, 10, 12 и так далее. Следовательно, здесь мы получаем ряд четных чисел.

Примечание: - Возможен пропуск счета по любому номеру.
- Помогает быстро сосчитать число
- Счет с пропусками широко применяется в таблицах умножения.
Счетчик с пропуском вперед
Здесь мы считаем число в прямом направлении числа. Это означает, что мы пропускаем счет для положительных чисел. Подсчет пропусков имеет большое применение в реальной жизни. Предположим, нам нужно посчитать шарики, которые состоят из сотен чисел. Подсчет шариков один к одному займет больше времени. Следовательно, если мы пропустим их подсчет на любое большое число, такое как 10 или 20, мы сможем быстро их сосчитать.
Здесь мы научимся пропускать счет по разным числам.
Пропустить счет до 2
Здесь мы добавляем число 2 для каждого счета таким образом, чтобы счет представлялся чередующимися числами. Предположим, мы начинаем считать с 2, тогда, пропуская счет на 2 для каждого шага, мы можем записать как;
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, ….  , и так далее
, и так далее Пропустить счет до 3
Здесь мы добавляем число 3 для каждого шага счета.
3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60 и так далее. Пропустить счет до 4
Когда мы пропускаем количество натуральных чисел на 4, мы прибавляем 4 на каждом шаге. Вот как это сделать:
Пропустить счет на 4 Результат 0+4 4 4+4 8 8+4 12 12+4 16 16+4 20 20+4 24 24+4 28 28+4 32 32+436 36+4 40 Итак, мы можем пропустить счет 4, мы получили таблицу из 4.

Пропустить счет до 5
Когда мы считаем, пропуская 5 чисел между ними, мы пропускаем счет на 5. Давайте начнем считать, пропуская 5 и записывая последующие числа.
5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, … Пропустить счет до 10
Когда мы пропускаем счет на 10 в промежутке между счетами, то говорят, что мы пропускаем счет на 10. Пропустить счет на 10 очень легко и быстро. См. приведенный ниже пример, чтобы понять его лучше.
- 0+10 = 10
- 10+10=20
- 20+10=30
- 30+10=40
- 40+10=50
- 50+10=60
- 60+10=70
- 70+10=80
- 80+10=90
- 90+10=100
- 100+10=110
- 110+10=120
- 120+10=130
- 130+10=140
- 140+10=150
И так далее
Пропустить подсчет большими числами
Здесь мы научимся пропускать счет на более крупные числа, такие как 25, 50, 100.

Пропустить счет до 25
Когда нам нужно сосчитать сотни вещей, мы также можем пропустить счет до 25. Это поможет быстро считать. Счетчик пропусков на 25 выполняется как:
25, 50, 75, 100, 125, 150, 175, 200, 225, 250, 275, 300, …. Вы можете попрактиковаться в написании большего количества чисел в прямом счете до 25.
Пропустить счет до 50
Пропустить подсчет на 50 означает подсчет объектов после каждых 50 объектов. Это можно сделать так:
50, 100, 150, 200, 250, 300, 350, 400, 450, 500, …. Пропустить счет до 100
Если нам нужно сосчитать предметы в очень большом количестве, скажем, 1000, то мы можем пропустить счет на 100. Давайте разберемся со счетом на 100 с помощью нескольких примеров, приведенных ниже;
100, 200, 300, 400, 500, 600, 700, 800, 900, 1000, …. 
В приведенном выше счете вы можете видеть, что цифра на сотом месте меняется после каждого счета.
Таблица подсчета пропусков (от 2 до 10)
Подготовим таблицу, в которой мы увидим пропущенные числа от 2 до 10.
Считать по Пропустить счет 2 шт. 2 4 6 8 10 12 14 16 18 20 22 24 3 3 6 9 12 15 18 21 24 27 30 33 36 4 шт. 4 8 12 16 20 24 28 32 36 40 44 48 5 5 10 15 20 25 30 35 40 45 50 55 60 6 6 12 18 24 30 36 42 48 54 60 66 72 7 из 7 14 21 28 35 42 49 56 63 70 77 84 Восьмерки 8 16 24 32 40 48 56 64 72 80 88 96 Девятки 9 18 27 36 45 54 63 72 81 90 99 108 10-е 10 20 30 40 50 60 70 80 90 100 110 120 Эта таблица напоминает таблицу умножения от 2 до 10.

Обратный счет с пропуском
Студенты также могут практиковаться в обратном счете в сторону отрицательных чисел. Предположим, мы хотим пропустить счет на -2, тогда
-2, -4, -6, -8, -10, ….
Математически это возможно, но в реальной жизни мы не пропускаем счет отрицательными числами.
Но для практики вы можете пропустить счет на -3,-4,-5 или любое отрицательное число.
Пропустить примеры подсчета
Q.1: Если есть 20 шариков, то что из следующего поможет быстро считать?
- Пропустить счет на 1
- Пропустить счет на 2
Решение: пропуск счета на 2 поможет считать быстрее, чем пропуск счета на 1. На подсчет шариков уйдет половина времени, а не на подсчет по одному.
Q.2: Если в корзине 40 мячей, и нам нужно пропустить счет на 5. Тогда сколько раз нам нужно считать мячи?
Решение: дано, количество шаров = 40
Если мы пропустим счет на 5, то получим
5, 10, 15, 20, 25, 30, 35, 40
Таким образом, здесь мы пропустим счет в 5, 8 раз.

Практические вопросы
- Как пропустить счет до 9?
- Пропустить счет до 15.
- Предположим, есть 100 шариков. Пропустите эти шарики до 20.
- Пропустить счет на -10.
Связанные статьи
Часто задаваемые вопросы – Часто задаваемые вопросы
Q1
Что такое подсчет пропусков?
Счет с пропуском — это метод прямого счета на любое число, кроме 1. Если мы пропускаем счет на число, это означает, что мы добавляем это число на каждом шаге, чтобы получить другое число.
Q2
Как пропустить счет?
Подсчет с пропуском — это метод подсчета чисел путем пропуска их с определенным номером.
Например, если мы пропустим счет на 1 и начнем считать с 0, то получим последовательность четных чисел, такую как 0, 2, 4, 6, 8, 10, 12, 14, 16, 18 и т. д. .Q3
Как пропустить счет до 10?
Пропуск счета на 10 дает таблицу умножения 10, если мы начнем считать с 10.

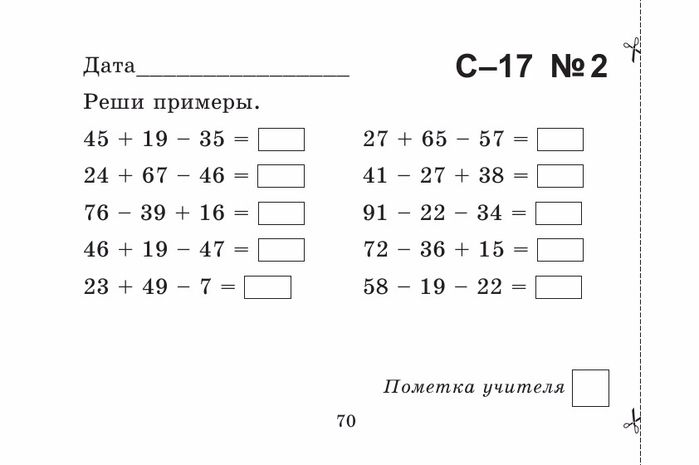
 Решение задач, часть 1 Через карту
Решение задач, часть 1 Через карту
 , и так далее
, и так далее