Математика Умножение двузначного числа на однозначное

Материалы к уроку

Конспект урока

27. Умножение двузначного числа на однозначное
Организационный этап   Математика вновь к вам пришла. В путь-дорогу с собой позвала. Все задачи и примеры, уравнения и схемы Одолеем без труда и узнаем всё тогда. Сегодня сама царица Математика приглашает нас в свою страну. Без конца твердят нам в школе: «Математика важна». На заводе, в классе, в поле Математика нужна. Сегодня на уроке мы будем учиться умножать двузначное число на однозначное.
Этап подготовки учащихся к активному сознательному усвоению знаний   Устный счёт   Всё считается со счета. Людям всюду нужен счет! Потому ему почёт! Начинаем устный счёт! И отправляемся в небольшое путешествие по стране Математике.   Задание 1 Посмотрите перед нами бурная математическая речка Слагайка, чтобы её переплыть, нужно заменить суммой разрядных слагаемых следующие числа: 15, 27, 38 Проверьте себя.   Задание 2 В стране Математике много интересного. Перед нами горы Считалы, чтобы на них подняться, нужно выполнить задание. Выберите выражение, значение которого равно 0. 1) 48 : 8 · 6 — 6 2) 48 : (1 · 6) + 6 3) 48 : 8 · (6 — 6) 4) 48 : 8 · 6 : 6 Проверьте себя. 3) 48 : 8 · (6 — 6)   Задание 3 В конкурсе портретов царицы Математики приняли участие: 5 учеников первого класса, каждый ученик предоставил по две работы. 7 учеников второго класса,  каждый ученик предоставил по две работы. 10 учеников третьего класса,  каждый ученик предоставил по три работы. Сколько работ от каждого класса было на выставке? Проверьте себя. Какое количество работ предоставлено от учеников 1 класса?                    5 · 2 = 10 Какое количество работ предоставлено от учеников 2 класса?                    7 · 2 = 14 Какое количество работ предоставлено от учеников 3 класса?                   10 · 3 = 30
Этап усвоения новых знаний   Ребята, смотрите, перед нами океан Знаний. И где-то там вдалеке есть остров Умножения. Побывать там нам поможет царица Математика. Научимся умножать двузначное число на однозначное. 42  умножаем на 6. 1. Раскладываем первый множитель на разрядные слагаемые. Что такое 42?  Это 40 и 2. 2. Применяем распределительный закон умножения: умножаем каждое разрядное слагаемое на второй множитель, а полученные результаты складываем. 42  ∙ 6 = (40  ∙ 6) + (2 ∙ 6) = 240 + 12 = 252   Запомните, чтобы умножить двузначное число на однозначное: 1.  Нужно разложить первый множитель на разрядные слагаемые. 2.  Применить распределительный  закон умножения: умножить каждое разрядное слагаемое на второй множитель, а полученные результаты сложить. Решим пример с объяснением. 17 умножить на 4. 17 раскладываем на разрядные слагаемые — это 10 и 7. Дальше применяем распределительный закон умножения: умножаем каждое разрядное слагаемое на второй множитель, а полученные результаты складываем. 10 умножаем на 4, получается 40, 7 умножаем на 4, получается 28, 40 плюс 28, получается 68.   Молодцы!   Для решения примеров подобного вида можно использовать последовательность команд, которые нужно выполнять поочерёдно или можно использовать алгоритм: Заменяем… Получится пример… Умножаем каждое слагаемое… Складываем результаты…
Этап закрепления новых знаний   Путешествуем дальше по стране Математике. Вот мы с вами уже находимся на острове Умножения. Посмотрите повсюду деревья, на которых растут числовые выражения, сорвем парочку.   Задание 1 Найдите произведение чисел 24 и 3; 19 и 4 Проверьте себя и оцените свои успехи. 24 · 3 = (20 + 4) · 3 = 20 · 3 + 4 · 3 = 60 + 12 = 72        19 · 4 = (10 + 9) · 4 = 10 · 4 + 9 · 4 = 40 + 36 = 76
Задание 2 Ребята, на острове Умножения растут даже цветы математические с задачами. На четырёх клумбах по пять кустов гвоздик и по шесть кустов роз. Сколько всего кустов на клумбах? Решите задачу, сделав схематический рисунок. Проверьте себя и оцените свои успехи. Сложим количество кустов роз и гвоздик и сумму умножим на 4, т. к. клумб всего 4: (5 + 6) · 4. Решить данное выражение можно двумя способами: 1 способ: умножим число на каждое слагаемое и полученные результаты сложим. (5 + 6) · 4 = 5 · 4 + 6 · 4 = 20 + 24 = 44 (к. ) 2 способ: вычислим сумму и умножим ее на число: (5 + 6) · 4 = 11 · 4 = 44 (к.) Ответ: на клумбах всего 44 куста.   Интересно задачи решать, Из решений можно много узнать: Сколько ниток пойдет на берет, Расход ткани на модный жакет, Сколько стоит билет на балет. Массу предметов и общий расход, Сколько ребят ушли в поход, И сколько остались полоть огород. У каждой задачи свой сюжет, И надо найти на вопрос ответ.   Во время путешествия все, конечно, проголодались, подкрепимся фруктами, решив задачу. 21 ученик получил по 3 груши. Сколько всего груш было? Решите задачу без краткой записи. Проверьте себя. 21 · 3 = (20 + 1) · 3 = 20 · 3 + 1 · 3 = 60 + 3 = 63 (г. ) Ответ: всего было 63 груши.   Задание от царицы Математики на внимание. Посмотрите на запись математических выражений и запишите только верное выражение. 17 · 2 = (10 + 7) · 2 = 10 · 2+ 7 = 20 + 7 = 34 17 · 2 = (10 + 7) · 2 = 10 · 2 + 7 · 2 = 20 + 14 = 34 Проверьте себя. 17 · 2 = (10 + 7) · 2 = 10 · 2 + 7 · 2 = 20 + 14 = 34
Этап подведения итогов   Для того чтобы умножить двузначное число на однозначное нужно: Представить двузначное число в виде суммы разрядных слагаемых. Применить правило умножения суммы на число.
Рефлексия   Ребята, наше путешествие по стране Математике подходит к концу. Но мы туда ещё обязательно вернёмся, ведь осталось ещё много математических вершин, которые мы не покорили. На прощание царица Математика дарит нам цветы, выберите себе тот, который вам подходит по итогам урока, и нарисуйте его у себя в тетради. Красный. Я работал на уроке с желанием, был уверен в себе. Желтый. Я работал на уроке с желанием, но чувствовал какое-то неудобство, волнение, но мне было интересно. Синий. Я работал на уроке без желания, боялся отвечать и выполнять работу….   Спасибо  за работу!

Остались вопросы по теме? Наши педагоги готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать педагогаОставить заявку на подбор

😃 Умножение — правила, секретные примеры, упражнения, игры

Основа математики – это четыре операции с числами и переменными: сложение, вычитание, деление и умножение. Как раз об операции умножения и пойдет речь в этой статье.

• Формулы умножения
• Сокращенное умножение
• Умножение дробей
• Таблица умножения
• Игры на развитие счета
• Развитие феноменального устного счета

Умножение чисел

Умножение чисел осваивается детьми во втором классе, и ничего в этом сложного нет. Сейчас мы рассмотрим умножение на примерах.

Пример 2*5. Это значит либо 2+2+2+2+2, либо 5+5. Берем 5 два раза или 2 пять раз. Ответ, соответственно, 10.

Пример 4*3. Аналогично, 4+4+4 или 3+3+3+3. Три раза по 4 или четыре раза по 3. Ответ 12.

Пример 5*3. Делаем так же как и предыдущие примеры. 5+5+5 или 3+3+3+3+3. Ответ 15.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Записаться на курсУзнать подробнее

---

Формулы умножения

Умножение – это сумма одинаковых чисел, например, 2 * 5 = 2 + 2 + 2 + 2 + 2 или 2 * 5 = 5 + 5. Формула умножения:

a1+a2+…+an=n*a.

Где, а – любое число, n – число слагаемых а. Допустим, а=2, тогда 2+2+2=6, тогда n=3 умножая 3 на 2, получаем 6.Рассмотрим в обратном порядке. Например, дано: 3 * 3, то есть. 3 умножить на 3 – это значит, что тройку надо взять 3 раза: 3 + 3 + 3 = 9. 3 * 3=9.

Сокращенное умножение

Сокращенное умножение – сокращение операции умножения в определенных случаях, и специально для этого выведены формулы сокращенного умножения. Которые помогут сделать вычисления наиболее рациональными и быстрыми:

Формулы сокращенного умножения

Пусть a, b принадлежат R, тогда:

1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения. 2)

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Записаться на курсУзнать подробнее

---

Умножение дробей

Рассматривая сложение и вычитание дробей, прозвучало правило, приведения дробей к общему знаменателю, чтобы выполнить расчет. При умножении этого делать не надо! При умножении двух дробей, умножается знаменатель на знаменатель, а числитель на числитель.

Например, (2/5) * (3 * 4). Умножим две трети на одну четверть. Умножаем знаменатель на знаменатель, а числитель на числитель: (2 * 3)/(5 * 4), тогда 6/20, совершаем сокращение, получаем 3/10.

Умножение 2 класс

Второй класс – это только начала изучения умножения, поэтому второклассники решают простейшие задачки на замену сложения умножением, умножают числа, учат таблицу умножения. Давайте рассмотрим задачи на умножение уровня второго класса:

1. Олег живет в пяти этажном доме, на самом верхнем этаже. Высота одного этажа равняется 2 метрам. Какова высота дома?

2. В коробке находятся 10 упаковок с печеньем. В каждой упаковке их 7 штук. Сколько печенья в коробке?

3. Миша расставил свои игрушечные машинки в ряд. В каждом ряду их 7, а рядов всего 8. Сколько у Миши машинок?

4. В столовой стоят 6 столов, а за каждым столом задвинуты 5 стульев. Сколько стульев в столовой?

5. Мама с магазина принесла 3 пакета с апельсинами. В пакетах находятся по 22 апельсина. Сколько апельсиновпринесла мама?

6. В саду растет 9 кустов клубники, а на каждом кустике растет 11 ягод. Сколько ягод растет на всех кустиках?

7. Рома положил друг за другом 8 деталей трубы, одинакового размера по 2 метра. Какова длина полной трубы?

8. В школу родители на первое сентября привезли детей. Приехало 12 машин, в каждой было по 2 ребенка. Сколькодетей привезли родители на этих машинах?

Умножение 3 класс

В третьем классе даются уже более серьезные задания. Помимо умножения будет так же проходиться Деление.

Среди заданий на умножение будет: умножение двузначных чисел, умножение столбиком, замена сложения умножением и наоборот.

Умножение столбиком:

Умножение столбиком – самый простой способ перемножить большие числа. Рассмотрим данный метод на примередвух чисел 427 * 36.

1 шаг. Запишем числа друг под другом, так чтобы 427 было на верху, а 36 внизу, то есть 6 под 7, 3 под 2.

2 шаг. Умножение начинаем с крайней правой цифры нижнего числа. То есть порядок умножения таков: 6 * 7, 6 * 2, 6 * 4, затем так же с тройкой: 3 * 7, 3 * 2, 3 * 4.

Итак, умножаем сначала 6 на 7, ответ:42. Записываем так: так как получилось 42, то 4 – десятки, а 2 – единицы, запись происходит аналогично сложению, а значит 2 записываем под шестеркой, а 4 прибавляем к двойке числа 427.

3 шаг. Затем аналогично делаем с 6 * 2. Ответ: 12. Первый десяток, который прибавляется к четверке числа 427, а второй – единицы. Складываем полученную двойку с четверкой от предыдущего умножения.

4 шаг. Умножаем 6 на 4. Ответа 24 и прибавляем 1 от предыдущего умножения. Получаем 25.

Итак, умножив 427 на 6, получился ответ 2562

ЗАПОМНИТЕ! Результат второго умножения нужно начать записывать под ВТОРОЙ цифрой первого результата!

5 шаг. Совершаем аналогичные действия с цифрой 3. Получаем ответ умножения 427 * 3=1281

6 шаг. Затем полученные ответы при умножении складываем и получаем итоговый ответ умножения 427 * 36. Ответ: 15372.

Умножение 4 класс

Четвертый класс – это уже умножение только больших чисел. Вычисление выполняются методом умножения в столбик. Метод описан выше доступным языком.

Например, найти произведение следующих пар чисел:

1. 988 * 98 =
2. 99 * 114 =
3. 17 * 174 =
4. 164 * 19 =

Презентация на умножение

Скачайте презентацию на умножение с простейшими заданиями для второклассников. Презентация поможет детям лучше ориентироваться в этой операции, потому что она составлена красочно и в игровом стиле – в лучшем варианте для обучения ребенка!

Презентация

Таблица умножения

Таблица умножения учится каждым школьником во втором классе. Ее обязан знать каждый!

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Записаться на курсУзнать подробнее

---

Примеры на умножение

Умножение на однозначное

1. 9 * 5 =
2. 9 * 8 =
3. 8 * 4 =
4. 3 * 9 =
5. 7 * 4 =
6. 9 * 5 =
7. 8 * 8 =
8. 6 * 9 =
9. 6 * 7 =
10. 9 * 2 =
11. 8 * 5 =
12. 3 * 6 =

Умножение на двузначное

1. 4 * 16 =
2. 11 * 6 =
3. 24 * 3 =
4. 9 * 19 =
5. 16 * 8 =
6. 27 * 5 =
7. 4 * 31 =
8. 17 * 5 =
9. 28 * 2 =
10. 12 * 9 =

Умножение двузначное на двузначное

1. 24 * 16 =
2. 14 * 17 =
3. 19 * 31 =
4. 18 * 18 =
5. 10 * 15 =
6. 15 * 40 =
7. 31 * 27 =
8. 23 * 25 =
9. 17 * 13 =

Умножение трехзначных чисел

1. 630 * 50 =
2. 123 * 8 =
3. 201 * 18 =
4. 282 * 72 =
5. 96 * 660 =
6. 910 * 7 =
7. 428 * 37 =
8. 920 * 14 =

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра «Быстрый счет»

Игра «быстрый счет» поможет вам усовершенствовать свое мышление. Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ «да» или «нет» на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.

Играть сейчас

Игра «Математические матрицы»

«Математические матрицы» великолепное упражнение для мозга детей, которое поможет вам развить его мыслительную работу, устный счет, быстрый поиск нужных компонентов, внимательность. Суть игры заключается в том, что игроку предстоит из предложенных 16 чисел найти такую пару, которая в сумме даст данное число, например на картинке ниже данное число «29», а искомая пара «5» и «24».

Играть сейчас

Игра «Числовой охват»

Игра «числовой охват» нагрузит вашу память во время занятий с данным упражнением.

Суть игры – запомнить цифру, на запоминание которой отводится около трех секунд. Затем нужно ее воспроизвести. По мере прохождения этапов игры, количество цифр растет, начинаете с двух и далее.

Играть сейчас

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Играть сейчас

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Играть сейчас

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Играть сейчас

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Играть сейчас

Игра «Математические сравнения»

Игра «Математические сравнения» развивает мышление и память. Главная суть игры сравнить числа и математические операции. В этой игре надо сравнить два числа. На верху, написан вопрос, прочитайте его и ответьте правильно на поставленный вопрос. Ответить можно при помощи кнопок расположенных внизу. Там нарисованы три кнопки «левое», «равно» и «правое». Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Играть сейчас

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Записаться на курсУзнать подробнее

---

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Записаться на курсУзнать подробнее

---

Развитие памяти и внимания у ребенка 5-10 лет

Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать.

После прохождения курса ребенок сможет:

1. В 2-5 раз лучше запоминать тексты, лица, цифры, слова
2. Научится запоминать на более длительный срок
3. Увеличится скорость воспоминания нужной информации

Записаться на курсУзнать подробнее

---

Супер-память за 30 дней

Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.

Записаться на курсУзнать подробнее

---

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Записаться на курсУзнать подробнее

Нахождение моделей умножения с помощью схем и таблиц (примеры)

Содержание

• Что такое таблица умножения?
• Таблица умножения чисел от 1 до 10
• Образцы в таблице умножения
• Образцы кратных четных и нечетных чисел
• Образец, связанный с распределительным свойством умножения
• Образец, связанный с коммуникативным свойством умножения
• Решенные примеры
• Часто задаваемые вопросы

Что такое таблица умножения?

Таблица умножения — это таблица, в которой представлены кратные двух чисел. Знакомство с таблицей умножения поможет нам легко решать математические задачи. Множители также известны как произведения, а два умноженных числа известны как множители.

Таблица умножения чисел от 1 до 10

Таблицу умножения чисел от 1 до 10 можно получить, умножая числа в одном диапазоне друг на друга. Таблица умножения чисел от 1 до 10 выглядит следующим образом:

и коэффициент, на который мы умножаем число.

Что такое закономерности в таблице умножения?

Паттерн — это то, что можно многократно наблюдать в определенных ситуациях. Узоры можно наблюдать в одежде, которую вы носите, в цветах в саду, в океане и во многих других вещах. Точно так же мы можем наблюдать закономерности и в таблице умножения.

Образцы кратных четных и нечетных чисел

Сначала рассмотрим произведение четных чисел.

Ясно, что кратные четным числам всегда четные числа. То есть произведения четных чисел всегда заканчиваются на 2, 4, 6, 8 или 0, 9.0005

С другой стороны, кратные нечетного числа чередуются между нечетными и четными числами. Если нечетное число умножить на нечетное число, произведение также будет нечетным числом. Если нечетное число умножить на четное, произведение всегда будет четным числом.

Например, 5 \( \times \) 5 = 25, 5 \( \times \) 6 = 30 и 5 \( \times \) 7 = 35, где 5 и 7 — нечетные числа, а 6 — четное число.

Среди кратных нечетных и четных чисел спрятан еще один шаблон. Все произведения числа 4 в два раза больше произведения числа 2. Все произведения числа 6 в два раза больше произведения числа 3. Точно так же все произведения числа 8 в два раза больше произведения числа 4, а все произведения числа 10 в два раза больше произведения числа 5.

Схема, связанная с распределительным свойством умножения

Мы можем наблюдать интересную закономерность в таблице умножения, глядя на ее столбцы. Рассмотрим столбцы для 3, 5 и 8 и сравните продукты в этих столбцах.

Мы знаем, что 3 + 5 = 8. Интересен тот факт, что кратные этим числам подчиняются тому же правилу. То есть числа, кратные 8, представляют собой сумму кратных 3 и 5 для данного фактора. Например, 15, 25 и 40 кратны 3, 5 и 8, которые мы получаем, когда умножаем эти числа на 5. И 15 + 25 = 40. Аналогично, 27 + 45 = 72, где 27, 45 и 72 кратны 3, 5 и 8, которые мы получаем, умножая их на 9..

Этот шаблон создан благодаря распределительному свойству умножения. Свойство утверждает, что умножение суммы двух или более слагаемых на число равносильно умножению каждого слагаемого по отдельности на число и последующему сложению произведений вместе. С точки зрения математики, если c = a + b, то 5 \( \times \) c = 5 \( \times \) (a + b) = 5 \( \times \) a + 5 \( \times \) б.

Рассмотрим пример. Мы знаем, что 3 + 5 = 8

Умножая обе части на 5:

(3 + 5) \( \раз \) 5 = 8 \( \раз \) 5

3 \( \раз \) 5 + 5 \( \раз \) 5 = 40

15 + 25 = 40

То же свойство наблюдается для всех столбцов, где сумма значений в любых двух столбцах равна значению другого столбца для данной строки.

Образец, связанный с переместительным свойством умножения

Найдите закономерность среди выделенных чисел на диагоналях. Одна из выделенных диагоналей имеет числа 7, 12, 15, 16, 15, 12 и 7. Когда мы достигнем середины первой диагонали, мы получим 4 \( \times \) 4 = 16. Произведения, следующие за этим номера такие же, как те, которые появились перед ним. Но они в обратном порядке.

Та же картина наблюдается на второй и третьей выделенных диагоналях. Числа на второй диагонали — 9, 16, 21, 24, 25, 24, 21, 16 и 9, а числа на третьей диагонали — 20, 27, 32, 35, 36, 35, 32, 27, и 20.

Этот шаблон создается благодаря коммутативному свойству умножения. Коммутативное свойство умножения гласит, что при умножении чисел в любом порядке мы получим один и тот же результат.

Например, 2 \( \times \) 3 = 6 и 3 \( \times \) 2 = 6, 5 \( \times \) 8 = 40 и 8 \( \times \) 5 = 40. Это относится к умножению всех чисел.

Числа на диагоналях повторяются в обратном порядке из-за множителей. Рассмотрим диагональ с числами 7, 12, 15, 16, 15, 12 и 7. 16 получается умножением 4 само на себя. С левой стороны 15 получается путем умножения 5 \( \times \) 3, а с правой стороны 15 получается путем умножения 3 \( \times \) 5, что дает тот же результат. Такая же тенденция наблюдается среди всех чисел во всех диагоналях.

Решенные примеры шаблонов для умножения

Пример 1: Выделенные строка и столбец таблицы умножения имеют одинаковый набор чисел. Опишите свойство, которое создает этот шаблон.

 

 

Решение:

Свойство, создающее этот шаблон, можно определить, наблюдая за числами в выделенной строке и столбце. Рассмотрим число 21 в выделенной строке и выделенном столбце. Число 21 в выделенном столбце получается путем умножения 7 \( \times \) 3, а число 21 в выделенной строке получается путем умножения 3 \( \times \) 7.

 

Свойство коммутативности утверждает, что 7 \( \times \) 3 = 3 \( \times \) 7 = 21. Этот шаблон является просто вариацией шаблона, который мы наблюдали на диагоналях таблицы.

 

Пример 2: Сравните строки 3 и 6. Опишите закономерность, наблюдаемую в кратных этим числам.

 

 

 

Решение:

Мы знаем, что 6 = 3 \( \times \) 2.

 

Итак, когда любое число умножается на 6, его можно переписать как это число, умноженное на двойное число 3. Например, 24 = 6\( \times \) 4 и 24 = 3 \( \times \) 2 \( \times \) 4 = 3 \( \times \) 8.

 

Следовательно, числа во второй выделенной строке в два раза больше чисел в первой выделенной строке.

 

Пример 3: Найдите пропущенное число в следующем наборе чисел. Опишите наблюдаемое в этом случае свойство.

 

9, 16, __, 24, 25, __, 21, __, 9

 

Решение:

таблица умножения.

 

 

 

Недостающие числа 21, 24 и 16. Таким образом, полный набор чисел становится следующим: 9, 16, 21, 24, 25, 24, 21, 16, и 9. Мы можем обратите внимание, что числа повторяются в обратном порядке после числа 25, что равно 5 \( \times \) 5.

 

Этот шаблон создан благодаря коммутативному свойству умножения.

 

Пример 4: Джоэл выращивает несколько кур на своем заднем дворе. Количество яиц, произведенных его фермой на заднем дворе, указано ниже.

 

 

 

Найдите количество дней, необходимое для производства 28 яиц.

 

Решение: 

Количество дней равно 3, 6 и 9, а количество произведенных яиц равно 12, 24 и 36. Нам нужно найти число, соединяющее эти два набора чисел.

 

 

Из таблицы умножения видно, что мы получаем 12, 24 и 36, когда умножаем 4 на 3, 6 и 9 соответственно. Это означает, что ферма может производить 4 яйца в день.

 

Чтобы найти количество дней, необходимых для производства 28 яиц, нам просто нужно найти число, относящееся к 28 и 4. необходимое количество дней произвести 28 яиц — 7,

Часто задаваемые вопросы о шаблонах таблицы умножения

Что вы видите в произведениях любого числа, умноженного на 1?

Произведение любого числа при умножении на 1 и есть само число. Когда 1 является одним из факторов, множители будут 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 и так далее.

Что вы наблюдаете в произведениях любого числа при умножении на 2?

Когда число умножается на два, мы фактически удваиваем число. Кроме того, произведение всегда будет четным числом.

Что вы видите на месте единиц, кратных 5?

Число, кратное 5, всегда заканчивается либо 0, либо 5. Если 5 умножается на четное число, цифра в разряде единиц всегда равна 0. С другой стороны, если 5 умножается на нечетное число, цифра на месте единиц всегда 5. 

Ознакомьтесь с другими нашими курсами

Массивы умножения с примерами из жизни

Что такое Массив умножения ? Разве это не более быстрый метод сложения? Таким образом, когда вы умножаете число на другое число, вы добавляете число столько же раз, сколько звонит другой номер.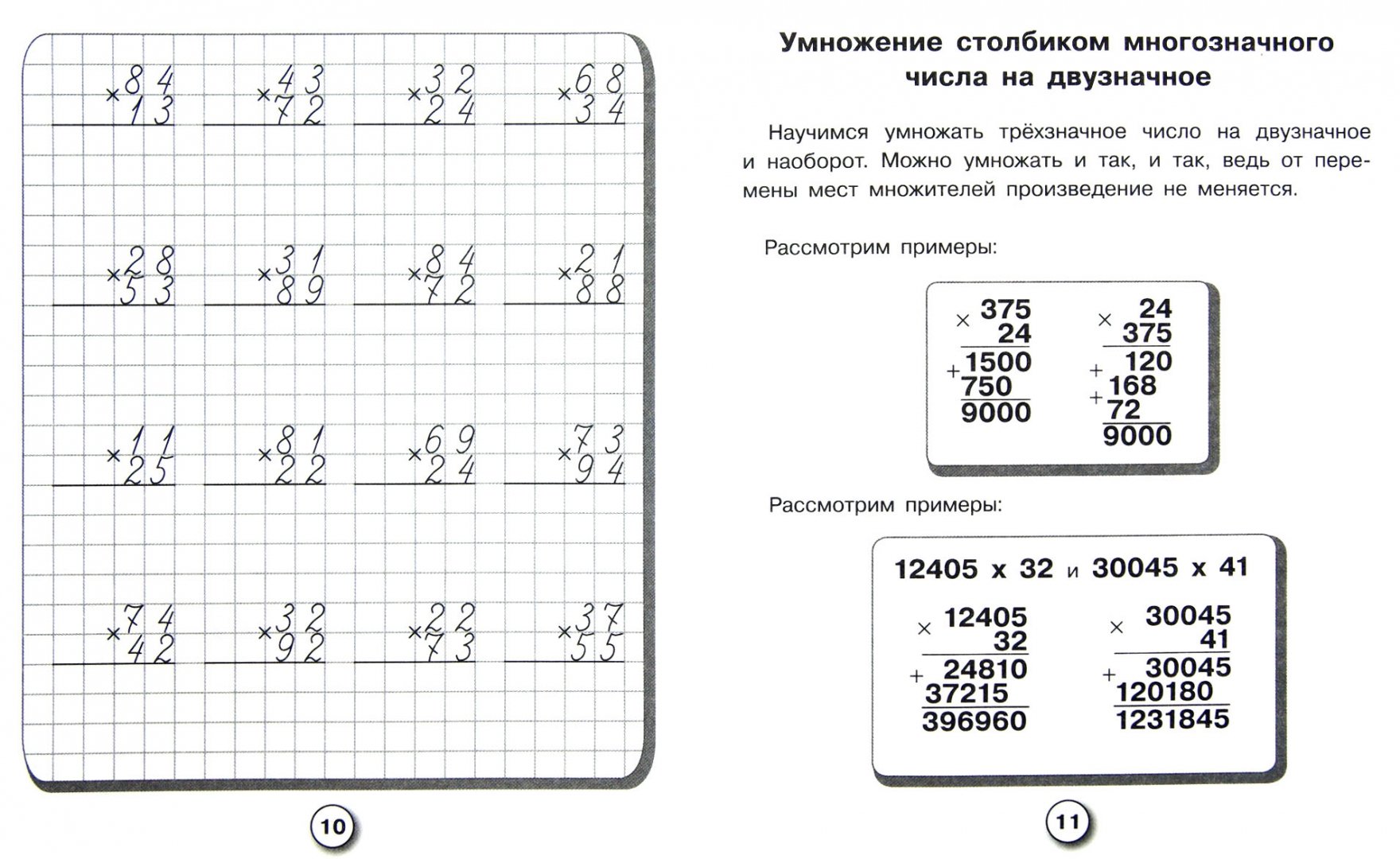 Умножение можно сделать проще, чем когда-либо, если вы выучите массив умножения. Они являются полезным представлением концепций умножения. Равномерно расставленные стулья в зрительном зале или марширующем строю изображают массивы.

Вы можете легко вычислить участвующих членов, если вы визуализируете их в строках и столбцах. Итак, что такое массив в умножении? Как массивы могут помочь быстрее решать задачи на умножение? Узнайте все о массиве умножения в статье ниже.

Вот что мы рассмотрим:

• Что такое массив при умножении?
• Как написать уравнения массива умножения?
• Как выполнить умножение массива с пропуском счета?
• Каковы преимущества массива умножения модели?
• Реальные примеры массива умножения

Визуальное видение вещей может помочь развить конкретное понимание важных математических концепций. Массив использует визуализацию элементов умножения в строках и столбцах. Массив — это расположение чисел, объектов или изображений в виде строк и столбцов. Строка располагается горизонтально (слева направо), а столбец (вверху и внизу) — вертикально.

Каждый столбец должен содержать одинаковое количество объектов в массиве, и то же самое относится к каждой строке. В них должно быть такое же количество объектов, как и в других рядах.

Как написать уравнения массива умножения?

Чтобы написать уравнение умножения массива, вы сначала считаете количество строк, а затем количество столбцов. Давайте рассмотрим несколько примеров ниже, чтобы понять массив умножения.

На следующем рисунке массив состоит из 2 строк и 4 столбцов смайликов. Его также можно описать как массив 2 на 4. Слово «по» можно представить крестом умножения.

Следовательно, математически вы записываете массив в виде 2 × 4. Дважды четыре равняется восьми, поэтому уравнение будет таким: 2 × 4 = 8

В этом массиве 3 строки и 4 столбца. Это массив 3 на 4, и вы можете записать его как 3 × 4. Уравнение умножения будет: 3 × 4 = 12

Итак, из приведенных выше примеров вы можете видеть, что первое число представляет количество строк, а второе число представляет количество столбцов. Итак, второй массив — это 3 × 4, а не 4 × 3, хотя вычисленное произведение, т. е. 12, в любом случае будет одинаковым.

Как выполнить массив умножения с пропуском счета?

Что такое подсчет пропусков? Счет с пропуском — это метод прямого счета по числам, отличным от 1. Таким образом, если вам нужно считать с пропуском по числу, вы будете продолжать прибавлять одно и то же число на каждом шагу к ранее полученному числу. Это похоже на многократное добавление. Предположим, вам нужно пропустить счет на 2, поэтому ваши ответы будут 4, 6, 8, 10, 12, 14 и так далее. Итак, каждый раз, когда вы прибавляете 2 к предыдущему числу, то есть прибавляете 2 к 4, чтобы получить 6, прибавляете 2 к 6, чтобы получить 8, и так далее.

Давайте рассмотрим следующий пример массива пончиков, чтобы понять, как пропустить счет для умножения массива на .

Приведенный выше массив состоит из трех строк, и в каждой строке пять пончиков. Итак, есть пять столбцов пончиков. Чтобы рассчитать общее количество пончиков, вы можете просто посчитать их. Но использование подсчета пропусков ускоряет процесс и делает его намного проще.

Здесь вы можете пропустить счет на 5 для каждой строки, чтобы подсчитать количество пончиков. В первом ряду пять пончиков, поэтому, если вы пропустите счет на 5, конец второго ряда составит десять, а конец третьего ряда даст пятнадцать, что и является вашим ответом. Это то же самое, что 3 × 5 = 15

На приведенном выше изображении вы также можете пропустить счет по столбцам. Вам придется пропустить счет на три, так как в каждом столбце есть три пончика. Таким образом, для пяти столбцов пропуск трехкратного счета будет выглядеть как 3, 6, 9, 12 и 15. 

Интересно, что один массив может иметь два уравнения: одно для столбцов, а другое для строк. В приведенном выше примере уравнения умножения таковы:

Для строк: 3 × 5 = 15

Для столбцов: 5 × 3 = 15

Каковы преимущества массива умножения модели?

Умножение массивов имеет несколько преимуществ в понимании и решении математических задач. Не только математика, компьютерные языки, такие как Python, используют умножение массива NumPy для умножения массива. Вот некоторые из ключевых преимуществ умножения моделей массивов в математике:

1. Умножение массивов упрощает визуализацию задач

Это может быть отличным способом ввести умножение с помощью практических объектов, но это может быть утомительно, когда работа с большими числами или решение нескольких задач. Вы можете использовать массив бумажных точек, чтобы надеть L-образную крышку на верхнюю часть массива. Таким образом, вы можете показать любой факт умножения, который вы хотите. На следующем изображении показан массив точек и L-образная крышка.

Вы можете использовать массив точек и L-образную крышку следующим образом. Предположим, вы хотите объяснить, как выглядит 6 × 8, то есть 6 групп по 8. Наденьте L-образную крышку на массив точек, как показано ниже.

Теперь есть шесть рядов, и в каждом ряду восемь точек. Вы можете легко подсчитать общее количество точек в массиве как 6 × 8 = 48.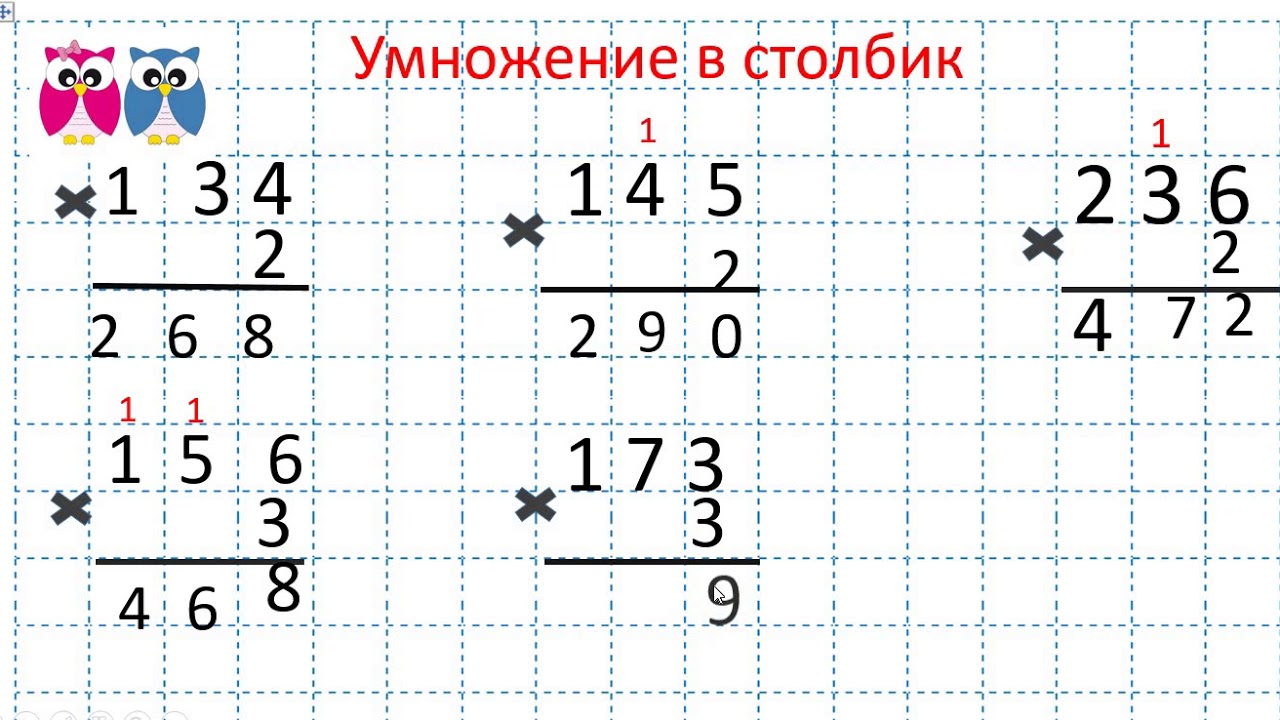

2. Умножение массива позволяет использовать стратегии вместо механического запоминания

Давайте рассмотрим пример 6 × 7, чтобы понять это. Ученикам становится трудно запоминать ответы на подобные умножения, но им становится легче, когда они используют 5 × 7 в качестве трамплина. Учащиеся в основном знакомы с числами, кратными пяти, с раннего возраста. Таким образом, становится намного проще, когда они видят 6 × 7 как еще одну группу из 7, чем 5 × 7. Им просто нужно сложить 35 + 7, чтобы найти ответ: 6 × 7 = 42.

3. Умножение массивов позволяет учащимся увидеть свойство коммутативности в действии

В соответствии со свойством коммутативности вы получите одинаковый ответ при умножении одних и тех же чисел в любом порядке. Например, если вы умножаете 4 × 7 или 7 × 4, оба дают один и тот же ответ: 28.

Используя умножение массива точек , вы можете объяснить факты умножения. Чтобы объяснить свойство коммутативности, поверните массив на 90 градусов. Массив точек покажет факт умножения, а общее количество точек не изменится.

В предложении умножения есть несколько чисел, каждое из которых имеет особое имя. Числа, которые вы умножаете, называются множителями. Ответ, полученный путем умножения множителей, называется произведением.

6 × 7 = 42 

Здесь 6 — это множитель, который представляет количество строк, множитель 7 представляет объекты в каждой строке, а произведение 42 представляет общее количество объектов.

Когда массив переворачивается на бок, все меняется следующим образом.

7 × 6 = 42

Здесь множитель 7 представляет количество строк, множитель 6 представляет объекты в каждой строке, а произведение 42 представляет собой общее количество объектов.

Порядок множителей меняется, но произведение остается прежним, демонстрируя математическое свойство, известное как коммутативное свойство умножения.

4. Использование массивов для больших чисел

Используя массивы, учащиеся могут легко изучить вычисления с большими числами, такими как 12 x 5. Массив можно разделить на полезные фрагменты. Например, 12 x 5 можно разбить для выполнения вычислений.

12 х 5 = (10 х 5) + (2 х 5).

Хотя рисование точек — хорошая техника для начинающих, она может быть утомительной. Метод пустого массива помогает решить сложные умножения, приняв неформальный способ. Они учат студентов, как использовать другие стратегии, такие как компенсация, для процесса умножения.

В следующем примере показан метод пустого массива для умножения. Здесь для вычисления 34 х 9 студент решил сделать 34 х 10. Далее он снимает 34 х 1, упрощая процесс.

Итак, 34 x 10 = 340

340 – 34 = 306

Вы также можете разбить 34 на 30 и 4. Затем вы вычтете 30 из 340, а затем 4 из 310.  

5. Умножение Рабочие листы массивов позволяют учащимся практиковать уравнения

Рабочие листы массива умножения — отличный способ попрактиковаться в уравнениях. Обычно учащимся предлагается заполнить уравнение для описания массива, как показано на рисунке ниже.

Реальные примеры массива умножения

Вы можете практиковаться в умножении массивов, где бы и когда бы вы ни столкнулись с массивами. Они присутствуют повсюду вокруг вас.

Ниже приведены некоторые распространенные примеры массивов для умножения из реальной жизни:

• Лоток с яйцами
• Форма для выпечки маффинов
• Забор
• Коробка шоколада
• Блистерные упаковки лекарств
• Бутылки для воды в картонных коробках
• шахматная доска
• Матрицы также являются массивами
• Контакты на сотовом телефоне
• Меню ресторана
• Бланк вопросов представляет собой набор пронумерованных вопросов, где каждому вопросу присваивается определенное количество баллов.

Часто задаваемые вопросы

1. Как перемножить все значения в массиве?

Самый простой способ перемножить все значения в массиве — сначала преобразовать массив в список.

Затем вы можете использовать функцию карты, чтобы умножить каждое значение в списке.

Приведенный ниже код будет умножать каждое значение в массиве:

а = [1,2,3]

л = список(а)

л * 2

[2, 4, 6]

2. Что означает массив в математике?

 Массив — это способ организации чисел, чтобы их можно было легко сортировать и искать. Это как электронная таблица Excel, но гораздо более продвинутая.

3. Какое числовое число умножения представляет массив?

Массив представляет предложение на умножение 5 × 3 = 15

4. Как вы решаете задачи на умножение?

Чтобы решить задачу на умножение, нужно умножить числа в первом наборе скобок на числа во втором наборе скобок. Например, если вы хотите узнать, сколько будет 8 x 7, вы должны записать 8 и умножить на 7. В результате вы получите 56.

5. Что такое массив по математике 4 класс?

 Массив – это набор чисел, организованных определенным образом.