3000 примеров по математике. Равенства. Сложение и вычитание в пределах 100. Два уровня сложности. Ответы. 2-3 классы
Автор(-ы): Узорова О.В.
Серия: 3000 примеров для начальной школы
По году издания: 2021
Тип обложки: Мягкая обложка
Издательства: АСТ
Количество страниц: 16
Формат: 60×84/8 (205×290 мм)
EAN: 9785171348069
Изготовитель:
ЗАО «КНИЖНЫЙ КЛУБ 36.
6″ 107078, РФ, г. Москва, ул. Бакунинская, д. 71, строение 10, этаж 8
Импортер: ООО «БиблиоБай», 220113, г.Минск, ул.Мележа, 1
4,80 руб
Кол-во:
Под заказ.
Поставка на склад 23 мая
- Описание товара
- Отзывы
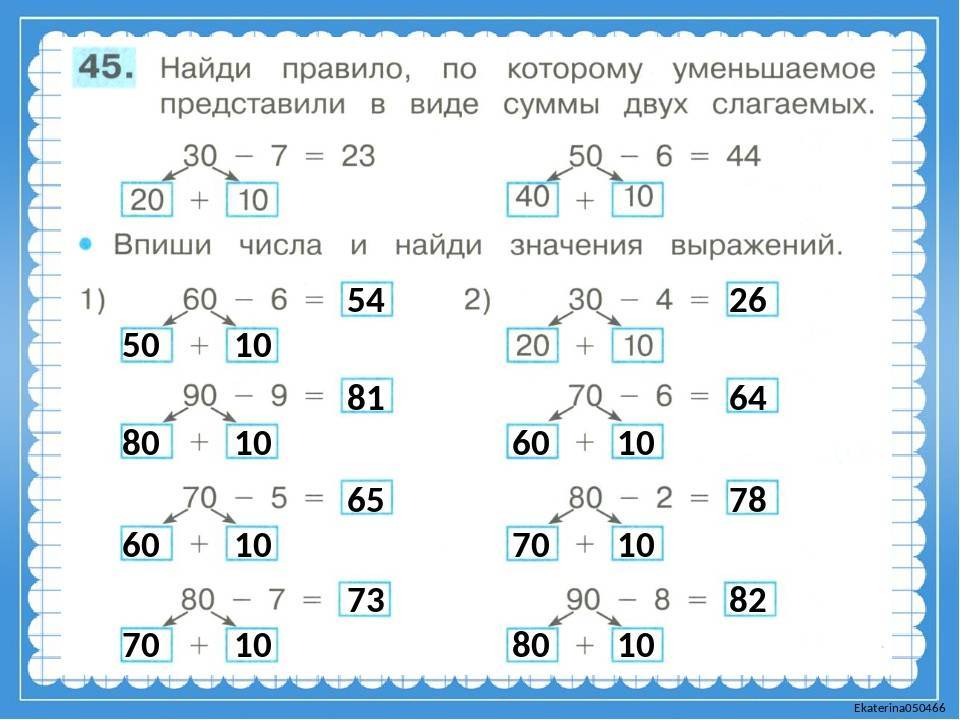
Пособие поможет сформировать и закрепить навык автоматизированного счёта по базовым темам начальной школы: «Счёт в пределах 10», «Счёт в пределах 20», «Счёт в пределах 100».
В пособии приведены цепочки равенств с пропущенными числами. Нужно вставить числа, чтобы равенства были верными.
Предложены примеры двух уровней сложности. Прежде чем ребёнок начнёт самостоятельно решать эти цепочки, можно объяснить ему, как это лучше делать. Например, возьмём цепочку равенств 1+2=___=10-___=___+0. Цепочка состоит из нескольких равенств, каждое из которых это пример с одним и тем же ответом.
Последовательно решая эти примеры, вписываем нужные числа. Первый пример цепочки 1+2=3. Вписываем число 3 и получаем второй пример 3=10-7. Наконец, третий пример 10-7=3+0. В конце книги даны ответы для самопроверки. Решение цепочек примеров – это эффективный тренинг, позволяющий довести до автоматизма вычислительные навыки ребёнка.
Автоматизированный навык счёта поможет сэкономить драгоценное время при решении задач, длинных примеров, неравенств и уравнений. Кроме того, автоматизированный счёт разовьёт у ребёнка память, логическое мышление, гибкость ума и сообразительность, а также значительно повысит работоспособность мозга – активизирует развитие речи и интеллекта, способность удерживать и переключать внимание.
Пособие будет полезно для работы в классе и самостоятельных занятий дома.
Отзывы пользователей
Напишите ваш собственный отзыв
Похожие товары
Стр. 99 — ГДЗ Математика 2 класс Учебник Моро Часть 2
org/BreadcrumbList»>Вернуться к содержанию учебника
Что узнали.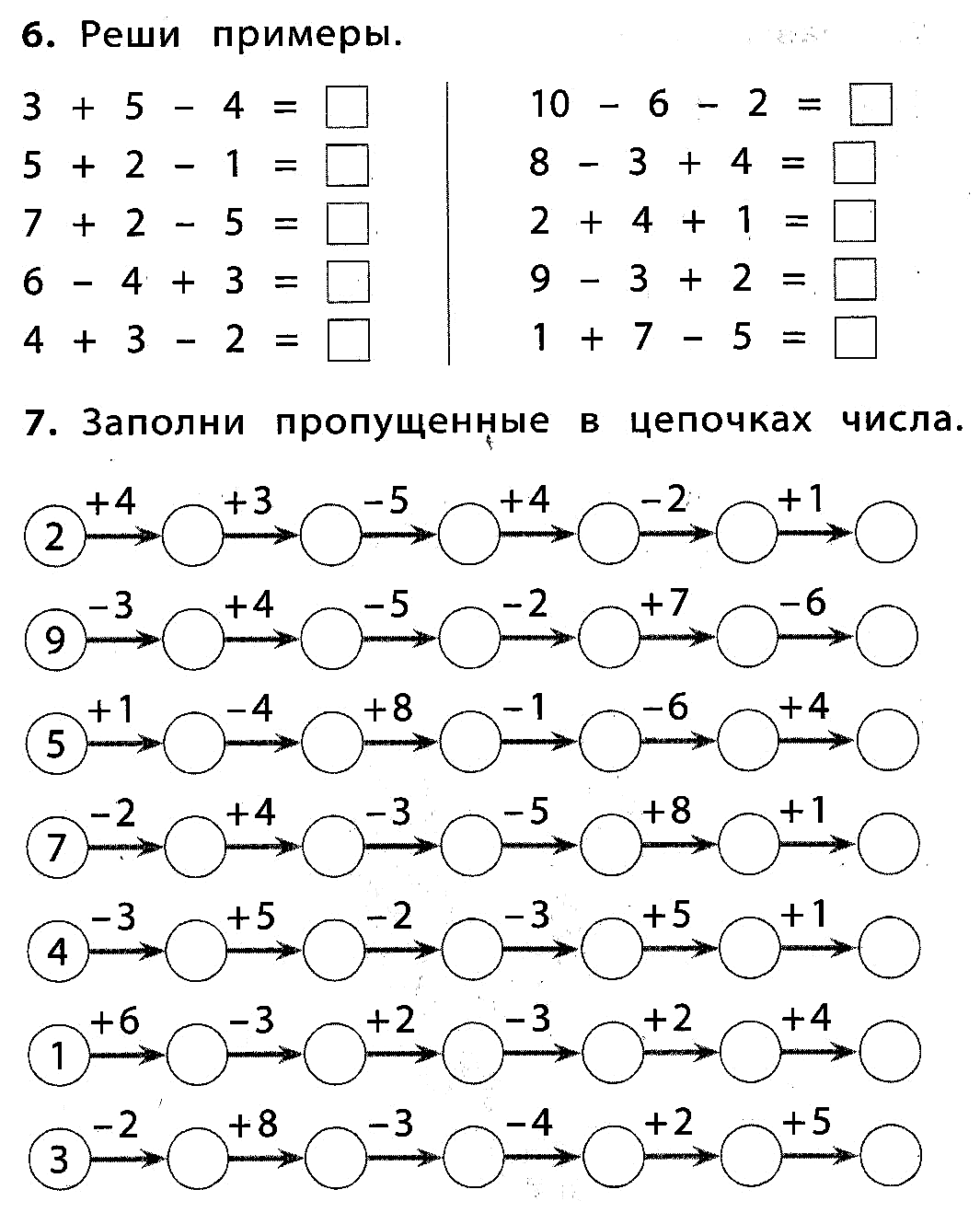
Чему научились
Вопрос
24. Вычисли и проверь решение:
| 52 + 37 | 38 + 16 |
| 90 — 73 | 58 + 27 |
| 68 — 25 | 71 — 24 |
| 69 — 27 | 75 + 16 |
Ответ
| Решение | ||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| |||||||||||||||||||||||||||||||||||||||||
| Проверка | ||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| |||||||||||||||||||||||||||||||||||||||||
| Решение | ||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| |||||||||||||||||||||||||||||||||||||||||
| Проверка | ||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| |||||||||||||||||||||||||||||||||||||||||
Пояснение
Сложение и вычитание выполняем в столбик
При выполнении вычитания, если единицы уменьшаемого меньше единиц вычитаемого, над десятками уменьшаемого ставим точку, чтобы не забыть о том, что один десяток забрали.
Если есть необходимость, то число, которое запоминают при выполнении сложения в столбик, можно писать сверху над разрядом, к которому это число будут прибавлять. Например,
| + | 3 | 8 |
| 1 | 6 | |
| 5 | 4 |
Чтобы проверить сложение, можно использовать любой из следующих способов:
- из суммы вычесть первое слагаемое и в результате вычитания должно получиться второе слагаемое;
- из суммы вычесть второе слагаемое и в результате вычитания должно получиться первое слагаемое.
Чтобы проверить вычитание, можно использовать любой из следующих способов:
- к разности прибавить вычитаемое и в результате сложения должно получиться уменьшаемое;
- из уменьшаемого вычесть разность и в результате вычитания должно получится вычитаемое.
Вопрос
25.
Прочитай выражение k + 8. Найди значения этой суммы, если
k = 36, k = 42, k = 57, k = 69.
Ответ
Решение
| k | k + 8 |
| 36 | 44 |
| 42 | 50 |
| 57 | 65 |
| 69 | 77 |
Пояснение
Читаю выражение: «ка плюс восемь» или «сумма ка и восьми».
Чтобы найти значение буквенного выражения, нужно в это выражение вместо буквы подставить число, которое дано в условии, и выполнить вычисления.
| k | k + 8 |
| 36 | 36 + 8 = 44 |
| 42 | 42 + 8 = 50 |
| 57 | 57 + 8 = 65 |
| 69 | 69 + 8 = 77 |
Вопрос
26.
| 20 + (42 + 8) + 6 | 10 + (35 — 15) |
| 50 + (34 + 6) + 7 | 70 — (84 — 40) |
Ответ
Решение
20 + (42 + 8) + 6 = 76
50 + (34 + 6) + 7 = 97
10 + (35 — 15) = 30
70 — (84 — 40) = 26
Пояснение
Если в выражении есть скобки, то сначала выполняют действия в скобках, а затем за скобками.
Также, если выражение содержит только действие сложение, то сложение выполняем удобным способом.
20 + (42 + 8) + 6 = (20 + 6) + 50 = 26 + 50 = 76 | 10 + (35 — 15) = 10 + 20 = 30 |
50 + (34 + 6) + 7 = (50 + 7) + 40 = 57 + 40 = 97 | 70 — (84 — 40) = 70 — 44 = 70 — 40 — 4 = 30 — 4 = 26 |
Вопрос
27.
Маме, папе и дочери вместе 68 лет. Сколько лет дочери, если маме 28 лет, а папе 32 года?
Ответ
Решение
1) 28 + 32 = 60 (л.) — маме и папе вместе.
2) 68 — 60 = 8 (л.)
Ответ: дочери 8 лет.
Пояснение
Вопрос
28. Катя принесла из сада 15 тюльпанов. Она составила 3 букета: первый — из 7 тюльпанов, второй — из 5 тюльпанов. Сколько тюльпанов в третьем букете?
Ответ
Решение
1) 7 + 5 = 12(т.) — в двух букетах.
2) 15 — 12 = 3 (т.)
Ответ: 3 тюльпана в третьем букете.
Пояснение
Вопрос
29. У хоккеистов школьной команды было 12 старых клюшек и 18 новых.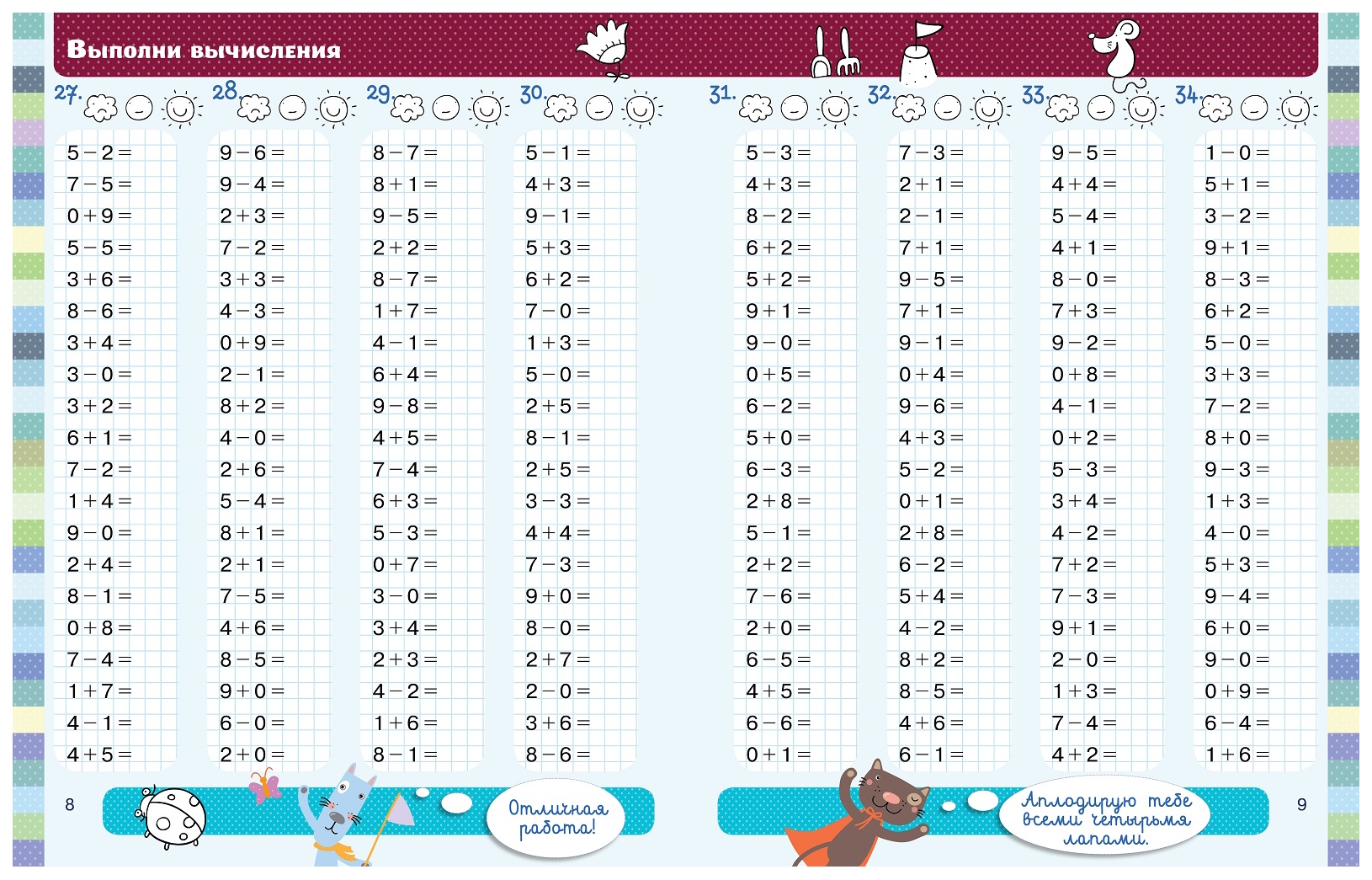
Во время игры 5 клюшек сломалось. Сколько клюшек осталось?
Ответ
Решение
1) 18 + 12 = 30 (к.) — всего.
2) 30 — 5 = 25 (к.)
Ответ: осталось 25 клюшек.
Пояснение
1 способ:
2 способ: 1) 12 — 5 = 7 (к.) — осталось, если сломались только старые клюшки 2) 18 + 7 = 25 (к.)- всего осталось Ответ: осталось 25 клюшек. | 3 способ: 1) 18 — 5 = 13 (к.) — осталось, если сломались только новые клюшки 2) 12 + 13 = 25 (к.)- всего осталось Ответ: осталось 25 клюшек. |
Вопрос
30. В детский сад привезли 20 кг муки. Из 4 кг муки испекли блины, а из 8 кг — булочки.
Сколько килограммов муки осталось?
Реши задачу разными способами.
Ответ
Решение
1 способ:
1) 8 + 4 = 12 (кг) — всего израсходовали.
2) 20 — 12 = 8 (кг)
Ответ: осталось 8 кг муки.
2 способ:
1) 20 — 4 = 16 (кг) — осталось после того как испекли блины.
2) 16 — 8 = 8 (кг)
Ответ: осталось 8 кг муки.
3 способ:
1) 20 — 8 = 12 (кг) — осталось после того как испекли булочки.
2) 12 — 4 = 8 (кг)
Ответ: осталось 8 кг муки.
Пояснение
Вопрос
31. Сыну 9 лет, а отцу 35 лет. На сколько лет отец старше сына?
Ответ
Решение
35 — 9 = 26 (л.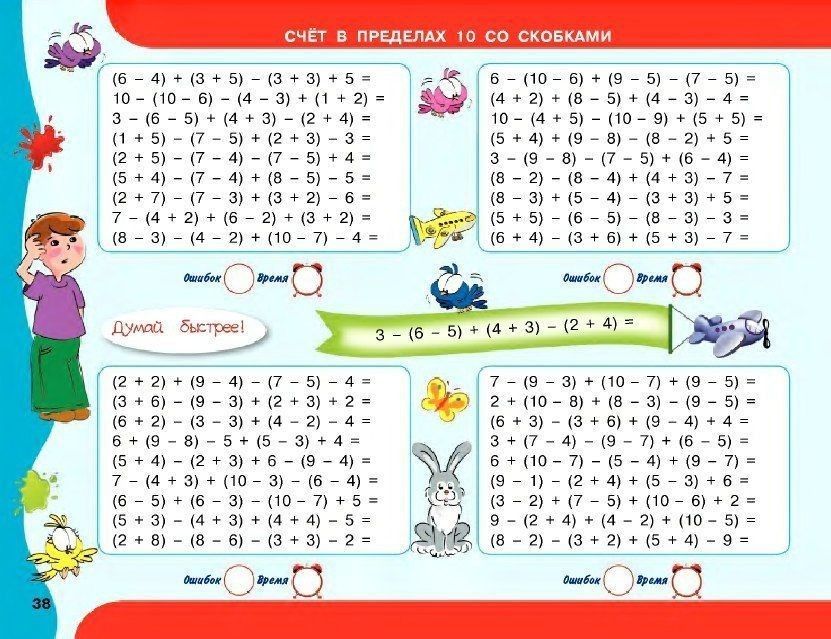
)
Ответ: отец старше на 26 лет.
Пояснение
Вопрос
32. Первый мультфильм шёл по телевизору 15 мин, второй — на 8 мин меньше, а третий — столько, сколько первый и второй вместе.
Поставь разные вопросы и реши задачи.
Ответ
Вопрос 1:
Сколько времени шел третий мультфильм?
1) 15 — 8 = 7 (мин) — шел второй мультфильм
2) 15 + 7 = 22 (мин)
Ответ: 22 минуты шёл третий мультфильм.
Вопрос 2:
Сколько времени шли все три мультфильма?
1) 15 — 8 = 7 (мин) — шел второй мультфильм.
2) 15 + 7 = 22 (мин) — шел третий мультфильм и первый и второй мультфильмы вместе.
3) 22 + 22 = 44 (мин)
Ответ: все мультфильмы шли 44 минуты.
Пояснение
Вопрос 1:
Сколько времени шел третий мультфильм?
Вопрос 2:
Сколько времени шли все три мультфильма?
Вопрос
33.
Оля вырезала для куклы из бумаги 2 разные кофточки и 3 юбки. Сколько есть разных способов одеть куклу, если каждый раз использовать 1 кофточку и 1 юбку?
Ответ
Решение
Есть 6 способов.
Пояснение
Вопрос
Проверочные работы, с. 64, 65.
Ответ
На нашем сайте есть решение варианта 1 проверочной работы на странице 64.
На нашем сайте есть решение варианта 2 проверочной работы на странице 65.
Вернуться к содержанию учебника
Развитие беглости речи в рамках и между классами в IM K-5 Math™, часть 2: сложение и вычитание 09 “ Мы должны отказаться от представления о том, что изучение математики должно быть линейным и процедурным усилием, осваиваемым посредством механического запоминания. Вместо этого мы должны признать и подчеркнуть, что взаимосвязанные концепции ведут к более прочным основаниям в математике и более сильной личной и математической идентичности».
TODOS: Математика для ВСЕХ (2020)
Из-за проблемной структуры нашей учебной программы идеи учащихся играют неотъемлемую роль в процессе обучения в IM K–5 Math™. Исходя из убеждения, что все учащиеся являются способными учениками с предварительными навыками и накопленными знаниями, мы разработали нашу учебную программу, чтобы дать учителям возможность оценить, что учащиеся уже знают, позволив им поиграть с математическими идеями, прежде чем формировать концепции. Учащиеся изучают математику, занимаясь математикой, даже для развития процедурной беглости с алгоритмами.
Во время пилотного бета-тестирования IM K-5 Math Кейли Ривера-Рамирес взяла интервью у своей мамы в рамках задания в 3-м классе Меган Кодер. Студентам было предложено спросить члена семьи, как они научились вычитать.
Запуск урока сложения и вычитания таким образом прославляет знания семей учащихся, способствует положительному математическому самосознанию и дает учителям возможность развивать культурные знания.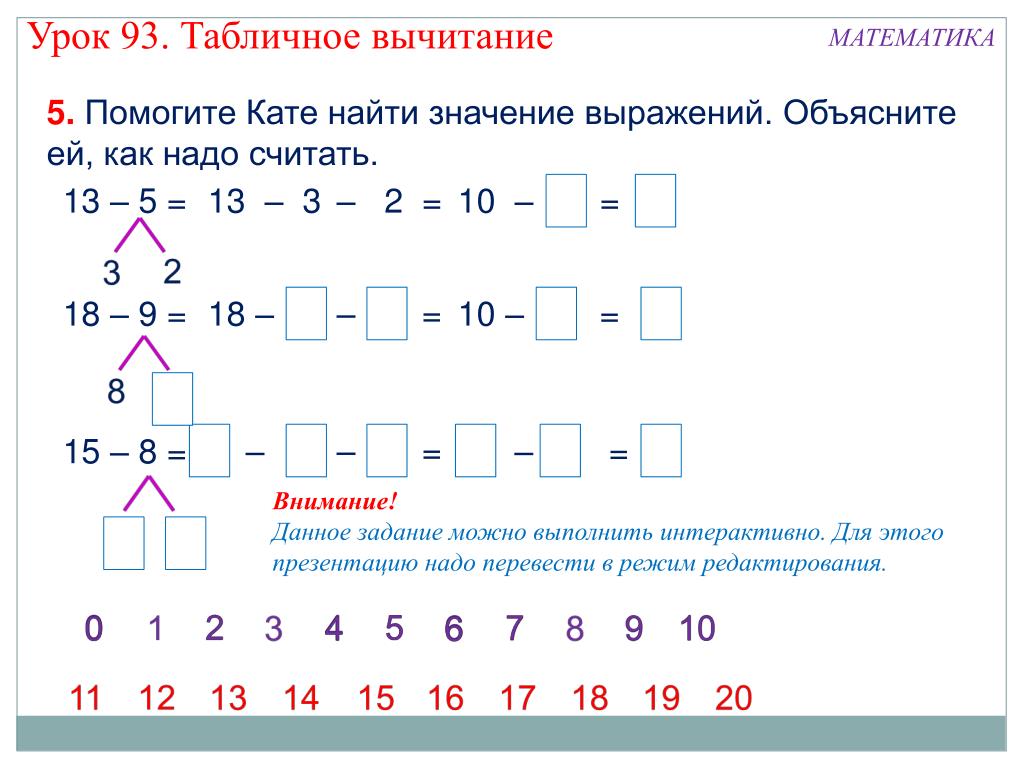
В нашем последнем посте мы поделились тем, как дизайн учебной программы способствует развитию беглости фактов. Сосредоточив внимание на требовании к беглости в 1 классе — бегло складывать и вычитать в пределах 10, — мы выделили места в нашем курсе для 1 класса, где учащиеся изучают и практикуют свои факты, опираясь на известные им факты и свое концептуальное понимание чисел и операций. В этом посте мы проливаем свет на то, как учебная программа помогает учащимся развивать беглость выполнения процедур с помощью алгоритмов сложения и вычитания во 2–5 классах.
Свободное владение алгоритмами сложения и вычитания в 2–5 классахНачиная со 2 класса, по мере того, как учащиеся развивают свободное владение фактами в пределах 20, наблюдается совпадающий прогресс в направлении развития беглости со стандартным алгоритмом сложения и вычитания многозначных чисел. набирать целые числа к концу 4 класса.
В IM K–5 Math™ процесс развития беглости с помощью алгоритма выглядит следующим образом:
- Учащиеся действуют понятным для них образом.
- Учащиеся анализируют и пробуют стратегии и алгоритмы, основанные на понимании стоимостных значений, свойствах операций и взаимосвязях между операциями.
- Учащиеся знают и используют стандартный алгоритм.
В этом процессе учащиеся начинают с того, что они знают, и строят на этом основе. Они разбираются в новых стратегиях, представлениях и алгоритмах, прежде чем их попросят использовать. Ниже мы освещаем продвижение к процедурной беглости с помощью алгоритмов сложения и вычитания в учебной программе во 2–5 классах.
Когда учащиеся переходят во 2-й класс, у них развивается понимание разрядного значения, свойств операций и отношения между сложением и вычитанием. Они применяют эти знания, чтобы точно и эффективно складывать и вычитать в пределах 100. Работая над достижением этой цели, они также учатся использовать стратегии, основанные на разрядности, свойствах операций и связи между сложением и вычитанием для сложения и вычитания в пределах 1000.
.
Эту последовательность развития беглости речи в нашем курсе для 2-го класса лучше всего видно, если посмотреть на разминку в течение года. Студентам предлагается мыслить гибко и использовать стратегии, которые имеют для них смысл. Учителя могут использовать эти учебные программы, чтобы понять мышление учащихся и оценить беглость математики.
2.
Учащиеся анализируют и пробуют стратегии и алгоритмы, основанные на понимании разрядного значения, свойствах операций и взаимосвязях между операциями. После нескольких разделов углубленного изучения, развития навыков счета и гибкости с помощью стратегий работы с большими числами, учащиеся начинают анализировать и пробовать письменные методы. В Разделе 7 2-го класса учащиеся используют блоки и диаграммы с основанием 10, чтобы связать то, что они знают о разрядном значении, свойствах операций и взаимосвязи между сложением и вычитанием в уравнениях. Они используют эти инструменты, чтобы изобразить сложение сотен с сотнями, десятков с десятками и единиц с единицами, и узнают, что при сложении или вычитании им может потребоваться составить или разложить десятку, сотню или и то, и другое.
В приведенном ниже примере учащиеся анализируют две разные стратегии нахождения 358 + 67. Они устанавливают связи между составлением десяти и сотен с использованием диаграммы с основанием десять и использованием письменного метода.
Эти концепции продолжают развиваться в 3-м классе, когда учащиеся практикуются в использовании алгоритмов, основанных на позиционном значении и поддерживающих продвижение к сложению и вычитанию больших чисел и десятичных дробей. В нашем курсе для 3-го класса учащиеся начинают с алгоритмов, демонстрирующих расширенную форму, а затем переходят к более эффективным алгоритмам. Студенты могут узнать и использовать стандартные алгоритмы сложения и вычитания в разное время. IM–5 Math™ структурирован таким образом, что концептуальное понимание может развиваться одновременно или даже после того, как учащиеся научились выполнять процедуры.
Приведенные ниже примеры взяты из наших курсов для 2-го и 3-го классов. Они показывают, как учащиеся изучают алгоритмы, связывая их со стратегиями, которые они знают.
Учащиеся используют свое понимание разрядного значения и свойств операций, чтобы разобраться в алгоритмах, а затем выполнить вычисления.
В 4-м классе учащиеся используют письменные методы, изученные во 2-м и 3-м классах, чтобы понять и использовать стандартный алгоритм сложения и вычитания многозначных чисел. В Разделе 4 нашего курса для 4 класса учащиеся отмечают сходства и различия между алгоритмом в развернутой форме и стандартным алгоритмом. Они разбираются в стандартном алгоритме, анализируя его, прежде чем их попросят попробовать самостоятельно.
Оценка беглости Помимо проверки вычислений учащихся, учителя могут оценить владение учащимися процедурами с помощью алгоритма несколькими способами. Учащимся может быть предложено проанализировать (правильную или неправильную) работу вымышленного ученика, или же учащихся можно попросить сравнить и противопоставить два разных вычислительных метода.
В приведенном ниже примере для 4-го класса учащиеся обращают внимание на потенциальные ошибки при использовании алгоритма, особенно когда необходимо разложить или составить десятичную единицу несколько раз, как в случае вычитания из числа с нулями. Учащиеся рассматривают различные стратегии подхода к многозначному вычитанию, включая использование взаимосвязи между сложением и вычитанием.
В разных классах вы можете видеть, как учащиеся переходят от использования стратегий, которые имеют для них смысл, к использованию стратегий и письменных методов, основанных на обобщенных концепциях. Процесс развития процедурной беглости с помощью алгоритмов очевиден в поисковых листах, которые учителя могут использовать для отслеживания успеваемости учащихся.
Развитие гибкости с помощью процедур Развитие навыков сложения и вычитания в детском саду до 4-го класса имеет решающее значение для операций с десятичными дробями в 5-м классе. Развивая понимание разряда справа от десятичной дроби, учащиеся узнают, что они могут применять то, что они знают о свойствах операций, понимании разрядного значения и взаимосвязи между сложением и вычитанием с целыми числами, чтобы гибко складывать и вычитать десятичные дроби до сотых.
Они используют понимание разрядности, чтобы решить, разумны ли суммы и различия, и убедиться, что цифры в числах правильно выровнены при использовании стандартного алгоритма.
На протяжении всего этого прогресса, по мере того как учащиеся учатся складывать и вычитать многозначные числа, используя стандартный алгоритм с точностью и эффективностью, они продолжают практиковаться и приобретают гибкость в умственной арифметике во время разминки. Эта практика не только помогает учащимся развивать и поддерживать счет, но также напоминает учащимся, что стандартный алгоритм не всегда может быть наиболее подходящей или эффективной стратегией.
Последовательный путь к точности, эффективности и гибкостиПродвижение к беглости сложения и вычитания в IM K–5 Math™ тщательно разработано, чтобы дать учащимся возможность связать то, что они знают, с последовательным рассказом о понятиях и процедурах сложения и вычитания.
Попутно мы поддерживаем развитие положительного математического самосознания, напоминая учащимся о знаниях, которые они привносят на каждый урок, выполняя упражнения для разминки.
Эти процедуры позволяют им напрячь свои умственные математические мускулы и продолжать использовать стратегии, которые имеют для них смысл. Эта последовательная практика в сочетании с последовательным развитием обучения предоставляет учащимся инструменты, необходимые им для беглых вычислений. Они не только приобретают навыки для точного, эффективного и гибкого использования процедур, но также приобретают способность определять из множества имеющихся в их распоряжении стратегий, какие из них наиболее подходят для данной проблемы.
Важные математические навыки для второго класса
Хотите помочь своему второкласснику освоить основы математики во втором классе? Вот некоторые из навыков, которые ваш ребенок будет осваивать в классе.
Числа
Счет до одной тысячи
Счет вперед в пределах 1000. Счет на 5 секунд. Сосчитайте и прибавьте по 10 и 100. К любому заданному числу от 100 до 900 мысленно прибавьте 10 или 100 или вычтите 10 или 100.
Четные и нечетные числа
Понимать нечетные и четные числа. Определите, нечетное или четное количество предметов в группе (до 20 предметов), разделив их на пары и/или сосчитав на два.
Чтение и запись больших чисел
Чтение и запись чисел до 1000, используя числа (352, 621, 1000) и названия чисел ( «триста пятьдесят два», «шестьсот двадцать один», «один тысяча» ).
Связь между большими числами
Понимать отношения между единицами, десятками и сотнями: десять единицы равны единице десять; десять десятки равны сотне, десять сотни равны одной тысяче. Поймите, что в трехзначном числе первая цифра представляет количество сотен, вторая цифра представляет количество десятков, а третья цифра представляет количество единиц, например, 843 равно 8 сотням (800), 4 десяткам. (40) и 3 единицы (3).
Сравнение больших чисел
Сравните трехзначные числа, используя символы > (больше или больше), = (равно) и < (меньше или меньше), и объясните, используя сотни, десятки и единицы.
Сложение, вычитание, умножение и деление
Большие числа
Быстро и точно складывать числа, которые в сумме не превышают 20, и вычитать из чисел до 20. 7
Решайте одноэтапные и двухэтапные задачи со словами, добавляя или вычитая числа до 100.
Сложение больших цифр
Учтите, что при сложении двух трехзначных чисел вы складываете сотни и сотни, десятки и десятки, единицы и единицы, и вам может понадобиться составить новую десятку или новую сотню. Используйте модели или рисунки и объясните свой письменный метод.
Сложение в пределах 1000
Научитесь складывать в пределах 1000.
Вычитание больших цифр
Поймите, что при вычитании одного трехзначного числа из другого трехзначного числа вы вычитаете сотни из сотен, десятки из десятков и единицы из единиц, и вам может понадобиться получить больше десятков и единиц чтобы вычесть. Используйте модели или рисунки и объясните свой письменный метод.
Вычитание в пределах 1000
Узнайте, как вычитать в пределах 1000.
Измерения и данные
Считывание показаний цифровых и аналоговых часов
Считывание показаний часов с круглым циферблатом и цифровых часов для определения времени с точностью до пяти минут. Поймите понятие утра и вечера. в 24-часовой день. Уметь называть время вслух и писать время разными способами, используя слова «утра» и «после полудня».
Измерение и оценка длины
Измерение и оценка длины линий или объектов в стандартных единицах измерения, таких как дюймы, футы, сантиметры и метры. Запишите и прочитайте размеры в дюймах (дюймах) или сантиметрах (см). Сравните размеры (на сколько больше, на сколько меньше).
Решение задач со словами
Решение задач со словами на сложение и вычитание с длинами в одних и тех же единицах (в пределах 100).
Пример:
Новый рулон ленты содержит 72 дюйма ленты.
Саре нужно 26 дюймов ленты, чтобы обернуть подарок на день рождения. Если она отрежет 26 дюймов от начала нового рулона, сколько дюймов ленты останется?
Решение задач на деньги
Решение задач на сложение и вычитание на деньги – монеты (пенни, никель, десятицентовик, четвертак) и долларовые купюры.
Пример:
У Антония есть четвертак, две десятицентовика и пять пенни. Он хочет купить свисток, который стоит один доллар. Сколько еще денег ему нужно? Какая комбинация монет даст ему нужные деньги?
Изображения и гистограммы
Чтение и создание графических изображений и гистограмм для отображения измерений, количеств или других данных в четырех категориях. Решайте задачи на сложение, вычитание и сравнение слов, используя информацию, представленную в виде гистограммы.
Фигуры
Определение общих фигур
Определение треугольников (трехсторонние фигуры), четырехугольников (четырехсторонние фигуры), пятиугольников (пятиугольники) и шестиугольников (шестиугольники).