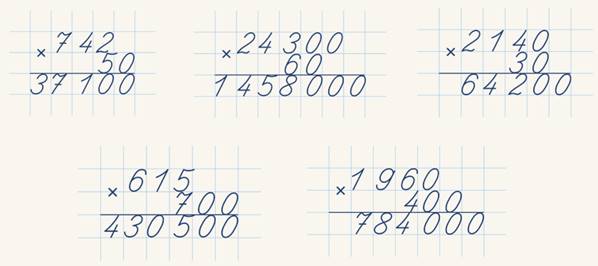Умножение трехзначного числа на однозначное по схеме
75,00 ₽
Задание поможет научиться умножать большие числа. Два вида решения примеров: столбиком и по схеме. Два уровня сложности: 1) простые примеры, в которых дается трехзначное число с нулем посередине; 2) сложные примеры, в которых трехзначное число полностью состоит из цифр. С ответами. Для печати А4.
Артикул: i-10081 Категория: Для учебы Метки: 3 класс, Умножение
- Описание
- Детали
- Отзывы (0)
Описание
Задание «Умножение трехзначного числа на однозначное» поможет научиться умножать большие числа.
В задании предлагается решить примеры умножения трехзначного числа на однозначное разными способами:
— С помощью разделения трехзначного числа на разрядные слагаемые;
— В столбик.
В программе два уровня сложности:
— Простые примеры, в которых дается трехзначное число с нулем посередине
— Сложные примеры, в которых трехзначное число полностью состоит из цифр.
Таким образом, сначала можно потренироваться на простых примерах, а затем переходить к более сложным.
Первый пример в задании — это образец умножения трехзначного числа на однозначное, по которому нужно решить примеры, выполняя последовательно несколько действий и записывая ответы в определенных местах.
Программа счета написана в Excel с помощью макросов. Формируются примеры на листе формата А4. Примеры генерируются случайным образом, количество генераций не ограничено. В конце карточки формируются ответы на примеры, которые после печати карточки можно отрезать. Нумерация карточек и ответов позволяет быстро находить ответы к каждой карточке, даже если их напечатано много.
Генератор примеров по математике будет очень удобен как для родителей, так и для учителей: не нужно заранее покупать задачники и пособия по математике с примерами. Можно скачать файл и сгенерировать карточки в любое время независимо от подключения к интернету и распечатать.
Можно скачать файл и сгенерировать карточки в любое время независимо от подключения к интернету и распечатать.
Для ознакомления с программой можно бесплатно скачать примеры, которые получаются при использовании программы. Для получения новой карточки примеров достаточно скачать, нажать на кнопку генерации и распечатать.
Данную программу также можно скачать в составе сборника заданий для 3 класса.
На сайте представлен каталог программ, в котором все программы распределены по группам. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.
Вам также будет интересно…
Задачи на движение (разные виды)
100,00 ₽В корзинуПорядок действий в пределах 1000 (все действия)
90,00 ₽В корзинуУмножение и деление в столбик
Оценка 4.67 из 5
100,00 ₽В корзинуРаскрытие скобок и порядок действий до 1000 (сложные примеры)
130,00 ₽Деление в столбик
75,00 ₽В корзинуСложение и вычитание в столбик
Оценка 5.
70,00 ₽В корзину 00 из 5
00 из 5Умножение в столбик
75,00 ₽В корзинуУмножение и деление по типам (табличное, внетабличное, круглых чисел)
120,00 ₽В корзинуУмножение в столбик 2 (с клеткой)
Оценка 5.00 из 5
85,00 ₽В корзину
ГДЗ по математике 4 класс учебник Моро, Бантова 2 часть
❤️️Ответ к странице 49. Математика 4 класс учебник 2 часть. Авторы: М.И. Моро, М.А. Бантова.
Задание вверху страницы
Рассмотри и сравни, как выполнено умножение.
Ответ:
Умножение трехзначного числа на трехзначное с нулем на месте десятков выполняют следующим образом: умножают первый множитель на количество единиц, умножение на количество десятков пропускается, потому что второе произведение равно 0, а третье произведение записывают под сотнями. Два неполных произведения (по сути три, но второе равно 0) складывают и записывают ответ.
Ответ:
При умножении 327 на 406 получаются три неполных произведения:1962, 0 и 1308.
При умножении 614 на 280 получаются три неполных произведения: 4912, 0 и 1228. Но для того, чтобы сократить работу первое неполное произведение не прописывают и не ищут его, так как нуль сдвинут и не участвует в умножении.
Но для того, чтобы сократить работу первое неполное произведение не прописывают и не ищут его, так как нуль сдвинут и не участвует в умножении.
Объясни, почему в таких случаях при умножении на трехзначное число записывают только два неполных произведения и как их подписывают.
Ответ:
При умножении трехзначного числа на трехзначное число с нулем на позиции десятков, получается три неполных произведения. Первое записывается под единицами, второе не записывается, но мысленно мы помним, что оно записывается под десятками, а третье неполное произведение записываем под сотнями. Складываем неполные произведения и читаем ответ.
Также есть особенность при умножении трехзначного числа на трехзначное число с нулем на позиции единиц. Второй множитель записывают со сдвигом влево на 1 знак и поэтому число, означающее десятки становится условно единицами, а сотни — десятками. У нас получаются всего два неполных произведения, потому что умножение на нуль не выполняют и первым неполным произведением, записываемым под единицами, становится уже число, полученное при умножении первого множителя на количество десятков.
Номер 185.
Вычисли с объяснением.
Ответ:
1) 254 ∙ 37
Умножу первый множитель на число единиц:
254 ∙ 7 = 1778
Получу первое неполное произведение 1778.
Умножу первый множитель на число десятков:
254 ∙ 3 = 762
Получу второе неполное произведение: 762.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения.
Читаю ответ: произведение чисел 254 и 37 равно 9398.
 Начну подписывать второе неполное произведение под десятками, а третье под сотнями.
Сложу неполные произведения.
Читаю ответ: произведение чисел 254 и 307 равно 77978.
Начну подписывать второе неполное произведение под десятками, а третье под сотнями.
Сложу неполные произведения.
Читаю ответ: произведение чисел 254 и 307 равно 77978.
3) 481 ∙ 360 Записываем второй множитель со сдвигом вправо на 1 знак и таким образом первым действием выполняем умножение первого множителя на количество десятков. Умножу первый множитель на число десятков: 481 ∙ 6 = 2886 Получу первое неполное произведение 2886. Умножу первый множитель на число сотен: 481 ∙ 3 = 1443 Получу второе неполное произведение: 1443. Начну подписывать первое неполное произведение под единицами, а второе неполное произведение под сотнями. Нуль припысываю к ответу справа. Сложу неполные произведения. Читаю ответ: произведение чисел 481 и 306 равно 173160.
Номер 186.
Ответ:
Номер 187.
Двум классам поручено расчистить школьный каток, длины которого 20 м, а ширина 10 м.
Ответ:
1) 20 ∙ 10 = 200 (м²) – площадь катка. 2) 26 + 24 = 50 (уч.) – в двух классах всего. 3) 200 : 50 = 4 (м²) – должен рассчитать один ученик. 4) 4 ∙ 26 = 104 (м²) – должны расчистить ученики первого класса. 5) 4 ∙ 24 = 96 (м²) – должны расчистить ученики второго класса. Ответ: 104 м² и 96 м².
Номер 188.
У фермера 4 лошади и 9 коров. Лошади требуется на месяц 135 кг сена, а трём коровам – столько сена, сколько необходимо семи лошадям. Сколько килограммов сена должен расходовать фермер ежемесячно на всех лошадей и коров?
Ответ:
4 лошади и 9 коров = ? кг сена всего
1 лошадь = 135 кг сена
3 коровы = 7 лошадей = ? кг сена
1) 135 ∙ 7 = 945 (кг) – сена нужно для 3 коров.
2) 9 : 3 = 3 (р.) – 9 коров больше в 3 раза, чем 3 коровы. 3) 945 ∙ 3 = 2835 (кг) – сена нужно для 9 коров.
4) 135 ∙ 4 = 540 (кг) – сена нужно для 4 лошадей.
5) 2835 + 540 = 3375 (кг)
II способ:
Ответ: 3375 кг сена должен расходовать фермер ежемесячно на всех лошадей и коров.
Номер 189.
Высота футбольных ворот 2 м 40 см, она в 2 раза больше высоты хоккейных ворот. Узнай высоту хоккейных ворот.
Ответ:
2 м 40 см = 240 см 1) 240 : 2 = 120 (см) – высота хоккейных ворот. Ответ: 1 м 20 см.
Номер 190.
1) Начерти отрезок длиной 8 см. Раздели его на 2 равные части. Какие доли отрезка получились? Сколько их? Раздели каждую половину ещё на 2 равные части. Какие доли отрезка получились? Сколько их в целом отрезке? Сколько четвёртых долей отрезка в его половине?
 Какие доли отрезка получились? Сколько восьмых долей в трёх четвёртых отрезка?
Какие доли отрезка получились? Сколько восьмых долей в трёх четвёртых отрезка?Ответ:
Если разделить отрезок на 2 равные части, то получается две доли, которые можно назвать половина или одна вторая.
Разобъём каждую половину пополам. Получились 4 доли, которые называют четвёртые доли или одна четвёртая или четвертина.
Разобъём каждую четвёртую часть пополам. Получились 8 равных долей. Их называют восьмые доли или одна восьмая часть.
В трёх четвёртых отрезка шесть восьмых долей.
Задание внизу страницы
Ответ:
Задание на полях страницыСравни площади фигур.
Ответ:
Площади всех фигур одинаковые, потому что если мы разобьем квадрат на 2 треугольника, то увидим, что эти треугольники, равны треугольникам, из которых составлены фигуры 2 и 3, а это значит, что все фигуры равны.
Методы и шаги с решенными примерами
Трехзначное умножение в математике — это метод умножения трехзначных чисел на однозначные, двузначные или трехзначные числа путем размещения чисел в столбцах в соответствии с их положением. ценности. Умножение трехзначных чисел затруднено с двузначными и трехзначными числами. Однако умножать трехзначные числа на однозначные числа довольно просто.
В этой статье по математике мы узнаем, что означает умножение трехзначного числа, умножение трехзначного числа на однозначное, умножение трехзначного числа на двузначное и умножение трехзначного числа на трехзначное вместе с перегруппировкой и без нее. перегруппировка чисел, и решать задачи на основе 3-значного умножения.
Трехзначное умножение
Трехзначное умножение — это метод умножения трехзначных чисел на другие числа. При умножении числа располагаются в столбцах в соответствии с их разрядностью. Трехзначные числа располагаются в соответствии со своим разрядом: единицы, десятки и сотни.
Когда мы умножаем два набора цифр, большее число остается сверху, а меньшее число помещается под ним. Число, расположенное сверху, называется 9.0003 множимое на и число, расположенное ниже, называется множителем .
Когда числа расположены в соответствии с их разрядами, мы умножаем множитель со всеми цифрами множимого один за другим, начиная с цифры единиц, за которой следуют цифры десятков, а затем цифры сотен. Все эти продукты написаны вместе, и они приводят к конечному продукту. Давайте разберемся с этим на некоторых примерах умножения.
Чтобы узнать о различных типах чисел с их определениями и примерами, нажмите здесь.
Примеры трехзначного умножения:
Пример 1: Умножьте \(123\) на \(3\).
Запишите данное умножение \(123 \times 3\), как показано ниже, где \(123\) — множимое, а \(3\) — множитель.
После умножения этих чисел мы получим произведение как \(269\).
Пример 2: Умножить \(211\) на \(3\).
Запишите данное умножение \(211 \times 3\), как показано ниже, где \(211\) — множимое, а \(3\) — множитель.
После умножения данных чисел мы получаем произведение как \(633\). Давайте теперь поймем, как сделать это умножение с разными числами.
3-значное умножение на 1-значное
Когда 3-значное число умножается на 1-значное число, мы имеем два случая, которые приведены ниже:
- 3-значное на 1-значное умножение без перегруппировки.
- Умножение 3 цифр на 1 цифру с перегруппировкой.
3-значное умножение на 1-значное без перегруппировки:
Чтобы найти произведение трехзначного числа на однозначное, умножаем однозначное число на каждую цифру трехзначного числа. Если произведение однозначного числа на каждую цифру числа является однозначной цифрой, то нет необходимости переносить какое-либо число. Давайте разберемся в этом с помощью примера.
Например: Умножить \(214\) на \(2\).
Следующие шаги показывают метод умножения \(214\) на \(2\).
Шаг 1: Расположите числа \(214\) и \(2\) в столбцах в соответствии с их разрядностью, как показано на рисунке ниже.
Шаг 2: Теперь сначала умножьте однозначное число (которое равно \(2\)) на каждую цифру трехзначного числа (которое равно \(214\)).
- \(2\4=8\).
- \(2 \умножить на 1 = 2\).
- \(2 \умножить на 2 = 4\).
Шаг 3: Следовательно, произведение \(214\) на \(2\) равно \(428\).
Чтобы узнать о системах счисления, их типах с решаемыми примерами, нажмите здесь.
3-значное умножение на 1-значное с перегруппировкой:
В этом разделе мы узнаем, когда умножение 3-значного числа умножается на 1-значное число с использованием переноса с помощью примера.
Например: Умножить \(347\) на \(3\).
Следующие шаги показывают метод умножения \(347\) на \(3\).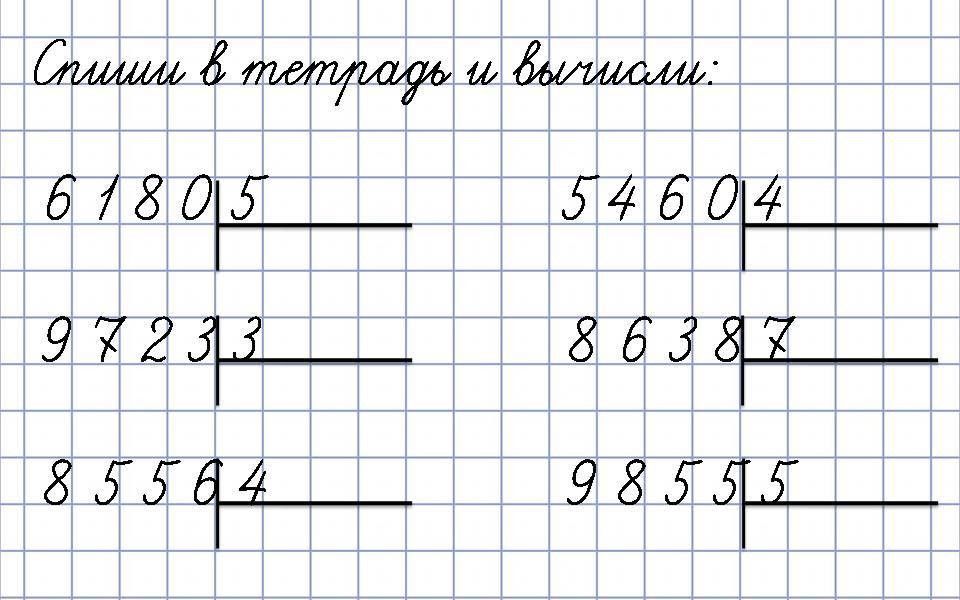
Шаг 1: Расположите числа \(347\) и \(3\) в столбцах в соответствии с их разрядностью, как показано на рисунке ниже.
Шаг 2: Умножьте \(3\) на каждую цифру \(347\).
- \(3\7 умножить на 21\). Так как \(21\) является двузначным числом, напишите \(1\) под столбцом единиц и перенесите \(2\) в столбец десятков над \(4\).
- \(3\4=12\). Здесь нам нужно добавить перенос \(2\) к \(12\), мы получим \(14\). Поскольку \(14\) является двузначным числом, напишите \(4\) под столбцом десятков и перенесите \(1\) в столбец сотен над \(3\).
- \(3 \х3 = 9\). Здесь нам нужно добавить перенос \(1\) к \(9\), мы получим \(10\). Так как другой цифры для умножения не осталось, мы пишем \(10\).
Шаг 3: Следовательно, произведение \(347\) на \(3\) равно \(1041\).
Чтобы узнать о различных типах арифметических операций с правилами и примерами, нажмите здесь.
Умножение 3-значного на 2-значное
Чтобы умножить 3-значное число на 2-значное, мы сначала записываем 3-значное число сверху, а 2-значное число — под ним. Когда 3-значное число умножается на 2-значное число, у нас есть два случая, которые приведены ниже:
Когда 3-значное число умножается на 2-значное число, у нас есть два случая, которые приведены ниже:
- 3-значное умножение на 2-значное без перегруппировки.
- 3-значное умножение на 2-значное с перегруппировкой.
Умножение 3-значного числа на 2-значное без перегруппировки:
Чтобы найти произведение 3-значного числа на 2-значное число, мы сначала умножаем цифру единиц множителя на множимое, затем умножаем разряд десятков множителя с множимым. Затем мы добавляем оба этих продукта, чтобы получить конечный продукт. Давайте разберемся в этом с помощью примера.
Например: Умножить \(411\) на \(31\).
Следующие шаги показывают метод умножения \(411\) на \(31\).
Шаг 1: Расположите числа \(411\) и \(31\) в столбцах в соответствии с их разрядностью, как показано на рисунке ниже.
Шаг 2: Теперь сначала умножьте \(1\) на каждую цифру \(411\).
- \(1\умножить на 1=1\).

- \(1 \умножить на 1 = 1\).
- \(1\4=4\).
Здесь у нас есть \(411\) как первое частичное произведение.
Шаг 3: Теперь поставьте \(0\) под первым частичным произведением, т. е. непосредственно перед записью второго частичного произведения в следующей строке. Этот \(0\) помещен здесь, потому что на этом шаге мы фактически умножаем \(411\) на \(30\).
Шаг 4: Теперь умножьте \(3\) на каждую цифру \(411\).
- \(3\1=3\).
- \(3 \умножить на 1 = 3\).
- \(3 \умножить на 12 = 12\).
Здесь у нас есть \(12330\) в качестве второго частичного произведения.
Шаг 5: Добавьте эти продукты, чтобы получить окончательный ответ.
Итак, \(411 + 12330 = 12741\). Следовательно, конечный продукт \(411\) на \(31\) равен \(12741\).
Чтобы узнать о сложении и вычитании полиномиальных выражений, нажмите здесь.
3-значное умножение на 2-значное с перегруппировкой:
В этом разделе мы узнаем, когда умножение 3-значного числа умножается на 2-значное с помощью переноса с помощью примера.
Например: Умножьте \(573\) на \(46\).
Следующие шаги показывают метод умножения \(573\) на \(46\).
Шаг 1: Расположите числа \(573\) и \(46\) в столбцах в соответствии с их разрядами, как показано на рисунке ниже.
Шаг 2: Теперь сначала умножьте \(6\) на каждую цифру \(573\).
- \(6 \умножить на 3 = 18\). Так как \(18\) является двузначным числом, напишите \(8\) в столбце единиц и перенесите \(1\) в столбец десятков над \(7\).
- \(6\7 умножить на 42\). Здесь прибавляем перенос \(1\) к \(42\), получаем \(43\). Поскольку \(43\) является двузначным числом, напишите \(3\) в столбце десятков и перенесите \(4\) в столбец сотен над \(5\).
- \(6 \умножить на 5 = 30\). Здесь прибавляем перенос \(4\) к \(30\), получаем \(34\). Поскольку другой цифры для умножения не осталось, мы пишем \(34\).
Здесь у нас есть \(3438\) как первое частичное произведение.
Шаг 3: Теперь поставьте \(0\) под первым частичным произведением, т. е. перед записью второго частичного произведения в следующей строке. Это потому, что на этом шаге мы фактически умножаем \(573\) на \(40\).
е. перед записью второго частичного произведения в следующей строке. Это потому, что на этом шаге мы фактически умножаем \(573\) на \(40\).
Шаг 4: Умножьте \(4\) на каждую цифру \(573\).
- \(4\3=12\). Поскольку \(12\) является двузначным числом, напишите \(2\) под столбцом десятков и перенесите \(1\) в столбец десятков над \(7\).
- \(4\7 умножить на 28\). Здесь прибавляем перенос \(1\) к \(28\), получаем \(29\). Поскольку \(29\) является двузначным числом, мы пишем \(9\) под столбцом сотен и переносим \(2\) в столбец сотен над \(5\).
- \(4\5=20\). Здесь прибавляем переносимое число \(2\) к \(20\), получаем \(22\). Так как другой цифры для умножения не осталось, мы пишем \(22\).
Здесь у нас есть \(22920\) в качестве второго частичного произведения.
Шаг 5: Добавьте эти продукты, чтобы получить окончательный ответ.
Итак, \(3438 + 22920 = 26358\). Следовательно, конечный продукт \(573\) на \(46\) равен \(26358\).
Чтобы узнать о сложении дробей с решенными примерами, нажмите здесь.
3-значное умножение на 3-значное
Умножение 3-значного числа на 3-значное число — процесс, аналогичный описанному в предыдущем разделе. Давайте разберемся с 3-значным умножением на 3-значное с помощью примера.
Например: Умножить \(123\) на \(456\).
Следующие шаги показывают метод умножения \(123\) на \(456\).
Шаг 1: Расположите числа \(123\) и \(456\) в столбцах в соответствии с их разрядностью, как показано на рисунке ниже.
Шаг 2: Теперь сначала умножьте \(6\) на каждую цифру \(123\).
- \(6 \умножить на 3 = 18\). Поскольку \(18\) является двузначным числом, запишите \(8\) в столбце единиц и перенесите \(1\) в столбец десятков над \(2\).
- \(6 \умножить на 2 = 12\). Здесь прибавляем перенос \(1\) к \(12\), получаем \(13\). Поскольку \(13\) является двузначным числом, напишите \(3\) под столбцом десятков и перенесите \(1\) в следующий столбец над \(1\).

- \(6 \умножить на 1 = 6\). Здесь прибавляем перенос \(1\) к \(6\), получаем \(7\). Так как другой цифры для умножения не осталось, мы пишем \(7\).
Здесь у нас есть \(738\) как первое частичное произведение.
Шаг 3: Теперь поставьте \(0\) под этим частичным произведением под единицами.
Шаг 4: Умножьте \(5\) на каждую цифру \(123\).
Повторите ту же процедуру, что и в шаге 2, чтобы получить второй частичный продукт. Итак, здесь у нас есть \(6150\) в качестве второго частичного произведения.
Шаг 5: Теперь поместите два нуля (\(0\)s) под столбцами единиц и десятков под частичным произведением, полученным на предыдущем шаге. Это потому, что на этом шаге мы фактически умножаем \(123\) на \(400\).
Шаг 6: Умножьте \(4\) на каждую цифру \(123\).
Повторите ту же процедуру, что и в шаге 2, чтобы получить третий частичный продукт. Итак, здесь мы имеем \(49200\) в качестве третьего частичного произведения.
Шаг 7: Сложите все частичные продукты, чтобы получить конечный продукт.
Итак, \(738 + 6150 + 49200 = 56088\). Следовательно, конечный продукт \(123\) на \(456\) равен \(56088\).
Чтобы узнать о сложении и вычитании десятичных дробей с примерами, нажмите здесь.
Решенные примеры трехзначного умножения
1. Умножьте \(712\) на \(23\)
Решение: Следуйте приведенным ниже инструкциям, чтобы найти произведение \(712\) на \(23\).
- Умножьте \(3\) на каждую цифру \(712\).
- Поставьте \(0\) на единицу ниже продукта, полученного выше.
- Умножьте \(2\) на каждую цифру \(712\).
- Добавьте два частичных продукта, чтобы получить конечный продукт.
Следовательно, конечный продукт \(712\) на \(23\) равен \(16376\).
2. Умножьте \(543\) на \(278\).
Решение: Следуйте приведенным ниже инструкциям, чтобы найти произведение \(543\) на \(278\).
- Умножьте \(8\) на каждую цифру \(543\).
- Поставьте \(0\) на единицу ниже продукта, полученного выше.
- Умножьте \(7\) на каждую цифру \(543\).
- Поместите два \(0\) под столбцами единиц и десятков под частичным произведением, полученным на предыдущем шаге.
- Умножьте \(2\) на каждую цифру \(543\).
- Добавьте все частичные продукты, чтобы получить конечный продукт.
Следовательно, конечный продукт \(543\) на \(278\) равен \(150954\).
Мы надеемся, что приведенная выше статья поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Часто задаваемые вопросы по 3-значному умножению
В.1 Как умножать трехзначные числа?
Ответ 1 Трехзначное умножение можно легко выполнить, если числа расположены в соответствии с их разрядами. Когда у нас есть набор из двух чисел для умножения, мы обычно держим большее число сверху, а меньшее число — под ним. Затем умножьте множитель на все цифры множимого по одному, начиная с цифры единиц, затем цифру десятков, а затем цифру сотен. Все эти продукты написаны вместе, и они приводят к конечному продукту.
Когда у нас есть набор из двух чисел для умножения, мы обычно держим большее число сверху, а меньшее число — под ним. Затем умножьте множитель на все цифры множимого по одному, начиная с цифры единиц, затем цифру десятков, а затем цифру сотен. Все эти продукты написаны вместе, и они приводят к конечному продукту.
В.2 Как умножить трехзначное число на двузначное?
Ответ 2 Когда трехзначное число умножается на двузначное, мы умножаем каждую цифру двузначного числа на каждую цифру трехзначного числа. Мы располагаем числа в столбцах в соответствии с их разрядными значениями, пишем частичные произведения одно под другим и складываем их, чтобы получить конечный продукт.
В.3 Как умножить трехзначное число на однозначное?
Ответ 3 Чтобы умножить трехзначное число на однозначное, мы умножаем однозначное число на каждую цифру трехзначного числа, чтобы получить произведение.
В. 4 Что вы подразумеваете под трехзначным умножением?
4 Что вы подразумеваете под трехзначным умножением?
Ответ 4 Трехзначное умножение — это метод умножения трехзначных чисел на однозначные, двузначные и трехзначные числа путем размещения чисел в столбцах в соответствии с их разрядными значениями. .
В.5 Что такое умножение трех цифр на три цифры?
Ответ 5 Умножение 3-значного на 3-значное означает, что 3-значное число умножается на другое 3-значное число. Это делается путем размещения чисел в столбцах, а затем умножения каждой цифры одного числа на каждую цифру другого числа. Частичные продукты записываются один под другим, а затем продукты добавляются, чтобы получить окончательный ответ.
Скачать публикацию в формате PDF| Бинарное вычитание: определение, правила, шаги с решающими примерами | |
| Прямоугольная пирамида: типы, формулы, свойства и примеры | |
. | Значение Cos 180 в градусах и радианах с решенными примерами |
| Верхняя и нижняя треугольная матрица: определитель, обратная и примеры |
3 идеи для обучения многозначному умножению
Вот 3 идеи FAST для обучения многозначному умножению. Эти вмешательства просты и быстры для занятых учителей.
Многозначное умножение
Звучит знакомо?
Вы уже неделю учите двузначное умножение, а ваши ученики просто не понимают .
Вы пробовали все обычные вещи, такие как раздача учащимся таблицы умножения, тестирование на время для изучения фактов и предложение поощрений. Я уверен, что вы очень старались. И ваши ученики, вероятно, тоже очень старались.
Но они до сих пор не понимают.
Закрепите это сейчас для дальнейшего использованияВы не одиноки. И это не твоя вина.
Многие учащиеся не готовы к многоэтапному традиционному алгоритму. Точно так же многие учащиеся не владеют основными фактами умножения.
Но с этим придется смириться.
3 идеи FAST Intervention, чтобы попробовать
Используйте эти 3 идеи FAST для обучения многозначному умножению. Они выдержали испытание временем и стоят времени и усилий.
1. Помогите учащимся содержать свою работу в чистоте.
Разборчивые, выстроенные в ряд числа так важны для успеха в математике. Учащиеся просто должны иметь разборчивый почерк и правильное выравнивание, чтобы цифры не выбивались из столбцов.
Следующие несколько советов касаются упорядочения номеров и столбцов.
Во-первых, поощряйте учеников писать красивыми острыми карандашами, чтобы их почерк был мелким и аккуратным. Тупые карандаши размазываются, а почерк жирнеет, занимает больше места.
Еще один совет, который поможет с выравниванием, — это использование математических графических органайзеров. Они отлично подходят для выравнивания чисел и столбцов.
На изображении ниже видно, как в органайзере все аккуратно расставлено. Выровненные числа и столбцы жизненно важны, когда студенты работают и учатся. Расстояние также имеет решающее значение; эти организаторы позволяют студентам работать, не перегружая их номера.
Выровненные числа и столбцы жизненно важны, когда студенты работают и учатся. Расстояние также имеет решающее значение; эти организаторы позволяют студентам работать, не перегружая их номера.
Вам следует попробовать использовать миллиметровую бумагу или бумагу с сеткой, если ваши ученики не нуждаются в большой поддержке или готовы продвигаться к независимости. Миллиметровая бумага помогала учащимся преуспевать в математике на протяжении десятилетий и работает до сих пор. Сетки легко сохраняют числа, столбцы и строки в чистоте и порядке.
Если у вас нет времени делать свои собственные, эти наборы подготовлены и готовы к занятиям сразу — просто распечатайте и вперед! Идеально подходит для занятых учителей со студентами, которым требуется много практики и повторений.
Щелкните по изображению, чтобы ознакомиться с полным комплектом. Бумага для тетрадей, перевернутая боком, позволяет учащимся сохранять аккуратность в работе. Эта стратегия дешевая и ТАК ЛЕГКАЯ!
Эта стратегия дешевая и ТАК ЛЕГКАЯ!
ПРИМЕЧАНИЕ: Некоторые ученики могут с трудом писать свои числа настолько мелкими, чтобы они аккуратно помещались между строк.
Но поскольку это бесплатно, попробовать стоит!
Быстроразлинованная бумага для аккуратностиЕсли вы не уверены, какие наборы подходят для ваших учеников, попробуйте один из них — БЕСПЛАТНО! Нажмите на изображение ниже, чтобы получить БЕСПЛАТНЫЙ набор для пробного использования!
Нажмите, чтобы посетить Учителя платят учителям.НАЖМИТЕ ЗДЕСЬ, чтобы узнать больше об использовании миллиметровки и органайзеров для умножения со своими учениками!
2. Давайте поработаем над беглостью фактов умножения.
Я считаю, что для обучения владению фактами можно использовать самые разные методы, и мои любимые занятия — игры.
Представленная выше игра идеально подходит для учащихся, которые впервые изучают факты умножения или нуждаются в интенсивном изучении основных фактов умножения.
Студенты просто запускают таймер и кладут карточки с ответами поверх соответствующего факта. В верхней части тренировочного коврика факты перечислены по порядку. Нижняя половина показывает перепутанные факты.
*Игра была специально разработана для того, чтобы учащиеся могли «обманывать», глядя на верхнюю часть. Это дает уверенность, поскольку их время улучшается, и студенты вскоре учатся решать проблемы, не полагаясь на верхнюю часть.
Другие варианты игр могут быть такими же простыми, как использование карточек с настольной игрой или крестики-нолики. Я предлагаю подбирать партнеров-студентов с одинаковым уровнем беглости, чтобы избежать чувства разочарования.
Даже простые игры можно использовать для закрепления фактов.Вы можете разрешить партнерам использовать таблицу умножения для проверки ответов друг друга.
Некоторым учащимся хорошо подходят онлайн-игры и обучающие программы. Xtramath.org — надежная и полезная программа, которую я использую уже много лет. Прочтите этот пост в блоге: Xtramath.org — отличная БЕСПЛАТНАЯ программа для занятий по математике!
Прочтите этот пост в блоге: Xtramath.org — отличная БЕСПЛАТНАЯ программа для занятий по математике!
Использование тестов на время по-прежнему является популярным способом обучения и мотивации учащихся к изучению фактов. Если вы ищете базовый набор тестов на время умножения, ознакомьтесь с этим универсальным набором.
Даже если вы не хотите ограничивать студентов по времени, это все равно отличная практика.
3 различных формата викторинЯ также приобрел и использовал этот ресурс у другого автора, работающего над платой учителям, созданного г-ном Хьюзом. Моим ученикам понравилось это задание, и они создали свой собственный додекаэдр, к тому же они довольно круто смотрятся в классе.
От Создано г-ном Хьюзом в Учителя платят учителям3. Предоставьте рекомендации — большие и маленькие.
Когда учащиеся решают задачи на многозначное умножение, им часто нужны напоминания и визуальные подсказки, поскольку для их решения требуется очень много шагов.
Опорные диаграммы и плакаты служат в качестве наглядных материалов и справочных материалов, которые помогают учащимся самостоятельно ответить на многие вопросы.
Нажмите на изображение, чтобы перейти на страницу «Учителя платят учителям».Справочные плакаты и опорные диаграммы (такие как приведенный выше) могут научить учащихся полагаться на себя при решении задач и ответах на вопросы. Это способствует независимости и уверенности. Кроме того, у учителя есть больше времени, чтобы поддержать отстающих учеников, а не отвечать на одни и те же вопросы снова и снова.
Я часто использую это для проверки двузначного умноженияЯ использую эту якорную таблицу двузначного умножения (выше) для частого просмотра двухзначного умножения на двузначное. Он следует тем же визуальным подсказкам, что и организаторы умножения. Он идеально подходит для учителей, которым нужно знать, как преподавать многозначное умножение.
И это многоразовый !
Обратите внимание на стикеры.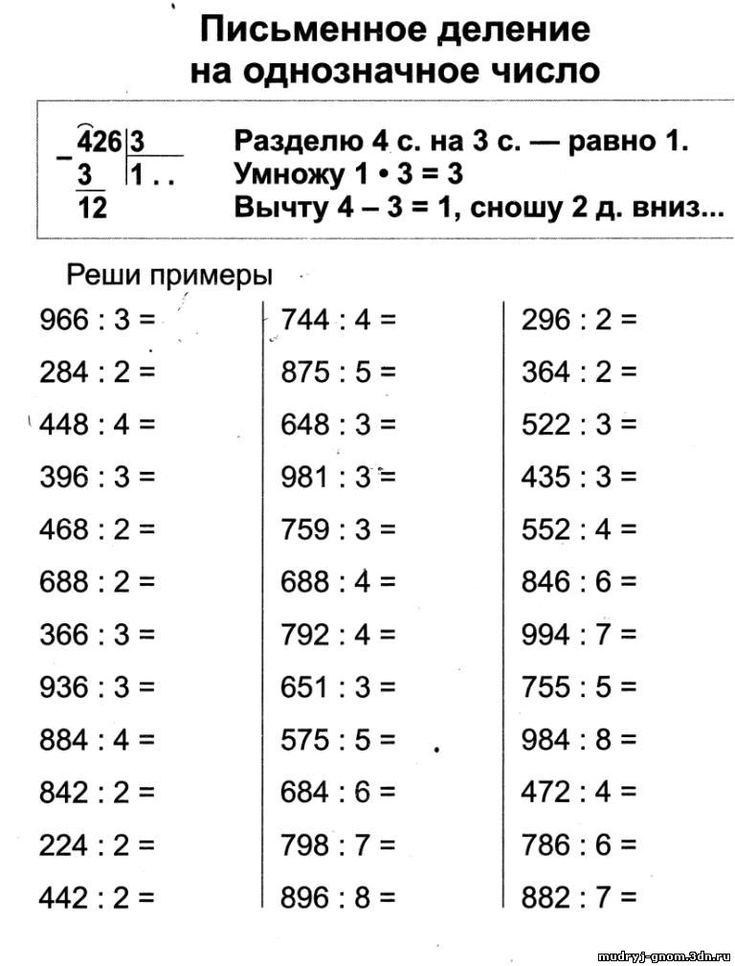 Меняйте их на разные числа каждый день для частой практики! Вы можете сделать задачи настолько простыми или сложными, насколько это необходимо вашему классу.
Меняйте их на разные числа каждый день для частой практики! Вы можете сделать задачи настолько простыми или сложными, насколько это необходимо вашему классу.
Используйте такие плакаты и якорные диаграммы ежедневно или еженедельно для начинающих, учащихся специальных учебных заведений или всех учащихся, которым полезно регулярно просматривать их.
Краткое руководство по обучению умножению
Несколько слов напоследок. . .
При обучении многозначному умножению то, что работает для одних учащихся, может не работать для других. Оставайтесь открытыми и гибкими, пробуя новые идеи и стратегии. Многим учащимся требуется повторение и несколько раз просмотр понятий, представленных различными способами, прежде чем они найдут отклик.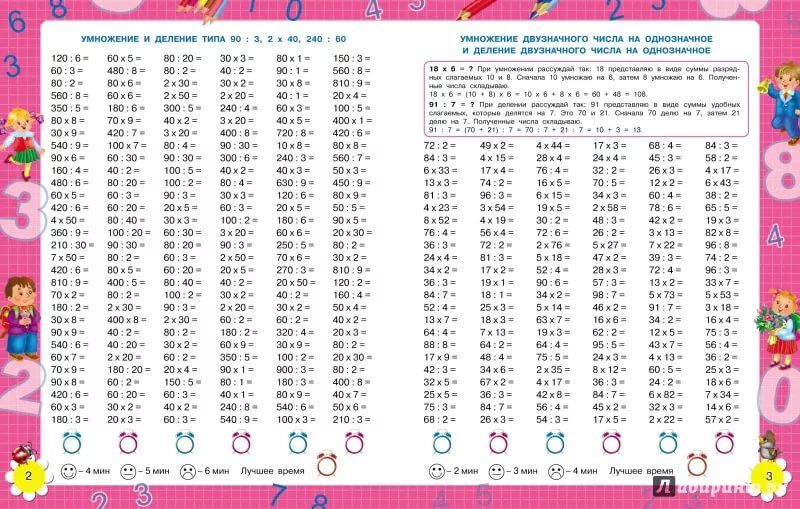
Другие статьи о многозначном умножении:
Рабочие листы по двузначному умножению: дифференцированные . Вот визуальный метод обучения двузначному умножению с использованием дифференцированных визуальных подсказок, помогающих ученикам добиться успеха.
Двузначное умножение стало проще! – Вот как использовать организаторы двузначного умножения и рабочие листы.
Статьи о длинном делении:
Дифференцированные рабочие листы длинного деления БЕСПЛАТНО – Получите БЕСПЛАТНО эти дифференцированные рабочие листы с делением на длинное деление и значительно повысьте успеваемость учащихся и свои успехи в обучении!
Как преподавать многозначное умножение и деление в длинное число – Эта статья в блоге познакомит вас с имеющимися у меня ресурсами по дифференцированному умножению и делению в длинное число. Затем вы узнаете, как именно я использую их в своем классе.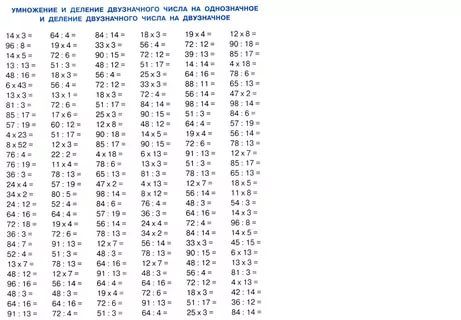
 00 из 5
00 из 5