16 тыс изображений найдено в Яндекс.Картинках — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Содержание
примеры по математике 4 класс на умножение и деление столбиком
Image Wallpaper and More collection of примеры по математике 4 класс на умножение и деление столбиком contain 30+ more images free download Презентация по математике на тему » игры, задания на умножение и …
Картинки по запросу деление в столбик 4 класс примеры | Деление …
Презентация на тему: «Математика 4 класс. Тема урока: Умножение и …
примеры на умножение и деление 4 класс в столбик карточки: 10 тыс …
30000 примеров по математике. 4 класс Елена Нефедова, Ольга …
контрольная работа умножение деление столбиком — Prakard
Скачать примеры в столбик на деление 4 класс
примеры на умножение и деление 4 класс в столбик карточки: 10 тыс …
Презентация по математике 3 класс «Закрепление решения примеров и …
Карточки по математике 4 класс «Деление многозначных чисел на …
Деление столбиком на однозначное число | Kid-mama
Картинки по запросу деление в столбик 4 класс примеры | Деление . ..
..
Книга 3000 новых примеров по математике. Внетабличное умножение и …
2
Купить книгу 3000 новых примеров по математике. Внетабличное …
Умножение в столбик: скачать и распечатать примеры — 3mu.ru
Карточки для отработки вычислительных навыков для 4 класса
Купить 3000 новых примеров по математике. 3 класс. Табличное …
Рабочие Листы на Умножение
3000 примеров по математике (Табличное умножение и деление). 2-3 …
Решебник деление в столбик 3 класс примеры — muemichi’s diary
Книга 3000 новых примеров по математике. Внетабличное умножение и …
Контрольная работа по математике по теме: «Умножение и деление на …
примеры на умножение и деление 4 класс в столбик карточки: 10 тыс …
КТП по математике 4 класс УМК » Школа России»
2
Таблица деления (математика для детей, 2, 3 класс)
ГДЗ (решебник) по математике 3 класс Моро, Бантова часть 1, 2 . ..
Презентация по математике на тему » игры, задания на умножение и …
Книга «Математика.
 3 класс. Табличное умножение и деление …
3 класс. Табличное умножение и деление …Образцы примеров на деление трехзначных чисел на однозначные и …
2
Умножение и деление многозначных чисел 4 класс примеры …
Умножение на числа, оканчивающиеся нулями — Математика 4 класс (Моро)
Иллюстрация 1 из 3 для Математика. 3-4 классы. Внетабличное …
Деление в столбик: скачать и распечатать примеры — 3mu.ru
Примеры в столбик для 2 класса hfccgtxfnfnm :: biocicacon
Купить 3000 новых примеров по математике. 3 класс. Табличное …
Книга 3000 новых примеров по математике. Внетабличное умножение и …
2
Примеры деление столбиком для 4 класса с ответами
примеры по математике 4 класс на умножение и деление столбиком Images Collection Математика, Практический справочник, 1-4 класс, Марченко И. С., 2012 Примеры на деление столбиком 3 класс — сайт с формами Как объяснить ребенку деление столбиком во 2-3 классе | rastishka.by
Умножение и деление многозначных чисел на однозначное.

Просмотр содержимого документа
«Контрольная работа 4 класс по теме: Умножение и деление многозначных чисел на однозначное.»
Контрольная работа 4 класспо теме: Умножение и деление многозначных
чисел на однозначное.
1 вариант.
1. Реши задачу:
В концертном зале 200 мест. В партере 120 мест. В амфитеатре мест в 3 раза меньше, чем в партере, а остальные места на балконе. Сколько мест на балконе?
2. Сначала определи, сколько цифр будет в записи частного, а потом выполни деление столбиком.
54663:7 80395:5 6543:9 860073:3
1836:4 7542:9 3906:6 9150:3
3. Найди значения выражений:
(10283 + 16789) : 9 5 ∙ (125 + 75) : 20 + 80
(200496 –134597) ∙ 2
4. Реши уравнение:
3 ∙ х = 87 -6
Задачи на смекалку.
5. Внук, родившийся в 1992 году, на 65 лет моложе деда. В каком году родился дед?
Внук, родившийся в 1992 году, на 65 лет моложе деда. В каком году родился дед?
6. В двух лодках разместились 12 человек, в одной – в два раза больше, чем в другой. Угадай, сколько человек в каждой лодке.
2 вариант.
1. Реши задачу:
На рынок привезли груши, яблоки и сливы, всего 4 00. Яблок было 150 кг, груш в 3 раза меньше, чем яблок, а остальные сливы. Сколько килограммов слив привезли на рынок?
2. Сначала определи, сколько цифр будет в записи частного, а потом выполни деление столбиком.
98560:7 83216:4 8656:4 91620:4
73170:9 3726:9 91728:9 705355:5
3. Найди значения выражений:
(18370 + 23679) : 7 156 – 96 : (12 : 4) : 2
(800035 – 784942) ∙ 6
4. Реши уравнение:
84 : х = 6 ∙ 7
Задачи на смекалку.
5. Бабушка родилась в 1934 году. В каком году родилась внучка, если она на 56 лет моложе бабушки?
6. У Оли и Кати вместе столько же яблок, сколько у Коли и Толи.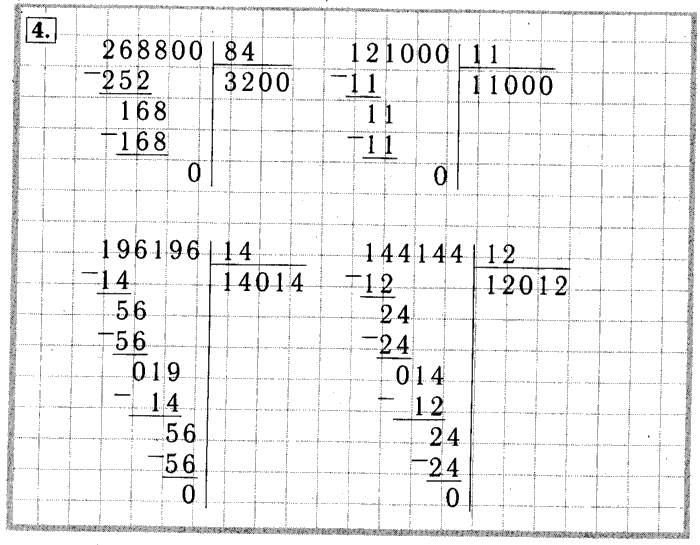 У Кати 5 яблок, а у Коли 8 яблок. У кого яблок больше: у Оли или у Толи?
У Кати 5 яблок, а у Коли 8 яблок. У кого яблок больше: у Оли или у Толи?
Страница 76 (учебник Моро 1 часть 4 класс) ответы по математике
Умножение и деление
325. Объясни записи в рамках на полях.
с * 1 = c — при умножении любого числа на 1 получается само это число.
b * 0 = 0 — при умножении любого числа на 0 получается 0. 326.
327. Запиши произведение чисел a и b и вычисли его значение при а = 72 и b = 3.
a * b = 72 * 3 = 216.
328. Составь разные задачи по выражению 16 * 4.
Задача 1:
Цена ручки 16 р. Сколько стоят 4 таких ручки?
16 * 4 = 64 p.
Ответ: 64 р.
Задача 2:
Ваня за месяц заработал 16 пятерок, а Саша в 4 раза больше. Сколько пятерок за месяц заработал Саша?
16 * 4 = 64 пятерок.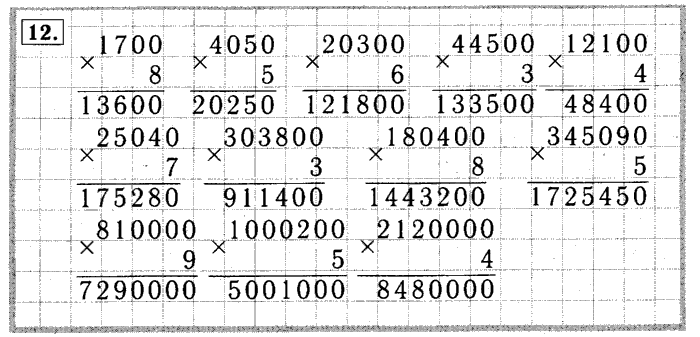
Ответ: 64 пятерок.
329. На 9 одинаковых парников надо 45 м плёнки. Сколько метров плёнки пойдёт на 3 таких парника? Составь и реши задачи, обратные данной.
1) 45 : 9 = 5 м плёнки идёт на 1 парник.
2) 5 * 3 = 15 м плёнки пойдёт на 3 парника.Ответ:
15 м.
Обратная задача:
На 3 парника нужно 15 м плёнки. Сколько метров плёнки пойдёт на 9 таких же парников?
1) 15 : 3 = 5 м плёнки идёт на 1 парник.
2) 5 * 9 = 45 м плёнки нужно на 9 парников.Ответ: 45 м.
330. Туристы в первый день прошли 16 км, что составило восьмую часть их маршрута. Сколько километров им осталось пройти?
1) 16 * 8 = 128 км составляет весь маршрут туристов.
2) 128 — 16 = 112 км осталось пройти туристам.Ответ: 112 км.
331.
332.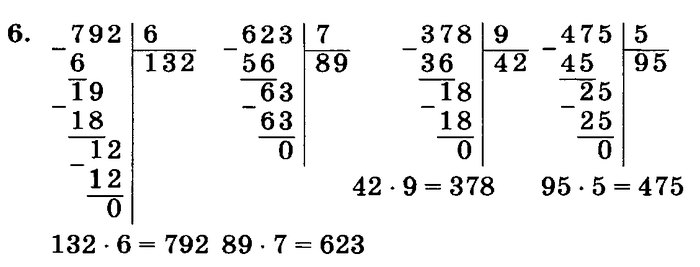 Начерти такой треугольник, дополни его до прямоугольника, найди площадь прямоугольника и каждого треугольника.
Начерти такой треугольник, дополни его до прямоугольника, найди площадь прямоугольника и каждого треугольника.
Площадь прямоугольника: 3 * 5 = 15 см2 = 1500 мм2.
Площадь треугольника: 1500 : 2 = 750 мм2.
Задание под знаком вопроса.
(14 + 7) * 3 = 21 * 3 = 63
8 * (100 — 99) = 8 * 1 = 8
Проверочные работы по математике, 4 класс
ПРОВЕРОЧНЫЕ МАТЕРИАЛЫ, ИСПОЛЬЗУЕМЫЕ ДЛЯ ОЦЕНКИ ПЛАНИРУЕМЫХ РЕЗУЛЬТАТОВ ПО МАТЕМАТИКЕ В 4 КЛАССЕ (ВХОДНОЙ КОНТРОЛЬ)
Содержание работы.
Вариант 1
1. Решите задачу.
С одного участка школьники собрали 160 кг моркови, а с другого – в 2 раза больше. Четвертую часть всей моркови они израсходовали на корм кроликам. Сколько килограммов моркови израсходовали на корм кроликам?
2. Найдите значения выражений.
18 + 36 : 9 + 6 · 8 – 50
400 – (80 + 180 : 3) + 60
3. Решите примеры столбиком.
138 + 567 152 · 6
447 – 189 867 : 3
4. Переведите.
125 см = …м …дм …см 7 м 3 см = …см
847 дм = …м …дм 700 см² = … дм²
5. Начертите прямоугольник со сторонами 5 см и 3 см. Найдите его площадь и периметр.
Вариант 2
1. Решите задачу.
На одном участке школьники вырастили 240 кг капусты, на другом – в 2 раза меньше. Четвертую часть всей капусты израсходовали на корм кроликам. Сколько килограммов капусты израсходовали на корм кроликам?
2. Найдите значения выражений.
(18 + 36) : 9 + 6 · 8 – 50
720 : (2 + 7) + (140 – 90)
3. Решите примеры столбиком.
523 + 197 279 · 3
831 – 369 792 : 2
4. Переведите.
8 м 4 см = …см 275 см = …м …дм …см
900 см² = … дм² 631 дм = …м …дм
5. Начертите прямоугольник со сторонами 6 см и 2 см. Найдите площадь и периметр этого прямоугольника.
Найдите площадь и периметр этого прямоугольника.
ПРОВЕРОЧНЫЕ МАТЕРИАЛЫ, ИСПОЛЬЗУЕМЫЕ ДЛЯ ОЦЕНКИ ПЛАНИРУЕМЫХ РЕЗУЛЬТАТОВ ПО МАТЕМАТИКЕ В 4 КЛАССЕ (ИТОГОВЫЙ КОНТРОЛЬ)
Содержание работы.
Вариант 1
1. Запиши числа:
а) два миллиона сто тринадцать тысяч двести двадцать семь;
б) 6 единиц третьего класса, 90 единиц второго класса, 9 единиц первого класса.
2. Вычисли.
б) 40 000 — 25 375;
д) 435 • 605;
е) 766 • 670 =
и) 206226 : 342
(479 484+113 796):72 – 146•18
3. Реши задачу.
От двух пристаней, находящихся на расстоянии 510 км, отплыли одновременно навстречу друг другу катер и моторная лодка. Встреча произошла через 15 ч. Катер шел со скоростью 19 км/ч. С какой скорость шла моторная лодка?
4. Сравни.
а) 5 т 7 кг … 50 ц 7 кг; в) 3 ч 24 мин … 324 мин;
б) 4700 м … 47 км; г) 5 м 2… 5000 см2.
5. Найди площадь и периметр прямоугольника со сторонами 30 и 600 см.
6. Реши уравнение с•12=1000 -280
7*. В первой корзине 87 яблок. После того как из нее взяли 17 яблок, в ней осталось
на 20 яблок больше, чем во второй и третьей корзинах вместе. Сколько яблок в третьей корзине, если во второй 18 яблок?
Вариант 2
1. Запиши числа:
а) четыре миллиона двести пятнадцать тысяч семьсот сорок один;
б) 240 единиц третьего класса, 8 единиц второго класса, 50 единиц первого класса.
2. Вычисли.
а) 50 000 — 23 876; в) 372272:53.
б) 492 • 304; г) 543 • 650;
86• (727 216:604+2018)-181708
3. Реши задачу.
От Москвы до Бреста 1199 км. Из этих городов одновременно навстречу друг другу вышли два поезда и встретились через 11 часов. С какой скоростью двигался второй поезд, если скорость первого 52 км/ч?
4. Сравни.
а) 4 т 2 кг … 40 ц 2 кг; в) 6 мин 45 с … 645
б) 7800 м … 78 км; г) 5 км2 … 50 000 м2.
5. Найди площадь и периметр прямоугольника со сторонами 40 и 500 см.
Найди площадь и периметр прямоугольника со сторонами 40 и 500 см.
6 . х:12 =1367-367
7*. В первой коробке 59 деталей конструктора. После того как в нее положили еще 11 деталей, в ней стало на 20 деталей больше, чем во второй и третьей коробках
вместе. Сколько деталей во второй коробке, если в третьей 15 деталей
СПЕЦИФИКАЦИЯ
ПРОВЕРОЧНЫХ МАТЕРИАЛОВ, ИСПОЛЬЗУЕМЫХ ДЛЯ ОЦЕНКИ ПЛАНИРУЕМЫХ РЕЗУЛЬТАТОВ ПО МАТЕМАТИКЕ В 4 КЛАССЕ
(ВХОДНОЙ КОНТРОЛЬ)
Цель и содержание работы по математике
Проверить базовые знания учащихся в период начала обучения в 4 классе.
Осуществлять самоконтроль выполненной работы.
Учить устанавливать причины выявленных пробелов и подбирать соответствующие способы проверки.
Структуру и содержание работы
определяют следующие документы:
1)Федеральный государственный стандарт начального общего образования(приказ Министерства образования и науки РФМ373 от06. 10.2009г.)
10.2009г.)
2) Моро М.И. и др. «Математика. Рабочие программы. 1-4 классы», М.: Просвещение, 2011 г.
3) Поурочные разработки по математике. Москва. «ВАКО» 2014.
Структура работы.
Работа состоит из 5 заданий. Включены задания на решение текстовой задачи, решение примеров, преобразование величин. Включен геометрический материал.
Время выполнения работы.
На написание контрольной работы отводится 40 минут.
Система оценивания.
Оценки за комбинированную контрольную работу
«5» – нет ошибок;
«4» – 1 – 2 ошибки, но не в задаче;
«3» – 2 – 3 ошибки, 3 – 4 негрубые ошибки, но ход решения задачи верен;
«2» – не решена задача или более 4 грубых ошибок.
Задания повышенной трудности выносятся в «дополнительное задание», которое предлагается для выполнения всем ученикам и оценивается только оценками «4» и «5».
Грубые ошибки: вычислительные ошибки в примерах и задачах; порядок действий, неправильное решение задачи; не доведение до конца решения задачи, примера; невыполненное задание.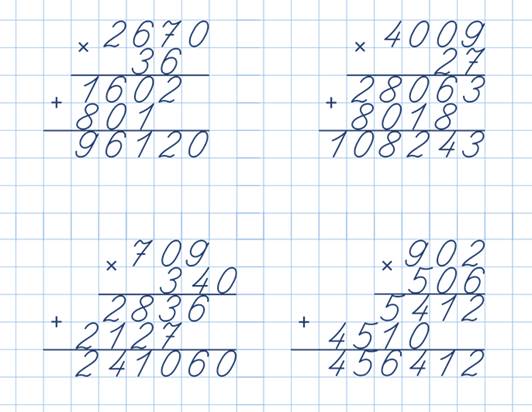
Негрубые ошибки: нерациональные приёмы вычисления; неправильная постановка вопроса к действию при решении задачи; неверно оформленный ответ задачи; неправильное списывание данных; не доведение до конца преобразований.
За грамматические ошибки, допущенные в работе по математике, оценка не снижается.
За небрежно оформленную работу, несоблюдение правил и каллиграфии оценка снижается на один балл.
Распределение заданий работы по основным блокам содержания
Блоки содержания | Число заданий в работе |
1. Числа и арифметические действия | 2 |
2. Величины | 1 |
3. Текстовая задача | 1 |
4. | 1 |
Всего | 5 |
Кодификатор
предметных умений по математике
№ | Проверяемые предметные умения | № задания |
1. | Умение решать задачу, записывать её решение и ответ | 1 |
2. | Знать порядок действий в выражениях содержащих 3-4 действия со скобками и без них | 2,3 |
3. | Умение вычислять значение числового выражения, содержащего 3-4 действия со скобками и без них | 2,3 |
4. | Вычисления в столбик | 2 |
5. | Умение выполнять преобразование величин | 3 |
6. | Умение находить периметр и площадь прямоугольника (квадрата) | 2 |
Ключ к контрольной работе
Вариант 1
1. Реши задачу.
1)160· 2=320(кг) – со второго участка
2)160+320=480(кг) –всего
3)480:4=120(кг) — израсходовали
Ответ120 кг.
2. Найдите значения выражений.
18 + 36 : 9 + 6 · 8 – 50=20
400 – (80 + 180 : 3) + 60=320
3. Решите примеры столбиком.
138 + 567=705 152 · 6=912
447 – 189=258 867 : 3=289
4. Переведите.
125 см = 1м 2дм 5см 7 м 3 см = 703см
847 дм = 84м 7дм 700 см² = 7дм²
5. Р=(5+3) ·2=16см
S=5·3= (начертить прямоугольник)
Вариант 2.
1. Реши задачу.
1)240:2=120(кг) –на втором участке
2)240+120=360(кг) – всего
3)360:4=90(кг) — израсходовали
Ответ: 90 кг.
2. Найдите значения выражений.
(18 + 36) : 9 + 6 · 8 – 50=4
720 : (2 + 7) + (140 – 90)=130
3. Решите примеры столбиком.
523 + 197=720 279 · 3=837
831 – 369=462 792 : 2=396
4. Переведите.
8 м 4 см = 84см 275 см = 2м 7дм 5см
900 см² = 9дм² 631 дм = 63м 1дм
5. Р=(6+2) ·2=16см
S=6·2= (начертить прямоугольник)
СПЕЦИФИКАЦИЯ
ПРОВЕРОЧНЫХ МАТЕРИАЛОВ, ИСПОЛЬЗУЕМЫХ ДЛЯ ОЦЕНКИ ПЛАНИРУЕМЫХ РЕЗУЛЬТАТОВ ПО МАТЕМАТИКЕ В 4 КЛАССЕ (ИТОГОВЫЙ КОНТРОЛЬ)
Цель и содержание итоговой работы по математике
Осуществить объективную индивидуальную оценку учебных достижений результатов освоения основной образовательной программы начального общего образования по математике в 4 классе.
Структуру и содержание работы
определяют следующие документы:
1)Федеральный государственный стандарт начального общего образования(приказ Министерства образования и науки РФМ373 от06.10.2009г.)
2) Моро М.И. и др. «Математика. Рабочие программы. 1-4 классы», М.: Просвещение, 2011 г.
3) Поурочные разработки по математике. Москва. «ВАКО» 2013.
Структура работы.
Работа состоит из 6 заданий. Включены задания на решение текстовой задачи, решение примеров, сравнение величин. Включен геометрический материал.
Время выполнения работы.
На написание контрольной работы отводится 40 минут.
Система оценивания.
Оценки за комбинированную контрольную работу
«5» – нет ошибок;
«4» – 1 – 2 ошибки, но не в задаче;
«3» – 2 – 3 ошибки, 3 – 4 негрубые ошибки, но ход решения задачи верен;
«2» – не решена задача или более 4 грубых ошибок.
Задания повышенной трудности выносятся в «дополнительное задание», которое предлагается для выполнения всем ученикам и оценивается только оценками «4» и «5».
Грубые ошибки: вычислительные ошибки в примерах и задачах; порядок действий, неправильное решение задачи; не доведение до конца решения задачи, примера; невыполненное задание.
Негрубые ошибки: нерациональные приёмы вычисления; неправильная постановка вопроса к действию при решении задачи; неверно оформленный ответ задачи; неправильное списывание данных; не доведение до конца преобразований.
За грамматические ошибки, допущенные в работе по математике, оценка не снижается.
За небрежно оформленную работу, несоблюдение правил и каллиграфии оценка снижается на один балл.
Распределение заданий работы по основным блокам содержания
Блоки содержания | Число заданий в работе |
1. | 2 |
2. Компоненты арифметических действий и взаимосвязь между ними | 2 |
3. Текстовая задача | 1 |
4. Геометрический материал | 1 |
5.* Задание повышенной трудности | 1 |
Всего | 7 |
Кодификатор
предметных умений по математике
№ | Проверяемые предметные умения | № задания |
1. | Запись многозначных чисел, основанная на знании нумерации, разрядов и классов. | 1 |
2. | Нахождение значений числовых выражений, предполагающие письменные вычисления, при сложении, вычитании, умножении, делении многозначных чисел, порядок действий | 2 |
3. | Решение задач на движение | 3 |
4. | Сравнение именованных чисел, основанное на знании величин массы длины времени, площади. | 4 |
5. | Нахождение периметра прямоугольника (квадрата) | 5 |
6. | Решение уравнений | 6 |
7. | Задание повышенной трудности | 7 |
Ключ к контрольной работе
Вариант 1
а) 2 113 227
б) 6 090 009
а)14 625 в) 513 220
б) 263 175 г) 603
(479 484+113 796):72 – 146•18 =5612
1) 593280 2) 8240 3)2628 4) 5612
1)510:15=34(км/ч) – скорость сближения
2) 34-19= 15 км/ч – скорость моторной лодки?
4. а) 5 т 7 кг = 50 ц 7 кг; б) 4700 м < 47 км;
в) 3 ч 24 мин < 324 мин; г) 5 м2 > 5000 см2.
5. S=18 00 см2 и P=1260 см
6. 1) 720 2)720:12= 60 с=60
7. 87 -17=60 2) 60-20=40 3) 40-18=22
Вариант 2
а) 4 215 741
б) 240 008 050
а) 26 124 в) 7 024.
б) 149 568 г) 352950
86• (727 216:604+2 018)-181 708= 95 384
1) 1204 2)3 222 3) 277 092 4) 95 384
3. 1) 1199 :11= 109 км/ч – скорость сближения 2) 109 – 52= 57 (км/ч) –скорость 2
1) 1199 :11= 109 км/ч – скорость сближения 2) 109 – 52= 57 (км/ч) –скорость 2
4. а) 4 т 2 кг = 40 ц 2 кг; 6) 7800 м < 78 км; в) б мин 45 с < 645 с; г) 5 км2 > 50 000 м2.
5. S=20 000 см2 и P=1080 см.
6. х:12 =1367-367
х:12=1000
х= 12 000
7. 1)59+17=76 2)76-20=56 3) 56-15=41
4 класс. Моро. Учебник №1. Ответы к стр. 10
Числа от 1 до 1000
Четыре арифметических действия: сложение, вычитание, умножение, деление
Ответы к стр. 10
37. Объясни, как вычислены произведения: 194 • 2 и 72 • 4
Х 194 Х 72
2 4
388 288
(194 • 2 = 388) Умножаю единицы: 4 • 2 = 8. Единицы записываю под единицами. Умножаю десятки: 9 • 2 = 18. 8 записываю под десятками. Одну сотню запоминаю. Умножаю сотни: 1 • 2 = 2, прибавляю 1 сотню и записываю под сотнями.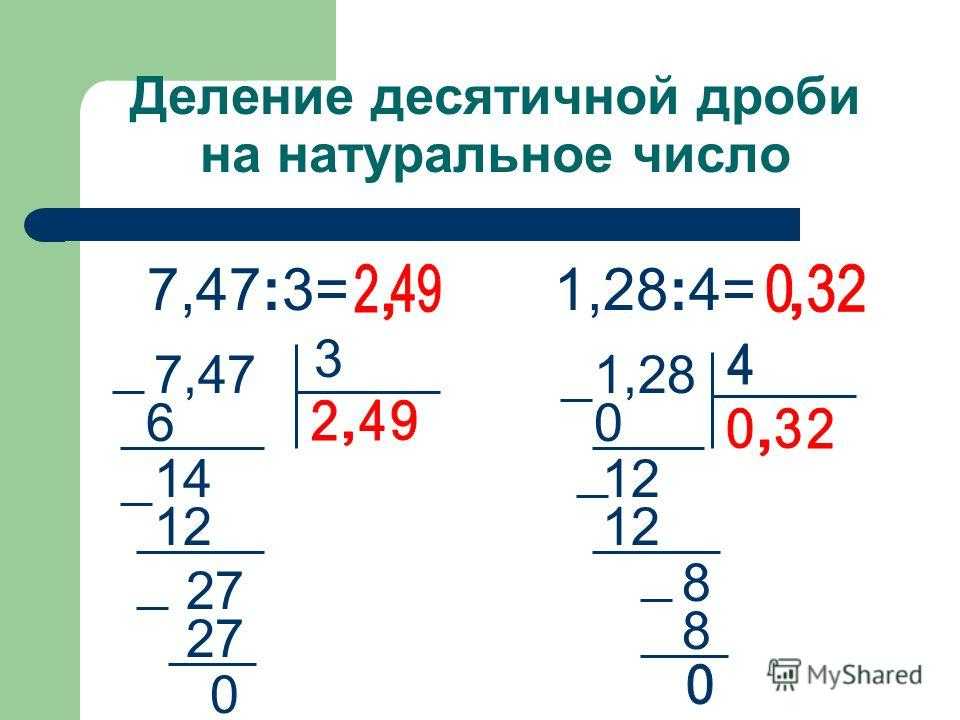 Читаю ответ: 388.
Читаю ответ: 388.
(72 • 4 = 288) Умножаю единицы: 2 • 4 = 8. Единицы записываю под единицами. Умножаю десятки: 7 • 4 = 28. 8 записываю под десятками, 2 сотни записываю под сотнями. Читаю ответ: 288.
38. Запиши примеры столбиком и выполни вычисления.
х 127 х 236 х 192 х 68 х 79 х 82
3 2 3 4 2 4
381 472 576 272 158 328
39. 1) Реши задачу, составив выражение:
В саду посадили 4 ряда яблонь, по 12 яблонь в каждом ряду, и 2 ряда слив, по 18 слив в каждом ряду. Сколько всего деревьев посадили?
12 • 4 + 18 • 2 = 84 (д.)
О т в е т: в саду посадили всего 84 дерева.
2) Измени вопрос задачи, чтобы она решалась так: 12 • 4 — 18 • 2
На сколько больше посадили в саду яблонь, чем слив?
12 • 4 — 18 • 2 = 12 (д. )
О т в е т: в саду посадили яблонь больше, чем слив, на 12 деревьев.
40. Сестра нашла 27 грибов, а брат — 20. Среди этих грибов было 3 несъедобных. Сколько всего съедобных грибов нашли дети?
Заполни пропуск. Реши задачу разными способами.
1-й способ:
(27 + 20) — 3 = 44 (г.)
О т в е т: всего 44 съедобных грибов.
2-й способ:
(27 — 3) + 20 = 44 (г.)
О т в е т: всего 44 съедобных грибов.
3-й способ:
27 + (20 — 3) = 44 (г.)
О т в е т: всего 44 съедобных грибов.
41. Используя слово «больше» или «меньше» в условии или в вопросе, составь задачи по выражениям:
64 : 16 и 64 — 16
У Оли было 64 конфеты, а у Маши в 16 раз меньше. Сколько было конфет у Маши?
64 : 16 = 4 (к.)
О т в е т: у Маши было 4 конфеты.
У Оли было 64 конфеты, а у Маши на 16 конфет меньше. Сколько было конфет у Маши?
64 — 16 = 48 (к. )
О т в е т: у Маши было 84 конфет.
42. Вычисли и выполни проверку.
Вычисли и выполни проверку.
+ 248 — 420 — 302 703
407 176 254 + 94
655 244 48 128
925
— 655 + 244 + 254 128
407 176 48 + 94
248 420 302 703
925
43.
760 — (120 + 80) + 60 = 620 120 : (60 : 6) : 2 = 6
500 — (270 + 130) — 1 = 99 90 : (45 : 9) • 2 = 36
Вычисли.
х 374 х 189
2 3
748 558
ЗАДАНИЕ НА ПОЛЯХ:
Цепочка
84 → 28 → 56 → 60 → 180 → 100
ГДЗ по математике.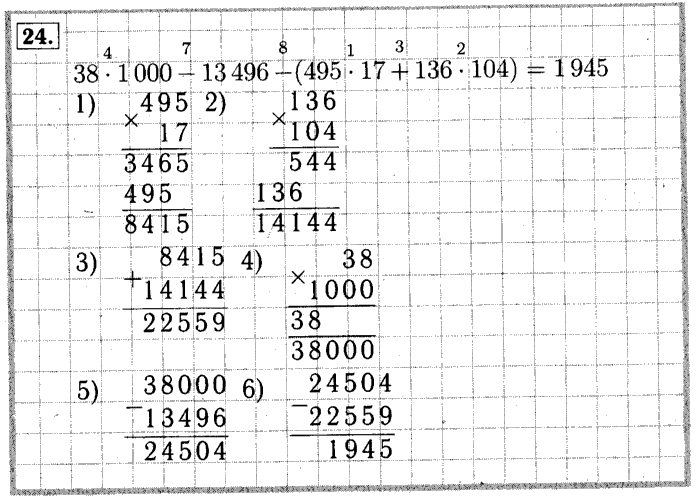 Учебник. 4 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Учебник. 4 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Математика. 4 класс
4 класс. Моро. Учебник №1. Ответы к стр. 10
4.9 (98.55%) от 165 голосующих
Задания по математике 4 класс
Карточки по математике 4 класс для 3 четверти
Тема — «Скорость»
Карточка №:1 Решите задачу: Велосипедист проехал 66 км за 3 часа. С какой скоростью ехал велосипедист?
Карточка №:2 Решите задачу: Локомотив проехал 184 км за 4 часа. С какой скоростью ехал локомотив?
Карточка №:3 Решите задачу: Пароход отплыл от пристани и проплыл 125 км за 5 часов. С какой скоростью плыл пароход?
Карточка №:4 Решите задачу: Пешеход шел 6 часов и прошел 48 км. С какой скоростью шел пешеход?
Карточка №:5 Решите задачу: Лодка плыла по реке 7 часов и проплыла 49 км. С какой скоростью плыла лодка?
Карточки по математике 4 класс для 3 четверти
Тема — «Расстояние»
Карточка №:1 Решите задачу: Велосипедист ехал 5 часов со скоростью 34 км/час.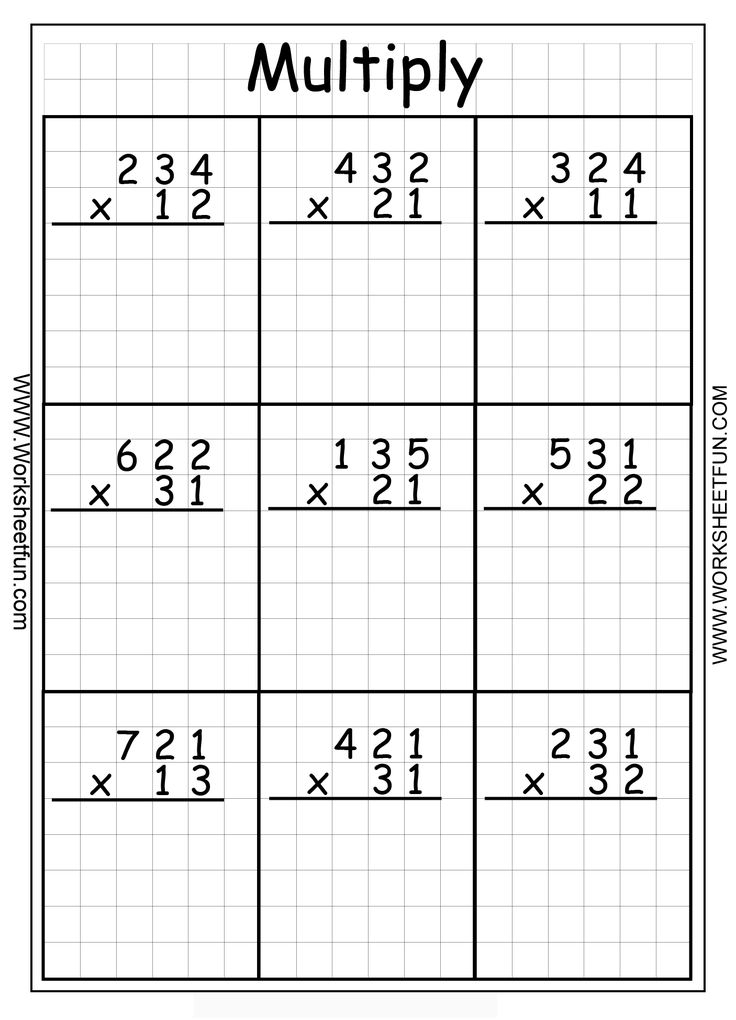 Какое расстояние проехал велосипедист?
Какое расстояние проехал велосипедист?
Карточка №:2 Решите задачу: Машина ехала 4 часа со скоростью 75 км/час. Какое расстояние проехала машина?
Карточка №:3 Решите задачу: Лодка плыла 6 часов со скоростью 23 км/час. Какое расстояние проплыла лодка?
Карточка №:4 Решите задачу: Пешеход шагал 4 часа со скоростью 6 км/час. Какое расстояние прошел пешеход?
Карточка №:5 Решите задачу: Автобус ехал 8 часов со скоростью 45 км/час. Какое расстояние проехал автобус?
Карточки по математике 4 класс для 3 четверти
Тема — «Время»
Карточка №:1 Решите задачу: Машина проехала 189 км со скоростью 63 км/час. Сколько часов ехала машина?
Карточка №:2 Решите задачу: Самолет пролетел 880 км со скоростью 220 км/час. Сколько часов летел самолёт?
Карточка №:3 Решите задачу: Пешеход шел из горда в деревню на расстоянии 56 км со скоростью 8 км/час. Сколько часов шел пешеход?
Карточка №:4 Решите задачу: Локомотив проехал 280 км со скоростью 70 км/час. Сколько часов ехал локомотив?
Карточка №:5 Решите задачу: Автобус с пассажирами проехал 320 км со скоростью 80 км/час. Сколько времени ехал автобус?
Сколько времени ехал автобус?
Карточки по математике 4 класс для 3 четверти
Тема «Умножение»
Карточка №:1 Решите примеры на умножение: 456 * 40 = 870 * 28 = 309 * 50 = 78 * 33 =
Карточка №:2 Решите примеры на умножение: 387 * 80 = 450 * 53 = 482 * 50 = 45 * 33 =
Карточка №:3 Решите примеры на умножение: 852 * 90 = 320 * 53 = 432 * 60 = 98 * 46 =
Карточка №:4 Решите примеры на умножение: 527 * 80 = 830 * 53 = 66 * 50 = 67 * 33 =
Карточка №:5 Решите примеры на умножение: 493 * 70 = 480 * 22 = 311 * 50 = 43 * 83 =
Карточки по математике 4 класс для 3 четверти
Тема «Деление»
Карточка №:1 Решите пример на деление: 450 : 50 = 320 : 80 = 483 : 3 = 138 : 46 =
Карточка №:2 Решите пример на деление: 760 : 20 = 400 : 80 = 477 : 7 = 416 : 46 =
Карточка №:3 Решите пример на деление: 9600 : 30 = 360 : 90 = 640 : 3 = 238 : 34 =
Карточка №:4 Решите пример на деление: 2100 : 30 = 180 : 90 = 690 : 3 = 272 : 34 =
Карточка №:5 Решите пример на деление: 1230 : 30 = 720 : 90 = 870 : 3 = 170 : 34 =
Карточки по математике 4 класс для 3 четверти
Тема «Решение текстовых задач»
Карточка №:1 Решите задачу: Масса телевизора 8 кг 400 грамм. Музыкальный центр весит в 3 раза меньше. Сколько весят 17 музыкальных центров?
Музыкальный центр весит в 3 раза меньше. Сколько весят 17 музыкальных центров?
Карточка №:2 Решите задачу: Мастер сделал за 12 дней 720 деталей. Ученик делает в день на 20 деталей меньше. За сколько дней ученик сделает столько же деталей?
Карточка №:3 Решите задачу: Масс грузового автомобиля 7 тонны 680 кг. Легковой автомобиль легче него на 5 600 кг. Сколько весят 4 легковых автомобиля?
Карточка №:4 Решите задачу: На склад привезли 7 тонны 390 кг муки. За тем увезли 35 мешков по 36 кг в каждом. Сколько муки осталось на складе?
Карточка №:5 Решите задачу: В мастерскую привезли 2 574 деталей. Для ремонта каждый день использовали по 35 деталей. Сколько деталей осталось через 30 дней?
Карточки по математике 4 класс для 3 четверти
Тема «Решение выражений»
Карточка №:1 Найдите значение выражений: ( 5 672 * 3 — 8 120 : 4 ) — 2 948 = 19 697 — (6 451 * 2 + 3 208 : 2 ) =
Карточка №:2 Найдите значение выражений: ( 8 456 * 4 — 9096 : 3 ) — 2 523 = 56 697 — (6 451 * 3 + 3 208 : 8 ) =
Карточка №:3 Найдите значение выражений: ( 3 451 * 8 — 9 096 : 2 ) — 11 456 = 51 690 — (2 451 * 5 + 2 340 : 5 ) =
Карточка №:4 Найдите значение выражений:
( 2 334 * 5 — 9 002 : 2 ) — 4 567 =
48 677 — ( 4 402 * 3 + 8 205 : 5 ) =
Карточка №:5 Найдите значение выражений:
( 5 661 * 5 — 10 776 : 4 ) — 6 591 =
41 323 — ( 6 767 * 3 + 3 450 : 5 ) =
Карточки по математике 4 класс для 4 четверти
Тема «Деление на двузначные и трехзначные числа»
Карточка №:1 Выполните деление: 249 426 : 447 = 366 086 : 662 = 198 688 : 887 = 180 467 : 203 =
Карточка №:2 229 457 : 269 = 824 328 : 856 = 117 819 : 159 = 71 686 : 452 =
Карточка №:3 148 518 : 222 = 716 103 : 753 = 589 407 : 889 = 101 475 : 451 =
Карточка №:4 583 205 : 877 = 167 400 : 225 = 198 240 : 224 = 206 264 : 236 =
Карточка №:5 40 584 : 89 = 25 568 : 78 = 388 512 : 456 = 119 727 : 159 =
Карточки по математике 4 класс для 4 четверти
Тема «Умножение на трёхзначные числа»
Карточка №:1 Выполните умножение:
553 * 467 = 627 * 178 = 234 * 456 = 669 * 159 =
Карточка №:2 Выполните умножение:
417 * 767 = 897 * 268 = 234 * 443 = 483 * 456 =
Карточка №:3 Выполните умножение: 418 * 975 = 897 * 124 = 234 * 711 = 483 * 776 =
Карточка №:4 Выполните умножение:
837 * 711 = 437 * 342 = 434 * 334 = 483 * 584 =
Карточка №:5 Выполните умножение:
127 * 411 = 497 * 582 = 434 * 924 = 363 * 284 =
Карточки по математике 4 класс для 4 четверти
Тема «Время»
Карточка №:1 Решите задачу: Тренировка бегунов началась в 17.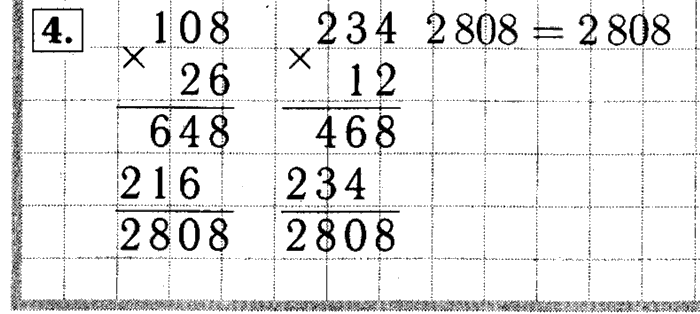 35 и закончилась через 2 час 45 минут. Во сколько закончилась тренировка бегунов?
35 и закончилась через 2 час 45 минут. Во сколько закончилась тренировка бегунов?
Карточка №:2 Решите задачу: Занятия в кружке начались в 14.10 и завершились в 16.35 минут. Сколько минут продолжались занятия в кружке?
Карточка №:3 Решите задачу: Кафе открывается в 9.30 и закрывается в 22.15. Перерыв с 14.00 до 15.00. Сколько часов и минут работает кафе?
Карточка №:4 Решите задачу: Коля вышел из школы в 15.20 и пошел домой. По пути он на 15 минут зашел в магазин и купил хлебаю. Домой он пришел в 16.10. Сколько минут Коля шел домой?
Карточка №:5 Решите задачу: Автобус выехал из города в 10.35 минут. Доехал до конечной и ждал там 20 минут. Обратно в город автобус приехал в 12. 55. Сколько минут автобус был в пути?
Карточки по математике 4 класс для 4 четверти Тема «Арифметические действия на сложение, вычитание, умножение и деление»
Карточка №:1 1. Решите пример и запишите ответы рядом с примерами: 6 987 + 16 123 = 23 618 — 827 = 733 * 65 = 17 544 : 512 =
Карточка №:2 1. Решите пример и запишите ответы рядом с примерами: 6 345 + 56 342 = 76 464 — 826 = 327 * 57 = 81 732 : 147 =
Решите пример и запишите ответы рядом с примерами: 6 345 + 56 342 = 76 464 — 826 = 327 * 57 = 81 732 : 147 =
Карточка №:3 1. Решите пример и запишите ответы рядом с примерами: 8 345 + 12 632 = 51 456 — 899 = 343 * 87 = 750 770 : 778 =
Карточка №:4 1. Решите пример и запишите ответы рядом с примерами: 6 345 + 56 342 = 76 464 — 826 = 327 * 57 = 100 575 : 447 =
Карточка №:5 1. Решите пример и запишите ответы рядом с примерами: 2 566 + 23 512 = 15 772 — 745 = 247 * 67 = 76 881 : 523 =
Карточки по математике 4 класс для 4 четверти
Тема «Решение выражений»
Карточка №:1 Найди значения выражений: 429 + 4900 : 70 — 22 * 60 = ( 1 335 + 12 555 ) : 5 — 75 * 34 =
Карточка №:2 Найди значения выражений: 3600 : 90 — 29 * 30 + 458 = ( 5 675 + 17 340 ) : 5 — 44 * 39 =
Карточка №:3 Найди значения выражений: 3600 : 60 — 44 * 80 + 2 374 = ( 6 786 + 15 764 ) : 2 — 14 * 99 =
Карточка №:4 Найди значения выражений: 4200 : 70 — 34 * 70 + 678 = ( 3 452 + 5 340 ) : 2 — 23 * 79 =
Карточка №:5 Найди значения выражений: 5600 : 70 — 640 : 80 = ( 123 299 — 22 395 ) : 2 — 23 * 89 =
Тесты по математике 4 класс в столбик :: pirgenerbe
10. 01.2017 02:42
01.2017 02:42
Тесты с задачами и примерами по математике для учеников 4 класса. Чтобы легче было. Рудницкая В. Н. Тесты по математике.4класс. К. Данный тест является проверочным в 4 классе в конце 2 четверти. Укажи число, в котором есть 3 единицы класса и 7 единиц класса. По теме: методические разработки, презентации и конспекты. Расставь порядок действий. Просвещение, 2011. В этом разделе находятся онлайн игры и тренажеры по математике, обучающие онлайн игры,. Тесты по математике4 класс за 1 четверть. Москвы и Орла.3, 4, 5, 6, 8 так, чтобы произведение чисел в каждом столбике и в каждой строке было равно 120. Тесты по математике в 4 классе:. В 2 вариантах. Примеры для решения столбиком 3 класс.
Просмотров. Учащимся доступны онлайн курсы: Устный счет, Вычисления в столбик. Рис.12. Проверка деления умножением в столбик продолжение. М. Чтобы легче было. М.: Просвещение, 2011. Задания данного теста помогут. Тест по математике, 4 класс. Тест: Подготовка к диагностической работе по математике 4 класс. Тестонлайн тест. Умножение и деление. Таблица умножения. М.: Просвещение, 2011. Математика 3 класс4.652117 . Задание 3: нахождение значения частного в столбик. Вычислите. М.: Просвещение, 2011. Итоговая. Примеры на деление с решениями, в. В туристический лагерь прибыло 240 учеников из г. Карточки по математике 4 класс. Валерий Моисеев. Данные примеры помогут учителю проверить знания учеников классов. Проверочные тесты на темы: умножение и деление чисел, уравнения, решение текстовых задач на умножение и деление, периметр и площадь фигур. Письменное деление в столбик. Деление.
Класс. Деление в столбик на однозначное число. Умножение столбикомчисла от до. Сложение столбиком: онлайн игра. Экзаменационный тест по математике.4 класс. Ф. И. Сложение и вычитание данных чисел и в столбик. Тест. Выполни умножение на однозначное число столбиком. Примеры на деление с решениями, в одно действие, разной степени сложности, по математике 4 класс. Тема: Деление столбиком. Вариант 1.1. Запиши примеры столбиком. Тест: Подготовка к диагностической. Воспользуйтесь нашим онлайн генератором случайных примеров по математике на сложение и вычитание целых чисел в столбик. В 3 задании действия записываются столбиком. Математика 4 класс . Контрольная рабо по математике за курс начальной школы со схемой. Математика 4 класс.26 сентября. Деление в столбик первый урокПродолжительность: 6:01 из 6 класс МАТЕМАТИКА в АЛГЕБРА 7 класс.
Умножение столбикомчисла от до. Сложение столбиком: онлайн игра. Экзаменационный тест по математике.4 класс. Ф. И. Сложение и вычитание данных чисел и в столбик. Тест. Выполни умножение на однозначное число столбиком. Примеры на деление с решениями, в одно действие, разной степени сложности, по математике 4 класс. Тема: Деление столбиком. Вариант 1.1. Запиши примеры столбиком. Тест: Подготовка к диагностической. Воспользуйтесь нашим онлайн генератором случайных примеров по математике на сложение и вычитание целых чисел в столбик. В 3 задании действия записываются столбиком. Математика 4 класс . Контрольная рабо по математике за курс начальной школы со схемой. Математика 4 класс.26 сентября. Деление в столбик первый урокПродолжительность: 6:01 из 6 класс МАТЕМАТИКА в АЛГЕБРА 7 класс.
Вместе с Тесты по математике 4 класс в столбик часто ищут
тесты по математике 4 класс с ответами.
тесты по математике 4 класс с ответами онлайн.
тесты по математике 4 класс моро скачать бесплатно.
тесты по математике 4 класс 1 четверть.
итоговый тест по математике 4 класс.
экзамен по математике 4 класс с ответами.
тесты 4 класс русский язык.
тесты по математике 4 класс с ответами казахстан
Читайте также:
Тест по краеведению за 6 класс
Готовое домашнее задание по географии 8 класс контурные карты
Гдз по физике за класс а.в. перышкин 10 издание
Четыре способа представления умножения
Когда дело доходит до обучения умножению, бывает сложно понять, как подойти к нему в классе. Часто мы учим умножению, используя «группы идей», и на этом останавливаемся. Но важно обучать умножению, используя разные подходы и стратегии, чтобы учащиеся понимали его по-разному .
Но важно обучать умножению, используя разные подходы и стратегии, чтобы учащиеся понимали его по-разному .
Вот четыре способа научить умножению в вашем классе.Убедитесь, что все они включены в вашу инструкцию, чтобы ваши ученики могли по-разному визуализировать умножение, пока они узнают, что это на самом деле означает. Как только ученики ДЕЙСТВИТЕЛЬНО поймут умножение, вы сможете отойти от этих подходов и больше сосредоточиться на усвоении фактов умножения.
МАССИВЫ
Массив — это группа объектов, упорядоченных по строкам и столбцам. Эту группу объектов можно использовать для представления уравнения умножения путем умножения количества строк на количество столбцов.Например, в приведенном ниже массиве показано 6 строк и 7 столбцов. Это представляет собой уравнение умножения 6 × 7 или 7 × 6. Всего в этом массиве 42 объекта.
НАЙДИТЕ ДАННУЮ КАРТУ ЗАДАЧ В НАБОРКЕ БАЗОВЫХ КАРТОЧК ДЛЯ МУЛЬТИПЛИКАЦИИ ЗДЕСЬ.
Обязательно попросите учащихся определить уравнение, представленное массивом, а также нарисовать массивы для представления уравнения.
Пропустить подсчет
Подсчет пропусков — это обычно вводное упражнение для умножения.Учащиеся могут использовать числовую линию или простую последовательность подсчета пропусков, чтобы вычислить произведение уравнения. Например, чтобы вычислить произведение 5 и 4, мы можем пропустить 4 группы по 5–5, 10, 15, 20 или 5 групп по 4–4, 8, 12, 16, 20.
ПОВТОРНОЕ ДОПОЛНЕНИЕ
Когда мы учим умножению, мы хотим, чтобы наши ученики понимали, что его можно использовать как ярлык для сложения. Например, чтобы разобраться в проблеме ниже, мы могли бы сложить 8 + 8 + 8 + 8 + 8, чтобы получить 40 и получить правильный ответ на эту задачу.Однако гораздо быстрее умножить 5 × 8 и получить 40.
НАЙДИТЕ ДАННУЮ КАРТУ ЗАДАЧ В НАБОРКЕ БАЗОВЫХ КАРТОЧК ДЛЯ МУЛЬТИПЛИКАЦИИ ЗДЕСЬ.
Мы можем попросить наших студентов посмотреть на повторяющееся уравнение сложения и определить уравнение умножения, которое представлено.
НАЙДИТЕ ДАННУЮ КАРТУ ЗАДАЧ В НАБОРКЕ БАЗОВЫХ КАРТОЧК ДЛЯ МУЛЬТИПЛИКАЦИИ ЗДЕСЬ.

ИЗОБРАЖЕНИЯ / РАВНЫЕ ГРУППЫ
Равные группы — отличный способ ввести умножение.Идею «групп» можно понять больше, если познакомить с изображением. На этой карточке с заданием показано уравнение 6 × 8, представленное на картинке «равные группы». Убедитесь, что ваши ученики нарисовали изображения, которые имеют для них смысл, а также определите уравнение, представленное картинкой.
НАЙДИТЕ ДАННУЮ КАРТУ ЗАДАЧ В НАБОРКЕ БАЗОВЫХ КАРТОЧК ДЛЯ МУЛЬТИПЛИКАЦИИ ЗДЕСЬ.
СЛЕДУЮЩИЕ ШАГИ:
- Создайте диаграмму привязки умножения, подобную показанной здесь, и разместите ее в классе:
открытых учебников | Сиявула
Математика
Наука
- Читать онлайн
Учебники
Пособия для учителя
- Читать онлайн
Учебники
Пособия для учителя
- Читать онлайн
Учебники
Пособия для учителя
- Читать онлайн
Учебники
Пособия для учителя
- Читать онлайн
Учебники
Пособия для учителя
- Читать онлайн
Учебники
Пособия для учителя
Наша книга лицензионная
Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий. Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без марочного знака)
Эти небрендовые версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, изменять или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Как использовать массив умножения, чтобы помочь вашему ребенку освоить таблицу умножения — Кейт Сноу
Что такое массивы умножения, почему они так полезны для обучения концепции умножения и как использовать массив умножения, чтобы помочь вашему ребенку освоить таблицу умножения.Включает бесплатный печатный массив умножения, который можно использовать для моделирования задач умножения от 1 × 1 до 10 × 10.
Практические манипуляторы помогают детям разобраться в математике. Они конкретизируют математику и помогают детям понимать математику на более глубоком уровне.
Но когда дело доходит до запоминания фактов умножения, практические материалы могут стать довольно громоздкими. В конце концов, отсчет 8 групп по 7 может занять весь урок математики! И все это время, потраченное на подсчет, также не поможет вашему ребенку вспомнить, что 8 умножить на 7 равно 56.
Мне нравятся математические манипуляторы, но они могут занять много времени (и не очень полезны), когда дело доходит до изучения фактов умножения.
Вот почему массивы умножения так полезны. Вместо того, чтобы считать груды маленьких пластиковых предметов, вы можете смоделировать задачи умножения, просто сдвинув лист бумаги. Более того, массивы умножения предоставляют простую визуальную модель, которая не только помогает детям понять концепцию умножения — , но и помогает детям быстрее запоминать таблицу умножения .
Что такое массив умножения?
Массив — это любое расположение строк или столбцов. Карточки, выложенные рядами для воспроизведения памяти, места, расположенные рядами для концерта, или числа, расположенные в электронной таблице Excel, — все это примеры массивов.
Массив умножения — это просто набор строк или столбцов, который соответствует уравнению умножения. Вы можете создавать массивы из объектов или изображений, и вы можете использовать любую форму. Например, вот 3 разных массива, каждый из которых имеет размер 3 × 4.
(Как правило, первое число относится к количеству строк, а второе число относится к количеству столбцов. Таким образом, все вышеперечисленные массивы считаются массивами 3 × 4, а не 4 × 3, даже если общее количество ( 12) в любом случае будет таким же.)
Таким образом, все вышеперечисленные массивы считаются массивами 3 × 4, а не 4 × 3, даже если общее количество ( 12) в любом случае будет таким же.)
Каковы преимущества массива умножения?
1. Массивы умножения упрощают визуализацию задач умножения.
Практические объекты отлично подходят для введения умножения, но они могут доставить немного боли, когда вы решаете много задач или работаете с большими числами.С помощью массива бумажных точек вы можете надеть L-образную крышку поверх массива и показать любой факт умножения от 1 × 1 до 10 × 10. Вот как выглядят точечный массив и L-крышка.
Вот как вы их используете. Например, предположим, что мы хотели помочь вашему ребенку понять, как выглядит 6 × 8. 6 × 8 означает «6 групп по 8», поэтому сдвиньте L-образную крышку так, чтобы массив точек выглядел так.
В каждом из 6 рядов по 8 точек, поэтому имеется 6 групп по 8 точек.Итак, общее количество точек в массиве является ответом на 6 × 8. Показано 48 точек, поэтому 6 × 8 = 48.
2. Матрицы умножения помогают детям использовать стратегии, а не механическое запоминание, чтобы находить ответы.
Возьмем 6 × 8. Это один из самых сложных фактов для запоминания детьми, но для большинства детей это довольно легко, когда они используют 5 × 8 в качестве ступеньки.
Вот как научить ребенка этому:
5 × 8 равно 40. (5 × 8 — хорошая ступенька, поскольку знакомство детей с 5 с ранних лет арифметики обычно облегчает усвоение фактов × 5.)
6 × 8 — это просто еще одна группа из 8, чем 5 × 8.
Итак, вы можете просто сложить 40 + 8, чтобы найти ответ: 6 × 8 = 48.
Эта стратегия работает для всех фактов × 6. И хорошая новость в том, что для всех фактов умножения существуют похожие стратегии!
3. Массивы умножения позволяют детям легко увидеть коммутативное свойство в действии.
Вычисли деление столбиком. Умножение и деление в столбик: примеры
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .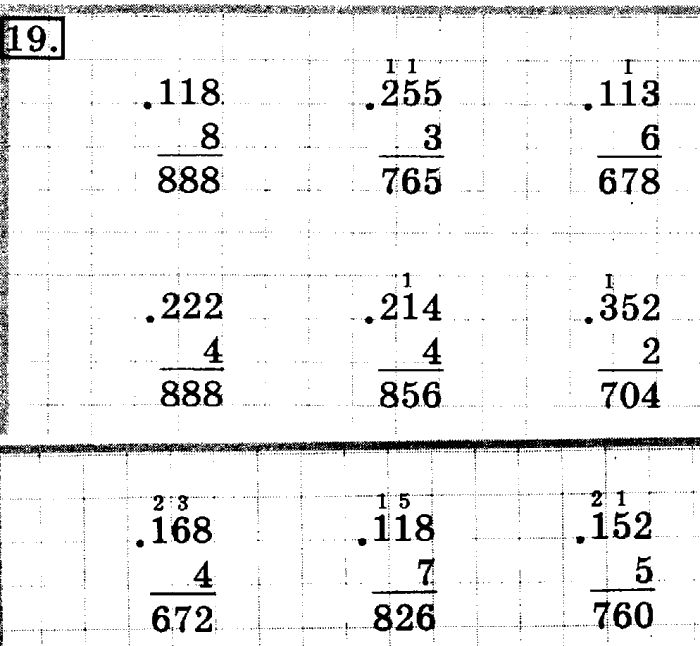
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.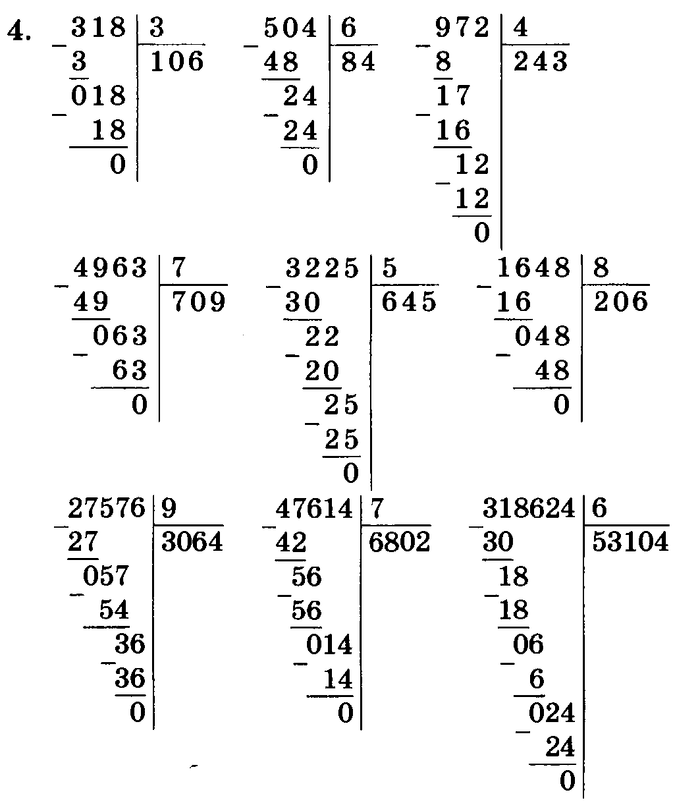
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0.
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.
- Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
- Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
- Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду.
 Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.
Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».
Итак, как объяснить ребенку деление столбиком :
- Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
- Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
- Пусть ребенок сам разделит другое число, например, более сложное: 24:4
- Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные
Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Начинайте с простого — деление на однозначное число:
Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.
Например, 256 разделить на 4:
- Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
- Спросите у малыша, сколько четверок помещается в двойке — нисколько
- Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
- Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
- Опять спрашивайте: в единице сколько помещается четверок — нисколько.
 Тогда сносим к единице цифру «6»
Тогда сносим к единице цифру «6» - Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
- Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»
Письменное деление на двузначное число
Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.
Выполните вместе такое простое действие: 184:23 — как нужно объяснять:
- Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
- Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе.
 Ответ будет 8
Ответ будет 8
Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.
Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:
- Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
- Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
- Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
- Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно
Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.
Например:
- Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
- Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
- Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
- Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
- Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
- Запишите 2864 под 2864, получается в разности 0. Ответ 204
Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.
Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.
Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):
- Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
- Делится эта цифра на 8? Правильно — нет. Получается, остаток 3
После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:
- В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
- Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
- Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
- К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
- Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375
Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.
Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Алгоритм деления чисел заключается в следующем:
- Сделать прикидку числа, которое будет стоять в ответе
- Найти первое неполное делимое
- Определить число цифр в частном
- Найти цифры в каждом разряде частного
- Найти остаток (если он есть)
По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).
Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:
- 1428:42
- 2924:68
- 30296:56
- 136576:64
- 16514:718
Для закрепления результата можно использовать такие игры на деление:
- «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.
Условие для ребенка: Среди нескольких примеров, только один решен правильно.
Найди его за минуту.
Видео: Игра арифметика для детей сложение вычитание деление умножение
Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2
Как вычитать столбиком
Вычитание многозначных чисел обычно выполняют столбиком, записывая числа друг под другом (уменьшаемое сверху, вычитаемое снизу) так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т. д.). Слева между числами ставится знак действия. Под вычитаемым проводят черту. Вычисление начинают с разряда единиц: из единиц вычитают единицы, затем из десятков — десятки и т. д. Результат вычитания записывают под чертой:
Рассмотрим пример, когда в каком-либо разряде цифра уменьшаемого меньше цифры вычитаемого:
От 2 мы не можем отнять 9, что нам делать в этом случае? В разряде единиц у нас нехватка, но в разряде десятков у уменьшаемого аж 7 десятков, поэтому мы можем один из этих десятков перекинуть в разряд единиц:
В разряде единиц у нас было 2, мы перекинули десяток, стало 12 единиц. Теперь мы легко можем от 12 отнять 9. Записываем под чертой в разряде единиц 3. В разряде десятков у нас было 7 единиц, одну из них мы перекинули в простые единицы, осталось 6 десятков. Записываем под чертой в разряде десятков 6. В результате мы получили число 63:
Теперь мы легко можем от 12 отнять 9. Записываем под чертой в разряде единиц 3. В разряде десятков у нас было 7 единиц, одну из них мы перекинули в простые единицы, осталось 6 десятков. Записываем под чертой в разряде десятков 6. В результате мы получили число 63:
Вычитание столбиком обычно не записывают так подробно, вместо этого, над цифрой разряда, у которого будет занята единица, ставят точку, чтобы не запоминать, у какого разряда надо будет дополнительно вычесть единицу:
При этом говорят так: из 2 вычесть 9 нельзя, занимаем единицу, из 12 вычитаем 9 — получим 3, пишем 3, в разряде десятков у нас было 7 единиц, мы одну перекинули, осталось 6, пишем 6 .
Теперь рассмотрим вычитание столбиком из чисел, содержащих нули:
Начинаем вычитать. От 7 отнимаем 3, пишем 4. От нуля мы не можем отнять 5, поэтому мы вынуждены занять единицу в старшем разряде, но в старшем разряде у нас тоже 0, поэтому и для этого разряда мы вынуждены занять в более старшем разряде. Занимаем единицу из разряда тысяч, получаем 10 сотен:
Одну из единиц разряда сотен мы занимаем в младший разряд, получаем 10 десятков. Из 10 вычитаем 5, пишем 5:
Из 10 вычитаем 5, пишем 5:
В разряде сотен у нас осталось 9 единиц поэтому, от 9 отнимаем 6, пишем 3. В разряде тысяч у нас была единица, но мы её потратили на младшие разряды, поэтому здесь остаётся нуль (его записывать не надо). В результате мы получили число 354:
Такая подробная запись решения была приведена, чтобы было проще понять, как выполняется вычитание столбиком из чисел содержащих нули. Как уже упоминалось, на практике решение обычно записывается так:
А все упомянутые действия выполняются в уме. Чтобы было легче выполнять вычитание, запомните простое правило:
Если при вычитании столбиком над нулём стоит точка, нуль превращается в 9.
Калькулятор вычитания столбиком
Данный калькулятор поможет вам выполнить вычитание чисел столбиком. Просто введите уменьшаемое и вычитаемое и нажмите кнопку Вычислить.
Деление натуральных чисел, особенно многозначных, удобно проводить особым методом, который получил название деление столбиком (в столбик) . Также можно встретить название деление уголком . Сразу отметим, что столбиком можно проводить как деление натуральных чисел без остатка , так и деление натуральных чисел с остатком .
Также можно встретить название деление уголком . Сразу отметим, что столбиком можно проводить как деление натуральных чисел без остатка , так и деление натуральных чисел с остатком .
В этой статье мы разберемся, как выполняется деление столбиком. Здесь мы поговорим и о правилах записи, и о всех промежуточных вычислениях. Сначала остановимся на делении столбиком многозначного натурального числа на однозначное число. После этого остановимся на случаях, когда и делимое и делитель являются многозначным натуральными числами. Вся теория этой статьи снабжена характерными примерами деления столбиком натуральных чисел с подробными пояснениями хода решения и иллюстрациями.
Навигация по странице.
Правила записи при делении столбиком
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида . Например, если делимым является число 6 105
, а делителем – 5
5, то их правильная запись при делении в столбик будет такой:
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком.
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места. Например, при делении столбиком натурального числа 614 808
на 51 234
(614 808
– шестизначное число, 51 234
– пятизначное число, разница в количестве знаков в записях равна 6−5=1
) для промежуточных вычислений потребуется меньше места, чем при делении чисел 8 058
и 4
(здесь разница в количестве знаков равна 4−1=3
). Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:
Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:
Теперь можно переходить непосредственно к процессу деления натуральных чисел столбиком.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком
Понятно, что разделить одно однозначное натуральное число на другое достаточно просто, и делить эти числа в столбик нет причин. Однако будет полезно отработать начальные навыки деления столбиком на этих простых примерах.
Пример.
Пусть нам нужно разделить столбиком 8 на 2 .
Решение.
Конечно, мы можем выполнить деление при помощи таблицы умножения , и сразу записать ответ 8:2=4 .
Но нас интересует, как выполнить деление этих чисел столбиком.
Сначала записываем делимое 8
и делитель 2
так, как того требует метод:
Теперь мы начинаем выяснять, сколько раз делитель содержится в делимом. Для этого мы последовательно умножаем делитель на числа 0
, 1
, 2
, 3
, … до того момента, пока в результате не получим число, равное делимому, (либо число большее, чем делимое, если имеет место деление с остатком).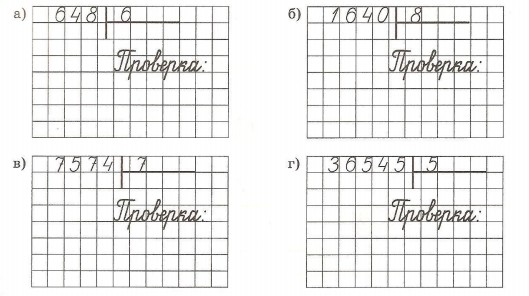 Если мы получаем число равное делимому, то сразу записываем его под делимым, а на место частного записываем число, на которое мы умножали делитель. Если же мы получаем число большее, чем делимое, то под делителем записываем число, вычисленное на предпоследнем шаге, а на место неполного частного записываем число, на которое умножался делитель на предпоследнем шаге.
Если мы получаем число равное делимому, то сразу записываем его под делимым, а на место частного записываем число, на которое мы умножали делитель. Если же мы получаем число большее, чем делимое, то под делителем записываем число, вычисленное на предпоследнем шаге, а на место неполного частного записываем число, на которое умножался делитель на предпоследнем шаге.
Поехали: 2·0=0
; 2·1=2
; 2·2=4
; 2·3=6
; 2·4=8
. Мы получили число, равное делимому, поэтому записываем его под делимым, а на место частного записываем число 4
. При этом запись примет следующий вид:
Остался завершающий этап деления однозначных натуральных чисел столбиком. Под числом, записанным под делимым, нужно провести горизонтальную черту, и провести вычитание чисел над этой чертой так, как это делается при вычитании натуральных чисел столбиком . Число, получающееся после вычитания, будет остатком от деления. Если оно равно нулю, то исходные числа разделились без остатка.
В нашем примере получаем
Теперь перед нами законченная запись деления столбиком числа 8
на 2
. Мы видим, что частное 8:2
равно 4
(и остаток равен 0
).
Мы видим, что частное 8:2
равно 4
(и остаток равен 0
).
Ответ:
8:2=4 .
Теперь рассмотрим, как осуществляется деление столбиком однозначных натуральных чисел с остатком.
Пример.
Разделим столбиком 7 на 3 .
Решение.
На начальном этапе запись выглядит так:
Начинаем выяснять, сколько раз в делимом содержится делитель. Будем умножать 3
на 0
, 1
, 2
, 3
и т.д. до того момента, пока не получим число равное или большее, чем делимое 7
. Получаем 3·0=07
(при необходимости обращайтесь к статье сравнение натуральных чисел). Под делимым записываем число 6
(оно получено на предпоследнем шаге), а на место неполного частного записываем число 2
(на него проводилось умножение на предпоследнем шаге).
Осталось провести вычитание, и деление столбиком однозначных натуральных чисел 7
и 3
будет завершено.
Таким образом, неполное частное равно 2 , и остаток равен 1 .
Ответ:
7:3=2 (ост. 1) .
Теперь можно переходить к делению столбиком многозначных натуральных чисел на однозначные натуральные числа.
Сейчас мы разберем алгоритм деления столбиком . На каждом его этапе мы будем приводить результаты, получающиеся при делении многозначного натурального числа 140 288 на однозначное натуральное число 4 . Этот пример выбран не случайно, так как при его решении мы столкнемся со всеми возможными нюансами, сможем подробно разобрать их.
Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
Первой слева цифрой в записи делимого 140 288
является цифра 1
. Число 1
меньше, чем делитель 4
, поэтому смотрим еще и на следующую слева цифру в записи делимого. При этом видим число 14
, с которым нам и предстоит работать дальше. Выделяем это число в записи делимого.
Выделяем это число в записи делимого.
Следующие пункты со второго по четвертый повторяются циклически, пока деление натуральных чисел столбиком не будет завершено.
Сейчас нам нужно определить, сколько раз делитель содержится в числе, с которым мы работаем (для удобства обозначим это число как x
). Для этого последовательно умножаем делитель на 0
, 1
, 2
, 3
, … до того момента, пока не получим число x
или число больше, чем x
. Когда получается число x
, то мы записываем его под выделенным числом по правилам записи, используемым при вычитании столбиком натуральных чисел. Число, на которое проводилось умножение, записывается на место частного при первом проходе алгоритма (при последующих проходах 2-4
пунктов алгоритма это число записывается правее уже находящихся там чисел). Когда получается число, которое больше числа x
, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место частного (или правее уже находящихся там чисел) записываем число, на которое проводилось умножение на предпоследнем шаге. (Аналогичные действия мы проводили в двух примерах, разобранных выше).
(Аналогичные действия мы проводили в двух примерах, разобранных выше).
Умножаем делитель 4
на числа 0
, 1
, 2
, …, пока не получим число, которое равно 14
или больше 14
. Имеем 4·0=014
. Так как на последнем шаге мы получили число 16
, которое больше, чем 14
, то под выделенным числом записываем число 12
, которое получилось на предпоследнем шаге, а на место частного записываем число 3
, так как в предпоследнем пункте умножение проводилось именно на него.
На этом этапе из выделенного числа вычитаем столбиком число, расположенное под ним. Под горизонтальной линией записывается результат вычитания. Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком). Здесь же для своего контроля не лишним будет сравнить результат вычитания с делителем и убедиться, что он меньше делителя. В противном случае где-то была допущена ошибка.
Нам нужно вычесть столбиком из числа 14
число 12
(для корректности записи нужно не забыть поставить знак «минус» слева от вычитаемых чисел). После завершения этого действия под горизонтальной чертой оказалось число 2
. Теперь проверяем свои вычисления, сравнивая полученное число с делителем. Так как число 2
меньше делителя 4
, то можно спокойно переходить к следующему пункту.
Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается. После этого выделяем число, образовавшееся под горизонтальной чертой, принимаем его в качестве рабочего числа, и повторяем с ним со 2 по 4 пункты алгоритма.
Под горизонтальной чертой справа от уже имеющейся там цифры 2
записываем цифру 0
, так как именно цифра 0
находится в записи делимого 140 288
в этом столбце. Таким образом, под горизонтальной чертой образуется число 20
.
Таким образом, под горизонтальной чертой образуется число 20
.
Это число 20
мы выделяем, принимаем в качестве рабочего числа, и повторяем с ним действия второго, третьего и четвертого пунктов алгоритма.
Умножаем делитель 4 на 0 , 1 , 2 , …, пока не получим число 20 или число, которое больше, чем 20 . Имеем 4·0=0
Проводим вычитание столбиком. Так как мы вычитаем равные натуральные числа, то в силу свойства вычитания равных натуральных чисел в результате получаем нуль. Нуль мы не записываем (так как это еще не завершающий этап деления столбиком), но запоминаем место, на котором мы его могли записать (для удобства это место мы отметим черным прямоугольником).
Под горизонтальной линией справа от запомненного места записываем цифру 2
, так как именно она находится в записи делимого 140 288
в этом столбце. Таким образом, под горизонтальной чертой мы имеем число 2
.
Число 2
принимаем за рабочее число, отмечаем его, и нам еще раз придется выполнить действия из 2-4
пунктов алгоритма.
Умножаем делитель на 0
, 1
, 2
и так далее, и сравниваем получающиеся числа с отмеченным числом 2
. Имеем 4·0=02
. Следовательно, под отмеченным числом записываем число 0
(оно было получено на предпоследнем шаге), а на месте частного справа от уже имеющегося там числа записываем число 0
(на 0
мы проводили умножение на предпоследнем шаге).
Выполняем вычитание столбиком, получаем число 2 под горизонтальной чертой. Проверяем себя, сравнивая полученное число с делителем 4 . Так как 2
Под горизонтально чертой справа от числа 2 дописываем цифру 8
(так как она находится в этом столбце в записи делимого 140 288
). Таким образом, под горизонтальной линией оказывается число 28
.
Принимаем это число в качестве рабочего, отмечаем его, и повторяем действия 2-4
пунктов.
Здесь никаких проблем возникнуть не должно, если Вы были внимательны до настоящего момента. Проделав все необходимые действия, получается следующий результат.
Осталось последний раз провести действия из пунктов 2
, 3
, 4
(предоставляем это Вам), после чего получится законченная картина деления натуральных чисел 140 288
и 4
в столбик:
Обратите внимание, что в самой нижней строчке записано число 0 . Если бы это был не последний шаг деления столбиком (то есть, если бы в записи делимого в столбцах справа оставались цифры), то этот нуль мы бы не записывали.
Таким образом, посмотрев на законченную запись деления многозначного натурального числа 140 288 на однозначное натуральное число 4 , мы видим, что частным является число 35 072 , (а остаток от деления равен нулю, он находится в самой нижней строке).
Конечно же, при делении натуральных чисел столбиком Вы не будете настолько подробно описывать все свои действия. Ваши решения будут выглядеть примерно так, как в следующих примерах.
Пример.
Выполните деление в столбик, если делимое равно 7 136
, а делителем является однозначное натуральное число 9
.
Решение.
На первом шаге алгоритма деления натуральных чисел столбиком мы получим запись вида
После выполнения действий из второго, третьего и четвертого пунктов алгоритма запись деления столбиком примет вид
Повторив цикл, будем иметь
Еще один проход дет нам законченную картину деления столбиком натуральных чисел 7 136
и 9
Таким образом, неполное частное равно 792 , а остаток от деления равен 8 .
Ответ:
7 136:9=792 (ост. 8) .
А этот пример демонстрирует, как должно выглядеть деление в столбик.
Пример.
Разделите натуральное число 7 042 035 на однозначное натуральное число 7 .
Решение.
Удобнее всего выполнить деление столбиком.
Ответ:
7 042 035:7=1 006 005 .
Деление столбиком многозначных натуральных чисел
Поспешим Вас обрадовать: если Вы хорошо усвоили алгоритм деления столбиком из предыдущего пункта этой статьи, то Вы уже почти умеете выполнять деление столбиком многозначных натуральных чисел . Это действительно так, так как со 2
по 4
этапы алгоритма остаются неизменными, а в первом пункте появляются лишь незначительные изменения.
Это действительно так, так как со 2
по 4
этапы алгоритма остаются неизменными, а в первом пункте появляются лишь незначительные изменения.
На первом этапе деления в столбик многозначных натуральных чисел нужно смотреть не на первую слева цифру в записи делимого, а на такое их количество, сколько знаков содержится в записи делителя. Если число, определяемое этими цифрами, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого. После этого выполняются действия, указанные во 2 , 3 и 4 пункте алгоритма до получения конечного результата.
Осталось лишь посмотреть применение алгоритма деления столбиком многозначных натуральных чисел на практике при решении примеров.
Пример.
Выполним деление столбиком многозначных натуральных чисел 5 562 и 206 .
Решение.
Так как в записи делителя 206
участвуют 3
знака, то смотрим на первые 3
цифры слева в записи делимого 5 562
. Эти цифры соответствуют числу 556
. Так как 556
больше, чем делитель 206
, то число 556
принимаем в качестве рабочего, выделяем его, и переходим к следующему этапу алгоритма.
Эти цифры соответствуют числу 556
. Так как 556
больше, чем делитель 206
, то число 556
принимаем в качестве рабочего, выделяем его, и переходим к следующему этапу алгоритма.
Теперь умножаем делитель 206
на числа 0
, 1
, 2
, 3
, … до того момента, пока не получим число, которое либо равно 556
, либо больше, чем 556
. Имеем (если умножение выполняется сложно, то лучше выполнять умножение натуральных чисел столбиком): 206·0=0556
. Так как мы получили число, которое больше числа 556
, то под выделенным числом записываем число 412
(оно было получено на предпоследнем шаге), а на место частного записываем число 2
(так как на него проводилось умножение на предпоследнем шаге). Запись деления столбиком принимает следующий вид:
Выполняем вычитание столбиком. Получаем разность 144
, это число меньше делителя, поэтому можно спокойно продолжать выполнение требуемых действий.
Под горизонтальной линией справа от имеющегося там числа записываем цифру 2
, так как она находится в записи делимого 5 562
в этом столбце:
Теперь мы работаем с числом 1 442
, выделяем его, и проходим пункты со второго по четвертый еще раз.
Умножаем делитель 206 на 0 , 1 , 2 , 3 , … до получения числа 1 442 или числа, которое больше, чем 1 442 . Поехали: 206·0=0
Проводим вычитание столбиком, получаем нуль, но сразу его не записываем, а лишь запоминаем его позицию, потому что не знаем, завершается ли на этом деление, или придется еще раз повторять шаги алгоритма:
Теперь мы видим, что под горизонтальную черту правее запомненной позиции мы не можем записать никакого числа, так как в записи делимого в этом столбце нет цифр. Следовательно, на этом деление столбиком закончено, и мы завершаем запись:
- Математика. Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.
- Математика. Любые учебники для 5 классов общеобразовательных учреждений.
Деление столбиком или, правильнее сказать, письменный прием деления уголком, школьники проходят уже в третьем классе начальной школы, но зачастую этой теме уделяется так мало внимания, что к 9-11 классу не все ученики могут им свободно пользоваться. Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.
Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.
Очевидно, что уделив делению столбиком больше внимания, чем заложено в школьной программе, ребенок облегчит себе выполнение заданий по математике вплоть до 11 класса. А для этого нужно немногое — понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.
Алгоритм деления столбиком на двузначное число
Как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к делению более мелких единиц.
1. Находим первое неполное делимое . Это число, которое делится на делитель с получением числа больше или равного 1. Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака.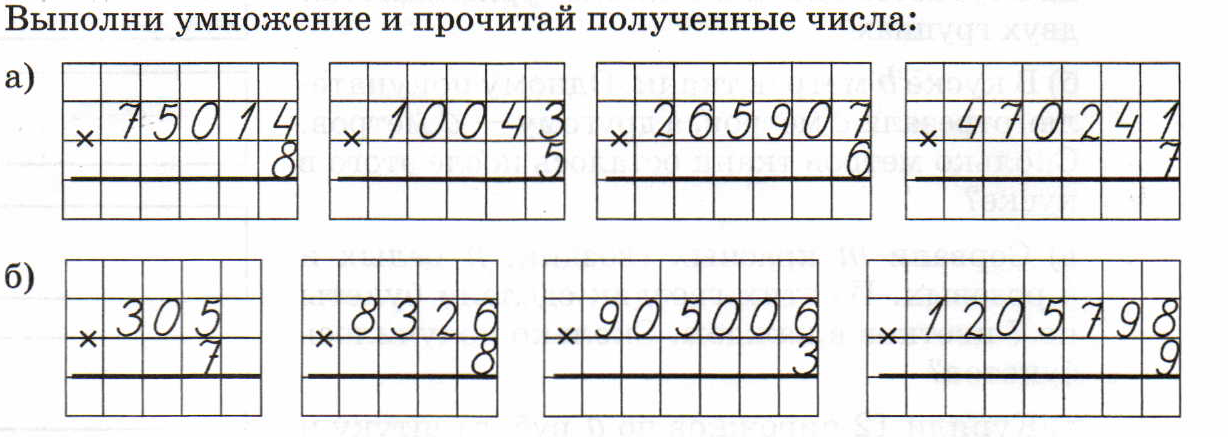
Примеры 76
8:24. Первое неполное делимое 76
265
:53 26 меньше 53, значит не подходит. Нужно добавить следующую цифру (5). Первое неполное делимое 265.
2. Определяем количество цифр в частном . Для определения числа цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого — еще по одной цифре частного.
Примеры 768:24. Первое неполное делимое 76. Ему соответствует 1 цифра частного. После первого неполного делителя есть еще одна цифра. Значит в частном будет всего 2 цифры.
265:53. Первое неполное делимое 265. Оно даст 1 цифру частного. Больше в делимом цифр нет. Значит в частном будет всего 1 цифра.
15344:56. Первое неполное делимое 153, а после него еще 2 цифры. Значит в частном будет всего 3 цифры.
3. Находим цифры в каждом разряде частного . Сначала найдем первую цифру частного. Подбираем такое целое число, чтобы при умножении его на наш делитель получилось число, максимально приближенное к первому неполному делимому. Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.
Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.
Затем находим вторую цифру частного. Переписываем в строку с остатком цифру, следующую за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.
4. Находим остаток (если есть).
Если цифры частного закончились и получился остаток 0, то деление выполнено без остатка. В ином случае значение частного записывается с остатком.
Так же выполняется деление на любое многозначное число (трехзначное, четырехзначное и т. д.)
Разбор примеров на деление столбиком на двузначное число
Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.
Найдем значение частного чисел 265 и 53.
Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.
Больше в делимом цифр нет. Значит в частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.
Значение частного чисел 265 и 53 равно 5.
Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.
Найдем значение частного чисел 184 и 23.
В частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.
Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.
Значение частного чисел 184 и 23 равно 8.
Рассмотрим более сложные случаи деления.
Найдем значение частного чисел 768 и 24.
Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.
Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.
Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.
Значение частного чисел 768 и 24 равно 32.
Найдем значение частного чисел 15344 и 56.
Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.
Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое 414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
Значение частного чисел 15344 и 56 равно 274.
Пример на деление с остатком
Чтобы провести аналогию, возьмем пример, похожий на пример выше, и отличающийся лишь последней цифрой
Найдем значение частного чисел 15345:56
Делим сначала точно так же, как в примере 15344:56, пока не дойдем до последнего неполного делимого 225. Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.
Значение частного чисел 15345 и 56 равно 274 (остаток 1).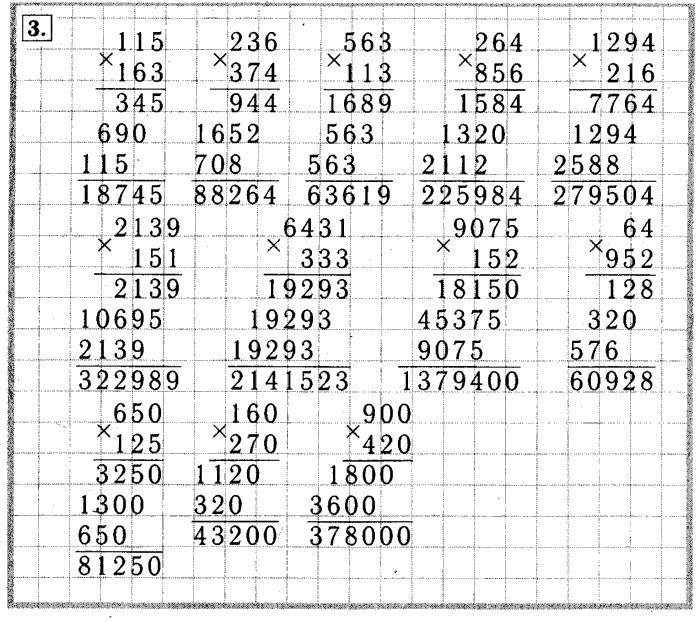
Деление с нулем в частном
Иногда в частном одним из чисел получается 0, и дети зачастую пропускают его, отсюда неправильное решение. Разберем, откуда может взяться 0 и как его не забыть.
Найдем значение частного чисел 2870:14
Первое неполное делимое — 28 сотен. Значит в частном будет 3 цифры. Ставим под уголок три точки. Это важный момент. Если ребенок потеряет ноль, останется лишняя точка, которая заставит задуматься, что где-то упущена цифра.
Определим первую цифру частного. Разделим 28 на 14. Подбором получается 2. Проверим, подойдет ли цифра 2. Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.
Получился нулевой остаток. Мы обозначили его розовым для наглядности, но записывать его не нужно. Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.
Теперь переписываем в ту же строку последнюю цифру делимого (количество единиц).
70:14=5 Записываем вместо последней точки в частном цифру 5. 70-70=0. Остатка нет.
Значение частного чисел 2870 и 14 равно 205.
Деление нужно непременно проверить умножением.
Примеры на деление для самопроверки
Найдите первое неполное делимое и определите количество цифр в частном.
3432:66 2450:98 15145:65 18354:42 17323:17
Усвоили тему, а теперь потренируйтесь решить несколько примеров столбиком самостоятельно.
1428: 42 30296: 56 254415: 35 16514: 718
Умножение и деление в столбик: примеры
Математика сродни головоломкам. Особенно это касается деления и умножения в столбик. В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Советы тем, кто хочет хорошо знать математику
Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.
Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.
Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.
Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.
Как умножаются в столбик натуральные числа?
Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:
- До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым.
 Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго. - Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
- То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.
Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.
Алгоритм умножения в столбик десятичных дробей
Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.
Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.
Именно столько их нужно отсчитать от конца ответа и там поставить запятую.
Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:
- Записать эти дроби нужно так, чтобы число 33 было под 25.
- Теперь правую тройку нужно умножить на 25. Получится 75. Записать его полагается так, чтобы пятерка оказалась под тройкой, на которую выполнялось умножение.
- Потом умножать 25 на первую 3. Опять будет 75, но написано оно будет так, чтобы 5 оказалось под 7 предыдущего числа.
- После сложения этих двух чисел получается 825. В десятичных дробях запятыми отделены 4 цифры. Поэтому в ответе нужно отделить запятой тоже 4 цифры. Но их всего три. Для этого перед 8 придется написать 0, поставить запятую, перед ней еще один 0.
- Ответом в примере окажется число 0,0825.
С чего начать обучение делению?
До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.
Второе (на него делят) — делитель. Ответ — частное.
После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?
После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.
Алгоритм деления чисел в столбик
Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:
- До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
- Записать делимое. Справа от него — делитель.
- Прочертить слева и снизу около последнего уголок.
- Определить неполное делимое, то есть число, которое будет минимальным для деления.
 Обычно оно состоит из одной цифры, максимум из двух.
Обычно оно состоит из одной цифры, максимум из двух. - Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
- Записать результат от умножения этого числа на делитель.
- Написать его под неполным делимом. Выполнить вычитание.
- Снести к остатку первую цифру после той части, которая уже разделена.
- Снова подобрать число для ответа.
- Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.
Как решать деление в столбик, если в делителе больше одной цифры?
Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.
Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Рассмотреть такое деление можно на примере — 12082 : 863.
- Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
- После вычитания получается остаток 345.
- К нему нужно снести цифру 2.
- В числе 3452 четыре раза умещается 863.
- Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
- Остаток после вычитания равен нулю. То есть деление закончено.
Ответом в примере будет число 14.
Как быть, если делимое заканчивается на ноль?
Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Что делать, если разделить нужно десятичную дробь?
Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.
Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.
Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей.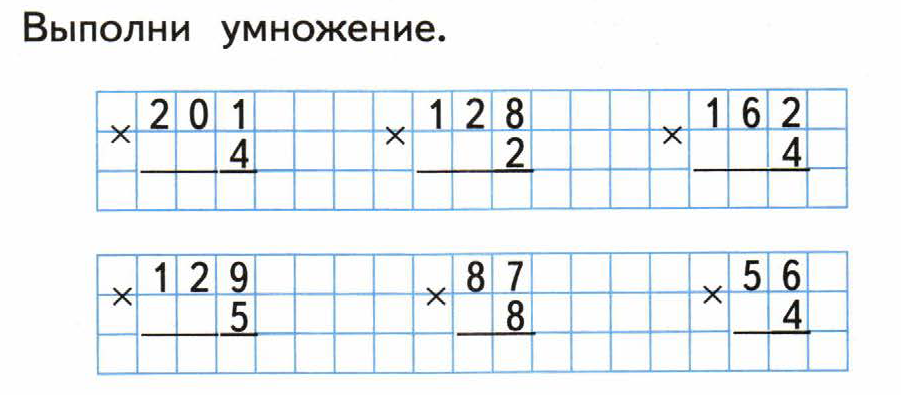 Иногда это нужно для того, чтобы доделить числа до конца.
Иногда это нужно для того, чтобы доделить числа до конца.
Деление двух десятичных дробей
Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.
Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.
Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.
В качестве примера: 28,4 делим на 3,2:
- Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.

- Их полагается разделить. Причем сразу все число 284 на 32.
- Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
- Деление целой части закончилось, и в ответ полагается поставить запятую.
- Снести к остатку 0.
- Снова взять по 8.
- Остаток: 24. К нему приписать еще один 0.
- Теперь брать нужно 7.
- Результат умножения — 224, остаток — 16.
- Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.
Деление закончено. Результат примера 28,4:3,2 равен 8,875.
Что делать, если делитель равен 10, 100, 0,1, или 0,01?
Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.
Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.
При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).
Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.
Деление периодических дробей
В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.
Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.
Если в примере разные дроби…
Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.
Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.
Умножение и деление в столбик
Рейтинг 4.50 из 5 на основе опроса 2 пользователей
(1 отзыв клиента)
80,00 ₽
Примеры на умножение и деление в столбик: на однозначные , двузначные и трехзначные числа. С ответами. Для печати А4.
С ответами. Для печати А4.
Артикул: i-2498 Категория: Для учебы Метки: 3 класс, 4 класс, 5-8 класс, Примеры в столбик
- Описание
- Детали
- Отзывы (1)
Описание
Примеры на умножение и деление в столбик решать просто. Но они требуют концентрации и внимания, особенно для очень торопливых детей. Практика счета таких примеров поможет развить внимательность и закрепить навыки счета больших чисел, а также добиться автоматизированного счета.
Программа представляет собой тренажер для счета. Она имеет внутренние настройки, изменяя которые можно создать примеры на умножение и деление в столбик для детей разного возраста и уровня подготовки:
- Умножение на однозначное, двузначное или трехзначное число,
- Деление на однозначное, двузначное или трехзначное число.

Поэтому программа будет полезна как для учеников начальной школы 3-4 классов, так и для более старших классов.
Программа счета написана в Excel с помощью макросов. Формируются примеры на листе формата А4. Примеры генерируются случайным образом, количество генераций не ограничено. При записи примеров разряды чисел формируются друг под другом, что позволяет легко ориентироваться в примерах.
В конце карточки формируются ответы на примеры, которые после печати карточки можно отрезать. Нумерация карточек и ответов позволяет быстро находить ответы к каждой карточке, даже если их напечатано много.
Генератор примеров по математике будет очень удобен как для родителей, так и для учителей. Не нужно заранее покупать задачники и пособия по математике с примерами. Можно скачать файл и сгенерировать карточки в любое время независимо от подключения к интернету и распечатать.
Для ознакомления с программой можно бесплатно скачать примеры, которые получаются при использовании программы.
Для получения новой карточки примеров достаточно скачать, нажать на кнопку генерации и распечатать.
Для решения примеров на умножение и деление в столбик на компьютере (без печати) можно скачать программы «Тренажер: умножение в столбик» и «Тренажер: деление в столбик«.
Другие программы, которые помогут закрепить навыки счета:
Также есть программы, в которых можно выбрать уровень сложности. В них можно начать с решения легких примеров, а затем перейти к более сложным.
На сайте представлен каталог программ, в котором все программы распределены по группам. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.
Вам также будет интересно…
Деление в столбик
60,00 ₽В корзинуДействия с именованными числами
80,00 ₽В корзинуЛогические задачи
175,00 ₽В корзинуУмножение в столбик
60,00 ₽В корзинуСложение и вычитание в столбик
Оценка 5.
60,00 ₽В корзину 00 из 5
00 из 5Деление с остатком на число (с выбором уровня сложности)
Оценка 5.00 из 5
75,00 ₽В корзинуТренажер: сложение и вычитание в столбик
60,00 ₽В корзинуТренажер: умножение в столбик
60,00 ₽В корзинуСложные примеры на порядок действий
100,00 ₽В корзинуУмножение и деление по типам (табличное, внетабличное, круглых чисел)
100,00 ₽В корзинуТренажер: деление в столбик
60,00 ₽В корзинуПорядок действий в пределах 1000 (все действия)
80,00 ₽В корзину
Способы и правила деления в столбик. Умножение и деление в столбик: примеры
Столбиком? Как дома самостоятельно отработать навык деления в столбик, если в школе ребенок что-то не усвоил? Делить столбиком учат во 2-3 классе, для родителей, конечно, это пройденный этап, но при желании можно вспомнить правильную запись и объяснить доступно своему школьнику то, что понадобится ему в жизни.
xvatit.com
Что должен знать ребенок 2-3 класса, чтобы научиться делить в столбик?
Как правильно объяснить ребенку 2-3 класса деление столбиком, чтобы в дальнейшем у него не было проблем? Для начала, проверим, нет ли пробелов в знаниях. Убедитесь, что:
- ребенок свободно выполняет операции сложения и вычитания;
- знает разряды чисел;
- знает назубок .
Как объяснить ребенку смысл действия «деление»?
- Ребенку нужно объяснить все на наглядном примере.
Попросите разделить что-либо между членами семьи или друзьями. Например, конфеты, кусочки торта и т.п. Важно, чтобы ребенок понял суть — разделить нужно поровну, т.е. без остатка. Потренируйтесь на разных примерах.
Допустим, 2 группы спортсменов должны занять места в автобусе. Известно сколько спортсменов в каждой группе и сколько всего мест в автобусе. Нужно узнать, сколько билетов нужно купить одной и второй группе. Или 24 тетради нужно раздать 12 ученикам, сколько достанется каждому.
- Когда ребенок усвоит суть принципа деления, покажите математическую запись этой операции, назовите компоненты.
- Объясните, что деление – это операция противоположная умножению, умножение наизнанку.
Удобнопоказать взаимосвязь деления и умножения на примере таблицы.
Например, 3 умножить на 4 равно 12.
3 — это первый множитель;
4 — второй множитель;
12 — произведение (результат умножения).
Если 12 (произведение) разделить на 3 (первый множитель), получим 4 (второй множитель).
Компоненты при делении называются иначе:
12 — делимое;
3 — делитель;
4 — частное (результат деления).
Нам, взрослым, проще «по старинке» записать «уголком» — и дело с концом. НО! Дети еще не проходили деление в столбик, что делать? Как научить ребенка делить двузначное число на однозначное не используя запись столбиком?
Возьмем для примера 72:3.
Все просто! Раскладываем 72 на такие числа, которые легко устно разделить на 3:
72=30+30+12.
Все сразу стало наглядно: 30 мы можем разделить на 3, и 12 ребенок легко разделит на 3.
Останется только сложить результаты, т.е. 72:3=10 (получили, когда 30 разделили на 3) + 10 (30 разделили на 3) + 4 (12 разделили на 3).
72:3=24
Мы не использовали деление в столбик, но ребенку был понятен ход рассуждений, и он выполнил вычисления без труда.
После простых примеров можно переходить к изучению деления в столбик, учить ребенка правильно записывать примеры «уголком». Для начала используйте только примеры на деление без остатка.
Как объяснить ребенку деление в столбик: алгоритм решения
Большие числа сложно делить в уме, проще использовать запись деления столбиком. Чтобы научить ребенка правильно выполнять вычисления, действуйте по алгоритму:
- Определить, где в примере делимое и делитель. Попросите ребенка назвать числа (что на что мы будем делить).

213:3
213 — делимое
3 — делитель
- Записать делимое — «уголок» — делитель.
- Определить, какую часть делимого мы можем использоваться, чтобы разделить на заданное число.
Рассуждаем так: 2 не делится на 3, значит — берем 21.
- Определить, сколько раз делитель «помещается» в выбранной части.
21 разделить на 3 — берем по 7.
- Умножить делитель на выбранное число, результат записать под «уголком».
7 умножить на 3 — получаем 21. Записываем.
- Найти разницу (остаток).
На этом этапе рассуждений научите ребенка проверять себя. Важно, чтобы он понял, что результат вычитания ВСЕГДА должен быть меньше делителя. Если вышло не так, нужно увеличить выбранное число и выполнить действие еще раз.
- Повторить действия, пока в остатке не окажется 0.
Как правильно рассуждать, чтобы научить ребенка 2-3 класса делить столбиком
Как объяснить ребенку деление 204:12=?
1. Записываем столбиком.
Записываем столбиком.
204 — делимое, 12 — делитель.
2. 2 не делится на 12, значит, берем 20.
3. Чтобы разделить 20 на 12 берем по 1. Записываем 1 под «уголком».
4. 1 умножить на 12 получим 12. Записываем под 20.
5. 20 минус 12 получим 8.
Проверяем себя. 8 меньше 12 (делителя)? Ок, все верно, идем дальше.
6. Рядом с 8 пишем 4. 84 разделить на 12. На сколько нужно умножить 12, чтобы получить 84?
Сразу сложно сказать, попробуем действовать методом подбора.
Возьмем, например, по 8, но пока не записываем. Считаем устно: 8 умножить на 12 получится 96. А у нас 84! Не подходит.
Пробуем поменьше… Например, возьмем по 6. Проверяем себя устно: 6 умножить на 12 равно 72. 84-72=12. Мы получили такое же число, как наш делитель, а должно быть или ноль, или меньше 12. Значит, оптимальная цифра 7!
7. Записываем 7 под «уголок» и выполняем вычисления. 7 умножить на 12 получим 84.
8. Записываем результат в столбик: 84 минус 84 равно ноль. Ура! Мы решили правильно!
Ура! Мы решили правильно!
Итак, вы научили ребенка делить столбиком, осталось теперь отработать этот навык, довести его до автоматизма.
Почему детям сложно научиться делить в столбик?
Помните, что проблемы с математикой возникают от неумения быстро делать простые арифметические действия. В начальной школе нужно отработать и довести до автоматизма сложение и вычитание, выучить «от корки до корки» таблицу умножения. Все! Остальное — дело техники, а она нарабатывается с практикой.
Будьте терпеливы, не ленитесь лишний раз объяснить ребенку то, что он не усвоил на уроке, нудно, но дотошно разобраться в алгоритме рассуждений и проговорить каждую промежуточную операцию прежде, чем озвучить готовый ответ. Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.
Уважаемые читатели! Расскажите, как вы учите ваших детей делить в столбик, с какими сложностями приходилось сталкиваться и какими способами вы их преодолели.
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг . Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг . Ставим точку под делителем.
5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Деление многозначных или многоразрядных чисел удобно производить письменно в столбик . Давайте разберем, как это делать. Начнем с деления многоразрядного числа на одноразрядное, и постепенно увеличим разрядность делимого.
Итак, поделим 354 на 2 . Для начала разместим эти числа как показано на рисунке:
Делимое размещаем слева, делитель справа, а частное будем записывать под делителем.
Теперь начинаем делить делимое на делитель поразрядно слева на право. Находим первое неполное делимое , для этого берем первый слева разряд, в нашем случае 3 и сравниваем с делителем.
3 больше 2 , значит 3 и есть неполное делимое. Ставим точку в частном и определяем, сколько ещё разрядов будет в частном – столько же, сколько осталось в делимом после выделения неполного делимого. В нашем случае в частном столько же разрядов, сколько в делимом, то есть старшим разрядом будут сотни:
Ставим точку в частном и определяем, сколько ещё разрядов будет в частном – столько же, сколько осталось в делимом после выделения неполного делимого. В нашем случае в частном столько же разрядов, сколько в делимом, то есть старшим разрядом будут сотни:
Для того чтобы 3 разделить на 2 вспоминаем таблицу умножения на 2 и находим число при умножении которого на 2 получим наибольшее произведение, которое меньше 3.
2 × 1 = 2 (2
2 × 2 = 4 (4 > 3)
2 меньше 3 , а 4 больше, значит, берем первый пример и множитель 1 .
Записываем 1 в частное на место первой точки (в разряд сотен), а найденное произведение записываем под делимым:
Теперь находим разность, между первым неполным делимым и произведением найденного разряда частного и делителем:
Полученное значение сравниваем с делителем. 15 больше 2 , значит, мы нашли второе неполное делимое. Для того чтобы найти результат деления 15 на 2 вновь вспоминаем таблицу умножения на 2 и находим наибольшее произведение, которое меньше 15 :
Для того чтобы найти результат деления 15 на 2 вновь вспоминаем таблицу умножения на 2 и находим наибольшее произведение, которое меньше 15 :
2 × 7 = 14 (14
2 × 8 = 16 (16 > 15)
Искомый множитель 7 , записываем его в частное на место второй точки (в десятки). Находим разность между вторым неполным делимым и произведением найденного разряда частного и делителя:
Продолжаем деление, для чего находим третье неполное делимое . Спускаем следующий разряд делимого:
Делим неполное делимое на 2, полученное значение ставим в разряд единиц частного. Проверим правильность деления:
2 × 7 = 14
Результат деления третьего неполного делимого на делитель пишем в частное, находим разность:
Разность мы получили равную нулю, значит деление произведено правильно .
Усложним задачу и приведем другой пример:
1020 ÷ 5
Запишем наш пример в столбик и определим первое неполное частное:
Разряд тысяч делимого составляет 1 , сравниваем с делителем:
1
Добавляем в неполное делимое разряд сотен и сравниваем:
10 > 5 – мы нашли неполное делимое.
Делим 10 на 5 , получаем 2 , записываем результат в частное. Разность между неполным делимым и результатом умножения делителя и найденного разряда частного.
10 – 10 = 0
0 мы не пишем, опускаем следующий разряд делимого – разряд десятков:
Сравниваем второе неполное делимое с делителем.
2
Нам следует добавить в неполное делимое ещё один разряд, для этого в частное, на разряд десятков ставим 0 :
20 ÷ 5 = 4
Записываем ответ в разряд единиц частного и проверяем: записываем произведение под второе неполное делимое и вычисляем разность. Получаем 0 , значит пример решён правильно .
И ещё 2 правила деления в столбик:
1. Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить, например:
Сколько нулей в младшем разряде делимого мы убираем, столько же нулей убираем в младших разрядах делителя.
2. Если в делимом после деления остались нули, то их следует перенести в частное:
Итак, сформулируем последовательность действий при делении в столбик.
- Размещаем делимое слева, делитель справа. Помним, что делимое мы делим, поразрядно выделяя неполные делимые и деля их последовательно на делитель. Разряды в неполное делимое выделяются слева направо от старших к младшим.
- Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить.
- Определяем первый неполный делитель:
а) выделяем в неполный делитель старший разряд делимого;
б) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (в) , если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4 ;
в) добавляем в неполное делимое следующий разряд и переходим к пункту (б) .
- Определяем сколько разрядов будет в частном, и ставим столько точек на месте частного (под делителем) сколько будет в нем разрядов.
 Одна точка (один разряд) за все первое неполное делимое и остальных точек (разрядов) столько же, сколько осталось разрядов в делимом после выделения неполного делимого.
Одна точка (один разряд) за все первое неполное делимое и остальных точек (разрядов) столько же, сколько осталось разрядов в делимом после выделения неполного делимого. - Делим неполное делимое на делитель, для этого находим число, при умножении которого на делитель получилось бы число либо равное неполному делимому, либо меньше его.
- Найденное число записываем на место очередного разряда частного (точки), а результат умножения его на делитель записываем под неполным делимым и находим их разность.
- Если найденная разность меньше или равна неполному делимому значит, мы правильно поделили неполное делимое на делитель.
- Если в делимом остались еще разряды, то продолжаем деление, иначе переходим к пункту 10 .
- Опускаем к разности следующий разряд делимого и получаем очередное неполное делимое:
а) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (б), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4;
б) добавляем к неполному делимому следующий разряд делимого, при этом в частное на место следующего разряда (точки) пишем 0;
в) переходим к пункту (а).
10. Если мы выполняли деление без остатка и последняя найденная разность равна 0 , то мы правильно выполнили деление .
Мы говорили о делении многоразрядного числа на одноразрядное. В случае, когда разрядность делителя больше, деление выполняется аналогично:
Конечно же, дети постигают азы математики на уроках в школе. Но не всегда малышу бывают понятны объяснения учителя. А может ребенок заболел и пропустил тему. В таких случаях родителям стоит вспомнить свои школьные годы, для того чтобы помочь ребенку не упустить важную информацию, без которой дальнейшее обучение будет нереально.
Учить ребенка столбиком начинают в третьем классе. К этому времени таблицей умножения школьник должен уже пользоваться с легкостью. Но если существуют с этим проблемы, стоит немедленно ведь перед тем, как научить ребенка делить столбиком, не должно возникать никаких сложностей с умножением.
Как научить делить столбиком?
Возьмем для примера трехзначное число 372 и поделим его на 6. Выбирайте любую комбинацию, но так, чтобы деление прошло без остатка. На первых порах это может запутать юного математика.
Выбирайте любую комбинацию, но так, чтобы деление прошло без остатка. На первых порах это может запутать юного математика.
Записываем числа, разделяя их уголком, и поясняем ребенку, что данное большое число мы будем постепенно делить на шесть равных частей. Попробуем сначала разделить первую цифру 3 на 6.
Она не делится, а значит, добавляем вторую, то есть попробуем, получится ли поделить 37.
Необходимо спросить у ребенка сколько раз шестерка поместится в цифре 37. Тот, кто без проблем знает математику, сразу догадается, что методом подбора можно подобрать нужный множитель. Итак, давайте подбирать, возьмем, к примеру, 5 и умножим на 6 – получается 30, вроде бы результат недалеко от 37, но стоит попробовать еще раз. Для этого 6 множим на 6 – равно 36. Вот это нам подходит, и первая цифра частного уже найдена – записываем ее под делителем, за линией.
Число 36 записываем под 37 и при вычитании получаем единицу. Она опять не делится на 6, а значит, к ней сносим оставшуюся наверху двойку. Теперь число 12 очень легко разделить на 6. В результате получаем второе число частного – двойка. Наш результат деления будет 62.
Теперь число 12 очень легко разделить на 6. В результате получаем второе число частного – двойка. Наш результат деления будет 62.
>> Урок 13. Деление на двузначное и трехзначное число
Разделим 876 на 24. Прикидка 800: 20 = 40 показывает, что в ответе должно получиться число, близкое к 40.
Как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к делению более мелких единиц.
Число сотен 8 является однозначным, поэтому делим 87 десятков на 24. Получится 3 десятка и еще 15 десятков останется (87 — 3 24 = 15). 15 десятков и 6 единиц — это 156. А если 156 разделить на 24, то получится 6 и 12 в остатке (156 — 24 6 = 12). Всего получится 3 десятка и 6 единиц, то есть 36, а в остатке 12. Это записывают так:
10*. Найди сумму всех возможных двузначных чисел, все цифры которых нечетные.
Петерсон Людмила Георгиевна. Математика. 4 класс. Часть 1. — М.: Издательство «Ювента», 2005, — 64 с. : ил.
: ил.
Планы конспектов уроков по математике 4 класса скачать , учебники и книги бесплатно, разработки уроков по математике онлайн
Содержание урока
конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации
аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения
рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие
Совершенствование учебников и уроковисправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей
идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные уроки
Сайт vpr-klass.
 com — впр-класс.ком : гдз, решебник, гиа, егэ, решение задач, задания, варианты, подготовка к экзамену, тесты, презентации.
com — впр-класс.ком : гдз, решебник, гиа, егэ, решение задач, задания, варианты, подготовка к экзамену, тесты, презентации.Error in links file
Сайт vpr-klass.com — впр-класс.ком : гдз, решебник, гиа, егэ, решение задач, задания, варианты, подготовка к экзамену, тесты, презентации. У нас вы найдете много учебных материалов: решебники, ГДЗ, тестовые задания, видео уроки, генераторы задач, решения упражнений гиа и егэ.
| Расскажи друзьям vpr-klass или впр-класс Презентации Детские презентации Презентации по математике Презентации по астрономии Демо-варианты: Математика Русский язык Физика Обществознание Английский язык Информатика История Биология Химия Литература География Математика Русский язык |  com (впр-класс) com (впр-класс) Последние новости ГИА и ЕГЭ 2017. Сайт Vpr-klass.com — это учебный-образовательно-познавательный сайт для школьников! Приветствуем на уникальном сайте помощи всем ученикам 1-11 классов. На образовательном ресурсе полно полезной, учебной информации от способов решения заданий по математике до разных генераторов задач по алгебре и онлайн калькуляторов по геометрии, которые облегчат жизнь школьника. В частности, сделан больший уклон на решебники и ГДЗ, ведь правильная домашняя работа — это хорошие оценки и учеба в школе. | Интересно Много разных решений Тесты ГИА онлайн. Видео — ГИА 2013: геометрия Видео — ГИА 2012 Видео — Демо-вариант 2012. Решение Демо-варианта 2013 года (2014 года). Задача №1, Вычислить. Задача №2, Числа и прямая. Задача №3, Сравнение чисел. Задача №4, Уравнения. Задача №5, Графики и формулы. Задача №6, Прогрессии. Задача №7, Упростить выражение. Задача №8, Неравенства, системы неравенств. Задача №9, Задания по геометрии. Генератор вариантов ГИА 2014 Много разных решений. Онлайн тесты. Видео уроки ЕГЭ по математике. Генератор вариантов ЕГЭ 2014 Книги, справочники Решение демо варианта ЕГЭ по математике 2014 Задания B1, задача. Задания B2, диаграммы. Задания B5, уравнения. Задания B8, производная. Задания B10, вероятность. Видео уроки |
Copyright © 2017 vpr-klass.com | Если какой-либо из материалов нарушает ваши авторские права, просим немедленно связаться с Администрацией!!! Наш e-mail: [email protected] | Правообладателям |
sitemap. xml
xml
Умножение и деление: определение, правила, свойства
- Автор Priya_Singh
- Последнее изменение 20-07-2022
- Автор Прия_Сингх
- Последнее изменение 20-07-2022
Арифметические операции математики включают сложение, вычитание, умножение и деление на все типы действительных чисел, включая целые числа. Символ деления представляет собой форму обела в виде горизонтальной линии с точкой над и под линией, \( \div .\). Впервые он был использован в качестве знака деления швейцарским математиком Иоганном Раном в его книге Teutsche Algebra in \(1659.\)
В математике термин умножение является одной из основных операций и означает многократное сложение числа относительно другого числа. Символ умножения — \(×.\). В этой статье мы предоставим подробную информацию об умножении и делении. Продолжайте читать, чтобы узнать больше!
Умножение: Умножение используется для нахождения произведения двух или более чисел. Умножение также известно как многократное сложение.
Умножение также известно как многократное сложение.
Пример: Когда вы хотите умножить числа \(4 \times 12 = 48\) или \(12 + 12 + 12 + 12 = 48.\)
Деление: Деление — это операция, обратная умножению. Так пытаются определить, сколько раз одно число содержится в другом.
Мы знаем, что деление \(20\) на \(5\) означает нахождение числа, которое при умножении на \(5\) дает нам \(20.\) Такое число есть \(4.\)
Следовательно , мы пишем \(20 \div 5 = 4\) или \(\frac{{20}}{5} = 4.\)
Аналогично, деление \(36\) на \( – 9\) означает нахождение число, которое при умножении на \( – 9\) дает \(\left( {36} \right).\) Такое число равно \( – 4.\)
Поэтому мы пишем \(36 \div \left( { – 9} \right) = – 4\) или \(\frac{{36}}{{ – 9}} = – 4\)
Деление \( – 35\) на \(\left( { – 7} \right)\) означает, какое число нужно умножить на \(\left( { – 7} \right)\), чтобы получить \(\left( { – 35 } \right).\)
Такое число равно \(5.\)
Следовательно, \(\left( { – 35} \right) \div \left( { – 7} \right) = 5\) или \(\frac{{ – 35}}{{ – 7}} = 5. \)
\)
Делимое: Число, которое нужно разделить, называется делимым.
Делитель: Число, которое делится, называется делителем.
Частное: Результат деления известен как частное.
Остаток: Число, оставшееся после деления, называется остатком.
Здесь \(r\) остаток, очевидно, \(r = a – bq.\)
Используя эти термины, алгоритм деления можно переформулировать следующим образом:
\({\rm{Дивиденд}} = { \rm{Делитель}} \times {\rm{Частное}} + {\rm{Остаток}}\)
Пример: Если мы разделим \(26\) на число \(6,\), то делимое равно \(26,\) делитель равен \(6,\), частное равно \(26,\), а остаток равен \(2.\)
Изучите концепции 11-го экзамена CBSE
Правила умножения и деленияПравила умножения и деления следующие:
Умножение Чтобы умножить числа, мы следуем заданным правилам:
Правило 1: Произведение двух чисел противоположных знаков равно аддитивному обратному произведению их абсолютных значений.
Пример: \(7 \times \left( { – 4} \right) = – \left( {7 \times 4} \right) = – 28\)
\(\left( { – 8} \right) \times 5 = – \left( {8 \times 5} \right) = – 40\)
Правило 2: Произведение двух чисел с одинаковыми знаками равно равны произведению их абсолютных величин.
Пример: \(7 \times 12 = 84\)
\(\left( { – 8} \right) \times \left( { – 13} \right) = 8 \times 13 = 104\)
Вы знаете, что если делимое отрицательно, а делитель отрицателен, то частное положительно. Если делимое — отрицательное число, а делитель — положительное число, то частное — отрицательное число.
Таким образом, мы имеем следующие правила деления чисел:
Правило \(1:\) Частное двух чисел, как положительных, так и отрицательных, есть положительное число, равное частному соответствующих фундаментальных значений цифры.
Таким образом, мы разделяем их значения независимо от их знака и ставим знак плюс в частном для деления двух чисел с одинаковыми символами.
Правило \(2:\) Частное положительного и отрицательного числа является отрицательным числом. Абсолютное значение равно частному соответствующих основных значений чисел.
Таким образом, мы делим их значения независимо от их знака и ставим знак минус в частное для деления чисел с разными знаками.
Свойства умножения и деления следующие:
Умножение: Ниже приведены свойства умножения:
1. Коммутативность: Умножение целого числа коммутативно. Другими словами,
, если \(a\) и \(b\) — любые два целых числа, то \(a \times b = b \times a\)
2. Умножение на ноль: Если \(a\) — любое целое число, то \(a \times 0 = 0 \times a = 0.\)
Другими словами, произведение любого целого числа на ноль всегда равен нулю.
3. Существование тождества умножения: Если \(a\) является целым числом, то \(a \times 1 = a = 1 \times a. \)
\)
Другими словами, произведение любого целого числа и \(1\) — это само число.
Число \(1\) известно как идентификатор умножения или элемент идентификации для умножения целых чисел, поскольку оно не изменяет идентичность (значение) чисел во время операции умножения.
4. Ассоциативность: если \(a,\,c\) целые числа, то
\(\left( {a \times b} \right) \times c = \left( {b \times c} \право)\)
Умножение целых чисел ассоциативно; то есть произведение трех действительных чисел не меняется при изменении их расположения.
5. Дистрибутивность умножения над сложением: Если \(a,\,b,\,c\) любые три целых числа, то
\(a \times \left( {b + c} \right) = a \times b + a \times c\)
\(\left( {b + c} \right) \times a = b \times a + c \times a\)
Умножение целых чисел распространяется на их сложение.
Деление: Ниже приведены некоторые свойства деления чисел:
1. Если \(a\) и \(b\) являются целыми числами, то \(a \div b\) не является обязательно целое число.
Пример: \(14 \div 2 = 7.\) Здесь частное является целым числом.
Но в \(15 \div 4,\) мы замечаем, что частное не является целым числом. Здесь результат равен
\(\frac{{15}}{4} = 3\frac{3}{4}.\) частное равно \(3;\) остаток равен \(3\)
2. Если \(a\) — целое число, отличное от \(0,\), то \(a \div a = 1.\)
3. Для каждого целого \(a,\) имеем \(a \ div 1 = a.\)
4. Если \(a\) ненулевое целое, то \(0 \div a = 0\)
5. Если \(a\) целое, то \( a \div 0\) не имеет смысла.
6. Если \(a,\,b,\,c\) целые числа, то
\(a > b \Rightarrow a \div c > b \div c,\), если \(c\) положительно.
\(a > b \Rightarrow a \div c > b \div c,\), если \(c\) отрицательно.
Формулы умножения и деления следующие:
УмножениеФормулы умножения чисел приведены ниже в таблице:
| Тип чисел | Операция | Результат | Пример |
| \(1 \times 7 = 7\) | |||
| Отрицательное \( \times \) Отрицательное | Умножить | Положительное \(\left( + \right)\) | \(\left( { – 1} \right) \times \left( { – 7} \right) = 7\) |
| Положительное \( \times \) Отрицательное | Умножить | Отрицательное \(\left( + \right)\) | \(1 \times \left( { – 7} \right) = – 7\) |
| Отрицательное \( \times \) Положительное | Умножить | Отрицательное \(\left( + \right)\ ) | \(\left( { – 1} \right) \times 7 = – 7\) |
В случае умножения чисел нужно умножать числа без знака. После того, как продукт приобретен, отметьте символ в соответствии с правилом умножения.
После того, как продукт приобретен, отметьте символ в соответствии с правилом умножения.
Практика 11-го экзамена CBSE Вопросы
ПодразделениеФормулы деления чисел приведены ниже в таблице:
| Тип номеров | Операция | Результат | Пример |
| положительный \div 6 = 2\) | |||
| Отрицательное \( \div \) Отрицательное | Разделить | Положительное \(\left( + \right)\) | \(\left( { – 12} \right) \div \left( { – 6} \right) = – 2\) |
| Положительный \( \div \) Отрицательный | Разделить | Отрицательное \[\left( – \right)\] | \(12 \div \left( { – 6} \right) = – 2\) |
| Отрицательное \( \div \) Положительный | Разделить | Отрицательный \[\left( – \right)\] | \(\left( { – 12} \right) \div 6 = – 2\) |
То же, что и умножение, Вы должны разделить числа без знака, а затем поставить символ в соответствии с правилом, указанным в таблице.
Деление двух чисел с одинаковыми знаками дает положительное частное, а деление двух чисел с разными знаками дает отрицательное частное.
Умножение: При умножении четных отрицательных целых чисел результат всегда положительный.
\(\влево(-\вправо) \раз \влево(-\вправо)\влево(-\вправо) \раз \влево(-\вправо) = \влево(+\вправо)\)
Деление: Для каждого факта умножения у нас есть два факта деления.
Пример: Для таблицы номер 5 фактами деления являются \(10 \дел 5 = 2,\,25 \дел 5 = 5\) и \(50 \дел 5 = 10\) и \(5 \ умножить на 2 = 10,\,2 \умножить на 5 = 10.\)
Q.1. Умножьте \(475\) на \(64\), используя свойство дистрибутивности.
Ответ: У нас есть, \(475 \times 64\)
\( = \left( {400 + 70 + 5} \right) \times 64\)
\( = 400 \times 64 + 70 \х 64 + 5 \х 64\) [Используя дистрибутивность]
\( = 25600 + 4480 + 320 = 30400\)
Q. 2. Найдите число, которое при делении на \(46\) дает частное \(11\) и остаток \(18.\)
2. Найдите число, которое при делении на \(46\) дает частное \(11\) и остаток \(18.\)
Ответ: Имеем
Делитель \(= 46,\) Частное \(= 11\) и Остаток \(= 18.\)
Нам нужно найти делимое. По алгоритму деления имеем
\({\rm{Дивиденд}} = {\rm{Делитель}} \times {\rm{Частное}} + {\rm{Остаток}}\)
\(\Rightarrow {\ rm{Дивиденд}} = 46 \умножить на 11 + 18\)
\( = 506 + 18 = 524.\)
Следовательно, искомый ответ равен \(524.\)
Q.3. Найдите произведение \(4 \times 4957 \times 25.\)
Ответ: Заметим, что
\(4 \times 25 = 100\)
Итак, мы можем расставить числа, чтобы найти желаемый продукт
\(4 \times 4925 \times 25 = \left( {4 \times 25} \right) \times 4957 = 100 \times 4957 = 495700\)
Следовательно, искомый ответ равен \(495700.\)
Q.4. Найдите значение: \(\left[ {32 + 2 \times 17 + \left( { – 6} \right)} \right] \div 15\)
Ответ: У нас есть,
\(\left[ {32 + 2 \times 17 + \left( { – 6} \right)} \right] \div 15\)
\( = \left[ {32 + 34 \div \left( { – 6} \right)} \right] \div 15 = \left( {66 – 6} \right) \div 15 = 60 \div 15 = \frac{{60}}{{15}} = 4\)
Следовательно, искомый ответ равен \(4. \)
\)
Q.5. Определить произведение наибольшего числа четырехзначных и наибольшего числа трехзначных.
Ответ: Мы знаем, что наибольшее четырехзначное число равно \(9999\), а наибольшее трехзначное число равно \(999.\)
\(\следовательно \) Требуемый продукт \( = 9999 \times 999\)
\( = 9999 \times \left( {1000 – 1} \right)\)
\( = 9999 \times 1000 – 9999 \times 1\,\,\,\left[ {\ ,a \times \left( {b – c} \right) = a \times b – a \times c} \right]\)
\( = \left( {1000 – 1} \right) \times 1000 – \влево( {1000 — 1} \вправо) \в 1\)
\( = 1000 \в 1000 — 1000 \время 1 — \влево( {1000 \время 1 — 1 \в 1} \вправо)\)
\(\left[ {\,\left( {a – b} \right) \times c = a \times c – b \times c} \right]\)
\( = 1000000 – 1000 – 10000 + 1\ )
\(= 1000000 – 11000 = 9989001\)
Попытка 11-го экзамена CBSE Пробные тесты
Резюме
Умножение помогает нам найти произведение двух или более чисел. Это также известно как повторное добавление. Деление помогает учащимся определить, сколько раз одно число содержится в другом. Деление также известно как повторное вычитание. Для деления используется символ \( \div .\). В делении используются четыре основных термина. Основными терминами, используемыми при делении, являются делимое, делитель, частное и остаток.
Это также известно как повторное добавление. Деление помогает учащимся определить, сколько раз одно число содержится в другом. Деление также известно как повторное вычитание. Для деления используется символ \( \div .\). В делении используются четыре основных термина. Основными терминами, используемыми при делении, являются делимое, делитель, частное и остаток.
Q.1. Как легко умножать и делить?
Ответ: Умножение
Например: Когда вы хотите умножить число \(5\) на любое четное число: \(5 \times 4 = \)
Вы должны взять число, которое умножается на \(5\) и разрезается пополам, что означает, что число \(4\) станет \(2.\)
Добавьте число ноль рядом с числом \(2,\), что означает, что вы получили число \(20,\), т. е. \(5 \times 4 = 20.\)
Когда вы хотите умножить число \(5 \times 4 = 20.\) на любое нечетное число:
Например: \(5 \times 3 = \)
Вы должны вычесть единицу из числа, умноженного на \( 5,\), что означает число \(3 – 1 = 2. \)
\)
Теперь снова нужно разделить пополам число \(2\), что означает \(2 – 1 = 1,\), и добавить цифру \ (5\) рядом с цифрой \(1,\), которая дает \(5 \times 3 = 15\)
Деление
Например: Деление на \(5:\) Здесь вам нужно просто- просто умножьте число на \(2\), а затем разделите полученное произведение на число \(10.\)
Если вы делите число \(65432\) на \(5\), то
Вы будете писать как \(65432 \div 5 = \left( {65432 \times 2} \right) \div 10 = 130864 \ деление 10 = 13086,4\)
Q.2. Объясните умножение и деление на примере?
Ответ: При умножении чисел мы находим произведение заданных чисел путем их умножения.
Пример: \(3 \times 10 = 30\) или \(10 + 10 + 10 = 30\)
При делении мы делим числа, чтобы получить недостающий множитель, когда заданы два других множителя. Деление также известно как повторное вычитание.
Пример: \(56 \дел 7 = 8,\,56 \дел 8 = 7\) или \(56 – 8 – 8 – 8 – 8 – 8 – 8 – 8. \)
\)
Q.3. Какие \(4\) способы показать умножение?
Ответ: 1. Умножьте числа, используя многократное сложение
2. Умножьте числа, используя метод длинного умножения.
3. Умножьте числа, используя метод сетки.
4. Умножить числа, разделив числа на единицы, десятки, сотни (по разрядности).
Q.4. Какие символы используются для умножения?
Ответ: Символ, который мы используем для представления умножения, — это знак креста \(\left( \times \right),\), а иногда мы также используем точку \(\left( * \right) \) для представления произведения чисел.
Q.5. Какие символы обозначают умножение и деление?
Ответ: Символ, который мы используем для умножения, — это знак креста \(\left( \times \right),\), а иногда мы также используем точку \(\left( \cdot \right) \) или \(\left( * \right)\) для представления произведения чисел. Символ, который используется для деления чисел: \( \div .\)
Символ, который используется для деления чисел: \( \div .\)
Уметь делить дроби здесь
Мы надеемся, что эта подробная статья об умножении и делении поможет вам в подготовке. Если вы застряли, сообщите нам об этом в разделе комментариев ниже, и мы свяжемся с вами в ближайшее время.
Практические вопросы по умножению и делению с советами и решениями
10.6: Умножение и деление чисел со знаком
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 48897
- Денни Бурзински и Уэйд Эллис-младший
- Колледж Южной Невады 900 04X через OpenStax 04X
Цели обучения
- уметь умножать и делить числа со знаком
- уметь умножать и делить числа со знаком с помощью калькулятора
Умножение чисел со знаком
Рассмотрим сначала произведение двух положительных чисел.
 Умножить: \(3\cdot 5\).
Умножить: \(3\cdot 5\).\(3 \cdot 5\) означает \(5 + 5 + 5 = 15\)
Это предполагает, что (В более поздних курсах математики слово «предполагает» превращается в слово «доказательство». доказывать утверждение Математические доказательства строятся для проверки утверждения во всех возможных случаях.)
\(\text{(положительное число)} \cdot \text{(положительное число)} = \text{(положительное число)}\)
Короче говоря,
(+) (+) = (+)
Теперь рассмотрим произведение положительного числа на отрицательное. Умножение: (3)(-5)
(3)(-5) означает (-5) + (-5) + (-5) = -15
Отсюда следует, что
\(\text{(положительно число)} \cdot \text{(отрицательное число)} = \text{(отрицательное число)}\)
Более кратко,
(+) (-) = (-)
По коммутативному свойству умножения, мы получаем
\(\text{(отрицательное число)} \cdot \text{(положительное число)} = \text{(отрицательное число)}\)
Короче говоря,
(-) (+) = (-)
Знак произведения двух отрицательных чисел можно предположить, взглянув на следующую иллюстрацию.

Умножить -2 соответственно на 4, 3, 2, 1, 0, -1, -2, -3, -4.
У нас есть следующие правила умножения чисел со знаком.
Правила умножения подписанных Чисел
Умножение чисел со знаком:- Чтобы умножить два действительных числа, имеющих одинаковый знак , умножьте их абсолютные значения. Продукт положительный.
(+) (+) = (+)
(-) (-) = (+) - Чтобы умножить два действительных числа, которые имеют противоположных знаков , умножьте их абсолютные значения. Произведение отрицательное.
(+) (-) = (-)
(-) (+) = (-)
Набор образцов A
Найдите следующие продукты.
\(8 \cdot 6\)
Решение
\(\begin{array} {ccl} {|8|} & = & {8} \\ {|6|} & = & {6} \end{array} \big \} \) Умножьте эти абсолютные значения.
\(8 \cdot 6 = 48\)
Так как числа имеют один и тот же знак, произведение положительное.

Таким образом, \(8 \cdot 6 = +48\), или \(8 \cdot 6 = 48\).
Набор образцов A
(-8)(-6)
Решение
\(\begin{array} {ccl} {|-8|} & = & {8} \\ {|-6 |} & = & {6} \end{array} \big \}\) Умножьте эти абсолютные значения.
\(8 \cdot 6 = 48\)
Так как числа имеют одинаковый знак, произведение положительное.
Таким образом, \((-8)(-6) = +48\), или \((-8)(-6) = 48\).
Набор образцов A
(-4)(7)
Решение
\(\begin{array} {ccl} {|-4|} & = & {4} \\ {|7|} & = & {7} \end{array} \big \}\) Умножьте эти абсолютные значения.
\(4 \cdot 7 = 28\)
Поскольку числа имеют противоположные знаки, произведение отрицательное.
Таким образом, (-4)(7) = -28.
Набор образцов A
6(-3)
Решение
\(\begin{array} {ccl} {|6|} & = & {6} \\ {|-3|} & = & {3} \end{array} \big \}\) Умножьте эти абсолютные значения.
\(6 \cdot 3 = 18\)
Поскольку числа имеют противоположные знаки, произведение отрицательное.

Таким образом, 6(-3) = -18.
Тренировочный набор A
Найдите следующие продукты.
3(-8)
- Ответить
-24
Тренировочный набор A
4(16)
- Ответить
64
Тренировочный набор A
(-6)(-5)
- Ответить
30
Тренировочный набор A
(-7)(-2)
- Ответить
14
Тренировочный набор A
(-1)(4)
- Ответить
-4
Тренировочный набор A
(-7)7
- Ответить
-49
Деление чисел со знаком
Чтобы определить знаки в задаче на деление, вспомните, что
\(\dfrac{12}{3} = 4\), так как \(12 = 3 \cdot 4\)
Это предполагает что
\(\dfrac{(+)}{(+)} = (+)\)
\(\dfrac{(+)}{(+)} = (+)\), так как (+) = (+ ) (+)
Что такое \(\dfrac{12}{-3}\)?
12 = (-3)(-4) предполагает, что \(\dfrac{12}{-3} = -4\).
 То есть
То есть\(\dfrac{(+)}{(-)} = (-)\)
(+) = (-) (-) предполагает, что \(\dfrac{(+)}{( -)} = (-)\)
Что такое \(\dfrac{-12}{3}\)?
-12 = (3)(-4) предполагает, что \(\dfrac{-12}{3} = -4\). То есть
\(\dfrac{(-)}{(+)} = (-)\)
(-) = (+) (-) предполагает, что \(\dfrac{(-)}{( +)} = (-)\)
Что такое \(\dfrac{-12}{-3}\)?
-12 = (-3)(4) предполагает, что \(\dfrac{-12}{-3} = 4\). То есть
\(\dfrac{(-)}{(-)} = (+)\)
(-) = (-)(+) предполагает, что \(\dfrac{(-)}{( -)} = (+)\)
У нас есть следующие правила деления чисел со знаком.
Правила деления чисел со знаком
Деление чисел со знаком:- Чтобы разделить два действительных числа, имеющих один и тот же знак , разделите их абсолютные значения. Коэффициент положительный.
\(\dfrac{(+)}{(+)} = (+)\dfrac{(-)}{(-)} = (+)\) - Чтобы разделить два действительных числа, которые имеют противоположных знаков , разделите их абсолютные значения.
 Коэффициент отрицательный.
Коэффициент отрицательный.
\(\dfrac{(-)}{(+)} = (-)\dfrac{(+)}{(-)} = (-)\)
Набор образцов B
Найдите следующие частные.
\(\dfrac{-10}{2}\)
Решение
\(\begin{array} {ccc} {|-10|} & = & {10} \\ {|2| } & = & {2} \end{array} \big \}\) Разделите эти абсолютные значения.
\(\dfrac{10}{2} = 5\)
Поскольку числа имеют противоположные знаки, частное отрицательно.
Таким образом, \(\dfrac{-10}{2} = -5\).
Набор образцов B
\(\dfrac{-35}{-7}\)
Решение
\(\begin{array} {ccc} {|-35|} & = & {35} \\ {|-7|} & = & {7} \end{массив} \big \}\) Разделите эти абсолютные значения.
\(\dfrac{35}{7} = 5\)
Поскольку числа имеют одинаковые знаки, частное положительно.
Таким образом, \(\dfrac{-35}{-7} = 5\).
Набор образцов B
\(\dfrac{18}{-9}\)
Решение
\(\begin{array} {ccc} {|18|} & = & {18} \\ {|-9|} & = & {9} \end{массив} \big \}\) Разделите эти абсолютные значения.

\(\dfrac{18}{9} = 2\)
Поскольку числа имеют противоположные знаки, частное отрицательно.
Таким образом, \(\dfrac{18}{-9} = -2\).
Тренировочный набор B
Найдите следующие частные.
\(\dfrac{-24}{-6}\)
- Ответить
4
Практический набор B
\(\dfrac{30}{-5}\)
- Ответить
-6
Практический набор B
\(\dfrac{-54}{27}\)
- Ответить
-2
Практический набор B
\(\dfrac{51}{17}\)
- Ответить
3
Набор образцов C
Найдите значение \(\dfrac{-6(4 — 7) — 2(8 — 9)}{-(4 + 1) + 1}\).
Решение
Используя порядок операций и то, что мы знаем о числах со знаком, мы получаем,
\(\begin{array} {rcl} {\dfrac{-6(4 — 7) — 2(8 — 9)}{-(4 + 1) + 1}} & = & {\dfrac{-6(-3) — 2(-1)}{-(5) + 1}} \\ {} & = & {\dfrac{18 + 2}{-5 + 1}} \\ {} & = & {\dfrac{20}{-4}} \\ {} & = & {-5} \end{array} \)
Тренировочный набор C
Найдите значение \(\dfrac{-5(2-6)-4(-8-1)}{2(3-10)-9(-2)}\).

- Ответить
14
Калькуляторы
Калькуляторы с ключом
можно использовать для умножения и деления чисел со знаком.
Набор образцов D
Используйте калькулятор, чтобы найти каждое частное или произведение.
\((-186) \cdot (-43)\)
Решение
Поскольку этот продукт включает \(\text{(отрицательное)} \cdot \text{(отрицательное)}\), мы знаем, что результатом должно быть положительное число. Мы проиллюстрируем это на калькуляторе.
Дисплей считывает Тип 186 186 Пресс -186 Пресс \(\раз\) -186 Тип 43 43 Пресс -43 Пресс = 7998 Таким образом, \((-186) \cdot (-43) = 7,998\)
Образец набора D
\(\dfrac{158.
 64}{-54.3}\). Округлить до одного десятичного знака.
64}{-54.3}\). Округлить до одного десятичного знака.Решение
Поскольку этот продукт включает \(\text{(отрицательный)} \cdot \text{(отрицательный)}\), мы знаем, что результатом должно быть положительное число. Мы проиллюстрируем это на калькуляторе.
Дисплей считывает Тип 158,64 158,64 Пресс \(\дел\) 158,64 Тип 54,3 54,3 Пресс -54,3 Пресс = -2, 6961Округляя до одного десятичного знака получаем -2,9.
Тренировочный набор D
Используйте калькулятор, чтобы найти каждое значение.

\((-51.3) \cdot (-21.6)\)
- Ответить
1 108,08
Тренировочный набор D
\(-2.5746 \дел -2.1\)
- Ответить
1,226
Тренировочный набор D
\((0,006) \cdot (-0,241)\). Округлить до трех знаков после запятой.
- Ответить
-0,001
Упражнения
Найдите значение каждого из следующих. Используйте калькулятор, чтобы проверить каждый результат.
Упражнение \(\PageIndex{1}\)
(-2)(-8)
- Ответить
16
Упражнение \(\PageIndex{2}\)
(-3)(-9)
Упражнение \(\PageIndex{3}\)
(-4)(-8)
- Ответить
32
Упражнение \(\PageIndex{4}\)
(-5)(-2)
Упражнение \(\PageIndex{5}\)
(3)(-12)
- Ответить
-36
Упражнение \(\PageIndex{6}\)
(4)(-18)
Упражнение \(\PageIndex{7}\)
(10)(-6)
- Ответить
-60
Упражнение \(\PageIndex{8}\)
(-6)(4)
Упражнение \(\PageIndex{9}\)
(-2)(6)
- Ответить
-12
Упражнение \(\PageIndex{10}\)
(-8)(7)
Упражнение \(\PageIndex{11}\)
\(\dfrac{21}{7}\)
- Ответить
3
Упражнение \(\PageIndex{12}\)
\(\dfrac{42}{6}\)
Упражнение \(\PageIndex{13}\)
\(\dfrac{-39}{3}\)
- Ответить
-13
Упражнение \(\PageIndex{14}\)
\(\dfrac{-20}{10}\)
Упражнение \(\PageIndex{15}\)
\(\dfrac{-45}{-5}\)
- Ответить
9
Упражнение \(\PageIndex{16}\)
\(\dfrac{-16}{-8}\)
Упражнение \(\PageIndex{17}\)
\(\dfrac{25}{-5}\)
- Ответить
-5
Упражнение \(\PageIndex{18}\)
\(\dfrac{36}{-4}\)
Упражнение \(\PageIndex{19}\)
8 — (-3)
- Ответить
11
Упражнение \(\PageIndex{20}\)
14 — (-20)
Упражнение \(\PageIndex{21}\)
20 — (-8)
- Ответ
28
Упражнение \(\PageIndex{22}\)
(-4) — (-1)
Упражнение \(\PageIndex{23}\)
0 — 4
- Ответить
-4
Упражнение \(\PageIndex{24}\)
0 — (-1)
Упражнение \(\PageIndex{25}\)
-6 + 1 — 7
- Ответить
-12
Упражнение \(\PageIndex{26}\)
15 — 12 — 20
Упражнение \(\PageIndex{27}\)
1 — 6 — 7 + 8
- Ответить
-4
Упражнение \(\PageIndex{28}\)
2 + 7 — 10 + 2
Упражнение \(\PageIndex{29}\)
3(4 — 6)
- Ответить
-6
Упражнение \(\PageIndex{30}\)
8(5 — 12)
Упражнение \(\PageIndex{31}\)
-3(1 — 6)
- Ответить
15
Упражнение \(\PageIndex{32}\)
-8(4 — 12) + 2
Упражнение \(\PageIndex{33}\)
-4(1-8) + 3(10-3)
- Ответить
49
Упражнение \(\PageIndex{34}\)
-9(0-2) + 4(8-9) + 0(-3)
Упражнение \(\PageIndex{35}\)
6(-2 — 9) — 6(2 + 9) + 4(-1 — 1)
- Ответить
-140
Упражнение \(\PageIndex{36}\)
\(\dfrac{3(4 + 1) — 2 (5)}{-2}\)
Упражнение \(\PageIndex{37}\)
\(\dfrac{4(8 + 1) — 3 (-2)}{-4 — 2}\)
- Ответить
-7
Упражнение \(\PageIndex{38}\)
\(\dfrac{-1(3 + 2) + 5}{-1}\)
Упражнение \(\PageIndex{39}\)
\(\dfrac{-3(4 — 2) + (-3)(-6)}{-4}\)
- Ответить
-3
Упражнение \(\PageIndex{40}\)
-1(4 + 2)
Упражнение \(\PageIndex{41}\)
-1(6 — 1)
- Ответить
-5
Упражнение \(\PageIndex{42}\)
92\).
Упражнение \(\PageIndex{45}\)
Найдите \(\dfrac{3}{8}\) из \(\dfrac{32}{9}\).
- Ответить
\(\dfrac{4}{3} = 1 \dfrac{1}{3}\)
Упражнение \(\PageIndex{46}\)
Запишите это число в десятичной форме, используя цифры: «пятьдесят две трехтысячных»
Упражнение \(\PageIndex{47}\)
Отношение хлора к воде в растворе составляет 2 к 7. Сколько мл воды содержится в растворе, содержащем 15 мл хлора?
- Ответить
\(52 \dfrac{1}{2}\)
Упражнение \(\PageIndex{48}\)
Выполнить вычитание -8 — (-20)
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Денни Бурзински и Уэйд Эллис-младший
- Лицензия
- СС BY
- Показать страницу TOC
- нет
- Метки

Методы умножения и деления – объяснение, методы и примеры решений
Умножение и деление чисел являются основой математики. Все проблемы математики зависят от умножения и деления чисел. Предположим, вы хотите раздать 5 шоколадок 15 своим друзьям. Сколько всего шоколадок вам нужно? что вы сделаете, чтобы получить результат, который вы прибавите 5, 15 раз, не так ли. Но умножение — это сокращение от многократного сложения. Используя умножение, вы можете напрямую умножить 15 × 5 = 75. Распределить — это не так просто и быстро. Точно так же, если вы хотите распределить 60 шоколадок поровну между 20 друзьями, как вы будете считать? А вот и деление, деление позволит вам легко найти это 60 ÷ 20 = 3. Таким образом, вы можете раздать каждому из них по 3 шоколадки. Но чтобы понять умножение и деление, необходимо запомнить таблицу умножения чисел.
Итак, давайте изучим, что такое умножение, и как делить число, и способы деления.

Что такое умножение?
Умножение – это арифметическая операция, позволяющая найти произведение двух чисел, в результате которого получится третье число. Умножение положительных целых чисел заключается в добавлении числа к самому себе заданное количество раз. Умножение называется повторным сложением, потому что оно упрощает повторное сложение. Например, 5 + 5 + 5 = 5 × 3 = 15. Однако, поскольку мы умножаем на целые числа, мы также можем умножать на дроби, десятичные дроби и т. д. Например, на рисунке ниже:
Число, которое нужно умножить, называется множимым, здесь 3 — множимое
Число, на которое умножается множимое, называется множителем, здесь 5 — множитель или множитель.
Результат умножения называется произведением, здесь 15 — произведение.
[Изображение будет загружено в ближайшее время]
Методы умножения
Однозначные числа легко умножаются, поскольку мы знаем таблицу умножения.
 А как насчет двузначного умножения, трехзначного умножения и так далее. Итак, давайте изучим простой метод умножения двух или более цифр.
А как насчет двузначного умножения, трехзначного умножения и так далее. Итак, давайте изучим простой метод умножения двух или более цифр.Умножение с помощью сетки
Пример: Найдите произведение 48 и 9
Шаг 1: Разделите 48 на 40 и 8
Шаг 2: Поместите числа в сетку
Шаг 3: умножьте 9 на 40 = 360 and place it below 40
Step 4: multiply 9 by 8 = 72 place it below 8
40
8
9
360
72
Шаг 5: Добавить 360 и 72 = 432
Следовательно, 48 x 9 = 432
Способность, с использованием колонны
. с большими числами.
Пример: 469 x 32
Решение:
Шаг 1: Запишите числа друг над другом.

Шаг 2: Начнем с тех, что расположены под последним номером. Это 2 из 32. Мы умножаем 2 на 469.и запишите его под чертой.
[Изображение будет загружено в ближайшее время]
Шаг 3: Поставьте ноль в разряде десятков
[Изображение будет загружено в ближайшее время]
Шаг 4: Умножьте 3 на верхнее число (469) и запишите это число рядом с ноль.
[Изображение будет загружено в ближайшее время]
Шаг 5: Если бы было больше чисел, мы бы добавили больше строк и продолжили бы добавлять больше нулей. Например, если бы в разряде сотен стояла цифра 3 (т. е. число внизу было 332), мы бы добавили два нуля в следующей строке, а затем умножили бы 469.на 3.
Шаг 6: После того, как мы умножили все числа внизу, мы складываем ряды чисел, чтобы получить ответ.
[Изображение будет загружено в ближайшее время]
Деление — это повторное вычитание.
 Деление означает деление на равные части,
Деление означает деление на равные части, В процессе деления число, которое должно быть разделено, называется делимым. Число, которое делится, называется делителем. Число раз, которое делитель делит делимое, является частным, а число, оставшееся после деления, называется остатком.
[Изображение будет загружено в ближайшее время]
Например, на приведенном выше рисунке делимое равно 68, делитель равен 5, частное равно 13, а остаток равен 0.
Методы деления
Как разделить 425 ÷ 5
Решение:
Шаг 1: Запишите делитель, равный 5, перед скобкой деления, а делимое (425) под ним.
5)425
Шаг 2. Рассмотрим первую цифру делимого, которая равна 4. Она меньше 5, поэтому мы не можем разделить ее на 5, поэтому возьмите первые два числа делимого (42) и определите, сколько 5′ держит. В этом случае 42 содержит пять восьмерок (5*8=40), но не (5*9=45).
 Запишите 8 как частное над скобкой деления.
Запишите 8 как частное над скобкой деления.8
5)425
Шаг 3: Умножьте 5 на 8 и запишите результат (40) под 42 делимого.
8
5)425
40
Шаг 4: Поставьте черту под 40 и вычтите ее из 42 (42-40=2) и запишите 2 под 40 делимого. Запишите следующее число, то есть 5 из 425, и запишите его справа от 2.
8
5)425
— 40
——-
25
Шаг 5: Разделите 25 на 5. В этом случае 25 содержит пять пятерок. Запишите 5 рядом с 8 как частное над скобкой деления справа от 8. 5 частного на делитель, равный 5, и запишите результат под делимым. Вычтите 25 из 25, чтобы получить ответ 0. Это приводит к тому, что ничего не остается, и 5 можно поровну разделить на 425, чтобы получить частное 85.
85
5) 425
40
——
25
25
———
00
SELED.

Решение:
5 6 2
X 2 2
——————
1 1 2 4
79 6 0 2 1 1 4 1 2 ———————
1 2 3 6 4
2. Разделить 342 ÷ 6
Решение:
5 7
6 ) 3 4 2
3 0
————
4 2
4 2
— —— —
0 0
Quiz Time
Multiply
67 x 7
561 x 89
Divide
678 ÷ 7
543 ÷ 5
Забавные факты
Китайский метод умножения первоначально включал использование бамбуковых палочек, чтобы помочь им с умножением, располагая их горизонтально и вертикально.

Деление обратное умножению.
Умножение и деление
Умножение и делениеБольше практики
Предположим, что население небольшого города составляет примерно 3,0 х 10 4 человек (это 30 000, но мы написали это таким образом, чтобы подчеркнуть, что мы не уверены в населения во второй цифре числа мы имеем два значащих фигуры). В этом же городе 1,15 х 10 4 (или 11 500 с тремя значащие цифры) дома. Означает ли это, что в среднем 2,608695652174 человека в каждом доме? Это может быть математический ответ, который вы получите разделить количество людей на количество домов, но это не имеет особого смысла отвечать. Где мы должны округлить это?
Этот ответ исходит из правила для значащих цифр, используемых при умножении и подразделение:
Ответ округлить до кратчайшего числа значащих цифры в числах, которые вы умножаете или делите. 
Наименьшее количество значащих цифр равно 2 (в 3,0 x 10 4 ). Это означает, что правильный способ сообщить ответ состоит в том, что в среднем 2,6 человека. за дом в этом городе, который тоже имеет 2 значащие цифры. Вот как происходит расчет сделано (цветовая кодировка используется на следующей диаграмме, чтобы проиллюстрировать важные цифры).
Необработанный ответ необходимо округлить до двух значащих цифр, поскольку более короткая из числа, которые мы используем (3,0 x 10 4 человека), имеют только две значащие цифры.
Обычно рекомендуется выполнять вычисления, как если бы значащих цифр не существовало, то округлить ответ до правильные значащие цифры после завершения всех вычислений. Нажмите здесь, чтобы узнать, почему правило для значащих цифр работает с умножением и делением.

Вот еще несколько примеров (синяя подсветка показывает меньшее количество значимых цифры):
Что такое (104,250 x 2,26) / 15,553?
Номер Номер
Значащие цифрыИсходный ответ Округленный ответ 104.250 6
(235,605)/15,553 = 15,14852440044
15,1 2,26 3
15.553 5
Что такое (0,002450 * 0,1478) / 0,120?
Номер Количество
Значащие цифрыИсходный ответ Округленный ответ 0,002450 4
(0,00036211) /0,120 = 0,003017583333333
0,00302 0,1478 4
0,120 3
В каждом случае обратите внимание, что ответ округляется до НАИМЕНЬШЕГО ЧИСЛА значащие цифры.

Как сообщать следующее? Предположим, что каждый число — это экспериментальный результат с правильным количеством значащих цифр. (32,987 x 0,23) / 5,0000 =
0,10246 х 0,0100 = Нет никакой разницы в работе с числами, записанными в экспоненциальном представлении. В на самом деле, это проще, потому что никогда не возникает путаницы в том, являются ли нули значительным или нет. Просто посчитайте количество цифр в самом коротком экспериментальном число, умножить (или разделить) числа, а затем округлить ответ до кратчайшего количество цифр.
Что такое (3,125 х 10 -6 ) х (2,50 х 10 -5 )?
Номер Количество
Значащие цифрыИсходный ответ Округленный ответ 3,125 x 10 -6 4
7,8125 x 10 -11 7,81 x 10 -11 2,50 x 10 -5 3
Что такое (1,3568 x 10 -3 x 2,6554) / 3,266 x 10 -7 ?
Номер Количество
Значащие цифрыИсходный ответ Округленный ответ 1,3568 x 10 -3 5
3,60284672 х 10 -3 =
3,266 х 10 -71,1031373
- х
10 4
1,103 x 10 4 2,6554 5
3,266 x 10 -7 4
Как сообщать следующее? Предположим, что каждый число — это экспериментальный результат с правильным количеством значащих цифр.  Убедиться
вы отвечаете в экспоненциальном представлении (например 1.23Е-45).
Убедиться
вы отвечаете в экспоненциальном представлении (например 1.23Е-45).3,2987 x 10 3 х 2,3 х 10 4 =
1,02467 х 10 -8 / 1,06 х 10 -11 = Сделайте еще несколько примеров для практики
Умножение и деление — предварительная алгебра
Все ресурсы предварительной алгебры
11 Диагностические тесты 177 практических тестов Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 3 4 Следующая →
Предварительная алгебра Справка » Операции и свойства » Операции » Умножение и деление
Выразите в градусах: радианы
Возможные ответы:
Правильный ответ:
Объяснение:
Так как , мы можем преобразовать следующим образом:
Сообщить об ошибке
Предположим, вы знаете значения и и хотите вычислить выражение:
В каком порядке вы бы выполнили четыре операции в выражении?
Возможные ответы:
Умножение, сложение, вычитание, деление
Деление, умножение, вычитание, сложение
Сложение, вычитание, умножение, деление , разделить
Правильный ответ:
Умножить, вычесть, сложить, разделить
Объяснение:
Дробная черта в выражении действует как символ деления и символ группировки, поэтому сначала мы оцениваем числитель.
 В числителе есть умножение, вычитание и сложение, поэтому по порядку операций мы сначала умножаем. Сложение и вычитание выполняются справа налево; вычитание осталось от сложения, поэтому мы сначала вычитаем, а затем прибавляем. Наконец, делим числитель на знаменатель.
В числителе есть умножение, вычитание и сложение, поэтому по порядку операций мы сначала умножаем. Сложение и вычитание выполняются справа налево; вычитание осталось от сложения, поэтому мы сначала вычитаем, а затем прибавляем. Наконец, делим числитель на знаменатель.Вкратце: умножение, вычитание, сложение, деление
Сообщить об ошибке
Максимально упростите следующее:
Возможные ответы:
Правильный ответ:
Объяснение:
Если мы используем метод фольги, мы получим следующее:
Первый:Внутренний:
Внешний:
Последний:
Если это упростить, у нас останется
Сообщить об ошибке
:
Возможные ответы:
Правильный ответ:
Объяснение:
Вся операция возведена в квадрат, поэтому для лучшего понимания, как ее решить, ее можно переписать так:
Используя порядок операций, мы получаем следующее:
Первая:Внутренняя:
Внешняя:
Последняя:
В упрощенном виде мы имеем
Сообщить об ошибке
Упрощение:
Возможные ответы:
Правильный ответ:
Объяснение:
Уравнение можно переписать как
Сначала следует использовать метод фольги, в результате чего мы получим:
Затем 2 можно распределить между каждым из факторов в скобках.
 Выход из решения:
Выход из решения:Сообщить об ошибке
Какое выражение упрощается до
Возможные ответы:
Правильный ответ:
Объяснение:
Результаты при упрощении с помощью метода фольги следующим образом:
Первый:Внутренний:
Внешний:
Последний:
Отчет о ошибке
. Что выражение упрощает до
98
.
Правильный ответ:
Объяснение:
При упрощении с использованием метода FOIL получается следующее:
Первый:
Внутренний:
Внешний:
Последний:
Когда 2 распределены, а выражение упрощено. % комиссии со всех продаж.
 Какова будет его комиссия за неделю, если он продаст три автомобиля на этой неделе: внедорожник за 55 000 долларов во вторник, автомобиль за 28 000 долларов в четверг и фургон за 42 000 долларов в пятницу?
Какова будет его комиссия за неделю, если он продаст три автомобиля на этой неделе: внедорожник за 55 000 долларов во вторник, автомобиль за 28 000 долларов в четверг и фургон за 42 000 долларов в пятницу?Возможных ответов:
Правильный ответ:
Пояснение:
Общая цена продажи автомобилей, которые он продает, составит
.
12% от 125 000 долларов США составляют
,
, что является комиссией продавца.
Сообщить об ошибке
Прочитайте следующую проблему, но не решайте ее.
Согласно завещанию г-на Смита, после его смерти каждому из его шести детей должен быть оставлен участок земли площадью 510 акров. Если эти шесть участков составляют всю ферму, то насколько велика сейчас ферма мистера Смита?
Какое из следующих выражений необходимо вычислить, чтобы ответить на этот вопрос?
Возможные ответы:
Правильный ответ:
Пояснение:
Имеется шесть посылок одинакового размера; Таким образом, общий размер составляет продукта общего размера (510 акров) и количества участков (6).
 Это
Это Сообщить об ошибке
У Бека 5 пар обуви одного и того же стиля, которые называются «пуговицы вверх». На каждом ботинке по 6 пуговиц. Сколько пуговиц в коллекции обуви Бекки «на пуговицах»?
Возможные ответы:
Правильный ответ:
Объяснение:
Если у Бека 5 пар обуви, это означает, что у него 10 туфель, потому что в паре 2 туфельки.
Поскольку на каждом ботинке по 6 пуговиц, значит, в коллекции 60 пуговиц.
Сообщить об ошибке
← Предыдущая 1 2 3 4 Следующая →
Уведомление об авторских правах
Все ресурсы Pre-Algebra
11 диагностических тестов 177 практических тестов Вопрос дня Карточки Learn by Concept
Сложение, вычитание, умножение и деление Повторение — 3-й класс математики
В математике есть 4 основных операции: сложение, вычитание, умножение и деление.

Давайте повторим, что вы узнали о каждом из них. 🤗
Что такое дополнение?
Объединение двух и более чисел называется сложением.
Сложение Уравнение состоит из двух или более сложений , символа плюс (+), символа равенства (=) и суммы .
Попробуем сложить числа.
Дополнение Пример 1
4,255 + 3,104 = ?
Давайте добавим числа, используя форму столбца .
Начните с единиц справа (👉) и решайте столбец за столбцом.

Итак, каков ответ? 🤓
Правильно! Это 7359.
Дополнение Пример 2
675 + 198 = ?
Запишите задачу в виде столбца.
На этот раз нам пришлось перегруппироваться!
Совет: Когда сумма в столбце больше 9, вам нужно перегруппировать !
Отлично! 😎
Теперь приступим к вычитанию.
Обзор вычитания
Вычитание отнимает часть числа.

Попробуем вычесть несколько чисел.
Пример вычитания 1
497 — 251 = ?
Давайте вычтем, используя форму столбца .
Как и в случае сложения, начните со столбца «Единицы».
Какая разница? 🤓
497 — 251 = 246
Хорошая работа! 👏
Пример вычитания 2
7,301 — 6,361 = ?
Вычитаем! На этот раз нам нужно перегруппировать .

Какая тебе разница? 😃
7 301 — 6 361 = 940
Так держать! 🤗
Давайте теперь рассмотрим умножение и деление.
Обзор умножения
Повторное добавление равных групп называется умножением .
👉 Например, если умножить 2 кругов 5 раз, получится 10 кругов.
5 × 2 = 10
Уравнения умножения состоят из множителей и произведения.
Давайте рассмотрим несколько примеров умножения.

Пример умножения 1
9 × 8 = ?
Умножение — это сокращение для повторного сложения .
Это означает Добавить до Сама 8 раз, или ADD до до .
9 × 8 =
9 + 9 + 9 + 9 + 9 + 9 + 9 + 9 = 72Итак,
9 × 8 = 72
Пример умножения 2
256 × 3 = ?
Давайте умножим эти большие числа, используя форму столбца .

Сначала мы умножаем цифру в разряде Единиц на 3.
Затем умножаем цифру в разряде Десятков на 3 и добавляем перенос.
Получаем 16, так что надо переносить на сотни.
Наконец, мы умножаем цифру на Сотни Поместите на 3 и добавьте перенос.
Отличная работа! 👏
Обзор отдела
Подразделение разбивает число на равные группы.
👉 Например, когда мы разбиваем 10 кружков на 5 равных групп, получаем по 2 кружка в каждой группе.

10 ÷ 5 = 2
A деление уравнение имеет делимое , делитель , символ деления (÷ или ⟌) и частное .
Давайте рассмотрим некоторые задачи на деление.
Раздел Пример 1
30 ÷ 6 = ?
Давайте решим это с помощью повторного вычитания.
✅ Мы начинаем с 30 и вычитаем 6 из и из , пока не достигнем 0. Количество раз, которое мы вычитаем, является нашим ответом.
Итак,
30 ÷ 6 = 5
Отлично! 🤗
Совет: Думайте о делении как о противоположности умножения.
 Если вы видите 30 ÷ 6 = ? только подумайте: какое число умножить на 6 будет 30?
Если вы видите 30 ÷ 6 = ? только подумайте: какое число умножить на 6 будет 30?6 х ? = 30
И вы получите тот же ответ: 5!
Раздел Пример 2
882 ÷ 7 = ?
Давайте решим этот вопрос, используя long Division .
✅ Начнем с расстановки чисел в длинном делении.
✅ Сейчас смотри в первой цифре, 8.
Можете ли вы сказать, сколько семерок поместится в 8? 🤔
Очень хорошо! 1.
Write the 1 on top , and write the product of 1 and 7 below the 8.

Now, вычтите этот продукт из 8 , чтобы получить остаток.
Отлично! 😎
Далее, введите следующую цифру и повторите процесс.
Наконец, введите последнюю цифру и повторите процесс.
Какой ответ вы получили?
882 ÷ 7 = 126
Отличная работа! 👏
🎉 Вы только что рассмотрели самые важные моменты о сложении, вычитании, умножении и делении.
А теперь приступайте к практике, которая поможет вам помнить дольше.

 Геометрический материал
Геометрический материал
 Числа и арифметические действия
Числа и арифметические действия 

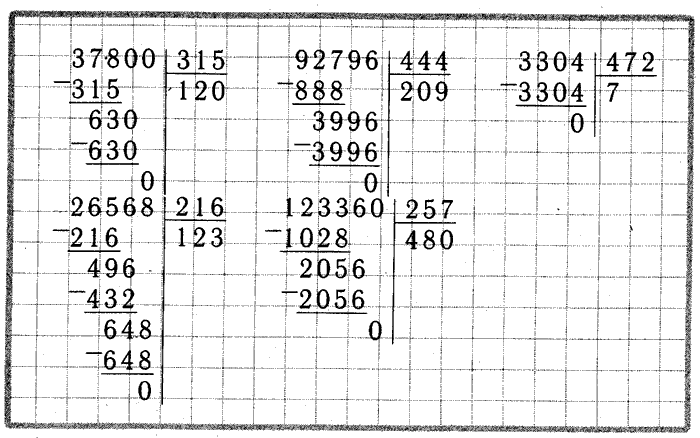 Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям Тогда сносим к единице цифру «6»
Тогда сносим к единице цифру «6» Ответ будет 8
Ответ будет 8 Найди его за минуту.
Найди его за минуту. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго. Обычно оно состоит из одной цифры, максимум из двух.
Обычно оно состоит из одной цифры, максимум из двух.
