Примеры на умножение с десятичными дробями. Дроби

Чтобы понять, как умножать десятичные дроби, рассмотрим конкретные примеры.

Правило умножения десятичных дробей

1) Умножаем, не обращая внимания на запятую.

2) В результате отделяем после запятой столько цифр, сколько их после запятых в обоих множителях вместе.

Примеры .

Найти произведение десятичных дробей:

Чтобы умножить десятичные дроби, умножаем, не обращая внимания на запятые. То есть мы умножаем не 6,8 и 3,4, а 68 и 34. В результате отделяем после запятой столько цифр, сколько их после запятых в обоих множителях вместе. В первом множителе после запятой одна цифра, во втором — тоже одна. Итого, отделяем после запятой две цифры.Таким образом, получили окончательный ответ: 6,8∙3,4=23,12.

Умножаем десятичные дроби, не принимая во внимание запятую. То есть фактически вместо умножения 36,85 на 1,14 мы умножаем 3685 на 14. Получаем 51590. Теперь в этом результате надо отделить запятой столько цифр, сколько их в обоих множителях вместе.

В первом числе после запятой две цифры, во втором — одна. Итого, отделяем запятой три цифры. Поскольку в конце записи после запятой стоит нуль, в ответ мы его не пишем: 36,85∙1,4=51,59.

Чтобы умножить эти десятичные дроби, умножим числа, не обращая внимания на запятые. То есть умножаем натуральные числа 2315 и 7. Получаем 16205. В этом числе нужно отделить после запятой четыре цифры — столько, сколько их в обоих множителях вместе (в каждом — по два). Окончательный ответ: 23,15∙0,07=1,6205.

Умножение десятичной дроби на натуральное число выполняется аналогично. Умножаем числа, не обращая внимания на запятую, то есть 75 умножаем на 16. В полученном результате после запятой должно стоять столько же знаков, сколько их в обоих множителях вместе — один. Таким образом, 75∙1,6=120,0=120.

Умножение десятичных дробей начинаем с того, что умножаем натуральные числа, так как на запятые не обращаем внимания. После этого отделяем после запятой столько цифр, сколько их в обоих множителях вместе.

В первом числе после запятой два знака, во втором — тоже два. Итого, в результате после запятой должно стоять четыре цифры: 4,72∙5,04=23,7888.

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цель урока:

• В увлекательной форме ввести учащимся правило умножения десятичной дроби на натуральное число, на разрядную единицу и правило выражения десятичной дроби в процентах. Выработать умение применения полученных знаний при решении примеров и задач.
• Развивать и активизировать логическое мышление учащихся, умение выявлять закономерности и обобщать их, укреплять память, умение сотрудничать, оказывать помощь, оценивать свою работу и работу друг друга.
• Воспитывать интерес к математике, активность, мобильность, умение общаться.

Оборудование: интерактивная доска, плакат с цифрограммой, плакаты с высказываниями математиков.

Ход урока

1. Организационный момент.
2. Устный счёт – обобщение раннее изученного материала, подготовка к изучению нового материала.
3. Объяснение нового материала.
4. Задание на дом.
5. Математическая физкультминутка.
6. Обобщение и систематизация полученных знаний в игровой форме при помощи компьютера.
7. Выставление оценок.

2. Ребята, сегодня у нас урок будет несколько необычным, потому что я буду проводить его не одна, а со своим другом. И друг у меня тоже необычный, сейчас вы его увидите. (На экране появляется компьютер-мультяшка). У моего друга есть имя и он умеет разговаривать. Как тебя зовут, дружок? Компоша отвечает: “Меня зовут Компоша”. Ты сегодня готов помогать мне? ДА! Ну тогда давай начнём урок.

Мне сегодня пришла зашифрованная цифрограмма, ребята, которую мы должны вместе решить и расшифровать. (На доске вывешивается плакат с устным счётом на сложение и вычитание десятичных дробей, в результате решения которого ребята получают следующий код 523914687. )

5	2	3	9	1	4	6	8	7
1	2	3	4	5	6	7	8	9

Расшифровать полученный код помогает Компоша. В результате расшифровки получается слово УМНОЖЕНИЕ. Умножение – это ключевое слово темы сегодняшнего урока. На мониторе высвечивается тема урока: “Умножение десятичной дроби на натуральное число”

Ребята, мы знаем, как выполняется умножение натуральных чисел. Сегодня мы с вами рассмотрим умножение десятичных чисел на натуральное число. Умножение десятичной дроби на натуральное число можно рассматривать как сумму слагаемых, каждое из которых равно этой десятичной дроби, а количество слагаемых равно этому натуральному числу. Например: 5,21·3 = 5,21 + 5, 21 + 5,21 = 15,63 Значит, 5,21·3 = 15,63. Представив 5,21 в виде обыкновенной дроби на натуральное число, получим

И в этом случае получили тот же результат 15,63. Теперь, не обращая внимания на запятую, возьмём вместо числа 5,21 число 521 и перемножим на данное натуральное число. Здесь мы должны помнить, что в одном из множителей запятая перенесена на два разряда вправо. При умножении чисел 5, 21 и3 получим произведение равное 15,63. Теперь в этом примере запятую перенесём влево на два разряда. Таким образом, во сколько раз один из множителей увеличили, во столько раз уменьшили произведение. На основании сходных моментов этих способов, сделаем вывод.

Чтобы умножить десятичную дробь на натуральное число, надо:
1) не обращая внимания на запятую, выполнить умножение натуральных чисел;

2) в полученном произведении отделить запятой справа столько знаков, сколько их в десятичной дроби.

На мониторе высвечиваются следующие примеры, которые мы разбираем вместе с Компошей и ребятами: 5,21·3 = 15,63 и 7,624·15 = 114,34. После показываю умножение на круглое число 12,6·50 = 630 . Далее перехожу на умножение десятичной дроби на разрядную единицу. Показываю следующие примеры: 7,423·100 = 742,3 и 5,2·1000 = 5200. Итак, ввожу правило умножения десятичной дроби на разрядную единицу:

Чтобы умножить десятичную дробь на разрядные единицы 10, 100, 1000 и т.д., надо в этой дроби перенести запятую вправо на столько знаков, сколько нулей в записи разрядной единицы.

Заканчиваю объяснение выражением десятичной дроби в процентах. Ввожу правило:

Чтобы выразить десятичную дробь в процентах, надо её умножить на 100 и приписать знак %.

Привожу пример на компьютере 0,5·100 = 50 или 0,5 = 50% .

4. По окончании объяснения даю ребятам домашнее задание, которое тоже высвечивается на мониторе компьютера: № 1030, № 1034, № 1032.

5. Чтобы ребята немного отдохнули, на закрепление темы делаем вместе с Компошей математическую физкультминутку. Все встают, показываю классу решённые примеры и они должны ответить, правильно или не правильно решён пример. Если пример решён правильно, то они поднимают руки над головой и делают хлопок ладонями. Если же пример решён не верно, ребята вытягивают руки в стороны и разминают пальчики.

6. А теперь вы немного отдохнули, можно и решить задания. Откройте учебник на странице 205, № 1029. в этом задании надо вычислить значение выражений:

Задания появляются на компьютере.

По мере их решения, появляется картинка с изображением кораблика, который при полной сборке уплывает.

№ 1031 Вычисли:

Решая это задание на компьютере, постепенно складывается ракета, решив последний пример, ракета улетает. Учитель делает небольшую информацию учащимся: “ Каждый год с казахстанской земли с космодрома Байконур взлетают к звёздам космические корабли. Рядом с Байконуром Казахстан строит свой новый космодром “Байтерек”.

№ 1035. Задача.

Какое расстояние пройдёт легковая машина за 4 часа, если скорость легковой машины 74,8 км/ч.

Данная задача сопровождается звуковым оформлением и вынесением на монитор краткого условия задачи. Если задача решена, верно, то машина начинает двигаться вперёд до финишного флажка.

№ 1033. Запиши десятичные дроби в процентах.

0,2 = 20%; 0,5 = 50%; 0,75 = 75%; 0,92 = 92%; 1,24 =1 24%; 3,5 = 350%; 5,61= 561%.

Решая каждый пример, при появлении ответа появляется буква, в результате чего появляется слово

Молодцы .

Учитель спрашивает Компошу, к чему бы появилось это слово? Компоша отвечает: “Молодцы, ребята!” и прощается со всеми.

Учитель подводит итоги урока и выставляет оценки.

1 урок

1. Организационный момент

Проверить готовность учащихся к уроку.

(Наличие учебных принадлежностей к уроку)

I .Актуализация знаний

Устная работа.

Цель: Систематизировать предыдущие знания,необходимые при изучении нового материала.

Учащиеся устно выполняют задания на умножение десятичной дроби на натуральное число и на умножение обыкновенных дробей..

Вычислите:

Затем учитель задает вопрос:Сформулируйте как выполнить умножение десятичной дроби на натуральное число?Учащиеся вспоминают определение.Сообщаются тема урока и цели урока.

II .Одновременное разделение на группы и на пары.

Учащиеся выбирают по одной карточке со стола учителя. На одних из них записаны примеры на действия с обыкновенными дробями, а на других соответствующие ответы. Они должны будут найти соответствия, и разделится на пары.Если же будут работать в группах,то разделятся таким образом:

1 группа- это учащиеся, которым попались примеры,2 группа- это те учащиеся, у которых окажутся соответствующие ответы.(см.Приложение №1)

III .Изучение новогоматериала

Цель: Познакомить учащихся с новым материалом.

Объяснение учителя:

3.1.Групповая работа.

Цель: Самостоятельно решив задачу двумя способами сформулировать правилоумножения десятичной дроби на десятичную дробь.

Учащимся предлагается следующая задача:

Длина прямоугольника 6,3см, ширина 2,8см. Найдите его площадь.

Каждая группа выполняет данное задание по указанному ей предложенному способу.

Способ 1: Записать числовые значения измерений прямоугольника в виде натуральных чисел, выразив в миллиметрах. Вычислять площадь и полученный ответ выразить в квадратных сантиметрах.

Способ 2: Представить измерения прямоугольника в виде обыкновенных дробей, найти площадь, перемножив обыкновенные дроби и перевести в десятичную дробь.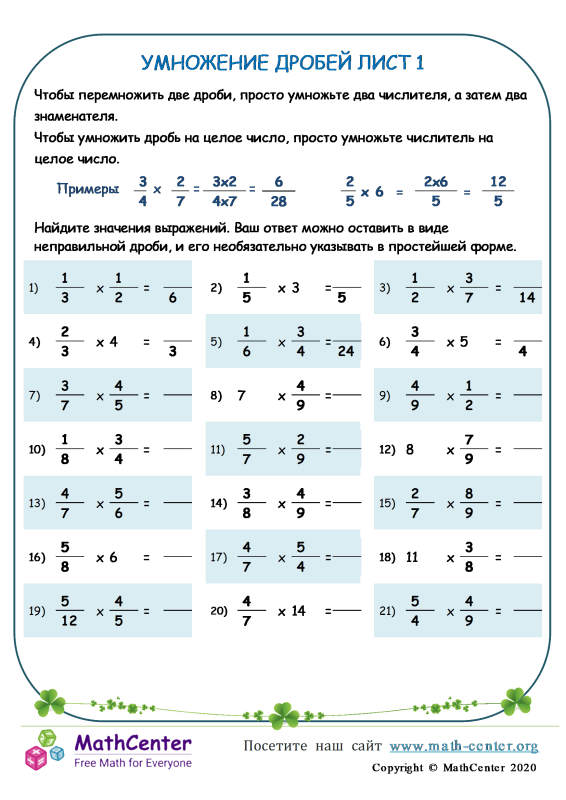

Затем представитель каждой группы объясняет решение данного примера учащимся другой группы у доски. Учащиеся обмениваются мнениями и из результатов решения задачи делают вывод:

Сколько десятичных знаков в множителях, столько же и десятичных знаков в их произведении.

Затем учитель комментирует работу групп, подводит итоги и делает вывод.

Учащиеся записывают в тетрадях для конспектов.

Вывод: Чтобы умножить десятичные дроби надо:

1)выполнить умножение, не обращая внимания на запятые;

2)отделить в полученном произведении запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе.

3.2 Разбор различных примеров.

Цель: Дальнейшая отработка умений выполнять умножение десятичных дробей.

Умножим данные числа не обращая внимания на запятые, получим в произведении число 20 496. В двух множителях после запятой всего имеется три десятичных знака. Поэтому в произведении нужно отделить справа три цифры. Итак, произведение равно 20,496.

VI .Решение задач

Цель: Отработка умений применять правило умножения десятичных дробей при решении задач.

Учащиеся работают в парах.

Выполняют задания: №812 ,№814

VII . Подведение итогов урока. Рефлексия

Цель: Выяснить достигли ли учащиеся целей урока,чтобы учесть при планировании следующего урока.

Действия ученика : Обобщив свои знания, отвечают на вопросы.

Вопросы для подведения итогов .(Устно).

1. Чему мы сегодня научились на уроке?

2. Какую цель мы сегодня на уроке изучили?

3. Повторим правило умножения десятичных дробей.

В конце урока учащиеся дают рефлексию:

Урок понравился / не понравился

Цель урока понял / не понял

Что узнал, чему научился______________________________

Что не понял полностью _______________________________

Над чем надо поработать_______________________________

Оценивание: Учитель поощряет ответы и работы учеников.

Задание на дом: №813 № 815

Как обычные числа.

2. Считаем число знаков после запятой у 1-ой десятичной дроби и у 2-ой. Их число складываем.

3. В итоговом результате отсчитываем справа налево такое число цифр, сколько получилось их в пункте выше, и ставим запятую.

Правила умножения десятичных дробей.

1. Умножить, не обращая внимания на запятую.

2. В произведении отделяем после запятой такое количество цифр, сколько их после запятых в обоих множителях вместе.

Умножая десятичную дробь на натуральное число, необходимо:

1. Умножить числа, не обращая внимания на запятую;

2. В результате ставим запятую так, чтобы справа от нее было столько цифр, сколько в десятичной дроби.

Умножение десятичных дробей столбиком.

Рассмотрим на примере:

Записываем десятичные дроби в столбик и умножаем их как натуральные числа , не обращая внимания на запятые. Т.е. 3,11 мы рассматриваем как 311, а 0,01 как 1.

Результатом является 311. Далее считаем число знаков (цифр) после запятой у обеих дробей. В 1-ой десятичной дроби 2 знака и во 2-рой — 2. Общее число цифр после запятых:

2 + 2 = 4

Отсчитываем справа налево четыре знака у результата. В итоговом результате цифр меньше, чем нужно отделить запятой. В этом случае необходимо слева дописать не хватающее количество нулей.

В нашем случае не достает 1-ой цифры, поэтому дописываем слева 1 ноль.

Обратите внимание:

Умножая любую десятичную дробь на 10, 100, 1000 и так далее, запятая в десятичной дроби переносится вправо на столько знаков, сколько нулей после единицы.

Например :

70,1 . 10 = 701

0,023 . 100 = 2,3

5,6 . 1 000 = 5 600

Обратите внимание:

Для умножения десятичной дроби на 0,1; 0,01; 0,001; и так далее, нужно в этой дроби перенести запятую влево на столько знаков, сколько нулей перед единицей.

Считаем и ноль целых!

Например:

12 . 0,1 = 1,2

0,05 . 0,1 = 0,005

1,256 . 0,01 = 0,012 56

Переходим к изучению следующего действия с десятичными дробями , сейчас мы всесторонне рассмотрим умножение десятичных дробей . Сначала обговорим общие принципы умножения десятичных дробей. После этого перейдем к умножению десятичной дроби на десятичную дробь, покажем, как выполняется умножение десятичных дробей столбиком, рассмотрим решения примеров. Дальше разберем умножение десятичных дробей на натуральные числа, в частности на 10, 100 и т.д. В заключение поговорим об умножении десятичных дробей на обыкновенные дроби и смешанные числа.

Сразу скажем, что в этой статье мы будем говорить лишь об умножении положительных десятичных дробей (смотрите положительные и отрицательные числа). Остальные случаи разобраны в статьях умножение рациональных чисел и умножение действительных чисел .

Навигация по странице.

Общие принципы умножения десятичных дробей

Обсудим общие принципы, которых следует придерживаться при проведении умножения с десятичными дробями.

Так как конечные десятичные дроби и бесконечные периодические дроби являются десятичной формой записи обыкновенных дробей, то умножение таких десятичных дробей по сути является умножением обыкновенных дробей . Иными словами, умножение конечных десятичных дробей , умножение конечной и периодической десятичных дробей , а также умножение периодических десятичных дробей сводится к умножению обыкновенных дробей после перевода десятичных дробей в обыкновенные .

Рассмотрим примеры применения озвученного принципа умножения десятичных дробей.

Пример.

Выполните умножение десятичных дробей 1,5 и 0,75 .

Решение.

Заменим умножаемые десятичные дроби соответствующими обыкновенными дробями. Так как 1,5=15/10 и 0,75=75/100 , то . Можно провести сокращение дроби , после чего выделить целую часть из неправильной дроби , а удобнее полученную обыкновенную дробь 1 125/1 000 записать в виде десятичной дроби 1,125 .

Ответ:

1,5·0,75=1,125 .

Следует отметить, что конечные десятичные дроби удобно умножать столбиком, об этом способе умножения десятичных дробей мы поговорим в .

Рассмотрим пример умножения периодических десятичных дробей.

Пример.

Вычислите произведение периодических десятичных дробей 0,(3) и 2,(36) .

Решение.

Выполним перевод периодических десятичных дробей в обыкновенные дроби:

Тогда . Можно полученную обыкновенную дробь перевести в десятичную дробь :

Ответ:

0,(3)·2,(36)=0,(78) .

Если среди умножаемых десятичных дробей присутствуют бесконечные непериодические, то все умножаемые дроби, в том числе конечные и периодические, следует округлить до некоторого разряда (смотрите округление чисел ), после чего выполнять умножение полученных после округления конечных десятичных дробей.

Пример.

Выполните умножение десятичных дробей 5,382… и 0,2 .

Решение.

Сначала округлим бесконечную непериодическую десятичную дробь, округление можно провести до сотых, имеем 5,382…≈5,38 . Конечную десятичную дробь 0,2 округлять до сотых нет необходимости. Таким образом, 5,382…·0,2≈5,38·0,2 . Осталось вычислить произведение конечных десятичных дробей: 5,38·0,2=538/100·2/10= 1 076/1 000=1,076 .

Ответ:

5,382…·0,2≈1,076 .

Умножение десятичных дробей столбиком

Умножение конечных десятичных дробей можно выполнять столбиком, аналогично умножению столбиком натуральных чисел .

Сформулируем правило умножения десятичных дробей столбиком . Чтобы умножить десятичные дроби столбиком, надо:

• не обращая внимания на запятые, выполнить умножение по всем правилам умножения столбиком натуральных чисел;
• в полученном числе отделить десятичной запятой столько цифр справа, сколько десятичных знаков в обоих множителях вместе, при этом если в произведении не хватает цифр, то слева нужно дописать нужное количество нулей.

Рассмотрим примеры умножения десятичных дробей столбиком.

Пример.

Выполните умножение десятичных дробей 63,37 и 0,12 .

Решение.

Проведем умножение десятичных дробей столбиком. Сначала умножаем числа, не обращая внимания на запятые:

Осталось в полученном произведении поставить запятую. Ей нужно отделить 4 цифры справа, так как в множителях в сумме четыре десятичных знака (два в дроби 3,37 и два в дроби 0,12 ). Цифр там хватает, поэтому нулей слева дописывать не придется. Закончим запись:

В итоге имеем 3,37·0,12=7,6044 .

Ответ:

3,37·0,12=7,6044 .

Пример.

Вычислите произведение десятичных дробей 3,2601 и 0,0254 .

Решение.

Выполнив умножение столбиком без учета запятых, получаем следующую картину:

Теперь в произведении нужно отделить запятой 8 цифр справа, так как общее количество десятичных знаков умножаемых дробей равно восьми. Но в произведении только 7 цифр, поэтому, нужно слева приписать столько нулей, чтобы можно было отделить запятой 8 цифр. В нашем случае нужно приписать два нуля:

На этом умножение десятичных дробей столбиком закончено.

Ответ:

3,2601·0,0254=0,08280654 .

Умножение десятичных дробей на 0,1, 0,01, и т.д.

Довольно часто приходится умножать десятичные дроби на 0,1 , 0,01 и так далее. Поэтому целесообразно сформулировать правило умножения десятичной дроби на эти числа, которое следует из рассмотренных выше принципов умножения десятичных дробей.

Итак, умножение данной десятичной дроби на 0,1 , 0,01 , 0,001 и так далее дает дробь, которая получается из исходной, если в ее записи перенести запятую влево на 1 , 2 , 3 и так далее цифр соответственно, при этом если не хватает цифр для переноса запятой, то нужно слева дописать необходимое количество нулей.

Например, чтобы умножить десятичную дробь 54,34 на 0,1 , надо в дроби 54,34 перенести запятую влево на 1 цифру, при этом получится дробь 5,434 , то есть, 54,34·0,1=5,434 . Приведем еще один пример. Умножим десятичную дробь 9,3 на 0,0001 . Для этого нам нужно в умножаемой десятичной дроби 9,3 перенести запятую на 4 цифры влево, но запись дроби 9,3 не содержит такого количества знаков.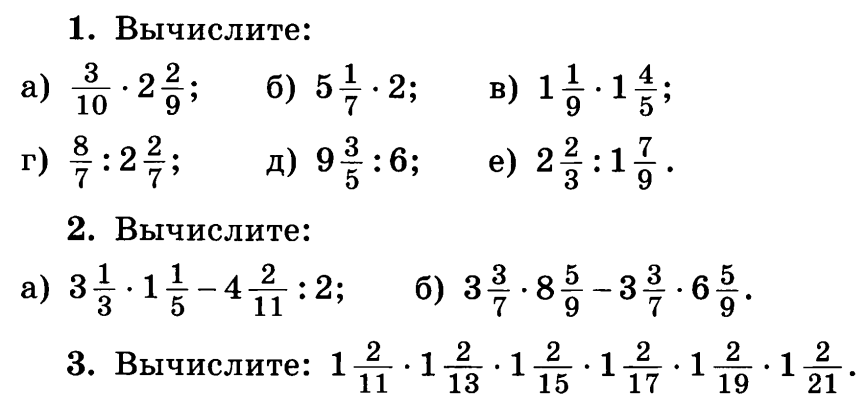 Поэтому нам нужно в записи дроби 9,3 слева приписать столько нулей, чтобы можно было беспрепятственно осуществить перенос запятой на 4 цифры, имеем 9,3·0,0001=0,00093 .

Заметим, что озвученное правило умножения десятичной дроби на 0,1, 0,01, … справедливо и для бесконечных десятичных дробей. К примеру, 0,(18)·0,01=0,00(18) или 93,938…·0,1=9,3938… .

Умножение десятичной дроби на натуральное число

По своей сути умножение десятичных дробей на натуральные числа ничем не отличается от умножения десятичной дроби на десятичную дробь.

Конечную десятичную дробь умножать на натуральное число удобнее всего столбиком, при этом следует придерживаться правил умножения столбиком десятичных дробей, рассмотренных в одном из предыдущих пунктов.

Пример.

Вычислите произведение 15·2,27 .

Решение.

Проведем умножение натурального числа на десятичную дробь столбиком:

Ответ:

15·2,27=34,05 .

При умножении периодической десятичной дроби на натуральное число, периодическую дробь следует заменить обыкновенной дробью.

Пример.

Умножьте десятичную дробь 0,(42) на натуральное число 22 .

Решение.

Сначала переведем периодическую десятичную дробь в обыкновенную дробь:

Теперь выполним умножение: . Этот результат в виде десятичной дроби имеет вид 9,(3) .

Ответ:

0,(42)·22=9,(3) .

А при умножении бесконечной непериодической десятичной дроби на натуральное число нужно предварительно провести округление.

Пример.

Выполните умножение 4·2,145… .

Решение.

Округлив до сотых исходную бесконечную десятичную дробь, мы придем к умножению натурального числа и конечной десятичной дроби. Имеем 4·2,145…≈4·2,15=8,60 .

Ответ:

4·2,145…≈8,60 .

Умножение десятичной дроби на 10, 100, …

Довольно часто приходится умножать десятичные дроби на 10, 100, … Поэтому целесообразно подробно остановиться на этих случаях.

Озвучим правило умножения десятичной дроби на 10, 100, 1 000 и т.д. При умножении десятичной дроби на 10, 100, … в ее записи нужно перенести запятую вправо на 1, 2, 3, … цифры соответственно и отбросить лишние нули слева; если в записи умножаемой дроби не хватает цифр для переноса запятой, то нужно дописать необходимое количество нулей справа.

Пример.

Умножьте десятичную дробь 0,0783 на 100 .

Решение.

Перенесем в записи дроби 0,0783 на две цифры вправо, при этом получим 007,83 . Отбросив два нуля слева, получаем десятичную дробь 7,38 . Таким образом, 0,0783·100=7,83 .

Ответ:

0,0783·100=7,83 .

Пример.

Выполните умножение десятичной дроби 0,02 на 10 000 .

Решение.

Чтобы умножить 0,02 на 10 000 , нам нужно перенести запятую на 4 цифры вправо. Очевидно, в записи дроби 0,02 не хватает цифр для переноса запятой на 4 цифры, поэтому допишем несколько нулей справа, чтобы можно было осуществить перенос запятой. В нашем примере достаточно дописать три нуля, имеем 0,02000 . После переноса запятой получим запись 00200,0 . Отбросив нули слева, имеем число 200,0 , которое равно натуральному числу 200 , оно и является результатом умножения десятичной дроби 0,02 на 10 000 .

Попробуйте решить простой пример по математике с дробью

В Японии завирусилось одно простое уравнение с дробями из начальной школы, которое ввело в ступор не только детей, но и многих взрослых. Тысячи людей пытались одолеть его, но не каждому эта задачка пришлась по зубам. Давайте посмотрим, чего в ней такого сложного.

Юлиана Качанова Отвечаю за тесты

Неужели мы все становимся все тупее и глупее, если уже не можем решить простой математический пример с дробями??

ВОПРОС 1 ИЗ 1

Чтобы получить правильный ответ в приведенном выше примере, необходимо знать, в каком порядке выполнять математические действия при решении. И сейчас мы напомним вам базовые правила.

Сумма дробей и разность дробей

При сложении и вычитании дробей с равными знаменателями нужно помнить о двух основных правилах: 

1. В результате сложения дробей с равными знаменателями мы получаем дробь, знаменатель которой остается тем же, а числитель будет равняться сумме обоих числителей дробей.
2. В результате вычисления разности дробей с одинаковыми знаменателями получаем дробь, знаменатель которой остается тот же, а из числителя первой дроби вычитается числитель второй.

А что делать, если знаменатели двух дробей разные? Наверное, подобные математические примеры с дробями становятся главной проблемой у школьников, которые не до конца усвоили правила и «плавают» в теме.

Но переживать не стоит, чтобы правильно решить такую задачу, нужно всего лишь привести дроби к одному знаменателю, и есть три способа, как это сделать:

• Домножаем числитель и знаменатель так, чтобы у обеих дробей знаменатели стали равными:

Но прежде чем использовать этот способ, оцените, делится ли больший знаменатель на меньший. И если делится, то смело выполняем преобразование — домножаем числитель и знаменатель так чтобы у обеих дробей знаменатели стали равными.

• Умножаем числитель и знаменатель первой дроби на знаменатель второй, а числитель и знаменатель второй дроби на знаменатель первой:

• Необходимо найти наименьшее общее кратное (НОК) знаменателей. Это и будет общий знаменатель. Что это за число такое? Это наименьшее натуральное число, которое делится на каждое из чисел.

  Для того, чтобы определить наименьшее общее кратное нескольких чисел, необходимо:
  — разложить каждое из чисел на ПРОСТЫЕ множители;
  — выписать разложение БОЛЬШЕГО из них;
  — умножить его на НЕДОСТАЮЩИЕ множители других чисел.

Произведение дробей

Правило решения примеров с дробями, где есть умножение, довольно простое — для нахождения произведения дробей умножаются их числители и знаменатели. И для этого не нужно приводить дроби к общему знаменателю.

Деление дробей

Решение примеров с дробями, в которых есть деление, тоже не очень сложное — главное, не запутаться. Чтобы разделить дроби, нужно перевернуть дробь, на которую делят, а затем выполнить умножение.

Вот как это выглядит на примере:

Как умножать дроби — JavaTpoint

следующий → ← предыдущая В арифметике умножение — это произведение двух или более чисел или дробей. В этом разделе мы узнаем , как умножать дроби. Как умножать дроби Чтобы найти умножение или произведение двух или более дробей, мы должны выполнить шаги, указанные ниже: Шаг 1: Умножьте числители дробей, чтобы получить числитель. Шаг 2: Умножьте знаменатели дробей, чтобы получить знаменатель. Шаг 3: При необходимости упростите дробь. Примечание. Чтобы упростить дробь, всегда используйте одно и то же число для деления числителя и знаменателя. Предположим, есть две дроби и мы хотим их умножить, тогда: Короче говоря, мы можем сказать, что умножение дробей равно: Давайте посмотрим несколько примеров. Теперь мы видим, что числитель и знаменатель делятся на 2. Итак, упростим дробь. При упрощении получаем. Следовательно, умножение andis. Умножение смешанных дробей Смешанная фракция – это фракция в форме . Имея дело со смешанными дробями, сначала преобразуйте смешанную дробь в неправильную дробь , а затем примените описанные выше шаги. Чтобы преобразовать смешанную дробь в неправильную, выполните следующие действия: Умножьте целое число (a) на знаменатель (c) . В результате получаем (a×c). К приведенному выше результату (a×c) добавьте числитель (b) . После сложения числителя мы получаем числитель неправильной дроби. Знаменатель неправильной дроби будет знаменателем смешанной дроби. В общем можно сказать что: Пример: Найдите произведение и . Решение: Сначала мы преобразуем смешанную дробь в неправильную дробь. Мы можем упростить дробь перед умножением или просто дробь в конце. В этом примере мы, наконец, упростим дробь. При делении дроби на 8 получается смешанная дробь. Видим, что дробь тоже делится на 2. Значит, еще упростим ее и гетор. Умножение целого числа и дроби Пример: умножьте дробь на 9. Решение: Следовательно, умножение и 9является . Пример: умножить 26 на. Решение: Или сначала разделим 26 на 13. В результате получится 2 и умножим на числитель, получим: 2×14=28 Следовательно, умножение 26 на 28. Умножение более двух дробей Давайте посмотрим еще несколько примеров. Другой способ найти умножение: Следовательно, умножение равно . Следующая темаКак найти процент ← предыдущая следующий →

Дробные операции

Горячая математика

К добавить (или вычесть) два дроби :

1) Найдите наименьший общий знаменатель .

2) Запишите обе исходные дроби в виде эквивалентные дроби с наименьшим общим знаменателем.

3) Сложите (или вычтите) числители.

4) Запишите результат со знаменателем.

Пример 1:

Добавлять 1 3 + 3 7 .

Наименьший общий знаменатель равен 21 .

1 3 + 3 7 знак равно 1 ⋅ 7 3 ⋅ 7 + 3 ⋅ 3 7 ⋅ 3 знак равно 7 21 + 921 знак равно 16 21

К умножить две дроби:

1) Умножить числитель на числитель.

2) Умножить знаменатель на знаменатель.

Для всех действительных чисел а , б , с , д ( б ≠ 0 , д ≠ 0 )

а б ⋅ с д знак равно а с б д

Пример 2:

Умножить 1 4 ⋅ 5 6 .

1 4 ⋅ 5 6 знак равно 1 ⋅ 5 4 ⋅ 6 знак равно 5 24

К разделять на дробь, умножить на нее взаимный .

Для всех действительных чисел а , б , с , д ( б ≠ 0 , с ≠ , д ≠ 0 )

а б ÷ с д знак равно а б ⋅ д с знак равно а д б с

Пример 3:

Разделять 3 4 ÷ 5 7 .

3 4 ÷ 5 7 знак равно 3 4 ⋅ 7 5 знак равно 3 ⋅ 7 4 ⋅ 5 знак равно 21 20

Смешанные номера можно записать как неделимая дробь а неправильную дробь можно записать как смешанное число.

Пример 4:

Напишите 7 2 5 как неправильная дробь.

7 2 5 знак равно 7 1 + 2 5 знак равно 7 ⋅ 5 1 ⋅ 5 + 2 5 знак равно 35 5 + 2 5 знак равно 37 5

Пример 5:

Напишите 11 7 как смешанное число в простой форме.

11 7 знак равно 11 ÷ 7 знак равно 1 р 4

Следовательно, 11 7 знак равно 1 4 7 .

Фракция находится в самые низкие условия когда числитель и знаменатель не имеют общего делителя, кроме 1 . Чтобы записать дробь в наименьшем виде, разделите числитель и знаменатель на наибольший общий делитель .

Пример 6:

Напишите 45 75 в самых низких условиях.