Конспект урока по математике: «Уравнения. Вычисление столбиком» (2 класс)

Здравствуйте, ребята! Начнем урок с интересной загадки:

Отгадайте без подсказки

Вы героев этой сказки:

Трое братьев до чего же

Друг на друга все похожи!

(Три поросенка)

 

Буквенные выражения

 Три весёлых поросёнка Ниф-Ниф, Наф-Наф и Нуф-Нуф приглашают нас с вами, ребята, в гости. Посмотрите, какие дома они построили!

 

Как вы думаете, можно ли вставить в окошки карточки с цифрами? Почему?

В домике Ниф-Нифа в открытом окошке может быть карточка с цифрой 5? Какое выражение можно записать?

5 + 4

А какое выражение запишем, если в доме Нуф-Нуфа в окошке будет цифра 2?

6 + 2

Можно ли в окошке Наф-Нафа увидеть цифру 1? А цифру 3?

 

С цифрой 1 запишем выражение: 1 – 1.

А вот цифра 3 не подходит, потому что из 1 нельзя вычесть 3.

Запишите получившиеся выражения и найдите их значения.

 

Проверь себя.

5 + 4= 9

6 + 2= 8

1 – 1= 0

 

Мы записали числовые выражения, ведь они содержат только числа.

Ребята, как вы думаете, можно ли в окошко вставить карточку с буквой?

В математике принято использовать латинские буквы. Может быть, вы уже знаете некоторые из них? Давайте, правильно назовем латинские буквы.

 

В окошки домиков поросят подставим карточки с буквами: x, y, d.

Запишем выражения: x + 4, 6 + y, 1 – d.

У нас получились буквенные выражения.

Найдём значение следующих буквенных выражений: 8 + а, d – 6, x + 5, y – 1.

Для этого вместо буквы подставим число: а = 12, d = 9, x = 14, y = 20.

8 + a d – 6 x + 5 y – 1

8 + 12 = 20 9 – 6 = 3 14 + 5 = 19 20 – 1 = 19

Найдите значение выражения: k + 20, если k = 3, k = 5, k = 9.

 

Проверь себя.

3 + 20 = 23

5 + 20 = 25

9 + 20 = 29

Уравнение. Решение уравнений методом подбора

 

Ребята, внимательно посмотрите на карточки с цифрами трех поросят. Чья карточка подходит для записи в рамке? Почему?

Подходит карточка с цифрой 8, потому что 8 + 2 = 10.

Вместо окошка запишем латинскую букву х (икс).

Получится запись: х + 2 = 10.

Это уравнение.

Ниф-Ниф просит из чисел 6, 5, 2, 1 подобрать для каждого уравнения такое значение у (игрек), при котором получится верное равенство:

8 + у = 9                12 – у= 10                у + 7 = 12                 у – 5 = 1

Мы решили уравнения методом подбора. Обязательно нужно сделать проверку. Для этого вместо у (игрек) подставим в уравнение нужное число и убедимся, что равенство верное.

8 + у = 9 у = 1 8 + 1 = 9 9 = 9

у + 7 = 12 у = 5 5+7=12 12 = 12

12 – у = 10 у = 2 12 – 2 = 10 10 = 10

у – 5 = 1 у = 6 6 – 5 = 1 1 = 1

А теперь задание от Наф-Нафа. Ребята, найдите среди этих записей уравнение и решите его методом подбора.

3 + у             10 – х               14 – 2               b < 3               у – 6 = 2               а + 5

 

Проверь себя.

у – 6 = 2

у = 8

8 – 6 = 2

2 = 2

 

Проверка сложения и вычитания

Ребята, по примеру на сложение составьте два примера на вычитание по образцу:

2 + 3 = 5                                     6 + 1 = 7                                        9 + 7 = 16

5 – 2 = 3                                     ………. .                                           …………

5 – 3 = 2                                     ………..                                           …………

 

Проверь себя:

 

Молодцы! Вспомните, как называются числа при сложении!

Это правило пригодится нам для проверки правильности вычислений.

Например, 2 + 1 = 3

Проверку выполним вычитанием: 3 – 1 = 2 или 3 – 2 = 1.

Выполните самостоятельно сложение и сделайте проверку вычитанием:

17 + 3                                     76 + 4                                    20 + 19

 

Проверь себя.

17 + 3 = 20 20 – 3 = 17

76+ 4 = 80 80 – 4 = 76

20 + 19 = 39 39 – 20 = 19

 

Задание от Нуф-Нуфа. Ребята, вспомните, как называются числа при вычитании?

Ребята, выполните вычитание и сделайте проверку сложением:

30 – 9         100 – 40

 

Проверь себя.

30 – 9 = 21

21 + 9 = 30

100 – 40 = 60

60 + 40 = 100

 

Выполните вычитание и сделайте проверку, пользуясь правилом:

72 – 30               60 – 20

 

Проверь себя.

72 – 30 = 42

72 – 42 = 30

60 – 20 = 40

60 – 40 = 20

Письменное сложение и вычитание. Запись столбиком

 

Ребята. Помогите трем поросятам посчитать!

Веселым поросятам для строительства прочного каменного дома нужно ещё 36 камней. У них уже есть 53 камня. Сколько всего камней нужно для строительства дома?

В этом примере мы к единицам прибавляли единицы, к десяткам прибавляли десятки.

Гораздо удобнее этот пример записать столбиком:

Алгоритм сложения

• Пишу десятки под десятками, а единицы под единицами.
• Складываю единицы: 6 плюс 3 будет 9.
• Пишу под единицами – 9.
• Складываю десятки: 3 плюс 5 будет 8.
• Пишу под десятками – 8.
• Читаю ответ: 89.

Вычитание тоже можно выполнять столбиком:

Алгоритм вычитания

• Пишу десятки под десятками, а единицы под единицами.
• Вычитаю единицы: 9 минус 4 будет 5.
• Пишу под единицами – 5.
• Вычитаю десятки: 6 минус 3 будет 3.
• Пишу под десятками – 3.
• Читаю ответ: 35.

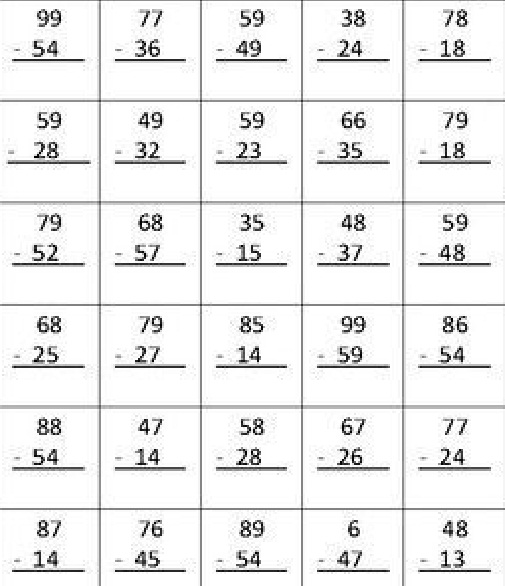
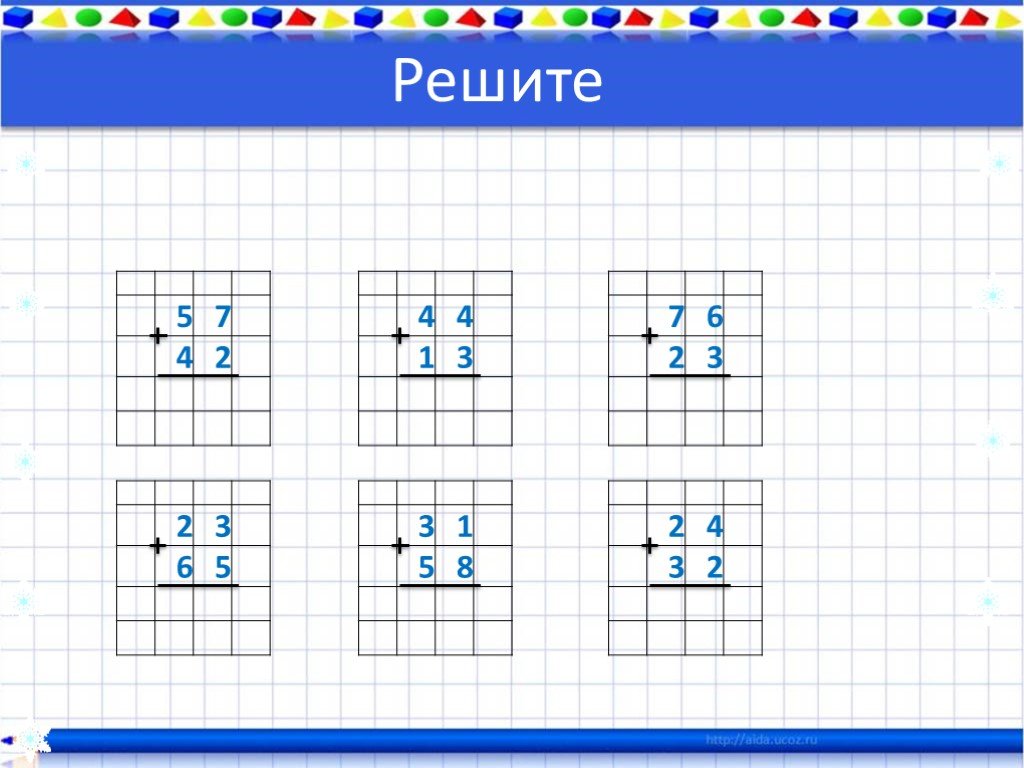
Ребята, веселые поросята записали для вас примеры столбиком. Используя алгоритмы, спишите примеры правильно и вычислите с устным объяснением:

Пока мы с вами решали примеры, в записях наших сказочных поросят кто-то стер некоторые цифры. Помогите восстановить примеры на сложение столбиком. Узнайте, какие числа складывали, какие результаты получились. Подумайте, какая цифра должна стоять на месте звездочки.

Правильный ответ вы найдете в конце урока со значком 

Ребята, все ли задания этого урока давались вам легко? Выберите мордочку одного из трёх поросят: Ниф-Нифа, Нуф-Нуфа или Наф-Нафа по своему настроению.

 

А вы помните, чем закончилась сказка про трех веселых поросят? Они спрятались от волка в крепком каменном доме Наф-Нафа. Крепким бывает не только дом, крепкой бывает дружба! Сообща можно многого добиться, даже если бывает очень трудно.

Напоследок три веселых задачки на смекалку от наших сказочных героев.

 

Задача от Ниф-Нифа.

Сколько лап и сколько ушей у трех зайцев?

 

Задача от Нуф-Нуфа.

Сколько клювов и сколько лапок у трех цыплят?

 

Задача от Наф-Нафа.

Сколько хвостов и сколько ушей у трех котов?

 

Проверь себя.

У трех зайцев 12 лап и 6 ушей.

У трех цыплят 3 клюва и 6 лапок.

У трех котов 3 хвоста и 6 ушей.

 

А вот и правильный ответ!

Ниф-Ниф, Наф-Наф и Нуф-Нуф прощаются с вами, ребята. До новых встреч!

  Вся информация взята из открытых источников.
Если вы считаете, что ваши авторские права нарушены, пожалуйста, напишите в чате на этом сайте, приложив скан документа подтверждающего ваше право.
Мы убедимся в этом и сразу снимем публикацию.

Сложение чисел столбиком. Онлайн калькулятор

• Сложение однозначных чисел
• Сложение многозначных чисел
• Сложение столбиком
• Калькулятор сложения столбиком

Сложение однозначных чисел

Однозначные числа складывают, используя таблицу сложения. Таблицу сложения, а точнее результаты сложения однозначных чисел, нужно помнить наизусть.

Пример. Сложим однозначные числа  4  и  9:

4 + 9 = 13.

Сложение многозначных чисел

Многозначные числа складывают по разрядам, используя переместительный и сочетательный законы сложения.

Пример. Сложим двузначные числа  26  и  48:

26 + 48 = (20 + 6) + (40 + 8) = 20 + 6 + 40 + 8 = (20 + 40) + (6 + 8) = 60 + 14 = 60 + (10 + 4) = 60 + 10 + 4 = (60 + 10) + 4 = 70 + 4 = 74.

Сначала мы разложили слагаемые на разряды, затем сгруппировали в одну группу десятки, в другую — единицы и выполнили сложение по разрядам, т.  е. сложили десятки с десятками и единицы с единицами, затем один десяток, получившийся от сложения единиц, прибавили к десяткам, которых у нас было 6 от сложения десятков, и в конце сложили десятки с единицами.

Форма записи сложения, которую мы использовали, слишком длинная и потому неудобная, поэтому при сложении многозначных чисел обычно используется другая, более удобная форма записи, которая называется сложением столбиком.

Сложение столбиком

Сложение многозначных натуральных чисел удобней выполнять в столбик.

Сложение столбиком — это форма записи и способ сложения, используемый при сложении многозначных чисел. Сложение столбиком иначе ещё называют сложением в столбик.

Рассмотрим сложение столбиком на примере сложения чисел  7056  и  483.

Сложение в столбик записывается так: одно слагаемое записывается под другим так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т.  д.). Для удобства обычно меньшее число записывают под большим. Слева между слагаемыми ставится знак плюс, а под нижним слагаемым проводится горизонтальная черта:

Полученную запись можно мысленно разбить на столбики так, как это показано на рисунке:

Все дальнейшие действия сводятся к сложению однозначных чисел, которые находятся в одном столбике. Вычисление выполняется поразрядно справа налево, начиная с разряда единиц.

Если в результате сложения получается число меньшее  10,  то оно записывается под чертой в этом же разряде.

Начинаем вычисление с разряда единиц: складываем числа  6  и  3.  В результате имеем число  9.  Так как  9 < 10,  то записываем это число под чертой, в том же разряде:

Если в результате сложения получается число, равное  10  или большее  10,  то под чертой в этом же разряде записывается значение разряда единиц полученного числа, а значение разряда десятков полученного числа запоминается (оно используется на следующем шаге).

Переходим к сложению чисел в следующем разряде, то есть к сложению значений разряда десятков. Складываем числа  5  и  8,  получаем число  13.  Так как  13 > 10,  то под чертой, в том же разряде, записываем число  3  (это значение разряда единиц числа  13),  а число  1  запоминаем (это значение разряда десятков числа  13),  при этом говорят  три пишем, а один в уме.  Чтобы не забыть о запомненном числе, его обычно записывают сверху над следующим (слева) разрядом:

Запомненное число прибавляется к сумме чисел следующего разряда.

Переходим к следующему разряду и складываем числа  0  и  4.  В результате имеем  4.  К полученному числу прибавляем запомненное число  1,  получаем  5.  Так как  5 < 10,  то под чертой, в том же разряде, записываем число  5:

После этого происходит переход на один разряд влево и действия повторяются. Данный процесс продолжается до тех пор, пока числа не закончатся.

Если в столбике содержится только одно число, и у нас нет запомненного числа (от предыдущего сложения), в этом случае мы просто записываем это число под чертой, в том же разряде.

Так как в следующем столбике находится лишь одно число —  7,  и в памяти у нас нет запомненного числа, то мы просто записываем  7  под чертой, в том же разряде:

Дальше никаких чисел нет и в памяти тоже чисел нет. На этом процесс сложения можно считать завершённым. Натуральное число, получившееся под чертой, является результатом сложения данных чисел. Теперь можно записать сумму данных чисел в обычном виде:

7056 + 483 = 7539.

Рассмотрим ещё пару примеров сложения столбиком, чтобы разобраться с оставшимися нюансами.

Пример 1. Сложим числа  29  и  6  столбиком.

Складываем  9  и  6,  в результате получаем число  15.  Так как  15 > 10,  то число  5  записываем, а число  1  запоминаем:

Если в столбике содержится только одно число, и у нас имеется запомненное число (от предыдущего сложения), то запомненное число просто прибавляется к этому одному числу.

В следующем столбике находится лишь одно число —  2.  Так как у нас в памяти имеется число  1,  то его нужно прибавить к  2.   В результате получаем число  3:

Дальше никаких чисел нет и запомненного числа тоже нет, следовательно, сложение столбиком завершено.

Пример 2. Сложим столбиком числа  43  и  94.

Складываем  3  и  4.  В результате имеем число  7.  Так как  7 < 10,  то записываем это число под чертой, в том же разряде:

Если в последнем разряде в результате сложения получается число, равное  10  или большее  10,  то под чертой в этом же разряде записывается значение разряда единиц полученного числа, а значение разряда десятков полученного числа записывается под чертой в следующий разряд.

В следующем разряде складываем числа  4  и  9,  получаем число  13.  Так как  13 > 10,  то под чертой, в том же разряде, записываем число  3,  а число  1  записываем под чертой в следующий разряд:

Дальше никаких чисел нет и в памяти числа тоже нет, следовательно, сложение в столбик завершено.

Удобство сложения в столбик заключается в том, что сложение многозначных натуральных чисел фактически сводится к сложению однозначных чисел и запись процесса сложения занимает меньше места.

Калькулятор сложения столбиком

Данный калькулятор поможет вам выполнить сложение столбиком. Просто введите слагаемые и нажмите кнопку Вычислить.

Что такое столбцовый метод сложения и вычитания?

Метод столбцов является одним из наиболее распространенных письменных методов, которые учащиеся изучают при сложении и вычитании все более больших чисел. Числа и расчеты составляют большую часть учебного плана по математике в начальной школе, и ожидается, что к концу 3-го класса учащиеся будут использовать письменные методы сложения и вычитания.

Что такое метод столбцов?

Метод столбцов — это математический способ выполнения вычислений, при котором числа, которые вы вычисляете, записываются с каждой цифрой в столбце правильного разряда. Это позволяет детям использовать свои знания о позиционном значении, чтобы понять сложение и вычитание.

Например:

Что такое добавление столбца?

Сложение столбцов — это формальный метод сложения двух чисел. Как и выше, числа представлены друг над другом, гарантируя, что каждая цифра выровнена правильно. Это позволяет детям понять сложение с перегруппировкой, когда мы пересекаем границу десятков.

Что такое вычитание столбцов?

Вычитание по столбцам использует те же принципы — представление цифр друг над другом и их выравнивание по разрядности. Преимущество использования вычитания столбцов как метода заключается в том, что он позволяет детям понять и визуализировать обмен.

Ищете ресурсы для занятий? Смотрите нашу коллекцию рабочих листов на сложение и вычитание

Присоединяйтесь к третьему космическому учебному математическому центру

Чтобы просмотреть всю нашу коллекцию бесплатных и премиальных математических ресурсов для учителей и родителей, зарегистрируйтесь, чтобы присоединиться к математическому центру Third Space Learning. Это быстро, легко и бесплатно! (Пожалуйста, используйте Google Chrome для доступа к Maths Hub)

Как упорядочить метод столбцов

Чтобы метод столбцов работал, важно, чтобы дети изложили его правильно.

Для этого они должны иметь надежное представление о разрядном значении и числах разбиения, чтобы показать это, чтобы цифры располагались в правильных столбцах. Именно здесь стандартная практика «одна цифра на квадрат» становится больше, чем просто представление.

При обучении столбцовому методу часто полезно сначала попросить учеников написать заголовки столбцов над своими расчетами (Th, H, T, O и т. д.) и напомнить им, что должна быть одна цифра. в каждом квадрате.

Этот совет позволяет избежать распространенных проблем, с которыми ученики могут столкнуться при составлении задания, что приводит к ошибкам в расчетах. Большинство этих ошибок связано с тем, что ученики не используют правильные столбцы при организации своей работы.

Приступая к столбцовому методу, многие ученики допускают ошибки из-за неправильной организации расчетов.

В 3-м классе, когда дети складывают и вычитают трехзначные и двузначные числа, один из способов убедиться, что они правильно расположили столбцы, — это использовать ноль в качестве заполнителя в столбце сотен для двузначного числа.

Ноль можно использовать в качестве заполнителя, чтобы помочь учащимся правильно организовать расчеты.

Существуют также соображения по стилю, касающиеся расположения столбцов. Кроме того, иногда нам нужно будет перегруппировать числа между столбцами, например, при вычислении 281 + 634.

В этот момент 8 десятков плюс 3 десятка равно 11 десяткам, что равно 110. Мы знаем, что не можем поместить 11 в столбец десятков. , значит, нам нужно обменять десять десятков на сто. Есть два варианта, как это устроить:

Я считаю, что вариант слева наиболее эффективен в классе, потому что ученики могут видеть сто, когда они добавляют столбец сотен. По моему опыту, ученики могут забыть, что мы перегруппировали сотню, если она находится ниже отработки, как на картинке справа.

Аналогично, при обмене в вычитании нужно учитывать, как мы его устроим. Наиболее распространенный способ сделать это следующим образом:

Пример слайда о вычитании столбцов в нашем онлайн-уроке один на один по математике.

Что такое метод расширенного столбца?

Метод расширенного столбца позволяет детям добавлять числа, требующие перегруппировки, добавляя каждый столбец разряда по отдельности. Обычно это используется в качестве первого шага к возможности использовать традиционное сложение столбцов.

Например:

В приведенном выше примере (взятом из учебного плана 3 класса) мы начинаем справа, что необходимо для добавления столбца. Мы добавляем столбец единиц (9 + 5) и пишем этот ответ после столбцов правильных разрядов.

Тот же метод используется для столбцов десятков и сотен. Написав цифры, которые они добавили, в скобках рядом со своей работой, дети могут увидеть, откуда берется их ответ.

Это также может работать с десятичными числами, начиная с 4-го класса:

Использование здесь метода сложения в столбик может помочь детям запомнить, где находится десятичная точка в числе, поскольку она всегда остается на одном и том же месте. В этом примере мы снова начинаем справа, складывая числа в одном столбце вместе.

Расчет с использованием метода столбцов

Шаг 1: Организуйте расчет с использованием столбцов разрядных значений.

Шаг 2: Начиная справа (в данном случае столбец единиц), завершите вычисление (9-8) и запишите ответ внизу, в том же столбце.

Шаг 3: Вычислите следующий столбец слева от этого – здесь это столбец десятков. Объясняя это детям, убедитесь, что они понимают, что из 7 десятков вычесть 2 десятка или 70-20, а не 7-2.

Шаг 4: Снова двигайтесь влево. В приведенном здесь примере нам нужно обменять столбец сотен. Мы не можем вычесть 5 сотен из 3 сотен, не обменяв 1 тысячу. Нам нужно обменять одну из тысяч на десять сотен, сделав вычисление тринадцать сотен вычесть пять сотен.

Шаг 5: Заполните последнюю колонку слева – три тысячи минус одна тысяча.

Когда дети узнают о методах столбцов в школе?

Национальная учебная программа определяет использование «формальных письменных методов сложения и вычитания в столбцах» с 3-го года обучения. Однако руководство предлагает для 2-го года «запись сложения и вычитания в столбцах поддерживает разрядное значение и готовит к формальным письменным методам с большими числами». поэтому некоторые школы могут решить ввести метод столбцов с двузначными числами во 2-м классе, однако это не является обязательным в учебной программе по математике KS1.

Начиная с 5-го класса в рамках национальной учебной программы, посвященной дробям, учащиеся будут решать задачи с десятичными дробями. На этом этапе они также используют метод столбца для сложения и вычитания десятичных чисел.

Какие еще методы сложения и вычитания используются в школе?

В то время как метод столбцов является основным формальным методом, упомянутым в национальной учебной программе и поэтому преподаваемым в школе, дети учатся складывать и вычитать, используя множество различных умственных методов и ресурсов во время учебы в начальной школе.

Знание сложения и вычитания начинается в раннем возрасте и сосредоточено на использовании конкретных материалов, чтобы добавлять больше и убирать из группы объектов.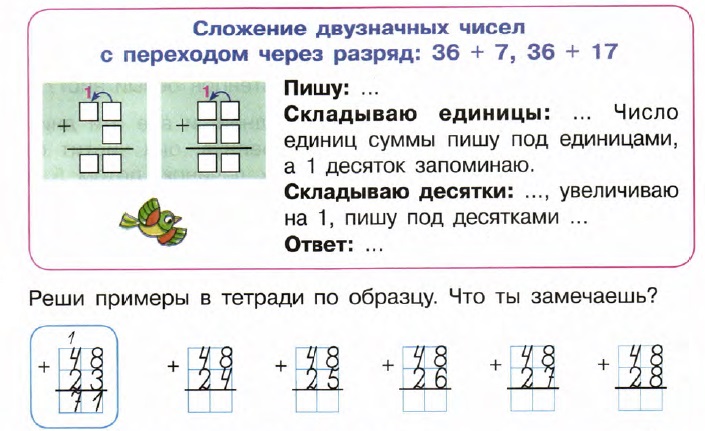 На этом этапе они будут использовать язык «больше чем» и «меньше чем», а затем перейдут к «добавить» и «вычесть» или к их синонимам.

В соответствии с национальным учебным планом дети должны использовать умственные методы, чтобы найти ответы на вычисления сложения и вычитания в пределах двадцати в течение 1-го года. Они используют конкретные и графические ресурсы, чтобы помочь им освоить это, поскольку это необходимо для того, чтобы впоследствии стать уверенными математиками. в своем образовании.

Дети используют конкретные математические ресурсы, такие как счетные кубики, нумикон, диены, бусины, счетчики разрядов и числовые линии, прежде чем приступить к вычислениям, чтобы убедиться, что они хорошо понимают числовое значение, смысл чисел, сложение и вычитание. Затем они переходят к формальным методам расчета, в первую очередь к методу столбцов, чтобы иметь возможность продемонстрировать свою работу в более сложных вычислениях и текстовых задачах.

В учебной программе по математике дети повторяют один и тот же материал с большими числами по спирали, поэтому в 3-м классе они изучают сложение и вычитание с трехзначными числами, в 4-м классе — с четырехзначными числами, а в 5-м классе — с числами вверх. до одного миллиона.

Какое отношение метод столбцов имеет к другим областям математики?

Метод столбца для сложения и вычитания изложен в тетради таким же образом, как и для метода умножения. Таким образом, прочная основа метода столбцов в 4-м классе поможет ученикам 5-го класса, когда они перейдут к умножению и делению в столбик.

Примеры работы методом столбца

1. 3_4 + 615 = 989. Вставьте пропущенную цифру.

Здесь ребенок нашел пропущенное число, используя обратную операцию. Они знают, что 8 десятков — это ответ в столбце десятков, и у них уже есть одна десятка. Поэтому, чтобы вычислить пропущенное число, они использовали обратную операцию, вычитая 1 десяток из 8 десятков, что равно 7 десяткам.

2. У школы есть 5500 фунтов стерлингов, которые можно потратить на новые ресурсы. Они покупают 10 планшетных компьютеров за 3468 фунтов стерлингов, а затем тратят 9 фунтов стерлингов.56 на зарядном устройстве. Сколько у них осталось в бюджете?

Этот вопрос состоит из двух слов. Вы можете вычесть каждое число из исходных 5500 фунтов стерлингов, но здесь я решил добавить две потраченные суммы, а затем вычесть это из общего бюджета. Это показывает применение как сложения столбца, так и вычитания для получения ответа на проблему 1076 фунтов стерлингов.

3. Верен этот расчет или нет? Докажите это

8,7 + 0,4 = 8,11

Это неверно. Как показано в расчете 9,1. Расчет служит доказательством. Вы можете расширить это, спросив, что, по их мнению, было сделано, чтобы получить ответ 8.11.

Примеры вопросов метода столбца

1. 3_57 + 4801 = 8058. Вставьте пропущенную цифру.

Ответ: 2 сотни

2. Самая высокая гора в мире — Эверест, высота которой 29 029 футов. Самая высокая гора в Великобритании — Бен-Невис, высота которой составляет 4411 футов. Насколько выше Эверест, чем Бен-Невис?

Ответ: 29029 футов – 4411 футов = 24 618 футов

3. Али вычисляет:

Объясните, что Али сделал неправильно.

24 нужно переставить на одно место, чтобы 2 равнялось 2 десяткам, а 4 — 4 единицам.

4. Чарли пошел в магазин и потратил 24,56 фунта стерлингов на две вещи. Она потратила 6,78 фунтов стерлингов на один предмет. Сколько стоил второй?

Ответ: £24,56 – £6,78 = £17,78

5. Какая ошибка была допущена? Как это можно исправить?

Ответ: В столбце десятков не учтены десятки, перегруппированные из столбца единиц, поэтому должно быть 12 десятков. Это также не было учтено в столбце сотен, который должен быть равен 9 сотням.

Как написать метод столбца?

Метод столбца записывается путем размещения каждого числа одно над другим, гарантируя, что цифры с одинаковым значением разряда находятся в одном столбце.

Что такое столбчатый метод для детей?

Метод столбца — это письменный метод для завершения вычислений сложения и вычитания.

Подробнее:

• Что такое числовые облигации?
• Как научить KS2 вычитанию: вычитание 5-й год
• Как учить сложению KS2: дополнение 5 класса
• Что такое субитизация?

Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Каждую неделю репетиторы-специалисты по математике Third Space Learning поддерживают тысячи учеников в сотнях школ еженедельными индивидуальными онлайн-уроками и математическими мероприятиями, предназначенными для заполнения пробелов и ускорения прогресса.

С 2013 года мы помогли более 150 000 учеников начальных и средних школ стать более уверенными в себе, способными математиками. Узнайте больше или запросите персональное предложение для вашей школы, чтобы рассказать нам о потребностях вашей школы и о том, как мы можем помочь.

Обучение в начальной школе ориентировано на потребности каждого ребенка и строго соответствует национальной учебной программе.

ячейки, столбцы, проценты, даты и время

В этом учебном пособии показано, как выполнять вычитание в Excel с использованием знака минус и функции СУММ. Вы также научитесь вычитать ячейки, целые столбцы, матрицы и списки.

Вычитание — одно из четырех основных арифметических действий, и каждый ученик начальной школы знает, что для вычитания одного числа из другого используется знак минус. Этот старый добрый метод работает и в Excel. Какие вещи вы можете вычитать в своих рабочих листах? Просто любые вещи: числа, проценты, дни, месяцы, часы, минуты и секунды. Вы даже можете вычитать матрицы, текстовые строки и списки. Теперь давайте посмотрим, как вы можете все это сделать.

Формула вычитания в Excel (формула минус)

Для ясности функция ВЫЧИТАНИЕ в Excel не существует. Чтобы выполнить простую операцию вычитания, вы используете знак минус (-).

Базовая формула вычитания в Excel проста:

= номер1 — номер2

Например, чтобы вычесть 10 из 100, напишите приведенное ниже уравнение и получите в результате 90:

=100-10

Чтобы ввести формулу на лист, сделайте следующее:

1. В ячейку, в которую вы хотите вывести результат, введите знак равенства ( = ).
2. Введите первое число, затем знак минус и второе число.
3. Завершите формулу, нажав клавишу Enter.

Как и в математике, в одной формуле можно выполнять более одной арифметической операции.

Например, чтобы вычесть несколько чисел из 100, введите все эти числа, разделенные знаком минус:

=100-10-20-30

Чтобы указать, какая часть формулы должна быть вычислена первой, используйте круглые скобки. Например:

=(100-10)/(80-20)

На снимке экрана ниже показаны еще несколько формул для вычитания чисел в Excel:

Как вычесть ячейки в Excel

Чтобы вычесть одну ячейку из другой, вы также используете формулу минуса, но указываете ссылки на ячейки вместо фактических чисел:

= ячейка_1 — ячейка_2

Например, чтобы вычесть число в B2 из числа в A2, используйте следующую формулу:

=А2-В2

Вам не обязательно вводить ссылки на ячейки вручную, вы можете быстро добавить их в формулу, выбрав соответствующие ячейки. Вот как:

1. В ячейке, в которую вы хотите вывести разницу, введите знак равенства (=), чтобы начать формулу.
2. Щелкните ячейку, содержащую уменьшаемое число (число, из которого необходимо вычесть другое число). Его ссылка будет добавлена ​​в формулу автоматически (A2).
3. Введите знак минус (-).
4. Щелкните ячейку, содержащую вычитаемое (число, которое необходимо вычесть), чтобы добавить его ссылку в формулу (B2).
5. Нажмите клавишу Enter, чтобы завершить формулу.

И у вас будет результат, подобный этому:

Как вычесть несколько ячеек из одной ячейки в Excel

Чтобы вычесть несколько ячеек из одной и той же ячейки, вы можете использовать любой из следующих методов.

Метод 1. Знак минус

Просто введите несколько ссылок на ячейки, разделенные знаком минус, как мы это делали при вычитании нескольких чисел.

Например, чтобы вычесть ячейки B2:B6 из B1, создайте формулу следующим образом:

=B1-B2-B3-B4-B5-B6

Метод 2.

Функция СУММ

Чтобы сделать формулу более компактной, сложите вычитаемые (B2:B6) с помощью функции СУММ, а затем вычтите сумму из уменьшаемого (B1):

=B1-СУММ(B2:B6)

Метод 3. Сумма отрицательных чисел

Как вы помните из курса математики, вычитание отрицательного числа — это то же самое, что и сложение. Итак, сделайте все числа, которые вы хотите вычесть, отрицательными (для этого просто введите знак минус перед числом), а затем используйте функцию СУММ, чтобы сложить отрицательные числа:

=СУММ(B1:B6)

Как вычесть столбцы в Excel

Чтобы вычесть 2 столбца построчно, напишите формулу минуса для самой верхней ячейки, а затем перетащите маркер заполнения или дважды щелкните знак плюс, чтобы скопировать формулу во весь столбец.

В качестве примера, давайте вычтем числа в столбце C из чисел в столбце B, начиная со строки 2:

=B2-C2

Из-за использования относительных ссылок на ячейки формула будет корректно корректироваться для каждой строки:

Вычесть одно и то же число из столбца чисел

Чтобы вычесть одно число из диапазона ячеек, введите это число в какую-нибудь ячейку (в данном примере F1) и вычтите ячейку F1 из первой ячейки в диапазоне:

=B2-$F$1

Ключевым моментом является блокировка ссылки на вычитаемую ячейку знаком $. Это создает абсолютную ссылку на ячейку, которая не изменяется независимо от того, куда копируется формула. Первая ссылка (B2) не заблокирована, поэтому она меняется для каждой строки.

В результате в ячейке C3 у вас будет формула =B3-$F$1; в ячейке C4 формула изменится на =B4-$F$1 и т. д.:

Если дизайн вашего рабочего листа не позволяет разместить в дополнительной ячейке вычитаемое число, ничто не мешает вам жестко закодировать его прямо в формуле:

=B2-150

Как вычесть проценты в Excel

Если вы хотите просто вычесть один процент из другого, вам поможет уже знакомая формула вычитания. Например:

=100%-30%

Или вы можете ввести проценты в отдельные ячейки и вычесть эти ячейки:

=А2-В2

Если вы хотите вычесть процент из числа, т.е. уменьшить число на процент , затем используйте эту формулу:

= Номер * (1 — %)

Например, вот как можно уменьшить число в A2 на 30%:

=А2*(1-30%)

Или вы можете ввести процент в отдельную ячейку (скажем, B2) и ссылаться на эту ячейку, используя абсолютную ссылку:

=A2*(1-$B$2)

Для получения дополнительной информации см. Как рассчитать проценты в Excel.

Как вычитать даты в Excel

Самый простой способ вычитания дат в Excel — ввести их в отдельные ячейки и вычесть одну ячейку из другой:

= Конечная_дата — Начальная_дата

Вы также можете указать даты непосредственно в формуле с помощью функции ДАТА или ДАТАЗНАЧ. Например:

=ДАТА(2018,2,1)-ДАТА(2018,1,1)

=ДАТАЗНАЧ("01.02.2018")-ДАТАЗНАЧ("1.01.2018")

Дополнительную информацию о вычитании дат можно найти здесь:

• Как складывать и вычитать даты в Excel
• Как рассчитать дни между датами в Excel

Как вычесть время в Excel

Аналогично строится формула вычитания времени в Excel:

= Время окончания — Время начала

Например, чтобы получить разницу между временем в A2 и B2, используйте следующую формулу:

=А2-В2

Чтобы результат отображался правильно, обязательно примените формат времени к ячейке формулы:

Тот же результат можно получить, указав значения времени непосредственно в формуле. Чтобы Excel правильно понял время, используйте функцию ВРЕМЗНАЧ:

=ЗНАЧ ВРЕМЕНИ("16:30")-ЗНАЧ ВРЕМЕНИ("12:00")

Для получения дополнительной информации о вычитании времени см.:

• Как рассчитать время в Excel
• Как добавить и вычесть время, чтобы показать более 24 часов, 60 минут, 60 секунд

Как сделать матричное вычитание в Excel

Предположим, у вас есть два набора значений (матриц) и вы хотите вычесть соответствующие элементы наборов, как показано на снимке экрана ниже:

Вот как это можно сделать с помощью одной формулы:

1. Выберите диапазон пустых ячеек с тем же количеством строк и столбцов, что и ваши матрицы.
2. В выбранном диапазоне или в строке формул введите формулу вычитания матрицы:
   =(A2:C4)-(E2:G4)
3. Нажмите Ctrl + Shift + Enter, чтобы сделать его формулой массива.
   

Результаты вычитания появятся в выбранном диапазоне. Если щелкнуть любую ячейку в результирующем массиве и посмотреть на строку формул, то вы увидите, что формула окружена {фигурными скобками}, что является визуальным признаком формул массива в Excel:

Если вам не нравится использовать формулы массива на ваших листах, вы можете вставить обычную формулу вычитания в самую верхнюю левую ячейку и скопировать вправо и вниз столько ячеек, сколько строк и столбцов вашей матрицы.

В этом примере мы могли бы поместить приведенную ниже формулу в C7 и перетащить ее в следующие 2 столбца и 2 строки:

=А2-С4

Из-за использования относительных ссылок на ячейки (без знака $) формула будет корректироваться на основе относительного положения столбца и строки, в которые она копируется:

Вычитание текста одной ячейки из другой ячейки

В зависимости от того, хотите ли вы считать прописные и строчные символы одинаковыми или разными, используйте одну из следующих формул.

Формула с учетом регистра для вычитания текста

Чтобы вычесть текст одной ячейки из текста другой ячейки, используйте функцию ПОДСТАВИТЬ, чтобы заменить вычитаемый текст пустой строкой, а затем ОБРЕЗАТЬ лишние пробелы:

ОТРЕЗАТЬ (ЗАМЕНИТЬ ( полный_текст , текст_для_вычитания ,»»))

С полным текстом в A2 и подстрокой, которую вы хотите удалить в B2, формула выглядит следующим образом:

=ОТРЕЗАТЬ(ЗАМЕНИТЬ(A2,B2,""))

Как видите, формула прекрасно работает для вычитания подстроки из начала и из конца строки:

Если вы хотите вычесть один и тот же текст из диапазона ячеек, вы можете «жестко закодировать» этот текст в своей формуле.

В качестве примера удалим слово «Яблоки» из ячейки A2:

=ОТРЕЗАТЬ(ЗАМЕНИТЬ(A2;"Яблоки",""))

Чтобы формула работала, обязательно вводите текст точно, включая регистр символов .

Формула без учета регистра для вычитания текста

Эта формула основана на том же подходе — замена вычитаемого текста пустой строкой. Но на этот раз мы будем использовать функцию REPLACE в сочетании с двумя другими функциями, которые определяют, с чего начать и сколько символов нужно заменить:

.

• Функция ПОИСК возвращает позицию первого вычитаемого символа в исходной строке без учета регистра. Это число идет к start_num аргумент функции ЗАМЕНИТЬ.
• Функция ДЛСТР находит длину удаляемой подстроки. Это число входит в аргумент num_chars команды REPLACE.

Полная формула выглядит следующим образом:

ОТРЕЗАТЬ(ЗАМЕНИТЬ( полный_текст , ПОИСК( текст_для_вычитания , полный_текст ), ДЛСТР( текст_для_вычитания ),»»))

Применительно к нашему выборочному набору данных он принимает следующую форму:

=ОТРЕЗАТЬ(ЗАМЕНИТЬ(A2,ПОИСК(B2,A2),ДЛСТР(B2),""))

Где A2 — исходный текст, а B2 — удаляемая подстрока.

Вычитание одного списка из другого

Предположим, у вас есть два списка текстовых значений в разных столбцах, причем меньший список является подмножеством большего списка. Возникает вопрос: как удалить элементы меньшего списка из большего списка?

Математически задача сводится к вычитанию меньшего списка из большего:

Большой список: {«A», «B», «C», «D»}

Меньший список: {«A», «C»}

Результат: {«B», «D»}

В терминах Excel нам нужно сравнить два списка на наличие уникальных значений, т. е. найти значения, которые появляются только в большем списке. Для этого используйте формулу, описанную в разделе Как сравнить два столбца на наличие различий:

.

=ЕСЛИ(СЧЕТЕСЛИ($B:$B, $A2)=0, "Уникальный", "")

Где A2 — первые ячейки большого списка, а B — столбец, содержащий меньший список.

В результате уникальные значения в большом списке помечаются соответствующим образом:

И теперь вы можете фильтровать уникальные значения и копировать их куда хотите.

Вот как вы вычитаете числа и ячейки в Excel. Чтобы поближе ознакомиться с нашими примерами, загрузите наш образец рабочей тетради ниже.