Самостоятельные работы по математике за 5 класс к учебнику Виленкина Н.Я. за 1, 2, 3 и 4 четверти — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Содержание
Самостоятельные работы по математике за 5 класс к учебнику Виленкина Н.Я. за 1, 2, 3 и 4 четверти
Дата публикации: .
Самостоятельные на темы: «Натуральные числа и их обозначения», «Сложение и вычитание натуральных чисел», «Сравнение натуральных чисел», «Отрезок, прямая, луч», «Умножение натуральных чисел», «Деление натуральных чисел», «Выражения и уравнения», «Квадрат и куб числа», «Окружность и круг», «Обыкновенные дроби», «Сравнение дробей» и др.
Некоторые понятия к учебному материалу.
1. Натуральные числа – используются для счета предметов в повседневной жизни.
2. Отрезок. Длина отрезка – расстояние между его крайними точками, концами. Обозначается заглавными латинскими буквами, например AB.
3. Шкала – специальная линейка с делениями (штрихами).
Шкала – специальная линейка с делениями (штрихами).
4. Единичный отрезок – отрезок с длиной равной единице.
5. Меньше и больше. Меньше, число, которое при счете называется раньше. Больше, число, которое при счете называется позже.
6. Слагаемые числа – числа, которые складываются.
7. Вычитание. Число из которого вычитают – это уменьшаемое. Число, которое вычитается – это вычитаемое. В итоге получаем разность.
Самостоятельная работа №1 (входная работа на повторение)
Вариант I.
1. Определение числа.
а) Определите натуральное число, которое следует за числом 699.
б) Определите натуральное число, которое на две единицы меньше числа 1001.
в) Определите натуральное число, которое на единицу больше числа 239 999.
г) Определите натуральное число, которое на единицу меньше числа 394 000.
2. Решите задачу.
В городском сквере посажено 340 деревьев. А в парке посажено 270 деревьев. На сколько деревьев больше в городском сквере, чем в парке?
А в парке посажено 270 деревьев. На сколько деревьев больше в городском сквере, чем в парке?
3. Решите примеры.
| а) 492 + 1 220 = | б) 3 495 — 593 = |
| в) 5112 : 6 = | г) 56 * 23 = |
Вариант II.
1. Определение числа.
а) Определите натуральное число, которое следует за числом 879.
б) Определите натуральное число, которое на единицу меньше числа 2 000.
в) Определите натуральное число, которое на единицу больше числа 722 999.
г) Определите натуральное число, которое на единицу меньше числа 24 000.
2. Решите задачу.
Рыбаки за первую неделю поймали 395 кг рыбы, а за вторую неделю – 239 кг. На сколько кг было поймано меньше за вторую неделю, чем за первую?
3. Решите примеры.
| а) 638 + 1 445 = | б) 6 112 — 2 598 = |
| в) 2688 : 3 = | г) 24 * 45 = |
Вариант III.
1. Определение числа.
а) Определите натуральное число, которое следует перед числом 699.
б) Определите натуральное число, которое на единицу меньше числа 3 000.
в) Определите натуральное число, которое на единицу больше числа 28 999.
г) Определите натуральное число, которое на единицу меньше числа 12 000.
2. Решите задачу.
В огороде посадили 2 грядки помидор. С первой грядки было собрано 427 помидор, а со второй грядки – 311. На сколько меньше помидор было собрано со второй грядки, чем с первой?
3. Решите примеры.
| а) 455 + 3 412= | б) 5 332 — 593 = |
| в) 3648 : 8 = | г) 29 * 41 = |
Самостоятельная работа №2 на тему: «Натуральные числа и их обозначения»
Вариант I.
1. Запишите следующие числа 3 раза подряд и запишите полученное в результате число в виде словосочетания.
а) число 20;
б) число 49.
2. Представьте следующие словосочетания в числовом виде.
а) Шесть миллиардов пятьсот три тысяча семь.
б) На единицу больше чем пятьсот девять тысяч девятьсот девяносто девять.
3. Определите все возможные трехзначные числа, состоящие из следующих чисел (числа не должны повторяться).
a) 2, 3 и 7.
b) 4, 0 и 9.
Вариант II.
1. Запишите следующие числа 3 раза подряд и запишите полученное в результате число в виде словосочетания.
а) число 60;
б) число 38.
2. Представьте следующие словосочетания в числовом виде.
а) Восемь миллиардов триста одна тысяча три.
б) На единицу больше чем сто девять тысяч девятьсот девяносто девять.
3. Определите все возможные трехзначные числа, состоящие из следующих чисел (числа не должны повторяться).
a) 1, 3 и 9.
b) 2, 4 и 0.
Вариант III.
1. Запишите следующие числа 3 раза подряд и запишите полученное в результате число в виде словосочетания.
а) число 30;
б) число 58.
2. Представьте следующие словосочетания в числовом виде.
а) Два миллиарда шестьсот два миллиона триста.
б) На единицу больше чем семьсот пять тысяч девятьсот девяносто восемь.
3. Определите все возможные трехзначные числа, состоящие из следующих чисел (числа не должны повторяться).
a) 5, 2 и 8.
b) 1, 3 и 0.
Самостоятельная работа №3
Вариант I.
1. Переведите из одной единицы измерения в другую.
| а) 8 дм 43 см = … см | б) 5 км 549 м = … м |
| в) 7 см 18 мм = … мм | г) 249 см =… дм … см |
2. Начертите отрезок AB, равный 17 см 5 мм. Отметьте на нем точки C и D.
AC равно 10 см 4 мм, CD равно 4 см 9 мм. Чему равна длина отрезка DB?
Начертите отрезок AB, равный 17 см 5 мм. Отметьте на нем точки C и D.
AC равно 10 см 4 мм, CD равно 4 см 9 мм. Чему равна длина отрезка DB?
3. Решите задачу.
Перед домом построили забор. Забор держится на 18 столбах, расстояние между столбами составляет пять метров. Каково расстояние между шестым и четырнадцатым столбами?
4. Начертите четырехугольник ABCD. Отметьте точкой T середину стороны BC. Соедините точки B и D, А и T. Выпишите все многоугольники, которые образовались.
Вариант II.
1. Переведите из одной единицы измерения в другую.
| а) 4 дм 23 см = … см | б) 25 км 50 м = … м |
| в) 16 см 65 мм = … мм | г) 456 см =… дм … см |
2. Начертите отрезок AB, равный 15 см 4 мм, отметьте на нем точки C и D. AC равен 8 см 2 мм, CD равен 3 см 7 мм.
Чему равна длина отрезка DB?
3. Решите задачу.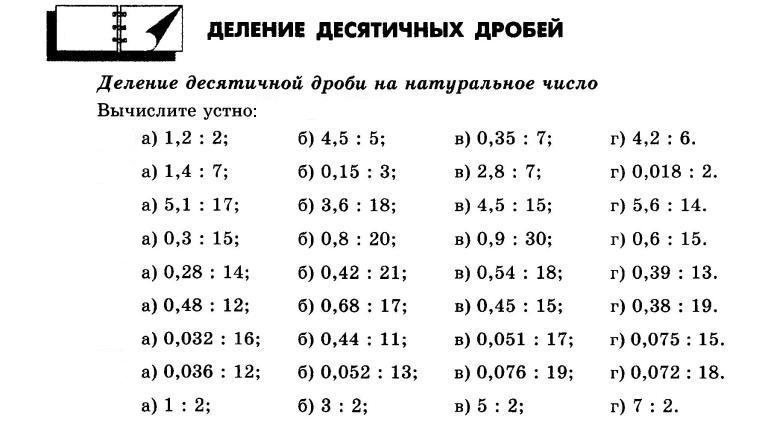
Перед домом построили забор. Забор держится на 19 столбах, расстояние между столбами составляет 4 метра. Каково расстояние между третьим и восьмым столбами?
4. Начертите четырехугольник ABCD. Отметьте середину AB и поставьте точку N. Проведите отрезки DN и АС. Выпишите все многоугольники, которые образовались.
Вариант III.
1. Переведите из одной единицы измерения в другую.
| а) 19 дм 5 см = … см | б) 21 км 678 м = … м |
| в) 43 см 8 мм = … мм | г) 503 см =… дм … см |
2. Начертите отрезок AB, равный 13 см 2 мм, отметьте на нем точки C и D. AC равен 7 см 3 мм. CD равен 3 см 6 мм. Чему равна длина отрезка DB?
3. Решите задачу.
Перед домом построили забор. Забор держится на 16 столбах, расстояние между столбами составляет 3 метра. Каково расстояние между пятым и одиннадцатым столбами?
4. Начертите четырехугольник ABCD. Отметьте середину CD и поставьте точку М. Проведите отрезки BM и АС. Выпишите все многоугольники, которые образовались.
Начертите четырехугольник ABCD. Отметьте середину CD и поставьте точку М. Проведите отрезки BM и АС. Выпишите все многоугольники, которые образовались.
Самостоятельная работа №4 на тему: «Сравнение натуральных чисел»
Вариант I.
1. Сравните числа.
| а) 3 485 660 … 3 458 660 | б) 303 559 … 330 559 |
| в) 2 596 440 … 2 569 440 | г) 45 696 … 44 696 |
2. Представьте в виде двойного неравенства: 18 т 347 кг … 18 т 4 ц 59 кг … 18 568 кг.
Вариант II.
1. Сравните числа.
| а) 34 686 887 … 34 868 887 | б) 3 855 … 3 585 |
| в) 40 955 999 … 40 595 999 | г) 455 776 … 445 776 |
2. Представьте в виде двойного неравенства: 13 км 845 м … 14675 м … 13 км 845 м 3 дм.
Вариант III.
1. Сравните числа.
| а) 678 881 … 687 881 | б) 782 223 … 728 223 |
| в) 2 490 606 … 2 490 660 | г) 13 799 . .. 13 977 .. 13 977 |
2. Представьте в виде двойного неравенства: 15 т 475 кг … 15657 кг … 157 ц 35 кг.
Самостоятельная работа №5 на тему: «Сложение и вычитание натуральных чисел»
Вариант I.
1. Выполните сложение.
| а) 348 588 667 + 239 586 394 = | б) 93 955 483 + 495 868 991 = |
| в) 23 394 596 + 5 697 345 = | г) 3 949 532 + 405 669 = |
2. Выполните вычитание.
| а) 348 588 667 — 283 745 733 = | б) 93 955 483 — 22 394 583 = |
| в) 23 394 596 — 192 485 = | г) 3 949 532 — 4 348 483 = |
3. Решите задачу.
Мастерская закупила 560 гаек. На ремонт первой машины потребовалось 203 гайки, а на ремонт второй машины – еще 293 гайки. Сколько гаек осталось в мастерской?
4. Решите задачу.
В концертном зале стояло 454 стула. Для проведения концерта принесли 123 новых стула, а после антракта – еще 13 стульев. Сколько всего стульев стало в концертном зале?
Сколько всего стульев стало в концертном зале?
Вариант II.
1. Выполните сложение.
| а) 3 484 558 + 9 499 834 = | б) 93 955 483 + 394 585 665 = |
| в) 3 495 863 + 35 384 588 = | г) 5 697 291 + 34 405 669 = |
2. Выполните вычитание.
| а) 4 856 342 — 3 495 384 = | б) 283 495 864 — 232 485 965 = |
| в) 5 965 493 — 3 449 594 = | г) 23 455 303 — 19 485 588 = |
3. Решите задачу.
В рулоне было смотано 327 м ленты. В первый день использовали 103 м, а во второй день – ещё 205 м. Сколько метров осталось в рулоне?
4. Решите задачу.
В магазине находилось 4 т 150 кг сахара. В первый день привезли 340 кг сахара, а во второй день – еще 4 ц сахара. Сколько кг сахара стало в магазине?
Вариант III.
1. Выполните сложение.
| а) 2 399 388 + 239 586 394 = | б) 435 483 + 495 868 991 = |
| в) 34 567 784 + 13 412 345 = | г) 6 563 544 + 23 876 554 = |
2. Выполните вычитание.
| а) 455 586 661 — 283 745 733 = | б) 40 954 586 — 22 394 583 = |
| в) 495 568 222 — 448 568 338 = | г) 3 949 532 — 2 349 588 = |
3. Решите задачу.
В моток смотано 459 м провода. В первый день истратили 119 м, а на второй день – 239 м провода. Сколько метров провода осталось в мотке?
4. Решите задачу.
На складе находилось 3 т и 450 кг муки. В первый день привезли 560 кг, через неделю привезли еще 5 ц муки. Сколько кг муки стало на складе?
Самостоятельная работа №6
Вариант I.
1. Найдите значение выражения: ( а + 46 ) : ( b — 48 ), если а = 35 и b = 57.
2. Упростите выражения.
а) с + 239 — 93;
б) 485 — 483 + d.
3. Составьте уравнение для решения задачи и решите его.
Было задумано некоторое число. К нему прибавили число 194, а потом прибавили ещё число 110 и получили число 322. Какое число было задумано?
4. Решите уравнения. a) (305 — ( ( 45 + х ) — 32 ) + 96 = 223;
б) 38 + ( 69 — y ) + 74 = 172.
Вариант II.
1. Найдите значение выражения: ( а — 34 ) * ( b + 9 ), если а = 60 и b = 11.
2. Упростите выражения.
а) 594 — 69 — а;
б) 149 + b — 54.
3. Составьте уравнение для решения задачи и решите его.
Было задумано некоторое число. Из этого числа вычли число 424, а затем прибавили число 392. В итоге, получилось число 632. Какое число было задумано?
4. Решите уравнения.
a) 209 — ( ( 145 + х ) — 12 ) + 96 = 123;
б) 18 + ( 159 — y ) + 34 = 172.
Вариант III.
1. Найдите значение выражения: ( а — 68 ) : b + 2 339, если а = 92 и b = 8.
2. Упростите выражения.
а) с + 239 — 193;
б) 485 — d + 384.
3. Составьте уравнение для решения задачи и решите его.
Было задумано некоторое число. Из этого числа вычли число 209, а затем прибавили число 47. В итоге, получилось число 217. Какое число было задумано?
4. Решите уравнения.
a) ( 111 — ( 45 + х ) ) + 96 = 123;
б) 29 + ( 59 — y ) + 15 = 72.
После завершения второй четверти, учащиеся должны:
1. уметь умножать натуральные числа и использовать эти знания;
2. уметь производить деление натуральных чисел, в том числе и деление с остатком, и использовать эти навыки при решении задач;
3. знать распределительное свойство умножения, уметь применять это свойство при устных вычислениях и при решении задач;
4. знать, что такое возведение числа в степень. Понимать, что такое корень и куб числа;
Понимать, что такое корень и куб числа;
5. понимать, что такое формула, и как производить вычисления по формуле.
Самостоятельная работа №7 на тему: «Действия с натуральными числами. Умножение»
Вариант I.
1. Выполните умножение.
| а) 283 * 46 = | б) 29 * 473 = | в) 841 * 93 = | г) 19 * 632 = |
| д) 570 * 340 = | е) 930 * 730 = | ж) 5100 * 360 = | з) 560 * 230 = |
2. Умножьте числа, используя наиболее удобный порядок действий.
а) 25 * 491 * 4 * 200 =
б) 4 * 324 * 25 * 300 =
3. Расположите уравнения в порядке убывания, не производя никаких действий.
| 35 * 34 = | 34 * 33 = | 34 * 36 = | 32 * 32 = |
4. Решите задачу.
В двухэтажной школе всего 32 кабинета и в каждом кабинете по 12 парт. В трехэтажной школе 45 кабинетов и в каждом кабинете по 14 парт. Сколько всего парт необходимо городским школам, если в городе 8 двухэтажных и 5 трехэтажных школ?
Сколько всего парт необходимо городским школам, если в городе 8 двухэтажных и 5 трехэтажных школ?
Вариант II.
1. Выполните умножение.
| а) 342 * 57 = | б) 64 * 268 = | в) 342 * 89 = | г) 32 * 864 = |
| д) 920 * 560 = | е) 470 * 990 = | ж) 2300 * 630 = | з) 430 * 540 = |
2. Умножьте числа, используя наиболее удобный порядок действий.
а) 25 * 376 * 4 * 500 =
б) 4 * 265 * 25 * 200 =
3. Расположите уравнения в порядке убывания, не производя никаких действий.
| 85 * 84 = | 84 * 83 = | 84 * 86 = | 82 * 82 = |
4. Решите задачу.
В поселке построено 18 домов. Из них 4 трехэтажных, 6 двухэтажных, остальные одноэтажные дома. В трехэтажных домах – 18 окон, в двухэтажных – 14 окон, в одноэтажных – 8 окон. Сколько окон необходимо для 4 таких же посёлков?
Вариант III.
1. Выполните умножение.
| а) 563 * 24 = | б) 32 * 441 = | в) 324 * 87 = | г) 23 * 728 = |
| д) 220 * 680 = | е) 240 * 580 = | ж) 7500 * 290 = | з) 920 * 630 = |
2. Умножьте числа, используя наиболее удобный порядок действий.
а) 25 * 376 * 4 * 300 =
б) 4 * 641 * 25 * 100 =
3. Расположите уравнения в порядке убывания, не производя никаких действий.
| 65 * 64 = | 64 * 63 = | 64 * 66 = | 62 * 62 = |
4. Решите задачу.
В один мешок помещается 26 кг картофеля, или 34 кг муки, или 38 кг сахара. Сколько всего весит груз, если в машину погрузили 32 мешка картофеля, 38 мешков муки и 52 мешка сахара?
Самостоятельная работа №8 на тему: «Деление натуральных чисел»
Вариант I.
1. Выполните деление.
| а) 475 860 : 5 = | б) 8 412 : 4 = | в) 492 000 000 : 1 000 = |
| г) 270 930 : 3 = | д) 386 240 : 5 = | е) 19 688 : 23 = |
2. Решите уравнения.
Решите уравнения.
| а) X : 85 = 2 210 | б) 36 690 : Y = 10 | в) 792 : X = 4 |
| г) 15 * ( 39 : X ) = 45 | д) Y : 42 = 168 | е) 65 065 : Y = 1 001 |
3. Решите задачу.
Фермеру необходимо вспахать поле размером 318500 м. За сколько дней он вспашет поле, если известно, что за день он может вспахать 45 500 м?
4. Остаток равен 18, неполное частное – 35 и делитель – 23. Найдите делимое.
Вариант II.
1. Выполните деление.
| а) 489 560 : 5 = | б) 36 690 : 3 = | в) 657 000 : 1 000 = |
| г) 960 552 : 6 = | д) 522 240 : 2 = | е) 67 065 : 85 = |
2. Решите уравнения.
| а) X : 26 = 456 | б) 4 760 : Y = 85 | в) 792 : X = 8 |
| г) 35 * ( 54 : X ) = 315 | д) Y : 3 = 3015 | е) 524 : Y = 131 |
3. Решите задачу.
Решите задачу.
Станок производит 1200 заготовок за 1 час. Сколько минут нужно машине, чтобы приготовить 48 000 заготовок?
4. Остаток равен 33, неполное частное – 41 и делитель – 25. Найдите делимое.
Вариант III.
1. Выполните деление.
| а) 236 560 : 4 = | б) 36 690 : 6 = | в) 612 345 000 : 1 000 = |
| г) 960 440 : 8 = | д) 678 350 : 2 = | е) 31 464 : 69 = |
2. Решите уравнения.
| а) X : 25 = 14 | б) 1 820 : Y = 28 | в) 1 836 : X = 6 |
| г) 52 * Y = 468 | д) Y : 3 = 7 659 | е) 1048 : Y = 131 |
3. Решите задачу.
Комбайн убирает 30 га пшеницы за 1 час. Сколько дней ему нужно, чтобы убрать площадь равную 1200 га, если в день он будет работать по 10 часов?
4. Остаток равен 24, неполное частное – 25 и делитель – 28. Найдите делимое.
Самостоятельная работа №9 на темы: «Выражения, уравнения и решение уравнений», «Квадрат и куб числа»
Вариант I.
1. Решите примеры.
а) 34 + ( 239 — 606 : 6 ) * 4 — 393 : 3 =
б) 152 =
в) 73 =
г) ( 14 + 7 )2 — ( 5 + 13 )2 + 287 =
2. Упростите выражение и найдите его значение при с=34: 47с + 34 — 58 + 12с — 58.
3. Решите уравнения.
а) 15 * х = 945
б) 3 * y — 45 = 44
4. Решите задачу.
Бабушка и внучка слепили 124 пельмени. Сколько пельменей слепили бабушка и сколько внучка, если бабушка лепила в 3 раза быстрее, чем внучка?
Вариант II.
1. Решите примеры.
а) 472 — ( 29 + 124 : 4 ) — 72 : 8 =
б) 182 =
в) 63 =
г) ( 5 + 27 )2 — ( 4 + 12 )2 — 64 =
2. Упростите выражение и найдите его значение при с=12: 19с + 57 — 58с + 29с — 38 + 5с.
Упростите выражение и найдите его значение при с=12: 19с + 57 — 58с + 29с — 38 + 5с.
3. Решите уравнения:
а) 15 * х = 180
б) 12 * y + 36 = 96
4. Решите задачу.
Инженер и студент отремонтировали 248 приборов. Инженер ремонтировал приборы в 3 раза быстрее, чем студент. Сколько приборов починил каждый?
Вариант III.
1. Решите примеры.
а) 365 + ( 299 — 342 : 2 ) * 5 — 687 : 3 =
б) 172 =
в) 83 =
г) ( 4 + 7 )2 — ( 5 + 23 )2 + 787 =
2. Упростите выражение и найдите его значение при с=12: 47 + 56с — 6с + 34 — 12с.
3. Решите уравнения.
а) 32 * х = 1280
б) 8 * y + 36 = 356
4. Решите задачу.
Портной и его ученик сшили 213 фартуков. Портной работал в 2 раза быстрее, чем его ученик. Сколько фартуков сшил портной, а сколько ученик?
Самостоятельная работа №10 на темы: «Окружность и круг».
 «Обыкновенные дроби»
«Обыкновенные дроби»Вариант I.
1. Нарисуйте окружность с центром в точке X и радиусом 4 см 6 мм. Нарисуйте отрезок CD так, чтобы он проходил через центр окружности и пересекал ее в точках C и D. Как называются отрезки СX и СD? Определите их длину.
2. Решите задачу.
Оля нашла 26 грибов, из них 18 маслят. Какую часть грибов составляют маслята?
3. Решите задачу.
Рыбаки поймали 112 кг рыбы. Из них 10⁄28 – караси. Сколько карасей поймали рыбаки?
4. Решите задачу.
Коля прочитал 85 страниц журнала, что составило 5⁄12 от общего числа страниц. Сколько страниц в журнале?
Вариант II.
1. Нарисуйте окружность с центром в точке Y и радиусом 3 см 8 мм.
Нарисуйте отрезок EF так, чтобы он проходил через центр окружности и пересекал ее в точках E и F. Как называются отрезки YE и EF? Определите их длину.
2. Решите задачу.
Коля собрал в корзину 31 фрукт, из них 22 фрукта – это груши. Какую часть собранных фруктов составляют груши?
3. Решите задачу.
Школьники собрали 104 кг овощей. 13⁄26 от общего числа овощей составляют помидоры. Сколько кг помидор собрали школьники?
4. Решите задачу.
Мастер отремонтировал 35 приборов, что составило 5⁄12 от общего количества приборов. Сколько всего приборов надо отремонтировать мастеру?
Вариант III.
1. Нарисуйте окружность с центром в точке Z и радиусом 2 см 6 мм. Нарисуйте отрезок GH так, чтобы он проходил через центр окружности и пересекал ее в точках G и H. Как называются отрезки GZ и GH? Определите их длину.
2. Решите задачу.
У Саши есть 29 карандашей. Из них 19 карандашей – это простые карандаши. Какую часть карандашей составляют цветные карандаши?
3. Решите задачу.
Решите задачу.
Мастер сделал 312 деталей. Из них 3⁄24 часть деталей – деревянные. Сколько деревянных деталей сделал мастер?
4. Решите задачу.
Ребята из 5 класса собрали 32 кг ягод. Это составляет 3⁄24 от всего количества собранных ягод. Сколько всего ягод было собрано?
Самостоятельная работа №11 на тему: «Сравнение дробей»
Вариант I.
1. Задан луч длиной в 12 единиц. Отметьте на числовом луче:
| а) 2⁄12 части | б) 6⁄12 части | 2⁄3 части | 5⁄4 части |
2. Сравните дроби.
а) 23⁄38 и 16⁄18
б) 21⁄45 и 15⁄26
3. Найдите три решения неравенства.
а) 21⁄22< x < 22⁄22
б) 7⁄11 < z < 8⁄11
4. При каких значениях х:
а) дробь х⁄22 будет правильной?
б) дробь 15⁄х будет неправильной?
Вариант II.
1. Задан луч длиной в 15 единиц. Отметьте на числовом луче:
| 4⁄15 части | 3⁄15 части | 3⁄5 части | 2⁄3 части |
2. Сравните дроби.
а) 26⁄34 и 15⁄17
б) 22⁄49 и 18⁄21
3. Найдите три решения неравенства.
а) 19⁄20 < x < 20⁄20
б) 7⁄9 < z < 8⁄9
4. При каких значениях y:
При каких значениях y:
а) дробь y⁄19 будет правильной?
б) дробь 23⁄y будет неправильной?
Вариант III.
1. Задан луч длиной в 18 единиц. Отметьте на числовом луче:
| 2⁄18 части | 6⁄18 части | 2⁄3 части | 5⁄6 части |
2. Сравните дроби.
а) 26⁄31 и 18⁄19
б) 23⁄41 и 17⁄18
3. Найдите три решения неравенства.
а) 9⁄10< y < 10⁄10
б) 5⁄7 < z < 6⁄7
4. При каких значениях z:
а) дробь z⁄29 будет правильной?
б) дробь 13⁄z будет неправильной?
Самостоятельная работа №12 на тему: «Сложение и вычитание обыкновенных дробей»
Вариант I.
1. Решите примеры.
а) 26⁄31 + 18⁄31 — 6⁄31;
б) 17⁄125 — 5⁄125 + 106⁄125;
в) 19⁄39 + ( 18⁄39 — 6⁄39 ) — 13⁄39;
2. Решите уравнения.
а) x + 6⁄18 = 16⁄18
б) 13⁄25 — ( y + 6⁄25 ) = 4⁄25
3. Решите задачу.
Первый спортсмен пробежал 5⁄7 км, а второй спортсмен за тоже время пробежал 6⁄7 км. На сколько метров больше пробежал первый спортсмен?
4. Решите задачу.
Из мешка взяли 2⁄9 части муки, а потом – ещё 3⁄9 части. В мешке осталось 14 кг. Сколько кг муки было в мешке?
В мешке осталось 14 кг. Сколько кг муки было в мешке?
Вариант II.
1. Решите примеры.
а) 15⁄38 + 12⁄38 — 11⁄38;
б) 23⁄192 — 8⁄192 + 48⁄192;
в) 19⁄56 + ( 21⁄56 — 12⁄56 ) — 16⁄56;
2. Решите уравнения.
а) x — 5⁄12 = 3⁄12
б) 18⁄23 — ( 7⁄23 + y ) = 5⁄23
3. Решите задачу.
Расстояние от дачи до пруда равно 3⁄5 км, а от дачи до леса равно 4⁄5 км. На сколько метров расстояние от дачи до пруда больше, чем расстояние от дачи до леса?
4. Решите задачу.
Из погреба вытащили 3⁄12 части картофеля, а потом – ещё 2⁄12 части. После этого в погребе осталось 56 кг картофеля. Сколько картофеля было в погребе?
После этого в погребе осталось 56 кг картофеля. Сколько картофеля было в погребе?
Вариант III.
1. Решите примеры.
а) 19⁄28 + 12⁄28 — 16⁄28;
б) 13⁄176 — 11⁄176 + 49⁄176;
в) 27⁄42 + ( 12⁄42 — 6⁄42 ) — 12⁄42;
2. Решите уравнения.
а) x + 12⁄23 = 20⁄23
б) 28⁄35 — ( y + 16⁄35 ) = 4⁄35
3. Решите задачу.
Расстояние от школы до больницы равно 8⁄9 км, а от школы до бассейна равно 4⁄9 км. На сколько метров расстояние от школы до больницы больше, чем расстояние от школы до бассейна?
4. Решите задачу.
Решите задачу.
Из рулона отрезали 3⁄8 части ткани, а потом – ещё 2⁄8 части. После этого в рулоне осталось 32 метра ткани. Сколько метров ткани было в рулоне?
Самостоятельная работа №13 на тему: «Сложение и вычитание смешанных чисел»
Вариант I.
1. Решите примеры.
а) 4 19⁄28 + 6 12⁄28;
б) 5 13⁄176 — 2 11⁄176;
в) 12 27⁄43 + 3 12⁄43.
2. Решите уравнения.
а) 23 18⁄38 + х =36 12⁄28;
б) 7 14⁄16 — y = 3 11⁄16;
в) y + 18 27⁄53 = 24 13⁄53;
3. Решите задачу.
В первый день в мастерской использовали 23 3⁄18 метра проволоки, а во второй день – ещё 18 2⁄18 части. После этого в рулоне осталось 32 метра проволоки. Сколько метров проволоки было в рулоне?
После этого в рулоне осталось 32 метра проволоки. Сколько метров проволоки было в рулоне?
Вариант II.
1. Решите примеры.
а) 3 13⁄22 + 3 12⁄22;
б) 8 15⁄126 — 4 15⁄126;
в) 13 22⁄49 + 3 14⁄49.
2. Решите уравнения.
а) 2 18⁄43 + х = 3 4⁄43;
б) 17 15⁄19 — y = 12 12⁄19;
в) y — 18 38⁄56 = 24 27⁄56.
3. Решите задачу.
В первый день в школе покрасили 17 5⁄23 метра коридора, а во второй день – ещё 23 4⁄23 метра. Сколько метров было покрашено за 2 дня?
Вариант III.
1. Решите примеры.
а) 5 19⁄23 + 6 12⁄23;
б) 7 13⁄48 — 3 11⁄48;
в) 82 25⁄78 + 34 12⁄78
2. Решите уравнения.
Решите уравнения.
а) 6 17⁄29 + х = 23 4⁄29;
б) 8 15⁄128 — y = 6 12⁄128;
в) y — 18 38⁄47 = 5 27⁄47.
3. Решите задачу.
Фермер убрал 13 6⁄13 метра грядки в первый день, а на следующий день – ещё 18 3⁄13 метра. После двух дней работы осталось убрать 6 метров. Какова длина грядки?
Самостоятельная работа №14 на темы: «Десятичная запись дробных чисел». «Сравнение десятичных дробей»
Вариант I.
1. Заданные дроби представьте, как десятичные дроби.
а) 5 59⁄10
б) 6 1⁄100
в) 17 137⁄1000
2. Сравните числа.
а) 5,596 и 5,629
б) 7,34 и 7,339
в) 0,684 и 0,6840
3. Переведите из одной единицы измерения в другую.
Переведите из одной единицы измерения в другую.
а) представьте в тоннах: 92 ц; 887 кг; 14 т 12 кг;
б) представьте в квадратных дециметрах: 8 м 2; 57 см 2; 8 м2 77 дм2.
4. Отметьте точки: 0,2; 0,8; 1,1; 2,3; 2,1; 3,7 на числовом отрезке, равном 5 единицам.
Вариант II.
1. Заданные дроби представьте, как десятичные дроби.
а) 18 59⁄1000
б) 7⁄10
в) 7 137⁄100
2. Сравните числа.
а) 35,97 и 35,971
б) 8,449 и 8,540
в) 0,92 и 0,920
3. Переведите из одной единицы измерения в другую.
а) представьте в тоннах: 3 ц; 239 кг; 23 т 28 кг;
б) представьте в квадратных дециметрах: 13 м 2; 2 см 2; 87 м2 32 дм2.
4. Отметьте точки: 0,5; 0,7; 1,1; 2; 2,3; 3,5 на числовом отрезке, равном 6 единицам.
Отметьте точки: 0,5; 0,7; 1,1; 2; 2,3; 3,5 на числовом отрезке, равном 6 единицам.
Вариант III.
1. Заданные дроби представьте, как десятичные дроби.
а) 15 43⁄100
б) 9 23⁄1000
в) 5⁄10
2. Сравните числа.
а) 29,345 и 29,354
б) 171,89 и 171,889
в) 0,93 и 0,930
3. Переведите из одной единицы измерения в другую.
а) представьте в тоннах: 18 ц; 56 кг; 3 т 9 кг;
б) представьте в квадратных дециметрах: 4 м 2; 23 см 2; 2 м2 56 дм2.
4. Отметьте точки: 0,4; 0,5; 1,4; 1,9; 2,4; 3,0 на числовом отрезке, равном 4 единицам.
Самостоятельная работа №15 на темы: «Сложение и вычитание десятичных дробей». «Округление чисел»
Вариант I.
1. Решите примеры на сложение десятичных дробей.
Решите примеры на сложение десятичных дробей.
а) 29,3 + 4,35 =
б) 68,9 + 19,1 =
в) 0,68 + 6,4 =
2. Решите примеры на вычитание десятичных дробей.
а) 35,1 — 13,2 =
б) 37 — 27,3 =
в) 13,28 — 5,327 =
3. Решите задачу:
В первый день плот проплыл 14,8 км, во второй день – на 1 км 700 м больше, чем в первый день. В третий день плот проплыл на 600 м меньше, чем во второй день. Сколько всего км проплыл плот?
4. Округлите:
а) целую часть числа 2539,48190 до сотен, до десятков, до единиц;
б) дробную часть числа 2539,48190 до тысячных, до сотен, до десятков.
Вариант II.
1. Решите примеры на сложение десятичных дробей.
а) 79,3 + 8,15 =
б) 18 + 8,8 =
в) 0,93 + 23,4 =
2. Решите примеры на вычитание десятичных дробей.
а) 48,2 — 4,98 =
б) 96 — 48,6 =
в) 37,67 — 13,168 =
3. Решите задачу.
Решите задачу.
В первом пакете было 15,7 кг песка, во втором – на 350 г больше, чем в первом. В третьем – на 1200 г меньше, чем в первом. Сколько кг песка в трех пакетах?
4. Округлите:
а) целую часть числа 3462,9470 до сотен, до десятков, до единиц;
б) дробную часть числа 3462,9470 до тысячных, до сотен, до десятков.
Вариант III.
1. Решите примеры на сложение десятичных дробей.
а) 34,3 + 13,11 =
б) 8 + 47,7 =
в) 0,123 + 23,942 =
2. Решите примеры на вычитание десятичных дробей.
а) 69,2 — 7,88 =
б) 91,76 — 18,6 =
в) 8,94 — 5,452 =
3. Решите задачу.
3 дня бабушка пекла блины. В первый день она использовала 1,2 кг муки, во второй день – на 500 г меньше, чем в первый день, а на третий день – на 300 г больше, чем во второй день. Сколько муки она использовала за три дня?
4. Округлите:
Округлите:
а) целую часть числа 4392,73910 до сотен, до десятков, до единиц;
б) дробную часть числа 4392,73910 до тысячных, до сотен, до десятков.
Самостоятельная работа №16 на тему: «Умножение десятичных дробей на натуральные числа»
Вариант I.
1. Выполните умножение.
| а) 8,3 * 8 = | б) 7,12 * 34 = | в) 0,235 * 93 = | г) 1,93 * 100 = |
2. Найдите значение выражения: х + ( 3,74х — 1,474х ) при х=3; 100; 374; 1000.
3. Решите задачу.
Одновременно навстречу друг другу из двух деревень, расстояние между которыми составляет 45,8 км, вышли пешеходы. Скорость первого пешехода составляет 4,2 км/ч, а скорость второго – 4,5 км/ч. Какое расстояние будет между ними через 4 часа?
4. Решите задачу.
Машина проехала 360 км за 6 часов. Какое расстояние она преодолеет, передвигаясь с той же скоростью, за 1⁄4 часа, за 2 1⁄3 часа?
Вариант II.
1. Выполните умножение.
| а) 7,48 * 12 = | б) 3,57 * 7 = | в) 0,873 * 87 = | г) 1,698 * 1000 = |
2. Найдите значение выражения: 5х + ( 6,59х + 2,483х ) при х=5; 100; 324; 1000.
3. Решите задачу.
Одновременно в противоположных направлениях из города выехали 2 машины. Скорость первой машины составляет 54,7 км/ч, а скорость второй – 76,2 км/ч. Какое расстояние будет между ними через 3 часа?
4. Решите задачу.
Велосипедист преодолел 72 км за 3 часа. Какое расстояние он преодолеет, перемещаясь с той же скоростью, за 5⁄6 часа, за 2 1⁄3 часа?
Вариант III.
1. Выполните умножение.
| а) 9,4 * 6 = | б) 8,34 * 56 = | в) 0,517 * 62 = | г) 6,787 * 1000 = |
2. Найдите значение выражения: ( 8,45х — 3,594х ) — х при х=8; 100; 843; 1000.
3. Решите задачу.
Одновременно навстречу друг другу из двух городов выехали мотоциклы. Расстояние между городами составляет 234,8 км. Скорость первого мотоциклиста составляет 34,5 км/ч, а скорость второго – 56,2 км/ч. Какое расстояние будет между ними через 2 часа?
4. Решите задачу.
Моторная лодка прошла 24 км за 2 часа. Какое расстояние она пройдет, перемещаясь с той же скоростью, за 1⁄4 часа, за 3 1⁄3 часа?
Самостоятельная работа №17 на тему: «Деление десятичных дробей на натуральные числа»
Вариант I.
1. Выполните деление.
| а) 2,729 : 6 = | б) 283,85 : 4 = | в) 4 : 13 = | г) 0,095 : 10 = |
2. Решите уравнения.
| а) 5X — 0,4 = 23,6 | б) 48,2 : Y = 10,4 |
3. Решите задачу.
За два дня рабочие отремонтировали 3,6 км дороги. В первый день они отремонтировали 1/4 части дороги. Сколько км дороги они отремонтировали во второй день?
В первый день они отремонтировали 1/4 части дороги. Сколько км дороги они отремонтировали во второй день?
4. Решите задачу.
4 класс и 5 класс собирали макулатуру. Пятиклассники собрали в 2 раза больше макулатуры, чем ребята из 4 класса. Вместе они собрали 239,7 кг. Сколько кг собрали ребята из 5 класса и сколько ребята из 4 класса?
Вариант II.
1. Выполните деление.
| а) 5,837 : 7 = | б) 291,49 : 5 = | в) 5 : 18 = | г) 0,023 : 10 = |
2. Решите уравнения.
| а) 8X + 2,8 = 18,6 | б) 28,1 : Y = 12,4 |
3. Решите задачу.
За два дня бригада собрала 147,6 кг ягод. В первый день они собрали 4/9 части урожая ягод. Сколько кг ягод они собрали во второй день?
4. Решите задачу.
Две бригады собирали картофель. Первая бригада собрала в 3 раза больше картофеля, чем вторая. Обе бригады вместе собрали 49,6 ц урожая. Сколько центнеров картофеля собрали первая бригада и сколько вторая бригада?
Обе бригады вместе собрали 49,6 ц урожая. Сколько центнеров картофеля собрали первая бригада и сколько вторая бригада?
Вариант III.
1. Выполните деление.
| а) 4,752 : 9 = | б) 472,49 : 6 = | в) 7 : 19 = | г) 0,044 : 10 = |
2. Решите уравнения.
| а) 5X + 2,5 = 24 | б) 14,2 : Y = 3,4 |
3. Решите задачу.
За 2 дня мотоциклист преодолел 394,1 км. В первый день он проехал 4⁄7 части пути. Сколько км он проехал во второй день?
4. Решите задачу.
Мама собрала в 5 раз больше ягод, чем дочка. Вместе они собрали 34,5 кг ягод. Сколько ягод собрала мама и сколько дочка?
Самостоятельная работа №18 на тему: «Среднее арифметическое»
Вариант I.
1. Найдите среднее арифметическое четырех чисел: 4,5; 5,6; 4,9; 5,1.
2. Решите задачу.
В течение часа машина двигалась со скоростью 67,5 км/ч, в течение второго часа – со скоростью 51,6 км/ч. В течение третьего часа её скорость составила 72,3 км/ч. Какова средняя скорость машины? Сколько км она преодолела за 3 часа?
3. Решите задачу.
Среднее арифметическое трех чисел составляет 14,5. Первое число – 14,1, а второе число на 0,8 больше третьего числа. Назовите эти числа.
4. Решите задачу.
Расстояние между двумя деревнями равно 340 км. Автомобиль преодолел половину пути со скоростью 58 км/ч, а вторую половину – со скоростью 49 км/ч. Какова средняя скорость автомобиля на протяжении всего пути?
Вариант II.
1. Найдите среднее арифметическое четырех чисел: 12,3; 12,9; 11,6; 13,1.
2. Решите задачу.
В течение первого часа спортсмен шел со скоростью 11,2 км/ч, в течение второго часа – со скоростью 10,7 км/ч, а в течение третьего часа его скорость составила 9,8 км/ч. Какова средняя скорость спортсмена? Какое расстояние он прошел за 3 часа?
Какова средняя скорость спортсмена? Какое расстояние он прошел за 3 часа?
3. Решите задачу.
Среднее арифметическое трех чисел составляет 28,5. Первое число – 28,2, а второе на 0,9 больше третьего числа. Назовите эти числа.
4. Решите задачу.
Расстояние между двумя городами составляет 52 км. Первую половину пути велосипедист передвигался со скоростью 18 км/ч, а вторую половину – со скоростью 22 км/час. Какова средняя скорость велосипедиста на всем протяжении пути?
Вариант III.
1. Найдите среднее арифметическое четырех чисел: 9,1; 9,9; 11,1; 10,7.
2. Решите задачу.
В течение первого часа лодка двигалась со скоростью 15,5 км/ч, во второй час движения её скорость составила 17,4 км/ч, а в течение третьего часа – 12,7 км/ч. Какая средняя скорость лодки? Сколько км она преодолела за 3 часа?
3. Решите задачу.
Среднее арифметическое трех чисел составляет 13,2. Первое число – 13,9, а второе – на 0,7 больше третьего числа. Назовите эти числа.
Первое число – 13,9, а второе – на 0,7 больше третьего числа. Назовите эти числа.
4. Решите задачу.
Расстояние между двумя деревнями составляет 24 км. Первую половину пути пешеход двигался со скоростью 8 км/ч, а вторую половину – со скоростью 9 км/ч. Какова средняя скорость пешехода на всем протяжении пути?
Самостоятельная работа №19 на тему: «Проценты, задачи на проценты»
Вариант I.
1. Решите задачу.
В спортивной секции занимается 60 учеников, из них 70% составляют девочки. Сколько мальчиков занимается в спортивной секции?
2. Решите задачу.
Ребята четвертых и пятых классов собирали макулатуру. Ребята пятого класса собрали 150 кг макулатуры, что составило 60% общего веса собранной макулатуры. Сколько кг макулатуры собрали ребята?
3. Решите задачу.
Из 15 кг яблок получается 12 кг яблочного пюре. Каков процент выхода пюре из яблок?
Каков процент выхода пюре из яблок?
Вариант II.
1. Решите задачу.
В 5 классе числится 30 учеников, 60% из них – мальчики. Сколько девочек учится в 5 классе?
2. Решите задачу.
2 бригады собирали помидоры. Первая бригада собрала 320 кг помидор, что составило 40% от общего урожая. Сколько всего помидор собрали обе бригады?
3. Решите задачу.
Из 60 семян взошли 55 растений. Найдите процент всхожести семян.
Вариант III.
1. Решите задачу.
В школе работает 40 человека. Из них 80% – женщины. Сколько мужчин работает в школе?
2. Решите задачу.
Бабушка и внучка собирали яблоки. Бабушка собрала 30 кг яблок, что составило 80% от общего сбора. Сколько кг яблок собрали бабушка и внучка вместе?
3. Решите задачу.
При перемалывании 40 кг зерна получили 25 кг муки. Найдите процент выхода муки.
Найдите процент выхода муки.
Математика 5 класс — Мир математики
I. Чтобы разделить десятичную дробь на натуральное число, нужно делить дробь на это число, как делят натуральные числа и поставить в частном запятую тогда, когда закончится деление целой части.
Примеры.
Выполнить деление: 1) 96,25:5; 2) 4,78:4; 3) 183,06:45.
Решение.
Пример 1) 96,25:5.
Делим «уголком» так, как делят натуральные числа. После того, как сносим цифру 2 (число десятых — первая цифра после запятой в записи делимого 96,25), в частном ставим запятую и продолжаем деление.
Ответ: 19,25.
Пример 2) 4,78:4.
Делим так, как делят натуральные числа. В частном поставим запятую сразу, как снесем 7 — первую цифру после запятой в делимом 4,78. Продолжаем деление дальше. При вычитании 38-36 получаем 2, но деление не окончено. Как поступаем? Мы знаем, что в конце десятичной дроби можно приписывать нули — от этого значение дроби не изменится. Приписываем нуль и делим 20 на 4. Получаем 5 — деление окончено.
В частном поставим запятую сразу, как снесем 7 — первую цифру после запятой в делимом 4,78. Продолжаем деление дальше. При вычитании 38-36 получаем 2, но деление не окончено. Как поступаем? Мы знаем, что в конце десятичной дроби можно приписывать нули — от этого значение дроби не изменится. Приписываем нуль и делим 20 на 4. Получаем 5 — деление окончено.
Ответ: 1,195.
Пример 3) 183,06:45.
Делим как 18306 на 45. В частном поставим запятую как только снесем цифру 0 — первую цифру после запятой в делимом 183,06. Так же, как в примере 2) нам пришлось приписать нуль к числу 36 — разности чисел 306 и 270.
Ответ: 4,068.
Вывод: при делении десятичной дроби на натуральное число в частном ставим запятую сразу после того, как сносим цифру в разряде десятых делимого. Обратите внимание: все выделенные красным цветом цифры в этих трех примерах относятся к разряду десятых долей делимого.
Смотрите видео: «Как разделить десятичную дробь на натуральное число».
II. Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д. нужно перенести запятую влево на 1, 2, 3 и т. д. цифр.
Примеры.
Выполнить деление: 1) 41,56:10; 2) 123,45:100; 3) 0,47:100; 4) 8,5:1000; 5) 631,2:10000.
Решение.
Перенос запятой влево зависит от того, сколько в делителе нулей после единицы. Так, при делении десятичной дроби на 10мы будем переносить в делимом запятую влево на одну цифру; при делении на100 — перенесем запятую влево на двецифры; при делении на 1000 перенесем в данной десятичной дроби запятую на три цифры влево.
В примерах 3) и 4) пришлось приписать нули перед десятичной дробью, чтобы удобнее было переносить запятую. Однако, приписывать нули можно мысленно, и вы будете это делать, когда хорошо научитесь применять правило II для деления десятичной дроби на 10, 100, 1000 и т. д.
Однако, приписывать нули можно мысленно, и вы будете это делать, когда хорошо научитесь применять правило II для деления десятичной дроби на 10, 100, 1000 и т. д.
Смотрите видео: «Как разделить десятичную дробь на 10, 100, 1000 и т.д.»
I. Чтобы умножить десятичную дробь на натуральное число, нужно умножить ее на это число, не обращая внимания на запятую, и в полученном произведении отделить запятой столько цифр справа, сколько их было после запятой в данной дроби.
Примеры. Выполнить умножение: 1) 1,25·7; 2) 0,345·8; 3) 2,391·14.
Решение.
Смотрите видео: « Как умножить десятичную дробь на натуральное число».
II. Чтобы умножить одну десятичную дробь на другую, нужно выполнить умножение , не обращая внимания на запятые, и в полученном результате отделить запятой справа столько цифр, сколько их было после запятых в обоих множителях вместе.
Примеры. Выполнить умножение: 1) 18, 2·0,09; 2) 3,2·0,065; 3) 0,54·12,3.
Решение.
Смотрите видео: «Умножение десятичных дробей.»
III. Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д. нужно перенести запятую вправо на 1, 2, 3 и т. д. цифр.
Примеры. Выполнить умножение: 1) 3,25·10; 2) 0,637·100; 3) 4,307·1000; 4) 2,04·1000; 5) 0,00031·10000.
Решение.
Смотрите видео: «Умножение десятичных дробей на 10, 100, 1000 и т. д.»
IV. Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д. нужно перенести запятую влево на 1, 2, 3 и т. д. цифр.
Примеры. Выполнить умножение: 1) 28,3·0,1; 2) 324,7·0,01; 3) 6,85·0,01; 4) 6179,5·0,001; 5) 92,1·0,0001.
Решение.
Смотрите видео: «Умножение десятичных дробей на 0,1; 0,001; 0,0001 и т. д.»
Поиск Поиск
-
Школьный помощник
- математика 5 класс
- математика 6 класс
- алгебра 7 класс
- алгебра 8 класс
- геометрия 7 класс
- русский язык 5 класс
- русский язык 6 класс
- русский язык 7 класс
- математика
- алгебра
- геометрия
- русский язык
«»
следующая предыдущая вернуться на предыдущую страницу
Такой страницы нет !!!
- Популярные запросы
- Обстоятельство
- Дополнение
- Определение
- Деление дробей
- Русский язык 7 класс
- Русский язык 6 класс
- Русский язык 5 класс
- Алгебра 7 класс
- Математика 6 класс
- Алгебра 8 класс
- Математика 5 класс
- Наименьшее общее кратное
- Наибольший общий делитель.
 Взаимно простые числа
Взаимно простые числа - Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
- Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
- Деление и дроби
- Квадратный корень из неотрицательного числа
- Доли. Обыкновенные дроби
- Окружность и круг
- Антонимы. Синонимы
- Десятичная запись дробных чисел
- Буквы о – а в корнях -лаг- / -лож-, -рос- / -раст- (-ращ-)
Примеры на умножение и деление натуральных чисел | Учебно-методический материал по алгебре (5 класс) на тему:
«Мастер-умножитель»
Предлагаются занимательные примеры. При решении каждого из них получается слово (для этого используем ключ).
1) Ключ 0 1 2 3 4 5 6 7 8 9
И ф л р н а м о г ь
689832 : 67 888982 : 43 181804 : 604
928564 : 91 595161 : 987 965280 : 32
147368 : 169 550940 : 65
767010 : 74 686868 : 546
2) Ключ 0 1 2 3 4 5 6 7 8 9
ь о л с т п а к р е
778 ∙ 73 1398 ∙ 25 102 ∙ 88
25945 ∙ 16 23458 ∙ 37 21333 ∙ 37
166 ∙ 49 83 ∙ 32 4102 ∙ 97
1023 ∙ 71 5489 ∙ 14
3) Ключ 0 1 2 3 4 5 6 7 8 9
к с о в а т е и н р
976968 : 27 947648 : 64 101188 : 82
956662 : 23 638638 : 77 657072 : 18
4) Ключ 0 1 2 3 4 5 6 7 8 9
ь л п е в о н к м а
128520 : 17 238280 : 28 87653 : 37
9972 : 12 73160 : 31 99374 : 22
96930 : 45 151656 : 71
5) Ключ 0 1 2 3 4 5 6 7 8 9
ь к у р п а н о л т
4127 ∙ 111 367 ∙ 34 2026 ∙ 76
3133 ∙ 155 28711 ∙ 16 883 ∙ 15
365 ∙ 131 452 ∙ 15 3367 ∙ 53
751 ∙ 165 1149 ∙ 85
1097 ∙ 443 10084 ∙ 45
328 ∙ 283 485 ∙ 17
6) Ключ 0 1 2 3 4 5 6 7 8 9
о м л ч п я с и а е
49110 : 321 967296 : 352 815670 : 19
81832 : 212 612469 : 143 511225 : 715
178192 : 344 865260 : 23
7) Ключ 0 1 2 3 4 5 6 7 8 9
а х м б н и о к е л
276504 : 984 922507 : 23 196317 : 99
954434 : 26 984256 : 14 778088 : 19
972928 : 32 962090 : 47
205407 : 787 826386 : 209
8) Ключ 0 1 2 3 4 5 6 7 8 9
л о с п р а к е т в
2591 ∙ 111 373 ∙ 244 2179 ∙ 28
1954 ∙ 175 142 ∙ 197 755 ∙ 47
773 ∙ 385 134 ∙ 187 508 ∙ 69
2113 ∙ 432 713 ∙ 905 375 ∙ 827
1477 ∙ 145 1993 ∙ 305
Задачи и примеры по математике за 5 класс: тренажер по математике для 5 класса онлайн
Ваш ребенок с трудом решает задачи и не может освоить десятичные дроби? Мы поможем решить эту проблему. Предлагаем пройти тест по математике за 5 класс на интеллектуальной платформе Skills4u абсолютно бесплатно. Всего за несколько минут вы сможете оценить уровень владения материалом и получите рейтинг, составленный на основе правильных ответов.
Предлагаем пройти тест по математике за 5 класс на интеллектуальной платформе Skills4u абсолютно бесплатно. Всего за несколько минут вы сможете оценить уровень владения материалом и получите рейтинг, составленный на основе правильных ответов.
Наша платформа предлагает интерактивные тесты по математике (5 класс), основанные на интеллектуальном алгоритме. Суть в том, что выдача заданий происходит на основе анализа результатов опроса. Это персонализированный подход, позволяющий учесть уровень подготовки каждого ученика и предложить примеры, которые ему по силам. При этом каждый раз задания могут быть иными, постепенно усложняясь по мере усвоения материала.
Посещает ли ваш ребенок частную или государственную школу, занимается дополнительно онлайн или ходит к репетитору – тестирование по математике за 5 класс выявит пробелы в знаниях и поможет сформировать прочные навыки решения любых задач. Весь материал разбит по темам. Вы можете выбрать ту, в которой ваш ребенок испытывает затруднения, или сделать полный срез успеваемости, чтобы составить полную картину. Пробный онлайн тест по математике за 5 класс вы можете пройти совершенно бесплатно прямо сейчас. Платформа оценит ответы, предложит исправить ошибки и составит рейтинг ученика.
Пробный онлайн тест по математике за 5 класс вы можете пройти совершенно бесплатно прямо сейчас. Платформа оценит ответы, предложит исправить ошибки и составит рейтинг ученика.
Для формирования устойчивого навыка, доходящего до автоматизма, необходимо решать примеры по вычислительным навыкам за 5 класс по математике в течение нескольких последующих дней для закрепления материала. Для этого следует оформить доступ к образовательной платформе Skills4u, выбрав один из планов: на 1 месяц, на полгода или на 12 месяцев. Стоимость невелика, а результат будет очень скоро заметен.
Если ваш ребенок будет регулярно проходить онлайн тестирование за 5 класс по математике на интерактивной платформе, он сможет быстро и безошибочно решать самые сложные примеры и уравнения, производить вычисления с десятичными дробями. Разумеется, гарантированный положительный результат дает только продолжительная подписка, но даже месяц занятий позволит сдвинуться с мертвой точки.
Увлекательная форма без дополнительных письменных заданий, интеллектуальный алгоритм выдачи примеров, позволяющий учитывать уровень подготовки каждого ребенка – вот залог успеха нашей программы. Присоединяйтесь!
Присоединяйтесь!
Урок 14. деление нацело — Математика — 5 класс
Математика
5 класс
Урок № 14
Деление нацело
Перечень вопросов, рассматриваемых в теме:
— деление натуральных чисел;
— свойства деления натуральных чисел.
Тезаурус
Деление – это математическое действие, обратное умножению.
Делимое – это число, которое делят.
Делитель – это число, на которое делят.
Частное – результат деления.
Делить на нуль нельзя.
Любое натуральное число а делится на 1 и само на себя:
а : 1 = а, а : а = 1
Важное свойство частного: делимое и делитель можно одновременно умножить или разделить на одно и то же натуральное число: частное от этого не изменится.
Обязательная литература
- Никольский С. М. Математика: 5 класс. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – М.: Просвещение, 2017. – 272 с.
- Потапов М.
 К. Математика. Книга для учителя. 5-6 классы. // М. К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010.- 256 с.
К. Математика. Книга для учителя. 5-6 классы. // М. К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010.- 256 с.
Дополнительная литература
- Бурмистрова Т. А. Математика. Сборник рабочих программ. 5-6 классы. // Составитель Т. А. Бурмистрова – М.: Просвещение, 2014.- 80 с.
- Потапов М. К. Математика: дидактические материалы. 6 класс. // М. К. Потапов, А. В. Шевкин – М.: Просвещение, 2010.- 118 с.
- Чесноков А. С. Дидактические материалы по математике 5 класс. // А. С. Чесноков, К. И. Нешков. – М.: Академкнига, 2014.- 124 с.
Теоретический материал для самостоятельного изучения
Давайте вспомним, что нам уже известно об операции деления. Пусть у нас есть натуральные числа a и b, причём а больше b или равно b (a ≥ b). Говорят, что а делится на b нацело, если существует натуральное число с, при умножении которого на b получается а: a = b ∙ c.
Обычно слово «нацело» в этой фразе опускается. При этом записывают: a : b = с и называют а – делимым, b – делителем, с – частным.
Любое натуральное число а делится на 1 и само на себя:
а : 1 = а, а : а = 1
так как а ∙ 1 = а, 1 ∙ а = а.
Например, 14 делится на 1 и на 14.
14 : 1 = 14, 14 : 14 = 1
При делении ноля на любое натуральное число получается ноль: 0 : а = 0, потому что 0 ∙ а = 0.
Запомните: делить на нуль нельзя!
Любое натуральное число а делить на нуль нельзя, потому что не существует такого числа с, для которого выполнялось бы равенство а : 0 = с (так как с ∙ 0 = 0 ≠ а). Принято считать, что нуль на нуль делить нельзя.
Для деления чисел из двух и более цифр (знаков) применяют деление уголком.
Вспомним, как делить уголком, на примере.
Вычислим 392 : 28 = ?
Для начала запишем делимое и делитель уголком:
Начнём делить 392 на 28 следующим образом.
Во-первых, определим неполное частное. Для этого слева направо сравниваем цифры делимого и делителя.
Рассмотрим цифру 3. Она меньше 28 – значит, нужно взять ещё одну цифру из делимого. 39 больше 28, следовательно, это неполное частное.
Она меньше 28 – значит, нужно взять ещё одну цифру из делимого. 39 больше 28, следовательно, это неполное частное.
Ставим точку в частном (под уголком делителя).
Посчитаем, сколько цифр осталось в делимом, после неполного частного. У нас после 39 стоит только одна цифра – 2. Значит, и в результат добавляем ещё одну точку.
Приступаем к делению: 28 помещается в 39 только один раз, поэтому ставим первой цифрой ответа единицу и вычитаем 28 из 39.
После вычитания в остатке получилось 11, это меньше, чем 28, поэтому к 11 дописываем 2.
112 делится на 28. Получаем 4. Записываем полученный результат второй цифрой в ответе.
В остатке получился нуль – значит, числа разделились нацело. Таким образом, 392 : 28 = 14.
Важное свойство частного: делимое и делитель можно одновременно умножить или разделить на одно и то же натуральное число: частное от этого не изменится.
Вычислим 50 : 25 = ?
Сначала одновременно умножим 50 и 25 на 2. Получим:
100 : 50 = 2.
Теперь разделим 50 и 25 на 5. Получим:
10 : 5 = 2.
В обоих случаях ответ оказался одинаковым. Значит, свойство частного верно.
Если каждое из натуральных чисел a и b делится на натуральное число с, то верно равенство:
(a+ b) : c = a : c + b : c.
Убедимся в правдивости данного свойства на примере.
Вычислим выражение: 124 : 4 + 36 : 4.
Рассмотрим два способа решения.
1 способ. Выполним деление и сложим результаты.
124 : 4 + 36 : 4 = 31 + 9 = 40.
2 способ. Заметим, что у нас есть общий делитель – 4. Вынесем его за скобки. Получим:
(124 + 36) : 4 = 160 : 4 = 40.
В обоих случаях у нас получился один и тот же ответ. Значит, свойство верно.
Разбор решения заданий тренировочного модуля
№ 1. Вычислите 812 : 14 = _____.
Решение: выполним деление уголком.
Ответ: 58.
№ 2. Найдите неизвестный множитель х из равенства: 15 ∙ х = 195.
Выберите верный ответ: х = 3; х = 13; х = 25; х = 15.
Решение: чтобы найти неизвестный множитель, надо произведение поделить на известный множитель, то есть:
15 ∙ х = 195
х = 195 : 15
Выполнив деление уголком, получим:
Ответ: х = 13.
Урок 17. деление с остатком — Математика — 5 класс
Математика
5 класс
Урок № 17
Деление с остатком
Перечень вопросов, рассматриваемых в теме:
— деление с остатком;
— неполное частное;
— остаток.
Тезаурус
Деление с остатком – это деление одного натурального числа на другое, при котором остаток меньше делителя.
Обязательная литература
- Никольский С. М. Математика: 5 класс. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – М.: Просвещение, 2017. – 272 с.
- Потапов М. К. Математика. Книга для учителя. 5-6 классы. // М. К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010.- 256 с.
Дополнительная литература
- Бурмистрова Т.
 А. Математика. Сборник рабочих программ. 5-6 классы. // Составитель Т. А. Бурмистрова – М.: Просвещение, 2014.- 80 с.
А. Математика. Сборник рабочих программ. 5-6 классы. // Составитель Т. А. Бурмистрова – М.: Просвещение, 2014.- 80 с. - Потапов М. К. Математика: дидактические материалы. 6 класс. // М. К. Потапов, А. В. Шевкин – М.: Просвещение, 2010.- 118 с.
- Чесноков А. С. Дидактические материалы по математике 5 класс. // А. С. Чесноков, К. И. Нешков. – М.: Академкнига, 2014.- 124 с.
Теоретический материал для самостоятельного изучения
Не всегда можно полностью разделить одно число на другое. В примерах на деление может оставаться остаток. Такое деление называется деление с остатком.
Рассмотрим пример. Разделим 16 на 5.
Запишем этот пример в столбик:
Получилось, что 5 помещается в 16 три раза, но остаётся 1 – это остаток.
Читается данное выражение следующим образом: «16 разделить на 5 получится 3, и остаток – 1».
Деление с остатком – это деление одного натурального числа на другое, при котором остаток меньше делителя.
Если при делении натуральных чисел остаток равен нулю, то договорились считать, что делимое делится на делитель без остатка, или делится нацело.
Запишем деление с остатком в общем виде.
Порядок решения выражений на деление с остатком:
1. находим наибольшее число до а, которое делится на b без остатка – это c;
2. вычитаем из делимого найденное число c.
a – c = r
Сравниваем остаток с делителем. Остаток всегда меньше делителя: r < b.
Если получилось, что остаток больше делителя – значит, наибольшее число, которое делится на делитель без остатка, найдено неверно.
При решении более сложных примеров не всегда можно легко найти наибольшее число из пункта 1. Иногда для этого необходимо произвести дополнительные расчёты в столбик.
Рассмотрим ещё один пример.
297 : 25 = ?
Запишем это выражение в столбик:
Получили остаток 22, он меньше, чем 25, значит:
297 : 25 = 11 ост (22)
Как проверить деление с остатком:
- умножить неполное частное на делитель;
- прибавить к полученному результату остаток;
- сравнить полученный результат с делимым.

Проверим ответ предыдущего примера.
297 : 25 = 11 ост (22)
25 · 11 = 275
275 + 22 = 297
Деление с остатком выполнено верно.
Разбор решения заданий модуля
№ 1. Вычислите выражение 312 : 15 = _____ ост (____)
Решение: выполним деление уголком:
Сравним неполное частное с делителем: 12 < 15.
Теперь проверим, верно ли мы нашли неполное частное и остаток:
20 ∙ 15 + 12 = 300 + 12 = 312
Ответ: 312 : 15 = 20 ост (12)
№ 2. Найдите неизвестное делимое в выражении:
х : 17= 18 (остаток 4)
Выберите верный ответ: х = 310; х = 120; х = 250; х = 110.
Решение: чтобы найти неизвестное делимое, надо неполное частное умножить на делитель и прибавить остаток.
х = 18 ∙ 17 + 4
х = 306 + 4
х = 310
Ответ: х = 310.
Стратегии разделения для 5-го класса
Боитесь ли вы преподавать разделение каждый год? Раньше я был в этом лагере. Мои ученики много боролись с делением, потому что им не хватало чувства числа и концептуального понимания. Однако, к счастью, я понял, что так быть не должно. Я могу использовать стратегии разделения, которые не только подходят для развития, но и имеют смысл для моих учеников.
Однако, к счастью, я понял, что так быть не должно. Я могу использовать стратегии разделения, которые не только подходят для развития, но и имеют смысл для моих учеников.
Фактически, как только я отказался от стандартного алгоритма в качестве моей стратегии деления, мои ученики начали осваивать деление влево и вправо.Некоторые все еще боролись? да. К сожалению, ни одна из стратегий или советов, которыми я делюсь, не станет волшебной пилюлей, но они сделают разделение доступным и концептуальным для ваших учеников.
Частные частные с помощью Easy Breezy Math
Частные частные изменили правила игры для моих учеников. Частные частные — это стратегия деления, которая использует фрагменты для более эффективного многократного вычитания групп делителя.
Но мне пришлось добавить эшафот для моих учеников.Мы называем этот эшафот нашей «Легкой и легкой математикой». По сути, мы берем известное нам умножение и списываем их в сторону. Мы устраняем эти проблемы, чтобы помочь нам решить проблему. Мы делаем это, потому что моим ученикам действительно не хватает чувства деления в начале года. Это также помогает им увидеть связь между умножением и делением.
Мы делаем это, потому что моим ученикам действительно не хватает чувства деления в начале года. Это также помогает им увидеть связь между умножением и делением.
По мере того, как год идет, они выйдут за рамки простой простой математики, поскольку они разовьют чувство числа и начнут видеть закономерности.
Совет: напомните им сложить множители вертикально в их Easy Breezy Math. Иногда я даю своим ученикам доски специально для этого, чтобы сделать их более интересными.
Чтобы получить более подробную информацию об этом методе разделения и получить помощь бесплатно, щелкните здесь.
Если эта стратегия для вас нова и вам нужно увидеть ее в действии, то посмотрите это видео и песню.
Коробочная модель
или коробочный метод с частичными частными
Box Model Division 1 был для меня новым годом назад и работает лучше всего, когда студенты знакомы с использованием этого типа органайзера при умножении на частичные произведения. Этот тип стратегии деления похож на частичное частное, но организован иначе.
Этот тип стратегии деления похож на частичное частное, но организован иначе.
Если это для вас совершенно в новинку, посмотрите видео, на котором учитель и ее класс проходят этапы. Этот метод лучше всего «увидеть в действии», а не читать о нем.
Это видео длиннее, но оно отлично помогает учителям понять стратегию деления и послушать некоторый язык, чтобы помочь ученикам понять его.Примечание. Часть работы What I Know совпадает с тем, что я называю « Easy Breezy Math. ”
Я настоятельно рекомендую представить эту стратегию (и действительно любую стратегию, но определенно эту) в контексте проблемы со словом, чтобы помочь студентам осмыслить стратегию и действительно понять, что происходит. Полезно называть дивиденд и делитель в зависимости от контекста.
Советы для преподавателей (с любой стратегией дивизиона)
1.) Представьте новые стратегии с увлекательным контекстом или проблемой со словом. По мере того, как вы проходите этапы стратегии, проходите через то, что может происходить в проблеме.
По мере того, как вы проходите этапы стратегии, проходите через то, что может происходить в проблеме.
2.) Если эти стратегии совершенно новые, то потратьте день (или больше) с однозначными делителями, прежде чем переходить к двузначным делителям. Это будет того стоить!
3.) Убедитесь, что ученики понимают цель Easy Breezy Math, если вы решите использовать эту платформу. Кроме того, убедитесь, что они понимают, что это означает и как работает (в нем представлены частичные частные, которые уже готовы для учащихся на выбор).
4.) Научите студентов проверять свои ответы умножением. Это поможет им в самооценке и позволит им обнаруживать небольшие ошибки, которые они допускают при вычитании или другие ошибки вычислений.
А как насчет традиционного алгоритма деления?
Поскольку в моем штате используется общее ядро, я не преподаю традиционный алгоритм деления в рамках учебной программы пятого класса. Однако после государственного тестирования мы делаем предварительный просмотр математики в шестом классе. В то время я всегда усиленно учил традиционный алгоритм.К этому моменту у моих учеников есть четкое понимание деления и лучшее чувство чисел. Это помогает им освоить алгоритм. Кроме того, я обнаружил, что многие учителя шестого класса ожидают, что они знают традиционный алгоритм, поэтому я определенно не хочу, чтобы мои ученики отставали, когда они пойдут в среднюю школу.
В то время я всегда усиленно учил традиционный алгоритм.К этому моменту у моих учеников есть четкое понимание деления и лучшее чувство чисел. Это помогает им освоить алгоритм. Кроме того, я обнаружил, что многие учителя шестого класса ожидают, что они знают традиционный алгоритм, поэтому я определенно не хочу, чтобы мои ученики отставали, когда они пойдут в среднюю школу.
Требуется БОЛЬШЕ ресурсов для подразделения?
БЕСПЛАТНЫЕ печатные формы «Дивизион»: Щелкните здесь, чтобы получить бесплатный пакет печатных материалов «Дивизион дня». Я использую их для утренней работы, проверки математики или домашних заданий после того, как ученики выучили деление и им нужно развить беглость речи и продолжить практику.
Дополнительные ресурсы отдела
: У меня также есть пакет отдела, который содержит печатные формы, простые центры, карточки задач и оценки. Ресурсы не требуют какой-либо конкретной стратегии, поэтому вы можете выбрать стратегии, которые вы хотите, чтобы ваши ученики применяли, или позволить им выбирать. Щелкните здесь, чтобы просмотреть дополнительные ресурсы Division в моем магазине Teachers Pay Teachers.
Щелкните здесь, чтобы просмотреть дополнительные ресурсы Division в моем магазине Teachers Pay Teachers.
Используете ли вы какую-либо из этих стратегий разделения? Вы используете другую стратегию разделения? Дайте мне знать в комментариях.Я всегда ищу новые стратегии разделения для 5-го класса!
Рабочие листы
Division для 3, 4 и 5 классов
Вы здесь: Главная → Рабочие листы → Division
Это бесплатные распечатываемые рабочие листы по разделам, сгенерированные случайным образом для учащихся 3-5 классов. Темы включают факты деления, умственное деление, деление в столбик, деление с остатками, порядок операций, уравнения и факторинг.
Вы можете распечатать их прямо из окна браузера, но сначала проверьте, как это выглядит в «Предварительном просмотре».Если рабочий лист не помещается на странице в режиме предварительного просмотра, настройте поля, верхний и нижний колонтитулы в настройках страницы в браузере.
Все рабочие листы имеют ключ ответа; однако вам нужно щелкнуть страницу ключа ответа сразу же, после создания рабочего листа, потому что ключ ответа также генерируется «на лету» и не будет существовать позже, если вы придете искать его позже.
Перейти к:
4 класс
Рабочие листы ментального деления
Практика деления фактов (таблицы 1-10)
Практика деления фактов (таблицы 1-12)
Отсутствует дивиденд или делитель (основные факты)
Разделить на 10 или 100
Разделить на целые десятки или сотни
Разделите в уме целые десятки и целые сотни на однозначные числа
Деление с остатком от 1 до 100 по основным фактам
Деление с остатком в пределах 1-100
Деление с остатком, делитель целых десяти
Порядок операций: сложение, вычитание, умножение,
деление и скобка — три операции
Порядок операций: сложение, вычитание, умножение,
деление и скобка — четыре операции
Порядок операций: сложение, вычитание, умножение,
разделение и скобка — пять операций
Листы с длинным делением
Практика деления фактов (с использованием символа длинного деления)
Длинное деление, двузначные дивиденды, однозначный делитель, точное деление
Деление в столбик, двузначные дивиденды, однозначный делитель, возможны остатки
Длинное деление, трехзначные дивиденды, однозначный делитель, точное деление
Деление в столбик, трехзначные дивиденды, однозначный делитель, возможны остатки
Длинное деление, 4-значные дивиденды, 1-значные делители, точное деление
Длинное деление, 4-значные дивиденды, 1-значные делители, возможны остатки
5 класс
Психическое подразделение
Разделите в уме трех- и четырехзначное число на однозначное
Деление с остатком в пределах 1-100
Деление с остатком, делитель целых десяти
Деление с остатком, делитель на целую сотню
Деление в длину
1-значный делитель, 4-значное делимое, без остатка
1-значный делитель, 4-значное делимое, остаток
2-значный делитель, 4-значное делимое, делитель между 11 и 35
2-значный делитель, 4-значное делимое, без остатка — (делителем является любое двузначное число)
2-значный делитель, 4-значное делимое, с остатком — (делителем является любое двузначное число)
Умножение
уравнения (пропущенный множитель; решить в столбик)
Уравнения деления (пропущенный делимый или делитель; решение путем длинного умножения или длинного деления)
Решите уравнения умножения — используя длинное деление, одно- или двухзначный делитель
Таблицы факторинга
Перечислить все множители данного числа
Факторинговые числа в пределах
4-100 до простых множителей
Сложный факторинг: числа множителей в пределах
4-500 в простых множителях
| Вы здесь: Главная → Задания → 5 класс Это исчерпывающий набор бесплатных распечатываемых рабочих листов по математике для 5 класса, организованных по таким темам, как сложение, вычитание, алгебраическое мышление, разряд, умножение, деление, разложение на простые множители, десятичные дроби, дроби, измерения, координатная сетка и геометрия. Рабочие листы генерируются случайным образом каждый раз, когда вы нажимаете на ссылки ниже. Вы также можете получить новый, другой, просто обновив страницу в своем браузере (нажмите F5). Вы можете распечатать их прямо из окна браузера, но сначала проверьте, как это выглядит в «Предварительном просмотре».Если рабочий лист не умещается на странице, отрегулируйте поля, верхний и нижний колонтитулы в настройках страницы вашего браузера. Другой вариант — настроить «масштаб» на 95% или 90% в предварительном просмотре печати. В некоторых браузерах и принтерах есть опция «Печатать по размеру», которая автоматически масштабирует рабочий лист по размеру области печати. Все рабочие листы содержат ключ ответа, расположенный на 2-й странице файла. АлгебраМатематика для начальных классов Эдвард ЗаккароХорошая книга по решению проблем с очень разнообразными текстовыми задачами и стратегиями решения проблем.Включает главы по следующим темам: последовательности, решение проблем, деньги, проценты, алгебраическое мышление, отрицательные числа, логика, отношения, вероятность, измерения, дроби, деление. Вопросы в каждой главе разбиты на четыре уровня: легкий, несколько сложный, сложный и очень сложный. Сложение и вычитание по столбцам (числа друг под другом)Место и округлениеПропускной счет
Округление
УмножениеУмножение умственных способностей Длинное умножение (в столбцах) ПодразделениеПсихологическое отделение Длинное деление
Следующие четыре типа рабочих листов выходят за рамки
Стандарт Common Core для пятого класса. ФакторингДробное сложение и вычитаниеКак дроби / дробные части В отличие от дробей / дробных частей
Умножение на дробьФракционное подразделениеСледующие типы рабочих листов выходят за рамки стандартов Common Core. Преобразование дробей в смешанные числа и наоборотЭквивалентные дроби и упрощенные дробиЗаписывать дроби как десятичные и наоборот В приведенных ниже таблицах ключ ответа не дает дроби в упрощенной форме. Сложение десятичной дробиМентальная математика От 0 до 1 десятичных цифр От 0 до 2 десятичных цифр Дополнительная колонка Десятичное вычитаниеМентальная математика От 0 до 1 десятичных цифр От 0 до 2 десятичных цифр Задачи: ментальная математика Вычитание по столбцу Вызовы: алгебраическое мышление Десятичное умножениеМентальная математика
Умножить по столбцам Десятичное делениеМентальная математика Длинное деление Единицы измеренияОбычная система
Метрическая система
Сетка координатГеометрияЕсли вы хотите иметь больший контроль над такими параметрами, как количество проблем, размер шрифта, интервал проблем или диапазон чисел, просто щелкните по этим ссылкам, чтобы самостоятельно использовать генераторы рабочих листов: |
Учебный план 5-го класса
Ниже приведены необходимые навыки со ссылками на ресурсы, которые помогут в освоении этого навыка. Мы также поощряем много упражнений и книжную работу. Curriculum Home
Мы также поощряем много упражнений и книжную работу. Curriculum Home
Важно: это только руководство.
Обратитесь в местный орган управления образованием, чтобы узнать их требования.
Класс 5 | Умножение
☐ Используйте различные стратегии для умножения трехзначных чисел на трехзначные числа. Примечание. Умножение на что-либо большее, чем трехзначный множитель / множимое, должно выполняться с использованием технологий.
☐ Уметь умножать на отрицательные числа
☐ Развивайте беглость речи с помощью умножения до 12x
5 класс | Раздел
☐ Используйте различные стратегии для деления трех- или четырехзначных чисел на одно- или двузначные числа. Примечание. Деление на что-либо большее, чем двузначный делитель, должно производиться с использованием технологий.
☐ Легко проверить, может ли одно число быть равномерно разделено на другое, используя правила делимости.
5 класс | Числа
☐ Чтение и запись целых чисел в миллионы
☐ Помните, что некоторые числа делятся только на одно и сами по себе (простое число), а другие имеют несколько делителей (составные)
☐ Вычислить кратное целого числа и наименьшее общее кратное двух чисел
☐ Определите факторы данного числа
☐ Найдите общие делители и наибольший общий делитель двух чисел
☐ Вычислить арифметическое выражение, используя порядок операций, включая умножение, деление, сложение, вычитание и скобки
☐ Сравните и закажите номера в миллионы
☐ Округление чисел до сотых и до ближайших 10 000
☐ Поймите структуру разрядных значений десятичной системы счисления: * 10 единиц = 1 десятка * 10 десятков = 1 сотня * 10 сот = 1 тысяча * 10 тысяч = 1 десять тысяч * 10 десятков тысяч = 1 сотня тысяч * 10 сотен тысяч = 1 миллион
☐ Поймите разницу между множителем и кратным целому числу,
5 класс | Десятичные дроби
☐ Сравните десятичные дроби, используя, или =
☐ Используйте различные стратегии для сложения, вычитания, умножения и деления десятичных знаков до тысячных
☐ Чтение, запись и порядок десятичных дробей с точностью до тысячных
☐ Конвертировать проценты в десятичные числа
5 класс | Дроби
☐ Упростите дроби до наименьших значений
☐ Преобразование неправильных дробей в смешанные числа и смешанных чисел в неправильные дроби
☐ Используйте различные стратегии для сложения и вычитания дробей с одинаковыми знаменателями
☐ Сложить и вычесть смешанные числа с одинаковыми знаменателями
☐ Оценивайте суммы и разности дробей с одинаковыми знаменателями.
☐ Создайте эквивалентные дроби, учитывая дробь
☐ Сравните и упорядочьте дроби, включая отличные от знаменателей (с использованием числовой линии и без нее). Примечание: часто используемые дроби, такие как те, которые могут быть указаны на линейке, мерной чашке и т. Д.
☐ Сравните дроби, используя, или =
☐ Сложение, вычитание, умножение и деление дробей (включая смешанные дроби), знаменателями которых являются степени десятичных дробей.
☐ Разделите дробь на целое число
☐ Умножить дробь на целое число
☐ Выражайте десятичные дроби как эквивалент дробей со знаменателями, которые являются степенями 10
☐ Перевести проценты в дроби
5 класс | Проценты
☐ Поймите, что процент означает часть 100
☐ Преобразование дробей или десятичных знаков в проценты
5 класс | Передаточные числа
☐ Понять концепцию передаточного числа
☐ Экспресс-коэффициенты в разных формах
5 класс | Измерение
☐ Используйте линейку для измерения с точностью до сантиметра или миллиметра
☐ Определите личные рекомендации для метрических единиц длины
☐ Определите общепринятые эквивалентные единицы длины (метрические)
☐ Преобразование длины в метрическую систему
☐ Определите инструменты и методы, необходимые для измерения с надлежащим уровнем точности: длины и углы
☐ Измерьте и начертите углы с помощью транспортира
☐ Понять температуру
☐ Понимание температурных шкал Цельсия и Фаренгейта, включая точки замерзания и кипения воды по двум шкалам
☐ Используйте линейку для измерения с точностью до дюйма, 1/2, 1/4 или 1/8 дюйма
☐ Определите личные рекомендации для стандартных единиц длины США
☐ Определите общепринятые эквивалентные единицы длины (США)
☐ Преобразование длины в системе США
5 класс | Время
☐ Вычислить прошедшее время в часах и минутах
☐ Преобразование времени из минут и секунд в секунды или часов и минут в минуты
5 класс | Геометрия (плоскость)
☐ Вычислить формулу периметра для заданных входных значений
☐ Рассчитать периметр правильных и неправильных многоугольников
☐ Определить соответствующие части равных треугольников
☐ Определить и провести линии симметрии основных геометрических фигур
☐ Постройте точки для образования основных геометрических фигур (определите и классифицируйте)
☐ Расчет периметра основных геометрических фигур, нарисованных на координатной плоскости (прямоугольники и фигуры, состоящие из прямоугольников, имеющих стороны с целой длиной и параллельных осям)
☐ Обозначить пары одинаковых треугольников или других геометрических фигур
☐ Определить соотношение сторон одинаковых треугольников
☐ Классифицируйте четырехугольники по свойствам их углов и сторон
☐ Знайте, что сумма внутренних углов четырехугольника составляет 360 градусов
☐ Классифицируйте треугольники по свойствам их углов и сторон
☐ Знайте, что сумма внутренних углов треугольника составляет 180 градусов
☐ Найдите недостающий угол, если даны два угла треугольника
☐ Определить пары совпадающих треугольников или других геометрических фигур
☐ Знайте, что прямой угол равен 90 градусам, прямой угол — 180 градусов, а полный круг — 360 градусов.
☐ Поймите, что подразумевается под порядком симметрии вращения плоской формы, и узнайте, как найти его значение.
☐ Разберитесь, что подразумевается под правильными и неправильными многоугольниками; выпуклые и вогнутые многоугольники; и сложные многоугольники.
☐ Понять, что подразумевается под точечной симметрией
☐ Понять, что подразумевается под вершиной угла и прилегающими углами
5 класс | Геометрия (твердое тело)
☐ Понять платоновы тела
☐ Постройте модели Платоновых тел из их сетей.
☐ Понимать многогранники и классифицировать их как Платоновы тела, призмы, пирамиды и т. Д.
5 класс | Алгебра
☐ Определите и используйте соответствующую терминологию при обращении к константам, переменным и алгебраическим выражениям
☐ Перевести простые словесные выражения в алгебраические
☐ Подставить присвоенные значения в выражения переменных и оценить, используя порядок операций
☐ Решите простые одношаговые уравнения, используя основные целочисленные факты
☐ Решите и объясните простые одношаговые уравнения, используя обратные операции с целыми числами
☐ Создавайте и объясняйте закономерности и алгебраические отношения (пример: 2,4,6,8… алгебраически 2n (удвоение))
☐ Создавайте алгебраические или геометрические узоры, используя конкретные объекты или визуальные рисунки (например, вращайте и закрашивайте геометрические фигуры)
☐ Знайте разницу между закрытым и открытым предложением.
5 класс | Координаты
☐ Определите и нанесите точки в первом квадранте
5 класс | Логика
☐ Используйте логические рассуждения для решения задач, требующих различных навыков
5 класс | Данные
☐ Собирать и записывать данные из различных источников (например,г., газеты, журналы, опросы, диаграммы и обзоры)
☐ Отображение данных в виде линейного графика, чтобы показать увеличение или уменьшение с течением времени
☐ Вычислить среднее значение для данного набора данных и использовать для описания набора данных
☐ Формулируйте выводы и делайте прогнозы по графикам
5 класс | Оценка
☐ Обосновать обоснованность оценки
☐ Оценка сумм, разностей, произведений и частных десятичных знаков
☐ Обоснуйте обоснованность ответов с помощью оценки
5 класс | Вероятность
☐ Перечислите возможные результаты для эксперимента с одним событием
☐ Запишите результаты эксперимента с использованием дробей / соотношений
☐ Создайте образец пространства и определите вероятность одного события, учитывая простой эксперимент (например,г. , катящий числовой куб)
, катящий числовой куб)
☐ Найдите вероятности в строке числа вероятностей
Важные математические навыки для пятиклассников
Хотите помочь своему пятикласснику освоить математику? Вот некоторые из навыков, которые ваш пятиклассник будет изучать в классе.
Сложение, вычитание, умножение и деление
Многозначные целые числа
Быстро и точно умножайте многозначные целые числа. Разделите целые числа (до четырех цифр) на двузначные числа.
Пример:
Решить 4,824 ÷ 12 =?
Объясните или проиллюстрируйте, как вы решили эту проблему.
Совет: выделите практическое применение математики.
По мере того, как математика, которую они изучают, становится более сложной и менее очевидно связанной с их повседневным опытом, у некоторых детей начинает развиваться математическая тревога. Важно, чтобы ваш ребенок занимался математикой и помогал ему понять, как в реальной жизни применяются концепции, которые ребенок изучает в школе.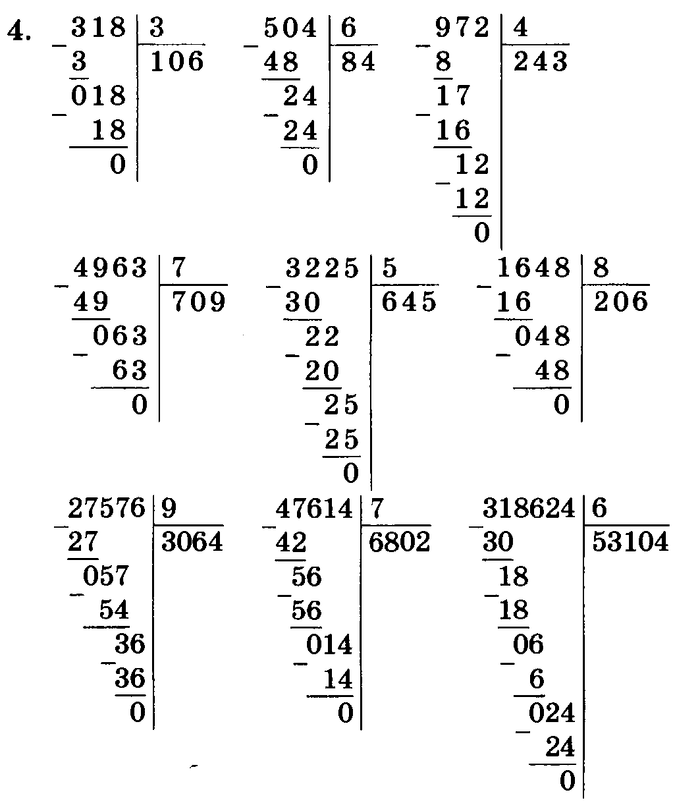 Составление бюджета на школьные принадлежности или их ежемесячное пособие — один из способов практиковать сложение и вычитание. Если вы попросите их помочь вам с приготовлением или выпечкой, это покажет им, как работают дроби. Помогать рассчитывать цены при покупке продуктов — тоже хорошая практика.
Составление бюджета на школьные принадлежности или их ежемесячное пособие — один из способов практиковать сложение и вычитание. Если вы попросите их помочь вам с приготовлением или выпечкой, это покажет им, как работают дроби. Помогать рассчитывать цены при покупке продуктов — тоже хорошая практика.
Связанные
Понимание разряда
Расширьте понимание разряда: в многозначном числе цифра в одном месте представляет 1⁄10 того, что она представляет в месте слева от него, и в 10 раз больше как он изображен справа от него.
Сравнение десятичных знаков
Чтение, запись и сравнение десятичных знаков с разрядами тысячных, используя символы> (больше чем) и
- Прочтите это десятичное число: 23,002.
- Запишите две и шестьдесят две тысячные в виде десятичного числа.
- Какой знак подтверждает это утверждение: 5,389 _? _ 5,420
- Исследователь измеряет количество бактерий, выросших на образцах неохлажденных продуктов.
 Ваш ребенок насчитывает 73.343 миллиона бактерий в образце A, 73,431 миллиона бактерий в образце B и 74,399 миллиона бактерий в образце C. Расположите образцы в порядке от наибольшего количества бактерий к наименьшему. Объясните или проиллюстрируйте, как вы приводите эти образцы в порядок.
Ваш ребенок насчитывает 73.343 миллиона бактерий в образце A, 73,431 миллиона бактерий в образце B и 74,399 миллиона бактерий в образце C. Расположите образцы в порядке от наибольшего количества бактерий к наименьшему. Объясните или проиллюстрируйте, как вы приводите эти образцы в порядок.
Связанные
Десятичные дроби с точностью до сотых
Сложение, вычитание, умножение и деление десятичных долей с точностью до сотых.
Совет: потренируйтесь в вычислениях с использованием десятичных знаков.
Свяжите работу с десятичными знаками, которую ваш ребенок делает в классе, с реальным миром, поощряя их делать покупки по выгодным ценам.Попросите их разделить стоимость товаров, упакованных оптом, на количество отдельных товаров, чтобы определить стоимость каждого товара. Итак, сколько вы платите за рулон бумажного полотенца или за банку газировки при покупке оптом? Или попросите ребенка подсчитать, сколько вы сэкономите на каждом товаре, если цены со скидкой предполагают оптовые скидки.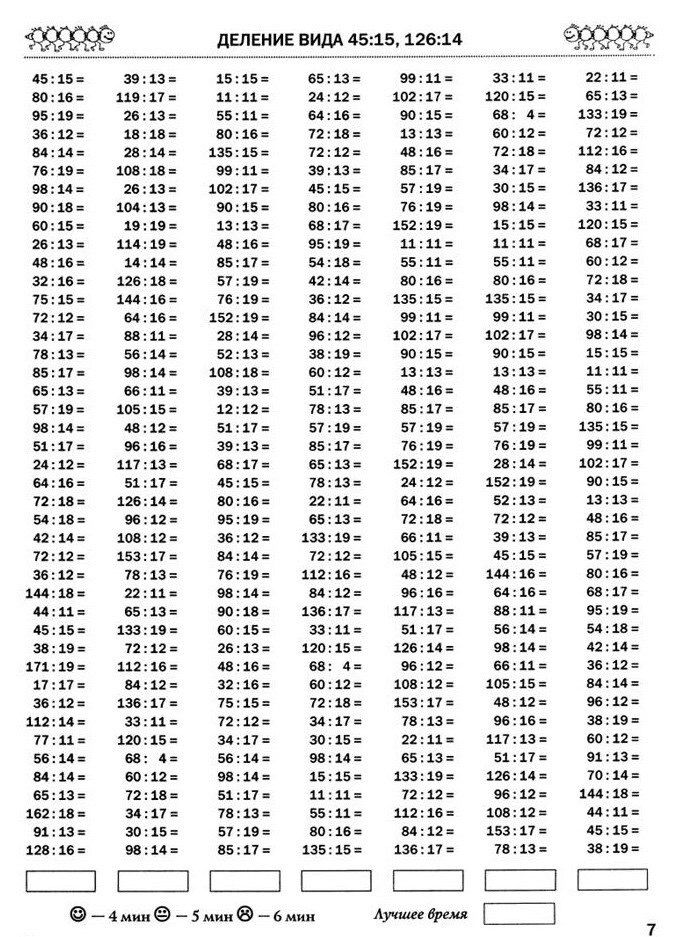
Что такое показатель степени
Понять, что такое показатель степени. Например, «2» в 10² указывает, сколько раз нужно умножить число само на себя. 10² можно читать как «10 в степени 2», «10 в степени 2» или «10 в квадрате» и означает 10 x 10 или 100.10³ (или «10 в третьей степени» или «10 в кубе») означает 10 x 10 x 10 или 1000.
Дроби
Решение задач со словами
Решение задач со словами, включающих сложение и вычитание дробей.
Пример:
Пятый класс собирает пазл из 600 деталей. Они начали вчера и собрали 100 частей — всего одну шестую (1⁄6) головоломки. Сегодня их собрано 400 штук. Какая часть головоломки завершена? Нарисуйте картинку И запишите математику, чтобы показать, как вы решили задачу.
Совет: выделите практическое применение математики.
По мере того, как математика, которую они изучают, становится более сложной и менее очевидно связанной с их повседневным опытом, у некоторых детей начинает развиваться математическая тревога.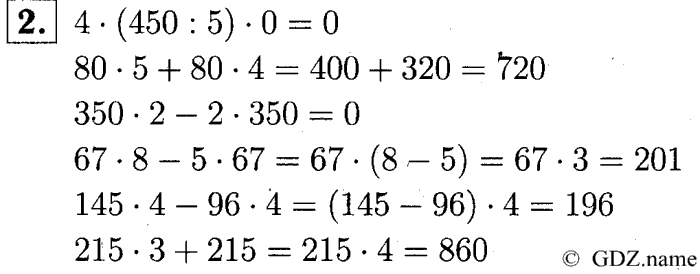 Важно, чтобы ваш ребенок занимался математикой и помогал ему понять, как в реальной жизни применяются концепции, которые он изучает в школе. Составление бюджета на школьные принадлежности или ежемесячное пособие — один из способов для нее практиковать сложение и вычитание.Если вы попросите ее помочь вам с приготовлением или выпечкой, это покажет ей, как работают дроби. Помогать рассчитывать цены при покупке продуктов — тоже хорошая практика.
Важно, чтобы ваш ребенок занимался математикой и помогал ему понять, как в реальной жизни применяются концепции, которые он изучает в школе. Составление бюджета на школьные принадлежности или ежемесячное пособие — один из способов для нее практиковать сложение и вычитание.Если вы попросите ее помочь вам с приготовлением или выпечкой, это покажет ей, как работают дроби. Помогать рассчитывать цены при покупке продуктов — тоже хорошая практика.
Нахождение общего знаменателя
Решите задачи со словами, включающие сложение и вычитание дробей с разными знаменателями (нижние числа), преобразовывая их в дроби с одинаковым знаменателем, называемые общим знаменателем.
Пример:
Самая высокая девочка в пятом классе имеет рост 51 7⁄8 дюйма.Самый высокий мальчик в пятом классе имеет рост 49 1⁄2 дюйма. Какая разница в их росте?
После вечеринки остались две чашки лимонада. В одной миске 1⁄3 галлона. В другом — 1⁄2 галлона лимонада. Друг говорит, что не стоит пытаться объединить их в 1-галлонный контейнер, потому что лимонад вытечет наверх. Ты согласен? Почему или почему нет?
Ты согласен? Почему или почему нет?
Умножение дробей
Решайте задачи со словами, включающие умножение дробей на другие дроби и умножение дробей на смешанные числа (целое число и дробь, например 11⁄4 или 21⁄2).
Пример:
- В оркестре средней школы 1⁄3 учащихся-музыкантов играют на струнных инструментах. Из учеников, играющих на струнных инструментах, 3⁄4 играют на скрипке. Какая часть оркестра играет на скрипке?
- Утром во время экскурсии в яблоневый сад пятиклассники собрали 4⁄5 бушеля яблок. После обеда в полдень они собрали в 2,5 раза больше яблок. Уместятся ли все яблоки, собранные ими днем, в ящик на 2 бушеля? Откуда вы знаете?
Совет: потренируйтесь использовать дроби.
Помогите своему ребенку познакомиться с дробями, попросив его масштабировать рецепты для вашей семьи. Пусть они начнут с того, что уменьшат рецепт вдвое или вдвое. Когда они почувствуют себя комфортно, попросите их преобразовать его на 1 1/2, чтобы рецепт, который должен был накормить семью из четырех человек, работал на семью из шести человек.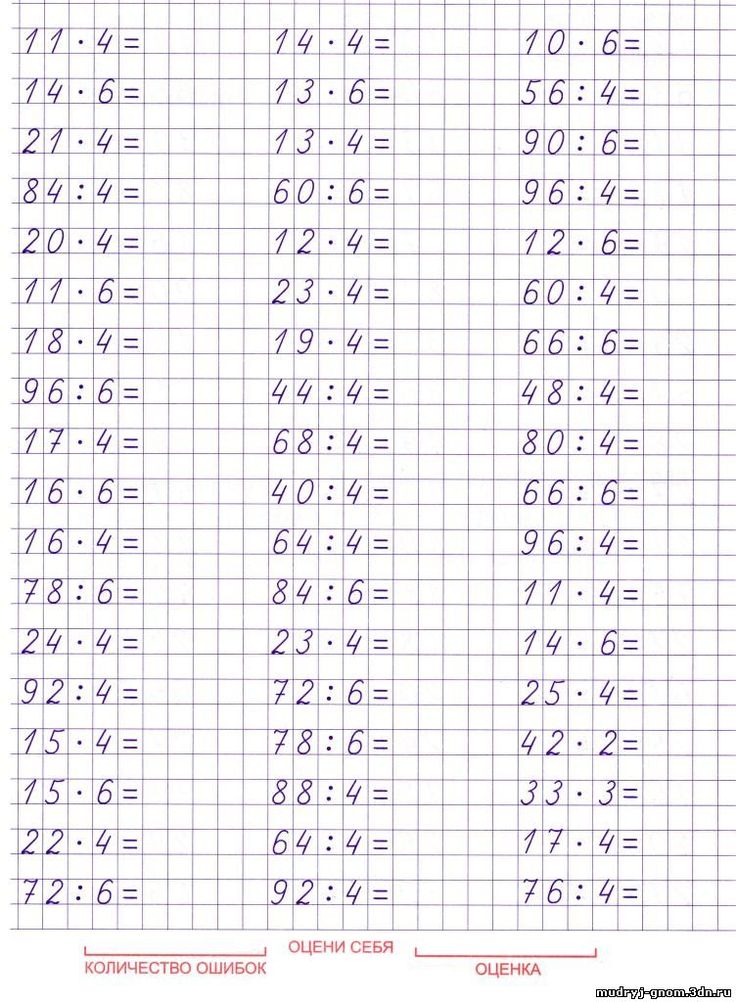
Единица деления дробей
Разделите единичные дроби (дроби с 1 в числителе или верхним числом) на целые числа. Разделите целые числа на единичные дроби.
Пример:
Если три человека разделят ½ фунта шоколада поровну, сколько шоколада получит каждый? Объясните или проиллюстрируйте, как вы решили эту проблему.
Умножение на дроби
Помните, что умножение числа на дробь меньше 1 даст ответ меньше числа — например: 12 x ¾ = 9. Умножение числа на дробь больше 1 даст результат в ответе больше числа — например: 12 x 2 ½ = 30.
Измерения и данные
Преобразование единиц и дробей
Преобразование единиц и долей единиц в одной системе измерения.
Пример:
Сколько минут составляет 1⁄5 часа? Объясните или проиллюстрируйте, как вы решили эту проблему.
Проблемы многоступенчатого преобразования единиц измерения
Решайте многоступенчатые задачи преобразования слов, используя преобразование стандартных единиц измерения разного размера.
Пример:
У меня 75 см ленты.Для выполнения проекта мне нужно в семь раз больше ленты. Сколько еще метров ленты мне нужно?
Объясните или проиллюстрируйте, как вы решили эту проблему.
Использование линейного графика
Решайте проблемы, используя информацию (в единицах дроби), представленную на линейном графике.
Геометрия
Понимание объема
Под объемом понимается измерение пространства внутри трехмерной или твердой фигуры. Используйте формулы длина x ширина x высота или основание x высота , чтобы измерить объем трехмерного или твердого объекта с прямоугольными сторонами, например куба. Измеряйте объем для решения реальных проблем.
Пример:
Прямоугольный контейнер для мороженого имеет длину 8 дюймов и высоту 4 дюйма. Каков объем контейнера, выраженный в кубических дюймах?
Советы, которые помогут вашему пятикласснику в уроке математики, можно найти на нашей странице с советами по математике для пятого класса.
Ресурсы Parent Toolkit были разработаны NBC News Learn с помощью профильных экспертов и соответствуют Общим основным государственным стандартам.
Математика Мамонт 5 класс Полная программа
Math Mammoth Grade 5 Grade Complete Curriculum — это полная математическая программа для 5-го класса, в которой вы найдете все необходимое для обучения математике в 5-м классе. Он доступен как в версии для скачивания, так и в виде печатных копий.
208 страниц
170 страниц уроков
201 страниц
176 страниц уроков
Содержимое 5-A и образцы
Содержимое и образцы 5-B
Руководство пользователя, класс 5
Выравнивание / содержимое CCS
FAQ
Цены и заказ
Вы можете приобрести Math Mammoth Grade 5 для загрузки, на компакт-диске или в виде уже распечатанных книг.
Цифровая версия
5 класс: $ 39,50 (скачать)
(два рабочих текста, ключи ответов, тесты, совокупные обзоры, средство создания рабочих листов, Soft-Pak)
Только часть 5-A:
$ 19,75 (загрузить)
(Все для первой половины 5-го класса по математике; включает Софт-Пак)
Только часть 5-B:
$ 19,75 (загрузить)
(Все для второй половины 5-го класса по математике; включает Софт-Пак)
Вы будете покупать загружаемые материалы у моего авторизованного реселлера Comecero, LLC.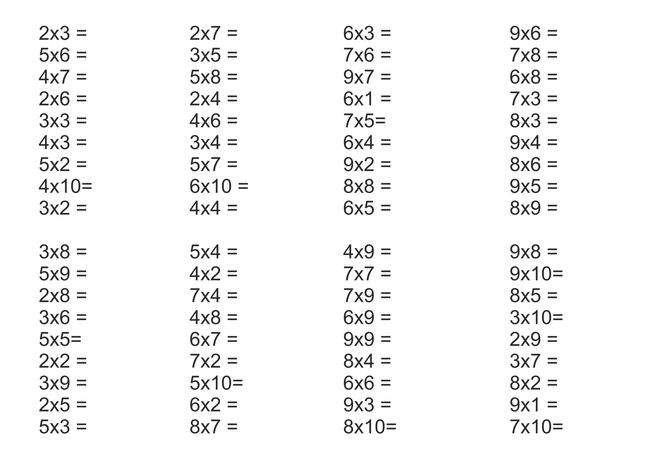
CD
Полная оценка 5: $ 44,50
(два рабочих текста, ключи ответов, тесты, совокупные обзоры, средство создания рабочих листов, Soft-Pak)
Печатные копии
Ресурсный центр Rainbow продает тексты с идеальным переплетом либо с полноцветными, либо с внутренними страницами в оттенках серого:
Математика Мамонт 5 класс (ч / б)
Математика Мамонт 5 класс (цвет)
Lulu продает в спиральном переплете (катушку) версии учебников для студентов и книг с тестами и обзорами.
Рабочий текст 5-A $ 18,45
Рабочий текст 5-B $ 18,45
Тесты и совокупные обзоры 10,25 $
Ключи ответов $ 12,95 (идеальная привязка)
Вспомогательные материалы
Включает ключи ответов, тесты, совокупные обзоры, средство создания рабочих листов и программное обеспечение Soft-Pak (цифровая загрузка).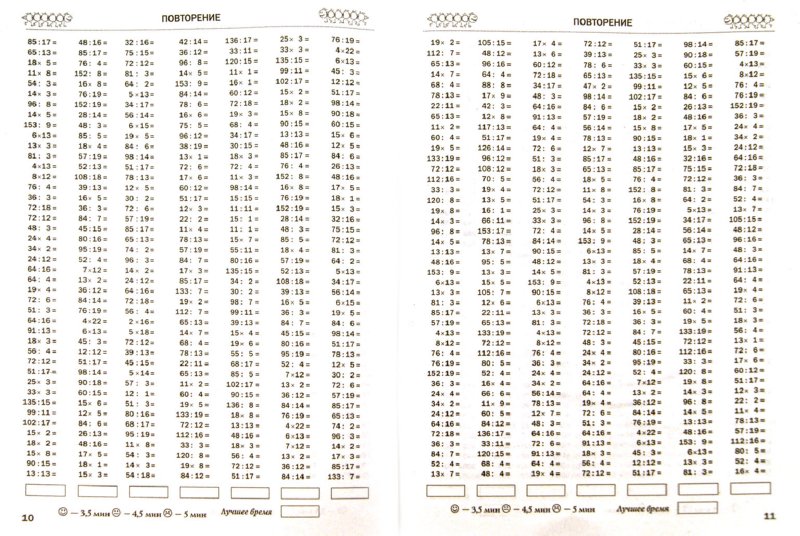 Купите это вместе с печатными учебниками для студентов. Не покупайте, если вы получили полную цифровую версию, как указано выше.
Купите это вместе с печатными учебниками для студентов. Не покупайте, если вы получили полную цифровую версию, как указано выше.
, издание 2019 г. (8,95 долл. США):
издание 2020 г. (8 долларов США.95):
План урока
Вы можете приобрести план уроков по математике Mammoth Grade 5, чтобы использовать его в онлайн-планировщике Homeschool Planet . Узнать больше.
В основе учебной программы лежат два студенческих рабочих текста (A и B), каждый из которых охватывает примерно полгода работы по математике. Эти рабочие тексты содержат все инструкции и упражнения из одной книги, что упрощает подготовку к уроку. Рабочие тексты написаны непосредственно ученику, и, таким образом, они позволяют многим ученикам учиться самостоятельно и учиться прямо из книг.
Вы также получите отдельные ключи ответов, тесты по главам, дополнительные совокупные обзоры (я рекомендую вам использовать хотя бы некоторые из них) и универсальное средство для создания рабочих листов (требуется доступ в Интернет) для тех случаев, когда вашему ребенку нужно немного больше практики .
Характеристики
- Math Mammoth фокусируется на концептуальном понимании . В нем объясняется «ПОЧЕМУ», так что ваши дети могут понимать математику, а не просто узнавать «КАК» это делать.
- Концепции часто объясняются с помощью визуальных моделей , за которыми следуют упражнения с использованием этих моделей.Эти визуальные модели могут заменить многие дети манипулятивными средствами; однако при желании очень легко добавить к урокам соответствующие манипуляторы.
- Учебная программа ориентирована на овладение знаниями . Это означает, что он довольно долго концентрируется на теме, вникая в ее различные аспекты. Это способствует концептуальному пониманию, в отличие от спиральных учебных программ, которые часто имеют тенденцию слишком много прыгать от темы к теме.
- Особое внимание уделяется умственной математике и пониманию чисел .
- Требуется очень небольшая подготовка учителей .
- Учебная программа не имеет отдельного руководства для учителя и не написана по сценарию.
 Во введении к каждой главе есть некоторые примечания для учителя относительно материала главы. Все инструкции написаны непосредственно для ученика в рабочем тексте, а также существуют сопроводительные видеоролики, где вы можете увидеть, как Мария сама преподает материал.
Во введении к каждой главе есть некоторые примечания для учителя относительно материала главы. Все инструкции написаны непосредственно для ученика в рабочем тексте, а также существуют сопроводительные видеоролики, где вы можете увидеть, как Мария сама преподает материал. - После введения каждой главы вы найдете список интернет-ссылок и ресурсов (игры, викторины, анимации и т. Д.).), которые можно использовать для развлечения, иллюстраций и дальнейшей практики.
Дополнительные возможности для цифровой версии (скачать / CD)
Файлы PDF включены для аннотации. Это означает, что при желании ваш ученик может заполнить их на компьютере, используя пишущую машинку и инструменты рисования в Acrobat Reader версии 9 или выше, или на планшетном устройстве, используя любое приложение PDF с возможностью аннотации. (Узнать больше.)
БОНУС! Если вы приобретете загружаемую версию или версию на компакт-диске, вы также получите программы Soft-Pak полностью БЕСПЛАТНО . 6 программ Soft-Pak (4 математических, 1 языковая, 1 составитель списков) предлагают как экранные, так и печатные задания в формате с низким содержанием графики и высоким содержанием. Подробнее читайте и смотрите скриншоты.
6 программ Soft-Pak (4 математических, 1 языковая, 1 составитель списков) предлагают как экранные, так и печатные задания в формате с низким содержанием графики и высоким содержанием. Подробнее читайте и смотрите скриншоты.
Обзор тем
Основными направлениями обучения в Math Mammoth Grade 5 являются:
- четыре операции с целыми числами
- разряда с большими числами и разумное использование калькулятора
- решение задач и простые уравнения
- десятичная арифметика (все операции с десятичными знаками)
- статистика и графики
- дробная арифметика (все операции с дробями)
- геометрия: обзор углов, площади и периметра; рисование кругов; классификация треугольников и четырехугольников; объем прямоугольных призм
См. Также оглавление 5-A и 5-B (в файлах примеров), которое позволит вам увидеть затронутые темы более подробно.
Дополнения
План урока
Мы предлагаем план уроков по математике Mammoth Grade 5 для онлайн-планировщика Homeschool Planet . Он доступен в двух версиях: обычный и план PLUS, который также включает файл плана в формате PDF. Узнать больше.
Он доступен в двух версиях: обычный и план PLUS, который также включает файл плана в формате PDF. Узнать больше.
Рабочая тетрадь по обзору навыков
Рабочая тетрадь по обзору навыков мамонта по математике, 5 класс предоставляет дополнительную практику по темам учебной программы по математике мамонта для 5 класса. Я рекомендую вам приобретать его только в том случае, если вы уверены, что вашему ученику действительно нужна дополнительная практика.Узнать больше.
Введение
Пятый сорт — это время для дробей и десятичных знаков, в частности. Мы изучаем дроби и десятичные дроби, а также операции с ними глубоко и детально. Студенты также углубляют свое понимание целых чисел, узнают больше о решении задач и знакомятся с калькулятором.
Год начинается с изучения целых чисел и их операций. Студенты могут просмотреть умножение нескольких цифр и выучить деление в столбик с двузначными делителями .Мы также рассматриваем делимость и множители из четвертого класса и изучаем разложение на простые множители .
Во второй главе основное внимание уделяется большим числам и с помощью калькулятора . Это первый раз, когда калькулятор вводится в полную учебную программу Math Mammoth — до сих пор все вычисления производились мысленно или с помощью бумаги и карандаша. Я хочу, чтобы учащиеся научились критически относиться к калькулятору и использовали его с здравым смыслом.Каждое упражнение, в котором разрешено использование калькулятора, помечено маленьким символом калькулятора.
Третья глава посвящена уравнениям и решению задач . Изучаем простые уравнения с помощью весов и стержней модели . Основная идея состоит в том, чтобы научить студентов понимать уравнение и то, что это значит для решения уравнения. Студенты также решают изрядное количество задач, используя модель визуальной панели.
В четвертой главе примерно знаков после запятой и некоторые операции с десятичными знаками (остальные будут изучены
в главе 6).Пятый класс — это время, когда ученики изучают все основные операции с десятичными знаками. В этом
В главе мы сосредоточимся на разрядах с десятичными знаками, сложении и вычитании десятичных знаков, а также
умножение и деление десятичных знаков на целые числа. Умножение десятичных знаков на десятичные и
разделение десятичных знаков на десятичные дроби рассматривается в главе 6.
В этом
В главе мы сосредоточимся на разрядах с десятичными знаками, сложении и вычитании десятичных знаков, а также
умножение и деление десятичных знаков на целые числа. Умножение десятичных знаков на десятичные и
разделение десятичных знаков на десятичные дроби рассматривается в главе 6.
В главе 5 мы изучаем график в координатной сетке, линейные и гистограммы, а также среднее значение и режим . Сегодняшний мир становится все более сложным из-за большого количества данных, представленных в СМИ, поэтому наши детям нужно хорошо разбираться в статистических графиках, чтобы понимать всю эту информацию.
Глава 6 продолжает наше исследование десятичных знаков . Основное внимание уделяется умножению десятичных знаков на десятичные дроби, делению десятичные дроби на десятичные дроби и преобразование между единицами измерения.
Глава 7 охватывает сложение и вычитание дробей — еще одна тема для 5-го класса, помимо десятичных дробей. Самая сложная тема этой главы — сложение и вычитание непохожих дробей.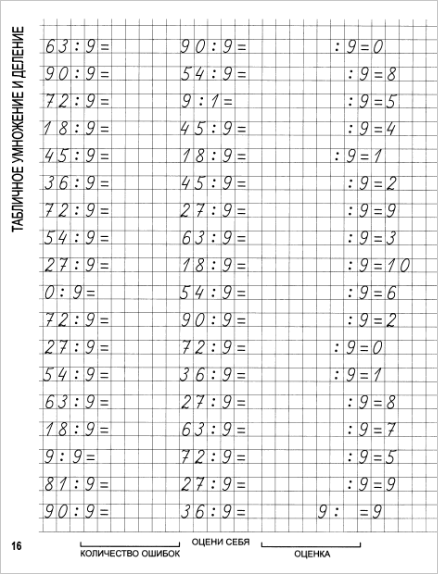 выполняется путем их предварительного преобразования в эквивалентные дроби с общим знаменателем.
выполняется путем их предварительного преобразования в эквивалентные дроби с общим знаменателем.
В главе 8 мы изучаем умножение и деление дробей под разными углами.
Глава 9 переносит нас к геометрии, начиная с обзора углов и многоугольников. Оттуда студенты будут научиться рисовать круги, классифицировать треугольники и четырехугольники и концепцию тома в контексте правильные прямоугольные призмы (коробки).
Манипуляторы
Вот список манипуляторов, которые необходимы или рекомендуются для 5 класса.
- Линейка в дюймах (для 5-B).
- Линейка сантиметров (для 5-B).
- Циркуль и транспортир (для 5-Б).
- Фракционные манипуляторы. Учебная программа содержит печатные формы для создания собственных манипуляторов с дробями. В тексте широко используются визуальные модели круговых диаграмм, и студенты даже учатся рисовать их сами для упражнений, поэтому изготовление или покупка манипуляторов является совершенно необязательным (необязательно; для 5-B).

Дополнения
План урока
За 9 долларов.95, вы можете приобрести план уроков по математике Mammoth Grade 3, чтобы использовать его в онлайн-планировщике Homeschool Planet . Узнать больше.
Обзоры и характеристики
Math Mammoth обзор на As They Grow Up блог
Обзор использования Math Mammoth 5-го класса с аутичным сыном в Через открытое окно блог
Это наш первый год обучения на дому, потому что мы хотели путешествовать. Мы начали выпускать Singapore Standard Edition, потому что этим она занималась в своей бывшей школе.Я сразу понимаю, что, несмотря на степень магистра делового администрирования и неплохое математическое образование, я понятия не имел, что мне делать, чтобы преподавать уроки. Итак, мы заявили, что ищем что-то еще, сложное, но что я могу понять и чему научить. Мы выбрали MM, а также используем CTC Math из-за видео, идеального сочетания. Мне нравится, что MM можно распечатать, потому что у нас не всегда есть подключение к Интернету в дороге, и они выставляют нам все оценки. Поскольку Сингапур пропускает некоторые основы в младших классах, я совмещаю уроки MM в 4-м и 5-м классах, чтобы определить, что нужно моему ребенку.Отличная программа, много практики и примеров, в отличие от Сингапура, действительно проясняют цель урока. Я очень рекомендую.
Поскольку Сингапур пропускает некоторые основы в младших классах, я совмещаю уроки MM в 4-м и 5-м классах, чтобы определить, что нужно моему ребенку.Отличная программа, много практики и примеров, в отличие от Сингапура, действительно проясняют цель урока. Я очень рекомендую.
MaryLu C
Октябрь 2016
Моим детям (первоклассникам и пятиклассникам) очень понравился Math Mammoth. Мне нравится, что я печатаю только то, что мне нужно, и им нравится, чтобы их не забрасывали слишком большим количеством проблем на концепцию. Как только они его получат, мы двинемся дальше. Мне нравятся такие занятия, как «Деньги», которые я могу использовать с обоими детьми. Очень рекомендую Math Mammoth!
— Кэрри В., Член кооператива
мая 2015 г.
Обзор
: Math Mammoth (Revisited) — Введение в дроби, раздел 2, светло-голубой класс 5 от Got Chai? блог.
Большое спасибо, Мария. Мы вас обожаем! Я действительно ценю доступ к такой исключительной программе.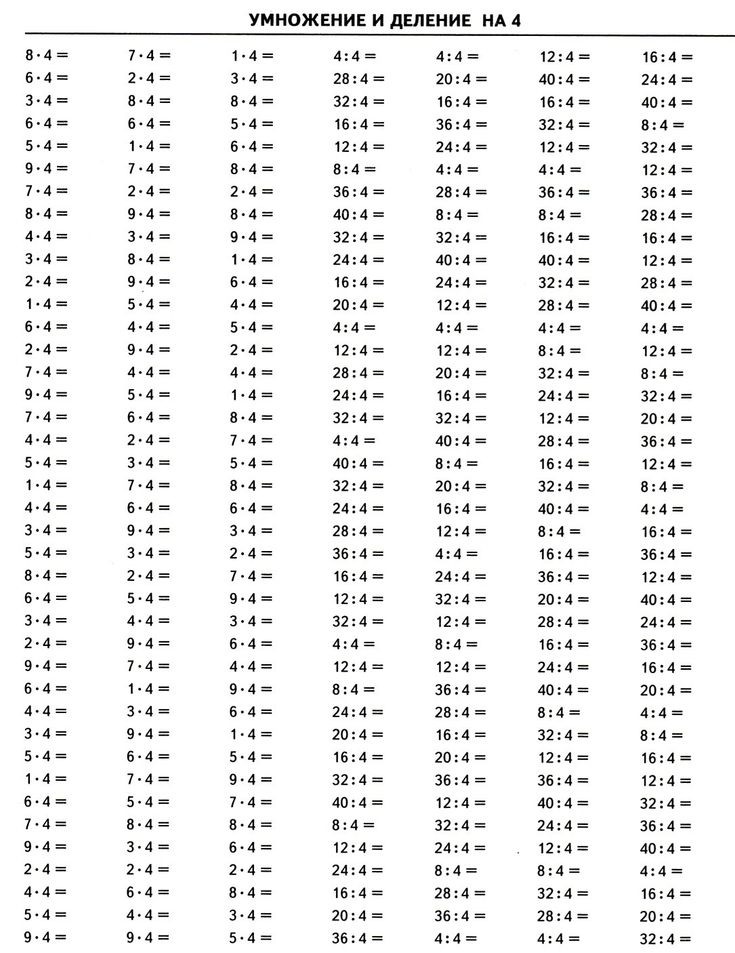 Что Бог послал. Вы являетесь таким благословением для нашей семьи и нашего сообщества, обучающегося на дому. Это лучшая математическая программа, которую мы когда-либо видели. И мы перепробовали многие за эти годы … Саксонию, Сингапур, Калверт и одну в системе государственных школ, которую мы смогли взять взаймы.Это бьет их руки вниз. Это основательно, хорошо продумано и заставляет наших детей думать о математике. Практики и повторений достаточно, чтобы концепции действительно усвоились, не утомляя их. Это единственная математическая программа, которую мы использовали, и мне не пришлось запускать ее в поисках добавки. Еще раз спасибо, Мария, очень рада, что мы тебя нашли.
Что Бог послал. Вы являетесь таким благословением для нашей семьи и нашего сообщества, обучающегося на дому. Это лучшая математическая программа, которую мы когда-либо видели. И мы перепробовали многие за эти годы … Саксонию, Сингапур, Калверт и одну в системе государственных школ, которую мы смогли взять взаймы.Это бьет их руки вниз. Это основательно, хорошо продумано и заставляет наших детей думать о математике. Практики и повторений достаточно, чтобы концепции действительно усвоились, не утомляя их. Это единственная математическая программа, которую мы использовали, и мне не пришлось запускать ее в поисках добавки. Еще раз спасибо, Мария, очень рада, что мы тебя нашли.
Дженнифер
августа 2014
Примечание: два обзора ниже относятся к более старой версии MM5. Однако принципиально он похож на новую, исправленную версию.
Зейн отлично учится по математике! Мне эта программа нравится намного больше, чем Saxon … мы уделяем достаточно времени каждой новой концепции, чтобы он действительно ее «понял»! Скачанный материал (5 класс) намного красочнее (и поэтому вызывает у него интерес!), Чем печатная версия Math Mammoth [использованная в 4 классе]. И со всей дополнительной «помощью», которую вы предоставляете; от подсказок, предложений и игр до списка других сайтов с играми, загрузками (фаворитом был math rider!) и халявой… вы сделали математику УДОВОЛЬСТВИЕМ для ОБЕИХ из нас! Я действительно не могу вас отблагодарить (а я уже обучил на дому двух мальчиков . .. один разработчик компьютерных веб-сайтов, а другой инженер-химик … так что я СТАРАЯ мама и, честно говоря, готова немного повеселиться с учеба в школе)!
И со всей дополнительной «помощью», которую вы предоставляете; от подсказок, предложений и игр до списка других сайтов с играми, загрузками (фаворитом был math rider!) и халявой… вы сделали математику УДОВОЛЬСТВИЕМ для ОБЕИХ из нас! Я действительно не могу вас отблагодарить (а я уже обучил на дому двух мальчиков . .. один разработчик компьютерных веб-сайтов, а другой инженер-химик … так что я СТАРАЯ мама и, честно говоря, готова немного повеселиться с учеба в школе)!
Math Mammoth УДИВИТЕЛЬНЫЙ!
Бонни
января 2012
Я мать двух прекрасных дочерей 13 и 11 лет, которые учатся в государственной школе французского погружения на острове Ванкувер, Канада.
У моей младшей дочери был трудный 5-й класс по математике, и в школе ей оказывали дополнительную помощь в обучении.Я часто беспокоился о том, что, поскольку все обучение ведется на французском, ее втором языке, ей в конечном итоге может быть труднее понять уроки математики или, возможно, способ ее преподавания. И хотя я пытался помочь ей в течение учебного года, это стало скорее упражнением в переводе, потому что я только год изучал базовый вводный французский в университете, и ей пришлось перевести мне вопрос, прежде чем я смог помочь.
И хотя я пытался помочь ей в течение учебного года, это стало скорее упражнением в переводе, потому что я только год изучал базовый вводный французский в университете, и ей пришлось перевести мне вопрос, прежде чем я смог помочь.
Я знал, что нам нужно поработать над этим летом.Я узнал, что в ее математических знаниях было больше пробелов, чем я думал ранее. Именно тогда я отказался от обучения ее математике на французском языке и начал искать рабочие листы в Интернете. Я был очень рад встретить ваши бесплатные рабочие листы, но после просмотра полных страниц с образцами рабочего текста Mammoth и клипов на Youtube, которые помогают обучать «учителя», я был так впечатлен, что купил голубой рабочий текст A и B. Мне очень нравится, насколько ясно объясняются уроки и как концепции плавно сочетаются друг с другом, и что вы персонализировали этот курс с инструкциями для «учителей».И когда я сказал своей дочери, что нашел в Интернете учителя математики, который может научить МЕНЯ преподавать, она, похоже, была довольна и, возможно, немного вздохнула (!!?)
Итак, вот и мы, день 4, страница 17, она набирает скорость, и ее отношение улучшилось, поскольку она начинает понимать уже пройденную математику.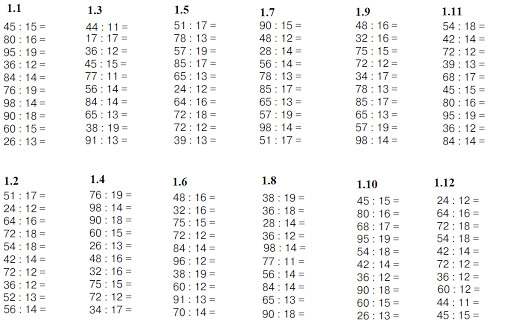 Мне очень нравится, что уроки или правила выделены или обрисованы в общих чертах, чтобы к ним было легче вернуться. Рабочий лист также выглядит привлекательно.
Я надеюсь, что этим летом мы сможем пройти весь курс, не будучи слишком утомительным, но я вижу, что она набирает чувство собственного достоинства и воодушевляется, она работает, задавая вопросы, с меньшим руководством с моей стороны.
Мне очень нравится, что уроки или правила выделены или обрисованы в общих чертах, чтобы к ним было легче вернуться. Рабочий лист также выглядит привлекательно.
Я надеюсь, что этим летом мы сможем пройти весь курс, не будучи слишком утомительным, но я вижу, что она набирает чувство собственного достоинства и воодушевляется, она работает, задавая вопросы, с меньшим руководством с моей стороны.
Итак, большое спасибо, Мария!
Я ожидаю, что куплю голубой рабочий текст 6-го класса, чтобы «работать вместе» с ней, когда она вернется к математике в 6-м классе по французскому языку в сентябре. Я уверен, что смогу отслеживать ее успехи, а затем предлагать помощь по мере необходимости (или, если необходимо!).
С уважением, Элейн 900 — 13 июля 2010 г.
% PDF-1.4
%
448 0 объект
>
эндобдж
xref
448 82
0000000016 00000 н.
0000002775 00000 н.
0000002922 00000 н.
0000003419 00000 п.
0000003751 00000 п.
0000004062 00000 н.
0000004260 00000 н.
0000004374 00000 п.
0000004486 00000 н. 0000004599 00000 н.
0000004708 00000 н.
0000005172 00000 п.
0000005199 00000 п.
0000005635 00000 п.
0000005662 00000 н.
0000006228 00000 п.
0000006624 00000 н.
0000006651 00000 п.
0000006678 00000 н.
0000007142 00000 п.
0000007282 00000 н.
0000007415 00000 н.
0000007550 00000 н.
0000007687 00000 н.
0000008233 00000 н.
0000008771 00000 н.
0000009330 00000 н.
0000009891 00000 н.
0000010435 00000 п.
0000010462 00000 п.
0000010856 00000 п.
0000010994 00000 п.
0000011520 00000 п.
0000011783 00000 п.
0000012286 00000 п.
0000012575 00000 п.
0000012846 00000 п.
0000014112 00000 п.
0000025731 00000 п.
0000025844 00000 п.
0000027008 00000 н.
0000027316 00000 н.
0000027431 00000 н.
0000030282 00000 п.
0000030600 00000 п.
0000030719 00000 п.
0000031960 00000 п.
0000032273 00000 п.
0000032400 00000 п.
0000034380 00000 п.
0000034704 00000 п.
0000034774 00000 п.
0000034854 00000 п.
0000038726 00000 п.
0000039000 00000 н.
0000039288 00000 п.
0000039358 00000 п.
0000039438 00000 п.
0000044340 00000 п.
0000044609 00000 п.
0000004599 00000 н.
0000004708 00000 н.
0000005172 00000 п.
0000005199 00000 п.
0000005635 00000 п.
0000005662 00000 н.
0000006228 00000 п.
0000006624 00000 н.
0000006651 00000 п.
0000006678 00000 н.
0000007142 00000 п.
0000007282 00000 н.
0000007415 00000 н.
0000007550 00000 н.
0000007687 00000 н.
0000008233 00000 н.
0000008771 00000 н.
0000009330 00000 н.
0000009891 00000 н.
0000010435 00000 п.
0000010462 00000 п.
0000010856 00000 п.
0000010994 00000 п.
0000011520 00000 п.
0000011783 00000 п.
0000012286 00000 п.
0000012575 00000 п.
0000012846 00000 п.
0000014112 00000 п.
0000025731 00000 п.
0000025844 00000 п.
0000027008 00000 н.
0000027316 00000 н.
0000027431 00000 н.
0000030282 00000 п.
0000030600 00000 п.
0000030719 00000 п.
0000031960 00000 п.
0000032273 00000 п.
0000032400 00000 п.
0000034380 00000 п.
0000034704 00000 п.
0000034774 00000 п.
0000034854 00000 п.
0000038726 00000 п.
0000039000 00000 н.
0000039288 00000 п.
0000039358 00000 п.
0000039438 00000 п.
0000044340 00000 п.
0000044609 00000 п.
методика выполнения операций и примеры реализации алгоритма
Математика
12.11.21
9 мин.
Одними из базовых математических операций являются умножение и деление натуральных чисел. В 5 классе они изучаются более подробно с учетом всех «тонкостей». Специалисты разработали специальные алгоритмы, позволяющие произвести расчеты без ошибок. Однако перед обучением нужно разобрать основные определения и понятия, а затем приступать к практике.
Оглавление:
- Общие сведения
- Методика умножения
- Алгоритм деления
- Примеры решений
Общие сведения
Умножением двух или нескольких чисел называется математическая операция, состоящая из множителей и результата (произведения). Следует отметить, что ее можно заменить сложением, т. е. 2*3=2+2+2=6. Иными словами, первый множитель указывает на число, а второй обозначает, какое количество раз его необходимо сложить с эквивалентным значением. Операция умножения (при не табличных значениях) выполняется в столбик.
Операция умножения (при не табличных значениях) выполняется в столбик.
Деление — вид арифметической операции, при которой одно число (делимое) делится на другое (делитель), а их результатом является частное. Ее можно заменить вычитанием, т. е. 36/6=36−6−6−6−6−6−6=0. Следует отметить, что деление является сложным типом операции, поскольку классифицируется на два вида: без остатка и с его наличием.
Натуральные — числа, при помощи которых производится счет, т. е. 1, 2, 3, 4 и т. д. Весь числовой ряд является натуральным. Он расположен только в порядке возрастания.
Методика умножения
При умножении чисел используется специальная методика, при которой два значения записываются в столбик: единицы под единицами, десятки под десятками и т. д. Алгоритм возможно применять для многозначных величин. Он имеет следующий вид:
- Написать числовые пары одну под другой.

- Выполнить умножение единиц второго числа на первое.
- Записать результат.
- Перемножить разряд десятков с первым значением и записать его со смещением влево.
- Повторить четвертый пункт методики (нужно не забывать о постоянном смещении влево на один разряд).
- Сложить обе величины и записать окончательный результат.
Следует отметить, что для оптимизации решения примеров по математике 5 класса на умножение применяются свойства. К ним относятся следующие:
- При произведении любого натурального числа на 0 получается нулевое значение.
- Произведение двух чисел, одно из которых 1, есть другое значение, т. е. а*1=а.
- Переместительное: перемена мест сомножителей не меняет результат (mnо=mоn=nоm=nmo=omn=onm).
- Сочетательный закон: перемножать можно в любом порядке. Например, если удобно умножить 1 на 3, то можно их перемножить, а затем подключить второе значение.
- Распределительное: умножение числа на сумму двух величин эквивалентно произведению общего множителя за скобкой на первое и второе значения, а затем полученные два результата требуется сложить.
 Это свойство может быть полезно при решении уравнений.
Это свойство может быть полезно при решении уравнений.
Следует отметить, что любое из вышеописанных свойств возможно применять несколько раз. Например, можно использовать переместительное и сочетательное.
Алгоритм деления
Деление, как и умножение, выполняется по определенному алгоритму. Однако следует учитывать факт, что результат может быть целым и с остатком. В первом и во втором случае применяется аналогичный алгоритм, но существуют некоторые особенности. Методика деления натурального числа на другое значение, принадлежащего к этому типу, имеет такой вид:
- Записать делимое, а с правой стороны — делитель, отделяя их прямой чертой.
- Взять количество разрядов, соответствующих делителю.
- Подобрать множитель, а затем записать его произведение на делитель под I разрядной группой и вычислить их разность.
- Взять II разрядную группу и выполнить аналогичную операцию.
- Продолжать до того момента, пока не получится 0 или величина (остаток), которая меньше делителя.

Следует отметить, что операция деления имеет несколько особенностей. К ним относятся следующие:
- Деление на 0 невозможно. Возможно только нуль разделить на любое число. Результат при этом будет равен 0. Пример деления для 5 класса имеет такой вид: 0/8=0.
- Деление на 1 имеет эквивалентное исходное значение: 5/1=5.
После рассмотрения алгоритмов нужно перейти решению примеров на умножение и деление для 5 класса.
Примеры решений
Для примера следует разобрать задачу на перемножение чисел 25 и 25. В этом случае рекомендуется воспользоваться таким алгоритмом:
- Записать первый множитель, а под ним второй.
- Провести результирующую горизонтальную линию после величин в первом пункте.
- Поставить слева знак произведения.
- Умножить 25 на 5 (разряд единиц), а затем записать под чертой: 125.

- Перемножить 25 и 2 (десятки): 50.
- Записать величину, полученную в пятом пункте под десятками первого результата.
- Сложить величины 125+50 (смещенное влево): 625.
Следующий пример — задание на операцию деления 625 на 5. Для этого следует воспользоваться вышеописанной методикой:
- Написать делимое и делитель, разделив их вертикальной чертой.
- Рассмотреть I разряд. Он делится на 5, но с остатком: 6/5=1 (1 — остаток).
- Записать в поле результата число 1.
- Перемножить 1 и 5, записав под шестеркой: 5.
- Отделить остаток: 1.
- Перенести к 1 второй разряд: 12.
- Подобрать множитель: 5*2=10<12.
- Перемножить 5 и 2, записав результат под 12.
- Выделить остаток: 2.
- Перенести к 2 III разряд: 25.
- Осуществить деление 25 на пятерку: 25/5=5.
- Искомое частное: 125.
Следует отметить, что множитель при выполнении операции деления подбирается по такому принципу: его произведение на делитель не должно превышать значения делимого.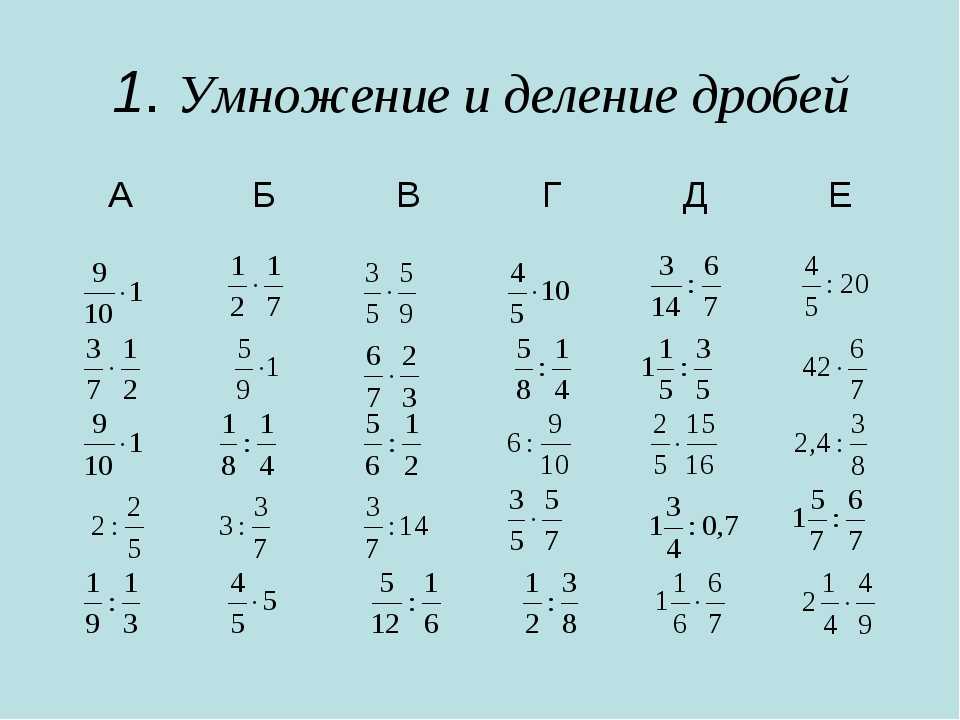 Операция с остатком реализуется аналогично. Например, в выражении 4/3 остаток равен единице, а результат записывается следующим образом: 4/3=1 (+1). Последнее значение «(+1)» указывает на положительный остаток, т. е. 3*1+1=4.
Операция с остатком реализуется аналогично. Например, в выражении 4/3 остаток равен единице, а результат записывается следующим образом: 4/3=1 (+1). Последнее значение «(+1)» указывает на положительный остаток, т. е. 3*1+1=4.
Иногда в математической литературе можно встретить запись «(-1)», которая указывает на отрицательную величину остатка. Например, запись «11 (-1)» при делении неизвестного числа на тройку определяет исходную величину следующим образом: 3*11−1=33−1=32. Пример возможно править и в таком виде: 32/3=10 (+2)=11 (-1).
Таким образом, арифметические операции умножения и деления рекомендуется при отсутствии калькулятора выполнять в столбик, но для этого следует знать основные методики.
Не успеваете написать работу?
Заполните форму и узнайте стоимость
Вид работыПоиск информацииДипломнаяВКРМагистерскаяРефератОтчет по практикеВопросыКурсовая теорияКурсовая практикаДругоеКонтрольная работаРезюмеБизнес-планДиплом MBAЭссеЗащитная речьДиссертацияТестыЗадачиДиплом техническийПлан к дипломуКонцепция к дипломуПакет для защитыСтатьиЧасть дипломаМагистерская диссертацияКандидатская диссертацияКонтактные данные — строго конфиденциальны!
Указывайте телефон без ошибок! — потребуется для входа в личный кабинет.
* Нажимая на кнопку, вы даёте согласие на обработку персональных данных и соглашаетесь с политикой конфиденциальности
Подтверждение
Ваша заявка принята.
Ей присвоен номер 0000.
Просьба при ответах не изменять тему письма и присвоенный заявке номер.
В ближайшее время мы свяжемся с Вами.
Ошибка оформления заказа
Кажется вы неправильно указали свой EMAIL, без которого мы не сможем ответить вам.
Пожалуйста проверте заполнение формы и при необходимости скорректируйте данные.
Основные правила математики с примерами. 5 класс
Основные правила математики с примерами. 5 класс
Содержание
- Натуральные числа
- Сравнение натуральных чисел
- Свойства сложения
- Формула пути
- Корень уравнения
- Правила решения уравнений
- Отрезок, прямая, луч
- Угол, биссектриса угла
- Углы: развернутый, прямой, острый, тупой
- Многоугольники.
 Равные фигуры
Равные фигуры - Треугольники: остроугольный, прямоугольный, тупоугольный
- Треугольники: равнобедренный, равносторонний, разносторонний
- Прямоугольник. Квадрат. Периметр
- Умножение. Свойства умножения
- Деление. Деление с остатком
- Площадь. Площадь квадрата, прямоугольника
- Объем. Объем прямоугольного параллелепипеда, куба
- Дроби: правильная, неправильная, сравнение дробей
- Сложение и вычитание дробей с одинаковыми знаменателями
- Сложение и вычитание смешанных чисел
- Преобразование неправильной дроби в смешанное число
- Преобразование смешанного числа в неправильную дробь
- Десятичные дроби: свойства, сравнение, округление
- Десятичные дроби: сложение, вычитание
- Десятичные дроби: умножение, деление
- Среднее арифметическое
- Процент
Натуральные числа
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., которые используют при счете предметов, называют натуральными.
Сравнение натуральных чисел
Число 0 меньше любого натурального числа.
0<1, 0<100
Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.
4352⏟4>999⏟3
Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр
3561>3559
Свойства сложения
Переместительный закон:
15+10=10+15
Сочетательный закон:
(23+15)+25=23+(15+25)
Формула пути
S=V·t,где S — пройденный путь, V — скорость движения, t — время, за которое пройден путь S
= 50км, = 2ч, = 25км/ч
, 50км = 25км/ч· 2ч
, 25км/ч = 50км : 2ч
, 2ч = 50км : 25км/ч
Корень уравнения
Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.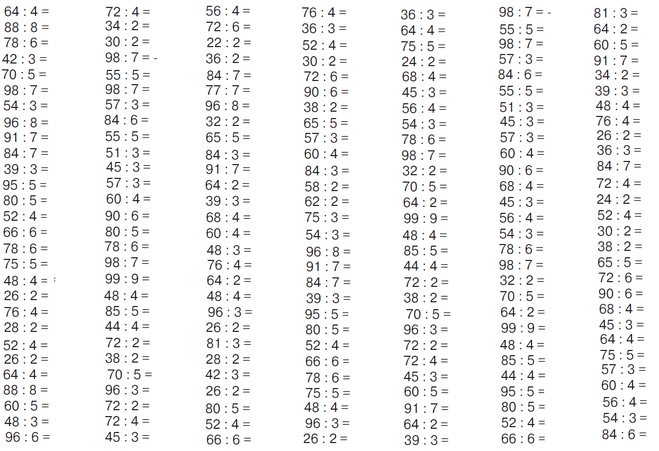
2·x+10=16
x = 3 — корень, так как 2·3+10=16
Что значит «Решить уравнение»
Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.
Правила решения уравнений
- Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
20слагаемое+xслагаемое=100суммаx = 100 — 20x = 80
- Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
xуменьшаемое—10вычитаемое=40разностьx = 40 + 10x = 50
- Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
50уменьшаемое—xвычитаемое=40разностьx = 50 — 40x = 10
- Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
xмножитель·7множитель=56произведениеx = 56 : 7x = 8
- Чтобы найти неизвестное делимое, надо делитель умножить на частное.
xделимое:8делитель=9частноеx = 9 · 8x = 72
- Чтобы найти неизвестный делитель, надо делимое разделить на частное.

42делимое:xделитель=7частноеx = 42 : 7x = 6
Отрезок, прямая, луч
Отрезок
Отрезок — часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)
Свойство длины отрезка
Если на отрезке отметить точку , то длина отрезка равна сумме длин отрезков и .
Равные отрезки
Два отрезка называют равными, если они совмещаются при наложении.
Свойство прямой
Через две точки проходит только одна прямая.
Измерить отрезок
Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается
Ломаная
Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом
Луч
Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча.В названии луча присутствуют две буквы, например, . Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
Угол, биссектриса угла
Угол
Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.
Равные углы
Два угла называют равными, если они совмещаются при наложении.
Свойство величины угла
Если между сторонами угла ∠ провести луч , то градусная мера ∠ равна сумме градусных мер углов ∠ и ∠, то есть ∠ = ∠+ ∠.
Биссектриса угла
Луч, который делит угол на два равных угла, называется биссектрисой угла.
Углы: развернутый, прямой, острый, тупой
Развернутый угол
Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.
Прямой угол
Угол, градусная мера которого равна 90°, называют прямым.
Острый угол
Угол, градусная мера которого меньше 90°, называют острым.
Тупой угол
Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.
Многоугольники.
 Равные фигуры
Равные фигурыРавные многоугольники
Два многоугольники называют равными, если они совмещаются при наложении.
Равные фигуры
Две фигуры называют равными, если они совмещаются при наложении.
Треугольники: остроугольный, прямоугольный, тупоугольный
Остроугольный треугольник
Если все углы треугольника острые, то его называют остроугольным треугольником.
Прямоугольный треугольник
Если один из углов треугольника прямой, то его называют прямоугольным треугольником.
Тупоугольный треугольник
Если один из углов треугольника тупой, то его называют тупоугольным треугольником.
Треугольники: равнобедренный, равносторонний, разносторонний
Равнобедренный треугольник
Если две стороны треугольника равны, то его называют равнобедренным треугольником.
Равносторонний треугольник
Если три стороны треугольника равны, то его называют равносторонним треугольником.
Периметр равностороннего треугольника
Если сторона равностороннего треугольника равна , то его периметр вычисляют по формуле
Разносторонний треугольник
Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.
Прямоугольник. Квадрат. Периметр
Прямоугольник
Если в четырехугольнике все углы прямые, то его называют прямоугольником.
Свойство прямоугольника
Противоположные стороны прямоугольника равны.
Периметр прямоугольника
Если соседние стороны прямоугольника равны и , то его периметр вычисляют по формуле
Квадрат
Прямоугольник, у которого все стороны равны, называют квадратом.
Периметр квадрата
Если сторона квадрата равна , то его периметр вычисляют по формуле .
Умножение. Свойства умножения
Умножение
- Произведением числа на натуральное число , которое не равно 1, называют сумму, состоящую из слагаемых, каждый из которых равен . В равенства числа и называют множителями, а число и запись — произведением.
- Если один из двух множителей равен 1, то произведение равно второму множителю.
- Если один из множителей равен нулю, то произведение равно нулю.

- Если произведение равно нулю, то хотя бы один из множителей равен нулю.
Свойства умножения
- Переместительный закон умножения:
- Сочетательный закон умножения:
- Распределительное свойство умножения относительно сложения:
2·(3+10) = 2·3 + 2·103·11 + 3·4 = 3·(11 + 4)
- Распределительное свойство умножения относительно вычитания:
2·(15—7) = 2·15 — 2·73·10 — 3·4 = 3·(10 — 4)
Деление. Деление с остатком
Деление
Для натуральных чисел равенство является правильным, если является правильным равенство
15 : 5 = 3 -правильное равенство, так как равенство 5 · 3 = 15 верное
В равенстве число называют делимым, число — делителем, число и запись — частным от деления, отношением, долей.
На ноль делить нельзя.
Для любого натурального числа правильными являются равенства:
,
Деление с остатком
, где — делимое, — делитель, — неполное частное, — остаток, .
154делимое=50делитель · 3неполное частное + 4остаток, 4<50
Если остаток равен нулю, то говорят, что число делится нацело на число .
Площадь. Площадь квадрата, прямоугольника
Свойства площади фигуры
Равные фигуры имеют равные площади;
Площадь фигуры равна сумме площадей фигур, из которых она состоит.
Площадь прямоугольника
Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.
Площадь квадрата
,
где — площадь квадрата, — длина его стороны.
Объем. Объем прямоугольного параллелепипеда, куба
Свойства объема фигуры
Равные фигуры имеют равные объемы;
Объем фигуры равен сумме объемов фигур, из которых она состоит.
Объем прямоугольного параллелепипеда
- ,
где — объем параллелепипеда, , и — его измерения, выраженные в одних и тех же единицах;
, где — площадь поверхности прямоугольного параллелепипеда.
- ,
где — площадь основания параллелепипеда, — его высота.
Объем куба
,
где — объем куба, — длина его ребра.
Дроби: правильная, неправильная, сравнение дробей
Правильная дробь
Дробь, числитель которой меньше знаменателя, называют правильной
Неправильная дробь
Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.
Сравнение дробей
- Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.
- Из двух дробей с одинаковыми числителями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.
- Все правильные дроби меньше единицы, а неправильные — больше или равны единице.
- Любая неправильная дробь больше любой правильной дроби.
Сложение и вычитание дробей с одинаковыми знаменателями
- Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.

- Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.
Сложение и вычитание смешанных чисел
- Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.
- Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.
Преобразование неправильной дроби в смешанное число
Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно
- числитель разделить на знаменатель;
- полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.
227= смешанное число? 7322—211 227=317
Преобразование смешанного числа в неправильную дробь
Чтобы преобразовать смешанное число в неправильную дробь нужно
- целую часть числа умножить на знаменатель дробной части;
- к полученному произведению прибавить числитель дробной части;
- эту сумму записать как числитель неправильной дроби;
- в его знаменателе записать знаменатель дробной части смешанного числа.

523= неправильная дробь?523=5*3+23=15+23=173
Десятичные дроби: свойства, сравнение, округление
Свойства десятичной дроби
Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.
Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.
2,23 = 2,230 = 2,230000005,50000=5,50000=5,5
Сравнение десятичных дробей
Из двух десятичных дробей больше та, у которой целая часть больше.
Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо
- с помощью приписывания нулей справа уравнять количество цифр в дробных частях,
- после чего сравнить полученные дроби поразрядно.
Сравнить 5,03 и 5,0375.5,03⏟2=5,0300⏟4 и 5,0375⏟4 ; 5,0300 < 5,0375.
Округление десятичных дробей
Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо
- все следующие за этим разрядом цифры отбросить.

- если при этом первая из цифр, которые отбрасывают равна 0,1, 2, 3, 4, то последнюю из цифр, которые оставляют, не меняют;
- если же первая из цифр, которые отбрасывют, равна 5, 6, 7, 8, 9, то последнюю из цифр, которые оставляют, увеличивают на единицу.
Округлить 5,248 и 3,952:а) до десятых:5,248≈5,2; 3,952≈4,0;б) до сотых:5,248≈5,25;3,952≈3,95.
Десятичные дроби: сложение, вычитание
Сложение десятичных дробей
Чтобы найти сумму двух десятичных дробей, нужно:
- уравнять количество цифр после запятых;
- записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
- сложить полученные числа так, как складывают натуральные числа;
- поставить в полученной сумме запятую под запятыми.
Сложить 2,5 и 3,623.2,500⏟3 и 3,263⏟3;2,500+3,2635,763
Вычитание десятичных дробей
Чтобы найти разность двух десятичных дробей, нужно:
- уравнять количество цифр после запятых;
- записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
- выполнить вычитание так, как вычитают натуральные числа;
- поставить в полученной разности запятую под запятыми.

Вычесть 3,27 и 3,009.3,270⏟3 и 3,009⏟3;3,270—3,0090,261
Десятичные дроби: умножение, деление
Умножение десятичных дробей
Чтобы перемножить две десятичные дроби, надо:
- перемножить их как натуральные числа, не обращая внимания на запятые;
- в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.
Умножить 1,5 и 2,25.2×2,2511,5+1125225·33,375 —количество цифр после запятой
Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.
Умножить 1,235 на 10, 100, 1000.а) на 10:1,235 ×10⏟1=12,35б) на 100:1,235 ×100⏟2 = 123,5в) на 1000:1,235 ×1000⏟3=1235,0 = 1235
Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.
Умножить 512,3 на 0,1, 0,01 и 0,001.а) на 0,1:512,3 ×0,1⏟1=51,23б) на 0,01:512,3 ×0,01⏟2=5,123в) на 0,001:512,3 ×0,001⏟3=0,5123
Деление десятичных дробей
Чтобы разделить десятичную дробь на десятичную, надо:
- перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;
- выполнить деление на натуральное число.

Разделить 24,2 на 0,02.24,2 : 0,02⏟ 2= 2420,0 : 2 = 2420 : 2 = 1210.
Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.
Разделить 25,5 на 10, 100, 1000.а) на 10:25,5 : 10⏟1=2,55;б) на 100:25,5 : 100⏟2=0,255;в) на 1000:25,5 : 1000⏟3=0,0255;
Среднее арифметическое
Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.
Найти среднее арифметическое чисел 15, 25 и 20.
15+25+20⏞сумма чисел3⏟количество чисел = 603= 20
Примечание:
Задача. Автомобиль 200 км ехал со скоростью 50 км/ч. Затем 120 км он ехал со скоростью 30 км/ч. Найти среднюю скорость.
Здесь
Vсредняя =Sобщtобщ .
1) 200 + 120 = 320(км) -весь путь;
2) 200 : 50 = 4(ч) — время, затраченное на 1-ую часть пути;
3) 120 : 30 = 4(ч) — время, затраченное на 2-ую часть пути;
4) 4 + 4 = 8(ч) — все время;
5) 320 : 8 = 40(км/ч) — средняя скорость.
Ответ: 40 км/ч.
Процент
Процентом называют сотую часть величины или числа 1%=
Найти 4% от числа 20.20 : 100 = 0,2 (0,2 —это 1% от числа 20);0,2 × 4 =0,8( 0,8—искомое число).Или 4% = 4100 = 0,04;0,04 ×20 = 0,8.
Умножение и деление десятичных дробей 5 класс онлайн-подготовка на Ростелеком Лицей
Введение
Что такое запись числа в десятичной системе счисления? Например, запись числа 2536?
Это краткая запись суммы:
Десятичная дробь – это тоже краткая запись суммы:
С помощью запятой отделяется целая часть от дробной. Умножение или деление на 10, 100, 0,1, 0,01 и так далее не меняет цифры в записи, а лишь сдвигает запятую.
Напоминание:
Кроме того, стоит помнить, что любую десятичную дробь можно представить в виде произведения:
Умножение десятичной дроби на целое число или другую десятичную дробь
В предыдущем разделе были повторены все необходимые правила для того, чтобы умножать десятичную дробь на целое число или на другую десятичную дробь.
Пример: а) ; б)
а)
б)
Каждый раз запятая была убрана, но информация о ней сохранялась с помощью множителя 0,1, 0,01 и так далее. Потом было выполнено умножение целых чисел. И снова запятая возвращалась на место, учитывая множитель.
Правило умножения дробного числа на целое число
Чтобы умножить дробь на целое число, нужно умножать, не обращая внимания на запятую, затем в ответе вернуть запятую на место, то есть отделить ею столько же цифр в дробной части, сколько было в исходном числе.
Пример:
Выполняя умножение, не стоит обращать внимания на запятую.
Затем необходимо поставить запятую так, чтобы в дробной части получилось, как и раньше, 3 цифры.
Умножение двух десятичных дробей. Правило
Для умножения двух десятичных дробей принцип абсолютно такой же.
Правило
Чтобы перемножить две десятичные дроби, нужно их перемножить, не обращая внимания на запятые, затем в ответе отделить запятой столько цифр, сколько их было у обоих чисел вместе.
Пример 1
Сначала необходимо переписать каждую дробь в виде целого числа и вспомогательного множителя. Таким образом, каждая дробь будет представлена в виде произведения.
Затем нужно выполнить умножение целых чисел отдельно, вспомогательных множителей отдельно. Полученный результат нужно умножить на 0,001, то есть выполняется отделение запятой дробной части длиной в 3 цифры.
Пример 2
Нужно выполнить умножение, не обращая внимания на запятые. Количество цифр после запятой – 3, поэтому запятая ставится, отделяя 3 цифры. Последний ноль можно убрать из записи.
Пример 3
Выполняется умножение в столбик, при этом не обращая внимания на запятые, но помня, что в конце надо будет также отделить запятой 4 цифры.
Пример 4
В ходе урока мы уже выяснили, что умножать десятичные дроби технически означает просто умножать целые числа. Далее в ответе нужно отделить запятой знаков столько, сколько их было у всех чисел вместе.
Далее в ответе нужно отделить запятой знаков столько, сколько их было у всех чисел вместе.
Конечно, это правило распространяется и на случай нескольких множителей:
Деление десятичных дробей
Ситуация с делением десятичных дробей такая же: если уметь делить целые числа одно на другое, то тогда получится и десятичную дробь делить на другую десятичную дробь.
Пример
Когда заканчивается целое число, которое надо разделить, то ставится запятая и продолжается выполнение вычислений:
Пример
Здесь ситуация ровно такая же: как только кончается целая часть – ставится запятая:
То есть технически не важно, что делить на целое число – дробь или другое целое число. Алгоритм одинаковый.
Общий алгоритм деления
Пусть надо число поделить на число . Это можно записать так:
или
Стоит помнить, что и можно умножить на одно и то же число, от этого результат не изменится.
В самом деле, можно делить , а можно , а можно . Можно все переписать в виде дробей. Результат все равно один – это равно 2.
Решение примеров
Пример. Одну десятичную дробь разделить на другую десятичную дробь:
Можно умножить обе части на одно и то же число. В данном случае это 10. Умножение на 10 означает сдвиг запятой вправо на одну позицию. Тогда второе число станет целым. А деление на целое число уже было изучено на этом уроке:
Задание: 1. ; 2.
1.
2.
Вывод
На этом уроке были изучены правила деления и умножения десятичных дробей. Кроме того, были также рассмотрены и решены различные примеры на данную тему.
Список литературы
1. Виленкин Н.Я.. Математика: учеб. для 5 кл. общеобр. учр. 17-е изд. – М.: Мнемозина, 2005.
2. Шевкин А.В. Текстовые задачи по математике: 5–6. – М.: Илекса, 2011.
– М.: Илекса, 2011.
3. Ершова А.П., Голобородько В.В. Вся школьная математика в самостоятельных и контрольных работах. Математика 5–6. – М.: Илекса, 2006.
4. Хлевнюк Н.Н., Иванова М.В.. Формирование вычислительных навыков на уроках математики. 5–9 классы. – М.: Илекса, 2011.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Портал «Школьный помощник» (Источник)
2. Портал «Школьная математика» (Источник)
3. Портал «МетаШкола» (Источник)
4. Портал Matematika-na.ru (Источник)
Домашнее задание
1. Вычислите:
а) ; б)
2. Вычислите:
а) ; б)
Умножение и деление натуральных чисел — правила и примеры для 5 класса » Kupuk.net
Одними из самых простых операций в математике являются умножение и деление натуральных чисел. В 5 классе после изучения арифметических действий школьников учат приёмам нахождения произведения и частного. Это знания, на которых базируется не только алгебра, геометрия, физика, химия, информатика, но даже и гуманитарные науки. Пожалуй, эти умения используются на практике больше любых других, полученных при обучении в средней школе.
Это знания, на которых базируется не только алгебра, геометрия, физика, химия, информатика, но даже и гуманитарные науки. Пожалуй, эти умения используются на практике больше любых других, полученных при обучении в средней школе.
Общие сведения
Математические вычисления сопровождают человека на всём протяжении его жизни. Когда произносится слово «число», имеется в виду определённый символ, определяющий количество чего-либо. Существуют различного вида выражения, например, целые, дробные, логарифмические. Но самыми простыми являются натуральные. Своё название они получили из-за применения в повседневной жизни. Их используют для счёта и определения порядка.
Таким образом, под натуральными числами понимают выражения, применяемые для определения количества любого физического объекта или присваивания порядкового номера. Например, 3, 1789, 9876, 100009. Если такие числа расположить в порядке увеличения, этот ряд называют натуральным. Последовательность 2, 3, 4, 5 будет именно такой. Нужно отметить, что натуральный ряд бесконечен, наибольшего значения в нём не существует.
Последовательность 2, 3, 4, 5 будет именно такой. Нужно отметить, что натуральный ряд бесконечен, наибольшего значения в нём не существует.
Есть несколько систем счисления. В зависимости от неё, для обозначения используется различный набор символов. В России, США, европейских странах применяют арабскую систему. При этом в повседневности используется десятичная разрядность, то есть для записи чисел берут знаки от 0 до 9.
С числами можно выполнять любые действия. Их складывают, вычитают, перемножают и делят. Кроме этого, возводят в степень, извлекают из-под корня, логарифмируют и дифференцируют.
К основным свойствам натуральных чисел относят:
- коммутативность при прибавлении;
- бинарность операции умножения;
- ассоциативность при сложении и умножении;
- дистрибутивность произведения относительно сложения.
Эти свойства важны. На них часто опираются при решении примеров на умножение и деление в 5 классе средней школы. Каждая запись числа состоит из определённого количества разрядов. По сути, она составляет совокупность разрядных слагаемых. В качестве единиц принимают десятки. Любое натуральное выражение можно представить в виде суммы таких чисел. Например, 89 состоит из 8 десятков и 9 единиц. Значит, равенство 89 = 80 + 9 будет справедливым.
Каждая запись числа состоит из определённого количества разрядов. По сути, она составляет совокупность разрядных слагаемых. В качестве единиц принимают десятки. Любое натуральное выражение можно представить в виде суммы таких чисел. Например, 89 состоит из 8 десятков и 9 единиц. Значит, равенство 89 = 80 + 9 будет справедливым.
Неизвестную натуральную цифру принято обозначать маленькой латинской буквой эн (n). Интересно то, что пересчитать все числа невозможно.
Их количество бесконечно. Самое большое, которое удалось определить называется гугол. Оно содержит 100 нулей и является мерой атомов в физике.
Принцип умножения
Операция умножения подразумевает действие, заменяющее собой многократное сложение. Один из аргументов называют множимым, а другой множителем. Результатом умножения является произведение. Найти его довольно просто, если знать свойства операции.
К достаточным правилам, зная которые можно найти произведение любых чисел, относят:
 Но при этом есть нюанс, что умножение выполняют сначала на уменьшаемое, а затем вычитаемое, и из первого вычитают второе.
Но при этом есть нюанс, что умножение выполняют сначала на уменьшаемое, а затем вычитаемое, и из первого вычитают второе.Для умножения до 100 существует специальная таблица, которую необходимо знать наизусть.
Следует также понимать, что при увеличении числа в десятки раз ответ увеличится на число нулей, стоящих в умножаемой цифре. Например, 34 * 10 = 340; 980 * 1000 = 980000. Так, выполняется сколь угодно сложное перемножение и для чисел большего десятка.
Произведение часто находят методом «столбик». Суть способа состоит в том, что аргументы записывают один под одним. При этом самая правая цифра верхнего числа должна стоять над самой правой нижнего. Далее выполняют поразрядное умножение начиная с младших членов. Если при этом образуется высший разряд, он прибавляется к перемножаемому.
Результат умножения следующего десятка сдвигается на единицу влево. Далее, складывают полученные результаты и получают искомое произведение.
Выполнение деления
Между нахождением частного и произведения существует тесная взаимосвязь. Особенно она просматривается при решении примеров на деление в 5 классе. По сути, эти 2 действия являются обратными друг другу. Математическим языком это можно описать как b * a = c → b = c / a. Эта зависимость в дальнейшем довольно сильно помогает решать сложные многозначные уравнения.
Существует несколько способов поиска частного:
 На самом деле этот способ используется редко из-за своей громоздкости.
На самом деле этот способ используется редко из-за своей громоздкости. Существуют методы, позволяющие проверить, насколько правильно найдено частное. Для этого нужно полученный ответ перемножить с делителем. Например, 12 / 4 = 3. Отсюда 3 * 4 = 12. Все три члена идентичные, значит, ответ найден верно.
Например, 12 / 4 = 3. Отсюда 3 * 4 = 12. Все три члена идентичные, значит, ответ найден верно.
Следует знать, что есть приёмы, позволяющие облегчить выполнение действия. При нахождении результата деления, когда нужно найти частное двух одинаковых чисел, в ответе будет единица: 345/ 345 = 78 / 78 = 89976 / 89976 = 1.
При этом 0, разделённый на любое число, даст в ответе 0. Делить же на него нельзя: выражение не будет иметь смысла.
Решение примеров
В 5 классе на математике всегда ученикам преподаватель предлагает решить определённые задания. Это нужно, чтобы школьник закрепил полученные теоретические знания и научился их применять на практике. Существуют сборники примеров по математике за 5 класс на умножение и деление для самостоятельной проработки. Прорешав успешно оттуда задачи, любой учащийся сможет утверждать, что он разобрался в теме.
Вот некоторые из примеров, содержащиеся в таких задачниках:

В начальных классах учителя при решении задач не разрешают пользоваться калькуляторами. Это необходимая мера.
youtube.com/embed/8jQVODj8vcI»/>Ведь чтобы научиться, важно не только понимать суть действий, но и набраться необходимого опыта. При этом обязательно нужно наизусть выучить таблицу умножения.
Онлайн уроки по математике за 5 класс
Учить урок
Цифры и числа. Множество натуральных чисел. Классы и разряды. Большие числа. Порядок действий
Учить урок
Составление выражений при решении задач. Знакомство с комбинаторными методами (размещение с повторениями)
Учить урок
Точка и отрезок. Обозначение и построение отрезков. Расположение точек по отношению к отрезку. Сравнение и измерение длин отрезков. Меры длины. Основные свойства измерения отрезков. Ломаная линия. Многоугольники и их основные элементы и характеристики. Треугольник, периметр треугольника.
Основные свойства измерения отрезков. Ломаная линия. Многоугольники и их основные элементы и характеристики. Треугольник, периметр треугольника.
Учить урок
Отрезок. Обозначение отрезков. Измерение длин. Точки. Расположение точек по отношению к геометрическим фигурам. Сравнение длин отрезков, нахождение/построение отрезков, равных данным
Учить урок
Измерение различных величин. Измерительные инструменты. Шкалы. Деления, цена деления
Учить урок
Измерительные инструменты. Шкалы. Деления, цена деления
Учить урок
Координаты. Координатный луч. Измерение расстояний между точками с помощью координатного луча. Сравнение длин отрезков
Координатный луч. Измерение расстояний между точками с помощью координатного луча. Сравнение длин отрезков
Учить урок
Составление выражений при решении задач. Знакомство с комбинаторными методами (размещение)
Учить урок
Сравнение чисел с одинаковым количеством знаков. Сравнение чисел по расположению на координатной прямой. Двойные неравенства. Сортировка по возрастанию и убыванию. Текстовые задачи, содержащие условия «меньше на..» или «больше на…»
Учить урок
Сложение натуральных чисел. Иллюстрация операции сложения натуральных чисел с помощью координатного луча. Переместительное и сочетательное свойство сложения. Сложение натуральных чисел с нулем. Демонстрация свойств сложения с помощью координатного луча. Группировка слагаемых. Округление натуральных чисел при сложении
Переместительное и сочетательное свойство сложения. Сложение натуральных чисел с нулем. Демонстрация свойств сложения с помощью координатного луча. Группировка слагаемых. Округление натуральных чисел при сложении
Учить урок
Разряды и классы. Разрядные слагаемые. Сумма разрядных слагаемых. Таблица сложения натуральных чисел. Поразрядное сложение натуральных чисел. Сложение натуральных чисел столбиком. Округление и группировка натуральных чисел при сложении.
Учить урок
Вычитание натуральных чисел. Иллюстрация операции вычитания натуральных чисел с помощью координатного луча. Свойства вычитания натуральных чисел. Демонстрация свойств вычитания с помощью координатного луча. Сравнение двух натуральных чисел с помощью вычитания.
Сравнение двух натуральных чисел с помощью вычитания.
Учить урок
Правила нахождения компонентов вычитания. Таблица сложения/вычитания натуральных чисел. Поразрядное вычитание натуральных чисел. Вычитание натуральных чисел «столбиком». Округление натуральных чисел при вычитании.
Учить урок
Задачи, решаемые с помощью сложения. Задачи, решаемые с помощью вычитания. Решение составных текстовых арифметических задач на сложение и вычитание. Округление натуральных чисел
Учить урок
Числовые выражения. Значение числового выражения. Буквенные выражения. Значение выражения при заданном значении переменной. Применение числовых и буквенных выражений в математике
Буквенные выражения. Значение выражения при заданном значении переменной. Применение числовых и буквенных выражений в математике
Учить урок
Выражения с переменной. Тождества. Тождественные преобразования числовых и буквенных выражений. Буквенная запись свойств сложения натуральных чисел. Буквенная запись свойств вычитания натуральных чисел
Учить урок
Уравнение. Корень уравнения. Запись уравнений. Равносильные уравнения. Решение уравнений. Решение задач с помощью уравнений
Учить урок
Смысл умножения. Компоненты умножения. Буквенная запись свойств умножения. Упрощение буквенных выражений с использованием свойств умножения
Буквенная запись свойств умножения. Упрощение буквенных выражений с использованием свойств умножения
Учить урок
Компоненты деления. Свойства деления. Алгоритм проверки правильности решения. Деление «уголком». Упрощение буквенных выражений и решение уравнений, содержащих действие деления
Учить урок
Деление натуральных чисел с остатком. Компоненты математической операции деления с остатком: делимое, делитель, неполное частное, остаток. Нахождение компонентов деления с остатком. Решение текстовых задач
Учить урок
Свойства умножения натуральных чисел. Свойства деления натуральных чисел
Свойства деления натуральных чисел
Учить урок
Виды простых арифметических задач на умножение и деление. Примеры решения задач арифметическим способом на умножение и деление. Правило проверки правильности вычислений умножения и деления натуральных чисел. Решение задач на умножение и деление алгебраическим способом
Учить урок
Упрощение выражения. Основные способы упрощения математического выражения. Упрощение математических выражений при решении уравнений и текстовых задач
Учить урок
Действия первой и второй ступени. Порядок выполнения действий в выражениях без скобок. Порядок выполнения действий в выражениях со скобками
Порядок выполнения действий в выражениях без скобок. Порядок выполнения действий в выражениях со скобками
Учить урок
Степень числа. Основание и показатель степени. Квадрат и куб числа. Таблицы квадратов и кубов первого десятка натуральных чисел. Порядок выполнения действий в выражениях, содержащих степень. Примеры нахождения значения выражений, содержащих квадраты и кубы чисел. Стандартный вид числа
Учить урок
Понятие формулы. Выражение одной величины через другие известные величины. Общие правила оформления и решения задач с использованием формул. Примеры зависимостей между величинами. Решение текстовых задач с помощью формул
Учить урок
Прямоугольник и квадрат. Понятие площади и ее единицы измерения. Свойства площади. Равные фигуры. Формулы площади прямоугольника и квадрата. Примеры решение текстовых задач по теме.
Понятие площади и ее единицы измерения. Свойства площади. Равные фигуры. Формулы площади прямоугольника и квадрата. Примеры решение текстовых задач по теме.
Учить урок
Единицы измерения длины и площади. Взаимосвязь единиц измерения площади между собой, правило перевода из одной единицы измерения в другую. Правила и способы измерения площадей. Примеры решение текстовых задач по теме
Учить урок
Прямоугольный параллелепипед и его элементы. Измерения прямоугольного параллелепипеда. Куб. Площадь поверхности прямоугольного параллелепипеда. Примеры решение текстовых задач по теме
Учить урок
Объем. Единицы измерения объема. Правило перевода из одной кубической единицы измерения в другую. Объем прямоугольного параллелепипеда. Объем куба. Основные свойства объема. Решение задач с использованием формулы объема прямоугольного параллелепипеда
Единицы измерения объема. Правило перевода из одной кубической единицы измерения в другую. Объем прямоугольного параллелепипеда. Объем куба. Основные свойства объема. Решение задач с использованием формулы объема прямоугольного параллелепипеда
Учить урок
Окружность и круг. Основные характеристики окружности и круга. Круговая диаграмма. Длина окружности. Циркуль. Построение окружности (круга) с заданным радиусом
Учить урок
Доли. Сравнение долей. Обыкновенные дроби. Числитель и знаменатель дроби. Чтение и запись обыкновенных дробей. Изображение дробных чисел на координатном луче
Учить урок
Нахождение части от целого. Нахождение целого по его части. Алгоритм и примеры решения задач на нахождение части от целого и целого по его части
Нахождение целого по его части. Алгоритм и примеры решения задач на нахождение части от целого и целого по его части
Учить урок
Сравнение дробей с одинаковым числителем. Сравнение дробей с одинаковым знаменателем. Сравнение дробей с различными числителями и знаменателями. Приведением дробей к общему знаменателю
Учить урок
Правильная дробь. Неправильная дробь. Сравнение правильных и неправильных дробей. Расположение правильных и неправильных дробей на координатном луче. Примеры решения задач на нахождение части от целого и целого по части
Учить урок
Правила сложения и вычитания обыкновенных дробей с одинаковыми знаменателями. Иллюстрация операции сложения и вычитания дробей с помощью координатного луча. Решение уравнений и простых текстовых задач с использованием правил сложения и вычитания дробей с одинаковыми знаменателями
Иллюстрация операции сложения и вычитания дробей с помощью координатного луча. Решение уравнений и простых текстовых задач с использованием правил сложения и вычитания дробей с одинаковыми знаменателями
Учить урок
Запись частного в виде дроби. Решение уравнений, содержащих дроби. Решение текстовых задач с использованием обыкновенных дробей
Учить урок
Смешанное число. Целая и дробная часть смешанного числа. Правило перевода смешанного числа в неправильную дробь. Правило выделения целой части из неправильной дроби. Изображение смешанных чисел на координатном луче
Учить урок
Сравнение смешанных чисел. Правила сложения смешанных чисел. Правила вычитания смешанных чисел. Решение текстовой задачи на сложение и вычитание смешанных чисел
Правила сложения смешанных чисел. Правила вычитания смешанных чисел. Решение текстовой задачи на сложение и вычитание смешанных чисел
Учить урок
Десятичные дроби. Правила записи и чтения десятичных дробей. История возникновения десятичных дробей. Перевод обыкновенной дроби в десятичную дробь и обратно
Учить урок
Разряды десятичных дробей. Разложение десятичной дроби по разрядам. Изображение десятичных дробей на координатном луче. Правила сравнения десятичных дробей
Учить урок
Правила сложения десятичных дробей. Правила вычитания десятичных дробей. Правила сложения и вычитания десятичных дробей столбиком. Решение текстовой задачи на сложение и вычитание десятичных дробей
Правила вычитания десятичных дробей. Правила сложения и вычитания десятичных дробей столбиком. Решение текстовой задачи на сложение и вычитание десятичных дробей
Учить урок
Приближенные значения с избытком. Приближенные значения с недостатком. Правило округления чисел до заданного разряда. Примеры округления чисел
Учить урок
Умножение десятичных дробей на натуральное число. Умножение десятичных дробей на 10, 100, 1000 и т.д. Примеры решение текстовых задач по теме
Учить урок
Деление десятичных дробей на натуральное число. Деление натуральных чисел без остатка. Деление десятичных дробей на 10, 100, 1000 и т.д. Примеры решения текстовых задач по теме
Деление натуральных чисел без остатка. Деление десятичных дробей на 10, 100, 1000 и т.д. Примеры решения текстовых задач по теме
Лэйдл предлагает пройти уроки математики за 5 класс в режиме онлайн. Дополнительные занятия позволят подтянуть знания по той или иной теме, разобраться в точных науках и значительно повысить успеваемость в школе.
Программа 5 класса включает в себя информацию о натуральных числах и арифметических операциях с ними, начальные знания о геометрических фигурах и вычислении их площади, а также сведения о дробях и остатках. Все это – база, без которой невозможно дальнейшее изучение математики. Вот почему дополнительные онлайн-уроки просто необходимы школьникам, испытывающим проблемы с точными науками.
3 причины выбрать Лэйдл
- Готовая программа.
Команда опытных преподавателей собрала самую важную информацию за 5 класс и представила ее в простой и структурированной форме, значительно облегчив процесс обучения.
- Мультимедийные материалы.
Красочные фото и детальные видео помогают освоить арифметику и геометрию – ребенок легче воспринимает теорию и учится применять полученные знания на практике. - Задачи и уравнения.
На сайте представлены не только теоретические уроки, но и многочисленные задачи и уравнения, которые полностью соответствуют школьной программе. После прохождения такого «испытания» вызов к доске будет не страшен.
Решите проблему с изучением математики раз и навсегда – зарегистрируйтесь на Лэйдл и радуйтесь успехам своего ребенка!
Математика 5 класс | Умножение и деление целых чисел
Краткое изложение раздела
В Разделе 2 учащиеся будут опираться на свою работу по многозначному умножению и делению из 4 класса, а также свое понимание структуры десятичной системы счисления в Блоке 1. развить беглость с многозначным умножением и расширить многозначное деление, чтобы включить двузначные делители.
В 4-м классе учащиеся овладели навыком сложения и вычитания многозначных чисел (4.NBT.4), необходимым навыком для вычисления сумм и разностей в стандартном алгоритме умножения и деления соответственно. Учащиеся также умножали целое число до четырех цифр на однозначное целое число, а также два двузначных числа (4.НБТ.5). К концу 4-го класса учащиеся могут вычислять эти продукты с помощью алгоритмов, но «постоянно рассуждают о связи между математическими рисунками и письменными вычислениями, помогая им увидеть алгоритмы умножения и деления как аббревиатуры или резюме своих рассуждений о количество» (Прогрессии для CCSSM, «Числа и операции в базе десяти, K-5», стр. 14). Учащиеся также находят целые числа в частных и остатках с до четырехзначных делимых и однозначных делителей (4. NBT.6). Подобно умножению, к концу 4 класса учащиеся могут вычислять эти частные, используя алгоритмы наряду с другими стратегиями и представлениями, так что алгоритмы имеют смысл, а не заучиваются.
Раздел 2 5 класса начинается с написания, оценки и интерпретации простых числовых выражений (5. OA.1, 5.OA.2). Это служит как для просмотра основных фактов умножения и деления, которые поддерживают основной контент позже в модуле, так и для записи вычислений, которые будут становиться все более сложными по мере продвижения модуля. Затем учащиеся закрепляют стандартный алгоритм умножения с вычислительными случаями из 4-го класса, прежде чем расширять его использование на все более и более крупные множители (5.NBT.5). Затем учащиеся следуют аналогичной последовательности с делением, сначала вычисляя частные случаи из 4-го класса, используя различные стратегии, а затем распространяя эти методы на вычисления, включающие двузначные делители. Однако обратите внимание, что, в отличие от умножения, свободное владение стандартным алгоритмом деления не ожидается до 6-го класса (6.NS.2). На протяжении всего модуля учащиеся «учатся использовать [] структуру [десятичных чисел] и свойства операций, чтобы свести вычисление многозначного… произведения или частного к набору однозначных вычислений в различных десятичных единицах.
OA.1, 5.OA.2). Это служит как для просмотра основных фактов умножения и деления, которые поддерживают основной контент позже в модуле, так и для записи вычислений, которые будут становиться все более сложными по мере продвижения модуля. Затем учащиеся закрепляют стандартный алгоритм умножения с вычислительными случаями из 4-го класса, прежде чем расширять его использование на все более и более крупные множители (5.NBT.5). Затем учащиеся следуют аналогичной последовательности с делением, сначала вычисляя частные случаи из 4-го класса, используя различные стратегии, а затем распространяя эти методы на вычисления, включающие двузначные делители. Однако обратите внимание, что, в отличие от умножения, свободное владение стандартным алгоритмом деления не ожидается до 6-го класса (6.NS.2). На протяжении всего модуля учащиеся «учатся использовать [] структуру [десятичных чисел] и свойства операций, чтобы свести вычисление многозначного… произведения или частного к набору однозначных вычислений в различных десятичных единицах. ” (MP.7) (Прогрессии для CCSSM, «Числа и операции в базе десяти, K-5», стр. 4). Далее, «повторное рассуждение (MP.8), основанное на единообразии десятичной системы система является частью этого процесса» (Прогрессии для CCSSM, «Число и действие в базе десяти, K-5», стр. 4).
” (MP.7) (Прогрессии для CCSSM, «Числа и операции в базе десяти, K-5», стр. 4). Далее, «повторное рассуждение (MP.8), основанное на единообразии десятичной системы система является частью этого процесса» (Прогрессии для CCSSM, «Число и действие в базе десяти, K-5», стр. 4).
Позже в этом году учащиеся будут полагаться на свои знания в области вычислений с целыми числами, чтобы выполнять их с десятичными дробями (5.NBT.7). Они также будут писать, оценивать и интерпретировать выражения с дробями и десятичными знаками в модулях 5 и 6 (5.OA.1, 5.OA.2). Эта работа «в 5 классе предвосхищает их более позднюю работу с переменными выражениями» (6–8.EE) (OA Progression, стр. 32). Кроме того, учащиеся закрепляют беглость с алгоритмом деления и расширяют беглость со всеми четырьмя операциями до десятичных дробей (6.EE.2-3). Они также распространяют эти вычисления на еще неизвестные части нашей системы счисления, такие как отрицательные числа (7.NS). Таким образом, к концу этого раздела учащиеся будут просто стесняться бегло выполнять все четыре операции с целыми числами и будут готовы выполнять эти операции с другими типами чисел. Они также будут готовы думать не только о вычислении числовых выражений, но и об их понимании и интерпретации, намекая на новый мир математики — алгебру.
Они также будут готовы думать не только о вычислении числовых выражений, но и об их понимании и интерпретации, намекая на новый мир математики — алгебру.
Темп: 23 учебных дня (20 уроков, 2 дня гибкого графика, 1 день оценки)
Fishtank Plus для математики
Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.
Узнать больше
Оценка
Следующие оценки сопровождают Модуль 2.
Предварительный модуль
Предложите учащимся выполнить предварительную оценку и самооценку учащихся перед началом модуля. Используйте Руководство по анализу предварительной оценки, чтобы определить пробелы в фундаментальном понимании и наметить план ускорения обучения на протяжении всего модуля.
Промежуточный модуль
Предложите учащимся выполнить промежуточную оценку после урока 10.
Последующий модуль
Используйте приведенные ниже ресурсы для оценки усвоения учащимися содержания модуля и плана действий для будущих модулей.
Постмодальная оценка
Ключ к ответам после модульной оценки
Руководство по анализу послемодульной оценки
92F25A3F-8529-4314-9899-6EE68694E3D0Пост-юнит самооценка
Расширенный пакет оценивания
Используйте данные учащихся для управления планированием с помощью расширенного набора модульных оценок, помогающих оценить уровень владения учащимися базовыми навыками и понятиями, а также их прогресс в изучении содержания модуля.
Скачать образец
Подготовка блока
Интеллектуальная подготовка
Предложения по подготовке к обучению данного модуля
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Запуск модуля
Подготовьтесь к преподаванию этого модуля, погрузившись в стандарты, большие идеи и связи с предыдущим и будущим содержанием. Запуск модулей включает в себя серию коротких видеороликов, целевую литературу и возможности для планирования действий.
Обновление до Plus
Интеллектуальная подготовка для всех модулей
- Прочтите и аннотируйте разделы «Сводка модуля» и «Основные сведения» плана модуля.
- Выполните все целевые задачи в модуле и аннотируйте их, учитывая «Сводку модуля» и «Основные сведения».
- Пройти итоговую оценку.
Интеллектуальная подготовка для конкретного модуля
- Прочтите статью «Моделирование с помощью математики» и посмотрите второе видео о трехактных задачах.
- Учащиеся будут использовать диаграммы с лентами для представления выражений и контекстных задач. Они широко использовали их в предыдущих классах для решения текстовых задач. Чтобы узнать больше об использовании ленточных диаграмм для моделирования текстовых задач, изучите наш инструмент для учителя здесь: Моделирование текстовых задач с помощью ленточных диаграмм.
- Просмотрите приведенную ниже таблицу, чтобы ознакомиться с моделями, используемыми в устройстве.

зональные модели | Пример: Решите 24 x 11 с использованием модели площади |
| Алгоритм частичного произведения | |
стандартный алгоритм умножения | |
алгоритм частных частных | |
стандартный алгоритм деления/длинного деления |
Основные понятия
Основные математические понятия, которые учащиеся поймут в этом модуле
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- При умножении более эффективно разлагать значение на меньшее количество ненулевых цифр. В стандартном алгоритме это означает запись числа с меньшим количеством ненулевых цифр внизу.
- При оценке с делением более эффективно использовать числа, которые легко вычислить в уме, а не округленные числа (например, $${413 \div 64 \rightarrow 420 \div 60}$$).

- Некоторые расчетные оценки могут быть лучше других, в зависимости от того, какие числа выбраны для использования вместо фактических значений. Вычислительные оценки могут быть слишком высокими или слишком низкими, в зависимости от того, как числа были первоначально оценены, от выполняемых вычислений и от того, где они расположены в числовом предложении.
- Общие десятичные методы умножения и деления (включая стандартный алгоритм) зависят от (1) понимания того, как вычислять произведения и частные числа, кратные 10, 100, 1000 и т. д., и однозначных чисел, и ( 2) распределительное имущество.
Запас слов
Термины и обозначения, которые учащиеся изучают или используют на уроке
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950уравнение
выражение
группировка символов (круглые скобки, скобки, фигурные скобки)
Чтобы увидеть весь словарный запас для модуля 2, просмотрите наш глоссарий лексики для 5-го класса.
Материалы
Материалы, иллюстрации и инструменты, которые потребуются преподавателям и учащимся для работы с этим модулем
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- модели для зон Алгоритм частичного произведения
- стандартный алгоритм умножения
- алгоритм частных частных
- стандартный алгоритм деления/длинного деления
- ленты схемы
Модульная практика
Речевые задачи и упражнения на беглость речи
Получите доступ к ежедневным репетициям текстовых задач и нашим ориентированным на содержание упражнениям на беглость речи, созданным, чтобы помочь учащимся укрепить свои навыки применения и беглости речи.
Предварительный просмотр
Узнать больше
Схема урока
Тема A: Написание и интерпретация числовых выражений
Оценивать числовые выражения, включающие символы сложения, вычитания, умножения, деления и группировки.
5.ОА.А.1
Напишите выражения, которые записывают вычисления с числами, и интерпретируйте выражения без их вычисления.
5.ОА.А.1 5.ОА.А.2
Напишите выражения, представляющие реальные ситуации, и оцените их.
5.ОА.А.1 5.ОА.А.2
Тема B: Умножение многозначных целых чисел
Умножить числа, кратные десяти. Оценивайте многозначные продукты, округляя числа до их наибольшего разряда.
5.НБТ.Б.5
Умножение двузначных, трехзначных и четырехзначных чисел на однозначные числа.
5.НБТ.Б.5
Умножение двузначных чисел на двузначные числа.
5.НБТ.Б.5
Умножение трехзначных чисел на двузначные числа.
5.НБТ.Б.5
Умножение четырехзначных чисел на двузначные числа.
5.НБТ.Б.5
Умножение трех- и четырехзначных чисел на трехзначные числа.
5.НБТ.Б.5
Умножьте многозначные числа и оцените разумность продукта.
5.НБТ.Б.5
Тема C: Разделение многозначных целых чисел
Разделить числа, кратные десяти, на числа, кратные десяти, без остатка. Оцените многозначные частные путем округления чисел до их наибольшего разрядного значения.
5.НБТ.Б.6
Оценить многозначное частное, используя совместимые числа.
5.НБТ.Б.6
Разделите двузначные, трехзначные и четырехзначные делимые на однозначные делители.
5.НБТ.Б.6
Разделите двузначные и трехзначные делимые на кратные 10 с однозначными частными и остатками в единицах.
5.НБТ.Б.6
Разделите двузначные делимые на двузначные делители с однозначными частными и остатками в единицах.
5.НБТ.Б.6
Разделите трехзначные делимые на двузначные делители с однозначными частными и остатками в единицах.
5.НБТ.Б.6
Разделить трехзначные делимые на двузначные делители с двузначными частными, рассуждая о разложении остатка в любом месте.
5.НБТ.Б.6
Разделить четырехзначные делимые на двузначные делители с двузначными и трехзначными частными, рассуждая о разложении остатка в любом месте.
5.НБТ.Б.6
Разделите многозначные числа на однозначные и двузначные делители и оцените достоверность частного.
5.НБТ.Б.6
Решите текстовые задачи на умножение и деление многозначных чисел.
5.НБТ.Б.5 5.НБТ.Б.6 5.ОА.А.1 5.ОА.А.2
Общие базовые стандарты
Ключ
Основной кластер
Вспомогательный кластер
Дополнительный кластер
Основные стандарты
Стандарты содержания, рассматриваемые в этом модуле
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Числа и операции в десятичной системе счисления
5.
 НБТ.Б.5 — Свободно умножайте многозначные целые числа по стандартному алгоритму.
НБТ.Б.5 — Свободно умножайте многозначные целые числа по стандартному алгоритму. 5.НБТ.Б.6 — Находить целые числа в частном целых чисел с делимыми до четырех цифр и делителями с двузначными цифрами, используя стратегии, основанные на разрядном значении, свойствах операций и/или связи между умножением и делением. Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.
Операции и алгебраическое мышление
5.ОА.А.1 — Используйте скобки, скобки или фигурные скобки в числовых выражениях и оценивайте выражения с этими символами.
5.ОА.А.2 — Пишите простые выражения, которые записывают вычисления с числами, и интерпретируйте числовые выражения без их вычисления. Например, выразите вычисление «сложите 8 и 7, затем умножьте на 2» как 2 × (8 + 7).
 Признайте, что 3 × (18932 + 921) в три раза больше, чем 18932 + 921, без необходимости вычислять указанную сумму или произведение.
Признайте, что 3 × (18932 + 921) в три раза больше, чем 18932 + 921, без необходимости вычислять указанную сумму или произведение.
Основополагающие стандарты
Стандарты, описанные в предыдущих модулях или классах, которые являются важной основой для текущего модуля
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Числа и операции в десятичной системе счисления
4.НБТ.Б.4
4.НБТ.Б.5
4.НБТ.Б.6
5.НБТ.А.1
5.НБТ.А.2
Операции и алгебраическое мышление
3.OA.D.8
4.ОА.А.3
Будущие стандарты
Стандарты будущих классов или разделы, связанные с содержанием данного раздела
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Выражения и уравнения
6.
 EE.A.2
EE.A.26.EE.A.3
6.EE.A.4
Система счисления
6.НС.Б.2
6.НС.Б.3
6.НС.Б.4
Стандарты математической практики
CCSS.MATH.PRACTICE.MP1 — Разбираться в проблемах и настойчиво решать их.
CCSS.MATH.PRACTICE.MP2 — Рассуждайте абстрактно и количественно.
CCSS.MATH.PRACTICE.MP3 — Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.
CCSS.MATH.PRACTICE.MP4 — Модель с математикой.
CCSS.MATH.PRACTICE.MP5 — Стратегически используйте соответствующие инструменты.
CCSS.MATH.
 PRACTICE.MP6
— Следите за точностью.
PRACTICE.MP6
— Следите за точностью.CCSS.MATH.PRACTICE.MP7 — Ищите и используйте структуру.
CCSS.MATH.PRACTICE.MP8 — Ищите и выражайте закономерность в повторяющихся рассуждениях.
Блок 1
Десятичное значение
значок/стрелка/вправо/большойБлок 3
Фигуры и объем
| Вы здесь: Главная → Рабочие листы → 5 класс Это обширная коллекция бесплатных печатных листов по математике для 5 класса, организованных по таким темам, как сложение, вычитание, алгебраическое мышление, разрядность, умножение, деление, разложение на простые множители, десятичные числа, дроби, измерения, координатная сетка и геометрия. Они генерируются случайным образом, могут быть распечатаны из вашего браузера и содержат ключ ответа. Рабочие листы поддерживают любую математическую программу для пятого класса, но особенно хорошо подходят для математической программы IXL для 5-го класса и их новых уроков в нижней части страницы. Скачки до: Рабочие листы генерируются случайным образом каждый раз, когда вы нажимаете на приведенные ниже ссылки. Вы также можете получить новый, другой, просто обновив страницу в браузере (нажмите F5). Вы можете распечатать их прямо из окна браузера, но сначала проверьте, как это выглядит в «Предварительном просмотре». Если рабочий лист не помещается на странице, отрегулируйте поля, верхний и нижний колонтитулы в настройках страницы вашего браузера. Другой вариант — настроить «шкалу» на 9.5% или 90% в режиме предварительного просмотра. Все рабочие листы поставляются с ключом ответа, размещенным на 2-й странице файла. Алгебра
Задача по математике для начальных классов Эдвард Заккаро Хорошая книга по решению проблем с очень разнообразными текстовыми задачами и стратегиями решения проблем. Сложение и вычитание в столбцах (числа друг под другом)
Разрядное значение и округление
 Пропуск счета
Округление
УмножениеУмножение в уме
 Длинное умножение (в столбцах)
ОтделМентальный отдел
Длинная часть
Следующие четыре типа рабочих листов не
Стандарты Common Core для пятого класса.
Факторинг
Сложение и вычитание дробейПодобные дроби/дробные части
В отличие от дробей/дробных частей
Умножение дробей
 Дробное деление
Следующие типы рабочих листов не соответствуют стандартам Common Core.
Преобразование дробей в смешанные числа и наоборот
Эквивалентные дроби и упрощение дробей
Запись дробей в виде десятичных и наоборот В таблицах ниже ключ ответа не дает дроби в упрощенной форме.
Десятичное сложениеМатематика в уме Десятичные цифры от 0 до 1
от 0 до 2 десятичных цифр
Дополнение к колонке
Десятичное вычитаниеМатематика в уме Десятичные цифры от 0 до 1
от 0 до 2 десятичных цифр
Задачи: арифметика в уме
Вычитание столбцов
Проблемы: алгебраическое мышление
Десятичное умножениеМатематика в уме
Умножить в столбцах
Десятичное делениеМатематика в уме
Длинная часть
Измерительные блокиТрадиционная система
 Метрическая система
Координатная сетка
Геометрия
Если вы хотите лучше контролировать такие параметры, как количество задач, размер шрифта, расстояние между задачами или диапазон чисел, просто щелкните по этим ссылкам, чтобы самостоятельно использовать генераторы рабочих листов: Меню математических листов 1 -й класс Рабочие листы римские цифры Классификация треугольников Канадские деньги |
Математика в пятом классе — обучение и практические занятия по математике для пятиклассника
[«`#», «Моя учетная запись»] Класс Описание: Учащиеся более глубоко изучают закономерности и операции с разрядными значениями. Их понимание расширяется и включает десятичные дроби в сотых и тысячных, операции с дробями и десятичными дробями, многозначное умножение и деление с остатками, модели площади, свойства умножения и деления, оценку и измерение объема. Введем координатную плоскость (квадрант I), которую учащиеся используют для решения задач.
Их понимание расширяется и включает десятичные дроби в сотых и тысячных, операции с дробями и десятичными дробями, многозначное умножение и деление с остатками, модели площади, свойства умножения и деления, оценку и измерение объема. Введем координатную плоскость (квадрант I), которую учащиеся используют для решения задач.
Pre-Kindergartenkindergartengrade 1grade 2grade 3grade 4grade 5
Pre-Kindergartenkindergartengrade 1grade 2grade 3grade 4grade 5
Модуль 1. Значение места и десятичные дни
Тема A: Умноженные шаблоны на Значите. Таблица значений разрядов и степеней десяти, учащиеся умножают и делят, чтобы решить задачи с десятичным числом в качестве множителя или частного.
Умножение на 10 с таблицей разрядов и без нее
Узнайте, как быстро умножить число на 10. Используйте таблицу разрядных значений, чтобы облегчить перестановку цифр с использованием концепции разрядного значения. Затем примените полученные знания, чтобы умножить на 10 без таблицы разрядных значений
Затем примените полученные знания, чтобы умножить на 10 без таблицы разрядных значений
Умножить на 100 с таблицей разрядных значений и без нее
Узнайте, почему умножение на 100 равносильно двукратному умножению на 10. Используйте таблицу разрядных значений, чтобы умножить число (до 4 цифр) на 100 путем сдвига цифр с использованием концепции разрядного значения. Затем примените полученные знания, чтобы умножить на 100
Умножение на 1000 с таблицей стоимостей и без нее
Узнайте, что умножение на 1000 равносильно трехкратному умножению на 10. Используйте таблицу разрядных значений для умножения числа (до 4 цифр) на 1000 путем сдвига цифр с использованием концепции разрядного значения
Умножение на 10, 100 и 1000
Потренируйтесь умножать число на 10, 100 или 1000 , Используйте понимание позиционного значения, чтобы переместить цифры в соответствующее место и добавить соответствующее количество нулей в конце произведения
Завершите схему умножения на 10 или 100
Изучите комбинацию чисел и вставьте число, которое правильно завершает схему. Используйте понимание умножения на 10, 100 или 1000, чтобы определить, какой фактор создает закономерность
Используйте понимание умножения на 10, 100 или 1000, чтобы определить, какой фактор создает закономерность
Деление на 10 с таблицей разрядных значений и без нее
Узнайте, как быстро разделить число на 10. Определите число, указанное на разряде график стоимости. Затем используйте диаграмму, чтобы помочь в смещении цифр, чтобы смоделировать деление. Наконец, примените полученные знания, чтобы разделить на 10
Разделение на 100 с таблицей стоимостей и без нее
Узнайте, почему деление на 100 равносильно двойному делению на 10. Используйте диаграмму разряда, чтобы разделить число на 100 путем сдвига цифр, используя концепцию разряда. Затем примените полученные знания для деления на 100 без таблицы
Разделите на 1000 с таблицей разрядных значений и без нее
Попрактикуйтесь в делении числа, состоящего из 4 или более цифр, на 1000. Первоначально вы можете выбрать использование таблицы разрядных значений смоделировать деление на 10 три раза. Затем примените полученное понимание, чтобы удалить правильное количество нулей из частного
Затем примените полученное понимание, чтобы удалить правильное количество нулей из частного
Деление на 10, 100 и 1000
Потренируйтесь делить 5-значные 6-значные числа на 10, 100 и 1000. Используйте понимание места, чтобы переместить цифры в соответствующее место и удалить правильное количество нулей с конца
Определите и заполните образец деления на 10 или 100
Рассмотрите образец чисел и вставьте число, которое правильно завершает образец. Используйте понимание деления на 10, 100 или 1000, чтобы определить, какой делитель создает шаблон
Чтобы умножить числа с одной ненулевой цифрой, вынесите на множители степени 10.
Узнайте, как умножать два числа, кратные 10. Во-первых, распознавать ненулевые цифры и практиковаться в написании до 6-значных чисел с одной ненулевой цифрой. нулевая цифра. Затем научитесь умножать два числа, разлагая на множители и переставляя ненулевые цифры
Умножайте числа с одной ненулевой цифрой
Потренируйтесь умножать два числа, кратные степени 10
Запишите соотношение между сотыми и тысячными с помощью таблицы стоимости места
Изучение соотношения между сотыми и тысячными разрядами десятичных дробей. Используйте десятичные счетчики и эквивалентные им дроби для сокращения дробей
Используйте десятичные счетчики и эквивалентные им дроби для сокращения дробей
Умножение десятичного числа на 10 с таблицей разрядов и без нее
Быстрое умножение десятичного числа на 10. Используйте диаграмму разряда, чтобы помочь в смещении цифр, используя концепцию разряда. Затем примените полученные знания, чтобы умножить на 10, не имея таблицы стоимостей
9.0079 Умножение десятичного числа на 100 с таблицей разрядов и без нееУзнайте, почему умножение на 100 равносильно двукратному умножению на 10. Используйте диаграмму разряда, чтобы умножить десятичную дробь на 100 путем сдвига цифр, используя концепцию разряда. Затем примените полученные знания, чтобы умножить на 100 без таблицы
Умножить десятичное число на 1000 с таблицей порядковых значений и без нее
Узнайте, что умножение на 1000 равносильно трехкратному умножению на 10. Первоначально вы можете использовать диаграмму разряда для моделирования умножения десятичного числа на 1000 путем сдвига цифр, используя концепцию разряда 9. 0006
0006
Умножение десятичного числа на 10, 100 и 1000
Потренируйтесь умножать десятичное число на 10, 100 или 1000. Используйте понимание разрядности, чтобы переместить цифры в нужное место. Кроме того, изучите взаимосвязь между нулями множителя и движением десятичной точки.
Заполните образец умножения на 10, 100 и 1000
Изучите образец десятичных чисел и вставьте число, которое правильно завершает образец. Используйте понимание умножения десятичной дроби на 10, 100 или 1000, чтобы определить, какой фактор создает закономерность
Преобразование единиц, десятых, сотых и тысячных в задачах на деление
Использование имен мест для помощи в задачах на деление. Создавайте эквивалентные выражения, вводя правильные термины
Разделите десятичное число на 10 с таблицей разрядов и без нее
Быстро разделите десятичное число на 10. Используйте диаграмму разряда, чтобы помочь в смещении цифр, используя концепцию разряда. Затем примените полученные знания, чтобы разделить на 10, не имея при себе таблицы стоимостей 9. 0006
0006
Разделить десятичное число на 100 с таблицей разрядов и без нее
Узнайте, почему деление на 100 равносильно двойному делению на 10. Используйте диаграмму разряда, чтобы разделить десятичную дробь на 100 путем сдвига цифр, используя концепцию разряда. Затем примените полученные знания для деления на 100 без таблицы
Разделите десятичное число на 1000 с таблицей порядковых значений и без нее
Узнайте, что деление на 1000 равносильно троекратному умножению на 10. Первоначально вы можете использовать диаграмму разряда для моделирования деления десятичной дроби на 1000 путем сдвига цифр с использованием концепции разряда. Затем примените понимание
Разделите число на 10, 100 и 1000
Попрактикуйтесь в делении десятичной дроби на 10, 100 или 1000. Используйте понимание разрядности, чтобы переместить цифры в нужное место. Кроме того, изучите соотношение между нулями делителя и движением десятичной точки
Заполните образец деления на 10, 100 и 1000
Изучите образец десятичных чисел и вставьте число, которое правильно завершает образец. Используйте понимание деления десятичной дроби на 10, 100 или 1000, чтобы определить, какой фактор создает закономерность
Используйте понимание деления десятичной дроби на 10, 100 или 1000, чтобы определить, какой фактор создает закономерность
Представление многократного умножения 10 в виде 10 с показателем степени
Изучите взаимосвязь между повторным умножением на 10 и количеством нулей в произведении. Представление повторяющихся множителей 10 в виде показателей степени 10
Представление 10 с показателем степени в виде повторного умножения
Узнайте взаимосвязь между экспоненциальным выражением и его выражением умножения. Определите показатель степени в выражении. Разверните показатель степени 10 в выражение умножения. Кроме того, потренируйтесь переписывать число как показатель степени 10 9.0006
Умножение десятичного числа на 10 с показателем степени
Узнайте, как умножить числа, умноженные на степень 10. Используйте понимание степени 10 и умножения десятичных дробей, чтобы расширить числа. Этот навык часто используется в науке для записи очень больших чисел в экспоненте
Разделить число на 10 с показателем степени
Расширить числа, которые делятся на степень 10. Используйте понимание показателей степени 10 и деления десятичных дробей, чтобы расширить числа
Используйте понимание показателей степени 10 и деления десятичных дробей, чтобы расширить числа
Тема B: Десятичные дроби и модели разрядов
Учащиеся используют знакомые символы (<, =, >) для сравнения чисел до тысячных. Они определяют, составляют и упорядочивают числа равной и неравной длины.
Запись десятичного числа в расширенной системе счисления
Узнайте, как преобразовать десятичное число в сумму его разрядных компонентов. Определите разрядное значение каждой цифры в десятичной дроби. Затем покажите развернутую сумму, из которой получилось число
9.0079 Сравнение чисел с точностью до сотых с таблицей разрядов и без нееНаучитесь сравнивать десятичные дроби. Используйте диаграмму стоимости мест, чтобы сравнить каждый набор значений мест слева направо. Затем используйте полученные знания для сравнения двух десятичных дробей без помощи таблицы.
Завершите неравенства, сравнивающие числа с точностью до сотых.
Потренируйтесь сравнивать десятичные дроби. Сначала вставьте правильный символ неравенства, чтобы сравнить два числа. Затем выберите правильное число, чтобы создать истинное утверждение о неравенстве. Затем проверьте свое понимание, вставив цифру, чтобы сделать утверждение о неравенстве
Сначала вставьте правильный символ неравенства, чтобы сравнить два числа. Затем выберите правильное число, чтобы создать истинное утверждение о неравенстве. Затем проверьте свое понимание, вставив цифру, чтобы сделать утверждение о неравенстве
Расположите десятичные числа в порядке от наименьшего к наибольшему (Уровень 1)
Узнайте, как расположить десятичные числа в порядке от наименьшего к наибольшему. Расставь три числа по порядку, поставив между ними правильный знак неравенства. Кроме того, потренируйтесь расставлять числа так, чтобы они были в правильном порядке.
Расположите десятичные числа в порядке от наименьшего к наибольшему (уровень 2)
Потренируйтесь расставлять десятичные числа по порядку. Переставить 4 числа от наименьшего к наибольшему
Расположить десятичные числа в порядке от наименьшего к наибольшему (уровень 3)
Потренируйтесь упорядочивать десятичные числа. Переставьте 4 числа в порядке от наименьшего к наибольшему
Тема C: Разрядное значение и округление десятичных дробей
Используя числовую прямую для предоставления контекста, учащиеся сначала определяют среднюю точку между двумя десятичными числами. Затем они переходят к округлению, используя числовую прямую и среднюю точку. Наконец, учащиеся округляют десятичные числа до любого заданного разряда без использования числовой строки.
Затем они переходят к округлению, используя числовую прямую и среднюю точку. Наконец, учащиеся округляют десятичные числа до любого заданного разряда без использования числовой строки.
Определить среднюю точку между двумя десятичными числами на числовой прямой
Узнайте, как легко определить середину между двумя десятичными знаками. Во-первых, используйте числовую строку, чтобы определить среднюю точку между двумя десятичными числами, отмеченными на этой числовой строке. Затем определите среднюю точку между двумя десятичными знаками, представленными в словесных выражениях
Определите, находится ли десятичное число больше или больше половины расстояния между двумя точками на числовой прямой
Узнайте, как определить, находится ли десятичное число меньше или больше половины между два заданных числа на числовой прямой. Сначала найдите десятичную дробь на числовой прямой. Затем найдите точку на полпути между двумя числами в строке чисел 9.0006
Составьте и примените правило округления чисел
Изучите правила округления десятичных дробей. Используйте числовую строку, чтобы определить, следует ли округлить данное десятичное число в большую или меньшую сторону, а затем выберите правильный ответ. Закончите предложения правил округления
Используйте числовую строку, чтобы определить, следует ли округлить данное десятичное число в большую или меньшую сторону, а затем выберите правильный ответ. Закончите предложения правил округления
Определите, округляется ли десятичное число вверх или вниз
Практика округления десятичных дробей. Учитывая десятичное число на баскетбольном мяче, выберите, в какую корзину должен попасть мяч, чтобы правильно округлить число
Округлите заданное число, сначала определив его ближайшие десятые
Научитесь округлять десятичные дроби, определяя ближайшие числа, до которых можно округлить данное десятичное число. Затем определите среднюю точку между ближайшими числами. Определите, меньше или больше заданное число середины, и соответственно округлите его.
Округлите данное число до сотых, десятых и единиц
Потренируйтесь округлять одно и то же число до ближайших сотых, десятых и единиц. Введите правильное значение, округленное до соответствующего разряда
Округление десятичного числа до заданного разряда (Уровень 1)
Практика округления чисел. Выберите правильный ответ на вопросы округления, чтобы решить головоломку с картинками
Выберите правильный ответ на вопросы округления, чтобы решить головоломку с картинками
Округлите десятичное число до заданного разрядного значения (Уровень 2)
Узнайте, как проверить разрядные значения для правильного округления. Определите разрядное значение, до которого вы хотите округлить, и разрядное значение справа от него. Затем определите, округляется ли значение вверх или вниз, и введите правильное округленное значение
Округление десятичного числа до заданного разряда (уровень 3)
Узнайте, как округлить до указанного разряда. Определите разрядное значение справа от значения, до которого следует округлить, затем определите, следует ли округлить в большую или меньшую сторону, и введите правильное округленное значение
Округлите десятичное число до заданного разрядного значения (уровень 4)
Практика округления чисел к заявленной стоимости места. Используйте свое понимание правил округления
Тема D: Сложение и вычитание десятичных знаков
На основе знакомой модели диска учащиеся складывают и вычитают числа до разряда тысяч. Они складывают и вычитают в уравнениях, требующих перегруппировки, и учатся использовать стандартный алгоритм (сложение столбцов и вычитание столбцов).
Они складывают и вычитают в уравнениях, требующих перегруппировки, и учатся использовать стандартный алгоритм (сложение столбцов и вычитание столбцов).
Сложение чисел до сотых с перегруппировкой с использованием модели диска
Научитесь складывать два десятичных числа (до сотых). Представьте каждое число моделью дисков для каждого разряда. Затем объедините диски с одинаковыми разрядами двух чисел, чтобы получить сумму 9.0006
Сложение чисел до тысячных с перегруппировкой с использованием модели диска
Научитесь складывать два десятичных числа (до тысячных). Представьте каждое число моделью дисков для каждого разряда. Затем соедините диски с одинаковыми разрядами двух чисел, чтобы получить сумму
Сложите числа до тысячных с перегруппировкой, используя сложение столбцов и модель диска
Сложите вместе два десятичных числа (до разряда тысяч). Перепишите задачу на сложение в виде столбцов и используйте модели дисков, чтобы помочь найти сумму с любой необходимой перегруппировкой
Добавление чисел до разряда тысячных с перегруппировкой с использованием сложения столбцов
Узнайте, как складывать два десятичных числа (до разряда тысяч). Перепишите задачу на сложение в виде столбца, чтобы лучше визуализировать любую необходимую перегруппировку при нахождении суммы
Перепишите задачу на сложение в виде столбца, чтобы лучше визуализировать любую необходимую перегруппировку при нахождении суммы
Вычитание чисел до сотых с перегруппировкой с использованием модели диска
Вычитание двух десятичных чисел (до сотых). Смоделируйте задачу на вычитание с помощью дисков, включая любую необходимую перегруппировку
Вычитание чисел до тысячных с перегруппировкой с использованием модели диска
Вычитание двух десятичных чисел (до сотых). Смоделируйте задачу на вычитание с помощью дисков, включая любую необходимую перегруппировку
Вычитание чисел до разряда тысячных с перегруппировкой с использованием вычитания столбцов и модели диска
Узнайте, как вычитать два десятичных числа (до разряда тысяч). Перепишите задачу на вычитание в виде столбцов и используйте модели дисков, чтобы помочь найти разницу с любой необходимой перегруппировкой
Вычитание чисел разной длины до тысячных с перегруппировкой с использованием вычитания столбцов и модели диска
Узнайте, как вычитать два десятичных числа разной длины. Перепишите задачу на вычитание в виде столбца и используйте модели дисков, чтобы помочь найти разницу с любой необходимой перегруппировкой
Перепишите задачу на вычитание в виде столбца и используйте модели дисков, чтобы помочь найти разницу с любой необходимой перегруппировкой
Вычитание чисел до тысячных с перегруппировкой с использованием вычитания столбцом
Узнайте, как вычитать два десятичных числа (до разряда тысяч). Перепишите задачу на вычитание в виде столбца, чтобы лучше визуализировать любую необходимую перегруппировку при поиске разницы
Тема E: Умножение десятичных чисел
Учащиеся делают первые шаги в понимании умножения десятичных чисел. Работая с однозначным целым числом и десятичным числом, учащиеся шаг за шагом выполняют процесс, используя знакомую модель диска. Они обмениваются дисками, чтобы смоделировать перегруппировку и изучить важность размещения десятичной точки.
Умножение десятичного числа с перегруппировкой с использованием модели диска
Узнайте, как умножить целое число на десятичное. Используйте модель диска, чтобы помочь представить десятичную дробь и ее умножение
Умножение десятичного числа с перегруппировкой с использованием модели диска и стандартного алгоритма
Умножение целого числа на десятичное. Используйте модель диска, чтобы представить десятичную дробь и ее умножение, и перепишите задачу в виде столбца
Используйте модель диска, чтобы представить десятичную дробь и ее умножение, и перепишите задачу в виде столбца
Сравните умножение целого числа с умножением числового числа на те же цифры
Узнайте, как использовать умножение целых чисел, чтобы помочь с умножением десятичная дробь, умноженная на целое число. Определите, используют ли десятичное число и связанное с ним целое число одни и те же цифры. Сравните произведение десятичного числа и целого числа с произведением
Умножение десятичного числа путем преобразования его в целое число и обратного преобразования произведения в десятичное число.
Преобразование десятичного числа в целое для облегчения решения задачи на умножение. Определите соответствующий коэффициент, чтобы преобразовать десятичную дробь в целое число. Затем найти продукт. Наконец, преобразуйте ответ обратно в десятичную форму
Тема F: Деление десятичных дробей
Учащиеся используют знакомые модели и процедуры, чтобы применить свои знания о делении десятичных дробей. Шаг за шагом они учатся правильно работать с помощью перегруппировки, использования нового разряда, использования нулей и добавления десятичной дроби в частное.
Шаг за шагом они учатся правильно работать с помощью перегруппировки, использования нового разряда, использования нулей и добавления десятичной дроби в частное.
Деление десятичного числа на однозначное число на основе модели
Узнайте, как делить десятичное число на целое число. Используйте модель диска, чтобы физически найти частичные частные каждого разрядного значения. Может потребоваться перегруппировка
Деление десятичного числа на однозначное число с перегруппировкой и без нее на основе модели
Деление десятичной дроби на целое число. Модель диска используется для представления десятичной дроби и для помощи в нахождении частичных частных каждого разрядного значения. Может потребоваться перегруппировка
Разделить десятичное число на однозначное число с перегруппировкой и без нее на основе модели
Научитесь делить десятичную дробь на целое число. Модель диска используется для представления десятичной дроби и для помощи в нахождении частичных частных каждого разрядного значения. Может потребоваться перегруппировка
Может потребоваться перегруппировка
Деление десятичного числа на однозначное число с перегруппировкой до нового разряда на основе модели
Узнайте, как разделить десятичное число на целое число, если в частном больше десятичных разрядов, чем в делимом. Модель диска используется для представления десятичной дроби и для помощи в нахождении частичных частных каждого разрядного значения. Перегруппировка на новое место значение будет
Деление десятичного числа на однозначное число с перегруппировкой и без нее с использованием деления в длинную и модели
Деление в длинную с делением десятичной дроби на целое число. Перепишите задачу на деление в длинном формате деления. Модель диска используется для представления десятичной дроби и для помощи в нахождении частичных частных каждого разрядного значения. Может потребоваться перегруппировка
Использование длинного деления для деления десятичного числа на однозначное с перегруппировкой и без нее
Научитесь делить десятичную дробь на целое число в длинное деление. Перепишите задачу на деление в длинном формате деления. Найдите частичные частные каждого разряда и запишите их в длинном делении. Может потребоваться перегруппировка
Перепишите задачу на деление в длинном формате деления. Найдите частичные частные каждого разряда и запишите их в длинном делении. Может потребоваться перегруппировка
Используйте длинное деление для деления десятичного числа на однозначное число с частными, включающими 0
Деление десятичного числа на целое с использованием длинного деления. Перепишите задачу на деление в длинном формате деления. Найдите частичные частные каждого разряда и запишите их в длинном делении. Иногда частичное частное может быть равно 0, поэтому перегруппировка может
Деление в длинное для деления десятичного числа на однозначное число с перегруппировкой в новое разрядное значение
Деление десятичного числа на целое с использованием деления в длинное и что делать, если последняя цифра не делится без остатка. Перепишите задачу на деление в длинном формате деления. Найдите частичные частные каждого разрядного значения и запишите их в длинном делении
МОДУЛЬ 2. Операции с многозначными целыми числами и десятичными дробями
Тема A: Умственные стратегии для умножения многозначных целых чисел
Учащиеся работают с круглыми числами, исчисляемыми десятками, сотнями и тысячами, чтобы увидеть, как вынесение на множители может упростить умственное умножение. При этом они применяют свойства умножения.
При этом они применяют свойства умножения.
Вынести 10, 100 или 1000 из заданного числа
Вынести 10, 100 или 1000 из числа. Сначала умножьте число на 10, 100 или 1000, а затем изучите, как эти два фактора формируют произведение. Затем укажите множители для заданных чисел, кратных 10, 100 или 1000
Решите задачи на умножение, используя ассоциативные и коммутативные свойства
Изучите ассоциативные и коммутативные свойства умножения. Изучите наборы факторов, чтобы определить, меняет ли их расположение ответ. Этот навык может помочь вам упростить задачи на умножение, чтобы вы могли быстро найти произведение с помощью меня
Решить задачу на умножение нескольких цифр, используя факторизацию и свойства умножения (Уровень 1)
Научитесь использовать факторизацию 10, 100, и 1000 и свойства умножения для умножения больших чисел. Вынесите на множители 10 100 или 1000, а затем сгруппируйте однозначные числа и степени 10 вместе
Решите в уме задачу на умножение нескольких цифр
Попрактикуйтесь в использовании ментальной арифметики для умножения больших чисел. Этот навык позволит вам быстрее решать задачи.
Этот навык позволит вам быстрее решать задачи.
Решите задачу на умножение нескольких цифр, используя факторизацию и свойства умножения (уровень 2)
Используйте факторизацию 10, 100 и 1000 и свойства умножения для умножения больших чисел. Вынесите на множители 10 100 или 1000, а затем сгруппируйте вместе однозначные числа и степени 10. Перестановка множителей позволяет быстро умножить
Округление многозначных чисел для оценки площади прямоугольника
Узнайте, как оценить площадь прямоугольника. Округлите измерения длины и ширины, а затем умножьте их, чтобы оценить площадь. Это позволяет быстро вычислить примерную площадь
Округление многозначных чисел для оценки произведения
Оценить ответ на задачу на умножение слов. Округлите большие числа до крайнего левого разряда. Затем используйте понимание степеней 10 и свойства умножения, чтобы быстро найти оценку ответа 9.0006
Тема B: Стандартный алгоритм умножения многозначных целых чисел
Учащиеся оттачивают свои навыки использования стандартного алгоритма умножения, работая с многозначными числами. Они осваивают использование перегруппировки и работу с нулями. Для дальнейшего концептуального понимания стандартный алгоритм представлен вместе с другими стратегиями, такими как модель площади и факторизация степеней 10.
Они осваивают использование перегруппировки и работу с нулями. Для дальнейшего концептуального понимания стандартный алгоритм представлен вместе с другими стратегиями, такими как модель площади и факторизация степеней 10.
Определение суммы, разности, произведения и частного в уравнениях
Выучите определения слов сумма, разность и частное. Выберите правильное слово для типа показанного уравнения. Затем сопоставьте тип задачи со словом ее результата
Составьте простые числовые выражения из текста
Научитесь преобразовывать словесные выражения в математические выражения. Из данного утверждения напишите математическое выражение, которое представляет слова. Этот навык поможет вам решать текстовые задачи, используя правильные операции
Составление выражений сложения и умножения с несколькими слагаемыми или множителями
Научитесь преобразовывать словесные выражения, содержащие более двух чисел, в математические выражения. Из данного утверждения напишите выражение сложения или умножения, которое представляет слова
Составьте сложные числовые выражения на основе модели (Часть 1)
Преобразуйте словесное выражение с тремя числами в математическое выражение. Используя диаграмму, вы выберете правильные действия и расставите числа в соответствующем порядке, чтобы образовать выражение
Используя диаграмму, вы выберете правильные действия и расставите числа в соответствующем порядке, чтобы образовать выражение
Составление сложных числовых выражений на основе модели (Часть 2)
Узнайте, как преобразовать словесное выражение с тремя числами в математическое выражение. Используя диаграмму, вы будете выбирать правильные операции и располагать числа в соответствующем порядке, чтобы образовать выражение
Составление сложных числовых выражений на основе модели (Часть 3)
Преобразование словесного выражения с тремя числами в математическое выражение. Используя диаграмму, вы выберете правильные действия и расставите числа в соответствующем порядке, чтобы образовать выражение
Умножение по стандартному алгоритму (1 цифра на 3 цифры)
Научитесь умножать однозначное число на трехзначное. Перепишите задачу в виде столбца с большим числом вверху. Понять, как умножать справа налево, переводя десятки частичного произведения в разрядное значение слева -цифровое число. Перепишите задачу в виде столбца с большим числом вверху. Понять, как умножать справа налево, переводя десятки частичного произведения в разрядное значение слева
Перепишите задачу в виде столбца с большим числом вверху. Понять, как умножать справа налево, переводя десятки частичного произведения в разрядное значение слева
Вынесение на множители степеней 10 для упрощения выражений умножения
Упрощение выражений умножения путем вынесения на множители степеней 10. Применение свойств умножения для перестановки множителей, чтобы иметь возможность использовать ментальную арифметику для быстрого завершения умножения
Решить связанные выражения умножения после разложение на множители степени числа 10
Узнайте, как быстро умножать большие числа. Умножьте на соответствующую однозначную цифру, а затем используйте понимание степеней 10 и их количество нулей, чтобы найти конечный продукт
Умножение в уме числа степени 10
Практикуйте математические приемы в уме, чтобы быстро умножать большие числа. Используйте понимание степеней 10. Вы можете использовать форму столбца для умножения связанной задачи перед добавлением соответствующего количества нулей к конечному результату
Умножьте на число со степенью 10, используя стандартный алгоритм
Узнайте, как умножить двузначное число на кратное 10, используя умножение в столбик. Используйте пошаговые инструкции, чтобы найти частичные продукты, которые формируют окончательный ответ
Используйте пошаговые инструкции, чтобы найти частичные продукты, которые формируют окончательный ответ
Умножение с использованием модели площади и стандартного алгоритма
Нахождение площади прямоугольника. Узнайте, как разбить прямоугольник на части с площадью, которую легче вычислить. Обратите внимание, как площади частей представлены в частичных произведениях стандартного алгоритма
Умножьте, используя стандартный алгоритм (3 цифры на 3 цифры) (Часть 1)
Узнайте, как умножать два трехзначных числа. Перепишите задачу в виде столбца. Поймите, как умножать справа налево, чтобы найти частичные произведения. Затем добавьте частичные произведения, чтобы найти окончательный ответ
Умножение по стандартному алгоритму (3 цифры на 3 цифры) (Часть 2)
Умножение двух трехзначных чисел. Перепишите задачу в виде столбца. Поймите, как умножать справа налево, чтобы найти частичные произведения, включая эффект цифры 0. Затем сложите частичные произведения, чтобы найти окончательный ответ.
Умножьте, используя стандартный алгоритм (3 цифры на 4 цифры) (Часть 1)
Узнайте, как умножить 3-значное и 4-значное числа вместе. Перепишите задачу в виде столбца. Понять, как умножать справа налево, чтобы найти частичные произведения, и как найти сумму этих произведений для окончательного ответа
Умножение по стандартному алгоритму (3 цифры на 4 цифры) (Часть 2)
Умножение 3-значного числа на 4-значное число. Перепишите задачу в виде столбца. Понять, как умножать справа налево, чтобы найти частичные произведения, в том числе влияние цифры 0
Умножать по стандартному алгоритму (2 цифры на 5 цифр)
Научиться умножать 5-значное число на 2-значный номер. Перепишите задачу в виде столбца. Понять, как умножать справа налево, чтобы найти частичные произведения, и как найти сумму этих произведений для окончательного ответа
Тема C: Десятичное многозначное умножение
Учащиеся расширяют свое понимание умножения десятичных чисел, увеличивая количество цифр в множителях. Работая с 2- или 3-значным целым числом и десятичным числом в десятых или сотых долях, учащиеся шаг за шагом выполняют процесс, используя стандартный алгоритм. Они узнают, как поставить десятичную дробь в своем ответе и как оценить, чтобы проверить обоснованность своего ответа.
Работая с 2- или 3-значным целым числом и десятичным числом в десятых или сотых долях, учащиеся шаг за шагом выполняют процесс, используя стандартный алгоритм. Они узнают, как поставить десятичную дробь в своем ответе и как оценить, чтобы проверить обоснованность своего ответа.
Умножение 2-значного десятичного числа на 2-значное целое с использованием частичных произведений с моделью площади
Умножение 2-значного десятичного числа на 2-значное целое число. Используйте сегментированный прямоугольник для представления частичных произведений в соответствующем умножении целого числа на целое число. Применить понимание разряда, чтобы найти произведение десятичных чисел
Умножить 2-значное десятичное число на 2-значное целое число, используя стандартный алгоритм (Уровень 1) как умножить двузначное десятичное число на двузначное целое число. Умножьте десятичную дробь на 10, затем используйте стандартный алгоритм, чтобы найти произведение целых чисел 9.0006
Умножение трехзначного десятичного числа на двузначное целое с использованием стандартного алгоритма (уровень 1) числа. Умножьте десятичную дробь на 100, затем используйте стандартный алгоритм, чтобы найти произведение целых чисел. Преобразование произведения целых чисел
Умножьте десятичную дробь на 100, затем используйте стандартный алгоритм, чтобы найти произведение целых чисел. Преобразование произведения целых чисел Умножение 2- или 3-значного десятичного числа на 2-значное целое число с использованием стандартного алгоритма (уровень 2)
Умножить 2-значное или 3-значное десятичное число на 2-значное целое число, используя родственное умножение двух целых чисел. Временно игнорируйте десятичную точку и используйте стандартный алгоритм для нахождения произведения целых чисел
Умножьте 2- или 3-значное десятичное число на 2-значное целое число, используя стандартный алгоритм (уровень 3) 2-значное или 3-значное десятичное число на 2-значное целое число. Используйте стандартный алгоритм для поиска произведения и определения положения десятичной точки на основе понимания десятичного умножения
Умножение десятичного числа на круглое путем вынесения на множители степени 10
Узнайте, как использовать круглые числа при умножении десятичного числа на целое число. Фактор степени 10 из целого числа. Переставить множители, чтобы упростить умножение
Фактор степени 10 из целого числа. Переставить множители, чтобы упростить умножение
Умножить десятичное число на круглое
Попрактиковаться в умножении десятичного числа на круглое число
Оценить произведение десятичного числа на трехзначное целое число (Часть 1)
Используйте округление для оценки произведения десятичного и трехзначного целого числа. Округлите каждый из факторов до их крайнего левого разряда. Умножьте округленные числа, чтобы приблизительно получить ответ.
Оцените произведение десятичного числа и трехзначного целого числа (Часть 2)
Потренируйтесь оценивать произведение десятичного числа и трехзначного целого числа. Округлите каждый из факторов до их крайнего левого разряда. Умножьте округленные числа, чтобы приблизиться к ответу
.Оцените произведение десятичного числа и трехзначного целого числа, затем решите с помощью стандартного алгоритма
Оцените произведение десятичного числа и трехзначного целого числа, а затем сравните оценку с фактическим произведением. Округлите каждый из факторов до их крайнего левого разряда. Умножьте округленные числа, чтобы приблизить ответ. Затем используйте стандартный
Округлите каждый из факторов до их крайнего левого разряда. Умножьте округленные числа, чтобы приблизить ответ. Затем используйте стандартный
Тема D: Умственные стратегии для деления многозначных целых чисел
Учащиеся полагаются на свое понимание степеней 10, деления, разрядности и округления, чтобы мысленно разделить многозначные целые числа.
Деление круглых чисел на степени 10
Научитесь быстро делить круглые числа на степени 10. Уменьшить количество нулей в частном на количество нулей в делителе
Разделить, вынеся из делителя степени 10
Упростить задачи деления, вынеся из множителя степени 10. Вынести из делителя степень десяти. Затем разделите делимое сначала на эту степень 10, а затем на другой множитель
Разделите мысленно многозначные круглые числа
Попрактикуйтесь в делении многозначных круглых чисел, используя математические вычисления в уме. Соберите головоломку с картинками, правильно решив задачи
Округлите многозначное число до заданного разряда (Уровень 1)
Узнайте, как округлить многозначное число до заданного разряда. Выберите значение справа от места, до которого вы хотите округлить, затем определите, следует ли округлять в большую или меньшую сторону
Выберите значение справа от места, до которого вы хотите округлить, затем определите, следует ли округлять в большую или меньшую сторону
Округление многозначного числа до заданного разряда (уровень 2) данное место
Список кратных заданному двузначному круглому числу
Пропустить счет путем перечисления нескольких кратных данному числу. Этот навык может помочь в решении задач на деление
Округление 3-значного числа до ближайшего кратного заданному 2-значному округленному числу (Уровень 1)
Научитесь округлять 3-значное число до ближайшего кратного заданной 2 -цифровое число. Назовите кратные двузначного числа. Определите, какое из кратных имеет наименьшую разницу с трехзначным числом
Округление 3-значного числа до ближайшего кратного заданного 2-значного круглого числа (Уровень 2)
Округление 3-значного числа до ближайшего кратного заданного 2-значного числа. Найдите кратные двузначного числа, которые стоят по обе стороны от трехзначного числа. Определите, какое из кратных имеет наименьшую разницу с трехзначным числом
Определите, какое из кратных имеет наименьшую разницу с трехзначным числом
Оцените частное, найдя ближайшее кратное
Узнайте, как вычислить частное. Округлите делитель до крайнего левого места. Затем округлить делимое до ближайшего кратного округленному делителю. Найдите приблизительное частное
Оценка частного уравнения многоразрядного деления (Уровень 1)
Оценка частного уравнения многоразрядного деления. Округлите и делитель, и делимое до крайнего левого места. Используйте степени 10, чтобы упростить задачу. Разделите округленное значение, чтобы найти приблизительное частное
Оцените частное уравнения многоразрядного деления (Уровень 2)
Оцените частное уравнения многоразрядного деления. Округлите и делитель, и делимое до крайнего левого места. Используйте степени 10 и разместите значения, чтобы упростить задачу. Разделите округленное значение, чтобы найти приблизительное частное
Тема E: Неполные частные и деление многоразрядных целых чисел
Учащиеся заглянут под капот деления, чтобы действительно понять концепцию остатка, а также шаги, связанные с делением на большие числа. Учащиеся работают с одно-, дву- и трехзначными делимыми и одно- и двузначными делителями. Они используют стандартный алгоритм деления в большую сторону, но по-разному подходят к нему, чтобы добиться математической гибкости.
Учащиеся работают с одно-, дву- и трехзначными делимыми и одно- и двузначными делителями. Они используют стандартный алгоритм деления в большую сторону, но по-разному подходят к нему, чтобы добиться математической гибкости.
Разделить группу объектов на группы заданного размера с остатком
Научитесь делить с остатком. Переведите словесную задачу в математическое выражение. Используйте модель для создания необходимых групп. Определите частное и остаток
Найдите частное и остаток, используя множители делителя
Научитесь делить с остатком. Используйте ближайшее кратное делителя, которое меньше делимого, чтобы найти частное. Затем определите остаток
Найдите частное и остаток, вычитая делитель из делимого (Часть 1)
Используйте повторное вычитание, чтобы найти остаток от задачи деления. Оцените частное, затем вычтите делитель из делимого столько раз, сколько возможно, чтобы найти остаток
Найдите частное и остаток, вычитая делитель из делимого (Часть 2)
Определите частное и остаток задачи деления через многократное вычитание. Вычтите делитель как можно больше раз. Посчитайте, сколько раз его вычли, чтобы найти частное. Число, оставшееся после вычитания, равно 9.0006
Вычтите делитель как можно больше раз. Посчитайте, сколько раз его вычли, чтобы найти частное. Число, оставшееся после вычитания, равно 9.0006
Оцените частное, затем решите, используя деление в большую сторону с однозначным частным (Часть 1)
Используйте оценку, чтобы научиться выполнять деление в большую. Округлите дивиденд до ближайшего кратного делителю, затем используйте коэффициенты 10, чтобы упростить оценку деления. Используйте оценку для завершения деления в большую сторону, включая нахождение остатка.
Оцените частное, затем решите, используя деление в большую сторону с однозначным частным (Часть 2)
Используйте оценку, чтобы научиться выполнять деление в большую сторону. Округлите делимое до ближайшего кратного делителя, чтобы получить частное. Перепишите задачу деления в длинной форме деления. Используйте оценку, чтобы завершить длинное деление, включая нахождение
Решите, используя деление в большую сторону с однозначным частным
Найдите частное, используя деление в большую сторону. Перепишите задачу деления в длинной форме деления. Используйте оценку, затем завершите частичные произведения в длинном делении. При необходимости можно использовать столбцовое умножение и вычитание
Перепишите задачу деления в длинной форме деления. Используйте оценку, затем завершите частичные произведения в длинном делении. При необходимости можно использовать столбцовое умножение и вычитание
Решить, используя деление в большую сторону с однозначным частным (завышение)
Узнайте, что делать, если оценочное частное слишком велико. Перепишите задачу деления в длинной форме деления. Округлите делитель и делимое. Если частичное произведение в длинном делении слишком велико, чтобы его можно было вычесть, уменьшите оценку на 1. Умножение столбца
Решите, используя деление в большую сторону с однозначным частным (занижение)
Распознайте, когда предполагаемое частное слишком мало. Перепишите задачу деления в длинной форме деления. Округлите делитель и делимое. Если остаток после вычитания в длинном делении больше или равен делителю, увеличьте оценку на
Решите, используя деление в длинное с однозначным частным
Попрактикуйтесь в делении в длинное с однозначным частным. Перепишите задачу в длинной форме деления. Если вы решите заполнить частное, вы можете решить задачу самостоятельно. Выбор оценки частного поможет вам решить проблему
Перепишите задачу в длинной форме деления. Если вы решите заполнить частное, вы можете решить задачу самостоятельно. Выбор оценки частного поможет вам решить проблему
Решите, используя деление в большую сторону с двузначным частным (Часть 1)
Найдите двузначное частное, используя деление в прямую. Перепишите задачу деления в длинной форме деления. Используйте оценку, затем завершите частичное частное в длинном делении. При необходимости можно использовать столбцовое умножение и вычитание
Решите, используя деление в большую сторону с двузначным частным (переоценка и занижение)
Узнайте, что делать, если расчетное частное слишком велико или слишком мало. Перепишите задачу деления в длинной форме деления. Используйте оценку, затем завершите частичные частные в длинном делении. Пересмотрите оценки, если вычитание не может быть завершено или
Решите, используя деление в большую сторону с двузначным частным (Часть 2)
Практика деления в большую сторону с двузначным частным. Перепишите задачу в длинной форме деления. Если вы решите заполнить частное, вы можете решить задачу самостоятельно. Выбор оценки частного проведет вас через проблему
Перепишите задачу в длинной форме деления. Если вы решите заполнить частное, вы можете решить задачу самостоятельно. Выбор оценки частного проведет вас через проблему
Решите, используя деление в большую сторону с трехзначным частным
Найдите частное из трех цифр, используя деление в большую сторону. Перепишите задачу деления в длинной форме деления. Используйте оценку, чтобы найти частичные частные. При необходимости можно использовать умножение и вычитание в столбик
Решите, используя деление в большую сторону с трехзначным частным (переоценка и занижение) (Часть 1)
Узнайте, что делать, если предполагаемое частное слишком велико или слишком мало. Перепишите задачу деления в длинной форме деления. Используйте оценку, затем завершите частичные частные в длинном делении. Пересмотрите оценки, если вычитание не может быть завершено, или
Решите, используя деление в длинное с 3-значным частным (переоценка и занижение) (Часть 2)
Практика деления в длинное с 2-значным частным. Перепишите задачу в длинной форме деления. Если вы решите заполнить частное, вы можете решить задачу самостоятельно. Выбор оценки частного поможет вам решить проблему
Перепишите задачу в длинной форме деления. Если вы решите заполнить частное, вы можете решить задачу самостоятельно. Выбор оценки частного поможет вам решить проблему
Тема F: Неполные частные и многозначное десятичное деление
Учащиеся заглянут под капот деления, чтобы действительно понять концепцию остатка, а также шаги, связанные с делением на большие числа. Учащиеся работают с одно-, дву- и трехзначными делимыми и одно- и двузначными делителями. Они используют стандартный алгоритм деления в большую сторону, но по-разному подходят к нему, чтобы добиться математической гибкости.
Переименование десятичных чисел в единицах измерения
Переименование десятичных чисел в виде десятых, сотых или тысячных долей. Сначала заполните пропуск количеством заданных единиц. Затем выберите правильную единицу для данного числа
Переименовать число в формате единиц в десятичное число
Записать число в единицах разряда в виде десятичного числа. Данные числа имеют возрастающее количество цифр
Переименовать целое число в виде единиц и десятичной форме
Переименовать целое число в разрядной форме единиц. Добавьте соответствующее количество нулей к каждому целому числу, чтобы записать его в виде десятых или сотых долей. Напишите правильное количество нулей после запятой, чтобы заменить целое число на заданное разрядное значение
Добавьте соответствующее количество нулей к каждому целому числу, чтобы записать его в виде десятых или сотых долей. Напишите правильное количество нулей после запятой, чтобы заменить целое число на заданное разрядное значение
Деление десятичной дроби на целое число (с использованием формы единиц и без нее)
Деление десятичной дроби на целое число с использованием разрядных значений. Во-первых, десятичная дробь указывается в форме единицы разряда. Затем выберите единицу стоимости места. Разделите и запишите ответ в виде десятичного числа. Наконец, попрактикуйтесь в делении десятичной дроби на целое число
Деление десятичной дроби на 10 или 100
Деление десятичной дроби на степень 10. Узнайте, как сместить десятичную точку в зависимости от количества нулей в делителе. Затем попрактикуйтесь в этом навыке деления 9.0006
Деление десятичного числа на кратное 10 или 100
Используйте коэффициенты 10, чтобы разделить десятичное число на двузначное или трехзначное круглое число. Вынесите из делителя степень числа 10. Затем разделите в два этапа, упростив деление
Вынесите из делителя степень числа 10. Затем разделите в два этапа, упростив деление
Оцените частное деления десятичного числа на двузначное число (Уровень 1)
Оцените частное деления десятичного числа на двузначное целое число. Округлите каждое число до крайнего левого разряда. Затем определите кратное делителя, ближайшего к делимому, и определите приблизительное частное. Этот навык поможет вам
Оценить частное деления десятичного числа на двузначное число (Уровень 2)
Оценить частное десятичного числа, деленного на двузначное целое число. Округлите делитель до крайнего левого разряда, а делимое — до ближайшего кратного округленному делителю. Затем определите приблизительное частное. Этот навык поможет вам в lon
Решите длинное деление до десятых разрядов
Научитесь находить частное двух целых чисел до десятого разряда вместо записи остатка. Перепишите задачу в длинной форме деления, затем выполните деление. Увеличьте делимое, добавив десятичную точку, за которой следует 0, чтобы продолжить деление
Решить длинное деление с точностью до сотых
Найти частное двух целых чисел с точностью до сотых вместо записи остатка. Перепишите задачу в длинной форме деления, затем выполните деление. Увеличьте делимое, добавив десятичную точку, за которой следуют нули, чтобы продолжить деление
Перепишите задачу в длинной форме деления, затем выполните деление. Увеличьте делимое, добавив десятичную точку, за которой следуют нули, чтобы продолжить деление
Решение деления десятичного числа в длинное число (Уровень 1)
Практика деления десятичного числа в длинное на двузначное целое число. Оцените частичные частные, корректируя оценки по мере необходимости. Добавление нулей не требуется для этих задач. Умножение столбцов и вычитание могут использоваться, если требуется
Деление десятичного числа в длинное (Уровень 2)
Практика деления десятичного числа в длинное на двузначное целое число. Оцените частичные частные, корректируя оценки по мере необходимости. Возможно, потребуется добавить нули для дополнительных разрядов, чтобы расширить деление. Умножение столбцов и вычитание
Решение деления десятичного числа в длинное число (сверх- и заниженное)
Использование деления в длинное деление десятичной дроби на двузначное целое число. Перепишите задачу на деление в длинном формате деления. Оцените частичные частные, узнав, когда корректировать оценки
Перепишите задачу на деление в длинном формате деления. Оцените частичные частные, узнав, когда корректировать оценки
Деление десятичного числа в длинное (Уровень 3)
Практика деления десятичного числа в длинное на двузначное целое число. На каждом шаге вы можете заполнить частное или руководствоваться оценкой частного. При необходимости можно использовать столбцовое умножение и вычитание.
Использовать длинное деление для решения словесной задачи с десятичным частным
Решать словесные задачи с помощью длинного деления. Используйте модель, чтобы представить ситуацию, и запишите задачу на деление в длинную сторону. На каждом шаге вы можете заполнить частное или руководствоваться оценкой частного. Нули, возможно, придется добавить для
Используйте длинное деление для решения задач на площади с десятичным частным.
Решите задачи на площади с использованием длинного деления. Обозначьте диаграмму полученной информацией и напишите задачу на деление в длинную сторону. На каждом шаге вы можете заполнить частное или руководствоваться оценкой частного.
На каждом шаге вы можете заполнить частное или руководствоваться оценкой частного.
МОДУЛЬ 3. Сложение и вычитание дробей
Тема A: Эквивалентные дроби
Учащиеся знакомятся с основами эквивалентности дробей. Они учатся умножать, чтобы найти эквивалентную дробь, и делить, чтобы уменьшить дробь. Также вводятся и применяются понятия общих множителей и наибольшего общего множителя.
Обозначьте числитель и знаменатель дроби
Запишите дробь, представленную моделью. Выучить названия частей дроби
Записать эквивалентную дробь (большего размера) на основе заданного множителя или знаменателя
Научиться записывать эквивалентные дроби. Во-первых, используйте модель. Затем используйте умножение, чтобы создать эквивалентные дроби. Наконец, дополните недостающую часть набора эквивалентных дробей
Напишите эквивалентную дробь (меньшую) на основе заданного делителя, числителя или знаменателя
Запишите уменьшенные эквивалентные дроби. Во-первых, используйте модель. Затем используйте деление, чтобы создать эквивалентные дроби. Наконец, дополните недостающую часть набора эквивалентных дробей
Во-первых, используйте модель. Затем используйте деление, чтобы создать эквивалентные дроби. Наконец, дополните недостающую часть набора эквивалентных дробей
Заполните эквивалентные дроби
Практикуйте эквивалентные дроби. во-первых, определите операцию, создавшую эквивалентные дроби. Затем дополните недостающую часть пары эквивалентных дробей. Наконец, сопоставьте эквивалентные дроби в игре на память
Определите общие делители двух заданных чисел
Найдите общие делители двух чисел. Перечислите все пары факторов обоих чисел, затем выберите общие факторы. Затем научитесь находить общие делители двух чисел, не перечисляя все пары делителей обоих чисел.
Определите общий делитель двух заданных чисел и разделите их на общий делитель
Определите общий делитель пары чисел. Разделите оба числа на этот множитель и проанализируйте, есть ли у этих частных еще общий множитель. Этот навык может помочь вам найти наибольший общий множитель и полностью сократить дроби
Приведение дроби к простейшей форме путем деления на наибольший общий множитель
Приведение дроби к простейшей форме. Выберите число, которое можно разделить как на числитель, так и на знаменатель. Выполните деление и определите, имеют ли части дроби еще один общий множитель. Продолжайте до тех пор, пока дробь не станет самой простой
Выберите число, которое можно разделить как на числитель, так и на знаменатель. Выполните деление и определите, имеют ли части дроби еще один общий множитель. Продолжайте до тех пор, пока дробь не станет самой простой
Тема B: Создание одинаковых единиц в картинках
Учащиеся полагаются на свои знания эквивалентности дробей, чтобы работать со всеми аспектами сложения и вычитания с дробями и смешанными числами. Благодаря большому количеству визуальной поддержки и пошаговым подсказкам они работают с одинаковыми и разными знаменателями. Учащиеся учатся преобразовывать смешанные числа в дроби для решения задач, писать ответы в простейшей форме и решать текстовые задачи.
Сложение дробей с одинаковыми знаменателями
Узнайте, как складывать дроби с одинаковыми знаменателями. Используйте модель, чтобы выполнить сложение, а затем введите ответ. Затем найдите сумму без модели
Перепишите неправильную дробь в виде смешанного числа
Перепишите неправильную дробь в виде смешанного числа. Запишите неправильную дробь, изображенную на модели. Затем используйте модель, чтобы найти целое число и дробь. Запишите неправильную дробь в виде суммы целого числа и дроби. Переход к написанию m
Запишите неправильную дробь, изображенную на модели. Затем используйте модель, чтобы найти целое число и дробь. Запишите неправильную дробь в виде суммы целого числа и дроби. Переход к написанию m
Сложите дроби с одинаковыми знаменателями и запишите сумму как смешанное число
Потренируйтесь складывать две дроби с одинаковыми знаменателями. Сумма должна быть переписана в виде смешанного числа
Разделить фигуры на равное количество частей (прекурсор нахождения общего знаменателя)
Разделить два прямоугольника на равное количество равных частей. Перетащите две разделенные фигуры друг на друга, чтобы найти общее количество частей. Этот навык поможет вам найти общие знаменатели дробей
Сложение дробей с разными знаменателями (перемножьте знаменатели, чтобы найти общий знаменатель)
Узнайте, как складывать дроби с разными знаменателями. Используйте модель прямоугольников, разделенных на равные части, чтобы помочь найти одинаковый знаменатель. Умножьте, чтобы получить эквивалентные дроби с одинаковым знаменателем
Умножьте, чтобы получить эквивалентные дроби с одинаковым знаменателем
Переименуйте дроби с разными знаменателями (Уровень 1)
Переименуйте две дроби, чтобы они имели общий знаменатель. Умножьте знаменатели вместе, затем запишите эквивалентные дроби с этими знаменателями
Переименование дробей с разными знаменателями (Уровень 2)
Определение общего знаменателя двух дробей. Перепишите эквивалентные дроби с общим знаменателем
Сложите дроби с разными знаменателями и запишите сумму в виде смешанного числа
Узнайте, как складывать дроби с разными знаменателями. Перемножьте знаменатели вместе, чтобы найти общий знаменатель, затем создайте эквивалентные дроби с тем же знаменателем. Добавьте переименованные дроби. Если сумма представляет собой неправильную дробь, перепишите ее на 9.0006
Сложите дроби с разными знаменателями и перепишите сумму в простейшей форме (Часть 1)
Сложите дроби с разными знаменателями. Составьте равнозначные дроби с одинаковыми знаменателями. Добавьте переименованные дроби. Уменьшите сумму, если она не выражена простым языком. Перепишите сумму как смешанное число, если это неправильная дробь
Добавьте переименованные дроби. Уменьшите сумму, если она не выражена простым языком. Перепишите сумму как смешанное число, если это неправильная дробь
Сложите дроби с разными знаменателями и запишите сумму в простейшей форме (Часть 2)
Потренируйтесь складывать дроби с разными знаменателями. Перемножьте знаменатели вместе, чтобы найти общий знаменатель, затем создайте эквивалентные дроби с тем же знаменателем. Добавьте переименованные дроби. Если сумма неправильная дробь, перепишите ее как
Вычитание дробей с одинаковыми знаменателями
Научитесь вычитать дроби с одинаковыми знаменателями. Используйте модель для выполнения вычитания, а затем введите ответ. Затем найдите разность без модели
Вычтите дроби с разными знаменателями (перемножьте знаменатели, чтобы найти общий знаменатель)
Используйте модели прямоугольников с равными частями, чтобы научиться вычитать дроби с разными знаменателями. Умножьте знаменатели, а затем создайте эквивалентные дроби с тем же знаменателем. Затем вычтите дроби
Затем вычтите дроби
Вычитание дробей с разными знаменателями
Вычитание дробей с разными знаменателями. Составьте равнозначные дроби с одинаковыми знаменателями. Вычитание переименованных дробей
Преобразование смешанного числа в неправильную дробь
Узнайте, как преобразовать смешанное число в неправильную дробь. Запишите целое число в виде дроби и прибавьте к дробной части. Затем отработайте этот навык, не выполняя шагов
. Вычтите дробь из смешанного числа с одинаковыми знаменателями (переименуйте смешанное число в дробь)
Потренируйтесь вычитать дробь из смешанного числа. Дроби имеют одинаковые знаменатели, но смешанные числа, возможно, придется переписать как неправильные дроби
Вычесть дробь из смешанного числа с разными знаменателями (переименовать смешанное число в дробь)
Вычесть дробь из смешанного числа с разными знаменателями знаменатели. Перепишите дроби с общими знаменателями. При необходимости замените смешанное число неправильной дробью. Затем вычтите
Затем вычтите
Вычтите дробь из смешанного числа с разными знаменателями и запишите разницу в простейшей форме
Потренируйтесь вычитать дробь из смешанного числа. Найдите общий знаменатель и перепишите смешанное число в виде неправильной дроби, если это необходимо. Запишите ответ в простейшей форме
Вычтите дробь из смешанного числа с разными знаменателями, чтобы решить задачу со словами
Решите задачи со словами, которые включают разность смешанного числа и дроби. Пометьте диаграмму, чтобы идентифицировать части проблемы и помочь составить выражение для решения. Найдите общий знаменатель и перепишите смешанное число как неправильное fra
Вычтите дробь из 1 целого, чтобы решить задачу со словами
Научитесь решать задачи со словами, в которых часть целого уже завершена или использована. Пометьте диаграмму, чтобы идентифицировать части проблемы и помочь составить выражение для решения. Затем вычтите, чтобы ответить на вопрос
Вычтите две дроби из одного целого, чтобы решить задачу со словами
Решите задачи со словами, которые включают вычитание двух дробей из целого. Используйте схему для систематизации информации. Найдите общий знаменатель и сложите две дроби. Вычтите эту сумму из 1
Используйте схему для систематизации информации. Найдите общий знаменатель и сложите две дроби. Вычтите эту сумму из 1
Сложение дробей для решения словесной задачи
Решение словесных задач на сложение дробей. Используйте схему для систематизации информации. Найдите общий знаменатель, а затем сложите две дроби
Тема C: Численное создание одинаковых единиц
Учащиеся усложняют операции сложения и вычитания, которые они могут решать, используя смешанные числа. Они закрепляют и применяют свое понимание эквивалентности чисел, переименовывая числа для решения задач.
Сложите смешанное число и целое число с одинаковыми знаменателями
Найдите сумму смешанного числа и целого числа. Сложите целые части числа вместе. Затем добавьте дробную часть
Вычтите дробь или смешанное число из целого числа с одинаковыми знаменателями с числовой линией и без нее
Найдите разность целого числа и дроби или смешанного числа. Во-первых, используйте числовую линию, чтобы помочь с вычитанием. Затем потренируйтесь без помощи числовой линии 9.0006
Затем потренируйтесь без помощи числовой линии 9.0006
Сложите смешанное число и дробь с одинаковыми знаменателями
Сложите смешанное число и дробь. Сначала найдите сумму дробных частей, а затем прибавьте их к целому числу. Для этих задач не требуется упрощение
Сложение смешанных чисел с одинаковыми знаменателями
Узнайте, как сложить два смешанных числа. Сначала сложите целые части числа, а затем добавьте дробные части. Переименуйте сумму дробных частей, если она равна 1 или если это неправильная дробь
Сложение смешанных чисел с разными знаменателями (Уровень 1)
Найдите сумму двух смешанных чисел с разными знаменателями. Сложите целые части числа. Затем найдите общий знаменатель дробных частей и переименуйте их перед сложением.
Сложите смешанные числа с разными знаменателями (Уровень 2)
Сложите два смешанных числа с разными знаменателями. Сложите целые части числа. Затем найдите общий знаменатель для дробных частей и переименуйте их перед добавлением. Если сумма дробных частей представляет собой неправильную дробь, перепишите ее как смешанное число 9.0006
Если сумма дробных частей представляет собой неправильную дробь, перепишите ее как смешанное число 9.0006
Вычитание смешанных чисел с одинаковыми знаменателями
Вычитание двух смешанных чисел с одинаковыми знаменателями. Вычтите целые части числа друг из друга, затем вычтите дробные части друг из друга. Для этих задач не требуется перегруппировка или упрощение.
Вычитание смешанных чисел с разными знаменателями (Уровень 1)
Вычитание двух смешанных чисел с разными знаменателями. Вычтите целые части числа друг из друга. Затем найдите общий знаменатель для дробных частей и переименуйте их перед вычитанием. Для этих 9 не требуется перегруппировка или упрощение.0006
Вычитание дроби из смешанного числа с одинаковыми знаменателями (переименование смешанного числа)
Научитесь вычитать дробь из смешанного числа, если дробь больше дробной части смешанного числа. Переименуйте смешанное число, переназначив 1 из целой части числа в дробную часть. Затем вычтите дроби
Вычтите смешанные числа с разными знаменателями (Уровень 2)
Вычтите смешанные числа с разными знаменателями. Сначала вычтите целые числа. Затем переименуйте дробные части смешанных чисел с общими знаменателями. При необходимости переименуйте смешанный номер, переназначив 1 из целой части номера на f
Сначала вычтите целые числа. Затем переименуйте дробные части смешанных чисел с общими знаменателями. При необходимости переименуйте смешанный номер, переназначив 1 из целой части номера на f
Вычитание смешанных чисел с разными знаменателями (Уровень 3)
Потренируйтесь вычитать смешанные числа с разными знаменателями. Сначала вычтите целые числа. Затем переименуйте дробные части смешанных чисел с общими знаменателями. При необходимости переименуйте смешанное число, переназначив 1 из целого числа p
Тема D: Дальнейшие приложения
Для поддержки более сложного понимания операций с дробями учащиеся поддерживаются наглядными моделями, числовой прямой и диаграммами. Они применяют свои знания о дробях для вычисления сумм и разностей и решения многошаговых задач со смешанными числами.
Сравните дроби с разными знаменателями с 1/2, чтобы вычислить сумму
Определите, является ли каждая дробь больше, меньше или равна 1/2. Затем определите, является ли сумма двух дробей больше, меньше или равна 1. Сначала используйте модели, чтобы визуализировать дроби. Затем потренируйтесь без моделей
Сначала используйте модели, чтобы визуализировать дроби. Затем потренируйтесь без моделей
Сравните дроби с разными знаменателями с отсутствующей единицей, чтобы оценить сумму.
Оцените сумму двух дробей с разными знаменателями. Сначала используйте числовую прямую для представления большей дроби и определите, насколько она близка к 1. Затем сравните разницу с другой дробью, чтобы определить, будет ли сумма больше или меньше 9.0006
Сравните дроби с разными знаменателями, чтобы оценить разность смешанного числа за вычетом дроби.
Оцените разность двух дробей с разными знаменателями. Сначала определите, какую дробь нужно вычесть из смешанного числа, чтобы получить 1. Затем сравните эту дробь с дробью, которую предполагается вычесть из смешанного числа
Сложите несколько смешанных чисел и дробей
Потренируйтесь складывать несколько дробей и смешанные числа вместе. Переставьте члены так, чтобы дроби с общими знаменателями стояли рядом друг с другом, и сначала найдите эти частичные суммы. Затем сложите частичные суммы вместе
Затем сложите частичные суммы вместе
Решите многошаговую задачу со смешанными числами с разными знаменателями (Часть 1)
Узнайте, как решать задачи со словами, в которых участвуют несколько дробей с разными знаменателями. Используйте диаграмму, чтобы систематизировать информацию, данную в задаче. Затем напишите и решите выражение для каждого шага задачи
Решите многошаговую задачу со смешанными числами с разными знаменателями (Часть 2)
Решите задачу со словами, включающую несколько дробей с разными знаменателями. Используйте диаграмму, чтобы систематизировать информацию, данную в задаче. Затем напишите и решите выражение для каждого шага задачи
МОДУЛЬ 4. Умножение и деление дробей и десятичных дробей
Тема A: Линейные графики измерений дробей
Учащиеся объединяют свои знания об измерениях, округлении и смешанных числах для создания линейных графиков. Затем они анализируют данные, требуя от них выполнения операций со смешанными числами.
Округлите по линейке до ближайшего полудюйма
Используйте линейку для измерения до ближайшего полудюйма. Определите приращения на линейке. Затем используйте промежуточные точки между приращениями, чтобы определить, следует ли округлять длину объекта в большую или меньшую сторону. Выберите правильную округленную длину на линейке
Округление на линейке до ближайшего полудюйма для создания линейного графика и анализа данных
Создание линейного графика на основе измерений длины нескольких объектов с округлением до ближайшего полудюйма. Проанализируйте данные для минимального и максимального измерения. Определите наиболее частое измерение, а также диапазон
Округлите по линейке до четверти дюйма
Используйте линейку для измерения до четверти дюйма. Определите приращения на линейке. Затем используйте промежуточные точки между приращениями, чтобы определить, следует ли округлять длину объекта в большую или меньшую сторону. Выберите правильную округленную длину на
Округлите по линейке до четверти дюйма, чтобы построить линейный график и проанализировать данные.

Измерьте длину нескольких объектов с точностью до четверти дюйма, создав линейный график измерений. Проанализируйте данные для минимального и максимального измерения. Определите наиболее частое измерение, а также разницу между двумя измерениями
Округлите по линейке до ближайшей восьмой фута
Используйте линейку для измерения до ближайшей восьмой фута. Определите приращения на линейке. Затем используйте промежуточные точки между приращениями, чтобы определить, следует ли округлять длину объекта в большую или меньшую сторону. Выберите правильную округленную длину на ру
Округлите на линейке до ближайшей восьмой дюйма, чтобы построить линейный график и проанализировать данные.
Измерьте длину нескольких объектов с точностью до восьмой дюйма, создав линейный график измерений. Проанализируйте данные для минимального и максимального измерения. Определите наиболее частое измерение, а также разницу между двумя измерениями
Тема B: Дроби как деление
Чтобы закрепить свое понимание дробей как деления, учащиеся работают над преобразованием между ними, используя дроби больше и меньше единицы. Затем они работают шаг за шагом, чтобы понять оставшуюся часть задачи деления как дробь. Вооружившись этим пониманием, учащиеся решают все более сложные задачи на деление слов.
Затем они работают шаг за шагом, чтобы понять оставшуюся часть задачи деления как дробь. Вооружившись этим пониманием, учащиеся решают все более сложные задачи на деление слов.
Переписать деление целых чисел в виде дроби на основе модели
Изучить взаимосвязь между делением количества и записью количества в виде дроби. Представьте деление как целое количество продуктов, разделенных между большим целым числом тарелок. Продукты будут разрезаны на количество частей, представленное pla
Перепишите деление целых чисел в виде дроби и сопоставьте дробь с соответствующим уравнением деления
Перепишите деление двух целых чисел в виде дроби. Делимое становится числителем, а делитель становится знаменателем. Практикуйте концепцию, сопоставляя дроби с соответствующим им выражением деления
Свяжите деление с дробями
Потренируйтесь записывать выражения деления как дроби. Вставьте пропущенное число в уравнение
Связать деление с дробями больше единицы
Представление деления в виде неправильной дроби. Во-первых, модель еды и тарелок используется для визуализации частного. Затем потренируйтесь переписывать выражения деления в виде дробей. Заполните пропущенное число в уравнении
Во-первых, модель еды и тарелок используется для визуализации частного. Затем потренируйтесь переписывать выражения деления в виде дробей. Заполните пропущенное число в уравнении
Разделите и сообщите остаток в виде дроби на основе модели
Научитесь делить два целых числа с остатком дроби. Модель еды и тарелок используется для физического представления разделения. Запишите частное в виде неправильной дроби и смешанного числа
Переименуйте дробь больше единицы в смешанное число (Уровень 1)
Перепишите неправильную дробь в смешанное число. Запишите дробь в виде выражения деления. Затем найдите частное и остаток задачи на деление, чтобы записать ответ в виде смешанного числа
.Переименовать дробь больше единицы в смешанное число (уровень 2)
Используйте деление в длинную сторону, чтобы преобразовать неправильную дробь в смешанное число. Запишите дробь в виде длинного деления, затем выполните деление. Частное становится целой частью, а остаток становится числителем дробной части.
Решайте задачи со словами на основе модели (Уровень 1)
Научитесь решать задачи со словами на дроби. Определите часть полосы, которая заштрихована. Затем с помощью линейки смоделируйте текстовую задачу и ответьте на вопрос 9.0006
Решение задач со словами на дроби на основе модели (уровень 2)
Использование модели для представления задачи со словами, включающей дроби. Обозначьте схему полученной информацией. Запишите нужное деление в виде дроби. Затем измените его на смешанное число и ответьте на вопрос
Решите задачи со словами на основе модели (Уровень 3)
Представьте задачу со словами, в которой используются дроби, используя модель. Обозначьте схему полученной информацией. Перепишите искомое деление в виде смешанного числа в простейшем виде и ответьте на вопрос 9.0006
Решение задач со словами на дроби на основе модели (уровень 4)
Решение задач со словами на дроби с использованием модели. Обозначьте схему полученной информацией. Запишите нужное деление в виде дроби. Затем используйте длинное деление, чтобы преобразовать дробь в смешанное число, и ответьте на вопрос
Запишите нужное деление в виде дроби. Затем используйте длинное деление, чтобы преобразовать дробь в смешанное число, и ответьте на вопрос
Решите задачи со словами на основе модели (Уровень 5)
Попрактикуйтесь в решении задач со словами на дроби. Запишите соответствующее выражение деления для задачи. Затем перепишите его в виде дроби или смешанного числа, если необходимо
Тема C: Умножение целого числа на дробь
Учащиеся начинают с нахождения единичной дроби целого числа и других дробей целого числа, используя знакомые модели. Затем они связывают этот процесс с умножением. Чтобы умножить целое число на дробь, учащиеся учатся находить общие множители и сокращать до или после умножения.
Определение частей целого числа на основе модели (уровень 1)
Найдите число, являющееся частью целого числа. Используйте модель, чтобы найти ответ. Затем сопоставьте дробь с моделью
Определить части целого числа на основе модели для решения текстовой задачи
Представьте текстовую задачу с помощью модели. Выберите, на сколько групп разделить целое число, исходя из информации в задаче. Найдите часть целого числа с помощью модели, затем ответьте на вопросы
Выберите, на сколько групп разделить целое число, исходя из информации в задаче. Найдите часть целого числа с помощью модели, затем ответьте на вопросы
Определите части целого числа на основе модели (Уровень 2)
Найдите часть целого числа с помощью модели. Представьте информацию, данную в задаче с моделью, выбрав количество частей. Затем напишите выражение для модели и решите. Если решение представляет собой неправильную дробь, перепишите
Определение долей целого числа на основе модели (уровень 3)
Вычисление доли целого числа с помощью модели. Представьте информацию, данную в задаче с моделью, выбрав количество частей. Вычислить значение одной части, затем выделить, сколько частей представлено дробями
Определить целое число по дробной части этого числа на основе модели
Найти целое число, если вы знаете дробную часть этого числа. Используйте модель для представления данной информации. Определите стоимость одной части, а затем используйте эту информацию для расчета общей суммы
Умножение целого числа на дробь
Узнайте, как умножить целое число на дробь. Запишите умножение как многократное сложение дроби. Обратите внимание на эти отношения повторного сложения и частей дроби. Затем отработайте эту концепцию, не переписывая ее как additio
Запишите умножение как многократное сложение дроби. Обратите внимание на эти отношения повторного сложения и частей дроби. Затем отработайте эту концепцию, не переписывая ее как additio
Свяжите часть целого числа с умножением и решите
Найдите часть целого числа путем умножения. Используйте модель для представления одной части целого числа, затем напишите необходимое выражение умножения. Затем найдите произведение
Определить долю измерения путем преобразования единиц и умножения
Определить долю измерения. Во-первых, преобразовать измерение в более мелкие единицы. Затем умножьте на дробь и упростите ответ
Определите общие делители двух целых чисел
Найдите общие делители двух чисел. Перечислите все пары факторов обоих чисел, затем выберите общие факторы. Затем определите общие множители двух чисел, не перечисляя все пары множителей обоих чисел.0006
Деление целых чисел на общий делитель
Определение общего делителя пары чисел. Разделите оба числа на этот множитель и проанализируйте, есть ли у этих частных еще общий множитель. Этот навык поможет вам найти наибольший общий множитель и полностью сократить дроби
Разделите оба числа на этот множитель и проанализируйте, есть ли у этих частных еще общий множитель. Этот навык поможет вам найти наибольший общий множитель и полностью сократить дроби
Уменьшить дробь путем деления на общий делитель
Научитесь приводить дроби к простейшим терминам. Найдите общий делитель числителя и знаменателя. Затем разделите оба числа на общий множитель. Продолжайте делить на общие множители до тех пор, пока в числителе и знаменателе не останется комм
Уменьшение коэффициентов перед умножением целого числа на дробь (Уровень 1)
Умножение дроби на целое число. Изучите, как уменьшение общего множителя перед умножением может упростить умножение. Выберите числа, которые имеют общий множитель, и определите этот множитель. Затем разделите общий множитель и умножьте
Сократите множители перед умножением целого числа на дробь (Уровень 2)
Потренируйтесь уменьшать общие множители перед умножением в знаменателе дроби. Выберите два числа, которые имеют общий делитель, и разделите их на общий делитель. При необходимости повторите. Затем умножьте оставшиеся числа в числителе. Если т
При необходимости повторите. Затем умножьте оставшиеся числа в числителе. Если т
Умножение целого числа на дробь путем уменьшения до или после умножения
Выберите, следует ли уменьшать до или после умножения в числителе дроби. Научитесь делать правильный выбор, чтобы иметь возможность использовать арифметику в уме
Тема D: Выражения дробей и словесные задачи
Учащиеся обобщают свое понимание дробей и операций для построения и решения выражений. Знакомые модели поддерживают их обучение, а словесные задачи помещают навыки в контекст.
Сопоставьте операции с терминами сумма, разность, произведение и частное
Попрактикуйтесь в словарных терминах, используемых для сложения, вычитания, умножения и деления. Сопоставьте словесное выражение с правильным математическим выражением
Составьте выражение на основе текста
Напишите математическое выражение для данного словесного выражения. Выберите правильную операцию для использования между двумя числами. Также расставьте цифры в правильном порядке, если необходимо
Также расставьте цифры в правильном порядке, если необходимо
Составление составного выражения на основе текста (Часть 1)
Составление математического выражения, включающего три значения, сложение и умножение. Определите операции, представленные словами в словесном выражении. Затем поместите числа в выражение с правильными операциями, вставив круглые скобки
Составьте составное выражение на основе текста (Часть 2)
Составьте математическое выражение, включающее три значения и умножение целых чисел на дробь. Определите операции, представленные словами в словесном выражении. Затем поместите числа в выражение с правильными операциями, ins
Составление составного выражения на основе текста (часть 3)
Напишите математическое выражение, включающее три значения, а также умножение и вычитание целых чисел и дробей. Определите операции, представленные словами в словесном выражении. Затем поместите числа в выражение с правильным
Составьте сложное уравнение на основе модели и решите (Часть 1)
Напишите и решите составное уравнение на основе показанной модели. Определите часть стержня, который помечен, и выражение, представляющее полную длину стержня. Затем организуйте числа и необходимые операции в выражении. Найдите с
Определите часть стержня, который помечен, и выражение, представляющее полную длину стержня. Затем организуйте числа и необходимые операции в выражении. Найдите с
Составьте составное уравнение на основе модели и решите (Часть 2)
Напишите и решите составное уравнение на основе показанной модели. Определите количество разделов на панели и выражение, которое представляет каждый раздел. Затем организуйте числа и необходимые операции в выражении. Найти решение, переписав i
Решить сложное уравнение с дробями и скобками
Найти решение сложного уравнения с дробями и скобками. Перепишите выражения деления в виде дробей. Следуйте порядку операций для решения. Запишите решение в виде упрощенных дробей или смешанных чисел
Решите задачу на умножение целого числа на дробь (Уровень 1)
Решите задачу на умножение целого числа на дробь. Составьте выражения, отвечающие на каждый вопрос. Затем решите выражения, упрощая перед умножением. Ответьте на все вопросы
Решите задачу на умножение целого числа на дробь (Уровень 2)
Решите задачу на умножение целого числа на дробь. Используйте схему для моделирования проблемы. Составьте выражения, отвечающие на каждый вопрос. Затем решите выражения, упрощая перед умножением на 9.0006
Используйте схему для моделирования проблемы. Составьте выражения, отвечающие на каждый вопрос. Затем решите выражения, упрощая перед умножением на 9.0006
Тема E: Умножение дроби на дробь
Учащиеся учатся умножать дроби, начиная с единичных дробей и используя модель площади. Затем они переходят к умножению, которое включает в себя смешанные числа, сокращение и единицы измерения.
Умножение долей единиц с использованием модели площади
Использование площади прямоугольника для моделирования произведения двух долей единиц. Обозначьте на схеме длины сторон прямоугольников. Затем найдите уравнение площади и свяжите его с произведением дробей
Умножение дробей с использованием модели площади
Моделирование произведения двух дробей с использованием площади прямоугольника. Обозначьте на схеме длины сторон прямоугольников. Затем найдите уравнение площади и свяжите его с умножением дробей
Умножьте дроби (уменьшите перед умножением)
Потренируйтесь умножать две дроби. Сократите общие все множители из числителя и знаменателя перед умножением, если это возможно. Кроме того, потренируйтесь писать выражения дробей и упрощайте их, прежде чем находить произведение 9.0006
Сократите общие все множители из числителя и знаменателя перед умножением, если это возможно. Кроме того, потренируйтесь писать выражения дробей и упрощайте их, прежде чем находить произведение 9.0006
Умножение дробей (уменьшение до или после умножения)
Умножение двух дробей. Решите, умножать или уменьшать на каждом шаге. Найдите упрощенный продукт
Решите текстовые задачи, умножив дроби, используя модель площади
Решите текстовые задачи, моделируя произведение двух дробей, используя площадь прямоугольника. Обозначьте диаграмму информацией, данной в задаче. Затем запишите полученное выражение и решите его, чтобы ответить на вопрос 9.0006
Преобразование смешанного числа в дробь для умножения на дробь
Преобразование смешанного числа в неправильную дробь перед умножением. Затем уменьшите общие множители от умножения, прежде чем найти произведение
Преобразование измерений путем умножения целого числа на дробь
Преобразование единиц измерения. Определить соотношение между меньшими и большими единицами. Затем умножьте целое число и дробь, чтобы преобразовать единицы. Запишите ответ в простейшей форме или в виде смешанного числа, в зависимости от ситуации
Определить соотношение между меньшими и большими единицами. Затем умножьте целое число и дробь, чтобы преобразовать единицы. Запишите ответ в простейшей форме или в виде смешанного числа, в зависимости от ситуации
Преобразование измерений путем умножения дробей
Преобразование единиц измерения. Определить соотношение между меньшими и большими единицами. Затем умножьте, чтобы преобразовать единицы. Смешанные числа, возможно, придется переписать как неправильные дроби, а общие множители следует разделить перед умножением
Преобразовать умножение на десятичную дробь в умножение на дробь и решить
Изучить взаимосвязь между умножением на 0,1 или 0,01 и умножением на эквивалентную дробь . Преобразование между десятичными дробями и дробями. Обратите внимание, что умножение на десятичную дробь можно переписать как деление на 9.0006
Умножение на 0,1 с использованием таблицы разрядных значений
Использование таблицы разрядных значений для умножения числа на 0,1. Определите число, изображенное на графике. Затем переместите цифры в правильное место для данного умножения. Узнайте, как перемещать десятичную точку для быстрого вычисления в уме
Определите число, изображенное на графике. Затем переместите цифры в правильное место для данного умножения. Узнайте, как перемещать десятичную точку для быстрого вычисления в уме
Умножение на 0,01 с помощью таблицы разрядных значений
Используйте таблицу разрядных значений для умножения числа на 0,01. Определите число, изображенное на графике. Затем переместите цифры в правильное место для данного умножения. Научитесь перемещать десятичную точку для быстрого счета в уме
Умножение на 0,1 или 0,01
Практика умножения числа на 0,1 или 0,01
Разложение десятичного числа для умножения
Разложение десятичного числа для простого умножения. Запишите десятичную дробь как произведение целого числа и 0,1 или 0,01. Затем переставьте множители, чтобы упростить умножение. Найти произведение
Определить место запятой в произведении двух десятичных чисел
Узнайте, как найти место запятой в произведении двух десятичных чисел. Перетащите десятичную дробь в нужное место
Умножение двух десятичных чисел с помощью умножения столбцов (Часть 1)
Использование умножения столбцов для нахождения произведения двух десятичных чисел. Перепишите задачу в виде столбца. Затем найдите частичные произведения без десятичной точки. Сложите частичные произведения и вставьте десятичную точку в нужное место для fina
Перепишите задачу в виде столбца. Затем найдите частичные произведения без десятичной точки. Сложите частичные произведения и вставьте десятичную точку в нужное место для fina
Умножьте два десятичных числа, используя умножение столбца (Часть 2)
Найдите произведение двух десятичных чисел, используя умножение столбца. Перепишите задачу в виде столбца. Затем найдите частичные произведения без десятичной точки. Добавьте частичные произведения и вставьте десятичную точку в правильном месте для последних
Умножение двух десятичных чисел с помощью умножения столбцов (часть 3)
Использование умножения столбцов для нахождения произведения двух десятичных чисел. Перепишите задачу в виде столбца. Затем найдите частичные произведения без десятичной точки. Сложите частичные произведения и вставьте десятичную точку в правильном месте для fina
Тема F: Умножение с дробями и десятичными дробями как масштабирование и текстовые задачи
Учащиеся изучают эффекты умножения на меньше, равно и больше 1 , Они решают задачи на умножение, вводят недостающие множители и дополняют неравенства, чтобы закрепить свое понимание.
Умножение дроби на дробь, равную 1
Нахождение эквивалентных дробей путем умножения дроби на дробь, равную 1. Узнайте, что дробь с одинаковым числом в числителе и знаменателе равна 1. Этот навык полезен при переименовании дроби с общими знаменателями для сложения o
Определите пропущенный множитель как дробь, равную 1
Потренируйтесь умножать дробь на другую дробь, равную 1. Сначала составьте дроби, равные 1, заполнив пропущенный числитель или знаменатель. Затем выберите правильную дробь, равную 1. Наконец, напишите любую дробь
Определить закономерности умножения на дроби меньше, равно и больше 1
Изучить эффект умножения на дроби меньше, равно или больше 1. Определить дробь как меньше, равно или больше чем 1. Затем определите, является ли произведение этой дроби и целого числа меньше, равно или больше
Используйте
<, = и > для сравнения результата умножения на дроби меньше, равно и больше 1 Используйте символы неравенства, чтобы сравнить дробь с 1. Затем сравните произведение этой дроби и другой дроби со значением второй дроби
Затем сравните произведение этой дроби и другой дроби со значением второй дроби
Определите дробь, которая завершает неравенство умножения.
Потренируйтесь определять связь между произведением двух дробей и значением одной из этих дробей. Во-первых, имея выбор из трех дробей, выберите ту, которая делает утверждение о неравенстве верным. Затем заполните недостающую часть
Преобразование дроби меньше единицы в десятичную форму (Уровень 1)
Узнайте, как преобразовать дробь в десятичную форму. Определите, какой множитель изменит знаменатель до степени 10, а затем умножьте, чтобы получить эквивалентную дробь. Затем запишите эту дробь как десятичную
Преобразование дроби больше единицы в десятичную форму
Преобразование неправильной дроби в десятичную. Определите, какой множитель изменит знаменатель до степени 10, а затем умножьте, чтобы получить эквивалентную дробь. Затем запишите эту дробь как десятичную
Преобразуйте дробь меньше единицы в десятичную форму (уровень 2)
Перепишите дробь как десятичную. Дополните множитель, который составит эквивалентную дробь с заданной степенью 10 в знаменателе. Затем умножьте числители и запишите дробь как десятичную 9.0006
Дополните множитель, который составит эквивалентную дробь с заданной степенью 10 в знаменателе. Затем умножьте числители и запишите дробь как десятичную 9.0006
Преобразование дроби меньше единицы в десятичную форму с помощью деления
Используйте длинное деление, чтобы преобразовать дробь в десятичную. Разделите числитель на знаменатель, добавив нули, чтобы продолжить деление без остатка
Преобразование дроби больше единицы в десятичную форму с помощью деления
Используйте длинное деление, чтобы преобразовать неправильную дробь в десятичную. Разделите числитель на знаменатель, добавив нули, чтобы продолжить деление без остатка
Определить результат умножения с помощью
<, = или > (Часть 1)Изучить эффект умножения на десятичную дробь меньше, равно или больше 1. Определить десятичную дробь как меньше, равно или больше 1. Затем определите, меньше, равно или больше произведение этого десятичного числа и целого числа
Полные неравенства, включающие умножение на десятичное число значение одного из этих десятичных знаков.
 Во-первых, имея выбор из трех десятичных знаков, выберите тот, который делает утверждение о неравенстве верным. Затем заполните недостающую часть де
Во-первых, имея выбор из трех десятичных знаков, выберите тот, который делает утверждение о неравенстве верным. Затем заполните недостающую часть деОпределите результат умножения с помощью
<, = или > (Часть 2)Умножьте на дробь или десятичную дробь, большую 1. Определите, меньше или больше произведение одного из множителей, используя символы неравенства. Демонстрация понимание концепции путем помещения правильного неравенства в выражение формулы
Определить результат умножения с помощью
<, = или > (Часть 3)Умножить на дробь или десятичную дробь меньше 1. Определить, меньше ли произведение или больше, чем один из факторов, используя символы неравенства. Продемонстрируйте понимание концепции, поместив правильное неравенство в выражение формулы
Тема G: Деление дробей и десятичных дробей
Учащиеся полагаются на свое понимание умножения дробей, чтобы научиться делить дроби. С помощью знакомых моделей, таких как ленточные диаграммы и модели с площадями, они изучают различные подходы к делению дробей. На этом этапе они используют единичные дроби с целыми числами и единичные дроби с единичными дробями.
На этом этапе они используют единичные дроби с целыми числами и единичные дроби с единичными дробями.
Переписать уравнение с умножением на дробь как уравнение деления на основе модели
Изучите взаимосвязь между умножением на дробь и делением. Используя данную модель, разрезанную на равные части, укажите, сколько частей составляет целое. Затем завершите выражения умножения и деления по модели
Составьте уравнение деления с дробью на основе модели
Напишите выражения деления на основе модели. Используя данную модель, разрезанную на равные части, укажите, сколько частей составляет целое. Затем завершите выражение деления о модели
Разделите целое число на дробную часть, используя ленточную диаграмму
Используйте ленточную диаграмму, чтобы разделить целое число на дробную часть. Обозначьте на схеме целые числа и дробные части. Используйте числовую строку, чтобы пропустить подсчет частей дроби. Затем определите общее количество разделов
Соотнесите деление на единичную дробь с умножением на знаменатель
Изучите взаимосвязь между делением на единичную дробь и умножением на знаменатель. Используя ленточную диаграмму, обозначьте на диаграмме целые числа и дробные части. Используйте числовую строку, чтобы пропустить подсчет частей дроби. Затем напишите мю
Используя ленточную диаграмму, обозначьте на диаграмме целые числа и дробные части. Используйте числовую строку, чтобы пропустить подсчет частей дроби. Затем напишите мю
Разделить целое число на дробную часть путем умножения на знаменатель
Переписать деление на дробь как умножение. Умножьте целое число на знаменатель дроби и запишите полученное произведение
Разделите целое число на дробную единицу
Разделите целое число на дробную единицу в контексте текстовой задачи. Перепишите деление как умножение и найдите произведение
Разделите дробную единицу на целое число на основе ленточной диаграммы (Часть 1)
Научитесь делить дробь на целое число. Используйте ленточную модель, чтобы представить дробь как равные части. Затем разделите каждую часть на количество частей, указанное целым числом. Ответьте, сколько всего секций
Разделите дробь на целое число на основе ленточной диаграммы (Часть 2)
Разделите дробь на целое число с помощью ленточной диаграммы. Используйте модель, чтобы представить дробь как равные части. Затем разделите каждую часть на количество частей, указанное целым числом. Перепишите дробь так, чтобы она представляла все части, показанные на цифре 9.0006
Используйте модель, чтобы представить дробь как равные части. Затем разделите каждую часть на количество частей, указанное целым числом. Перепишите дробь так, чтобы она представляла все части, показанные на цифре 9.0006
Разделить дробную часть на целое число
Попрактиковаться в делении дробной части на целое число. Переименуйте дробь, вставив пропущенный знаменатель. Затем разделите и приведите дробь к простейшей форме
Умножьте единичную дробь на единичную дробь с моделью площади и без нее (Часть 1)
Умножьте две единичные дроби вместе. Используйте модель площади для представления обеих дробей на одном прямоугольнике. Найдите заштрихованную площадь, представляющую произведение двух дробей. Затем примените эту концепцию к задачам на умножение без использования режима площади 9.0006
Умножение единичной дроби на единичную дробь с моделью площади и без нее (Часть 2)
Использование модели площади для представления деления дроби единицы на целое число. Перепишите деление как умножение на дробь. Используйте получившуюся заштрихованную область, чтобы найти произведение двух дробей
Перепишите деление как умножение на дробь. Используйте получившуюся заштрихованную область, чтобы найти произведение двух дробей
Свяжите деление на целое число с умножением на дробную часть
Используйте ленточную диаграмму, чтобы обнаружить взаимосвязь между делением на целое число и умножением на дробную единицу. Разделите диаграмму на участки в соответствии со значениями, указанными в задаче. Перепишите полученное выражение деления как множитель
Решите уравнения деления с дробями единиц и целыми числами
Попрактикуйтесь в делении дробей единиц на целые числа. Перепишите выражение деления как умножение и найдите произведение
Умножьте десятичное число на десятую степень
Найдите произведение десятичного числа на десятую степень. Узнайте, как сдвинуть десятичную точку для быстрого вычисления в уме.
Упростите дробь, используя основное свойство дробей.
Используйте основное свойство дробей, чтобы упростить дроби. Сначала выведите из дроби общий множитель. Затем выберите уравнения дробей, которые показывают основное свойство дробей. Наконец, дополните пропущенное число в основном свойстве дробей eq 9.0006
Затем выберите уравнения дробей, которые показывают основное свойство дробей. Наконец, дополните пропущенное число в основном свойстве дробей eq 9.0006
Преобразуйте дробь в заданный знаменатель, используя основное свойство дробей.
Напишите эквивалентные уравнения, используя основное свойство дробей. Учитывая дробь и новое значение знаменателя, определите, на какое число нужно умножить, чтобы получить этот знаменатель. Затем запишите эквивалентную дробь
Преобразование между выражениями деления и дробями
Перепишите выражение деления как дробь. Запишите делимое как числитель, а делитель как знаменатель. Также потренируйтесь писать выражение деления из дроби
Полное выражение дробей с использованием основного свойства дробей
Использование основного свойства дробей для упрощения дробей. Сначала выведите из дроби общий множитель. Затем дополните пропущенное число в уравнении основного свойства дробей
Преобразование дробей с десятичными знаменателями в дроби с целыми знаменателями (Уровень 1)
Используйте основное свойство дробей для преобразования дробей, содержащих десятичные числа, в дроби, содержащие только целые числа. Превратите выражение деления в дробь. Затем выберите правильный множитель, который делает знаменатель целым числом. Упростить фр
Превратите выражение деления в дробь. Затем выберите правильный множитель, который делает знаменатель целым числом. Упростить фр
Преобразование дробей с десятичными знаменателями в дроби с целыми знаменателями (Уровень 2)
Преобразование дробей, содержащих десятичные числа, в дроби, содержащие только целые числа. Превратите выражение деления в дробь. Затем выберите правильный множитель, который делает знаменатель целым числом. Упростить дробь
Преобразование дробей с десятичными знаменателями в дроби с целыми знаменателями (уровень 3)
Преобразование дробей, содержащих десятичные дроби, в дроби, содержащие только целые числа. Перепишите выражение деления в виде дроби. Затем выберите правильный множитель, который делает знаменатель целым числом. Найдите частное, при необходимости используя длинное деление
Преобразование дробей с десятичными знаменателями в дроби с целыми знаменателями (Уровень 4)
Используйте основное свойство дробей для преобразования дробей, содержащих десятичные дроби, в дроби, содержащие только целые числа. Выберите правильный множитель, который делает знаменатель целым числом. Затем умножьте и упростите дробь
Выберите правильный множитель, который делает знаменатель целым числом. Затем умножьте и упростите дробь
Преобразование выражений деления с десятичными делителями в выражения с делителями целых чисел (Уровень 1)
Узнайте, как преобразовать деление десятичных дробей в выражение деления, содержащее целые числа. Сдвиньте запятую делителя вправо на столько знаков, сколько необходимо, чтобы он стал целым числом. Сдвиньте запятую делимого на то же число
Преобразование выражений деления с десятичными делителями в выражения с делителями целых чисел (Уровень 2)
Преобразование деления десятичных дробей в выражение деления, содержащее целые числа. Сдвиньте запятую вправо на столько разрядов, сколько необходимо, чтобы получилось целое число. Сдвиньте запятую делимого на такое же количество знаков. Затем найдите
МОДУЛЬ 5: Алгебраические выражения
Тема A: Решение сложных уравнений с отсутствующими слагаемыми
Описание темы: Учащиеся решают все более сложные уравнения с отсутствующими слагаемыми. В этих предварительных алгебраических уравнениях проблема заключается не в числовых значениях, а в логике того, как числа и уравнения могут быть объединены для решения чисел, представленных символами.
В этих предварительных алгебраических уравнениях проблема заключается не в числовых значениях, а в логике того, как числа и уравнения могут быть объединены для решения чисел, представленных символами.
Решите отсутствующие уравнения слагаемых
Найдите отсутствующий член в уравнении сложения или вычитания. Каждое уравнение имеет символ вместо одного из членов. Найдите пропущенное число
Решите многошаговые уравнения с отсутствующими слагаемыми
Решите уравнения с более чем одним пропущенным членом. Каждое уравнение будет иметь один и тот же символ вместо двух или трех членов. Найдите пропущенное число
Найдите пропущенные слагаемые в парных уравнениях (Уровень 1)
Найдите два пропущенных члена в паре уравнений. Каждое уравнение имеет один или два символа вместо члена. Найдите пропущенные числа
Найдите пропущенные слагаемые в системе из трех уравнений.
Найдите три пропущенных члена в системе из трех уравнений. Каждое уравнение имеет один или два символа вместо члена. Найдите пропущенные числа
Найдите пропущенные числа
Найдите пропущенные слагаемые в парных уравнениях (Уровень 2)
Найдите пропущенные члены в паре уравнений. Каждое уравнение имеет один или два символа вместо члена. Узнайте, как заменить набор терминов, если общее значение известно. Найдите недостающие числа
Решите уравнения с отсутствующими слагаемыми, содержащие 0
Решите два отсутствующих члена в паре уравнений. Каждое уравнение имеет символы вместо термина. Найдите недостающие числа. Изучите эффект добавления 0 в уравнение
Найдите пропущенные слагаемые в парных уравнениях, содержащих 0
Попрактикуйтесь в решении уравнений с более чем одним пропущенным членом. Каждое уравнение имеет символы вместо двух или трех членов. Найди недостающие числа
Рабочие листы по математике для 5-го класса
Дополнительные рабочие листы
Это главная страница дополнительных рабочих листов. Перейдите по ссылкам, чтобы найти рабочие листы сложения по математике космического корабля, рабочие листы сложения нескольких цифр, рабочие листы сложения без переноса и другие темы сложения. Эти дополнительные рабочие листы бесплатны для личного или классного использования.
Эти дополнительные рабочие листы бесплатны для личного или классного использования.
Рабочие листы на сложение
Рабочие листы на вычитание
Это главная страница рабочих листов на вычитание. Перейдите по ссылкам, чтобы найти рабочие листы по математическому вычитанию космического корабля, тесты на вычитание по времени, рабочие листы по вычитанию нескольких цифр, простые рабочие листы по заимствованию и перегруппировке, а также математические рабочие листы со смешанными задачами на сложение и вычитание
Рабочие листы вычитания
Рабочие листы умножения
Это главная страница для рабочих листов умножения. Уберите пальцы, потому что это первая математическая операция, требующая запоминания фактов. Вы найдете рабочие листы умножения для восьми простых правил папы для освоения таблицы умножения, умножения RocketMath, многозначного умножения, квадратов и других тем рабочего листа умножения. Все эти рабочие листы по умножению содержат ключи для ответов, их можно мгновенно распечатать и использовать в классе или дома.
Все эти рабочие листы по умножению содержат ключи для ответов, их можно мгновенно распечатать и использовать в классе или дома.
Рабочие листы на умножение
Рабочие листы на деление
Это главная страница рабочих листов на деление. Сюда входят рабочие листы математического отдела космического корабля, рабочие листы для деления на несколько цифр, рабочие листы для квадратных корней, кубических корней, смешанные рабочие листы для умножения и деления. Эти рабочие листы разделения бесплатны для личного или классного использования.
Рабочие листы на деление
Таблица умножения
Пытаетесь запомнить факты умножения? Эта страница содержит печатные таблицы умножения, которые идеально подходят для справки. Существуют различные варианты каждой таблицы умножения с фактами от 1 до 9.(продукты 1-81), 1-10 (продукты 1-100), 1-12 (продукты 1-144) и 1-15 (продукты 1-255). Каждая из этих диаграмм умножения представляет собой SVG с высоким разрешением, поэтому факты умножения печатаются красиво!
Таблица умножения
Таблица умножения
Вы ищете распечатанную таблицу умножения, в которой есть не только факты? Один с некоторыми дополнительными математическими фактами о множителях? Или уникальный дизайн? В цвете? Все таблицы умножения на этой странице представляют собой файлы SVG с высоким разрешением, которые прекрасно распечатываются на вашем принтере и являются отличным ресурсом для изучения таблицы умножения в классе начальной школы или дома!
Таблица умножения
Рабочие листы семейства фактов
Рабочие листы семейства фактов сосредоточены на наборах связанных математических фактов, а не на конкретных операциях. Научите своих детей сложению и вычитанию одновременно и укрепите отношения в семье фактов! На каждом уровне вводятся два семейства фактов, которые позволяют прогрессивно практиковаться, или просто используйте рабочие листы в конце для всестороннего обзора семейства фактов.
Научите своих детей сложению и вычитанию одновременно и укрепите отношения в семье фактов! На каждом уровне вводятся два семейства фактов, которые позволяют прогрессивно практиковаться, или просто используйте рабочие листы в конце для всестороннего обзора семейства фактов.
Рабочие листы семейства фактов
Рабочие листы длинного деления
Вводные рабочие листы с делением в длинное число, листы с делением в длинное с остатком и без него, деление в длинное с десятичными знаками. Все эти длинные листы деления включают подробные, развернутые ответы.
Рабочие листы длинного деления
Графические дроби
Отличное введение в дроби с использованием круговой графики. Учащихся просят идентифицировать числовые формы дробей на графике или создать свои собственные представления.
Графические дроби
Сокращение дробей
Практические рабочие листы для сокращения дробей. Рабочие листы с различными дробями в этом разделе посвящены сокращению простых дробей, неправильных дробей и смешанных дробей.
Рабочие листы с различными дробями в этом разделе посвящены сокращению простых дробей, неправильных дробей и смешанных дробей.
Сокращение дробей
Сравнение дробей
Практические рабочие листы для сравнения дробей. Задачи на дроби на этих листах требуют от детей сравнения одинаковых и непохожих знаменателей, неправильных дробей и смешанных дробей.
Сравнение дробей
Сложение дробей
Рабочие листы для сложения дробей с общими знаменателями, с разными знаменателями, в виде простых дробей и смешанных дробей. Полная работа с шагами показана для каждой задачи на ключах ответов.
Сложение дробей
Вычитание дробей
Рабочие листы для вычитания дробей с общими знаменателями, с разными знаменателями, в виде простых дробей и смешанных дробей. Полные ключи ответов, которые показывают работу!
Вычитание дробей
Умножение дробей
Эти математические рабочие листы служат для практики умножения дробей. Включает задачи с целыми и без них, а также с кросс-отменами и без них. Каждый рабочий лист в формате PDF здесь имеет подробный ключ ответа, который показывает работу, необходимую для решения проблемы, а не только окончательный ответ!
Включает задачи с целыми и без них, а также с кросс-отменами и без них. Каждый рабочий лист в формате PDF здесь имеет подробный ключ ответа, который показывает работу, необходимую для решения проблемы, а не только окончательный ответ!
Умножение дробей
Деление дробей
Рабочие листы для деления дробей с делением на две дроби. Включает в себя простые дроби, смешанные дроби и неправильные дроби, а также задачи, для решения которых используется шаг перекрестного умножения.
Деление дробей
Дроби как десятичные числа
Рабочие листы для преобразования дробей в десятичные, в том числе с использованием деления в большую сторону.
Дроби как десятичные дроби
Задачи со словами
На этой странице представлены задачи со словами, охватывающие ряд трудностей для всех основных операций, включая задачи с большими значениями, а также с неиспользованной информацией. Словесные задачи — отличный способ применить эти математические факты на практике и развить реальное понимание того, что означают операции в реальном мире!
Словесные задачи — отличный способ применить эти математические факты на практике и развить реальное понимание того, что означают операции в реальном мире!
Словесные задачки
Предалгебраические словесные задачи
Предалгебраические словесные задачи на сложение, вычитание, умножение и деление, связанные с отношениями между числами в простых уравнениях… Отличный первый шаг для облегчения в алгебре!
Предварительные алгебраические задачи
Денежные задачи
Реальные задачи на сложение, вычитание, умножение и деление, связанные с деньгами. Отличное первое введение в прикладную математику для студентов, знакомых с десятичной арифметикой!
Задачи на деньги
Отрицательные числа
Эти рабочие листы с отрицательными числами комбинируют отрицательные числа с другими целыми числами (как положительными, так и отрицательными) с использованием основных математических операций, умножения многозначных отрицательных чисел и деления в длинную сторону с отрицательными числами.
Отрицательные числа
Проценты
Рабочие листы для практики использования и вычисления процентов других чисел, включая преобразование между дробями и процентами.
Проценты
Округление чисел
В этом разделе представлены рабочие листы округления для округления целых чисел и округления десятичных чисел, начиная с относительно простых задач, которые вводят алгоритм округления, а затем переходят к более сложным задачам, где учащиеся должны определить правильную разрядную цифру для проверьте, а также правильную цифру для округления в большую или меньшую сторону..
Округление чисел
Упорядочивание чисел
Практика упорядочивания рабочих листов с несколькими числами в порядке возрастания (от наибольшего к наименьшему) и убывания (от наименьшего к наибольшему). Включает в себя целые числа, десятичные числа и отрицательные числа. Аналогичные наборы рабочих листов с порядковыми номерами представлены как в горизонтальном, так и в вертикальном форматах.
Аналогичные наборы рабочих листов с порядковыми номерами представлены как в горизонтальном, так и в вертикальном форматах.
Номера для заказа
Стандартная, расширенная и словесная форма
Практические рабочие листы для преобразования чисел между стандартной формой (цифры), расширенной формой (разрядное значение) и формой слова (прописью или устным представлением).
Стандартная, расширенная и словесная формы
Шаблоны чисел
Эти рабочие листы шаблонов чисел помогают учащимся развить необходимые навыки для определения шаблонов и отношений между числами.
Шаблоны номеров
Шаблоны с отрицательными значениями
Числовые шаблоны, которые пересекают ноль и могут начинаться или заканчиваться отрицательными значениями.
Шаблоны с негативами
Среднее, медиана, диапазон
Рабочие листы для определения среднего, медианы, моды и диапазона для наборов чисел. Задачи включают в себя наборы всех положительных целых чисел, все отрицательные целые числа и смешанные наборы знаков, а также практику работы с калькулятором.
Задачи включают в себя наборы всех положительных целых чисел, все отрицательные целые числа и смешанные наборы знаков, а также практику работы с калькулятором.
Среднее, Медиана, Диапазон
Отсутствующие операции
Рабочие листы, в которых даны ответы, но отсутствует операция. Это отличный способ выучить группы фактов «в обратном порядке» или обеспечить подкрепление, если запоминание с помощью других упражнений кажется застопорившимся.
Отсутствующие операции
Римские цифры
Рабочие листы по римским цифрам, включая преобразование римских цифр, упорядочивание римских цифр и заполнение шаблонов римских цифр. Римские цифры — идеальная тема для учащихся 3-х, 4-х и 5-х классов, и эти рабочие листы обеспечивают практику чтения и письма римскими цифрами, а также базовые навыки восприятия чисел.
Римские цифры
Таблица римских цифр
Если вы пытаетесь научиться читать и писать римскими цифрами, пытаетесь найти причудливый способ написать свой год рождения, или вам просто нужна «шпаргалка» для быстрого Для справки, каждая таблица с римскими цифрами на этой странице позволит вам работать с этой древней системой счисления в кратчайшие сроки. Все диаграммы печатаются на одной странице в версиях для 1-10, 1-100 и 1-1000 с правилами для римских цифр и без них. Пытаетесь понять, что означает эта странная римская цифра после Суперкубка? Взгляните на новую таблицу римских цифр Super Bowl!
Все диаграммы печатаются на одной странице в версиях для 1-10, 1-100 и 1-1000 с правилами для римских цифр и без них. Пытаетесь понять, что означает эта странная римская цифра после Суперкубка? Взгляните на новую таблицу римских цифр Super Bowl!
Таблица с римскими цифрами
Судоку
Головоломки судоку для детей и взрослых, в том числе простые и сложные, злые судоку, самурайские судоку и многое другое!
Судоку
Магический квадрат
Головоломки с магическим квадратом — отличное введение в логику и решение задач… Попробуйте эти 3×3, 4×4 и 5×5, чтобы улучшить свои математические навыки!
Волшебный квадрат
Головоломки с числовой сеткой
В этом разделе представлены листы математических логических головоломок в виде сетки, включающие сложение, вычитание, умножение и деление для разных классов и уровней навыков. Существуют версии этих логических головоломок с пропущенными числами, а также с пропущенными операциями.
Существуют версии этих логических головоломок с пропущенными числами, а также с пропущенными операциями.
Головоломки с числовой сеткой
Факторизация, НОД, НОК
Распечатываемые на этой странице рабочие листы факторизации простых чисел требуют, чтобы учащиеся разлагали все большие целые числа на простые множители. Это первый шаг для определения наибольших общих делителей двух чисел или определения наименьшего общего кратного двух чисел, но дополнительно простая факторизация вводит понятия простых чисел и составных чисел.
Факторизация, НОД, НОК
Предварительная алгебра
Предварительные алгебраические навыки, включая поиск пропущенных значений.
Pre-Algebra
Exponents Worksheets
Знакомит с квадратами, кубами и показателями степени в сочетании с другими базовыми операциями. Включает в себя практику, которая создаст память сайта общих экспоненциальных терминов
Рабочие листы Exponents
Рабочие листы порядка операций
Эти рабочие листы порядка операций смешивают основные арифметические операции, включая круглые скобки и показатели степени. Если вы ищете рабочие листы с порядком операций, которые проверяют знание правил PEMDAS, эти математические листы — хорошее начало. Вы также можете найти рабочие листы порядка операций с отрицательными числами и рабочие листы порядка операций со сравнениями на этих других страницах рабочего листа.
Если вы ищете рабочие листы с порядком операций, которые проверяют знание правил PEMDAS, эти математические листы — хорошее начало. Вы также можете найти рабочие листы порядка операций с отрицательными числами и рабочие листы порядка операций со сравнениями на этих других страницах рабочего листа.
Порядок действий Рабочие листы
Базовая геометрия
Простая маркировка линий, углов и треугольников. Определение фигур
Базовая геометрия
Больше и меньше
Практические рабочие листы для сравнения чисел. Эти рабочие листы содержат больше и меньше операций, сравнений и тестов на равенство для многозначных чисел, времени и многого другого!
Больше и меньше
Миллиметровая бумага
Бесплатная печатная миллиметровая бумага, бумага с сеткой и бумага с точками для математических задач, ремесел, зентанглинга, ландшафтного дизайна, архитектуры или просто рисования. Все стили графической бумаги включают дюймовые и сантиметровые варианты. Все эти PDF-файлы предназначены для печати на бумаге размером 8,5 x 11 дюймов.
Все стили графической бумаги включают дюймовые и сантиметровые варианты. Все эти PDF-файлы предназначены для печати на бумаге размером 8,5 x 11 дюймов.
Миллиметровая бумага
Координатная плоскость
Пустые координатные плоскости на этой странице включают варианты с метками либо на оси, либо на краю сетки, а также версии с метками квадрантов. Вы можете найти полные 4-квадрантные координатные плоскости, а также пустые 1-квадрантные координатные плоскости в настройках макетов для решения нескольких домашних задач на одной странице.
Координатная плоскость
Измерение в дюймах
Эти листы измерения в дюймах (обычные единицы измерения) позволят развить навыки выполнения линейных измерений либо одной точки, либо измерения длины объекта. Существуют различные измерительные рабочие листы с задачами, подходящие для учащихся детского сада, первого, второго или третьего класса по математике.
Измерение в дюймах
Метрическое измерение
Рабочие листы для определения измеренных положений и измерения объектов в сантиметрах и миллиметрах на линейке. Эти рабочие листы являются отличной практикой для учащихся первого, второго, третьего и четвертого классов, а также могут обеспечить практическую практику вычитания при измерении длины объектов на линейке.
Метрическая единица измерения
Преобразование единиц метрической системы СИ
В этих таблицах для преобразования единиц измерения из одной единицы измерения в другую используются единичные дроби. Этот подход более распространен на уроках химии, физики или других естественных наук и требует, чтобы учащиеся сосредоточились на сокращении единиц, чтобы найти решение с правильным значением и правильными единицами.
Преобразование метрических единиц СИ
Преобразование обычных единиц
Традиционная практика преобразования единиц измерения расстояния (дюймы в футы), объема (унции в галлоны) и массы (унции в фунты). Эти рабочие листы также используют дроби единицы для преобразования значений единиц измерения из одного измерения в другое. Этот подход более распространен на уроках химии, физики или других естественных наук и требует, чтобы учащиеся сосредоточились на сокращении единиц, чтобы найти решение с правильным значением и правильными единицами.
Эти рабочие листы также используют дроби единицы для преобразования значений единиц измерения из одного измерения в другое. Этот подход более распространен на уроках химии, физики или других естественных наук и требует, чтобы учащиеся сосредоточились на сокращении единиц, чтобы найти решение с правильным значением и правильными единицами.
Преобразование обычных единиц измерения
Традиционные и метрические единицы
В этих рабочих листах используются единичные дроби для преобразования значений между единицами СИ (метрическими) и обычными единицами. Темы в этом разделе включают практику преобразования дюймов в метры, литров в галлоны и граммов в фунты.
Обычная и метрическая система
Дополнительные раскраски по номерам
Эти листы дополнительных раскрасок требуют, чтобы учащиеся решили простые математические факты, чтобы найти правильный цвет для раскрашивания, чтобы показать изображение их собственного творения. Вы найдете растущий набор праздничных и сезонных тематических страниц, которые я буду добавлять со временем… Пожалуйста, заходите почаще на наличие обновлений или, если у вас есть предложения, отправьте мне сообщение по контактной ссылке ниже!
Вы найдете растущий набор праздничных и сезонных тематических страниц, которые я буду добавлять со временем… Пожалуйста, заходите почаще на наличие обновлений или, если у вас есть предложения, отправьте мне сообщение по контактной ссылке ниже!
Сложение цветов по номерам
Вычитание цветов по номерам
Эти рабочие листы раскрашивания методом вычитания требуют, чтобы учащиеся решили простые математические факты, чтобы найти правильный цвет для растушевки, чтобы показать изображение собственного творения. Вы найдете растущий набор праздничных и сезонных тематических страниц, которые я буду добавлять со временем… Пожалуйста, заходите почаще на наличие обновлений или, если у вас есть предложения, отправьте мне сообщение по контактной ссылке ниже!
Вычитание цвета по номеру
Умножение по номерам
Ищете рабочие листы, чтобы сделать изучение математики в День святого Валентина немного веселее? На этой странице собраны листы для умножения в цвете на число, подходящие для учащихся третьего, четвертого или пятого классов.
Умножение по номерам
Разделение по номерам
Ищете рабочие листы, чтобы сделать изучение математики в День святого Валентина немного веселее? На этой странице собраны листы с цветовым делением по номерам, подходящие для учащихся третьего, четвертого или пятого классов.
Цвет деления по номеру
Таблица квадратных корней
Ищете ли вы список полных квадратных корней или полную таблицу квадратных корней от 1 до 100, таблица квадратных корней на этой странице будет иметь ваши радикалы покрытый! Существуют как цветные, так и черно-белые версии диаграмм в формате PDF для печати.
Таблица квадратного корня
Таблица дробей
Эта уникальная визуализация эквивалентных дробей объединяет значения дробей на числовой прямой для создания элегантной симметрии. Он не только выделяет дроби в их наименьшей, наиболее сокращенной форме, но и предоставляет удобный десятичный эквивалент для наиболее часто используемых дробей. Это действительно одна из лучших справочных диаграмм, которые я создал за 10 лет создания математических ресурсов!
Это действительно одна из лучших справочных диаграмм, которые я создал за 10 лет создания математических ресурсов!
Таблица дробей
Головоломки по поиску слов
Используйте эти математические головоломки для поиска слов, чтобы познакомить учащихся начальной школы со словарным запасом и терминами, когда они знакомятся с новыми математическими понятиями! Эти головоломки для поиска слов включают в себя наборы для различных уровней обучения, согласованных с Common Core, а также конкретные темы для геометрии, алгебры и многого другого!
Головоломки с поиском слов
Таблица вероятностей
Таблица привязки вероятностей для решения задач со словами! Эта иллюстрированная таблица описывает сценарии с монетами, костями и игральными картами. Он включает коэффициенты на наиболее вероятные и наименее вероятные исходы.
Таблица вероятностей
Таблица измерений
Эта таблица измерений является хорошим справочным пособием для решения текстовых задач, связанных с переводом единиц объема, длины или температуры из одной системы в другую. Значения показаны на одной шкале как в обычной, так и в метрической системах. Отлично подходит для измерения кухни и приготовления пищи!
Значения показаны на одной шкале как в обычной, так и в метрической системах. Отлично подходит для измерения кухни и приготовления пищи!
Диаграмма измерений
Линейные уравнения
Рабочие листы линейных уравнений, включая расчет наклона по двум точкам, расчет точек пересечения по оси Y, построение графиков уравнений в форме пересечения наклона, построение графиков уравнений в форме точечного наклона, построение графиков систем уравнений, построение графиков линейных уравнений, построение графиков линейные неравенства и многое другое!
Линейные уравнения
Числовая линейка
Числовая линейка может быть мощным инструментом для изучения отрицательных чисел, отношений или просто вводных операций сложения и вычитания. PDF-файлы с числовыми строками на этой странице включают различные диапазоны (10, 12, 15, 20, 15 и 100) как с нуля, так и с отрицательными диапазонами. Полный набор строк чисел дроби, отмеченных общими знаменателями, включен в диапазоны от -5 до 5. Существуют также специальные строки с номерами для прошедшего времени, температуры и денег, а также пустые строки с номерами для обычных диапазонов и дробей.
Существуют также специальные строки с номерами для прошедшего времени, температуры и денег, а также пустые строки с номерами для обычных диапазонов и дробей.
Числовая строка
Рабочие листы по математике для печати для 5-го класса
Пятиклассники изучат широкий спектр математических тем, укрепляя свои арифметические навыки. Рабочие листы по математике на этой странице охватывают многие из основных тем математики 5-го класса, но уверенность во всех основных операциях необходима для успеха как в 5-м классе, так и после него. Учащиеся 5-го класса должны быть на таком уровне, чтобы их факты умножения и деления можно было вспомнить мгновенно; если нет, рабочие листы для каждой операции в этом разделе следует регулярно пересматривать. Применение математики важно в 5-м классе, и другие математические рабочие листы здесь обеспечивают практику решения текстовых задач по различным темам. Существуют также рабочие листы числовых шаблонов, рабочие листы факторизации, рабочие листы среднего / медианы / режима и рабочие листы с подчеркнутыми навыками предварительной алгебры.
Игры на деление для пятиклассников онлайн
Часто задаваемые вопросы:Q1: Как вы решаете задачи на деление?
Ответ: Чтобы решить задачи на деление, мы читаем задачу и определяем делимое и делитель. Затем мы делим делимое на делитель либо мысленно, либо методом длинного деления. Нам также может понадобиться решить проблему дальше, чтобы получить окончательный ответ.
Q2: Что такое факт разделения для 5-классников?
Ответ: Факты деления — это предложения с номером деления, относящиеся к таблицам умножения. Следовательно: 30 ÷ 3 = 10, 27 ÷ 3 = 9 и 24 ÷ 3 = 8 — все это факты деления для таблицы трех умножений. К 5 годам дети знают все свои таблицы умножения до 12 х 12 и соответствующие факты деления. Они используют факты деления для решения задач на деление с участием больших чисел.
Q3: Как вы делите числа, используя деление в большую сторону?
Ответ: Чтобы разделить числа с помощью длинного деления, мы помещаем делитель вне поля деления и делимое внутри него. Мы идентифицируем первые одну или две цифры, которые ближе всего к кратному делителю, который либо равен, либо меньше первых одной или двух цифр. Мы записываем кратное в частное и под цифрами в делимом. Затем мы вычитаем кратное делителя из первых цифр делимого. Тогда полученный ответ является остатком в этом случае. Мы опускаем следующую цифру делимого и повторяем тот же процесс, пока не получим последний остаток, который равен либо 0, либо числу меньше делителя.
Мы идентифицируем первые одну или две цифры, которые ближе всего к кратному делителю, который либо равен, либо меньше первых одной или двух цифр. Мы записываем кратное в частное и под цифрами в делимом. Затем мы вычитаем кратное делителя из первых цифр делимого. Тогда полученный ответ является остатком в этом случае. Мы опускаем следующую цифру делимого и повторяем тот же процесс, пока не получим последний остаток, который равен либо 0, либо числу меньше делителя.
Предыдущий класс развивает у детей навыки рассуждения для получения арифметического выражения из заданной задачи. С подходящими операторами для быстрого сложения, вычитания, умножения и деления 4-значных чисел на однозначное число; результат операции «деления» вычисляется через частное и остаток. Также методы деления в длину и на кратные 10 и 100 позволяют быстро делить числа и получать точный ответ.
В 5 классе вводятся двузначные делители, чтобы еще больше улучшить навыки продвинутой математики. Понимание таких концепций, как ноу-хау для составления таблицы умножения; дети усваивают умение вычислять делитель и делимое с точностью до ближайшего числа, кратного 10. Этот метод улучшает быстрые математические навыки и позволяет детям также оценивать частные. Понимание «деления» на дробные числа и разрядную систему полезно для изучения измерений и знакомых методов преобразования.
Этот метод улучшает быстрые математические навыки и позволяет детям также оценивать частные. Понимание «деления» на дробные числа и разрядную систему полезно для изучения измерений и знакомых методов преобразования.
Что такое «Отдел»?
«Деление» как математический прием для учащихся 5-х классов озвучивается как:
«Формулирование модели справедливого деления числа (дивиденда) на указанное количество групп (делителя)».
Например:
Математические игры для учебного отдела
Абстрактные знания основных математических навыков улучшаются в каждом классе, чтобы изучить применимость и практические аспекты. «Деление» как математическая основа начинается с создания модели раздела для концептуализации и связывания ее с визуальным наблюдением. Увлекательные обучающие математические игры для SplashLearn еще больше оттачивают навыки деления четырехзначных чисел на однозначное число и вычисления частного и остатка (если есть). Простые в понимании математические игры, соответствующие основным математическим стандартам для 5-го класса, расширяют навыки деления чисел, включая дроби и двузначные делители.
Хорошо продуманные игры помогают детям преуспеть в математике и участвовать в эффективном домашнем обучении.
Обучение и результат:
В 5-м классе умение рассуждать, необходимое для понимания словесной задачи, развивается путем формулирования допустимых выражений. Дети учатся использовать стандартные алгоритмы и соответствующие свойства математических операций (такие как распределительное свойство умножения; a x b = b x a). Со знанием системы счисления с основанием 10 и оценкой ближайшего кратного 10, соответствующего числу; дети учатся стратегически разбивать делимое и делитель на части в десятичных единицах для оценки частного.
Прогнозируемые результаты обучения перечислены ниже:
- Обнаружение шаблона или структуры для сложения, вычитания, умножения и деления целых чисел, дробей и чисел для графического представления
- Понимание и обобщение шаблонов для решения арифметических выражений с использованием арифметических операций
- Понимание модели справедливого распределения путем вычисления частного в десятичной форме
- Применение распределительного свойства для нахождения частного места за местом, начиная с самого высокого места
- Оценка ближайшего множителя с основанием 10 для делимого и делителя для включения умственных вычислений и развития быстрых математических навыков
- Деление дробей и четырехзначных чисел на двузначный делитель и дробь
- Представление математических выражений и частного с использованием разрядной системы значений
Требуемые математические навыки:
Чтобы изучить операцию «деления», включающую дроби и двузначное деление, необходимые математические основы настаивают на беглом решении одноэтапных и многоэтапных математических операций. Это операции сложения, вычитания, умножения и деления четырехзначных чисел. Значимая команда умножения двузначного числа на однозначное число для точной оценки полезна при работе с методом деления на длинные.
Это операции сложения, вычитания, умножения и деления четырехзначных чисел. Значимая команда умножения двузначного числа на однозначное число для точной оценки полезна при работе с методом деления на длинные.
Понимание системы позиционных значений наряду с интерпретацией блоков с основанием 10 и блоков единиц способствует развитию навыков визуального наблюдения для деления на дробные делители.
Engagement:
Рабочие листы SplashLearn поощряют детей к логическому мышлению с рассуждениями и пониманием языка для понимания математических концепций. Уникальный, привлекательный и интерактивный интерфейс с красочным тематическим дисплеем воспитывает у детей глубоко укоренившиеся понятия. Следование хорошо спланированному распорядку выполнения комплексных упражнений помогает быстро выполнять вычисления в уме и преуспевать в математике без страха.
В следующем разделе обсуждаются различные случаи с двузначными числами и дробными значениями в качестве делителя и соответствующей десятичной арифметики.
Деление на двузначные числа
Чтобы разделить число (от 10 до 10 000) на двузначный делитель (от 10 до 99), используется метод деления в большую сторону. Два возможных ответа в таком делении: либо целое число в частном, либо частное с остатком. Остаток всегда будет меньше делителя.
Деление без остатка
Чтобы разделить число на двузначный делитель, рассмотрим следующий пример:
- Разделить 425 на 25
- 25 )¯425 ( 17 → Частное
— 25 ↓ _ → 25 x 1 = 25
175
— 175 → 25 x 7 = 175
000 → Нет остальных
, чтобы решить проблему с использованием быстрой математической навыки, оценить самое близкое значение (множество из 10 и ближе к делимому), что при вычитании даст 0 или остаток меньше делителя. Например,
- 25 х 4 = 100
- Итак, 25 х 8 = 200
- As, 200 – 25 = 175, таким образом, 25 x 7 = 175, и его можно вычесть из оставшегося делимого.

Деление с остатком
Как обсуждалось ранее, результат деления может заканчиваться на частное и на остаток. Рассмотрим следующий пример:
- Разделите 738 на 22 .
- 22 )¯738 ( 33 → Частное
– 66↓ _ →22 x 3 = 66
078
— 066 → 22 x 3 = 66
012 → Остаток
- А 20 ближе к 22, чем 30, переписывайте дивизор как 20
- Точно так же 738 можно записать как 700
- Таким образом, новое уравнение: 700 ÷ 20
- 20 )¯700 ( 35 → Частное
– 60↓ _ →20 x 3 = 60
100
— 100 → 20 x 5 = 100
000 → без остатков
- С оценкой дивидендов и делителя дети могут легко найти ближайшее значение коэффициента в математических утечках.
Деление с дробными значениями
По мере того, как дети изучают методы деления целых чисел и деления числа на многозначный делитель (однозначный и двузначный), изучение «деления» на дробные значения становится легким.
Следующая диаграмма иллюстрирует множественные случаи деления с дробными значениями единиц.
Разделить дробную часть на целое
Чтобы разделить дробную часть на целое число, иллюстрация, подобная линейному графику, полезна для понимания метода.
- Например, разделить 1/7 на 3
- Разделить линию на 7 равных частей, далее каждую из них разделить на 3 равные части
- Общее количество порций можно рассчитать как:
- ÷ 3 ➔ X ➔ ➔
- Свойство умножения единиц множителей используется для создания уравнения
Исходное изображение: Чтобы разделить 1/7 на 3, разделите 1/7 на 3 блока каждый.
Разделить целое на дробную часть
Поскольку числа меняются местами, в случае, когда делимое представляет собой целое число, а делитель представляет собой дробную часть, уравнение «деления» аналогично построено с использованием линейного графика. Разница только в числителе, а не в знаменателе.
- Например, разделить 3 на 1/5
- Разделить линию на 3 равные части, далее каждую из них разделить на 5 равных частей
- Общее количество порций можно рассчитать как:
- 3 ÷ ➔ 3 X ➔ ➔ ➔ 15
- Свойство умножения единиц множителей используется для создания уравнения
- Проблему можно визуально наблюдать как общее количество коробок, содержащихся в пределах 3 единиц.
Справочное изображение: Чтобы разделить 3 на 1/5, подсчитайте количество блоков
Деление в десятичной арифметике
В предыдущем разделе показано деление единичных дробей на целые числа и целых чисел на единичные дроби. В десятичной арифметике деление выполняется путем представления десятичных значений в дробной форме со знаменателем, кратным 10. Знаменатель оценивается разрядным значением десятичного числа.
Следующая таблица иллюстрирует некоторые примеры задач на деление, связанных с десятичной арифметикой.
Деление десятичного числа на кратное 10
Чтобы разделить десятичное число на кратное 10, первым шагом является корректировка десятичного разряда. Десятичная дробь сдвигается влево на один разряд для каждой единицы 10.
Деление десятичной дроби на целое
Чтобы разделить десятичную дробь на целое число, система разрядных значений для перезаписи десятичной дроби удобна для упрощения деления. уравнение. Следуя методу длинного деления или короткого деления в соответствии с многозначным делителем, можно решить уравнение, как показано в примере.
Десятичное деление
Чтобы разделить десятичное число на другое десятичное число, уравнения деления составляются с учетом разрядной системы значений и сокращения десятичных множителей друг с другом. Концепция проиллюстрирована примером для понимания техники.
Приложение
Операция «деление» с использованием десятичной арифметики, единичных дробей и многозначного делителя является основой обучения измерению, представлению данных и геометрии. Кроме того, в практических аспектах эта концепция широко используется для рисования карт, пропорционального изменения масштаба таких измерений, как длина и высота, преобразования физических величин, таких как вес, вместимость и т. д., в различные единицы (метрические и общепринятые в США) для облегчения интерпретации.
Кроме того, в практических аспектах эта концепция широко используется для рисования карт, пропорционального изменения масштаба таких измерений, как длина и высота, преобразования физических величин, таких как вес, вместимость и т. д., в различные единицы (метрические и общепринятые в США) для облегчения интерпретации.
SplashLearn Division Games Рабочие листы для 5-го класса
Полезность основных математических операций при изучении сложных математических понятий очевидна из сложности текстовых задач в 5-м классе. С развитием навыков деления на дробные и двузначные делители; дети понимают и понимают математику, связанную с представлением данных, измерением и геометрией, а также понимают «модель справедливого распределения».
Кроме того, ежедневные математические задачи укрепляют умственные способности детей. Рабочие листы SplashLearn на «деление», состоящие из головоломок, математических загадок, одноэтапных и многоэтапных текстовых задач , являются идеальным помощником во время летних каникул, чтобы предотвратить потерю навыков. Тщательно спланированная учебная программа pre-k получила особую оценку наставников, занимающихся домашним обучением. Начните практиковаться в увлекательных математических играх уже сегодня, чтобы повысить уверенность и преуспеть в математике.
Тщательно спланированная учебная программа pre-k получила особую оценку наставников, занимающихся домашним обучением. Начните практиковаться в увлекательных математических играх уже сегодня, чтобы повысить уверенность и преуспеть в математике.
Повторение основ умножения и деления с пятиклассниками {бесплатные}
| 11 комментариев | Рубрики: Математика, умножение и деление
Многие из моих учеников в прошлом приходили ко мне, не имея концептуального понимания основных математических понятий, которые были введены еще во 2-м и 3-м классах. Самая важная часть моего обучения математике — это развитие концептуального понимания, и это действительно важно, поскольку пятый класс переходит к более абстрактным математическим концепциям. Имея это в виду, это первый концептуальный урок, который я каждый год преподаю своим пятиклассникам. Нажмите здесь, чтобы увидеть математические таблицы начала учебного года, которые я составляю в первые недели учебы.
Примечание : Я также буду делать записи обо всех изменениях, которые я хотел бы внести, когда снова буду делать урок в следующем году. Как учителя, мы постоянно растем и совершенствуемся так же, как мы хотим, чтобы наши ученики, и я хочу убедиться, что я делюсь с вами любыми улучшениями.
Наличие концептуального понимания основ умножения и деления является ключевым в 5-м классе. В 5-м классе мы переходим к десятичному и дробному умножению, что требует от учащихся понимания того, что умножение также является частью целого или части части. Однако, если у них нет даже базового понимания умножения, это может быть очень сложно для них. Я делаю этот урок ОЧЕНЬ простым, но это одна из записей в интерактивной тетради, к которой некоторые ученики возвращаются в течение всего года.
Обзор умножения
Для начала поговорим о том, что такое умножение. Некоторые учащиеся могут отбарабанить «повторяющееся сложение» или «равные группы», но я хочу, чтобы они могли привести примеры и обсудить это своими словами. Это одно из ключевых различий между механическим заучиванием концепции и более глубоким ее пониманием.
Это одно из ключевых различий между механическим заучиванием концепции и более глубоким ее пониманием.
Обсудив это, мы переходим к определению каждого числа в задаче на умножение. Это приводит к обсуждению того, что при умножении целых чисел (я делаю различие со студентами, чтобы посеять семя для десятичного и дробного умножения) у вас есть группы, и вы ищете общее количество чего-то. Это удобно, когда мы переходим к задачам на умножение и деление слов с большими числами. Я постоянно спрашиваю студентов: что вы ищете? Я хочу, чтобы они поняли, что если они имеют равные группы и ищут общую сумму, то они умножаются.
Мы также обсуждаем массивы и скорости, когда говорим об умножении. Я хочу, чтобы учащиеся увидели связь между проблемами скорости и равными группами.
Вот несколько снимков интерактивного шаблона, который я использовал. Этому посвящено гораздо больше дискуссий, и, к сожалению, многие из этих дискуссий не были отражены в заметках этого конкретного студента.
Изменения в этой части урока
Вот некоторые вещи, которые я бы изменил, чтобы улучшить этот урок на следующий год:
- Предложите учащимся нарисовать несколько изображений умножения вместо простого круга. Вместо этого мы будем рисовать массивы и числовые линии в дополнение к круговому представлению для каждой операции.
Обзор деления
После рассмотрения понятия умножения мы переходим непосредственно к рассмотрению понятия деления. Проделываем те же шаги, что и с умножением. Мы подробно обсудим, что такое деление и что оно означает. Я хочу, чтобы учащиеся увидели связь между умножением и делением, поэтому мы используем фразу «распределение общего количества чего-либо на равные группы». Это напрямую связано с концепцией, согласно которой умножение определяет общую сумму в равных группах. Разделение, с другой стороны, берет общее количество чего-либо, объединяя его в группы. Это язык, который я использую со студентами. Это действительно нравится многим из них, которые никогда не понимали связи между ними.
После обсуждения основной концепции деления мы переходим к двум типам деления: количество групп неизвестно и размер группы неизвестен. Некоторым из моих учеников это действительно трудно. Я должен думать, что это потому, что они не знакомятся с этими терминами и/или их не просят решить различные проблемы деления. Имея это в виду, учащиеся выполняют две разные модели, чтобы показать оба типа деления. В будущем я обязательно попрошу учащихся обозначить каждую модель как «Размер группы неизвестен» или «Количество групп неизвестно».
Я ссылаюсь на эти интерактивные математические шаблоны в нашем блоке умножения и деления. На самом деле это первая интерактивная записная книжка года и одна из самых важных. К тому времени, когда мы перейдем к умножению десятичных и дробных чисел, учащиеся будут готовы понять этот аспект умножения.
Изменения в этой части урока
Вот некоторые вещи, которые я бы изменил, чтобы улучшить этот урок на следующий год:
- Предложите учащимся использовать термин «разделение» в дополнение к слову «поместить».
 Это не только более правильно с математической точки зрения, но и подготавливает их к делению единичных дробей, когда они разбивают целое на дробные количества.
Это не только более правильно с математической точки зрения, но и подготавливает их к делению единичных дробей, когда они разбивают целое на дробные количества. - Я бы использовал несколько представлений так же, как и в части урока, связанной с умножением.
Загрузите шаблоны умножения и деления здесь
Щелкните здесь или на изображении, чтобы загрузить шаблоны умножения и деления, используемые в этом уроке.
Следующие шаги
Вот что я делаю в дни, следующие за этим уроком:
- На следующий день раздайте бланк с просьбой дать ученикам определение умножения и деления и, в зависимости от класса, также сравните эти две операции.
- Ежедневно ставьте перед учащимися задачу на умножение или деление. Я бы внимательно следил за учениками и смотрел, какие из них борются. Возьмите несколько задач со свободными словами, которые идеально подходят для этого, нажав здесь.
- Соберите небольшие группы для продолжения обучения с использованием манипуляций для учащихся, которым необходимо более интенсивное обучение умножению и делению.

- Оцените беглость моих учеников по математике и отправьте домой наборы для умножения и деления тем, у кого проблемы.
Ваши ученики приходят к вам, не имея базового концептуального понимания, или они достаточно сильны в понятиях умножения и деления?
11 комментариев | Рубрики: Математика, умножение и раздел
У вас есть ученики, которые еще не усвоили математические факты?
Зарегистрируйтесь в более чем 30 БЕСПЛАТНЫХ партнерских играх, чтобы улучшить навыки умножения и деления ваших учащихся.
Имя Адрес электронной почтыВводя свои данные, вы соглашаетесь получать от меня сообщения по электронной почте. Согласно моей политике конфиденциальности, вы можете отказаться от подписки в любое время.
Вам также могут понравиться эти посты
Добро пожаловать, друзья! Я Дженнифер Финдли: учитель, мать и заядлый читатель. Я считаю, что с правильными ресурсами, мышлением и стратегиями все учащиеся могут достичь высокого уровня и научиться любить учиться.
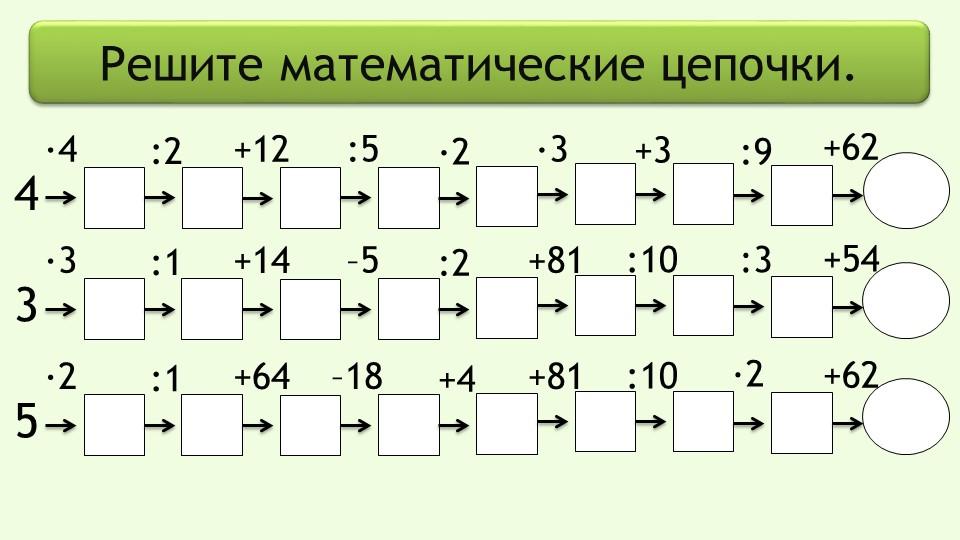 Взаимно простые числа
Взаимно простые числа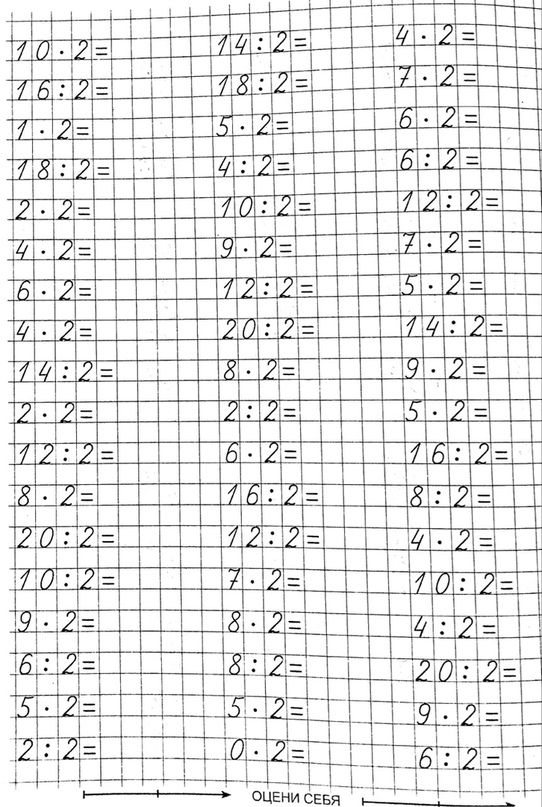 К. Математика. Книга для учителя. 5-6 классы. // М. К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010.- 256 с.
К. Математика. Книга для учителя. 5-6 классы. // М. К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010.- 256 с. А. Математика. Сборник рабочих программ. 5-6 классы. // Составитель Т. А. Бурмистрова – М.: Просвещение, 2014.- 80 с.
А. Математика. Сборник рабочих программ. 5-6 классы. // Составитель Т. А. Бурмистрова – М.: Просвещение, 2014.- 80 с.
 Они генерируются случайным образом, их можно распечатать в вашем браузере и включать в себя ключ ответа. Рабочие листы подходят для любой математической программы для пятого класса, но особенно хорошо подходят для программы IXL по математике для 5-го класса и их новых уроков внизу страницы.
Они генерируются случайным образом, их можно распечатать в вашем браузере и включать в себя ключ ответа. Рабочие листы подходят для любой математической программы для пятого класса, но особенно хорошо подходят для программы IXL по математике для 5-го класса и их новых уроков внизу страницы.

 Например, 0,24 задается как 24/100, а не как 6/25. Если хотите, вы можете спросить
студент упростить.
Например, 0,24 задается как 24/100, а не как 6/25. Если хотите, вы можете спросить
студент упростить. 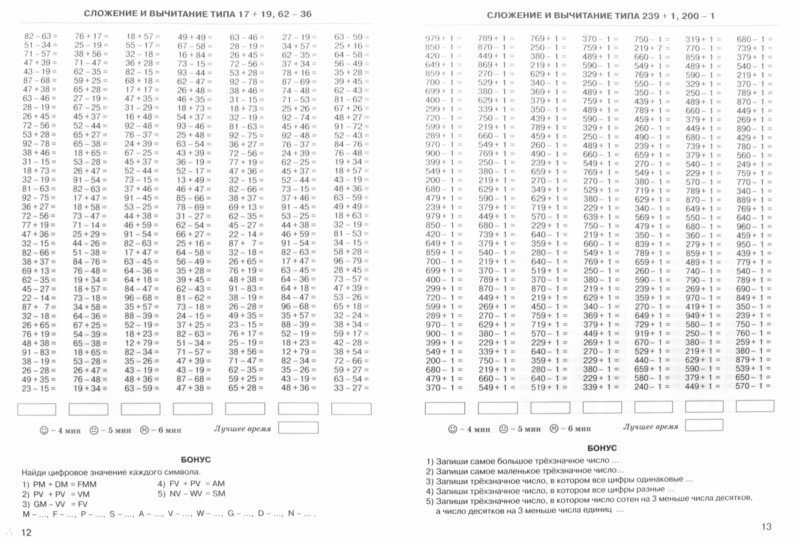 Ваш ребенок насчитывает 73.343 миллиона бактерий в образце A, 73,431 миллиона бактерий в образце B и 74,399 миллиона бактерий в образце C. Расположите образцы в порядке от наибольшего количества бактерий к наименьшему. Объясните или проиллюстрируйте, как вы приводите эти образцы в порядок.
Ваш ребенок насчитывает 73.343 миллиона бактерий в образце A, 73,431 миллиона бактерий в образце B и 74,399 миллиона бактерий в образце C. Расположите образцы в порядке от наибольшего количества бактерий к наименьшему. Объясните или проиллюстрируйте, как вы приводите эти образцы в порядок. Во введении к каждой главе есть некоторые примечания для учителя относительно материала главы. Все инструкции написаны непосредственно для ученика в рабочем тексте, а также существуют сопроводительные видеоролики, где вы можете увидеть, как Мария сама преподает материал.
Во введении к каждой главе есть некоторые примечания для учителя относительно материала главы. Все инструкции написаны непосредственно для ученика в рабочем тексте, а также существуют сопроводительные видеоролики, где вы можете увидеть, как Мария сама преподает материал.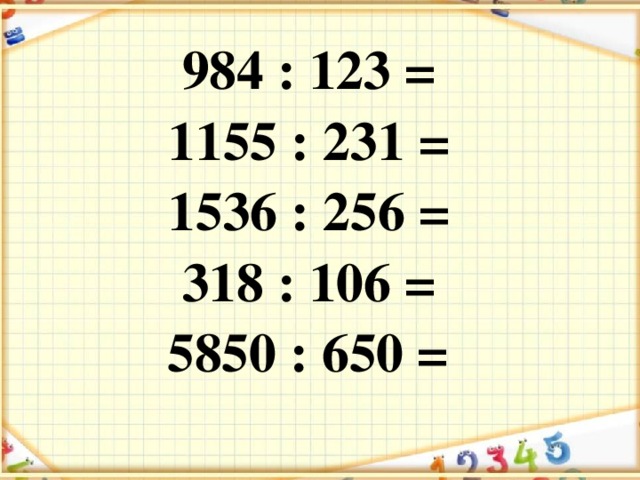
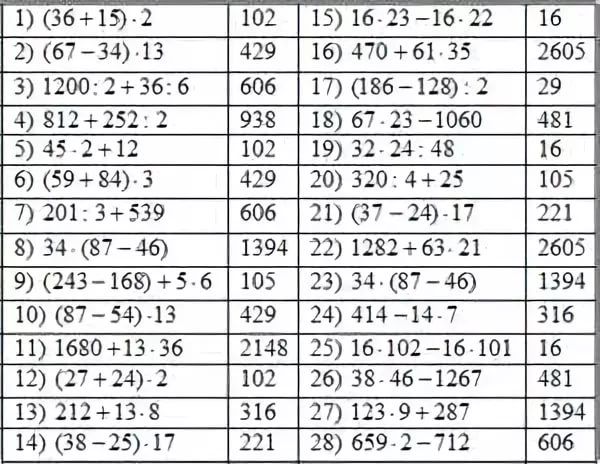
 Это свойство может быть полезно при решении уравнений.
Это свойство может быть полезно при решении уравнений.
 Равные фигуры
Равные фигуры