3000 примеров по математике с ответами и методическими рекомендациями. 2 класс. Устный счет. Сложение и вычитание в пределах 100 (Елена Нефёдова, Ольга Узорова)

Читать отрывок

Купить офлайн

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

В наличии в 181 магазине. Смотреть на карте

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

Одно из условий успешного обучения математике — автоматизированные навыки устного счёта. Неспособность к устному счёту ведёт к проблемам с общей успеваемостью. .Как развить способности устного счёта? Больше считать устно. .При устных вычислениях развиваются не только внимание и память, но и смекалка, самостоятельность, гибкость ума, а также автоматизируется быстрота реакции и повышается работоспособность мозга. .В этой книге отрабатываются приёмы сложения и вычитания в пределах 100. Разнообразие формулировок и видов заданий позволит не только отработать до автоматизма счёт, но и научить ребёнка искать и находить рациональные пути решения примеров и задач. .Ответы в конце книги и подробные методические рекомендации на второй и третьей сторонках обложки помогут эффективно организовать работу в классе и дома и будут полезны учителям и родителям. .Книга предназначена для коллективной и индивидуальной работы на уроке и самостоятельных занятий дома. .

Описание

Характеристики

Одно из условий успешного обучения математике — автоматизированные навыки устного счёта. Неспособность к устному счёту ведёт к проблемам с общей успеваемостью. .Как развить способности устного счёта? Больше считать устно. .При устных вычислениях развиваются не только внимание и память, но и смекалка, самостоятельность, гибкость ума, а также автоматизируется быстрота реакции и повышается работоспособность мозга. .В этой книге отрабатываются приёмы сложения и вычитания в пределах 100.

Разнообразие формулировок и видов заданий позволит не только отработать до автоматизма счёт, но и научить ребёнка искать и находить рациональные пути решения примеров и задач. .Ответы в конце книги и подробные методические рекомендации на второй и третьей сторонках обложки помогут эффективно организовать работу в классе и дома и будут полезны учителям и родителям. .Книга предназначена для коллективной и индивидуальной работы на уроке и самостоятельных занятий дома. .

АСТ

На товар пока нет отзывов

Поделитесь своим мнением раньше всех

Как получить бонусы за отзыв о товаре

1

Сделайте заказ в интернет-магазине

2

Напишите развёрнутый отзыв от 300 символов только на то, что вы купили

3

Дождитесь, пока отзыв опубликуют.

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Книга «3000 примеров по математике с ответами и методическими рекомендациями. 2 класс. Устный счет. Сложение и вычитание в пределах 100» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене. Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом другом регионе России, вы можете оформить заказ на книгу Елена Нефёдова, Ольга Узорова «3000 примеров по математике с ответами и методическими рекомендациями.

2 класс. Устный счет. Сложение и вычитание в пределах 100» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.

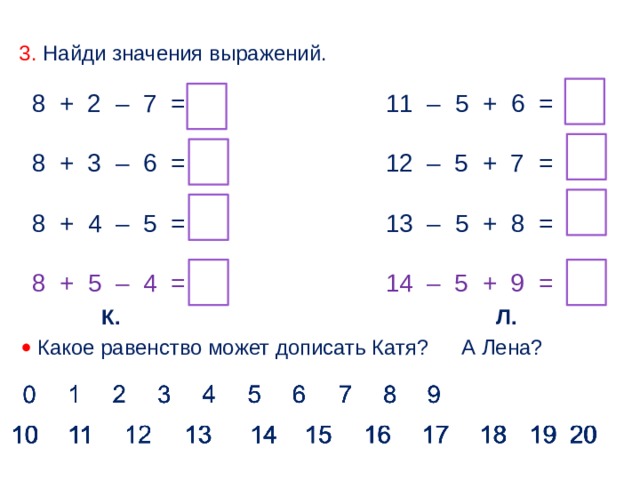
Урок по математике «Сложение и вычитание в пределах 100 без перехода через десяток» 2 класс

 

 

 

 

 

 

 

Урок по математике

«Сложение и вычитание в пределах 100 без перехода через десяток»

 

 

 

 

 

 

 

 

 

Виноградова Светлана Владимировна

учитель начальных классов

 

 

 

 

2022

 

Тема: «Сложение и вычитание чисел без перехода через десяток в столбик»

I.                   Пояснительная записка.

Недостаточно обладать мудростью, нужно уметь пользоваться ею.

(Цицерон)

Математика является одной из самых значимых дисциплин, которая является необходимой в жизни каждого человека. Математика, как учебный предмет содержит необходимые предпосылки для развития познавательных способностей учащихся, она формирует и корригирует такие формы мышления, как синтез, сравнение, анализ, развивает способность к обобщению, к конкретизации, создает условия для коррекции памяти, концентрации внимания, развития наблюдательности.  

Умения и навыки уметь проводить основные арифметические действия (сложение, вычитание) являются основополагающими не только в начальной школе, но и в целом курсе обучения математики в школе, институте.

Целью выбранного урока является закрепление и совершенствование вычислительных навыков письменного приёма сложения и вычитания в столбик без перехода через десяток

Основными задачами урока я ставлю закрепление устных и письменных приемов сложения и вычитания в столбик без перехода через десяток; вырабатывание навыков решения задач разных видов на сложение и вычитание; развитие математической речи, наблюдательности, памяти, логического мышления, воображения; воспитание активности, уважения друг к другу, дисциплины, самостоятельности.

II. Разработка урока.

Тема урока: Сложение и вычитание чисел без перехода через десяток в столбик.

Тип урока: урок закрепления знаний и умений (обобщения и систематизации знаний).

Цель урока: закреплять умения устного и письменного сложения и вычитания чисел без перехода через десяток в столбик; совершенствовать умение решать простые и составные задачи; формирование и развитие ценностного отношения обучающихся к совместной учебной деятельности.

Задачи урока:

1. Повторять и закреплять устный и письменный приемы алгоритма сложения и вычитания чисел без перехода через десяток в столбик;

2. Закреплять знания табличных случаев умножения и деления;

3. Вырабатывать навыки решения задач разных видов на сложение и вычитание;

4.  Развивать вычислительные навыки, логическое мышление, математическую речь.

5.  Формировать навыки самоконтроля, умение работать в паре и группе.

УУД:

Предметные:

— знать алгоритм сложения двузначных чисел вычитания без перехода через десяток в столбик;

— уметь выполнять устные и письменные приемы сложения и вычитания без перехода через десяток в столбик;

— решать задачи, соотносить текст задачи с ее краткой записью; 

— использовать приемы сложения, вычитания, умножения, деления для выполнения математических заданий.

Личностные:

— принимают и осваивают социальную роль обучающегося;

— развитие навыков сотрудничества с одноклассниками и учителем;

— развивают учебно-познавательный интерес к применению раннее полученных знаний по теме сложения и вычитания без перехода через десяток в столбик;

— умение признавать собственные ошибки;

— умение оценивать трудность предлагаемого задания;

— восприятие математики как части общечеловеческой культуры.

Метапредметные:

Познавательные: 

 — умение анализировать объекты с выделением существенных признаков;

 — умение ориентироваться в своей системе знаний и осознавать необходимость применения знания;

— осуществлять поиск необходимой информации для выполнения учебных заданий, находить ответы на вопросы, используя свой жизненный опыт, учебник;

— выделения существенных признаков и их синтеза;

— осознанно и произвольно строить речевое высказывание в устной форме.

Коммуникативные:

— умение слушать собеседника и вести диалог,

— высказывать свою точку зрения;

— умение работать в сотрудничестве: ученик-учитель, ученик-ученик, работать в паре;

— задавать вопросы, необходимые для организации собственной деятельности.

Регулятивные: 

— умение принимать и сохранять учебную задачу;

— умение контролировать и оценивать свои действия;

— умение провести рефлексию своих действий на уроке. 

Межпредметные связи: русский язык, окружающий мир

Ресурсы:

— основные Учебник Г.В. Дорофеева, Т.Н. Миракова Математика 2 класс, Рабочая тетрадь Г.В. Дорофеева, Т.Н. Миракова, Т.Б. Бука Математика 2 класс.

— дополнительные: методические пособия.

Оборудование:

Учебник, рабочая печатная тетрадь, рабочая тетрадь, наборные цифры, предметные картинки, карточки с заданием, геометрические фигуры.

Формы организации деятельности обучающихся:

Фронтальная, работа в группах, индивидуальная, дифференцированная работа, работа в парах, работа по рядам, творческая работа с задачей.

Структура урока:

1. Организационный этап. (1 мин)

2. Этап актуализация опорных знаний и способов действий. (7 мин)

3. Этап повторение и закрепление знаний изученного материала. (7 мин)

4. Этап организация контроля и самоконтроля (взаимоконтроля). (25мин)

5. Рефлексивно-оценочный этап. (4мин)

6. Домашнее задание (1мин)

Ход урока:

I. Организационный этап.

Прозвенел звонок для нас!

Встали все у парт красиво,

Поздоровались учтиво,

Тихо сели, спинки прямо.

Все легонечко вздохнем.

Урок математики начнем!

Присаживаемся, вспомните, как правильно сидеть за партой!

II. Этап актуализация знаний.

Ребята на уроках математики мы с Вами учимся считать и решать задачи, а зачем нам это надо? Знания, которые мы получаем на уроках нужны ли нам вне школы?

Итак, сегодня нам с Вами очень понадобятся знания, полученные на предыдущих уроках, поэтому соберитесь и включите свой «умный компьютер».

Но для начала откроем рабочую тетрадь и запишем сегодняшнюю дату: 14 марта и классная работа. Не забываем, что от предыдущей работы отступаем 4 клеточки вниз. В словах «классная работа» какие орфограммы встречаются? (словарные, удвоенный согласный, безударная гласная в корне, начало предложения, конец предложения)

Что можете сказать про число 14 (двухзначное, четное, состоит из 1 д 4 ед).

Минутка чистописания.

На доске у меня записаны числа:

5,10,15, ….

Найдите закономерность и запишите следующее число (20).

Обратите на написание цифры 2 и 0 (плакат «Пиши цифры правильно»).

Устный счет.

Математический диктант:

ответы

1) Назовите число, которое больше 24, но меньше 26.

(25)

2) Найдите сумму слагаемых 6 и 4, запиши.

(10)

3) Найдите разность чисел 25 и 4.

(21)

4) Первый множитель 2, второй множитель 4. Найдите произведение.

(4)

5)Частное равно 3, а делимое 9. Найти делитель.

(3)

Параллельно 2 учащихся решают примеры у доски в столбик.

36+12= 34-14= 54-2=

37-5=  32-30=  36+42=

Проверку осуществляют учащиеся класса.

Подведение мини итога.  

Какое задание вызвало затруднение в математическом диктанте?

Какие знания (правила) использовали ученики при решении выражений у доски?

III. Этап повторение и закрепление знаний изученного материала

Постановка учебной задачи.

Сейчас мы с вами побудем и ученикам, и учителями. У вас у каждого карточка с равенствами, которые надо решить.

Разрезные карточки

12+14= 31+17= 22-11=	78-26= 56+22= 23-12=	26+31= 57-22= 84+14=
27+52= 13+12= 18-16=	88+11= 34+21= 27-25=	45+23= 89-16= 22+24=

 

47+22= 89-16= 13+12=	36+33= 76+11= 24-21=	56-23= 24+12= 37-13=
87-65= 34+11= 12+14=	96-32= 23+35= 14+12=	56-23= 42+21= 14+15=
67-23= 12+16= 95-13=	99-66= 15+13= 45-23=	48-13= 11+13= 47+21=

Затем поменяйтесь карточками. Возьмите простой карандаш и проверьте работу соседа, если решено правильно поставьте +, если нет -.

Ребята, скажите, с какими цифрами вы сейчас работали? (двузначные)

Какие задачи поставим перед собой сегодня на уроке? (будем продолжать учиться складывать двузначные числа)

Что повторим? (алгоритм сложения двузначных чисел)

Какие умения закрепим? (продолжим закреплять алгоритм решения сложения в столбик, применение алгоритма при решении примеров и задач).

Откройте учебник на стр. 27 и повторите правило. (При выполнении сложения и вычитания столбиком десятки пишутся под десятками, а единицы – под единицами)

IV. Этап организация контроля и самоконтроля (взаимоконтроля)

На доске записать:

25 + 14

Подскажите, каким способом мы еще можем записать это равенство?

(в столбик)

К доске выходит ученик и составляет этот пример в столбик на доске из наборных цифр

25 +     14     39

Напомните мне алгоритм (правило) письменного сложения двузначных чисел в столбик без перехода через десяток.

У доски ученик отвечает:

1. читаю выражение

2. пишу десятки под десятками, единицы под единицами

3. складываю единицы

4. складываю десятки

5. читаю ответ

Не забывайте, что каждая цифра имеет свою клеточку, десятки-слева, единицы-справа.

Всегда начинаем считать? (с единиц)

Учебник стр.27 №2 (1 строка)

Запишите в столбик и решите эти выражения в тетради.

37+21=         56+23=                  82+15=               45=20=

На доске ученики составляют данные выражения из наборных цифр и решают, класс сверяет свой ответ в тетради с ответом на доске.

Проверьте свои ответы, если все правильно на полях поставьте +, если нет — исправьте.

На доске записываю:

28-15=

Чем отличается это равенство от предыдущих? (действие вычитание)

Как мы вычитаем двузначные числа в столбик без перехода через десяток? (повторяем алгоритм действия вычитания в столбик)

1. читаю выражение

2. пишу десятки под десятками, единицы под единицами

3. вычитаю единицы

4. вычитаю десятки

5. читаю ответ

У доски ученик составляет пример в столбик из наборных цифр

28 —    15    13

Учебник стр.27 №2 (2 строка)

Запишите в столбик и решите эти выражения в тетради.

64-32=      49-17=      56-30=      87-83=

На доске ученики составляют данные выражения из наборных цифр и решают, класс сверяет свой ответ в тетради с ответом на доске.

Проверьте свои ответы, если все правильно на полях поставьте +, если нет — исправьте.

Физкультминутка

А теперь немного отдохнем.

И спортивную минутку проведем:

В ладошки мы похлопаем

И чуть-чуть потопаем.

Раз – присели, два – привстали,

Три – нагнулись и достали

Правой ручкой башмачок,

Левой ручкой – потолок.

И еще разок присядем!

А теперь на место сядем.

Мы устали чуточку,

Отдохнем минуточку.

Молодцы, присаживаемся, продолжим урок!

Мне нужны два помощника. Ознакомьтесь с заданием на карточках (карточки с задачами).

Карточки с задачами:

Прочитай, устно решите. Прочитай ребятам задачу. Выслушай ответ учеников. Правильно ответили ребята?   Десять пингвинов катались на льдине, Трое на санках, Один на коньках. Сколько пингвинов осталось кататься, Если четыре полезли купаться?

Прочитай, устно решите. Прочитай ребятам задачу. Выслушай ответ учеников. Правильно ответили ребята?   ·         У Кузьмы в руках корзина, В ней лежат три апельсина, Десять слив и две хурмы. Сколько фруктов у Кузьмы?

А пока ребята готовятся, мы не будем терять время и откроем печатную тетрадь на стр. 51 номер 6. 

Задача: В корзину сначала положили 20 картофелин, а потом ещё 36 картофелин. Для приготовления супа взяли 4 картофелины. Сколько картофелин осталось в корзине?

Прочитайте самостоятельно задачу.

Мы можем сразу ответить на вопрос задачи? (нет)

Это задача простая или составная? (составная)

Что нам известно? (что в корзине было 20 и 36 картофелин, а 4 картофелины взяли для супа)

Что надо найти? (сколько осталось картофелин)

Какое первое действие, что узнаем? (сложение, сколько было всего картофелин)

Следующее действие, что мы найдем? (вычитание, сколько осталось картофелин в корзине)

Мы ответили на вопрос задачи? (Ответили на вопрос)

Запишите решение и ответ:

1)20+36=56(к) — было.

2)56-4=52(к)

Ответ: 52 картофелины осталось в корзине.

Сколько картофелин осталось в корзине? (52 картофелины)

Если у вас такой же ответ, то поставьте + рядом с решением задачи.

Физкультминутка (зарядка для глаз)

Закройте глаза

Раз – налево, два – направо, 
Три – наверх, четыре — вниз. 
А теперь по кругу смотрим, 
Чтобы лучше видеть мир. 
Взгляд направим ближе, дальше, 
Тренируя мышцу глаз. 
Видеть скоро будем лучше, 
Убедитесь вы сейчас! 

Открываем глазки

Подведение мини итога.

Сейчас мы с вами должны решить устно задачи, которые предлагают нам Миша и Маша (задачи в стихах на карточках, розданных учащимся)

Ученики зачитывают задачу.  

Устное решение задач:

1.     (10+3+1)-4=10 пингвинов остались кататься.

2.     3+10+2=15 фруктов у Кузьмы.

Творческая работа с задачей в группе (геометрический материал)

Быстро ответившие ребята (или по желанию учеников) (3 чел-ка) получают задание на карточке (задание для творческой работы) раздаточным материалом (3 прямоугольника, 3 линейки, 3 карандаша, 3 ножниц).

Карточка задание для творческой работы:

Прочитайте внимательно задание. Выполните задание с помощью линейки, карандаша и ножниц. Можете попробовать сначала на белом прямоугольнике   Крышка стола имеет форму прямоугольника. Отпилите части так, чтобы получился треугольник, четырехугольник и пятиугольник

Ответ:  

 

 

 

Самостоятельная работа.

Мы тоже не будем скучать, в рабочей тетради выполните самостоятельно задание номер 7, стр.53 (многоугольник, изображенный на рисунке, разделили на треугольники, проводя отрезки и не добавляя новых вершин. Сколько получилось треугольников? Раскрась их разным цветом). Ответ: 17 треугольников.

Подведение мини итога.

Ребятам надо было распилить стол, чтоб получились треугольник, четырёхугольник и пятиугольник. Покажите свой результат.

Трудное было задание или нет? Какую отметку поставим ребятам за выполнение этого задания?

Слава, Юния, Тимофей покажите, как вы выполнили свое задание в печатной тетради. Кто не справился с этим заданием, поднимите руку, и ребята помогут вам найти и исправить ошибку.

V. Рефлексивно-оценочный этап.

Ребята какую тему мы сегодня повторяли и закрепляли?

Повторите алгоритм сложении и вычитании двухзначных чисел в столбик?

Трудно было на уроке, покажите жестом (большой палец руки вверх — легко, вниз- трудно)? С каким заданием было сложно справиться?

А теперь посчитайте слои плюсики в рабочей и печатной тетради и подумайте, какую отметку вы бы себе поставили за урок, покажите на пальцах?

Выставляю отметки в журнал.

VI. Домашнее задание

Печатная тетрадь стр. 53 № 4, № 6, задание на карточках (записать и решить в рабочей тетради).

 

Карточки разрезные для выполнения домашней работы:

12+14= 31+17= 22-11=	78-26= 56+22= 23-12=	26+31= 57-22= 84+14=
27+52= 13+12= 18-16=	88+11= 34+21= 27-25=	45+23= 89-16= 22+24=
47+22= 89-16= 13+12=	36+33= 76+11= 24-21=	56-23= 24+12= 37-13=
87-65= 34+11= 12+14=	96-32= 23+35= 14+12=	56-23= 42+21= 14+15=
67-23= 12+16= 95-13=	99-66= 15+13= 45-23=	48-13= 11+13= 47+21=

III.            Заключение.

В начальной школе на уроках математики дети очень часто воспринимают тему повторения и закрепления сложения и вычитания чисел без перехода через десяток в столбик, как скучный и однообразный урок.

Проводя свой урок математики, я попытались показать, как можно применять различные методы и способы для того, чтобы преподнести информацию по повторению и закреплению знаний как можно более понятно, наглядно, доступно. Попыталась активировать познавательные способности ребят в процессе урока, показывая детям значимость данной темы в повседневной жизни человека. Учащиеся становятся более заинтересованными и внимательными, настраиваются на целенаправленную осмысленную работу по применению имеющихся знаний, умений и навыков в процессе обучения.

В ходе урока, я считаю, учащиеся достигли главных планируемых предметных результатов, таких, как возможность закрепить умение решать примеры на сложение и вычитание чисел в столбик без перехода через десяток, применять алгоритм сложения и вычитания в столбик, закреплять и применять умение правильно читать выражения и находить их значение; решать задачи разных видов.

Таким образом, урок повторения и закрепления по теме сложения и вычитания без перехода через десяток приобрел иной смысл и значение в глазах второклассников, становясь разнообразным и увлекательным, и имеющим важное значение, не только для дальнейшего обучения, но и для применения ими своих знаний в повседневной жизни.

Что такое вычесть? Определение, метод, примеры, факты

Вычитание: Введение

Предположим, мы покупаем мороженое на определенную сумму денег, скажем, $\$140$, и отдаем $\$200$ кассиру. Теперь кассир возвращает лишнюю сумму, выполняя вычитание, например, 200 – 140 = 60 долл. США. Тогда кассир вернет $\$60$.

Что именно здесь происходит?

Ответ на этот вопрос — вычитание.

Что такое вычитание в математике?

Вычитание — одно из четырех основных арифметических действий в математике. Остальные три — сложение, умножение и деление.

Мы можем наблюдать применение вычитания в нашей повседневной жизни в различных ситуациях.

Например, если у нас есть 3 конфеты, и наш друг просит у нас 1 конфету, сколько конфет у нас останется? Проще говоря,

3 долл. США – 1 = 2 

долл. Давайте разберемся с концепцией на следующем примере с яблоками.

В приведенном выше примере, если у Гарри есть 6 яблок, и он дает 3 яблока Джиму, сколько яблок останется у него?

Мы можем вычислить это, вычитая 3 из 6:

$6 − 3 = 3$

У Гарри осталось 3 яблока.

Родственные игры

Определение вычитания

Операция или процесс нахождения разницы между двумя числами или величинами называется вычитанием. Вычитание числа из другого числа также называется «вычитанием одного числа из другого». В некоторых случаях мы используем вычитание при совершении платежей, переводе денег нашим друзьям и во многих других случаях.

Связанные рабочие листы

Символ вычитания

В математике мы обычно использовали разные символы для разных операторов. У нас есть такие символы, как $+, −, /, *$ и многие другие. Символ вычитания $»−»$ — один из самых важных математических символов, которые мы используем. В предыдущем разделе мы читали о вычитании двух чисел 6 и 3. Если мы наблюдаем это выражение: $(6 − 3 = 3)$, символ $(−)$ между двумя числами обозначает вычитание. Этот символ также известен как знак минус $(−)$.

Формула операции вычитания

Когда мы вычитаем два числа, мы обычно используем некоторые термины, которые используются в выражении вычитания:

Уменьшаемое : Уменьшаемое число — это число, из которого вычитается другое число.

Вычитаемое : Вычитаемое — это число, которое нужно вычесть из уменьшаемого.

Разность : Разность – это окончательный результат после вычитания вычитаемого из уменьшаемого.

Формула вычитания написана как

Minuend $ — долл. США. =$ Вычитаемое

$4 =$ Разность

Что такое минус в математике?

Минус — это знак или символ, который представлен горизонтальной линией.

Мы используем минус в математике для множественных представлений.

Операция вычитания

Минус представляет собой арифметическую операцию вычитания между двумя числами. Мы используем знак минус для обозначения вычитания, уменьшения на, удаления и т. д. 

Например,  

Знак минус также означает, насколько одно значение больше другого.

Например, у Дарби есть 8 имбирных пряников, а у Оливии 3 имбирных пряника.

У Дарби больше имбирных пряников на $(8 − 3) = 5$

Для представления отрицательных целых чисел

Целые числа — это числа, которые не представлены в десятичной или дробной форме и включают положительные и отрицательные числа наряду с 0. Мы используем минус знак для представления отрицательных целых чисел, то есть целых чисел, меньших нуля (без дробей). 9{\circ} \text{C}$

Для представления противоположных направлений

Мы также используем знак минус для представления отрицательного направления на миллиметровой бумаге, чтобы показать координаты.

График также движется в отрицательном направлении.

1. В первом квадранте координаты имеют вид $(x,y)$.
2. Во втором квадранте координаты имеют вид $(−x,y)$.
3. В третьем квадранте координаты имеют вид $(−x,−y)$.
4. В четвертом квадранте координаты имеют вид $(x,−y)$.

• Умножение двух отрицательных чисел дает положительное число.

Отрицательное $\times$ Отрицательное  $=$ Положительное

Например, $(− 5) \times (− 15) = + 75$

• Умножение отрицательного числа на положительное число дает отрицательное число.

Отрицательный $\times$ Положительный $=$ Отрицательный

Например, $(− 5) \times (15) = − 75$

• Добавление отрицательного числа к отрицательному числу всегда дает отрицательное число.

Отрицательное $+$ Отрицательное $=$ Отрицательное

Например, $(− 3) + (− 4) = (− 7)$

• Вычитание положительного числа из отрицательного числа будет всегда давайте отрицательное число.

Если мы вычтем положительное число из отрицательного числа, мы начнем с отрицательного числа и будем считать в обратном порядке.

Отрицательный $−$ Положительный $=$ Отрицательный

Например: Скажем, у нас есть задача $(− 2) − 3$.

Используя числовую прямую, начнем с $− 3$.

Теперь сосчитайте назад 3 единицы. Итак, продолжая отсчитывать три пробела от $− 2$ на числовой прямой, мы получаем

Ответ: $(− 2) − 3 = − 5$.

• Вычитание отрицательного числа из отрицательного числа

Знак минус, за которым следует знак минус, превращает два знака в знак плюс. Таким образом, вместо вычитания минуса вы добавляете плюс. Ответ может быть как положительным, так и отрицательным, в зависимости от величины чисел.

Отрицательное $−$ Отрицательное $=$ Отрицательное $+$ Положительное

По сути, $− (− 5)$ становится $+ 5$, а затем вы складываете числа.

Например, у нас есть $(− 2) − (− 5)$. Мы можем прочитать это как «минус два минус минус 5». Мы меняем два отрицательных знака на положительные, поэтому теперь уравнение принимает вид $(− 2) + 5$.

В числовой строке он начинается с $− 2$.

Затем продвигаемся вперед на 5 единиц: $+ 5$.

Ответ: $− 2 − (− 5) = 3$.

• Вычитание отрицательного числа из положительного всегда дает положительное число.

Когда мы вычитаем отрицательное число из положительного числа, мы превращаем знак вычитания, за которым следует отрицательный знак, в знак плюса. Таким образом, вместо вычитания минуса вы добавляете плюс. Таким образом, уравнение превращается в простую задачу на сложение.

Положительный – Отрицательный = Положительный + Положительный

Например, допустим, у нас есть задача $2 − (− 4)$. Это читается как «два минус четыре». $− (− 4)$ превращается в $+ 4$.

На числовой прямой начинаем с 2.

Затем продвигаемся вперед на три единицы: $2 + 4$.

Ответ: $2 − (− 4) = 6$.

Методы вычитания

Существуют различные методы вычитания. В этой статье мы обсудим три из них.

Визуальное представление

Один из методов — использовать диаграмму, показывающую, с чего вы начинаете, что вы забираете и что у вас остается.

Например, у нас есть 5 мячей, теперь друг просит 2 мяча, мы можем легко подсчитать, что у нас осталось 2 мяча, используя концепцию вычитания, изобразив это с помощью диаграммы, как показано ниже: 

Другой способ выполнения вычитания — использование числовой строки.

Вычитание в числовых рядах

Если мы хотим вычислить 5 минус 2, мы начинаем с 5. Поскольку нам нужно вычесть 2, мы делаем 2 шага назад. Наконец, мы видим, что стоим на 3. 

Итак, вот как на числовой прямой вычисляется $5 − 2$.

Это числовое представление выражения.

Метод столбца

Обычно используется метод столбца вычитания, когда мы разделяем числа на единицы, десятки, сотни и т. д. и записываем уменьшаемое над вычитаемым, где все единицы находятся в одном столбце, все десятки в другом столбце и так далее. В этом методе мы всегда начинаем вычитание с единиц и действуем справа налево.

Перегруппировка в математике

Перегруппировка в математике может быть определена как процесс создания/разбиения групп при выполнении таких операций, как сложение и вычитание. Перегруппировать означает переставить группы по значению места для выполнения операции. Мы используем перегруппировку при вычитании, когда цифры в уменьшаемом меньше, чем цифры в том же месте вычитаемого.

Этот процесс называется перегруппировкой, поскольку мы перегруппировываем числа или переставляем их в их позиционное значение для выполнения этого процесса. Когда мы используем перегруппировку при вычитании, это также иногда называют заимствованием.

Вычитание с перегруппировкой

При вычитании мы иногда используем концепцию перегруппировки между числами. Когда числа вычитаются методом столбца и нижняя цифра больше старшей, мы перегруппировываем числа, чтобы иметь возможность вычитать.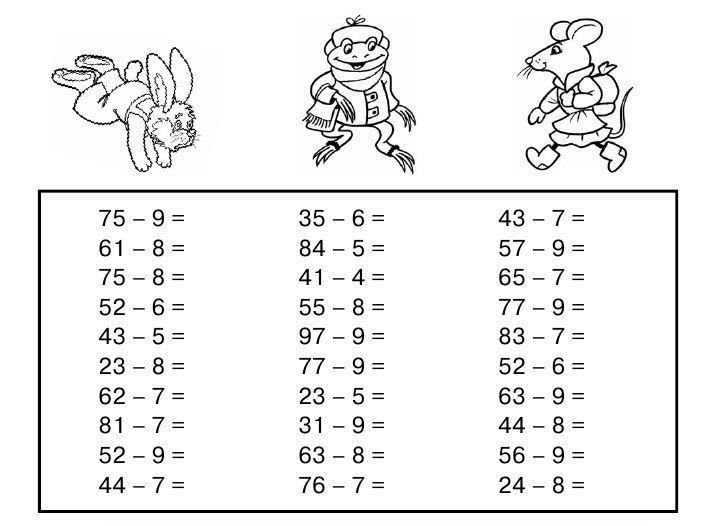

Давайте разберемся с вычитанием, используя этот пример перегруппировки, который включает в себя поиск ответа на выражение $31 − 19$.

Здесь мы сначала вычитаем разряд единицы числа в нижнем слоте с верхним слотом. Если число в нижнем слоте больше, чем число в верхнем слоте, происходит перегруппировка, также называемая заимствованием. В этом случае мы вычитаем единицу из разряда десятков из номера верхнего слота и записываем над ним оставшееся число, то есть из 3 берем 1, делая его 2, который мы написали выше 3, а этот 1, который мы вычли, равен « одолжил» на место единицы, сделав его равным 10 и добавив его к существующему номеру единицы, получив двузначное число. Проще говоря, 10 заимствовано из разряда десятков и добавлено к разряду единиц. В приведенном выше примере к цифре разряда единиц добавляется 10, т. е. 1, и мы пишем 11 над цифрой разряда единиц.

Теперь мы переходим к реальному вычитанию двух чисел. Номер единичного места верхнего слота теперь можно вычесть из номера единичного места нижнего слота, т.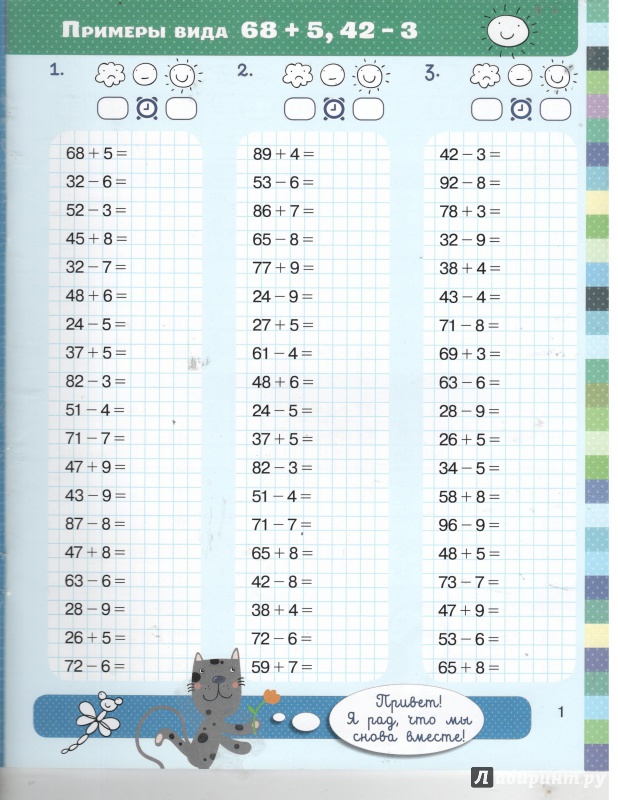 е. номер слота из него, т. Е. $ 2 − 1 $, что дает нам 1, что оставляет нам 12 в качестве окончательного ответа.

Вот как мы перегруппируем сотни и десятки, чтобы вычесть 182 из 427:

Свойства вычитания

Вот несколько важных свойств вычитания в нашей повседневной жизни.

• Коммутативное свойство вычитания:

Коммутативное свойство утверждает, что замена чисел не изменяет результат. Но при вычитании мы не можем получить тот же результат, если подставим уменьшаемое вместо вычитаемого и наоборот. Следовательно, свойство коммутативности невозможно в случае вычитания.

Например, $8 − 5$ не равно $5 − 8$.

• Идентичность свойства вычитания:

Свойство Identity утверждает, что при вычитании «0» из числа результатом является само число.

Например, $5 − 0 = 5$.

• Обратное свойство вычитания (вычитание числа само по себе):

Когда мы вычитаем число из самого себя, результат всегда равен «0».

$\text{A} − \text{A} = 0$

Например, $9 − 9 = 0$.

• Свойство равенства вычитания

В соответствии со свойством, если мы вычтем любое число из обеих частей уравнения, равенство уравнения останется в силе.

Для данного алгебраического уравнения;

$\Rightarrow \times − 3 = 5$

Если мы вычтем одно и то же число с обеих сторон, уравнение останется верным. Здесь мы вычтем 8 с обеих сторон.

$\Rightarrow \times − 3 − 8 = 5 − 8$

$\Rightarrow \times − 11 = − 3$

• Распределительное свойство вычитания

По свойству умножение вычитания чисел равно вычитанию произведения отдельных чисел.

$\text{A} \times (\text{B} — \text{C}) = \text{A} \times \text{B} — \text{A} \times \text{C}$

Например: $3 \times (5 − 2) = 3 \times 3 = 9$ и $3 \times 5 − 3 \times 2 = 15 − 6 = 9$

Заключение

В этой статье мы узнали о вычитании, его определение с примером, используемые для него символы, общие методы, используемые для вычитания. Мы также узнали о знаке минус. Знак минус используется для разных целей. Давайте потренируем наше понимание на нескольких решенных примерах и попрактикуемся в задачах и решенных примерах.

Решенные примеры

1. В футбольном матче команда A забила 5 голов, а команда B забила 9 голов. Какая команда забила больше голов и на сколько?

Решение:

Голы, забитые командой $\text{A}  = 5$;

Голы забиты Командой $\text{B} = 9$

Мы ясно видим, что Команда Б забила больше голов. Чтобы подсчитать количество голов, на которое превзошла команда Б, вычтем 5 из 9. 

$9 − 5 = 4$

Следовательно, команда Б забила на 4 гола больше, чем команда А.

2. У Джеффа 120 ручек. У ее друга Тима на 50 ручек меньше, чем у Джеффа. Сколько ручек у Тима?

Решение:

Как мы знаем, термин «меньше чем» относится к операции вычитания.

Дано,

Джефф $= 120$

Тим $= 120 − 50 = 70$

Следовательно, у Тима 70 ручек.

3. Во время ежегодной охоты за пасхальными яйцами участники нашли в клубе 52 яйца, из которых 14 пасхальных яиц были разбиты. Сможете ли вы узнать точное количество неразбитых яиц?

Решение:

Количество пасхальных яиц, найденных в клубе $= 52$;

Количество разбитых пасхальных яиц $= 14$;

Общее количество неразбитых яиц $=$ ?

Теперь мы вычтем количество разбитых яиц из общего количества яиц.

Таким образом, количество неразбитых яиц равно 38.

4. Джерри собрал 194 рыбы, а Эван собрал 132 рыбы. Кто набрал больше рыбы и на сколько?

Решение:

Количество пойманных Джерри рыб $= 194$;

Количество рыб, пойманных Эваном $= 132$

Это показывает, что Джерри собрал больше рыбы. Давайте вычтем $194 − 132$, чтобы получить разницу.

Таким образом, Джерри собрал на 62 рыбы больше, чем Эван.

5. На сколько 5251 меньше 6556?

Решение:

Из приведенного видно, что 6556 больше 5251 .

Теперь из 6556 вычтите 5251. 9{\circ} \text{F}$ 

8. Какими будут координаты A, если $x = −5$ и $y = − 7$ . В каком квадранте будет лежать А?

Решение: Поскольку известно, что $x = − 5$ и  $y = − 7$, координаты A будут $(− 5, − 7)$. Кроме того, поскольку обе координаты отрицательны, т. е. $( − x, − y)$, A будет лежать в третьем квадранте.

9. Лифт на восемнадцатом этаже. Он спускается на 13 этажей. На каком этаже сейчас лифт?

Решение: Этаж, на котором сейчас стоит лифт $= 18 − 13 = 5$-й этаж

10. Является ли $(4 − 6) = (6 − 4)$ ?

Решение: Найдем решение для обоих.

В левой части $4 − 6 = − 2$ 

Тогда как в правой части $6 − 4 = 2$

Мы ясно видим, что $2 \neq − 2$.

Итак, $(4 − 6)$ не равно $(6 − 4)$.

Практические задачи

1

Вычитая 69 из 108, получаем

35

36

37

39

Правильный ответ: 39
Воспользуемся этапами вычитания с повторным вычитанием.

2

В чем разница между 155 и 56?

100

102

95

99

Правильный ответ: 99
Давайте воспользуемся шагами для вычитания с перегруппировкой.

3

У Дерека 25 яблок, и 18 яблок он отдал своему брату. Сколько яблок осталось у Дерека?

5

6

7

8

Правильный ответ: 7
Здесь мы вычтем 18 из 25, чтобы найти ответ.

4

Посмотрите на данную числовую строку. Какое уравнение будет правильно соответствовать решению на числовой прямой?

$5 + 2 = 7$

$7 − 2 = 5$

$7 − 5 = 2$

$7 + 2 = 9$

Правильный ответ: $7 − 5 = 2$
Начиная с 7, мы сделал 5 шагов назад и приземлился на 2. Итак, изображение показывает уравнение $7 − 5 = 2$.

5

При вычитании 1267 из 1513 мы получаем

250

235

246

264

Правильный ответ: 246
C

Часто задаваемые вопросы

. WATHTRACT называется разница?

Потому что если вы вычтете меньшее число из большего числа, результатом будет разница между двумя числами.

Пример: вычесть 2 из 6

$6 − 2 = 4$

Но число 6 также на 4 больше, чем на 2. Это разница между двумя числами.

У какой другой операции выход меньше, чем вход?

Другая операция, при которой выход меньше, чем вход, — это деление.

Является ли вычитание ассоциативным?

Нет, вычитание не ассоциативно. Давайте рассмотрим это на примере. $10 − (5 − 1) \neq (10 − 5) − 1$

Можем ли мы вычесть большее число из меньшего?

Да, мы можем вычесть большее число из меньшего числа. В результате получится отрицательное число.

С математической точки зрения, почему вычитание путем «подсчета» работает?

Когда мы вычитаем 2 числа, мы можем сделать это двумя способами. Давайте возьмем пример вычитания 5 из 8. Вы можете либо взять 8 и вычесть из него 5, либо начать с 5 и сосчитать до 8. Когда вы начинаете с 5 и считаете до 8, вы делаете это 3 раза: 6, 7 и 8. Итак, 3 будет разницей между 5 и 8.

В чем разница между знаком минус и плюсом?

Знак минус обозначается горизонтальным символом, т. е. $−$, и означает вычитание или удаление. Принимая во внимание, что знак плюс обозначается пересечением горизонтальных и вертикальных линий, то есть $+$, что означает сложение или нахождение суммы.

Верно ли свойство коммутативности для вычитания?

Свойство коммутативности не выполняется для вычитания. Это означает, что для любых двух целых чисел $\text{A} − \text{B} \neq \text{B} − \text{A}$. Например: $3 − 5 = − 2$ и $5 − 3 = 2$ и $− 2 \neq 2$.

Справедливо ли ассоциативное свойство для вычитания?

Ассоциативность не выполняется для вычитания. Это означает для любых трех целых чисел A, B и C.

$\text{A} – (\text{B} – \text{C}) \neq (\text{A} – \text{B} ) – \text{C}$ Например: $(2 – 3) – 5 = – 1 – 5 = – 6$ и $2 – (3 – 5) = 2 + 2$ и $– 6 \neq 4$.

Что такое уменьшаемое и вычитаемое?

В уравнении вычитания уменьшаемое — это наибольшее число, из которого вычитается компонент. Вычитаемое — это термин, обозначающий число, которое вычитается из другого.

Кто открыл знак минус?

Роберт Рекорд ввел современное использование минуса в Великобритании в 1557 году. Первое появление знака минус было дано Йоханнесом Видманном в 1489 году и было найдено в его книге «Торговая арифметика».

Рабочие листы для сложения и вычитания для 2-го класса

• Интерактивные рабочие листы
• Рабочие листы для печати

Easy

Сложение чисел в пределах 100

Easy

Добавление чисел в пределах 1000

. чисел, используя свойства операций и различные мыслительные стратегии. Рабочие листы включают целевые вопросы и реальные задачи с числами до 1000, которые ваш ребенок может научиться решать.

Разнообразие тем

Рабочие листы на сложение и вычитание для 2 класса охватывают многие темы в легкой для понимания форме. Они освещают основные понятия сложения и вычитания одно- и двузначных чисел путем подсчета, сложения и вычитания чисел с перегруппировкой и без нее, математических вычислений в уме и даже с использованием числовой строки.

Хорошо структурированные рабочие листы

Рабочие листы на сложение и вычитание для 2 класса были разработаны специально для детей. Рабочие листы следуют хорошо структурированному образцу с суммами и практическими тестами, расположенными в порядке возрастания сложности и понимания.

Много практики

Онлайн-таблицы на сложение и вычитание для 2 класса содержат задачи на сложение и вычитание, которые должен решить ваш ребенок. Как только ваш ребенок освоит основы этих понятий, он сможет перейти на более высокие уровни и решать различные головоломки и задачи.

Простота обучения

Рабочие листы на сложение и вычитание для 2 класса основаны на простом и увлекательном подходе к изучению основ арифметики. Они предназначены для объяснения сложения и вычитания с использованием примеров, иллюстраций, головоломок и забавных фактов. Красочные визуальные эффекты и изображения еще больше добавляют привлекательности.

Задания для печати

Онлайн-таблицы сложения и вычитания для 2 класса призваны сделать математику в начальной школе интересной для учащихся. У них есть интерактивные действия в виде головоломок, числовых игр, викторин и задач. Рабочие листы также доступны для печати.

Рабочие листы на сложение и вычитание для 2 класса. Объяснение  

Рабочие листы для сложения

В рабочих листах для сложения и вычитания для 2 класса используется метод обучения, основанный на деятельности. Дополнительные рабочие листы для 2 класса охватывают такие темы, как:

• Свойства сложения         
• Сложение номинальных и разрядных значений чисел
• Сложение с перегруппировкой и без нее
• Сложение различных единиц, таких как вес, деньги, расстояния, возраст или просто числа.
• Сложение с 3 числами в столбцах
• Задачи Word 

Инструкции просты для выполнения, поэтому ваш ребенок может заниматься самостоятельно, а к каждому рабочему листу прилагается ключ для ответа. Ваш ребенок найдет математические понятия настолько интересными, что захочет учить их каждый день!

Рабочие листы по вычитанию

Использование рабочих листов по вычитанию может помочь вашему ребенку освоить вычитание во 2-м классе. В рабочих листах есть игры и ресурсы для вычитания второго класса на основе деятельности, созданные специально для них.

Вычитание является важным навыком, поэтому эти рабочие листы являются всеобъемлющими и основаны на приложениях для тщательного изучения. Они охватывают темы, связанные с вычитанием, такие как:

• Вычитание однозначных чисел
• Вычитание двухзначных чисел без перегруппировки
• Вычитание двух цифр с перегруппировкой
• Вычитание трех цифр
• Головоломки и игры на вычитание
• Словесные задачи

Рабочие листы на сложение и вычитание для 2 класса, которые можно распечатать, содержат наглядные пособия и иллюстрации, которые оживляют математику. С помощью этих рабочих листов учащиеся могут укрепить свои арифметические навыки. Есть множество текстовых задач, практических упражнений и головоломок, которые превращают учебное время в игровое!

Сделайте изучение математики вашим ребенком увлекательным и занимательным с помощью рабочих листов для сложения и вычитания для 2 класса для практики и тестов. Они подходят как для программы K-12, так и для домашнего обучения.

Часто задаваемые вопросы

О чем должен быть дополнительный лист для 2-го класса?

Сложение — это математическая операция, которая представлена ​​символом «+», указывающим на объединение двух или более чисел. Проще говоря, рабочие листы второго сложения помогают практиковать сумму двух или более чисел.

О чем задание на вычитание для 2-го класса?

Вычитание — это математическая операция, представленная символом «-», указывающим на уменьшение некоторой величины от заданного числа. Проще говоря, рабочие листы по вычитанию для 2-го класса помогают учащимся практиковать разницу двух чисел.

Почему ученику во втором классе важно выполнять задание на вычитание и сложение?

Вычитание и сложение являются основными математическими операциями, которые помогают учащимся в их повседневной жизни так же, как подсчет изменений или подсчет общей суммы. Обе операции также связаны и обратны друг другу. Рабочий лист сложения и вычитания во втором классе помогает учащемуся понять эту взаимосвязь.

Какие приемы используются при решении заданий на сложение и вычитание для 2 класса?

В рабочих листах для сложения и вычитания во 2-м классе учащиеся будут использовать и изучать вертикальный метод, горизонтальный метод, разрядное значение, модели сложения и вычитания двух чисел.

Что это за лист на сложение и вычитание для 2-го класса?

Рабочий лист на сложение и вычитание — это веселый и интерактивный рабочий лист для учащихся 2-х классов, который содержит вопросы по понятиям сложения и вычитания, решаемые с использованием различных методов.