Сайт vpr-klass.com — впр-класс.ком : гдз, решебник, гиа, егэ, решение задач, задания, варианты, подготовка к экзамену, тесты, презентации.
Error in links file
Сайт vpr-klass.com — впр-класс.ком : гдз, решебник, гиа, егэ, решение задач, задания, варианты, подготовка к экзамену, тесты, презентации. У нас вы найдете много учебных материалов: решебники, ГДЗ, тестовые задания, видео уроки, генераторы задач, решения упражнений гиа и егэ.
| Расскажи друзьям vpr-klass или впр-класс Презентации Детские презентации Презентации по математике Демо-варианты: Математика Русский язык Физика Обществознание Английский язык Информатика История Биология Химия Литература География Математика Русский язык |  com (впр-класс) Последние новости ГИА и ЕГЭ 2017. ЕГЭ по математике. КДР по математике. Математика 1-4 класс. Математика 5-6 класс. Алгебра и геометрия 7-9 класс. Алгебра и геометрия 10-11 класс. ГДЗ, решебники по математике, алгебре, геометрии. Онлайн калькуляторы по математике. Генераторы случайных примеров и задач по математике. Презентации. Другие школьные предметы. Сайт Vpr-klass.com — это учебный-образовательно-познавательный сайт для школьников! Приветствуем на уникальном сайте помощи всем ученикам 1-11 классов. На образовательном ресурсе полно полезной, учебной информации от способов решения заданий по математике до разных генераторов задач по алгебре и онлайн калькуляторов по геометрии, которые облегчат жизнь школьника. В частности, сделан больший уклон на решебники и ГДЗ, ведь правильная домашняя работа — это хорошие оценки и учеба в школе. | Интересно Много разных решений Тесты ГИА онлайн. Видео — ГИА 2013: геометрия Видео — ГИА 2012 Видео — Демо-вариант 2012. Решение Демо-варианта 2013 года (2014 года). Задача №1, Вычислить. Задача №2, Числа и прямая. Задача №3, Сравнение чисел. Задача №4, Уравнения. Задача №5, Графики и формулы. Задача №6, Прогрессии. Задача №8, Неравенства, системы неравенств. Задача №9, Задания по геометрии. Генератор вариантов ГИА 2014 Много разных решений. Онлайн тесты. Видео уроки ЕГЭ по математике. Генератор вариантов ЕГЭ 2014 Книги, справочники Решение демо варианта ЕГЭ по математике 2014 Задания B1, задача. Задания B2, диаграммы. Задания B5, уравнения. Задания B8, производная. Задания B10, вероятность. Видео уроки |
Copyright © 2017 vpr-klass.com | Если какой-либо из материалов нарушает ваши авторские права, просим немедленно связаться с Администрацией!!! Наш e-mail: [email protected] | Правообладателям |
sitemap.
xml
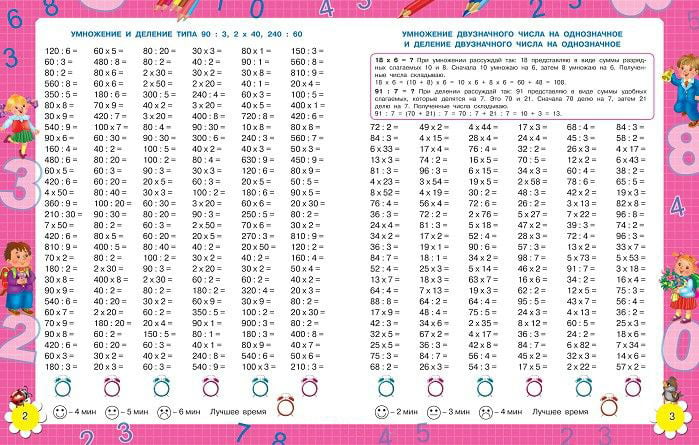
Примеры на умножение и деление. Второе полугодие.
Примеры на умножение и деление. Второе полугодие. Задачи по математике 3 класс
MAT-ZADACHI.RU
Задачи для 3 класса
- Математические диктанты
- Комбинаторные задачи
- Нестандартные задачи
- Множество и его элементы
- Способы задания множеств
- Пустое множество
- Диаграмма Венна
- Диаграмма Венна. Часть 2
- Подмножество
- Множество. Задачи
- Скорость, время, расстояние
Числа от 1 до 100
- Сложение и вычитание
- Буквенные выражения
- Единицы длины
Контрольные работы
- Умножение и деление
- Итоговая контрольная работа
- 1 четверть
- 2 четверть
- Контрольная работа 1
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Контрольная работа 1
- Итоговые контрольные работы 3 класс
- Контрольная работа 1
Тесты.
3 класс.
- Тесты по математике 3 класс
- Табличное умножение и деление чисел
- Особые случаи умножения и деления
Примеры, уравнения
- Примеры
- Уравнения
- Кроссворды
| | Математика 3 класс ->> Примеры Первое полугодиеВторое полугодие |
| 49 : 7 = 7 | 117 : 9 = 13 | 8 * 16 = 128 | 72 : 9 = 8 | 90 : 6 = 15 | 24 : 24 = 1 |
| 23 * 7 = 161 | 6 * 17 = 102 | 171 : 9 = 19 | 11 * 4 = 44 | 48 : 2 = 24 | 13 * 2 = 26 |
| 85 : 5 = 17 | 16 : 8 = 2 | 49 : 7 = 7 | 10 * 22 = 220 | 35 : 7 = 5 | 32 : 8 = 4 |
| 24 * 2 = 48 | 56 : 7 = 8 | 189 : 9 = 21 | 12 * 5 = 60 | 4 * 22 = 88 | 126 : 9 = 14 |
| 28 : 7 = 4 | 198 : 9 = 22 | 3 * 21 = 63 | 26 : 2 = 13 | 21 * 5 = 105 | 17 * 2 = 34 |
| 138 : 6 = 23 | 90 : 5 = 18 | 8 * 16 = 128 | 20 * 10 = 200 | 115 : 5 = 28 | 10 * 17 = 170 |
| 192 : 24 = 8 | 3 * 14 = 42 | 54 : 9 = 6 | 75 : 15 = 5 | 48 : 6 = 8 | 4 * 23 = 92 |
| 18 : 3 = 6 | 198 : 22 = 9 | 9 * 24 = 216 | 12 * 3 = 36 | 7 * 24 = 168 | 12 * 4 = 48 |
| 7 * 15 = 105 | 36 : 12 = 3 | 24 : 3 = 8 | 140 : 20 = 7 | 14 * 8 = 112 | 7 * 16 = 112 |
| 207 : 9 = 23 | 16 : 4 = 4 | 135 : 9 = 15 | 56 : 7 = 8 | 20 * 9 = 180 | 19 * 6 = 114 |
| 55 : 5 = 11 | 72 : 8 = 9 | 30 : 2 = 15 | 12 * 9 = 108 | 6 * 6 = 36 | 99 : 9 = 11 |
| 50 : 5 = 10 | 114 : 6 = 19 | 15 : 5 = 3 | 42 : 3 = 14 | 0 * 25 = 0 | 13 * 4 = 52 |
| 65 : 5 = 13 | 66 : 6 = 11 | 9 * 9 = 81 | 12 * 8 = 96 | 8 * 17 = 136 | 51 : 17 = 3 |
| 144 : 6 = 24 | 11 * 8 = 88 | 24 * 7 = 168 | 95 : 19 = 5 | 207 : 23 = 9 | 5 * 21 = 105 |
| 15 * 4 = 60 | 114 : 19 = 6 | 48 : 24 = 2 | 17 * 9 = 153 | 18 * 6 = 108 | 152 : 8 = 19 |
| 45 : 3 = 15 | 63 : 3 = 21 | 176 : 8 = 22 | 20 * 3 = 60 | 7 * 16 = 112 | 70 : 14 = 5 |
| 91 : 13 = 7 | 9 * 22 = 198 | 18 : 3 = 6 | 32 * 6 = 192 | 110 : 5 = 21 | 41 * 3 = 123 |
| 168 : 7 = 24 | 78 : 13 = 6 | 161 : 7 = 23 | 12 * 17 = 204 | 19 * 4 = 76 | 21 * 8 = 168 |
| 115 : 23 = 5 | 56 * 3 = 168 | 32 * 5 = 160 | 27 * 3 = 81 | 207 : 23 = 9 | 60 : 3 = 20 |
| 144 : 16 = 9 | 85 : 5 = 17 | 48 : 12 = 4 | 13 * 10 = 130 | 52 * 2 = 104 | 31 * 4 = 124 |
| 21 : 3 = 7 | 24 : 12 = 2 | 95 : 19 = 5 | 40 * 2 = 80 | 92 * 2 = 184 | 39 * 4 = 156 |
| 72 * 3 = 216 | 124 : 2 = 62 | 147 : 21 = 7 | 77 : 7 = 11 | 126 : 18 = 7 | 3 * 62 = 186 |
| 102 : 17 = 6 | 72 : 4 = 18 | 12 : 4 = 3 | 45 * 3 = 135 | 19 * 6 = 114 | 31 * 2 = 62 |
| 36 : 3 = 12 | 168 : 21 = 8 | 126 : 21 = 6 | 84 : 12 = 6 | 41 * 5 = 205 | 12 * 9 = 108 |
| 33 * 3 = 99 | 85 : 17 = 5 | 77 : 7 = 11 | 114 : 19 = 6 | 32 : 2 = 16 | 44 * 2 = 88 |
| 96 : 3 = 32 | 21 * 6 = 126 | 32 * 7 = 224 | 14 * 7 = 98 | 133 : 7 = 19 | 92 : 4 = 23 |
| 152 : 8 = 19 | 216 : 9 = 24 | 18 * 11 = 198 | 53 * 3 = 159 | 12 * 9 = 108 | 38 : 2 = 19 |
| 49 * 4 = 196 | 0 * 15 = 0 | 12 * 6 = 72 | 48 : 8 =6 | 195 : 3 = 65 | 21 * 10 = 210 |
| 17 * 4 = 68 | 154 : 7 = 22 | 34 * 2 = 68 | 135 : 15 = 9 | 104 : 13 = 8 | 68 * 2 = 136 |
| 11 * 6 = 66 | 96 : 3 = 32 | 87 : 3 = 29 | 37 * 5 = 185 | 44 * 5 = 220 | 98 * 1 = 98 |
| _______________ | _______________ | _______________ | _______________ | _______________ | _______________ |
Простые задачи
- Задачи на умножение
- Задачи на деление по содержанию и на равные части
- Задачи на 1 действие
Составные задачи
- Задачи на нахождение суммы
- Задачи на нахождение уменьшаемого, вычитаемого, разности
- Задачи на 2 действия
- Задачи на 3 действия
- Задачи на разностное и кратное сравнение
Действия с натуральными числами — Умскул Учебник
На этой странице вы узнаете:- Рассчитаться на раз-два-три! Какие числа мы используем при счете?
- Упрощаем: как разложить число на простые множители?
- Где могут пригодиться НОК и НОД?
Математика невозможна без чисел.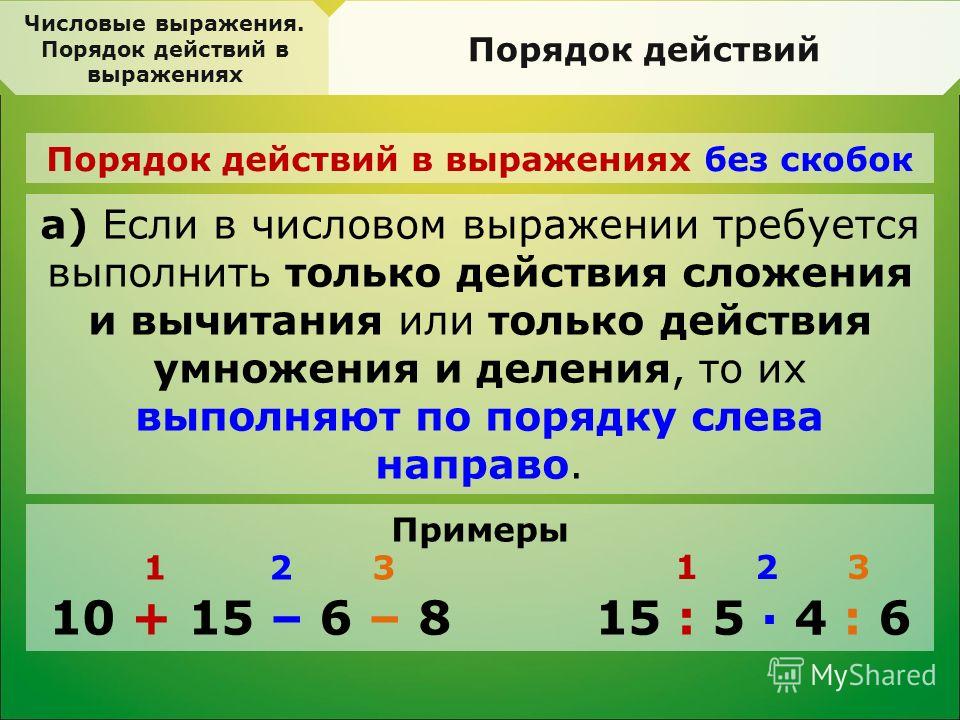
Из них состоят примеры, задачи и модели. Чтобы случайно не наступить на математические грабли, нужно хорошо разбираться в действиях с натуральными числами, их свойствами и особенностями.
Существует несколько множеств чисел: натуральные, целые, рациональные и так далее. Но какие же числа мы можем отнести к натуральным? Может те, в которых нет ГМО, консервантов и красителей?
Натуральные числа – это числа, употребляемые при счете.
Натуральные числа начинаются с 1 и образуются путем сложения некоторого количества единиц. Примерами натуральных чисел могут служить 1, 2, 3, 10, 1320, 130024, 1248640 и т.д.
| Рассчитаться на раз-два-три! Какие числа мы используем при счете? Натуральные числа – это числа, употребляемые при счете. Они начинаются с единицы. Например, 1, 2, 3, 4, 5, 11, 123, 15964 и так далее. |
Рассмотрим основные действия, которые проводятся с натуральными числами.
Сложение – это арифметическая операция, в результате которой объединяются единицы двух чисел.
Например, 2 + 3 = 5.
2 состоит из двух единиц, 3 состоит из трех единиц, тогда (1 + 1) + (1 + 1 + 1) = 5.
Допустим, вместо наших единиц будут апельсины. У Саши будет 4 апельсина, а у Маши 3 апельсина. Если девочки сложат апельсины в один пакет, то получится 7 апельсинов. Это действие можно записать через сложение как 4 + 3 = 7.
| Сложение можно записать как m + n = p, где m и n — слагаемые, p – сумма. |
1 свойство. Переместительное свойство: a + b = b + a.
Иначе можно сказать, что от перемены слагаемых сумма не меняется.
Например, 1 + 3 = 4 и 3 + 1 = 4. Если бы у Маши оказалось 4 апельсина, а у Саши 3, то вместе у них также останется 7 апельсинов.
2 свойство. Сочетательное свойство: a + (b + c) = (a + b) + c.
При сложении чисел не имеет значения, какие из них складывать в первую очередь: сумма не изменится.
Например, 1 + (2 + 3) = 1 + 5 = 6 и (1 + 2) + 3 = 3 + 3 = 6.
ВычитаниеВычитание – это арифметическое действие, обратное сложению.
Если при сложении мы ищем сумму через слагаемые, то в вычитании можем найти слагаемое через сумму и другое слагаемое. Например, 6 — 2 = 4.
| Вычитание можно записать как p — n = m, p — уменьшаемое, n – вычитаемое, m — разность. |
1 свойство. а — (b + c) = a — b — c.
Если из числа нужно вычесть сумму других двух чисел, то можно вычесть эти числа последовательно.
Например, 10 — (2 + 5) = 10 — 2 — 5 = 3.
2 свойство. (a + b) — c = (a — c) + b.
Если из суммы чисел нужно вычесть другое число, то сначала можно вычесть число из любого слагаемого, а потом сложить получившийся результат и оставшееся число.
Например, (8 + 2) — 3 = (8 — 3) + 2 = 7.
УмножениеУмножение – это действие, в результате которого определенное слагаемое берется несколько раз.
Например, в записи 35 * 3, число 35 берется три раза: 35 + 35 + 35.
| Умножение можно записать как m * n = p, где m и n — множители, p – произведение. |
1 свойство. Переместительное. a * b = b * a.
От перестановки множителей произведение не изменяется.
Например, 3 * 4 = 4 * 3 = 12.
2 свойство. Сочетательное свойство умножения: a * (b * c) = (a * b) * c.
От изменения порядка умножения чисел произведение не меняется.
Например, 34 * (2 * 4) = (34 * 2) * 4 = 272.
3 свойство. Распределительное свойство умножения: a * (b + c) = a * b + a * c.
При умножении числа на сумму, можно умножить это число на каждое слагаемое, а после сложить результаты.
Например, 2 * (59 + 91) = 2 * 59 + 2 * 91 = 300.
ДелениеДеление – это действие, обратное умножению.
Например, 35 : 5 = 7.
| Деление можно записать как m : n = p, где m — делимое, n — делитель, p – частное. |
Следует запомнить, что делить на 0 натуральные числа нельзя.
Однако не всегда получается разделить число нацело, тогда при делении появляется остаток. Например, при делении 36 на 8 получается частное 4 и остаток 4. Иначе эту операцию можно записать так: 36 = 8 * 4 + 4.
| Деление с остатком можно записать как m = n * p + r, где m — делимое, n — делитель, p – частное и r – остаток. |
Существуют признаки делимости, которые помогают сразу определить, делится ли число нацело или нет. Вот некоторые из них:
- Число делится на 2, если последняя цифра его записи четная или ноль.
Например, 1946032 будет делиться на 2, поскольку последняя цифра четная. 1946032 : 2 = 973016.
- Число делится на 3, если сумма его цифр делится на 3.
Число 951 будет делиться на 3, поскольку 9 + 5 + 1 = 15, 15 : 3 = 5. Поэтому 951 : 3 = 317.
- Число делится на 4, если две его последние цифры кратны четырем или ноли.
45216 будет делиться на 4, поскольку 16 кратно 4, тогда 45216 : 4 = 11304. Так же 700 будет кратно 4, поскольку две последние цифры – ноли, тогда 700 : 4 = 175.
- Число делится на 5, если последняя его цифра 0 или 5.
Например, 63795 : 5 = 12759, 25570 : 5 = 5114.
- Число делится на 9, если сумма его цифр делится на 9.
Сумма цифр числа 927 равна 9 + 2 + 7 = 18, то есть кратна 9, поэтому 927 : 9 = 103.
- Число делится на 10, если последняя его цифра – ноль.
Например, 2561470 : 10 = 256147.
Заметим, что при сложении и умножении натуральных чисел всегда получаются натуральные числа, тогда как при вычитании и делении не всегда получаются натуральные числа (результат будет зависеть от конкретного примера). Например, 7 — 14 = -7, где -7 – не натуральное число, 21 : 4 = 5,25, где 5,25 – не натуральное число.
Возведение в степеньВозведение в степень очень похоже на умножение, но чтобы возвести число в степень нужно умножить его на само себя. Сколько раз число будет умножено на само себя, такая степень у него и будет.
Например, 405 = 40 * 40 * 40 * 40 * 40.
| Возведение в степень можно представить как mn = p, где m – основание степени, n – показатель степени. |
Извлечение корня – действие, обратное возведению в степень.
При извлечении корня мы узнаем, в какую степень нужно возвести число, чтобы получилось данное число.
| Извлечение корня можно записать как \(\sqrt[n]{m} = p\), где n – показатель корня, m – подкоренное выражение, p – корень. |
О том, как не запутаться в корнях, смотри статью “Понятие корня”
Подведем итог:
Натуральные числа можно складывать, вычитать, умножать, делить, возводить в степень и извлекать из них корень.
Для понимания дальнейших рассуждений необходимо ввести понятие простого числа.
Простое число – это число, которое делится только на себя и на единицу.
Например, у числа 2 делителями будут только 2 и 1, у числа 17 – 17 и 1, у числа 151 – 151 и 1.
Помимо простых чисел существуют и составные числа – это числа, у которых есть другие делители, кроме 1 и самого себя.
Любое составное число можно разложить на простые множители (причем только одним способом).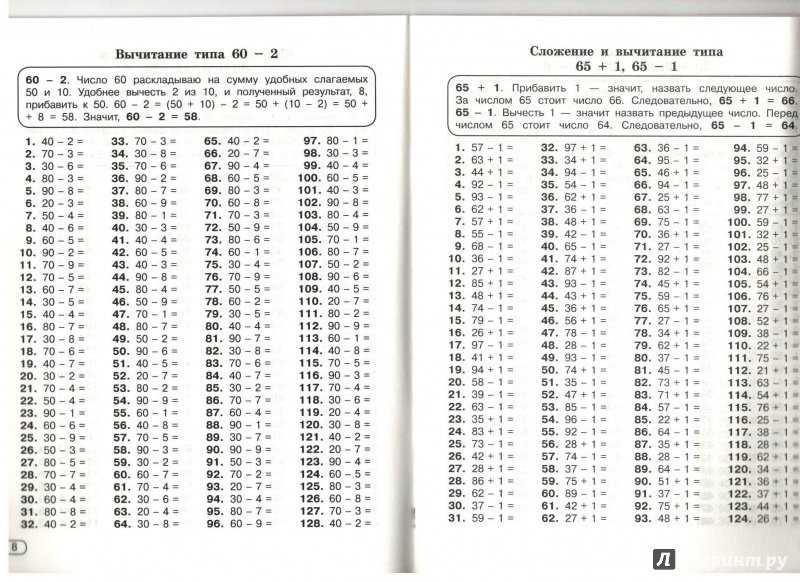
Например, 6 = 2 * 3, где 2 и 3 – простые числа.
Разложение на простые множители – это действие, в результате которого мы можем представить любое составное число в виде произведения нескольких простых множителей.
Умение раскладывать числа на простые множители может пригодиться для анализа чисел и их свойств.
| Упрощаем: как разложить число на простые множители? Любое число состоит из нескольких простых множителей. Разложить число на простые множители значит представить это число в виде произведения нескольких его простых множителей. Например, 18 = 2 * 3 * 3 |
Чтобы разложить число на простые множители, необходимо последовательно делить его на простые множители, начиная с наименьшего возможного.
Для примера разложим число 123896.
Первый подходящий делитель будет равен 2: 123896 = 61948 * 2.
61948 не является простым числом, поэтому продолжаем раскладывать, следующий делитель также равен 2: 123896 = 30974 * 2 * 2.
Продолжаем раскладывать число до тех пор, пока справа не получится произведение только из простых чисел: 123896 = 2 * 2 * 2 * 17 * 911. Для удобства повторяющиеся числа можно записать в виде степеней: 123896 = 23 * 17*911.
Процесс разложения на простые множители можно записать в виде столбика, где слева будут получившиеся в результате деления числа, а справа множители. Для примера разложим число 156:
Разложение множителей удобно применять, если необходимо найти все делители числа. Например, в числе 156 мы можем выделить не только простые множители, но и составные: 2 * 2 * 3 = 12 (156 : 12 = 13) или 2 * 3 = 6 (156 : 6 = 26) и т.д.
| Любой делитель числа равен произведению нескольких его простых множителей. |
У любых двух составных чисел можно найти общие делители, то есть такие числа, на которые будут нацело делиться данные числа.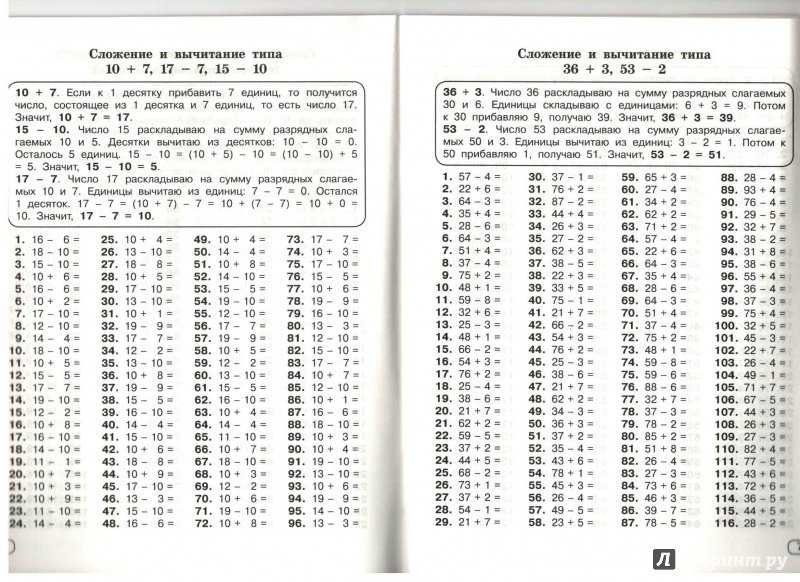
Например, рассмотрим числа 150 и 315.
Разложим их на простые множители: 150 = 2 * 3 * 52, 315 = 32 * 5 * 7.
У числа 150 можно выделить следующие делители: 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150.
У числа 315: 1, 3, 5, 7, 9, 15, 21, 35, 45, 63, 105, 315.
Из них совпадают: 3, 5, 15.
Совпадающие делители будут называться общими, а наибольший из них – наибольшим общим делителем (НОД). Он обозначается D(a,b).
Если НОД чисел a и b равен единице, то это взаимно простые числа. Взаимно простыми числами могут быть и составные, например, 15 и 16.
| Чтобы найти НОД чисел, необходимо: — Каждое из них разложить на простые множители; |
Найдем НОД чисел 45 и 105:
- 45 = 32 * 5
- 105 = 3 * 5 * 7.
Совпадающие простые множители: 3 и 5, тогда D(45, 105) = 3 * 5 = 15.
У любых составных чисел можно найти наименьшее общее кратное (НОК). Это такое число, которое нацело будет делиться на данные числа.
Например, рассмотрим числа 9 и 12. Числа, кратные 9: 9, 18, 27, 36, 45, 54, 63, 72 и т.д. Числа, кратные 12: 12, 24, 36, 48, 60, 72 и т.д. Среди этих чисел есть повторяющиеся 36 и 72, они будут общими кратными для чисел 9 и 12, а меньшее из них – это наименьшее общее кратное данных чисел (НОК). НОК обозначается как К(a, b).
| Чтобы найти НОК чисел, необходимо: — Разложить их на простые множители; |
Например, найдем НОК чисел 184 и 624.
- 184 = 23 * 23
- 624 = 24 * 3 * 13
Тогда К(184, 624) = 24 * 3 * 13 * 23 = 14352.
Наименьшее общее кратное двух взаимно простых чисел будет равно произведению этих чисел.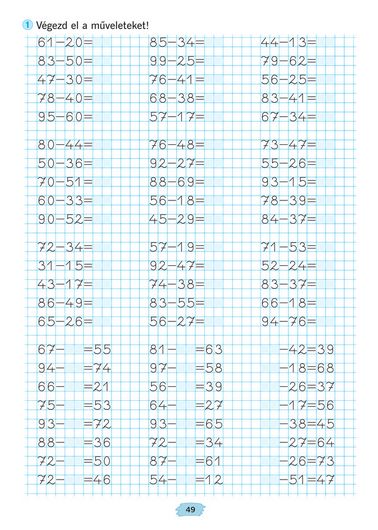
К(а, b) = a * b, где a, b – взаимно простые числа.
Между НОК и НОД существует следующая связь: произведение НОК и НОД некоторых чисел равно произведению этих чисел.
D(a, b) * K(a, b) = a * b
| Где могут пригодиться НОК и НОД? НОК и НОД активно используются в дробях. С помощью НОД можно сразу сократить дробь. Например, D(228, 1650) = 6, следовательно дробь с такими числами сразу можно сократить на 6: \(\frac{228}{1650} = \frac{38}{275}\) С помощью НОК можно привести дроби к общему знаменателю. Например, К(6, 22) = 66, тогда дроби \(\frac{1}{6}\) и \(\frac{1}{22}\) можно привести к общему знаменателю и получить \(\frac{11}{66}\) и \(\frac{3}{66}\). |
Рассмотренные операции являются основными для вычислений в задачах. Применение описанных свойств облегчает и ускоряет счет, что даст дополнительное время на экзамене и сократит количество вычислительных ошибок.
Фактчек- Натуральные числа – это числа, используемые при счете.
- Натуральные числа можно складывать, вычитать, умножать, делить, возводить в степень и извлекать корень,. При сложении и умножении натуральных чисел можно получить только натуральные числа, а при вычитании и делении – нет.
- Существуют простые и составные числа: простые числа делятся только на единицу и само себя; составные числа имеют еще и другие делители. Каждое составное число можно разложить на произведение простых множителей, причем только одним способом.
- У нескольких чисел можно найти наибольший общий делитель и наименьшее общее кратное. Если НОД двух чисел равен 1, то это взаимно простые числа. НОК двух взаимно простых чисел будет равен произведению этих чисел.
- Произведение НОК и НОД некоторых чисел равно произведению этих чисел.
Задание 1.
Какие числа называются натуральными?
- Числа, используемые при счете.
- Все числа, которые существуют.
- Все положительные и отрицательные целые числа.
- Все четные числа.
Задание 2.
Ответь, не вычисляя, какое число делится на 3?
- 113;
- 239;
- 158726;
- 26841.
Задание 3.
Ответь, не вычисляя, какое число делится на 4?
- 7673438;
- 2850;
- 526982;
- 264864.
Задание 4.
Какое число является составным?
- 26;
- 17;
- 3;
- 97.
Задание 5.
Какое число является простым?
- 39;
- 91;
- 59;
- 93.
Ответы: 1. — 1 2. — 4 3. — 4 4. — 1 5. — 3
Конспект урока «Сложение, вычитание, умножение, деление десятичных дробей»
5 класс
Цель деятельности педагога: создать условия для развития умений выполнять вычитание суммы из числа и числа из суммы.
Предметные: моделируют ситуации, иллюстрирующие арифметическое действие и ход его выполнения.
Личностные: проявляют устойчивый и широкий интерес к способам решения познавательных задач, положительное отношение к урокам математики, дают адекватную оценку результатов своей учебной деятельности.
Метапредметные:
– регулятивные: составляют план выполнения задач, решения проблем творческого и поискового характера;
– познавательные: делают предположения об информации, которая нужна для решения предметной учебной задачи;
– коммуникативные: умеют взглянуть на ситуацию с иной позиции и договориться с людьми иных позиций.
Ресурсный материал: плакат для устного счета.
Ход урока
I. Устные упражнения.
Сложение десятичных дробей выполняется по правилам сложения в столбик.
При сложении десятичные дробизаписываются «столбиком», так чтобы одноимённые разряды находились друг под другом без смещения.
При этом запятые должны стоять чётко друг под другом.
Неправильная запись
Правильная запись
Складывают десятичные дроби в столбик как натуральные числа, не обращая внимания на запятые.
В ответе запятую ставим под запятыми в исходных дробях.
Реши:
22,25 + 17,70
75,36 – 29,201
33,29 + 17,001
28,46 + 261,046
Также как и сложение, вычитание десятичных дробей производим по правилам вычитания в столбик натуральных чисел.
Основные правила вычитания десятичных дробей.
Уравниваем количество знаков после запятой.
Записываем десятичные дроби друг под другом так, чтобы запятые были друг под другом.
Выполняем вычитание десятичных дробей, не обращая внимания на запятые, по правилам вычитания в столбик натуральных чисел.
Ставим в ответе запятую под запятыми. Реши:
39,35 – 24,065
24,66 – 13,77
75,79 – 41,091
27,28 – 1,33
Умножение десятичных дробей происходит в три этапа.
Десятичные дроби записывают в столбик и умножают как обыкновенные числа.
Считаем количество знаков после запятой у первой десятичной дроби и у второй. Их количество складываем.
В полученном результате отсчитываем справа налево столько же цифр, сколько получилось их в пункте выше и ставим запятую.
Как умножать десятичные дроби
Пример:
Записываем десятичные дроби в столбик и умножаем их как натуральные числа, не обращая внимания на запятые. То есть 3,11мы рассматриваем как311, а0,01как1.
Получили 311. Теперь считаем количество знаков (цифр) после запятой у обеих дробей. В первой десятичной дроби два знака и во второй — два. Общее количество цифр после запятых: 2 + 2 = 4
Отсчитываем справа налево 4знака (цифры) у полученного числа. В полученном результате цифр меньше, чем нужно отделить запятой.
В таком случае нужно слеваприписать недостающее число нулей.
В таком случае нужно слеваприписать недостающее число нулей.У нас не хватает одной цифры, поэтому приписываем слева один ноль.
Запомните!
При умножении любой десятичной дробина 10; 100; 1000и т.д. запятая в десятичной дроби перемещается вправо на столько знаков, сколько нулей стоит после единицы.
Запомните!
Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001и т.д., надо в этой дроби перенести запятую влево на столько знаков, сколько нулей стоит перед единицей.
Считаем и ноль целых!
Реши:
27,8 • 0,1 0,5 • 0,2
55,89 • 10 0,05 • 2
371 • 0,01 2,5 • 4
71,26 • 100 0,25 • 0,4
Деление десятичной дроби на натуральное число
Для деления десятичной дроби на натуральное число пользуемся следующими правилами.
Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимание на запятую.
Ставим в частном запятую, когда заканчивается деление целой части делимого.
Пример:
0,806 : 31 =
Обратите внимание, что целая часть десятичной дроби (у нас это 0) меньше, чем делитель (31). Поэтому в частном сразу ставим 0 в целой части.
Не забываем записывать ответ в пример:
0,806 : 31 = 0,026
Реши:
0,39 : 13
23,1 : 7
0,231 : 7
Запомните!
Чтобы разделить десятичную дробь на 10, 100, 1000 и т.д., надо перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит после единицы в делителе.
Реши:
310,1 : 10
27,56 : 100
0,75 : 10
IV. Домашнее задание: п. 32 повторить п. 7; карточки
Арифметические действия с числами: сложение, вычитание, умножение, деление
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.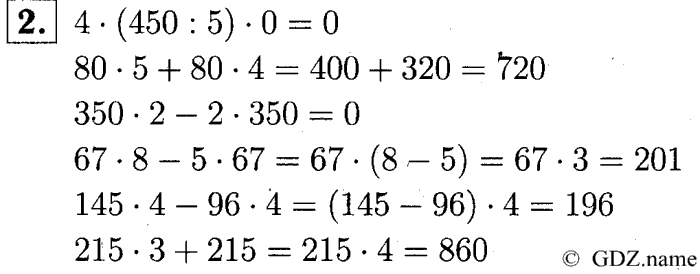
ru Математика Арифметика Основные арифметические действия: определения, примеры
В данной публикации мы рассмотрим определения, общие формулы и примеры 4 основных арифметических (математических) действий с числами: сложения, вычитания, умножения и деления.
- Сложение
- Вычитание
- Умножение
- Деление
Сложение
Сложение – это математическое действие, в результате которого находится сумма.
Сумма (s) чисел a1, a2,… an получается путем их сложения, т.е. s = a1 + a2 + … + an.
- s – сумма;
- a1, a2,… an – слагаемые.
Обозначается сложение специальным знаком “+“ (плюс), а сумма – “Σ“.
Пример: найдем сумму чисел.
1) 3, 5 и 23.
2) 12, 25, 30, 44.
Ответы:
1) 3 + 5 + 23 = 31
2) 12 + 25 + 30 + 44 = 111.
Вычитание
Вычитание чисел – это обратное сложению математическое действие, в результате коротого находится разность (c). Например:
c = a1 – b1 – b2 – … – bn
- c – разность;
- a1 – уменьшаемое;
- b1, b2,… bn – вычитаемые.
Обозначается вычитание специальным знаком “–“ (минус).
Пример: найдем разность чисел.
1) 62 минус 32 и 14.
2) 100 минус 49, 21 и 6.
Ответы:
1) 62 – 32 – 14 = 16.
2) 100 – 49 – 21 – 6 = 24.
Умножение
Умножение – это арифметическое действие, в результате которого вычисляется произведение.
Произведение (p) чисел a1, a2,… an рассчитывается путем их умножения, т.е. p = a1 · a2 · … · an.
Обозначается умножение специальными знаками “·“ или “x“.
Пример: найдем произведение чисел.
1) 3, 10 и 12.
2) 7, 1, 9 и 15.
Ответы:
1) 3 · 10 · 12 = 360.
2) 7 · 1 · 9 · 15 = 945.
Деление
Деление чисел – это обратное умножению действие, в результате коротого вычисляется частное (d). Например:
d = a : b
- d – частное;
- a – делимое;
- b – делитель.
Обозначается деление специальными знаками “:“ или “/“.
Пример: найдем частное чисел.
1) 56 разделим на 8.
2) 100 разделим на 5, затем на 2.
Ответы:
1) 56 : 8 = 7.
2) 100 : 5 : 2 = 10 (100 : 5 = 20, 20 : 2 = 10).
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Математические действия на английском языке
| Работаем с 10 до 21 без выходных!
Работаем с 10 до 21 без выходных! |
| Заказать звонок методиста |
Даже если ваша учеба, работа или сфера деятельности никак не связана с точными науками, простые математические действия на английском знать важно, т.
к. они встречаются не только в академических источниках, но и в фильмах, книгах и в повседневной речи.
Само слово «математика» в английском языке может звучать двумя способами. Первый и самый главный – это термин mathematics [ˌmæθəˈmætɪks]. Такой вариант употребляется, если речь идет о научной дисциплине или предмете изучения.
Mathematics includes the study of many topics. — Математика включает в себя изучение многих тем.
А в разговорной речи более уместен сокращенный вариант – maths [maθs], который принято использовать в Великобритании, а в США широко распространено применение еще более укороченного варианта math [mæθ].
My son has always been good at maths [масс]. — Мой сын всегда был хорош в математике.
Основные математические действия на английском: сложение, вычитание, умножение и деление.В английском языке, как и в русском, существует 4 арифметических действия: сложение (addition), вычитание (subtraction), умножение (multiplication) и деление (division).
Для удобства можно разделить термины, употребляемые в этих действиях, в небольшие таблицы:
сложение (addition)
| складывать | to add |
слагаемое | summand/addend | |
сумма | sum | |
плюс | plus |
2+2=4 – Two plus two equals four.
вычитание (subtraction)
| вычитать | to subtract |
вычитаемое | subtrahend | |
уменьшаемое | minuend | |
разница | difference / remainder | |
минус | minus |
7-2=5 – Seven minus two equals five.
умножение (multiplication)
| умножать на | multiply by |
умножить, разг. | times | |
умножаемое | multiplicand | |
множитель | multiplier | |
произведение | product |
5×3=15 – Five times three is fifteen.
деление (division)
| делить на | divide by |
разделить | divided by | |
делимое | dividend / numerator | |
делитель | divisor / denominator | |
частное | quotient |
15:3=5 — Fifteen divided by three equals five
И термины, которые связаны с результатом действия:
равно | total, equals |
ответ | answer |
Знак равенства | equal mark |
решение | solution |
Часто вместо equals или is equal to говорят is или get:
23 – 3 = 20 — Twenty-three minus three is twenty.
9 ÷ 3 = 3 – 9 divided by 3 is 3.
6 Х 4 = 24 — Multiply 6 by 4 and you’ll get 24.
Дроби на английском языке.Простые дроби (common fractions) состоят из числителя (numerator) и знаменателя (denominator).
3/4 – three fourths.
1/8 – one eighth.
Смешанные дроби или смешанные числа (mixed numeral) включают в себя целое число и дробь, например, 2 ½.
1¼ – one and a quarter.
1½ – one and a half.
1¾ – one and three quarters.
Числитель в дроби выражается количественным числительным, а знаменатель порядковым. Наиболее употребляемые в речи дроби 1/2, 1/3, 1/4 имеют упрощенные названия: половина, треть, четверть:
1/2 – a half, one half.
1/3 – a third, one third.
1/4 – a quarter, one fourth.
В случаях, когда числитель больше одного, к окончанию добавляется -s, так как знаменатель используется во множественном числе (как и в русском: две третьих, три четвертых).
3/4– three fourths.
Существительное, которое определяется простой дробью, используется с предлогом of:
3/4 mile – Three fourths of a mile.
Существительное, определяемое смешанной дробью, используется без предлога, но во множественном числе:
2 ½ miles – Two and a half miles.
Десятичные дроби (decimal fractions, decimals) – дроби, где в английском языке разделителем между целой и дробной частью числа служит точка (point), в отличие от русской запятой. Ноль перед точкой называется zero или в британском варианте nought. Ноль после точки может называться oh (как буква “o”), zero, nought. Если целое число в дроби равно нулю, его часто опускают в речи, начиная говорить сразу с “point”.
1.25 – One point two five.
0.1 – Point one, zero point one.
Целое число читается как обычное количественное числительное, например,
45. 1 – forty five point one – сорок пять целых одна сотая.
А в дробной части каждая цифра читается отдельно тоже как количественное:
2.45 – two point four five (не two point forty five) – две целых сорок пять сотых.
Проценты в английском языкеСотые доли могут выражаться с помощью процентов, тогда используется стандартный значок % и слово percent, всегда использующееся в единственном числе.
1% – One percent.
10% – Ten percent.
17% – Seventeen percent.
Глагол в предложениях с процентами согласуется с существительным, которое употреблено после частицы of:
Единственное число:
The remaining twenty percent of the script has been rewritten — Оставшиеся 20% сценария были переписаны.
Множественное число:
Twenty percent of the students are present — 20% студентов присутствуют.
Возведение в степень в английском.Для обозначения степени используются выражения to the power of five, to the fifth power, raised to the power of five, raised to the fifth power. Вторая и третья степень имеют упрощенные термины “в квадрате” (squared) и “в кубе” (cubed).
32 – Three squared, three to the second power.
33 – Three cubed, three to the third power.
104 – Ten to the fourth power, ten to the power of four.
3024 – Thirty to the power of twenty four.
Квадратный корень называется squareroot:
√25 = 5 – The square root of twenty five is five.
Математические выражения со скобками.Круглые скобки называются parentheses (ед. число parenthesis) или round brackets. Если выражение стоит в скобках, и к нему применяется операция, используется слово quantity.
(2+3)×4=24 – Two plus three quantity times four equals to twenty four.
(3+5)2=64 Three plus five quantity squared is sixty four.
Математические термины из этой статьи можно выучить с помощью PDF-карточек для распечатки.
Что такое коммутативное свойство? — Определения Факты и примеры
Переместительное свойство
Переместительное свойство утверждает, что числа, с которыми мы работаем, могут быть перемещены или заменены местами без изменения ответа. Это свойство справедливо для сложения и умножения, но не для вычитания и деления. Посмотрим.
Приведенные выше примеры ясно показывают, что свойство коммутативности верно для сложения и умножения, но не для вычитания и деления. Итак, если мы поменяем местами числа в операторах вычитания или деления, это изменит всю проблему.
Итак, математически коммутативное свойство сложения и умножения выглядит так:
Коммутативное свойство сложения:
a + b = b + a; где a и b — любые 2 целых числа
Коммутативное свойство умножения:
a × b = b × a; где a и b — любые 2 ненулевых целых числа
Варианты использования коммутативного свойства
- У Майры 6 яблок и 2 персика. У Ким 2 яблока и 6 персиков. У кого больше фруктов?
Даже если у обоих разное количество яблок и персиков, у них одинаковое количество фруктов, потому что 2 + 6 = 6 + 2.
- Сара покупает 3 упаковки булочек. В каждой упаковке по 4 булочки. Мила покупает 4 упаковки булочек, в каждой по 3 булочки. Кто купил больше булочек?
Даже если у обоих разное количество упаковок с булочками и в каждом из них разное количество булочек, они оба купили одинаковое количество булочек, потому что 3 × 4 = 4 × 3,
Решенные примеры по свойству переместимости
Пример 1: Заполните пропущенные числа, используя свойство переместимости.
- _________ + 27 = 27 + 11
- 45 + 89 = 89 + _________
- 84 × ______ = 77 × 84
- 118 × 36 = ________ × 118
. Решение: 292923
Пример 2: Используйте 14 × 15 = 210, чтобы найти 15 × 14.
Решение: Так как 14 × 15 = 210, то 15 × 14 также равно 210. Пример 3: Используйте 827 + 389 = 1,216, чтобы найти 389 + 827. дополнение, 827 + 389= 389 + 827. Поскольку 827 + 389 = 1216, значит, 389 + 827 также равно 1216. Пример 4: Используйте свойство коммутативности сложения, чтобы записать уравнение 3 + 5 + 9 = 17 в другой последовательности слагаемых. Решение: 3 + 9 + 5 = 17 (поскольку 5 + 9 = 9 + 5) 5 + 3 + 9 = 17 (поскольку 3 + 5 = 5 + 3) 5 + 9 + 3 = 17 (потому что 3 + 9 = 9 + 3) Точно так же мы можем переставить слагаемые и написать: 9 + 3 + 5 = 17 9 + 5 + 3 = 17 Пример 4: Бен купил 3 упаковки по 6 ручек в каждой. Миа купила 6 упаковок по 3 ручки в каждой. Они купили одинаковое количество ручек или нет? Решение: Бен купил 3 упаковки по 6 ручек в каждой. Итак, общее количество ручек, которые купил Бен = 3 × 6 Мия купила 6 упаковок по 3 ручки в каждой. Итак, общее количество ручек, которые купил Бен = 6 × 3 По свойству перестановочности умножения 3 × 6 = 6 × 3. Итак, Бен и Миа купили одинаковое количество ручек. Пример 5: У Лизы 78 красных и 6 синих шариков. У Бет есть 6 упаковок по 78 шариков в каждой. У них одинаковое количество шариков? Решение: Так как у Лизы 78 красных и 6 синих шариков. Итак, общее количество шариков у Лизы = 78 + 6 У Бет 6 пакетов по 78 шариков в каждом. Итак, общее количество шариков с Бет = 6 × 78 Очевидно, что сложение и умножение двух чисел дает разные результаты. (Кроме 2 + 2 и 2 × 2. То есть 78 + 6 ≠ 6 × 78 Итак, у Лизы и Бет не одинаковое количество шариков. 8 + 5 = 5 + 8 8 × 5 = 5 × 8 8 + 5 = 8 – 5 8 + 5 = 5 × 8 Правильный ответ: 8 + 5 = 5 + 8 7 × $\frac{1}{7}$ = 1 7 × 1 = 7 7 × 3 = 3 × 7 7 × 0 = 0 Правильный ответ: 7 × 3 = 3 × 7 15 ÷ 3 15 × 3 15 – 3 3 ÷ 15 Правильный ответ: 15 × 3 5, 5 4, 4 5, 4 4, 5 Правильный ответ: 4, 5 Можете ли вы применить свойство коммутативности сложения/умножения к трем числам? Да. По определению коммутативность применяется к 2 числам, но результат остается тем же и для 3 чисел. Это потому, что мы можем применить это свойство к двум числам из 3 в различных комбинациях. Какие операции не следуют свойству коммутативности? Коммутативное свойство не применимо к вычитанию и делению. Что такое ассоциативное свойство сложения (или умножения)? Это свойство указывает, что при сложении (или умножении) трех или более чисел сумма (или произведение) остается одинаковой независимо от группировки слагаемых (или множимых). То есть (a + b) + c = a + (b + c) Для каких операций выполняется свойство ассоциативности? Ассоциативное свойство справедливо для сложения и умножения. Какое распределительное свойство умножения? Под распределительным свойством умножения над сложением мы подразумеваем, что умножение суммы двух или более слагаемых на число даст тот же результат, что и умножение каждого слагаемого по отдельности на число, а затем сложение произведений вместе. То есть a × (b + c) = (a × b) + (a × c), где a, b и c — целые числа. Свойства номераРуководство для учащихся Автор Линдси Гатлин Прочная основа в числовых свойствах помогает создать прочную основу для всех математических концепций. Это пособие для учащихся посвящено положительным и отрицательным числам. Мы обсудим сложение и вычитание положительных и отрицательных чисел, умножение и деление положительных и отрицательных чисел, а также правила для положительных и отрицательных чисел. Это пятая статья в нашей серии «Свойства чисел». Если вы не видели наши первые четыре поста, посмотрите эти ссылки! Множители и простые множители Кратные и наименьшие общие кратные Правила делимости Четные и нечетные числа Каждый день мы работаем и взаимодействуем с положительными числами. Это потому, что есть так много случаев, когда нам приходится считать вещи или выполнять какие-либо важные операции (сложение, вычитание, умножение и деление). Прежде чем мы углубимся в операции с положительными и отрицательными числами, очень важно сначала понять числовую прямую и то, где на числовой прямой находятся различные числа. По мере того, как мы идем влево по числовой прямой, наши числа становятся меньше. Например, -7 < -5 По мере продвижения вправо по числовой прямой наши числа становятся больше. Например, 5 < 7 Число ноль (0) не является ни положительным, ни отрицательным. Итак, когда мы движемся по числовой прямой, прежде чем перейти от отрицательного к положительному или наоборот, мы должны помнить, что нужно считать число ноль. Как только мы привыкнем к числовой прямой и сравниваем различные числа, мы можем попрактиковаться в том, как эти числа взаимодействуют друг с другом. Эти взаимодействия происходят посредством математических операций. Мы можем использовать числовую линейку, чтобы решать задачи на сложение и вычитание. Как правило, когда мы вычитаем, мы двигаемся влево по числовой строке, а когда мы складываем, мы двигаемся вправо по числовой строке. Давайте рассмотрим некоторые взаимодействия с числами и начнем с того, как складывать и вычитать положительные и отрицательные числа. Когда мы складываем или вычитаем положительные и отрицательные числа, мы можем задать себе эти два вопроса. 1. С какого числа мы начинаем на числовой прямой? 2. В каком направлении мы будем двигаться по числовой прямой? Эти вопросы помогают нам понять, с чего начать и что происходит в ходе операции. Давайте рассмотрим некоторые из этих взаимодействий более подробно. Когда мы складываем два положительных числа, сумма этих чисел дает большее положительное число. Например, 5 + 7 = 12 Когда мы складываем вместе два или более положительных числа, наша сумма будет большим положительным значением. Когда мы складываем (или суммируем) два отрицательных числа, ответом будет меньшее отрицательное число. Например, -5 + -7 = -12 Но мы также должны помнить, что эту задачу можно записать несколькими способами. Например, это также может быть записано как эта задача на вычитание ниже. -5 – 7 = -12 Каждый раз, когда мы видим задачу на сложение двух отрицательных чисел, мы можем переписать задачу так, чтобы она больше походила на задачу на вычитание. -5 – 7 = -12 Даже без плюса посередине проблема остается той же. Мы бы решили это, как и любую другую задачу на вычитание. Мы начинаем с -5 на числовой прямой и идем налево семь раз, пока не получим наш ответ -12. Когда мы вычитаем два числа, мы должны уделять больше внимания порядку задачи. Возьмем пример: 7 – 5 = 2 Поскольку первое число 7 больше второго числа 5, результат будет положительным. Мы можем рассмотреть это более внимательно на числовой прямой. вычитание-положительных-отрицательных-чисел-1 Представление в числовой строке, показывающее, как вычитать, 7-5=2 вычитание-положительных-отрицательных-чисел-2 Представление в числовой строке, показывающее, как вычитать, 5-7 = -2 Но если порядок чисел изменить на обратный, мы получим ответ с другим знаком. 5 – 7 = -2 При решении задач на вычитание мы можем задавать себе те же вопросы, что и раньше. 1. С какого числа мы начинаем на числовой прямой? 2. В каком направлении мы будем двигаться по числовой прямой? Во втором случае первое положительное число 5 меньше второго числа 7, что означает, что наш ответ будет отрицательным. (Совет: Эту задачу можно записать и так: 5 + -7 = -2) Для задач с более отрицательными знаками мы должны быть осторожны с нашими операциями и вычислениями. Важным правилом для положительных и отрицательных чисел является , когда мы вычитаем отрицательное число, мы превращаем его в задачу на сложение. Например, -5 – (-7) → -5 + 7 -5 + 7 = 2 Когда мы вычитаем отрицательное число, мы делаем следующее: 1. 2. Заменить знак минус на знак плюс 3. Изменить знак второго числа (сложить наоборот) -7 – (-5) → -7 + 5 -7 + 5 = -2 Когда мы умножаем и делим положительные и отрицательные числа, самое главное — отслеживать количество отрицательных знаков в задаче. Одно из правил умножения и деления положительных и отрицательных чисел состоит в том, что ответ будет положительным, если мы умножим или разделим два отрицательных числа. Давайте рассмотрим несколько задач. Если в задаче на умножение нет отрицательных знаков, мы можем решить ее как обычно. 2 x 5 = 10 4 x 6 = 24 . отрицательное число, произведение будет отрицательным. Например, 2 x -5 = -10 -4 x 6 = -24 Когда мы умножаем и делим, какое число является отрицательным, а какое отрицательным, не имеет значения. Однако ответ или произведение будет отрицательным, если мы умножим одно положительное число на одно отрицательное число. В этом сценарии мы умножаем два отрицательных числа. Как гласит правило, умножение двух отрицательных чисел даст положительное число. -2 x -5 = 10 -4 x -6 = 24 При умножении (и делении) число в произведении одинаково, несмотря ни на что, но мы должны обращать внимание на знак нашего произведения. Мы также можем продвинуть наше первое правило умножения и деления на один шаг дальше: , когда присутствует нечетное количество отрицательных знаков, ответ будет отрицательным. С другой стороны, когда присутствует четное количество отрицательных знаков, ответ будет положительным. Теперь, когда мы рассмотрели несколько задач на умножение с положительными и отрицательными числами, давайте рассмотрим несколько задач на деление. Когда мы делим два положительных числа, мы можем просто разделить, и ответ останется положительным. 10 ÷ 5 = 2 24 ÷ 6 = 4 Независимо от знака фактическая операция остается неизменной. Таким образом, нам нужно только обратить более пристальное внимание на количество присутствующих отрицательных знаков, чтобы узнать знак нашего ответа или частного. Когда мы складывали и вычитали, расположение знака минус играло решающую роль в определении нашего окончательного ответа. Размещение не так важно при делении и умножении, как количество отрицательных чисел. Например, -10 ÷ 5 = -2 10 ÷ -5 = -2 -24 ÷ 6 = -4 Практические задачи
Согласно свойству перестановочности сложения , сумма остается той же при перестановке слагаемых, то есть a + b = b + a. 0005
Согласно коммутативному свойству умножения, произведение остается тем же самым при замене местами множимого и множителя. То есть а × b = b × а.
Коммутативное свойство не выполняется для деления и вычитания.
5 + 4 = 4 + 5
(по коммутативному свойству) Часто задаваемые вопросы
(a × b) × c = a × (b × c), где a, b и c — целые числа. Как складывать, вычитать, умножать и делить положительные и отрицательные числа — Delta Learning
Понимание того, как взаимодействуют числа, может помочь вам предсказать результаты решения проблемы, лучше понять уравнения и проверить проделанную работу. Но не каждое число является положительным. Даже если мы этого не осознаем, отрицательные числа играют важную роль во многих математических темах. Например, в классе отрицательные числа обычно встречаются в функциях, а за пределами класса это обычная тема в финансах. Если вы студент, читающий это, вы должны решить, с какой из них вам больше нравится работать, и постараться, чтобы все задачи выглядели одинаково. Первое число оставить прежним
Аналогично любой другой пример вычитания, мы должны обратить пристальное внимание на порядок проблемы, чтобы сообщить нам наш результат. Если мы изменим порядок, проблема теперь будет такой: При отсутствии отрицательных знаков наш продукт будет положительным. Например,
Положительный номер, умноженное на отрицательное число Например, Например,
4 Этот сценарий будет очень похож на то, что мы видели при умножении двух отрицательных чисел. Мы точно так же делим, но мы должны следить за нашими отрицательными числами и помнить правило, что когда мы разделим два отрицательных числа, ответ будет положительным. Например,
-10 ÷ -5 = 2
-24 ÷ -6 = 4
В задачах на сложение и вычитание помните, с какой позиции мы начинаем на числовой прямой и в каком направлении хотим двигаться.
Когда мы вычитаем отрицательное число, мы сохраняем первое число прежним, меняем минус на знак плюс, а второе число меняем на положительное число.
В задачах на деление и умножение нечетное количество отрицательных чисел даст отрицательный результат.
С другой стороны, четное количество отрицательных чисел даст положительный результат.ВСЕГДА следите за своими отрицательными числами.
числовые свойстваположительные и отрицательные числасложение и вычитание положительных и отрицательных чиселумножение и деление положительных и отрицательных чисел
Линдси Гэтлин
Матрицы – умножение, деление, сложение и вычитание
Перейти к содержимомуУмножение
Умножение
Деление
Матрица представляет собой массив чисел, в котором есть строки и столбцы, которые показывают размер или размеры матриц.
Умножить матрицу на одно число очень просто –
Вычисления выполняются по следующей формуле –
Все мы знаем, что число 2 в этом состоянии является скаляром, поэтому оно известно как скалярное умножение.
Умножение матрицы на другую матрицу
Но для умножения матрицы на другую матрицу нам нужно решить скалярное произведение строк и столбцов, и что это значит? Теперь давайте посмотрим на пример для выработки ответа или решения для строки 1 st и столбца 1 st .
Скалярный продукт — это умножение совпадающих членов и их суммирование —
(1, 2, 3). (7, 9, 10) = 1 * 7 + 2 * 9 + 3 * 10 = 7 + 11 + 30 = 48. 2 и членов, таких как 2 и 9, и 3 и членов, которые являются 3 и 10, а затем, наконец, суммируйте все это.
Хотите решить еще один пример? Тогда вот для 1-й строки и 2-го столбца —
(2, 3, 4). (7, 8 ,9) = 2 * 7 + 3 * 8 + 4 * 9 = 14 + 24 + 36 = 74
Теперь мы можем сделать то же самое для 2 -й ряд и 1-й столбец –
(1, 2, 1). (2, 3, 4) = 1 * 2 + 2 * 3 + 1 * 4 = 2 + 6 + 4 = 12
И тогда для 2 -й строки и 2-го столбца –
(3, 1, 2 ). (1, 2, 3) = 3 * 1 + 1 * 2 + 2 * 3 = 3 + 2 + 6 = 11
Тогда мы окончательно получим результат.
Надеюсь, теперь вы разобрались с методом и решениями?
Дивизия
А что такое деление? На самом деле мы не делим матрицы, так как делаем это таким образом.
X / Y = X * (1/Y) = X * B -1
Где, B обратная означает обратную матрицу B. поэтому здесь нам не нужно делить ее, а умножить на обратную матрицы. Есть несколько специальных способов узнать обратную матрицу.
Для обратной матрицы вам нужно выписать матрицу и идентифицировать матрицу рядом, а также выполнить некоторые операции со строками, чтобы матрица B идентична матрице. Выполняя операции со строками, B затем станет единичной матрицей, а фактическая единичная матрица станет обратной матрице B, поскольку все операции будут выполняться в единичной матрице.
После получения обратной матрицы вам нужно умножить обратную матрицу B на A, что будет делением матриц.
Сложение и вычитание
Прежде всего, давайте выясним, что такое матрица. Матрица может быть добавлена или вычтена из другой матрицы только в том случае, если обе матрицы имеют одинаковые размеры. Для добавления двух матриц просто добавьте записи и получите сумму вместо полученной матрицы.
Давайте решим несколько примеров и разберемся в них глубже –
Пример – 1
[1 2] + [2 -3]
Во-первых, обратите внимание, что обе матрицы являются матрицами 1 * 1, затем мы можем добавить их.
[1 2] + [2 -3]
= [1+2 2+(-3)]
= [3 -1]
Вычитание также является очень простой процедурой с матрицами. Давайте посмотрим на некоторые примеры, чтобы мы могли иметь четкое представление о них.
Пример – 2
[4 5] – [2 1]
Сначала ясно видим, что обе матрицы имеют одинаковую размерность, а затем начинаем вычитать –
[4 5] – [2 1]
= [4-2 5-1]
= [2 4]
Сложение матрицы очень простое и выполняется с каждой записью.
Давайте решим несколько критических примеров, которые дадут лучшее понимание матриц:
Добавьте следующие матрицы
Теперь нам просто нужно добавить эту пару записей, а затем упростить окончательное решение.
Итак, окончательный ответ —
До сих пор вы научились складывать две вещи в матрицах, такие как переменные, числа, уравнения и другие. Но сложение не всегда работает с матрицами.
Оцените приведенную ниже задачу или, если это невозможно, укажите причину.
Хотя матрицы добавляются при каждой записи, нам нужно сложить два числа, например 2 и 2, 1 и 8, затем 3 и 4, 4 и 6. Но что еще мы можем сделать при сложении чисел 6 и 7 и у которых нет прямых чисел в другой матрице? Итак, ответ –
Эти матрицы нельзя складывать, так как они не имеют одинаковых размеров и размеров.
Это всегда так при добавлении матриц, нужны обе матрицы одинакового размера. Если они не одинакового размера, то дополнение не применяется. В нем нет никакой математической логики для сложения неравных матриц.
Вычитание также работает с каждой записью и при тех же условиях. Вычитание матриц, как и сложение, невозможно выполнить, если матрицы имеют разную размерность или размеры. Это касается как сложения, так и вычитания матриц.
Найдите значения x и y для следующих уравнений –
Во-первых, вам нужно легко вычислить левую часть с помощью стороны и входа –
Таким образом, при равенстве матрицы работает с вводом, мы сравниваем эти записи для создания простых уравнений, которые мы можем решить. В таких случаях
X + 6 = 7 и 2y -3 = -5
X = 7 – 6
X = 1
And
2y – 3 = -5
Y = -5 + 3 / 2
Y = -2 / 2
Д = -1
Перейти к началу
Глава 3 Сложение, вычитание, умножение и деление.
ЦЕЛИ
По завершении этой главы учащийся должен уметь:
1. Найдите суммы.
2. Найдите отличия.
3. Проверить вычитание путем сложения.
4. Найдите произведения с помощью таблицы умножения.
5. Используйте пошаговую процедуру поиска продуктов.
6. Проверьте точность произведения умножения.
7. Найдите частные.
8. Найдите остаток.
9. Проверьте точность частного деления.
КЛЮЧЕВЫЕ СЛОВА
дополнение
сумма
вычитание
минусенд
вычитаемое
разница
торговля (заимствование)
умножение
множимое
множитель
товар
подпродукты
подразделение
дивиденд
делитель
частное
остаток
В этой главе четыре самых основных и важных математических
функции — сложение, вычитание, умножение и деление — будут
покрытый. На этих страницах вы не только вернетесь к основам всех
вычисления, но вы также увидите, насколько эти вычисления являются интегральными
к работе общественного питания.
СОВЕТЫ ... Для обеспечения идеальных решений Читаем слова слева направо. Решаем математические задачи работает справа налево.
ДОПОЛНЕНИЕ
Сложение можно считать одной из самых популярных математических функций.
потому что это означает, что происходит увеличение. В любом деловом предприятии,
это желание оператора, чтобы увеличение проявлялось в форме
приятной прибыли.
Сложение – это действие по соединению или объединению вещей или единицы, которые похожи, чтобы получить общее количество. Это общее количество называется суммой. Если у вас есть 6,00 долларов, а вам дали 10,00 долларов, у вас есть всего $16.00. Эту простую задачу на сложение можно записать двумя различные пути. Например:
6,00 $ + 10,00 $ = 16,00 $
Записывается цифрами, расположенными в ряд или строку, это называется
горизонтальное положение. Горизонтальное положение используется редко.
проблема, связанная с большими числами, потому что числа
position затрудняет вычисление ответа.
Эта же задача может быть записана и в том, что называется вертикальное или столбцовое положение.
6,00 $ +10,00/16,00 $
[РИСУНОК 3-1 ОПУЩЕН]
СОВЕТЫ ... Для обеспечения идеальных решений Сложение плюс сложение равно сумме или же Добавить + Добавить Сумма
В обоих случаях знак плюс, символ операции, используется для указать, что числа должны быть добавлены. На рис. 3-1 показан пример того, как добавка используется в сфере общественного питания.
В качестве другого примера, при подаче на ужин стейка из вырезки, если есть
25 стейков готовы к подаче, 18 готовятся на гриле и 125
хранится в холодильнике, предприятие общественного питания имеет в общей сложности
из 168 стейков в наличии. Поскольку все добавляемые единицы одинаковы,
Нет необходимости писать, что это за единицы. Следовательно, добавление
можно записать одним из следующих способов:
25 + 18 + 125 = 168 (или) 25
18
+ 125
168
Нет необходимости использовать знак плюс, если три или более цифр складываются вместе в вертикальном положении, потому что это не может быть спутать с любой другой арифметической операцией. Помните, что каждая цифра должны быть помещены в правильный столбец, чтобы дать ему правильное значение.
Вычисление задач на сложение вручную можно считать задачей
прошлое, потому что сегодня все пользуются калькуляторами. Тем не менее, это
все еще разумно понять правила и правильные шаги для решения сложения
проблемы таким образом, потому что могут возникнуть ситуации, когда калькулятор
недоступен, или, что еще хуже, батарея может разрядиться, пока вы
выполнить важный расчет. Никогда не разумно полностью зависеть
на калькуляторах или счетных машинах. Впитывайте информацию и примеры
представлены в этой главе, чтобы вы могли быстро и точно добавлять
если автоматизация когда-нибудь подведет вас.
Рекомендации
Существует несколько основных указаний, которым можно следовать при арифметические задачи для экономии времени и повышения точности.
Будьте аккуратны. Если вас интересует карьера в сфере общественного питания, опрятность имеет важное значение как для вашего внешнего вида, так и для личной гигиены. Аккуратность также важна в математике. Не требует дополнительного времени писать аккуратно и аккуратно, помещая каждую цифру в соответствующую колонку непосредственно под номером над ним, как показано ниже.
2 1 5 8
3 6
5 2 6
2 0 9
8 5
+ 1 9 2 2
4 9 3 6
СОВЕТЫ ... Для обеспечения идеальных решений
Всегда записывайте сделки (переносы).
Аккуратность также важна при обмене (переносе) номеров
от одного столбца к другому. Сумма столбца единиц в предыдущем
проблема 36 а не б. 3 (на самом деле 30) проданы (перенесены) в
столбец десятков. Когда сделка (перенос) 3 написана, она ставится
аккуратно в верхней части столбца десятков, чтобы его не упустили из виду при
считая этот столбец. Сумма столбца десятков равна 23 (фактически 230).
2 переносится (переносится) в столбец сотен. Опять же, поместите
2 аккуратно поверх столбца сотен. Следуйте этой процедуре для
каждый столбец в задаче, как показано ниже:
(1)(2)(3)
2 1 5 8
3 6
5 2 6
2 0 9
8 5
+ 1 9 2 2
4 9 3 6
Проверьте свою работу. Вся работа должна быть проверена, даже при использовании калькулятор, чтобы убедиться, что ваше дополнение правильное. Ошибки могут быть сделаны даже при автоматическом расчете. Даже если вы обнаружите, проверив, что ваша работа всегда правильная, практика все равно должна быть продолжение. Штраф за математические ошибки в классе составляет всего более низкий класс; штраф за ошибки в работе службы общественного питания может привести к денежным потерям как для вас, так и для вашего работодателя.
Обычный метод проверки добавления состоит в добавлении отдельных
столбцы в обратном порядке. Например, если вы изначально добавили
столбцы сверху вниз, что является обычной практикой, вы можете проверить
свою работу, добавив второй раз, снизу вверх. Просто переверни свой
процедура.
Увеличьте свою точность и скорость. Добавление часто упрощается, если числа объединяются, а затем добавляются. Например, в задаче 7 + 3 + 8 + 2 + 5 + 3 = 28, сложение значительно упрощается при объединении 7 и 3 в 10, и 8 и 2 в 10, что в сумме дает двадцать. Добавление оставшиеся числа (5 и 3) дают 8, что в сумме дает 28.
Удалите ненужные шаги при добавлении. Один из способов увеличения ваша скорость и точность в том, что вместо того, чтобы думать, что 7 плюс 3 равно 10, автоматически видеть комбинацию 7 и 3 как 10. При добавлении проблемы в предыдущем абзаце, не думайте, что 10 плюс 10 равно 20, плюс 5 равно 25, плюс 3 равно 28. Думайте 10, 20, 28.
Если следовать этим рекомендациям, они помогут вам обеспечить
точность и скорость, необходимые для любого типа задач на сложение, особенно
те, что связаны с общественным питанием. Некоторые из этих рекомендаций, например
опрятности и проверки своей работы, относятся ко всем арифметическим действиям.
ОБЗОР 3-1
Найдите сумму каждой из следующих задач на сложение. Использовать методы и рекомендации, предложенные в этой главе. Чтобы улучшить свою математику навыки, рассчитать эти проблемы вручную, а затем проверить свою работу.
1. 6
+ 7
2. 4
7
6
+ 3
___
3. 3 + 5 + 8 + 17 = --
4. 24 + 19 + 12 + 28 = --
5. 259
+ 148
6. 338
225
+ 648
7. $56,17
490,54
26.38
+ 18,67
8. 312
422
345
239
+ 751
9. $366,26
441,31
374,43
223,23
+154,73
10. 8
28
335
2765
222
589
17
259
+ 126
11. $43,16
42.19
41.20
31.42
29,73
25.43
27,63
18,64
+ 12.25
12. 555,25 долларов США
216,11
140,18
713,14
726,12
2890,82
326,22
129.10
+ 222,12
13. Если гостевой чек включает омлет на сумму 6,99 долл. США, Французский тост по 5,99 доллара и кофе по 1,25 доллара, сколько стоит общий чек? —
14. При приготовлении салатницы с фруктами
использовано: апельсины 1,98 доллара, яблоки 0,79 доллара, виноград 0,92 доллара, бананы 1,69 доллара,
клубника 2,68 доллара, персики 1,47 доллара и ананас 0,98 доллара. В чем был
общая стоимость фруктового салатника? —
15. В ресторане было 203 заказа курицы в морозилке, 126 в встроенный холодильник и 109 в выдвижном холодильнике. Как много заказы на курицу у них были под рукой? —
ВЫЧИТАНИЕ
Вычитание означает отнять. Это удаление одного числа вещи из другого количества вещей (см. рис. 3-2). Слово «вычитание» используется очень редко, за исключением его математических смысл. Популярное слово, используемое в деловом мире, «вычесть», что также означает отнять. Например, вместо сказать: «Он вычел скидку в размере 2 долларов из моего счета», утверждение будет таким: «он вычел скидку в размере 2 долларов с моего законопроект.»
[РИСУНОК 3-2 ОПУЩЕН]
Если у вас есть 12 долларов, а вы тратите 8,25 доллара, задача на вычитание написано следующим образом:
$12.
Знак минус (-) должен использоваться всегда, чтобы проблема не путают с другой математической операцией.
У каждого фактора вычитания есть имя. Исходный номер перед вычитанием или перед удалением чего-либо называется уменьшаемое. В приведенном выше примере уменьшаемое значение равно 12,00 долларов. Номер удален от уменьшаемого называется вычитаемым. В итоге осталась сумма или оставшееся после решения задачи называется разницей.
1585 г. - 742 Вычитаемое 843 Разница
Торговля (заимствование)
Вычитание часто требует торговли (заимствования). При торговле, прибавьте десять к единицам в уменьшаемом конце. При этом уменьшить число в столбце десятков на единицу. Хотя minuend обычно большее число, чем вычитаемое, конкретная цифра в уменьшаемом может быть меньше, чем цифра под ней в вычитаемом, поэтому торговля (заимствование) требуется. Пример: 1 723 — 688 = 1 038. Когда эта проблема устанавливается в вертикальном положении, выглядит так:
[Иллюстрация опущена]
СОВЕТЫ .
Уменьшаемое (1,723) намного больше, чем вычитаемое (688). Однако цифра 8 в столбце единиц вычитаемого равна больше, чем цифра 3 в столбце единиц уменьшаемого конца. С 8 нельзя вычесть из 3, возникает необходимость торговать (занимать) из столбец десятков.
Чтобы указать, что десятка была продана (заимствована), зачеркните 2 в столбце десятков и напишите над ним 1. Если пренебречь этим шагом, вы иногда может забыть, что вы торговали (брали взаймы).
1 13
1 723
- 688
5
Прибавьте проданные (взятые взаймы) десять к 3 в столбце единиц, что увеличивает 3 до 13. Затем вычтите 13 — 8 = 5. 5 записывается под чертой в колонке единиц.
113
1723
- 688
5
В столбце десятков нельзя вычесть 8 из 1 (фактически 80 из
10), значит, надо торговать (занимать) сотней из сотен
столбец. Это делается путем зачеркивания цифры 7 в сотнях.
столбец и запись 6 над ним.
6 11 13
1 7 2 3
- 6 8 8
5
Вернитесь к столбцу десятков и вычтите 8 из 11 (фактически 80 из 110), чтобы получить 3 (на самом деле 30). Напишите 3 в колонке десятков под бар.
6 11 13
1 7 2 3
- 6 8 8
35
Переходя к столбцу сотен, 6 можно вычесть из 6 (что равно на самом деле 600 из 600). Даже если ничего не останется, ноль используется удержать место. Таким образом, торговля (заимствование) в данном случае не требуется. столбец.
6 11 13 1 7 2 3 - 6 8 8 0 3 5
Задача решается сбиванием единицы, оставшейся в столбец тысяч. Завершенная задача представлена ниже:
6 11 13 1 7 2 3 - 6 8 8 1 0 3 5
Проверка вычитания
Проверка любой математической задачи — всегда мудрый шаг, даже если
с помощью калькулятора, потому что так легко сделать ошибку. Общий способ
проверка ответа на вычитание состоит в том, чтобы сложить вычитаемое и
разница. Сумма этих двух чисел должна равняться уменьшаемому.
Вычитание: 3 6 4 2 - 2 1 3 2 Вычитаемое 1 5 1 0 Разница Проверять: 2 1 3 2 Вычитаемое + 1 5 1 0 Разница 3 6 4 2
ОБЗОР 3-2
Найдите разницу в следующих задачах на вычитание. Рассчитайте эти проблемы вручную, а затем проверьте свою работу.
1. 955 - 314 = --
2. 688 - 520 = --
3. 4925 - 1649 = --
4. 743
- 526
5. 828
- 593
6. 5197
- 2058
7. 24,43 доллара США
- 18.20
8. $76,32
- 56,54
9. $132,77
- 59,99
10. 7 333,64 доллара США
- 6 132,45
_________
11. 221 004,03 доллара США
- 79625,07
12. Счет за свадебную вечеринку составил 1585,21 доллара. Они были учитывая скидку в размере 121,00 долларов США, поскольку гарантированное количество людей присутствовал. Каков был общий счет? —
13. В ресторане думали, что у них есть 76 живых лобстеров.
Проведя быструю инвентаризацию, было обнаружено, что 29 человек мертвы. Как много
живых лобстеров в ресторане не осталось? —
14. В морозилке ресторана было 240 цыплят. Они использовали 31 для особенная вечеринка. Сколько их осталось? —
15. Ресторан купил 268 фунтов вырезки. Сорок восемь фунты были потеряны при обвалке и обрезке. Сколько фунтов осталось? —
УМНОЖЕНИЕ
Умножение — еще одна математическая операция, при которой требуется увеличение. место. Методы, вызывающие увеличение, такие как сложение, кажутся быть самым популярным, особенно если увеличение написано по буквам «прибыль» или имеет знак доллара. Умножение может быть задуман как ярлык для определенного типа задачи на сложение. В умножение, целое число прибавляется к себе заданное количество раз. Например, 4 x 2 = 8 — это еще один способ выражения 4 + 4 = 8. Цифра 4 прибавляется сама к себе два раза.
Поскольку между сложением и умножением существует связь,
не имеет значения, какая операция используется в простых задачах, таких как
один выше. Однако, когда проблема состоит из проблем, связанных с
большие числа (например, 4531 X 6580 = ?), сложение непрактично
ее решения. Это когда умножение становится полезным в качестве ярлыка
для доп. Решить предыдущую задачу довольно долго, используя
умножение, как показано в следующем примере. Теперь только представьте, что
было бы задействовано, если бы это было сделано путем добавления:
6580 х 4531 6580 19740 32900 26320 29813980 СОВЕТЫ ... Для обеспечения идеальных решений Множитель, умноженный на множитель, равен произведению или же Множитель х множимое Товар
Каждое число, участвующее в процессе умножения, имеет имя.
число, которое складывается само с собой (в примере 4, 4 х 2 = 8), называется
множимое (что означает «будет умножаться»).
число, представляющее количество раз, которое должно быть добавлено множимое
на себя называется множителем (цифра 2 в примере). Результат
произведением множимого на множитель называется произведение. Произведение в нашем примере равно 8.
В следующем примере приведены названия и функции различных числа, участвующие в операции умножения.
362 множимое х 32 Множитель 724 Подпродукт 10860 Подпродукт 11584 Продукт Имя функции Число, которое нужно добавить к самому себе Множимое Количество раз, которое нужно добавить к самому себе Множитель Продукт столбца единиц Произведение столбца десятков Подпроизведение Конечный результат (ответ) Продукт
В этом примере показаны субпродукты. Подпродукты (подзначение
под, под или перед; произведение, являющееся результатом умножения) происходят
всякий раз, когда множитель состоит из двух или более цифр. В таком случае,
множитель равен 32. Первый подпродукт является результатом произведения
362 x 2 = 724. Второй подпроизведение (10 860) является результатом
умножение 362 x 30. Ноль в конце этого подпроизведения не
необходимо, потому что 4 + 0 = 4. Это не влияет на результат
проблема, и показан здесь только для иллюстрации того, что произведение
умножение 362 x 30 равно 10860, а не 1086. Это также помогает сохранить все
цифры в соответствующих колонках (единицы в колонке единиц, десятки в
столбец десятков и т. д.), как упоминалось ранее в отношении
вычитание.
После того, как все субпродукты определены, они складываются вместе для получения конечного итога или произведения (в данном примере 11 584). Знак умножения (также называемый знаком умножения) всегда используется в задачу на умножение, чтобы отличить ее от любого другого типа арифметическая операция.
Таблица умножения
Теперь вам было продемонстрировано на примерах, что умножение — это кратчайший путь к некоторым типам задач на сложение. А Быстрый метод ценен только в том случае, если его можно использовать эффективно и точно. Ключом к эффективному использованию умножения является таблица умножения (см. рис. 3-3, дающая произведения до 12 x 12). Точность зависит от ваших усилий и от того, насколько хорошо вы развили навыки умножения.
Упражняйтесь в таблице умножения, пока не запомните ее. Тестировать
насколько хорошо вы запомнили эту таблицу, напишите каждую задачу на одной стороне
каталожной карточки и продукта на другой стороне. Вы должны быть в состоянии
смотреть на задачу и знать ответ в течение пяти секунд, не
глядя на другую сторону.
СОВЕТЫ ... Для обеспечения идеальных решений Помните старую поговорку: практика делает совершенным.
Другой способ представления таблицы умножения показан на
Рисунок 3-4. Эта уникальная таблица дает произведения чисел до 25 x
25 = 625. Он относительно прост в использовании. Например, чтобы найти
произведение 8 х 9, найдите цифру 8 по вертикали (вверх и вниз)
столбец в крайнем левом углу. Затем перемещайте палец вправо, пока не появится цифра 9.
находится в горизонтальной (слева направо) колонке в верхней части
стол. Число 72 находится в том месте, где 8-й столбец и 9-й столбец
пересекаются. Следовательно, 72 — это произведение 8 х 9. Посмотрите на одно место ниже.
72 и найдите число 81. Это произведение 9 x 9. Выпадающий список
другое место, чтобы найти, что 10 х 9 = 90.
Упрощение умножения с помощью пошаговой процедуры. Этот пример умножения предназначен для иллюстрации шаг за шагом процедуры, связанные с поиском продукта. Как упоминалось ранее, умножение является разновидностью и имеет очень тесную связь с добавление. В этом примере будет показано, что произведение проблема является результатом сложения подпродуктов каждого шага проблема.
СОВЕТЫ ... Для обеспечения идеальных решений
Положите карточку или лист бумаги горизонтально на стол.
помогает найти произведения различных чисел.
Пример: 924
х 65
Столбец единиц:
Шаг 1. 5 х 4 = 20
Шаг 2. 5 х 20 = 100
Шаг 3. 5 х 900 = 4500
Подпроизведение одного столбца 4620
Столбец десятков:
Шаг 4. 60 х 4 = 240
Шаг 5. 60 х 20 = 1200
Шаг 6. 60 х 900 = 54 000
Подпроизведение столбца десятков 55 440
Добавьте субпродукты:
Шаг 7. 4 620 + 55 440 = 60 060 (Произведение)
В этом примере показаны действия по нахождению произведения 924 X 65. Как правило, когда проблема решается, ненужные нули удаляются,
но используются переносные номера, как показано в следующем примере:
9 2 4 множимое
х 6 5 Множитель
4 6 2 0 Подпроизведение единичного столбца
5 5 4 4 Подпроизведение столбца десятков
6 0 0 6 0 Товар
2 — номер переноса для столбца единиц.
1 — переносимое число для столбца десятков.
Обратите внимание, что подпроизведение столбца единиц в обоих методах работая проблема 4,620. То же верно и для субпродукта столбец десятков, 55 440. Нуль остается вне субпродукта во втором метод, потому что его единственная цель состоит в том, чтобы удержать место. Пока другой цифры стоят на своих местах, ноль не нужен.
Проверка изделия
Принятый и распространенный метод проверки точности произведение умножения состоит в том, чтобы инвертировать или перевернуть множимое с множитель и проработайте задачу с обратной позиции.
Исходное умножение
3 4 8 множимое
х 5 4 Множитель
1 3 9 2 Субпродукт
1 7 4 0 Субпродукт
1 8 7 9 2 Продукт
Проблема проверена
5 4 Множитель
х 3 4 8 множимое
4 3 2 Субпродукт
2 1 6 Подпродукт
1 6 2 Субпродукт
1 8 7 9 2 Продукт
Если проблема решена точно в обоих случаях, продукты
будет то же самое. Если получаются два разных продукта, инвертируйте
верните проблему в первоначальный вид и повторите попытку с немного лучшим
усилие. Сегодня проверку можно произвести на калькуляторе. Тем не менее, это
хорошая практика решать проблемы вручную, а затем перепроверять
работа на калькуляторе. Помните, что выполнение задач вручную обостряет
ваши математические способности, и что наступят времена, когда вы должны
без автоматики.
Рекомендации
Здесь предлагается несколько рекомендаций, которые помогут обеспечить скорость и точность работы умножения.
Будьте аккуратны. Аккуратность очень важна, как указывалось ранее в этом глава. Обычный метод умножения исключает конечные нули (нули, которые появляются в конце числа), и поэтому вы должны быть очень внимательно записывайте каждую цифру на своем месте.
Будьте осторожны с переносом номеров. Помните, что переходящие числа
добавляются к произведению двух умноженных чисел.
переходящие числа не умножаются, как указано в следующем
пример. (Примечание: нет необходимости записывать номера переноса как
показано в следующем примере.)
(4)(5) 7 5 8 х 7 5 3 0 6
Первые числа, на которые нужно умножить, это 7 x 8 = 56. Запишите букву b в столбец единиц под чертой и перенесите 5 в столбец десятков. Далее, 7 x 5 = 35. К этому мы добавляем переносимое число 5. Таким образом, 35 + 5 = 40. Напишите 0 в колонке десятков под чертой и перенесите 4 на столбец сотен. Следующий шаг в правильном порядке: 7 x 7 = 49. Чтобы это, добавьте перенос номер 4. Это становится 49+ 4 = 53. Запишите 3 в столбце сотен под чертой и 5 в столбце тысяч под баром. 7 х 758 = 5 306.
СОВЕТЫ ... Для обеспечения идеальных решений Будьте осторожны, когда множитель состоит из двух и более цифр. отметить переходящие номера.
Для быстрого определения произведения при умножении на 10, 100, 1000,
и т. д. Добавьте правильное количество нулей к множимому. За
пример: 10 х 222 = 2220. Так как в числе 10 один ноль, прибавьте один ноль
до 222, чтобы получить продукт. При умножении на 100 два нуля будут
быть добавлено. 100 х 222 = 22 200. При умножении на 1000 три нуля
добавлен.
Используйте единицы в произведении, когда они используются в множимом. А единица была объяснена в предыдущем уроке как единичное количество подобных вещи. Большинство задач на умножение в мире труда связаны с некоторыми своего рода обозначенные единицы. Если на птицеперерабатывающем заводе 45 цыплят каждый в 15 отдельных загонах, сколько цыплят у него в наличии? (45 х 15 = 675) Произведение не просто 675, а 675 цыплят. Этот тип единицу не нужно писать рядом с множимым при работе проблему, но помните, какой тип единиц умножается, чтобы результатом будет определенное количество этих обозначенных единиц.
ОБЗОР 3-3
Найдите ответ на следующие задачи на умножение. Если единицы указаны, укажите единицу измерения в ответе. Решите эти проблемы вручную а потом проверить свою работу. Округлить до ближайшего цента.
1. 156 х 3 2.
9. Говяжий бок весит 323 фунта и стоит 2,73 доллара за фунт. Как сторона сколько стоит? —
10. Если передняя часть телятины весит 46 фунтов и стоит 7,60 долл. фунтов, какова общая стоимость? —
11. Грузовик Джима проезжает 13 миль на каждый галлон бензина. Сколько миль он может проехать на 128 галлонах бензина? —
12. При приготовлении мясного рулета требуется четыре фунта говяжий фарш входит в каждую буханку. Сколько фунтов говяжьего фарша должно быть заказали при приготовлении 65 буханок? —
13. Говяжьи ребрышки весят 24 фунта и стоят 2,97 доллара за фунт. Что такое общая стоимость ребер? —
14. Свадебный банкет рассчитан на 575 человек. Кейтеринг взимается 25,75 долларов США с человека. Каков общий счет? —
15. Повар зарабатывает 125 долларов в день. Сколько можно заработать за год, если
повар работает 328 дней? —
ОТДЕЛ
Деление – это действие по разделению целого количества на части. Это является разделением всей этой части, процессом деления одного числа на еще один. Деление — это, по сути, способ узнать, сколько раз одно число содержится в другом числе. В некотором смысле это обратная сторона умножения, как показано ниже:
Умножение 5 х 8 = 40
Деление 40 / 8 = 5
40 / 5 = 8
Посмотрите на деление с другой точки зрения. Предположим, что ваш работодатель
обещает платить вам 8 долларов в час. Поставив восемь трудных
часов, вы получаете чек всего на 56,00 долларов США (до вычетов,
курс). Просто глядя на общую сумму, вы понимаете, что что-то не так. А
простая задача на деление покажет вам, что 56 долларов / 8 = 7 долларов. Вы были только
вам платят 7 долларов в час, или вам платят только за семь часов. С использованием
Таким образом, деление может помочь вам обнаружить, что была допущена ошибка.
Подразделение часто используется в сфере общественного питания, потому что продукты постоянно делятся. Стрип-филей делится на стейки, овощи на порции, пирожные на порции и т. д. (см. рис. 3-5, на котором показан другой пример). Пример, иллюстрирующий Разделение пищи можно увидеть, наблюдая за тем, как находится решение проблемы. следующая проблема:
Банка яблочного пюре № 10 содержит около 105 унций. Как много гости могут быть обслужены, если каждый гость получит порцию в 3 унции?
105/3 = 35
Тридцать пять гостей могут быть поданы из банки на 105 унций яблочное пюре. Использование деления помогло повару узнать, сколько банок должны открываться при обслуживании определенного количества человек.
При делении делимое число называется делимым. В
задача 80 / 4 = 20, число 80 является делимым. Название для
число, на которое делится делимое (число 4 в данном примере) равно
делитель. Результат деления делимого на делитель равен
называется частным. Частное в этом примере — это число 20.
СОВЕТЫ ... Для обеспечения идеальных решений Дивиденд, разделенный на делитель, равен частному частное Делитель) Дивиденд
[РИСУНОК 3-5 ОПУЩЕН]
СОВЕТЫ ... Для обеспечения идеальных решений При делении с помощью калькулятора сначала введите делимое.
В ситуациях, когда делитель не содержится в делимом равное или точное число раз, лишняя или оставшаяся цифра называется остаток. Например: 83/4 = 20 с 3 остатками, потому что 4 слишком велико, чтобы поместиться в 3. В этой задаче 3 является остаток.
Есть несколько знаков разделения, которые можно использовать при работе
проблемы деления. Обычно выбранный знак зависит от того, как долго или
сложная проблема может быть. До этого момента в наших примерах
операция деления, деление обозначено чертой с точкой
над и под (/). Этот символ в основном используется, когда проблема
простой или при первой постановке задачи на деление, которую необходимо решить. Простые задачи также пишутся с использованием дробной черты. Например, 84
/ 7 = 12 также можно записать как 84/7 = 12.
В так называемой задаче на деление в длину принятый знак использование имеет вид закрытой скобки с прямой линией выходит из топа:
[Иллюстрация опущена]
Пошаговое разделение
При рассмотрении основных математических операций деление обычно обсуждается последним, потому что он включает в себя как умножение, так и вычитание в его работе (включая переходящие номера и торговлю). Например: 8,295/15 = ?
Так как эта задача будет считаться длинной, длинная используется форма деления.
[Иллюстрация опущена]
Задача на длинное деление начинается слева, а не с
право, как сложение, вычитание и умножение. Первый
шаг состоит в том, чтобы оценить, сколько раз 15 содержится в 82 (на самом деле
8200). Известно, что 5 х 15 = 75, поэтому ваша первая оценка будет 5.
5 пишется над чертой деления в разряде сотен.
[Иллюстрация опущена]
Чтобы убедиться, что число 5 правильное, его умножают на 15. Произведение равно 75. Число 7 записано в колонке тысяч под 8 и 5 в столбце сотен под цифрой 2. Затем вычитается 75. из 82. Если разница меньше 15, оценка 5 в сотни место частного правильно. 82 — 75 = 7. Так как 7 меньше чем 15, оценка верна.
[Иллюстрация опущена]
Следующим шагом будет получение 9 в разряде десятков делимого вниз справа от 7, что дает 79. Мы оцениваем, что 79 содержит 15 всего 5 раз. 79 — 75 = 4, что меньше 15. (Обратите внимание, что иногда оценка слишком низкая или слишком высокая. Когда это происходит, оценка должна быть соответственно увеличена или уменьшена.)
Пока наша проблема дошла до этой точки:
[Иллюстрация опущена]
Следующим шагом сбиваем оставшуюся цифру 5 из тех
столбец и поместите его справа от 4 (оставшегося от вычитания 75
от 79). Снова оцените, сколько раз 45 содержит 15. Легко
увидеть, что 3 должно быть оценочной цифрой, чтобы проблема вышла
даже. Готовая задача выглядит следующим образом:
[Иллюстрация опущена]
Остаток
Как объяснялось ранее, фигура в задаче на деление, которая может быть остаток, когда делимое не содержит делителя точно называется остаток. Например:
[Иллюстрация опущена]
На данный момент больше нет цифр, которые можно было бы вывести из списка. дивиденд. В числе 18 нет 33-х. Следовательно, остаток 18 называется остатком. Следовательно, решение будет 65 Р18. Остаток также может быть записан в дробной или десятичной форме, как показано ниже:
2,163 / 33 = 65 18/33 (дробь) или 65,545 (десятичная дробь)
Контрольный отдел
Обычный метод проверки деления — умножение частного по делителю. Произведение делителя и частного вместе должны быть такими же, как дивиденд.
[Иллюстрация опущена]
Чтобы проверить деление: 1 3 2 Частное х 2 2 Делитель 2 6 4 2 6 4 2 9 0 4 Дивиденд
Если частное включает остаток, умножьте частное на
делитель, как показано в предыдущем примере, затем добавьте остаток к
продукт.
[Иллюстрация опущена]
Для проверки деления с наличием остатка:
2 7 5 Коэффициент х 3 1 делитель 2 7 5 8 2 5 8 5 2 5 Товар + 1 9Остаток 8 5 4 4 Дивиденд
ОБЗОР 3-4
Найдите частное для следующих задач на деление. Нести отвечает на три знака справа от запятой. Рассчитать эти проблемы вручную, а затем проверить все работает.
1. 45/15 = —
2. 96/3 = —
3. [МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII]
4. [МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII]
5. [МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII]
6. [МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII]
7. [МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII]
8. [МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII]
9. Говядина весом 480 фунтов куплена за 950,40 долларов. Что это стоимость за фунт? —
10. В течение недели доставка от компании «Прайм Тайм Кейтеринг»
грузовик проехал 336 миль. Они использовали 24 галлона бензина. Как много
мили они в среднем на галлон? —
11. Шеф-повар ресторана Starlight зарабатывает 43 200 долларов в год. Если этот повар работает 48 недель в году, сколько она зарабатывает за одну неделю? —
12. Повар в ресторане Blue Star работает пять дней в неделю и зарабатывает 356 долларов в неделю. Сколько он зарабатывает за один день? —
13. Ресторан заказывает 392 фунта свиной корейки. Каждая корейка весит 14 фунтов. Сколько филейных частей содержится в посылке? —
14. Грузовик компании «Делюкс Кейтеринг» имеет в среднем 13 миль на галлон бензина. За 30 дней эксплуатации грузовик проходит 2028 миль. Сколько бензина используется? —
15. Содержится сто двадцать восемь унций апельсинового сока в одном галлоне. Сколько стаканов сока по 8 унций можно подать? —
Шеф Сез... Математика никогда не была одним из моих любимых предметов в старших классах школы. Я все время думал: «Почему я нужно знать математику?» Сегодня, как руководитель шеф-повар в больнице Fairview Southdale, я использую математика каждую минуту дня! Мой бюджет на еду составляет 96 000 долларов в месяц.
Боб Ньюэлл, сертифицированный шеф-повар (CEC)
Шеф-повар
Содексо
Больница Fairview Southdale
Эдина, Миннесота
Больница Fairview Southdale, расположенная в пригороде Миннеаполиса, Миннесота, это учреждение на 390 коек. В больнице работает более 1000 человек врачей, 2200 поставщиков медицинских услуг и более 500 добровольцев. Г-н. У Ньюэлла была разнообразная карьера шеф-повара в различных больницах. а также для частного сектора, такого как Dow Corning Corporation, Alma Колледж и отели. Он также управлял собственным ресторанным бизнесом.
Рисунок 3-3 Таблица умножения чисел от 1 до 12 1 х 1 = 1 1 х 2 = 2 1 х 3 = 3 1 х 4 = 4 1 х 5 = 5 1 х 6 = 6 1 х 7 = 7 1 х 8 = 8 1 х 9 = 9 1 х 10 = 10 1 х 11 = 11 1 х 12 = 12 2 х 1 = 2 2 х 2 = 4 2 х 3 = 6 2 х 4 = 8 2 х 5 = 10 2 х 6 = 12 2 х 7 = 14 2 х 8 = 16 2 х 9 = 18 2 х 10 = 20 2 х 11 = 22 2 х 12 = 24 3 х 1 = 3 3 х 2 = 6 3 х 3 = 93 х 4 = 12 3 х 5 = 15 3 х 6 = 18 3 х 7 = 21 3 х 8 = 24 3 х 9 = 27 3 х 10 = 30 3 х 11 = 33 3 х 12 = 36 4 х 1 = 4 4 х 2 = 8 4 х 3 = 12 4 х 4 = 16 4 х 5 = 20 4 х 6 = 24 4 х 7 = 28 4 х 8 = 32 4 х 9 = 36 4 х 10 = 40 4 х 11 = 44 4 х 12 = 48 5 х 1 = 5 5 х 2 = 10 5 х 3 = 15 5 х 4 = 20 5 х 5 = 25 5 х 6 = 30 5 х 7 = 35 5 х 8 = 40 5 х 9 = 45 5 х 10 = 50 5 х 11 = 55 5 х 12 = 60 6 х 1 = 6 6 х 2 = 12 6 х 3 = 18 6 х 4 = 24 6 х 5 = 30 6 х 6 = 36 6 х 7 = 42 6 х 8 = 48 6 х 9= 54 6 х 10 = 60 6 х 11 = 66 6 х 12 = 72 7 х 1 = 7 7 х 2 = 14 7 х 3 = 21 7 х 4 = 28 7 х 5 = 35 7 х 6 = 42 7 х 7 = 49 7 х 8 = 56 7 х 9 = 63 7 х 10 = 70 7 х 11 = 77 7 х 12 = 84 8 х 1 = 8 8 х 2 = 16 8 х 3 = 24 8 х 4 = 32 8 х 5 = 40 8 х 6 = 48 8 х 7 = 56 8 х 8 = 64 8 х 9 = 72 8 х 10 = 80 8 х 11 = 88 8 х 12 = 96 9 х 1 = 9 9 х 2 = 18 9 х 3 = 27 9х 4 = 36 9 х 5 = 45 9 х 6 = 54 9 х 7 = 63 9 х 8 = 72 9 х 9 = 81 9 х 10 = 90 9 х 11 = 99 9 х 12 = 108 10 х 1 = 10 10 х 2 = 20 10 х 3 = 30 10 х 4 = 40 10 х 5 = 50 10 х 6 = 60 10 х 7 = 70 10 х 8 = 80 10 х 9 = 90 10 х 10 = 100 10 х 11 = 110 10 х 12 = 120 11 х 1 = 11 11 х 2 = 22 11 х 3 = 33 11 х 4 = 44 11 х 5 = 55 11 х 6 = 66 11 х 7 = 77 11 х 8 = 88 11 х 9= 99 11 х 10 = 110 11 х 11 = 121 11 х 12 = 132 12 х 1 = 12 12 х 2 = 24 12 х 3 = 36 12 х 4 = 48 12 х 5 = 60 12 х 6 = 72 12 х 7 = 84 12 х 8 = 96 12 х 9 = 108 12 х 10 = 120 12 х 11 = 132 12 х 12 = 144 Рисунок 3-4 Таблица умножения чисел от 1 до 25 1 2 3 4 5 6 7 8 9 10 2 4 6 8 10 12 14 16 18 20 3 6 912 15 18 21 24 27 30 4 8 12 16 20 24 28 32 36 40 5 10 15 20 25 30 35 40 45 50 6 12 18 24 30 36 42 48 54 60 7 14 21 28 35 42 49 56 63 70 8 16 24 32 40 48 56 64 72 80 9 18 27 36 45 54 63 72 81 90 10 20 30 40 50 60 70 80 90 100 11 22 33 44 55 66 77 88 99 110 12 24 36 48 60 72 84 96 108 120 13 26 39 52 65 78 91 104 117 130 14 28 42 56 70 84 98 112 126 140 15 30 45 60 75 90 105 120 135 150 16 32 48 &4 80 96 112 128 144 160 17 34 51 &8 85 102 119 136 153 170 18 36 54 72 90 108 126 144 162 180 19 38 57 76 95 114 133 152 171 190 20 40 60 80 100 120 140 160 180 200 21 42 63 84 105 126 147 168 189 210 22 44 66 88 110 132 154 176 198 220 23 46 69 92 115 138 161 184 207 230 24 48 72 96 120 144 168 192 216 240 25 50 75 100 125 150 175 200 225 250 1 2 3 4 5 6 7 8 9 10 1 11 12 13 14 15 16 17 18 192 22 24 26 28 30 32 34 36 38 3 33 36 39 42 45 48 51 54 57 4 44 48 52 56 60 64 68 72 76 5 55 60 65 70 75 80 85 90 95 6 66 72 78 84 90 96 102 108 114 7 77 84 91 98 105 112 119 126 133 8 88 96 104 112 120 128 136 144 152 9 99 108 117 126 135 144 153 162 171 10 110 120 130 140 150 160 170 180 190 11 121 132 143 154 165 176 187 198 209 12 132 144 156 168 180 192 204 216 228 13 143 156 169 182 195 208 221 234 247 14 154 168 182 196 210 224 238 252 266 15 165 180 195 210 225 240 255 270 285 16 176 192 208 224 240 256 272 288 304 17 187 204 221 238 255 272 289 306 323 18 198 216 234 252 270 288 306 324 342 19209 228 247 266 285 304 323 342 361 20 220 240 260 280 300 320 340 360 380 21 231 252 273 294 315 336 357 378 399 22 242 264 286 308 330 352 374 396 418 23 253 276 299 322 345 368 391 414 437 24 264 288 312 336 360 384 408 432 456 25 275 300 325 350 375 400 425 450 475 1 11 12 13 14 15 16 17 18 19 1 20 21 22 23 24 25 2 40 42 44 46 48 50 3 60 63 66 6972 75 4 80 84 88 92 96 100 5 100 105 110 115 120 125 6 120 126 132 138 144 150 7 140 147 154 161 168 175 8 160 168 176 184 192 200 9 180 189 198 207 216 225 10 200 210 220 230 240 250 11 220 231 242 253 264 275 12 240 252 264 276 288 300 13 260 273 286 299 312 325 14 280 294 308 322 336 350 15 300 315 330 345 360 375 16 320 336 352 368 384 400 17 340 357 374 391 408 425 18 360 378 396 414 432 450 19 380 399 418 437 456 475 20 400 420 440 460 480 500 21 420 441 462 483 504 525 22 440 462 484 506 528 550 23 460 483 506 529 552 575 24 480 504 528 552 576 600 25 500 525 550 575 600 625 1 20 21 22 23 24 25
2.
2: Полиномиальное сложение, вычитание, умножение и мономиальное деление- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 83116
- Дженнифер Фрейденрайх
- Колледж Диабло Вэлли
Большая часть раздела \(2.2\) посвящена математике, которую вы уже знаете, например, комбинированию одинаковых терминов при сложении многочленов, но мы будем держать вас в напряжении введением обозначения функций! Вы также получите дополнительную практику, которую вы жаждете для различных свойств экспоненты. Этот раздел направлен на укрепление вашей способности работать с полиномиальными функциями, используя нотацию функций. 92 + 6 &\text{Упростить, объединив одинаковые термины. 2 — 8x — 4\) и \(g(x) = 3x — 95} &\text{Ответ с положительными показателями.} \end{массив}\)
Определение: рациональная функция
Рациональная функция — это функция \(\dfrac{f(x)}{g(x)}\), где как \(f(x)\), так и \(g (x)\) — полиномиальные функции, а \(g(x)\) не равно нулю.
Мы более подробно изучим рациональную функцию в главе \(5\).
1. Пусть \(f(x) = 8x + 2\) и \(g(x) = 3 − 4x\). Найдите каждое из следующего:
- \((f+g)(x)\) 92-4\). Найдите каждое из следующего:
- \((f+g)(x)\)
- \((фг)(х)\)
- \((f \cdot g)(x)\)
- \((f+g)(x)\)
- \((фг)(х)\) 92\).
- \((f \cdot g)(2)\)
- \((f\cdot g)(0)\)
- \((f\cdot g)(-1)\)
- \((f\cdot g)(-2)\)
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Дженни Фрейденрайх
- Лицензия
- СС BY-SA
- Версия лицензии
- 4,0
- Показать страницу Оглавление
- нет
- Теги
- Одночленный отдел
- Полиномиальное сложение
- Полиномиальное умножение
- Полиномиальное вычитание
- рациональная функция
Подготовка к экзамену по математике THEA
Подготовка к экзамену по математике THEAПодготовка к экзамену по математике THEA
Основы математикиПравила экспоненты
Примеры:
Посмотрите видео: Math Help Exponents 1: Definitions by Pat McKeague
Смотреть видео: Math Help Exponents 3: Multiplication by Pat McKeague
Операции над числами/целыми числами со знаком (правила с add/sub/mult/div)
Сложение и вычитание
- Одинаковые знаки ДОБАВЬТЕ и СОХРАНИТЕ этот знак.
- Различные (непохожие) знаки ВЫЧИТАТЬ и СОХРАНИТЬ знак большего абсолютного значения.
Примеры:
Умножение и деление целых чисел
- Умножить или разделить, если знаки одинаковые, то знак произведения или частного будет положительным.
- Умножить или разделить, если знаки разные (не похожие) знак произведения или частного будет отрицательным.
Примеры:
Смотреть видео: сложение/вычитание отрицательных чисел от Академии Кана
Операции с дробями и десятичными знаками Add/Sub/Mult/Div
Правила умножения- Поместите все СМЕШАННЫЕ ЧИСЛА в НЕПРАВИЛЬНУЮ ФОРМУ.
- Уменьшить все дроби перед умножением
- Умножьте числитель на числитель и знаменатель на знаменатель.
Для умножения десятичных чисел:
Посмотрите видео: Основы арифметики: умножение десятичных дробей Патрика ДжМТ
Правила отдела
- ЗАМЕНИТЬ знак деления на знак умножения.
- Напишите ОБРАТНУЮ ЧИСЛО от делителя (число 2 nd ).
- Соблюдайте правила умножения.
до ДЕЛИТЬ десятичных чисел:
Смотреть видео: Основы арифметики: Деление десятичных дробей от Патрика ДжМТ
Смотреть видео: дроби — умножение и деление Патрика ДжМТ
Правила сложения и вычитания
- Должен иметь общий знаменатель
- Складывать или вычитать только числители
- Знаменатель остается прежним
- Сократить до минимума
- При сложении или вычитании смешанных чисел
а.
Сложение или вычитание целых чиселб. При сложении и вычитании может потребоваться дополнительный шаг (перенос или заимствование)
с. Ответы всегда должны быть самыми низкими
Примеры:
Примеры:
Добавьте следующие числа: 2,046, 0,658 и 1,39.
Вычтите следующие числа: 10,8–3,52
Смотреть видео: Дроби 1: Сокращение, Пэт МакКег
Посмотрите видео: Дроби 2: Умножение Пэта МакКега
Посмотрите видео: сложение и вычитание дробей от Khan Academy
Смотреть видео: Вычитание дробей от Khan Academy
Смотреть видео: сложение дробей с разными знаменателями от Khan Academy
Смотреть видео: Вычитание десятичных дробей от Khan Academy
Смотреть видео: добавление десятичных дробей от Khan Academy
Расчеты с использованием экспоненциальной записиПосмотрите видео Преобразование между научной записью и десятичной записью от PatrickJMT
Порядок операций, расчеты с использованием процентов
1.
4. Является ли \((f-g)(x)\) тем же, что и \((g-f)(x)\)? Объяснять.
5а. Ширина прямоугольника описывается функцией \(f(x) = 2x − 5\). Длина прямоугольника описывается функцией \(g(x) = 3x + 1\). Что из следующего описывает площадь прямоугольника?