Сложение и вычитание чисел в пределах 100. | Материал по математике (2 класс) по теме:
Сложение и вычитание в пределах 100
20-6 80-60 40-17 12+46 62+19 93-38
60-5 90-30 60-23 23+54 47+39 86-28
40-8 40-20 90-45 47+32 23+48 72-36
50-9 50-40 80-34 36+52 17+35 61-29
30-1 20+60 70-42 54+33 35+28 84-37
70+9 80+10 50-25 19+40 54+37 55-39
80+4 30+50 30-18 65+24 78+14 43-14
40+5 80-50 60-36 42+37 26+57 75-48
10+2 80+10 90-34 98-76 37+58 86-59
90-4 90-90 20-19 65-34 65+29 56-38
30-8 50+50 80-57 75+24 57+24 63-27
50+7 20+70 30-25 86-43 37+55 92-56
20+8 60-30 70-41 76-54 56+29 78-39
80-5 40-10 40-16 64+23 45+27 64-27
40+9 10+90 60-52 45+33 27+44 32-17
10+7 80-20 50-26 87-65 19+77 66-38
90-3 100-40 20-15 49-38 35+28 75-48
60+3 30+70 90-67 62+26 22+39 66-39
40-7 70-50 30-13 44+35 33+58 87-49
50-8 60-60 80-46 87-41 38+57 69-49
90+1 100-50 40-37 68-42 45+39 74-25
70-2 90-40 70-23 26+53 26+37 45-28
20+9 50+30 50-17 83+11 33+48 51-34
10+1 80-70 60-28 43+46 47+29 62-47
30-3 20+80 90-87 37+52 36+37 87-38
20-8 60-50 20-14 98-65 54+47 46-28
80+5 40+60 80-56 89-53 63+18 91-34
40+7 100-10 30-17 87-65 56+25 83-38
20-6 60+20 70-48 68-47 12+59 63-27
90+9 40+50 30-26 54+35 36+28 73-59
20+2 10+70 60-31 37+61 29+35 62-39
30+3 40+40 40-25 55+44 45+28 53-25
90+9 90-40 50-29 78-54 36+27 46-29
60-6 90-60 20-16 65-33 13+38 82-56
30-6 80-60 40-23 87-55 36+26 73-37
50+5 30+70 60-48 69-47 32+58 62-19
80+4 30+50 80-36 45+34 54+27 74-45
10+5 90-90 100-38 36+43 25+55 52-37
70-5 100-30 100-58 78-54 34+19 41-39
13+6 90-24 7+18 23+7 28+7
81+5 94-20 9+33 20-5 16+4
42+6 100-2 0+50 66+4 39+7
30+24 100-30 43-4 77+8 15-8
53+10 60-27 58-9 19+6 14-7
65+30 60-7 86-86 83-9 13-6
4+73 67-20 36-8 29+0 70-24
20+73 83-50 24-6 0+0 80-37
86-5 80-53 18-0 17-17 50-26
78-60 80-3 36+2 18+2 80-7
47-20 38+5 36+20 34-34 63+30
54+30 64+9 38-2 34-14 78-40
76-20 63+7 56-20 56-50 26+4
76+20 63+9 7+18 70-50 90-36
54+20 78+2 6+27 13-7 72-67
60+18 78+6 40-16 42+7 34+39
97+3 54+8 40-6 49-7 47+28
6+71 62+9 46-10 27+3 51-38
46+30 6+75 78-30 4+56 83+6
20+14 8+46 70-38 20+68 40-29
78+2 42-6 70-8 35+40 100-48
64+3 54-9 6+24 40-9 76+17
50-6 26-8 5+75 12-5 80-46
70-4 26+8 7+93 74-40 94-48
90-3 32-6 100-5 82-30 48+38
100-9 27+8 100-15 100-20 37+39
70-5 75-9 100-25 100-8 100-28
80-4 86+7 12-4 42-8 37+29
100-4 32-4 36-30 90-54 45+45
100-9 65+8 46+3 64+6 77-29
52+8 84-3 46-3 28+9 28+37
60-8 62+7 28+30 35-6 62-38
43-20 67+5 73+20 86-80 50-27
43-2 32-9 96-40 57+40 35+28
60-24 46+9 87-20 45+9 60-38
70-28 95-6 42+8 63-4 73-54
30-23 78+9 50-7 32-8 39+31
50-46 36+5 89+4 73-4 70-25
70-38 92+0 73-5 56-9 54+26
➕➖ Сложение и вычитание в пределах 100.
 Упражнения для школьников
Упражнения для школьниковДля решения данного упражнения необходимо выполнить сложение и вычитание в пределах 100 (в зависимости от каждого конкретного примера). Каждое из чисел (от 1 до 100), а также математические символы, появляется в случайном порядке.
Отличительной особенностью упражнений на данную тему являются их продвинутость до начального уровня средней школы, что делает упражнения универсальными, кроме старших классов.
Математически значимые упражнения решаются с применением действий сложения и вычитания. при этом действия сложения решаются учениками гораздо проще, чем действия вычитания. Это обусловлено восприятием мышления как основополагающего действия в математике.
Подсказка! Правильный ответ находится в пределах от 0 до 100.
Для решения более сложных примеров вы можете решить примеры на тему «Сложение и вычитание двух натуральных чисел».
Желаем удачи!
Примеры на тему Сложение и вычитание в пределах 100
Выполните 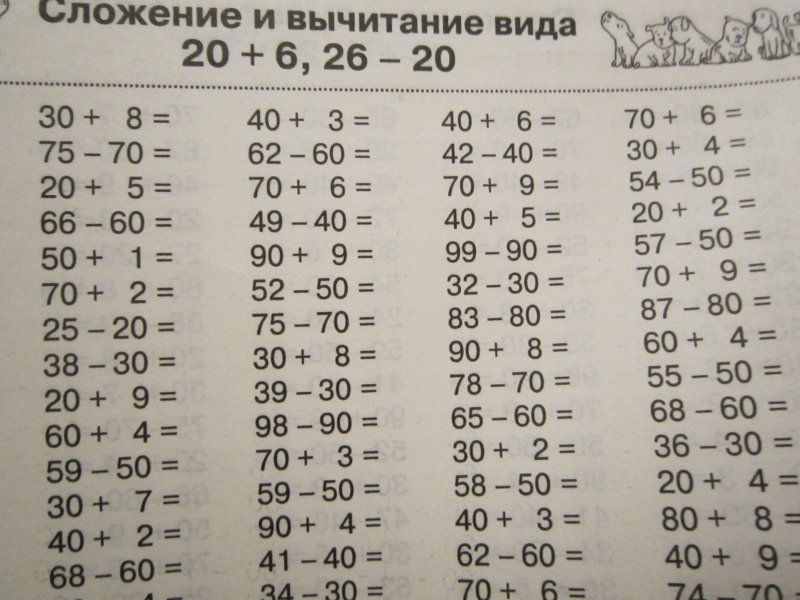
Внимание! Очерёдность примеров не повторяется, примеры появляются в случайном порядке при перезагрузке страницы и могут быть использованы для разных вариантов.
19+76=…
31+25=…
1+15=…
31-2=…
2+35=…
57-48=…
40+14=…
52-23=…
7+61=…
3+23=…
55-2=…
22+71=…
51-16=…
28+42=…
97-66=…
13+3=…
31+49=…
62-43=…
74-21=…
31+31=…
26+41=…
25+59=…
91+4=…
11-3=…
4+72=…
50+37=…
70-46=…
53-34=…
65-49=…
83-38=…
8+77=…
54+12=…
73-59=…
78-40=…
80-12=…
6+35=…
17+30=…
86-14=…
67-43=…
18-9=…
70+7=…
94-53=…
61+20=…
100-75=…
32+9=…
40+10=…
18-14=…
45-25=…
81-77=…
Примеры на сложение и вычитание в пределах 10 и 20 (математический тренажер для 1 класса)
Самые первые примеры, с которыми знакомится ребенок еще до школы — это сложение и вычитание. Не так уж сложно посчитать животных на картинке и, зачеркнув лишних, посчитать оставшихся. Или перекладывать счетные палочки, а потом считать их. Но для ребенка несколько труднее оперировать с голыми цифрами. Именно поэтому нужна практика и еще раз практика. Не бросайте заниматься с ребенком и летом, поскольку за лето школьная программа из маленькой головки просто выветривается и долго приходится наверстывать потерянные знания.
Не так уж сложно посчитать животных на картинке и, зачеркнув лишних, посчитать оставшихся. Или перекладывать счетные палочки, а потом считать их. Но для ребенка несколько труднее оперировать с голыми цифрами. Именно поэтому нужна практика и еще раз практика. Не бросайте заниматься с ребенком и летом, поскольку за лето школьная программа из маленькой головки просто выветривается и долго приходится наверстывать потерянные знания.
Если ваш ребенок первоклашка или только идет в первый класс — начните с повторения состава числа по домикам. А теперь можно браться и за примеры. Фактически сложение и вычитание в пределах десяти — это и есть первое практическое применение ребенком знания состава числа.
Кликайте по картинкам и открывайте тренажер в максимальном увеличении, далее можно скачать изображение себе на компьютер и распечатать в хорошем качестве.
Есть возможность разрезать А4 пополам и получить 2 листа с заданиями , если хотите уменьшить нагрузку на ребенка, или давать решать по столбику в день, если решили позаниматься летом.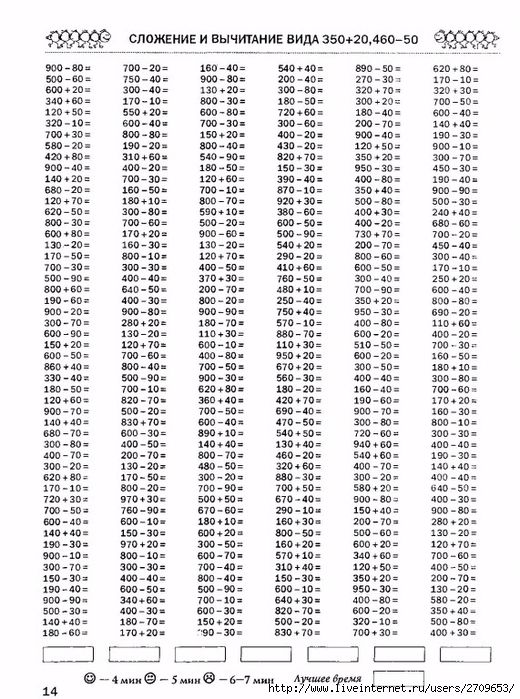
Решаем столбик, отмечаем успехи: тучка — не очень хорошо решили, смайлик — хорошо, солнышко — замечательно!
Сложение и вычитание в пределах 10
А теперь вразброс!
Примеры на сложение и вычитание в пределах 20
К моменту, когда ребенок приступит к изучению этой темы математики, он должен очень хорошо, на зубок знать состав чисел первого десятка. Если ребенок состав чисел не освоил, ему сложно придется в дальнейших вычислениях. Поэтому постоянно возвращайтесь к теме состава чисел в пределах 10, пока первоклассник не освоит его до автоматизма. Также первоклассник должен знать, что значит десятичный (разрядный) состав чисел. На уроках математики учитель рассказывает, что 10 — это, по-другому, 1 десяток, поэтому число 12 состоит из 1 десятка и 2 единиц. При сложении единицы складываются с единицами. Именно на знании десятичного состава чисел основываются приемы сложения и вычитания в пределах 20 без перехода через десяток.
Примеры для печати без перехода через десяток вперемешку:
Сложение и вычитание в пределах 20 с переходом через десяток основаны на приемах добавления до 10 или убавления до 10 соответственно, то есть на теме «состав числа 10», поэтому ответственно подойдите к изучению с ребенком этой темы.
Примеры с переходом через десяток (половина листа сложение, половина вычитание, лист также можно распечатать в формате А4 и разрезать пополам на 2 задания):
Мы надеемся, наши весёлые картинки с примерами воодушевят ребятишек на их решение с удовольствием 🙂
А еще у нас есть отличный онлайн тренажер по математике! Родителям не нужно ничего распечатывать и проверять, все это за вас совершенно бесплатно сделаем мы! Выбирайте режим и вперед >>
3000 примеров по математике (Сложение и вычитание в пределах 100). 2-3 класс — Узорова О.В. | 978-5-17-108563-6
Стоимость товара может отличаться от указанной на сайте!Наличие товара уточняйте в магазине или по телефону, указанному ниже.

г. Воронеж, площадь Ленина, д.4
8 (473) 277-16-90
г. Воронеж, ул. Маршака, д.18А
8 (473) 231-87-02
г. Липецк, пл.Плеханова, д. 7
8 (4742) 47-02-53
г. Воронеж, ул. Г. Лизюкова, д. 66 а
Лизюкова, д. 66 а
8 (473) 247-22-55
8 (47396) 5-29-29
г. Лиски, ул. Коммунистическая, д.7
8 (47391) 2-22-01
г.Воронеж, ул. Жилой массив Олимпийский, д.1
8 (473) 207-10-96
г. Калач, пл. Колхозного рынка, д. 21
Калач, пл. Колхозного рынка, д. 218 (47363) 21-857
г. Воронеж, ул.Челюскинцев, д 88А
8 (4732) 71-44-70
г. Старый Оскол, ул. Ленина, д.22
8 (4725) 23-38-06
8 (473) 300-41-49
г. Липецк, ул.Стаханова,38 б
Липецк, ул.Стаханова,38 б
8 (4742) 78-68-01
г. Курск, ул. Щепкина, д. 4Б
8 (4712) 73-31-39
|
|
Сложение и вычитание в пределах 100
При обучении сложению и вычитанию в пределах 100 собл! ются все требования, которые предъявляются к обучению вьн нению действий в пределах 20.
Многие трудности, которые испытывают школьники с нару нием интеллекта при выполнении действий сложения и вычита в пределах 20, не снимаются и при выполнении этих же деист! в пределах 100. Как показывают опыт и специальные йсследс ния по-прежнему большие затруднения учащиеся испытывают I выполнении действия вычитания. Наибольшее количество оши( возникает при решении примеров на сложение и вычитание переходом через разряд. Характерная ошибка при вычитании, единиц вычитаемого вычитают единицы уменьшаемого. Напримг, 35-17=22. Наблюдается также тенденция замены одного деж ‘ вия другим. Например: 64-16=80, 17+2=15 (вместо вычитании выполнено сложение и наоборот). При выполнении действий < двузначными числами учащиеся часто принимают во вниманш только единицы одного разряда, единицы другого разряда (первого или второго компонентов) переписывают без изменении (36+11=46, 85-24=64). Допускаются и такие ошибки: учащиеся складывают или вычитают, не обращая внимания на разряды: еди ницы складывают с десятками (37+2=57, 38-20=36), из меньше го числа вычитают большее (17-38=21), при решении сложных примеров выполняют только одно действие (12+14-8=26).
Допускаются и такие ошибки: учащиеся складывают или вычитают, не обращая внимания на разряды: еди ницы складывают с десятками (37+2=57, 38-20=36), из меньше го числа вычитают большее (17-38=21), при решении сложных примеров выполняют только одно действие (12+14-8=26).
Характерно, что учащиеся школы VIII вида долгое время не овладевают рациональными приемами вычисления, задерживаясь на приемах пересчитывания конкретных предметов, присчитывания по единице.
Причины ошибок заключаются в недостаточно твердом знании таблиц сложения и вычитания в пределах 10 и 20 (39-7=31, 42+7=48), в недостаточно твердом знании и понимании позиционного значения цифр в числе или в неумении использовать свои знания на практике, а также в особенностях мышления школьников с интеллектуальным недоразвитием.
Последовательность изучения действий сложения и вычитания обусловлена нарастанием степени трудности при рассмотрении различных случаев.
1.Сложение и вычитание круглых десятков (30+20, 50-20,
решение основано на знании нумерации круглых десятков).
2.Сложение и вычитание без перехода через разряд.
154
В+5 35-5=30 41-2=45
|В+30 3.5-20=5 47-32=47-30-2
5+26=30+20+6 56-20=5 47-42=47-40-2
86+30 56-26=56-20-6 47-27=47-20-7
145+2=40+5+2
145+32=45+30+2
р8. Сложение двузначного числа с однозначным, когда в сумме йучаются круглые десятки. Вычитание из круглых десятков Нозначного и двузначного числа:
40-5=
40-23=40-20-3
40-33=40-30-3
4. Сложение и вычитание с переходом через разряд.
35+ 7
7+35
35+27
Г Все действия с примерами 1, 2 и 3-й групп выполняются прие-»ами устных вычислений, т. е. вычисления надо начинать с единиц высших разрядов (десятков). Запись примеров производится в строчку. Приемы вычислений основываются на знании учащимися нумерации, десятичного состава чисел, таблиц сложения и вычитания в пределах 10.
Действия сложения и вычитания изучаются параллельно. Каждый случай сложения сопоставляется с соответствующим случаем вычитания, отмечается их сходство и различие. дс1..=ои
дс1..=ои
К решению примеров привлекаются все пособия, которые и<
пользуются при изучении нумерации. Действия производятся о6>
зательно на счетах.
2) 30+26 26+30 „„ „„
Объяснение решения примеров данного вида проводится также на пособиях (абак, арифметический ящик, счеты). Полезно пока зать учащимся подробную запись выполнения действия:
30+26
56=50+ 6 50-30=20 20+ 6=26
или 30+26=30+20+6=50+6=56.
Этой записью учитель пользуется только при объяснении. Ученикам же нужно показать короткую форму записи, но требовать устного комментирования при выполнении действий, при записи — подчеркивания десятков:
Указанные выше случаи сложения, а также вычитания решаются ответственно одинаковыми приемами. Однако по трудности они не—юзначны. Для школьника с нарушением интеллекта значительно 1уднее к меньшему числу прибавить большее. (2+7)-9-7 — это |иболее трудный случай табличного вычитания. Все это говорит о ом, что, соблюдая требование постепенности нарастания трудностей (фи решении примеров, необходимо учитывать не только приемы вы-(шслений, но и числа, над которыми выполняются действия. Объяснение:
Объяснение:
«В числе 45 — 4 десятка и 5 единиц. Отложим число на абаке. [Прибавим 2 единицы. Получим 4 десятка и 7 единиц, или число 47».
45+12
12=10+ 2 45+10=55 55+ 2=57
или
45+12=45+10+2 57-12=57-10-2
Такой прием целесообразен потому, что при вычитании с переходом через разряд применение приема разложения на разрядные слагаемые двух компонентов приведет к вычитанию из меньшего числа единиц уменьшаемого большего числа единиц вычитаемого (43-17, 43=40+3, 17=10+7, 40-10, 3-7).
30+26=56 26+30=56
Полезно выполнять действия на счетах.
Следует отметить, что некоторые учащиеся долгое время не могут научиться проводить рассуждения при решении примеров, но с их решением на счетах легко справляются, не смешивают разряды. Этим ученикам можно разрешать пользоваться счетами.
Для большей наглядности, лучшего понимания позиционного значения цифр в числе запись единиц и десятков на доске и в тетрадях некоторое время можно делать разными цветами. Это важ*ю для тех учащихся, которые плохо различают разряды.
Это важ*ю для тех учащихся, которые плохо различают разряды.
| 3) 45+2 42+7 | 47-2 49-7 | 4) 45+12 42+17 | 57-12 59-17 57-52 |
50- 5 70-25, 50+45
50-5 _ 70-25
45+25
| 45=40+ 5 5+ 5=10 40+10=50 | 25=20+ 5 45+20=65 65+ 5=70 | 50=40+10 10- 5= 5 40+ 5=45 | 25=20+ 5 70-20=50 50- 5=45 |
Рассуждения при решении этих примеров на сложение ничем не отличаются от рассуждений при решении примеров на сложение двух предыдущих видов, хотя последние и более трудны для учащихся.
При рассмотрении случаев вида 50-5 надо указать на то, что необходимо занять один десяток, так как в числе 50 число единиц равно 0, раздробить десяток в единицы, от десяти отнять 5, а оставшиеся десятки сложить с разностью.
ч
Для удобства и большей четкости изложения вычислительна приемов мы рассмотрели каждый новый случай изолированно. 1 процессе обучения учащихся устным вычислительным прием! необходимо каждый новый случай сложения или вычитания ря сматривать в неразрывной связи с предыдущими, постетч включая новые знания в уже имеющиеся, постоянно их сопост ляя. Например, 45+2, 45+5, 45+32, 45+35. Сопоставить примеры, найти общее и различное. Составить примеры такого вида.
Такого рода задания позволят увидеть сходство и различие примерах, заставят учащихся думать, рассматривать каждый он чай сложения не изолированно, а в связи и взаимообусловленном ти. Это позволит выработать обобщенный способ устных вычислс ний. (Решить, сравнить вычисления и составить похожие приме ры: 40-6, 40-26, 40-36, 40-30.)
4) Сложение и вычитание с переходом через разряд (2-я труп па примеров) выполняются приемами письменных вычислений т. е. вычисления начинаются с единиц низших разрядов (с еди ниц), за исключением деления, а запись дается в столбик.
100 100
5 ~ 35
Учащиеся знакомятся с записью и алгоритмами письменного сложения и вычитания и учатся комментировать свою деятельность. Необходимо сопоставлять различные случаи сначала сложения, затем вычитания, устанавливать черты сходства и различия, включать учащихся в процесс составления аналогичных примеров, учить их рассуждать. Только подобные приемы могут дать коррек-ционный эффект.
Когда учащиеся научатся выполнять действия сложения и вычитания с переходом через разряд в столбик, их знакомят с выполнением этих действий приемами устных вычислений.
т т
41-23 41-33
Объяснение обычно проводится на абаке, палочках, брусках или кубиках арифметического ящика, счетах. 158
штель предлагает прочитать пример, отложить на абаке 38, предварительно выяснив его десятичный состав. Снача-I единицам нужно прибавить 3 единицы: число 8 добавляется :ятка, т. е. прибавляются 2 единицы; образовавшиеся десять иииц заменяются одним десятком, получается 4 десятка. К 4 Гнткам прибавляется еще 1 единица.
При вычитании из двузначного числа однозначного с перехо-через разряд сначала вычитаются все единицы уменьшаемого, I затем из круглых десятков вычитаются оставшиеся единицы Считаемого.
Подробная 38+3=41 38+2=40 40+1=41
Как при сложении, так и при вычитании надо разложить второе лагаемое или уменьшаемое на два числа. При сложении второе лагаемое раскладывается на такие два числа, чтобы первое допол-яло число единиц двузначного числа до круглого десятка.
При вычитании вычитаемое раскладывается на такие два Числа, чтобы одно было равно числу единиц уменьшаемого, т. е., I чтобы при вычитании получилось круглое число.
При выполнении действий трудность для учащихся представляет умение правильно разложить число, выполнить последовательность нужных операций, запомнить и прибавить или вычесть оставшиеся единицы.
Например, выполняя действие 54+8, ученик может правильно дополнить 54 до 60. Затруднение вызывает разложение числа 8 на 6 и 2. Число 6 ученик использует, чтобы получить круглое число, но сколько еще единиц осталось прибавить к круглым десяткам (к 60), он забывает.
Учитывая это, необходимо, прежде чем рассматривать случаи данного вида, еще и еще раз повторить состав чисел первого десятка, провести упражнения на дополнение чисел до круглых десятков, например: «Сколько единиц не хватает до 50 в числах 42, 45, 48, 43, 4? Какое число нужно прибавить к числу 78, чтобы получить 80?» Надо рассматривать случаи вида 37+3+2=40+2=42 и добиваться ответа на вопрос: «Сколько всего единиц прибавили к числу (37)?»
43-3-2=40-2=38
«Сколько всего единиц вычли из числа 43?» Значит, 43-5=я Для некоторых учащихся школы VIII вида при решении тал вида примеров используется частичная наглядность, наприм 38+7. должны уметь выполнять на счетах.
Например: 56+27. Сначала отложим число 56. Прибавим 20. Получилось 76. Прибавим 7. 76 дополним до 80, заменим 10 единиц одним десятком, прибавим к 8 десяткам еще 3 единицы.
Выполним вычитание на счетах (рис. 11): 41-24.
Чтобы учащиеся приобрели умения и навыки в решении приме-на сложение и вычитание с переходом через разряд, надо |полнить достаточно много упражнений. Примеры можно давать
с двумя, и с тремя компонентами, чередуя действия сложения и пычитания. Решаются и такие примеры: 48+(39-30).
Расположение материала с постепенно нарастающей степенью Фудности позволяет учащимся овладеть необходимыми приемами при выполнении действий сложения и вычитания. Успех овладения вычислительными приемами во многом зависит от активности | лмих учащихся.
В школе VIII вида всегда будет группа детей, которым оказываем ся недоступным овладение устным вычислительным приемом при Решении примеров с переходом через разряд (27+38, 65-28). Такие учащиеся будут решать примеры приемами письменных вычислений (в столбик).
При изучении сотни закрепляется название компонентов и результатов действий сложения и вычитания. Чтобы названия компонентов вошли в активный словарь учащихся, необходимо при чтении выражений пользоваться этими названиями, например: «Первое слагаемое 45, второе слагаемое 30. Найти сумму. Уменьшаемое 80, вычитаемое 32. Найти разность. Найти сумму трех чисел: 30, 18, 42. Как называются числа при сложении? От суммы чисел 20 и 35 отнять 40» и т. д.
При изучении сотни учащиеся знакомятся с нахождением неизвестных компонентов сложения и вычитания.
При изучении действий сложения и вычитания в пределах 10 и 20 учащиеся решали примеры с неизвестными компонентами, используя прием подбора, например: П+3=10, 4+П=7, П-4=6, 10-П=4.
При изучении сотни неизвестный компонент обозначается буквой и учащиеся знакомятся с правилом нахождения неизвестных компонентов.
Прежде чем познакомить учащихся с решением примеров, содержащих неизвестный компонент, надо создать ситуацию, придумать такую жизненно-практическую задачу, которая дала бы учащимся возможность понять, что по двум известным компонентам и одному неизвестному можно найти этот третий неизвестный компонент.
6 Перова М. Н.
Например: «В коробке лежит несколько карандашей, туда но. жили еще 3 карандаша. В коробке стало 8 карандашей. Скол) карандашей было в коробке?»
Эту задачу следует драматизировать. Ученик берет коробку карандашами (количество карандашей в ней неизвестно), кла; туда 3 карандаша. Пересчитывает все карандаши в коробке. I оказывается 8. Учитель предлагает количество карандашей, ко1 рое было (т. е. неизвестное), обозначить буквой х. и записа х+3=8. Если от 8 карандашей отнимем 3 карандаша, котор добавили, то останется 5 карандашей: *+3=8, х=8-3, х=5.
Проверка. 5+3=8 8=8
После решения еще нескольких задач с реальными предметами можно сделать вывод: «Чтобы найти неизвестное слагаемо! нужно из суммы вычесть известное слагаемое».
5+лг=8
Нахождение неизвестного уменьшаемого также лучше всей как показывает опыт, показать на решении жизненно-практиче кой задачи, например: «В корзине лежит несколько грибов (х), г нее взяли 5 грибов (берем), осталось в корзине 4 гриба (сосчит.1 ли). Сколько грибов было в корзине?»
Задача обыгрывается. Обозначим грибы, которые были в корзи не, буквой х и запишем: х-5=4. «Каким действием можно уз нать, сколько грибов было?» (Сложением.)
л:=4+5
Проверка. 9-5=4 4=4
Вопросы и задания
1.Составьте тематический план изучения нумерации чисел первой сотни
в 3-м классе школы VIII вида.
2.Назовите этапы изучения нумерации чисел первой сотни.
3.Какова последовательность изучения сложения и вычитания в пределах
100?
4.Составьте конспект урока, целью которого является ознакомление уча
щихся с алгоритмом письменного сложения или вычитания в пределах 100.
5.Выпишите из учебника по математике для 3-го класса 3-5 видов
упражнений на развитие и коррекцию анализа и синтеза, сравнение. Со
ставьте по 5-б упражнений, направленных на решение аналогичных задач.
Глава 11
Конспект урока- игры «Сложение и вычитание в пределах 100»
Урок-сказка.
Тема: Сложение и вычитание в пределах 100. Закрепление.
Необходимое оборудование и материалы: учебники, тетради, компьютер, проектор, экран.
Цели урока:
Образовательные.
- Закрепление умения учащихся прибавлять и вычитать в пределах 100.
- Совершенствование умения решать задачи разных видов.
- Формирование умения работать самостоятельно, в группе.
Развивающие.
- Развитие логического мышления, творческого воображения, внимания памяти, познавательной деятельности и творческих способностей обучающихся.
Воспитательные.
- Воспитывать положительное отношение к учебному процессу, интерес к предмету и литературе.
- Воспитывать взаимопонимание, взаимопомощь, культуру поведения на уроке, аккуратность, самостоятельность, терпение друг к другу.
Слайд 1
Ход урока:
I. Организационный момент.
Прозвенел звонок на урок. — Добрый день, ребята! Мне приятно вас всех видеть. Давайте подарим друг другу хорошее настроение:
На части не делится солнце лучистое
И вечную землю нельзя поделить,
Но искорку счастья луча золотистого
Ты можешь, ты в силах друзьям подарить.
II. Психологический настрой.
Слайд 2
— Сегодня необычный урок математики. На нём все ученики класса отправятся в волшебный мир.
Наш урок будет похож на сказку,
Нам без знаний никуда.
Взяв с собой тетрадь, учебник, ручку и указку
Отправляемся туда.
— И так, готовы вы отправиться в сказку?
Когда колокольчик прозвенит 3 раза надо:
2 раза топнуть левой ногой,
3 раза хлопнуть над головой.
Повернуться в правую сторону,
левую, назад.
Произнести: 1, 2, 3 — сказка в гости приходи!
III. Постановка цели.
— Какую тему мы изучали на прошлых уроках. (Сложение и вычитание в пределах 100. Решение задач)
-Какие цели мы себе поставим на этот урок? ( Сегодня мы закрепим полученные раннее знания по этой теме, умение решать задачи.)
Нашего героя будут ждать испытания, а мы должны будем ему помогать своими знаниями.
-Скажите, где нам в жизни может пригодиться умение прибавлять и вычитать? (при покупке товара, при составлении чертежей, для дальнейшего обучения)
— А как называется сказка, кто её герои и кто написал вы узнаете выполнив первое задание.
V. Актуализация, повторение, закрепление и отработка полученных знаний.
Слайд 2
Задание 1.
— Перед вами числа: 5, 3, 19, 7, 1, 67, 43
— На какие две группы разделим числа? (двухзначные — (43, 67,19) (однозначные –1, 3, 5, 7, )
— Расположите их в порядке возрастания и расшифруйте название сказки. 1, 3,5,7,19,43,67
— Название сказки узнали, Колобок
— Главного героя тоже, Колобок
А кто написал? ( народ)
Слайд 3
— А чтобы продолжить путешествие и встретиться со следующими героями вот вам
Задание 2.
Слайд 4.
Перед вами выражения разделите их на две группы и решите их .
47 +12 = 32 + 16=
73 – 11 = 82 + 18 =
96 – 52 = 25 – 15 =
46 – 35 =
— По какому признаку вы поделили выражения на группы?
— Вспомним названия компонентов действия “ + ” и “ – ” слагаемое, слагаемое, сумма
Уменьшаемое, вычитаемое, разность.
Проверьте свои вычисления по образцу. Слайд 5.
47+12 = 59 Д 73 – 11 = 66 Б
32 + 16 =48 Е 96 – 52 = 44 А
82 + 18 = 100 Д 25 – 15 = 10 Б
46 – 35 = 11 А
Cлайд 6
— И так, в домике с резными окнами жили — поживали дедушка да бабушка.
Вот дедуля и просит: “Испеки мне жёнушка колобок как в сказке, благо, что муки у нас вдоволь.
— А на двери замок висит, да не простой, а кодовый. Заторопилась, заволновалась бабуля, а комбинацию цифр то и позабыла
— Давайте поможем ей вспомнить код замка.
|
10 |
20 |
30 |
40 |
50 |
|
10 |
8 |
6 |
4 |
2 |
— Необходимо заполнить пустые ячейки, соответствующими
числами и объяснить выбор.
Слайд 7
— Открыла бабуля с нашей помощью замок, вошла в кладовую, взяла муки, замесила тесто на сметанке, скатала колобок. Испекла и поставила на окошко студиться.
Полежал колобок, посмотрел по сторонам, а потом скатился на завалинку, с завалинки на травку, с травки на дорожку и покатился по дорожке
Слайд 8. (Загадка)
— Привет, Зайчишка!
— Привет, какая встреча, я тебя Колобок сейчас съем. Ты такой румяненький!
— Нет, ты меня не съешь, я тебе нужен. Ведь смотрю, ты задание выполнить не можешь. А задания то в Лесной школе не простые, а я могу тебе помочь.
— Обрадовался Зайка, поблагодарил Колобка за помощь и пожелал ему счастливого пути.
— А колобок устал немного и предлагает отдохнуть.
VI. Физ. минутка
Вы устали, засиделись?
Вам размяться захотелось?
Отложите вы тетрадки,
Приступаем мы к зарядке.
Раз – подняться, потянуться,
Два – согнуться, разогнуться,
Три – в ладоши три хлопка, головою три кивка,
На четыре – руки шире,
Пять – руками помахать,
Шесть – за парту тихо сесть.
Семь, восемь — лень отбросим.
Слайд 9.
— Отдохнул колобок вместе с ребятами и покатился дальше.
— Здравствуй, Колобок. Вот ты мне и попался.
— А зачем я тебе?-
— Съесть хочу, проголодался малость.
— Ничего у тебя не получится. Ты плохо в математике разбираешься, а я со своими друзьями могу тебе помочь.
— Это верно, задали мне задание не простое.
А) 27 < 16 +22
Б) 42+5 < 47 б) в)
В) 55 + 13 < 68
— Молодцы снова мы выручили колобка и помогли волку.
— Он доволен остался, а колобок покатился дальше.
Слайд 10,
— Катится и видит сидит…
— Медведь и читает задачу:
В ведро вмещается 10 л мёда, а в бочонок на 39 л больше.
Сколько литров мёда в ведре бочонке вместе?
— Увидел Мишенька колобка, забыл про задачу и говорит: Здравствуй, колобок, уж больно ты аппетитный, съем я тебя!
— Где тебе косолапому съесть меня, задачу решить не можешь. Давай лучше я тебе помогу.
— Поможем, ребятки?
Составим краткую запись
— прочтите условие задачи
— вопрос
— Что известно,
— что неизвестно,
— что надо найти?
— Какое первое действие?
— Почему именно сложение?
— Какое второе действие?
(дети записывают решение, взаимопроверка) 1)39 + 10 = 49(л) в бочонке
2) 40 + 39 = 79 (л) всего
Слайд 11. Хитрая задача Лисы.
Задача 2. Волк, медведь и заяц до встречи с колобком собирали на поляне цветы: ромашки, колокольчики и васильки. Волк собирал не колокольчики и не васильки. Медведь – не васильки. Какие цветы собирал каждый из героев? (Волк – ромашки, медведь – колокольчики, заяц – васильки)
Слайд 12. Молодцы.
Итог урока.
Рефлексия
— Давайте оценим свою работу.
-Вспомним, что удалось повторить за урок?
— Что показалось трудным?
— Какое задание было самым интересным?
— А с каким настроением вы уходите с урока выразите на лице колобка
и поместите на доску . (изображение лиц колобка)
.
— Я вам тоже хочу сказать за такое удивительное общение ,спасибо.
— Спасибо что вы дружно помогали друг другу и героям сказки. Но помните: -
— В мире много сказок грустных и смешных
Нам нельзя без дружбы.
Пусть герои сказок
Дарят нам тепло.
Пусть добро навеки побеждает зло!
Обучение сложению и вычитанию чисел до 100
Это третья из 4-х частей серии обсуждений по обучению сложению и вычитанию на начальных уровнях начальной школы. Для других частей этой серии, посвященных другим диапазонам чисел, перейдите по следующим ссылкам:
Изучение сложения и вычитания чисел до 100 — это следующий этап после чисел до 20. В этой серии мы поговорим о подходы к обучению, которые мы рекомендуем для чисел от 20 до 100 и общих проблем, с которыми сталкиваются студенты.
Базовое мастерство сложения и вычитания до 20 является основополагающим для мастерства в числах до 100. Для обсуждения распространенных ошибок и стратегий обучения числам до 20, пожалуйста, обратитесь к Части 2 этой серии обсуждений по Сложению и Вычитанию.
Общая стратегия и порядок инструкцийЭтот диапазон чисел (от 20 до 100) может быть обучен в двух частях:
- Числа от 20 до 40 и
- Числа от 40 до 100.
Если возможно, примените спиральный подход и преподайте эти две темы отдельно, с небольшой темой, например Измерения или формы между ними. Этот спиральный подход не только позволяет студентам усвоить и усвоить нижний диапазон 20-40, прежде чем они займутся более требовательным диапазоном 40-100, он также разбивает, казалось бы, гигантские задачи обучения: умело складывать и вычитать в пределах 100 на два. меньшие шаги.
В рамках каждой из этих двух тем / диапазона номеров мы рекомендуем преподавать в следующей последовательности:
- Добавление
- числовая строка
- значение разряда
- сложение кратных 10
- Без перегруппировки
- прибавление 2-значного числа к 1 -цифровой номер, эл.грамм. 23 + 5
- добавить 2-значное число к 2-значному номеру, например 23 + 15
- При перегруппировке
- добавьте 2-значное число к 1-значному номеру, например 37 + 8
- добавить 2-значное число к 2-значному номеру, например 29 + 23
- Вычитание
- числовая строка
- значение разряда
- вычесть кратные 10
- Без перегруппировки
- Вычесть однозначное число из двузначного числа, например 38-2
- Вычесть двузначное число из двузначного числа e.g 33-12
- С перегруппировкой
- Вычтите однозначное число из двухзначного числа, например 43-7
- Вычтите двузначное число из двузначного числа, например, 51-18
Имея это в виду, мы далее обсудим, что включает в себя каждый элемент, и выделим некоторые распространенные ошибки.
Числовая строкаРаспространенная ошибка студентов, когда они мысленно рассчитывают (и аналогично при обратном счете), является включение начального числа, например.g 28 + 3 равно 28, 29, 30 вместо 29, 30, 31. Чтобы минимизировать это, мы считаем целесообразным начать с числовой строки. Хорошее понимание числовой прямой также имеет решающее значение для развития сильного чувства числа.
Сложение с числовой линиейВ общем, первоклассники и второклассники должны уметь использовать числовую линию как для счета, так и для обратного счета.
Таблицы стоимости местаСтоимость места — ключевая концепция перегруппировки. Дети должны в полной мере понять, например, что 36 = ? десятков и ? единиц = 3 десятков 6 единиц
Однако многие дети могут отвечать на вопросы сложения и вычитания, не понимая полностью разницы.Они просто разбивают числа, например 36 на 3 и 6 и поместите их в соответствующие поля десятков и единиц. Хороший способ проверить их понимание — спросить их следующее.
36 = 1 десять ? единиц = 1 десятков 26 единиц
36 = 2 десятков ? единиц = 2 десятков 16 единиц
Сложение и вычитание кратных 10Учащимся должно быть комфортно складывать и вычитать кратные десятки, e.грамм.
14 + 20 = 34
Хотя это может показаться тривиальным, нередки случаи, когда студенты борются с этим. Мы считаем, что для этого особенно полезен подход «Конкретно — Изобразительное — Абстрактное». После использования юни-кубов в десятках и единицах для сложения чисел 14 и 20 учащиеся переходят от конкретного к графическому изображению, чтобы связать свой существующий опыт. Необходимо следить за тем, чтобы конкретные и графические изображения были тесно связаны. Многие ученики способны ухватить конкретные представления, но быстро теряются, когда графические представления имеют мало общего с их физическими манипуляциями.
Ученики должны понимать, что число 14 состоит из 1 десятки и 4 единиц, а число 20 состоит из 2 десятков. Чтобы сложить числа, мы складываем единицы и десятки отдельно. На этом этапе могут быть очень полезны числовые связи, напоминающие ученикам, что 14 состоит из 10 и 4.
Сложение без перегруппировки
Еще одним хорошим учебным пособием является диаграмма сотен, где учащиеся могут указать, что числа увеличиваются в десять раз по мере того, как они спускаются вниз по столбцам диаграммы.
В этом примере ниже учеников просят заполнить недостающие числа в таблице частичных сотен.
Сложение и вычитание, умноженное на десять с диаграммой частичных сотен Сложение без перегруппировкиУ студентов обычно нет проблем с правильным ответом на сложение без перегруппировки. Тем не менее, стоит понимать стратегии, которые используют учащиеся. На этом этапе многие еще рассчитывают. Хотя это не является математически неверным, исследования показали, что учащиеся, которые могут использовать и применять свое понимание ценности места, как правило, добиваются большего успеха в более поздние годы.
При добавлении 2-значного числа к 1-значному числу (например, 23 + 5) простой и эффективный способ состоит в том, чтобы разложить 23 на 2 десятки и 3 единицы, а затем добавить единицы и десятки по отдельности.
Сложение с перегруппировкойСложение с перегруппировкой часто бывает сложнее, и студентам нужны 2 базовых навыка, чтобы преуспеть.
- Добавляйте плавно в пределах 20.
- Прочный фундамент в виде стоимости.
Студенты должны быть в состоянии ответить на эти вопросы о числовом значении, прежде чем продолжить.
16 единиц =? десять ? единиц = 1 десять 6 единиц
3 десятка 12 единиц = 42
а. Конкретный — графический — абстрактный подход
На примере 26 + 7,
- Конкретное представление : Используя манипуляторы, 26 представлено как 2 десятка 6 единиц, а 7 представлено как 7 единиц на диаграмме значений разряда;
- Иллюстрированное представление : В числовом предложении число 26 разложено на 2 десятки и 6 единиц графически с использованием числовых связей;
- Абстрактное представление : Продолжая фокусироваться на разрядах, мы находим сумму, складывая единицы и десятки, где 2 десятка 13 единиц равны 33.
Для учащихся важно соединить эти три представления и понять концепцию разряда. Это очень важно для настройки стандартного алгоритма на следующем этапе.
Сложение с перегруппировкой с разметкойb. Стандартный алгоритм
Многие студенты не испытывают проблем с правильными ответами на стандартный алгоритм. Однако бывает сложно выяснить, «следуют ли они процедурам» или «действуют с пониманием».Вот несколько методов, которые мы используем.
- Учиться с пониманием
a. Существует тщательная настройка, чтобы обеспечить тесную связь между настройкой разряда и стандартным алгоритмом. В настройке разряда 26 разложено на 2 десятки и 6 единиц. На следующем шаге 6 единиц добавляются к 7 единицам, где сумма 13 единиц прибавляется к 2 десяткам, чтобы получить 33. Это сразу же связывается со стандартным алгоритмом.
Сложить в пределах 100: соединение разряда значений со стандартным алгоритмомb.Мы используем язык расстановок в обучении и изучении стандартного алгоритма. Например, вместо того, чтобы сказать «1 плюс 1 равно 2», мы говорим «1 десять плюс 1 десять это 2 десятка».
Сложите в пределах 100, используя язык разряда2. Тест на понимание
a. Часто компоненты стандартного алгоритма сложения или вычитания предварительно заполняются правильными числами. Чтобы проверить понимание учащимися значения места, мы используем промежуточный шаг, предоставляя учащимся пустые поля, чтобы они могли заполнить соответствующие числа.
Тестирование на понимание значения разрядаВ приведенном выше примере многие ученики будут указывать «7» в значении десятков для 7 + 26. Однако, получив ответ и сравнив с предыдущим ответом на 26 + 7, они понял бы, что, поскольку 26 + 7 должно иметь то же значение, что и 7 + 26 (коммутативное свойство), что-то должно быть не так с их работой!
г. Многие студенты привыкли составлять десятку при вычислении стандартного алгоритма. Непримеры — это очень полезный способ показать, что число, которое «переносится», представляет собой разряды десятков и не обязательно должно быть «1».Например, опросите учащихся на такие суммы, как «56 + 8 + 7». Сумма единиц — 21, составленных десятков — «2», а не «1».
Тестирование на понимание значения места Вычитание — Концепции для обученияВычитание обычно представлено как «убрать». В статье «Сила математики — как помочь вашему ребенку полюбить математику, даже если вы этого не сделаете» Патрисия Кларк говорит о важности ознакомления наших учеников с различными концепциями вычитания.
Искусственное разделение значений вычитания создает ненужные барьеры.Детям необходимо одновременно выучить четыре способа вычитания. Включите все четыре в свой разговор.
— Сила математики: как помочь ребенку полюбить математику, даже если вы этого не сделаете, Патрисия Кларк.
Ниже приведены некоторые примеры.
- Взять — например, У меня 5, и я забираю 3. Сколько у меня?
- Сравнение / различие — например, У меня 5, а у вас 3, у кого больше? На сколько больше?
- Отсутствует добавление — например, У меня есть 25 долларов. Мне нужно 30 долларов, чтобы купить сумку. Сколько еще мне нужно?
- Движение — эл.грамм. Я проезжаю 7 миль до библиотеки, разворачиваюсь и еду 5 миль обратно по тому же маршруту. Как далеко я от отправной точки?
Вычитание чисел от 20 до 100 обычно занимает в два раза больше времени, чем сложение. Для этого есть две основные причины. Во-первых, у них нет сильного чувства ценности места. Во-вторых, они все еще борются с вычитанием в пределах 20.
Вычитание без перегруппировкиПодобно сложению без перегруппировки, многие студенты не испытывают трудностей с вычитанием без перегруппировки.Тем не менее, снова важно внимательно изучить стратегии, которые могут использовать некоторые студенты. В статье «При чем тут математика?» Профессор математики Стэнфордского университета Джо Булер говорит о «сложной математике, которую использовали дети ниже среднего». При вычислении 16-13, вместо разложения 16 и 13 на десятки и единицы, вычитания десятков и вычитания единиц, дети ниже среднего начнут с 16 и начнут считать в обратном порядке (16-15-14-13-12-11-10- 9-8-7-6-5-4-3).
Когнитивная сложность этой задачи огромна, а место для ошибок огромно.
— «При чем тут математика?» Стэнфордский профессор математики Джо Булер
Эта математическая трудность, если не вмешиваться на более раннем этапе, может распространиться на большие числа до 40 и выше. Учащиеся, у которых есть прочная основа для числового значения, часто могут придумать смысл сложения и вычитания больших чисел без каких-либо дополнительных инструкций со стороны своих учителей.
В этом примере (1) учащимся нужно разложить 55 и 23 на десятки и единицы. (2) учащимся нужно отдельно вычесть десятки и единицы.
Вычитание в пределах 100: разложение десятков и единиц с использованием разряда Вычитание с перегруппировкойПри использовании стандартного алгоритма важно использовать «язык разряда».
Используя следующий пример, мы можем использовать «16 единиц вычитают 9 единиц» и «4 десятка вычитают 3 десятки» вместо «16 вычитают 9» и «4 вычитают 3». Это позволит учащимся увидеть, что мы вычитаем 30 из 40 вместо дискретных чисел 3 из 4. Это особенно важно, когда мы переходим к большим числам, исчисляемым сотнями.
Вычитание соединительного разряда со стандартным алгоритмом Связь между сложением и вычитаниемЧтобы лучше понять взаимосвязь между сложением и вычитанием, вопросы с пропущенными слагаемыми можно задавать в дополнение к обычным. По нашему опыту, ученики нередко сталкиваются с проблемами с пропущенными дополнениями. Чтобы помочь студентам, можно использовать числовую связь с отсутствующими частями. Связь с числами также особенно полезна при решении сложных задач со словами.
Связь между сложением и вычитанием Ментальная математикаБольшинство предыдущих стратегий, используемых для чисел до 20, следует пересмотреть для этого диапазона чисел, например
Кроме того, еще одна хорошая стратегия для внедрения на этом этапе — сокращение числа вдвое. Как правило, учащимся легко удваивать числа, но наоборот (деление пополам) им сложно. Детям обычно очень нравится разбивать «большие» числа пополам.
Например,
половина 60 равна 30.
половина 36 равна 18.
Для более продвинутых учеников они могут быть представлены стратегии разделения, например:
Умственная математика деление чисел вдвоеВ приведенном выше примере число 74 разбито на 60 и 14. В то время как оно не интуитивно понятно разделить 74 на 2 равные части, конечно проще с 60 и 14!
Числовые навыки, подобные этим, очень пригодятся позже в 5-6 классах, где ученики будут выполнять процедуры поиска наименьшего общего кратного, наибольшего общего множителя, простого факторизации, квадратного корня и кубического корня.По нашим наблюдениям, учащиеся, не овладевшие этими навыками на старших классах начальной школы, часто тратят слишком много времени на обработку простой математики, такой как 72 делить на 2 и т. Д., Что замедляет их при выполнении сложных процедур, что часто приводит к разочарованию и «отказу». ».
Чувство чиселНа этом этапе дети могут практиковаться в использовании мысленной числовой линии для интуитивного мышления. Например, они могут рассуждать, что 23 + 5 меньше 33 + 5, а 37-20 меньше 40-20.Они должны уметь сравнивать два набора чисел, не выясняя ответы.
Чувство числа Интуитивное рассуждениеЗаключение
Мы надеемся, что это обсуждение обучения «сложению и вычитанию чисел до 100» окажется полезным. На следующей неделе мы поговорим о типичных проблемах, с которыми сталкиваются при расширении обучения сложению и вычитанию чисел до 1000 и выше.
Подробнее об обучении сложению и вычитанию:
Использование сложения и вычитания в пределах 100 для решения одно- и двухэтапных задач со словами: CCSS.Math.Content.2.OA.A.1
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Задачи на сложение и вычитание для 2-го класса
Добро пожаловать на страницу задач на сложение и вычитание слов для 2-го класса.
Вот наша подборка бесплатных распечатанных рабочих листов с задачами на вычитание, которые помогут вашему ребенку
попрактикуйтесь в решении ряда задач на сложение и вычитание, используя числа до 100.
Каждый лист состоит из 5 или 6 задач на сложение и вычитание слов с числами до 100.
На каждом листе есть место для тренировки, чтобы ваш ребенок мог записать задачу и решить ее.
Мы разделили рабочие листы на текстовые задачи с перегруппировкой и без нее.
Использование этих листов поможет вашему ребенку:
- складывать и вычитать числа до 100;
- решать задачи на сложение и вычитание слов с перегруппировкой и без нее.
- распознавать язык, используемый при сложении и вычитании — сумма, сумма, разница, сколько еще и т. д.
Существует две версии каждого листа.
Первая версия (версия A) содержит проблемы, в которых перегруппировка не требуется.
Вторая версия (версия B) содержит похожие проблемы, но для их решения требуется перегруппировка.
Листы 1A, 1B, 2A, 2B, 3A и 3B содержат простые задачи со словами, в которых одно число нужно вычесть из другого.
На листах 4A, 4B, 5A и 5B есть двухэтапные задачи сложения и вычитания, где для решения проблемы требуются два шага.
К каждому листу прилагаетсяответов, а также расчет, необходимый для решения проблемы.
Все следующие листы представляют собой одноступенчатые задачи на сложение или вычитание слов.
Эти проблемы сложнее, чем перечисленные выше.
Каждая задача включает два шага для решения и может включать только сложение, вычитание или оба оператора.
Взгляните на наши задачи на вычитание слов для первоклассников.
На этой странице ваш ребенок научится решать простые задачи на вычитание слов с числами до 20.
У нас есть ряд таблиц вычитания из 3 цифр, которые разбиты на столбцы.
Взгляните на еще несколько наших рабочих листов, похожих на эти.
Здесь вы найдете еще несколько наших генераторов таблиц сложения и вычитания для создания ваших собственных таблиц сложения и вычитания.
Вот несколько листов для решения задач для второклассников.Большинство листов содержат «реальные» проблемы, связанные с животными.
Использование листов поможет вашему ребенку:
- применять свои навыки сложения, вычитания и умножения;
- применить свои знания об округлении и разметке;
- решить ряд проблем «реальной жизни».
Саламандры по математике надеются, что вам понравятся эти бесплатные распечатанные рабочие листы по математике. и все другие наши математические игры и ресурсы.
Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле комментариев Facebook внизу каждой страницы.
Рабочие листы для дополнений
Добро пожаловать на страницу дополнительных листов на Math-Drills.com, где мы добавим много положительных качеств к вашему обучению! На этой странице вы найдете рабочие листы сложения с фактами сложения и добавление двузначных чисел к добавлению столбцов и добавление с играми. В первый раздел мы включили несколько дополнительных печатных форм, которые должны помочь начинающему студенту.Обучение дополнительным фактам лучше всего проводить с помощью некоторых интересных обучающих стратегий.
Некоторые учителя и родители используют манипуляторы сложения, чтобы помочь ученикам понять основные факты сложения. Например, добавление групп «яблочных валетов» (хлопьев для завтрака) путем подсчета быстро приведет учащихся к пониманию концепции сложения. Чем раньше вы познакомите своих учеников с десятью базовыми блоками, тем лучше. Если вы еще не использовали их для подсчета, используйте их для базового сложения и покажите студентам, как работает перегруппировка.
Самые популярные дополнительные рабочие листы на этой неделе
Дополнительные таблицы фактов
Бесспорно, не лучший способ узнать дополнительные факты, но, несомненно, отличный способ подвести итоги. Таблицы дополнительных фактов являются бесценным ресурсом в любом домашнем или школьном классе.
Дополнительные таблицы
Сложение очень хорошо работает как таблица, поскольку слагаемые могут быть последовательными. Призовите студентов искать закономерности и научите их различным стратегиям усвоения фактов сложения.Для учащихся, которые еще не запомнили свои факты сложения, но которым необходимо знать их для более сложного урока математики, такого как сложение двузначных чисел, предоставьте им таблицу фактов сложения, чтобы они могли быстро найти факты сложения. Через некоторое время они, скорее всего, узнают факты, используя таблицу, и станут меньше полагаться на нее. Чтобы столы были более прочными, распечатайте их на картоне и ламинируйте. Их можно отобразить на экране или увеличить и распечатать на плакатной бумаге для использования всем классом.
Таблицы пятиминутного безумия
Пятиминутные диаграммы безумия — это сетки 10 на 10 для практики сложения фактов. В каждом квадрате учащиеся записывают сумму номера столбца и номера строки.
Кто-то называет безумными минутами или рассчитанными на время упражнениями, пятиминутное безумие предназначено для того, чтобы добавить немного больше волнения к отработке фактов сложения. Они идеально подходят для повышения способности учащегося быстро вспоминать дополнительные факты, что дает всевозможные преимущества в дальнейшей школьной жизни, в том числе предотвращает жалование школьных учителей на то, «что их ученики не могут даже складывать однозначные числа без использования калькулятора. .«
Общая цель состоит в том, чтобы заполнить одну таблицу менее чем за пять минут и набрать 98 процентов или выше, однако мы рекомендуем устанавливать личные цели для учащихся на основе первоначального теста. Если они бьются головой об стену через пару минут, задав всего несколько вопросов, им действительно не следует в данный момент завершать тренировку по сложению фактов по времени. Им еще предстоит кое-чему научиться. На этом этапе мы бы рекомендовали отказаться от манипуляторов.Если они ответят на вопросы за 1,5 минуты и ответят почти на все вопросы, они, вероятно, готовы к чему-то более сложному.
Five Minute
Addition Frenzies , которые включают одну таблицу сложения на страницеБезумное добавление одной страницы на страницу — не самое эффективное использование бумажных ресурсов, но они являются хорошей отправной точкой, особенно для младших школьников, которые недостаточно освоили свой почерк, чтобы уместить свои числа в меньшую таблицу.Они также отлично подходят для отображения на экранах или мониторах при групповых занятиях. Например, вы можете использовать интерактивную доску для заполнения таблицы.
Five Minute
Addition Frenzies , которые включают в себя четыре таблицы сложения на страницеБолее разумное использование ограничений на количество бумаги и фотокопий, наличие четырех таблиц на странице позволяет выполнять многодневную практику, совместную работу или использовать резак для бумаги, быструю стопку страниц для практики для студентов, которые заканчивают раньше.
Рабочие листы для сложения однозначных чисел
Большинство людей согласятся, что умение складывать однозначные числа быстро и в уме является важным навыком для успеха в математике. Различные дополнительные рабочие листы в этом разделе сосредоточены на навыках, которые учащиеся будут использовать на протяжении всей своей жизни. Эти рабочие листы не заставят учащегося учиться волшебным образом, но они ценны для подкрепления и практики, а также могут использоваться в качестве инструментов оценки.
Вертикально расположенное однозначное сложение
Итак, вам нужны практические листы для дополнения фактов? Вы их нашли.Используйте их для практики, оценивания, игр или просто для развлечения.
Сложение однозначных цифр с горизонтальным расположением
Не торопитесь? Эти дополнительные рабочие листы помогут учащимся, испытывающим трудности, делать это шаг за шагом, не беспокоясь о перегруппировке. Просто кучка красивых однозначных сумм.
Make Ten Стратегия добавленияСтратегия сложения «сделать десять» включает «разделение» второго слагаемого на две части.Первая часть объединяется с первым добавлением, чтобы получить десять, а вторая часть — это оставшаяся сумма. Эта стратегия помогает студентам быстро складывать в уме суммы более десяти. Например, складывая 8 + 7, ученики сначала понимают, что им нужно прибавить 2 к 8, чтобы получить 10, поэтому они делят 7 на 2 + 5. 8 + 2 дает 10, а еще 5 — 15. Навык может быть расширен. Во многих ситуациях, например, складывая 24 + 9, учащиеся понимают, что им нужно еще 6, чтобы получить 30, а 9 можно разделить на 6 + 3, поэтому 24 + 6 = 30 и еще 3 дает 33.Продолжая, учащиеся могут работать над распознаванием «дополнений» других важных чисел (см. Раздел ниже) для дальнейшей разработки этой стратегии.
Вопросы на сложение однозначных чисел с фокусными числами
Некоторым учащимся необходимо уделять внимание одному числу за раз. Может быть, они перегружены информацией, и им нужно добиваться успеха маленькими шагами.
Рабочие листы для сложения нескольких цифр
Для изучения сложения многозначных чисел можно использовать различные стратегии; не обязательно полагаться только на бумажные и карандашные методы.Базовые десять блоков могут помочь учащимся осмыслить сложение. Обучение студентов навыку сложения в уме слева направо поможет им в будущих исследованиях математики и жизни в целом. Например. 34 + 78 будет 30 + 70 = 100, 100 + 4 = 104, 104 + 8 = 112. Не забывайте об использовании оценок с этими листами.
Сложение нескольких цифр с перегруппировкой
НЕКОТОРЫЕКлассические таблицы сложения, некоторые этапы которых требуют перегруппировки, а другие нет.Версии со ВСЕМИ перегруппировками и БЕЗ перегруппировки следуют за этим разделом. Версии с разделителями тысяч находятся немного дальше по странице.
Сложение нескольких цифр с перегруппировкой
ВСЕПерегруппировка — вот в чем суть длинного сложения; эти рабочие листы дают студентам много практики, поскольку каждый шаг требует перегруппировки.
Сложение нескольких цифр с
NO перегруппировкойЕсли вы еще не освоили все факты сложения или длинный алгоритм сложения, этот раздел может быть для вас.Эти рабочие листы не требуют перегруппировки, поэтому они предоставляют дополнительный промежуточный навык для студентов, которым требуется немного больше руководства.
Горизонтально сложениеГоризонтальное сложение может побудить учащихся использовать математику в уме или другие методы сложения чисел. Одна из наиболее распространенных стратегий сложения в уме — это стратегия сложения слева направо (также называемая внешним интерфейсом). Это включает в себя сначала добавление более высоких разрядов.Другие стратегии для добавления многозначных чисел включают использование десятичных блоков или других манипуляций, числовых линий, разложение чисел и сложение частей, а также использование калькулятора.
Добавление
чисел фокусировки больше 9Эти рабочие листы включают числа больше, чем те, которые расположены вверху страницы.
Сложение нескольких цифр с
тысячами, разделенными запятымиИспользование запятой для разделения тысяч — самый распространенный способ форматирования больших чисел в английском мире.
Сложение нескольких цифр с
тысячами, разделенными пробеламиИспользование пробела для разделения тысяч больших чисел распространено в некоторых языках. В английском мире вы, скорее всего, встретите канадцев, форматирующих свои числа таким образом.
Сложение нескольких цифр с
тысячами, разделенными точкамиИспользование точки в качестве разделителя тысяч обычно не встречается в англоязычных странах, но, поскольку есть люди со всего мира, которые используют эти рабочие листы сложения, они включены.
Многозначное сложение с крупным шрифтом
По разным причинам иногда требуются дополнительные вопросы, выделенные более крупным шрифтом. Они должны соответствовать всем требованиям.
Различные другие рабочие листы для дополнений
Столбец Дополнительные рабочие листыДобавление столбцов — это не только упражнение в бухгалтерском учете, оно также развивает умственные навыки сложения, которые пригодятся в повседневной жизни. Для добавления столбцов чисел доступны различные стратегии.Традиционный метод — использовать карандаш и бумагу, также известный как сложение справа налево, когда учащиеся складывают и перегруппировываются, начиная с наименьшего места (в данном случае с единиц), и переходят к наибольшему месту. Мысленный подход может включать в себя учеников, идущих слева направо, где сначала добавляется большее место. Это легче уследить в уме, но время от времени требуется корректировка в предыдущих ответах. Например, сложите 345 + 678 + 901. Сначала сложите 300, 600 и 900, чтобы получить 1800, затем сложите по очереди 40, 70 и 0, чтобы получить 1910, затем обработайте 5, 8 и 1, чтобы получить 1924.Попутно вам приходилось корректировать итоговую сумму, но держать ее в голове намного проще, чем переносить в голову метод карандаша и бумаги.
Добавление с поддержкой сетки
Добавление с поддержкой сетки помогает учащимся, у которых возникают проблемы с составлением разметочных значений. Возможно, немного попрактиковавшись, они смогут лучше понять не только выстраивание значений разряда, но и то, почему это делается. Например, указание на то, что 5 из 659 означает 50, полезно для того, чтобы помочь учащимся понять значение разряда в том, что касается сложения.
Добавление с помощью
игрЭти дополнительные рабочие листы также помогают учащимся развивать умственные навыки сложения, но используют игровой контекст для знакомства и интереса. В рабочих листах с игральными картами валет считается за 11, королева — за 12, король — за 13, а туз — за 1. Игра в математические игры, наслаждаясь общением с друзьями, — отличный способ развить стратегическое мышление и свободное владение математикой у детей.
Добавление дополнений различных суммПоиск дополнительных чисел может очень помочь учащимся в развитии умственных арифметических навыков и углублении их понимания чисел.
Сложение
двойников чиселИспользование стратегии сложения удвоений может помочь учащимся быстрее обрабатывать дополнительные вопросы с помощью мысленной математики. Чтобы использовать эту стратегию, учащиеся должны понимать, что два числа близки к одному и тому же значению (обычно на одно или два). Они также должны распознавать, насколько оно больше или меньше первого слагаемого. Типичный диалог с вопросом 15 + 16 может выглядеть так: «Я вижу, что второе число больше первого на 1.Если я удвою первое число и добавлю 1, я получу свой ответ. 15 удвоенных — 30 плюс один — 31. 15 + 16, следовательно, 31 ».
Добавление
других систем счисленияНе обычно преподают в современных школах, добавление в другие системы счисления может растянуть умы учащихся и найти немало важных приложений, особенно в сфере технологий. Например, вы обнаружите, что двоичная, восьмеричная и шестнадцатеричная системы довольно часто используются в компьютерных технологиях.Четвертичные числа могут использоваться в генетике для хранения последовательностей ДНК. Двенадцатеричная система иногда предлагается как система, превосходящая десятичную
.Сложение и вычитание двух цифр (с целью и значением)
Сложение и вычитание двузначных чисел — сложная задача, требующая сочетания навыков. Обретение этой способности не происходит случайно: оно начинается с выработки твердого понимания двузначных чисел, задействует способность использовать понимание значения места и завершается использованием свойств операций для сложения и вычитания.Это чрезвычайно важная цель (и не самая легкая), поскольку свободное владение многозначными числами будет основываться на этих знаниях.
На протяжении всего курса Happy Numbers мы развиваем у учащихся навыки счета в трех областях для поддержки обучения:
1. Значение числа и разряда
2. Работа с круглыми числами
3. Сложение и вычитание 2-значных чисел
Эти этапы подготавливают учащихся к успешному сложению и вычитанию двузначных чисел и пониманию значения математики.
В этом посте мы расскажем вам о некоторых упражнениях, которые мы используем для понимания этих трех областей, и дадим вам всестороннее представление о том, что за ними стоит. Итак, давайте погрузимся в мир ощущения чисел и посмотрим, как сочетание технологий и педагогики может помочь вашим ученикам овладеть математикой!
Все упражнения, упомянутые здесь, являются частью курса HappyNumbers.com.
Этап 1: смысл числа и значение места
Для того, чтобы складывать и вычитать двузначные числа с пониманием, учащимся требуется прочная основа чувства числа и разметки.Затем они будут готовы узнать, что сложить 20 + 50 так же просто, как сложить 2 + 5 (при этом концептуально понимая разницу между 20 + 50 и 2 + 5). Начиная с первого класса, Happy Numbers усиливает концепцию «десять» и то, как использовать разрядную ценность для добавления или вычитания десяти или единицы.
Например, в этом упражнении используется таблица сотен и забавная игровая цель по кормлению кролика для закрепления этих навыков:
Мы ведем студентов по извилистой тропинке к пещере кролика, предлагая им заполнить недостающие числа.Для этого они должны понимать структуру диаграммы сотен, а также уметь прибавлять или вычитать 1 или 10 из любой позиции на диаграмме:
В другой версии диаграммы сотен фигура поднимается по лестнице из одного окна в другое, чтобы представить сложение и вычитание десятков. Сначала ученики определяют номер, на который он приземляется:
.Сначала студентам предоставляется множество окружающих цифр на диаграмме.По мере того, как они продвигаются в этом упражнении, мы удаляем числа, чтобы представить большую проблему:
Когда ученики знают начальную и конечную точки, они заполняют соответствующее уравнение, указывая круглое число, представленное подъемом:
Другие упражнения направляют внимание учащегося на единичное место, как это, в котором используются блоки с основанием 10, чтобы представить добавление однозначного числа к двузначному числу. Это упражнение имеет дополнительное преимущество в подготовке учащихся к работе с круглыми числами.
Учащиеся определяют недостающее слагаемое, необходимое для получения круглого числа:
Это моделирование позволяет познакомиться с алгебраическими выражениями, что важно для концептуального понимания:
Если учащиеся ответят неправильно, появится выделенная стопка розовых кубиков, указывающая им на пропущенное число:
Как только учащиеся продемонстрируют мастерство с помощью модели, мы переходим к использованию только уравнений:
Happy Numbers продолжает отслеживать ответы студентов, снова предоставляя модель в случае ошибки:
Это похоже на то, как учитель строит урок, предоставляя или удаляя поддержку, но Happy Numbers может сделать это немедленно, индивидуально.
После того, как учащиеся научатся складывать, чтобы получить круглое число, мы предлагаем аналогичное упражнение, которое требует, чтобы учащиеся как складывали, так и вычитали, чтобы получить ближайшие круглые числа:
В этом упражнении учащимся отображается числовая линия для поддержки в случае ошибки. Учащиеся сначала кладут мяч на числовую линию (задание, с которым они знакомы по предыдущим упражнениям):
, а затем определите число, которое нужно добавить или вычесть:
Стрелки и подсказки помогают ученикам определить правильный ответ, как если бы учитель работал с учеником один на один.
Такая же поддержка возникает для ошибок с вычитанием, используя знакомые цвета и символы:
Уравнения чередуют сложение и вычитание, чтобы учащиеся учились обращать внимание на знаки:
Случайное отображение + или -, наряду с немедленной поддержкой ошибок, удерживает учащихся вовлеченными, поскольку они укрепляют уверенность в выполнении этой задачи. И снова использование числовой линии в качестве модели расширяет их понимание задачи и чувство чисел.
Когда они будут готовы, увеличиваем сложность, убирая одну цифру из круглого числа:
Это небольшое изменение заставляет учащихся упражняться в чувстве числа при определении следующего большего или меньшего круглого числа. Опять же, поддержка числовой линии предоставляется каждый раз, когда студенту это нужно. В конце концов ученики понимают, что недостающую цифру легко вычислить, потому что они всегда добавляют или вычитают однозначное число. Это упражнение ставит учащихся в несколько «нестандартную» ситуацию, что очень полезно для концептуального понимания и решения проблем.
Этап 2: Работа с круглыми числами
Мы начинаем с упражнения, в котором основное внимание уделяется сложению или вычитанию двух круглых чисел. Это упрощенная версия двухзначного сложения / вычитания, которую легко смоделировать с помощью кубов для понимания. Чтобы подготовить учащихся к выполнению более сложных задач, мы подходим к этому упражнению поэтапно.
Шаг 1 начинается с уравнения и его модели, которые учащиеся выполняют для решения упражнения:
Шаг 2 продолжает это понимание, моделируя вычитание аналогичным образом:
Шаг 3 приближает учащихся к более абстрактному пониманию, заменяя кубики анимированными числовыми подсказками.Сначала выделяются разряды десятков:
Затем ученикам предлагается добавить их:
Наконец, учащиеся связывают эту упрощенную задачу сложения или вычитания с исходным уравнением:
Этот последний шаг этого упражнения дает студентам практическую стратегию решения +/- круглых чисел, показывая, что 60 + 20 так же просто, как 6 + 2, в то время как первые два шага дают студентам представление о действиях.
После изучения того, как складывать / вычитать два круглых числа, пора ученикам узнать, что делать, если одно число не является круглым. Еще раз, это упражнение приближается к навыку поэтапно.
Шаг 1 демонстрирует добавление круглого числа к некруглому числу, показывая уравнение и модель (с анимацией, добавляющей розовые стержни):
Когда учащиеся увидят уравнение, смоделированное с помощью анимации, им будет предложено указать сумму.Если они допустят ошибку, Happy Numbers немедленно предоставит строительные леса, чтобы помочь им прийти к правильному ответу:
Шаг 2 аналогичен, но здесь студентов сначала просят ввести уравнение на основе данной модели:
И затем решите, как они делали ранее:
Еще одно упражнение следует в том же формате, что и предыдущее, но использует вычитание:
Наконец, несколько упражнений помогают студентам повторять и укреплять сложение и вычитание круглых и некруглых чисел.Им представлены уравнения, которые необходимо решить:
Но поддерживаются кубиками (леса!), В случае ошибки:
Мы также бросаем вызов их пониманию, предлагая им решать нетрадиционные проблемы. Это упражнение было разработано специально, чтобы помочь студентам понять концепции сложения и вычитания двузначных чисел. Вместо того, чтобы запоминать факты или методы обучения для решения уравнений, это упражнение требует от учащихся определить, какой метод будет эффективным при решении проблемы.Это ценный навык, даже если представленный метод не является тем методом, который учащиеся, возможно, использовали сами для решения проблемы:
После того, как учащиеся выберут правильный метод, их просят решить уравнение:
Если учащиеся выберут неправильный метод, им будет предложено решить уравнение, чтобы показать, почему оно неверно. Для этого студенты должны применить знания из предыдущего обучения:
Еще одно упражнение бросает вызов мышлению учащихся, выходящему за рамки простого выполнения сложения или вычитания.Это на самом деле помогает студентам обнаружить отношения между сложением и вычитанием и понять, что это обратные операции.
Во-первых, Happy Numbers представляет учащимся несколько задач на сложение, которые укрепляют навыки, полученные в предыдущих упражнениях:
После того, как учащиеся решат их, им предлагаются три задачи на вычитание, которые, как вы можете заметить, имеют «что-то общее» с тремя задачами сложения, которые они только что решили:
Наконец, студентов просят сопоставить каждую задачу сложения с соответствующей задачей вычитания:
Это побуждает учащихся открывать группы фактов и думать о вычитании как о инверсии сложения!
Этап 3. Сложение и вычитание 2-значных чисел
Мы начинаем более сложные двузначные операции с некруглыми числами, которые не требуют обмена.Упражнения направлены на то, чтобы научить студентов складывать / вычитать единицы с единицами и десятки с десятками, чтобы получить ответ. Учащиеся изучают модели, лежащие в основе таких задач сложения / вычитания, а также находят практические методы их решения.
Шаг 1 представляет учащимся уравнение, моделируемое кубиками:
Happy Numbers использует анимацию для разделения первого числа на десятки и единицы, а затем предлагает студентам сделать то же самое со вторым числом:
После этого учащиеся следуют подсказкам, чтобы разобраться в вновь объединенных стержнях и кубах:
Наконец, учащиеся используют эту информацию для решения уравнения:
Если их ответ неверен, они поддерживаются выделением, которое указывает правильное значение:
Шаг 2 этого упражнения предоставляет кубики для первого числа в уравнении, но требует, чтобы учащиеся добавляли кубики, чтобы сами показать второе число:
Затем студенты ответят на исходное уравнение аналогичным образом:
Шаг 3 представляет собой уравнение:
Но предоставляет кубики еще раз в случае ошибки:
Аналогичное упражнение следует в том же формате, но использует вычитание:
Happy Numbers использует анимацию для моделирования «выталкивания» или вычитания кубиков и стержней.
Используя знания, полученные в предыдущих упражнениях, пора ученикам начать использовать практическую стратегию сложения двузначных чисел — сложения десятков с десятками и единиц с единицами.
Во-первых, Happy Numbers использует анимацию для демонстрации стратегии:
А затем предлагает студентам использовать стратегию самостоятельно:
Представляем аналогичное упражнение на вычитание:
«Счастливые числа» содержит множество других упражнений, позволяющих развивать беглость речи с помощью сложения и вычитания двух цифр.Как только учащиеся продемонстрируют понимание этой концепции, мы перейдем к изучению другой полезной и связанной концепции — достижения 100. Это специальное упражнение отлично подходит для закрепления того, как изменить доллар, среди других навыков.
Мы начинаем с уравнения и модели, аналогичных предыдущим упражнениям, которые учили студентов складывать, чтобы получить круглое число:
Учащимся предлагается добавить к модели розовые кубики, чтобы получить цифру 100. Затем они определяют решение.В конце концов, модель забирают, и студентам предоставляется только уравнение:
Конечно, если они ошибаются, Happy Numbers снова предоставляет модель:
Предыдущее упражнение дополняется веселым игровым упражнением из нашей серии «НЛО». Здесь ученики развивают беглость в достижении 100, находя пары слагаемых, которые дают эту сумму:
Happy Numbers — это отличное введение для ваших учеников, как начать складывать и вычитать двузначные числа.С помощью наших многочисленных упражнений с каркасом они разовьют новые навыки, а также концептуальное понимание, которое подготовит их к сложению и вычитанию с перегруппировкой или обменом. Как только у ваших учеников будет такая основа, не забудьте продолжить наши уроки по обмену!
—
С уважением,
Команда Happy Numbers
Ваш первоклассник и математика в соответствии со стандартами Common Core
Помните пазлы, с которыми ваш ребенок играл — используя треугольники для создания квадратов и прямоугольников? Оказывается, это была хорошая практика для первого класса по математике.
К концу первого класса вашему ребенку необходимо освоить 11 математических навыков:
- Считать до 120 — начиная с любого места, например, с 3 или 72.
- Сложение и вычитание чисел до 20.
- Зная, что этот знак «=» означает «равно».
- Решение проблем со словами с тремя однозначными числами (например, 2 + 3 + 9), которые в сумме составляют 20 или меньше.
- Понимание того, почему сложение и вычитание противоположны друг другу.
- Добавление до 100, включая добавление двузначного числа и однозначного числа (например,грамм. 82 + 7).
- Умение складывать двузначные числа на основе разряда.
- Сложение или вычитание 10 с помощью математических вычислений (например, 31 плюс 10 равно 41).
- Приступаем к измерениям, например, к выяснению, сколько его следов может уместиться на следе его отца.
- Указание и запись времени с точностью до часа и получаса (например, 13:00 и 13:30).
- Соединение двух фигур вместе для создания новой формы и разделение фигур на две и четыре части.
Я возьму по математике за 120, пожалуйста
Считаем до 100 — это для детсадовцев.Первоклассники считают до 120, но загвоздка в том, что они могут начинать с любого числа, например, 72, и считать до 73, 74, 75 и так далее. Дети также учатся вычитать числа до 20, например, 19–7 = 12. Студенты учатся решать задачи со словами, используя предметы, рисунки и, да, даже уравнения. Например, если у Теда 4 карандаша, у Даниэль 6 карандашей, а у Вики 9 карандашей, сколько карандашей у них всего вместе?
Ваша первоклассница может сначала нарисовать эту задачу и сосчитать карандаши, но к концу года она будет знать уравнение и то, как его решать.
Первоклассники также изучают взаимосвязь между счетом, сложением и вычитанием. Например, подсчет от 1 до 2 — это то же самое, что и прибавление 1 + 1. Добавление еще одного означает подсчет одного, а добавление еще двух означает подсчет двух и так далее. Точно так же вычитание можно рассматривать как обратный или обратный отсчет. Сделав еще один шаг, дети учатся думать о вычитании как об обратном или «отмене» сложения. Так, например, если 15 + 4 = 19, то 19 — 4 = 15.
Все на своих местах
В детском саду ваш ребенок начал учить разряды с помощью десятков и единиц.В двузначном числе, таком как 19, 1 представляет десятки, а 9 — единицы. Теперь ваш первоклассник будет опираться на это, научившись складывать двузначное число, например 54, и однозначное число, например 5, или двузначное число, кратное 10, например 10, 20, 30, 40 и т. Д.
Одна стратегия, которую усвоит ваш ребенок, — складывать десятки и единицы отдельно.
Например: 54 + 5 = 50 + 0 = 50 и 4 + 5 = 9, всего 59.
Иногда бывает необходимо создать десятку из единиц.
Например: 54 + 7 = 50 + 0 = 50 и 4 + 7 = 10 + 1. Переместите 10 в десятки, так что 50 + 10 = 60 и 1, всего 61.
Ожидается, что ваш ребенок также будет придумывать в своей голове — не считая — как найти на 10 больше или меньше другого числа. Если у Джеммы 68 леденцов на палочке и она отдаст 10, она должна знать, что это то же самое, что вычесть одну группу десятков, и у нее останется 58 леденцов.
Как это оценивается?
Первоклассники должны уметь объяснять длину двух предметов, сравнивая их с третьим предметом.Например, первый лист бумаги короче второго, но длиннее третьего.
Дети начинают применять понятие дополнения к измерению вещей. Допустим, ваш ребенок измеряет длину одеяла по хвосту собаки. он может обнаружить, что одеяло состоит из пяти с половиной хвостов. Это отличная практика, когда дети начинают пользоваться линейками.
Первоклассники также учатся определять время (и записывать его правильно, например, 13:30) с точностью до ближайшего часа и получаса, считывая как цифровые часы, так и старомодные круглые часы с минутной и часовой стрелками.
Приобретение форм
Первоклассники разбираются в свойствах форм, комбинируя две формы для образования новой, например, складывая два треугольника вместе, чтобы получился квадрат или прямоугольник. Они будут делать это на бумаге (в двух измерениях) и с объектами (в трех измерениях).
Дети также учатся разделять фигуры на две или четыре равные части и выучить слова для этих частей: половинки и четверти (или четверти).
Так что разбивайте блоки и конструкторы Lego и получайте удовольствие, пока вы можете практиковать все математические навыки вашего ребенка дома, играя на полу.
• Посмотрите, как выглядит знание разрядов единиц и десятков в этом видеоролике «Вехи» по математике для первого класса.
• Может ли ваш первоклассник решить такую словесную задачу?
Поделиться в Pinterest
Обновлено: 2 декабря 2019 г.
Вычитание сложением (метод дополнений)
(также называемый методом дополнений)
Здесь мы видим, как выполнять вычитание с помощью сложения!
(Я не рекомендую это для обычной работы по вычитанию, но это по-прежнему действительный и интересный способ вычитания.А в некоторых случаях это может сэкономить время.)
ступеней
Выполните следующие действия:
- возьмите « дополнение » из числа, которое мы вычитаем (посмотрим, как скоро)
- прибавьте к числу, которое мы вычитаем из
- отменить лишняя «1» слева
Дополнение
«Дополнение» — это число , чтобы добавить , чтобы получить 10 (или 100, 1000 и т. Д., В зависимости от того, сколько цифр у нас есть)
Пример Дополнение до 3 равно 7 , потому что 3 + 7 = 10 (мы прибавляем 7 , чтобы получить 10)
Пример: дополнение до 85 равно 15 , потому что 85 + 15 = 100
Пример: дополнение 111 равно 889 , потому что 111 + 889 = 1000
Вычисление дополнения
Дополнение найти легко!
Основная идея состоит в том, чтобы найти разницу в между каждой цифрой и 9 .Это приведет нас к «999 …», поэтому нам нужно только добавить 1, чтобы получилось «1000 …»
.На практике легко использовать этот метод:
- Старт с позиции «единицы»
- Пропускать любые нули
- Тогда:
| Для первой цифры , которая не равна нулю: | найдите, что делает его 10 | |
| Для все остальные цифры : | найдите, что делает его 9 |
Вот два примера:
(Вы можете проверить его работу, добавив номер и его дополнение,
например 372 + 628 = 1000 )
При небольшом опыте «что прибавляет к 10» или «что прибавляет к 9» становится автоматическим, и получение дополнения становится быстрым и легким.
Вот еще один пример, где нам нужно пропустить некоторые нули:
Пример: Какое дополнение к 1700 ?
- Пропустить два нуля
- Дополняющая цифра «10» — это 3 , .
- Дополнение «9» к 1: 8 ,
Итак, ответ:
8300
(Чек: 1700 + 8300 = 10000 )
Теперь добавьте их!
Теперь сложите два числа (используя сложение столбцов), но не забудьте отбросить лишнюю «1» слева.
Вот 3 шага ( дополнение , добавить , отбросить ):
И мы обнаружили, что 653 — 372 = 281 (отметьте, если хотите!)
Что делать, если в вычитаемом числе меньше цифр?
Как мы можем, например, сделать 4567 — 56?
После взятия дополнения мы просто заполняем все недостающие места девятками.
Пример: 4567 — 56
Ну, дополнение к 56 — 44, но нам нужно «дополнить» его до 4 цифр, чтобы получилось 9944.Теперь складываем их:
4567
+9944
14511
Затем отбросьте лишнюю «1» слева, и ответ будет:
4511
В этом случае было бы проще использовать быстрое вычитание, но он показывает, как работает метод « дополнить , добавить , отбросить ».
 Настраивается сложность примеров: с переходом через десяток или без перехода, сложение или вычитание, действия с «удобными» числами или примеры повышенной сложности…
Настраивается сложность примеров: с переходом через десяток или без перехода, сложение или вычитание, действия с «удобными» числами или примеры повышенной сложности…
 п.
п.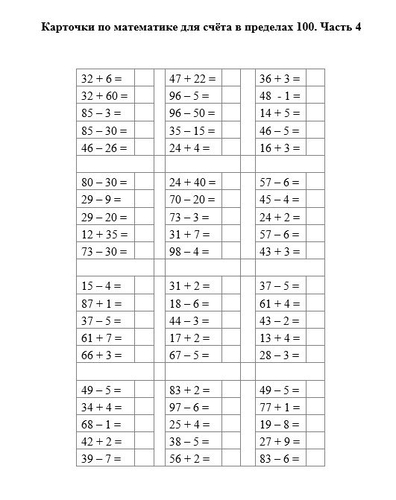 В файле заданий будут только задания с прочерками вместо ответов, а в файле ответов — примеры с ответами.
В файле заданий будут только задания с прочерками вместо ответов, а в файле ответов — примеры с ответами.
