ВСЕ ПРОГРАММЫ

Математика
Рабочие листы для 4 класса

 

1 цикл: Космос
Сложение, вычитание, умножение и деление в пределах 100 (устно и письменно). Название компонентов действия при сложении, вычитании, умножении и делении. Алгоритм решения текстовых задач. Значение переменной. Простейшие виды письменного сложения и вычитания в пределах 10 000. Скобки и порядок действий. Вычитание суммы и разности из числа. Умножение и деление суммы на число.

1. Сложение и вычитание в пределах 100
2. Решение текстовых заданий
3. Значение переменной
4. Письменное сложение и вычитание
5. Переместительный закон сложения
6. Сочетательный закон умножения

7. Вычитание суммы из числа
8. Умножение в пределах 100
9. Деление в пределах 100
10. Деление — действие, обратное умножению
11. Переместительный закон умножения
12. Законы умножения
13. Умножение суммы на число
14. Умножение суммы на число
15. Деление суммы на число
16. Деление суммы на число
17. Вычисление удобным способом. Порядок действий
18. Вычисление удобным способом. Порядок действий
19. Повторение

2 цикл: Было время…
Величины (единицы длины, массы, времени, площади) и их соотношения. Периметр квадрата и прямоугольника.  Числа до 1 000 000 и их состав.

1. Деление с остатком
2. Повторение
3. Единицы длины
4. Периметр прямоугольника
5. Единицы массы
6. Денежные единицы
7. Единицы времени

8. Скорость, время и расстояние
9. Повторение
10. Разряды числа. Сумма разрядных слагаемых.
11. Разряды. Сумма разрядных слагаемых.
12. Разряды тысяч
13. Десятки тысяч
14. Сотни тысяч

3 цикл: Земля в огненном кольце
Сравнение площадей предметов, вычисление площади квадрата и прямоугольника. Письменное сложение и вычитание 5- и 6-значных чисел. Проверка суммы и разности при письменном сложении и вычитании. Порядок действий и скобки. Письменное сложение и вычитание именованных величин.

1-1. Сравнение площадей фигур. Равные по площади фигуры
1-2. Квадратный сантиметр. Площадь прямоугольника
2. Площадь квадрата
3. Единицы площади
4. Повторение
5. Повторение
6. Алгоритм устного счета
7-1. Алгоритм письменных вычислений

7-2. Алгоритм письменных вычислений
8-1. Сравнение алгоритмов устного и письменного вычислений
8-2. Сравнение алгоритмов устного и письменного вычислений
9-1. Повторение
9-2. Повторение
10. Письменное значение пяти- и шестизначных чисел
11-1. Письменное значение пяти- и шестизначных чисел
11-2. Письменное значение пяти- и шестизначных чисел
12. Сложение нескольких чисел
13. Сложение нескольких чисел
14. Письменное значение пяти- и шестизначных чисел
15-1. Письменное значение пяти- и шестизначных чисел
15-2. Письменное значение пяти- и шестизначных чисел
16. Закрепление
18. Проверка письменного сложения и вычитания
19. Повторение
20. Повторение

4 цикл: Кукольный театр
Анализ и решение задач до трех действий. Устное умножение с числами 10, 100, 1000. Умножение однозначного числа на числа, оканчивающиеся на 0. Письменное умножение на однозначное число.

1-1. Значение выражений. Скобки и порядок действий
1-2. Значение выражений. Скобки и порядок действий
2-1. Значение выражений. Скобки и порядок действий
2-2. Значение выражений. Скобки и порядок действий
3-1. Письменное сложение и вычитание величин
3-2. Письменное сложение и вычитание величин
4-1. Письменное сложение и вычитание величин
4-2. Письменное сложение и вычитание величин
5-1. Повторение
5-2. Повторение
6-1. Решение текстовых заданий
6-2. Решение текстовых заданий
7-1. Решение текстовых заданий
7-2. Решение текстовых заданий
8-1. Повторение
8-2. Повторение
9-1. Повторение
9-2. Повторение

10. Сложение в уме
11. Умножение в уме
12. Деление в уме
13. Деление в уме
14-1. Повторение
14-2. Повторение
15-1. Повторение
15-2. Повторение

5 цикл: Секреты энергии
Повторение письменного умноженияна на однозначное число. Решение выражений (порядок действий). Письменное деление на однозначное число.

1-1. Письменное умножение многозначного числа на однозначное число
1-2. Письменное умножение многозначного числа на однозначное число
2. Письменное умножение многозначного числа на однозначное число
3. Письменное умножение многозначного числа на однозначное число
4. Письменное умножение многозначного числа на однозначное число
5-1. Письменное умножение многозначного числа на однозначное число
5-2. Письменное умножение многозначного числа на однозначное число

6. Значение выражений. Порядок действий
7. Повторение
8. Письменное деление многозначного числа на однозначное число
9. Письменное умножение многозначных чисел с 0 на однозначное число
10. Письменное умножение многозначных чисел с 0 на однозначное число
11. Письменное деление многозначного числа на однозначное число
12. Письменное деление многозначного числа на однозначное число
13. Письменное деление многозначного числа на однозначное число
14. Письменное деление многозначного числа на однозначное число
15-1. Повторение
15-2. Повторение

6 цикл: Кем быть?
Решение выражений (порядок действий). Письменное умножение и деление на двузначное число.

1-1. Решение выражений (порядок действий)
1-2. Значение выражений (порядок действий)
2-1. Письменное умножение на двузначное число
2-2. Письменное умножение на двузначное число
3-1. Письменное умножение множителей, оканчивающихся на ноль
3-2. Письменное умножение множителей, оканчивающихся на ноль
4-1. Письменное умножение на двузначное число
4-2. Повторение
5-1. Значение выражений
5-2. Значение выражений
6-1. Значение выражений
6-2. Значение выражений
7-1. Письменное деление на двузначное число
7-2. Письменное деление на двузначное число
8-1. Письменное деление на двузначное число с 0 в частном
8-2. Письменное деление на двузначное число с 0 в частном
9-1. Письменное деление на двузначное число с 0 в частном

9-2. Письменное деление на двузначное число с 0 в частном
10-1. Письменное деление на двузначное число
10-2. Письменное деление на двузначное число
11. Письменное деление на двузначное число
12-1. Письменное деление на двузначное число в случае, когда делимое и делитель оканчиваются на 0
12-2. Письменное деление на двузначное число в случае, когда делимое и делитель оканчиваются на 0
13. Письменное деление на двузначное число в случае, когда делимое и делитель оканчиваются на 0

7 цикл: Государство сквозь века
Повторение умножения на двузначное число. Решение выражений (порядок действий). Письменное деление с остатком. Письменное умножение на трехзначное число. Умножение именных величин на одно- и двузначное число. Решение текстовых заданий путем составления выражений и уравнений.

1-1. Письменное деление на двузначное число
1-2. Письменное деление на двузначное число
2. Значение выражения и порядок действий
3. Значение выражения и порядок действий
4. Письменное деление с остатком
5. Письменное деление с остатком
6. Повторение письменного деления и умножения
7. Умножение на трехзначное число
8. Умножение на трехзначное число
9. Письменное умножение множителей, содержащих 0
10. Письменное умножение множителей, содержащих 0
11. Повторение письменного умножения на трехзначное число
12. Умножение величин
13. Деление величин
14. Составление и решение уравнений
15. Решение текстовых заданий
16. Решение текстовых заданий
17. Повторение
18-1. Дроби
18-2. Дроби
18-3. Дроби

8 цикл: Рука об руку в политике

Решение текстовых заданий путем составления выражений и уравнений. Дроби (числительное, знаменательное, дробная черта; деление фигур на равные части; 1/2, 1/3 и 1/4 фигуры). Нахождение половины, трети и четверти числа.  Нахождение части заданных величин. Нахождение дроби по закрашенной или незакрашенной части фигуры. Решение   текстовых задач с дробями.   Повторение и углубление: счет, составление и чтение чисел до миллиона,  сравнение чисел, устное и письменное сложение и вычитание.

1. Нахождение части величин
2. Нахождение дроби по раскрашенной части
3. Текстовые задания с дробями
4. Повторение
5. Повторение
6. Счет
7-1. Состав, чтение и запись чисел до миллиона
7-2. Сравнение чисел
8. Письменное и устное сложение в пределах миллиона
9. Устное и письменное вычитание в пределах миллиона

10. Связь сложения и вычитания
11. Устное и письменное умножение
12. Письменное умножение на двузначное число
13-1. Устное и письменное деление на однозначное число
13-2. Письменное деление на двузначное число

9 цикл: Классифицируем природу
Связь сложения и вычитания. Устное и письменное умножение на одно- и двузначное число в пределах миллиона. Письменное умножение на двузначное число в пределах миллиона.  Устное и письменное деление на одно- и двузначное число в пределах миллиона. Письменное деление на двузначное число в пределах миллиона. Связь умножения и деления. Выражения и равенства. Буква в равенстве. Числа 0 и 1 и действия с ними. Порядок действий и скобки. Измерение величин (длина, вес, скорость, время, вычисление площади). Различение, называние и черчение  геометрических фигур — точка, отрезок, ломаная, треугольник, четырехугольник, квадрат, прямоугольник. Вычисление периметра треугольника и четырехугольника. Решение текстовых задач до трех действий. Задачи на самоконтроль и смекалку.

1. Связь деления и умножения
2. Выражение и равенство. Переменная в равенстве.
3. Числа 0 и 1
4. Скобки и порядок
5. Измерение длины
6. Измерение массы
7. Измерение времени
8. Измерение скорости
9. Измерение стоимости
10. Измерение площади
11. Геометрические фигуры
12. Периметр прямоугольника и четырехугольника
13. Периметр и площадь треугольника и четырехугольника
14. Решение текстовых заданий
15. Задания на повторение и смекалку

 

 

” Алгоритм умножения и деления на трехзначное число. 4 класс – Балабақша әлемі

Математика.
Краткосрочный план урока № 60.
Предмет: Математика
Урок: 60 Школа: Х. Бижанова
Дата:
05.12.19 ФИО учителя:
Отамурадова А.А
Класс: 4 А Количество
присутствующих: Количество
отсутствующих:
Раздел (сквозная тема): Раздел 2А. Умножение и деление «Культурное наследие».
Тема урока: Обобщение изученного.
Алгоритм умножения и деления на трехзначное число.
Древние города
Цели обучения, которым посвящен урок: 4.1.2.12** – применять алгоритм умножения и деления многозначных чисел, оканчивающихся нолями, на трехзначное число;
4.1.2.13** – применять алгоритм деления многозначных чисел на двух/трехзначное число, когда в записи частного есть ноли и алгоритм обратного действия умножения
Развитие навыков: 1.2 Операции над числами
Языковые цели
Учащиеся могут:
применять алгоритм умножения и деления многозначных чисел на двузначные и трехзначные.
Предметная лексика и терминология:
названия компонентов действий, неполное произведение, неполное делимое, пробная цифра частного.
Полезные выражения для диалогов и письма:
Обсуждение
Для чего нужно определить количество цифр в частном?
Почему используется пробная цифра частного?
Письмо
Запись умножения и деления столбиком
Критерии оценивания
Применяет алгоритм деления многозначных чисел на двузначное и трехзначное. Проверяет вычисления.
Материал прошедших уроков: Алгоритм умножения и деления.

Ход урока:
Этапы урока Запланированная деятельность на уроке Ресурсы
0-1 мин Создание положительного эмоционального настроя:
– Здравствуйте, те, кто родился зимой! (те, кто родился зимой, здороваются и садятся)
– Здравствуйте, те, кто родился летом! (те, кто родился летом, здороваются и садятся)
– Здравствуйте, те, кто родился весной! (те, кто родился весной, здороваются и садятся)
– Здравствуйте, те, кто родился осенью! (те, кто родился осенью, здороваются и садятся)
– Ещё раз, все, здравствуйте!
– Здороваться – это желать здоровья!
Я желаю, чтобы во все времена года у вас было отличное здоровье и мы могли дружно общаться и выполнять работу.
Эмоциональный настрой

Середина урока
2-5 мин

21-22 мин

23-28 мин

29-30 мин

31-37 мин

38-40 мин 1.Актуализация жизненного опыта.
1) Записать число, классная работа
2) Минутка чистописания
Назовите самое большое трехзначное число? (999)
– Давайте это число пропишем в мин. чистописания
3)(К) Математический диктант:
1)Какое число надо прибавить к 12560, чтобы получить 13000? (440)
2)На сколько 10ч. меньше 1 суток? ( на 14 ч)
3) Произведение 490, первый множитель 7. Чему равен второй множитель? (70)
4)Увеличьте 67 в 100 раз (6700)
5)Найдите разность чисел 930 и 200. (730)
6)Найдите восьмую часть числа от числа 800. (100)
7)Сумма двух чисел 650, одно из них 250. Найдите другое число. (400)
8)Сколько минут составляют 180 с.? (3 мин)
9) Частное 6, делитель 50. Чему равно делимое? (300)
10)Найдите частное чисел 54000 и 6. (9000)
Проверка работы. Взаимооценивание в парах. ( на полях оценивают себя карандашами светофор)
2. Постановка цели (проблемная ситуация).
Вспомните алгоритм умножения и деления, найдите ошибки в примерах.
1235 * 201 = 248235 29200 : 73 = 4
Учащиеся находят ошибки в записи первого примера и в ответе второго.
( на доске листы с примерами дети подходят и устраняют ошибки красным маркером)
– Какова тема и цель нашего урока?
Обобщить всё, что мы изучали.
3. Выполнение задания №1 с. 72
Определи количество цифр в частном, не выполняя вычислений.
Расположи ответы (количество цифр в частном) в порядке возрастания, и ты прочтёшь, какое второе название имел древний город Испиджаб.
Р-5. А-3. М-7. С-2. А-6. Й-4 Сайрам

Выступление детей и просмотр видеоролика
4.Работа по теме урока.
Выполнение №3 с. 72 второй столбик у доски с объяснением
2210 * 402 = 888420 181944 : 361 = 504
Оценивание работы учащимися.
Физминутка
Руки в стороны и вверх
Повторяем дружно
Засиделся ученик
Разминаться нужно
Мы сначала всем в ответ
Головой покрутим НЕТ!
Энергично, как всегда
Головой покрутим ДА!
Чтоб коленки не скрипели
Чтобы ножки не болели
Приседаем глубоко
Поднимаемся легко
Раз, два, три чеканим шаг
Подает учитель знак
Это значит что пора
Нам за парты сесть УРА!
5. (И) Самостоятельная работа.
Выполнение №3 с. 72 третий столбик.
• критерии оценивания:
Знать алгоритм деления на двузначное и трехзначное числа
Применить алгоритм при вычислениях.
Я могу
Могу применить алгоритм деления многозначных чисел на двузначное и трехзначное числа.
Могу выполнить проверку

Проверка работы. Лист оценивания.

6. (П) Работа в парах.
Исследуй.
Составь выражение по схеме и обозначь в нём порядок действий.

( 2.432*203+ 40.000)+ (60.950:50+14.000)- (7.809:3*2)
Проверка работы. Самооценивание.
(Молодец, если допустили ошибку напишите старайся) Дети пишут в тетрадках сами
-Давайте повторим вместе правила работы в группе
7. Работа в группах. Решить примеры, составить слово.
4167 : 463 = 9 (о) 3918:653=6(м)
2541*205=520905 (ы) 2311*203=469133 (ц)

8400:28=300 (л) 1261*324=408564 (д)
3200*12=38400 (о)
С каждой группы выходят по два ученика находят свои ответы
Выступление групп.
– Расположите ответы в порядке возрастания и прочитайте слово «МОЛОДЦЫ»
Резерв стр 73 № 6 (устно)
Нам надо узнать сколько раз по 11л входит в 55 литров.
55:11=5(раз)
100*5=500(км)
Щучинск 239+239=478(км)

2 слайд
3 слайд

4 слайд

Учебник
тетрадь

5 слайд

Учебник
На доске

На доске

Тетрадь

6 слайд

Учебник
7 слайд

Учебник

8 слайд

9 слайд(проверка)

10 слайд

11 слайд(проверка)
Конец урока
Итог урока.
-Какую цель мы поставили на сегодняшнем уроке?
– Достигли ли мы этой цели?
– Какие затруднения были у вас на уроке?
– Что нужно сделать чтобы эти затруднения не
повторялись?
Рефлексия.
Предлагает оценить свою работу при помощи смайликов Картинки к рефлексии.
Дифференциация Оценивание Межпредметные
связи
Мотивированные дети рассказывают по схеме о живой и неживой природе о взаимосвязи в природе Формативное оценивание.
Самооценивание по «Шкале трудности» в тетради.
Взаимооценивание при работе в паре, группе классом
Результаты наблюдения учителем качества ответов учащихся
на уроке.
Определение уровня усвоения навыка по (Творческая тетрадь) – литература
– физическая культура
– самопознание
– познание мира
Рефлексия для учителя:
Важные вопросы
по уроку:

Итоговая оценка (с точки зрения преподавания и обучения)
Какие два момента были наиболее успешны?
Какие два момента улучшили урок?
Что я узнал из урока о классе и отдельных людях, что я расскажу на следующем уроке?

Приемы умножения и деления на 10. 2-й класс, «Школа России»

Тип урока: овладение новыми знаниями.

Цели: познакомить с приемами умножения и деления на 10. Совершенствовать вычислительные навыки навыки устного счёта, умение решать задачи, развивать  внимание и логическое мышление.

Педагогические задачи: дать первичное представление об умножении и делении числа на 10, продолжать формировать умения находить результат действия деления с помощью примера на умножение, развивать вычислительные навыки, продолжать работу над задачами.

Планируемые образовательные результаты:

Предметные УУД: умение правильно умножать и делить на число 10, знание названия компонентов умножения и деления, понимание сути переместительного закона умножения, умение выделять геометрические фигуры, применение формулы периметра квадрата.

Метапредметные УУД:

• Регулятивные: умение формулировать учебную задачу урока на основе соотнесения того ,что уже известно и усвоено, и того, что еще неизвестно, умение контролировать и оценивать учебные действия в соответствии с поставленной задачей; способность к самопроверке, самооценке, проверке по образцу и корректировке, взаимопроверке.
• Познавательные: проявлять познавательную инициативу в учебном сотрудничестве, умение выделять необходимую информацию, создавать алгоритм деятельности, сравнивать, анализировать, устанавливать причинно-следственные связи, делать выводы.
• Коммуникативные: оказывать необходимую взаимопомощь, договариваться и приходить к общему решению в совместной деятельности, слушать, слышать и понимать партнеров, планировать учебное сотрудничество с учителем и сверстниками, достаточно полно и четко выражать свои мысли.
• Личностные УУД: принятие и освоение социальной роли обучающегося, развитие мотивов учебной деятельности и формирование личностного смысла учения; развитие навыков сотрудничества с взрослыми и сверстниками в разных социальных ситуациях, проявление самостоятельности, личной ответственности.

Методы и формы обучения: частично-поисковый, фронтальная и групповая работа, индивидуальная.

Оборудование: компьютер, электронная доска, доска, карточки с заданием, математический веер, карта путешествия, сундучок с призами.

1. Организационный момент

— Ребята, сегодня у нас необычный урок. Мы с вами отправимся в увлекательное морское путешествие и побудем командой моряков. С нами на борту присутствуют пассажиры. Только от нашей слаженной, дружной работы, зависит найдем ли мы сегодня клад.

2. Актуализация знаний

— Давайте вспомним правила поведения на корабле (Отвечаем по руке, задание дослушиваем до конца, сидим ровно прямо).

— Чтобы отправиться в путь нам нужно проложить курс корабля. Найдем значение данных математических выражений, показывая ответы на математическом веере.

(Выводим картинку корабля на электронную доску).

— Ребята, прочитайте данные математические выражения, назвав их компоненты и найдите значение (если дети затрудняются, необходимо напомнить арифметическое действие).

— 14 + 6 (1 слагаемое — 14, 2 слагаемое – 6, сумма равна 20).

— 43 — 4 (Уменьшаемое – 43, вычитаемое – 4, разность равна 39).

— 16 : 4 (Делимое – 16, делитель – 4, частное равно 4).

— 4 * 3 (1 множитель – 4, 2 множитель -3, произведение равно 12).

— 8 * 0 (1 множитель – 8, 2 множитель — 0, произведение равно 0).

— 40 — 33 (Уменьшаемое – 40, вычитаемое – 33, разность равна 7).

— 5 * 10 (1 множитель – 5, 2 множитель -10, произведение равно 50).

— 24 : 4 (Делимое – 24, делитель – 4, частное равно 6).

— 10 * 5 (1 множитель – 10, 2 множитель — 5, произведение равно 50).

— 17 + 15 (1 слагаемое — 17, 2 слагаемое – 17, сумма равна 32).

— Ребята, что мы сейчас с вами делали? (Считали математические выражения, вспоминали название математических компонентов).

— Молодцы! Мы отправляем наш корабль в добрый путь!

3. Самоопределение к деятельности

— Ребята, а что вы заметили, работая с данными  математическими выражениями? (Мы заметили, что два выражения с одинаковыми числами и одинаковым результатом. Это 5*10 и 10*5).

Учитель записывает выражение на доске (5*10 … 10*5).

— Ребята, сравните это выражение. Какой знак мы поставим? (Равно.)

— Какое математическое свойство вы  использовали для сравнения выражения? (Переместительное свойство умножения. От перестановки множителей результат умножения не изменяется).

 — Вычислите  значение этих выражений, заменяя умножение сложением  (Один ребенок работает у доски.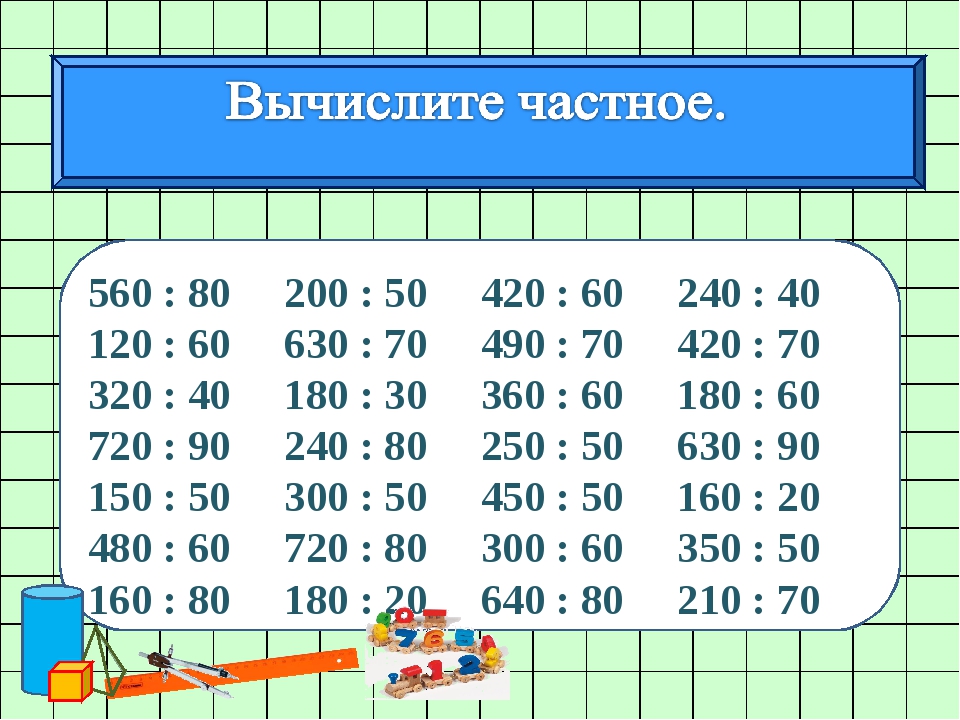 5* 10 = 5+5+5+5+5+5+5+5+5+5 = 50 и 10 * 5 = 10+10+10+10+10 = 50)

— Хорошо. Ребята, чтобы дальше отправиться в путь на нашем корабле, нам нужно составить по этим выражениям два примера на деление (50 : 10 = 5  и 50 : 5 = 10)

— А как вы нашли значение  выражений? (Зная значение произведения чисел 5 и 10, можно найти их частное)

— Какое правило взаимосвязи компонентов и результата действия вам помогло? (Если произведение разделить на один из множителей, то получится другой множитель)

— На сегодняшнем уроке мы продолжим учиться выполнять умножение и деление чисел и познакомимся с новым приёмом.
А кто догадался, что это за приём? (Приём умножения и деления на число 10)

— Ребята, что мы сейчас с вами делали? (Сравнивали выражения, повторяли переместительное свойство умножения и деления).

— Молодцы, отправляемся далее в наше путешествие.

— Проверьте своё предположение, откройте с. 74 и прочитайте задачи урока.

— Прочитайте объяснение вычислительного приема рядом с красной чертой.

— Послушаем объяснение и обратим наше внимание на электронную доску (Числа от 1 до 100. Приемы умножения и деления на 10).

— Что вы можете сказать о наших выводах и выводах в учебнике? (От перестановки множителей результат умножения не изменяется. Если произведение разделить на один из множителей, то получится другой ).

— Хорошо, что мы сейчас с вами сделали? (Убедились, что наши предположения правильны).

— Отправляемся дальше в наше увлекательное путешествие.

4. Физминутка

— Мы с вами моряки и нам необходимо быть внимательными, чтобы не попасть в руки к пиратам или не наткнуться на айсберг.
Игра «Запрещенное движение». Учитель говорит запретное движение, а дети должны быть внимательными и не повторять его, если учитель сказал или показал его.

5. Работа по учебнику

Минутка чистописания.

— Откройте тетради, запишите: сегодняшнее  число, Классная работа.

Цифра вроде буквы О —
Это ноль иль ничего.
Круглый ноль такой хорошенький,
Но не значит ничегошеньки!
Если ж слева рядом с ним
Единицу примостим,
Он побольше станет весить,
Потому что это — десять.

— Какое число будем прописывать? (10)

— Что можно сказать о числе 10? (чётное, двузначное, круглое, 1 десяток, 0 ед., в числовом ряду стоит после числа 9, перед числом 11)

— Что в жизни  бывает круглым? (Солнце, арбуз, мяч, часы, пуговица и т.п.)

— А в математике? (Круг, шар, числа)

— Какие числа называют круглыми? (Круглыми называют числа, оканчивающиеся на ноль).

— Назовите все круглые числа в числовом ряду до 100? (10, 20, 30, 40, 50, 60, 70, 80, 90).

— Назовите самое маленькое круглое двузначное число? Самое маленькое  круглое трехзначное число? (10; 100).

— Прописываем число 10 через клеточку.

(Прописная цифра 1. — Начинают писать маленькую палочку немного выше и правее центра клетки, ведут линию вверх к правому верхнему углу клетки. Затем пишут большую палочку от верхнего правого угла почти до середины нижней стороны клетки.

Прописная цифра 0. — Овал начинают писать немного левее правого верхнего угла клетки. Ведут линию вниз, закругляя на середине нижней стороны клетки. Затем ведут руку вверх к началу овала.)

— Молодцы, наш корабль плывет дальше.

— №1 стр.74 – фронтальная работа.

Составление таблицы. Дети устно поочередно читают примеры.

— Как связаны между собой четыре столбика примеров? (При составлении 2 столбика используется переместительное свойство умножения, при составлении 3 и 4 столбика – правило о том, что если значение произведения разделить на один множитель, то получится другой множитель).

10 * 2 = 20	2 * 10 = 20	20 : 2 = 10	20 : 10 = 2
10 * 3 = 30	3 * 10 = 30	30 : 3 = 10	30 : 10 = 3
10 * 4 = 40	4 * 10 = 40	40 : 4 = 10	40 : 10 = 4
10 * 5 = 50	5 * 10 = 50	50 : 5 = 10	50 : 10 = 5
10 * 6 = 60	6 * 10 = 60	60 : 6 = 10	60 : 10 = 6
10 * 7 = 70	7 * 10 = 70	70 : 7 = 10	70 : 10 = 7
10 * 8 = 80	8 * 10 = 80	80 : 8 = 10	80 : 10 = 8
10 * 9 = 90	9 * 10 = 90	90 : 9 = 10	90 : 10 = 9
10 * 10 = 100	10 * 10 = 100	100 : 10 = 10	100 : 10 = 10

— Ребята, какой вывод мы можем сделать об умножении и делении на 10? (Вывод: при умножении на 10  к числу справа дописывается 0.

При делении на 10 у числа 0 убирается!)

Дети читают на электронной доске стихотворение-правило.

— Наш корабль доплыл до середины пути, продолжаем наш путь. Что мы сейчас делали? (Выявили правило умножения и деления на 10.)

6. Физминутка

— Моряки должны быть не только внимательными, но и ловкими и смелыми.

— Как мы будем плыть на спасательной шлюпке? (Упражнение гребля)

— Как будем залезать по висячей лестнице? (Упражнение как будто лезем по лестнице руками)

— Как будем смотреть вдаль? (Упражнение тянемся на мысочках)

7. Закрепление изученного материала

— Ребята, как называется кухня на корабле? (Камбуз)

— Как называют повара на корабле? (Кок)

— Кок приготовил нам пирожки, но (скажу вам по секрету) кок – это бывший пират и он не умеет считать. Нам ему необходимо помочь разложить пирожки. Читаем условие задачи на стр.74 № 3.

Задача №3.

— Прочитай задачу про себя.

— Прочитай вслух.

— Сколько пирожков раскладывал повар? (40)

— Как он их раскладывал? (Поровну).

— Что значит «поровну»? (На каждую тарелку одинаковое количество).

— Как будем раскладывать пирожки на 10 тарелок? (По 1 пирожку на каждую тарелку).

(Один ученик работает у доски. 10 магнитных тарелок закрепляем на доске, раскладываем пирожки (из бумаги) по тарелкам).

— Сколько пирожков оказалось на каждой тарелке? (1)  

— Поровну разложили все 40 пирожков? (Нет).

— Уточните, как будем раскладывать пирожки? (До тех пор, пока все не закончатся).

— Сколько пирожков стало на каждой тарелке? (По 4 пирожка).

— Запишите решение задачи и ответ.

40:10=4 (п.)

Ответ: на каждой тарелке по 4 пирожка.

— Что обозначает число 40?  (Количество пирожков)

— Что обозначает число 10? (Количество тарелок)

-Что обозначает число 4? (Сколько пирожков на каждой тарелке).

— Решим 2 задачи обратные данной (с помощью магнитных рисунков составляем условие задач).

1. Повар разложил 40 пирожков на тарелки.  В каждой тарелке получилось по 4 пирожка. На сколько тарелок повар разложил пирожки?

40: 4 = 10 (т.)

Ответ: на 10 тарелок.

— Что обозначает число 40?  (количество пирожков)

— Что обозначает число 4? (Сколько пирожков на каждой тарелке).

— Что обозначает число 10? (Количество тарелок)

2. Повар разложил на 10 тарелок пирожки. В каждой тарелке получилось по 4 пирожка. Сколько всего пирожков было?

10 * 4 = 40 (п.)

Ответ: 40 пирожков всего.

— Что обозначает число 10? (Количество тарелок)

— Что обозначает число 4? (Сколько пирожков на каждой тарелке).

— Что обозначает число 40?  (Количество пирожков)

— Молодцы! Что мы сейчас с вами делали? (Решали задачу и составляли задачи обратной данной).

— Хорошо, наш корабль следует дальше. И перед нами разрушенный мост. Чтобы проплыть дальше, нам необходимо восстановить мост, решая примеры самостоятельно (Выводим картинку моста с примерами на электронную доску. Примеры из №5 с.74. Решаем в столбик. После выполнения задания проверка.)

• 74 – 58 = 16
• 46 + 37 = 83
• 83 – 29 = 54
• 64 + 36 = 100

— Молодцы! Корабль наш держит путь далее и мы с вами находим сундук с сокровищами. Чтобы открыть сундук нам надо узнать длину его стороны, зная уже периметр.

— Какую фигуру представляет сундук? (Квадрат)

— Что такое квадрат? (Прямоугольник, у которого все стороны равны)

— Что такое периметр? (Сумма длин всех сторон)

— Как найти периметр квадрата? (Сложить длины всех сторон)

— Прочитайте задание №4 на стр. 74.

— Какая формула периметра квадрата?

(Р = а + а +а +а
Р = а * 4)

— Чему равен периметр квадрата по условию задачи? (20 см.)

— Подставьте это значение в равенство (а * 4 = 20.)

— Что у вас получилось? (Уравнение.)

— Решите уравнение и узнайте длину стороны этого квадрата.

а * 4 =20
а = 20:4
а =5

Ответ: а = 5 см.

— Молодцы! Что мы сейчас делали? (Закрепляли изученный материал)

8. Рефлексия

— Решение задания по компьютеру № 1.

Работа в группах.

— Мы продолжаем наше путешествие и находим на острове бутылку с посланием. На листочках детям дается задание составить числовые выражения на деление. Проверка проходит фронтально.

— Составьте числовые выражения на деление.

1) 3, 30, 10 0, 50, 4, 10, 40 60, 6, 5
30 : 3 = 10
100 : 10 = 10
50 : 5 = 10
40 : 4 = 10
60 : 6 = 10

2) 90, 70, 7, 80,9 ,10, 100, 20, 8, 2
90 : 9 = 10
70 : 7 = 10
80 : 8 = 10
100 : 10 = 10
20 : 2 = 10

Фронтальная проверка.

9. Подведение итогов урока

— Ребята, мы с вами возвращаемся домой из нашего увлекательного путешествия.

— Какую тайну математики вы сегодня открыли? Чему научились? Всем ли было легко? Какие трудности испытывали? (Мы освоили приемы умножения и деления на 10.)

— Какое правило использовали при умножении числа на 10? (При умножении на 10 к числу справа дописывается 0.)

— Как находить результат при делении круглого числа на 10? (При делении на 10 у числа 0 убирается.)

— Молодцы! Вы были сегодня активны, внимательны, сообразительны, поэтому мы справились со всеми заданиями и нашли сундук с сокровищами. Спасибо вам за хорошую работу.

Выставление отметок.

10. Домашнее задание

— Открываем наш бортовой журнал – дневник и записываем домашнее задание. Учебник – стр.74 № 6.

Сундучок с призами – шоколадные монеты.

Применение распределительного свойства умножения 6 класс онлайн-подготовка на Ростелеком Лицей

51. Применение распределительного свойства умножения.

Напомню, что распределительное свойство умножения относительно сложения и вычитания записывается так.

(a + b) · c = a · c + b · c = ac + bc;

(a — b) · c = a · c — b · c = ac — bc.

Распределительное свойство умножения относительно сложения и относительно вычитания позволяет решать примеры.

Пример 1. 35-13∙15=35∙15-13∙15=3∙155-1∙153=9-5=4.

Пример 2. Найдем значение произведения

2314∙7=2+314∙7=2∙7+314∙7=14+3*714=1512.

Чтобы умножить смешанное число на натуральное число, можно:

1. Умножить целую часть на это число.
2. Умножить дробную часть на это число.
3. Сложить полученные результаты.

Пример 3. Найдем значение выражения

538∙28+258∙28=538+258∙28=8∙28=2.

Используя распределительное свойство умножения, можно упрощать выражения вида:

58a+34a=58+34∙a=148а=134 а

34x-15x=34-15x=1520-420x=1120x.

Пример 4. Квартира состоит из двух комнат. Длина большей комнаты 5110, а ширина 4 м. Длина меньшей комнаты 4 м, а ширина 3110 м. На сколько площадь одной комнаты меньше площади другой?

Площадь первой комнаты

S=a∙b=5110∙4=5+110∙4=5∙4+110∙4=20+25=2025 м².

Площадь второй комнаты

S=a∙b=3110∙4=3+110∙4=3∙4+110∙4=12+25=1225 м².

Разница площадей 2025-1225=8 м².

Чтобы умножить смешанное число на смешанное число, можно:

1. Перевести одно смешанное число в неправильную дробь.
2. Умножить целую часть второго множителя на неправильную дробь.
3. Умножить дробную часть второго множителя на неправильную дробь.
4. Сложить полученные результаты.

Пример 5. Найдем значение выражения

225∙412=225∙92=2∙92+25∙92=9+95=1045 .

Урок математики 4 класс «Деление числа на произведение»

Слайды и текст этой онлайн презентации

Слайд 1

УРОК МАТЕМАТИКИ 4 КЛАСС
Автор: Четкина Г. В. учитель начальных классов МБОУ «Атратская СОШ»

Слайд 2

1
4
55
+
23
99
100
5
=

Слайд 3

560 : 7
250 * 200
15 0* 200
20180 : 10
800 * 60
200 : 2
3500 : 5
30 * 20
50150 : 10
90 * 3000
500 * 40
320 : 8
810 : 9
5400 : 6
600
5015
70
80
900
270000
40
20000
90
48000
100
30000
2018
50000
30000
2018
700
100
48000
50000
5015
900
270000
40
20000
90

Слайд 4

ВСЕХ
2
5
3
4
,
ЦАРИЦА
,
МАТЕМАТИКА
,
НАУК.
Вычислите, запишите ответ: 355 – 50*7
Реши задачу, запиши ответ: Ученик решает 10 примеров за 40 минут. Сколько минут в среднем идёт на решение одного примера?
Запишите номер примера, в котором допущена ошибка: 1. 96000 : 100 = 960 2. 1250 : 10 = 125 3. 95000 : 1000 = 950

Запишите номер верного утверждения: Чтобы найти делитель, нужно: 1. Делимое умножить на частное. 2. Делимое разделить на частное.
—
3, 5, 2, 4.

Слайд 5

Чтоб врачом, моряком Или лётчиком стать, Надо твёрдо на «5» Математику знать!
Добро пожало вать!
МАТЕМАТИКА

Слайд 6

Частное чисел 350 и 7 увеличь на 20.
Из 800 вычти произведение чисел 30 и 9.
К 50 прибавь частное чисел 36 и 6.
Чему равно 3/5 тонны?
Найди периметр квадрата со стороной 9 см.
Чему равна ширина сада, если его S=54 кв.м, а его длина 9 м?
70
530
56
600 кг
36 см
6 м
Сколько дм в 240 см?
24 дм

Слайд 7

500 * 6 : 100
4000 * 3 : 100
950 – 720 + 42
140 : 7 * 2
(270 – 50) * 10
Е
Н
Д
И
Л
272
30
2200
30
120
40
30
Д е л е н и е

Слайд 8

Деление числа на произведение
познакомиться и отработать приёмы деления числа на произведение

Слайд 9

Составь задачу и реши её.
12км/ч t=2ч 13км/ч
?

Слайд 10

Слайд 11

Слайд 12

Молодцы! Спасибо за урок!
Д/З № 90, с. 20

Слайд 13

Рефлексия
ВО ВРЕМЯ ПУТЕШЕСТВИЯ БЫЛО ИНТЕРЕСНО И ЛЕГКО, ПОТОМУ ЧТО УМЕЮ БЫСТРО И ПРАВИЛЬНО ВЫЧИСЛЯТЬ, РЕШАТЬ ЗАДАЧИ
ПУТЕШЕСТВИЕ БЫЛО ИНТЕРЕСНОЕ, НО НЕКОТОРЫЕ ЗАДАНИЯ ВЫЗЫВАЛИ ЗАТРУДНЕНИЯ
МНЕ БЫЛО СКУЧНО! Я МЕДЛЕННО СЧИТАЮ, МНЕ ТРУДНО БЫЛО ВЫПОЛНИТЬ ЗАДАНИЯ.

Поколения компьютеров — история развития вычислительной техники

☰

В короткой истории компьютерной техники выделяют несколько периодов на основе того, какие основные элементы использовались для изготовления компьютера. Временное деление на периоды в определенной степени условно, т.к. когда еще выпускались компьютеры старого поколения, новое поколение начинало набирать обороты.

Можно выделить общие тенденции развития компьютеров:

1. Увеличение количества элементов на единицу площади.
2. Уменьшение размеров.
3. Увеличение скорости работы.
4. Снижение стоимости.
5. Развитие программных средств, с одной стороны, и упрощение, стандартизация аппаратных – с другой.

Нулевое поколение. Механические вычислители

Предпосылки к появлению компьютера формировались, наверное, с древних времен, однако нередко обзор начинают со счетной машины Блеза Паскаля, которую он сконструировал в 1642 г. Эта машина могла выполнять лишь операции сложения и вычитания. В 70-х годах того же века Готфрид Вильгельм Лейбниц построил машину, умеющую выполнять операции не только сложения и вычитания, но и умножения и деления.

В XIX веке большой вклад в будущее развитие вычислительной техники сделал Чарльз Бэббидж. Его разностная машина, хотя и умела только складывать и вычитать, зато результаты вычислений выдавливались на медной пластине (аналог средств ввода-вывода информации). В дальнейшем описанная Бэббиджем аналитическая машина должна была выполнять все четыре основные математические операции. Аналитическая машина состояла из памяти, вычислительного механизма и устройств ввода-вывода (прямо таки компьютер … только механический), а главное могла выполнять различные алгоритмы (в зависимости от того, какая перфокарта находилась в устройстве ввода). Программы для аналитической машины писала Ада Ловлейс (первый известный программист). На самом деле машина не была реализована в то время из-за технических и финансовых сложностей. Мир отставал от хода мыслей Бэббиджа.

В XX веке автоматические счетные машины конструировали Конрад Зус, Джорж Стибитс, Джон Атанасов. Машина последнего включала, можно сказать, прототип ОЗУ, а также использовала бинарную арифметику. Релейные компьютеры Говарда Айкена: «Марк I» и «Марк II» были схожи по архитектуре с аналитической машиной Бэббиджа.

Первое поколение. Компьютеры на электронных лампах (194х-1955)

Быстродействие: несколько десятков тысяч операций в секунду.

Особенности:

• Поскольку лампы имеют существенные размеры и их тысячи, то машины имели огромные размеры.
• Поскольку ламп много и они имеют свойство перегорать, то часто компьютер простаивал из-за поиска и замены вышедшей из строя лампы.
• Лампы выделяют большое количество тепла, следовательно, вычислительные машины требуют специальные мощные охладительные системы.

Примеры компьютеров:

Колоссус – секретная разработка британского правительства (в разработке принимал участие Алан Тьюринг). Это первый в мире электронный компьютер, хотя и не оказавший влияние на развитие компьютерной техники (из-за своей секретности), но помог победить во Второй мировой войне.

Эниак. Создатели: Джон Моушли и Дж. Преспер Экерт. Вес машины 30 тонн. Минусы: использование десятичной системы счисления; множество переключателей и кабелей.

Эдсак. Достижение: первая машина с программой в памяти.

Whirlwind I. Слова малой длины, работа в реальном времени.

Компьютер 701 (и последующие модели) фирмы IBM. Первый компьютер, лидирующий на рынке в течение 10 лет.

Второе поколение. Компьютеры на транзисторах (1955-1965)

Быстродействие: сотни тысяч операций в секунду.

По сравнению с электронными лампами использование транзисторов позволило уменьшить размеры вычислительной техники, повысить надежность, увеличить скорость работы (до 1 млн. операций в секунду) и почти свести на нет теплоотдачу. Развиваются способы хранения информации: широко используется магнитная лента, позже появляются диски. В этот период была замечена первая компьютерная игра.

Первый компьютер на транзисторах TX стал прототипом для компьютеров ветки PDP фирмы DEC, которые можно считать родоначальниками компьютерной промышленности, т.к появилось явление массовой продажи машин. DEC выпускает первый миникомпьютер (размером со шкаф). Зафиксировано появление дисплея.

Фирма IBM также активно трудится, производя уже транзисторные версии своих компьютеров.

Компьютер 6600 фирмы CDC, который разработал Сеймур Крей, имел преимущество над другими компьютерами того времени – это его быстродействие, которое достигалось за счет параллельного выполнения команд.

Третье поколение. Компьютеры на интегральных схемах (1965-1980)

Быстродействие: миллионы операций в секунду.

Интегральная схема представляет собой электронную схему, вытравленную на кремниевом кристалле. На такой схеме умещаются тысячи транзисторов. Следовательно, компьютеры этого поколения были вынуждены стать еще мельче, быстрее и дешевле.

Последнее свойство позволяло компьютерам проникать в различные сферы деятельности человека. Из-за этого они становились более специализированными (т.е. имелись различные вычислительные машины под различные задачи).

Появилась проблема совместимости выпускаемых моделей (программного обеспечения под них). Впервые большое внимание совместимости уделила компания IBM.

Было реализовано мультипрограммирование (это когда в памяти находится несколько выполняемых программ, что дает эффект экономии ресурсов процессора).

Дальнейшее развитие миникомпьютеров (PDP-11).

Четвертое поколение. Компьютеры на больших (и сверхбольших) интегральных схемах (1980-…)

Быстродействие: сотни миллионов операций в секунду.

Появилась возможность размещать на одном кристалле не одну интегральную схему, а тысячи. Быстродействие компьютеров увеличилось значительно. Компьютеры продолжали дешеветь и теперь их покупали даже отдельные личности, что ознаменовало так называемую эру персональных компьютеров. Но отдельная личность чаще всего не была профессиональным программистом. Следовательно, потребовалось развитие программного обеспечения, чтобы личность могла использовать компьютер в соответствие со своей фантазией.

В конце 70-х – начале 80-х популярностью пользовался компьютера Apple, разработанный Стивом Джобсом и Стивом Возняком. Позднее в массовое производство был запущен персональный компьютер IBM PC на процессоре Intel.

Позднее появились суперскалярные процессоры, способные выполнять множество команд одновременно, а также 64-разрядные компьютеры.

Пятое поколение?

Сюда относят неудавшийся проект Японии (хорошо описан в Википедии). Другие источники относят к пятому поколению вычислительных машин так называемые невидимые компьютеры (микроконтроллеры, встраиваемые в бытовую технику, машины и др.) или карманные компьютеры.

Также существует мнение, что к пятому поколению следует относить компьютеры с двухядерными процессорами. С этой точки зрения пятое поколение началось примерно с 2005 года.

Пособие по стандартам »Математика 4 класс Общие основные стандарты

В 4 классе учебное время должно быть сосредоточено на трех важнейших областях: (1) развитие понимания и беглости речи с помощью многозначного умножения и развитие понимания деления для нахождения частных, включающих многозначное умножение. цифровые дивиденды; (2) развитие понимания эквивалентности дробей, сложения и вычитания дробей с одинаковыми знаменателями и умножения дробей на целые числа; (3) понимание того, что геометрические фигуры можно анализировать и классифицировать на основе их свойств, таких как наличие параллельных сторон, перпендикулярных сторон, определенных угловых размеров и симметрии.

1. Учащиеся обобщают свое понимание разряда до 1 000 000, понимая относительные размеры чисел в каждом разряде. Они применяют свое понимание моделей умножения (группы равного размера, массивы, модели площадей), разметки и свойств операций, в частности свойства распределения, при разработке, обсуждении и использовании эффективных, точных и универсальных методов для вычислить произведения многозначных целых чисел. В зависимости от цифр и контекста они выбирают и точно применяют соответствующие методы для оценки или мысленного расчета продуктов.Они развивают беглость с помощью эффективных процедур умножения целых чисел; понимать и объяснять, почему процедуры работают на основе числовой стоимости и свойств операций; и используйте их для решения проблем. Учащиеся применяют свое понимание моделей деления, разметки, свойств операций и отношения деления к умножению по мере того, как они разрабатывают, обсуждают и используют эффективные, точные и обобщаемые процедуры для нахождения частных, включающих многозначные дивиденды. Они выбирают и точно применяют подходящие методы для оценки и мысленного вычисления частных, а также интерпретируют остатки в зависимости от контекста.

2. Студенты развивают понимание эквивалентности дробей и операций с дробями. Они признают, что две разные дроби могут быть равными (например, 15/9 = 5/3), и разрабатывают методы для создания и распознавания эквивалентных дробей. Студенты расширяют предыдущие представления о том, как дроби строятся из единичных дробей, составляя дроби из единичных дробей, разлагая дроби на единичные дроби и используя значение дробей и значение умножения для умножения дроби на целое число.

3. Учащиеся описывают, анализируют, сравнивают и классифицируют двухмерные формы. Создавая, рисуя и анализируя двумерные формы, учащиеся углубляют свое понимание свойств двумерных объектов и их использования для решения задач, связанных с симметрией.

Домен	Кластер	Код	Единое ядро ​​ГОСТ
Операции и алгебраическое мышление	Используйте четыре операции с целыми числами для решения проблем.	4.OA.1	Интерпретируйте уравнение умножения как сравнение, например, интерпретируйте 35 = 5 x 7 как утверждение, что 35 в 5 раз больше 7 и 7 раз больше 5. Представьте словесные утверждения мультипликативных сравнений как уравнения умножения.
		4.OA.2	Умножение или деление для решения словесных задач, включающих мультипликативное сравнение, например, используя рисунки и уравнения с символом неизвестного числа для представления проблемы, отличая мультипликативное сравнение от аддитивного сравнения.
		4.OA.3	Решайте многоступенчатые задачи со словами, поставленные с целыми числами и имеющие ответы с целыми числами, используя четыре операции, включая задачи, в которых необходимо интерпретировать остатки. Представьте эти проблемы, используя уравнения с буквой, обозначающей неизвестную величину. Оцените разумность ответов с помощью мысленных вычислений и стратегий оценки, включая округление.
	Ознакомьтесь с факторами и мультипликаторами.	4.OA.4	Найдите все пары факторов для целого числа в диапазоне 1–100. Помните, что целое число является кратным каждому из его факторов. Определите, является ли данное целое число в диапазоне 1–100 кратным заданному однозначному числу. Определите, является ли данное целое число в диапазоне 1–100 простым или составным.
	Создание и анализ шаблонов.	4.OA.5	Создает рисунок числа или фигуры в соответствии с заданным правилом.Определите очевидные особенности шаблона, которые не были явными в самом правиле. Например: учитывая правило «сложить 3» и начальное число 1, сгенерируйте термины в результирующей последовательности и обратите внимание, что термины кажутся чередующимися между нечетными и четными числами. Неформально объясните, почему числа будут и дальше меняться таким образом.
Число и операции в базе Ten	Обобщить понимание разрядов для многозначных целых чисел.	4.NBT.1	Помните, что в многозначном целом числе цифра в одном месте в десять раз больше, чем в месте справа. Например, узнайте, что 700 ÷ 70 = 10, применив концепции числового значения и деления. (Ожидания 4-й степени в этой области ограничены целыми числами, меньшими или равными 1 000 000.)
		4.NBT.2	Чтение и запись многозначных целых чисел с использованием десятичных цифр, числовых имен и расширенной формы.Сравните два многозначных числа на основе значений цифр в каждом месте, используя>, = и
		4.NBT.3	Используйте разметку знаков для округления многозначных целых чисел до любого места. (Ожидания 4-й степени в этой области ограничены целыми числами, меньшими или равными 1 000 000.)
	Используйте понимание разряда и свойства операций для выполнения многозначной арифметики.	4.NBT.4	Свободно вычисляйте и вычитайте многозначные целые числа, используя стандартный алгоритм.(Ожидания 4-го класса в этой области ограничены целыми числами, меньшими или равными 1 000 000. Можно использовать ряд алгоритмов.)
		4.NBT.5	Умножьте целое число до четырех цифр на однозначное целое число и умножьте два двузначных числа, используя стратегии, основанные на разрядах и свойствах операций. Проиллюстрируйте и объясните расчет с помощью уравнений, прямоугольных массивов и / или моделей площадей. (Ожидания 4-го класса в этой области ограничены целыми числами, меньшими или равными 1 000 000.Может использоваться ряд алгоритмов.)
		4.NBT.6	Найдите целочисленные частные и остатки с дивидендами до четырех цифр и однозначными делителями, используя стратегии, основанные на разряде, свойствах операций и / или взаимосвязи между умножением и делением. Проиллюстрируйте и объясните расчет с помощью уравнений, прямоугольных массивов и / или моделей площадей. (Ожидания 4-го класса в этой области ограничены целыми числами, меньшими или равными 1 000 000.Может использоваться ряд алгоритмов.)
Число и операции: дроби	Расширить понимание эквивалентности дробей и упорядочения.	4.NF.1	Объясните, почему дробь a / b эквивалентна дроби (n × a) / (n × b), используя модели визуальных дробей, обращая внимание на то, как количество и размер частей различаются, даже если сами две дроби являются тот же размер. Используйте этот принцип, чтобы распознавать и генерировать эквивалентные дроби.(Ожидаемые оценки 4-го класса в этой области ограничены дробями со знаменателями 2, 3, 4, 5, 6, 8, 10, 12, 100.)
		4.NF.2	Сравните две дроби с разными числителями и разными знаменателями, например, создав общие знаменатели или числители, или сравнив с эталонной дробью, такой как 1/2. Признайте, что сравнения действительны только тогда, когда две дроби относятся к одному и тому же целому. Запишите результаты сравнений с помощью символов>, = или
	Постройте дроби из дробных единиц, применяя и расширяя предыдущие представления об операциях над целыми числами.	4.NF.3	Дробь a / b с a> 1 понимается как сумма дробей 1 / b. а. Под сложением и вычитанием дробей следует понимать соединение и разделение частей, относящихся к одному целому. г. Разложите дробь на сумму дробей с одинаковым знаменателем более чем одним способом, записывая каждое разложение по формуле . Обоснуйте разложение, например, используя визуальную модель дроби. Примеры: 3/8 = 1/8 + 1/8 + 1/8; 3/8 = 1/8 + 2/8; 2 1/8 = 1 + 1 + 1/8 = 8/8 + 8/8 + 1/8. г. Сложите и вычтите смешанные числа с одинаковыми знаменателями, например, заменив каждое смешанное число эквивалентной дробью, и / или используя свойства операций и взаимосвязь между сложением и вычитанием. г. Решайте задачи со словами, включающие сложение и вычитание дробей, относящихся к одному целому и имеющих одинаковые знаменатели, , например, используя визуальные модели дробей и уравнения для представления проблемы.
		4.NF.4	Применяйте и расширяйте предыдущие представления об умножении, чтобы умножать дробь на целое число. а. Дробь a / b следует понимать как кратное 1 / b. Например, используйте модель визуальной дроби, чтобы представить 5/4 как произведение 5 × (1/4), записав вывод по уравнению 5/4 = 5 × (1/4). г. Поймите, что кратное a / b является кратным 1 / b, и используйте это понимание для умножения дроби на целое число. Например, использует модель визуальной дроби, чтобы выразить 3 × (2/5) как 6 × (1/5), распознавая этот продукт как 6/5. (Как правило, n × (a / b) = (n × a) / b.) c. Решать задачи со словами, связанные с умножением дроби на целое число, например.g., используя модели визуальных фракций и уравнения для представления проблемы. Например, если каждый человек на вечеринке съест 3/8 фунта ростбифа, а на вечеринке будет 5 человек , сколько фунтов ростбифа потребуется? Между какими двумя целыми числами лежит ваш ответ?
	Разберитесь в десятичной системе счисления дробей и сравните десятичные дроби.	4.NF.5	Выразите дробь со знаменателем 10 как эквивалентную дробь со знаминателем 100 и используйте этот метод для сложения двух дробей с соответствующими знаменателями 10 и 100.Например, выразите 3/10 как 30/100 и добавьте 3/10 + 4/100 = 34/100. (Учащиеся, которые могут генерировать эквивалентные дроби, могут разработать стратегии сложения дробей с разными знаменателями в целом. Но сложение и вычитание с разными знаменателями в целом не является обязательным требованием в этом классе.)
		4.NF.6	Используйте десятичную запись для дробей со знаменателем 10 или 100. Например, перепишите 0,62 как 1 62/100; опишите длину как 0,62 метра; найдите 0.62 на числовой линейной диаграмме. (Ожидаемые оценки 4-го класса в этой области ограничены дробями со знаменателями 2, 3, 4, 5, 6, 8, 10, 12, 100.)
		4.NF.7	Сравните два десятичных знака с сотыми, исходя из их размера. Помните, что сравнения сравнения действительны только тогда, когда два десятичных знака относятся к одному и тому же целому. Запишите результаты сравнений с помощью символов>, = или
Измерения и данные	Решает проблемы, связанные с измерением и преобразованием измерений из более крупной единицы в меньшую.	4.MD.1	Знать относительные размеры единиц измерения в одной системе единиц, включая км, м, см; кг, г; фунт, унция; л, мл; час, мин, сек. В рамках единой системы измерения выразите измерения в большей единице через меньшую единицу. Запишите эквиваленты измерений в таблицу из двух столбцов. Например: знайте, что 1 фут в 12 раз больше 1 дюйма. Выразите длину 4-футовой змеи как 48 дюймов. Создайте таблицу преобразования для футов и дюймов, перечислив пары чисел (1, 12), (2, 24 ), (3, 36),….
		4.MD.2	Используйте четыре операции для решения текстовых задач, связанных с расстояниями, интервалами времени, объемами жидкости, массами объектов и деньгами, включая задачи, связанные с простыми дробями или десятичными знаками, а также задачи, требующие выражения измерений, данных в большей единице, в меньших Блок. Представляйте измеряемые величины с помощью диаграмм, таких как диаграммы с числовыми линиями, которые имеют шкалу измерений.
		4.MD.3	Применяйте формулы площади и периметра для прямоугольников в реальных и математических задачах. Например, найдите ширину прямоугольной комнаты с учетом площади пола и длины, просмотрев формулу площади как уравнение умножения с неизвестным коэффициентом.
	Представление и интерпретация данных.	4.MD.4	Постройте линейный график для отображения набора данных измерений в долях единицы (1/2, 1/4, 1/8). Решайте задачи, связанные с сложением и вычитанием дробей, используя информацию, представленную на линейных графиках.Например, с помощью линейного графика найдите и интерпретируйте разницу в длине между самым длинным и самым коротким экземплярами в коллекции насекомых.
	Геометрические измерения — понимание понятий угла и измерения углов.	4.MD.5	Распознавать углы как геометрические формы, которые образуются там, где два луча имеют общую конечную точку, и понимать концепции измерения углов: a. Угол измеряется относительно круга с центром в общем конце лучей, принимая во внимание долю дуги окружности между точками, где два луча пересекают круг.Угол, который составляет 1/360 окружности, называется «углом в один градус» и может использоваться для измерения углов. г. Угол, который поворачивается на n углов в один градус, называется угловой мерой n градусов.
		4.MD.6	Измерьте углы в целых градусах с помощью транспортира. Нарисуйте углы указанной меры.
		4.MD.7	Распознать угловую меру как добавочную. Когда угол разбивается на неперекрывающиеся части, угловая мера целого является суммой угловых величин частей.Решайте задачи сложения и вычитания, чтобы найти неизвестные углы на диаграмме в реальных и математических задачах, например, используя уравнение с символом для неизвестной угловой меры.
Геометрия	Нарисуйте и обозначьте линии и углы, а также классифицируйте формы по свойствам их линий и углов.	4.G.1	Нарисуйте точки, линии, отрезки, лучи, углы (прямые, острые, тупые), а также перпендикулярные и параллельные линии. Обозначьте их на двухмерных фигурах.
		4.G.2	Классифицируют двумерные фигуры на основании наличия или отсутствия параллельных или перпендикулярных линий либо наличия или отсутствия углов заданного размера. Считайте прямоугольные треугольники категорией и определяйте прямоугольные треугольники.
		4.G.3	Распознает линию симметрии двумерной фигуры как линию, пересекающую фигуру, так что фигуру можно сложить вдоль этой линии на совпадающие части.Определите линейно-симметричные фигуры и проведите линии симметрии.

Оценка: 4 — Расчет 2

Особенности специального образования

Рекомендации по специальному образованию, написанные учителями специального образования штата Индиана, предназначены для повышения вовлеченности и поддержки роста учащихся в рамках специального образования. Это не исчерпывающий список стратегий, но эта поддержка поможет вам сделать обучение математике более доступным для учащихся. Педагоги должны адаптировать стратегии к потребностям ваших учеников и убедиться, что вы создаете возможности для всех учеников, чтобы они могли взаимодействовать с строгим содержанием.

Универсальные стратегии для учащихся с трудностями
Использование манипуляторов	Кубики Все материальное, чем можно манипулировать Карточки с номерами Сотни или 120 диаграмм Создание собственной книги до 1000 Пачка соломок Фракционные прутки / круги
Модель / Рисование рисунка	1 к 1 соответствие номера объекту (представление объекта) 10 кадров Размещение блоков значений Определить набор / группы Учитель моделирует — думает вслух — повторяется
Строительные ресурсы	Готовые заметки с заполнением пробелов Готовые диаграммы с заполнением пробелов Готовая числовая строка с заполненными пробелами Справочная таблица формул
Ежедневное подкрепление	Календарное время (при необходимости) Общественный кружок / утреннее собрание
Карты памяти	Известные факты с неизвестными фактами
Взаимодействие с точками соприкосновения
Визуальные подсказки	Плакаты со словарным запасом Словарь с картинками
Несколько способов доставки	Номерные строки Моделирование Демонстрация мышления

% PDF-1.5 % 1599 0 объект > эндобдж xref 1599 72 0000000016 00000 н. 0000003056 00000 н. 0000003183 00000 п. 0000003883 00000 н. 0000004106 00000 п. 0000004315 00000 н. 0000004539 00000 н. 0000004747 00000 н. 0000004984 00000 н. 0000005211 00000 н. 0000005438 00000 н. 0000005650 00000 н. 0000005877 00000 н. 0000006100 00000 н. 0000006307 00000 н. 0000006514 00000 н. 0000006721 00000 н. 0000006913 00000 н. 0000007119 00000 н. 0000007345 00000 н. 0000007555 00000 н. 0000007794 00000 н. 0000008120 00000 н. 0000008446 00000 н. 0000008756 00000 н. 0000009082 00000 н. 0000009290 00000 н. 0000009529 00000 н. 0000009755 00000 н. 0000009965 00000 н. 0000010204 00000 п. 0000010426 00000 п. 0000010632 00000 п. 0000010854 00000 п. 0000011078 00000 п. 0000011304 00000 п. 0000011514 00000 п. 0000011753 00000 п. 0000011979 00000 п. 0000012152 00000 п. 0000012287 00000 п. 0000012460 00000 п. 0000012637 00000 п. 0000012877 00000 п. 0000013111 00000 п. 0000013140 00000 п.