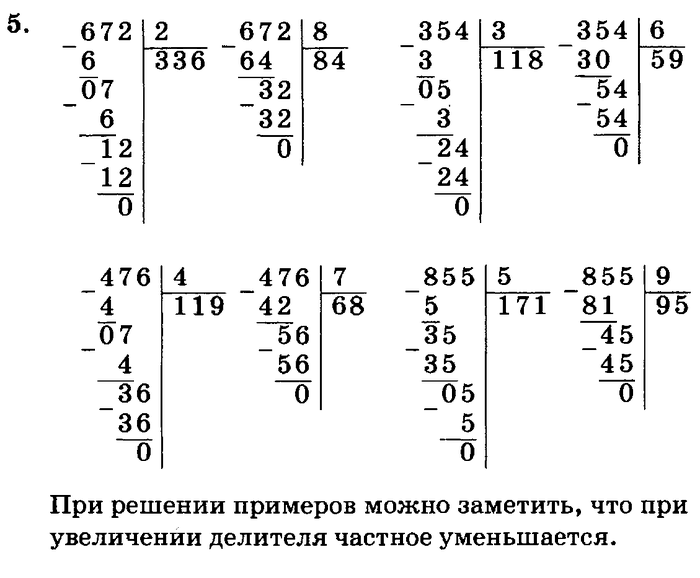
Деление в столбик 2 (с клеткой)
Рейтинг 5.00 из 5 на основе опроса 1 пользователя
(1 отзыв клиента)
85,00 ₽
Примеры на деление в столбик с учетом схемы решения: для каждого примера предусмотрено поле в клетку и разметка для заполнения, чтобы помочь правильно расставить цифры по разрядам. Примеры на деление на однозначное, двузначное или трехзначное число. С ответами. Для печати А4.
Количество товара Деление в столбик 2 (с клеткой)
Артикул: i-14972 Категория: Для учебы Метки: 3 класс, 4 класс, Примеры в столбик
- Описание
- Детали
- Отзывы (1)
Описание
Примеры на деление в столбик формируются с учетом схемы решения

Такая форма решения примеров поможет правильно расставить цифры по разрядам для правильного вычисления: вычесть разряды единиц одного числа из разрядов единиц другого числа, затем из разрядов десятков первого числа разряды десятков другого и т.д. Таким образом, карточки с примерами помогут закрепить последовательность и правильность решения примеров.
Программа имеет внутренние настройки, изменяя которые можно создать примеры для детей разного возраста и уровня подготовки: на однозначное , двузначное или трехзначное число. Поэтому программа будет полезна как для учеников начальной школы 3-4 классов, так и для более старших классов.
Программа счета написана в Excel с помощью макросов. Формируются примеры на листе формата А4. Примеры генерируются случайным образом, количество генераций не ограничено. В конце карточки формируются ответы на примеры, которые после печати карточки можно отрезать. Нумерация карточек и ответов позволяет быстро находить ответы к каждой карточке, даже если их напечатано много.
Нумерация карточек и ответов позволяет быстро находить ответы к каждой карточке, даже если их напечатано много.
Генератор примеров по математике будет очень удобен как для родителей, так и для учителей. Не нужно заранее покупать задачники и пособия по математике с примерами. Можно скачать файл и сгенерировать карточки в любое время независимо от подключения к интернету и распечатать.
Для ознакомления с программой можно бесплатно скачать примеры, которые получаются при использовании программы. Для получения новой карточки примеров достаточно скачать
Другие программы на деление в столбик:
- Деление в столбик (простое)
- Деление в столбик 3 (со словами для самоконтроля)
- Тренажер: деление в столбик» — решение на компьютере (без печати)
Другие программы, которые помогут закрепить навыки счета:
- Сложение и вычитание в столбик (простое)
- Сложение и вычитание в столбик 2 (с клеткой)
- Сложение и вычитание в столбик 3 (со словами для самоконтроля)
- Тренажер на сложение и вычитание в столбик — решение на компьютере (без печати)
- Умножение в столбик (простое)
- Умножение в столбик 2 (с клеткой)
- Тренажер: умножение в столбик — решение на компьютере (без печати)
- Примеры на все действия в столбик
- Умножение трехзначного числа на однозначное по схеме
- Умножение и деление в столбик
- Примеры в столбик на сложение, вычитание и умножение: заполнить пропуски
- Деление с остатком на число (с выбором уровня сложности)
- Умножение и деление по типам (табличное, внетабличное, круглых чисел)
На сайте представлен каталог программ, в котором все программы распределены по группам. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.
С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.
Вам также будет интересно…
Сложение и вычитание в столбик 2 (с клеткой)
80,00 ₽В корзинуДеление с остатком на число (с выбором уровня сложности)
Оценка 5.00 из 5
80,00 ₽В корзинуТренажер: умножение в столбик
75,00 ₽В корзинуВсе действия в столбик 3 (со словами для самоконтроля)
Оценка 5.00 из 5
175,00 ₽В корзинуДеление в столбик 3 (со словами для самоконтроля)
Умножение и деление в столбик
Оценка 4.67 из 5
100,00 ₽В корзинуТренажер: сложение и вычитание в столбик
70,00 ₽В корзинуРаскрытие скобок и порядок действий до 1000 (сложные примеры)
130,00 ₽В корзинуТренажер: деление в столбик
75,00 ₽В корзинуУмножение и деление по типам (табличное, внетабличное, круглых чисел)
120,00 ₽В корзинуУмножение в столбик 2 (с клеткой)
Оценка 5.
85,00 ₽В корзину 00 из 5
00 из 5Примеры в столбик на сложение, вычитание и умножение: заполнить пропуски
Оценка 5.00 из 5
120,00 ₽В корзину
Тренажер сложения, вычитания, умножения и деления столбиком
Skip Navigation Links
Тренажер сложения, вычитания, умножения и деления столбиком оснащен функцией автоматической проверки решения, индикатором времени и статистикой правильных и неправильных ответов. Тренажер будет полезен детям учащимся во 2, 3 и 4 классе.
Тип примера
СложениеВычитаниеУмножениеДелениеЛюбой типСложение и вычитаниеСложение и умножениеСложение и делениеВычитание и умножениеВычитание и делениеУмножение и деление
Уровень сложности
1
2
3
4
Правильно:   0
Ошибок:   0
00:00:00
| + | − |
| × | ÷ |
Тренажер по математике Тренажер по математике предназначен для развития навыков устного счета, таких математических операций как: сложение, вычитание, умножение и деление. Для начала работы выберите тип примера и уровень сложности. Тренажер оснащен функцией автоматической проверки решения, индикатором времени и статистикой правильных и неправильных ответов.
Для начала работы выберите тип примера и уровень сложности. Тренажер оснащен функцией автоматической проверки решения, индикатором времени и статистикой правильных и неправильных ответов.
| 49 | 17 |
| 25 | 12 |
Тренажер решения примеров. Найди правильный ответ. Тренажер решения примеров позволит улучшить навыки сложения, вычитания, умножения и деления. Для того чтобы начать тренировку, выберете математическую операцию и уровень сложности, далее необходимо выбрать правильный ответ из трех предложенных вариантов. Тренажер отображает время прошедшее от начала тренировки, а также количество верных ответов и ошибок. Данный тренажер будет полезен детям с 1 по 5 класс, а также всем, кто хочет улучшить навыки быстрого счета в уме.
5 × 5 = 25
Тренажер таблицы умножения Тренажер таблицы умножения отображает количество правильных и неправильных ответов.
45
_________
15
Тренажер сложения, вычитания, умножения и деления столбиком Тренажер сложения, вычитания, умножения и деления столбиком оснащен функцией автоматической проверки решения, индикатором времени и статистикой правильных и неправильных ответов. Тренажер будет полезен детям учащимся во 2, 3 и 4 классе.
Тренажер счета для дошкольников Данный тренажер поможет выучить цифры от 0 до 10 детям дошкольного возраста. В процессе занятия ребенку необходимо сосчитать количество предметов и выбрать правильный ответ из двух предложенных вариантов. Данный тренажер послужит хорошей альтернативой счету на палочках и закрепит знание цифр у детей.
Тренажер счета на внимательность для дошкольников Данный тренажер поможет выучить цифры от 0 до 10 и повысит внимательность у детей дошкольного возраста. В процессе занятия ребенку необходимо сосчитать количество предметов среди других и выбрать правильный ответ из двух предложенных вариантов. Данный тренажер послужит хорошей альтернативой счету на палочках и закрепит знание цифр у детей.
В процессе занятия ребенку необходимо сосчитать количество предметов среди других и выбрать правильный ответ из двух предложенных вариантов. Данный тренажер послужит хорошей альтернативой счету на палочках и закрепит знание цифр у детей.
Тренажер решения примеров с разными действиями Данный тренажер предназначен для тренировки решения примеров на различные действия как со скобками, так и без скобок. Вы быстро научитесь правильно расставлять действия в выражении. Для записи промежуточных решений воспользуйтесь окном в самом низу тренажера.
Что такое обратные операции? — Определение Факты и примеры
Операции
Математическая «операция» относится к вычислению значения с использованием операндов и математического оператора. Числа, используемые для операции, называются операндами. В зависимости от типа операции операндам назначаются разные термины. Операторы — это символы, обозначающие математическую операцию, например:
- + для сложения
- — для вычитания
- × для умножения
- ÷ для отдела
- = равно, указывает на равенство, то есть значение левой части равно значению правой части.

Родственные игры
Что такое обратные операции?
Обратное означает обратное. Таким образом, в математике обратная операция может быть определена как операция, которая отменяет то, что было сделано предыдущей операцией. Множество двух противоположных операций называется обратными операциями.
Например: Если мы сложим 5 и 2 ручки, мы получим 7 ручек. Теперь вычтите 7 ручек и 2 ручки, и мы получим 5 обратно. Здесь сложение и вычитание являются обратными операциями.
Примеры обратных операций приведены ниже:
Связанные рабочие листы
Сложение и вычитание
Сложение и вычитание являются обратными операциями, что означает, что сложение отменяет вычитание, а вычитание отменяет сложение. Мы можем переставить числа, данные в уравнении сложения, а затем мы можем использовать уравнение сложения, чтобы получить два разных уравнения вычитания.
Например: $15 + 6 = 21$
Образуются два уравнения вычитания: $21$ $–$ $6 = 15$ и $21$ $–$ $15 = 6$
После этого мы даже можем показать, что если взять число, например 15, прибавить и вычесть то же число до 15, мы снова получим 15.
т. е. $15 + 6$ $–$ $6 = 0$
Точно так же мы можем переставить числа, данные в уравнении вычитания, и тогда мы можем составить два уравнения сложения.
Например: $30$ $–$ $14 = 16$
Получаются следующие уравнения сложения: $14 + 16 = 30$ и $16 + 14 = 30$
Когда мы складываем число и вычитаем его позже, эффект обратный.
$16 – 4 + 4 = 0$
Умножение и деление
Умножение и деление являются обратными операциями, что означает, что умножение отменяет деление, а деление отменяет умножение. Мы можем переставить числа, данные в уравнении умножения, и тогда мы можем сделать два разных уравнения деления.
Например: $7 х 4 = 28$
Получаются два уравнения деления: $28\div4=7$ и $28\div7=4$
Кроме того, когда мы умножаем число, а затем делим его позже на, эффект обратный.
$12\times4=48; 48\div4=12$
Точно так же мы можем переставить числа, данные в уравнении деления, и тогда мы можем составить два уравнения умножения.
Например: $45\div9=5$
Образуются следующие уравнения умножения: $9\times 5 = 45$ и $5\times 9 = 45$
Также, когда мы делим число, а затем умножаем то же число позже на, эффект обратный.
$1\div24=3; 3\times4=12$
Свойства обратных операций
- Обратное аддитивное свойство
Значение, которое при добавлении к исходному числу дает 0, известно как обратная добавка.
Предположим, что x является исходным числом, тогда его аддитивный обратный будет минус x, т. е. $-$$\text{x}$, такой, что:
$\text{x + ( – x ) = x – x} = 0$
Например, $6+( $ $-$ $ 6)=0$. Следовательно, $–6$ является аддитивной инверсией 6 и наоборот.
Предположим, что $-$$\text{x}$ — исходное число, тогда его аддитивным обратным будет положительное значение x, т. е. x.
- Свойство обратного умножения
Значение, которое при умножении на исходное число дает 1, называется обратным мультипликативным.
Предположим, что x исходное число, тогда его мультипликативное обратное число будет обратным $\text{x}$, т. е. $\frac{1}{\text{x}}$, таким образом, что:
$ \text{x}\times\frac{1}{\text{x}}=1$
Например, $6\times\frac{1}{6}=1$. Следовательно, $\frac{1}{6}$ является мультипликативным, обратным 6, и наоборот.
Предположим, что $\frac{1}{x}$ — исходное число, тогда его мультипликативное обратное число будет обратным $\frac{1}{x}$, т. е. $x$.
Например: мультипликативное обратное значение $\frac{3}{4}$ равно $\frac{4}{3}$.
Решенные примеры
Пример 1: Составление уравнений вычитания из $24 + 13 = 37$ .
Решение : 37$ $–$ 24$ = 13$ и 37$ $-$ 13$ = 24$
2. Какая аддитивная величина обратна –10?
Решение : Поскольку -10 является отрицательным числом, его обратная аддитивная величина будет положительным числом. Таким образом, аддитивное обратное значение –10 будет равно 10.
Таким образом, аддитивное обратное значение –10 будет равно 10.
3. Чему равно мультипликативное обратное число $(3-\frac{1}{4})$ ?
Ответ: $(3-\frac{1}{4})=\frac{12-1}{4}=\frac{11}{4}$
Мультипликативное значение, обратное $\frac{11} {4}$ равно $\frac{4}{11}$ .
Практические задачи
1
Если $15$ $-$ $12=3$, каким будет уравнение сложения?
15$ + 3 = 12$
12$ + 3 = 15$
15$ $-$ 3 = 12$
Ничего из этого
Правильный ответ: 12$ + 3 = 15$
Уравнение сложения для 15$ $ $-$ $12 = 3$ равно $12 + 3 = 15$.
2
Если $34=12$, какое будет уравнение деления?
$12\div3=4$
$12\div4=3$
$4\div3=12$
Оба A и B
Правильный ответ: Оба A и B
Уравнения деления будут $12\div3= 4$ и $12\div4=3$. 92=64$, тогда $\sqrt{64}=8$.
Каково назначение обратной операции?
Обратные операции используются для изменения влияния одной операции на другую. Цель обратных операций — понять взаимосвязь между основными математическими операторами $+$, $−$, $\times$, $\div$, чтобы упростить решение уравнения и сэкономить время.
Цель обратных операций — понять взаимосвязь между основными математическими операторами $+$, $−$, $\times$, $\div$, чтобы упростить решение уравнения и сэкономить время.
Как используется обратная операция при решении уравнений?
Обратные операции используются при решении уравнений для выделения переменных путем применения обратных операций с обеих сторон.
Разделение по специальным номерам Разделение по специальным номерам (определение, типы и примеры)
- Разделение по специальным номерам
- Что такое разделение?
- Деление на 2, 5 или 10
- Деление на 3, 4, 6, 7, 8 и 9
- Деление на 0 и 1
Трое детей: Сэм, Роб и Боб. Райан покупает для них 6 шоколадок, но не понимает, сколько конфет можно дать каждому.
Райан дал 3 шоколадки Сэму, 2 Бобу и только 1 Робу. Это делает Сэма счастливым, но Роба грустным.
Райан задумался и раздал им 6 шоколадок поровну.

Каждый получает по 2 шоколадки. Это означает, что Райан поровну делит конфеты между тремя детьми.
Что такое деление
Деление — это метод распределения или разбиения числа на равные части. Это обратное умножение чисел. Знак деления – «÷». Когда мы знаем общее количество объектов и количество равных групп, мы можем разделить, чтобы найти размер каждой группы. И наоборот, если мы знаем общее количество объектов и размер каждой группы, мы можем разделить их, чтобы найти общее количество равных групп. Следовательно, деление — это операция, которая дает размер каждой равной группы или количество равных групп.
Число, которое делится, называется делимым. Число, на которое мы делим, называется делителем, а полученный результат — частным. Число, оставшееся в конце деления, называется остатком.
Например:
Имеется 35 счетчиков. Есть 5 равных рядов. Сколько фишек в каждом ряду?
Всего имеется 35 счетчиков, которые нужно расположить в 5 рядов.
 Чтобы найти количество фишек в каждом ряду, делим 35 на 5. Результат деления равен 7.
Чтобы найти количество фишек в каждом ряду, делим 35 на 5. Результат деления равен 7.Разделить на 2, 5 или 10
Если вы сделаете массив из 2, 5 или 10 счетчиков в каждой строке, количество полученных строк будет частным от деления. В противном случае, если вы разместите одинаковые счетчики в каждом столбце, количество столбцов будет частным.
Или предположим, что у вас есть определенное количество счетчиков. Вы хотите разделить их на 2, 5 или 10. Затем подумайте о числе, которое при умножении на 2, 5 или 10 дает количество счетчиков. Это число и будет частным от деления.
Например , если мы хотим разделить 14 на 2,
Мы знаем 2 × 7 = 14
Следовательно,
Следовательно, нам нужно 7 столбцов по 2 счетчика по 7 счетчиков.
Используя ту же стратегию, мы можем разделить любое число на 5 или 10.
Например, 30 ÷ 5 можно вычислить как
Сначала подумай 5 раз, какое число равно 30.
 Из пяти фактов мы знаем, что
Из пяти фактов мы знаем, что5×6 = 30. Итак, нам нужно создать 5 рядов по 6 фишек или 6 рядов по 5 фишек
каждый, чтобы получить 30 счетчиков
Опять же, для 40 ÷ 10,
10 раз сколько будет 40?
Используя факт 10, мы получаем, 10 × 4 = 40
Это означает, что мы делаем 10 рядов по 4 фишки в каждом или 4 ряда по 10 фишек в каждом.
Деление на 3, 4, 6, 7, 8 и 9
Деление на 3, 4, 6, 7, 8 или 9 аналогично делению на 2, 5 и 10.
Если у вас есть определенное количество счетчиков, сделайте массив счетчиков. Поставьте жетоны равные делителю (в данном случае 3, 4, 6, 7, 8 или 9) в каждой строке или столбце. Затем заполните строки и столбцы счетчиков, чтобы легко понять деление.
Например,
Мы можем найти 36 ÷ 4 как,
Подумайте 4 раза, какое число равно 36. Из факта 4s мы получим 4 × 9 = 36.
Или мы можем составить массив счетчиков 4 ряда по 9 фишек в каждом ряду.

Таким образом, деление можно выполнить следующим образом:
Разделить на 0 и 1
Когда любое число делится на 1, частное есть само число. Например,
Мы можем найти 8 ÷ 1 as,
Сначала подумайте, сколько будет 1 умножить на 8.
Ответ: 1 умножить на 8 равно 8 или 1 × 8 = 8
Следовательно, 8 ÷ 1 = 8
Деление 0 довольно интересно.
1. Мы не можем делить любое число на 0.
Например, у вас есть 6 игрушек. Вы хотите поделиться теми среди 0 детей. Сколько игрушек вы дадите каждому ребенку?
Этот вопрос не имеет никакого смысла. Поэтому деление на 0 невозможно.
Опять же,
2. Если мы разделим 0 на любое число (кроме числа 0), то получим частное 0.
Например, если у вас 5 друзей и нет денег из ваших, кто хочет денег. Подумайте, сколько денег вы дадите каждому из них.

Итак, если у вас нет денег, вы не можете их никому отдать. Таким образом, вы дадите всем по 0 долларов. Если ноль разделить на любое число, то в частном будет 0,9.0005
Например, 0 ÷ 5 можно получить как
Следовательно, 0 ÷ 5 = 0, поскольку ноль, деленный на любое число (кроме 0), сам равен 0.
Решенные примеры
Пример 1: Найдите коэффициент для 42 ÷ 7.
Решение:
Сначала. Подумайте 7 из 6 фактов, что 7 умножить на 6 равно 42, то есть 7 × 6 = 42.
В противном случае
Подумайте, сколько столбцов вы получите, используя счетчики.
Если нужно сделать 7 одинаковых рядов фишек из 42 фишек или по 7 фишек в каждом ряду из 42 фишек.
Следовательно, деление можно выполнить следующим образом:
Мы можем разделить 42 на 7 строк по 6 счетчиков в каждом или 6 столбцов по 7 счетчиков в каждом.
 Частное равно 6.
Частное равно 6.Пример 2: 5 друзей собираются вместе купить электрический вентилятор. Стоимость вентилятора $45. Найдите долю стоимости каждого друга.
Решение:
Есть 5 друзей. Стоимость вентилятора $45. Нам нужно найти вклад каждого друга, чтобы купить вентилятор.
Чтобы найти стоимость для каждого человека, мы разделим сумму 45 долларов США между 5 друзьями. Это означает, что мы делим 45 на 5.
Мы знаем, что 5 × 9 = 45
Следовательно, 45 $ ÷ 5 = 9
Вклад каждого друга должен составлять 9 долларов, чтобы купить вентилятор.
Пример 3: Дэвид покупает коробку с вазами для цветов. Коробка имеет 2 ряда, по 3 вазы в каждом ряду. Коробка стоила 36 долларов. Сколько стоит каждая ваза?
Решение:
В коробке два ряда ваз. В каждом ряду по 3 вазы.
 Коробка стоит 36 долларов.
Коробка стоит 36 долларов.Нам нужно узнать, сколько стоит каждая ваза.
Чтобы решить эту задачу, сначала умножим 2 на 3, чтобы узнать количество ваз в коробке. Затем разделите стоимость 36 долларов на продукт.
Следовательно, количество ваз = 2 × 3 = 6
Стоимость каждой вазы = 36 $ ÷ 6 = 6 $ [6 умножить на 6 равно 36, т. е. 6 × 6 = 36] стоимость каждой вазы $6.
Часто задаваемые вопросы
Как мы можем разделить число на другое число, которое не является фактом умножения данного числа?
Если какое-либо число не является точным кратным числа, оно оставляет остаток при делении. Это означает, что счетчики не могут быть разделены на равные группы.
Например, , 44 ÷ 7
44 не встречается в фактах умножения 7.
группы остаются счетчиками, если в каждой строке есть счетчики: 44 . Эти 2 дополнительных счетчика называются остатком.

 00 из 5
00 из 5

 Чтобы найти количество фишек в каждом ряду, делим 35 на 5. Результат деления равен 7.
Чтобы найти количество фишек в каждом ряду, делим 35 на 5. Результат деления равен 7. Из пяти фактов мы знаем, что
Из пяти фактов мы знаем, что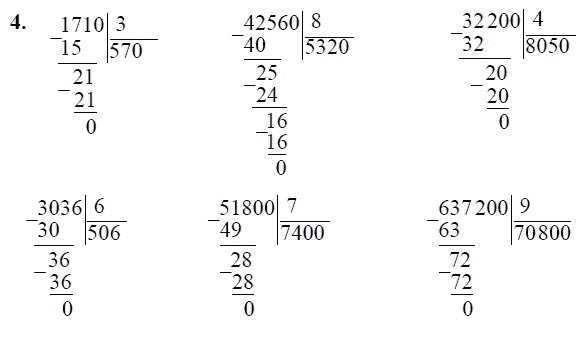

 Частное равно 6.
Частное равно 6. Коробка стоит 36 долларов.
Коробка стоит 36 долларов.