Умножение столбиком. Онлайн калькулятор | Математика

• Как умножать столбиком
• Калькулятор умножения столбиком

Как умножать столбиком

Умножение многозначных чисел обычно выполняют столбиком, записывая числа друг под другом так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т. д.). Для удобства сверху обычно записывается то число, которое имеет больше цифр. Слева между числами ставится знак действия. Под множителем проводят черту. Под чертой пишут цифры произведения по мере их получения.

Рассмотрим для начала умножение многозначного числа на однозначное. Пусть требуется умножить  846  на  5:

Умножить  846  на  5  — значит, сложить  5  чисел, каждое из которых равно  846.  Для этого достаточно взять сначала  5  раз по  6  единиц, потом  5  раз по  4  десятка и наконец  5  раз по  8  сотен.

1.   5  раз по  6  единиц =  30  единиц, т. е.  3  десятка. Пишем  0  под чертой на месте единиц, а  3  десятка запоминаем. Для удобства, чтобы не запоминать можно написать  3  над десятками множимого:

2.   5  раз по  4  десятка =  20  десятков, прибавляем к ним ещё  3  десятка =  23  десятка, т. е.  2  сотни и  3  десятка. Пишем  3  десятка под чертой на месте десятков, а  2  сотни запоминаем:

3.   5  раз по  8  сотен =  40  сотен, прибавляем к ним ещё  2  сотни =  42  сотни. Пишем под чертой  42  сотни, т. е.  4  тысячи и  2  сотни. Таким образом, произведение  846  на  5  оказывается равным  4230:

Теперь рассмотрим умножение многозначных чисел. Пусть требуется умножить  3826  на  472:

Умножить  3826  на  472  — значит, сложить  472  одинаковых числа, каждое из которых равно  3826.  Для этого надо сложить  3826  сначала  2  раза, потом  70  раз, потом  400  раз, т. е. умножить множимое отдельно на цифру каждого разряда множителя и полученные произведения сложить в одну сумму.

2  раза по  3826  =  7652.  Пишем полученное произведение под чертой:

Это не окончательное произведение, пока мы умножили только на одну цифру множителя. Полученное число называется частичным произведением. Теперь наша задача умножить множимое на цифру десятков. Но перед этим надо запомнить один важный момент: каждое частичное произведение нужно записывать под той цифрой, на которую происходит умножение.

Умножаем  3826  на  7.  Это будет второе частичное произведение  (26782):

Умножаем множимое на  4.  Это будет третье частичное произведение  (15304):

Под последним частичным произведением проводим черту и выполняем сложение всех полученных частичных произведений. Получаем полное произведение  (1 805 872):

Если во множителе встречается нуль, то обычно на него не умножают, а сразу переходят к следующей цифре множителя:

Когда множимое и (или) множитель оканчиваются нулями, умножение можно выполнить не обращая на них внимания, и в конце, к произведению добавить столько нулей, сколько их во множимом и во множителе вместе.

Например, необходимо вычислить  23 000 · 4500.  Сначала умножим  23  на  45,  не обращая внимание на нули:

И теперь, справа к полученному произведению припишем столько нулей, сколько их во множимом и во множителе вместе. Получится  103 500 000.

Калькулятор умножения столбиком

Данный калькулятор поможет вам выполнить умножение столбиком. Просто введите множимое и множитель и нажмите кнопку Вычислить.

Умножение: по-японски, по-итальянски и методом майя

• Аналия Йоренте
• BBC Mundo

13 января 2018

Подпишитесь на нашу рассылку ”Контекст”: она поможет вам разобраться в событиях.

Автор фото, Getty Images

Подпись к фото,

Не заболела бы голова…

«Математика такая трудная…» Вы наверняка не раз слышали эту фразу, а, может быть, даже сами ее произносили вслух.

Для многих математические вычисления — дело непростое, но вот вам три несложных способа, которые помогут выполнить хотя бы одно арифметическое действие — умножение. Без калькулятора.

Вполне вероятно, что в школе вы познакомились с наиболее традиционным способом умножения: сначала вы выучили на память таблицу умножения, а уж затем стали в столбик перемножать каждую из цифр, которыми записываются многозначные числа.

Если вам надо перемножить многозначные числа, то, чтобы найти ответ, потребуется большой лист бумаги.

Но если от этого длинного набора идущих одна под другой строчек с цифрами у вас голова идет кругом, то есть и другие, более наглядные методы, которые могут вам помочь в этом деле.

Но тут пригодятся некоторые художественные навыки.

Давайте порисуем!

Как минимум три способа умножения связаны с рисованием пересекающихся линий.

1. Способ индейцев майя, или японский метод

Относительно происхождения этого способа существует несколько версий.

Для просмотра этого контента вам надо включить JavaScript или использовать другой браузер

Подпись к видео,

Трудно умножать в уме? Попробуйте метод майя и японцев

Пропустить Подкаст и продолжить чтение.

Подкаст

Что это было?

Мы быстро, просто и понятно объясняем, что случилось, почему это важно и что будет дальше.

эпизоды

Конец истории Подкаст

Некоторые говорят, что его придумали индейцы цивилизации майя, населявшие районы Центральной Америки до прибытия туда конкистадоров в XVI веке. Он также известен как японский метод умножения, поскольку учителя в Японии используют именно этот визуальный способ, когда учат младших школьников умножению.

Суть в том, что параллельные и перпендикулярные линии представляют цифры тех чисел, которые нужно перемножить.

Давайте умножим 23 на 41.

Для этого нам надо нарисовать две параллельные линии, представляющие 2, и, немного отступя, еще три линии, представляющие 3.

Затем, перпендикулярно к этим линиям мы нарисуем четыре параллельные линии, представляющие 4 и, чуть отступя, еще одну линию для 1.

Теперь нам надо пересчитать все точки пересечения этих линий. Именно так мы и получаем наш результат — 943, как если бы мы умножали в столбик.

Ну как, неужели трудно?

2. Индийский способ, или итальянское умножение «решеткой» — «джелозия»

Происхождение этого способа умножения тоже не ясно, однако он хорошо известен по всей Азии.

«Алгоритм «джелозия» передавался из Индии в Китай, затем в Аравию, а оттуда в Италию в XIV-XV веках, где он получил название «джелозия», поскольку внешне был похож на венецианские решетчатые ставни», — пишет Марио Роберто Каналес Виллануэва в своей книге, посвященной различным способам умножения.

Автор фото, Getty Images

Подпись к фото,

Индийская или итальянская система умножения похожа на венецианские жалюзи

Давайте снова возьмем пример с умножением 23 на 41.

Теперь нам потребуется начертить таблицу из четырех клеток — по клетке на цифру.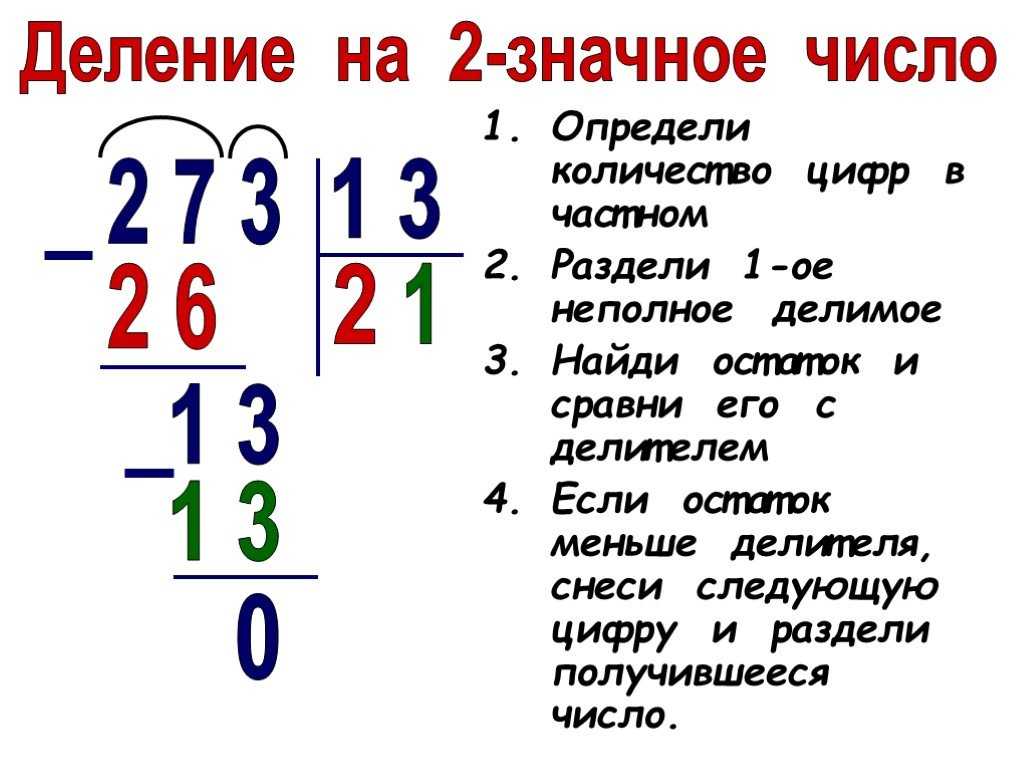 Подпишем сверху у каждой клетки соответствующую цифру — 2,3,4,1.

Затем надо разделить каждую клетку надвое по диагонали, чтобы получились треугольники.

Теперь мы сначала умножим первые цифры каждого числа, то есть 2 на 4, и запишем в первом треугольнике 0, а во втором 8.

Потом перемножим 3×4 и запишем 1 в первом треугольнике, а 2 во втором.

Проделаем то же самое и с другими двумя цифрами.

Когда все клетки нашей таблицы будут заполнены, мы складываем цифры в такой последовательности, как показано на видео, и записываем получившийся результат.

Для просмотра этого контента вам надо включить JavaScript или использовать другой браузер

Подпись к видео,

Трудно умножать в уме? Попробуйте индийский метод

Первая цифра у нас будет 0, вторая 9, третья 4, четвертая 3. Таким образом, результат получился: 943.

Как вам показалось, проще этот способ или нет?

Давайте попробуем еще один метод умножения с помощью рисунка.

3. «Массив», или метод таблицы

Как и в предыдущем случае, для этого потребуется нарисовать таблицу.

Возьмем тот же пример: 23 x 41.

Тут нам надо разделить наши числа на десятки и единицы, поэтому 23 мы запишем как 20 в одной колонке, и 3 в другой.

По вертикали мы запишем наверху 40, а внизу 1 .

Затем мы перемножим числа по горизонтали и вертикали.

Для просмотра этого контента вам надо включить JavaScript или использовать другой браузер

Подпись к видео,

Трудно умножать в уме? Нарисуйте таблицу.

Но вместо того чтобы умножать 20 на 40, мы отбросим нули и просто перемножим 2 x 4, получив 8.

То же самое сделаем, умножая 3 на 40. Мы удерживаем в скобках 0 и умножаем 3 на 4 и получаем 12.

Проделаем то же самое с нижним рядом.

Теперь добавим нули: в левой верхней клетке у нас получилось 8, но мы отбросили два нуля — теперь мы их допишем и получится 800.

В правой верхней клетке, когда мы умножали 3 на 4(0), у нас получилось 12; теперь мы допишем ноль и получим 120.

Сделаем так же со всеми прочими удержанными нулями.

И наконец, мы складываем все четыре числа, полученных умножением в таблице.

Результат? 943. Ну как, помогло?

Важно разнообразие

Автор фото, Getty Images

Подпись к фото,

Все способы хороши, главное — чтобы ответ сошелся

Что точно можно утверждать, — так это то, что все эти разные способы дали нам один и тот же результат!

Нам все-таки пришлось кое-что перемножить в процессе, но каждый шаг был проще, чем при умножении традиционным способом, и гораздо более наглядный.

Так почему же мало где в мире в обычных школах учат этим методам вычисления?

Одной из причин может быть упор на обучение «вычислениям в уме» — чтобы развивать умственные способности.

Однако Дэвид Уиз, учитель математики из Канады, работающий в государственных школах в Нью-Йорке, объясняет это иначе.

«Недавно я прочитал, что причина, по которой используется традиционный метод умножения, — это экономия бумаги и чернил. Этот метод не был придуман как самый простой для использования, но как самый экономный с точки зрения ресурсов, поскольку чернила и бумага были в дефиците», — объясняет Уиз.

Автор фото, Getty Images

Подпись к фото,

Для некоторых методов вычисления только головы недостаточно, нужны еще и фломастеры

Невзирая на это, он полагает, что альтернативные методы умножения очень полезны.

«Я не думаю, что это полезно — сразу учить школьников умножению, заставляя их выучивать таблицу умножения, но не объясняя им при этом, откуда она взялась. Поскольку если они забудут одно число, то как они смогут продвинуться в решении задачи? Метод майя или японский метод необходим, потому что с его помощью вы можете понять общую структуру умножения, а это хорошее начало», — полагает Уиз.

Существует и ряд других способов умножения, например, русский или египетский, они не требуют дополнительных навыков рисования.

Как говорят специалисты, с которыми мы беседовали, все эти методы помогают лучше понять процесс умножения.

«Понятно, что все идет на пользу. Математика в сегодняшнем мире открыта как внутри, так и снаружи классной комнаты», — резюмирует Андреа Васкес, учительница математики из Аргентины.

Именование семейств фактов – Элементарная математика

Чтобы попрактиковаться в математических фактах, соединив семейства фактов с массивами.

Материалы

Нет

Обзор

Нарисуйте на доске массив точек, например массив 3 на 5. Спросите учащихся о семействе фактов, которое описывает массив. В этом примере семейство фактов будет 3 × 5 = 15, 5 × 3 = 15, 15 ÷ 3 = 5 и 15 ÷ 5 = 3. Нарисуйте другие массивы с достаточно малыми размерами, чтобы поддерживать быстроту этой деятельности, и продолжайте спрашивать учащихся о семействе фактов, которое описывает массив. Когда учащиеся освоятся, вы можете дать член семейства фактов, например 4 × 3 = 12, и попросить учащихся описать соответствующий массив, а затем дать другие члены семейства фактов. В этом примере подойдет массив из 4 строк и 3 столбцов или массив из 3 строк и 4 столбцов. Другими членами семейства фактов являются 3 × 4 = 12, 12 ÷ 3 = 4 и 12 ÷ 4 = 3,9.0004

О последовательности

В части 1 учащимся предлагается визуализировать массивы меньших размеров и назвать семейство фактов, описывающее каждый массив. Часть 2, и расширение переходит к либо , именующему семейство фактов из визуализации массива , либо , описывающему массив из знания факта из семейства фактов.

Часть 1

Давайте изобразим несколько массивов и назовем семейство фактов, описывающее каждый из них. Например, я думаю о массиве, который имеет 3 строки и 5 столбцов. Какое семейство фактов описывает этот массив?

(5 × 3 = 15, 3 × 5 = 15, 15 ÷ 5 = 3 и 15 ÷ 3 = 5)

Примеры:

• 2 строки и 4 столбца (2 × 4 = 8, 4 × 2 = 8, 8 ÷ 4 = 2, 8 ÷ 2 = 4)
• 2 строки и 2 столбца (2 × 2 = 4, 4 ÷ 2 = 2)
• 3 ряда и 2 столбца (3 × 2 = 6, 2 × 3 = 6, 6 ÷ 3 = 2, 6 ÷ 2 = 3)
• 3 ряда и 3 столбца (3 × 3 = 9, 9 ÷ 3 = 3)
• 3 ряда и 4 столбца (3 × 4 = 12, 4 × 3 = 12, 12 ÷ 4 = 3 и 12 ÷ 3 = 4)

Пока дети наслаждаются своим мастерством, не стесняйтесь повторять. Когда дети хотят большего, попробуйте Часть 2.

Часть 2

Давайте рассмотрим более крупные массивы и их семейства фактов. На этот раз вам будет предоставлен массив для изображения или член семейства фактов. Если вам дан массив для изображения, вы назовете членов его семейства фактов. Если дан факт, вы описываете массив, связанный с этим фактом, и называете других членов семейства фактов. Вот так!

Примеры:

• 6 рядов и 5 столбцов (6 × 5 = 30, 5 × 6 = 30, 30 ÷ 5 = 6, 30 ÷ 6 = 5)
• 6 рядов и 3 столбца (6 × 3 = 18, 3 × 6 = 18, 18 ÷ 3 = 6, 18 ÷ 6 = 3)
• 6 x 6 = 36 (опишите массив с 6 строками и 6 столбцами, 36 ÷ 6 = 6)
• 7 рядов и 6 столбцов (7 × 6 = 42, 6 × 7 = 42, 42 ÷ 6 = 7, 42 ÷ 7 = 6)
• 7 x 4 = 28 (опишите массив из 7 строк и 4 столбцов, 4 × 7 = 28, 28 ÷ 4 = 7, 28 ÷ 7 = 4)
• 7 рядов и 7 столбцов (7 × 7 = 49, 49 ÷ 7 = 7)

Как всегда, когда дети кажутся взволнованными новой задачей, двигайтесь дальше.

Extension

Теперь представим еще большие массивы и их семейства фактов.

Примеры:

• 10 строк и 8 столбцов (10 × 8 = 80, 8 × 10 = 80, 80 ÷ 8 = 10, 80 ÷ 10 = 8)
• 11 × 10 (описать массив с 11 строками и 10 столбцами, 10 × 11 = 110, 110 ÷ 10 = 11, 110 ÷ 11 = 10)
• 11 строк и 11 столбцов (11 × 11 = 121, 121 ÷ 11 = 11)
• 12 × 10 (описать массив с 12 строками и 10 столбцами, 10 × 12 = 120, 120 ÷ 10 = 12, 120 ÷ 12 = 10)
• 12 рядов и 12 столбцов (12 × 12 = 144, 144 ÷ 12 = 12)

Умножение матриц | Как умножать матрицы

В линейной алгебре матрицы играют важную роль при работе с различными понятиями. Матрица представляет собой прямоугольный массив или таблицу чисел, символов или выражений, расположенных в строках и столбцах в математике. Мы можем выполнять различные операции с матрицами, такие как сложение, вычитание, умножение и так далее. В этой статье вы узнаете, как умножить матрицу на другую матрицу, его алгоритм, формулу, умножение матриц 2×2 и 3×3 с подробными примерами.

Содержание: Определение Умножение на скаляр Состояние Как умножить Формула Алгоритм Правила Умножение матриц 2×2 Умножение матриц 3×3 Свойства Пример Практические задачи Часто задаваемые вопросы

Умножение матриц Определение

Умножение матриц, , также известное как произведение матриц и умножение двух матриц, дает одну матрицу. Это тип бинарной операции.

Если две матрицы A и B, то произведение двух матриц A и B обозначается:

Х = АВ

Следовательно, произведение двух матриц является скалярным произведением двух матриц.

Умножение матрицы на скаляр

Умножение целого числа на матрицу — это просто скалярное умножение.

Мы знаем, что матрица — это массив чисел.

Он состоит из строк и столбцов. Если вы умножаете матрицу на скалярное значение, то это называется скалярным умножением. Другой случай состоит в том, что можно умножить матрицу на другую матрицу. Давайте посмотрим на пример, приведенный ниже для того же самого.

Мы можем определить умножение матрицы на скаляр математически как:

Если A = [a _ij ] _{m × n} — матрица, а k — скаляр, то kA — другая матрица, полученная путем умножения каждого элемента A на скаляр k.

Другими словами, kA = k [a _ij ] _{m × n}  = [k (a _ij )] _{m × n} , то есть (i, j)-й элемент kA равен ka _ij  для всех возможных значений i и j.

Пример:

\(\begin{array}{l} Умножьте\ the\ matrix\ A=\begin{bmatrix} 3 &4 &-1 \\ 0 &9 & 5 \end{bmatrix}  на\ 4. \конец{массив} \)

Решение:

Дано,

\(\begin{array}{l}A=\begin{bmatrix} 3 &4 &-1 \\ 0 &9& 5 \end{bmatrix}\end{массив} \)

\(\begin{array}{l}4 \times A = 4\times \begin{bmatrix} 3 &4 &-1 \\ 0 &9 & 5 \end{bmatrix}\end{массив} \)

Теперь нам нужно умножить каждый элемент матрицы A на 4.

\(\begin{array}{l}=\begin{bmatrix} 12 &16 &-4 \\ 0 &36 & 20 \end{bmatrix}\end{array} \)

Это искомая матрица после умножения данной матрицы на константное или скалярное значение, т.е. 4.

Умножение матриц Условие

Чтобы выполнить умножение двух матриц , мы должны убедиться, что количество столбцов в 1-й матрице равно количеству строк во 2-й матрице. Следовательно, результирующее матричное произведение будет иметь количество строк 1-й матрицы и количество столбцов 2-й матрицы. Порядок результирующей матрицы равен порядку умножения матрицы .

Также читайте:

Теперь давайте разберемся как выполнять умножение матриц 9{b} A_{xk}B_{ky}\end{массив} \)

Для x = 1…… a и y = 1…….c

Это одна из самых важных тем в 12 классе. Матрицы для 12 класса подробно объясняет типы матриц.

Обозначение

Если A — матрица размера m×n, а B — матрица размера p×q, то матричное произведение A и B представлено следующим образом:

Х = АВ

Где X — результирующая матрица размера m×q.

Формула умножения матриц

Давайте рассмотрим пример, чтобы понять эту формулу.

Предположим, что A и B — две матрицы, такие, что

\(\begin{array}{l}A =\begin{bmatrix} A_{11} &A_{12} & \cdots & A_{1n}\\ A_{21} & A_{22} &\cdots & A_ {2n} \\ &…………. &\\ A_{m1} & A_{m2} &\cdots & A_{mn} \end{bmatrix}, B= \begin{bmatrix} B_{11} &B_{ 12} & \cdots & B_{1n}\\ B_{21} &B_{22} &\cdots & B_{2n} \\ &………….& \\ B_{m1} & B_{m2} &\ cdots & B_{mn} \end{bmatrix}\end{массив} \)

Тогда матрица C = AB обозначается цифрой 9{b} A_{xk}B_{ky}\end{массив} \)

Для x = 1……a и y= 1…….c

Алгоритм умножения матриц

В последние годы было проведено значительное количество работ в области алгоритмов умножения матриц, поскольку они нашли свое применение во многих областях. Существует четыре типа алгоритмов:

• Итеративный алгоритм
• Алгоритм «разделяй и властвуй»
• Субкубические алгоритмы
• Параллельные и распределенные алгоритмы

В основном используется в различных языках программирования, таких как C, Java и т. д., для онлайн-умножения. Наиболее распространены 2×2, 3×3 и 4×4, умножение матриц.

Операция является двоичной с записями в наборе, на котором определены операции сложения, вычитания, умножения и деления. Эти операции аналогичны соответствующим операциям над действительными и рациональными числами.

Несмотря на то, что существует множество применений матриц, умножение матриц, по сути, является операцией в линейной алгебре. Линейное отображение, которое включает скалярное сложение и умножение, представлено умножением матриц.

Также можно найти широкий спектр алгоритмов на сетках. Этот тип алгоритма предназначен для минимизации присущей алгоритмам стандартных массивов неэффективности, когда может быть задержка в поступлении данных из двух разных матриц.

Правила умножения матриц

Из определенной выше формулы и процедуры мы можем записать следующие правила и свойства для умножения матриц.

• Произведение двух матриц A и B определяется, если количество столбцов матрицы A равно количеству строк матрицы B.
• Если AB определен, то BA не нужно определять
• Если и A, и B являются квадратными матрицами одного порядка, то и AB, и BA определены.
• Если определены и AB, и BA, нет необходимости, чтобы AB = BA.
• Если произведение двух матриц является нулевой матрицей, то необязательно, чтобы одна из матриц была нулевой матрицей.

Умножение матриц 2×2

Рассмотрим простое умножение матриц 2 × 2

\(\begin{array}{l}A = \begin{bmatrix} 3 и 7\\ 4 и 9\end{bmatrix} \ и\  B = \begin{bmatrix} 6 и 2\\ 5 и 8 \end{bmatrix}\end{массив} \)

Теперь каждый из элементов матрицы произведения AB можно рассчитать следующим образом:

• AB ₁₁ = 3 × 6 + 7 × 5 = 53
• AB ₁₂ = 3 × 2 + 7 × 8 = 62
• AB ₂₁ = 4 × 6 + 9 × 5 = 69
• AB ₂₂ = 4 × 2 + 9 × 8 = 80

Следовательно,

\(\begin{array}{l}AB = \begin{bmatrix} 53&62 \\ 69& 80 \end{bmatrix}\end{массив} \)

Умножение матриц 3×3

Чтобы понять произведение двух матриц 3 × 3, рассмотрим две матрицы 3 × 3 A и B.

\(\begin{array}{l} A = \begin{bmatrix} 12 &8 &4 \\ 3&17 &14 \\ 9 & 8& 10 \end{bmatrix} ,\ B = \begin{bmatrix} 5 & 19 &3 \ \ 6 &15 &9 \\ 7& 8 & 16 \end{bmatrix}\end{массив} \)

Каждый элемент матрицы продукта AB можно рассчитать следующим образом:

• AB ₁₁ = 12×5 + 8×6 + 4×7 = 136
• AB ₁₂ = 12×19 + 8×15 + 4×8 = 380
• АВ ₁₃ = 12×3 + 8×9+4×16 = 172
• АВ ₂₁ = 3×5 + 17×6 + 14×7 = 215
• АВ ₂₂ = 3×19 + 17×15 + 14×8 = 424
• АВ ₂₃ = 3×3 + 17×9 + 14×16 = 386
• AB ₃₁ = 9×5 + 8×6 + 10×7 = 163
• AB ₃₂  = 9 × 19 + 8 × 15 + 10 × 8 = 371
• АБ ₃₃ = 9×3 + 8×9 + 10×16 = 259

Следовательно,

\(\begin{array}{l}AB =\begin{bmatrix} 136 & 380 &172 \\ 215 &424 &386 \\ 163& 371 & 259 \end{bmatrix}\end{массив} \)

Попробуйте : Калькулятор умножения матриц

Свойства умножения матриц

Ниже приведены свойства умножения матриц:

Коммутативное свойство

Умножение матриц не является коммутативным.

Предположим, что если A и B являются двумя матрицами 2×2, 

АВ ≠ ВА

При умножении матриц порядок имеет большое значение.

Например,

\(\begin{array}{l}If\ A = \begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix} \ and\  B = \begin{bmatrix} 3 & 2\\ 1 & 4 \end{bmatrix} \ являются\ двумя\ матрицами,\ then\end{массивом} \)

\(\begin{array}{l}A\times B = \begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix}\times \begin{bmatrix} 3 & 2\\ 1 & 4 \ конец{bматрица}\конец{массив} \)

\(\begin{array}{l}A\times B = \begin{bmatrix} 5 и ​​10\\ 13 и 22 \end{bmatrix}\end{массив} \)

Но,

\(\begin{array}{l}B\times A = \begin{bmatrix} 3 & 2\\ 1 & 4 \end{bmatrix}\times \begin{bmatrix} 1 & 2\\ 3 & 4 \ конец{bmatrix}\конец{массив} \)

\(\begin{array}{l}B\times A = \begin{bmatrix} 9 и 14\\ 13 и 18 \end{bmatrix}\end{массив} \)

Это показывает, что матрица AB ≠BA.

Следовательно, умножение двух матриц некоммутативно.

Ассоциативное свойство

Если A, B и C являются тремя матрицами, ассоциативное свойство матричного умножения утверждает, что

(АВ) С = А(ВС)

 

\(\begin{array}{l} Пусть\ A =\begin{bmatrix} 1 и 2\\ 1& 1 \end{bmatrix}\end{массив} \)

\(\begin{array}{l}B =\begin{bmatrix} 3 & 2\\ 1& 2 \end{bmatrix}\end{array} \)

\(\begin{array}{l}C =\begin{bmatrix} 0 & 1\\ 2& 3 \end{bmatrix}\end{array} \)

LHS = (AB) C

\(\begin{array}{l}A\times B = \begin{bmatrix} 1 & 2\\ 1 & 1 \end{bmatrix} \times \begin{bmatrix} 3 & 2 \\ 1 & 2 \ конец {bmatrix}\конец {массив} \)

\(\begin{array}{l}A\times B = \begin{bmatrix} 5 и ​​6\\ 4 и 4 \end{bmatrix}\end{массив} \)

\(\begin{array}{l}(AB)C = \begin{bmatrix} 5 & 6\\ 4 & 4 \end{bmatrix} \times \begin{bmatrix} 0 & 1\\ 2 & 3 \ конец {bmatrix}\конец {массив} \)

\(\begin{array}{l}(AB)C = \begin{bmatrix} 12 и 23\\ 8 & 16 \end{bmatrix}\end{array} \)

RHS =  A(BC)

\(\begin{array}{l}BC = \begin{bmatrix} 3 & 2\\ 1 & 2 \end{bmatrix}\times \begin{bmatrix} 0 & 1\\ 2 & 3 \end{bmatrix }\конец{массив} \)

\(\begin{array}{l}BC = \begin{bmatrix} 4 & 9\\ 4 & 7 \end{bmatrix}\end{array} \)

\(\begin{array}{l}A(BC)= \begin{bmatrix} 1 & 2\\ 1 & 1 \end{bmatrix}\times \begin{bmatrix} 4 & 9\\ 4 & 7 \ конец {bmatrix}\конец {массив} \)

\(\begin{array}{l}A(BC)= \begin{bmatrix} 12 и 23\\ 8 & 16 \end{bmatrix}\end{array} \)

Таким образом, ассоциативность матричного умножения доказана.

Распределительная собственность

Если A, B и C являются тремя матрицами, дистрибутивное свойство матричного умножения утверждает, что

• (В+С)А = БА +КА
• А(В+С) = АВ + АС

Свойство мультипликативной идентичности

Свойство идентичности матричного умножения утверждает, что

1. I = I. А = А

Где A — матрица размера n × n, а «I» — единичная матрица порядка n.

 

\(\begin{array}{l} Пусть\ A = \begin{bmatrix} 2 и 3\\ 1 и 6 \end{bmatrix} \ и\ I = \begin{bmatrix} 1 & 0\\ 0 и 1 \end{bmatrix}\end{массив} \)

\(\begin{array}{l}A . I = \begin{bmatrix} 2 & 3\\ 1 & 6 \end{bmatrix}\times \begin{bmatrix} 1 & 0\\ 0 & 1 \end {bmatrix}\конец{массив} \)

\(\begin{array}{l}A . I = \begin{bmatrix} 2 & 3\\ 1 & 6 \end{bmatrix} = A\end{массив} \)

Свойство измерения

При умножении матриц произведение матрицы m × n и матрицы n × a равно матрице m × a.

Например, матрица A — это матрица 2 × 3, а матрица B — это матрица 3 × 4, тогда AB — это матрица 2 × 4.

Мультипликативное свойство Зеро

Если матрица умножается на нулевую матрицу, результирующая матрица является нулевой матрицей.

\(\begin{array}{l}If\ A = \begin{bmatrix} 2 & 1\\ 1 & 2 \end{bmatrix} \ is\ умножается\ на\ ноль\ матрица\end{массив} \)

\(\begin{array}{l}т.е.,\ \begin{bmatrix} 0 & 0\\ 0 & 0 \end{bmatrix},\end{array} \)

\(\begin{array}{l}Продукт\ становится\ \begin{bmatrix} 0 & 0\\ 0 & 0 \end{bmatrix}\end{array} \)

Решенный пример

Умножение матриц 4×4 объясняется ниже для двух матриц 4×4 A и B.

\(\begin{array}{l}A =\begin{bmatrix} 7 & 14 & 15 & 6 \\ 4 & 8 & 12 & 3 \\ 14 & 21 & 6 & 9 \\ 13 & 7 & 6 & 4 \end{ bmatrix},\  B = \begin{bmatrix} 5& 7 & 14 & 2\\ 8& 16 & 4 & 9\\ 13 & 6& 8 & 4\\ 6& 3 & 2 & 4 \end{bmatrix}\end{array } \)

Следуя тем же шагам, что и в предыдущих двух примерах, мы можем построить матрицу AB.

\(\begin{array}{l}AB = \begin{bmatrix} 378 &381 & 286 &224 \\ 258 & 237 & 190 & 140\\ 370 & 497& 346 & 277\\ 223& 251& 266 & 129 \end{ bmatrix}\end{массив} \)

Практические задачи на умножение матриц

Решите следующие проблемы:

1. \(\begin{array}{l}Найти\ произведение:\ 3\begin{bmatrix} 7 и 5\\ 2 & 1 \end{bmatrix}\end{array} \)

2. \(\begin{array}{l}Упростите\ следующие\ 3×3 \ матрицу:\ \begin{bmatrix} 1 & 6 & 2 \\ 2 & 3 & 1\\ 1 & 1 & 5 \ end{bmatrix}\times \begin{bmatrix} 1 & 8 & 7 \\ 4 & 2 & 3 \\ 2 & 6 & 1 \end{bmatrix}\end{массив} \)

3. \(\begin{array}{l}Найти\ произведение\ AB,\ если\ A =\begin{bmatrix} 5 & 3\\ 9 & 1 \end{bmatrix} \ and\ B = \begin{bmatrix} 1 и 0\\ 6 и 12 \end{bmatrix}\end{массив} \)

4. \(\begin{array}{l}Найти\ произведение\ матрицы\,\ если\ A = \begin{bmatrix} 4\\ 2\\ 1 \end{bmatrix} \ и\ \ begin{bmatrix} 2 & 4 & 6 \end{bmatrix}\end{массив} \)

5. \(\begin{array}{l}Вычислить:\ \frac{-4}{7}\begin{bmatrix} -22\\ 49\\ 35 \end{bmatrix}\end{array} \)

Узнайте больше о матрицах и других связанных темах в увлекательной и увлекательной форме. Загрузите BYJU’S — обучающее приложение сегодня.

Часто задаваемые вопросы – Часто задаваемые вопросы

Что такое умножение матриц?

Умножение матриц — это метод нахождения произведения двух матриц для получения результата в виде одной матрицы. Это тип бинарной операции.

Как умножить две заданные матрицы?

Чтобы умножить одну матрицу на другую, нужно сначала проверить, равно ли количество столбцов первой матрицы количеству строк второй матрицы. Теперь умножьте каждый элемент столбца первой матрицы на каждый элемент строк второй матрицы и сложите их все. Нам нужно сделать скалярное произведение столбцов и строк здесь.

Какой результат умножения матрицы (2×3) на матрицу (3×3)?

Результатом умножения матрицы (2×3) и матрицы (3×3) будет только матрица 2×3.

Как умножить матрицу 3×3?

Умножьте каждую строку первой матрицы на каждый столбец второй матрицы и сложите все, чтобы получить первый элемент.