Задания для детей 9-10 лет
В этом разделе сайта «Разумейкин» собраны упражнения для детей 9-10 лет, которые помогут ребенку расширить его кругозор и послужат дополнением занятий по школьным предметам. При разработке комплекса заданий для школьников наши специалисты старались сделать их не только максимально понятными и увлекательными, но и действительно полезными в практическом плане.
В блоке «Развитие» представлены интересные задания для детей 9-10 лет, способствующие улучшению логического и пространственного мышления, памяти, внимания. Все эти навыки помогают упростить процесс усвоения школьной программы. Задания-тесты в блоке «Развитие» построены в форме интересной компьютерной онлайн игры для детей 9-10 лет. Выполняя их, маленькие ученики отрабатывают навыки счета и чтения и стремятся узнавать что-то новое.
Интересные занимательные задания для детей 9 лет в блоке «Обучение» помогут школьникам закрепить знания, которые они получили в начальных классах. Представленные здесь упражнения соответствуют задачам, которые встречаются в аттестационных испытаниях.
- Подготовиться к экзаменам по математике, русскому языку, чтению, окружающему миру.
- Вспомнить литературные произведения, пройденные в начальной школе.
- Попрактиковаться в решении задач повышенной сложности по математике и русскому языку.
- Освежить в памяти темы, которые были изучены в рамках предмета «Окружающий мир».
Для большинства задач-вопросов для детей 9 лет мы предусмотрели подробное объяснение решения. Оно дается ребенку, если данный им ответ был неверным или неполным. Блок «Науки» включает в себя занимательные детские игры и задачи для 10 лет, справляясь с которыми ребенок узнаёт о химических элементах, особенностях строения веществ, давлении воздуха, преломлении солнечных лучей, изучает увлекательные факты о нашей планете и т. д. В большинстве упражнений предусмотрена вводная информация, которую мы изложили в доступной форме.
Несколько слов о подаче материала
Чтобы маленькие ученики могли усвоить информацию в процессе занятий, для каждого упражнения для детей 10 лет специалисты сайта «Разумейкин» подготовили тематические картинки и озвученный текст. Мы убеждены, что такой подход позволит лучше выучить материал. Для многих интересных игр-тестов для детей 10 лет мы подготовили обучающие видео, которые помогут справиться с онлайн-заданиями.
Как оцениваются результаты?
Справляясь с заданиями-тестами, дети 10 лет получают награды в режиме онлайн: кубки, медали и т. д. Они помогают повысить интерес школьника к самостоятельным занятиям. Большинство упражнений оценивается в зависимости от того, с какой попытки ученик дал правильный ответ.
При этом ребенок имеет возможность вернуться к выполненным заданиям, чтобы, к примеру, улучшить собственный результат.
Для определения сильных и слабых сторон в развитии детей 9 лет советуем перед выполнением познавательных заданий-игр бесплатно пройти онлайн-тесты.
Полученные результаты помогут понять, на каких темах потребуется остановиться более подробно.
6 приложений и сервисов для тренировки навыков счета
Мария Герке
опробовала сервисы
После школы многим из нас не пригодились навыки расчета нелинейных уравнений или тригонометрических функций.
Но что действительно оказалось важным, так это умение быстро считать в уме, поэтапно совершать сложные вычисления, разбираться в пропорциях и процентах, применять формулы для расчета расстояний и площадей.
Если вы чувствуете, что вам не хватает математических навыков — например, трудно составить бюджет, вычислить сложный процент по вкладу или определить, сколько продуктов нужно по рецепту, когда вы готовите на трех человек вместо пяти, — никогда не поздно эти навыки подтянуть.
Вот шесть ресурсов, которые с этим помогут. Все сервисы, кроме Euclidia, на английском языке.
Khan Academy
Сколько стоит: бесплатно
Подробнее: на сайте
Где скачать: Google Play, App Store
Khan Academy — платформа с бесплатными курсами по алгебре и геометрии от начального до университетского уровня.
Многие из них составлены по принципу «один курс — один год школьной программы», но есть и такие, что покрывают сразу все главные темы в одном из разделов математики. Например, общий курс алгебры начинается с простых линейных уравнений и заканчивается тригонометрическими функциями.
Обучение в Khan Academy состоит из теоретической и практической части. Сначала пользователи смотрят видео по теме урока и читают короткие статьи с примерами решения задач. Затем закрепляют изученное на практике: проходят тесты и сами решают примеры. Заниматься можно на сайте и в мобильном приложении.
/list/courses-for-life/
Переговоры, ремонт и здоровый сон: 25 образовательных курсов для жизни
Sumaze!
Стоимость: бесплатно
Подробнее: на сайте
Где скачать: Google Play, App Store
Это мобильное приложение с математическими головоломками.
Пользователь управляет синей плиткой: цель игры — довести ее до пункта назначения, совершив по пути нужные арифметические операции. Головоломки разделены по темам: например, в приложении можно отработать задачи с положительными и отрицательными числами, неравенствами, степенями, логарифмами и модульными функциями.
Разработчик Sumaze — британский благотворительный фонд MEI, который популяризирует математическое образование и старается улучшить его качество. У фонда есть еще два приложения из той же серии, рассчитанные на учеников средней школы: Sumaze 2 и Sumaze Adventure. Так что если головоломки в обычном Sumaze покажутся слишком сложными, можно начать с версии попроще.
6 финансовых калькуляторов для расчета ипотеки и оценки ваших финансовых возможностей
Euclidea
Стоимость: бесплатно
Где скачать: Google Play, App Store
Еще одно приложение с головоломками, но уже геометрическими: здесь пользователю нужно достраивать фигуры с помощью готового набора инструментов.
Например, можно соединить две точки прямыми, очертить окружность или провести перпендикуляр: чем выше сложность, тем больше инструментарий. Чтобы получить высшую оценку, нужно справиться с заданием за минимальное количество ходов.
Каждый уровень сопровождает краткая справка, которая поможет освежить в памяти определения и свойства геометрических фигур. Кроме того, в приложении есть подсказки: они бесплатно открываются по одной в час, но за 99 Р можно купить моментальный доступ ко всем подсказкам.
/sravnyator-main/
Сравнятор: сервис по подбору ИТ-курсов
7 min Math Genius
Стоимость: бесплатно
Где скачать: Google Play, App Store
Приложение с ежедневными семиминутными тренировками устного счета. Каждая минута посвящена отдельному типу операций: сложению, вычитанию, умножению, делению, работе с процентами и квадратами.
Задача пользователя — решить за отведенное время максимальное количество примеров, сложность которых растет с каждым правильным ответом.
Brilliant
Стоимость: первые 7 дней бесплатно, далее 6890 Р в год
Подробнее: на сайте
Где скачать: Google Play, App Store
Brilliant — это библиотека онлайн-курсов по математике, финансовым расчетам, физике и информатике от инструкторов из Массачусетского технологического университета, Калтеха, Университета Джонса Хопкинса и других известных учебных заведений.
В Brilliant нет привычного разделения на теорию и практику: пользователь сразу вовлекается в решение математических задач и получает в процессе все необходимые объяснения. При этом цель сервиса — не научить пользователя решать типовые задания, а объяснить логику, которая стоит за поиском правильного ответа.
/list/summer-math-school/
Летние математические лагеря для школьников
«Введение в математическое мышление» на Coursera
Стоимость: бесплатно
Подробнее: на странице курса
«Введение в математическое мышление» — это курс от британского математика и научно-популярного писателя Кита Девлина.
В школе нас учили решать задачи по готовым формулам и алгоритмам, а Девлин рассказывает об университетском подходе к математике, который основывается на умениях рассуждать о проблеме, самостоятельно разрабатывать пути ее решения и предоставлять стройные доказательства в защиту своих утверждений.
Этот курс не самый простой для восприятия, поэтому его стоит смотреть уже после того, как вы освежили в голове школьную программу по математике. Лучше всего он подойдет тем, кто работает по техническим специальностям и хочет развить аналитические способности.
/list/creativity-apps/
6 сервисов для развития логики, критического и креативного мышления
Решение неравенств с помощью пошагового решения математических задач
В этой главе мы разработаем некоторые приемы, помогающие решать задачи, сформулированные словами. Эти методы включают переписывание задач в виде символов. Например, поставленная задача
«Найдите число, которое при прибавлении к 3 дает 7»
можно записать так:
3 + ? = 7, 3 + n = 7, 3 + x = 1
и т.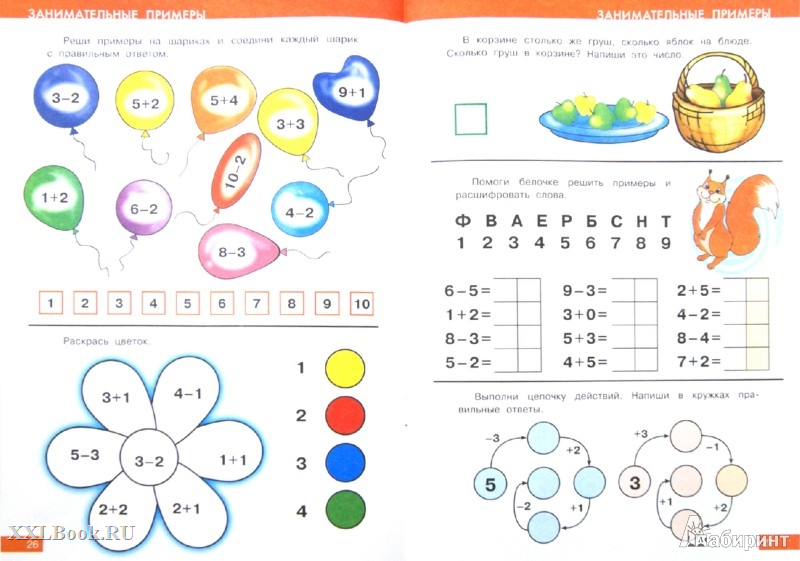
д., где символы ?, n и x представляют число, которое мы хотим найти. Такие сокращенные версии поставленных задач мы называем уравнениями или символическими предложениями. Такие уравнения, как x + 3 = 7, являются уравнениями первой степени, поскольку показатель степени равен 1. Члены слева от знака равенства составляют левый член уравнения; те, что справа, составляют правый член. Таким образом, в уравнении x + 3 = 7 левая часть равна x + 3, а правая часть равна 7.
РЕШЕНИЕ УРАВНЕНИЙ
Уравнения могут быть истинными или ложными, так же как словесные предложения могут быть истинными или ложными. Уравнение:
3 + x = 7
будет ложным, если вместо переменной подставить любое число, кроме 4. Значение переменной, для которой уравнение верно (4 в этом примере), называется решением уравнения. Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.
Пример 1.
Определить, является ли значение 3 решением уравнения член.
4(3) — 2 = 3(3) + 1
12 — 2 = 9 + 1
10 = 10
Ответ. 3 это решение.
Уравнения первой степени, которые мы рассматриваем в этой главе, имеют не более одного решения. Решения многих таких уравнений можно определить путем проверки.
Пример 2 Найдите решение каждого уравнения путем проверки.
а. х + 5 = 12
б. 4 · x = -20
Решения а. 7 является решением, так как 7 + 5 = 12,
b. -5 является решением, поскольку 4(-5) = -20.
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
В разделе 3.1 мы решили некоторые простые уравнения первой степени путем проверки. Однако решения большинства уравнений не сразу очевидны при осмотре. Следовательно, нам нужны некоторые математические «инструменты» для решения уравнений.
ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ
Эквивалентные уравнения – это уравнения, имеющие одинаковые решения. Таким образом,
3x + 3 = x + 13, 3x = x + 10, 2x = 10 и x = 5
эквивалентны уравнениям, поскольку 5 является единственным решением каждого из них.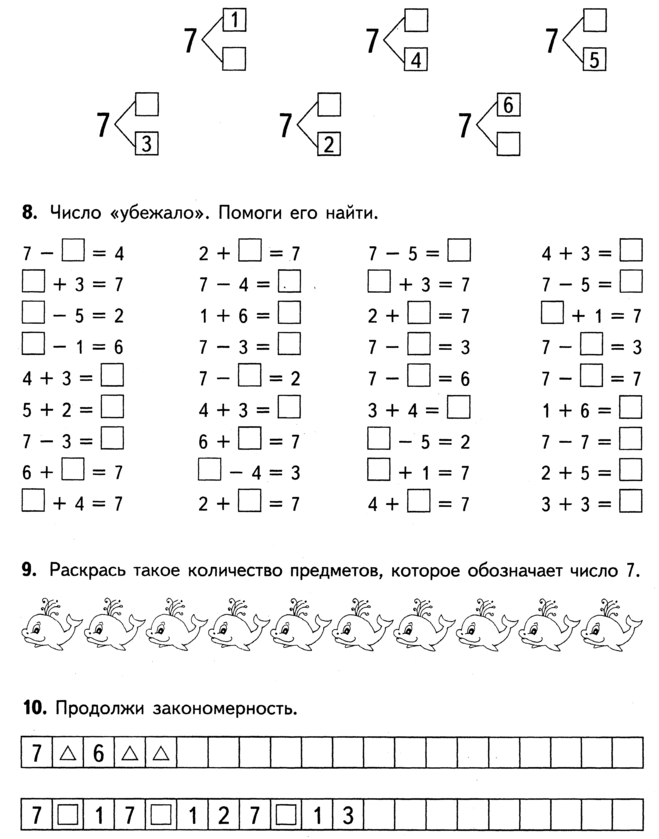
Следующее свойство, иногда называемое свойством сложения-вычитания , является одним из способов генерирования эквивалентных уравнений.
Если к обоим элементам добавляется или вычитается одно и то же количество уравнения, полученное уравнение эквивалентно исходному уравнение.
В символах
a — b, a + c = b + c и a — c = b — c
являются эквивалентными уравнениями.
Пример 1 Напишите уравнение, эквивалентное
x + 3 = 7
путем вычитания 3 из каждого члена.
Решение Вычитание 3 из каждого члена дает
x + 3 — 3 = 7 — 3
или
x = 4
Обратите внимание, что x + 3 = 7 и x = 4 являются эквивалентными уравнениями, поскольку решение одно и то же.
для обоих, а именно 4. Следующий пример показывает, как мы можем сгенерировать эквивалентные уравнения, сначала упростив один или оба члена уравнения.
Пример 2 Напишите уравнение, эквивалентное
4x- 2-3x = 4 + 6
путем объединения одинаковых терминов, а затем добавления 2 к каждому элементу.
Объединение одинаковых членов дает
x — 2 = 10
Добавление 2 к каждому члену дает
x-2+2 = 10+2
x = 12
Чтобы решить уравнение, мы используем сложение-вычитание свойство преобразовывать данное уравнение в эквивалентное уравнение формы x = a, из которого мы можем найти решение путем проверки.
Пример 3 Решить 2x + 1 = x — 2.
Мы хотим получить эквивалентное уравнение, в котором все члены, содержащие x, находятся в одном члене, а все члены, не содержащие x, — в другом. Если мы сначала прибавим -1 к каждому элементу (или вычтем из него 1), мы получим
2x + 1- 1 = x — 2- 1
2x = x — 3
Если мы теперь прибавим -x к каждому члену (или вычтем x из него), мы получим
2x-x = x — 3 — х
х = -3
где решение -3 очевидно.
Решением исходного уравнения является число -3; однако ответ часто отображается в виде уравнения x = -3.
Поскольку каждое уравнение, полученное в процессе, эквивалентно исходному уравнению, -3 также является решением 2x + 1 = x — 2. В приведенном выше примере мы можем проверить решение, подставив — 3 вместо x в исходном уравнение
2(-3) + 1 = (-3) — 2
-5 = -5
Симметричное свойство равенства также полезно при решении уравнений. Это свойство указывает
Если a = b, то b = a
Это позволяет нам менять местами члены уравнения в любое время, не заботясь о смене знака. Таким образом,
Если 4 = x + 2, то x + 2 = 4
Если x + 3 = 2x — 5, то 2x — 5 = x + 3
Если d = rt, то rt = d
Может быть несколько различные способы применения вышеуказанного свойства сложения. Иногда один метод лучше другого, а в некоторых случаях также полезно симметричное свойство равенства.
Пример 4 Решите 2x = 3x — 9. (1)
Решение Если мы сначала прибавим -3x к каждому элементу, мы получим
2x — 3x = 3x — 9 — 3x
-x = -9
где переменная имеет отрицательный коэффициент.
Хотя при проверке мы видим, что решение равно 9, поскольку -(9) = -9, мы можем избежать отрицательного коэффициента, добавляя -2x и +9 к каждому члену уравнения (1). В этом случае получаем
2х-2х + 9 = 3х- 9-2х+ 9
9 = х
откуда решение 9очевидно. Если мы хотим, мы можем записать последнее уравнение как x = 9 по симметричному свойству равенства.
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВА ДЕЛЕНИЯ
Рассмотрим уравнение
3x = 12
Решением этого уравнения является 4. Также обратите внимание, что если мы разделим каждую часть уравнения на 3, мы получим уравнения
, решение которого также равно 4. В общем случае мы имеем следующее свойство, которое иногда называют свойством деления.
Если оба члена уравнения разделить на одно и то же (отличное от нуля) полученное уравнение эквивалентно исходному уравнению.
В символах
эквивалентны уравнениям.
Пример 1 Напишите уравнение, эквивалентное
-4x = 12
, разделив каждый член на -4.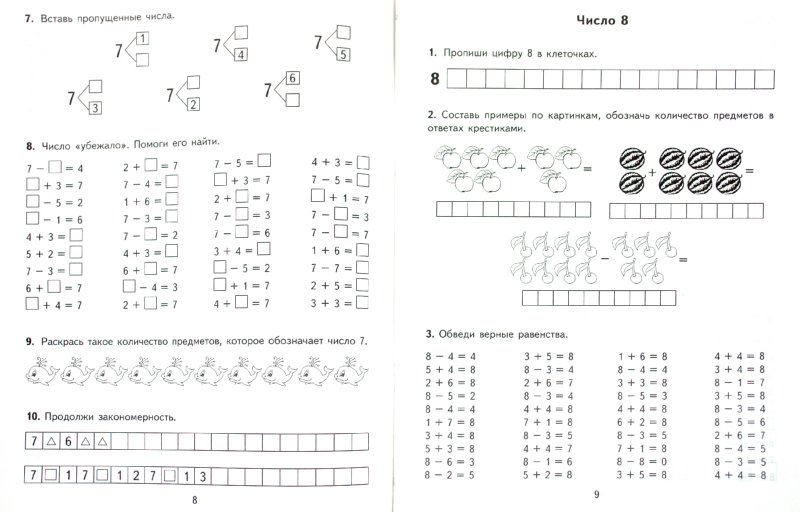
Решение Деление обоих членов на -4 дает
При решении уравнений мы используем вышеуказанное свойство для получения эквивалентных уравнений, в которых переменная имеет коэффициент 1.
Пример 2 Решите 3y + 2y = 20.
Сначала мы объединяем одинаковые члены, чтобы получить
5y = 20
Затем, разделив каждый член на 5, мы получаем
В следующем примере мы используем сложение — свойство вычитания и свойство деления для решения уравнения.
Пример 3 Решить 4x + 7 = x — 2.
Решение Сначала мы добавляем -x и -7 к каждому члену, чтобы получить
4x + 7 — x — 7 = x — 2 — x — 1
Далее , объединение одинаковых членов дает
3x = -9
Наконец, мы делим каждый член на 3, чтобы получить
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВА УМНОЖЕНИЯ
Рассмотрим уравнение
Решение этого уравнения умножая каждый член уравнения на 4, мы получаем уравнения
, решение которых также равно 12.
В общем случае мы имеем следующее свойство, которое иногда называют свойством умножения.
Если оба члена уравнения умножить на одну и ту же ненулевую величину, полученное уравнение эквивалентно исходному уравнению.
В символах
a = b и a·c = b·c (c ≠ 0)
являются эквивалентными уравнениями.
Пример 1 Напишите уравнение, эквивалентное
, умножив каждый член на 6.
Решение Умножив каждый член на 6, получим
дроби.
Пример 2 Решить
Решение Сначала умножьте каждый член на 5, чтобы получить
Теперь разделите каждый член на 3,
Пример 3 Решите .
Решение Сначала упростим над дробной чертой, чтобы получить
Затем умножим каждый член на 3, чтобы получить
Наконец, разделив каждый член на 5, получим
ДОПОЛНИТЕЛЬНЫЕ РЕШЕНИЯ 90 все методы, необходимые для решения большинства уравнений первой степени.
Нет определенного порядка, в котором следует применять свойства. Любой один или несколько из следующих шагов, перечисленных на странице 102, могут быть подходящими.Шаги для решения уравнений первой степени:
- Объедините одинаковые члены в каждом члене уравнения.
- Используя свойство сложения или вычитания, напишите уравнение со всеми членами, содержащими неизвестное в одном члене, и всеми членами, не содержащими неизвестного в другом.
- Объедините одинаковые термины в каждом элементе.
- Используйте свойство умножения для удаления дробей.
- Используйте свойство Division, чтобы получить коэффициент 1 для переменной.
Пример 1 Решите 5x — 7 = 2x — 4x + 14.
Решение Сначала мы объединяем одинаковые члены, 2x — 4x, чтобы получить
5x — 7 = -2x + 14
Затем мы добавляем +2x и +7 к каждому члену и объединяем одинаковые члены, чтобы получить
5x — 7 + 2x + 7 = -2x + 14 + 2x + 1
7x = 21
Наконец, мы делим каждый член на 7, чтобы получить
В следующем примере мы упрощаем дробную черту перед применением свойств, которые мы изучали.
Пример 2 Решить
Решение Сначала мы объединяем одинаковые члены, 4x — 2x, чтобы получить
Затем мы добавляем -3 к каждому члену и упрощаем
Затем мы умножаем каждый член на 3, чтобы получить
Наконец, мы делим каждый член на 2, чтобы получить
РЕШЕНИЕ ФОРМУЛ
Уравнения, которые включают переменные для измерения двух или более физических величин, называются формулами. Мы можем найти любую переменную в формуле, если известны значения других переменных. Мы подставляем известные значения в формулу и находим неизвестную переменную методами, которые мы использовали в предыдущих разделах.
Пример 1 В формуле d = rt найдите t, если d = 24 и r = 3.
Решение Мы можем найти t, подставив 24 вместо d и 3 вместо r. То есть
d = rt
(24) = (3)t
8 = t
Часто бывает необходимо решать формулы или уравнения, в которых имеется более одной переменной для одной из переменных в терминах другие.
Мы используем те же методы, что и в предыдущих разделах.
Пример 2 В формуле d = rt найдите t через r и d.
Решение Мы можем найти t через r и d, разделив оба члена на r, чтобы получить
, откуда по симметричному закону
В приведенном выше примере мы нашли t, применив свойство деления для создания эквивалентного уравнения. Иногда необходимо применить более одного такого свойства.
Пример 3 В уравнении ax + b = c найдите x через a, b и c.
Решение Мы можем найти x, сначала добавив -b к каждому члену, чтобы получить
затем разделив каждый член на a, мы получим
Решить неравенства с помощью программы «Пошаговое решение математических задач»
В главе 2 мы установили правила решения уравнений с использованием арифметических чисел. Теперь, когда мы изучили операции над числами со знаком, мы будем использовать те же правила для решения уравнений, в которых участвуют отрицательные числа.
Мы также изучим методы решения и построения графиков неравенств с одним неизвестным.
РЕШЕНИЕ УРАВНЕНИЙ, ВКЛЮЧАЮЩИХ ЗНАКОВЫЕ ЧИСЛА
ЗАДАЧИ
По завершении этого раздела вы сможете решать уравнения с числами со знаком.
Пример 1 Найдите x и проверьте: x + 5 = 3
Решение
Используя те же процедуры, описанные в главе 2, мы вычтем 5 из каждой части уравнения, получив
Пример 2 на x и проверяем: — 3x = 12
Решение
Разделив каждую сторону на -3, получим
| Всегда проверяйте исходное уравнение. |
| Другой способ решения уравнения 3x — 4 = 7x + 8 состоит в том, чтобы сначала вычесть 3x с обеих сторон, получив -4 = 4x + 8, затем вычесть 8 с обеих сторон и получить -12 = 4х. Теперь разделите обе части на 4, чтобы получить — 3 = x или x = — 3.  |
| Сначала удалите скобки. Затем следуйте процедуре, описанной в главе 2. |
ЛИТЕРАЛЬНЫЕ УРАВНЕНИЯ
ЦЕЛИ
По завершении этого раздела вы должны уметь:
- Найдите буквальное уравнение.
- Применить ранее изученные правила для решения буквенных уравнений.
Уравнение, состоящее более чем из одной буквы, иногда называют буквальным уравнением . Иногда бывает необходимо решить такое уравнение для одной из букв через другие. Пошаговая процедура, рассмотренная и использованная в главе 2, по-прежнему действительна после удаления любых символов группировки.
Пример 1 Решите для c: 3(x + c) — 4y = 2x — 5c
Решение
Сначала удалите скобки.
Здесь мы отмечаем, что, поскольку мы вычисляем с, мы хотим получить с с одной стороны и все остальные члены с другой стороны уравнения.
Таким образом, мы получаем
| Помните, abx это то же самое, что и 1abx. Делим на коэффициент при x, который в данном случае равен ab. |
| Решите уравнение 2x + 2y — 9x + 9a, сначала вычитая 2.v из обеих частей. Сравните решение с полученным в примере. |
Иногда форма ответа может быть изменена. В этом примере мы могли бы умножить и числитель, и знаменатель ответа на (-l) (это не меняет значения ответа) и получить
Преимущество этого последнего выражения перед первым состоит в том, что много отрицательных знаков в ответе.
| Умножение числителя и знаменателя дроби на одно и то же число является использованием фундаментального принципа дробей. |
Наиболее часто используемые буквенные выражения — это формулы из геометрии, физики, бизнеса, электроники и т.
д.
Пример 4 – это формула площади трапеции. Решите для с.
| Трапеция имеет две параллельные стороны и две непараллельные стороны. Параллельные стороны называются основаниями. Удаление скобок не означает просто их стирание. Мы должны умножить каждый член в скобках на множитель, стоящий перед скобками. Менять форму ответа не обязательно, но вы должны уметь распознавать правильный ответ, даже если форма отличается. |
Пример 5 представляет собой формулу, определяющую проценты (I), полученные за период D дней, когда известны основная сумма долга (p) и годовая ставка (r). Найдите годовую ставку, если известны сумма процентов, основная сумма долга и количество дней.
Решение
Задача требует решения для r.
Обратите внимание, что в этом примере r было оставлено справа, и поэтому вычисления были проще. Мы можем переписать ответ по-другому, если захотим.
ГРАФИЧЕСКИЕ НЕРАВЕНСТВА
ЦЕЛИ
По завершении этого раздела вы должны уметь:
- Используйте символ неравенства для обозначения относительного положения двух чисел на числовой прямой.
- Нарисуйте неравенства на числовой прямой.
Мы уже обсуждали множество рациональных чисел как те, которые могут быть выражены как отношение двух целых чисел. Существует также набор чисел, называемый иррациональными числами, , которые нельзя выразить как отношение целых чисел. В этот набор входят такие числа как и так далее. Множество, состоящее из рациональных и иррациональных чисел, называется действительных чисел.
Для любых двух действительных чисел a и b всегда можно утверждать, что Много раз нас интересует только, равны ли два числа, но бывают ситуации, когда мы также хотим представить относительный размер чисел, которые не равны.
Символы представляют собой символы неравенства или отношений порядка и используются для отображения относительных размеров значений двух чисел.
Обычно мы читаем этот символ как «больше чем». Например, a > b читается как «а больше, чем b». Обратите внимание, что мы заявили, что обычно читаем
| Утверждение 2 |
a
| Какое положительное число можно прибавить к 2, чтобы получить 5? |
Проще говоря, это определение утверждает, что а меньше b, если мы должны добавить что-то к а, чтобы получить b. Конечно, «что-то» должно быть положительным.
Если вы думаете о числовой строке, вы знаете, что добавление положительного числа эквивалентно перемещению вправо по числовой строке. Это приводит к следующему альтернативному определению, которое может быть легче визуализировать.
Пример 1 3
Мы могли бы также написать 6 > 3. |
Пример 2 — 4
| Мы могли бы также написать 0 > — 4. |
Пример 3 4 > — 2, потому что 4 находится справа от -2 на числовой прямой.
Пример 4 — 6
Математическое утверждение x
| Вы понимаете, почему невозможно найти наибольшее число меньше 3? |
На самом деле, назвать число x, которое является наибольшим числом меньше 3, — невозможная задача. Однако это может быть указано в числовой строке. Для этого нам нужен символ, представляющий значение утверждения, такого как x
Символы ( и ), используемые на числовой прямой, указывают на то, что конечная точка не включена в набор.
Пример 5 График x
Решение
Обратите внимание, что на графике есть стрелка, указывающая, что линия продолжается без конца влево.
| Этот график представляет каждое действительное число меньше 3. |
Пример 6 График x > 4 на числовой прямой.
Решение
| На этом графике представлены все действительные числа больше 4. |
Пример 7 График x > -5 на числовой прямой.
Решение
| На этом графике представлены все действительные числа больше -5. |
Пример 8 Постройте линейный график, показывающий, что x > — 1 и x
Решение
Утверждение x > — 1 и x
| На этом графике представлены все действительные числа от — 1 до 5. |
Пример 9 График — 3
Решение
Если мы хотим включить конечную точку в набор, мы используем другой символ, :.
Мы читаем эти символы как «равно или меньше» и «равно или больше».
Пример 10 х >; 4 указывает число 4 и все действительные числа справа от 4 на числовой прямой.
| Что означает x |
Символы [ и ], используемые в числовой строке, указывают, что конечная точка включена в набор.
| Вы обнаружите, что такое использование скобок и квадратных скобок соответствует их использованию в будущих курсах по математике. |
| Этот график представляет число 1 и все действительные числа больше 1. |
| Этот график представляет число 1 и все действительные числа, меньшие или равные -3. Пример 14 Напишите алгебраическое выражение для следующего графика.
Пример 15 Напишите алгебраическое выражение для следующего графика.
Пример 16 График на числовой прямой. Решение В этом примере представлена небольшая проблема. Как мы можем указать на числовой прямой? Если мы оценим точку, то другой человек может неправильно понять утверждение. Не могли бы вы сказать, представляет ли точка или, может быть, ? Поскольку целью графика является уточнение, всегда обозначают конечную точку.
РЕШЕНИЕ НЕРАВЕНСТВЗАДАЧИПо завершении этого раздела вы должны уметь решать неравенства с одним неизвестным. Решения неравенств обычно основаны на тех же основных правилах, что и уравнения. Есть одно исключение, которое мы вскоре обнаружим. Однако первое правило аналогично тому, которое используется при решении уравнений. Если к каждой стороне неравенства добавить одинаковое количество, результаты будут неравными в том же порядке. Пример 1 Если 5 Пример 2 Если 7
Это правило можно использовать для решения некоторых неравенств. Пример 3 Решить для x: x + 6 Решение Если мы прибавим -6 к каждой стороне, мы получим Отобразив это решение на числовой прямой, мы получим
Теперь мы воспользуемся правилом сложения, чтобы проиллюстрировать важную концепцию умножения или деления неравенств. Предположим, х > а. Теперь добавьте — x к обеим сторонам по правилу сложения.
Теперь добавьте -a с обеих сторон. Последнее выражение -a > -x можно переписать как -x < -a. Поэтому мы можем сказать: «Если х > а, то — х Если неравенство умножить или разделить на отрицательное число, результаты будут неравны в порядке , противоположном .
Пример 5 Найдите x и нарисуйте решение: -2x>6 Решение Чтобы получить x в левой части, мы должны разделить каждый член на — 2.
Обратите внимание на этот факт. Каждый раз, когда вы делите или умножаете на отрицательное число, вы должны изменить направление символа неравенства. Это единственная разница между решением уравнений и решением неравенств.
После того, как мы удалили круглые скобки и в выражении остались только отдельные члены, процедура поиска решения почти такая же, как в главе 2. Теперь рассмотрим пошаговый метод из главы 2 и отметим разница при решении неравенств. Первый Удалите дроби, умножив все члены на наименьший общий знаменатель всех дробей. (Без изменений, когда мы умножаем на положительное число.)
РЕЗЮМЕКлючевые слова
Процедуры
|