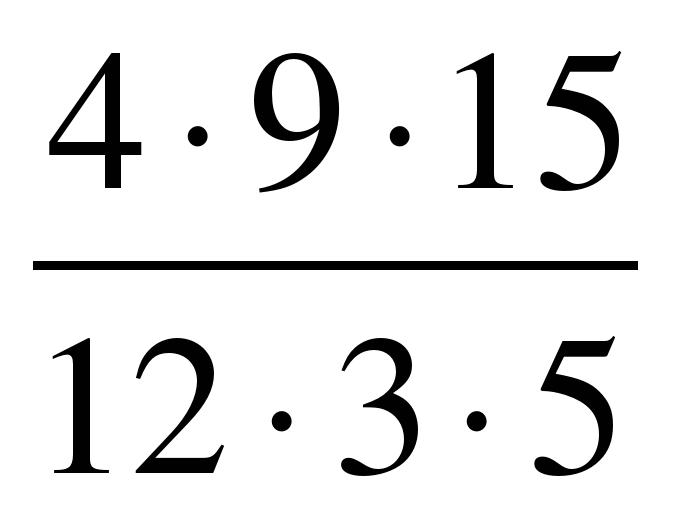Умножение дробей онлайн с решением. Калькулятор умножения дробей.

Чтобы умножить дробь на дробь нужно перемножить их числители и знаменатели, первое произведение записать числителем, а второе знаменателем.

Правила умножения дробей

Произведение двух дробей равно дроби. В числителе которой произведение числителей, а в знаменателе произведение знаменателей.

×

=

a × c

b × d

Как умножать обыкновенные дроби

Для умножения обыкновенных дробей нужно найти произведение числителей и произведение знаменателей. Первое произведение записать числителей а второе знаменателем.

Разберём пример: умножим дроби 1/4 × 1/3. Для этого перемножим числители 1 × 1 = 1 и знаменатели 4 × 3 = 12 в итоге у нас получится дробь 1/12

×

=

1 × 1

4 × 3

=

Как умножать натуральное число на дробь

Чтобы умножить дробь на натуральное число нужно числитель умножить на это число а знаменитель оставить без изменения.

×

=

a × b

c

Как умножать 3 и более дробей

При умножении 3 и более дробей мы пользумеся теми же правилами что и при умножении двух дробей.

Разберём пример: умножим правильную дробь 1/4 на натуральное число 5 и на смешанную дробь 3 целые 1/8.

Перед умножением нужно смешанную дробь перевести в неправильную 3 целые 1/8 = 25/8. Затем перемножить числители 1*5*25 = 125 и знаменатели 4*8 = 32. Полученное записать в виде дроби 125/32. При необходимости сократить и перевести в смешанную дробь.

×

×

=

×

×

=

1 × 5 × 25

4 × 8

=

=

Как умножить смешанную дробь на целое число

Чтобы умножить смешанную дробь на целое число нужно смешанную дробь перевести в неправильную. Затем числитель неправильной дроби умножить на целое число. Знаменатель оставить без изменения.

Разберём пример: умножим смешанную дробь 2 целые 1/4 на целое число 6.

Перед умножением нужно смешанную дробь перевести в неправильную 2 целые 1/4 = 9/4. Затем умножить числитель неправильной дроби на целое число 9*6 = 54 а знаменатель останется без изменения 4. При необходимости сократить и перевести в смешанную дробь.

×

=

×

=

9 × 6

4

=

=

=

Как перемножить смешанные дроби

Чтобы перемножить смешанные дроби, нужно их перевести в неправильные. Затем перемножить числители и знаменатели.

Разберём пример: умножим смешанную дробь 1 целая 2/5 на смешанную дробь 2 целые 1/3.

Переведём смешанные дроби в нерпавильные 1 целая 2/5 = 7/5 и 2 целые 1/3 = 7/3. Затем перемножим числители 7*7 = 49 и знаменатели 5*3 = 15. Получится дробь 49/15. При необходимости сократить и перевести в смешанную дробь.

×

=

×

=

7 × 7

5 × 3

=

=

Умножить дробь 13/11 на дробь 12/22
Умножить дробь 10/15 на дробь 4/7
Умножить дробь 2/2 на дробь 2/19
Умножить дробь 25/25 на дробь 13/12
Умножить дробь 22/20 на дробь 13/12
Умножить дробь 5/13 на дробь 18/20

Похожие калькуляторы

Перевести бесконечную периодическую дробь в обыкновенную дробь

Перевести десятичную дробь в обыкновенную

Привести дробь к новому знаменателю

Деление дробей

Преобразовать смешанную дробь в неправильную дробь

Преобразовать неправильная дробь в смешанную дробь

Сравнение дробей

Сложение дробей

Вычитание дробей

Приведение дробей к наименьшему общему знаменателю

Сократить дробь

деление и умножение смешанных дробей

Вы искали деление и умножение смешанных дробей? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и как дробь умножить на дробь с разными знаменателями, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «деление и умножение смешанных дробей».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как деление и умножение смешанных дробей,как дробь умножить на дробь с разными знаменателями,как дробь умножить на другую дробь,как перемножать дроби с разными знаменателями,как перемножить дроби с разными знаменателями,как решать дроби с разными знаменателями на умножение и деление,как умножать дроби неправильные,как умножать дроби с разными знаменателями,как умножать дроби с разными знаменателями и целыми числами,как умножать дроби с разными знаменателями и числителями,как умножать дроби с целыми числами и разными знаменателями,как умножать и делить дроби с разными знаменателями и числителями,как умножать смешанные числа с разными знаменателями,как умножаются дроби с разными знаменателями,как умножить две дроби с разными знаменателями,как умножить дроби с разными знаменателями,как умножить дроби с разными знаменателями и целыми числами,как умножить дроби с разными знаменателями и числителями,как умножить дробь на дробь с разными знаменателями,как умножить дробь на дробь с разными знаменателями и числителями,как умножить дробь на неправильную дробь,как умножить неправильную дробь на дробь,перемножение дробей с разными знаменателями,правило умножения дробей с разными знаменателями,при умножении дробей с разными знаменателями,произведение дробей с разными знаменателями,смешанную дробь умножить натуральное число на дробь,сокращение дробей умножение дробей,умножение дробей с неизвестными,умножение дробей с разным знаменателем,умножение дробей с разными,умножение дробей с разными знаменателями,умножение дробей с разными знаменателями примеры с решением,умножение дробей с разными знаменателями с целыми числами,умножение дробей с целыми числами и разными знаменателями,умножение и деление дробей с разными знаменателями умножение и деление,умножение и деление смешанных дробей,умножение неправильных дробей,умножение с дробей,умножение смешанных дробей,умножение смешанных дробей с разными знаменателями,умножения дробей с разными знаменателями,умножить дроби.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и деление и умножение смешанных дробей. Просто введите задачу в окошко и нажмите «решить» здесь (например, как дробь умножить на другую дробь).

Решить задачу деление и умножение смешанных дробей вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Умножение дробей

> … Математика > Фракции > Умножение дробей

Теперь, когда мы научились складывать и вычитать дроби, мы научимся умножать дроби. Умножать дроби намного проще, чем складывать или вычитать дроби, потому что нам не нужно находить общий знаменатель. Вместо этого мы умножаем числители и знаменатели. Следующее видео объяснит, почему это работает, и покажет несколько примеров.

Умножение дробей

Источник видео (05:48 мин.) | Стенограмма

При умножении дробей мы просто умножаем числители вместе и знаменатели вместе. Помните, что любое целое число можно представить в виде дроби, поставив его над 1.

Пример: \(\displaystyle 3=\frac{3}{1}\)

При необходимости уменьшите.

Пример, когда сокращение не требуется: \(\displaystyle \frac{2}{5}\cdot\frac{2}{3}=\frac{2\cdot2}{5\cdot3}=\frac{4} {15}\)

Пример, когда требуется сокращение: \(\displaystyle \frac{2}{5}\cdot\frac{3}{4}=\frac{2\cdot3}{5\cdot2\cdot2}=\frac{2 }{2}\cdot\frac{3}{5\cdot2}=1\cdot\frac{3}{10}=\frac{3}{10}\)

Дополнительные ресурсы

• Академия Хана: введение в умножение 2 дробей (05:05 мин. , расшифровка)
• Академия Хана: умножение 2 дробей: модель дробей (04:56 мин., расшифровка)
• Академия Хана: дроби — числовая строка (04:45 мин., стенограмма)
• Академия Хана: умножение 2 дробей: 5/6 x 2/3 (02:25 мин., Стенограмма)

Практические задачи

Умножьте следующие дроби:

1. \(\displaystyle \frac{1}{4}\cdot \frac{1}{3}=\) (

   Решение

   x

   Решение : \(\displaystyle \frac{1}{4}\cdot \frac{1}{3}=\frac{1}{12}\)
   Детали :

   Когда мы умножаем две дроби вместе, мы умножаем прямо. У нас есть:
   \(\displaystyle \frac{1}{4}\times\frac{1}{3}\)

   Что равно следующему:
   \(\displaystyle \frac{1\times1}{4\times3 }\)

   Что равно, как показано:
   \(\dfrac{1}{12}\)

   )
2. \(\displaystyle \frac{1}{4}\cdot \frac{5}{8}=\) (

   Решение

   x

   Решение : \(\displaystyle \frac{1}{4}\times \frac{5}{8}=\frac{5}{32}\)
   Детали :

   
   Когда мы умножаем две дроби вместе, мы умножаем прямо.

   У нас есть:
   \(\displaystyle \frac{1}{4}\times\frac{5}{8}\)

   Что равно следующему:
   \(\displaystyle \frac{1\times5}{4\times8 }\)

   Что равно, как показано:
   \(\dfrac{5}{32}\)

   )
3. \(\displaystyle \frac{3}{7}\cdot \frac{2}{5}=\) (

   Решение

   x

   Решение :
   \(\displaystyle \frac{3}{7}\cdot \frac{2}{5}=\frac{6}{35}\)

   )
4. \(\displaystyle \frac{3}{4}\cdot \frac{2}{9}=\) (

   Видео решение

   x

   Решение : \(\displaystyle \frac{3}{4}\cdot \frac{2}{9}=\frac{1}{6}\)
   Детали :

   ( Источник видео | Стенограмма)

   )
5. \(\displaystyle \frac{3}{4}\cdot 10=\) (
   Решение

   x

   Решение :
   \(\displaystyle \frac{3}{4}\cdot10=\frac{3}{4}\cdot\frac{10}{1}=\frac{30} {4}=\frac{15}{2}\)

   )
6. \(\displaystyle 6\cdot \frac{2}{3}=\) (

   Видео решение

   x

   Решение : \(\displaystyle 6 \cdot \frac{2}{3}=4\)
   Детали :

   (Источник видео | Стенограмма)

   )

Нужна дополнительная помощь?

1. Изучите другие уроки математики в Ресурсном центре.
2. Посетите онлайн-ресурсы для обучения в Ресурсном центре.
3. Свяжитесь со своим инструктором.
4. Если вам все еще нужна помощь, назначьте репетитора.

Умножение дробей — Математика: базовые учебные пособия

Умножение дробей

Умножение дробей может показаться пугающим, но знание того, как это сделать, делает его намного проще. В этом разделе шаг за шагом рассматривается процесс умножения двух дробей.

Примеры

Примеры

Нажмите на заголовки ниже, чтобы просмотреть каждый пример.

Пример 1

Пример 1
Умножьте и запишите ответ в упрощенной форме:
Умножьте числители и умножьте знаменатели. Обратите внимание, что, поскольку дроби имеют разные знаки, произведение будет отрицательным.
Упростить.
Найдите общие факторы и перепишите, показав общие факторы.
Удалить общие факторы.

Строка 1: Умножьте следующие дроби и запишите ответ в упрощенной форме: минус 5 на 8 раз 2 на 3

Строка 2: Умножьте числители вместе, чтобы числитель был отрицательным 5 раз 2. Затем умножьте знаменатели

вместе, поэтому знаменатель равен 8, умноженному на 3. Обратите внимание, что знаки дробей противоположны, поэтому произведение будет отрицательным.

Строка 3. Упростите числитель и знаменатель, чтобы дробь была отрицательной 10 на 24.

Строка 4: Найдите общие множители в числителе и знаменателе. Перепишите дробь, показывающую общий делитель 2, так, чтобы числитель был записан как минус 5 умножить на 2, а знаменатель был записан как 12 умножить на 2.

Строка 5: Удалите общий делитель 2 в числителе и знаменателе, чтобы окончательное упрощение дробь отрицательна 5 больше 12.

Пример 2

Пример 2
Умножьте и запишите ответ в упрощенной форме:
Преобразуйте смешанное число в неправильную дробь.
Умножьте числители и умножьте знаменатели.
Показать общие факторы и удалить их.
Умножить остальные коэффициенты.

Строка 1: Умножьте следующие дроби и запишите ответ в упрощенной форме: 3 и 1 на 3 умножить на 5 на 8. 3 умножить на 5 на 8.

Строка 2: Умножьте числители вместе, чтобы числитель был 10 умножить на 5. Затем умножьте знаменатели вместе, чтобы знаменатель был 3 умножить на 8.

Строка 4: Найдите общие множители в числителе и знаменателе. Перепишите дробь, показывающую общий делитель 2, чтобы числитель был записан как отрицательное 2 умножить на 5 умножить на 5, а знаменатель записал как 3 умножить на 2 умножить на 4.