Правило вычитания дробей с разными знаменателями: Урок 40. сложение и вычитание дробей — Математика — 6 класс

Содержание

общий знаменатель, алгоритм, решение примеров

Математика

12.11.21

14 мин.

Пожалуй, одной из самых популярных арифметических операций в алгебре является вычитание дробей с разными знаменателями. Алгоритм выполнения этого действия несложен и ничем не отличается, по сути, от сложения.

Оглавление:

Общие сведения

Нахождение общего знаменателя

Алгоритм вычитания

Решение примеров

Базируется он на основном свойстве отношений, позволяющем домножить числитель и знаменатель на одно и то же число. Следует отметить, что знание операции позволяет в дальнейшем приводить сложные выражения к простому виду, упрощая вычисления.

Общие сведения

Для того чтобы успешно научиться вычитать дроби, нужно понимать суть термина. В математике под ним понимают число, которое состоит из одной или нескольких долей единицы. Простыми словами, это отношение чего-то к целому. Например, пусть имеется арбуз. Его можно разрезать на равные части, то есть как бы подробить. По факту количество ягоды не изменится. Но если съесть один кусочек, то на тарелке останется три. Количественно в математике это действие можно описать дробью. Для рассматриваемого примера запись будет иметь вид: ¾.

В верхней части цифра обозначает долю от целого, а в нижней — на сколько равных кусков было разделено целое.

Делимое, то есть число, которое изменяется, называют числителем, а делитель — знаменателем. Дробь всегда будет меньше целой части.

В зависимости от соотношения частей, дробные выражения принято разделять на следующие типы:

Правильные. Рациональные числа, в которых делимое количественно меньше делителя.
Неправильные. Простые выражения, у которых значение знаменателя меньше величины числителя или совпадает с ним по численности.
Смешанные. Отношения, состоящие из натурального числа и правильной дроби.
Практически они представляют собой их сумму.

Кроме этого, существует ещё отдельный класс выражений, называемый десятичным. К нему относят отношения, в которых знаменатель — это число десять в степени с любым натуральным числом.

Записывают десятичные выражения, используя в качестве разделителя запятую. Например, 1/10 = 0,1.

С дробями, так как по факту это числа, разрешено выполнять любые математические действия. Самые простые из них — это умножение и деление, немного сложнее сложение и вычитание. Чтобы вычитать обыкновенные дроби, нужно знать их основное свойство. Сформулировать его можно следующим образом: если делитель и делимое умножить или разделить на одну и ту же величину, то результат отношения не изменится. Причём такую операцию можно выполнять сколько угодно раз.

Естественно, это не должен быть ноль, иначе выражение потеряет смысл. Например, ¾ = (3 * n)/(4 * n). Это свойство позволяет не только преобразовывать выражение, делая вычисления проще и удобнее, но и выполнять вычитание.

Всё дело в том, что при выполнении действия находят так называемые дополнительные множители, которые можно определить, опираясь на основное свойство.

Нахождение общего знаменателя

Основная сложность, которая может возникнуть при нахождении разности дробей, — это правильное определение общего знаменателя.

В качестве него выступает положительное число, делящееся на делители вычитаемых выражений без остатка. Искомый параметр можно находить как для двух дробей, так и сразу для нескольких.

В простейшем понимании такое число можно получить простым перемножением знаменателей.

Но такой подход будет нерациональным, хотя назвать его в корне неправильным нельзя.

Общее правило для вычисления наименьшего общего знаменателя (НОЗ):

Из чисел, стоящих в делимых, выбрать наибольшее и исследовать его на возможность деления с оставшимися. Если такое действие возможно, то выбранное значение и будет НОЗ. В ином случае переходят ко второму пункту.
Наибольший знаменатель умножают на два и проверяют делимость полученного числа на все остальные.
На этом шаге наибольший знаменатель умножают на три и повторяют проверку.
Если НОЗ не найден, делители раскладывают на простые множители. В результате повторяющиеся числа убирают, а оставшиеся перемножают. Получившееся произведение и будет НОЗ.

Таким образом, чтобы найти нужный знаменатель, необходимо уметь раскладывать простые числа на множители. Эта операция является тождественным преобразованием. Выполняется она в несколько этапов.

Сначала ищется наименьшее число, на которое можно разделить исходное без остатка. Затем выполняют деление и повторяют действие, но уже для полученного значения. Операцию повторяют до тех пор, пока в ответе не получится единица.

Понять процедуру проще на примере. Пусть нужно выполнить вычитание двух дробей, у которых в знаменателях стоит 15 и 40. Следуя алгоритму, нужно наибольшее из этих чисел умножить на два и попробовать выполнить деление. В ответе получится число 80, которое на 15 разделить без остатка невозможно. Поэтому можно попробовать выполнить умножение на три: 40 * 3 = 120. Полученное произведение можно разделить на 15, в ответе будет восемь. Значит, 120 и будет искомым общим знаменателем.

Это значение можно было найти и пойдя путём разложения. Так, 15 можно представить как 5 * 3, а 40 в виде произведения 2 * 2 * 2 * 5. При сравнении записей видно, что и в первой, и во второй стоит цифра пять. Поэтому в одной из них её нужно убрать, а оставшиеся члены перемножить: 3 * 2 * 2 * 2 * 5 = 120. Ответ идентичен.

Алгоритм вычитания

Следует отметить, что сложение и вычитание дробей выполняется по одинаковому алгоритму. Единственное отличие в арифметическом знаке действия. Если нужно из одного дробного выражения вычесть другое, рекомендуется придерживаться следующего алгоритма:

если в многочлене стоит смешанная дробь, то преобразовать её в неправильную;
исследовать вычитаемое и уменьшаемое на возможность упрощения;
найти наименьшее общее кратное среди знаменателей;

вычислить дополнительные множители;
домножить числители на найденные для них значения;
записать в знаменатель НОЗ, а в числитель разницу произведений делимых;
при возможности сократить дробь;
привести ответ к виду смешанного числа в случае получения неправильной дроби.

Как можно заметить, алгоритм простой. Но может возникнуть вопрос по нахождению дополнительных множителей, несмотря на то что действие относят к простым операциям. После того как найден общий знаменатель, нужно делитель вычитаемого и уменьшаемого разделить на это число. Полученные значения и будут являться искомыми аргументами, предназначенными для домножения.

Кроме этого, необходимо обратить внимание на вычитание дробей разного типа

. Чтобы правильно их вычесть, желательно вначале выполнить преобразование. Смешанное выражение можно довольно просто представить в виде неправильного числа. Для этого следует умножить целую часть на знаменатель и к полученному произведению добавить делимое. Затем результат сложения записать в числитель, а знаменатель оставить неизменным.

Существует и другой путь, обратный, то есть неправильную дробь превратить в смешанное число. Для этого числитель нужно разделить на знаменатель. По результату операции остаток записывают в делимое, а делитель оставляют без изменения. Целую же часть прибавляют к дробной. После того как два числа будут смешанными, алгоритм вычитания немного изменяется. Так, целые части вычитают отдельно от дробных чисел, а затем результаты просто складывают.

Какой алгоритм использовать для того, чтобы отнять дроби друг от друга, не принципиально.

Всё дело в привычке и навыках решающего.

Но, пожалуй, способ, заключающийся в переводе смешанного числа в неправильное выражение, проще. Другой же метод лучше использовать, когда надо вычесть из целого числа дробное или же наоборот.

Решение примеров

Чтобы научиться правильно вычитать дроби с разными знаменателями, нужно самостоятельно решить несколько задач. Обычно хватает проработать порядка пяти примеров, чтобы получить необходимый опыт. Вот некоторые наиболее интересные задания:

Вычислить разницу: (4 / 7) — (2 / 21). Придерживаясь алгоритма, вначале нужно найти общий знаменатель. Число в вычитаемом можно разделить на делитель уменьшаемого без остатка. Поэтому оно и будет искомым выражением. Далее, для первого члена дополнительным множителем будет 21: 7 = 3, а для второго 21: 21 = 1. Значит, решение примет следующий вид: (4 / 7) — (2 / 21) = ((3 * 4) — 2) / 21 = 10 / 21.
Определить результат действия: 4 (1 / 3) — 1 / 7. Перед началом выполнения вычитания нужно смешанную дробь привести к неправильному виду, а уже после действовать по алгоритму. Итак, 4 (1 / 3) = ((4 * 3) + 1) / 3 = 13 / 3. Отсюда (13 / 3) — 1 / 7 = ((7 * 13) — (3 * 1)) / 21 = (91 — 3) / 21 = 88 / 21. Полученный ответ нужно представить в виде смешанного выражения: 88 / 21 = (4 + 4 * 21) / 21 = 4 (4 / 21).
Сравнить два выражения по модулю: 4 / 5 — 12 / 4 — 4 (5 / 6) и 11 — 3 (1 / 3) + 8 / 7. Чтобы определить, какое из них больше, необходимо выполнить действия. Первый многочлен будет равен: 4 / 5 — 25 / 4 — 4 (5/6) = 4 / 5 — 12/ 4 — (4 * 6 + 5) / 6 = 4 / 5 — 25 / 4 — 29 / 6 = ((12*4) — (15 * 25) — (29 * 10)) / 60 = (48 — 375 — 290) / 60 = — 617 / 60 = -(17 + 10 * 60) / 60 = -10 (17 / 60). Второе выражение можно вычислить так: 11 — 3 (1 / 3) — 8 / 7 = 11 — 3 + 1 / 3 — 8 / 7 = 8 + 1 /3 — 8 / 7 = 8 + ((1*7) — (8 * 3)) / 21 = 8 + (7 — 24) / 21 = 8 — 17 / 21 = (8 / 1) — (17 / 21) = (168 — 17) / 21 = 151 / 21 = 74 / 21. Полученные ответы нужно сравнить без учёта знака. Поэтому можно утверждать, что первое выражение будет больше второго.

Таким образом, отнимать дроби с разными знаменателями не так уж и сложно. Нужно просто найти общий знаменатель, дополнительные множители и выполнить вычитание. При этом следует упомянуть так называемые онлайн-калькуляторы. Это веб-сервисы, которые в автоматическом режиме выполняют вычитание.

Их довольно удобно использовать не только для проверки самостоятельно решённых примеров, но и на стадии обучения.

Всё дело в том, что, кроме быстрого решения, эти сайты могут предоставить пользователям подробные решения того или иного примера.

Сравнение, сложение и вычитание дробей с разными знаменателями / Обыкновенные дроби / Справочник по математике 5-9 класс

Главная
Справочники
Справочник по математике 5-9 класс
Обыкновенные дроби
Сравнение, сложение и вычитание дробей с разными знаменателями

Мы уже умеем сравнивать, складывать и вычитать дроби с одинаковыми знаменателями. Теперь рассмотрим сравнение, сложение и вычитание дробей с разными знаменателями.

Чтобы сравнить две дроби с разными знаменателями, надо:

1) привести данные дроби к общему знаменателю;

2) применить правило сравнения дробей с одинаковыми знаменателями.

Пример:

Сравним дроби .

Приведем данные дроби к наименьшему общему знаменателю 10, получим:

Чтобы сложить (вычесть) две дроби с разными знаменателями, надо:

1) привести данные дроби к общему знаменателю;

2) применить правило сложения (вычитания) дробей с одинаковыми знаменателями.

Примеры:

1) Найдем сумму .

Наименьший общий знаменатель дробей равен 15. Каждую из этих дробей заменим на ей равную со знаменателем 15. Этой заменой мы сложение дробей с разными знаменателями сведем к сложению дробей с одинаковыми знаменателями, получим:

2) Найдем разность .

Наименьший общий знаменатель дробей равен 35. Каждую из этих дробей заменим на ей равную со знаменателем 35. Этой заменой мы вычитание дробей с разными знаменателями сведем к вычитанию дробей с одинаковыми знаменателями, получим:

Для дробей, как и для натуральных чисел, выполняются свойства сложения:

1) Переместительное свойство:

2) Сочетательное свойство:

Сложение и вычитание смешанных чисел

Чтобы выполнить сложение смешанных чисел, нужно:

1) привести дробные части этих чисел к наименьшему общему знаменателю;

2) отдельно выполнить сложение целых частей и отдельно дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части.

Пример:

Чтобы выполнить вычитание смешанных чисел, нужно:

1) привести дробные части этих чисел к наименьшему общему знаменателю; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь, уменьшив на единицу целую часть;

2) отдельно выполнить вычитание целых частей и отдельно дробных частей.

Пример:

Обычно, примеры такого вида, как пример 2, записывают коротко:

Обратите внимание: если в результате сложения или вычитания дробей получается сократимая дробь, то нужно выполнить сокращение.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Доли. Обыкновенные дроби

Сравнение дробей

Делители и кратные

Признаки делимости на 10, на 5 и на 2

Четные и нечетные числа

Признаки делимости на 9 и на 3

Простые и составные числа

Разложение на простые множители

Наибольший общий делитель

Наименьшее общее кратное

Деление и дроби

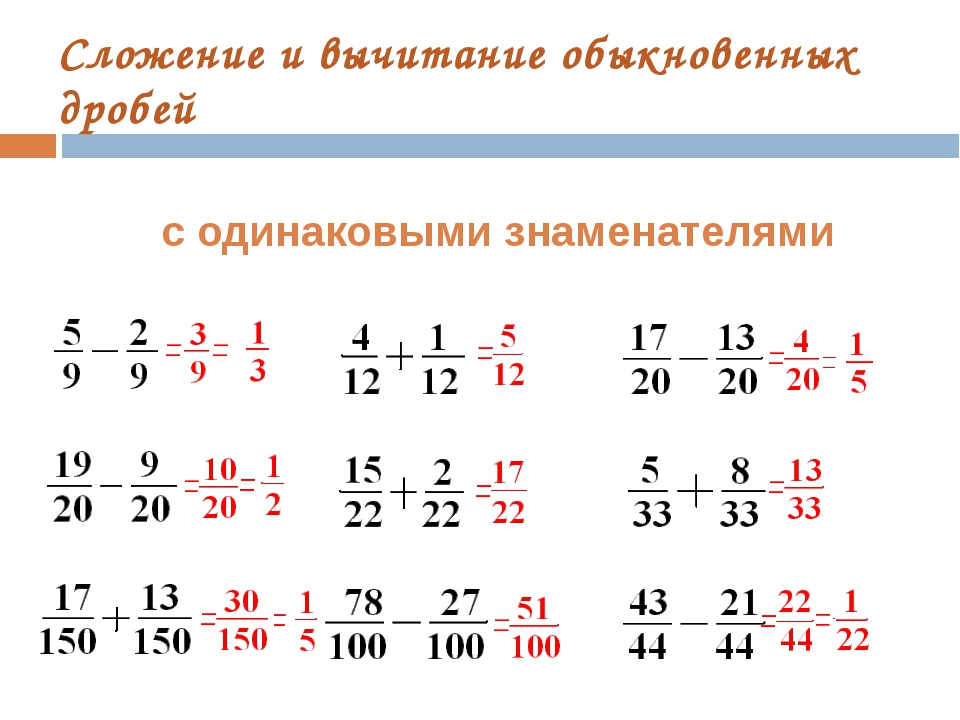
Сложение и вычитание дробей с одинаковыми знаменателями

Смешанное число

Сложение и вычитание смешанных чисел

Основное свойство дроби

Решето Эратосфена

Приведение дробей к общему знаменателю

Умножение обыкновенных дробей

Деление обыкновенных дробей

Обыкновенные дроби

Правило встречается в следующих упражнениях:

6 класс

Номер 252, Мерзляк, Полонский, Якир, Учебник

Номер 280, Мерзляк, Полонский, Якир, Учебник

Номер 281, Мерзляк, Полонский, Якир, Учебник

Номер 533, Мерзляк, Полонский, Якир, Учебник

Номер 1004, Мерзляк, Полонский, Якир, Учебник

Задание 317, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 846, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1132, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1283, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1284, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 5, Мерзляк, Полонский, Якир, Учебник

Номер 34, Мерзляк, Полонский, Якир, Учебник

Номер 39, Мерзляк, Полонский, Якир, Учебник

Номер 75, Мерзляк, Полонский, Якир, Учебник

Номер 139, Мерзляк, Полонский, Якир, Учебник

Номер 197, Мерзляк, Полонский, Якир, Учебник

Номер 297, Мерзляк, Полонский, Якир, Учебник

Номер 389, Мерзляк, Полонский, Якир, Учебник

Номер 429, Мерзляк, Полонский, Якир, Учебник

Номер 787, Мерзляк, Полонский, Якир, Учебник

Сложение и вычитание алгебраических дробей с разными знаменателями (основные правила, простейшие случаи) 8 класс

Сложение и вычитание обыкновенных дробей с разными знаменателями

Чтобы складывать и вычитать алгебраические дроби с разными знаменателями, проведём аналогию с обыкновенными дробями и перенесём её на алгебраические дроби.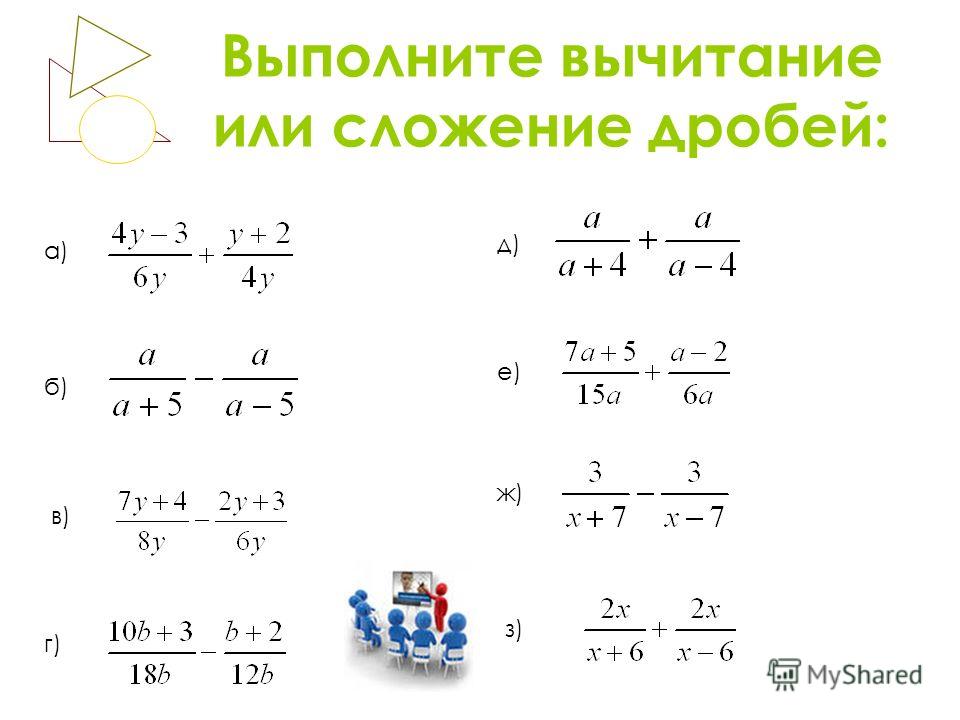

Рассмотрим простейший пример для обыкновенных дробей.

Пример 1. Сложить дроби: .

Решение:

Вспомним правило сложения дробей. Для начала дроби необходимо привести к общему знаменателю. В роли общего знаменателя для обыкновенных дробей выступает наименьшее общее кратное (НОК) исходных знаменателей.

Определение

– наименьшее натуральное число, которое делится одновременно на числа и .

Для нахождения НОК необходимо разложить знаменатели на простые множители, а затем выбрать все простые множители, которые входят в разложение обоих знаменателей.

; . Тогда в НОК чисел должны входить две двойки и две тройки: .

После нахождения общего знаменателя, необходимо для каждой из дробей найти дополнительный множитель (фактически, поделить общий знаменатель на знаменатель соответствующей дроби).

Затем каждая дробь умножается на полученный дополнительный множитель. Получаются дроби с одинаковыми знаменателями, складывать и вычитать которые мы научились на прошлых уроках.

Получаем: .

Ответ:.

Рассмотрим теперь сложение алгебраических дробей с разными знаменателями. Сначала рассмотрим дроби, знаменатели которых являются числами.

Сложение и вычитание алгебраических дробей с разными знаменателями

Пример 2. Сложить дроби: .

Решение:

Алгоритм решения абсолютно аналогичен предыдущему примеру. Легко подобрать общий знаменатель данных дробей: и дополнительные множители для каждой из них.

Ответ:.

Итак, сформулируем алгоритм сложения и вычитания алгебраических дробей с разными знаменателями:

1. Найти наименьший общий знаменатель дробей.

2. Найти дополнительные множители для каждой из дробей (поделив общий знаменатель на знаменатель данной дроби).

3. Домножить числители на соответствующие дополнительные множители.

4. Сложить или вычесть дроби, пользуясь правилами сложения и вычитания дробей с одинаковыми знаменателями.

Рассмотрим теперь пример с дробями, в знаменателе которых присутствуют буквенные выражения.

Пример 3. Сложить дроби: .

Решение:

Поскольку буквенные выражения в обоих знаменателях одинаковы, то следует найти общий знаменатель для чисел . Итоговый общий знаменатель будет иметь вид: . Таким образом, решение данного примера имеет вид:.

Ответ:.

Пример 4. Вычесть дроби: .

Решение:

Если «схитрить» при подборе общего знаменателя не удаётся (нельзя разложить на множители или воспользоваться формулами сокращённого умножения), то в качестве общего знаменателя приходится брать произведение знаменателей обеих дробей.

Ответ:.

Вообще, при решении подобных примеров, наиболее сложным заданием является нахождение общего знаменателя.

Пример вычитания алгебраических дробей с разложением знаменателя на множители

Рассмотрим более сложный пример.

Пример 5. Упростить: .

Решение:

При нахождении общего знаменателя необходимо прежде всего попытаться разложить знаменатели исходных дробей на множители (чтобы упростить общий знаменатель).

В данном конкретном случае:

;

Тогда легко определить общий знаменатель: .

Определяем дополнительные множители и решаем данный пример:

Ответ:.

Примеры на закрепление правил сложения и вычитания алгебраических дробей с разными знаменателями

Теперь закрепим правила сложения и вычитания дробей с разными знаменателями.

Пример 6. Упростить: .

Решение:

Ответ:.

Пример 7. Упростить: .

Решение:

Ответ:.

Пример сложения трёх алгебраических дробей с разными знаменателями

Рассмотрим теперь пример, в котором складываются не две, а три дроби (ведь правила сложения и вычитания для большего количества дробей остаются такими же).

Пример 8. Упростить: .

Решение:

Ответ:.

Пример вычитания алгебраических дробей с предварительным сокращением

Теперь рассмотрим пример, в котором необходимо сначала сократить дроби, а затем уже их складывать (вычитать).

Пример 9. Упростить: .

Решение:

Рассмотрим первую дробь:

. При этом следует указать, что .

Проведём аналогичные преобразования со второй дробью:

. При этом следует указать, что .

Таким образом, получаем следующее преобразование:

Ответ:.

На данном уроке мы рассмотрели правила сложения и вычитания дробей с разными знаменателями, а также решили типовые несложные задачи с использованием этих правил. В дальнейшем мы рассмотрим более сложные примеры задач на эти правила.

Список литературы

Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Фестиваль педагогических идей «Открытый урок» (Источник).
Учеба-Легко (Источник).

Домашнее задание

№№48–51, 53, 54. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
Упростить выражение: а) , б) , в) .
Вычислить значение выражения при .
Упростить выражение .

Сложение и вычитание обыкновенных дробей правило. Сложение дробей с целыми числами и разными знаменателями

Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками. Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.

Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.

Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.

Умножение дробей с разными знаменателями

Изначально стоит определить разновидности дробей :

правильные;
неправильные;
смешанные.

Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.

При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:

a/ b * c/ d = a*c / b*d.

Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.

Стоит рассмотреть умножение дробей с разными знаменателями на примерах:

8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
4/ 6 * 3/ 7 = 2/ 3 * 3/7 2*3 / 3*7 = 6/ 21 .

В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.

Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:

1 4/ 11 =1 + 4/ 11.

Как происходит перемножение

Предлагается несколько примеров для рассмотрения.

2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.

В примере используется умножение числа на обыкновенную дробную часть , записать правило для этого действия можно формулой:

a * b/ c = a*b / c.

По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:

4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.

Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:

d * e/ f = e/ f: d.

Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.

Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:

1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.

В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:

a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.

Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».

Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.

В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.

Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения , но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.

В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».

Содержание урока

Сложение дробей с одинаковыми знаменателями

Сложение дробей бывает двух видов:

Сложение дробей с одинаковыми знаменателями
Сложение дробей с разными знаменателями

Сначала изучим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения:

Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:

Пример 2. Сложить дроби и .

В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два равно единице:

Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:

Пример 3 . Сложить дроби и .

Опять же складываем числители, а знаменатель оставляем без изменения:

Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:

Пример 4. Найти значение выражения

Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:

Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.

Как видите в сложении дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:

Чтобы сложить дроби с одинаковыми знаменателя, нужно сложить их числители, а знаменатель оставить без изменения;

Сложение дробей с разными знаменателями

Теперь научимся складывать дроби с разными знаменателями.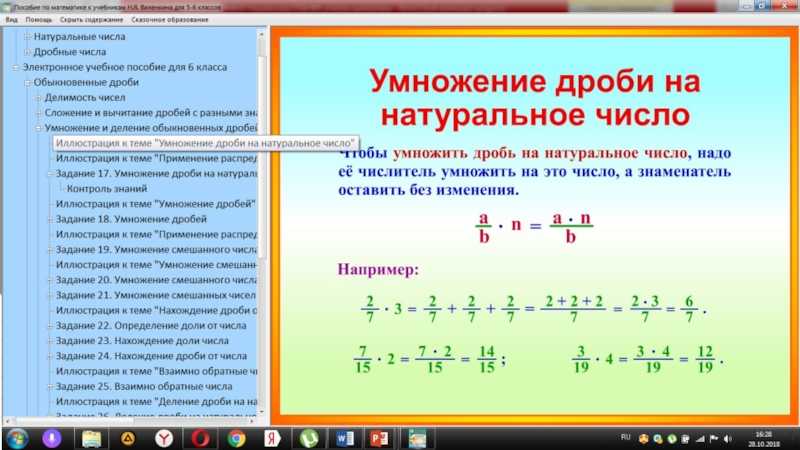 Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.

Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.

А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.

Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.

Суть этого способа заключается в том, что сначала ищется (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.

Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.

Пример 1 . Сложим дроби и

В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6

НОК (2 и 3) = 6

Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.

Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:

Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.

Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:

Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:

Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:

Таким образом, пример завершается. К прибавить получается .

Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:

Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).

Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).

Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:

Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби? «.

Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:

Найти НОК знаменателей дробей;
Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
Умножить числители и знаменатели дробей на свои дополнительные множители;
Сложить дроби, у которых одинаковые знаменатели;
Если в ответе получилась неправильная дробь, то выделить её целую часть;

Пример 2. Найти значение выражения .

Воспользуемся инструкцией, которая приведена выше.

Шаг 1. Найти НОК знаменателей дробей

Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4

Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби

Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:

Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:

Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:

Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители

Умножаем числители и знаменатели на свои дополнительные множители:

Шаг 4. Сложить дроби у которых одинаковые знаменатели

Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:

Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.

Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть

У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:

Получили ответ

Вычитание дробей с одинаковыми знаменателями

Вычитание дробей бывает двух видов:

Вычитание дробей с одинаковыми знаменателями
Вычитание дробей с разными знаменателями

Сначала изучим вычитание дробей с одинаковыми знаменателями. Тут всё просто. Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним.

Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:

Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:

Пример 2. Найти значение выражения .

Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:

Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:

Пример 3. Найти значение выражения

Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:

Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:

Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.

Вычитание дробей с разными знаменателями

Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.

Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.

Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.

Пример 1. Найти значение выражения:

У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.

Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12

НОК (3 и 4) = 12

Теперь возвращаемся к дробям и

Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:

Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:

Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:

Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:

Получили ответ

Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы

Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:

Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):

Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.

Пример 2. Найти значение выражения

У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.

Найдём НОК знаменателей этих дробей.

Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30

НОК (10, 3, 5) = 30

Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.

Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:

Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:

Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:

Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:

Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.

Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:

В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.

Чтобы сократить дробь , нужно разделить её числитель и знаменатель на (НОД) чисел 20 и 30.

Итак, находим НОД чисел 20 и 30:

Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10

Получили ответ

Умножение дроби на число

Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить прежним.

Пример 1 . Умножить дробь на число 1 .

Умножим числитель дроби на число 1

Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы

Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:

Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:

Пример 2 . Найти значение выражения

Умножим числитель дроби на 4

В ответе получилась неправильная дробь. Выделим в ней целую часть:

Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы

А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:

Умножение дробей

Чтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.

Пример 1. Найти значение выражения .

Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:

Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:

Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:

И взять от этих трех кусочков два:

У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:

Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:

Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно

Пример 2 . Найти значение выражения

Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:

В ответе получилась неправильная дробь. Выделим в ней целую часть:

Пример 3. Найти значение выражения

В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.

Итак, найдём НОД чисел 105 и 450:

Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15

Представление целого числа в виде дроби

Любое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:

Обратные числа

Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».

Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.

Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:

Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.

Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:

Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:

Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:

Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.

Обратное число можно найти также для любого другого целого числа.

Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.

Деление дроби на число

Допустим, у нас имеется половина пиццы:

Разделим её поровну на двоих. Сколько пиццы достанется каждому?

Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.

Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.

Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.

Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.

Итак, требуется разделить дробь на число 2 . Здесь делимым является дробь , а делителем число 2.

Чтобы разделить дробь на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить на

Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь , которую вы получили.

Вычитание дробей с одинаковыми знаменателями, примеры:

Вычитание правильной дроби из единицы.

Если необходимо вычесть из единицы дробь, которая является правильной , единицу переводят к виду неправильной дроби , у нее знаменатель равен знаменателю вычитаемой дроби.

Пример вычитания правильной дроби из единицы:

Знаменатель вычитаемой дроби = 7 , т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.

Вычитание правильной дроби из целого числа.

Правила вычитания дробей — правильной из целого числа (натурального числа) :

Переводим заданные дроби, которые содержат целую часть, в неправильные. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
Далее вычисляем разность дробей, которые мы получили. В результате мы почти найдем ответ;
Выполняем обратное преобразование, то есть избавляемся от неправильной дроби — выделяем в дроби целую часть.

Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.

Пример вычитания дробей:

В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.

Вычитание дробей с разными знаменателями.

Или, если сказать другими словами, вычитание разных дробей .

Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ) , и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.

Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.

Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители , то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!

Порядок действий при вычитании дробей с разными знаменателями.

найти НОК для всех знаменателей;
поставить для всех дробей дополнительные множители;
умножить все числители на дополнительный множитель;
полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.

Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.

Вычитание дробей, примеры:

Вычитание смешанных дробей.

При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.

Первый вариант вычитания смешанных дробей.

Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).

Например:

Второй вариант вычитания смешанных дробей.

Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.

Например:

Третий вариант вычитания смешанных дробей.

Дробная часть уменьшаемого меньше дробной части вычитаемого.

Пример:

Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.

Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого. 3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.

В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:

Правила сложения дробей с разными знаменателями очень простые.

Рассмотрим правила сложения дробей с разными знаменателями по шагам:

1. Найти НОК (наименьшее общее кратное) знаменателей. Полученный НОК будет общим знаменателем дробей;

2. Привести дроби к общему знаменателю;

3. Сложить дроби, приведенные к общему знаменателю.

На простом примере научимся применять правила сложения дробей с разными знаменателями.

Пример

Пример сложения дробей с разными знаменателями.

Сложить дроби с разными знаменателями:

1	+	5
6	+	12

Будем решать по шагам.

1. Найти НОК (наименьшее общее кратное) знаменателей.

Число 12 делится на 6.

Отсюда делаем вывод, что 12 есть наименьшее общее кратное чисел 6 и 12.

Ответ: нок чисел 6 и 12 равен 12:

НОК(6, 12) = 12

Полученный НОК и будет общим знаменателем двух дробей 1/6 и 5/12.

2. Привести дроби к общему знаменателю.

В нашем примере привести к общему знаменателю 12 нужно только первую дробь, ведь у второй дроби знаменатель уже равен 12.

Разделим общий знаменатель 12 на знаменатель первой дроби:

2 есть дополнительный множитель.

Умножим числитель и знаменатель первой дроби (1/6) на дополнительный множитель 2.

Одной из важнейших наук, применение которой можно увидеть в таких дисциплинах, как химия, физика и даже биология, является математика. Изучение этой науки позволяет развить некоторые умственные качества, улучшить и способность концентрироваться. Одна из тем, которые заслуживают отдельного внимания в курсе «Математика» — сложение и вычитание дробей. У многих учеников ее изучение вызывает затруднение. Возможно, наша статья поможет лучше понять эту тему.

Как вычесть дроби, знаменатели которых одинаковые

Дроби — это те же числа, с которыми можно производить различные действия. Их отличие от целых чисел заключается в присутствии знаменателя. Именно поэтому при выполнении действий с дробями нужно изучить некоторые их особенности и правила. Наиболее простым случаем является вычитание обыкновенных дробей, знаменатели которых представлены в виде одинакового числа. Выполнить это действие не составит особого труда, если знать простое правило:

Для того чтобы из одной дроби вычесть вторую, необходимо из числителя уменьшаемой дроби вычесть числитель вычитаемой дроби. Это число записываем в числитель разницы, а знаменатель оставляем тот же: k/m — b/m = (k-b)/m.

Примеры вычитания дробей, знаменатели которых одинаковы

7/19 — 3/19 = (7 — 3)/19 = 4/19.

От числителя уменьшаемой дроби «7» отнимаем числитель вычитаемой дроби «3», получаем «4». Это число мы записываем в числитель ответа, а в знаменатель ставим то же число, что было в знаменателях первой и второй дроби — «19».

На картинке ниже приведено еще несколько подобных примеров.

Рассмотрим более сложный пример, где произведено вычитание дробей с одинаковыми знаменателями:

29/47 — 3/47 — 8/47 — 2/47 — 7/47 = (29 — 3 — 8 — 2 — 7)/47 = 9/47.

От числителя уменьшаемой дроби «29» отниманием по очереди числители всех последующих дробей — «3», «8», «2», «7». В итоге получаем результат «9», который записываем в числитель ответа, а в знаменатель записываем то число, которое находится в знаменателях всех этих дробей, — «47».

Сложение дробей, имеющих одинаковый знаменатель

Сложение и вычитание обыкновенных дробей осуществляется по одному и тому же принципу.

Для того чтобы сложить дроби, знаменатели которых одинаковы, необходимо числители сложить. Полученное число — числитель суммы, а знаменатель останется тот же: k/m + b/m = (k + b)/m.

Рассмотрим, как это выглядит на примере:

1/4 + 2/4 = 3/4.

К числителю первой слагаемой дроби — «1» — добавляем числитель второй слагаемой дроби — «2». Результат — «3» — записываем в числитель суммы, а знаменатель оставляем тот же, что присутствовал в дробях, — «4».

Дроби с различными знаменателями и их вычитание

Действие с дробями, которые имеют одинаковый знаменатель, мы уже рассмотрели. Как видим, зная простые правила, решить подобные примеры достаточно легко. Но что делать, если необходимо произвести действие с дробями, которые имеют различные знаменатели? Многие учащиеся средних школ приходят в затруднение перед такими примерами. Но и здесь, если знать принцип решения, примеры уже не будут представлять для вас сложности. Здесь также существует правило, без которого решение подобных дробей просто невозможно.

Чтобы произвести вычитание дробей с разными знаменателями, необходимо их привести к одинаковому наименьшему знаменателю.

О том, как это сделать, мы поговорим подробнее.

Свойство дроби

Для того чтобы несколько дробей привести к одинаковому знаменателю, нужно использовать в решении главное свойство дроби: после деления или умножения числителя и знаменателя на одинаковое число получится дробь, равная данной.

Так, например, дробь 2/3 может иметь такие знаменатели, как «6», «9», «12» и т. д., то есть она может иметь вид любого числа, которое кратно «3». После того как числитель и знаменатель мы умножим на «2», получится дробь 4/6. После того как числитель и знаменатель исходной дроби мы умножим на «3», получим 6/9, а если аналогичное действие произвести с цифрой «4», получим 8/12. Одним равенством это можно записать так:

2/3 = 4/6 = 6/9 = 8/12…

Как привести несколько дробей к одному и тому же знаменателю

Рассмотрим, как привести несколько дробей к одному и тому же знаменателю. Для примера возьмем дроби, приведенные на картинке ниже. Для начала необходимо определить, какое число может стать знаменателем для их всех. Для облегчения разложим имеющиеся знаменатели на множители.

Знаменатель дроби 1/2 и дроби 2/3 на множители разложить нельзя. Знаменатель 7/9 имеет два множителя 7/9 = 7/(3 х 3), знаменатель дроби 5/6 = 5/(2 х 3). Теперь необходимо определить, какие же множители будут наименьшими для всех этих четырех дробей. Так как в первой дроби в знаменателе имеется число «2», значит, оно должно присутствовать во всех знаменателях, в дроби 7/9 присутствуют две тройки, значит, они также обе должны присутствовать в знаменателе. Учитывая вышесказанное, определяем, что знаменатель состоит из трех множителей: 3, 2, 3 и равен 3 х 2 х 3 = 18.

Рассмотрим первую дробь — 1/2. В ее знаменателе имеется «2», но нет ни одной цифры «3», а должно быть две. Для этого мы знаменатель умножаем на две тройки, но, согласно свойству дроби, мы и числитель должны умножить на две тройки:
1/2 = (1 х 3 х 3)/(2 х 3 х 3) = 9/18.

Аналогично производим действия с оставшимися дробями.

2/3 — в знаменателе не хватает одной тройки и одной двойки:
2/3 = (2 х 3 х 2)/(3 х 3 х 2) = 12/18.
7/9 или 7/(3 х 3) — в знаменателе не хватает двойки:
7/9 = (7 х 2)/(9 х 2) = 14/18.
5/6 или 5/(2 х 3) — в знаменателе не хватает тройки:
5/6 = (5 х 3)/(6 х 3) = 15/18.

Все вместе это выглядит так:

Как вычесть и сложить дроби, имеющие различные знаменатели

Как уже говорилось выше, для того чтобы произвести сложение или вычитание дробей, имеющих различные знаменатели, их необходимо привести к одному знаменателю, а дальше воспользоваться правилами вычитания дробей, имеющих одинаковый знаменатель, о котором уже рассказывалось.

Рассмотрим это на примере: 4/18 — 3/15.

Находим кратное чисел 18 и 15:

Число 18 состоит из 3 х 2 х 3.
Число 15 состоит из 5 х 3.
Общее кратное будет состоять из следующих множителей 5 х 3 х 3 х 2 = 90.

После того как знаменатель будет найден, необходимо вычислить множитель, который будет отличным для каждой дроби, то есть то число, на которое необходимо будет умножить не только знаменатель, но и числитель. Для этого число, которое мы нашли (общее кратное), делим на знаменатель той дроби, у которой нужно определить дополнительные множители.

90 поделить на 15. Полученное число «6» будет множителем для 3/15.
90 поделить на 18. Полученное число «5» будет множителем для 4/18.

Следующий этап нашего решения — приведение каждой дроби к знаменателю «90».

Как это делается, мы уже говорили. Рассмотрим, как это записывается в примере:

(4 х 5)/(18 х 5) — (3 х 6)/(15 х 6) = 20/90 — 18/90 = 2/90 = 1/45.

Если дроби с маленькими числами, то можно общий знаменатель определить, как в примере, приведенном на картинке ниже.

Аналогично производится и имеющих различные знаменатели.

Вычитание и имеющих целые части

Вычитание дробей и их сложение мы уже детально разобрали. Но как произвести вычитание, если у дроби есть целая часть? Опять же, воспользуемся несколькими правилами:

Все дроби, имеющие целую часть, перевести в неправильные. Говоря простыми словами, убрать целую часть. Для этого число целой части умножаем на знаменатель дроби, полученное произведение добавляем к числителю. То число, которое получится после этих действий, — числитель неправильной дроби. Знаменатель же остается неизменным.
Если дроби имеют различные знаменатели, следует привести их к одинаковому.
Произвести сложение или вычитание с одинаковыми знаменателями.
При получении неправильной дроби выделить целую часть.

Есть и иной способ, при помощи которого можно осуществить сложение и вычитание дробей с целыми частями. Для этого производятся отдельно действия с целыми частями, и отдельно действия с дробями, а результаты записываются вместе.

Приведенный пример состоит из дробей, которые имеют одинаковый знаменатель. В том случае, когда знаменатели различны, их необходимо привести к одинаковому, а далее выполнить действия, как показано на примере.

Вычитание дробей из целого числа

Еще одной из разновидностей действий с дробями является тот случай, когда дробь необходимо отнять от На первый взгляд подобный пример кажется трудно решаемым. Однако здесь все довольно просто. Для его решения необходимо перевести целое число в дробь, причем с таким знаменателем, который имеется в вычитаемой дроби. Далее производим вычитание, аналогичное вычитанию с одинаковыми знаменателями. На примере это выглядит так:

7 — 4/9 = (7 х 9)/9 — 4/9 = 53/9 — 4/9 = 49/9.

Приведенное в этой статье вычитание дробей (6 класс) является основой для решения более сложных примеров, которые рассматриваются в последующих классах. Знания этой темы используются впоследствии для решения функций, производных и так далее. Поэтому очень важно разобраться и понять действия с дробями, рассматриваемые выше.

правила, примеры, решения, решение дробей

Следующее действие, которое можно выполнять с обыкновенными дробями, — вычитание. В рамках этого материала мы рассмотрим, как правильно вычислить разность дробей с одинаковыми и разными знаменателями, как вычесть дробь из натурального числа и наоборот. Все примеры будут проиллюстрированы задачами. Заранее уточним, что мы будем разбирать лишь случаи, когда разность дробей дает в итоге положительное число.

Как найти разность дробей с одинаковыми знаменателями

Начнем сразу с наглядного примера: допустим, у нас есть яблоко, которое разделили на восемь частей. Оставим пять частей на тарелке и заберем две из них. Это действие можно записать так:

58-28

В итоге у нас осталось 3 восьмых доли, поскольку 5−2=3. Получается, что 58-28=38.

Благодаря этому простому примеру мы увидели, как именно работает правило вычитания для дробей, знаменатели которых одинаковы. Сформулируем его.

Определение 1

Чтобы найти разность дробей с одинаковыми знаменателями, нужно из числителя одной вычесть числитель другой, а знаменатель оставить прежним. Это правило можно записать в виде ab-cb=a-cb.

Такую формулу мы будем использовать и в дальнейшем.

Возьмем конкретные примеры.

Пример 1

Вычтите из дроби 2415 обыкновенную дробь 1715.

Решение

Мы видим, что эти дроби имеют одинаковые знаменатели. Поэтому все, что нам нужно сделать, – это вычесть 17 из 24. Мы получаем 7 и дописываем к ней знаменатель, получаем 715.

Наши подсчеты можно записать так: 2415-1715=24-1715=715

Если необходимо, можно сократить сложную дробь или выделить целую часть из неправильной, чтобы считать было удобнее.

Пример 2

Найдите разность 3712-1512.

Решение

Воспользуемся описанной выше формулой и подсчитаем: 3712-1512=37-1512=2212

Легко заметить, что числитель и знаменатель можно разделить на 2 (об этом мы уже говорили ранее, когда разбирали признаки делимости). Сократив ответ, получим 116. Это неправильная дробь, из которой мы выделим целую часть: 116=156.

Как найти разность дробей с разными знаменателями

Такое математическое действие можно свести к тому, что мы уже описывали выше. Для этого просто приведем нужные дроби к одному знаменателю. Сформулируем определение:

Определение 2

Чтобы найти разность дробей, у которых разные знаменатели, необходимо привести их к одному знаменателю и найти разность числителей.

Рассмотрим на примере, как это делается.

Пример 3

Вычтите из 29 дробь 115.

Решение

Знаменатели разные, и нужно привести их к наименьшему общему значению. В данном случае НОК равно 45. Для первой дроби необходим дополнительный множитель 5, а для второй – 3.

Подсчитаем: 29=2·59·5=1045115=1·315·3=345

У нас получились две дроби с одинаковым знаменателем, и теперь мы легко можем найти их разность по описанному ранее алгоритму: 1045-345=10-345=745

Краткая запись решения выглядит так: 29-115=1045-345=10-345=745.

Не стоит пренебрегать сокращением результата или выделением из него целой части, если это необходимо. В данном примере нам этого не нужно делать.

Пример 4

Найдите разность 199 — 736.

Решение

Приведем указанные в условии дроби к наименьшему общему знаменателю 36 и получим соответственно 769 и 736.

Считаем ответ: 7636-736=76-736=6936

Результат можно сократить на 3 и получить 2312. Числитель больше знаменателя, а значит, мы можем выделить целую часть. Итоговый ответ — 11112.

Краткая запись всего решения — 199-736=11112.

Как вычесть из обыкновенной дроби натуральное число

Такое действие также легко свести к простому вычитанию обыкновенных дробей. Это можно сделать, представив натуральное число в виде дроби. Покажем на примере.

Пример 5

Найдите разность 8321 – 3.

Решение

3 – то же самое, что и 31. Тогда можно подсчитать так: 8321-3=2021.

Если в условии необходимо вычесть целое число из неправильной дроби, удобнее сначала выделить из нее целое, записав ее в виде смешанного числа. Тогда предыдущий пример можно решить иначе.

Из дроби 8321 при выделении целой части получится 8321=32021.

Теперь просто вычтем 3 из него: 32021-3=2021.

Как вычесть обыкновенную дробь из натурального числа

Это действие делается аналогично предыдущему: мы переписываем натуральное число в виде дроби, приводим обе к единому знаменателю и находим разность. Проиллюстрируем это примером.

Пример 6

Найдите разность: 7-53.

Решение

Сделаем 7 дробью 71. Делаем вычитание и преобразуем конечный результат, выделяя из него целую часть: 7-53=513.

Есть и другой способ произвести расчеты. Он обладает некоторыми преимуществами, которыми можно воспользоваться в тех случаях, если числители и знаменатели дробей в задаче – большие числа.

Определение 3

Если та дробь, которую нужно вычесть, является правильной, то натуральное число, из которого мы вычитаем, нужно представить в виде суммы двух чисел, одно из которых равно 1. После этого нужно вычесть нужную дробь из единицы и получить ответ.

Пример 7

Вычислите разность 1 065 -1362.

Решение

Дробь, которую нужно вычесть – правильная, ведь ее числитель меньше знаменателя. Поэтому нам нужно отнять единицу от 1065 и вычесть из нее нужную дробь: 1065-1362=(1064+1)-1362

Теперь нам нужно найти ответ. Используя свойства вычитания, полученное выражение можно записать как 1064+1-1362. Подсчитаем разность в скобках. Для этого единицу представим как дробь 11.

Получается, что 1-1362=11-1362=6262-1362=4962.

Теперь вспомним про 1064 и сформулируем ответ: 10644962.

Используем старый способ, чтобы доказать, что он менее удобен. Вот такие вычисления вышли бы у нас:

1065-1362=10651-1362=1065·621·62-1362=6603062-1362==66030-1362=6601762=106446

Ответ тот же, но подсчеты, очевидно, более громоздкие.

Мы рассмотрели случай, когда нужно вычесть правильную дробь. Если она неправильная, мы заменяем ее смешанным числом и производим вычитание по знакомым правилам.

Пример 8

Вычислите разность 644 — 735.

Решение

Вторая дробь – неправильная, и от нее надо отделить целую часть.

735=1435

Теперь вычисляем аналогично предыдущему примеру: 630-35=(629+1)-35=629+1-35=629+25=62925

Свойства вычитания при работе с дробями

Те свойства, которыми обладает вычитание натуральных чисел, распространяются и на случаи вычитания обыкновенных дробей. Рассмотрим, как использовать их при решении примеров.

Пример 9

Найдите разность 244-32-56.

Решение

Схожие примеры мы уже решали, когда разбирали вычитание суммы из числа, поэтому действуем по уже известному алгоритму. Сначала подсчитаем разность 254-32, а потом отнимем от нее последнюю дробь:

254-32=244-64=194194-56=5712-1012=4712

Преобразуем ответ, выделив из него целую часть. Итог — 31112.

Краткая запись всего решения:

254-32-56=254-32-56=254-64-56==194-56=5712-1012=4712=31112

Если в выражении присутствуют и дроби, и натуральные числа, то рекомендуется при подсчетах сгруппировать их по типам.

Пример 10

Н айдите разность 98+1720-5+35.

Решение

Зная основные свойства вычитания и сложения, мы можем сгруппировать числа следующим образом: 98+1720-5+35=98+1720-5-35=98-5+1720-35

Завершим расчеты: 98-5+1720-35=93+1720-1220=93+520=93+14=9314

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Как складывать неправильные дроби с разными знаменателями. Как научиться вычитать дроби с разными знаменателями

Вычитание дробей с одинаковыми знаменателями, примеры:

Вычитание правильной дроби из единицы.

Пример вычитания правильной дроби из единицы:

Вычитание правильной дроби из целого числа.

Правила вычитания дробей — правильной из целого числа (натурального числа) :

Переводим заданные дроби, которые содержат целую часть, в неправильные. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
Далее вычисляем разность дробей, которые мы получили. В результате мы почти найдем ответ;
Выполняем обратное преобразование, то есть избавляемся от неправильной дроби — выделяем в дроби целую часть.

Пример вычитания дробей:

Вычитание дробей с разными знаменателями.

Или, если сказать другими словами, вычитание разных дробей .

Порядок действий при вычитании дробей с разными знаменателями.

найти НОК для всех знаменателей;
поставить для всех дробей дополнительные множители;
умножить все числители на дополнительный множитель;
полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.

Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.

Вычитание дробей, примеры:

Вычитание смешанных дробей.

Первый вариант вычитания смешанных дробей.

Например:

Второй вариант вычитания смешанных дробей.

Например:

Третий вариант вычитания смешанных дробей.

Дробная часть уменьшаемого меньше дробной части вычитаемого.

Пример:

Как вычесть дроби, знаменатели которых одинаковые

Для того чтобы из одной дроби вычесть вторую, необходимо из числителя уменьшаемой дроби вычесть числитель вычитаемой дроби. Это число записываем в числитель разницы, а знаменатель оставляем тот же: k/m — b/m = (k-b)/m.

Примеры вычитания дробей, знаменатели которых одинаковы

7/19 — 3/19 = (7 — 3)/19 = 4/19.

На картинке ниже приведено еще несколько подобных примеров.

Рассмотрим более сложный пример, где произведено вычитание дробей с одинаковыми знаменателями:

29/47 — 3/47 — 8/47 — 2/47 — 7/47 = (29 — 3 — 8 — 2 — 7)/47 = 9/47.

Сложение дробей, имеющих одинаковый знаменатель

Сложение и вычитание обыкновенных дробей осуществляется по одному и тому же принципу.

Для того чтобы сложить дроби, знаменатели которых одинаковы, необходимо числители сложить. Полученное число — числитель суммы, а знаменатель останется тот же: k/m + b/m = (k + b)/m.

Рассмотрим, как это выглядит на примере:

1/4 + 2/4 = 3/4.

Дроби с различными знаменателями и их вычитание

О том, как это сделать, мы поговорим подробнее.

Свойство дроби

2/3 = 4/6 = 6/9 = 8/12…

Как привести несколько дробей к одному и тому же знаменателю

Аналогично производим действия с оставшимися дробями.

2/3 — в знаменателе не хватает одной тройки и одной двойки:
2/3 = (2 х 3 х 2)/(3 х 3 х 2) = 12/18.
7/9 или 7/(3 х 3) — в знаменателе не хватает двойки:
7/9 = (7 х 2)/(9 х 2) = 14/18.
5/6 или 5/(2 х 3) — в знаменателе не хватает тройки:
5/6 = (5 х 3)/(6 х 3) = 15/18.

Все вместе это выглядит так:

Как вычесть и сложить дроби, имеющие различные знаменатели

Рассмотрим это на примере: 4/18 — 3/15.

Находим кратное чисел 18 и 15:

Число 18 состоит из 3 х 2 х 3.
Число 15 состоит из 5 х 3.
Общее кратное будет состоять из следующих множителей 5 х 3 х 3 х 2 = 90.

90 поделить на 15. Полученное число «6» будет множителем для 3/15.
90 поделить на 18. Полученное число «5» будет множителем для 4/18.

Следующий этап нашего решения — приведение каждой дроби к знаменателю «90».

Как это делается, мы уже говорили. Рассмотрим, как это записывается в примере:

(4 х 5)/(18 х 5) — (3 х 6)/(15 х 6) = 20/90 — 18/90 = 2/90 = 1/45.

Аналогично производится и имеющих различные знаменатели.

Вычитание и имеющих целые части

Все дроби, имеющие целую часть, перевести в неправильные. Говоря простыми словами, убрать целую часть. Для этого число целой части умножаем на знаменатель дроби, полученное произведение добавляем к числителю. То число, которое получится после этих действий, — числитель неправильной дроби. Знаменатель же остается неизменным.
Если дроби имеют различные знаменатели, следует привести их к одинаковому.
Произвести сложение или вычитание с одинаковыми знаменателями.
При получении неправильной дроби выделить целую часть.

Вычитание дробей из целого числа

7 — 4/9 = (7 х 9)/9 — 4/9 = 53/9 — 4/9 = 49/9.

Разные действия с дробями можно выполнять, например, сложение дробей. Сложение дробей можно разделить на несколько видов. В каждом виде сложения дробей свои правила и алгоритм действий. Рассмотрим подробно каждый вид сложения.

Сложение дробей с одинаковыми знаменателями.

На примере посмотрим, как складывать дроби с общим знаменателем.

Туристы пошли в поход из точки A в точку E. В первый день они прошли от точки A до B или $\frac{1}{5}$ от всего пути. Во второй день они прошли от точки B до D или $\frac{2}{5}$ от всего пути. Какое расстояние они прошли от начала пути до точки D?

Чтобы найти расстояние от точки A до точки D нужно сложить дроби $\frac{1}{5} + \frac{2}{5}$.

Сложение дробей с одинаковыми знаменателями заключается в том, что нужно числители этих дробей сложить, а знаменатель останется прежний.

$\frac{1}{5} + \frac{2}{5} = \frac{1 + 2}{5} = \frac{3}{5}$

В буквенном виде сумма дробей с одинаковыми знаменателями будет выглядеть так:

$\bf \frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}$

Ответ: туристы прошли $\frac{3}{5}$ всего пути.

Сложение дробей с разными знаменателями.

Рассмотрим пример:

Нужно сложить две дроби $\frac{3}{4}$ и $\frac{2}{7}$.

Чтобы сложить дроби с разными знаменателями нужно сначала найти , а потом воспользоваться правилом сложения дробей с одинаковыми знаменателями.

Для знаменателей 4 и 7 общим знаменателем будет число 28. Первую дробь $\frac{3}{4}$ нужно умножить на 7. Вторую дробь $\frac{2}{7}$ нужно умножить на 4.

$\frac{3}{4} + \frac{2}{7} = \frac{3 \times \color{red} {7} + 2 \times \color{red} {4}}{4 \times \color{red} {7}} = \frac{21 + 8}{28} = \frac{29}{28} = 1\frac{1}{28}$

В буквенном виде получаем такую формулу:

$\bf \frac{a}{b} + \frac{c}{d} = \frac{a \times d + c \times b}{b \times d}$

Сложение смешанных чисел или смешанных дробей.

Сложение происходит по закону сложения.

У смешанных дробей складываем целые части с целыми и дробные части с дробными.

Если дробные части смешанных чисел имеют одинаковые знаменатели, то числители складываем, а знаменатель остается тот же.

Сложим смешанные числа $3\frac{6}{11}$ и $1\frac{3}{11}$.

$3\frac{6}{11} + 1\frac{3}{11} = (\color{red} {3} + \color{blue} {\frac{6}{11}}) + (\color{red} {1} + \color{blue} {\frac{3}{11}}) = (\color{red} {3} + \color{red} {1}) + (\color{blue} {\frac{6}{11}} + \color{blue} {\frac{3}{11}}) = \color{red}{4} + (\color{blue} {\frac{6 + 3}{11}}) = \color{red}{4} + \color{blue} {\frac{9}{11}} = \color{red}{4} \color{blue} {\frac{9}{11}}$

Если дробные части смешанных чисел имею разные знаменатели, то находим общий знаменатель.

Выполним сложение смешанных чисел $7\frac{1}{8}$ и $2\frac{1}{6}$.

Знаменатель разный, поэтому нужно найти общий знаменатель, он равен 24. Умножим первую дробь $7\frac{1}{8}$ на дополнительный множитель 3, а вторую дробь $2\frac{1}{6}$ на 4.

$7\frac{1}{8} + 2\frac{1}{6} = 7\frac{1 \times \color{red} {3}}{8 \times \color{red} {3}} = 2\frac{1 \times \color{red} {4}}{6 \times \color{red} {4}} =7\frac{3}{24} + 2\frac{4}{24} = 9\frac{7}{24}$

Вопросы по теме:
Как складывать дроби?
Ответ: сначала надо определиться к какому типу относиться выражение: у дробей одинаковые знаменатели, разные знаменатели или смешанные дроби. В зависимости от типа выражения переходим к алгоритму решения.

Как решать дроби с разными знаменателями?
Ответ: необходимо найти общий знаменатель, а дальше по правилу сложения дробей с одинаковыми знаменателями.

Как решать смешанные дроби?
Ответ: складываем целые части с целыми и дробные части с дробными.

Пример №1:
Может ли сумма двух в результате получить правильную дробь? Неправильную дробь? Приведите примеры.

$\frac{2}{7} + \frac{3}{7} = \frac{2 + 3}{7} = \frac{5}{7}$

Дробь $\frac{5}{7}$ это правильная дробь, она является результатом суммы двух правильных дробей $\frac{2}{7}$ и $\frac{3}{7}$.

$\frac{2}{5} + \frac{8}{9} = \frac{2 \times 9 + 8 \times 5}{5 \times 9} =\frac{18 + 40}{45} = \frac{58}{45}$

Дробь $\frac{58}{45}$ является неправильной дроби, она получилась в результате суммы правильных дробей $\frac{2}{5}$ и $\frac{8}{9}$.

Ответ: на оба вопроса ответ да.

Пример №2:
Сложите дроби: а) $\frac{3}{11} + \frac{5}{11}$ б) $\frac{1}{3} + \frac{2}{9}$.

а) $\frac{3}{11} + \frac{5}{11} = \frac{3 + 5}{11} = \frac{8}{11}$

б) $\frac{1}{3} + \frac{2}{9} = \frac{1 \times \color{red} {3}}{3 \times \color{red} {3}} + \frac{2}{9} = \frac{3}{9} + \frac{2}{9} = \frac{5}{9}$

Пример №3:
Запишите смешанную дробь в виде суммы натурального числа и правильной дроби: а) $1\frac{9}{47}$ б) $5\frac{1}{3}$

а) $1\frac{9}{47} = 1 + \frac{9}{47}$

б) $5\frac{1}{3} = 5 + \frac{1}{3}$

Пример №4:
Вычислите сумму: а) $8\frac{5}{7} + 2\frac{1}{7}$ б) $2\frac{9}{13} + \frac{2}{13}$ в) $7\frac{2}{5} + 3\frac{4}{15}$

а) $8\frac{5}{7} + 2\frac{1}{7} = (8 + 2) + (\frac{5}{7} + \frac{1}{7}) = 10 + \frac{6}{7} = 10\frac{6}{7}$

б) $2\frac{9}{13} + \frac{2}{13} = 2 + (\frac{9}{13} + \frac{2}{13}) = 2\frac{11}{13} $

в) $7\frac{2}{5} + 3\frac{4}{15} = 7\frac{2 \times 3}{5 \times 3} + 3\frac{4}{15} = 7\frac{6}{15} + 3\frac{4}{15} = (7 + 3)+(\frac{6}{15} + \frac{4}{15}) = 10 + \frac{10}{15} = 10\frac{10}{15} = 10\frac{2}{3}$

Задача №1:
За обедам съели $\frac{8}{11}$ от торта, а вечером за ужином съели $\frac{3}{11}$. Как вы думаете торт полностью съели или нет?

Решение:
Знаменатель дроби равен 11, он указывает на сколько частей разделили торт. В обед съели 8 кусочков торта из 11. За ужином съели 3 кусочка торта из 11. Сложим 8 + 3 = 11, съели кусочков торта из 11, то есть весь торт.

$\frac{8}{11} + \frac{3}{11} = \frac{11}{11} = 1$

Ответ: весь торт съели.

Рассмотрим дробь $\frac63$. Ее величина равна 2, так как $\frac63 =6:3 = 2$. А что произойдет, если числитель и знаменатель умножить на 2? $\frac63 \times 2=\frac{12}{6}$. Очевидно, величина дроби не изменилась, так $\frac{12}{6}$ как у также равно 2. Можно умножить числитель и знаменатель на 3 и получить $\frac{18}{9}$, или на 27 и получить $\frac{162}{81}$ или на 101 и получить $\frac{606}{303}$. В каждом из этих случаев величина дроби, которую мы получаем, разделив числитель на знаменатель, равна 2. Это означает, что не изменилась.

Такая же закономерность наблюдается и в случае других дробей. Если числитель и знаменатель дроби $\frac{120}{60}$ (равной 2) разделить на 2 (результат $\frac{60}{30}$), или на 3 (результат $\frac{40}{20}$), или на 4 (результат $\frac{30}{15}$) и так далее, то в каждом случае величина дроби остается неизменной и равной 2.

Это правило распространяется также на дроби, которые не равны целому числу .

Если числитель и знаменатель дроби $\frac{1}{3}$ умножить на 2, мы получим $\frac{2}{6}$, то есть величина дроби не изменилась. И в самом деле, если вы разделите пирог на 3 части и возьмете одну из них или разделите его на 6 частей и возьмете 2 части, вы в обоих случаях получите одинаковое количество пирога. Следовательно, числа $\frac{1}{3}$ и $\frac{2}{6}$ идентичны. Сформулируем общее правило.

Числитель и знаменатель любой дроби можно умножить или разделить на одно и то же число, и при этом величина дроби не изменяется.

Это правило оказывается очень полезным. Например, оно позволяет в ряде случаев, но не всегда, избежать операций с большими числами.

Например, мы можем разделить числитель и знаменатель дроби $\frac{126}{189}$ на 63 и получить дробь $\frac{2}{3}$ с которой гораздо проще производить расчеты. Еще один пример. Числитель и знаменатель дроби $\frac{155}{31}$ можем разделить на 31 и получить дробь $\frac{5}{1}$ или 5, поскольку 5:1=5.

В этом примере мы впервые встретились с дробью, знаменатель которой равен 1 . Такие дроби играют важную роль при вычислениях. Следует помнить, что любое число можно разделить на 1 и при этом его величина не изменится. То есть $\frac{273}{1}$ равно 273; $\frac{509993}{1}$ равно 509993 и так далее. Следовательно, мы можем не разделять числа на , поскольку каждое целое число можно представить в виде дроби со знаменателем 1.

С такими дробями, знаменатель которых равен 1, можно производить те же арифметические действия, что и со всеми остальными дробями: $\frac{15}{1}+\frac{15}{1}=\frac{30}{1}$, $\frac{4}{1} \times \frac{3}{1}=\frac{12}{1}$.

Вы можете спросить, какой прок от того, что мы представим целое число в виде дроби, у которой под чертой будет стоять единица, ведь с целым числом работать удобнее. Но дело в том, что представление целого числа в виде дроби дает нам возможность эффективнее производить различные действия, когда мы имеем дело одновременно и с целыми, и с дробными числами. Например, чтобы научится складывать дроби с разными знаменателями . Предположим, нам надо сложить $\frac{1}{3}$ и $\frac{1}{5}$.

Мы знаем, что складывать можно только те дроби, знаменатели которых равны. Значит, нам нужно научиться приводить дроби к такому виду, когда их знаменатели равны. В этом случае нам опять пригодится то, что можно умножать числитель и знаменатель дроби на одно и то же число без изменения ее величины.

Сначала умножим числитель и знаменатель дроби $\frac{1}{3}$ на 5. Получим $\frac{5}{15}$, величина дроби не изменилась. Затем умножим числитель и знаменатель дроби $\frac{1}{5}$ на 3. Получим $\frac{3}{15}$, опять величина дроби не изменилась. Следовательно, $\frac{1}{3}+\frac{1}{5}=\frac{5}{15}+\frac{3}{15}=\frac{8}{15}$.

Теперь попробуем применить эту систему к сложению чисел, содержащих как целую, так и дробную части.

Нам надо сложить $3 + \frac{1}{3}+1\frac{1}{4}$. Сначала переведем все слагаемые в форму дробей и получим: $\frac31 + \frac{1}{3}+\frac{5}{4}$. Теперь нам надо привести все дроби к общему знаменателю, для этого мы числитель и знаменатель первой дроби умножаем на 12, второй — на 4, а третьей — на 3. В результате получаем $\frac{36}{12} + \frac{4}{12}+\frac{15}{12}$, что равно $\frac{55}{12}$. Если вы хотите избавиться от неправильной дроби , ее можно превратить в число, состоящее из целой и дробной частей: $\frac{55}{12} = \frac{48}{12}+\frac{7}{12}$ или $4\frac{7}{12}$.

Все правила, позволяющие проводить операции с дробями , которые мы с вами только что изучили, также справедливы и в случае отрицательных чисел. Так, -1: 3 можно записать как $\frac{-1}{3}$, а 1: (-3) как $\frac{1}{-3}$.

Поскольку как при делении отрицательного числа на положительное, так и при делении положительного числа на отрицательное в результате мы получаем отрицательные числа, в обоих случаях мы получим ответ в виде отрицательного числа. То есть

$(-1) : 3 = \frac{1}{3}$ или $1: (-3) = \frac{1}{-3}$. Знак минус при таком написании относится ко всей дроби целиком, а не отдельно к числителю или знаменателю.

С другой стороны, (-1) : (-3) можно записать как $\frac{-1}{-3}$, а поскольку при делении отрицательного числа на отрицательное число мы получаем положительное число, то $\frac{-1}{-3}$ можно записать как $+\frac{1}{3}$.

Сложение и вычитание отрицательных дробей проводят по той же схеме, что и сложение, и вычитание положительных дробей. Например, что такое $1- 1\frac13$? Представим оба числа в виде дробей и получим $\frac{1}{1}-\frac{4}{3}$. Приведем дроби к общему знаменателю и получим $\frac{1 \times 3}{1 \times 3}-\frac{4}{3}$, то есть $\frac{3}{3}-\frac{4}{3}$, или $-\frac{1}{3}$.

Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с разными знаменателями
Понятие о НОК
Приведение дробей к одному знаменателю
Как сложить целое число и дробь

1 Сложение и вычитание дробей с одинаковыми знаменателями

Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же, например:

Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же, например:

Чтобы сложить смешанные дроби, надо отдельно сложить их целые части, а затем сложить их дробные части, и записать результат смешанной дробью,

Если при сложении дробных частей получилась неправильная дробь, выделяем из нее целую часть и прибавляем ее к целой части, например:

2 Сложение и вычитание дробей с разными знаменателями

Для того, чтобы сложить или вычесть дроби с разными знаменателями, нужно сначала привести их к одному знаменателю, а дальше действовать, как указано в начале этой статьи. Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное). Для числителя каждой из дробей находятся дополнительные множители с помощью деления НОК на знаменатель этой дроби. Мы рассмотрим пример позже, после того, как разберемся, что же такое НОК.

3 Наименьшее общее кратное (НОК)

Наименьшее общее кратное двух чисел (НОК) — это наименьшее натуральное число, которое делится на оба эти числа без остатка. Иногда НОК можно подобрать устно, но чаще, особенно при работе с большими числами, приходится находить НОК письменно, с помощью следующего алгоритма:

Для того, чтобы найти НОК нескольких чисел, нужно:

Разложить эти числа на простые множители
Взять самое большое разложение, и записать эти числа в виде произведения
Выделить в других разложениях числа, которые не встречаются в самом большом разложении (или встречаются в нем меньшее число раз), и добавить их к произведению.
Перемножить все числа в произведении, это и будет НОК.

Например, найдем НОК чисел 28 и 21:

4Приведение дробей к одному знаменателю

Вернемся к сложению дробей с разными знаменателями.

Когда мы приводим дроби к одинаковому знаменателю, равному НОК обоих знаменателей, мы должны умножить числители этих дробей на дополнительные множители . Найти их можно, разделив НОК на знаменатель соответствующей дроби, например:

Таким образом, чтобы привести дроби к одному показателю, нужно сначала найти НОК (то есть наименьшее число, которое делится на оба знаменателя) знаменателей этих дробей, затем поставить дополнительные множители к числителям дробей. Найти их можно, разделив общий знаменатель (НОК) на знаменатель соответствующей дроби. Затем нужно умножить числитель каждой дроби на дополнительный множитель, а знаменателем поставить НОК.

5Как сложить целое число и дробь

Для того, чтобы сложить целое число и дробь, нужно просто добавить это число перед дробью, при этом получится смешанная дробь, например.

Как вычитать дроби с разными знаменателями

Вычитание дробей, особенно с разными знаменателями, может показаться сложным на первый взгляд. Однако, как только вы освоите некоторые основные правила, все будет довольно просто.

Во-первых, нам нужно понять состав дроби. Здесь есть две части – числитель и знаменатель, разделенные разделительной чертой.

В знаменателе находится нижняя цифра. Это показывает нам, на сколько равных частей было разделено одно целое. Числитель является верхней цифрой и показывает, сколько частей целого присутствует.

Чтобы успешно отделить одну дробь от другой, нужно добиться того, чтобы целое, с которым мы имеем дело, в обоих случаях делилось на одинаковое количество равных частей, т. е. чтобы знаменатели были одинаковыми.

Есть несколько быстрых приемов, которые можно использовать при вычитании дробей с разными знаменателями. Ниже мы объясняем традиционный метод, поскольку именно его вам нужно будет применить, когда вас попросят показать свои работы на любом официальном экзамене.

Одни и те же правила применяются при работе с правильными дробями (где числитель меньше знаменателя) или неправильными дробями (где числитель больше знаменателя).

4 простых шага о том, как вычитать дроби с разными знаменателями:

Шаг 1. Найдите наименьший общий знаменатель

Наименьший общий знаменатель (НОД) — это наименьшее общее кратное двух знаменателей, с которыми вы работаете.

Например, если нас попросили вычесть 2/3 из 2/6, мы знаем, что 6 кратно 3, поэтому 6 — это наш LCD.

Шаг 2: Найдите эквивалентную дробь

После того, как вы нашли ЖК-дисплей, вам нужно сохранить значение ваших дробей прежним. Таким образом, при изменении знаменателя вам нужно применить то же изменение к числителю.

Используя приведенный выше пример, чтобы заменить знаменатель на 6, мы умножаем 3 на 2. Чтобы сохранить дробь равного значения, мы также должны умножить 2 (числитель) на 2. Это дает нам эквивалент дроби 4 /6.

Повторите этот процесс и для второй фракции. В нашем примере знаменатель уже равен 6, поэтому никаких изменений не требуется.

Теперь у нас есть пересмотренное уравнение 4/6 — 2/6.

Шаг 3: Вычтите новые числители

Следующий этап прост: просто вычтите числители, которые есть в вашем новом уравнении. В этом случае 4 — 2 = 2,

Возьмите полученную цифру и поместите ее над общим знаменателем. Это дает нам 2/6.

Шаг 4: При необходимости упростите ответ

Последний шаг – по возможности упростить дробь. Для этого вам нужно найти наибольший общий множитель, общий для обеих частей дроби, и разделить их на него.

В случае 2/6 наибольший общий множитель равен 2. Поскольку 2 ÷ 2 = 1, а 6 ÷ 2 = 3, наша упрощенная дробь равна 1/3.

2/3 — 2/6 = 1/3

Примеры вопросов

Ниже вы найдете два примера вопросов, в которых вам предлагается вычесть дроби с разными знаменателями. Первое выражается в виде стандартного уравнения, второе — в виде более сложной словесной задачи.

Пример вопроса 1

Сколько будет 5/6 минус 13/25?

Начните с поиска ЖК-дисплея. В этом примере это не так просто, поэтому вам может быть полезно записать кратные наибольшему текущему знаменателю, чтобы помочь вам: 25, 50, 75, 100, 125, 150…

Теперь мы можем видеть, что первое кратное 25 делится на 6 равно 150, так что это наш ЖК-дисплей.

Затем нам нужно найти наши эквивалентные дроби:

6 x 25 = 150, поэтому нам нужно использовать то же значение, чтобы умножить числитель, что даст 5 x 25 = 125. Таким образом, наша первая эквивалентная дробь будет 125/150.

Теперь перейдем ко второй:

25 х 6 = 150 и 13 х 6 = 78. Наша вторая эквивалентная дробь 78/150.

Вычтите числители и поместите результат на ЖК-дисплей: 125/150 — 78/150 = 47/150.

Эта фракция уже имеет простейшую форму.

Ответ: 5/6 минус 13/25 = 47/150

Пример вопроса 2

Эмма готовится к марафону и поставила перед собой цель пробежать к концу недели. В понедельник она пробегает 7/15 дистанции. В среду она пробегает 4/5 дистанции.

Насколько дальше пробежала Эмма в среду по сравнению с понедельником?

Чтобы решить эту задачу, нам нужно вычесть расстояние, которое Эмма пробежала в понедельник, из того, сколько она пробежала в среду, поэтому наше уравнение будет выглядеть так: 4/5 — 7/15.

Затем мы находим наш ЖК-дисплей, который, как мы видим, равен 15. Мы находим эквивалент нашей первой дроби, умножая обе части на одно и то же значение: 5 x 3 = 15 и 4 x 3 = 12.

Наша эквивалентная дробь поэтому 12/15.

Так как во второй дроби наш знаменатель уже равен 15, здесь никаких изменений не требуется.

Теперь мы можем вычесть наши числители (12 — 7 = 5) и поставить наш ответ над знаменателем: 5/15.

Наконец, мы идентифицируем наибольший общий делитель 5 и 15 как 5 и делим обе части дроби для упрощения: 5 ÷ 5 = 1 и 15 ÷ 5 = 3.

Ответ: 4/5 минус 7/15 = 1/3

Вычитание дробей с разными знаменателями

Вычитание дробей с разными знаменателями — это метод вычитания дробей с разными знаменателями. Мы можем вычитать дроби с разными знаменателями, превращая дроби в одинаковые дроби. Чтобы преобразовать разные дроби в одинаковые дроби, мы берем НОК знаменателей и находим эквивалентные дроби с одинаковыми знаменателями. Вычитание дробей с разными знаменателями — сложный процесс, поэтому для облегчения вычислений делаем знаменатели одинаковыми.

В этой статье мы обсудим концепцию вычитания дробей с разными знаменателями. Мы поймем его значение и шаги по вычитанию дробей с разными знаменателями. Мы также рассмотрим концепцию вычитания смешанных чисел с разными знаменателями и решим несколько примеров для лучшего понимания концепции.

1.	Что такое вычитание дробей с разными знаменателями?
2.	шагов для вычитания дробей с разными знаменателями
3.	Примеры вычитания дробей с разными знаменателями
4.	Вычитание смешанных чисел с разными знаменателями
5.	Часто задаваемые вопросы о вычитании дробей с разными знаменателями

Что такое вычитание дробей с разными знаменателями?

Прежде чем научиться вычитать дроби с разными знаменателями, вспомним значение одинаковых и разных дробей. У одинаковых дробей один и тот же знаменатель, а у разных дробей знаменатели разные. Например, дроби 4/9 и 2/5 отличаются от дробей тем, что имеют разные знаменатели. С другой стороны, дроби 2/5 и 4/5 похожи на дроби, поскольку имеют одинаковые знаменатели. Для вычитания дробей с разными знаменателями мы преобразуем неодинаковые дроби в одинаковые дроби. Чтобы преобразовать их в одинаковые дроби, мы найдем НОК различных знаменателей и умножим дроби на подходящее число, чтобы найти их эквивалентные дроби. Давайте разберемся, как вычитать дроби с разными знаменателями.

шагов для вычитания дробей с разными знаменателями

Чтобы вычесть дроби с разными знаменателями, мы выполняем определенные шаги, чтобы найти разницу. Ниже приведены шаги для вычитания дробей с разными знаменателями:

Шаг 1: Найдите НОК различных знаменателей дробей.
Шаг 2: Умножьте и разделите дроби на подходящее число, чтобы получить знаменатель в виде НОК, полученного на шаге 1.
Шаг 3: Теперь мы получили одинаковые дроби, эквивалентные исходным дробям.
Шаг 4: Вычтите числители полученных одинаковых дробей.
Шаг 5: Упростите дробь, полученную после вычитания, до наименьшей формы, если это возможно.

Давайте теперь решим несколько примеров, используя описанные выше шаги, чтобы понять процесс вычитания дробей с разными знаменателями.

Примеры вычитания дробей с разными знаменателями

Теперь, когда мы поняли шаги по вычитанию дробей с разными знаменателями, давайте решим пример, чтобы лучше понять концепцию.

Пример: Вычтите дроби 2/3 и 4/5.

Решение: Давайте решим задачу, выполнив шаги вычитания дробей с разными знаменателями, описанные в предыдущем разделе:

Шаг 1: Найдите НОК 3 и 5

НОК (3, 5) = 15

Шаг 2: Умножьте и разделите дроби 2/3 и 4/5 на подходящее число, чтобы изменить их знаменатель на 15.

2/3 = (2 × 5) / (3 × 5) = 10/15

4/5 = (4 × 3) / (5 × 3) = 12/15

Шаг 3: 10/15 и 12/15 — подобные дроби, эквивалентные исходным дробям.

Шаг 4: Вычтите одинаковые дроби.

10/15 — 12/15 = (10-12)/15

= -2/15

Шаг 5: -2/15 больше нельзя уменьшить.

Ответ: 2/3 — 4/5 = -2/15

Вычитание смешанных чисел с разными знаменателями

Итак, мы поняли принцип вычитания дробей с разными знаменателями. Давайте теперь научимся вычитать смешанные дроби с разными знаменателями. Чтобы найти разность смешанных чисел с разными знаменателями, мы сначала упростим смешанные дроби до неправильных, а затем проделаем те же шаги, которые мы обсуждали ранее. Рассмотрим пример и вычтем смешанные числа с разными знаменателями.

Пример: Вычтите 3 2/3 из 4 1/2.

Решение: Сначала мы заменим смешанное число на неправильную дробь, а затем вычтем.

4 1/2 = 9/2 и 3 2/3 = 11/3

Теперь нам нужно вычесть 11/3 из 9/2. Поскольку знаменатели разные, мы найдем НОК 2 и 3.

НОК (2, 3) = 6

Умножьте и разделите дроби 11/3 и 9/2 на подходящее число, чтобы изменить их знаменатель на 6

11/3 = (11 × 2) / (3 × 2) = 22/6

9/2 = (9 × 3) / (2 × 3) = 27/6

Вычитая 22/6 из 27/6, получаем

27/6 — 22/6 = 5/6

⇒ 9/2 — 11/3 = 5/6

⇒ 4 1/2 — 3 2 /3 = 5/6

Так как 5/6 не может быть далее сокращено, разность смешанных чисел с разными знаменателями 3 2/3 и 4 1/2 равна 5/6.

Важные замечания по вычитанию дробей с разными знаменателями

Мы можем вычитать дроби с разными знаменателями, превращая дроби в одинаковые дроби.
Для вычитания смешанных чисел с разными знаменателями мы сначала упрощаем смешанные дроби до неправильных дробей.
Для вычитания дробей с разными знаменателями мы преобразуем разные дроби в одинаковые, находя НОК знаменателей.

☛ Связанные темы:

Сложение дробей с отличающимися знаменателями
Сложение и вычитание дробей
Вычитание смешанных дробей

Часто задаваемые вопросы о вычитании дробей с разными знаменателями

Что такое вычитание дробей с разными знаменателями?

Вычитание дробей с разными знаменателями — это метод вычитания дробей с разными знаменателями.

Как вычитать дроби с разными знаменателями?

Мы можем вычитать дроби с разными знаменателями, вычитая эквивалентные дроби данных дробей.

Каковы шаги для вычитания дробей с разными знаменателями?

Ниже приведены шаги для вычитания дробей с разными знаменателями:

Шаг 1: Найдите НОК различных знаменателей дробей.
Шаг 2: Умножьте и разделите дроби на подходящее число, чтобы получить знаменатель в виде НОК, полученного на шаге 1.
Шаг 3: Теперь мы получили одинаковые дроби, эквивалентные исходным дробям.
Шаг 4: Вычтите числители полученных одинаковых дробей.
Шаг 5: Упростите дробь, полученную после вычитания, до наименьшей формы, если это возможно.

Каково правило вычитания дробей с разными знаменателями?

Основное правило для вычитания дробей с разными знаменателями состоит в том, чтобы сделать знаменатели одинаковыми, найдя НОК разных знаменателей.

Приведите пример вычитания дробей с разными знаменателями.

Пример вычитания дробей с разными знаменателями:

Решение 3/4 — 1/5.

НОК (4, 5) = 20

3/4 — 1/5 = 15/20 — 4/20

= 11/20

Вычитание дробей

Сначала вы можете прочитать «Сложение дробей».

Есть 3 простых шага для вычитания дробей

Шаг 1. Убедитесь, что нижние числа (знаменатели) совпадают
Шаг 2. Вычтите верхние числа (числители). Положите ответ над тем же знаменателем.
Шаг 3. Упростите дробь (при необходимости).

Пример 1:

3 4 − 1 4

Шаг 1 . Нижние цифры уже одинаковые. Сразу переходите к шагу 2.

Шаг 2 . Вычтите верхние числа и положите ответ над тем же знаменателем:

3 4 − 1 4 знак равно 3 − 1 4 знак равно 2 4

Шаг 3 . Упростите дробь:

2 4 знак равно 1 2

(Если вы не уверены в последнем шаге, см. Эквивалентные дроби.)

Пример 2:

1 2 − 1 6

Шаг 1 . Нижние цифры разные. Видите, как кусочки разного размера? Нам нужно сделать их одинаковыми, прежде чем мы сможем продолжить, потому что мы не можем вычесть их следующим образом:

1 2	−	1 6	=	?

Чтобы нижние числа были одинаковыми, умножьте верхние и нижние части первой дроби ( ¹ / ₂ ) на 3 следующим образом:

1 × 3

1 2

3 6

× 3

А теперь наш вопрос выглядит так:

3 6	−	1 6

Нижние числа (знаменатели) совпадают, поэтому мы можем перейти к шагу 2.

Шаг 2 . Вычтите верхние числа и положите ответ над тем же знаменателем:

3 6 − 1 6 знак равно 3 − 1 6 знак равно 2 6

На картинке это выглядит так:

3 6	−	1 6	=	2 6

Шаг 3 . Упростите дробь:

2 6 знак равно 1 3

С ручкой и бумагой

А вот как это сделать ручкой и бумагой (нажмите кнопку воспроизведения):

Поиграй!

Попробуйте вычитать дроби.

Вычитание смешанных дробей

У меня есть специальная страница о сложении и вычитании смешанных дробей.

Уравнивание знаменателей

В предыдущем примере было легко сделать знаменатели одинаковыми, но это может быть сложнее … поэтому вам может понадобиться использовать либо

Метод общего знаменателя или
Метод наименьшего общего знаменателя

Они оба работают, используйте тот, который вам больше нравится!

Пример: кексы

Вы хотите продавать кексы на рынке:

Вам платят 2 5 от общего объема продаж
Но ты должен заплатить 1 4 от общего объема продаж для киоска

Сколько вы получаете?

Нам нужно вычесть 1 4 из 2 5

2 5 − 1 4 знак равно ? ?

Сначала сделайте нижние числа (знаменатели) одинаковыми.

Умножить верх и низ ² / ₅ на 4 :

2 × 4 5 × 4 − 1 4 знак равно ? ?

И умножить верх и низ ¹ / ₄ на 5 :

2 × 4 5 × 4 − 1 × 5 4 × 5 знак равно ? ?

Теперь делаем вычисления:

8 20 − 5 20 знак равно 8 − 5 20 знак равно 3 20

Ответ: у вас останется 3 20 от общего объема продаж.

рабочих листа

Сложение и вычитание дробей с разными знаменателями

Поиск
Нам нужно сделать несколько дополнительных шагов, чтобы сложить или вычесть дроби с разными знаменателями. Общая стратегия обсуждается ниже. В этом уроке мы рассмотрим несколько примеров, чтобы убедиться, что вы знакомы с этой процедурой.
Шаг 1: Даны две разные дроби, знаменатели которых НЕ совпадают.
Шаг 2: Сделайте знаменатели одинаковыми, найдя наименьшее общее кратное (НОК) их знаменателей. Этот шаг точно такой же, как нахождение наименьшего общего знаменателя (LCD).
Шаг 3: Преобразуйте каждую дробь в эквивалентную ей дробь со знаменателем, равным наименьшему общему кратному, найденному на шаге 2.
Шаг 4: Теперь добавьте или вычтите «новые» дроби из шага №3. Всегда сокращайте ответ до самых низких условий.
Примеры сложения и вычитания дробей с разными знаменателями
Пример 1: Сложение дробей с разными знаменателями.
Знаменатели двух дробей не равны . Нам нужно сделать их равными, найдя их наименьшее общее кратное, которое будет служить их наименьшим общим знаменателем (LCD).
Начните с перечисления кратных каждого знаменателя и определите наименьшее число, общее для них обоих.
У первой дроби уже есть знаменатель, равный НОК = 15, поэтому мы оставим его в покое.
Вторая дробь требует некоторой корректировки, чтобы сделать ее знаменатель равным 15. Сделайте это, умножив ее числитель и знаменатель на число 3.
Когда их знаменатели равны, сложите дроби, добавив их числители, а затем знаменатель.
Дробь {{11} \over {15}} является нашим окончательным ответом, потому что она уже находится в наименьшем члене.
Пример 2: Сложите дроби с разными знаменателями.
Мы пока не можем сложить две дроби, потому что у них разные знаменатели, а именно 5 и 9. Начните с перечисления их кратных и выберите наименьшее число, общее для обеих дробей. Это станет их общим знаменателем.
Теперь преобразуйте каждую дробь в эквивалентную дробь с НОК в качестве знаменателя, затем продолжите обычное сложение.
Найдите возможность сократить ответ до наименьшего члена. Числитель и знаменатель {{33} \over {45}} делятся на 3 .
Пример 3: Сложите дроби с разными знаменателями.
Иногда нет необходимости находить наименьший общий знаменатель методом списка. Мы можем немедленно найти его, если оба числа являются простыми.
Простое число — это целое число больше 1, которое делится на 1 и само на себя.
Обратите внимание, что знаменатели 3 и 5 — простые числа. LCD будет просто их произведением, то есть 3 x 5 = 15.
Пример 4: Сложите дроби с разными знаменателями.
Решение :
Найдите наименьшее общее кратное знаменателей.
Внесите необходимые коррективы в знаменатель и действуйте как обычно. Сократите свой окончательный ответ до наименьшего члена.
Пример 5: Сложите дроби с разными знаменателями.
Решение :
Поскольку знаменатели 11 и 13 являются простыми числами, их произведение будет наименьшим общим знаменателем.
Преобразуйте текущие знаменатели двух дробей в ЖКИ и продолжите обычное сложение.
Пример 6: Вычтите дроби с разными знаменателями.
Вычитание дробей с неравными знаменателями очень похоже на сложение.
Приравняйте их знаменатели, используя принцип наименьшего общего кратного. Затем вычтите их числители соответственно.
Перепишите каждую дробь в эквивалентную ей дробь со знаменателем, равным НОК = 30 , затем вычтите их числители. Обязательно сократите свой ответ до наименьшего члена.
Пример 7: Вычтите дроби с разными знаменателями.
Поскольку оба знаменателя являются простыми числами, их НОК является просто их произведением, таким образом, 7 x 5 = 35.
Пример 8: Вычтите дроби с разными знаменателями.
Решение :
Найдите наименьший общий знаменатель, определив НОК знаменателей.
Перепишите две дроби с общим знаменателем, равным НОК = 42 . Вычтите их числители и, если возможно, уменьшите ответ до наименьшего члена.
Пример 9: Вычтите дроби с разными знаменателями.
Решение :
Найдите наименьший общий знаменатель, определив наименьшее общее кратное знаменателей.
Вносим поправки в существующие дроби, чтобы их знаменатель был равен LCD = 40 . После этого вычтите их числители и скопируйте общий знаменатель.
Вас также может заинтересовать:
Сложение и вычитание дробей с одинаковым знаменателем
Умножение дробей
Деление дробей
Упрощение дробей
Равные дроби
Дробь 90, обратная a0
Сложение и вычитание дробей с одинаковыми или одинаковыми знаменателями
Поиск
При сложении или вычитании дробей считайте задачу простой, если знаменатели равны или одинаковы. Правила изложены ниже.
К ДОБАВЬТЕ дробей с одинаковыми или одинаковыми знаменателями, просто добавьте числители, а затем скопируйте общий знаменатель. Всегда сокращайте свой окончательный ответ до наименьшего термина.
Чтобы ВЫЧИТАТЬ дробей с одинаковыми или одинаковыми знаменателями, просто вычтите числители, а затем скопируйте общий знаменатель. Всегда сокращайте свой окончательный ответ до наименьшего термина.
Примеры сложения и вычитания дробей с одинаковыми знаменателями
Пример 1 : Сложите дроби.
Знаменатели обеих дробей равны 7. Поскольку у них один и тот же знаменатель, мы можем легко сложить эти дроби, добавив их числители и скопировав общий знаменатель, который равен 7.
Мы также можем показать процесс сложения с помощью кружков.
Первую дробь \Large{3 \over 7} можно представить в виде круга, разделенного поровну на семь частей с тремя частями, заштрихованными красным цветом.
Обратите внимание на : числитель говорит нам, сколько областей заштриховано, а знаменатель говорит нам, на сколько равных частей разделен круг.
Таким же образом вторая дробь \Large{2 \over 7} выглядит следующим образом:
Поскольку оба круга разделены на семь (7) равных частей, мы должны их перекрыть. Новый круг после добавления имеет пять (5) заштрихованных областей, которые представляют собой накопление красных и синих фигур.
Пример 2 : Добавьте дроби.
Объединим эти дроби по правилу сложения. Снова добавьте числители, затем скопируйте общий знаменатель.
После сложения дробей всегда находите возможность упростить результат, сократив его до наименьшего члена. Мы можем сделать это, разделив числитель и знаменатель на их наибольший общий делитель.
Общий делитель — это целое число, отличное от нуля, которое может без остатка делить два или более чисел.
Наибольший общий делитель (НОД) — это наибольшее число среди общих делителей двух или более чисел.
Очевидно, что числитель и знаменатель имеют общий делитель 2. Однако существует ли число больше 2, на которое они оба могут делиться без остатка?
Да, есть! Число 4 является наибольшим общим делителем 12 и 16. Поэтому мы будем использовать это число, чтобы сократить дробь до ее наименьшего члена.
Разделить верх и низ на GCD = 4 , чтобы получить окончательный ответ.
Пример 3: Сложите дроби.
Решение :
Поскольку знаменатели двух дробей равны, сложите числители и скопируйте общий знаменатель.
Верхнее и нижнее числа дроби делятся на 2 и 6. Однако мы всегда хотим, чтобы наибольший общий делитель приводил дробь к наименьшему члену. Таким образом, НОД = 6 .
Разделите верхнее и нижнее число на 6.
Пример 4: Сложите дроби.
Решение :
Все три дроби имеют одинаковый знаменатель. Добавим как обычно.
Получите сумму трех числителей, затем скопируйте общий знаменатель.
Наибольший общий делитель между числителем и знаменателем равен 5.
Разделить верхнее и нижнее число на 5.
Пример 5: Вычесть дроби.
На этот раз мы будем вычитать числители, а не складывать их.
Глядя на результат после вычитания, только общий делитель между числителем и знаменателем равен 1 . Таким образом, окончательный ответ остается как \Large{{3 \over 5}}. Подумайте об этом, деление верхней и нижней части на 1 не изменит значение дроби.
Предположим, у вас есть зеленый торт. И вы разрезаете его на 5 равных частей. Это можно представить в виде дроби \Large{{5 \over 5}}.
Если вы съели два куска торта ( \Large{- {2 \over 5}} ), у вас должно остаться три куска ( \Large{{3 \over 5}} ).
Табличка должна выглядеть примерно так.
Пример 6: Вычтите дроби.
Две дроби имеют одинаковый знаменатель, а это значит, что мы сможем легко вычесть их числители.
Ответ можно еще больше упростить, используя общий делитель 3. Итак, разделите числитель и знаменатель на 3, чтобы сократить дробь до наименьшего члена.
Пример 7: Вычтите дроби.
Решение :
Поскольку знаменатели двух дробей равны, вычтите их числителей, затем скопируйте общий знаменатель.
Числитель и знаменатель делятся на 3 и 9. Однако мы всегда хотим, чтобы наибольший общий делитель приводил дробь к наименьшему члену. Таким образом, НОД = 9 .
Разделите верхнее и нижнее число на 9.
Пример 8: Вычтите дроби.
Решение :
Вычтите числители, скопируйте общий знаменатель и сократите полученную дробь до наименьшего члена, используя НОД = 11 .
Вас также могут заинтересовать:
Сложение и вычитание дробей с разными знаменателями
Умножение дробей
Деление дробей
Упрощение дробей
Равные дроби
Обратная дробь
Используйте пропорциональные отношения для решения многошаговых задач на соотношение и проценты. | СС | 7 | 7.РП | 7.RP.A
Popular Tutorials
in Использование пропорциональных отношений для решения многошаговых задач на соотношение и проценты.
Как решить задачу со словами, используя процентную долю?
Задачи Word позволяют увидеть, как математика используется в реальном мире! В этом уроке показано, как взять задачу со словами и превратить ее в процентную пропорцию. Затем посмотрите, как найти ответ, используя свойство пропорций средних экстремумов. Взглянем!
Как составить пропорцию из задачи Word?
Иногда самая трудная часть задачи со словами — понять, как превратить слова в уравнение, которое можно решить. В этом учебном пособии вы увидите шаги, которые нужно предпринять, чтобы превратить задачу со словами, включающую чертеж, в пропорцию. Взглянем!
Как с помощью пропорции найти часть целого?
Взять процент от числа? Пытаетесь понять результат? Используйте процентную пропорцию, чтобы решить! Этот урок покажет вам, как!
Как использовать формулу простых процентов?
Если у вас уже есть счет в банке или вы планируете открыть его в будущем, обязательно прочитайте это руководство! Следите за тем, как в этом учебнике рассматривается задача со словами, включающая простые проценты.
Что такое формула простых процентов?
Проценты можно найти во многих местах: сберегательные счета, ипотечные кредиты, кредиты, инвестиции, кредитные карты и многое другое! Посмотрите этот урок и узнайте, как рассчитать простые проценты!
Как вычислить процент изменения?
Задачи Word позволяют увидеть, как математика используется в реальном мире! В этом руководстве вы узнаете, как рассчитать процент увеличения, используя формулу процента изменения.
Что такое процент изменения?
Многие вещи в этом мире меняют свою ценность, например, автомобили, видеоигры и компьютеры. Когда что-то либо увеличивается, либо уменьшается в цене, может быть полезно знать процент этого изменения стоимости. Чтобы вычислить этот процент, вам понадобится формула процента изменения. Узнайте это с помощью этого урока!
Как узнать, насколько что-то уценено?
Собираетесь за покупками? Что-то, что вы хотите в продаже? Пытаетесь выяснить цену продажи этого предмета? Следуйте за этой задачей слова, и вы увидите, как рассчитать эту цену!
Как настроить процентную долю от задачи Word?
Иногда самая трудная часть задачи со словами — понять, как превратить слова в уравнение, которое можно решить. Этот учебник позволит вам увидеть шаги, которые нужно предпринять, чтобы сделать именно это! Взглянем! Вы будете рады, что сделали!
Как рассчитать налог с продаж?
Ходить по магазинам может быть очень весело, но все может испортиться, когда вы доберетесь до кассы и поймете, что налог с продаж превышает ваш бюджет. Всегда оставайтесь в рамках бюджета, определяя общую стоимость ДО того, как вы нажмете на оплату. Посмотрите этот урок и узнайте, как рассчитать налог с продаж!
Как с помощью уравнения найти часть целого?
Взять процент от числа? Пытаетесь понять результат? Преобразуйте проценты в десятичные числа и умножьте на число! Этот урок покажет вам, как!
Как решить пропорцию, используя перекрестные произведения?
Хотите решить процентную пропорцию? Просто используйте свойство экстремумов средних пропорций, чтобы крест умножить! Решите переменную, и вы получите ответ! Узнайте, как с помощью этого руководства.
Как с помощью пропорции определить, сколько процентов составляет часть целого?
Часть – это несколько процентов от целого. Пытаетесь вычислить проценты? Используйте процентную пропорцию, чтобы решить! Этот урок покажет вам, как!
Что такое среднее-экстремальное свойство пропорций?
Свойство пропорций средние-крайние позволяет умножать крест, взяв произведение средних и приравняв их произведению крайних. Это свойство пригодится, когда вы пытаетесь решить пропорцию. Посмотрите этот урок, чтобы узнать больше!
Каковы средние и крайние значения пропорций?
Пропорция — это просто уравнение, в котором два отношения равны, и каждая часть пропорции имеет особое имя. Этот учебник научит вас этим именам, и это поможет вам понять перекрестное умножение, когда вы будете изучать его позже!
Как решить задачу с помощью пропорции?
В этом учебном пособии представлено отличное практическое применение математики. Вы увидите, как использовать масштаб чертежа дома, чтобы найти фактическую высоту дома. В этом уроке показано, как использовать пропорцию для решения!
Как рассчитать чаевые?
Если вам нужно оставить чаевые в ресторане, вы можете быстро прикинуть сумму в уме! В этом руководстве показано, как использовать оценку и вычисления в уме для расчета чаевых!
Как вы оцениваете продажную цену?
Продажи велики, но сколько вы на самом деле экономите? В этом руководстве показано, как оценить продажную цену товара.
Как вычислить процентное отношение части к части?
Словесные задачи и проценты могут быть забавной комбинацией! Этот урок покажет вам, как найти процент чего-то в корзине, используя коэффициенты!
Как вычислить процентное отношение части к целому?
Если вы хотите найти процент в словесной задаче, вы можете использовать отношение, чтобы помочь вам! Этот урок покажет вам, как сделать именно это!
Как решить пропорцию, найдя эквивалентное отношение?
Пытаетесь найти пропущенное значение, чтобы создать пропорцию с двумя отношениями? Представьте отношения в виде дроби и определите их отношение. Используйте это отношение, чтобы найти недостающее значение. Этот урок покажет вам, как!
Как решить пропорцию, используя свойство равенства умножения?
Пытаетесь найти пропущенное значение в отношении для создания пропорциональных соотношений? Вы можете использовать свойство умножения равенства! В этом руководстве показано, как использовать это свойство для поиска пропущенного значения в соотношении.