правила, примеры, решения, как вычесть из десятичной дроби обыкновенную дробь

Изучаем другие действия, которые можно совершать с десятичными дробями. В этом материале мы узнаем, как правильно подсчитать разность десятичных дробей. Отдельно разберем правила для конечных и бесконечных дробей (как периодических, так и непериодических), а также посмотрим, как считать разность дробей столбиком. Во второй части мы объясним, как вычесть десятичную дробь из натурального числа, обыкновенной дроби, смешанного числа.

Отметим заранее, что в этой статье рассмотрены только случаи, когда меньшая дробь вычитается из большей, т.е. результат этого действия положителен; другие случаи относятся к нахождению разности рациональных и действительных чисел и должны быть объяснены отдельно.

Основные правила вычитания десятичных дробей

Процесс вычисления как конечных, так и бесконечных периодических десятичных дробей можно свести к нахождению разности дробей обыкновенных. Раньше мы говорили о том, что десятичные дроби можно записывать в виде обыкновенных дробей. Исходя из этого правила, разберем несколько примеров нахождения разности.

Пример 1

Найдите разность 3,7-0,31.

Решение 

Переписываем десятичные дроби в виде обыкновенных: 3,7=3710 и 0,31=31100.

Что делать потом, мы уже изучали. Мы получили ответ, который переводим обратно в десятичную дробь: 339100=3,39.

Подсчеты, связанные с десятичными дробями, удобно производить столбиком. Как же пользоваться этим методом? Покажем, решив задачу.

Пример 2

Вычислите разность между периодической дробью 0, (4) и периодической десятичной дробью 0,41(6).

Решение

 Переведем записи периодических дробей в обыкновенные и подсчитаем.

0,4(4)=0,4+0,004+…=0,41-0,1=0,40,9=49.0,41(6)=0,41+(0,006+0,0006+…)=41100+0,0060,9==41100+6900=41100+1150=123300+2300=125300=512

Итого: 0,(4)-0,41(6)=49-512=1636-1536=136  

Если нужно, ответ мы можем представить в виде десятичной дроби:

Ответ: 0,(4) −0,41(6) =0,02(7).  

Разберем далее, как найти разность, если у нас в условиях стоят бесконечные непериодические дроби. Такой случай также можно свести к нахождению разности конечных десятичных дробей, для чего понадобится округлить бесконечные дроби до определенного разряда (обычно самого меньшего из возможных).

Пример 3

Найдите разность 2, 77369…-0,52.

Решение

Вторая дробь в условии – конечная, а первая – бесконечная непериодическая. Мы можем округлить ее до четырех знаков после запятой: 2,77369…≈2,7737. После этого можно выполнять вычитание: 2,77369…−0,52≈2,7737−0,52.

Ответ: 2,2537. 

Как считать разность десятичных дробей столбиком

Вычитание столбиком – быстрый и наглядный способ узнать разность конечных десятичных дробей. Процесс подсчета очень схож с аналогичным для натуральных чисел.

Определение 1

Чтобы подсчитать разность десятичных дробей столбиком, необходимо:

1. если в указанных десятичных дробях отличается количество знаков после запятой, уравняем его. Для этого допишем к нужной дроби нули;
2. запишем вычитаемую дробь под уменьшаемой, разместив значения разрядов строго друг под другом, а запятую под запятой;
3. выполним подсчет столбиком так же, как мы это делаем для натуральных чисел, запятую при этом игнорируем;
4. в ответе отделим нужное количество чисел запятой так, чтобы она располагалась на том же месте. 

Разберем конкретный пример использования этого метода на практике.

Пример 4

Найдите разность 4 452,294-10,30501.

Решение 

Для начала выполним первый шаг – уравняем количество десятичных знаков. Допишем два нуля в первую дробь и получим дробь вида 4 452,29400, значение которой идентично исходной.

Запишем получившиеся числа друг под другом в нужном порядке, чтобы получился столбик:

Считаем как обычно, игнорируя запятые:

В получившемся ответе поставим запятую в нужном месте:

Подсчеты окончены.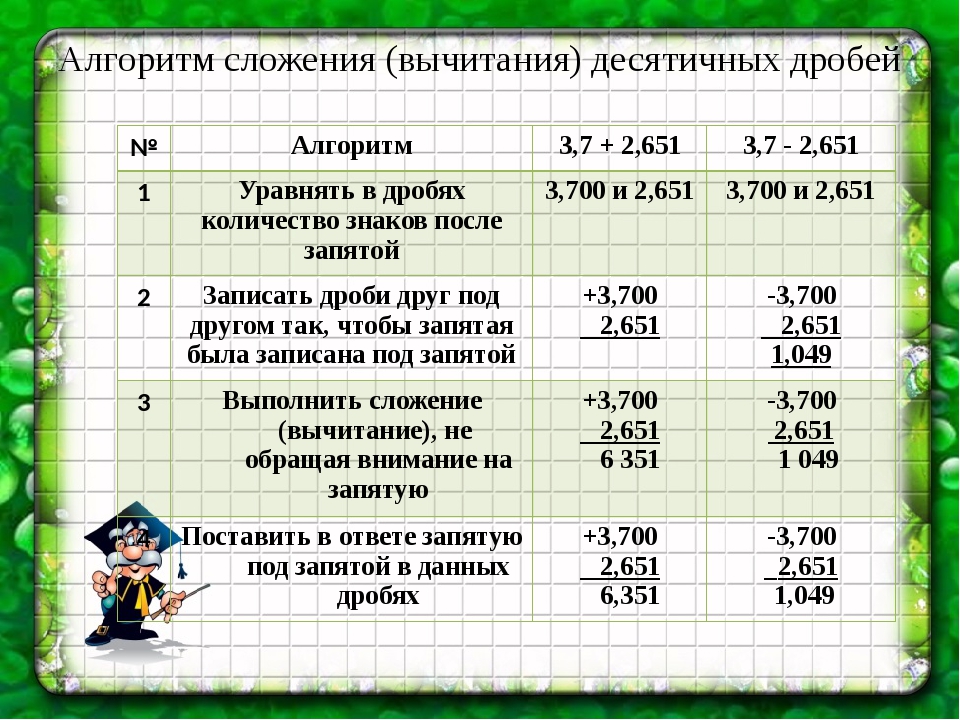

Наш результат : 4 452,294−10,30501=4 441,98899.

Как вычесть натуральное число из десятичной дроби и наоборот

Найти разность между конечной десятичной дробью и натуральным числом легче всего описанным выше способом – столбиком. Для этого число, из которого мы вычитаем, необходимо записать в виде десятичной дроби, в дробной части которой стоят нули.

Пример 5

Вычислите 15-7,32.

Запишем уменьшаемое число 15 в виде дроби 15,00, поскольку дробь, которую нам нужно вычесть, имеет два знака после запятой. Далее выполняем подсчет столбиком, как обычно:

Таким образом, 15−7,32=7,68.

Если из натурального числа нам нужно вычесть бесконечную периодическую дробь, то мы опять же сводим эту задачу к аналогичному вычислению. Заменяем периодическую десятичную дробь на обыкновенную.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание Пример 6

Вычислите разность 1-0, (6).

Решение

Указанной в условии периодической десятичной дроби соответствует обычная 23.

Считаем: 1−0,(6)=1−23=13.

Полученный ответ можно перевести в периодическую дробь 0,(3).

Если данная в условии дробь непериодическая, поступаем так же, предварительно округлив ее до нужного разряда.

Пример 7

Отнимите 4,274… от 5.

Решение 

Указанную бесконечную дробь мы округлим до сотых и получим 4,274…≈4,27.

После этого вычисляем 5−4,274…≈5−4,27.

Преобразуем 5 в 5,00 и запишем столбик:

В итоге 5−4,274…≈0,73. 

Если перед нами стоит обратная задача – вычесть натуральное число из десятичной дроби, то мы выполняем вычитание из целой части дроби, а дробную часть не трогаем совсем. Мы поступаем так и с конечными, и с бесконечными дробями.

Пример 8

Найдите разность 37,505 – 17.

Решение

Отделяем от дроби целую часть 37 и вычитаем требуемое число из нее. Получаем 37,505−17=20,505.  

Как вычесть десятичную дробь из смешанного числа или обыкновенной дроби и наоборот

Эту задачу также необходимо свести к вычитанию обыкновенных дробей – как в случае со смешанными числами, так и с десятичными дробями.

Пример 9

Вычислите разность 0,25-45.

Решение

Представим 0,25 в виде обыкновенной дроби – 0,25=25100=14.

Теперь нам нужно найти разность между 14и 45.

Считаем: 45−0,25=45−14=1620−520=1120.

Запишем ответ в виде десятичной записи: 0,55. 

Если в условии стоит смешанное число, из которого надо вычесть конечную или периодическую десятичную дробь, то поступаем аналогично.

Пример 10

Условие: отнимите 0,(18) от 8411.

Решение

Перепишем периодическую дробь в виде обыкновенной. 0,(18)=0,18+0,0018+0,000018+…=0,181-0,01=0,180,99=1899=211

Получается, что 8411-0,(18)=8411-211=8211.

В виде десятичной дроби ответ можно записать как 8,(18). 

Таким же образом мы действуем, когда вычитаем смешанное число или обыкновенную дробь из конечной или периодической дроби.

Пример 11

Подсчитайте 940-0,03.

Решение 

Заменяем дробь 0,03 на обыкновенную 3100.

У нас получается, что: 940−0,03=940−3100=90400−12400=78400=39200

Ответ можно оставить так или преобразовать в десятичную дробь 0,195. 

Если нам требуется выполнять вычитание с участием бесконечных непериодических дробей, то нам нужно будет свести их к конечным. Со смешанными числами поступаем аналогично. Для этого запишем обыкновенную дробь или смешанное число в виде десятичной дроби и округлим вычитаемую дробь до определенного разряда. Проиллюстрируем нашу мысль примером:

Пример 12

Отнимите 4,38475603…. из 1027.

Решение

Преобразуем смешанное число в неправильную дробь.

 

1027=10·7+27=727

Далее эту дробь запишем в десятичном виде и получим 10, (285714).

В итоге 1027-4,38475603…=10,(285714)-4,38475603…. 

Теперь округлим вычитаемые числа до седьмого знака: 10, (285714) =10,285714285714…≈10,2857143 и  4,38475603…≈4,3847560 

Тогда 10, (285714) −4,38475603…≈10,2857143−4,3847560.

Единственное, что осталось сделать – вычесть одну конечную десятичную дробь из другой. Выполним подсчет столбиком:

Ответ: 1027-4,38475603…≈5,9009583 

Вычитание десятичных дробей | Математика

Как и сложение, вычитание десятичных дробей зависит от правильной записи чисел.

Правило вычитания десятичных дробей

1) ЗАПЯТАЯ ПОД ЗАПЯТОЙ!

Эта часть правила самая важная. При вычитании десятичных дробей их следует записать так, чтобы запятые уменьшаемого и вычитаемого находились строго одна под другой.

2) Уравниваем количество цифр после запятой. Для этого в том числе, где количество цифр после запятой меньше, дописываем после запятой в конце нули.

3) Вычитаем числа, не обращая внимания на запятую.

4) Сносим запятую под запятыми.

Примеры на вычитание десятичных дробей.

1) 9,7-3,5

Чтобы найти разность десятичных дробей 9,7 и 3,5, запишем их так, чтобы запятые в обоих числах находились строго одна под другой. Затем вычитаем, не обращая внимания на запятую. В полученном результате запятую сносим, то есть записываем под запятыми уменьшаемого и вычитаемого:

9,7-3,5=6,2.

2) 23,45 — 1,5

Чтобы из одной десятичной дроби вычесть другую, надо записать их так, чтобы запятые располагались точно одна под другой. Так как у 23,45 после запятой две цифры, а у 1,5 — только одна, дописываем в 1,5 нуль. После этого ведем вычитания, не обращая внимания на запятую. В результат сносим запятую под запятыми:

23,45 — 1,5=21,95.

3) 63,5-8,921

Вычитание десятичных дробей начинаем с их записи так, чтобы запятые были расположены ровно одна под одной. В первом числе после запятой одна цифра, во втором — три, поэтому на место недостающих двух цифр в первом числе записываем нули. Затем вычитаем числа, не обращая внимания на запятую. В полученном результате сносим запятую под запятыми:

63,5-8,921=54,579.

4) 2,8703 — 0,507

Чтобы вычесть эти десятичные дроби, записываем их так, чтобы запятая второго числа расположилась точно под запятой первого. В первом числе после запятой четыре цифры, во втором — три, поэтому второе число дополняем после запятой нулем в конце. После этого вычитаем эти числа, как обычные натуральные, не учитывая запятую. В полученном результате записываем запятую под запятыми :

2,8703 — 0,507 = 2,3663.

5) 35,46 — 7,372

Вычитание десятичных дробей начинаем с записи чисел таким образом, чтобы запятые находились одна под другой. Дополняем нулем после запятой первое число, чтобы в обоих дробях после запятой было по три цифры. Затем вычитаем, не обращая внимания на запятую. В ответе сносим запятую под запятыми:

35,46 — 7,372 = 28,088.

6) 45 — 7,303

Чтобы из натурального числа вычесть десятичную дробь, в его записи в конце ставим запятую и приписываем необходимое количество нулей после запятой. Зачем вычитаем, не беря во внимание запятую. В ответ сносим запятую ровно под запятыми:

45 — 7,303 = 37,698.

7) 17,256 — 4,756

Этот пример на вычитание десятичных дробей выполняем аналогично. В результате получили число с нулями после запятой в конце. Их в ответе не пишем: 17,256 — 4,756 =12,5.

урок с примерами, карточками и видео

Простые арифметические действия — это основа дальнейшего обучения детей точным наукам. Математика сопровождает людей повсюду на протяжении всей жизни, а потому важно понимать её с самых азов. Вычитание десятичных дробей в столбик вызывает у многих школьников трудности, тогда как с действиями с простыми числами они отлично справляются. На самом деле в этом нет ничего сложного — главное уяснить алгоритм решения.

Как вычитать десятичные дроби в столбик

При записи десятичных дробей нижние и верхние разряды чисел должны соотвествовать друг другу: целые под целыми, десятые под десятыми, сотые под сотыми, тысячные под тысячными

Действия с десятичными дробями производятся так же, как и с натуральными. Основные правила, которые важно знать при решении примеров на вычитание в столбик:

1. Сначала следует уравнять количество знаков после запятой. Это делается путём добавления нулей. Например, необходимо вычесть из дроби 5,5 число 2,03. Как видно из примера, количество знаков после запятой разное. Чтобы сделать их одинаковым, в дробь 5,5 (пять целых пять десятых) в конце добавляем ноль и получаем 5,50 (пять целых пятьдесят сотых). Это правило следует из правил вычитания простых дробей. Как известно, дроби с разными знаменателями нельзя складывать или вычитать. Прежде их необходимо привести в общему знаменателю. В приведённом примере десятичные дроби можно записать в виде 5 5/10 и 2 3/100. Из целых чисел нужно вычитать целые, из дробных — дробные. В примере знаменатели у дробей разные, наименьший общий знаменатель равен 100. Следовательно, числитель и знаменатель дроби 5/10 следует умножить на 10, в итоге получим 50/100, что в переводе в десятичную дробь будет выглядеть как 5,50.
2. Числа записать таким образом, чтобы запятая нижнего находилась в том же месте, что и у верхнего. Проще всего записывать числа, начиная с запятой. Поставить две запятые сверху и снизу, а затем уже расписывать знаки по обе стороны. Это правило, кстати, действует на основании того же правила вычитания простых дробей — из целого вычитаются целые, а из дробных — дробные. Запятая в результате должна располагаться точно под двумя верхними.
3. Выполнить действие, не обращая внимания на запятую. Вычитают десятичные дроби справа налево, то есть начиная с самой правой цифры после запятой.
4. Поставить в ответе запятую под запятой. Так мы сможем правильно отразить результат вычисления.

Вычитать нужно по цифрам разрядов: целые из целых, сотые из сотых и так далее

Вычитание всегда можно проверить сложением.

Карточки для уроков

Чтобы было проще изучить алгоритм действий, можно распечатать для детей специальные карточки-памятки, которые помогут быстрее освоить новый материал.

Фотогалерея: варианты карточек для занятий

Видео: как вычитать десятичные дроби столбиком

Освоив это простое действие, дети смогут в дальнейшем лучше учиться, ведь примеры с десятичными дробями решают не только на математике, но и на физике, химии, астрономии. Главное — понять алгоритм.

Оцените статью: Поделитесь с друзьями!

Математика – 5 класс. Вычитание десятичных дробей

Дата публикации: 08 апреля 2017.

Способы вычитания десятичных дробей

Вычитать десятичные дроби можно двумя способами.

Первый способ аналогичен вычитанию натуральных чисел столбиком.
Давайте рассмотрим этот способ на примере. Даны десятичные дроби: 45,68 и 4,1, определим: чему равна их разность?
Сначала уравняем количество знаков после запятой. Для этого справа к десятичной дроби 4,1 припишем ноль и получим 4,10. Значение десятичной дроби при этом не меняется, т.к. десятичную разделительную запятую мы не переносили.
Далее расположим десятичные дроби друг под другом и, начиная с самого крайнего правого столбца, будем вычитать цифры нижнего ряда из цифр верхнего ряда. В конце не забываем поставить запятую.
В результате этих операций мы получим разность десятичных дробей.
Все просто и понятно. Единственное затруднение может возникнуть, если при вычитании разряд числа уменьшаемого меньше разряда числа вычитаемого.

Рассмотрим еще один пример вычитания десятичных дробей.
Даны десятичные дроби: 23,18 и 3,2.
Сначала выравняем количество разрядов и получим: 23,18 и 3,20.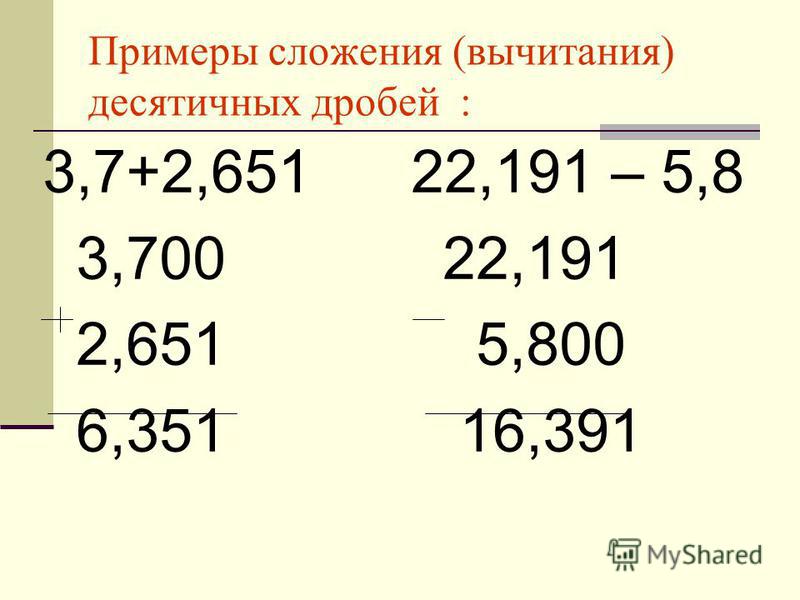
Запишем десятичные дроби в столбик друг под другом/

Начиная с правого крайнего ряда, вычитаем цифры нижнего ряда из цифр верхнего ряда. Если из цифры 1 вычесть цифру 2, то получим отрицательное число. Поэтому мы берем десяток единиц из соседнего разряда и получается, что производим вычитание числа 2 из числа 11. В результате имеем:
Алгоритм вычитания десятичных дробей:
1. Выравниваем десятичные дроби по количеству цифр после запятой.
2. Записываем десятичные дроби в столбик друг под другом.
3. Производим вычитание десятичных дробей по правилам вычитания натуральных чисел, не обращая внимания на наличие десятичной запятой.
4. После окончания вычитания, не забываем поставить десятичную запятую.

Второй способ вычитания десятичных дробей

Этот способ более сложен, менее нагляден и требует небольшого опыта. Зато он более быстр, поскольку здесь нет необходимости записывать числа в столбик и уравнивать количество знаков после запятой.
Самое главное в этом методе запомнить правило: десятые доли числа можно вычитать только из десятых долей, сотые – из сотых и т. д. Если в каком-либо разряде уменьшаемое меньше вычитаемого, то десяток единиц берем из соседнего слева разряда.

Рассмотрим пример. Заданы десятичные дроби: 5,13 и 3,4.
Вычитаем сотые доли, получаем 3.

5,13 — 3,4 =    3

Вычитаем десятые доли. В данном пример нам необходимо взять десять единиц из соседнего разряда, т.к. при вычитании десятых долей, уменьшаемое меньше вычитаемого.

5,13 — 3,4 =   73

Далее вычитаем единицы и получаем ответ.

5,13 — 3,4 = 1,73

И как обычно, результаты вычитания нужно проверить сложением. Для нашего примера, это:

1,73 + 3,4 = 5,13

Сложение и вычитание десятичных дробей 5 класс онлайн-подготовка на Ростелеком Лицей

Сложение и вычитание десятичных дробей

Научимся складывать и вычитать десятичные дроби.

Сложим десятичные дроби 3,7 и 2,651. Сначала уравняем количество цифр после запятой, приписав к первой дроби два нуля справа: 3,7=3,700. Потом запишем числа в смешанной форме.

Если сложить числа столбиком, получим тот же результат.

Теперь вычтем из 3,7 число 2,651.

Попробуем вычесть столбиком, и снова результат совпадёт.

Сформулируем правило сложения и вычитания десятичных дробей.

Чтобы сложить (вычесть) десятичные дроби, нужно:

1. Уравнять в этих дробях количество знаков после запятой.

2. Записать их друг под другом так, чтобы запятая была записана под запятой.

3. Выполнить сложение (вычитание), не обращая внимание на запятую.

4. Поставить в ответе запятую под запятой в данных дробях.

Теперь мы можем представлять дробь как сумму.

Число 0,444 равно сумме 4 десятых, 4 сотых, 4 тысячных:

Первый разряд после запятой называют разрядом десятых, второй – разрядом сотых, а третий – разрядом тысячных.

Сумму 0,4 + 0,004 + 0,004 называют разложением числа 0,444 по разрядным слагаемым.

Рассмотрим число 3258,912, в котором высшим разрядом являются тысячи, а низшим разрядом – тысячные. Это число содержит 3 тысячи, 2 сотни, 5 десятков, 8 единиц, 9 десятых, 1 сотую, 2 тысячные. Его разложением на сумму разрядных слагаемых будет 3258,912 = 3000 + 200 + 50 + 8 + 0,9 + 0,01 + 0,002

Десятичные дроби можно сравнивать по разрядам.

Например, 2,67<4,7, так как 2<4. Мы сравнили только высший разряд (единицы).

Сравним числа 2,681 и 2,69. Целые части одинаковы, и цифры в разряде десятых тоже одинаковы. Но число в разряде сотых меньше у первой десятичной дроби, чем у второй (8˂9). Значит, 2,681<2,69.

Как вычитать десятичные дроби. Правило сложения и вычитание десятичных дробей

Урок на тему: «Правила вычитания десятичных дробей. Примеры»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 5 класса
Тренажер к учебнику Истоминой Н.Б.    Тренажер к учебнику Н.Я. Виленкина

Способы вычитания десятичных дробей

Вычитать десятичные дроби можно двумя способами.

Первый способ аналогичен вычитанию натуральных чисел столбиком.
Давайте рассмотрим этот способ на примере. Даны десятичные дроби: 45,68 и 4,1, определим: чему равна их разность?
Сначала уравняем количество знаков после запятой. Для этого справа к десятичной дроби 4,1 припишем ноль и получим 4,10. Значение десятичной дроби при этом не меняется, т.к. десятичную разделительную запятую мы не переносили.
Далее расположим десятичные дроби друг под другом и, начиная с самого крайнего правого столбца, будем вычитать цифры нижнего ряда из цифр верхнего ряда. В конце не забываем поставить запятую.
В результате этих операций мы получим разность десятичных дробей.
Все просто и понятно. Единственное затруднение может возникнуть, если при вычитании разряд числа уменьшаемого меньше разряда числа вычитаемого.

Рассмотрим еще один пример вычитания десятичных дробей.
Даны десятичные дроби: 23,18 и 3,2.
Сначала выравняем количество разрядов и получим: 23,18 и 3,20.
Запишем десятичные дроби в столбик друг под другом/

Начиная с правого крайнего ряда, вычитаем цифры нижнего ряда из цифр верхнего ряда. Если из цифры 1 вычесть цифру 2, то получим отрицательное число. Поэтому мы берем десяток единиц из соседнего разряда и получается, что производим вычитание числа 2 из числа 11. В результате имеем:
Алгоритм вычитания десятичных дробей:
1. Выравниваем десятичные дроби по количеству цифр после запятой.
2. Записываем десятичные дроби в столбик друг под другом.
3. Производим вычитание десятичных дробей по правилам вычитания натуральных чисел, не обращая внимания на наличие десятичной запятой.
4. После окончания вычитания, не забываем поставить десятичную запятую.

Второй способ вычитания десятичных дробей

Этот способ более сложен, менее нагляден и требует небольшого опыта. Зато он более быстр, поскольку здесь нет необходимости записывать числа в столбик и уравнивать количество знаков после запятой.
Самое главное в этом методе запомнить правило: десятые доли числа можно вычитать только из десятых долей, сотые — из сотых и т. д. Если в каком-либо разряде уменьшаемое меньше вычитаемого, то десяток единиц берем из соседнего слева разряда.

Рассмотрим пример. Заданы десятичные дроби: 5,13 и 3,4.
Вычитаем сотые доли, получаем 3.

Вычитаем десятые доли. В данном пример нам необходимо взять десять единиц из соседнего разряда, т.к. при вычитании десятых долей, уменьшаемое меньше вычитаемого.

5,13 — 3,4 = 1,73

И как обычно, результаты вычитания нужно проверить сложением. Для нашего примера, это:

Как и сложение, вычитание десятичных дробей зависит от правильной записи чисел.

Правило вычитания десятичных дробей

1) ЗАПЯТАЯ ПОД ЗАПЯТОЙ!

Эта часть правила самая важная. При вычитании десятичных дробей их следует записать так, чтобы запятые уменьшаемого и вычитаемого находились строго одна под другой.

2) Уравниваем количество цифр после запятой. Для этого в том числе, где количество цифр после запятой меньше, дописываем после запятой в конце нули.

3) Вычитаем числа, не обращая внимания на запятую.

4) Сносим запятую под запятыми.

Примеры на вычитание десятичных дробей .

Чтобы найти разность десятичных дробей 9,7 и 3,5, запишем их так, чтобы запятые в обоих числах находились строго одна под другой. Затем вычитаем, не обращая внимания на запятую. В полученном результате запятую сносим, то есть записываем под запятыми уменьшаемого и вычитаемого:

2) 23,45 — 1,5

Чтобы из одной десятичной дроби вычесть другую, надо записать их так, чтобы запятые располагались точно одна под другой. Так как у 23,45 после запятой две цифры, а у 1,5 — только одна, дописываем в 1,5 нуль. После этого ведем вычитания, не обращая внимания на запятую. В результат сносим запятую под запятыми:

23,45 — 1,5=21,95.

Вычитание десятичных дробей начинаем с их записи так, чтобы запятые были расположены ровно одна под одной. В первом числе после запятой одна цифра, во втором — три, поэтому на место недостающих двух цифр в первом числе записываем нули. Затем вычитаем числа, не обращая внимания на запятую. В полученном результате сносим запятую под запятыми:

63,5-8,921=54,579.

4) 2,8703 — 0,507

Чтобы вычесть эти десятичные дроби, записываем их так, чтобы запятая второго числа расположилась точно под запятой первого. В первом числе после запятой четыре цифры, во втором — три, поэтому второе число дополняем после запятой нулем в конце. После этого вычитаем эти числа, как обычные натуральные, не учитывая запятую. В полученном результате записываем запятую под запятыми:

2,8703 — 0,507 = 2,3663.

5) 35,46 — 7,372

Вычитание десятичных дробей начинаем с записи чисел таким образом, чтобы запятые находились одна под другой. Дополняем нулем после запятой первое число, чтобы в обоих дробях после запятой было по три цифры. Затем вычитаем, не обращая внимания на запятую. В ответе сносим запятую под запятыми:

35,46 — 7,372 = 28,088.

Чтобы из натурального числа вычесть десятичную дробь, в его записи в конце ставим запятую и приписываем необходимое количество нулей после запятой. Зачем вычитаем, не беря во внимание запятую. В ответ сносим запятую ровно под запятыми:

45 — 7,303 = 37,698.

7) 17,256 — 4,756

Этот пример на вычитание десятичных дробей выполняем аналогично. В результате получили число с нулями после запятой в конце. Их в ответе не пишем: 17,256 — 4,756 =12,5.

Дата: 25.02.16г. Утверждаю:

Тема: Вычитание десятичных дробей

Цели:

Сформировать у учащихся знания о вычитании десятичных дробей

Развивать у учащихся интеллект и познавательный интерес

Осуществлять трудовое воспитание

Оборудование: учебник, классная доска

Тип урока : комбинированный

Метод: работа с отстающими

Ход урока :

Приветствие

Проверка отсутствующих

Проверка домашнего задания

Фронтальный опрос

Объяснение нового материала:

Также как и сложение, вычитание десятичных дробей производим по правилам натуральных чисел.

Основные правила вычитания десятичных дробей.

Уравниваем количество знаков после запятой.

Записываем десятичные дроби друг под другом так, чтобы запятые были друг под другом.

Выполняем вычитание десятичных дробей, не обращая внимания на запятые, по правилам вычитания в столбик натуральных чисел.

Ставим в ответе запятую под запятыми.

Если вы чувствуете себя уверенно в десятичных дробях и хорошо понимаете, что называется десятыми, сотыми и т.д., предлагаем вам попробовать другой способ вычитания (сложения) десятичных дробей без их записи в столбик. Другой способ вычитания десятичных дробей , как и сложение, основывается на трёх основных правилах.

Вычитают десятичные дроби справа налево . То есть, начиная с самой правой цифры после запятой.

При вычитании большей цифры из меньшей, у соседа слева меньшей цифры занимаем десяток.

Как обычно, рассмотрим пример:

Вычитаем справа налево с самой правой цифры. У нас самая правая цифра в обеих дробях — сотые. 1 — в первом числе, 1 — во втором. Вот их и вычитаем. 1 − 1 = 0. Получилось 0, значит, на месте сотых нового числа пишем ноль.

Десятые вычитаем из десятых. 2 — в первом числе, 3 — во втором числе. Так как из 2 (меньшего) мы не можем вычесть 3 (большее), занимаем десяток у соседа слева для 2. У нас это 5. Теперь мы не из 2 вычитаем 3, а из 12 вычитаем 3.
12 − 3 = 9.
На месте десятых нового числа пишем 9. Не забываем, что после занятия десятка из 5, мы должны вычесть из 5 единицу. Чтобы это не забыть ставим над 5 пустой кружок.

И наконец, вычитаем целые части. 14 — в первом числе (не забудьте, что мы из 5 вычли 1), 8 — во втором числе. 14 − 8 = 6

Запомните!

Во втором числе самая правая цифра это 2 (сотые), а в первом числе сотых нет в явном виде. Поэтому, к первому числу справа от 9 добавляем ноль и вычитаем согласно основным правилам.

Такие арифметические вычислительные действия, как сложение и вычитание десятичных дробей , необходимы для того, чтобы, оперируя дробными числами получать искомый результат. Особая важность проведения этих операций состоит в том, что во многих сферах деятельности человека меры многих сущностей представлены именно десятичными дробями . Поэтому для осуществления определенных действий со многими предметами материального мира требуется складывать или вычитать именно десятичные дроби . Следует заметить, что на практике эти операции используются практически повсеместно.

Процедуры сложения и вычитания десятичных дробей по своей математической сути осуществляется практически точно так же, как аналогичные операции для целых чисел. При ее осуществлении значение каждого разряда одного числа нужно записывать под значением аналогичного разряда другого числа.

Подчиняется следующим правилам:

Сначала необходимо произвести уравнивание количество тех знаков, что располагаются после запятой;

Затем нужно произвести запись десятичных дробей друг под другом таким образом, чтобы содержащиеся в них запятые располагались строго друг под другом;

Осуществить процедуру вычитания десятичных дробей в полном соответствии с теми правилами, которые действуют для вычитания целых чисел. При этом не нужно обращать никакого внимания на запятые;

После получения ответа запятую в нем нужно поставить строго под теми, которые имеются в исходных числах.

Операция сложения десятичных дробей осуществляется в соответствии с теми же правилами и алгоритмом, которые описаны выше для процедуры вычитания.

Пример сложения десятичных дробей

Две целых две десятых плюс одна сотая плюс четырнадцать целых девяносто пять сотых равняется семнадцать целых шестнадцать сотых.

2,2 + 0,01 + 14,95 = 17,16

Примеры сложения и вычитания десятичных дробей

Математические операции сложения и вычитания десятичных дробей на практике используются чрезвычайно широко, причем они нередко касаются многих предметов окружающего нас материального мира. Ниже приводится несколько примеров таких вычислений.

Пример 1

Согласно проектно-сметной документации, для строительства небольшого производственного объекта требуется десять целых пять десятых кубометров бетона. Используя современные технологии возведения зданий, подрядчикам без ущерба для качественных характеристик сооружения удалось использовать для проведения всех работ всего девять целых девять десятых кубометров бетона. Размер экономии составляет:

Десять целых пять десятых минус девять целых девять десятых равно ноль целых шесть десятых кубометра бетона.

10,5 – 9,9 = 0,6 м 3

Пример 2

Двигатель, устанавливаемый на старую модель автомобиля, потребляет в городском цикле восемь целых две десятых литра топлива на сто километров пробега. Для нового силового агрегата этот показатель составляет семь целых пять десятых литров. Размер экономии составляет:

Восемь целых две десятых литра минус семь целых пять десятых литра равно ноль целых семь десятых литра на сто километров пробега в городском режиме движения.

8,2 – 7,5 = 0,7л

Операции сложения и вычитания десятичных дробей применяются чрезвычайно широко, и их осуществление не составляет никаких проблем. В современной математике эти процедуры отработаны практически идеально, и ими практически все хорошо владеют еще со школьной скамьи.

Цели урока:

• формирование знаний о правилах сложения и вычитания десятичных дробей и умения применять их в простейших случаях;
• развитие умений сравнивать, выявлять закономерности, обобщать;
• воспитание самостоятельности при выполнении заданий.

Оборудование: компьютер, проектор, магнитные доски для учащихся, индивидуальные разноуровневые карточки.

Структура урока:

1. Организационный момент.
2. Активизация ранее полученных знаний.
3. Изучение нового материала.
4. Первичное закрепление изученного материала.
5. Тест.
6. Постановка домашнего задания.
7. Подведение итогов урока.

ХОД УРОКА

I. Организационный момент

Проверяется готовность класса к уроку. Отмечается, что учащиеся недавно познакомились с понятием «десятичная дробь», научились читать и сравнивать десятичные дроби. На уроке будет рассмотрен вопрос о том, как складывать и вычитать десятичные дроби. Записывается тема урока. Слайд 1.

II. Активизация ранее полученных знаний

Коль скоро речь сегодня пойдет о десятичных дробях, давайте вспомним:

• Какие из этих дробей можно записать в виде десятичных:

Слайд 2. (Учащиеся называют дроби).

Представьте дроби в виде десятичных. (Учащиеся показывают на магнитных досках) .
Еще раз вспомним, какие дроби можно записать в виде десятичных. (Ученики дают ответ).

Представьте в виде десятичных дробей:

Слайд 3. (На магнитных досках учащиеся показывают записи).

0,62; 7,321; 21,0001; 63,01246. Слайд 4.

III. Изучение нового материала

– Ребята, а какой из приведенных примеров касается сегодняшней темы. (Учащиеся отвечают, что последний).
– Давайте запишем этот пример в тетрадь и найдем сумму.

Давайте запишем этот пример в виде десятичных дробей.

Тот же самый результат мы получим, складывая числа в столбик.

– Что мы с вами получили? (Сумму десятичных дробей).
– Давайте проговорим, как мы это сделали. Слайд 6.

– Хорошо!

Ученикам предлагается найти сумму десятичных дробей, у которых разное количество цифр после запятой 6,23 + 173,3. Учащимся задается вопрос: «Как действовать в этом случае?». (Учащиеся отвечают, что в слагаемых разное количество знаков после запятой).

– Как же быть? (Нужно уравнять, дописав нуль справа у второго слагаемого).

6,32 + 173,7 = 6,32 + 173,70

А теперь можно записать числа в столбик и найти сумму.

Алгоритм сложения десятичных дробей дополняется и выглядит следующим образом:

– А как найти разность двух десятичных дробей? (Точно так же).

Алгоритм дополняется и выглядит так:

– Итак, как сложить или вычесть десятичные дроби?

Алгоритм повторяется учащимися и появляется на экране.

IV. Первичное закрепление полученных знаний

1. Вычислим устно (примеры учащимся предлагаются на табличках, а ответы – на магнитных досках):

2. Решение упражнений.

№1213 (а, г, б), №1214 (а, д, е), №1219 (в, е, л).

Примеры решаются у доски с комментариями . Слайд 7.

V. Тест

– Итак, а сейчас мы проверим, как вы запомнили правила сложения и вычитания десятичных дробей.
Устно повторяется еще раз алгоритм.
Учащимся предлагаются карточки трех типов (Приложение 3 )
Ответы учащиеся демонстрируют на табличках. При успешном выполнении заданий у всех учащихся на табличках должно быть написано слово «плюс». Слайд 8.

VI. Подведение итогов урока

– Что вам понравилось на сегодняшнем уроке?
– Что не понравилось?
– Чему мы с вами научились на уроке? (Складывать и вычитать десятичные дроби).
– Какой способ нам позволит это сделать быстро? (Сложение и вычитание «в столбик»).
– А как это сделать?

Учащиеся проговаривают алгоритм.

VII. Постановка домашнего задания

– Пользуясь этим алгоритмом дома, вы выполните следующие задания: № 1255 (а, г, е), №1256 (е, з), а также ознакомитесь с пунктом параграфом 32 учебника. Сравните алгоритм, предложенный в учебнике, с нашим.
– Урок окончен.

Урок 58. вычитание положительных десятичных дробей — Математика — 6 класс

Математика

6 класс

Урок № 58

Вычитание положительных десятичных дробей

Перечень рассматриваемых вопросов:

• десятичная запись дробей;
• десятичная дробь;
• поразрядное сложение;
• поразрядное вычитание;
• перевод из одних единиц измерения в другие.

Тезаурус

Десятичная дробь – это дробь, у которой знаменатель является степенью числа 10.

Десятичные дроби записывают без знаменателей, выделяя целую часть (целая часть правильной дроби считается равной 0) и отделяя её запятой от числителя дробной части.

Обязательная литература:

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.

Дополнительная литература:

1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.

Теоретический материал для самостоятельного изучения

Уметь правильно выполнять действие вычитания так же важно, как уметь выполнять сложение. Например, при ремонте электрического провода от куска длиной 3,51 м отрезали 2,387 м. Как узнать, сколько осталось провода, и хватит ли его на проведение дальнейших работ? В этом нам поможет умение вычитать десятичные дроби.

Вычитание десятичных дробей, как и сложение, можно выполнить в столбик. Рассмотрим подробно, как это сделать. Уравняем количество знаков после запятой, для этого припишем к числу 3,51 справа один ноль. Получим число 3,510. Запишем числа в столбик, запятая под запятой, разряд под разрядом.

Из 0 тысячных вычесть 7 тысячных и получить положительное число нельзя, поэтому занимаем в уменьшаемом одну сотую и раздробляем её в 10 тысячных. Тогда 10 тысячных минус 7 тысячных получится 3 тысячных. Пишем в разряде тысячных цифру 3.

Из 0 сотых вычесть 8 сотых нельзя. Занимаем в уменьшаемом одну сотую и раздробляем её на 10 сотых. 10 сотых минус 8 сотых получится 2 сотых. Пишем в разряде сотых цифру 2.

4 десятых минус 3 десятых будет 1 десятая. В разряде десятых пишем цифру 1.

3 единицы минус 2 единицы будет 1 единица. Пишем в разряде единиц цифру 1. Получаем ответ 1,123.

Алгоритм вычитания десятичных дробей:

– уравнять в числах количество цифр после запятой.

– записать уменьшаемое и вычитаемое друг под другом так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого, а запятая была под запятой.

– произвести вычитание десятичных дробей так же, как вычитание натуральных чисел – поразрядно, не обращая внимания на запятую.

– поставить в полученной разности запятую под запятыми.

– записать результат.

Рассмотрим несколько заданий

1. Найдите разность.

17,2 – 3,148

Используем алгоритм. Уравняем количество знаков после запятой, приписывая нули. Получаем 17,200 – 3,148. Записываем в столбик, запятая под запятой. Выполняем вычитание, не обращая внимания на запятую. В ответе ставим запятую под запятыми. Получаем: 14,052.

16 – 4,256

Число 16 целое, значит, дробная часть равна нулю. Чтобы уравнять количество знаков после запятой, припишем три нуля в дробную часть числа 16. Получаем 16,000 – 4,256. Записываем в столбик, запятая под запятой. Выполняем вычитание. Ставим запятую под запятыми. Получаем ответ: 11,744.

2. Найдите разность удобным способом.

15,75 – 4,68 + 12,68 – 4,25

Удобнее поменять местами числа, сохраняя знаки, стоящие перед ними. Сделаем это и сразу сгруппируем. Получаем

(15,75 – 4,25) + (12,68 – 4,68).

Выполним действия в каждой группе и сложим результаты. Получаем 11,5+8=19,5.

3. Найдите разность, используя правила раскрытия скобок.

4,756 – (2,395 – 1,244)

Вспомним правило раскрытия скобок. Если перед скобкой стоит знак «минус», то скобки можно опустить, изменив знаки слагаемых на противоположные. Если перед скобкой стоит знак «плюс», скобки можно опустить, знаки при этом не меняются.

Раскроем скобки.

4,756 – 2,395 + 1,244.

Используем переместительное свойство, оставляя знаки перед числами неизменными.

4,756 + 1,244 – 2,395 = 6 – 2,395 = 3,605

4. Найдите разность, приведя дроби к одному виду.

Удобнее перевести обыкновенную дробь в десятичную. Для этого умножим числитель и знаменатель дробной части на 25. Получим 2,25. Теперь выполним вычитание.

7,3 – 2,25 = 7,30 – 2,25 = 5,05

В данном случае удобнее десятичную дробь перевести в обыкновенную, так как знаменатель 3 в обыкновенной дроби не позволит нам привести его к виду единицы с нулями.

5. Найдите разность.

12,3 дм – 45 см – 35 мм

Чтобы произвести вычисления, нужно выразить все величины в одной единице измерения. Например, в дециметрах.

45 см = 4,5 дм,

35 мм = 0,35 дм.

Получаем

12,3 дм – 4,5 дм– 0,35 дм = 7,45 дм.

Умение вычитать десятичные дроби поможет нам и при решении задач. Рассмотрим некоторые из них.

Задача 1. Собственная скорость теплохода равна 23,8 км/ч, скорость течения реки1,6 км/ч. Найти скорость теплохода против течения.

Решение. Чтобы найти скорость движения против течения, нужно из собственной скорости теплохода вычесть скорость течения. Таким образом, 23,8 км/ч – 1,6 км/ч = 22,2 км/ч.

Задача 2. Из двух пунктов, расстояние между которыми 2 км, вышли в одном направлении одновременно два пешехода. Скорость первого пешехода 4,9км/ч, скорость второго 2,9км/ч. Через какое время первый пешеход догонит второго?

Решение. Составив схему, мы видим, что это задача на движение вдогонку. Поскольку из условия точно известно, что первый пешеход догонит второго, речь пойдёт о скорости сближения.

Чтобы найти скорость сближения, нужно из скорости первого (догоняющего) пешехода вычесть скорость второго.

4,9 км/ч – 2,9 км/ч = 2 (км/ч) – скорость сближения.

Чтобы найти время до встречи, нужно расстояние между пешеходами разделить на скорость сближения.

Получаем: 2 : 2 = 1 (ч) – время.

Ответ: через 1 ч.

Разбор заданий тренировочного модуля

№ 1. Тип задания. Ввод с клавиатуры пропущенных элементов в тексте.

В магазине было 5 видов сладостей. Шоколадных конфет было больше, чем карамели, на 2,4 кг, но меньше, чем ириса, на 3,8 кг. Печенья было больше, чем пирожных, на 1,5 кг, но меньше, чем ириса, на 1,9 кг. Печенья было 7,3 кг. А всего в магазине было … кг сладостей.

Решение

1) 7,3 + 1,9 = 9,2 (кг) ириса было в магазине;

2) 7,3 – 1,5 = 5,8 (кг) пирожных;

3) 9,2 – 3,8 = 5,4 (кг) шоколадных конфет;

4) 5,4 – 2,4 = 3 (кг) карамели;

5) 7,3 + 9,2 + 5,8 + 5,4 + 3 = 30,7 (кг).

Ответ: всего в магазине было 30,7 кг сладостей.

№ 2. Вычислите периметр прямоугольника и зачеркните неверные ответы.

Вычислите периметр прямоугольника, если его ширина равна 4,03 м, а длина на 1,756 м меньше.

Варианты ответов:

12,578

11,170

12,608

Решение.

Периметр это сумма длин всех сторон. Найдём длину прямоугольника. По условию она на 1,756 м меньше ширины.

4,03 м – 1,756 м = 2,274 м

Теперь вычислим периметр.

4,03 м + 4,03 м + 2,274 м + 2,274 м = 12,608 м

Ответ:

с вычитанием десятичных знаков

Вычитать десятичные дроби легко, если работа ведется аккуратно

Чтобы вычесть десятичные дроби, выполните следующие действия:

• Запишите два числа, одно под другим, с десятичными точками.
• Добавьте нули, чтобы числа имели одинаковую длину
• Затем вычтите обычным образом, не забывая поставить десятичную точку в ответе

Пример: вычесть 0.03 из 1.1

Выровняйте десятичные знаки вверх:			1,1
		–	0,03
«Pad» с нулями:			1,10
		–	0. 03
Вычесть:			1,10
		–	0,03
			1.07

Ответ: 1.07

Это было точно так же, как 110 — 3 = 107, но с десятичной запятой в другой позиции

Пример: вычислить 7.005-0,55

Выровняйте десятичные знаки вверх:			7.005
		–	0,55
«Pad» с нулями:			7.005
		–	0.550
Вычесть:			7.005
		–	0,550
			6.455

Ответ: 6.455

И это было точно так же, как 7005 — 550 = 6455

5.3: Сложение и вычитание десятичных знаков

Добавление десятичных знаков

Сложение десятичных чисел очень похоже на сложение целых чисел. Например, предположим, что нас просят добавить 2,34 и 5,25. Мы можем изменить эти десятичные числа на , смешанные дроби и сложить.

\ [\ begin {выровнено} 2,34 + 5,25 & = 2 \ frac {34} {100} + 5 \ frac {25} {100} \\ & = 7 \ frac {59} {100} \ end {выровнено} \ nonumber \]

Однако мы также можем выровнять десятичные числа по десятичным точкам и сложить по вертикали, как показано ниже.

\ [\ begin {массив} {r} 2.34 \\ + 5.25 \\ \ hline 7.59 \ end {array} \ nonumber \]

Обратите внимание, что эта процедура выравнивания дает тот же результат: «семьдесят девять сотых». Это мотивирует следующую процедуру сложения десятичных чисел.

Добавление десятичных знаков

Чтобы добавить десятичные числа, действуйте следующим образом:

1. Поместите добавляемые числа в вертикальном формате, выравнивая десятичные точки.
2. Сложите числа, как если бы они были целыми числами.
3. Поместите десятичную точку в ответе в тот же столбец, что и десятичные точки над ней.

Пример 1

Складываем 3,125 и 4,814.

Раствор

Разместите числа в вертикальном формате, выровняв их по десятичным точкам. Добавьте, а затем поместите десятичную точку в ответе в тот же столбец, что и десятичные точки, которые появляются над ответом.

\ [\ begin {array} {r} 3.125 \\ +4.814 \\ \ hline 7.939 \ end {array} \ nonumber \]

Таким образом, 3.125 + 4,814 = 7,939.

Упражнение

Добавить: 2.864 + 3.029

Ответ

5,893

Пример 2

У Джейн в кошельке 4,35 доллара. У Джима в кошельке 5,62 доллара. Если они суммируют свои деньги, какова общая сумма?

Раствор

Расположите числа в вертикальном формате, выравнивая десятичные точки, затем сложите.

\ [\ begin {array} {r} \ $ 4.35 \\ + \ $ 5.62 \\ \ hline \ $ 9.97 \ end {array} \ nonumber \]

Упражнение

У Алисы в кошельке 8,63 доллара, а у Джоанны — 2,29 доллара. Если они объединят свои деньги, какова общая сумма?

Ответ

$ 10.91

Прежде чем рассматривать другой пример, напомним одно важное наблюдение.

Важное замечание

Добавление нулей в конец дробной части десятичного числа не меняет его значения.Точно так же удаление завершающих нулей в конце десятичного числа не меняет его значения.

Например, мы могли бы добавить два нуля в конце дробной части 7,25, чтобы получить 7,2500. Числа 7.25 и 7.2500 идентичны, как показывает следующий аргумент:

\ [\ begin {Выровнено} 7.2500 & = 7 \ frac {2500} {10000} \\ & = 7 \ frac {25} {100} \\ & = 7.25 \ end {Выровнено} \ nonumber \]

Пример 3

Складываем 7.5 и 12.23.

Раствор

Расположите числа в вертикальном формате, выровняв их десятичные точки в столбце.Обратите внимание, что мы добавляем завершающий ноль, чтобы улучшить выравнивание по столбцам.

\ [\ begin {массив} {r} 7.50 \\ +12.23 \\ \ hline 19.73 \ end {array} \ nonumber \]

Следовательно, 7,5 + 12,23 = 19,73.

Упражнение

Добавить: 9.7 + 15.86

Ответ

25,56

Пример 4

Найдите сумму: 12,2 + 8,352 + 22,44.

Раствор

Расположите числа в вертикальном формате, выровняв их десятичные точки в столбце.Обратите внимание, что мы добавляем нули в конце, чтобы улучшить выравнивание по столбцам.

\ [\ begin {array} {r} 12.200 \\ 8.352 \\ + 22.440 \\ \ hline 42.992 \ end {array} \ nonumber \]

Следовательно, 12,2 + 8,352 + 22,44 = 42,992.

Упражнение

Добавить: 12.9 + 4.286 + 33.97

Ответ

51.156

Вычитание десятичных знаков

Вычитание десятичных чисел происходит примерно так же, как и сложение десятичных чисел.

Вычитание десятичных знаков

Чтобы вычесть десятичные числа, действуйте следующим образом:

1. Поместите числа для вычитания в вертикальном формате, выравнивая десятичные точки.
2. Вычтите числа, как если бы они были целыми числами.
3. Поместите десятичную точку в ответе в тот же столбец, что и десятичные точки над ней.

Пример 5

Вычтем 12,23 из 33,57.

Раствор

Расположите числа в вертикальном формате, выровняв их десятичные точки в столбце, а затем вычтите. Обратите внимание, что мы вычитаем 12,23 из 33,57.

\ [\ begin {массив} {r} 33,57 \\ -12,23 \\ \ hline 21,34 \ end {array} \ nonumber \]

Следовательно, 33,57 — 12,23 = 21,34.

Упражнение

Вычесть: 58,76 — 38,95

Ответ

19,81

Как и при сложении, мы добавляем конечные нули к дробной части десятичных чисел, чтобы облегчить выравнивание по столбцам.

Пример 6

Найдите разницу: 13.3 — 8,572.

Раствор

Расположите числа в вертикальном формате, выровняв их десятичные точки в столбце. Обратите внимание, что мы добавляем нули в конце дробной части 13,3, чтобы улучшить выравнивание по столбцам.

\ [\ begin {array} {r} 13.300 \\ -8.572 \\ \ hline 4.728 \ end {array} \ nonumber \]

Следовательно, 13,3 — 8,572 = 4,728.

Упражнение

Вычесть: 15,2 — 8,756

Ответ

6.444

Сложение и вычитание десятичных чисел со знаком

Мы используем те же правила для сложения десятичных чисел со знаком, что и для сложения целых чисел.

Сложение двух десятичных знаков с одинаковыми знаками

Чтобы добавить два десятичных знака с одинаковыми знаками, действуйте следующим образом:

1. Сложите величины десятичных чисел.
2. Префикс общего знака.

Пример 7

Упростить: −3,2 + (- 18,95).

Раствор

Чтобы добавить одинаковые знаки, сначала добавьте величины.

\ [\ begin {array} {r} 3.20 \\ +18.95 \\ \ hline 22.15 \ end {array} \ nonumber \]

Префикс общего знака. Следовательно, −3,2 + (- 18,95) = −22,15

.

Упражнение

Упростить: -5,7 + (-83,85)

Ответ

−89,55

Мы используем то же правило, что и для целых чисел, при добавлении десятичных дробей с разными знаками.

Сложение двух десятичных знаков с разными знаками

Чтобы добавить два десятичных знака с разными знаками, действуйте следующим образом:

1. Вычтите меньшую звездную величину из большей.
2. Префикс знака десятичного числа с большей величиной.

Пример 8

Упростить: −3 + 2,24.

Раствор

Чтобы добавить непохожие знаки, сначала вычтите меньшую величину из большей.

\ [\ begin {array} {r} 3.00 \\ -2,24 \\ \ hline 0,76 \ end {array} \ nonumber \]

Префикс знака десятичного числа с большей величиной. Следовательно, −3 + 2.24 = −0.76.

Упражнение

Упростить: −8 + 5,74

Ответ

-2,26

Вычитание по-прежнему означает, что прибавляет противоположное .

Пример 9

Упростить: −8,567 — (−12,3).

Раствор

Вычитание сначала нужно заменить на сложение, добавив противоположное.

\ [- 8,567 — (-12,3) = -8,567 + 12,3 \ nonumber \]

У нас есть непохожие знаки. Во-первых, вычтите меньшую величину из большей.

\ [\ begin {array} {r} 12.300 \\ — 8.567 \\ \ hline 3.733 \ end {array} \ nonumber \]

Префикс знака десятичного числа с большей величиной. Отсюда:

\ [\ начало {выровнено} -8,567 — (-12,3) & = -8,567 + 12,3 \\ & = 3,733 \ конец {выровнено} \ nonumber \]

Упражнение

Упростить: −2.384 — (−15,2)

Ответ

12,816

Порядок операций требует, чтобы мы сначала упростили выражения, содержащиеся в круглых скобках.

Пример 10

Упростить: −11,2 — (−8,45 + 2,7).

Раствор

Сначала нужно добавить в круглые скобки. Поскольку у нас разные знаки, вычтите меньшую величину из большей.

\ [\ begin {array} {r} 8. 45 \\ — 2.70 \\ \ hline 5.75 \ end {array} \ nonumber \]

Префикс знака числа с большей величиной. Следовательно,

\ [- 11,2 — (−8,45 + 2,7) = −11,2 — (−5,75) \ nonumber \]

Вычитание означает сложение противоположного.

\ [- 11,2 — (-5,75) = -11,2 + 5,75 \ nonumber \]

Опять же, у нас непохожие знаки. Вычтите меньшую величину из большей.

\ [\ begin {array} {r} 11.20 \\ — 5.75 \\ \ hline 5.45 \ end {array} \ nonumber \]

Префикс знака числа с большой величиной.

\ [-11,2 + 5,75 = -5,45 \ nonumber \]

Упражнение

Упростить: −12,8 — (−7,44 + 3,7)

Ответ

−9,06

Письмо по математике

Решение предыдущего примера должно быть записано следующим образом:

\ [\ begin {выровнено} -11,2 — (-8,45 + 2,7) & = -11,2 — (-5,75) \\ & = -11,2 + 5,75 \\ & = -5,45 \ конец {выровнено} \ nonumber \]

Любая скретч-работа, такая как вычисления в вертикальном формате в предыдущем примере, должна выполняться на полях или в блокноте.

Пример 11

Упростить: −12,3 — | — 4,6 — (−2,84) |.

Раствор

Сначала мы упрощаем выражение внутри столбцов абсолютного значения, берем абсолютное значение результата, а затем вычитаем.

\ [\ begin {align} -12,3 — | -4,6 — (- 2,84) | ~ \\ = -12,3 — | -4,6 + 2,84 | ~ & \ textcolor {red} {\ text {Добавьте противоположное.}} \\ = -12,3 — | -1,76 | ~ & \ textcolor {красный} {\ text {Добавить:} -4,6 + 2,84 = -1,76.} \\ = -12,3-1,76 ~ & \ textcolor {красный} {| -1.76 | = 1,76.} \\ = -12,3 + (-1,76) ~ & \ textcolor {red} {\ text {Добавить противоположное.}} \\ = -14,06 ~ & \ textcolor {red} {\ text {Добавить :} -12,3 + (-1,76) = -14,06.} \ End {выровнено} \ nonumber \]

Упражнение

Упростить: −8,6 — | — 5,5 — (−8,32) |

Ответ

−11,42

Упражнения

В упражнениях 1–12 сложите десятичные дроби.

1. \ (31.9 + 84.7 \)

2. \ (9.39 + 7.7 \)

3.\ (4 + 97,18 \)

4. \ (2.645 + 2.444 \)

5. \ (4 + 87.502 \)

6. \ (23,69 + 97,8 \)

7. \ (95,57 + 7,88 \)

8. \ (18.7 + 7 \)

9. \ (52.671 + 5.97 \)

10. \ (9.696 + 28.2 \)

11. \ (4,76 + 2,1 \)

12. \ (1,5 + 46,4 \)

---

В упражнениях 13-24 вычтите десятичные дроби.

13. \ (9 — 2.261 \)

14. \ (98,14 — 7,27 \)

15. \ (80.9 — 6 \)

16.\ (9,126 — 6 \)

17. \ (55,672 — 3,3 \)

18. \ (4,717 — 1,637 \)

19. \ (60,575 — 6 \)

20. \ (8.91 — 2.68 \)

21. \ (39,8 — 4,5 \)

22. \ (8,210 — 3,7 \)

23. \ (8.1 — 2.12 \)

24. \ (7,675 — 1,1 \)

---

В упражнениях 25–64 складывайте или вычитайте десятичные дроби, как показано.

25. \ (- 19,13 — 7 \)

26. \ (- 8 — 79,8 \)

27. \ (6,08 — 76,8 \)

28.\ (5,76 — 36,8 \)

29. \ (- 34,7 + (- 56,214) \)

30. \ (- 7,5 + (- 7,11) \)

31. \ (8,4 + (- 6,757) \)

32. \ (- 1,94 + 72,85 \)

33. \ (- 50,4 + 7,6 \)

34. \ (1,4 + (- 86,9) \)

35. \ (- 43,3 + 2,2 \)

36. \ (0,08 + (-2,33) \)

37. \ (0,19 — 0,7 \)

38. \ (9 — 18.01 \)

39. \ (- 7 — 1,504 \)

40. \ (- 4,28 — 2,6 \)

41. \ (- 4.47 + (−2) \)

42. \ (- 9 + (- 43.67) \)

43. \ (71,72 — (−6) \)

44. \ (6 — (−8,4) \)

45. \ (- 9,829 — (−17,33) \)

46. \ (- 95,23 — (-71,7) \)

47. \ (2.001 — 4.202 \)

48. \ (4 — 11.421 \)

49. \ (2,6 — 2,99 \)

50. \ (3.57 — 84.21 \)

51. \ (- 4.560 — 2.335 \)

52. \ (- 4,95 — 96,89 \)

53. \ (- 54,3 — 3,97 \)

54. \ (- 2 — 29,285 \)

55. \ (- 6,32 + (-48,663) \)

56. \ (- 8,8 + (- 34,27) \)

57. \ (- 8 — (−3,686) \)

58. \ (- 2,263 — (−72,3) \)

59. \ (9,365 + (−5) \)

60. \ (- 0,12 + 6,973 \)

61. \ (2,762 — (−7,3) \)

62. \ (65,079 — (-52,6) \)

63. \ (- 96,1 + (- 9,65) \)

64. \ (- 1.067 + (−4.4) \)

---

В упражнениях 65–80 упростите данное выражение.

65. \ (- 12,05 — | 17,83 — (-17,16) | \)

66. \ (15,88 — | — 5,22 — (-19,94) | \)

67.\ (- 6.4 + | 9.38 — (−9.39) | \)

68. \ (- 16,74 + | 16,64 — 2,6 | \)

69. \ (- 19,1 — (1,51 — (−17,35)) \)

70. \ (17,98 — (10,07 — (−10,1)) \)

71. \ (11,55 + (6,3 — (-1,9)) \)

72. \ (- 8,14 + (16,6 — (-15,41)) \)

73. \ (- 1,7 — (1,9 — (−16,25)) \)

74. \ (- 4,06 — (4,4 — (-10,04)) \)

75. \ (1,2 + | 8,74 — 16,5 | \)

76. \ (18,4 + | 16,5 — 7,6 | \)

77. \ (- 12,4 — | 3,81 — 16,4 | \)

78.\ (13,65 — | 11,55 — (−4,44) | \)

79. \ (- 11,15 + (11,6 — (-16,68)) \)

80. \ (8,5 + (3,9 — 6,98) \)

---

81. Крупные банки . Рыночная капитализация четырех крупнейших банков страны (по состоянию на 23 апреля 2009 г.)

JPMorgan Chase & Co	124,8 миллиарда долларов
Wells Fargo & Co	85,3 миллиарда долларов
Goldman Sachs Group Inc.	61,8 миллиарда долларов
Банк Америки	56,4 миллиарда долларов

Какова общая стоимость четырех крупнейших банков страны? Associated Press Times-Standard 22.04.09

82. Зеркало телескопа. Недавно запущенный телескоп Herschel имеет зеркало диаметром 11,5 футов, а зеркало Хаббла — 7,9 футов в диаметре. Насколько больше по диаметру зеркало Гершеля, чем зеркало Хаббла?

83. Средняя температура . Средние температуры в июле в Сакраменто, штат Калифорния, — это высокая дневная температура 93,8 градуса по Фаренгейту и низкая ночная температура 60,9 градусов по Фаренгейту. Какое изменение температуры днем ​​и ночью? Подсказка: См. Раздел 2.3, где приведена формула для сравнения температур.

84. Средняя температура . Средние температуры в июле в Реддинге, штат Калифорния, представляют собой высокую дневную температуру 98,2 градуса по Фаренгейту и низкую ночную температуру 64.9 градусов по Фаренгейту. Какое изменение температуры днем ​​и ночью? Подсказка: См. Раздел 2.3, где приведена формула для сравнения температур.

85. Собственный капитал . Чистая стоимость активов определяется как активы за вычетом обязательств. Активы — это все, что может быть конвертировано в наличные, а обязательства — это все долги. General Growth Properties, владельцы торгового центра Bayshore Mall, владеют активами на 29,6 млрд долларов и обязательствами на 27 млрд долларов и обанкротились. Какова была чистая стоимость активов General Growth Properties до банкротства? Times-Standard 17.04.2009

86. Виноградная дробленка . Предварительный отчет Департамента продовольствия и сельского хозяйства Калифорнии показывает, что в 2009 году в штате было произведено 3,69 миллиона тонн винного винограда. Это всего лишь меньше рекордных 3,76 миллиона тонн в 2005 году. На сколько тонн меньше рекордного показателя 2009 года? Associated Press-Times-Standard Calif. Урожай винограда в 2009 году подскочил на 23%.

87. Оборот . Обследование вакансий и текучести кадров Департамента труда утверждает, что работодатели наняли около 4 человек.08 миллионов человек в январе 2010 года, в то время как 4,12 миллиона человек были уволены или иным образом уволились с работы. Насколько больше людей потеряли работу, чем были наняты? Преобразуйте свой ответ в целое число. Associated Press-Times-Standard 03/10/10 Количество вакансий резко увеличилось в январе до 2,7 млн.

---

Вычитание путем перегруппировки или заимствования — Полный курс арифметики

(Урок 2, вопрос 7.)

Мы не можем взять 9 из 4.

Таким образом, мы возьмем 1 у 3, получив 2, и перегруппируем 1 с 4.

«9 из 14 это 5.» Потому что 9 плюс 5 равно 14.

Далее, мы не можем взять 8 из 2, поэтому возьмем 1 из 8, получив 7 —

— и перегруппируем это 1 с 2.

«8 из 12 равно 4. 1 из 7 равно 6.»

Мы всегда можем проверить разницу 645 на , прибавив к меньшему числу. «5 плюс 9 равно 14. 4 плюс 8 равно 12, плюс 1 равно 13.» И так далее.

В интересах мастерства ученик должен стараться не писать зачеркиванием или перегруппированными числами.Эти шаги следует практиковать мысленно. Ответ всегда можно проверить, добавив.

Другими словами, с практикой ученик должен уметь сказать:

«9 из 14 равно 5.»

«8 из 12 это 4.»

«1 из 7 равно 6.»

Вот развернутая форма:

Мы не можем взять 4 единицы из 0, и мы не можем разложить 0 десятков.Мы должны двигаться влево и начинать разложение с первого места, которое не равно 0, а именно 6.

6 находится в разряде тысяч. Мы разложим 1 из этих тысяч на 10 сотен и перегруппируем их с 0 сотнями.

Сейчас у нас 5 тысяч 10 соток.

Теперь разложим 1 из 10 сотен на 10 десятков.

Наконец, мы можем разложить 1 из 10 десятков на 10 единиц.

На этом декомпозиция и перегруппировка завершены.Вычитание выполняется легко:

Ответ: 4766.

Проблема будет возникать, конечно, вот так:

По мере практики ученик должен уметь сказать:

«4 из 10 равно 6.»

«3 из 9 равно 6.»

«2 из 9 равно 7. »

«1 из 5 это 4.»

Опять же, мы всегда можем проверить ответ, добавив.

(Сравните, пожалуйста, простоту сложения обоих чисел.)

Пример 8. Выравнивание. 68 . 27–3

Ответ . 3 — 3 шт. . Мы должны вычесть его из 8 единиц. Ответ: 6 5 . 27.

Кроме того, мы должны выровнять цифры, которые имеют одинаковое разрядное значение.

Пример 9. На вашем текущем счете есть остаток в размере 310 долларов США. 12, и вы выписываете чек на 45 долларов . 24. Затем вы вносите депозит в размере 126 . 75, и вы выписываете еще один чек на 22 доллара. 50. Каков ваш текущий баланс?

Ответ . Каждый раз, когда вы выписываете чек, вы должны вычесть его. И каждый раз, когда вы делаете депозит, вы добавляете. Вот последовательность вычитаний и сложений:

310 . 12		Начальное сальдо
— 45 . 24		Шах
264 . 88
+ 126 . 75		Залог
391 . 63
-22 . 50		Шах
369 . 13		Текущий остаток

Пожалуйста, «переверните» страницу и выполните несколько задач .

или

Переходите к следующему уроку.

Введение | Главная | Содержание

---

Авторские права © 2021 Лоуренс Спектор

Вопросы или комментарии?

Электронная почта: themathpage @ яндекс.com

Операции с десятичными знаками — Математика для учителей начальной школы

Конечно, мы можем складывать, вычитать, умножать и делить десятичные числа, переписывая их как дроби и используя известные нам алгоритмы. Конечно, иногда преобразование в дроби требует гораздо больше работы, чем просто работа с десятичными дробями (если вы знаете, что делаете). Итак, давайте подумаем о числовых значениях и вычислениях с десятичными знаками.

Помните, что когда мы использовали модель «Точки и прямоугольники» для добавления, она выглядела так.

Пример: 163 + 489

Затем мы проводим взрывы до тех пор, пока в каждом квадрате не останется меньше десяти точек, и мы обнаружим, что:

Вычитание было немного сложнее.

Пример: 921 — 551

Начнем с представления 921:

Поскольку мы хотим «убрать» 551, это означает, что мы убираем пять точек из поля сотен, оставляя четыре точки.

Теперь мы хотим убрать пять точек из поля десятков, но мы не можем этого сделать! Там всего две точки.Что мы можем сделать? Что ж, у нас все еще есть несколько сотен, поэтому мы можем «взорвать» сотню точку и вместо этого поставить десять точек в поле десятков. Тогда мы сможем забрать пятерых из них, оставив семь.

(Обратите внимание, что у нас на одну точку меньше в поле сотен; теперь там только три точки.)

Теперь мы хотим взять одну точку из поля единиц, и это не оставляет точек там.

Мы заключаем, что:

Самостоятельно

Работайте над следующими упражнениями самостоятельно или с партнером.

1. Для каждого расчета нарисуйте модель «Точки и прямоугольники» и используйте ее, чтобы найти результат расчета.

2. Для каждого вычисления, приведенного ниже, быстро добавьте десятичные дроби, используя те же соображения, что и в предыдущих задачах.

Думать / Пара / Поделиться

• Хлоя добавила и получила ответ. В чем была вероятная ошибка Хлои? Как ее учитель, как вы могли бы помочь Хлое лучше понять операцию сложения?

• В начальной школе учеников учат складывать и вычитать десятичные дроби, «ставя десятичные точки в ряд. Используйте модель «Точки и прямоугольники», чтобы объяснить, почему это сокращение имеет смысл.

Давайте быстро рассмотрим модель «точки и прямоугольники» для умножения целых чисел, прежде чем мы вернемся к разговору о десятичных дробях.

Самостоятельно

Работайте над следующими упражнениями самостоятельно или с партнером.

1. Выполните каждое вычисление, используя рассуждения, как в приведенном выше примере умножения.

2. Выполните каждое вычисление, используя рассуждения, как в примерах «Деление и десятичные дроби».

Вы знаете, что умножение целого числа по основанию десять на 10 приводит к добавлению нуля к правому концу числа. Ваша работа, приведенная выше, должна убедить вас, что это не работает с десятичными знаками!

Думать / Пара / Поделиться

• Напишите новое правило, которое работает как для целых, так и для десятичных чисел:

Если я умножу целое или десятичное число на 10, простой способ найти результат —

.

___________________________.

• Обоснуйте заявление, которое вы сделали выше.
• С этим мышлением можно пойти гораздо дальше. Каков эффект деления числа, записанного в десятичной системе счисления, на десять? К сотне? Обоснуйте то, что вы говорите.

Вы, наверное, знаете алгоритм умножения десятичных чисел вручную. Но если вы хорошо обдумаете алгоритм, должно иметь смысл , исходя из того, что представляют собой десятичные числа и что означает умножение.Давайте начнем с числового умножения целых чисел на десятичные.

Думать / Пара / Поделиться

Рассмотрим выражение

Заполните поле целым или десятичным числом, чтобы получилось:

• Больше 100.
• Больше 64, но меньше 100.
• Не менее 17, но менее 32.
• Равно 16.
• Больше 8, но меньше 16.
• Меньше 8, но больше 0.

Обязательно обосновываю свои ответы. Вам следует использовать свое чувство чисел, а не вычислять вручную или с помощью калькулятора!

Один из способов умножения десятичных чисел путем преобразования их в дроби и последующего использования того, что вы знаете об умножении дробей. Есть и другие способы думать об умножении, которые сосредоточены на чувстве числа и расстановке значений, а не на механике вычислений.

Вы должны заметить, что ученик использует ассоциативное свойство умножения:

Проблема 15

Для каждого вычисления ниже результат вычисления отображается правильно, но десятичная точка отсутствует.Используйте числовой смысл и рассуждения, чтобы правильно расставить десятичную точку и вкратце обосновать, откуда вы знаете, что правы.

(Не пользуйтесь калькулятором, не вычисляйте умножение вручную и не используйте уловку «подсчета количества десятичных знаков». Используйте свое понимание чисел!)

Самостоятельно

Работайте над следующими упражнениями самостоятельно или с партнером.

1. Запишите каждое число в виде дроби.(Запишите их как «неправильные дроби», а не «смешанные числа».)

2. В упражнении (1) выше, как количество цифр справа от десятичной точки соотносится с количеством нулей в знаменателе? Используйте то, что вы знаете о числовой стоимости, чтобы объяснить, почему ваш ответ всегда верен (не только для приведенных выше примеров).
3. Найдите каждый продукт.

4. В упражнении (3) выше, как количество нулей в произведении связано с количеством нулей в двух множителях? Используйте то, что вы знаете о числовой стоимости, чтобы объяснить, почему ваш ответ всегда верен (не только для приведенных выше примеров).
   1. Если вы запишете дробью, сколько нулей будет в знаменателе?
   2. Что, если вы запишете дробью, сколько нулей будет в знаменателе?
   3. Сколько нулей было бы в знаменателе произведения и? (Не вычисляйте произведение, чтобы ответить на этот вопрос!)
5. Используйте тот факт, что и ваши ответы на приведенные выше упражнения, чтобы найти. Объясните, как вы получили ответ.

Стандартный алгоритм умножения

Стандартный алгоритм умножения десятичных чисел можно описать так:

Шаг 1

Вычислите произведение, как если бы два множителя были целыми числами.(Не обращайте внимания на десятичные точки.)

Шаг 2

Подсчитайте количество цифр справа от десятичной точки в каждом множителе и сложите эти числа. Назовите результат.

Шаг 3

Сумма, которую вы нашли на шаге 2, будет числом цифр справа от десятичной точки в произведении. Поэтому поместите десятичную точку в соответствии с отсчетом соответствующего количества знаков справа.

Думать / Пара / Поделиться

• Запишите два примера умножения десятичных чисел с использованием стандартного алгоритма, описанного выше.

• Используйте то, что вы знаете о разрядах, дробях и умножении, чтобы получить , внимательно объясните, почему стандартный алгоритм, описанный выше, имеет смысл.

Как и следовало ожидать, разделение десятичных знаков сложнее объяснить, чем любые другие операции. Трудно адаптировать нашу модель «точки и квадраты» для деления. Предположим, мы хотим вычислить. Конечно, мы можем нарисовать картинку, но как мы можем составить группы точек?

Думать / Пара / Поделиться

Давайте начнем с того, что вы уже знаете.Выполните это вычисление (вручную, а не с помощью калькулятора), показывая всю свою работу. Объясните партнеру свой метод и посмотрите, рассчитывает ли он так же.

Самостоятельно

Работайте над следующими упражнениями самостоятельно или с партнером.

1. Объясните, почему эти две дроби эквивалентны.

2. Объясните, почему эти два вычисления деления дают одинаковый результат.

3. Объясните, почему эти три дроби эквивалентны.

4. Объясните, почему эти три вычисления деления дают одинаковый результат.

5. Заполните поле, чтобы уравнение соответствовало действительности. Обязательно обоснуйте свой ответ.

Стандартный алгоритм деления

Стандартный алгоритм деления чисел, представленных конечными десятичными разложениями, выглядит примерно так:

Шаг 1

Переместите десятичную точку делителя в конец числа.

Шаг 2

Переместите десятичную точку делимого на такое же количество позиций (на то же расстояние и в том же направлении).

Шаг 3

Разделите новое десятичное делимое (из шага 2) на новый делитель целого числа (из шага 1). Поскольку мы делим на целое число, наши стандартные методы имеют смысл.

Это довольно механическое описание, которое не дает подробного понимания , почему работает этот алгоритм .

Проблема 16

Внимательно объясните , почему алгоритм, описанный выше в три этапа, работает для вычисления деления десятичных чисел. Вам необходимо объяснить, что происходит, когда вы «перемещаете десятичную точку» на шагах 1 и 2, и почему результат, вычисленный на шаге 3, совпадает с исходной задачей.

Неопределенность при сложении и вычитании

Цели обучения

• Укажите правило округления значений, полученных путем сложения или вычитания.
• Примените правило к соответствующим проблемам.

Как вы думаете, сколько лет этому калькулятору?

Калькуляторы — отличные устройства. Их изобретение позволило проводить быстрые вычисления на работе, в школе или в других местах, где манипуляции с числами должны выполняться быстро и точно. Но они хороши настолько, насколько хороши введенные в них числа. Калькулятор не может определить, насколько точен каждый из набора чисел, и ответ, отображаемый на экране, должен быть оценен пользователем на предмет надежности.

Рассмотрим два отдельных измерения массы: 16,7 г и 5,24 г. Первое измерение массы (16,7 г) известно только с точностью до десятых долей или одной цифрой после десятичной точки. Нет информации о его сотых долях, поэтому эту цифру нельзя считать нулевой. Второе измерение (5,24 г) известно с точностью до сотых долей или двумя цифрами после десятичной точки.

Если сложить эти массы, на калькуляторе получится 16,7 + 5,24 = 21,94 г. Сообщая ответ как 21.94 г говорит о том, что сумма известна до сотых долей. Однако это не может быть правдой, потому что сотые доли первой массы были совершенно неизвестны. Расчетный ответ необходимо округлить таким образом, чтобы отразить достоверность каждого из измеренных значений, которые на него повлияли. Для задач сложения и вычитания ответ должен быть округлен до того же числа десятичных знаков, что и результат измерения с наименьшим числом десятичных знаков. Сумма вышеуказанных масс будет правильно округлена до 21.9 г.

При работе с целыми числами обратите внимание на последнюю значащую цифру слева от десятичной точки и округлите свой ответ до той же точки. Например, рассмотрим вычитание: 78 500 м — 362 м. Расчетный результат — 78 138 м. Однако первое измерение известно только разрядам сотен, так как 5 — это последняя значащая цифра. Округление результата до той же точки означает, что правильный результат равен 78 100 м.

Сводка

• Для задач сложения и вычитания ответ должен быть округлен до того же числа десятичных знаков, что и измерение с наименьшим числом десятичных знаков.

Практика

Прочтите информацию и работайте над проблемами на следующем веб-сайте:

http://sigfigscalculator.appspot.com/tutorial/add_and_subtract

Обзор

1. Каков основной принцип работы со сложением и вычитанием?
2. На что вы обращаете внимание при работе с целыми числами?

Двоичное сложение и вычитание — Правила и примеры

Сложение и вычитание в двоичной системе счисления аналогично десятичной системе счисления. Единственное отличие состоит в том, что десятичная система счисления состоит из цифр от 0 до 9 и их основание — 10, тогда как двоичная система счисления состоит только из двух цифр (0 и 1), что упрощает их работу. Сложение и вычитание двоичных систем счисления подробно поясняются ниже.

Для понимания, двоичное сложение сначала рассматривает сложение двух десятичных чисел, как показано ниже.

Когда мы добавляем единичный столбец двоичной цифры (то есть 7 + 4), мы получаем число, которое больше основания десятичного числа (основание числа — 10, а сумма цифр — 11).Теперь добавьте столбец десятков двоичной цифры, сумма которой равна 9 и, следовательно, меньше основания. Таким образом, в десятичном столбце двоичной цифры нет переноса.

Решение указанной выше суммы объясняется ниже.

Бинарное сложение

В двоичной системе счисления используются только две цифры 0 и 1, благодаря чему их сложение несложно. Как упоминалось выше, существует четыре основных операции для двоичного сложения.

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10

Приведенные выше первые три уравнения очень идентичны двоичному числу.Добавление двоичных файлов по столбцам подробно описано ниже. Рассмотрим сложение 11101 и 11011.

Вышеупомянутая сумма выполняется следующим шагом

1 + 1 = 10 = 0 с переносом 1.

1 + 0 + 1 = 10 = 0 с переносом 1

1 + 1 + 0 = 10 = 10 = 0 с переносом 1

1 + 1 + 1 = 10 + 1 = 11 = 1 с переносом 1

1 +1 +1 = 11

Внимательно обратите внимание на , что 10 + 1 = 11, что эквивалентно двум + один = три (следующее двоичное число после 10)

Таким образом, требуется результат 111000.

Двоичное вычитание

Вычитание двоичной цифры зависит от четырех основных операций

0-0 = 0
1-0 = 1
1-1 = 0
10-1 = 1

Приведенные выше первые три операции легко понять, поскольку они идентичны десятичному вычитанию. Четвертую операцию можно понять по логике два минус один — один.

Для двоичного числа с двумя или более цифрами вычитание выполняется столбец за столбцом, как при десятичном вычитании.Кроме того, иногда приходится брать деньги из следующего более высокого столбца. Рассмотрим следующий пример.

Вышеупомянутое вычитание выполняется с помощью следующих шагов.

0 — 0 = 0

Для 0 — 1 = 1, взяв в долг 1, а затем 10 — 1 = 1

Для 1-0, поскольку 1 уже задано, становится 0-0 = 0

1 — 1 = 0

Следовательно, результат будет 0010.

математических правил вычитания | Sciencing

Обновлено 1 декабря 2020 г.

Кевин Бек

Вычитание, наряду со сложением, умножением и делением, является одной из четырех основных операций арифметики.Говоря простым языком, вычитание одного числа из другого означает уменьшение значения второго числа точно на величину первого. Хотя в принципе это простой процесс, на практике задачи вычитания часто являются частью более сложных вычислений, и в этих случаях полезно знать правила, чтобы не застрять.

Несколько примеров математических правил вычитания:

Вычитание с использованием отрицательных и положительных чисел

Когда вы вычитаете положительное число из меньшего положительного числа, результатом будет отрицательное число:

8-11 = — 3

Вычитание отрицательного числа приводит к сложению положительного эквивалента этого числа.Другими словами, отрицательные числа сокращаются для создания положительного:

7 — (- 5) = 7 + 5 = 12

Значимые числа и вычитание

Значимые числа — это все цифры, показанные справа от десятичная точка в любом числе. Например, 2.35608 имеет пять значащих цифр, 12.75 — две, а 163.922 — три.

При вычитании одного десятичного числа из другого или нескольких таких чисел друг из друга дайте ответ, содержащий наименьшее количество значащих цифр любого числа в задаче.