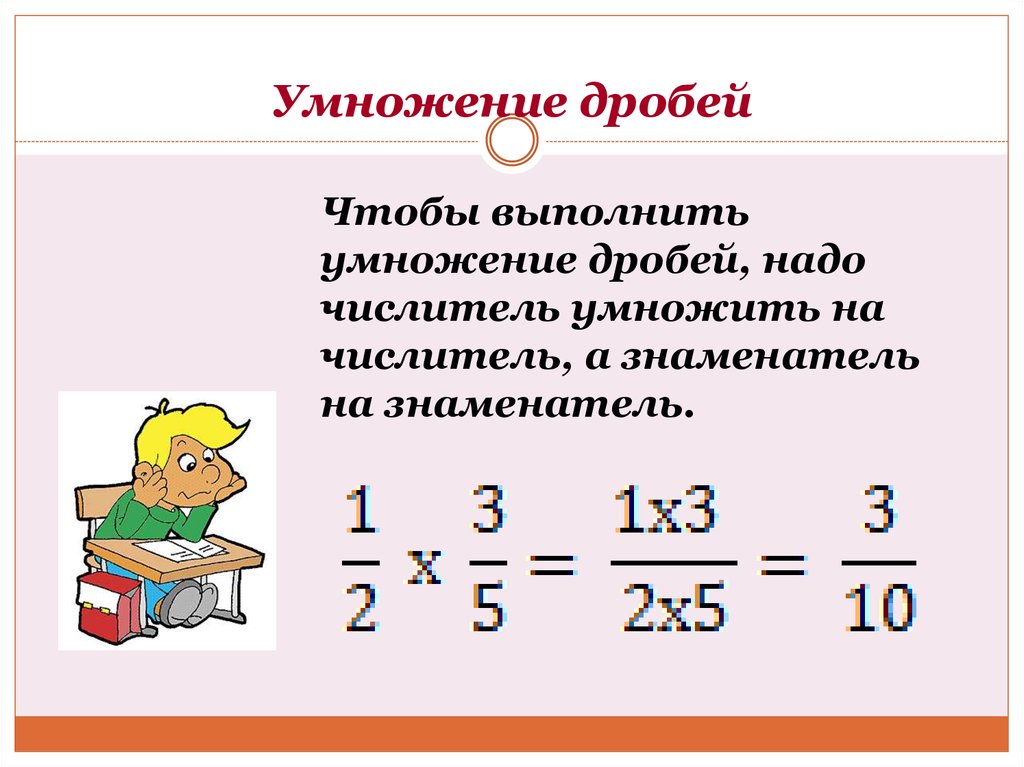
Как выполнить умножение двух смешанных чисел. Дробь

Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками. Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.

Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.

Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский.

Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.

Умножение дробей с разными знаменателями

Изначально стоит определить разновидности дробей :

• правильные;
• неправильные;
• смешанные.

Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.

При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:

a/ b * c/ d = a*c / b*d.

Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.

Стоит рассмотреть умножение дробей с разными знаменателями на примерах:

• 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
• 4/ 6 * 3/ 7 = 2/ 3 * 3/7 2*3 / 3*7 = 6/ 21 .

В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.

Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:

1 4/ 11 =1 + 4/ 11.

Как происходит перемножение

Предлагается несколько примеров для рассмотрения.

2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.

В примере используется умножение числа на

обыкновенную дробную часть , записать правило для этого действия можно формулой:

a * b/ c = a*b / c.

По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:

4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.

Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:

d * e/ f = e/ f: d.

Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.

Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:

1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.

В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:

a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.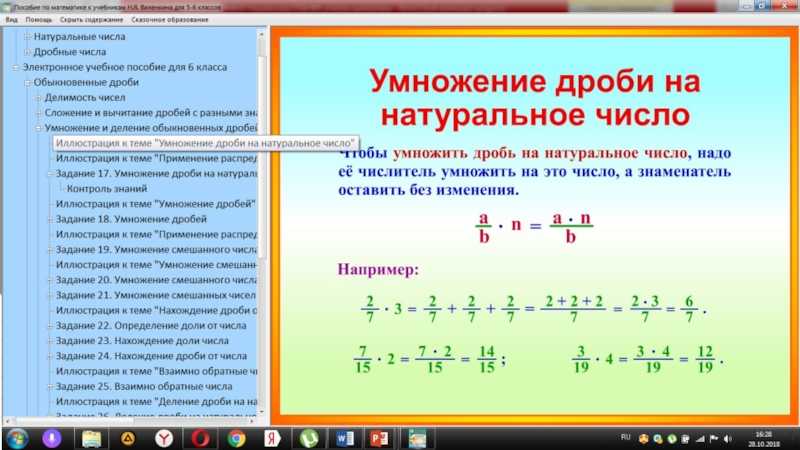

Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».

Умножение неправильных дробей

производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.

В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить».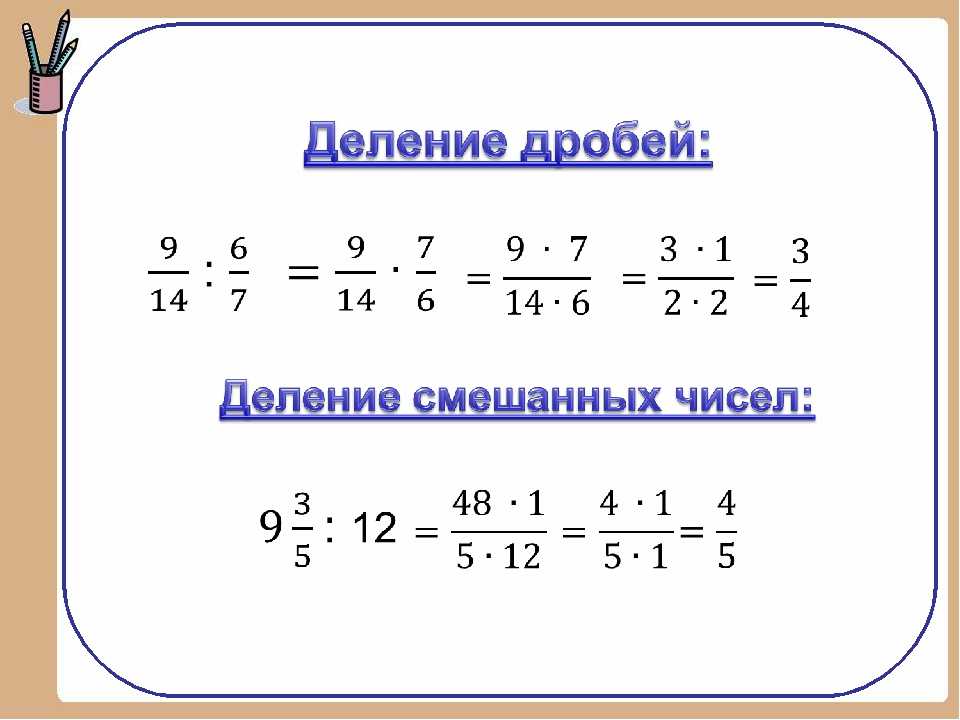 Программа считает автоматически.

Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а

целые дробные выражения , но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.

В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».

В курсе средней и старшей школы учащиеся проходили тему «Дроби». Однако это понятие гораздо шире, чем дается в процессе обучения. Сегодня понятие дроби встречается достаточно часто, и не каждый может провести вычисления какого-либо выражения, к примеру, умножение дробей.

Что такое дробь?

Так исторически сложилось, что дробные числа появились из-за необходимости измерять. Как показывает практика, часто встречаются примеры на определение длины отрезка, объема прямоугольного прямоугольника.

Первоначально ученики знакомятся с таким понятием, как доля. К примеру, если разделить арбуз на 8 частей, то каждому достанется по одной восьмой арбуза. Вот эта одна часть из восьми и называется долей.

Доля, равная ½ от какой-либо величины, называется половиной; ⅓ — третью; ¼ — четвертью. Записи вида 5 / 8 , 4 / 5 , 2 / 4 называют обыкновенными дробями. Обыкновенная дробь разделяется на числитель и знаменатель. Между ними находится черта дроби, или дробная черта. Дробную черту можно нарисовать в виде как горизонтальной, так и наклонной линии. В данном случае она обозначает знак деления.

Знаменатель представляет, на сколько одинаковых долей разделяют величину, предмет; а числитель — сколько одинаковых долей взято. Числитель пишется над дробной чертой, знаменатель — под ней.

Удобнее всего показать обыкновенные дроби на координатном луче. Если единичный отрезок разделить на 4 равные доли, обозначить каждую долю латинской буквой, то в результате можно получить отличное наглядное пособие. Так, точка А показывает долю, равную 1 / 4 от всего единичного отрезка, а точка В отмечает 2 / 8 от данного отрезка.

Разновидности дробей

Дроби бывают обыкновенные, десятичные, а также смешанные числа. Кроме того, дроби можно разделить на правильные и неправильные. Эта классификация больше подходит для обыкновенных дробей.

Под правильной дробью понимают число, у которого числитель меньше знаменателя. Соответственно, неправильная дробь — число, у которого числитель больше знаменателя. Второй вид обычно записывают в виде смешанного числа. Такое выражение состоит из целой и дробной части. Например, 1½. 1 — целая часть, ½ — дробная. Однако если нужно провести какие-то манипуляции с выражением (деление или умножение дробей, их сокращение или преобразование), смешанное число переводится в неправильную дробь.

Правильное дробное выражение всегда меньше единицы, а неправильное — больше либо равно 1.

Что касается то под этим выражением понимают запись, в которой представлено любое число, знаменатель дробного выражения которого можно выразить через единицу с несколькими нулями. Если дробь правильная, то целая часть в десятичной записи будет равна нулю.

Чтобы записать десятичную дробь, нужно сначала написать целую часть, отделить ее от дробной с помощью запятой и потом уже записать дробное выражение. Необходимо помнить, что после запятой числитель должен содержать столько же цифровых символов, сколько нулей в знаменателе.

Пример . Представить дробь 7 21 / 1000 в десятичной записи.

Алгоритм перевода неправильной дроби в смешанное число и наоборот

Записывать в ответе задачи неправильную дробь некорректно, поэтому ее нужно перевести в смешанное число:

• разделить числитель на имеющийся знаменатель;
• в конкретном примере неполное частное — целое;
• и остаток — числитель дробной части, причем знаменатель остается неизменным.

Пример . Перевести неправильную дробь в смешанное число: 47 / 5 .

Решение . 47: 5. Неполное частное равняется 9, остаток = 2. Значит, 47 / 5 = 9 2 / 5 .

Иногда нужно представить смешанное число в качестве неправильной дроби. Тогда нужно воспользоваться следующим алгоритмом:

• целая часть умножается на знаменатель дробного выражения;
• полученное произведение прибавляется к числителю;
• результат записывается в числителе, знаменатель остается неизменным.

Пример . Представить число в смешанном виде в качестве неправильной дроби: 9 8 / 10 .

Решение . 9 х 10 + 8 = 90 + 8 = 98 — числитель.

Ответ : 98 / 10.

Умножение дробей обыкновенных

Над обыкновенными дробями можно совершать различные алгебраические операции. Чтобы перемножить два числа, нужно числитель перемножить с числителем, а знаменатель со знаменателем. Причем умножение дробей с разными знаменателямине отличается от произведения дробных чисел с одинаковыми знаменателями.

Случается, что после нахождения результата нужно сократить дробь. В обязательном порядке нужно максимально упростить получившееся выражение. Конечно, нельзя сказать, что неправильная дробь в ответе — это ошибка, но и назвать верным ответом ее тоже затруднительно.

Пример . Найти произведение двух обыкновенных дробей: ½ и 20 / 18 .

Как видно из примера, после нахождения произведения получилась сократимая дробная запись. И числитель, и знаменатель в данном случае делится на 4, и результатом выступает ответ 5 / 9 .

Умножение дробей десятичных

Произведение десятичных дробей довольно сильно отличается от произведения обыкновенных по своему принципу. Итак, умножение дробей заключается в следующем:

• две десятичные дроби нужно записать друг под другом так, чтобы крайние правые цифры оказались одна под другой;
• нужно перемножить записанные числа, несмотря на запятые, то есть как натуральные;
• подсчитать количество цифр после знака запятой в каждом из чисел;
• в получившемся после перемножения результате нужно отсчитать справа столько цифровых символов, сколько содержится в сумме в обоих множителях после запятой, и поставить отделяющий знак;
• если цифр в произведении оказалось меньше, тогда перед ними нужно написать столько нулей, чтобы покрыть это количество, поставить запятую и приписать целую часть, равную нулю.

Пример . Вычислить произведение двух десятичных дробей: 2,25 и 3,6.

Решение .

Умножение смешанных дробей

Чтобы вычислить произведение двух смешанных дробей, нужно использовать правило умножения дробей:

• перевести числа в смешанном виде в неправильные дроби;
• найти произведение числителей;
• найти произведение знаменателей;
• записать получившийся результат;
• максимально упростить выражение.

Пример . Найти произведение 4½ и 6 2 / 5.

Умножение числа на дробь (дроби на число)

Помимо нахождения произведения двух дробей, смешанных чисел, встречаются задания, где нужно помножить на дробь.

Итак, чтобы найти произведение десятичной дроби и натурального числа, нужно:

• записать число под дробью так, чтобы крайние правые цифры оказались одна над другой;
• найти произведение, несмотря на запятую;
• в полученном результате отделить целую часть от дробной с помощью запятой, отсчитав справа то количество знаков, которое находится после запятой в дроби.

Чтобы умножить обыкновенную дробь на число, следует найти произведение числителя и натурального множителя. Если в ответе получается сократимая дробь, ее следует преобразовать.

Пример . Вычислить произведение 5 / 8 и 12.

Решение . 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.

Ответ : 7 1 / 2.

Как видно из предыдущего примера, необходимо было сократить получившийся результат и преобразовать неправильное дробное выражение в смешанное число.

Также умножение дробей касается и нахождения произведения числа в смешанном виде и натурального множителя. Чтобы перемножить эти два числа, следует целую часть смешанного множителя умножить на число, числитель помножить на это же значение, а знаменатель оставить неизменным. Если требуется, нужно максимально упростить получившийся результат.

Пример . Найти произведение 9 5 / 6 и 9.

Решение . 9 5 / 6 х 9 = 9 х 9 + (5 х 9) / 6 = 81 + 45 / 6 = 81 + 7 3 / 6 = 88 1 / 2.

Ответ : 88 1 / 2.

Умножение на множители 10, 100, 1000 или 0,1; 0,01; 0,001

Из предыдущего пункта вытекает следующее правило. Для умножения дроби десятичной на 10, 100, 1000, 10000 и т. д. нужно передвинуть запятую вправо на столько символов цифр, сколько нулей во множителе после единицы.

Пример 1 . Найти произведение 0,065 и 1000.

Решение . 0,065 х 1000 = 0065 = 65.

Ответ : 65.

Пример 2 . Найти произведение 3,9 и 1000.

Решение . 3,9 х 1000 = 3,900 х 1000 = 3900.

Ответ : 3900.

Если нужно перемножить натуральное число и 0,1; 0,01; 0,001; 0,0001 и т. д., следует передвинуть влево запятую в получившемся произведении на столько символов цифр, сколько нулей находится до единицы. Если необходимо, перед натуральным числом записываются нули в достаточном количестве.

Пример 1 . Найти произведение 56 и 0,01.

Решение . 56 х 0,01 = 0056 = 0,56.

Ответ : 0,56.

Пример 2 . Найти произведение 4 и 0,001.

Решение . 4 х 0,001 = 0004 = 0,004.

Ответ : 0,004.

Итак, нахождение произведения различных дробей не должно вызывать затруднений, разве что подсчет результата; в таком случае без калькулятора просто не обойтись.

Чтобы правильно умножить дробь на дробь или дробь на число, нужно знать простые правила. Эти правила сейчас разберем подробно.

Умножение обыкновенной дроби на дробь.

Чтобы умножить дробь на дробь необходимо посчитать произведение числителей и произведение знаменателей этих дробей.

\(\bf \frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\\\)

Рассмотрим пример:
Мы числитель первой дроби умножаем с числителем второй дроби, также и знаменатель первой дроби умножаем со знаменателем второй дроби.

\(\frac{6}{7} \times \frac{2}{3} = \frac{6 \times 2}{7 \times 3} = \frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\)

Дробь \(\frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\) сократили на 3.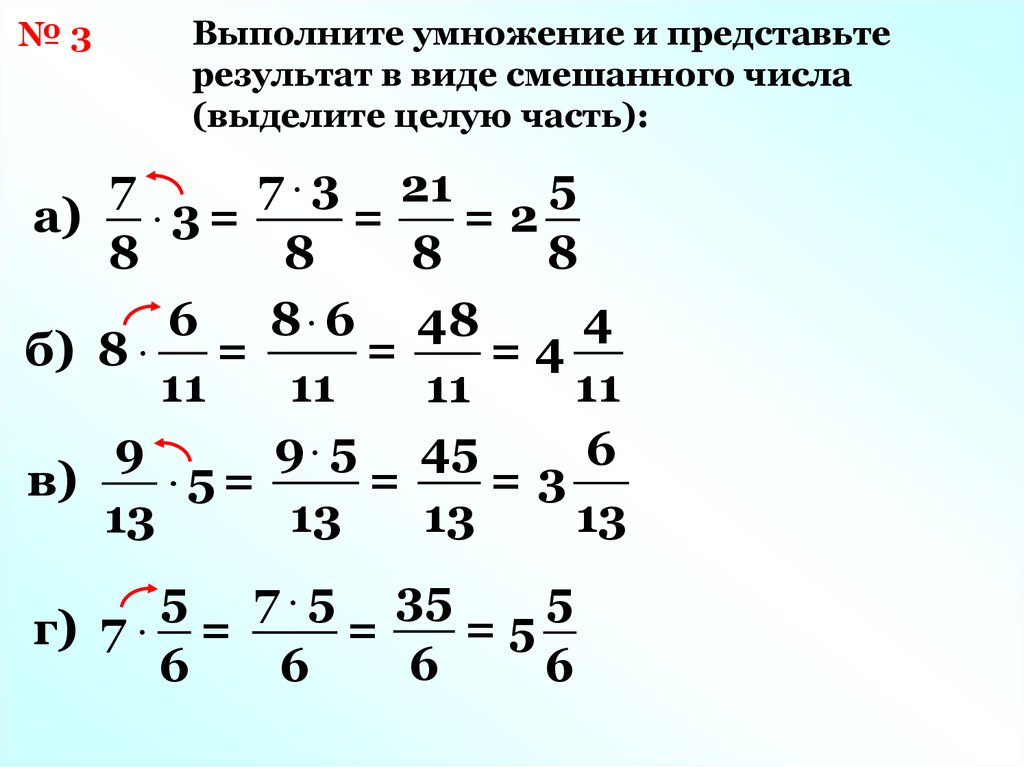

Умножение дроби на число.

Для начала вспомним правило, любое число можно представить в виде дроби \(\bf n = \frac{n}{1}\) .

Воспользуемся этим правилом при умножении.

\(5 \times \frac{4}{7} = \frac{5}{1} \times \frac{4}{7} = \frac{5 \times 4}{1 \times 7} = \frac{20}{7} = 2\frac{6}{7}\\\)

Неправильную дробь \(\frac{20}{7} = \frac{14 + 6}{7} = \frac{14}{7} + \frac{6}{7} = 2 + \frac{6}{7}= 2\frac{6}{7}\\\) перевели в смешанную дробь.

Другими словами, при умножении числа на дробь, число умножаем на числитель, а знаменатель оставляем без изменения. Пример:

\(\frac{2}{5} \times 3 = \frac{2 \times 3}{5} = \frac{6}{5} = 1\frac{1}{5}\\\\\) \(\bf \frac{a}{b} \times c = \frac{a \times c}{b}\\\)

Умножение смешанных дробей.

Чтобы перемножить смешанные дроби, нужно сначала каждую смешанную дробь представить в виде неправильно дроби, а потом воспользоваться правилом умножения. Числитель умножаем с числителем, знаменатель умножаем со знаменателем.

Пример:
\(2\frac{1}{4} \times 3\frac{5}{6} = \frac{9}{4} \times \frac{23}{6} = \frac{9 \times 23}{4 \times 6} = \frac{3 \times \color{red} {3} \times 23}{4 \times 2 \times \color{red} {3}} = \frac{69}{8} = 8\frac{5}{8}\\\)

Умножение взаимно обратных дробей и чисел.

Дробь \(\bf \frac{a}{b}\) является обратной для дроби \(\bf \frac{b}{a}\), при условии a≠0,b≠0.
Дроби \(\bf \frac{a}{b}\) и \(\bf \frac{b}{a}\) называются взаимно обратными дробями. Произведение взаимно обратных дробей равно 1.
\(\bf \frac{a}{b} \times \frac{b}{a} = 1 \\\)

Пример:
\(\frac{5}{9} \times \frac{9}{5} = \frac{45}{45} = 1\\\)

Вопросы по теме:
Как умножить дробь на дробь?
Ответ: произведение обыкновенных дробей является умножение числитель с числителем, знаменатель со знаменателем. Чтобы получить произведение смешанных дробей нужно перевести их в неправильную дробь и перемножить по правилам.

Как выполнить умножение дробей с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, умножение происходит по правилу нахождения произведения числитель с числителем, знаменатель со знаменателем.

Как умножать смешанные дроби?
Ответ: в первую очередь надо перевести смешанную дробь в неправильную дробь и далее находить произведение по правилам умножения.

Как умножить число на дробь?
Ответ: число умножаем с числителем, а знаменатель оставляем тот же.

Пример №1:
Вычислите произведение: а) \(\frac{8}{9} \times \frac{7}{11}\) б) \(\frac{2}{15} \times \frac{10}{13}\)

Решение:
а) \(\frac{8}{9} \times \frac{7}{11} = \frac{8 \times 7}{9 \times 11} = \frac{56}{99}\\\\\)
б) \(\frac{2}{15} \times \frac{10}{13} = \frac{2 \times 10}{15 \times 13} = \frac{2 \times 2 \times \color{red} {5}}{3 \times \color{red} {5} \times 13} = \frac{4}{39}\)

Пример №2:
Вычислите произведения числа и дроби: а) \(3 \times \frac{17}{23}\) б) \(\frac{2}{3} \times 11\)

Решение:
а) \(3 \times \frac{17}{23} = \frac{3}{1} \times \frac{17}{23} = \frac{3 \times 17}{1 \times 23} = \frac{51}{23} = 2\frac{5}{23}\\\\\)
б) \(\frac{2}{3} \times 11 = \frac{2}{3} \times \frac{11}{1} = \frac{2 \times 11}{3 \times 1} = \frac{22}{3} = 7\frac{1}{3}\)

Пример №3:
Напишите число обратное дроби \(\frac{1}{3}\)?
Ответ: \(\frac{3}{1} = 3\)

Пример №4:
Вычислите произведение двух взаимно обратных дробей: а) \(\frac{104}{215} \times \frac{215}{104}\)

Решение:
а) \(\frac{104}{215} \times \frac{215}{104} = 1\)

Пример №5:
Могут ли взаимно обратные дроби быть:
а) одновременно правильными дробями;
б) одновременно неправильными дробями;
в) одновременно натуральными числами?

Решение:
а) чтобы ответить на первый вопрос приведем пример. Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.

б) практически при всех переборах дробей это условие не выполняется, но существуют некоторые числа, которые выполняют условие быть одновременно неправильной дробью. Например неправильная дробь \(\frac{3}{3}\) , обратная ей дробь равна \(\frac{3}{3}\). Получаем две неправильные дроби. Ответ: не всегда при определённых условиях, когда числитель и знаменатель равны.

в) натуральные числа – это числа которые мы используем при счете, например, 1, 2, 3, …. Если возьмем число \(3 = \frac{3}{1}\), то обратная ей дробь будет \(\frac{1}{3}\). Дробь \(\frac{1}{3}\) не является натуральным числом. Если мы переберем все числа, получать обратное число всегда дробь, кроме 1. Если возьмем число 1, то обратная ей дробь будет \(\frac{1}{1} = \frac{1}{1} = 1\). Число 1 натуральное число. Ответ: могут быть одновременно натуральными числами только в одном случае, если это число 1.

Пример №6:
Выполните произведение смешанных дробей: а) \(4 \times 2\frac{4}{5}\) б) \(1\frac{1}{4} \times 3\frac{2}{7}\)

Решение:
а) \(4 \times 2\frac{4}{5} = \frac{4}{1} \times \frac{14}{5} = \frac{56}{5} = 11\frac{1}{5}\\\\ \)
б) \(1\frac{1}{4} \times 3\frac{2}{7} = \frac{5}{4} \times \frac{23}{7} = \frac{115}{28} = 4\frac{3}{7}\)

Пример №7:
Могут ли два взаимно обратных числа быть одновременно смешанными числами?

Рассмотрим на примере. Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.

Умножение смешанных чисел. 6-й класс

Этапы урока	Формируемые УУД	Деятельность учителя	Деятельность учащегося
Самоопределение к деятельности Цели: – психологический настрой уч-ся на работу; – создать условия для возникновения у учеников внутренней потребности включения в учебную деятельность.	Личностные: осмысление внутренней позиции ученика на уровне положительного отношения к уроку. Регулятивные: самоорганизация и организация своего рабочего места.	Упражнение «Ладошки» – Ребята, потрите ладошки так, чтобы они стали горячими. Быстро передайте тепло соседу по парте, соединив свои ладошки с ладошками товарища. Пусть тепло вашей души поддерживает вас и помогает вам. – А девиз нашего сегодняшнего урока такой: «О, сколько нам открытий чудных готовит просвещения дух». (На доске ) – Значит, чему будет посвящён наш урок? – А были ли открытия в вашей жизни? Как вы думаете, что такое открытие?	Проявляют психологическую готовность к познавательной деятельности.   – Открытию нового знания. Ребята с места отвечают на вопросы
Актуализация знаний Цель: повторение изученного материала необходимого для «открытия нового знания» и выявление затруднений.	Личностные: осознание своих эмоций, интереса к изучению математике. Познавательные: актуализация изученных способов действий, развитие мыслительных операций; умение из предложенной информации выделять главное. Регулятивные: учатся работать по предложенному учителем плану; умение разбивать на группы, делать  выводы, мотивация к учебной деятельности.  Коммуникативные: планирование учебного сотрудничества с учителем и со сверстниками; уметь выслушивать и понимать речь других.	Фронтальный опрос: Давайте вспомним, что мы изучали ранее, для этого ответим на вопросы: – Что называют сокращением дроби?  – Какую дробь называют несократимой?  – К какому новому знаменателю можно привести данную дробь?  – Как найти дополнительный множитель?  – Какая дробь называется правильной (неправильной)?  – Как из неправильной дроби выделить целую часть?  – Как записать число в виде неправильной дроби?  – Как умножить дробь на натуральное число?  – Как выполнить умножение двух дробей?  – Свойства нуля при умножении?	С места называют ответы.
Постановка учебной проблемы Цель: выявить место затруднения, зафиксировать во внешней речи причину затруднения.	Познавательные: уметь ориентироваться в своей системе знаний; отличать новое от уже известного с помощью учителя. Регулятивные: подготовка к самостоятельной формулировки темы урока. Коммуникативные: формирование способности сохранять доброжелательное отношение друг к другу в учебной деятельности.	– Теперь, ребята, мы с вами поработаем в парах. – О чём вы должны помнить, работая в парах?	Выслушивать друг друга, не перебивая. Рассуждать спокойно, не мешая другим. Помнить пословицу: «Умеешь сам – научи другого».
		– Итак,  у Вас на столах лежат карточки с примерами. Вам необходимо решить их. Вычислите: = После решения выполнить проверку, на слайде появились ответы.	Решают в группах.
		– Какое задание вызвало затруднение?	–
		– Почему?	– Мы еще не умеем умножать такие примеры.
		– Как называется число ?	– Смешанным.
		– Как вы думаете какова тема нашего сегодняшнего урока?	– Умножение смешанных чисел.
		– Какие цели на сегодняшний урок вы перед собой ставите?	Формулируют цели урока
Открытие уч-ся нового знания Цель: организовать устранение и фиксирование преодоления затруднения.	Познавательные: активизация мыслительной деятельности через проблемное задание; добывать новые знания извлекать информацию, представленную в разных формах; ориентирование в условных обозначениях. Регулятивные: определение и формулирование цели деятельности на уроке с помощью учителя; осмысление выделенных педагогом ориентиров действия в новом учебном материале; участвовать в оценке и обсуждении полученного результата. Коммуникативные: оформление своих мыслей согласно заданным рамкам обсуждения, аргументация своих суждений; участвовать в обсуждениях, работая в паре. Личностные: понимать свои желания и цели по  отношению к  общим учебным задачам.	– Давайте вспомним, как мы складывали и вычитали смешанные числа? – Можем ли мы перемножать неправильные дроби? – Попробуйте составить алгоритм умножения смешанных чисел? Параллельно ответам появляется алгоритм на доске, каждому учащемуся раздается памятка – «Алгоритм умножения смешанных чисел».	– Мы для этого переводили в неправильные дроби – Да 1. Перевести смешанные числа в неправильную дроб 2.Выполнить умножение по правилу умножения дробе 3. Сократить полученное произведени 4. Выделить целую часть
Первичное закрепление Цель: зафиксировать новое знание в речи и знаках; уточнить тему урока.	Познавательные: умение следовать образцу и правилу. Регулятивные: проявление самостоятельности и инициативы в разных видах деятельности. Коммуникативные: умение вести диалог, выполнять различные роли (продавец, покупатель).	Давайте на практики попробуем применить данный алгоритм для этого решим следующие примеры.
Физкультминутка	Личностные: умение применять правила охраны своего здоровья.
Самостоятельная работа с самопроверкой по образцу Цель: организовать выполнение учащимися самостоятельной работы на новое знание; – организовать самопроверку по эталону.	Познавательные: понимание смысла задания; возможность применить первоначальные способы поиска информации. Коммуникативные: осуществление взаимоконтроля по ходу выполнения задания.	– А сейчас, ребята вы будете работать самостоятельно с последующей проверкой по образцу (каждому учащемуся раздаются карточки с  заданиями) Проверка по образцу (презентация) – Кто решил всё правильно? Погладьте себя по головке и похвалите себя. – Кто допустил ошибки, не расстраивайтесь, вы ещё позанимаетесь и у вас всё получится.
Включение нового знания в систему знаний и повторение Цель: включить новое знание в систему уже имеющихся.	Познавательные: находить ответы на вопросы используя учебник, свой жизненный опыт и информацию, полученную на уроке. Находить и формулировать решение задачи с помощью простейшей модели(рисунка). Коммуникативные: слушать и понимать речь других.	– А сейчас откроем учебник стр.73 № 450. Что нам нужно сделать? – Прочитайте задачу.	– Решить задачу
		– Как двигались два велосипедиста?	– В одном направлении
		– Зная скорость первого велосипедиста и то, что скорость второго в 1 раза больше, что можно найти?	– Скорость второго велосипедиста
		– Как найти скорость второго велосипедиста?	– Скорость первого велосипедиста умножить на 1
		– Зная скорости двух велосипедистов, что можно найти?	– Скорость удаления
		– Как найти скорость удаления?	– Из большей скорости вычесть меньшую скорость
		– Зная скорость удаления и время, что можно найти?	– Расстояние которое будет между двумя велосипедистами через 1
		– Оформите решение задачи самостоятельно.
Рефлексия Цели: – зафиксировать  содержание урока; – организовать рефлексию собственной учебной деятельности.	Регулятивные: формирование умения адекватно оценивать свою деятельность. Личностные: оценивание разного вида деятельности на уроке.	– Итак, каждый ставил перед собой цель, поднимите руки, кто достиг ее. – Что помогало, что мешало вашей успешной работе? – Скажите, пожалуйста люди какой профессии сталкиваются со смешанными числами и применяют алгоритм умножения смешанных чисел? – Итак, повара, продавцы, бухгалтера применяют в своей работе алгоритм умножения смешанных чисел. – Повторите алгоритм умножения смешанных чисел.  – Спасибо, дети за урок,  сегодня  мы сделали еще одно открытие в  изучении математики. Вы все просто МОЛОДЦЫ!	Ответы учеников.

Операции со смешанными числами

Горячая математика

Добавление смешанных номеров

Чтобы добавить смешанные числа , сначала преобразуйте каждое смешанное число в неделимая дробь . Затем сложите неправильные дроби и запишите ответ в простейшая форма .

Пример :

3 2 5 + 4 1 5 «=» 17 5 + 21 5 «=» ( 17 + 21 ) 5 «=» 38 5 или 7 3 5

Примечание: Вы можете использовать другой метод для добавления смешанных чисел. Сначала сложите целые части числа, а затем сложите дробные части отдельно. Затем запишите ответ в простейшей форме. Например:

3 2 5 + 4 1 5 «=» ( 3 + 4 ) + ( 2 5 + 1 5 ) «=» 7 + 2 + 1 5 «=» 7 + 3 5 «=» 7 3 5

Вычитание смешанных чисел

Чтобы вычесть смешанные числа, сначала запишите каждое смешанное число как неправильную дробь. Затем вычтите неправильные дроби и запишите ответ в простейшей форме.

Пример :

9 1 6 − 5 2 6 «=» 55 6 − 32 6 «=» 55 − 32 6 «=» 23 6 или 3 5 6

Умножение смешанных чисел

Чтобы умножить смешанные числа, сначала запишите каждое смешанное число как неправильную дробь. Затем умножьте неправильные дроби и запишите результат в простейшей форме.

Пример :

2 2 3 ⋅ 3 1 5 «=» 8 3 ⋅ 16 5 «=» 128 15 «=» 8 8 15

Разделение смешанных чисел

Чтобы разделить смешанные числа, сначала запишите каждое смешанное число как неправильную дробь. Затем, чтобы разделить неправильную дробь, умножьте первую дробь на мультипликативное обратное второй фракции.

Пример :

3 1 2 ÷ 4 2 3 «=» 7 2 ÷ 14 3

Мультипликативная инверсия 14 3 является 3 14 .

«=» 7 2 ⋅ 3 14 «=» 21 28 «=» 3 4

правила, примеры, решения. Фракции. Умножение и деление дробей Умножение и деление смешанных чисел

Тема урока: «Умножение и деление смешанных дробей»

Цель: выработать у учащихся умение и умение применять правило умножения и деления смешанных дробей;

развитие у учащихся аналитического мышления, формирование у учащихся умения выделять главное и обобщать.

Задания: повторить правило умножения и деления обыкновенных дробей.

Проверить умение применять правило умножения и деления обыкновенных дробей,

правило умножения дроби на натуральное число и наоборот. Проверьте умение преобразовывать неправильную дробь в смешанное число и наоборот.

Выведите новое правило и алгоритм умножения и деления смешанных чисел.

Разработать новое правило выполнения заданий.

Предметные результаты: алгоритм умножения и деления смешанных дробей (памятка)

Метапредметные и личные результаты :

Регуляторные РЭК: постановка целей; планировать, получая результат

УУД познавательный: общеобразовательный, логический, постановка задачи и решение

УУД коммуникативный: работа в парах

Оборудование: учебник математики 6 класс

Раздаточный материал.

Проектор.

На занятиях:

I. Проблемная ситуация и актуализация знаний

1. Анкетирование детей на повторение изученного материала по теме умножение и деление дробей (алгоритм выполнения, правило умножения дроби на натуральное число).

2. Иллюстрация примеров на проекторе. Виды обыкновенных дробей. Как получить смесь из неправильной дроби и наоборот.

3.По окончании опроса самостоятельная работа, включающая примеры на умножение и деление обыкновенных дробей и содержащая два примера на умножение и деление смешанных дробей, где дети сталкиваются с проблемой. Правильные ответы для проверки с учащимися отражаются на проекторе.

4. Обсуждение проблемы. Ведите по теме урока.

II. Совместное открытие знаний.

1/ Предлагается обсуждение в парах для озвучивания варианта решения проблемы. Запишите версии на доске. Как узнать, какая версия правильная?

2 / Предложите учащимся обратиться к учебнику по соответствующей теме.

3/ Выполните ознакомительное чтение, найдите нужный абзац и изучите его, чтобы составить алгоритм умножения и деления смешанных дробей. Контроль за выполнением поставленной задачи.

4/ Прослушайте версии, чтобы составить общий алгоритм из основного. Отобразите его на проекторе и раздайте учащимся в качестве памятки.

III. Самостоятельное применение знаний

1/ Вернуться к задаче с решением примеров из самостоятельной работы и использованием полученного алгоритма для их решения. Проверьте в парах. Покажите результаты на проекторе для проверки.

2/ Дайте задание из учебника. Исполнительный контроль.

IV. Итог урока

Начните с проблемы, возникшей в начале урока, обсудите пути ее решения и результат.

Оценка работ учащихся.

Домашнее задание.

В этой статье мы разберем умножение смешанных чисел . Сначала озвучим правило умножения смешанных чисел и рассмотрим применение этого правила при решении примеров. Далее поговорим об умножении смешанного числа на натуральное число. Наконец, мы научимся умножать смешанное число и обыкновенную дробь.

Навигация по страницам.

Умножение смешанных чисел.

Умножение смешанных чисел можно свести к умножению обыкновенных дробей. Для этого достаточно смешанные числа перевести в неправильные дроби.

Запишем правило умножения смешанных чисел.

Во-вторых, нужно использовать правило умножения дроби на дробь.

Рассмотрим примеры применения этого правила при умножении смешанного числа на смешанное число.

Пример.

Перемножьте смешанные числа и.

Раствор.

Сначала представим смешанные числа, подлежащие умножению, в виде неправильных дробей: и … Теперь мы можем заменить умножение смешанных чисел умножением обыкновенных дробей: … Применяя правило умножения дробей, получаем … полученная дробь несократимая (см. дроби сократимые и несократимые), но неправильная (см. дроби правильные и неправильные), поэтому для получения окончательного ответа остается отделить от неправильной дроби целую часть: .

Запишем все решение одной строкой:.

Ответ:

.

Для закрепления навыков умножения смешанных чисел рассмотрим решение другого примера.

Пример.

Выполнить умножение.

Раствор.

Забавные числа и равны соответственно дробям 13/5 и 10/9. Тогда… На этом этапе самое время вспомнить о приведении дроби: мы заменим все числа в дроби их разложениями на простые множители, и выполним приведение тех же множителей.

Ответ:

Умножение смешанного числа на натуральное

После замены смешанного числа на неправильную дробь умножение смешанного числа на натуральное число сводится к умножению обыкновенной дроби на натуральное число .

Пример.

Умножьте смешанное число на натуральное 45.

Решение.

Смешанное число равно дроби, тогда… Заменяем числа в полученной дроби их разложениями на простые множители, выполняем приведение, а затем выделяем целую часть: .

Ответ:

Иногда удобно умножать смешанное число на натуральное, используя свойство распределения умножения относительно сложения. В этом случае произведение смешанного числа на натуральное число равно сумме произведений целой части на данное натуральное число и дробной части на данное натуральное число, то есть .

Пример.

Рассчитать произведение.

Далее действуем по правилу: умножаем первую дробь на дробь, обратную второй (то есть на перевернутую дробь, у которой числитель и знаменатель переставлены местами). При умножении дробей числитель умножается на числитель, а знаменатель на знаменатель.

Рассмотрим примеры деления смешанных чисел.

Начнем делить смешанные числа с преобразования их в неправильные дроби. Затем делим полученные дроби. Для этого умножьте первую дробь на перевернутую вторую. 20 и 25 на 5, 3 и 9 — на 3. Получилась неправильная дробь, поэтому надо.

Преобразуем смешанные числа в неправильные дроби. Далее по правилу деления дробей оставляем первое число и умножаем его на число, обратное второму. Уменьшить 15 и 25 на 5, 8 и 16 — на 2. Выделить из получившейся неправильной дроби целую часть.

Заменяем смешанные числа неправильными дробями и делим их. Для этого перепишите первую дробь без изменений и умножьте ее на перевернутую вторую. Сократите 18 и 36 на 18, 35 и 7 на 7. Получится неправильная дробь. Выделите из него всю часть.

) и знаменатель на знаменатель (получаем знаменатель произведения).

Формула умножения дробей:

Например:

Перед тем, как приступить к перемножению числителей и знаменателей, необходимо проверить возможность сокращения дроби. Если вы сможете сократить дробь, то вам будет проще производить дальнейшие вычисления.

Деление обыкновенной дроби на дробь.

Деление дробей с участием натурального числа.

Это не так страшно, как кажется. Как и при сложении, преобразуйте целое число в дробь со знаменателем. Например:

Умножение смешанных дробей.

Правила умножения дробей (смешанных):

• перевод смешанных дробей в неправильные;
• умножить числители и знаменатели дробей;
• уменьшаем дробь;
• если вы получили неправильную дробь, то преобразуйте неправильную дробь в смешанную.

Внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно сначала привести их к виду неправильных дробей, а затем умножить по правилу умножения обыкновенных дробей.

Второй способ умножения дроби на натуральное число.

Может быть удобнее использовать второй способ умножения обыкновенной дроби на число.

Внимание! Чтобы умножить дробь на натуральное число, необходимо разделить знаменатель дроби на это число, а числитель оставить без изменений.

Из приведенного примера видно, что этот вариант удобнее использовать, когда знаменатель дроби делится без остатка на натуральное число.

Фракции многоэтажные.

В старших классах часто встречаются трехэтажные (или более) дроби. Пример:

Для приведения такой дроби к обычному виду используется деление через 2 точки:

Примечание! При делении дробей очень важен порядок деления. Будьте осторожны, здесь легко запутаться.