алгоритм, как ставить запятую, правила переноса, примеры

Умножение десятичных дробей — общие принципы

Десятичная дробь — форма записи обыкновенной дроби, у которой знаменатель равен 10, 100, 1000 и т.д. 

Числа со знаменателями 10, 100, 1000 и т.д. записывают без знаменателя. Сначала пишут целую часть, а потом числитель дробной части. Целую часть отделяют от дробной части запятой.

Например, вместо  пишут 5,7 (читают: «5 целых 7 десятых»).

Вместо  пишут 3,17 (читают: «3 целых 17 сотых»).

Десятичные дроби перемножают как целые числа, на запятые внимания не обращают. В результате отделяют запятой столько цифр справа, сколько их стоит после запятой во всех множителях вместе.

Пример 1

Найдите значение выражения: .

Задания подобного плана выполняют по следующему алгоритму:

1. Перемножить десятичные дроби как целые числа, на запятые не обращать внимания.
2. Посчитать количество цифр после запятой в каждом множителе.
3. В ответе отделить запятой справа количество цифр, которое получили.
4. Если последняя цифра после запятой — нуль или нули, то необходимо переписать результат без нулей.
5. Записать ответ.

В двух множителях три цифры после запятой. Нужно отделить три цифры справа в результате и поставить запятую.

Умножение десятичной дроби на обыкновенную дробь или смешанное число

Для того, чтобы умножить десятичную дробь на обыкновенную дробь, необходимо:

1. Перевести десятичную дробь в обыкновенную дробь.
2. Перемножить обыкновенные дроби — числитель с числителем, знаменатель со знаменателем.
3. При выполнении умножения по возможности следует сократить дробное выражение:

• найти общие делители числителя и знаменателя;
• разделить числитель и знаменатель на их общие делители;
• получить несократимую дробь: у числителя и знаменателя нет общих делителей, кроме единицы.

1. Числа, которые остались после сокращения, перемножить отдельно в числителе и знаменателе.

• если получилась неправильная дробь ‒ числитель больше знаменателя, то выделить целую часть.

1. Обыкновенную дробь или смешанное число перевести в десятичную дробь, если возможно.
2. Если десятичная дробь заканчивается нулем или нулями, то переписать результат без нулей.
3. Записать ответ.

Для того, чтобы умножить десятичную дробь на смешанное число, необходимо:

1. Перевести десятичную дробь в обыкновенную дробь.
2. Перевести смешанное число в обыкновенную дробь.
3. Перемножить эти дроби.
4. Сократить дробное выражение до несократимой дроби.
5. Перемножить числа в числителе и знаменателе.
6. Дробь перевести в десятичную дробь или смешанное число.
7. Если десятичная дробь заканчивается нулем или нулями, то переписать результат без нулей.
8. Записать ответ.

Умножение десятичной дроби на натуральное число

Произведение десятичной дроби и натурального числа — сумма слагаемых, каждое из которых равно этой дроби, а количество слагаемых определяется натуральным числом.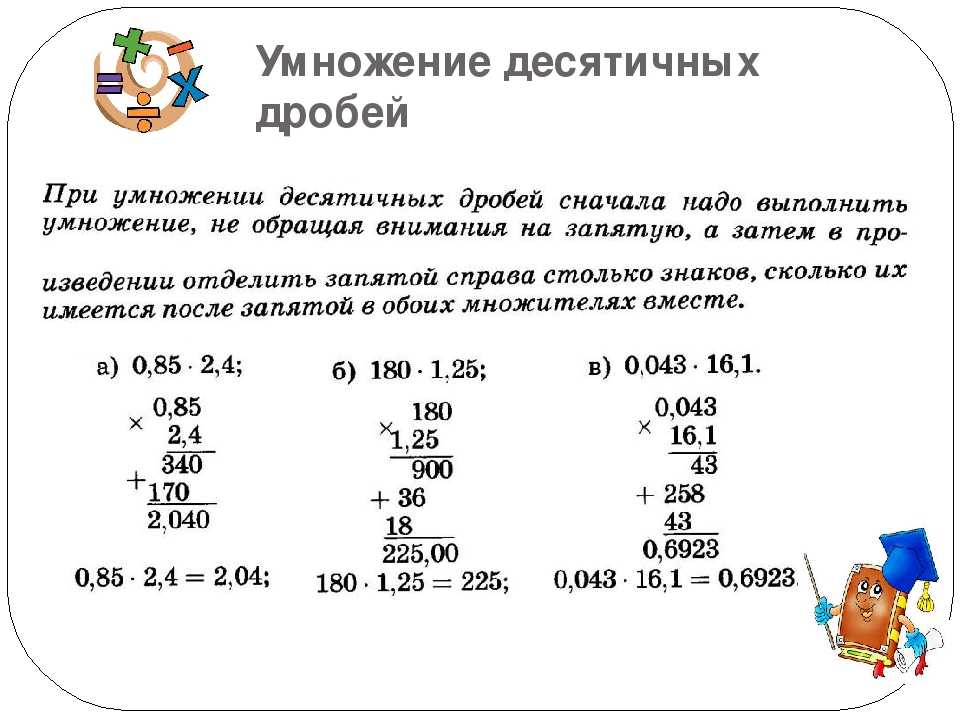

Пример 2

Выражение представляют в виде суммы, в которой слагаемое 0,25 повторяется четыре раза:

Для того, чтобы умножить десятичную дробь на натуральное число, необходимо:

1. Умножить десятичную дробь на натуральное число, не обращая внимания на запятую.
2. Посчитать количество цифр после запятой в десятичной дроби.
3. В произведении отделить столько цифр справа, сколько их отделено запятой в десятичной дроби.
4. Если последняя цифра после запятой — нуль или нули, то переписать результат без нуля или нулей.
5. Записать ответ.

Алгоритм, как ставить запятую, правила переноса

Для того, чтобы в результате умножения правильно поставить запятую, надо:

• посчитать количество цифр после запятой в каждом множителе;
• в результате отделить запятой справа это количество цифр.

Свойство 1

При умножении десятичной дроби на 10, 100, 1000 и т. д. запятую в десятичной дроби переносят вправо на столько цифр, сколько нулей стоит в множителе после единицы.

Если количество цифр в десятичной дроби после запятой меньше количества нулей после единицы, то нужно:

• уравнять количество разрядов — поставить нули после последней цифры десятичной дроби;
• перенести запятую на столько цифр вправо, сколько нулей после единицы в множителе.

Свойство 2

При умножении десятичной дроби на 0,1; 0,01; 0,001 и т. д. переносят запятую влево на столько цифр, сколько нулей стоит перед единицей в множителе. Нуль целых также учитываем.

Примеры решения задач

Пример 3

Выполните умножение: 

Для объяснения решения действуем по алгоритму:

1. Переводим десятичную дробь в обыкновенную дробь:

• «как слышим, так и пишем»: одна целая, две десятых —  — получили смешанное число;
• сокращаем дробную часть смешанного числа: 
• переводим смешанное число в неправильную дробь:  — знаменатель переписываем без изменений, в числителе умножаем целую часть на знаменатель и прибавляем числитель.

1. Полученную неправильную дробь умножаем на множитель:

• ищем общий делитель чисел в числителе и знаменателе — 6 и 4 делятся нацело на 2;
• делим числитель и знаменатель на 2, получаем: 
• больше общих делителей у числителя и знаменателя нет, кроме 1, поэтому умножаем числа в числителе и в знаменателе: 

1. Переводим полученную обыкновенную дробь в десятичную:

• знаменатель дроби равен 10, после единицы один нуль, значит после запятой отделяем одну цифру: 

Пример 4

Выполните умножение: 

Чтобы умножить десятичную дробь на смешанное число:

1. Переводим десятичную дробь в обыкновенную дробь: 
2. Переводим смешанное число в неправильную дробь: 
3. Перемножаем полученные числа: 
4. Прежде чем дальше перемножать числа в числителе и знаменателе, ищем общие делители числителя и знаменателя:

• числа 21 и 7 делятся нацело на 7. Получаем 
• числа 18 и 10 делятся нацело на 2. Получаем 
• больше общих делителей, кроме единицы, у числителя и знаменателя нет. Перемножаем числа в числителе и числа в знаменателе: 

1. Дробь неправильная — числитель больше знаменателя — выделяем целую часть: 
2. Это смешанное число переводим в десятичную дробь. Умножаем числитель и знаменатель дробной части на 2 (чтобы в знаменателе стало 10): 
3. Записываем ответ.

Пример 5

Выполните умножение: 

Решаем пример по схеме:

• перемножаем как целые числа, на запятую внимание не обращаем;
• считаем количество цифр после запятой: две цифры;
• отсчитываем справа в результате две цифры и ставим запятую.

Пример 6

Выполните умножение: 

Запятую в десятичной дроби переносим вправо на две цифры, так как в множителе после единицы стоит два нуля.

Пример 7

Выполните умножение: 

Запятую переносим влево на четыре цифры, так как в множителе перед единицей стоит четыре нуля.

Пример 8

Решите уравнение: 

Чтобы решить уравнение, нужно найти его корни или доказать, что корней нет.

Находим делимое. Для этого умножаем делитель на частное:  

Ответ: x =2,665

Для закрепления навыков умножения десятичных дробей используют математические тренажеры.

Умножение десятичных дробей: правила, примеры, решения

Данный материал будет посвящен изучению дробных чисел. А именно десятичных дробей их основных свойств и правил умножения.

Мы рассмотрим все виды дробей и как с ними работать. Какие способы применяют для их быстрого и точного вычисления

Для начала дадим определение десятичной дроби. Это число, которое после запятой имеет характерный остаток

Примеры десятичных дробей: 145,14; 12,85; 1,23.

В свою очередь данный вид дробей подразделяется на следующие категории:

• Конечные — если после запятой присутствует окончательное число.

Например: \[\pm a_{0} a_{1} a_{2} a_{3} \ldots . {-k}\]

Основные свойства дробей:

Изменение величины десятичной дроби не произойдет, даже если к ней добавить справа несколько нулей. Это свойство принято считать одним из самых главных для данного вида дробей.

Если в рассматриваемом дробном значении наблюдается множество нулевых значений, тогда их просто исключают, так как никакого влияния на значение они не имеют.

 Рассмотрим несколько простых и понятных для ознакомления примеров решения данных дробей

• 0,900 = 0,9;
• 22,10200000 = 22,102;
• 0,45000=0,45;
• 0,12569000=0,12569;
• 0,780=0,78.

Основные характеристики десятичных дробей

1. Дробное число, не будет иметь какого — либо значения, если в знаменателе нулевое число. Деление на ноль в математике строго запрещено.
2. Нулю будет равна дробь, у которой в числителе значится нулевое значение. В знаменатель — нет.
3. Если значения, которые находятся в числителе и знаменателе разделить или умножить на любое действительное число. То получится дробь равная ей по значении.
4. Если взять две дроби: \[\frac{a}{b} \text { и } \frac{c}{d}\] то они называться будут равными при \[a \cdot d \text { или } b \cdot c\].

Существующая взаимосвязь между дробями различных категорий и видов

• Целая часть десятичной дроби всегда будет равной такой части дроби, только смешанного типа;
• Когда значение в числителе меньше значения знаменателя, то нулю равна целая часть дроби;
• Количество значений после запятой, определяется в зависимости от количества нулей, которые записаны в знаменателе обыкновенной дроби.

Правило записи десятичной дроби

Пример №1. Нужно преобразовать  обыкновенную дробь \[\frac{16}{10}\] в десятичную.

Принцип решения задачи:

Если в знаменателе число 10, а по правилам это будет только один ноль. Справа налево отсчитываем, в числителе один знак. И после этого ставим запятую. Получаем десятичную дробь, где: число один является целой частью, а шесть дробной.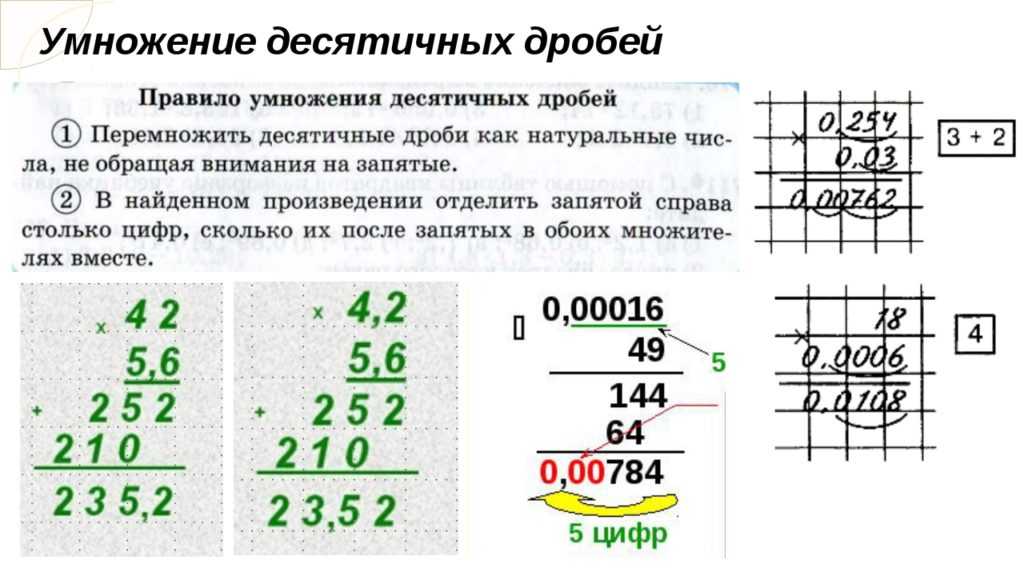

\[\frac{16}{10}=1,6\]

Пример №2: Перевести \[\frac{39}{1000}\] в десятичную дробь.

Теперь видим, что, знаменатель равен 1000 и нужно использовать для решения три нуля. Проводим те же действия что и в первом примере. Получаем десятичную дробь. Где нулевое значение — это целая часть, а все остальное — это дробная часть.

\[\frac{39}{1000}=0,039\]

Ознакомившись кратко с десятичными дробями, перейдем к изучению правил их умножения.

Принцип умножения десятичных дробей

Для умножения десятичных дробей необходимо, произвести следующие действия.

• Дробь записать в виде так называемого математического столбика. Далее рассмотреть заданное значение, как обыкновенные действительные числа и подсчитать их;
• Все знаки за запятой подсчитать и сложить сумму;
• Полученную сумму справа налево отложить и поставить запятую.

Для данного вида дробей характерны все те же действия, что и для остальных чисел.

Если переставить местами множители, на окончательный ответ это не повлияет.

если мы хотим умножить число на произведение двух и более. Сначала умножаем данное число на первый множитель затем полученное значение на второй и так далее.

Чтобы умножить сумму на множитель. Нужно по отдельности умножить числа и полученную сумму сложить.

Если проводим умножение на разность чисел, то для начала умножаем на уменьшаемое, а затем на вычитаемое. Следовательно полученные значения вычитаем.

Также процесс умножения можно упростить. Десятичные дроби умножить как действительные целые числа, и поставить запятую.

Для наглядности рассмотрим несколько примеров:

Пример №1:

Определить произведение чисел \[1,5 \cdot 0,75\]

Первым делом преобразуем дробь. Заменим десятичную. на обыкновенную.

0,75=75/100

\[1,5=\frac{15}{10}\]

Затем проводим сокращение дробных значений и выделяем, по уже изученным правилам целую часть.

\[\frac{125}{1000}\]  можно преобразовать и получить следующую дробь 1,125.

Ответ: 1,125.

Пример №2:

Определить произведение чисел \[5,382 \ldots \cdot 0,2\]

Первое значение является бесконечной дробью. Ее рекомендуется округлить до сотых значений. Получается \[5,382 \ldots \approx 5,38\].

Второй множитель округлять не требуется, это не имеет смысла.

Далее можно произвести вычисление \[5,38 \cdot 0,2=\frac{538}{100} \cdot \frac{2}{10}=\frac{1,076}{1000}=1,076\]

Следовательно, получаем ответ к нашей задаче: 1,076.

Пример №3:

Необходимо умножить две периодические дроби.

\[0,(3) \cdot 2,(36)\]

Преобразуем заданные значения в обыкновенную дробь.

\[0,(3)=0,3+0,03+0,003+0,003+\ldots=\frac{0,3}{1-0,1}=\frac{0,3}{9}=\frac{3}{9}=\frac{1}{3}\]

\[2,(36)=2+(0,36+0,0036+\ldots)=2+\frac{0,36}{1-0,01}=2+\frac{36}{99}=2+\frac{4}{11}=2 \cdot \frac{4}{11} \frac{26}{11}\]

\[\Rightarrow 0,(3) \cdot 2,(36)=\frac{1}{3} \cdot \frac{26}{11}=\frac{26}{33}\]

Полученную в конечном итоге обыкновенную дробь приводим к десятичной.  В столбик разделим числитель на знаменатель.

Окончательный ответ : \[0,(3) \cdot 2,(36)=0,(78)\].

Умножение десятичных дробей при помощи столбика

Умножение столбиком выполняя на условии, что на запятые никакого внимания не уделяется (они игнорируются)

В итоговом результате ставится знак запятой справа. Отделяется столько запятых, сколько множители имеют десятичных знаков вместе.

Если не хватает цифр, то принято в окончательном ответе дописывать нули.

Рассмотрим примеры решения подобных задач.

Пример №1:

Нужно найти значение произведения, следующих чисел: 63,37 и 0,12.

Выполняем умножение, не обращая внимание на запятые.

Далее определяемся с запятой, где ее ставить. Она будет через четыре цифры справа. Потому что сумма десятичных знаков двух множителей равна 4.

Нули в данной ситуации не записываются. Это связано с достаточным количеством чисел.

Получаем окончательное значение равное 7,6044.

Пример №2:

Заданные числовые, дробные выражения 3,2601 и 0,0254, необходимо умножить между собой.

Для этого применим умножение столбиком.

Мы будем ставить запятую, отделяющую 8 цифр с правой стороны.  Потому что заданные дроби, вместе, имеют восемь знаков после запятой.

Нули в данной ситуации записываются. Это связано с недостаточным количеством значений.

Получаем окончательное значение равное: 0 , 08280654

Как правильно умножить десятичные дроби на 0,001;0,01;0,1.

Для того чтобы умножить десятичную дробь на следующие значения: 0,1;0,01; 0,001, необходимо перенести знак запятой. Переносится знак в левую сторону, на количество знаков равное количеству нулей перед единицей.

Значение ноль целых, так же отсчитывается. При нехватке количества цифр, нужно дописать недостающее количество нулей.  

Примеры

 

\[35,9 \cdot 0,1=3,59;\]

\[1,9 \cdot 0,1=0,19;\]

\[145,6 \cdot 0,01=1,456;\]

\[9644,1 \cdot 0,001=9,6441;\]

\[22,9 \cdot 0,0001=0,00229.\]

Решим несколько примеров для закрепления материала.

Пример 1

Нужно произвести умножение значение: 9,4 и 0,0001.

Так как 0,0001 имеет четыре нуля, то переносим запятую в первом множителе заданное количество и получаем следующее значение.

\[9,4 \cdot 0,0001=0,00094\]

Ответ: 0,00094.

Пример 2

Нужно произвести умножение значение: 11.4 и 0,001.

Так как 0,001 имеет три нуля, то переносим запятую в первом множителе заданное количество и получаем следующее значение.

\[11,4 \cdot 0,001=0,00114\]

Ответ: 0,00114.

Пример 3

Умножаем следующие значения: 6,4 и 0,01.

Так как 0,01 имеет два нуля, то переносим запятую в первом множителе заданное количество и получаем следующее значение.

\[6,4 \cdot 0,01=0,064\]

Ответ: 0,064.

Условие умножения десятичной дроби с натуральным показателем

Принцип умножения дробей данного вида, такой же как и между десятичными. Используются и принимаются к сведению все те правила, которые были изучены ранее.

Подробно рассмотрим на примерах и решим их.

Пример №1:

Нам нужно вычислить произведение из числовых значений.

\[15 \cdot 2,27\]

Для этого воспользуемся правилом умножения через столбик.

Следовательно, ответ задачи, исходя из вычисления равен: 34,05.

Пример №2:

Даны числовые значения 0,(42) и 22. Необходимо найти их произведение.

Для начала преобразуем периодическую дробь в обычную.

И получим следующее выражение:

\[0,(42)=0,42+0,0042+0,000042+\ldots=\frac{0,42}{1-0,1}=\frac{0,42}{0,99}=\frac{42}{99}=\frac{14}{33}\]

Следом проводим умножение: \[0,(42) \cdot 22=\frac{14}{33} \cdot 22=\frac{14 \cdot 22}{3}=\frac{28}{3}=9 \frac{1}{3}\].

Итоговый результат, будет записываться в виде периодической дроби, как и было задано изначально.

Ответ: \[0,(42) \cdot 22=9,(3)\]

Пример №3:

Даны значения и нужно их умножить \[(4 \cdot 2,145)\]

Для начала округляем бесконечную дробь до сотых значений. Умножаем полученные значения и получаем окончательный ответ к задаче.

\[4 \cdot 2,145 \ldots \approx 4 \cdot 2,15=8,60\]

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Как умножить десятичную дробь на 1000, 100, 10

Чтобы выполнить умножение на перечисленные числовые значения, нужно вспомнить правило переноса запятой. Это перенос вправо на количество нулей в множителе. Имеющиеся лишние нули можно просто убрать. А при недостатке нулевых значений, их можно дописать.

Примеры

\[1,11 \cdot 10=11,1\]

\[22,335 \cdot 100=2233,5\]

\[8,79 \cdot 1000=8790\]

\[0,34678 \cdot 10000=3467,8\]

\[0,02 \cdot 1000=20\]

\[0,00045 \cdot 100=0,045\]

Разберем на числовом примере принцип решения подобных задач:

Пример №1:

Вычислить значения 100 и 0,0783

Сначала переносим в десятичной дроби знак запятой. Так как в значении 100 два нуля, то запятая вправо переносится на два значения.

Следовательно, мы получаем следующее значение 007,83. Первые два нуля убираем, за ненадобностью и получаем ответ 7,83.

Ответ: \[0,0783 \cdot 100=7,83\]

Пример №2:

В этой задаче нужно найти значение двух числовых данных 0,2 и 10 000.

Вправо переносим запятую на четыре цифры. Так как второй множитель имеет четыре нуля. Так как нулей в исходном значении недостаточно их нужно дописать. Нам необходим только один ноль.  Из этого получаем следующее число 0,02000. Переносим знак запятой вправо и получаем 0200,0. Передний ноль перед двойкой убираем. Он нам не нужен. И получаем следующий ответ задачи: 200.

Принцип умножения десятичной дроби с обыкновенной и со смешанной дробью

Чтобы произвести данную операцию, необходимо выполнить следующие требования:

1. Десятичную дробь преобразовывают в обыкновенную и умножаем с нужным числом.
2. В десятичную переводим обыкновенную или смешанную дробь и далее умножаем друг с другом.

Ниже приведены примеры решения задач.

Пример №1. Найти произведение \[\frac{3}{5}\] на 0,9.

Поэтапный процесс решения.

1) Записываем 0,9 в виде обыкновенной дроби, а именно \[0,9=\frac{9}{10}\]

2) Умножаем цифры по правилам математики \[\frac{3}{5} \cdot \frac{9}{10}=\frac{27}{50}=0,54\].

Ответ: \[\frac{3}{5} \cdot 0,9=0,54\]

Пример №2. Найти произведение чисел \[0,18 \text { на } 3 \frac{1}{4}\].

Выполняем следующие действия:

1) Записываем \[3 \frac{1}{4}\] в виде десятичной дроби: \[3 \frac{1}{4}=3,25\].

2) Вычисляем известные нам значения: \[0,18 \cdot 3,25=0,585\]

Ответ: \[0,18 \cdot 3 \frac{1}{4}=0,585\]

Пример №3:

Даны следующие значения \[0,4 \text { и } 3 \frac{3}{5}\]. По условию задач нужно найти их произведение, иными словами умножить.

Первым делом 0,4 переведем в десятичную дробь и получим значение: \[0,4=\frac{4}{10}=\frac{2}{5}\].

Затем проводим вычисление: \[0,4 \cdot 3 \frac{3}{5}=\frac{2}{5} \cdot \frac{23}{6}=\frac{23}{15}=1 \frac{8}{15}\].

Полученный ответ является смешанным значением. Его необходимо перевести в значение периодической дроби.  А именно: 1,5(3).

Следовательно, это и ответ задачи. 1,5(3).

Пример №4:

Вычислить произведение заданных чисел: \[3,5678 \ldots . . \text { и } \frac{2}{3}\]

Второй множитель, можно рассмотреть и записать как \[\frac{2}{3}=0,666 \ldots \ldots\]

Затем оба множителя распишем, и получим тысячный разряд. Получаем десятичные дроби и вычисляем значения. 3,568 и 0,667.

Для расчета применяем расчет с помощью столбика.

Получим итоговый результат и округлим его до трех знаков после запятой. Потому что именно до тысячных знаков, мы округляем исходные данные.

\[2,379856 \approx 2,380\]

Тема десятичных дробей материал довольно емкий. Который включает в себя много различных моментов. Их необходимо учитывать при решении задач и примеров. А именно:

• принцип переноса знака запятой, на количество нулей;
• преобразование десятичных дробей в иной вид дроби.

Обязательно помнить один из главных моментов в алгебре, а именно деление на ноль. Точнее сказать его запрет. Всегда нужно, помнить, что на ноль деление запрещается. И если нулевое значение имеет числитель дроби, то она всегда будет приравнена к нулю.

Соблюдая все изученные характеристики и свойства дробей, а также главные правила математики, можно решать задачи данного типа без особых трудностей.

Умножение десятичных дробей

Умножение десятичных дробей

Показать рекламу

Скрыть рекламу
О рекламе

Умножьте без десятичной точки, а затем снова вставьте его в нужное место!

Как умножать десятичные числа

Просто выполните следующие действия:

• Умножайте как обычно, игнорируя десятичные точки.
• Затем поставьте в ответе запятую — в нем будет столько знаков после запятой, сколько вместе взятых двух исходных чисел.

Другими словами, просто подсчитайте, сколько чисел после запятой в обоих чисел, которые вы умножаете, тогда в ответе должно быть столько же чисел после и десятичной запятой.

 

Пример: умножить 0,03 на 1,1

начать с:		0,03 × 1,1
умножить без десятичной точки:		3 × 11 = 33
0.03 имеет 2 десятичных знака , и 1.1 имеет 1 десятичный знак , поэтому ответ имеет 3 десятичных знака : 900 38		0,033

 

См. анимацию умножения десятичных знаков

Как это работает?

Потому что, когда вы умножаете без десятичной точки, вы действительно сдвигаете десятичную точку вправо до убрать с дороги :

Оригинал:		1 ход:		2 хода:		3 хода:
0,03 × 1,1		0,3  × 1,1		3.  × 1,1		3.  ×  11.

Тогда мы делаем (теперь легко) умножение:

3. × 11. = 33.

Но помните, мы сделали 3 движения десятичной точки, поэтому нам нужно отменить это:

3 Ходы:		2 хода:		1 ход:		Правильно
33.		3,3		0,33		0,033

Вот еще несколько примеров:

Пример: умножьте 0,25 на 0,2

начните с:		0,25 × 0,2
умножить без десятичной точки:		25 × 2 = 50
0,25 имеет 2 знаков после запятой, и 0,2 имеет 1 знаков после запятой, , поэтому ответ имеет 3 знаков после запятой:		0,050

Пример: умножьте 102 на 0,22

начните с:		102 × 0,22
умножить без десятичной точки:		102 × 22 = 2244
102 имеет 0 знаков после запятой, и 0,22 имеют 2 знаков после запятой, , поэтому ответ имеет 2 знаков после запятой:		22,44

Здравый смысл

В качестве последней проверки вы можете надеть шляпу здравого смысла и подумать «это правильный размер?» , потому что вы не хотите ни за что платить в десять раз больше, ни получать только одну десятую того, что вам нужно!

И все.

Только помните: в ответе должно быть столько знаков после запятой, сколько в обоих числах, которые вы умножаете.

 

Десятичные рабочие листы
 

Copyright © 2017 MathsIsFun.com

Как умножать десятичные дроби? Определение, примеры, факты

Знакомство с умножением десятичных дробей

Умножение — жизненно важный навык, который должен знать каждый. Умножение десятичных дробей — это более продвинутый навык умножения, повышающий навык по сравнению с простым умножением целых чисел. Знакомство детей с чем-то немного сложным, например, с десятичными умножениями, научит их использовать более сложные математические понятия.

Умножение десятичных дробей может показаться сложным и пугающим для юных умов. Как родитель или учитель, как вы можете преодолеть этот разрыв между неприязнью и жизненно важными математическими навыками? Растущий интерес и любопытство могут противостоять неприязни или страху перед предметом. SplashLearn — это платформа, созданная для помощи юным умам в понимании сложных математических концепций, соответствующих школьной программе, с помощью игр.

Да, вы правильно прочитали. В конце концов, что может быть более заманчивым и интерактивным для детей, чем игры? Игры SplashLearn — это увлекательный и инновационный способ обучения детей теориям и концепциям, которые в противном случае были бы для них утомительным занятием.

Родственные игры

Умножение десятичных чисел на целое число

Умножение десятичного числа на целое похоже на умножение целых чисел. Однако из-за десятичных знаков в одном из чисел это может показаться трудным. Итак, давайте посмотрим, как мы можем упростить этот процесс для вас.

Шаг 1: Забудьте о десятичных дробях. Да, они не играют никакой роли, пока вы выполняете реальную операцию. Теперь умножьте два числа, как если бы вы делали это с целыми числами.

Шаг 2: Подсчитайте количество цифр после запятой.

Шаг 3: Поставьте десятичную точку в произведении, оставив такое же количество цифр справа, как десятичные разряды в коэффициенте.

Совет для профессионалов: Всегда помните, что произведение после умножения должно иметь такое же количество знаков после запятой, как и множители.

Теперь давайте посмотрим на примеры умножения десятичных дробей:

Пример: Найдите произведение 0,2$ \умножить на 3$

Шаг 1: Берем два числа без учета десятичной дроби, т.е. 2 и 3. Перемножаем их . Итак, мы получаем $2\times 3 = 6$.

Шаг 2: Считаем количество цифр после запятой. Здесь у нас есть только одна цифра после запятой.

Шаг 3: Ставим запятую в произведении, оставляя после себя одну цифру справа. Поскольку произведение равно 6, мы должны поставить десятичную дробь перед ним.

Итак, ответ будет 0,6.

Пример: Найдите произведение 0,4 доллара х 3 доллара

Аналогично, чтобы найти произведение 0,4 и 3, умножьте числа без десятичных знаков, т. е. 4 доллара х 3 = 12 долларов.

Теперь есть одна цифра после запятой, поэтому давайте поместим десятичную точку в произведение, оставив одну цифру справа: 1,2

Таким образом, $0,4 \ умножить на 3 = 1,2 $

Связанные рабочие листы

Умножение двух десятичных чисел

При умножении двух десятичных чисел необходимо учитывать десятичные разряды обоих множителей.

Шаг 1: Сначала игнорируйте десятичные разряды. Выполните умножение данных чисел.

Шаг 2: Подсчитайте количество знаков после запятой в обоих множителях и рассчитайте их сумму.

Шаг 3: Поставьте запятую с правого конца в соответствии с количеством знаков после запятой, которое вы подсчитали на шаге 2.

Пример: Найдите произведение 15,62$ х 0,7$

Шаг 1: Игнорируем десятичные дроби и умножаем заданные числа.

1562$ \умножить на 7 = 10934$

Шаг 2: Считаем количество знаков после запятой в обоих числах и вычисляем их сумму.

15,62 имеет 2 знака после запятой, а 0,72 имеет 1 знак после запятой. Следовательно, сумма десятичных множителей равна 3.

Шаг 3: Ставим десятичную дробь в произведении, оставляя после себя три цифры справа.

Итак, 15,62 доллара США \ умножить на 0,7 = 10,934 доллара  

Умножение десятичных дробей на 10, 100 и 1000

Когда мы умножаем десятичное число на 10, десятичная дробь сдвигается вправо от числа на один разряд.

Например, $15,2705 \×10 = 152,705$

Здесь в решении происходит только одно изменение: десятичный сдвиг от его позиции в 15,2705 на один знак вправо. Итак, в качестве ответа мы получаем 152.705.

Когда мы умножаем десятичное число на 100, десятичная дробь сдвигается вправо от числа на два знака.

Например, $15,2705 \х100 = 1527,05$

Когда мы умножаем десятичное число на 1000, десятичное число сдвигается вправо от числа на три знака.

Например, 15,2705 долл. США х 1000 = 15270,5 долл. США

Итак, когда нам нужно умножить десятичное число на 10, 100 или 1000, мы сдвигаем десятичное число справа от числа в соответствии с количеством нулей после 1. .  

Рассмотрим несколько примеров:

• 53,5$ \ умножить на 10 = 535$
• 469,127$ \ умножить на 10 = 4691,27$
• 398,16 $ \ умножить на 100 = 39816
$
• 826,3 $ \ умножить на 100 = 82630,0
$
• 0,137$ \умножить на 100 = 13,7$

Решенные примеры

1) Найдите произведение числа $9,2 \times 0,08$ .

Решение :

Шаг 1: Мы игнорируем десятичные дроби и умножаем заданные числа.

92$ х 8 = 736$

Шаг 2: Заметим, что 9,2 имеет 1 десятичный знак, а 0,08 имеет 2 десятичных знака. Следовательно, сумма десятичных множителей равна 3. 

Шаг 3: Подставляем десятичную дробь в произведение, оставляя после себя три цифры справа.

Таким образом, 9,2$ х 0,08 = 0,736$

2) Найдите произведение 20,1$ х 6,0$ .

Решение :

Шаг 1: Мы игнорируем десятичные дроби и умножаем заданные числа.

201$ х 60 = 12060$

Шаг 2: Заметим, что 20.1 имеет 1 десятичный разряд, а 6.0 имеет 1 десятичный разряд. Следовательно, сумма десятичных множителей равна 2. 

Шаг 3: Подставляем десятичную дробь в произведение, оставляя две цифры справа.

Таким образом, 20,1$ х 6,0 = 120,60$

3) Найдите произведение 36$ х 0,5$ .

Решение :

Шаг 1: Мы игнорируем десятичные дроби и умножаем заданные числа.

36$ \умножить на 5 = 180$

Шаг 2: Заметим, что 0,5 имеет 1 десятичный знак.

Шаг 3: Ставим десятичную дробь в произведении, оставляя после себя одну цифру справа.

Итак, $36 х 0,5 = 18,0$

Практические задачи

1

Что получится, если 341,58 умножить на 4?

136632

1366,32

136,623

13363,2

Правильный ответ: 1366,32
Мы игнорируем десятичную дробь и умножаем заданные числа.
Получаем $34158 х 4 = 136632$
Поскольку $341,58$ имеет два десятичных знака, мы помещаем десятичную дробь в произведение, оставляя две цифры справа.
Итак, ответ $1366,32$.

2

Какой из следующих ответов является правильным для данной задачи на умножение? 64$\умножить на 8.3$

531,2

351,2

53,12

5,312

Правильный ответ: 531,2
Мы игнорируем десятичную дробь и умножаем заданные числа.
Получаем $64 х 83 = 5312$
Поскольку $8,3$ имеет один десятичный знак, мы помещаем десятичную дробь в произведение, оставляя после себя одну цифру справа.
Итак, ответ равен 531,2$

3

Найдите произведение 5,27$ х 3,9$.

2055,3

17,553

20,553

25,053

Правильный ответ: 20,553
Мы игнорируем десятичные дроби и умножаем заданные числа.
Получаем $527 х 39 = 20553$
Так как 5,27 имеет два десятичных знака, а 3,9 — один десятичный знак, мы помещаем десятичную дробь в произведение, оставляя после себя три цифры справа.
Итак, ответ $20.553$.

Часто задаваемые вопросы

Как умножить десятичные дроби на 10 и 100?

При умножении десятичного числа на 10 сдвиньте десятичное число вправо на один разряд. А при умножении десятичной дроби на 100 сдвиньте запятую на два знака.

Например, 4,89 доллара США х 10 = 48,9 доллара и 3,4 доллара х 100 = 340 долларов

Каково правило умножения десятичных дробей?

Для десятичного умножения нет особого правила.