Умножение целых чисел, правила, примеры, как умножать не целые числа, произведение двух чисел

В этом материале мы покажем, как правильно выполнять умножение целых чисел. Начнем, как всегда, с основных понятий и обозначений и выясним, какой смысл вкладывается в умножение двух целых чисел. Затем сформулируем правила, по которым перемножают целые положительные и целые отрицательные числа, а также числа, имеющие разные знаки. Как всегда, нашу мысль будем пояснять наглядными примерами решений задач. Далее рассмотрим те случаи, когда один из множителей нулевой или равен единице, посмотрим, как можно проверить верность результата, полученного после умножения, а в конце объясним, как правильно перемножать 3, 4 и большее количество целых чисел.

Основные определения при умножении целых чисел

При умножении целых чисел используются те же термины и знаки, о которых мы говорили ранее в статье об умножении натуральных чисел. У нас есть два множителя, которые являются целыми числами, результат, называемый произведением, и знак умножения в виде точки, звездочки или знака «x» (в целях единообразия в дальнейшем будем использовать точку).

Если обозначить множители и произведение буквами a, b и c, то действие умножения можем записать в виде равенства a·b=c. Само числовое выражение a·b тоже называется произведением. Произведение двух целых чисел также является целым числом.

В чем состоит смысл умножения целых чисел?

До этого мы уже объясняли смысл умножения на примере натуральных чисел. Произведение натуральных чисел a и b представляет собой сумму b слагаемых, каждое из которых равно a.

Целые положительные числа – это натуральные числа, поэтому смысл действия умножения для них точно такой же. В буквенном виде его также можно представить как

(значения a и b – целые положительные числа).

В принципе, этот смысл распространяется на все произведения, где одно слагаемое целое и положительное. Второе при этом также должно быть целым, однако оно может быть отрицательным или даже равным нулю. Так, схема умножения числа -3 на 5 будет выглядеть как (−3)·5=(−3)+(−3)+(−3)+(−3)+(−3).

Если вторым множителем является единица, то результат умножения – это сумма одного слагаемого, которое равно другому множителю. Это можно записать как a·1=a. Результат умножения целого числа на единицу есть само это число.

А как быть в случае, если одно из множителей нулевое? Получается, что в ответе будет сумма из 0 слагаемых. Очевидно, что это будет 0. Запишем, что a·0=0 для любого целого a. Умножение целого числа на ноль дает в результате ноль.

В случае с отрицательными числами общий смысл действия умножения сформулировать достаточно сложно. Примем это действие как данность и подчеркнем, что правила умножения в таком случае должны сохранять справедливыми свойства умножения для целых положительных чисел. В частности, такое числовое выражение должно обладать переместительным и сочетательным свойствами.

Основные правила, применяемые при умножении целых чисел

Можно выполнить умножение исходя из того, что оно по сути представляет собой сложение одинаковых слагаемых. Но, как мы уже отмечали, это долгий и трудный процесс, если таких слагаемых у нас много. А если одним из множителей является отрицательное число, то воспользоваться этим способом мы не можем. Поэтому нам надо вывести особые правила для умножения целых чисел. Сформулируем и запишем их.

Как умножать одно целое положительное число на другое

Целые положительные числа относятся к натуральным, поэтому правила умножения натуральных чисел распространяются и на них. В итоге мы, разумеется, получим целый положительный результат, т.е. натуральное число. Разберем конкретные примеры.

Пример 1

Подсчитайте, сколько будет 9 умножить на 7.

Решение

Обратимся к таблице умножения и возьмем из нее готовый результат.

Получим: 9·7=63.

Ответ: 63.

Пример 2

Сколько будет 127 умножить на 5?

Решение

Представим первый из множителей как сумму разрядных слагаемых, т.е. 100+20+7.

Теперь последовательно умножим слагаемые на данное число: 127·5=(100+20+7)·5=100·5+20·5+7·5.

Заканчиваем вычисление: 100·5+20·5+7·5=500+100+35=600+35=635.

Ответ: 635.

Чтобы перемножать многозначные числа, удобно пользоваться методом подсчета в столбик.

Пример 3

Условие: умножьте 712 на 92.

Решение: запишем множители в столбик и вычислим результат.

Ответ: 65 504.

Как правильно перемножить целые числа, имеющие разные знаки

Для того чтобы вывести правило для такого случая, приведем пример.

Итак, нам надо вычислить произведение числа -5 на 3. Вспомним смысл умножения и запишем: (−5)·3=(−5)+(−5)+(−5)=−15. Если учесть переместительное свойство, то должно быть верным и (−5)·3=3·(−5). Очевидно, что модуль числа, полученного в результате, соответствует произведению данных множителей. Таким образом, произведение двух чисел с разными знаками есть число отрицательное.

Определение 1

Чтобы умножить одно отрицательное число на одно положительное, надо перемножить между собой модули этих чисел и поставить перед результатом минус.

Разберем несколько примеров, подтверждающих это правило.

Пример 4

Умножьте 7 на -14.

Решение

Запишем отдельно модули исходных множителей. Получим 7 и 14. Подсчитаем, чему будет равно их произведение: 7·14=98. Все, что нам нужно сделать дальше, – это поставить знак минуса перед полученным числом.

Ответ: 7·(−14)=−98.

Пример 5

Подсчитайте, сколько будет (−36)·29.

Решение

Согласно правилу умножения чисел с разными знаками, нам нужно начать с умножения модулей. Считаем: 36·29=1 044. Здесь удобно будет воспользоваться методом умножения в столбик. Нам осталось поставить минус перед результатом и записать готовый ответ.

Ответ: (−36)·29=−1 044.

В последней части параграфа мы попробуем доказать, что равенство a·(−b)=−(a·b) справедливо (a и b здесь – любые целые числа). Правило умножения целых чисел с разными знаками, которое мы записали выше, является частным случаем этого равенства.

Задача сводится к тому, что нам надо доказать, что значениями выражений a·(−b) и a·b будут противоположные числа.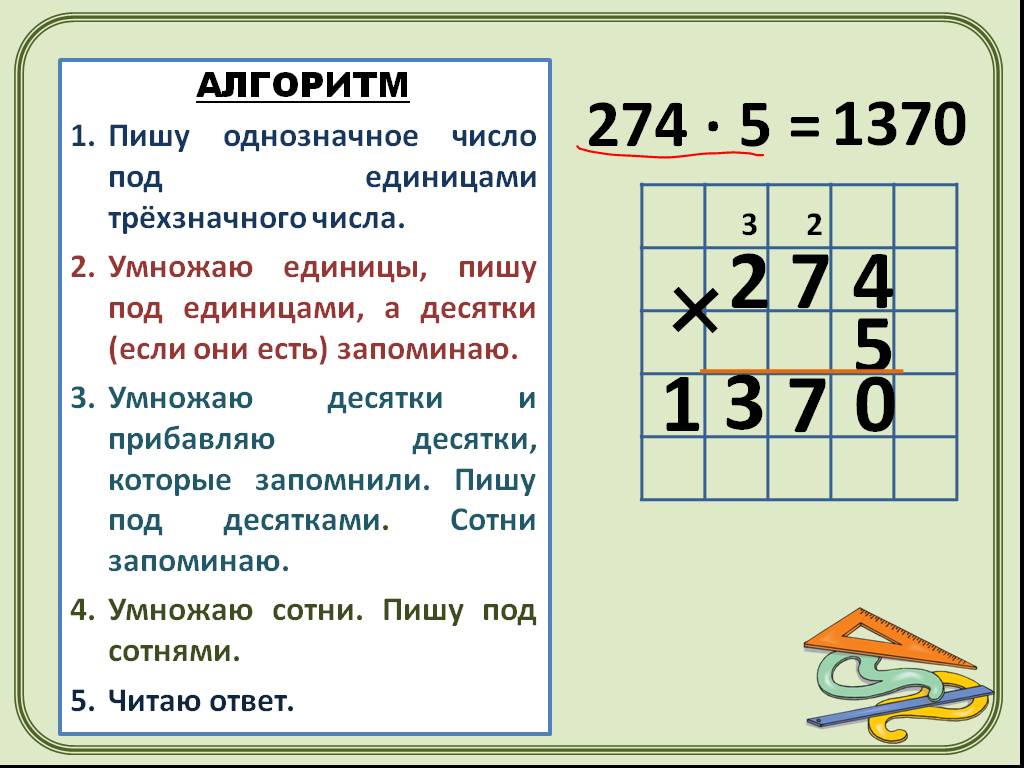

Для этого вычислим сумму a·(−b)+a·b. Она будет равна 0. Учитывая распределительное свойство умножения целых чисел относительно сложения,  справедливым будет a·(−b)+a·b=a·((−b)+b). Сумма (−b)+b –это ноль, потому что это сумма противоположных чисел, в итоге получается, что a·((−b)+b)=a·0. Итоговое произведение равно 0, согласно свойству умножения целого числа на 0. Получается, что a·(−b)+a·b=0, значит, a·(−b) и a·b являются противоположными числами. Отсюда вытекает справедливость равенства a·(−b)=−(a·b). Таким же образом можно показать, что (−a)·b=−(a·b).

Как перемножить целые отрицательные числа

Для получения этого правила нам понадобится равенство (−a)·(−b)=a·b. Ниже мы приведем его доказательство.

Перед этим мы писали, почему a·(−b)=−(a·b) и (−a)·b=−(a·b), следовательно, мы можем записать цепочку равенств (−a)·(−b)=−(a·(−b))=−(−(a·b)).

У  нас получилось выражение −(−(a·b)), которое идентично a·b в силу определения противоположных чисел. Таким образом, (−a)·(−b)=a·b.

Теперь мы можем перейти к формулировке правила умножения целых отрицательных чисел.

Определение 2

Чтобы найти произведение целых отрицательных чисел, нам надо вычислить произведение их модулей.

Из правила ясно, что результат умножения двух отрицательных свойств есть число положительное.

Посмотрим, как применить это правило на практике.

Пример 6

Умножьте (−34)·(−2).

Решение

Воспользуемся правилом и просто перемножим между собой модули: -34=34 и -2=2.

Весь ход решения можно записать как (−34)·(−2)=34·2=68.

Ответ: 68.

Пример 7

Умножьте −1 041 на -538.

Решение

Вычисляем модули и перемножаем их столбиком.

 

Ответ: (−1 041)·(−538)=560 058.  

Как умножить целое число на единицу

Мы уже упоминали, что если мы умножим на единицу любое целое число, то результат будет равен этому же числу, то есть a·1=a. Так как числовое выражение с умножением обладает переместительным свойством, то a·1=1·a тоже должно быть верным. Получается, что 1·a=a. Выведем основное правило и запомним его:

Определение 3

Если умножить два целых числа, одно из которых равно 1, то результат будет равен второму числу.

К примеру, 58·1=58, 1·0=0 и 1·(−602)=−602. Как видно, от значения второго множителя результат не зависит: произведение −53 и 1 – это −53, а результат умножения 1 и отрицательного целого числа −989 981 – это  −989 981.

Как умножить целое число на нуль

Умножение любого целого числа на нуль дает нам в итоге нулевой результат, т.е. a·0=0. С учетом переместительного свойства умножения мы получим, что 0·a=0 тоже будет верно. Запомним:

Определение 4

Если умножить два целых числа, одно из которых равно 0, то результат тоже будет равен 0. Умножение нуля на нуль в итоге также дает нуль.

Так, произведение 678 на 0 – это 0; произведение -45 на нуль – тоже нуль; (−90 7789)·0=0.

Обратное утверждение тоже будет верным: если произведение двух чисел равно нулю, то один или оба множителя тоже равны нулю.

Как проверить результат умножения целых чисел

Для проверки точности результата умножения нам потребуется вспомнить действие деления. Нужно разделить итоговый результат на один из множителей. Если в итоге мы получим второй множитель, то мы все посчитали правильно. Если же результат будет отличен от значения другого множителя, значит, расчет ошибочен и его нужно переделать.

Посмотрим на примерах, как правильно проверить результат умножения целых чисел.

Пример 8

После умножения 21 на -5 получилось -115. Проверьте, верен ли результат.

Решение

Для проверки нам надо разделить произведение на любой множитель. Возьмем -5. Делимое и делитель у нас отрицательные, значит, в итоге мы получим частное от деления их модулей: (−115):(−5)=115:5 (посмотрите статью о том, как делить целые отрицательные числа).

В итоге мы получим 23, хотя второй множитель в исходных данных равен 21. Значит, вычисления были ошибочными.

Ответ: результат деления неверен.

Пример 9

Умножьте -17 на -67 и проверьте точность результата.

Решение

Вспоминаем, как правильно умножать целые отрицательные числа. Считаем: (−17)·(−67)=17·67=1 139. Теперь переходим к проверке. Для этого делим столбиком результат на любой множитель, например, на -67.

Согласно правилам деления чисел с разными знаками, сначала мы проводим подсчеты с их модулями:

Теперь перед результатом мы должны поставить минус.

У нас получилось -17, что соответствует первоначальному условию. Значит, мы все сделали правильно.

Ответ: (−17)·(−67)=1 139. 

Как перемножить три целых числа и более

Зная, что числовое выражение с умножением имеет сочетательное свойство, мы можем точно подсчитать произведение 3,4, 5 и большего количества множителей. А благодаря остальным свойствам можно сказать, что результат произведения не будет определяться положением множителей в примере и способом расстановки скобок. Ранее мы уже приводили обоснования этих утверждений в случае с натуральными числами. Для примера с целыми множителями эти правила работают таким же образом.

Посмотрим на конкретный пример.

Пример 10

Найдите произведение 5-ти множителей: 5, −12, 1, −2 и 15.

Решение

Заменим соседние множители их произведением и запишем, что

 5·(−12)·1·(−2)·15=(−60)·1·(−2)·15=(−60)·(−2)·15=120·15=1 800

С расстановкой скобок можно записать так: (((5·(−12))·1)·(−2))·15. Это позволит нам делать вычисления быстрее и проще.

Можно было переставить множители и по-другому: 1·5·(−12)·(−2)·15, в таком случае скобки надо было расставить так: ((1·5)·(−12))·((−2)·15)=(5·(−12))·((−2)·15)=(−60)·(−30)=1 800.

Мы видим, что результат будет одинаков вне зависимости от метода расстановки скобок и последовательности вычислений.

Ответ: 1800. 

Если хоть один из множителей в примере был бы нулевым, то подсчет не имел бы смысла. Мы сразу могли бы сказать, что результат будет равен 0. Это не зависит от значения других множителей, они могли бы быть любыми. Обратное утверждение также будет справедливо: если произведение нескольких множителей равно 0, то один из этих множителей будет нулевым.

Умножение целых чисел, правила, примеры, как умножать не целые числа, произведение двух чисел

В этом материале мы покажем, как правильно выполнять умножение целых чисел. Начнем, как всегда, с основных понятий и обозначений и выясним, какой смысл вкладывается в умножение двух целых чисел. Затем сформулируем правила, по которым перемножают целые положительные и целые отрицательные числа, а также числа, имеющие разные знаки. Как всегда, нашу мысль будем пояснять наглядными примерами решений задач. Далее рассмотрим те случаи, когда один из множителей нулевой или равен единице, посмотрим, как можно проверить верность результата, полученного после умножения, а в конце объясним, как правильно перемножать 3, 4 и большее количество целых чисел.

Основные определения при умножении целых чисел

При умножении целых чисел используются те же термины и знаки, о которых мы говорили ранее в статье об умножении натуральных чисел. У нас есть два множителя, которые являются целыми числами, результат, называемый произведением, и знак умножения в виде точки, звездочки или знака «x» (в целях единообразия в дальнейшем будем использовать точку).

Если обозначить множители и произведение буквами a, b и c, то действие умножения можем записать в виде равенства a·b=c. Само числовое выражение a·b тоже называется произведением. Произведение двух целых чисел также является целым числом.

В чем состоит смысл умножения целых чисел?

До этого мы уже объясняли смысл умножения на примере натуральных чисел. Произведение натуральных чисел a и b представляет собой сумму b слагаемых, каждое из которых равно a.

Целые положительные числа – это натуральные числа, поэтому смысл действия умножения для них точно такой же. В буквенном виде его также можно представить как

(значения a и b – целые положительные числа).

В принципе, этот смысл распространяется на все произведения, где одно слагаемое целое и положительное. Второе при этом также должно быть целым, однако оно может быть отрицательным или даже равным нулю. Так, схема умножения числа -3 на 5 будет выглядеть как (−3)·5=(−3)+(−3)+(−3)+(−3)+(−3).

Если вторым множителем является единица, то результат умножения – это сумма одного слагаемого, которое равно другому множителю. Это можно записать как a·1=a. Результат умножения целого числа на единицу есть само это число.

А как быть в случае, если одно из множителей нулевое? Получается, что в ответе будет сумма из 0 слагаемых. Очевидно, что это будет 0. Запишем, что a·0=0 для любого целого a. Умножение целого числа на ноль дает в результате ноль.

В случае с отрицательными числами общий смысл действия умножения сформулировать достаточно сложно. Примем это действие как данность и подчеркнем, что правила умножения в таком случае должны сохранять справедливыми свойства умножения для целых положительных чисел. В частности, такое числовое выражение должно обладать переместительным и сочетательным свойствами.

Основные правила, применяемые при умножении целых чисел

Можно выполнить умножение исходя из того, что оно по сути представляет собой сложение одинаковых слагаемых. Но, как мы уже отмечали, это долгий и трудный процесс, если таких слагаемых у нас много. А если одним из множителей является отрицательное число, то воспользоваться этим способом мы не можем. Поэтому нам надо вывести особые правила для умножения целых чисел. Сформулируем и запишем их.

Как умножать одно целое положительное число на другое

Целые положительные числа относятся к натуральным, поэтому правила умножения натуральных чисел распространяются и на них. В итоге мы, разумеется, получим целый положительный результат, т.е. натуральное число. Разберем конкретные примеры.

Пример 1

Подсчитайте, сколько будет 9 умножить на 7.

Решение

Обратимся к таблице умножения и возьмем из нее готовый результат.

Получим: 9·7=63.

Ответ: 63.

Пример 2

Сколько будет 127 умножить на 5?

Решение

Представим первый из множителей как сумму разрядных слагаемых, т. е. 100+20+7.

Теперь последовательно умножим слагаемые на данное число: 127·5=(100+20+7)·5=100·5+20·5+7·5.

Заканчиваем вычисление: 100·5+20·5+7·5=500+100+35=600+35=635.

Ответ: 635.

Чтобы перемножать многозначные числа, удобно пользоваться методом подсчета в столбик.

Пример 3

Условие: умножьте 712 на 92.

Решение: запишем множители в столбик и вычислим результат.

Ответ: 65 504.

Как правильно перемножить целые числа, имеющие разные знаки

Для того чтобы вывести правило для такого случая, приведем пример.

Итак, нам надо вычислить произведение числа -5 на 3. Вспомним смысл умножения и запишем: (−5)·3=(−5)+(−5)+(−5)=−15. Если учесть переместительное свойство, то должно быть верным и (−5)·3=3·(−5). Очевидно, что модуль числа, полученного в результате, соответствует произведению данных множителей. Таким образом, произведение двух чисел с разными знаками есть число отрицательное.

Определение 1

Чтобы умножить одно отрицательное число на одно положительное, надо перемножить между собой модули этих чисел и поставить перед результатом минус.

Разберем несколько примеров, подтверждающих это правило.

Пример 4

Умножьте 7 на -14.

Решение

Запишем отдельно модули исходных множителей. Получим 7 и 14. Подсчитаем, чему будет равно их произведение: 7·14=98. Все, что нам нужно сделать дальше, – это поставить знак минуса перед полученным числом.

Ответ: 7·(−14)=−98.

Пример 5

Подсчитайте, сколько будет (−36)·29.

Решение

Согласно правилу умножения чисел с разными знаками, нам нужно начать с умножения модулей. Считаем: 36·29=1 044. Здесь удобно будет воспользоваться методом умножения в столбик. Нам осталось поставить минус перед результатом и записать готовый ответ.

Ответ: (−36)·29=−1 044.

В последней части параграфа мы попробуем доказать, что равенство a·(−b)=−(a·b) справедливо (a и b здесь – любые целые числа). Правило умножения целых чисел с разными знаками, которое мы записали выше, является частным случаем этого равенства.

Задача сводится к тому, что нам надо доказать, что значениями выражений a·(−b) и a·b будут противоположные числа. Для этого вычислим сумму a·(−b)+a·b. Она будет равна 0. Учитывая распределительное свойство умножения целых чисел относительно сложения,  справедливым будет a·(−b)+a·b=a·((−b)+b). Сумма (−b)+b –это ноль, потому что это сумма противоположных чисел, в итоге получается, что a·((−b)+b)=a·0. Итоговое произведение равно 0, согласно свойству умножения целого числа на 0. Получается, что a·(−b)+a·b=0, значит, a·(−b) и a·b являются противоположными числами. Отсюда вытекает справедливость равенства a·(−b)=−(a·b). Таким же образом можно показать, что (−a)·b=−(a·b).

Как перемножить целые отрицательные числа

Для получения этого правила нам понадобится равенство (−a)·(−b)=a·b. Ниже мы приведем его доказательство.

Перед этим мы писали, почему a·(−b)=−(a·b) и (−a)·b=−(a·b), следовательно, мы можем записать цепочку равенств (−a)·(−b)=−(a·(−b))=−(−(a·b)).

У  нас получилось выражение −(−(a·b)), которое идентично a·b в силу определения противоположных чисел. Таким образом, (−a)·(−b)=a·b.

Теперь мы можем перейти к формулировке правила умножения целых отрицательных чисел.

Определение 2

Чтобы найти произведение целых отрицательных чисел, нам надо вычислить произведение их модулей.

Из правила ясно, что результат умножения двух отрицательных свойств есть число положительное.

Посмотрим, как применить это правило на практике.

Пример 6

Умножьте (−34)·(−2).

Решение

Воспользуемся правилом и просто перемножим между собой модули: -34=34 и -2=2.

Весь ход решения можно записать как (−34)·(−2)=34·2=68.

Ответ: 68.

Пример 7

Умножьте −1 041 на -538.

Решение

Вычисляем модули и перемножаем их столбиком.

 

Ответ: (−1 041)·(−538)=560 058.  

Как умножить целое число на единицу

Мы уже упоминали, что если мы умножим на единицу любое целое число, то результат будет равен этому же числу, то есть a·1=a. Так как числовое выражение с умножением обладает переместительным свойством, то a·1=1·a тоже должно быть верным. Получается, что 1·a=a. Выведем основное правило и запомним его:

Определение 3

Если умножить два целых числа, одно из которых равно 1, то результат будет равен второму числу.

К примеру, 58·1=58, 1·0=0 и 1·(−602)=−602. Как видно, от значения второго множителя результат не зависит: произведение −53 и 1 – это −53, а результат умножения 1 и отрицательного целого числа −989 981 – это  −989 981.

Как умножить целое число на нуль

Умножение любого целого числа на нуль дает нам в итоге нулевой результат, т.е. a·0=0. С учетом переместительного свойства умножения мы получим, что 0·a=0 тоже будет верно. Запомним:

Определение 4

Если умножить два целых числа, одно из которых равно 0, то результат тоже будет равен 0. Умножение нуля на нуль в итоге также дает нуль.

Так, произведение 678 на 0 – это 0; произведение -45 на нуль – тоже нуль; (−90 7789)·0=0.

Обратное утверждение тоже будет верным: если произведение двух чисел равно нулю, то один или оба множителя тоже равны нулю.

Как проверить результат умножения целых чисел

Для проверки точности результата умножения нам потребуется вспомнить действие деления. Нужно разделить итоговый результат на один из множителей. Если в итоге мы получим второй множитель, то мы все посчитали правильно. Если же результат будет отличен от значения другого множителя, значит, расчет ошибочен и его нужно переделать.

Посмотрим на примерах, как правильно проверить результат умножения целых чисел.

Пример 8

После умножения 21 на -5 получилось -115. Проверьте, верен ли результат.

Решение

Для проверки нам надо разделить произведение на любой множитель. Возьмем -5. Делимое и делитель у нас отрицательные, значит, в итоге мы получим частное от деления их модулей: (−115):(−5)=115:5 (посмотрите статью о том, как делить целые отрицательные числа).

В итоге мы получим 23, хотя второй множитель в исходных данных равен 21. Значит, вычисления были ошибочными.

Ответ: результат деления неверен.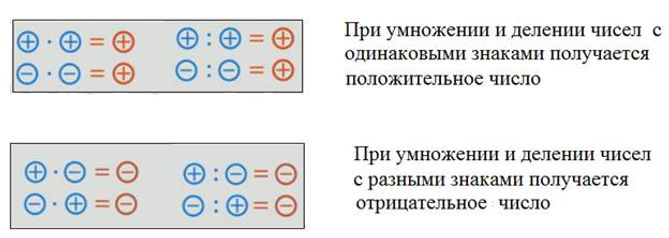

Пример 9

Умножьте -17 на -67 и проверьте точность результата.

Решение

Вспоминаем, как правильно умножать целые отрицательные числа. Считаем: (−17)·(−67)=17·67=1 139. Теперь переходим к проверке. Для этого делим столбиком результат на любой множитель, например, на -67.

Согласно правилам деления чисел с разными знаками, сначала мы проводим подсчеты с их модулями:

Теперь перед результатом мы должны поставить минус.

У нас получилось -17, что соответствует первоначальному условию. Значит, мы все сделали правильно.

Ответ: (−17)·(−67)=1 139. 

Как перемножить три целых числа и более

Зная, что числовое выражение с умножением имеет сочетательное свойство, мы можем точно подсчитать произведение 3,4, 5 и большего количества множителей. А благодаря остальным свойствам можно сказать, что результат произведения не будет определяться положением множителей в примере и способом расстановки скобок. Ранее мы уже приводили обоснования этих утверждений в случае с натуральными числами. Для примера с целыми множителями эти правила работают таким же образом.

Посмотрим на конкретный пример.

Пример 10

Найдите произведение 5-ти множителей: 5, −12, 1, −2 и 15.

Решение

Заменим соседние множители их произведением и запишем, что

 5·(−12)·1·(−2)·15=(−60)·1·(−2)·15=(−60)·(−2)·15=120·15=1 800

С расстановкой скобок можно записать так: (((5·(−12))·1)·(−2))·15. Это позволит нам делать вычисления быстрее и проще.

Можно было переставить множители и по-другому: 1·5·(−12)·(−2)·15, в таком случае скобки надо было расставить так: ((1·5)·(−12))·((−2)·15)=(5·(−12))·((−2)·15)=(−60)·(−30)=1 800.

Мы видим, что результат будет одинаков вне зависимости от метода расстановки скобок и последовательности вычислений.

Ответ: 1800. 

Если хоть один из множителей в примере был бы нулевым, то подсчет не имел бы смысла. Мы сразу могли бы сказать, что результат будет равен 0. Это не зависит от значения других множителей, они могли бы быть любыми. Обратное утверждение также будет справедливо: если произведение нескольких множителей равно 0, то один из этих множителей будет нулевым.

Свойство мультипликативной идентичности единицы

Свойство мультипликативной идентичности 1

Я номер один.

Суммы, в которые я вовлечен, легкие и веселые.

Я умный и сообразительный.

Проблемы со мной, ты всегда справишься!

Родственные игры

Что такое номер 1?

Это очень простой номер. Но и очень важно. В математике число 1 представляет собой единое целое. Это количество или значение 1. Единица — первое положительное нечетное число в числовой строке.

Сегодня мы узнаем о свойстве мультипликативной идентичности единицы. Уникально и интересно. Давайте сразу приступим.

Связанные рабочие листы

Определение идентичности Свойство умножения?

Свойство мультипликативной идентичности числа 1. Звучит сложно, не правда ли? Это не. Подать заявку на недвижимость с таким длинным названием легко. Это также довольно простой математический закон.

Формула мультипликативной идентичности выражается как  ✕  1 = a. Здесь «а» может быть любым вещественным числом.

В нем говорится, что любое число, умноженное на 1, дает тот же результат, что и само число. Его также называют тождественным свойством умножения. Это потому, что идентичность номера остается прежней.

Вот несколько примеров тождественности умножения.

Что вы видите на графике выше? Что произойдет, если 1 умножить на любое число? Ничего, это не меняет номер. Получим то же число, что и в результате, когда умножим его на 1. Число не изменится, а значит сохранит свои identity , что является причиной названия свойства. И мы можем сказать, что 1 — это мультипликативная идентичность .

Интересные факты!

• Египтяне были первой цивилизацией, которая изобрела различные символы. Они сделали это для разных чисел. У них был символ для одного. Это была просто линия.
• 1 — натуральное число.
• 1 не является ни простым, ни составным числом.
• 1 — единственный делитель 1.
• Что происходит, когда число делится на 1? Оно дает то же частное, что и само число. Это называется тождественным свойством деления.
• 1 также называют «единицей» или «единицей».

Решенные примеры

  Пример 1. Если 35  ✕  n = 35, каково значение n? Укажите используемое имущество.

Решение:

35 ✕ n = 35 (дано)

n = 35 ÷ 35 = 1

n = 1

. используется тождественное свойство умножения . Результатом является исходное число, когда вы умножаете число на 1.

Пример 2. Используйте свойство идентичности умножения, чтобы найти правильное значение «z», если z  ✕  1 = 9/17.

Решение:

z ✕ 1 = 9/17 (дано)

Воспользуемся мультипликативным тождеством. Если 1 умножается на число, возвращается исходное число.

Следовательно, z = 9/17 

Пример 3. Какое из двух уравнений иллюстрирует тождественное свойство умножения?

A) 54 ✕ 1 = 54 B) -54 ✕ -1 = 54

Решение:

A) 54 ✕ 1 = 54. Да, это уравнение иллюстрирует свойство идентификационную свойство умножения. Число 54, умноженное на 1, дает тот же результат, что и само число, 54.

б) -54  ✕  -1 = 54: Нет, это уравнение не иллюстрирует тождественное свойство умножения. Число -54 при умножении на -1 дает результат, отличный от исходного числа.

Практические задачи

1

Что такое мультипликативный элемент идентичности для действительных чисел?

1

-1

Само число

Правильный ответ: 1
Мультипликативное тождество действительного числа равно 1. Когда мы умножаем 1 на любое действительное число, мы получаем одно и то же число.
Например, 59 ✕ 1 = 59.

2

Используйте свойство мультипликативной идентичности, чтобы найти правильное значение «n», если n ✕ 1 = -27.

1

27

-27

Правильный ответ: -27
n ✕ 1 = -27 (дано). Согласно мультипликативной идентичности, если 1 умножается на число, произведение является исходным числом. Итак, поскольку произведение равно -27, n также равно -27.
-27 ✕ 1 = -27

3

Какое уравнение демонстрирует свойство мультипликативной идентичности? 1010151 Любое число, умноженное на 1, дает тот же результат, что и само число.

Это свойство показано в варианте b. -101 ✕ 1 = — 101.

Часто задаваемые вопросы

Почему цифра 1 называется уникальной?

1 (единица, также называемая единицей и единицей) — это число. Числовая цифра используется для представления этого числа цифрами. Число 1 называют уникальным числом по следующим причинам:

• Это не простое и не составное число.
• Имеет только один фактор, то есть само число.

Применяется ли свойство идентичности умножения к -1?

Нет, мультипликативная идентичность не применяется, когда любое число умножается на -1. Это потому, что результат не будет тем же числом. Например, 31  ✕  -1 = -31.

К каким числам можно применить свойство идентичности умножения?

Свойство идентичности умножения можно применить ко всем действительным числам. Это включает в себя натуральные числа, целые числа, а также рациональные числа.

4 простых способа умножения показателей степени [+ Действия] | Блог Prodigy Math

Что общего между землетрясениями, фондовым рынком, информатикой и ядерной физикой?

Все они включают умножение степени .

Экспоненты являются неотъемлемой частью алгебры, полиномиальных уравнений и курсов математики более высокого уровня, но многие студенты с трудом понимают, как с ними работать. Вы прошли через правила экспоненты с вашим классом, и теперь пришло время применить их в действии. 95 = 243

Первое число называется основанием . Представляет число, которое умножается.

Второе, меньшее число — это показатель степени . Он представляет собой количество раз, когда основание умножается само на себя.

Существует семь правил экспоненты :

1. Правило произведения степеней : Сложение степеней при умножении одинаковых оснований
2. Правило отношения степеней : Вычитание степеней при делении одинаковых оснований
3. Правило степени степеней : Умножение степеней вместе при возведении степени в другую степень
4. Степень произведения rul e: Распределение мощности по каждому основанию при возведении нескольких переменных в степень
5. Степень правила частного : Распределить степень ко всем значениям в частном
6. Правило нулевой степени : Любое основание, возведенное в нулевую степень, становится единицей
7. Правило отрицательного порядка взаимный

Понял? Тогда продолжим.

Как умножать экспоненты 4 способами

Помните, что все эти стратегии — всего лишь ярлыки, помогающие упростить более сложные уравнения. Чтобы найти фактическое значение показателя степени, учащиеся должны сначала понять, что это значит:  повторное умножение .

Познакомьте учащихся с основами, такими как выражение показателей степени в виде произведений, прежде чем переходить к умножению показателей степени.

Когда они освоятся с концепцией, пора начинать. 92 не имеют ничего общего, что можно было бы объединить, ответ не может быть упрощен до одного показателя степени и должен быть выражен в виде обычного числа.

4. Умножение отрицательных показателей степени

Это может показаться сложным, но умножение показателей степени с отрицательными числами точно такое же, как умножение показателей степени с неотрицательными числами.

Начните с изучения свойств отрицательных чисел. В частности, просмотрите, как складывать и умножать их. Ваши ученики должны чувствовать себя комфортно, работая с отрицательными числами, прежде чем они перейдут к отрицательным показателям. 92

Сначала преобразуйте отрицательные показатели в обратные, затем вычислите.

Когда вы умножаете экспоненты, напомните студентам:

• Добавить экспоненты , если основания одинаковы
• , умножженные базы . , просто решите

Упражнения для тренировки умножения в степени

1. Prodigy

Развитие беглости математики является важной частью того, чтобы учащиеся чувствовали себя уверенно на математических курсах средней школы и колледжа. Учащиеся могут практиковаться в умножении показателей и других математических понятиях с Prodigy, а вы задаете индивидуальные вопросы в игре, основанные на содержании урока.

Ваш класс будет исследовать мир, наполненный увлекательными квестами, экзотическими домашними животными и изучением математики. Вы сможете выбирать, на какие вопросы они будут отвечать, и получать в режиме реального времени данные о том, что они освоили, над чем работают и где им может понадобиться дополнительная помощь.

Имея 1400 навыков и подсчет, вы сможете предоставлять материалов, соответствующих учебной программе,  по любой теме, которую вы изучаете, включая умножение показателей.

2. Экспонентная война

Education.com

Классическая карточная игра, но с экспоненциально интересным поворотом!

Учащиеся работают в командах по два человека и противостоят другой паре. Дайте каждой команде по колоде карт (с вынутыми дамами, валетами и королями) и попросите каждого игрока вытащить по две карты. Первая карта является основанием, а вторая карта является показателем степени.

Каждая пара должна решить свое уравнение и найти произведение. Побеждает команда с наибольшим ответом. Установите таймер для класса и посмотрите, кто наберет больше всего очков.

Пока ученики играют, пройдитесь по классу и убедитесь, что они не пропускают ни одного шага. Если вы видите много ошибок или неуспевающих учеников, воспринимайте это как знак того, что вам, возможно, нужно что-то пересмотреть.

3. Exponent Scavenger Hunt

Дайте своим ученикам возможность найти сокровища и исследовать класс с помощью показательной охоты за мусором.

Разделите свой класс на группы по три или четыре человека. В зависимости от количества групп, которые у вас есть, сделайте несколько разных наборов карточек. Начинайте каждый набор с карты, на которой есть проблема. Напишите ответ на задачу на следующей карточке, а на обороте поставьте еще одну задачу. Продолжайте, пока у вас не будет трех или четырех наборов задач (или больше).

Начиная с первой карточки, каждая группа должна решить задачу и найти правильный ответ где-то еще в классе . Когда они находят карточку с правильным ответом, они могут перевернуть ее и решить следующую задачу. Дайте учащимся листочки для решения и позвольте им начать искать свои ответы. Какая команда финиширует первой, та и победительница!

4. Exponent Jeopardy

Каждый ученик любит классическую игру Jeopardy. Используя настраиваемый шаблон, замените викторины вопросами, которые дают учащимся возможность попрактиковаться в умножении показателей, и разделите класс на две команды.

Вот несколько советов, как обеспечить бесперебойную работу игры:

• Если у вас большой класс, подумайте о том, чтобы разделить класс на несколько игр, чтобы у каждого ученика была возможность принять участие.
• предложить учащимся самим сделать игру. Дайте им шаблон (или пусть более продвинутые ученики начнут с нуля) и попросите их сделать короткую игру.
• Используйте его в качестве проверки в конце модуля перед тестом и комбинируйте более важные вопросы с более сложными ответами

5. Рабочие листы для умножения показателей степени

Рабочие листы — это проверенный метод развития математических навыков в определенном наборе навыков. Они также могут быть индикатором понимания учащимися, если используются как часть стратегии формативного оценивания. Вот некоторые из наших любимых:

• Папины рабочие листы
• Education.com
• Math Drills

).

Чтобы получить что-то более уникальное, попробуйте умножение многочленов. Как и в обычном рабочем листе, в нем есть вопросы, на которые должны ответить учащиеся, но он также содержит «банк ответов» для учащихся. Вырежьте соответствующие полоски и перемешайте их. Предложите учащимся сопоставить ответы с правильным разделом на своем рабочем листе после решения уравнения и показа своей работы.

Умножение показателей: Давайте повторим

Если ваши ученики помнят только три вещи, убедитесь, что это следующие понятия:

• Сложение степеней при умножении подобных оснований
• Умножение оснований при умножении как показателей степени
• Показатель степени является продуктом многократного умножения

Если они запомнят эти три правила, у них будет прочный фундамент, построенный еще до их первого максимума школьный урок алгебры.