Правила умножения и деления любого числа на ноль
Число ноль занимает особое место в такой науке, как математика, даже несмотря на то, что оно буквально означает «ничто», «пустоту».
Ноль используют для обозначения «пустых» разрядов в десятичных дробях, как после запятой, так и до, для начала отсчёта координат в системах координат, а также именно нолю принадлежит одно из основных правил арифметики – на ноль делить нельзя.
С ним выполняются все арифметические действия: деление, умножение, сложение и вычитание, но именно деление и умножение на ноль мы сейчас рассмотрим подробнее, так как в них содержатся некоторые нюансы.
Что такое умножение в математике, определение.
Для того, чтобы разобраться, чем отличается умножение числа на ноль от умножения других чисел на друг друга, нужно для начала дать определение, что такое операция умножения в целом.
Умножение – одно из основных действий в математике, в котором участвуют два аргумента – множитель и сомножитель. Зачастую, особенно в школах, первый аргумент называют множимым, а второй множителем. Результат их умножения называют произведением.
Зачастую, особенно в школах, первый аргумент называют множимым, а второй множителем. Результат их умножения называют произведением.
Для натуральных чисел умножением, по сути, является многократное сложение. Таким образом получаем, чтобы умножить число a на число b, необходимо b раз сложить a.
a ⋅ b = a + a + … + a} b
Умножение на ноль, правило математики.Основное правило гласит: при умножении числа на ноль и ноль на число в ответе всегда будет получаться ноль.
a ⋅ 0 = 0
0 ⋅ a = 0
Не всегда всем понятно, почему же в итоге получается ноль. Правило сухо заучивается, а вопрос так и остается без ответа, хотя ничего сверхъестественного и скрытого в этом нет, всё многим проще, чем может показаться изначально.
Ответ кроется в самом действии умножения, о котором мы подробно поговорили выше. Рассмотрим самое логичное и примитивное объяснение, дабы понять, что данное умножение бесполезно, так как при умножении числа на ноль результат всё равно будет один – ноль.
Допустим, число a – это яблоко, а число b – это количество яблок, которое необходимо взять. Если b будет равняться нолю, получается, мы берем яблоко ноль раз, а, следовательно, как не было яблок, так и нет.
И наоборот, если у нас нет яблок, то и взять ничего не получится.
Данный пример – настолько простой и понятный в понимании правил умножения на ноль, что даже самый далёкий от математических формул человек сможет в своей голове всё по полочкам разложить.
Примеры умножения на ноль.
0 ⋅ 3 = 0 + 0 + 0 = 0
0 ⋅ 4 = 0 + 0 + 0 + 0 = 0
756 ⋅ 0 = 0
293 ⋅ 0 = 0
Что такое деление в математике, определение.
Деление – в математике действие обратное умножению, также состоящее из двух аргументов – делимого и делителя. Результат деления называют частным. Остатком называют то число, что осталось после деления делимого на делитель.
Результат деления называют частным. Остатком называют то число, что осталось после деления делимого на делитель.
Деление в математике принято обозначать двоеточием :, косой чертой /, горизонтальной чертой — или обелюсом ÷.
Если умножение для натуральных чисел заменяет многократное сложение, то, соответственно, деление будет заменять многократное вычитание.
Чтобы стало понятнее, рассмотрим на простом примере, таком как деление числа15 на число 2.
Из действия вычитания мы находим, что число 2 содержится в 15 семь полных раз, и еще остается единица.
В данном случае 15 – делимое, 2 – делитель, 7 – неполное частное, а 1 – остаток.
Также иногда результат деления называют отношением.
Деление на ноль, правило математики.
С начальной школы всем пытаются привить, что на ноль делить нельзя. Все это заучивают, не требуя лишних доказательств, ну нельзя и нельзя. Однако стоит спросить взрослого человека – а почему, собственно, нельзя? Мало кто сможет достаточно внятно ответить на поставленный вопрос из школьной программы, так как это правило вызывает довольно много противоречий.
Большинство людей и правда не делит на ноль только исходя из этого правила, не пытаясь найти ответ, по которому станет понятен этот запрет. Хотя ответ лежит прямо перед глазами.
Как оказалось, не все действия в арифметике полноправны, а точнее только сложение и умножение, следовательно, все остальные действия с числами исходят от них.
Рассмотрим в качестве примера выражение: 14 : 0
Данное выражение можно представить и в виде уравнения: 0 ⋅ x = 14
Становится понятно, что при делении на ноль, необходимо найти такое число, при умножении на которое получится 14, а это априори невозможно исходя из всего того, что мы выяснили ранее.
Примеры деления на ноль.
56 : 0 = 0
15 : 0 = 0
0 : 9 = 0
Действия с нулём. Правило умножения любого числа на ноль Любое число умноженное на 0 равняется
Ещё в школе учителя нам всем старались вбить в голову простейшее правило: «Любое число, умноженное на ноль, равняется нулю!» , — но всё равно вокруг него постоянно возникает куча споров. Кто-то просто запомнил правило и не забивает себе голову вопросом «почему?». «Нельзя и всё тут, потому что в школе так сказали, правило есть правило!» Кто-то может исписать полтетради формулами, доказывая это правило или, наоборот, его нелогичность.
Кто-то просто запомнил правило и не забивает себе голову вопросом «почему?». «Нельзя и всё тут, потому что в школе так сказали, правило есть правило!» Кто-то может исписать полтетради формулами, доказывая это правило или, наоборот, его нелогичность.
Вконтакте
Кто в итоге прав
Во время этих споров оба человека, имеющие противоположные точки зрения, смотрят друг на друга, как на барана, и доказывают всеми силами свою правоту. Хотя, если посмотреть на них со стороны, то можно увидеть не одного, а двух баранов, упирающихся друг в друга рогами. Различие между ними лишь в том, что один чуть менее образован, чем второй.
Чаще всего, те, кто считают это правило неверным, стараются призвать к логике вот таким способом:
У меня на столе лежит два яблока, если я положу к ним ноль яблок, то есть не положу ни одного, то от этого мои два яблока не исчезнут! Правило нелогично!
Действительно, яблоки никуда не исчезнут, но не из-за того, что правило нелогично, а потому что здесь использовано немного другое уравнение: 2+0 = 2. Так что такое умозаключение отбросим сразу — оно нелогично, хоть и имеет обратную цель — призвать к логике.
Так что такое умозаключение отбросим сразу — оно нелогично, хоть и имеет обратную цель — призвать к логике.
Что такое умножение
Изначально правило умножения было определено только для натуральных чисел: умножение — это число, прибавленное к самому себе определённое количество раз, что подразумевает натуральность числа. Таким образом, любое число с умножением можно свести вот к такому уравнению:
- 25×3 = 75
- 25 + 25 + 25 = 75
- 25×3 = 25 + 25 + 25
Из этого уравнения следует вывод, что умножение — это упрощённое сложение .
Что такое ноль
Любой человек с самого детства знает: ноль — это пустота, Несмотря на то, что эта пустота имеет обозначение, она не несёт за собой вообще ничего. Древние восточные учёные считали иначе — они подходили к вопросу философски и проводили некие параллели между пустотой и бесконечностью и видели глубокий смысл в этом числе. Ведь ноль, имеющий значение пустоты, встав рядом с любым натуральным числом, умножает его в десять раз. Отсюда и все споры по поводу умножения — это число несёт в себе столько противоречивости, что становится сложно не запутаться. Кроме того, ноль постоянно используется для определения пустых разрядов в десятичных дробях, это делается и до, и после запятой.
Отсюда и все споры по поводу умножения — это число несёт в себе столько противоречивости, что становится сложно не запутаться. Кроме того, ноль постоянно используется для определения пустых разрядов в десятичных дробях, это делается и до, и после запятой.
Можно ли умножать на пустоту
Умножать на ноль можно, но бесполезно, потому что, как ни крути, но даже при умножении отрицательных чисел всё равно будет получаться ноль. Достаточно просто запомнить это простейшее правило и никогда больше не задаваться этим вопросом. На самом деле всё проще, чем кажется на первый взгляд. Нет никаких скрытых смыслов и тайн, как считали древние учёные. Ниже будет приведено самое логичное объяснение, что это умножение бесполезно, ведь при умножении числа на него всё равно будет получаться одно и то же — ноль.
Возвращаясь в самое начало, к доводу по поводу двух яблок, 2 умножить на 0 выглядит вот так:
- Если съесть по два яблока пять раз, то съедено 2×5 = 2+2+2+2+2 = 10 яблок
- Если их съесть по два трижды, то съедено 2×3 = 2+2+2 = 6 яблок
- Если съесть по два яблока ноль раз, то не будет съедено ничего — 2×0 = 0×2 = 0+0 = 0
Ведь съесть яблоко 0 раз — это означает не съесть ни одного. Это будет понятно даже самому маленькому ребёнку. Как ни крути — выйдет 0, двойку или тройку можно заменить абсолютно любым числом и выйдет абсолютно то же самое. А если проще говоря, то ноль — это ничего , а когда у вас ничего нет , то сколько ни умножай — всё равно будет ноль . Волшебства не бывает, и из ничего не получится яблоко, даже при умножении 0 на миллион. Это самое простое, понятное и логичное объяснение правила умножения на ноль. Человеку, далёкому от всех формул и математики будет достаточно такого объяснения, для того чтобы диссонанс в голове рассосался, и всё встало на свои места.
Это будет понятно даже самому маленькому ребёнку. Как ни крути — выйдет 0, двойку или тройку можно заменить абсолютно любым числом и выйдет абсолютно то же самое. А если проще говоря, то ноль — это ничего , а когда у вас ничего нет , то сколько ни умножай — всё равно будет ноль . Волшебства не бывает, и из ничего не получится яблоко, даже при умножении 0 на миллион. Это самое простое, понятное и логичное объяснение правила умножения на ноль. Человеку, далёкому от всех формул и математики будет достаточно такого объяснения, для того чтобы диссонанс в голове рассосался, и всё встало на свои места.
Деление
Из всего вышеперечисленного вытекает и другое важное правило:
На ноль делить нельзя!
Это правило нам тоже с самого детства упорно вбивают в голову. Мы просто знаем, что нельзя и всё, не забивая себе голову лишней информацией. Если вам неожиданно зададут вопрос, по какой причине запрещено делить на ноль, то большинство растеряется и не сможет внятно ответить на простейший вопрос из школьной программы, потому что вокруг этого правила не ходит столько споров и противоречий.
Все просто зазубрили правило и не делят на ноль, не подозревая, что ответ кроется на поверхности. Сложение, умножение, деление и вычитание — неравноправны, полноценны из перечисленного только умножение и сложение, а все остальные манипуляции с числами строятся из них. То есть запись 10: 2 является сокращением уравнения 2 * х = 10. Значит, запись 10: 0 такое же сокращение от 0 * х = 10. Получается, что деление на ноль — это задание найти число, умножая которое на 0, получится 10. А мы уже разобрались, что такого числа не существует, значит, у этого уравнения нет решения, и оно будет априори неверным.
Расскажу тебе позволь,
Чтобы не делил на 0!
Режь 1 как хочешь, вдоль,
Только не дели на 0!
Евгений Ширяев, преподаватель и руководитель Лаборатории математики Политехнического музея , рассказал АиФ.ru о делении на ноль:
1. Юрисдикция вопроса
Согласитесь, особенную провокационность правилу придает запрет. Как это нельзя? Кто запретил? А как же наши гражданские права?
Как это нельзя? Кто запретил? А как же наши гражданские права?
Ни конституция РФ, ни Уголовный кодекс, ни даже устав вашей школы не возражают против интересующего нас интеллектуального действия. А значит, запрет не имеет юридической силы, и ничто не мешает прямо тут, на страницах АиФ.ru, попробовать что-нибудь разделить на ноль. Например, тысячу.
2. Разделим, как учили
Вспомните, когда вы только узнали, как делить, первые примеры решали спроверкой умножением: результат, умноженный на делитель должен был совпасть сделимым. Не совпал — не решили.
Пример 1. 1000: 0 =…
Забудем на минуту про запретное правило и сделаем несколько попыток угадать ответ.
Неправильные отсечёт проверка. Перебирайте варианты: 100, 1, −23, 17, 0, 10 000. Для каждого из них проверка даст один и тот же результат:
100 · 0 = 1 · 0 = − 23 · 0 = 17 · 0 = 0 · 0 = 10 000 · 0 = 0
Ноль умножением все превращает в себя и никогда в тысячу. Вывод сформулировать несложно: никакое число не пройдет проверку. Т. е. ни одно число не может быть результатом деления ненулевого числа на ноль. Такое деление не запрещено, а просто не имеет результата.
Т. е. ни одно число не может быть результатом деления ненулевого числа на ноль. Такое деление не запрещено, а просто не имеет результата.
3. Нюанс
Чуть не упустили одну возможность опровергнуть запрет. Да, мы признаем, что ненулевое число не разделится на 0. Но может быть, сам 0 сможет?
Пример 2. 0: 0 = …
Ваши предложения для частного? 100? Пожалуйста: частное 100, умноженное на делитель 0, равно делимому 0.
Еще варианты! 1? Тоже подходит. И −23, и 17, и все-все-все. В этом примере проверка на результат будет положительной для любого числа. И по-честному, решением в этом примере надо называть не число, а множество чисел. Всех. А так недолго договориться и до того, что Алиса это не Алиса, а Мэри-Энн, а обе они — сон кролика.
4. Что там про высшую математику?
Проблема разрешена, нюансы учтены, точки расставлены, все прояснилось — ответом для примера с делением на ноль не может быть ни одно число. Такие задачки решать — дело безнадежное и невозможное.
Пример 3. Придумать, как разделить 1000 на 0.
А никак. Зато 1000 можно без трудностей делить на другие числа. Ну, давайте хотя бы делать, что получается, пусть даже изменив поставленную задачу. А там, глядишь, увлечемся, и ответ сам собой объявится. Забываем на минуту про ноль и делим на сто:
Сотня далека от нуля. Сделаем шаг к нему, уменьшив делитель:
1000: 25 = 40,
1000: 20 = 50,
1000: 10 = 100,
1000: 8 = 125,
1000: 5 = 200,
1000: 4 = 250,
1000: 2 = 500,
1000: 1 = 1000.
Очевидная динамика: чем ближе делитель к нулю, тем больше частное. Тенденцию можно наблюдать и дальше, переходя к дробям и продолжая уменьшать числитель:
Осталось заметить, что к нулю мы можем подойти как угодно близко, делая частное сколь угодно большим.
В этом процессе нет нуля и нет последнего частного. Мы обозначили движение к ним, заменив число на последовательность, сходящуюся к интересующему нас числу:
При этом подразумевается аналогичная замена и для делимого:
1000 ↔ { 1000, 1000, 1000,. .. }
.. }
Стрелки не зря поставлены двусторонними: некоторые последовательности могут сходиться к числам. Тогда мы можем поставить в соответствие последовательности ее числовой предел.
Посмотрим на последовательность частных:
Она растет неограниченно, не стремясь ни к какому числу и превосходя любое. Математики добавляют к числам символ ∞, чтобы иметь возможность рядом с такой последовательностью поставить двустороннюю стрелку:
Сопоставление числам последовательностей, имеющих предел, позволяет предложить решение к третьему примеру:
При поэлементном делении последовательности, сходящейся к 1000, на последовательность из положительных чисел, сходящуюся к 0, получим последовательность, сходящуюся к ∞.
5. И здесь нюанс с двумя нулями
Что будет результатом деления двух последовательностей положительных чисел, сходящихся к нулю? Если они одинаковые, то тождественная единица. Если к нулю быстрее сходится последовательность-делимое, то в частном последовательность снулевым пределом. А когда элементы делителя убывают гораздо быстрее, чем у делимого, последовательность частного будет сильно расти:
А когда элементы делителя убывают гораздо быстрее, чем у делимого, последовательность частного будет сильно расти:
Неопределенная ситуация. И так и называется: неопределенность вида 0/0 . Когда математики видят последовательности, подходящие под такую неопределенность, они не бросаются делить два одинаковых числа друг на друга, а разбираются, какая из последовательностей быстрее бежит к нулю и как именно. И в каждом примере будет свой конкретный ответ!
6. В жизни
Закон Ома связывает силу тока, напряжение и сопротивление в цепи. Часто его записывают в такой форме:
Позволим себе пренебречь аккуратным физическим пониманием и формально посмотрим на правую часть как на частное двух чисел. Вообразим, что решаем школьную задачу по электричеству. В условии дано напряжение в вольтах и сопротивление в омах. Вопрос очевиден, решение в одно действие.
А теперь заглянем в определение сверхпроводимости: это свойство некоторых металлов обладать нулевым электрическим сопротивлением.
Ну что, решим задачку для сверхпроводящей цепи? Просто так подставить R = 0 не выйдет, физика подкидывает интересную задачу, за которой, очевидно, стоит научное открытие. И люди, сумевшие поделить на ноль в этой ситуации, получили Нобелевскую премию. Любые запреты полезно уметь обходить!
Ноль сам по себе цифра очень интересная. Сам по себе означает пустоту, отсутствие значения, а рядом с другой цифрой увеличивает ее значимость в 10 раз. Любые числа в нулевой степени всегда дают 1. Этот знак использовали еще в цивилизации майя, причем он у них еще обозначал понятие «начало, причина». Даже календарь у начинался с нулевого дня. А еще эта цифра связана со строгим запретом.
Еще с начальных школьных лет все мы четко усвоили правило «на ноль делить нельзя». Но если в детстве многое воспринимаешь на веру и слова взрослого редко вызывают сомнения, то со временем иногда хочется все-таки разобраться в причинах, понять, почему были установлены те или иные правила.
Почему нельзя делить на ноль? На этот вопрос хочется получить понятное логическое объяснение. В первом классе учителя это сделать не могли, потому как в математике правила объясняются с помощью уравнений, а в том возрасте мы и представления не имели о том, что это такое. А теперь пришла пора разобраться и получить понятное логическое объяснение того, почему нельзя делить на ноль.
В первом классе учителя это сделать не могли, потому как в математике правила объясняются с помощью уравнений, а в том возрасте мы и представления не имели о том, что это такое. А теперь пришла пора разобраться и получить понятное логическое объяснение того, почему нельзя делить на ноль.
Дело в том, что в математике лишь две из четырех основных операций (+, — , х, /) с числами признаются независимыми: умножение и сложение. Остальные же операции принято считать производными. Рассмотрим простенький пример.
Вот скажите, сколько получится, если от 20 отнять 18? Естественно, в нашей голове моментально возникает ответ: это будет 2. А как мы пришли к такому результату? Кому-то этот вопрос покажется странным — ведь и так все ясно, что получится 2, кто-то пояснит, что от 20 копеек отнял 18 и у него получилось две копейки. Логически все эти ответы не вызывают сомнений, однако с точки зрения математики решать эту задачу следует по-другому. Еще раз напомним, что главными операциями в математике являются умножение и сложение и поэтому в нашем случае ответ кроется в решении следующего уравнения: х + 18 = 20. Из которого и вытекает, что х = 20 — 18, х =2. Казалось бы, зачем так подробно все расписывать? Ведь и так все элементарно просто. Однако без этого тяжело объяснить почему нельзя делить на ноль.
Из которого и вытекает, что х = 20 — 18, х =2. Казалось бы, зачем так подробно все расписывать? Ведь и так все элементарно просто. Однако без этого тяжело объяснить почему нельзя делить на ноль.
А теперь посмотрим что получится если мы пожелаем 18 разделить на ноль. Снова составим уравнение: 18: 0 = х. Поскольку операция деления является производной от процедуры умножения, то преобразовав наше уравнение получим х * 0 = 18. Вот здесь как раз и начинается тупик. Любое число на месте икса при умножении на ноль даст 0 и получить 18 нам никак не удастся. Теперь становится предельно ясно почему нельзя делить на ноль. Сам ноль можно делить на какое-угодно число, а вот наоборот — увы, никак нельзя.
А что получится, если ноль разделить на самого себя? Это можно записать в таком виде: 0: 0 = х, или х * 0 = 0. Это уравнение имеет бесчисленное число решений. Поэтому в итоге получается бесконечность. Поэтому операция и в этом случае тоже не имеет смысла.
Деление на 0 лежит в корне многих мнимых математических шуток, которыми при желании можно озадачить любого несведущего человека. К примеру, рассмотрим уравнение: 4*х — 20 = 7*х — 35. Вынесем за скобки в левой части 4, а в правой 7. Получим: 4*(х — 5) = 7*(х — 5). Теперь умножим левую и правую часть уравнения на дробь 1 / (х — 5). Уравнение примет такой вид: 4*(х — 5)/(х — 5) = 7*(х — 5)/ (х — 5). Сократим дроби на (х — 5) и у нас выйдет, что 4 = 7. Из этого можно сделать вывод, что 2*2 = 7! Конечно, подвох здесь в том, что равен 5 и сокращать дроби было нельзя, поскольку это приводило к делению на ноль. Поэтому при сокращении дробей нужно всегда проверять чтобы ноль случайно не оказался в знаменателе, иначе результат получится совсем непредсказуемым.
К примеру, рассмотрим уравнение: 4*х — 20 = 7*х — 35. Вынесем за скобки в левой части 4, а в правой 7. Получим: 4*(х — 5) = 7*(х — 5). Теперь умножим левую и правую часть уравнения на дробь 1 / (х — 5). Уравнение примет такой вид: 4*(х — 5)/(х — 5) = 7*(х — 5)/ (х — 5). Сократим дроби на (х — 5) и у нас выйдет, что 4 = 7. Из этого можно сделать вывод, что 2*2 = 7! Конечно, подвох здесь в том, что равен 5 и сокращать дроби было нельзя, поскольку это приводило к делению на ноль. Поэтому при сокращении дробей нужно всегда проверять чтобы ноль случайно не оказался в знаменателе, иначе результат получится совсем непредсказуемым.
Число 0 можно представить, как некую границу, отделяющую мир реальных чисел от мнимых или отрицательных. Благодаря двусмысленному положению, многие операции с этой числовой величиной не подчиняются математической логике. Невозможность деления на нуль — яркий тому пример. А разрешенные арифметические действия с нулем могут быть выполнены с помощью общепринятых определений.
История нуля
Ноль является точкой отсчета во всех стандартных системах исчисления. Европейцы стали использовать это число сравнительно недавно, но мудрецы Древней Индии пользовались нулем за тысячу лет до того, как пустое число стало регулярно использоваться европейскими математиками. Ещё раньше индийцев ноль являлся обязательной величиной в числовой системе майя. Этот американский народ использовал двенадцатеричную систему исчисления, а нулем у них начинался первый день каждого месяца. Интересно, что у майя знак, обозначающий «ноль», полностью совпадал со знаком, определяющим «бесконечность». Таким образом, древние майя делали вывод о тождественности и непознаваемости этих величин.
Математические действия с нулем
Стандартные математические операции с нулем можно свести к нескольким правилам.
Сложение: если к произвольному числу добавить ноль, то оно не изменит своего значения (0+x=x).
Вычитание: при вычитании нуля из любого числа значение вычитаемого остается неизменным (x-0=x).
Умножение: любое число, умноженное на 0, дает в произведении 0 (a*0=0).
Деление: ноль можно разделить на любое число, не равное нулю. При этом значение такой дроби будет 0. А деление на ноль запрещено.
Возведение в степень. Это действие можно выполнить с любым числом. Произвольное число, возведенное в нулевую степень, даст 1 (x 0 =1).
Ноль в любой степени равен 0 (0 а =0).
При этом сразу возникает противоречие: выражение 0 0 не имеет смысла.
Парадоксы математики
О том, что деление на ноль невозможно, многие знают со школьной скамьи. Но объяснить причину такого запрета почему-то не получается. В самом деле, почему формула деления на ноль не существует, а вот другие действия с этим числом вполне разумны и возможны? Ответ на этот вопрос дают математики.
Все дело в том, что привычные арифметические действия, которые школьники изучают в начальных классах, на самом деле далеко не так равноправны, как нам кажется. Все простые операции с числами могут быть сведены к двум: сложению и умножению. Эти действия составляют суть самого понятия числа, а остальные операции строятся на использовании этих двух.
Эти действия составляют суть самого понятия числа, а остальные операции строятся на использовании этих двух.
Сложение и умножение
Возьмем стандартный пример на вычитание: 10-2=8. В школе его рассматривают просто: если от десяти предметов отнять два, останется восемь. Но математики смотрят на эту операцию совсем по-другому. Ведь такой операции, как вычитание, для них не существует. Данный пример можно записать и другим способом: х+2=10. Для математиков неизвестная разность — это просто число, которое нужно добавить к двум, чтобы получилось восемь. И никакого вычитания здесь не требуется, нужно просто найти подходящее числовое значение.
Умножение и деление рассматриваются так же. В примере 12:4=3 можно понять, что речь идет о разделении восьми предметов на две равные кучки. Но в действительности это просто перевернутая формула записи 3х4=12.Такие примеры на деление можно приводить бесконечно.
Примеры на деление на 0
Вот тут и становится понемногу понятным, почему нельзя делить на ноль. Умножение и деление на ноль подчиняется своим правилам. Все примеры на деление этой величины можно сформулировать в виде 6:0=х. Но это же перевернутая запись выражения 6 * х=0. Но, как известно, любое число, умноженное на 0, дает в произведении только 0. Это свойство заложено в самом понятии нулевой величины.
Умножение и деление на ноль подчиняется своим правилам. Все примеры на деление этой величины можно сформулировать в виде 6:0=х. Но это же перевернутая запись выражения 6 * х=0. Но, как известно, любое число, умноженное на 0, дает в произведении только 0. Это свойство заложено в самом понятии нулевой величины.
Выходит, что такого числа, которое при умножении на 0 дает какую-либо осязаемую величину, не существует, то есть данная задача не имеет решения. Такого ответа бояться не следует, это естественный ответ для задач такого типа. Просто запись 6:0 не имеет никакого смысла, и она ничего не может объяснить. Кратко говоря, это выражение можно объяснить тем самым бессмертным «деление на ноль невозможно».
Существует ли операция 0:0? Действительно, если операция умножения на 0 законна, можно ли ноль разделить на ноль? Ведь уравнение вида 0х 5=0 вполне легально. Вместо числа 5 можно поставить 0, произведение от этого не поменяется.
Действительно, 0х0=0. Но поделить на 0 по-прежнему нельзя. Как было сказано, деление — это просто обратная операция умножения. Таким образом, если в примере 0х5=0, нужно определить второй множитель, получаем 0х0=5. Или 10. Или бесконечность. Деление бесконечности на ноль — как вам это понравится?
Как было сказано, деление — это просто обратная операция умножения. Таким образом, если в примере 0х5=0, нужно определить второй множитель, получаем 0х0=5. Или 10. Или бесконечность. Деление бесконечности на ноль — как вам это понравится?
Но если в выражение подходит любое число, то оно не имеет смысла, мы не можем из бесконечного множества чисел выбрать какое-то одно. А раз так, это значит и выражение 0:0 не имеет смысла. Получается, что на ноль нельзя делить даже сам ноль.
Высшая математика
Деление на ноль — это головная боль для школьной математики. Изучаемый в технических вузах математический анализ немного расширяет понятие задач, которые не имеют решения. Например, к уже известному выражению 0:0 добавляются новые, которые не имеют решения в школьных курсах математики:
- бесконечность, разделенная на бесконечность: ∞:∞;
- бесконечность минус бесконечность: ∞−∞;
- единица, возведенная в бесконечную степень: 1 ∞ ;
- бесконечность, умноженная на 0: ∞*0;
- некоторые другие.

Элементарными методами решить такие выражения невозможно. Но высшая математика благодаря дополнительным возможностям для ряда подобных примеров дает конечные решения. Особенно это видно в рассмотрении задач из теории пределов.
Раскрытие неопределенности
В теории пределов значение 0 заменяется условной бесконечно малой переменной величиной. А выражения, в которых при подставлении нужного значения получается деление на ноль, преобразовываются. Ниже представлен стандартный пример раскрытия предела при помощи обычных алгебраических преобразований:
Как видно в примере, простое сокращение дроби приводит ее значение к вполне рациональному ответу.
При рассмотрении пределов тригонометрических функций их выражения стремятся свести к первому замечательному пределу. При рассмотрении пределов, в которых знаменатель обращается в 0 при подставлении предела, используют второй замечательный предел.
Метод Лопиталя
В некоторых случаях пределы выражений можно заменить пределом их производных. Гийом Лопиталь — французский математик, основоположник французской школы математического анализа. Он доказал, что пределы выражений равны пределам производных этих выражений. В математической записи его правило выглядит следующим образом.
Гийом Лопиталь — французский математик, основоположник французской школы математического анализа. Он доказал, что пределы выражений равны пределам производных этих выражений. В математической записи его правило выглядит следующим образом.
На данном уроке будет рассмотрено, как выполнять умножение и деление на числа вида 10, 100, 0,1, 0,001. Также будут решены различные примеры на данную тему.
Упражнение. Как умножить число 25,78 на 10?
Десятичная запись данного числа — это сокращенная запись суммы. Необходимо расписать ее более подробно:
Таким образом, нужно умножить сумму. Для этого можно просто умножить каждое слагаемое:
Выходит, что.
Можно сделать вывод, что умножить десятичную дробь на 10 очень просто: нужно запятую сдвинуть вправо на одну позицию.
Упражнение. Умножить 25,486 на 100.
Умножить на 100 — это то же самое, что и умножить два раза на 10. Иными словами, необходимо сдвинуть запятую вправо два раза:
Упражнение. Разделить 25,78 на 10.
Разделить 25,78 на 10.
Как и в предыдущем случае, необходимо представить число 25,78 в виде суммы:
Так как нужно поделить сумму, то это эквивалентно делению каждого слагаемого:
Выходит, чтобы разделить на 10, нужно запятую сдвинуть влево на одну позицию. Например:
Упражнение. Разделить 124,478 на 100.
Разделить на 100 — это то же самое, что два раза разделить на 10, поэтому запятая сдвигается влево на 2 позиции:
Если десятичную дробь нужно умножить на 10, 100, 1000 и так далее, нужно запятую сдвинуть вправо на столько позиций, сколько нулей у множителя.
И наоборот, если десятичную дробь нужно поделить на 10, 100, 1000 и так далее, нужно запятую сдвинуть влево на столько позиций, сколько нулей у множителя.
Пример 1
Умножить на 100 значит сдвинуть запятую вправо на две позиции.
После сдвига можно обнаружить, что после запятой уже нет цифр, а это значит, что дробная часть отсутствует. Тогда и запятая не нужна, число получилось целое.
Пример 2
Сдвигать нужно на 4 позиции вправо. Но цифр после запятой всего две. Стоит вспомнить, что для дроби 56,14 есть эквивалентная запись.
Теперь умножить на 10 000 не составляет труда:
Если не очень понятно, почему можно дописать два нуля к дроби в предыдущем примере, то дополнительное видео по ссылке сможет помочь в этом.
Эквивалентные десятичные записи
Запись 52 означает следующее:
Если впереди поставить 0, получим запись 052. Эти записи эквивалентны.
Можно ли поставить два нуля впереди? Да, эти записи эквивалентны.
Теперь посмотрим на десятичную дробь:
Если приписать ноль, то получается:
Эти записи эквивалентны. Аналогично можно приписать несколько нулей.
Таким образом, к любому числу можно приписать несколько нулей после дробной части и несколько нулей перед целой частью. Это будут эквивалентные записи одного и того же числа.
Пример 3
Так как происходит деление на 100, то необходимо сдвинуть запятую на 2 позиции влево. Слева от запятой не осталось цифр. Целая часть отсутствует. Такую запись часто используют программисты. В математике же, если целой части нет, то ставят ноль вместо нее.
Слева от запятой не осталось цифр. Целая часть отсутствует. Такую запись часто используют программисты. В математике же, если целой части нет, то ставят ноль вместо нее.
Пример 4
Сдвигать нужно влево на три позиции, но позиций всего две. Если перед числом написать несколько нулей, то это будет эквивалентная запись.
То есть при сдвиге влево, если цифры кончились, необходимо восполнить их нулями.
Пример 5
В данном случае стоит помнить, что запятая всегда стоит после целой части. Тогда:
Умножение и деление на числа 10, 100, 1000 — очень простая процедура. Точно так же дело обстоит и с числами 0,1, 0,01, 0,001.
Пример . Умножить 25,34 на 0,1.
Выполним запись десятичной дроби 0,1 в виде обыкновенной. Но умножить на — то же самое, что разделить на 10. Поэтому необходимо сдвинуть запятую на 1 позицию влево:
Аналогично умножить на 0,01 — это разделить на 100:
Пример. 5,235 разделить на 0,1.
Решение данного примера строится аналогичным образом: 0,1 выражается в виде обыкновенной дроби, а делить на — это все равно, что умножить на 10:
То есть чтобы поделить на 0,1, нужно запятую сдвинуть вправо на одну позицию, что равносильно умножению на 10.
Умножить на 10 и разделить на 0,1 — это одно и то же. Запятую нужно сдвинуть вправо на 1 позицию.
Разделить на 10 и умножить на 0,1 — это одно и то же. Запятую нужно сдвинуть вправо на 1 позицию:
что такое умножение, свойства 0, можно ли делить на 0
Ещё в школе учителя нам всем старались вбить в голову простейшее правило: «Любое число, умноженное на ноль, равняется нулю!», — но всё равно вокруг него постоянно возникает куча споров. Кто-то просто запомнил правило и не забивает себе голову вопросом «почему?». «Нельзя и всё тут, потому что в школе так сказали, правило есть правило!» Кто-то может исписать полтетради формулами, доказывая это правило или, наоборот, его нелогичность.
…
Оглавление:
- Кто в итоге прав
- Что такое умножение
- Что такое ноль
- Можно ли умножать на пустоту
- Деление
Кто в итоге прав
Во время этих споров оба человека, имеющие противоположные точки зрения, смотрят друг на друга, как на барана, и доказывают всеми силами свою правоту. Хотя, если посмотреть на них со стороны, то можно увидеть не одного, а двух баранов, упирающихся друг в друга рогами. Различие между ними лишь в том, что один чуть менее образован, чем второй.
Хотя, если посмотреть на них со стороны, то можно увидеть не одного, а двух баранов, упирающихся друг в друга рогами. Различие между ними лишь в том, что один чуть менее образован, чем второй.
Это интересно: разрядные слагаемые — что это?
Чаще всего, те, кто считают это правило неверным, стараются призвать к логике вот таким способом:
У меня на столе лежит два яблока, если я положу к ним ноль яблок, то есть не положу ни одного, то от этого мои два яблока не исчезнут! Правило нелогично!
Действительно, яблоки никуда не исчезнут, но не из-за того, что правило нелогично, а потому что здесь использовано немного другое уравнение: 2+0 = 2. Так что такое умозаключение отбросим сразу — оно нелогично, хоть и имеет обратную цель — призвать к логике.
Это интересно: Как найти разность чисел в математике?
Что такое умножение
Изначально правило умножения было определено только для натуральных чисел: умножение — это число, прибавленное к самому себе определённое количество раз, что подразумевает натуральность числа. Таким образом, любое число с умножением можно свести вот к такому уравнению:
Таким образом, любое число с умножением можно свести вот к такому уравнению:
- 25×3 = 75
- 25 + 25 + 25 = 75
- 25×3 = 25 + 25 + 25
Из этого уравнения следует вывод, что умножение — это упрощённое сложение.
Это интересно: что такое хорда окружности в геометрии, определение и свойства.
Что такое ноль
Любой человек с самого детства знает: ноль — это пустота, Несмотря на то, что эта пустота имеет обозначение, она не несёт за собой вообще ничего. Древние восточные учёные считали иначе — они подходили к вопросу философски и проводили некие параллели между пустотой и бесконечностью и видели глубокий смысл в этом числе. Ведь ноль, имеющий значение пустоты, встав рядом с любым натуральным числом, умножает его в десять раз. Отсюда и все споры по поводу умножения — это число несёт в себе столько противоречивости, что становится сложно не запутаться. Кроме того, ноль постоянно используется для определения пустых разрядов в десятичных дробях, это делается и до, и после запятой.
Это интересно: какой четырёхугольник называется квадратом?
Можно ли умножать на пустоту
Умножать на ноль можно, но бесполезно, потому что, как ни крути, но даже при умножении отрицательных чисел всё равно будет получаться ноль. Достаточно просто запомнить это простейшее правило и никогда больше не задаваться этим вопросом. На самом деле всё проще, чем кажется на первый взгляд. Нет никаких скрытых смыслов и тайн, как считали древние учёные. Ниже будет приведено самое логичное объяснение, что это умножение бесполезно, ведь при умножении числа на него всё равно будет получаться одно и то же — ноль.
Это интересно: что такое модуль числа?
Возвращаясь в самое начало, к доводу по поводу двух яблок, 2 умножить на 0 выглядит вот так:
- Если съесть по два яблока пять раз, то съедено 2×5 = 2+2+2+2+2 = 10 яблок
- Если их съесть по два трижды, то съедено 2×3 = 2+2+2 = 6 яблок
- Если съесть по два яблока ноль раз, то не будет съедено ничего — 2×0 = 0×2 = 0+0 = 0
Ведь съесть яблоко 0 раз — это означает не съесть ни одного. Это будет понятно даже самому маленькому ребёнку. Как ни крути — выйдет 0, двойку или тройку можно заменить абсолютно любым числом и выйдет абсолютно то же самое. А если проще говоря, то ноль — это ничего, а когда у вас ничего нет, то сколько ни умножай — всё равно будет ноль. Волшебства не бывает, и из ничего не получится яблоко, даже при умножении 0 на миллион. Это самое простое, понятное и логичное объяснение правила умножения на ноль. Человеку, далёкому от всех формул и математики будет достаточно такого объяснения, для того чтобы диссонанс в голове рассосался, и всё встало на свои места.
Это будет понятно даже самому маленькому ребёнку. Как ни крути — выйдет 0, двойку или тройку можно заменить абсолютно любым числом и выйдет абсолютно то же самое. А если проще говоря, то ноль — это ничего, а когда у вас ничего нет, то сколько ни умножай — всё равно будет ноль. Волшебства не бывает, и из ничего не получится яблоко, даже при умножении 0 на миллион. Это самое простое, понятное и логичное объяснение правила умножения на ноль. Человеку, далёкому от всех формул и математики будет достаточно такого объяснения, для того чтобы диссонанс в голове рассосался, и всё встало на свои места.
Это интересно: формулировка и доказательство признаков параллелограмма.
Деление
Из всего вышеперечисленного вытекает и другое важное правило:
На ноль делить нельзя!
Это правило нам тоже с самого детства упорно вбивают в голову. Мы просто знаем, что нельзя и всё, не забивая себе голову лишней информацией. Если вам неожиданно зададут вопрос, по какой причине запрещено делить на ноль, то большинство растеряется и не сможет внятно ответить на простейший вопрос из школьной программы, потому что вокруг этого правила не ходит столько споров и противоречий.
Если вам неожиданно зададут вопрос, по какой причине запрещено делить на ноль, то большинство растеряется и не сможет внятно ответить на простейший вопрос из школьной программы, потому что вокруг этого правила не ходит столько споров и противоречий.
Все просто зазубрили правило и не делят на ноль, не подозревая, что ответ кроется на поверхности. Сложение, умножение, деление и вычитание — неравноправны, полноценны из перечисленного только умножение и сложение, а все остальные манипуляции с числами строятся из них. То есть запись 10: 2 является сокращением уравнения 2 * х = 10. Значит, запись 10: 0 такое же сокращение от 0 * х = 10. Получается, что деление на ноль — это задание найти число, умножая которое на 0, получится 10. А мы уже разобрались, что такого числа не существует, значит, у этого уравнения нет решения, и оно будет априори неверным.
Расскажу тебе позволь,
Чтобы не делил на 0!
Режь 1 как хочешь, вдоль,
Только не дели на 0!
youtube.com/embed/KcBOMIh3-3g» allowfullscreen=»allowfullscreen»>
примеры 4 класс, ошибка, правила, формула, умножение, бесконечность, презентация, дроби, остаток
Математика – это интересная наука, которая сначала может ставить определенные запреты, а затем сама же их нарушать. Это хорошо можно проследить, начав изучать высшую алгебру в ВУЗе. Уже тогда вчерашние школьники понимают всю неоднозначность некоторых математических вопросов, к примеру, таких как извлечение квадратного корня или же деление на ноль. Ведь учителя все время твердили, что делить на ноль нельзя. Но не все так однозначно в этом вопросе.
Ноль можно назвать одной из самых интересных цифр. У нее нет значения, она означает пустоту в прямом смысле слова. Однако, если ее поставить рядом с какой-либо цифрой, то значение последней станет больше в несколько раз.
Ноль загадочен сам по себе. Его использовал еще древний народ майя. У майя он означал «начало», а отсчет календарных дней также начинался с него.
Очень интересным фактом является то, что знак ноля и знак неопределенности у них были похожи. Этим майя хотели показать, что 0 является таким же тождественным знаком, как и неопределенность. В Европе же в обиход он вошел сравнительно недавно.
Также многим известен запрет, связанный с нолем. Любой человек скажет, что на него нельзя делить. Это говорят учителя в школе, а дети обычно верят им на слово. Обычно детям либо просто не интересно это знать, либо они знают, что будет, если, услышав важный запрет, сразу же спросить «А почему делить нельзя?». Но когда становишься старше, то просыпается интерес, и хочется побольше узнать о причинах такого запрета. Однако существует разумное доказательство. Чтобы его понять, следует для начала изучить, какие действия в математике можно производить с нулем и как это на нем сказывается. Отдельно следует рассматривать алгебраические операции из высшей математики, так как там действуют несколько иные законы.
Действия с нулем
Для начала необходимо определить, какие действия с нулем можно выполнять. Существует несколько видов, которые объясняют еще в школьной программе:
Существует несколько видов, которые объясняют еще в школьной программе:
- сложение;
- умножение;
- вычитание;
- деление;
- возведение в степень.
[stop]Если при сложении к любой цифре прибавить 0, то она останется прежней и не поменяет своего числового значения. То же произойдет, если отнять 0.[/stop]
При умножении и делении все обстоит немного иначе. Если умножить любое число на 0, то и произведение тоже станет нулевым.
Рассмотрим пример:
0*5=0
Запишем это как сложение:
0+0+0+0+0=0
Всего складываемых нолей пять, вот и выходит:
0*5=0
Попробуем один умножить на 0. Результат также будет нулевым.
Ноль можно разделить на любое другое число, не равное ему. В этом случае выходит дробь, значение которой будет нулевым.
Если 0 делить на отрицательное число, то выйдет все тот же 0:
0/(-5)=0
Можно возвести 0 в нулевую степень. В таком случае выйдет 1. При этом важно помнить, что выражение «0 в нулевой степени» абсолютно бессмысленно. Если попытаться возвести его в любую степень, то все-равно будет 0. Пример:
Если попытаться возвести его в любую степень, то все-равно будет 0. Пример:
04=0*0*0*0
Пользуемся правилом умножения, получаем 0.
Читайте также: Свойства натуральных логарифмов
Так можно ли делить или нет?
Чтобы понять, можно делить на 0 или нет, обращаемся к высшей математике. Школьные учителя утверждают, что данная цифра — это ничто. То есть когда говорят, что 0 ручек, это значит, что совсем нет ручек. В высшей математике понятие «ноль» более широкое. Оно вовсе не означает пустоту. Здесь это неопределенность, так как если провести исследование, то получается, что при делении 0 на 0 мы можем в результате получить другое число.
Для математиков нет понятий «деление» и «вычитание». Допустим: если от пяти отнять три, то останется два. Так выглядит вычитание. Однако, математики запишут это таким образом:
X+3=5
Таким образом, неизвестной разностью является некое число, которое прибавляют к 3, чтобы вышло 5. То есть, не нужно ничего вычитать, нужно найти подходящий показатель. Это правило действует для сложения.
Это правило действует для сложения.
Иначе дела обстоят с правилами умножения и деления. Известно, что умножение на ноль приводит к нулевому результату. Например, если 3/0=X, тогда, если перевернуть запись, получится 3*X=0. А число, которое умножалось на 0 даст 0 и в произведении. Как результат, числа, которое бы давало в произведении с 0 величину, отличную от ноля, не существует. А значит, деление на ноль бессмысленно, то есть оно подходит к нашему правилу.
Но что будет, если попытаться поделить 0 на себя же? Возьмем как X некую неопределенную цифру. Образуется уравнение 0*X=0. Его можно решить.
Если мы попробуем взять вместо X ноль, то мы получим 0/0=0. Но если вместо X взять, например, 1, и провести деление, то в конечном итоге окажется 0/0=1.
В этом случае выйдет, что в качестве множителя можно использовать другое число. Итогом будет бесконечное множество разных чисел. Деление на 0 имеет смысл, но тогда появляется некое условие, благодаря которому мы сможем все-таки выбрать одну подходящую цифру. Это действие называется «раскрытием неопределенности». В арифметике же деление на ноль снова потеряет смысл, так как не будет возможности выбрать из множеств
Это действие называется «раскрытием неопределенности». В арифметике же деление на ноль снова потеряет смысл, так как не будет возможности выбрать из множеств
Деление на ноль и высшая математика
Школьная арифметика основывалась преимущественно на проведении математических операций с вещественными числами. Большая их часть имеет целый ряд аксиом:
- коммутативность и ассоциативность сложения и умножения;
- существование 0 и 1;
- существование обратного и противоположного элементов.
Кроме этого для вычисления их свойств применяют еще 2 аксиомы – порядка и непрерывности. Так как деление – это процедура противоположная умножению, то при ее проведении возникает 2 проблемы.
Проблема первая – если провести деление на 0, то полученный результат не будет возможности проверить при помощи умножения. Каким бы числом не выступало частное, если его умножить на 0, то делимое все-равно не выйдет получить.
Проблема вторая – если разделить 0 на 0, в итого ответом может выступать любая цифра, которая в случае перемножения с делителем станет нулем.
Все это стало причиной табу в школьной программе на такую операцию, как деление на 0. Но в высшей математике есть возможность его обойти. Например, если построить другую алгебраическую структуру, которая будет отличаться от привычной нам числовой прямой. Примером может служить колесо. У него иные правила и законы. Одним из них является следующий – деление никаким образом не привязано к умножению и трансформируется из бинарной операции в унарную.
Делить на 0 в высшей математике можно, но для этого потребуется выйти за рамки привычного представления о законах и операциях в алгебре.
Ноль и бесконечность
Бесконечность часто встречается в высшей математике. Так как школьникам просто не важно знать о том, что существуют еще математические действия с ней, то и объяснить детям, почему деление на 0 выполнить нельзя, учителя как следует не могут.
Бесконечность отличается от неопределенности, она один из ее видов
Математические секреты ученики начинают узнавать на первом курсе института. Высшая математика предоставляет комплекс задач, которые не имеют решения. Самыми известными являются задачи с бесконечностью. Их решают при помощи математического анализа.
Высшая математика предоставляет комплекс задач, которые не имеют решения. Самыми известными являются задачи с бесконечностью. Их решают при помощи математического анализа.
К бесконечности применимы математические действия: сложение, умножение. Еще применяют вычитание и деление, но в конечном итоге они все равно сводятся к двум простейшим операциям.
Но что будет, если попытаться:
- Бесконечность умножить на 0. По идее, если попробуем умножить на 0 любое число, то получим 0. Но бесконечностью является неопределенное множество цифр. Так как мы не можем выбрать из этого множества одну, то выражение ∞*0 не имеет решения и является абсолютно бессмысленным.
- Ноль делить на бесконечность. Здесь происходит та же история, что и выше. Не можем выбрать одну цифру, а значит не знаем на что разделить. Выражение не имеет смысла.
Теперь попробуем поделить бесконечность на 0. Должна выйти неопределенность. Но если попробуем заменить деление умножением, то получится определенный ответ.
Например: ∞/0=∞*1/0= ∞*∞ = ∞.
Как результат, выходит такой математический парадокс.
Ответ, почему нельзя делить на ноль:
Мысленный эксперимент, пробуем делить на ноль:
Итак, теперь известно, что 0 подчиняется практически всем операциям, которые производят с обычными числами, кроме одной единственной. На 0 делить нельзя только потому, что в результате получается неопределенность.
Ноль
НольГЛАВНАЯ МАТЕМАТИКА ГЕОМЕТРИЯ
сложение с нулём, вычитание нуля, умножение на ноль, деление на ноль, степень и ноль, факториал нуля, правописание слова ноль.
Согласно общепринятому определению, ноль — это число, отделяющее положительные числа от отрицательных на числовой прямой. Ноль — это самое проблематичное место в математике, которое не подчиняется логике, а все математические действия с нулём основаны не на логике, а на общепринятых определениях.
Первый пример проблематичности нуля — это натуральные числа. В русских школах ноль не является натуральным числом, в других школах ноль является натуральным числом. Поскольку понятие «натуральные числа» — это искусственное отделение некоторых чисел от всех остальных чисел по определённым признакам, то математического доказательства натуральности или не натуральности нуля быть не может. Ноль считается нейтральным элементом по отношению операций сложения и вычитания.
Ноль считается целым, беззнаковым числом. Также ноль считается чётным числом, поскольку при делении нуля на 2 получается целое число ноль.
Ноль является первой цифрой во всех стандартных системах счисления. В позиционных системах счисления, к которым принадлежит привычная нам десятичная система счисления, цифрой ноль обозначают отсутствие значения данного разряда при записи числа. Индейцы майя использовали ноль в принятой у них двенадцатиричной системе счисления за тысячу лет до индийских математиков. С нулевого дня в календаре майя начинался каждый месяц. Интересно, что тем же самым знаком ноль математики майя обозначали и бесконечность — вторую проблему современной математики.
С нулевого дня в календаре майя начинался каждый месяц. Интересно, что тем же самым знаком ноль математики майя обозначали и бесконечность — вторую проблему современной математики.
Слово «ноль» в арабском языке звучит как «сыфр». От арабского слова ноль (сыфр) произошло слово «цифра».
Как правильно пишется — ноль или нуль? Слова ноль и нуль совпадают в значении, но различаются употреблением. Как правило, ноль употребляется в обиходной речи и в ряде устойчивых сочетаний, нуль — в терминологии, в научной речи. Правильными будут оба варианта написания этого слова. Например: Деление на ноль. Ноль целых. Ноль внимания. Ноль без палочки. Абсолютный нуль. Ноль целых пять десятых.
В грамматике производные слова от слов ноль и нуль пишутся так: нолевой или нулевой, нолик или нулик, ноля или нуля, нулевой или реже встречающееся нолевой, ноль-ноль. Например: Ниже нуля. Равно нулю. Свести к нулю. Нулевой мередиан. Нулевой пробег. В двенадцать ноль-ноль.
Нулевой мередиан. Нулевой пробег. В двенадцать ноль-ноль.
В математических действиях с нулем на сегодняшний день определены следующие результаты:
сложение — если к любому числу прибавить ноль, число останется неизменным; если к нулю прибавить любое число результатом сложения будет то же самое любое число:
a + 0 = a
0 + a = a
вычитание — если из любого числа вычесть ноль, число останется неизменным; если из нуля вычесть любое число в результате получится то же самое любое число с противоположным знаком:
a — 0 = a
0 — a = -a
умножение — если любое число умножить на ноль, результатом будет ноль; если ноль умножить на любое число в результате получится ноль:
a х 0 = 0
0 х a = 0
деление — деление на ноль запрещено, поскольку результат не существует; общепринятый взгляд на проблему деления на ноль изложен в работе Александра Сергеева «Почему нельзя делить на ноль?»; для любознательных написана другая статья, в которой рассматривается возможность деления на ноль:
a : 0 = делить на ноль запрещено, при этом а не равно нулю
ноль разделить на ноль — выражение не имеет смысла, так как не может быть определено:
0 : 0 = выражение не имеет смысла
ноль разделить на число — если ноль разделить на число в результате всегда будет ноль, не зависимо от того, какое число находится в знаменателе (исключением из этого правила является число ноль, смотри выше):
0 : a = 0, при этом а не равно нулю
ноль в степени — ноль в любой степени равен нулю:
0a = 0, при этом а не равно нулю
возведение в степень — любое число в степени ноль равняется единице (число в степени 0):
a0 = 1, при этом а не равно нулю
ноль в степени ноль — выражение не имеет смысла, так как не может быть определено (ноль в нулевой степени, 0 в степени 0):
00 = выражение не имеет смысла
извлечение корня — корень любой степени из нуля равен нулю:
01/a = 0, при этом а не равно нулю
факториал — факториал нуля, или ноль факториал, равняется единице:
0! = 1
распределение цифр — при подсчете распределения цифр ноль считается незначащей цифрой. Изменение подхода в правилах подсчета распределения цифр, когда ноль считается ЗНАЧАЩЕЙ цифрой позволит получать более точные результаты распределения цифр во всех стандартных системах счисления, в том числе в двоичной системе счисления.
Изменение подхода в правилах подсчета распределения цифр, когда ноль считается ЗНАЧАЩЕЙ цифрой позволит получать более точные результаты распределения цифр во всех стандартных системах счисления, в том числе в двоичной системе счисления.
Кому интересен вопрос возникновения нуля, предлагаю прочесть статью «История нуля» Дж. Дж. О’Коннора и Е. Ф. Робертсона в переводе И. Ю. Осмоловского.
30 августа 2010 года — 10 июля 2022 года.
© 2006 — 2022 Николай Хижняк. Все права защищены.
Умножение на ноль — правило в математике и примеры
Правило арифметики о том, что при умножении на ноль любого числа получается 0, изучают еще в младших классах средней школы. Дети верят учителям на слово, но при взрослении у многих возникает интерес к этой теме. Людям хочется больше узнать, почему с нулем связаны разные ограничения. Математики объясняют подобные факты свойствами этой удивительной цифры.
Содержание
- История возникновения
- Сложение, умножение, степень
- Деление на ноль
- Раскрытие неопределенностей
История возникновения
Ноль означает ничто, пустоту. Он используется для обозначения пустых разрядов чисел в позиционной системе счисления, а также в десятичных дробях до и после запятой. Вокруг этой цифры всегда велось много споров. Использовать ноль начали еще в древности, о чем свидетельствуют трактаты вавилонян и надписи майя.
Он используется для обозначения пустых разрядов чисел в позиционной системе счисления, а также в десятичных дробях до и после запятой. Вокруг этой цифры всегда велось много споров. Использовать ноль начали еще в древности, о чем свидетельствуют трактаты вавилонян и надписи майя.
Но повсеместно применять в вычислениях его начали лишь спустя несколько тысячелетий. Это произошло в Индии. Нулю там придавали не только математический, но и философский смысл. Он означает отсутствие всего, а его форма соответствовала кругу жизни.
Индусы использовали 0 как любое другое число. Его складывали, вычитали, на него умножали. С делением на 0 возникла проблема, но благодаря ей в дальнейшем возникла другая область математики — математический анализ. Идею использования нуля подхватили исламские ученые на Ближнем Востоке и внесли его в арабскую систему счисления.
В Европе до Крестовых походов применялась Римская система счисления. Это непозиционная система, и ноль в ней отсутствует. Делать расчеты в ней очень тяжело. Для вычислений использовали специальные разграфленные таблицы — абаки. Расчеты с их применением производились часами, в то время как сегодня любой школьник сможет легко получить результат, например, перемножая или складывая числа в столбик.
Делать расчеты в ней очень тяжело. Для вычислений использовали специальные разграфленные таблицы — абаки. Расчеты с их применением производились часами, в то время как сегодня любой школьник сможет легко получить результат, например, перемножая или складывая числа в столбик.
Во времена первых Крестовых походов арабские цифры вместе с нолем и позиционной системой счисления пришли в Европу. К этим новшествам сначала отнеслись с большим недоверием. Во Флоренции даже был издан закон о запрещении использования арабских цифр вместе с нулем.
Считалось, что они поощряют мошенничество: 0 легко переделать на цифру 9 или приписать в конце счета, чтобы величина долга возросла многократно. Лишь в XV веке, когда началось развитие в сфере математики и механики, люди оценили преимущество нуля и арабских цифр и стали использовать их повсеместно.
Сложение, умножение, степень
В математике используется несколько действий. Они следующие:
Они следующие:
- сложение;
- вычитание;
- умножение;
- деление;
- возведение в степень.
Сложение с нулем обычно вопросов не вызывает. Если к любому числу добавить 0, это значит, что к нему не прибавилось ничего. Слагаемое каким было, таким и осталось, сколько раз ноль ни прибавляй. То же самое будет, если отнять ноль.
Операция умножения гораздо менее очевидна. Не все понимают, почему при умножении на ноль получается ноль. Это объясняется особенностями операции умножения. Изначально ее определяли как число, прибавленное к самому себе определенное количество раз, что справедливо для натуральных чисел. Так, 5 х 3 = 15. Этот пример можно заменить следующим выражением: 5 + 5 + 5 = 15. То есть число 5 было взято 3 раза. Согласно этому правилу, умножение на 0 числа 5 дает нулевой результат, и 5 х 0 = 0.
Чтобы было нагляднее, можно привести следующий пример:
- если мальчик съел 2 раза по 2 яблока, то окажется, что он позавтракал 4 яблоками;
- если он съел 3 раза по 2 яблока, то в результате получится 6 яблок;
- если же он съел 0 раз по 2 яблока, то ответ будет 0.

Иногда юные скептики выдвигают следующее возражение: допустим, у мальчика в руке 2 яблока. Если он не съел их, то яблоки не пропадут, они так и останутся в него в руке. Почему же тогда результат равен нулю? Действительно, яблоки из руки никуда не денутся. Но в примере учитываются лишь те из них, которые были съедены, проще говоря, оказались в желудке у мальчика. В последнем случае они туда не попали.
Правило умножения на ноль в математике действительно для любых чисел:
- положительных;
- отрицательных;
- целых;
- дробей;
- разрядных;
- рациональных;
- иррациональных;
- 0 можно умножать на 0.
В любом случае произведение будет нулевым. С нулем можно производить следующие действия:
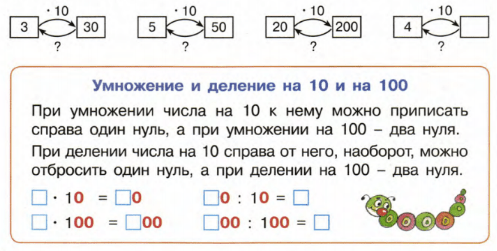 Ноль в нулевую степень возводить нельзя, это бессмысленно.
Ноль в нулевую степень возводить нельзя, это бессмысленно.Деление на ноль
Математики говорят, что четыре арифметических действия: сложение, вычитание, умножение и деление неравноправны. Базовыми считаются первое и третье из них (сложение и умножение), а деление и вычитание — производными.
Например, разность между 5 и 2 равна 3. Это действие также можно записать в виде следующего выражения: Х + 2 = 5. Решением уравнения будет число 3. Аналогичное правило действует и для умножения. Деление 6 на 3 можно записать так: Х * 2 = 3.
Для действий с нулем можно использовать следующий прием. Выражение записывают так: Х * 0 = 0. Здесь X может быть равен любому числу. Из этого следует, что невозможно найти число, умножение которого на 0 давало бы произведение, отличное от 0.
Из этого следует, что невозможно найти число, умножение которого на 0 давало бы произведение, отличное от 0.
Если попытаться найти результат от деления ненулевого числа (например, 5) на ноль, то это действие можно записать так: Х * 0 = 5. Так, при умножении любого числа на ноль получается ноль, у этого уравнения в арифметике нет решения.
Раскрытие неопределенностей
Действиями, связанными с делением на 0, занимается один из разделов высшей математики — математический анализ. В нем используется такое понятие, как бесконечность (бесконечно большая величина). Одно из ее определений — это предел, к которому стремится выражение а/Х при Х, стремящемся к нулю. Здесь а — любое ненулевое действительное число. Если в этом выражении уменьшать значение X, то результат будет увеличиваться, пока, в конце концов, не подойдет к бесконечности. С этой величиной можно делать различные математические действия:
- прибавлять любые числа;
- вычитать числа, не равные бесконечности;
- умножать на значения, не равные 0 и бесконечности;
- возводить в степень, не равную 0.

В результате получится бесконечность. Следующие выражения дают в результате полную неопределенность:
- бесконечность минус бесконечность;
- бесконечность умножить на 0;
- бесконечность разделить на бесконечность;
- ноль разделить на ноль;
- ноль умножить на бесконечность;
- ноль в нулевой степени;
- бесконечность в степени ноль;
- единица в степени бесконечность.
Задачи с неопределенностями возникают при вычислении пределов функций, которые заданы формулами, дающими подобные выражения при подстановке предельных значений аргумента. Математики говорят, что результатом таких уравнений будет бесконечное множество чисел. Обычно для их решения используют различные схемы и алгоритмы. Это называется раскрытием неопределенности.
Над нулем можно проделывать все арифметические операции. Единственное ограничение — он не может быть делителем для любого действительного числа. Результатом деления ненулевого числа на ноль в высшей математике считается бесконечность, а деление нуля на ноль дает неопределенность. В арифметике подобные действия считаются невозможными и бессмысленными.
Результатом деления ненулевого числа на ноль в высшей математике считается бесконечность, а деление нуля на ноль дает неопределенность. В арифметике подобные действия считаются невозможными и бессмысленными.
Предыдущая
МатематикаКоординатная плоскость — определение расположения точек и фигур
Следующая
МатематикаПочему на ноль делить нельзя — правило, доказательство и и примеры
Урок Видео: Правила деления на 0 и 1
Стенограмма видео
Правила деления на ноль и единицу
В этом видео мы будем учиться
как смоделировать то, что происходит, когда мы делим, используя числа один и ноль. Вам будет приятно узнать, что
деление на ноль на самом деле не приведет к появлению черных дыр. Но это одна из тех идей в
математика, которая может быть довольно сложной для понимания. Итак, для начала начнем с
легче наших двух чисел.
Итак, для начала начнем с
легче наших двух чисел.
Что произойдет, если мы разделим число одним? Ну, если вы помните, есть два способа, которыми мы можем думать о разделении, как о группировке и разделении. Давайте используем девять, разделенных на один, как пример. Теперь, если мы думаем об этом деление как группировку, то, что мы говорим, это если мы начнем с девяти и разделим это разбей на группы по одному, сколько будет групп? Конечно, у нас будет девять групп, не так ли? Это такая же идея, как если бы в вашем классе было девять человек. И твой учитель сказал: «Правильно, сегодня после обеда вам нужно поработать индивидуально». Вы все будете работать за столом самостоятельно. Вам понадобится девять столов, не так ли? Девять разделить на один равно девять.
Мы можем найти тот же ответ,
думая о делении на один как об обмене. Другими словами, что произойдет, если мы
начнем с девяти, и мы разделим его с, ну, с одним? Представьте, что у вас было девять конфет, и вы
поделился ими только с собой. В некотором смысле, это не совсем то,
это? Есть только один из вас. Вы получите все девять конфет. Девять, разделенные на одну группу, равны
девять. Теперь вы можете заметить что-нибудь
интересно об этом отделении? Мы начали с девяти. И к тому времени, когда мы разделили его на
один, он вообще не изменился. Наш ответ тот же самый номер, который мы
начал дивизию с.
Другими словами, что произойдет, если мы
начнем с девяти, и мы разделим его с, ну, с одним? Представьте, что у вас было девять конфет, и вы
поделился ими только с собой. В некотором смысле, это не совсем то,
это? Есть только один из вас. Вы получите все девять конфет. Девять, разделенные на одну группу, равны
девять. Теперь вы можете заметить что-нибудь
интересно об этом отделении? Мы начали с девяти. И к тому времени, когда мы разделили его на
один, он вообще не изменился. Наш ответ тот же самый номер, который мы
начал дивизию с.
И это приводит нас к правилу, что
мы можем вспомнить, когда мы делим на единицу, независимо от того, какое число. И это то, что любое число делится
на единицу равняется самому себе. И так, 14 разделились на одну группу
равно 14. 35 разделить на единицу равно 35. А 296 352 разделить на единицу равно
296,3 — ну вы поняли. Что-то еще, что мы могли бы использовать, чтобы помочь
мы понимаем, что происходит, когда мы делим на единицу, это умножение. Так, например, если мы хотим найти
того, чему равно 12, деленное на единицу, мы могли бы придумать противоположное или обратное действие,
что есть умножение, и спросим себя: «Что будет умножено на единицу, чтобы получить
ответ 12?» Мы знаем, что 12 умножить на один равно
12. А если мы знаем, что 12 лотов одного
сделать 12, мы также знаем, что если мы разделим 12 на один, мы получим ответ 12.
Что-то еще, что мы могли бы использовать, чтобы помочь
мы понимаем, что происходит, когда мы делим на единицу, это умножение. Так, например, если мы хотим найти
того, чему равно 12, деленное на единицу, мы могли бы придумать противоположное или обратное действие,
что есть умножение, и спросим себя: «Что будет умножено на единицу, чтобы получить
ответ 12?» Мы знаем, что 12 умножить на один равно
12. А если мы знаем, что 12 лотов одного
сделать 12, мы также знаем, что если мы разделим 12 на один, мы получим ответ 12.
До сих пор мы только думали
о делении на единицу. И мы видели, что любое число
разделить на единицу равно самому себе. Но вы знаете, мы можем изменить это
утверждение вокруг, чтобы сделать другое правило. Любое число, деленное само на себя, равно
один. Если мы возьмем шесть, разделенных на шесть, как
например, если у нас есть шесть счетчиков и мы разделим их на группы по шесть, мы будем только
возможность составить одну группу. Шесть разделить само на себя равно
один. Итак, 18 разделить на 18 равно
один. Неважно, какой номер мы
работать с. Если мы разделим его на себя, то
ответ всегда будет один. Итак, мы узнали два разных
факты или правила здесь для случаев, когда деление включает в себя номер один. Любое число, деленное на единицу, остается
такой же. И любое число, деленное само на себя
равняется единице. Давайте попробуем ответить на
теперь пара вопросов, где мы можем применить на практике эти правила.
Шесть разделить само на себя равно
один. Итак, 18 разделить на 18 равно
один. Неважно, какой номер мы
работать с. Если мы разделим его на себя, то
ответ всегда будет один. Итак, мы узнали два разных
факты или правила здесь для случаев, когда деление включает в себя номер один. Любое число, деленное на единицу, остается
такой же. И любое число, деленное само на себя
равняется единице. Давайте попробуем ответить на
теперь пара вопросов, где мы можем применить на практике эти правила.
Полное: Четыре разделить на что равняется четырем.
В этом вопросе нам дается
деление, где делитель, то есть число, на которое мы делим, отсутствует. Число, которое мы делим, равно
четыре. И тогда мы делим это на что-то
и ответ тоже четыре. Это интересно. На какое число мы можем разделить так
что число, с которого мы начинаем, не меняется? Давайте нарисуем модель стержня, чтобы помочь
нас. Если мы разделим четыре на группы
определенную сумму, и мы обнаруживаем, что можем составить четыре группы, какой будет каждая группа
стоит? Каждая группа будет иметь значение
одного. Четыре разделены на равные группы по одному
равняется четырем. И мы знаем, что это правильно, потому что
нам напоминают о важном факте, связанном с делением на единицу. И это то, что любое число делится
на единицу равняется самому себе. Поэтому, как только мы увидели, что наш
стартовый номер в этом дивизионе не изменился, мы поняли, что должны были его разделить
одним. Четыре разделить на один равно
четыре. Наше недостающее число — один.
Если мы разделим четыре на группы
определенную сумму, и мы обнаруживаем, что можем составить четыре группы, какой будет каждая группа
стоит? Каждая группа будет иметь значение
одного. Четыре разделены на равные группы по одному
равняется четырем. И мы знаем, что это правильно, потому что
нам напоминают о важном факте, связанном с делением на единицу. И это то, что любое число делится
на единицу равняется самому себе. Поэтому, как только мы увидели, что наш
стартовый номер в этом дивизионе не изменился, мы поняли, что должны были его разделить
одним. Четыре разделить на один равно
четыре. Наше недостающее число — один.
Выполните следующее: Два разделенных на то, что равно единице.
В этом вопросе нам дается
деление с пропущенным номером. На что мы делим два, чтобы дать нам
ответ один? Ну, мы знаем это деление и
умножение — обратные операции; они противоположности. Таким образом, чтобы помочь найти недостающее число в
такое деление, мы можем подумать о сопутствующем ему факте умножения,
противоположность этому. Поэтому вместо того, чтобы спрашивать себя,
«На что мы поделим два, чтобы получить ответ один?», мы можем пойти в обратном направлении и спросить
себя: «На что нам умножить один, чтобы получить ответ два?» ну это совсем просто
Факт умножения, не так ли? Один раз два равно двум. И если мы знаем, что есть много
два на два, если мы разделим само на себя, мы получим ответ один.
Таким образом, чтобы помочь найти недостающее число в
такое деление, мы можем подумать о сопутствующем ему факте умножения,
противоположность этому. Поэтому вместо того, чтобы спрашивать себя,
«На что мы поделим два, чтобы получить ответ один?», мы можем пойти в обратном направлении и спросить
себя: «На что нам умножить один, чтобы получить ответ два?» ну это совсем просто
Факт умножения, не так ли? Один раз два равно двум. И если мы знаем, что есть много
два на два, если мы разделим само на себя, мы получим ответ один.
Другой способ узнать, что это правда, это
потому что мы знаем правило, которое применяется каждый раз, когда число делится само на себя. Любое число, деленное само на себя, равно
один. А так, ведь наша дивизия показала
ответ один, мы знали, что первое число должно быть разделено само на себя. Два разделить на два равно одному. Наше недостающее число — два.
Наше недостающее число — два.
Теперь, если вы помните, название это видео было «Правила деления на ноль и единицу». И хотя мы рассмотрели правила деления, когда речь идет о числе один, пора подумать о нуль. Что происходит, когда мы делим с помощью нуль? Ты помнишь тот мультик, который мы используется два персонажа, падающие в черную дыру, потому что один из них только что пробовал делить на ноль. Теперь это было просто немного весело. Но вы знаете, деление на ноль может на самом деле сделать вашу голову кружиться немного. Итак, что мы сделаем, это возьмем это очень медленно, чтобы попытаться понять это. Возможно, на этот раз это могло бы имеет смысл начать с правила.
Это правило очень легко
помните, возможно, не так просто понять, но определенно легко
запомнить. И это то, что мы не можем разделить на
нуль. Попробуем объяснить, почему
нет, и мы попробуем 100 разделить на ноль в качестве примера. Итак, вот 100 счетчиков. А если разбить их на группы
100, групп хватило бы только на одного человека. Если мы разделим 100 на группы по 50,
тогда два человека получат группу по 50 человек каждый. И затем, как еще один пример,
если мы разделим наши 100 счетчиков на группы по одному, все 100 человек получат счетчик
каждый. Теперь глядя на эти деления можно
помогите нам, когда дело доходит до размышлений о делении на ноль.
Попробуем объяснить, почему
нет, и мы попробуем 100 разделить на ноль в качестве примера. Итак, вот 100 счетчиков. А если разбить их на группы
100, групп хватило бы только на одного человека. Если мы разделим 100 на группы по 50,
тогда два человека получат группу по 50 человек каждый. И затем, как еще один пример,
если мы разделим наши 100 счетчиков на группы по одному, все 100 человек получат счетчик
каждый. Теперь глядя на эти деления можно
помогите нам, когда дело доходит до размышлений о делении на ноль.
Обратите внимание, как число, которое мы
деление на идет вниз, ответ на каждое деление идет вверх. И поэтому мы ожидаем ответа на
100 разделить на ноль, чтобы снова увеличить. Но если мы остановимся и подумаем об этом,
100 фишек, разделенных на группы по 0, означают, что может подойти один человек, а затем
мы могли бы поделиться с ними нулевыми счетчиками, но у нас все равно было бы столько же счетчиков
как мы должны были начать с. И это все еще было бы так, если бы
пришел еще кто-то или даже еще 100 человек. Сотни и даже сотни
тысячи людей могли постучать в нашу дверь с просьбой об нулевых счетчиках, и мы все равно
быть в состоянии сделать это, потому что ноль ничто. Это не влияет на наши 100 счетчиков
вообще. Мы просто не можем разделить
до 100 до нуля.
И это все еще было бы так, если бы
пришел еще кто-то или даже еще 100 человек. Сотни и даже сотни
тысячи людей могли постучать в нашу дверь с просьбой об нулевых счетчиках, и мы все равно
быть в состоянии сделать это, потому что ноль ничто. Это не влияет на наши 100 счетчиков
вообще. Мы просто не можем разделить
до 100 до нуля.
Некоторые другие вещи, которые мы можем использовать
чтобы помочь нам понять, что мы не можем делить на ноль, факты умножения. Например, если нас попросят сделать
невозможное и разделить 15 на ноль, мы бы подумали об обратной операции и
мы спрашивали себя: «Какое число нужно умножить на ноль, чтобы получить ответ 15?» И тогда, надеюсь, мы начнем
хмуриться и говорить себе: «Это невозможно». Если каждая тарелка, которая у нас есть, имеет ноль
бананов на нем, сколько этих пустых тарелок нам нужно, чтобы иметь 15 бананов? Ну, это не имеет смысла, не так ли
Это? Мы просто не можем ответить на это. У нас может быть полмиллиона пустых
кусочков бананов, и у нас все равно не было бы 15 съеденных. Мы могли бы также вычеркнуть
расчеты такие. Они просто не имеют смысла.
У нас может быть полмиллиона пустых
кусочков бананов, и у нас все равно не было бы 15 съеденных. Мы могли бы также вычеркнуть
расчеты такие. Они просто не имеют смысла.
Но что, если у нас есть подразделение, которое
начинается с нуля? Есть ли правило для этого? Как насчет деления нуля на 10 для
пример? Вот изображение нулевой овцы. Некоторые из вас могут подумать, что это выглядит
больше похоже на ноль слонов, но это точно ноль овец. Вам нужно посмотреть внимательнее. А что, если мы возьмем нашу нулевую овцу
и разделить их на 10 равных групп? Мы здесь. Что вы имеете в виду, вы не можете видеть
их? конечно не будет
все овцы в этих группах присутствуют, потому что у нас изначально не было овец. Ноль разделить на 10 равно нулю. На самом деле, мы могли бы разделить ноль
на любое количество групп. Ответ всегда будет
одинаковый.
И это подводит нас ко второму Правило деления на ноль. И это если мы начнем с нуль, и мы делим его на любое число вообще, это всегда дает ноль. Давайте попрактикуем то, что мы узнали о делении на ноль тогда.
Заполните следующее: Что разделить на 12 равно нулю.
Это может показаться необычным
деление, потому что оно заканчивается ответом ноль. И не часто мы видим
деление, оканчивающееся нулем. В начале этого номера
предложение, мы видим, что у нас есть пропущенное число, которое нам нужно заполнить. Какое число если разделить на 12
дал бы ответ ноль? Чтобы помочь нам найти это пропавшее без вести
число, мы можем начать с конца этого деления и двигаться в обратном направлении, потому что мы знаем
что обратным или противоположным делению является умножение. Если мы разделим число на 12 и получим
есть нулевые партии из 12, то чтобы найти это недостающее число, нам просто нужно найти ноль
много 12.
Мы можем использовать наши знания о умножение на ноль, чтобы помочь нам здесь, потому что мы знаем, что любое число, умноженное на ноль равен нулю. И вот как мы знаем, что пропали без вести число должно быть равно нулю. Это напоминает нам о факте, который мы знаем делать с работой с нулем в делениях. Деление нуля на любое число вообще всегда приводит к нулю. И, как мы знаем, наш ответ равен нулю, мы знаем, что число, которое мы разделили на 12, тоже должно быть нулем. Ноль разделить на 12 равно нулю. Наше недостающее число равно нулю.
Итак, что мы узнали из этого
видео? Мы научились моделировать то, что
происходит, когда мы делим единицу или ноль, а также когда мы делим число на единицу или
нуль. Мы узнали эти факты. Любое число деленное на единицу равно
само по себе, и любое число, деленное само на себя, равно единице. Кроме того, ноль, разделенный на любое число, равен
нуль. И делить на ноль нельзя
возможный.
Кроме того, ноль, разделенный на любое число, равен
нуль. И делить на ноль нельзя
возможный.
Умножение на ноль — свойства, деление, примеры решений и часто задаваемые вопросы
Что происходит при умножении числа на 0? Умножение числа на 0 делает произведение равным нулю. Помните, что произведение любого действительного числа на 0 равно 0. Для любого действительного числа m m⋅0 = 0. Согласно нулевому свойству умножения, произведение любого числа на ноль (0) равно 0. Теперь мы уже узнали, что ноль является аддитивной идентичностью, учитывая, что его можно добавить к любому числу без изменения идентичности числа.
Основные свойства Zero
Ноль и единица на самом деле являются особыми числами и поэтому обладают особыми свойствами. Но у нуля также есть некоторые уникальные свойства, касающиеся умножения и деления.
Ноль является аддитивным идентификатором, поскольку его можно добавить к любому числу без изменения идентификатора номера. Но ноль обладает некоторыми особыми свойствами, когда дело доходит до умножения и деления. При умножении числа на 0 произведение становится равным нулю, поэтому произведение любого действительного числа на 0 равно 0.
Но ноль обладает некоторыми особыми свойствами, когда дело доходит до умножения и деления. При умножении числа на 0 произведение становится равным нулю, поэтому произведение любого действительного числа на 0 равно 0.
Прибавление 0 к числовой цифре оставляет ее неизменной. 0 известен как аддитивная идентичность, а свойство называется свойством аддитивной идентичности.
6 + 0 = 6
1 + 0 = 1
Ноль является аддитивным идентификатором, поскольку его можно добавить к любому числу без изменения идентификатора номера. Нулевое свойство умножения гласит, что при умножении числа на ноль произведение всегда равно нулю. Ноль может стоять до или после числа, что означает, что позиция нуля не влияет на свойство.
Итак, 2 x 0 = 0. Нулевое свойство умножения применимо ко всем типам чисел, будь то целые числа, дроби, десятичные дроби или даже алгебраические термины. Его не следует рассматривать как тождественное свойство умножения, которое включает 1 в качестве элемента идентичности и в котором произведение является самим числом.
Ноль, умноженный на любую числовую цифру, равен нулю, а это означает, что умножение любого числа на 0 дает 0.
0 × 6 = 0
1 × 0 = 0 мощность 0 равна единице. Например,
290 = 1
-570 = 1
Показатель степени нуля
Число 0 в любой степени остается 0.
Ноль как числитель
0 разделить на любое ненулевое число равно 0. Например,
0 ÷ 7 = 0
0 ÷ 45 = 0
Любое деление на 0 неопределенно. Например,
51 ÷ 0 = не определено
12 ÷ 0 = не определено
Способы представления умножения
Число «a», умноженное на число «b», может быть представлено несколькими способами, как показано ниже в таблица:
a⋅b | Использование точки по центру. | Сопоставление проще и предпочтительнее для переменных. Центрированная точка очень полезна для констант: например, 2⋅3 = 6. |
ab | Использование сопоставления Размещение элементов рядом. | Это стандартный формат записи константы перед переменной. Например, мы пишем 3а, а не а3. |
(a)(b) | Использование скобок. | Сопоставление проще и предпочтительнее для переменных. Круглые скобки необходимы в подобных ситуациях: (a + 1)(b + 3) |
Примечание. В алгебре и выше при выборе переменной x не используйте символ умножения ‘×’ для обозначения умножение, так как это может привести к путанице с переменной x.
(Исключение: принято использовать «×» для научного обозначения).
Деление нуля
Деление любого числа на ноль не определено. Разделение означает разделение чего-либо на равные части или группы, чтобы это можно было разделить поровну между всеми. Хотя значение нуля как числа ничто. Если он стоит перед единицей, то это четное число, которое не является ни положительным, ни отрицательным.
Для любого действительного числа m, кроме 0, 0/m = 0 и 0 ÷ m = 0.
Ноль, деленный на любое действительное число, отличное от 0, равен 0.
Обратите внимание, что мы всегда можем проверить деление с помощью соответствующий факт умножения. Итак, мы знаем, что
0 ÷ 5 = 0, так как 0⋅5 = 0
Деление на ноль
Как насчет деления числа на 0? Только представьте реальный пример: если в банке нет конфет и пять видов хотят ими поделиться, сколько конфет получит каждый ребенок? Есть 0 конфет, которыми можно поделиться, поэтому нет смысла делиться тем, чего нет.
5÷ 0 = не определено
Решенные примеры с нулевым свойством умножения
Вот несколько примеров нулевого свойства умножения. Это поможет вам узнать свойство умножения, как умножить на 0 и его результаты.
Пример:
Упростите выражение 7/9 × 0
Решение:
Поскольку оно включает умножение на 0 и любое число, мы умножаем на 0 = 0
Таким образом, 7/9 × 0 = 0.
Забава Факты
Если при умножении 0, то ответ всегда будет 0.
Даже большее число, умноженное на 0, равно 0. Например,
65 × 0 = 0. не имеет значения, идет ли 0 первым или нет в уравнении. Например, x умножить на 0 = 0. Или: 0 × 7 = 0 или: 9× 0 = 0.
На самом деле не имеет значения, сколько чисел.
 Если происходит только умножение, а затем 0, результатом будет 0. Например, = 459 × 9 × 0 × 5 = 0.
Если происходит только умножение, а затем 0, результатом будет 0. Например, = 459 × 9 × 0 × 5 = 0.Количество операций не имеет значения. Если происходит только умножение и есть 0, результатом будет просто 0. Например, 459 + 7 — 6 × 0 = 0.
0 × 0 = 0 (поскольку у нас есть ноль 0).
Использование свойств умножения и деления нуля | Преалгебра |
Результаты обучения
- Определение свойств умножения и деления нуля
Использование свойств нуля
Мы уже узнали, что ноль — это аддитивная идентичность, поскольку его можно добавить к любому числу без изменения идентичности числа. Но ноль также обладает некоторыми особыми свойствами, когда дело доходит до умножения и деления.
Умножение на ноль
Что произойдет, если вы умножите число на
0?0?0?
Умножение на
000
делает произведение равным нулю. Произведение любого действительного числа и
Произведение любого действительного числа и
000
равно
000
.
Умножение на ноль
Для любого действительного числа
aaa
,
a⋅0=0a\cdot 0=0a⋅0=0
Упражнения
Упростить:
1.
−8⋅0-8\cdot 0−8⋅0
2.
512⋅0\frac{5}{12}\cdot 0125⋅0
3.
0(2.94)0\left(2.94\right)0(2.94)
5 Решение:
5
| 1. | |
−8⋅0-8\cdot 0−8⋅0 | |
| Произведение любого действительного числа на 0 равно 0. | 000 |
| 2. | |
512⋅0\frac{5}{12}\cdot 0125⋅0 | |
Произведение любого действительного числа на 0 равно 0. | 000 |
| 3. | |
0(2,94)0\влево(2,94\вправо)0(2,94) | |
| Произведение любого действительного числа на 0 равно 0. | 000 |
ПОПРОБУЙТЕ
Деление с нулем
Как насчет деления на
0?0?0?
Подумайте о реальном примере: если в банке с печеньем нет печенья и трое человек хотят ими поделиться, сколько печенья получит каждый? Есть
000
файлов cookie, которыми можно поделиться, поэтому каждый человек получает
000
файлов cookie.
0÷3=00\div 3=00÷3=0
Помните, что мы всегда можем проверить деление с помощью соответствующего факта умножения. Итак, мы знаем, что
0÷3=0 потому что 0⋅3=00\div 3=0\text{ потому что }0\cdot 3=00÷3=0 потому что 0⋅3=0
.
Отдел Зеро
Для любого вещественного числа
aaa
, кроме
0,0a=00,\frac{0}{a}=00,a0=0
и
0÷a=00\div a=00÷ а=0
.
Ноль, разделенный на любое действительное число, кроме нуля, равен нулю.
Упражнения
Упростить:
1.
0÷50\дел 50÷5
2.
0−2\frac{0}{-2}−20
3.
0÷780\div \frac {7}{8}0÷87
Показать решение
Решение:
| 1. | |
0÷50\дел 50÷5 | |
| Ноль, разделенный на любое действительное число, кроме 0, равен нулю. | 000 |
| 2. | |
0−2\frac{0}{-2}−20 | |
Ноль, разделенный на любое действительное число, кроме 0, равен нулю. | 000 |
| 3. | |
0÷780\дел\фрак{7}{8}0÷87 | |
| Ноль, разделенный на любое действительное число, кроме 0, равен нулю. | 000 |
ПОПРОБУЙТЕ
Теперь давайте подумаем о делении числа на нулей. Каков результат деления
444
на
0?0?0?
Подумайте о родственном факте умножения. Есть ли число, которое умножается на
000
дает
4?4?4?
4÷0=4\div 0=4÷0=
означает
⋅0=4\cdot 0=4⋅0=4
Так как любое действительное число, умноженное на
000
0равно 0 900
, не существует действительного числа, которое можно умножить на
000
и получить
444
. Мы можем заключить, что нет ответа на
Мы можем заключить, что нет ответа на
4÷04\div 04÷0
, поэтому мы говорим, что деление на ноль не определено.
Деление на ноль
Для любого действительного числа
a,a0a,\frac{a}{0}a,0a
и
a÷0a\div 0a÷0
не определены.
Деление на ноль не определено.
Упражнения
Упростить:
1.
7.5÷07.5\дел 07.5÷0
2.
−320\frac{-32}{0}0−32
3.
49÷0\frac{49÷0\frac{-32}{0}0−32 {9}\div 094÷0
Показать решение
Решение:
| 1. | |
7.5÷07.5\дел 07.5÷0 | |
| Деление на ноль не определено. | не определено |
| 2. | |
−320\frac{-32}{0}0−32 | |
Деление на ноль не определено. | не определено |
| 3. | |
49÷0\frac{4}{9}\div 094÷0 | |
| Деление на ноль не определено. | не определено |
ПОПРОБУЙТЕ
Ниже мы суммируем свойства нуля.
Свойства нуля
Умножение на ноль: Для любого действительного числа
aaa
,
a⋅0=0 Произведение любого числа на 0 равно 0.\begin{array}{c}a cdot 0=0\text{ Произведение любого числа и 0 равно 0.}\qquad \end{array}a⋅0=0 Произведение любого числа и 0 равно 0.
Деление на ноль: Для любого действительного числа деленное на любое действительное число, кроме самого себя, равно нулю.
a0\frac{a}{0}0a
не определено. Деление на ноль не определено.
Посмотрите следующее видео, чтобы увидеть больше примеров использования свойства умножения и деления нуля.
Лицензии и атрибуты
Контент под лицензией CC, ранее опубликованный
- Умножение и деление на ноль. Автор : Джеймс Соуза (Mathispower4u.com). Лицензия : CC BY: Атрибуция
Лицензионный контент CC, Конкретная атрибуция
- Преалгебра. Предоставлено : OpenStax. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно на http://cnx.org/contents/[email protected]
Zero’s Strange Properties — How Zero Works
То, что ноль может быть как неотрицательным, так и неположительным целым числом, но при этом не быть ни отрицательным, ни положительным, является лишь одним из уникальных свойств числа. На самом деле существует группа этих странных характеристик, называемых свойствами нуля .
На самом деле существует группа этих странных характеристик, называемых свойствами нуля .
Свойство сложения нуля говорит о том, что если вы прибавите или вычтете ноль из любого другого числа, результатом всегда будет другое число. 5+0=5 и 9 000 017-0=9 000 017, например. Он отражает концепцию нуля как ничего не представляющего, поэтому ничего не прибавляя к чему-то, оставляет это что-то неизменным — ноль — это единственное число, которое не изменяет другие числа при сложении или вычитании.
Реклама
Аддитивное обратное свойство нуля отражает его позицию точки опоры между отрицательными и положительными целыми числами. Любые два числа, сумма которых равна нулю, являются аддитивными инверсиями друг друга. Например, если вы прибавите -5 к 5, вы получите ноль. Таким образом, -5 и 5 являются аддитивными инверсиями друг друга.
Свойство умножения гласит то, что знает каждый третьеклассник: умножение любого числа на ноль дает в сумме ноль. Это очевидно, когда-то укоренившееся, но, возможно, причина упускается из виду. Умножение, в одном эффекте, является ярлыком для сложения. 3×2 — это то же самое, что 2+2+2, поэтому идея о том, что число может быть добавлено ноль раз или что ноль может быть добавлен к самому себе любое количество раз, математически бессмысленна [источник: Carasco].
Умножение, в одном эффекте, является ярлыком для сложения. 3×2 — это то же самое, что 2+2+2, поэтому идея о том, что число может быть добавлено ноль раз или что ноль может быть добавлен к самому себе любое количество раз, математически бессмысленна [источник: Carasco].
Понятие деления на ноль еще более бессмысленно, настолько, что для него нет свойства; концепции просто не существует, поскольку она не может быть осуществлена. Даже математики часто пытаются объяснить, почему деление на ноль не работает. Причина в основном связана со свойством умножения. При делении числа на другое число, например 6/2, результат (в данном случае 3) можно осмысленно подставить в формулу, где ответ, умноженный на делитель, равен делимому. Другими словами, 6/2=3 и 3×2=6. Это не работает с нулем, когда мы заменяем им 2 в качестве делителя; 3×0=0, а не 6 [источник: Utah Math]. Концепция деления на ноль чревата настолько нелогичными последствиями, что ее мифическая разрушительная сила стала шуткой в Интернете.
Существует также свойство нулевого показателя; из-за существования отрицательных показателей, числа в отрицательной степени, числа в нулевой степени всегда равны единице. Хотя это работает математически, это также создает логические проблемы. В основном, ноль в нулевой степени по-прежнему равен единице, хотя ноль, добавленный или вычитаемый или умноженный сам на себя, должен равняться нулю [источник: Stapel].
Вот сила нуля.
Похожие статьи
Источники
- Аршам, Хоссейн. «Ноль в четырех измерениях». Университет Балтимора. По состоянию на 18 апреля 2011 г. http://home.ubalt.edu/ntsbarsh/zero/zero.htm
- Ask Dr. Math. «Деление на ноль.» Математический форум в Университете Дрекселя. По состоянию на 5 апреля 2011 г. http://mathforum.org/dr.math/faq/faq.divideby0.html
- Караско, Шут. «Свойства нуля». Basic-Mathematics.com. По состоянию на 18 апреля 2011 г. http://www.basic-mathematics.com/properties-of-zero.html
- Forex Realm.
 «Биография и факты Фибоначчи». По состоянию на 15 апреля 2010 г. http://www.forexrealm.com/technical-analysis/fibonacci/fibonacci-biography-history-facts.html
«Биография и факты Фибоначчи». По состоянию на 15 апреля 2010 г. http://www.forexrealm.com/technical-analysis/fibonacci/fibonacci-biography-history-facts.html - Грей, Джереми. «Рецензия на книгу: Ноль: биография опасной идеи». Уведомления АМС. October 200. http://www.ams.org/notices/200009/rev-gray.pdf
- Knott, Dr. Ron. «Кем был Фибоначчи?» Университет Суррея. 11 марта 1998 г. http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibBio.html
- Мэтсон, Джон. «Происхождение нуля». Научный американец. 21 августа 2009 г. http://www.scientificamerican.com/article.cfm?id=history-of-zero
- О’Коннор, Дж.Дж. и Робертсон, Э. Ф. «История нуля». Университет Сент-Эндрюс. Ноябрь 2000 г. http://www-history.mcs.st-and.ac.uk/HistTopics/Zero.html
- Пепперберг, Ирэн и Гордон, Джесси Д. «Понимание чисел серым попугаем (Psittacus erithacus), включая концепцию, подобную нулю». Журнал сравнительной психологии. 2005. http://www.alexfoundation.org/papers/JCPAlexComp.
 pdf
pdf - Saudi Aramco World. «Ноль, ключ к числам». Ноябрь 1961 г. http://www.saudiaramcoworld.com/issue/196109/zero.key.to.numbers.htm
- Сейф, Чарльз. «Ноль: биография опасной идеи». Пингвин. 2000. http://books.google.com/books?id=obJ70nxVYFUC 9.0076
- Сингх, Саймон. «5 цифр — ноль». Би-би-си. 11 марта 2002 г. http://www.bbc.co.uk/radio4/science/5numbers1.shtml
- Стапель, Элизабет. «Отрицательные показатели». Пурпурная математика. По состоянию на 18 апреля 2011 г. http://www.purplemath.com/modules/exponent2.htm
- Stockton, J.K. «Дата альманаха I». 10 марта 2010 г. http://www.merlyn.demon.co.uk/miscdate.htm#AstDat
- Терези, Дик. «Нуль.» Атлантический океан. Июль 1997 г. http://www.theatlantic.com/past/docs/issues/97jul/zero.htm
- The Straight Dope. — Ноль — это число? По состоянию на 5 апреля 2011 г. http://www.straightdope.com/columns/read/1633/is-zero-a-number
- Математический факультет Университета Юты. «Почему нельзя делить на ноль?» 17 февраля 1997 г.
 http://www.math.utah.edu/~pa/math/0by0.html
http://www.math.utah.edu/~pa/math/0by0.html - Wolfram Math World. «Натуральное число.» По состоянию на 5 апреля 2011 г. http://mathworld.wolfram.com/NaturalNumber.html
Процитируйте это!
Пожалуйста, скопируйте/вставьте следующий текст, чтобы правильно цитировать эту статью HowStuffWorks.com:
Джош Кларк
«Как работает ноль»
4 мая 2011 г.
HowStuffWorks.com.
Что это такое и как его использовать
Цифра 0 уже давно ставит в тупик людей, изучающих математические понятия. Ноль это число? Как мы это используем? Хотя все мы на каком-то уровне знаем, что ноль означает ничего или ничего, это не всегда помогает нам включить его в математические задачи. Ниже мы рассмотрим несколько основных функций нуля и способы решения уравнений, содержащих ноль, с использованием этих функций.
Что такое число 0?
Является ли ноль числом? Ноль или 0 это 9Число 0666 и цифра, используемая для представления числа 0 , широко используются в математике и могут использоваться как самостоятельные числа или как заполнители в уравнениях.
История
Число 0 использовалось для представления идеи «ничто» со времен древнего шумерского общества, которое использовало его для обозначения отсутствия числа при записи чисел и уравнений.
Овальная форма , известная нам сегодня как 0, появилась в арабском языке в конце 700-х годов . Зеро не появлялся в европейском обществе до конца 12 века.
Современное использование
Ноль обычно используется в языке для выражения концепции отсутствия, а в математике используется как целое число. Число 0 в сегодняшней математике может быть сложным; зачем что-то вычислять, когда на самом деле там ничего нет? Но ноль можно использовать в различных математических задачах, и важно знать, что делать с нулем, когда вы его видите.
Операции с 0
Хотя этот список функций с использованием нуля не охватывает все математические функции , эти основные арифметические инструкции с использованием нуля помогут вам решать задачи на тестах и, возможно, даже в реальном мире.
Сложение
Тождество Закон сложения гласит, что любое число, добавленное к 0, равно самому себе .
Таким образом, вы можете добавить любое число и получить ту же сумму. Таким образом, вы можете добавить 0 к 1, 107 и 1 000 000 и все равно получить то же число, с которого вы начали.
Вычитание
Как и при сложении, если вычесть 0 из любого числа, вы получите ту же сумму. Например, 12-0 = 12.
Если вы вычитаете, вам может понадобиться заимствование для решения проблемы. Заимствование — это метод, используемый для вычитания чисел, состоящих более чем из одной цифры.
Вот пример заимствования (разберусь как форматировать):
1572-125 = х
В этой задаче из 2 нельзя вычесть 5. Значит, надо заимствовать из 7.
70 это 7 десятков. Итак, вы можете убрать десятку, и 7 станет 2; затем 2 становится 12. Теперь вам нужно вычесть 5 из 12.
12-5 равно 7.
6-2 равно 4.
5-1 равно 4.
1-0 (пустое место) равно 1.
Следовательно, ответ равен 1447.
Итак, если 0 — это ничто, как мы можем заимствовать его в задаче на вычитание? Ключ заключается в том, чтобы заимствовать из следующей цифры слева. Вы можете идти так далеко влево, как вам нужно.
Итак, если бы вы сделали 306-98 вы должны сначала позаимствовать из 3, чтобы сделать 0 равным 10. Затем вы можете позаимствовать из 10, чтобы сделать 6 равным 16. Таким образом, ваша задача будет выглядеть так: 16-8=8.
9-9=0.
2-0=2.
Таким образом, ваш ответ 208.
Не стесняйтесь заниматься математикой, добавляя котят в свою жизнь
Умножение
Умножение на 0 на самом деле является одной из самых простых функций. , ответ всегда 0.
12 × 0 = 0
255 × 0 = 0
1679 × 0=0
И знаете что? 123596395539 x 0 = 0
Деление
Число 0, деленное на любое число, равно нулю. Подумайте об этом так: деление означает деление или разделение вещей поровну, верно ? Если у вас есть коробка с 8 кексами и за вашим столом 4 человека, вы разделите 8 на 4 и обнаружите, что каждый получает по два кекса. Но если у вас за столом 4 человека и в коробке 0 кексов, вам фактически нечего делить. Каждый получает 0 кексов.
Подумайте об этом так: деление означает деление или разделение вещей поровну, верно ? Если у вас есть коробка с 8 кексами и за вашим столом 4 человека, вы разделите 8 на 4 и обнаружите, что каждый получает по два кекса. Но если у вас за столом 4 человека и в коробке 0 кексов, вам фактически нечего делить. Каждый получает 0 кексов.
К сожалению, деление числа на ноль не столь очевидно логично. Любое число, деленное на ноль, считается неопределенным; если вы поместите его в свой калькулятор прямо сейчас, вы, вероятно, получите сообщение об ошибке.
При делении вы всегда можете перепроверить свой ответ, умножив частное (ответ на задачу о делении) на делимое . В нашей задаче о кексах это 2 x 4. Число должно равняться нашему первоначальному делителю, 8.
Однако это помогает нам понять, почему мы не можем разделить число на 0. Поскольку мы знаем из наших правил умножения, что все, что умножается на 0, равно 0, изложенная выше концепция не работает, если 0 является делимым, потому что ответ всегда будет 0, даже если это не исходный делитель.
Если по какой-то причине вы встретили 0 как делимое в задаче, вы можете выразить его как 1, даже если ответ технически не определен .
Возведение в степень
Как и в делении, 0 в экспоненте считается неопределенным. Однако, когда вы решаете задачи, и вы сталкиваетесь с чем-то, что равно 0 в степени другого числа или числу в степени 0, помните правило степени 0
Правило степени 0 гласит, что любое основание с показателем степени 0 или 0 равно 1. Итак, x¹ = 1,
Между тем, 0 в любой степени равно 0. Таким образом, 0² = 0.
Факториал нуля
Факториал — это математическое выражение, выражаемое как ! равно числу, полученному путем умножения всех чисел между 1 и заданным целым числом.
Итак, 2! означает, что мы умножаем все числа от 1 до 2. Это означает, что 2! = 2×1 = 2 и, следовательно, 2! = 24
6! означает, что мы умножаем все числа от 1 до 6. Итак, 6! = 1×2×3×4×5×6 = 720 и, следовательно, 6! = 720
Нулевой факториал, часто записывается как 0! Определяется как равный 1. По сути, поскольку факториал представляет собой выражение произведения всех целых чисел между заданными числами и 1, это единственный технически правильный ответ для 0! потому что единственное число между 0 и 1 — это 1.
По сути, поскольку факториал представляет собой выражение произведения всех целых чисел между заданными числами и 1, это единственный технически правильный ответ для 0! потому что единственное число между 0 и 1 — это 1.
Использовать число ноль может быть сложно, но есть несколько правил, которые помогут вам правильно выполнять математические операции, когда используется ноль. Обязательно придерживайтесь этих правил и помните, что ноль вам не враг. Если вы знаете, как работать с числом ноль, использовать его будет проще простого.
Что дальше?
Очарованы числом ноль? Узнайте, сколько нулей в миллиарде и сколько нулей в гуголе и гуголплексе.
Нужна дополнительная помощь по математике? Узнайте, как преобразовывать десятичные дроби в дроби, складывать и вычитать дроби, а также все о составных и рациональных числах. И не забудьте нашу удобную таблицу умножения.
Нужна дополнительная помощь по этой теме? Проверьте Tutorbase!
Наша база данных проверенных преподавателей включает ряд опытных преподавателей, которые могут помочь вам отшлифовать эссе по английскому языку или объяснить, как производные работают в исчислении. Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.
Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.
Есть друзья, которым тоже нужна помощь в подготовке к экзаменам? Поделись этой статьей!
Об авторе
Кэрри имеет степень бакалавра письма, литературы и издательского дела в Колледже Эмерсон и в настоящее время получает степень магистра иностранных дел. Она несколько лет работала в издательстве и считает, что книги могут открывать новые миры. Она любит читать, гулять на свежем воздухе и узнавать что-то новое.
Объяснение «правила нулевой мощности». Показатели кажутся довольно простыми… | Бретт Берри | Math Hacks
Экспоненты кажутся довольно простыми, не так ли? Возведение числа в степень 1 означает, что у вас есть одно из этого числа, возведение в степень 2 означает, что у вас есть два числа, умноженные вместе, степень 3 означает, что число равно трем, и так далее.
А как же нулевая мощность? Почему любое ненулевое число, возведенное в нулевую степень, равно 1? А что произойдет, если мы возведем ноль в нулевую степень? Это все еще 1?
Посмотрите видео или прочитайте ниже, чтобы узнать!
Нажмите здесь, чтобы подписаться на Math HacksДавайте начнем с изучения деления значений с показателями степени.
Вызов показателей степени представляют собой повторное умножение . Таким образом, мы можем переписать приведенное выше выражение как:
Поскольку 2/2 = 1, сокращаем три набора 2/2. Это оставляет 2 • 2, или 2 в квадрате.
Конечно, мы можем сократить путь и вычесть количество двоек внизу из числа двоек сверху. Поскольку эти величины представлены их соответствующими показателями степени, все, что нам нужно сделать, это записать общее основание с разницей в значениях степени в качестве степени.
Если мы обобщим это правило, то получим следующее, где n представляет собой ненулевое действительное число, а x и y также являются действительными числами.
Отсюда легко вывести объяснение, почему любое ненулевое число, возведенное в нулевую степень, равно 1. Опять же, давайте рассмотрим конкретный пример.
Мы знаем, что любое ненулевое число, деленное само на себя, равно 1 . Итак, я могу написать следующее:
Это то же самое, что написать:
Теперь я воспользуюсь приведенным выше правилом экспоненты, чтобы переписать левую часть этого уравнения.
Конечно, это эквивалентно:
Мы можем использовать тот же процесс, что и в этом примере, вместе с приведенным выше обобщенным правилом, чтобы показать, что любое ненулевое действительное число, возведенное в нулевую степень, должно дать 1.
Здесь все становится сложнее. Приведенный выше метод не работает, потому что, конечно, делить на ноль нельзя. Давайте рассмотрим, почему.
Начнем с обычного деления на ноль ОШИБКА .
Как насчет 2÷0? Давайте посмотрим, почему мы, , не можем этого сделать.
Деление на самом деле просто форма умножения, так что же произойдет, если я перепишу приведенное выше уравнение как:
Какое значение может удовлетворять этому уравнению для x?
Нет значения! Любое число, умноженное на ноль, дает ноль, оно никогда не может равняться 2. Поэтому мы говорим 9.0666 деление на ноль не определено . Возможного решения нет.
Теперь давайте посмотрим на 0÷0.
Опять же, перепишите это как задачу на умножение.
Здесь мы сталкиваемся с совершенно другой ситуацией. Решением для x может быть ЛЮБОЕ действительное число! Невозможно определить, что такое x. Следовательно, 0/0 считается неопределенным*, а не неопределенным.
Если мы попытаемся использовать описанный выше метод с нулем в качестве основы, чтобы определить, какой будет ноль в нулевой степени, мы немедленно остановимся и не сможем продолжать, потому что знаем, что 0÷0 ≠ 1, но это неопределенно.
Так чему же равен ноль в нулевой степени?
Это вызывает большие споры. Некоторые считают, что это должно быть определено как 1, в то время как другие считают, что это 0, а некоторые считают, что это не определено. Для каждого есть хорошие математические аргументы, и, пожалуй, правильнее всего считать неопределенным .
Несмотря на это, математическое сообщество выступает за то, чтобы определял ноль в нулевой степени как 1, по крайней мере, для большинства целей.
Возможно, полезное определение показателей для математика-любителя выглядит следующим образом:
Включив «1» в определение, мы можем заключить, что любое число (включая ноль) повторенное ноль умноженное на дает 1. Простой пример того, почему 0/0 является неопределенным, можно найти, изучив некоторые основные ограничения.
Подписывайтесь на Math Hacks в Instagram Эти ограничения нельзя оценить напрямую, поскольку они являются неопределенными формами. Вместо этого мы должны использовать Правило Лопиталя 9.0667 , взяв производную от числителя и знаменателя отдельно, найти решения равные 2 и 3 соответственно.
Вместо этого мы должны использовать Правило Лопиталя 9.0667 , взяв производную от числителя и знаменателя отдельно, найти решения равные 2 и 3 соответственно.
При работе с уравнением, которое приводит к неопределенной форме нуля в степени нуль, во время практики исчисления обязательно применяйте методы для неопределенных величин, такие как правило Лопиталя, чтобы правильно оценить предел.
❤ ОСТАВАЙТЕСЬ НА СВЯЗИ ❤
Будьте в курсе всех новостей Math Hacks!
Инстаграм | Фейсбук | Твиттер
Следующий урок: Распространенное заблуждение о вероятности
Подпишитесь прямо сейчас! Math Hacks уже на YouTube!
Присоединяйтесь ко мне, пока мы вместе решаем математические задачи. Распространение любви к математике + расширение прав и возможностей. Подпишитесь на новые…
www.youtube.com
10 главных секретов треугольника Паскаля
Биномиальная теорема, последовательность Фибоначчи, треугольник Серпинского и многое другое
medium.



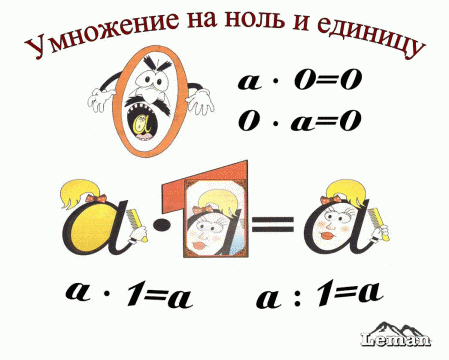
 Если происходит только умножение, а затем 0, результатом будет 0. Например, = 459 × 9 × 0 × 5 = 0.
Если происходит только умножение, а затем 0, результатом будет 0. Например, = 459 × 9 × 0 × 5 = 0. «Биография и факты Фибоначчи». По состоянию на 15 апреля 2010 г. http://www.forexrealm.com/technical-analysis/fibonacci/fibonacci-biography-history-facts.html
«Биография и факты Фибоначчи». По состоянию на 15 апреля 2010 г. http://www.forexrealm.com/technical-analysis/fibonacci/fibonacci-biography-history-facts.html pdf
pdf http://www.math.utah.edu/~pa/math/0by0.html
http://www.math.utah.edu/~pa/math/0by0.html